Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure
Abstract
1. Introduction
2. Quantum Competitive Learning
3. Qubits and Quantum Gates
3.1. Qubit
3.2. Quantum Gates
4. Methodology
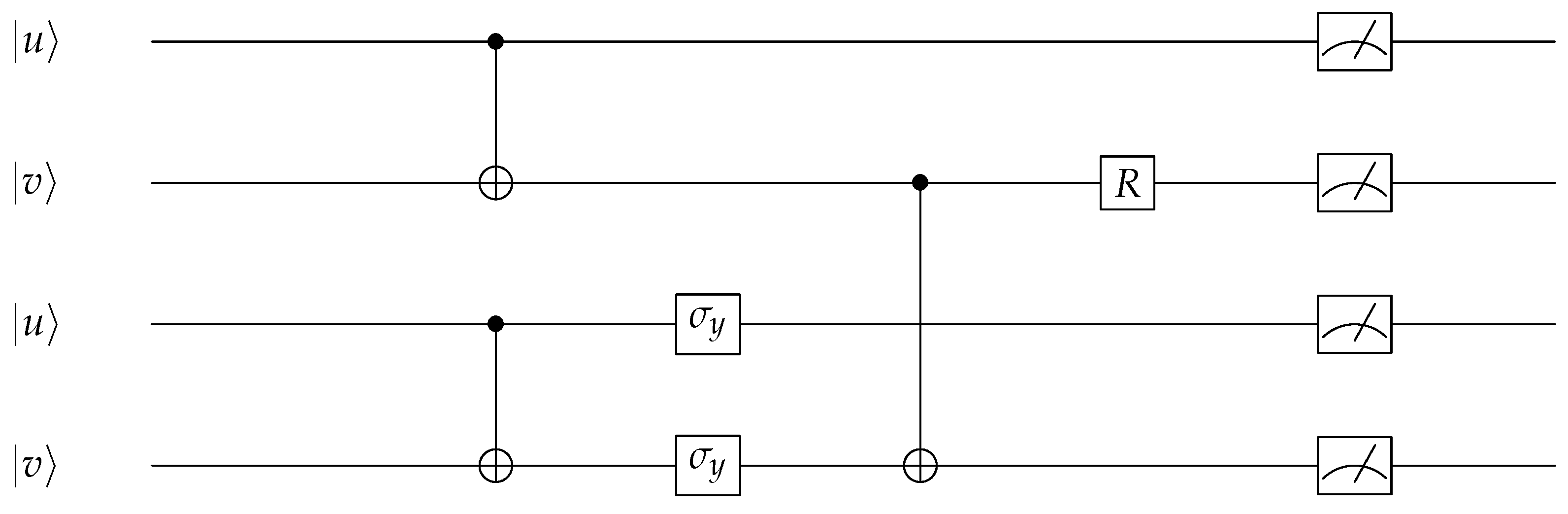
- Prepare two copies of the two-qubit state given by Equation (2) as follows:
- gate is applied between the second and the forth qubits, respectively, followed by the rotation R gate as follows:where the subscripts in the gate represent the control and the target gate, respectively. However, the unitary R gate rotate the state of the qubit as follows:Therefore, the state of the system is as follows:Comparing Equation (3) and Equation (4), we obtainwhere and are the success probability for obtaining the state and , respectively.
5. The proposed Quantum Classification Algorithm Based on Competitive Learning and Entanglement Measure: Case Study
| Algorithm 1 The proposed Quantum Classification Algorithm based on Competitive Learning and Entanglement Measure (QCPNN). |
|
5.1. Case Study
5.1.1. Quantum-Storing Layer Using Zhou’s Storage Model
- Step 1: The quantum system is initialized by the three registers , and as = . Assuming that the input state is given by , where the first pattern in Equation (9) is considered, so the initial state can be described as = .
- Step 2: = where is the toffli gate (Equation (1)).
- Step 3: =
- Step 4: =
- Step 6: =
- Step 7: =
- Step 8: =
5.1.2. Classification an Input Using the Proposed Algorithm
- Initialization Step:Here, the input register is , is the memory register that holds the prototypes patterns and its state is given by Equation (11), and is initialized by the state . Due to the input, test, pattern has two well known values in the first and third qubits, so . Therefore, the state of the system is described as follows:
- Apply the competitive detection operator between the input register and the prototype register as .
- Apply the Toffoli-gate between qubits of the register and the qubit as control qubits and target qubit, respectively.Hence, the state of the two-qubit system is
- Repeat the steps 1, 2 and 3 to get another decoupled copy of the state .
- Apply the operator on the state yields the state:Here, it is obvious that the probability of the state , , or is non-zero, so according to Equation (7) the concurrence value . Then, the test pattern belongs to the class label “1”.
6. Application
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hagan, M.; Demuth, H.; Beale, M. Neural Network Design; PWS publishing Company: Boston, MA, USA, 1996. [Google Scholar]
- Feynman, R. Simulating Physics with Computers. Int. J. Theor. Phys. 1982, 21, 467. [Google Scholar] [CrossRef]
- Jha, P.K.; Eleuch, H.; Rostovtsev, Y.V. Coherent control of Atomic Excitation using Off-resonant Strong Few-cycle Pulses. Phys. Rev. 2010, 82, 045805. [Google Scholar] [CrossRef]
- Mohamed, A.-B.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Sete, E.A.; Svidzinsky, A.A.; Rostovtsev, Y.V.; Eleuch, H.; Jha, P.K.; Suckewer, S.; Scully, M.O. Using Quantum Coherence to Generate Gain in the XUV and X-Ray: Gain-Swept Superradiance and Lasing Without Inversion. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 541–553. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Das, S. Semiconductor cavity QED with squeezed light: Nonlinear regime. Phys. Rev. 2011, 84, 053817. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Eleuch, H.; Hassouni, Y. Beam splitting and entanglement generation: Excited coherent states. Quantum Inf. Process. 2013, 12, 69–82. [Google Scholar] [CrossRef]
- Kak, S.C. Quantum Neural Computing. Adv. Imaging Electron. Phys. 1995, 94, 259–314. [Google Scholar]
- Ventura, D.; Martinez, T. Quantum Associative Memory. Inf. Sci. 2000, 124, 273–296. [Google Scholar] [CrossRef]
- Trugenberger, C.A. Probabilistic quantum memories. Phys. Rev. 2001, 87, 067901. [Google Scholar] [CrossRef]
- Guptaa, S.; Ziab, R.K.P. Quantum Neural Networks. J. Comput. Syst. Sci. 2001, 63, 355–383. [Google Scholar] [CrossRef]
- De Paula Neto, F.M.; Ludermir, T.B.; de Oliveira, W.R.; da Silva, A.J. Quantum Perceptron with Dynamic Internal Memory. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Xu, Y.; Zhang, X.; Gai, H. Quantum Neural Networks for Face Recognition Classifier. Procedia Eng. 2011, 15, 1319–1323. [Google Scholar] [CrossRef]
- Siomau, M. A quantum model for autonomous learning automata. Quantum Inf. Process. 2014, 13, 1211–1221. [Google Scholar] [CrossRef]
- Paparo, G.D.; Dunjko, V.; Makmal, A.; Martin-Delgado1, M.A.; Briegel, H.J. Quantum Speedup for Active Learning Agents. Phys. Rev. 2014, 4, 031002. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayshiy, I.; Petruccione, F. The quest for a quantum Neural Network. Quantum Inf. Process. 2014, 13, 2567–2586. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. Simulating a perceptron on a quantum computer. Phys. Lett. 2015, 379, 660–663. [Google Scholar] [CrossRef]
- Da Silva, A.J.; Ludermir, T.B.; de Oliveira, W.R. Quantum perceptron over a field and neural network architecture seclection in a quantum computer. Neural Netwo. 2016, 76, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Cao, Y.; Yang, S.; Xu, X. Quantum Storage Network. In Proceedings of the 3rd International Conference on Natural Computation (ICNC), Haikou, Hainan, China, 24–27 August 2007. [Google Scholar]
- Zhou, R. Quantum Competitive Neural Network. Int. J. Theor. Phys. 2010, 49, 110–119. [Google Scholar] [CrossRef]
- Altaisky, M.V. Quantum Neural Networks. Available online: https://arxiv.org/abs/quant-ph/0107012 (accessed on 5 July 2001).
- Ventura, D. Implementing competitive learning in a quantum system. In Proceedings of the International Joint Conference on Neural Networks (IJCNN’99), Washington, DC, USA, 10–16 July 1999; pp. 462–466. [Google Scholar]
- Fei, L.; Baoyu, Z. A study of quantum neural networks. Neural Netw. Signal Process. IEEE 2003, 1, 539–542. [Google Scholar]
- Zhou, R.; Qin, L.; Jiang, N. Quantum perceptron network. LNCS 2006, 4131, 651–657. [Google Scholar]
- Zhou, R.; Ding, Q.; Quantum, M.P. Neural network. Int. J. Theor. Phys. 2007, 46, 3209–3215. [Google Scholar] [CrossRef]
- Li, P.; Xiao, H. Model and algorithm of Quantum-inspired Neural Network with Sequence Input based on Controlled Rotation Gates. Appl. Intell. 2014, 40, 107. [Google Scholar] [CrossRef]
- Shang, F. Quantum-inspired neural network with quantum weights and real Weights. Open J. Appl. Sci. 2015, 5, 609–617. [Google Scholar] [CrossRef]
- Cao, M.; Li, P. Quantum-inspired neural networks with applications. Int. J. Comput. Inf. Technol. 2014, 3, 83–92. [Google Scholar]
- Li, Z.; Li, P. Quantum-Inspired Neural Network with Sequence Input. Open J. Appl. Sci. 2015, 5, 259–269. [Google Scholar] [CrossRef]
- Mahajan, R.P. Hybrid Quantum Inspired Neural Model for Commodity Price Prediction. In Proceedings of the ICACT, Seoul, Korea, 13–16 February 2011; pp. 1353–1357. [Google Scholar]
- Bhattacharyya, S.; Bhattacharjee, S.; Mondal, N.K. A Quantum Backpropagation Multilayer Perceptron (QBMLP) for Predicting Iron Adsorption Capacity of Calcareous Soil from Aqueous Solution. Appl. Soft Comput. 2015, 27, 299–312. [Google Scholar] [CrossRef]
- Sagheer, A.; Zidan, M. Autonomous Quantum Perceptron Neural Network. arXiv 2013, arXiv:1312.4149. Available online: https://arxiv.org/abs/1312.4149 (accessed on 15 December 2013).
- Zidan, M.; Abdel-Aty, A.; El-Sadek, A.; Zanaty, E.A.; Abdel-Aty, M. Low-Cost Autonomous Perceptron Neural Network Inspired by Quantum Computation. AIP Conf. Proc. 2017, 1905, 020005. [Google Scholar]
- Li, P.; Xiao, H.; Shang, F.; Tong, X.; Li, X.; Cao, M. A hybrid quantum-inspired neural networks with sequence inputs. Neurocomputing 2013, 117, 81–90. [Google Scholar] [CrossRef]
- Xiao, H.; Cao, M. Hybrid Quantum Neural Networks Model Algorithm and Simulation. In Proceedings of the 5th International Conference on Natural Computation, Tianjin, China, 14–16 August 2009; pp. 164–168. [Google Scholar]
- Panchi, L.; Shiyong, L. Learning Algorithm and Application of Quantum BP Neural Networks based on universal quantum gates. Syst. Eng. Electron. 2008, 19, 167–174. [Google Scholar] [CrossRef]
- Zidan, M.; Sagheer, A.; Metwally, N. An Autonomous Competitive Learning Algorithm using Quantum Hamming Neural Networks. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–7. [Google Scholar]
- Rojas, R. Unsupervised Learning and Clustering Algorithms, Neural Networks; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Zhong, Y.; Yuan, C. Quantum Competition Network Model Based On Quantum Entanglement. J. Comput. 2012, 7, 2312–2317. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys. Rev. Lett. 1997, 79, 325. [Google Scholar] [CrossRef]
- Sagheer, A.; Metwally, N. Communication via Quantum Neural Networks. In Proceedings of the 2nd World Congress on Nature and Biologically Inspired Computing, NaBIC, Fukuoka, Japan, 15–17 December 2010; pp. 418–422. [Google Scholar]
- Huang, Z.M.; Qiu, D.W. Geometric quantum discord under noisy environment. Quantum Inf. Process. 2016, 15, 1979. [Google Scholar] [CrossRef]
- Mohamed, A.B. Non-local correlation and quantum discord in two atoms in the non-degenerate model. Ann. Phys. 2012, 327, 3130–3137. [Google Scholar] [CrossRef]
- Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. 2008, 77, 022301. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of corre- lations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Luo, S.; Fu, S. Geometric measure of quantum discord. Phys. Rev. 2010, 82, 034302. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Eleuch, H. Dynamical behavior of entanglement in semiconductor microcavities. Phys. E 2010, 42, 2091–2096. [Google Scholar] [CrossRef]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Zhou, L.; Sheng, Y.B. Concurrence Measurement for the Two-Qubit Optical and Atomic States. Entropy 2015, 17, 4293. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. 2002, 65, 032314. [Google Scholar] [CrossRef]
- Islam, R.; Ma, R.; Preiss, P.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Greine, M. Measuring entanglement entropy in a quantum many-body system. Nature 2015, 528, 48. [Google Scholar] [CrossRef]
- Romero, G.; López, C.E.; Lastra, F.; Solano, E.; Retamal, J.C. Direct measurement of concurrence for atomic two-qubit pure states. Phys. Rev. 2007, 75, 032303. [Google Scholar] [CrossRef]
- Walborn, S.P.; Ribeior, P.H.S.; Davidovich, L.; Mintert, F.; Buchleitner, A. Experimental determination of entanglement with a single measurement. Nature 2006, 440, 1022. [Google Scholar] [CrossRef] [PubMed]
- Zidan, M.; Abdel-Aty, A.; Younes, A.; Zanaty, E.A.; El-khayat, I.; Abdel-Aty, M. A Novel Algorithm based on Entanglement Measurement for Improving Speed of Quantum Algorithms. Appl. Math. Inf. Sci. 2018, 12, 265–269. [Google Scholar] [CrossRef]
- El-Wazan, K.; Younes, A.; Doma, S.B. A Quantum Algorithm for Testing Junta Variables and Learning Boolean Functions via Entanglement Measure. arXiv, 2017; arXiv:1710.10495. [Google Scholar]
- El-Wazan, K. A Measuring Hamming Distance between Boolean Functions via Entanglement Measure. arXiv, 2019; arXiv:1903.04762. [Google Scholar]
- Hong-Fu, W.; Shou, Z. Application of quantum algorithms to direct measurement of concurrence of a two-qubit pure state. Chin. Phys. B 2009, 18, 2642. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A Single Quantum Cannot be Cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Cheon, S.W.; Chang, S.H.; Chung, H.Y.; Bien, Z.N. Application of neural networks to multiple alarm processing and diagnosis in nuclear power plants. IEEE Trans. Nucl. Sci. 1993, 40, 11–20. [Google Scholar] [CrossRef]
- Maa, J.; Jiang, J. Applications of fault detection and diagnosis methods in nuclear power plants: A review. Prog. Nucl. Energy 2011, 53, 255–266. [Google Scholar] [CrossRef]


| Alarm Signal | Description |
|---|---|
| Bearing flow low | |
| Thermal barrier flow low | |
| No.1 seal differential pressure low | |
| Standpipe level low | |
| Charging pump flow low | |
| No.1 seal leak off flow low | |
| Bearing temperature high | |
| Seal injection flow low | |
| No.1 Seal leak off flow high | |
| Seal injection filter differential pressure high | |
| Standpipe level high | |
| Thermal barrier temperature high |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zidan, M.; Abdel-Aty, A.-H.; El-shafei, M.; Feraig, M.; Al-Sbou, Y.; Eleuch, H.; Abdel-Aty, M. Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure. Appl. Sci. 2019, 9, 1277. https://doi.org/10.3390/app9071277
Zidan M, Abdel-Aty A-H, El-shafei M, Feraig M, Al-Sbou Y, Eleuch H, Abdel-Aty M. Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure. Applied Sciences. 2019; 9(7):1277. https://doi.org/10.3390/app9071277
Chicago/Turabian StyleZidan, Mohammed, Abdel-Haleem Abdel-Aty, Mahmoud El-shafei, Marwa Feraig, Yazeed Al-Sbou, Hichem Eleuch, and Mahmoud Abdel-Aty. 2019. "Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure" Applied Sciences 9, no. 7: 1277. https://doi.org/10.3390/app9071277
APA StyleZidan, M., Abdel-Aty, A.-H., El-shafei, M., Feraig, M., Al-Sbou, Y., Eleuch, H., & Abdel-Aty, M. (2019). Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure. Applied Sciences, 9(7), 1277. https://doi.org/10.3390/app9071277








