Electronic, Optical, Mechanical and Lattice Dynamical Properties of MgBi₂O₆: A First-Principles Study

Abstract

Electronic structure, optical, mechanical, and lattice dynamical properties of the tetragonal MgBi₂O₆ are studied using a first-principles method. The band gap of MgBi₂O₆ calculated from the PBE0 hybrid functional method is about 1.62 eV and agrees well with the experimental value. The calculations on elastic constants show that MgBi₂O₆ exhibits mechanical stability and strong elastic anisotropy. The detailed analysis of calculated optical parameters and effective masses clearly indicate that MgBi₂O₆ has strong optical response in the visible light region and high separation efficiency of photoinduced electrons and holes.

1. Introduction

Currently, Bi-based oxides have received considerable attention due to their particular physical properties and wide applications in different fields like multiferroics [1,2], superconductivity [3,4], and photocatalysis [5,6]. Generally, Bi exists as the trivalent state (Bi³⁺) in most of the Bi-based oxides like Bi₂O₃ [7], BiVO₄ [8], Bi₂WO₆ [9], Bi₂Sn₂O₇ [10], BiFeO₃ [11], and BiMnO₃ [12]. However, some Bi-containing oxides with the unusual pentavalent state (Bi⁵⁺) have also attracted research interest. For example, NaBiO₃ has been found to show the absorption of visible light and can be used as a prominent material for photooxidation of organics [13]. A recent work by Gong et al. [14] shows that AgBiO₃ can self-produce significant amounts of reactive oxygen species without light illumination or any other additional oxidant and has an excellent oxidizing reactivity. BaBiO₃, as one kind of Bi-based oxides containing Bi³⁺ and Bi⁵⁺ mixed valent states, has been found to show the potential use for the absorber of all-oxide photovoltaics [15] and can be an active photocatalyst under visible-light irradiation [16].

MgBi₂O₆ adopting the trirutile-type structure is also a Bi⁵⁺-containing compound. Kumada et al. [17] first successfully prepared MgBi₂O₆ by the low-temperature hydrothermal method and characterized its crystal structure in detail. In 2003, Mizoguchi et al. [18] investigated the optical and electrical properties of MgBi₂O₆ and found that MgBi₂O₆ is a degenerate n-type semiconductor with the band gap of about 1.8 eV, and it is possible to produce an optical band gap that extends into the visible region of the spectrum by tuning the Bi⁵⁺ 6s–O 2p interaction in order to produce a disperse conduction band. The band structure makes MgBi₂O₆ a good candidate of visible light-sensitive photocatalysts for decomposition of organic species. Comparing with other pentavalent bismuthates such as LiBiO₃, NaBiO₃, KBiO₃, ZnBi₂O₆, SrBi₂O6, AgBiO₃, BaBi₂O₆, and PbBi₂O₆, MgBi₂O₆ does not possess the highest photocatalytic activity, but there is no adsorption observed in the decomposition of methylene blue [19]. It may be a good idea to adjust the wide band gap of some traditional photocatalysts such TiO₂ by building complex compounds with MgBi2O₆. In our recent work, the photocatalytic activity of MgBi₂O₆ has been found to be significantly enhanced via constructing AgBr/MgBi₂O₆ heterostructured composites [20]. Theoretically, the band gap of MgBi₂O₆ was calculated to be about 1.10 eV using the Heyd-Scuseria-Ernzerhof (HSE) functional method within the framework of the density functional theory (DFT), and was found to be widely tuned by applying external strain [21]. On the basis of theoretical calculations, however, the deeper understanding of the physical properties of MgBi₂O₆ is still in lacking. In this work, we investigated the electronic structure, optical, mechanical, and lattice dynamical properties MgBi₂O₆ using first-principles calculations.

2. Computational Details

All calculations were carried out using the Vienna ab-initio simulation package (VASP) [22,23], which is an implement of DFT. The projector augmented wave (PAW) method [24,25] was used to describe the ion-electron interactions. The generalized gradient approximation (GGA) parameterized by Perdew, Burke and Ernzerhof (PBE) [26] was applied for the exchange-correlation function. The cutoff energy for the plane wave basis set was fixed at 500 eV. The Brillouin zone is sampled by a Monkhorst-Pack type k-point mesh with density of 2π × 0.03 Å⁻¹. Full relaxation of MgBi₂O₆ unit cell was performed until the changes in total energy and force on each atom are less than 10⁻⁵ eV and 10⁻³ eV/Å, respectively. In this work, Mg-3s, Mg-2p, Bi-6s, Bi-6p, O-2s, and O-2p states are taken as valence electrons. Based on the DFT calculation, a more accurate screened coulomb hybrid functional (HF) developed by Heyd, Scuseria, and Ernzerhof (PBE0) [27,28] (containing 30% of the exact exchange, and 70% of the PBE exchange, and 100% of the PBE correlation energy in this work) was used to calculate the electronic structure. In the calculations of optical properties, a dense k-point density of 2π × 0.015 Å⁻¹ including the Γ point was used to ensure the accurate precision. Moreover, 88 extra empty bands are included in the calculations to hold the excited electronic states. Phonon calculations were performed within the framework of density functional perturbation theory to investigate the lattice dynamical properties of MgBi₂O₆. The phonon dispersion curve and phonon density of states (PDOS) were calculated by the PHONOPY code [29] on the basis of force constants obtained from VASP code. In the phonon calculations, a 2 × 2 × 1 supercell was used.

3. Results and Discussion

3.1. Optimized Crystal Structure of MgBi₂O₆

At ground state, MgBi₂O₆ crystallizes in a tetragonal trirutile-type structure with P4₂/mnm space group. It can be seen from the crystal structure depicted in Figure 1 that BiO₆ and MgO₆ octahedrons connect with the sharing edges and stack along the $\left[001\right]$ direction by 2:1 ratio. In the $\left[110\right]$ and $\left[\overline{1}10\right]$ directions, BiO₆ and MgO₆ octahedrons are connected with each other by sharing O vertices. The optimized lattice constants listed in Table 1 are in good agreement with the experimental values [17]. The BiO₆ octahedrons are slightly distorted and the bond lengths of Bi-O(8j) are not completely identical.

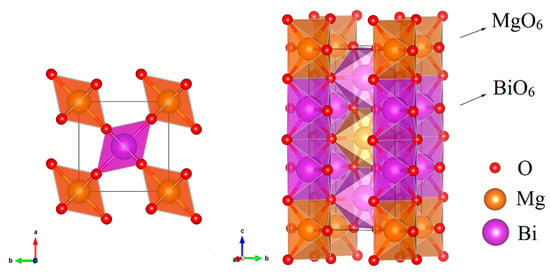
Figure 1. Crystal structure of the trirutile-type MgBi₂O₆ represented as two different views.

Table 1. Optimized structural parameters of MgBi₂O₆, Bi-O and Mg-O interatomic distances. The experimental values [17] are listed in brackets for comparison.

Lattice Constants (Å)	Atomic Coordinates (Fractional)
	Atom	Site	x	y	z
a = 4.920 (4.826)	Bi	4e	0	0	0.333 (0.332)
c = 9.924 (9.719)	Mg	2a	0	0	0
	O1	4f	0.302 (0.305)	0.302 (0.305)	0
	O2	8j	0.309 (0.307)	0.309 (0.307)	0.336 (0.335)
BiO6 octahedron			MgO6 octahedron
Bi-O(1)	2.156 (2.114) × 2		Mg-O(1)	2.107 (2.084) × 2
Bi-O(2)	2.153 (2.102) × 2		Mg-O(2)	2.103 (2.073) × 4
Bi-O(3)	2.141 (2.084) × 2

3.2. Electronic Properties of MgBi₂O₆

To study the electronic property of tetragonal MgBi₂O₆, the electronic band structure along high symmetry directions in the Brillouin zone (BZ) and density of states are calculated. The band structure calculated by conventional DFT (dotted line in Figure 2) shows that there is a bit of overlap between the conduction band and valence band, indicating the metallic feature of MgBi₂O₆. This contradicts the experimental findings. It is well known that DFT calculations do not take into account the effects of electron excitation and thus tend to underestimate the electronic band gap. To acquire the more accurate results, the calculations based on the HF PBE0 method are further performed. The HF corrected band structure (solid line in Figure 2) shows that MgBi₂O₆ is a direct semiconductor with a band gap of about 1.62 eV, which is well consistent with the experimental measured data (1.6~1.8 eV) [18,19,20] and larger than the previously calculated value (1.10 eV) based on the HF method [21]. The valence band near the Fermi level (E_F) is flat, while the dispersion of the conduction band close to the E_F is relative strong.

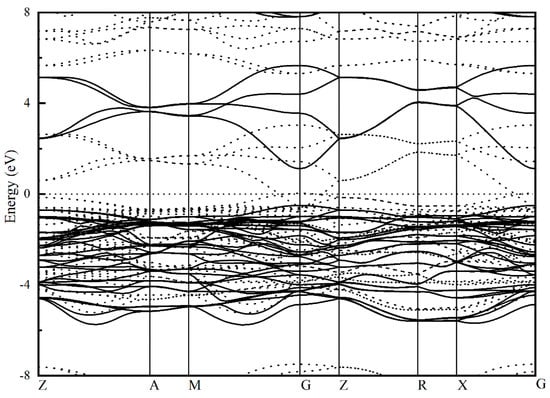
Figure 2. Calculated electronic band structure of MgBi₂O₆ using hybrid functional PBE0 method. Band structure from conventional DFT calculation (dotted line) is also presented for comparison.

The effective mass (m^*) of carriers is an important parameter, because it determines the transfer and separation efficiency of electrons and holes, and directly influences the photophysical properties of semiconductors. m^* can be calculated as follows:

$${\left(\frac{1}{m^{*}}\right)}_{ij}=\frac{1}{{\hslash }^2}\frac{{\partial }^{2}E\left(k\right)}{\partial k_i{k}_j},i,j=x,y,z,$$

(1)

where E_n(k) represents the band energy, k is the wave vector, and $\hslash$ is the reduced Planck constant. For MgBi₂O₆, the effective electron mass (m_e^*) at the conduction band and hole mass (m_h^*) at the valence band at the Γ point are calculated and listed in Table 2. The calculated tensors of m^* clearly show that m_e^* is fairly isotropic and m_h^* shows a relatively strong anisotropy. m_h^* along the [001] direction is larger than those along the [100] and [010] directions. The values of m_e^* in Table 2 are also comparable to the previously calculated value (0.277) for MgBi₂O₆ [21]. Moreover, the values of m_h^* are distinctly larger than those of m_e^*, which indicates that the mobility of holes at the valence band is obviously slower than that of electrons at the conduction band. The big difference in mobility between electrons and holes is undoubtedly beneficial to the separation of charge carriers and the reduction of the recombination rate of electron-hole pairs. In addition, the values of m_h^*/m_e^* of MgBi₂O₆ are in the range of 6.2~10.9, being larger than the corresponding value (2.1) of anatase TiO₂ [30] widely investigated as an important photocatalytic material. Thus, semiconducting MgBi₂O₆ can be considered as a photocatalyst with highly efficient separation of photoinduced electrons and holes.

Table 2. Calculated effective electron mass (m_e^*) and hole mass (m_h^*) along the three principal directions at the Γ point. All values are in units of free electron mass (m₀).

	Conduction Band	Valence Band
Γ	$\left(\begin{array}{ccc}0.221& 0& 0\\ 0& 0.206& 0\\ 0& 0& 0.171\end{array}\right)$	$\left(\begin{array}{ccc}-1.572& 0& 0\\ 0& -1.370& 0\\ 0& 0& -1.871\end{array}\right)$

The calculated electronic total and partial density of states (DOS) of MgBi₂O₆ is shown in Figure 3. It can be clearly seen that the DOS near the top of the valence band is derived from the Bi-5d, Mg-2p and O-2p states. The bottom of the conduction band is mainly composed of O-2p, Bi-6s, and Mg-3s states. The strong hybridizations between Bi-5d and O-2p states in BiO₆ octahedrons and bonding interactions between Mg-2p or Mg-3s and O-2p states in MgO₆ octahedrons should be directly responsible for the structural stability of MgBi₂O₆.

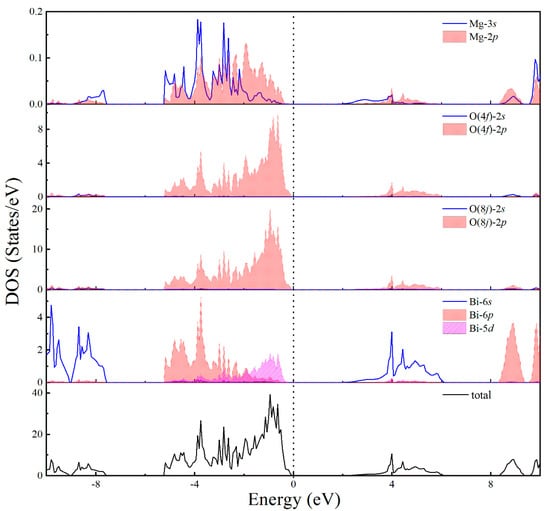
Figure 3. Calculated electronic density of states of MgBi₂O₆ using PBE0 method.

To get a deeper understanding of the bonding nature of Bi, Mg, and O atoms, the electron localization function (ELF) was further calculated. According to the original definition, the ELF values are scaled in the range from 0 to 1. The high ELF means strong covalent bonding interaction between atoms and the very low ELF close to 0 corresponds to the ionic bonding. Figure 4 shows the calculated ELF for (110) plane of MgBi₂O₆ passing through Bi, Mg, and O atoms. The ELF values between Mg and O atoms are extremely low, indicating the ionic bonding in MgO₆ octahedrons. This can be well understood on the basis of the previously obtained recognition on MgO, which is usually considered as one kind of classical ionically bonded compounds. The maximal value of ELF between Bi and O atoms reaches about 0.61, which clearly identifies the partially Bi-O covalent bonding interaction in BiO₆ octahedrons.

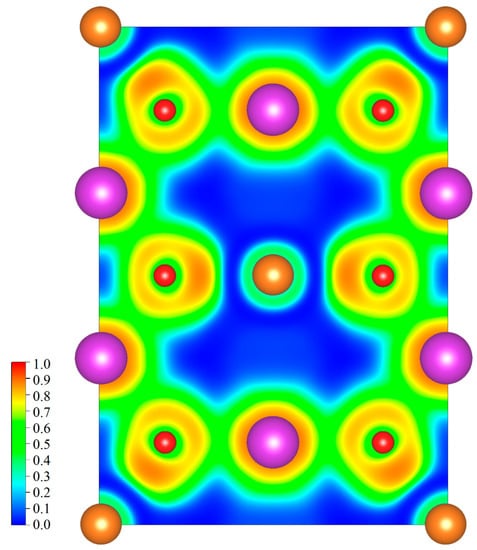
Figure 4. Calculated electron localization function for (110) plane across Bi, Mg, and O atoms.

3.3. Optical Properties of MgBi₂O₆

In order to understand the optical performance of semiconducting MgBi₂O₆, we calculated its dielectric functions using the hybrid functional PBE0 method, and further computed its optical properties such as complex refractive index n, extinction coefficient k, reflectivity R, absorption coefficients α, and electron energy-loss function L. The calculated dielectric functions are depicted in Figure 5. It can be clearly seen that the static dielectric function is found to be 4.1 at 0 eV. With the increase of the polarization intensity and energy, the dielectric function, the real part ε₁ is also gradually increased and reaches a maximum value of 5.4 when the energy value is about 2.8 eV. When the photon energy reaches 1.6 eV, which is the width of electronic band gap, the electrons in the valence bands begin to excite and transit to conduction bands. As the carrier concentration increases, the degree of polarization decreases and the dielectric function decreases slightly. With the further increment of photon energy, the dielectric function values begins to fluctuate, which corresponds to the change of carrier concentration in the crystal. The imaginary part ε₂ reflects the transition between occupied and non-occupied electrons and can be used to characterize the light absorption behavior of the crystal. The first two peaks of the imaginary part of the dielectric function ε₂ are, respectively, at about 2.0 and 3.0 eV, which probably results from the electron transition from the top of the valence bands to the bottom of the conduction bands.

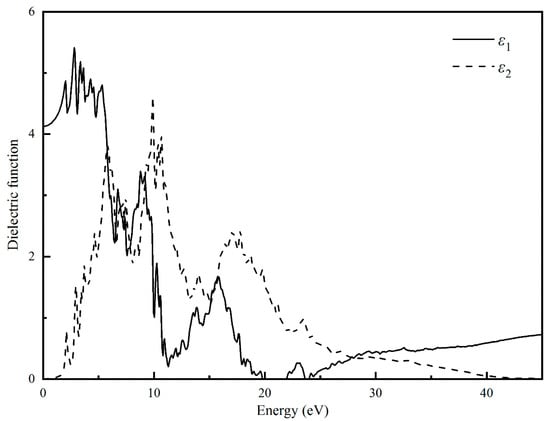
Figure 5. Calculated complex dielectric function of MgBi₂O₆.

The calculated refractive index n, extinction coefficient k, absorption coefficient α, reflectivity R, and electron energy loss function L of MgBi₂O₆ are shown in Figure 6. As presented in Figure 6a, the higher value of n is in the energy range of 1.5–5.8 eV and the corresponding wavelength range is from 214 to 826 nm, indicating that MgBi₂O₆ has a strong refractive effect in both ultraviolet (UV) and visible light region. The value of k rapidly starts to increase from 2.0 eV, also showing a response in the visible and UV light region. The calculated α in Figure 6c shows that the light absorption edge is about 1.6 eV and is comparable with the band gap calculated by the PBE0 method. The value of optical absorption edge also agrees with literatural values [18,20]. With the increase of energy, α also gradually increases and a series of absorption peaks appear in the energy range from 1.6 to 27 eV. Combining with the calculated dielectric function and density of states, we can find that the first two absorption peaks at 4.5 and 6.0 eV are probably related to the electron migration of the O-2p, Bi-6s, Bi-5d, and Mg-2p states. The reflectivity R and the electron energy loss function L can be used to represent the resonant frequency of the incident light and the resonant frequency of the plasma. As shown in Figure 6d, the average value of R is about 13.8%, indicating that MgBi₂O₆ can be used as a light absorbing material. The calculated L presented in Figure 6e completely locates in the continuous energy range of 0–45 eV, indicating that the characteristics of plasma oscillation in MgBi₂O₆ are not obvious. This is strongly different from the behavior appearing in Bi₂Sn₂O₇ [31].

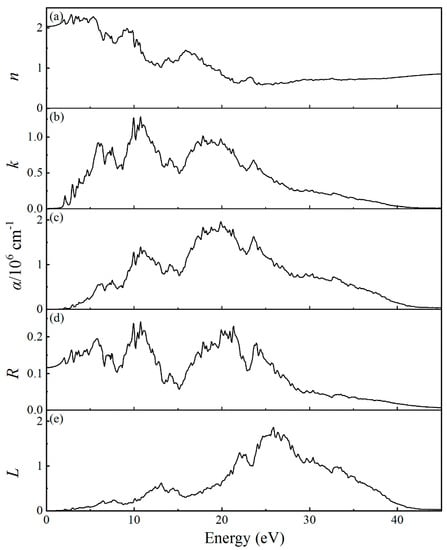
Figure 6. Calculated optical properties of MgBi₂O₆: (a) complex refractive index n, (b) extinction coefficient k, (c) absorption coefficient α, (d) reflectivity R, and (e) electron energy loss function L.

3.4. Mechanical Properties of MgBi₂O₆

To investigate the mechanical properties of tetragonal MgBi₂O₆, the six independent elastic constants C_ij are calculated by applying finite distortions of the lattice. The results are listed in Table 3. For the tetragonal system, the mechanical stability criterion [32] is given by the following relationships:

(C₁₁ − C₁₂) > 0, (C₁₁ + C₃₃ − 2C₁₃) > 0,

C₁₁ > 0, C₃₃ > 0, C₄₄ > 0, C₆₆ > 0,

(2C₁₁ + C₃₃ + 2C₁₂ + 4C₁₃) > 0,

(2)

Table 3. Calculated elastic constants C_ij, bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio υ of MgBi₂O₆.

Elastic Constants (GPa)						Mechanical Moduli (GPa)			υ
C11	C12	C13	C33	C44	C66	B	G	E
171.8	110.4	98.1	280.3	66.2	141.9	137.7	76.2	193.0	0.27

The calculated values of C_ij in Table 3 satisfy the stability criterion mentioned above, indicating that the tetragonal MgBi₂O₆ has mechanical stability. As listed in Table 3, C₁₁ is significantly smaller than C₃₃, indicating that the chemical bonding strength in the (100) and (010) directions is significantly weaker than the bonding strength in the (001) direction. In addition, C₄₄ is obviously smaller than C₆₆, which demonstrates that it is easier for shear deformation to occur along the (001) direction in comparison with the (010) direction. The shear elastic anisotropy of the material can be estimated by the relation A = 2C₆₆/(C₁₁ − C₁₂). Typically, if A has a value of 1, meaning that the material is isotropic. The more the value of A deviates from 1, the elastic anisotropy would be more prominent. For MgBi₂O₆, the calculated A value is 4.6, indicating that MgBi₂O₆ is highly anisotropic.

For the tetragonal system, the bulk modulus B and the shear modulus G are calculated as follows:

B = (2C₁₁ + C₃₃ + 2C₁₂ + 4C₁₃)/9,

(3)

G = (2C₁₁ + C₃₃ − C₁₂ − 2C₁₃ + 6C₄₄ + 3C₆₆)/15,

(4)

Young’s modulus E and Poisson’s ratio υ can be estimated from the bulk and shear moduli

E = 9BG/(G + 3B),

(5)

υ = (3B − 2G)/[2(3B + G)],

(6)

The calculated B, G, E, and υ are listed in Table 3. The B/G value is about 1.81. According to Pugh’s criteria of brittleness and ductility [33], MgBi₂O₆ exhibits some toughness, but it is not obvious, which is consistent with the Poisson’s ratio υ = 0.27. In addition, the elastic anisotropy of MgBi₂O₆ can be directly determined by the direction-dependent Young’s modulus. The Young’s modulus in a specific direction can be expressed by the elastic compliances ($s^{\prime }$):

$$E^{\prime }=\frac{1}{s^{\prime }},$$

(7)

with

$$s^{\prime }=A_{1i}{A}_{1j}{A}_{1k}{A}_{1l}{s}_{ijkl},$$

(8)

where A is the matrix associated with the change of axes:

$$A_{11}=\cos \theta \sin \phi ,A_{12}=\sin \theta \sin \phi ,A_{13}=\cos \phi ,$$

(9)

Using the reduction of s_ijkl for the tetragonal crystal class [34], the reduced Young’s modulus with orientation can be expressed as follows:

$$E^{\prime }=\frac{1}{\left\{s_{11}+\left[s_{66}-2\left(s_{11}-s_{12}\right)\right]\frac{{\sin }^2\theta }{4}\right\}{\sin }^4\theta +s_{33}{\cos }^4\theta +\left(2s_{13}+s_{44}\right)\frac{{\sin }^{2}2\phi }{4}},$$

(10)

The calculated directional dependence of Young’s modulus depicted in Figure 7 is a significantly distorted spherical shape. The calculated values along the [001], [110], and [-110] directions are obviously larger than those along the [100] and [010] directions. Tetragonal MgBi₂O₆ exhibits the highly elastic anisotropy.

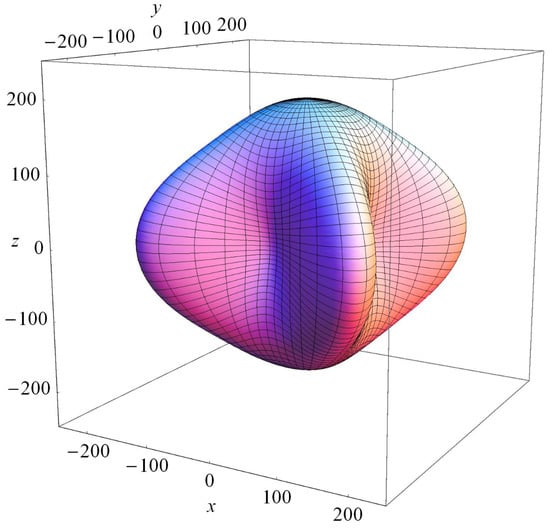
Figure 7. Directional dependence of Young’s modulus (in GPa) of MgBi₂O₆.

3.5. Lattice Dynamical Properties of MgBi₂O₆

The phonon dispersion curves along high symmetry directions and the phonon density of states are shown in Figure 8. There are 18 atoms in MgBi₂O₆ cells, so there is a total of 54 vibration modes in the phonon spectrum, including three acoustic modes and 51 optical modes. The calculated phonon spectrum shows no imaginary frequency, indicating the dynamical stability of MgBi₂O₆. Along F-Q and Q-Z paths in the Brillouin zone, the vibration modes are double degenerate. The acoustic modes phonons reflect the vibration of the centroid of the original cell and occupy the 0–3 THz frequency region. Among the three acoustic modes passing through the Γ point, the longitudinal mode has higher frequency in comparison with the other two transverse acoustic modes. There is no gap at the frequency range of about 3 THz between the longitudinal acoustic and transverse optical modes. Thus, phonons can transition from the acoustic mode to the optical mode without any momentum transfer [35]. Further combining with the calculated PDOS shown in Figure 8, we can find that the coupled vibrations of Bi, Mg, and O atoms including the O-Bi-O and O-Mg-O bending vibrations in BiO₆ and MgO₆ octahedrons within the frequency range from 3 to 9.8 THz and the Bi-O and Mg-O stretching vibrations in the frequency range from 12 to 16.4 THz are obvious. The phonon branches above 16.4 THz are completely ascribed to the vibrations of O atoms.

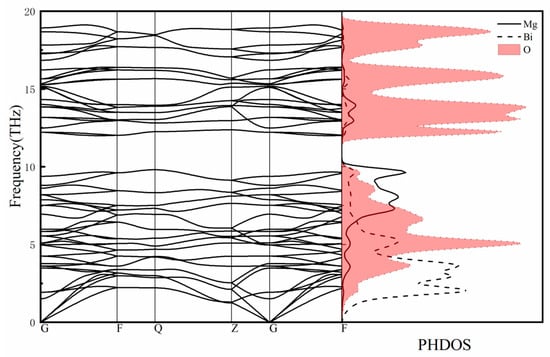
Figure 8. Calculated phonon dispersion curves and phonon density of states of MgBi₂O₆.

4. Conclusions

In this work, we have investigated the structural, electronic, optical, mechanical, and lattice dynamical properties of the trirutile-type MgBi₂O₆ in detail using the first-principles calculations. The calculated band gap of MgBi₂O₆ from the Heyd-Scuseria-Ernzerhof hybrid functional PBE0 electrical is about 1.62 eV and consistent with the experimental data (1.6~1.8 eV). The calculated effective masses show that the mobility of holes at conduction band is obviously slower than that of electrons at valence band, indicating high separation efficiency of electrons and holes in MgBi₂O₆. The calculated results of optical parameters clearly show that MgBi₂O₆ has strong light response in the visible light region and can be used as a light absorbing material. The calculated elastic constants and phonon dispersion clearly show that MgBi₂O₆ is mechanically and dynamically stable. Moreover, MgBi₂O₆ exhibits significantly elastic anisotropy.