Abstract
The dynamics of the photoelectric effect in solid-state systems can be investigated via attosecond-time-resolved photoelectron spectroscopy. This article provides a comparison of delay information accessible by the two most important techniques, attosecond streaking spectroscopy and reconstruction of attosecond beating by interference of two-photon transitions (RABBITT) at solid surfaces, respectively. The analysis is based on simulated time-resolved photoemission spectra obtained by solving the time-dependent Schrödinger equation in a single-active-electron approximation. We show a continuous transition from the few-cycle RABBITT regime to the streaking regime as two special cases of laser-assisted photoemission. The absolute delay times obtained by both methods agree with each other, within the uncertainty limits for kinetic energies >10 eV. Moreover, for kinetic energies >10 eV, both streaking delay time and RABBITT delay time coincide with the classical time of flight for an electron propagating from the emitter atom to the bulk-vacuum interface, with only small deviations of less than 4 as due to quantum mechanical interference effects.
1. Introduction
The availability of attosecond extreme-ultraviolet (EUV) pulses enabled access to electron dynamics on their natural time scales [1,2,3]. This progress in laser technology opened up the new research field of attosecond science [4]. Photoionization and photoemission dynamics are studied in various systems, ranging from atoms [5,6,7] and molecules (for a review, see Reference [8]) to condensed matter systems like solid surfaces [9,10,11,12] and nanoparticles [13]. Moreover, in this context, fundamental questions arise regarding the role and concept of time in quantum mechanics [14,15]. Experimental access to relative delay in solid-state photoemission between different initial states triggered various theoretical approaches to understand these phenomena. Since a comprehensive ab initio many-body theory of this process is still missing, various approaches were taken to tackle different aspects of these phenomena. Among others, there are ballistic approaches [16,17,18] as well as approaches including influences of the crystal lattice [19,20]. Aspects like inelastic mean free path, or excited state lifetime, respectively [18], electron-hole interaction [16], infrared (IR) field screening [21,22], final-state effects [20,23], coupling between Coulomb potential and light field [6,24,25], and intra-atomic Eisenbud–Wigner–Smith (EWS) delays [10] have also been recently investigated.
The key to attosecond laser pulses is the energy upconversion of an ultrashort few-cycle near-infrared laser pulse (IR) to shorter wavelengths in the EUV regime via the high harmonic generation (HHG) process [26,27]. Typically, an attosecond EUV burst is used to excite electrons from a bound core level or valence state into the continuum. To obtain temporal resolution, photoelectrons are probed by the fundamental IR pulse. Here, the most important techniques are the reconstruction of attosecond beating by interference of two-photon transitions (RABBITT) [2,28], and attosecond streaking spectroscopy [29].
The main difference between these techniques is that RABBITT uses an attosecond pulse train (APT) to excite photoelectrons, while streaking spectroscopy is based on excitation with a single-attosecond pulse (SAP). In both cases, the time delay between the EUV and IR pulse is varied to obtain an energy- and time-resolved spectrogram.
The photoemission process can be envisioned as follows: The EUV pulse (train) excites a wave packet from an initial state into a final state inside the material (Figure 1). However, because of the different time structure and corresponding EUV energy spectrum, the generated electron-wave packets exhibit different momentum or kinetic-energy distributions. In a streaking experiment, excitation with a single-attosecond pulse led to broad excitation-energy distribution in the order of several eV (Figure 1a), whereas in RABBITT the femtosecond envelope of the APT resulted in a highly modulated distribution that exhibited rather narrow spectral features (Figure 1b). Because of the HHG process, these spectral features are separated by twice the fundamental photon energy. In both cases, the so-generated continuum electron wave packet propagates towards the surface. Note that the part of the wave packet that propagates into the bulk is irrelevant for the simulations considered here and is therefore not shown in Figure 1. If the wave packet was excited by a single-attosecond pulse, a single electron wave packet travels to the surface. In case of excitation by an APT, a train of electron pulses moves toward the surface, where they are emitted into the vacuum.
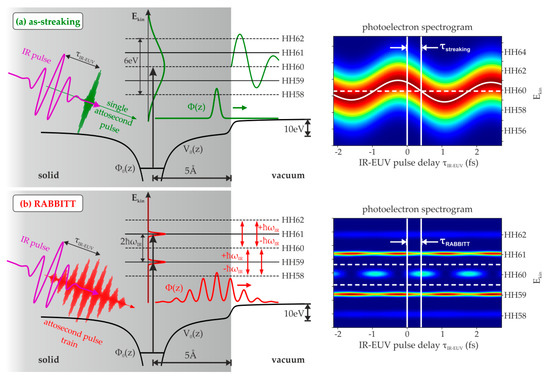
Figure 1.
Principle of (a) as-streaking and (b) reconstruction of attosecond beating by interference of two-photon transitions (RABBITT) at solid surfaces: Initial state is excited into the continuum by a single-attosecond extreme-ultraviolet (EUV) pulse (green) or by an attosecond pulse train (red), respectively. The time–energy bandwidth product results in broad energy distribution in the continuum in the case of a single-attosecond pulse (SAP, green) and two narrow lines in the case of an attosecond pulse train (APT, red). The continuum wave packet , i.e., a single electron wave packet (streaking) or an electron pulse train (RABBITT), travels toward the surface and is emitted into the vacuum (schematic wave packet and laser-pulse plots are not true to scale). As soon as the photoelectron leaves the surface, it starts interacting with the infrared (IR) pulse (violet). In the case of a single electron wave packet, the energy distribution accumulates a shift determined by IR vector potential. This results in a streaking spectrogram (upper-right panel). Here, the white solid line corresponds to the streaked momentum expectation value, while the white dashed line corresponds to the momentum expectation value without IR interaction. White vertical lines indicate the delay between streaking trace and zero IR–EUV pulse delay. If it is excited by an APT (RABBITT), at each half-cycle of the IR field, a photoelectron wave packet is emitted. Absorption and emission of IR photons leads to the formation of side bands in the RABBITT spectrum (lower-right panel). Intensity oscillation in the central side band (between white dashed lines) is shifted with respect to zero IR–EUV pulse delay (white vertical lines).
In a streaking experiment, the photoelectron is excited at inside the solid. At a certain point in time , when the electron passes the surface, the electron starts interacting with the IR field in the vacuum that, in our model, is completely screened inside the material. This photoemission time corresponds to the time that the whole photoemission process takes from excitation until emission into the vacuum. In a classical picture, photoemission time is the transport time from the emitter atom to the surface.
In vacuum, the electron is accelerated by the IR field in its polarization direction (Figure 1a):
After the IR pulse has interacted with the photoelectron (, the photoelectron has acquired the momentum
Hence, variation of IR–EUV time delay results in a replica of the vector potential of IR pulse shifted by a delay with respect to zero delay between EUV and IR pulse (upper-right panel of Figure 1).
Equation (2) is valid for vanishing IR fields inside the solid, and instantaneous EUV excitation [29]. Under these conditions, streaking delay is equal to absolute photoemission time [22]. Note that this is a rather classical view on the streaking process, motivated here by the fact that the correspondence principle is applicable. The quantum wave packet for the streaking process converges toward classical behavior for large quantum numbers.
In a RABBITT experiment, an attosecond pulse train is used to photoexcite the system. The excitation spectrum consists of a series of rather narrow lines located at the odd multiples of fundamental energy , where is the initial state energy of the core level under investigation (Figure 1b) [2]. The photoelectron wave packet is then composed of several subpulses. Interaction with the IR field leads to side bands in photoemission spectra located at the even multiples of fundamental IR energy by absorbing or emitting an additional IR photon. This is the well-known laser-assisted photoemission process at solid surfaces (LAPE) [30]. At moderate IR intensities, there are two interfering pathways for photoelectrons to contribute to the central side band at : photoelectrons excited by the -th harmonic via emission of one IR photon, and those excited by the -th harmonic via the absorption of one IR photon. Hence, the intensity of the side band depends on the relative phase between both quantum paths. Variation of the IR–EUV delay results in intensity oscillation of the central side band, with an oscillation frequency that is twice as large as that of the fundamental IR radiation (lower-right panel of Figure 1). Moreover, side-band oscillations are shifted with respect to the maximum of the EUV pulse by a RABBITT delay . Note that, since side-band oscillation in a RABBITT experiment is determined by phase differences between two quantum pathways, which is a genuine quantum property, in contrast to streaking spectrograms, RABBITT spectrograms cannot be interpreted within a classical picture. Hence, for the RABBITT process, the correspondence principle is not directly applicable, and it is not a priori obvious that RABBITT delay directly reveals photoemission time .
Therefore, an important question that arises is whether delays determined by RABBITT () and streaking () for solid-state photoemission agree with each other. Different quantum-interference pathways compared to the streaking case might influence the shift of the RABBITT side-band oscillations on the delay axis. For illustration, photoelectrons in a RABBITT experiment only move inside the material with kinetic energies corresponding to (N−1)-th or (N+1)-th harmonics, while oscillations at the N-th harmonic are evaluated. However, the kinetic energy distribution inside the material is zero around the N-th harmonic. In contrast, in the streaking case, electrons move inside the material with kinetic energy centered on the N-th harmonic. This consideration also raises the question of how delays determined by both techniques are related to each other.
In the gas phase, Cattaneo et al. experimentally demonstrated delay agreement within an accuracy of tens of attoseconds, determined from streaking and RABBITT spectra for the photoionization of Ne and Ar atoms [31]. For more complex many-body systems like solids, experimental proof for the equivalence of both methods is still missing. For instance, transport of the electron from inside the solid to the surface substantially contributes to photoemission delay. Moreover, in a solid-surface photoemission experiment, the interaction region with EUV field and IR field, respectively, are spatially separated if the IR field is screened at the surface. Therefore, delay contributions from Coulomb–laser coupling (streaking) [24,25] and continuum–continuum coupling (RABBITT) [6] do not occur if the IR field inside the solid can be neglected. Hence, conclusions from gas-phase experiments cannot be directly transferred to solids. The goal of this article is to numerically explore the similarities and differences in time delays obtained from RABBITT and streaking spectroscopy as applied to solid-state photoemission.
Note, however, that this is a theoretical view on attosecond-time-resolved spectroscopy. In a streaking or RABBITT experiment, relative delays between different emission channels are usually measured. For the present investigation, such relative delays would make identification of the underlying physics more difficult to present and would not provide additional information.
Time delays obtainable from both methods are compared in this article by solving the one-dimensional time-dependent Schrödinger equation (TDSE) for potential contributions that were successfully applied to explain experiment results in time-resolved photoemission from solid surfaces [10,16]. Note that a possible impact of local atomic effects such as, for example, initial- and final-state angular momenta were not considered in the present case. To guarantee comparability, we applied identical 5fs IR pulses for RABBITT and streaking calculations. Note that RABBITT experiments are usually performed with longer IR pulses (>20 fs) [2,6,23,32]. Although the application of longer IR pulses reduces experimental difficulties, there is no fundamental obstacle to perform RABBITT experiments with carrier-envelope-phase-stabilized few-cycle IR pulses.
In Section 2, model contributions and calculation methods are introduced. Section 3.1 demonstrates the transition from the RABBITT regime to the streaking regime by varying the EUV excitation spectrum. Extracted delays are compared in Section 3.2.
2. Methods
We describe all steps of the photoemission process from excitation to detection by the TDSE in one dimension and in a single-active-electron picture,
where is the time-independent effective one-electron potential, and and are the IR and EUV interaction potentials in length and velocity gauge, respectively.
All calculations shown here are based on an approach introduced by Kazansky and Kabachnik to describe atomic photoionization [33], as well as by Kazansky and Echenique, which was used to describe photoemission dynamics from a metal surface [16]. Note that the present implementation of the 1D model does not account for angular momentum effects and thus cannot be used to describe atomic-photoemission processes.
The central idea of this approach is to express the wave function as a sum of initial state and final state to separate fast phase oscillations. In the following, it is assumed that the IR field vanishes inside the solid and that EUV interaction is such a small perturbation that depopulation of the initial and final states by EUV excitation can be neglected. Then, the initial state wave function can be treated as time-independent, and the full wave function can be expressed as:
where is the initial state wave function that fulfills
Photoelectron wave function is zero before the EUV pulse arrives. The rapidly oscillating exponential is separated for computational efficiency. Here, is the center frequency of EUV light. Inserting Equation (4) into Equation (3), and using Equation (5) as well as the rotating-wave approximation, results in a differential equation for photoelectron wave function [10,16]:
where is the envelope of the EUV pulse vector potential.
Note that this approach is nonperturbative with respect to solid potential and IR potential, i.e., it does not apply strong field approximation, but describes the laser field and the solid’s effective potential on equal footing.
The unperturbed solid is described by the sum of jellium-type potential and electron–hole interaction. Jellium potential is given by:
where is the surface position, is the width of the transition region, and is the depth of the potential well. The screened electron–hole interaction is described by a one-dimensional Yukawa potential:
Here, is the effective initial position, μ is the screening length, and a is a regularization parameter [16].
The spatial distribution of IR potential is assumed as a smooth but narrow step at the surface because modeling of IR field penetration is beyond the scope of this article. Damping of the photoelectron wave function due to inelastic scattering processes is neglected here. Instead, damping enters the effective initial position via the inelastic mean free path.
This approach can be used to calculate streaking spectra as well as RABBITT spectra. In the case of streaking, is the envelope of a single-attosecond pulse, while it is the envelope of an attosecond pulse train for RABBITT calculations.
If not specified, the time-independent potential parameters used here are , Å, eV, Å, and Å. These values are not optimized for any specific material, but are in the order of typical values used to successfully reproduce experimental results [10,16].
Computations are performed on a one-dimensional spatial grid ranging from −185 to 185 nm using 32,768 grid points. Time integration is performed via a split-step Fourier method [34,35] with a step size of dt = 0.24 as. Equation (6) is integrated until the IR pulse is terminated. The split-step Fourier method using fast Fourier transforms (FFTs) implicitly enforces periodic boundary conditions, which is not a proper description for the photoemission process into the semi-infinite vacuum half-space. Therefore, spatial grid size was chosen such that the photoelectron wave packet did not reach the boundaries during whole time integration.
3. Results
We start our discussion with a short introduction into the generation of single-attosecond pulses and attosecond pulse trains, which are obtained by the HHG process in noble-gas atoms. The latter can be envisioned in a three-step process [36,37]: During each cycle of the laser pulse, the atom is ionized by the strong electric field of the laser pulse. The electron is subsequently further accelerated by the laser field. When the electric field reverses its sign during the cycle, a certain fraction of the electron wave packet is accelerated back toward the parent ion and recollides. Since it gained kinetic energy during the acceleration process, the recombined atom emits a photon with energy corresponding to an odd high-order multiple of the fundamental photon energy. A typical gas target HHG spectrum of a near-infrared few-cycle pulse can be divided into three regimes (Figure 2): The intensity of the spectral lines rapidly decays at the lowest odd harmonic orders due to decreasing conversion efficiency in this regime. At intermediate harmonic orders, there is a plateau regime with distinguishable lines of constant intensity located at the odd multiples of fundamental frequency. A dropping cutoff continuum is formed at the highest harmonic orders within reach where only recolliding electrons from a single half-cycle of the IR pulse with maximum electric field strength contribute. Cutoff energy depends on the ponderomotive potential of the laser-driven motion, and thus increases with increasing laser intensity [26].
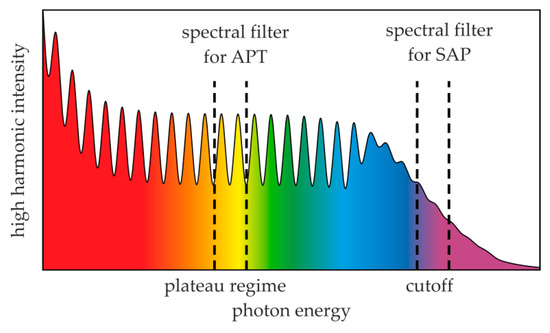
Figure 2.
Schematic high harmonic spectrum of a few-cycle IR pulse. In the intermediate energy regime, separated harmonic lines of equal height form a plateau. Spectral filtering in this regime leads to EUV APTs. In the high-energy regime, a cutoff continuum is formed. To obtain SAPs, this regime needs to be spectrally filtered.
RABBITT and streaking experiments require filtering different regions of the HHG spectrum. In a RABBITT experiment, the excitation spectrum is restricted to the plateau region where separate EUV lines can form attosecond pulse trains [28]. For streaking, a broad part of the cutoff continuum needs to be spectrally filtered to generate single-attosecond pulses. To obtain sufficient spectral width in the cutoff regime for single-attosecond pulses, the fundamental pulse duration is restricted to less than two optical cycles [1]. The goal here is to study the possibility of direct experimental comparison of streaking and RABBITT measurements of identical initial and final states. Hence, it is required that single-attosecond pulses and attosecond pulse trains with identical mean photon energy are available. Therefore, either HHG cutoff is brought into overlap with a spectral filter that then transmits a single pulse, or the cutoff is shifted to significantly higher energies, so that the plateau regime is transmitted through the filter, resulting in an attosecond pulse train. For the following analysis, we assume that we can independently adjust the EUV spectrum from the IR pulse. In an experiment, this is, in principle, possible if the IR pulse is separated from that part of the IR pulse driving the HHG process. The pulse duration and intensity of the part of the IR pulse responsible for HHG needs to be adjusted to tune the EUV spectrum. Furthermore, effects related to the spectral phase of the EUV spectrum are omitted.
3.1. From RABBITT Regime to Streaking Regime
To demonstrate the transition from the conditions of a RABBITT to a streaking experiment in a simplified solid-surface system, EUV attosecond pulse duration is successively reduced. A reduction of attosecond EUV pulse duration in the time domain implies a broadening of the corresponding EUV excitation spectrum. The attosecond excitation pulses corresponding to the EUV spectra applied in the following are shown in Figure 3.
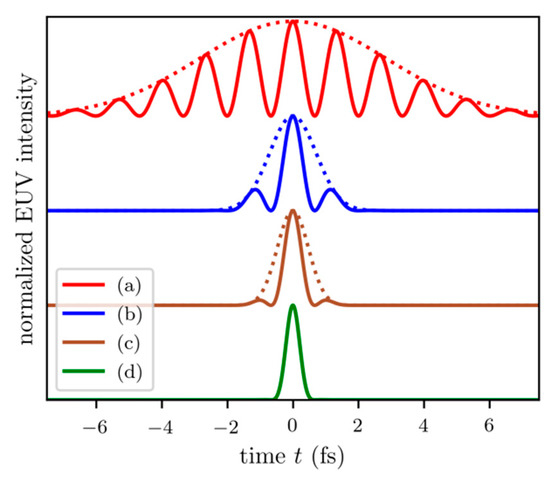
Figure 3.
Normalized intensity of EUV excitation pulses (solid line) in the time domain corresponding to the EUV spectra shown in Figure 4a–d. Pulse train envelopes are also shown (dotted lines). The envelope full width at half maximum (FWHM) pulse durations are (a) 6.7 fs, (b) 1.7 fs, (c) 1.1 fs, and (d) 474 as.
In a RABBITT experiment, an attosecond pulse train is applied as the excitation pulse. Here, its envelope full width at half maximum (FWHM) pulse duration is 6.7 fs (Figure 3, red line). The corresponding excitation spectrum in the RABBITT regime consists of two well-separated narrow spectral EUV lines located at the 59th and 61st harmonic order (Figure 4a) corresponding to 91.3 and 94.4 eV, respectively.
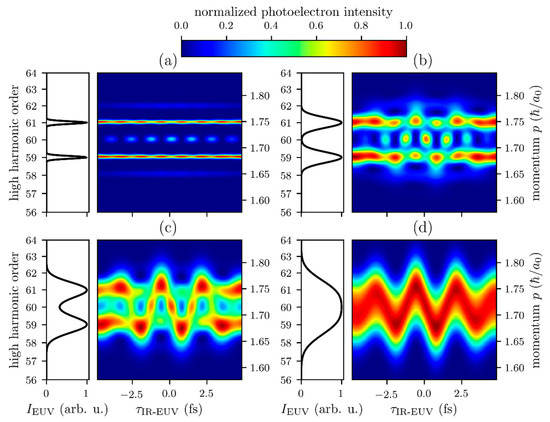
Figure 4.
Simulated photoelectron spectra (color plots) corresponding to four different EUV excitation spectra (black lines). All spectra were individually normalized. EUV pulse (train) was given by the Fourier transform of the EUV spectra. IR pulse was treated independently, with a center wavelength of 800 nm, pulse duration of 5 fs, and maximum electric field amplitude . Effective propagation distance was 5 Å, and initial-state binding energy was .
Now, we move from a pure RABBITT regime to a pure streaking regime by reducing the duration of the APT envelope. As fewer and fewer subpulses of the EUV pulse train interfere with each other, the resulting spectral features of the harmonics become broader. For a 1.7 fs (FWHM) long attosecond pulse train envelope, three EUV pulses interact with the system (Figure 3, blue line), resulting in two broad but still fully separated lines in the EUV spectrum (Figure 4b). Further reduction of the APT envelope duration to 1.1 fs leads to very weak side pulses and a pronounced main attosecond pulse in the APT (Figure 3, brown line). Spectral lines in the corresponding EUV spectrum overlap (Figure 4c). A single-attosecond pulse (Figure 3, green line) of 474 as duration was obtained for broad spectral distribution (Figure 4d).
Time-resolved photoelectron spectra are calculated by solving the full one-particle TDSE while the excitation spectrum is varied. The initial wave function of the electron is localized at 5 Å below the surface. This initial depth inside the material was chosen since it closely fits the effective mean free path of the photoelectrons considered here. Note that the kinetic energies of the photoelectrons are close to the minimum of the universal curve [38]. The time-independent potential consists of jellium potential and screened Yukawa potential. The electron is excited by the EUV pulse (train) and propagates toward the surface, where it is emitted into the vacuum. For all EUV excitation pulses, the electron wave packet starts to interact with the same 5 fs 800 nm IR cosine pulse with electric field amplitude .
For excitation by an attosecond pulse train (Figure 3, red line), the resulting time-resolved photoelectron spectrum is a typical RABBITT spectrogram, as shown in Figure 4a. For delays between the IR and EUV pulse beyond the temporal overlap of both pulses, there are two photoelectron peaks located at energies corresponding to odd harmonics (not shown). If the EUV and IR pulses overlap, there are additional side bands at even harmonic orders (LAPE) [30]. The additional side band (60th harmonic) located between the 59th and 61st harmonic order, oscillates as a function of IR–EUV time delay due to interference between photoelectrons that emit one IR photon after absorption of a 61st-order EUV photon and those that absorb one IR photon after absorption of a 59th-order EUV photon. For constructive interference at the side band, there is destructive interference in the odd-order single-photon peaks, and vice versa. Note that, here, a bandwidth-limited EUV pulse train is assumed and, hence, the different harmonics interact with the initial state at the exact same time.
If the photoelectron were excited by a 1.7 fs APT (Figure 3, blue line), the spectrogram would show deviations from a pure RABBITT spectrogram (Figure 4b). For IR–EUV delays at which a higher yield at the 59th band is observed, the yield is reduced at the 61st band, and vice versa. In addition, the 59th- and 61st-order bands show IR-induced and IR–EUV delay-dependent broadening.
For even shorter duration of the APT envelope (1.1 fs, Figure 3, brown line), where EUV lines overlap (Figure 4c), the resulting spectrogram shows a signature of the vector potential of the IR pulse. However, for certain IR–EUV delays , the direct photoemission peaks corresponding to the odd harmonics can still be distinguished. This intermediate regime (Figure 4b,c) exhibits features of both RABBITT and streaking spectra.
Further reduction of the pulse train envelope leads to excitation with a single-attosecond pulse (Figure 3, green line) and correspondingly broad kineticenergy distribution of the excited electron wave packet (Figure 4d). This results in a typical streaking spectrogram, where the peak shift as function of reproduces IR vector potential. This transition illustrates that RABBITT and attosecond-streaking are two extremal cases of laser-assisted photoemission [30]. The manifestation of the LAPE mechanism critically depends on the time structure of the involved EUV and IR fields. In the limit of rather long IR and EUV pulses, photoemission side-band formation is observed. For very short EUV pulses (streaking case) and rapidly amplitude-modulated EUV fields (RABBITT case) the interference of different excitation pathways leads to a streaking and a RABBITT spectrogram, respectively. Note that all sprectrograms are calculated for the same IR pulse. Thus, the appearance of either a RABBITT or a streaking type of spectrum is not at all related to IR field properties, but is basically determined by the time structure of the EUV field.
Interestingly, continuous transition between both regimes seen in Figure 4 can be understood as an example of the quantum-classical correspondence principle: In the RABBITT regime, we observed discrete photoelectron side-band peaks caused by exchange of IR photons with the electron wave packet. The time structure of the electron wave packet created by the APT and this interaction with the photon field results in final electron momentum distribution that is characteristic for quantized light–matter interaction, i.e., discrete side bands appear. Moreover, the information of photoemission dynamics is imprinted on the RABBITT signal via the phase of the photoelectron wave function, which is a genuine quantum property. RABBITT, as an interferometric measurement, works as a quantum clock [14]. In contrast, the streaking regime exhibits classical behavior. Here, photoelectrons also undergo multiple interactions with the photon field but, due to different accessible interference pathways, resulting in continuously varying momentum distribution, and quantized light–matter interaction is no longer evident. The attosecond streak camera [29] acts as a classical clock [14] where time information can be analogously extracted to a streaking camera, in the sense that, here, a transient electric field directly imposes the time reference.
3.2. Comparison of Streaking and RABBITT Delays with Classical Photoemission Times
To compare the delay information that can be obtained from a streaking or RABBITT experiment at solid surfaces, streaking and RABBITT spectrograms were calculated for different center EUV energies. Again, the initial state is effectively localized at –5 Å, and the potential specified in the Methods section is used as an example system. Spectra were calculated for , ranging from 5 to 90 eV. The IR pulse has a central energy of 1.55 eV, and pulse duration of 5 fs. The delay axis was sampled by 101 -delay steps between −2.4 and 2.4 fs. From the resulting spectrograms, the corresponding streaking and RABBITT delays were extracted following the procedures described in Appendix A.
Resulting delays and are shown in Figure 5, and compared with (Figure 5a). Photoemission times were determined by calculating the classical transport time for a free electron at the same potentials propagating from emission depth ( Å) to the surface ( Å).
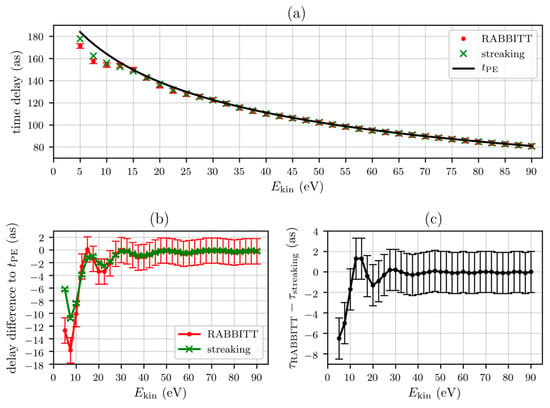
Figure 5.
Comparison of streaking and RABBITT delays with classical photoemission transport times . (a) Variation of streaking (green crosses) and RABBITT delays (red dots), as well as classical photoemission times (black) as a function of (vacuum) kinetic energy. For the streaking data, error bars are not shown because they are smaller than the symbol size. Streaking and RABBITT delays were extracted from spectrograms, calculated by solving the one-dimensional time-dependent Schrödinger equation (TDSE) (Equation (6)) for potential properties described in the main text. (b) Difference between RABBITT and streaking delays and classical photoemission times. (c) Difference between RABBITT and streaking delays.
Streaking delays can be determined from simulated photoelectron spectra with an accuracy of (Appendix A, Figure A1a). Due to the lack of an appropriate evaluation method for few-cycle RABBITT data (Appendix A, Figure A1b), RABBITT delays are subject to a larger systematic error, and can only be specified here with the accuracy . decreases for longer IR pulses that would, however, significantly increase simulation computation time.
Figure 5b shows the difference between classical photoemission times and (red), as well as (green), respectively. Consistently with the quantum-classical correspondence principle, streaking and RABBITT delays from TDSE calculations approach the classical results with increasing kinetic energy. The difference becomes smaller than 1 as for , and one can conclude that the extracted delays from the spectrograms indeed reveal photoemission time. Note that deviation from classical behavior is not significant for in the RABBITT case because of larger systematic error. For smaller energies, streaking and RABBITT results exhibit oscillatory deviations from the classical case toward smaller delays. This is a quantum mechanical interference effect caused by partial reflections of the excited state wave packet at the inhomogeneities of the potential. In TDSE calculations, the actual shape of the potential composed of the potential step at the surface and the Yukawa potential determine energy-dependent transmission and reflection coefficients. Therefore, parts of the wave packet undergo reflections before being emitted through the surface. The corresponding interference pattern that emerges in the spatial region between the initial position and the surface step is more pronounced for low kinetic energies. This results in modulated photoelectron energy distribution. Consequently, this imprints temporal modulation onto the wave packet that affects the delay extracted from the time-resolved photoelectron spectrogram. In the case of streaking, there is a maximum difference between streaking delay and classical photoemission time of −11 as at 7.5 eV. The same behavior can also be observed for RABBITT delays.
Unfortunately, we have no knowledge about the exact potential shape of a solid at the interface. Still, we can conclude that quantum effects due to scattering at potential inhomogeneities have more impact to lower kinetic energies. Hence, we conclude that the validity of classical photoemission time deteriorates as final state energy approaches vacuum energy.
The difference between delays determined from streaking spectra and RABBITT spectra is shown in Figure 5c. For kinetic energies <10 eV, there are significant differences between these two cases. We attribute this difference to the modulated energy distributions mentioned above. The impact of this effect on different electron distributions generated in RABBITT and streaking experiments results in different extracted temporal delays. Additional differences can arise due to ambiguities in streaking spectrogram analysis for low kinetic energies where asymmetries of the resulting momentum distribution are ignored. Note that IR field-driven recollision dynamics of the photoelectron with the surface were negligible at the investigated field strength for this energy range.
For kinetic energies higher than 10 eV within the accuracy available here, there was no significant difference between RABBITT and streaking spectra for solid-state systems at this level of description. It is necessary to improve the method to evaluate simulated RABBITT spectra to clarify if these small differences (<2 as) have a physical origin or if it is an analysis issue.
4. Conclusions
We calculated time-resolved photoelectron spectra for photoemission from solid surfaces in a one-dimensional single-active-electron model using jellium-type potential and electron-hole interaction. Thus, a band structure does not exist in this model. For RABBITT and streaking spectra, we applied the same IR field strength of 1 V/nm, i.e., peak intensity, at a pulse duration of 5 fs. Both methods yielded analyzable signals. This corresponds to a streaking amplitude of 1.2 eV at eV and to a streaking amplitude of 1.7 eV at eV, which is comparable to typical results for streaking at solid surfaces [9,10,11,39]. IR intensity applied in the RABBITT experiments was in the same order of magnitude [23,32,40].
We could show for solid surfaces that RABBITT and streaking yield identical delay information within evaluation accuracy. Analysis revealed that differences between these techniques are expected to play a role only for photoelectrons with kinetic energy below 10 eV in the investigated system. In core-level photoemission spectra from solid samples, photoelectrons in this kinetic energy range are impossible to determine in practice because these photoemission peaks would be covered by a strong secondary electron background. Based on our analysis, differences between RABBITT and streaking delays determined at surfaces with vanishing internal IR field in an accessible energy range are smaller than ±3 as. Obviously, this is also valid for delay differences.
For experimental proof of our model calculations, van der Waals crystals might be a suitable set of samples, because streaking delays of WSe2 photoemission spectra were successfully explained by the model applied here using jellium-type potential and including electron–hole interaction for electron transport while treating angular momentum influences as intra-atomic effects. Additionally, they exhibited stable surface conditions, which is helpful for such a challenging experiment [10].
Moreover, it can be stated that both streaking and RABBITT delay reflect photoemission time within our model for sufficiently high kinetic energy as long as the IR field inside the material can be neglected.
In a system described by homogeneous inner potential, i.e., a jellium model, the EUV transition matrix element is a rather flat function with respect to energy. However, if the EUV transition matrix element in a system exhibits narrow features, photoelectron yield at narrow harmonic lines is sensitive to these features in a RABBITT measurement. This could lead to asymmetric spectral distributions. In a streaking spectrogram, broad energy distribution might average out these features, and the method might be less sensitive to transition matrix properties, and differences to RABBITT could arise. So, for more advanced models of solid-state photoemission, taking, for example, band-structure effects into account, deviations between RABBITT and streaking spectroscopy might appear. Hence, similar investigations as are needed for a more advanced description of electron dynamics in solids.
Author Contributions
Formal analysis, A.G.; funding acquisition, M.A. and W.P.; investigation, A.G.; project administration, W.P.; software, A.G.; supervision, M.A. and W.P.; validation, A.G. and S.N.; writing—original draft, A.G.; writing—review and editing, A.G., S.N., W.E., B.S., M.A., and W.P.
Funding
This research was funded by the German Research Foundation within Priority Program SPP “Quantum Dynamics in Tailored Intense Fields” (grant number PF317/10-1).
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; and in the decision to publish the results.
Appendix A. Extraction of Delays
Streaking delays can be determined by least-square fitting of IR vector potential (Equation (2)) to the momentum expectation value of the spectrum (Figure A1a). In order to obtain , continuum wave packet is evaluated for . Keeping the streaking amplitude as a free fit-parameter accounts for squeezing the streaking amplitude due to a finite EUV pulse duration. The fit works reliably and gives a standard error for the streaking delay fit parameter of . There are systematic deviations between model function and simulation results in the order of of the maximum streaking shift.
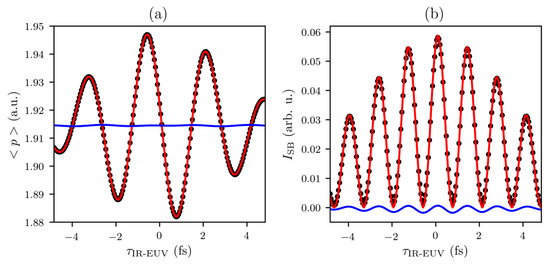
Figure A1.
Analysis of simulated photoelectron spectra for a 50 eV photoelectron interacting with an IR pulse with a center wavelength of 800 nm, pulse duration of 5 fs, and maximum electric field amplitude = . (a) Photoelectron is generated by a single-attosecond pulse (streaking). IR vector potential (red line) is fitted to the simulated data points. The residuum between model function and data points (blue line) exhibits systematic deviations in the order of with respect to the streaking amplitude. (b) Photoelectron is generated by an attosecond pulse train (RABBITT). Equation (9) (red line) is fitted to the simulated data points. Here, the residuum between model function and data points (blue line) shows systematic deviations in the order of a few percent of maximum side-band intensity.
In a RABBITT experiment using longer IR pulses (>20 fs), side-band delays are usually determined by fitting a cosine function to side-band intensity [2,6,23,32]. However, in the simulations presented here, background-free few-cycle RABBITT spectra were calculated using a 5 fs IR pulse, i.e., its finite spectral width comes into play. The corresponding nonresonant two-photon transition matrix elements scale with . Therefore, low-energy parts of the IR spectrum contribute more strongly to side-band intensity than the high-energy parts. This leads to a red-shift of side-band oscillation with respect to IR center frequency [41]. Determination of RABBITT delays becomes nontrivial, because neglecting the envelope of the EUV pulse train and IR pulses leads to systematic deviations between model function and results. The best agreement was obtained for fitting the square modulus of the convolution of the EUV pulse train envelope with the IR electric field (Equation (9)) to the integrated side-band intensity (Figure A1b):
Here, delay , IR oscillation frequency, IR pulse duration, and are used as fit parameters to account for the red shift. The red shift of the side-band oscillation amounts to 60 meV at for a 5 fs pulse with 1.55 eV central energy. However, as shown in Figure A1b, there are systematic deviations for short IR pulses in the order of a few percent of the maximum side-band intensity, i.e., one order of magnitude larger than in the streaking case. These systematic errors cause instabilities in the fitting procedure that prevent convergence with respect to delay-axis sampling. For our analysis, we compared fit results for different distributions of IR–EUV delay sampling points. The scattering of results provides an accuracy estimate. Thus, RABBITT delays determined with this procedure are subject to a systematic error of .
References
- Drescher, M.; Hentschel, M.; Kienberger, R.; Tempea, G.; Spielmann, C.; Reider, G.A.; Corkum, P.B.; Krausz, F. X-ray Pulses Approaching the Attosecond Frontier. Science 2001, 291, 1923–1927. [Google Scholar] [CrossRef] [PubMed]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Gallmann, L.; Cirelli, C.; Keller, U. Attosecond Science: Recent Highlights and Future Trends. Annu. Rev. Phys. Chem. 2012, 63, 447–469. [Google Scholar] [PubMed]
- Schultze, M.; Fiess, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in Photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef] [PubMed]
- Klünder, K.; Dahlström, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guénot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing Single-Photon Ionization on the Attosecond Time Scale. Phys. Rev. Lett. 2011, 106, 143002. [Google Scholar] [CrossRef] [PubMed]
- Dahlström, J.M.; Guénot, D.; Klünder, K.; Gisselbrecht, M.; Mauritsson, J.; L’Huillier, A.; Maquet, A.; Taïeb, R. Theory of attosecond delays in laser-assisted photoionization. Chem. Phys. 2013, 414, 53–64. [Google Scholar] [CrossRef]
- Nisoli, M.; Decleva, P.; Calegari, F.; Palacios, A.; Martín, F. Attosecond Electron Dynamics in Molecules. Chem. Rev. 2017, 117, 10760–10825. [Google Scholar] [CrossRef]
- Neppl, S.; Ernstorfer, R.; Cavalieri, A.L.; Lemell, C.; Wachter, G.; Magerl, E.; Bothschafter, E.M.; Jobst, M.; Hofstetter, M.; Kleineberg, U.; et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 2015, 517, 342–346. [Google Scholar] [CrossRef]
- Siek, F.; Neb, S.; Bartz, P.; Hensen, M.; Strüber, C.; Fiechter, S.; Torrent-Sucarrat, M.; Silkin, V.M.; Krasovskii, E.E.; Kabachnik, N.M.; et al. Angular momentum–induced delays in solid-state photoemission enhanced by intra-atomic interactions. Science 2017, 357, 1274–1277. [Google Scholar] [CrossRef]
- Ossiander, M.; Riemensberger, J.; Neppl, S.; Mittermair, M.; Schäffer, M.; Duensing, A.; Wagner, M.S.; Heider, R.; Wurzer, M.; Gerl, M.; et al. Absolute timing of the photoelectric effect. Nature 2018, 561, 374–377. [Google Scholar] [CrossRef] [PubMed]
- Cavalieri, A.L.; Müller, N.; Uphues, T.; Yakovlev, V.S.; Baltuška, A.; Horvath, B.; Schmidt, B.; Blümel, L.; Holzwarth, R.; Hendel, S.; et al. Attosecond spectroscopy in condensed matter. Nature 2007, 449, 1029–1032. [Google Scholar] [CrossRef] [PubMed]
- Seiffert, L.; Liu, Q.; Zherebtsov, S.; Trabattoni, A.; Rupp, P.; Castrovilli, M.C.; Galli, M.; Süßmann, F.; Wintersperger, K.; Stierle, J.; et al. Attosecond chronoscopy of electron scattering in dielectric nanoparticles. Nat. Phys. 2017, 13, 766–770. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765–802. [Google Scholar] [CrossRef]
- Maquet, A.; Caillat, J.; Taïeb, R. Attosecond delays in photoionization: time and quantum mechanics. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 204004. [Google Scholar] [CrossRef]
- Kazansky, A.K.; Echenique, P.M. One-Electron Model for the Electronic Response of Metal Surfaces to Subfemtosecond Photoexcitation. Phys. Rev. Lett. 2009, 102, 177401. [Google Scholar] [CrossRef] [PubMed]
- Lemell, C.; Solleder, B.; Tőkési, K.; Burgdörfer, J. Simulation of attosecond streaking of electrons emitted from a tungsten surface. Phys. Rev. A 2009, 79, 062901. [Google Scholar] [CrossRef]
- Krasovskii, E.E.; Friedrich, C.; Schattke, W.; Echenique, P.M. Rapid propagation of a Bloch wave packet excited by a femtosecond ultraviolet pulse. Phys. Rev. B 2016, 94, 195434. [Google Scholar] [CrossRef]
- Borisov, A.G.; Sánchez-Portal, D.; Kazansky, A.K.; Echenique, P.M. Resonant and nonresonant processes in attosecond streaking from metals. Phys. Rev. B 2013, 87, 121110. [Google Scholar] [CrossRef]
- Krasovskii, E.E. Attosecond spectroscopy of solids: Streaking phase shift due to lattice scattering. Phys. Rev. B 2011, 84, 195106. [Google Scholar] [CrossRef]
- Liao, Q.; Thumm, U. Attosecond Time-Resolved Photoelectron Dispersion and Photoemission Time Delays. Phys. Rev. Lett. 2014, 112, 023602. [Google Scholar] [CrossRef] [PubMed]
- Gebauer, A.; Neb, S.; Enns, W.; Heinzmann, U.; Kazansky, A.K.; Pfeiffer, W. Photoemission time versus streaking delay in attosecond time-resolved solid state photoemission. Submitted to EPJ Web Conf. 2018. [Google Scholar]
- Tao, Z.; Chen, C.; Szilvasi, T.; Keller, M.; Mavrikakis, M.; Kapteyn, H.; Murnane, M. Direct time-domain observation of attosecond final-state lifetimes in photoemission from solids. Science 2016, 353, 62–67. [Google Scholar] [CrossRef]
- Smirnova, O.; Mouritzen, A.S.; Patchkovskii, S.; Ivanov, M.Y. Coulomb–laser coupling in laser-assisted photoionization and molecular tomography. J. Phys. B At. Mol. Opt. Phys. 2007, 40, F197–F206. [Google Scholar] [CrossRef]
- Nagele, S.; Pazourek, R.; Feist, J.; Doblhoff-Dier, K.; Lemell, C.; Tőkési, K.; Burgdörfer, J. Time-resolved photoemission by attosecond streaking: extraction of time information. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 081001. [Google Scholar] [CrossRef]
- Li, X.F.; L’Huillier, A.; Ferray, M.; Lompré, L.A.; Mainfray, G. Multiple-harmonic generation in rare gases at high laser intensity. Phys. Rev. A 1989, 39, 5751–5761. [Google Scholar] [CrossRef]
- McPherson, A.; Gibson, G.; Jara, H.; Johann, U.; Luk, T.S.; McIntyre, I.A.; Boyer, K.; Rhodes, C.K. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 1987, 4, 595. [Google Scholar] [CrossRef]
- Muller, H.G. Reconstruction of attosecond harmonic beating by interference of two-photon transitions. Appl. Phys. B 2002, 74, s17–s21. [Google Scholar] [CrossRef]
- Itatani, J.; Quéré, F.; Yudin, G.L.; Ivanov, M.Y.; Krausz, F.; Corkum, P.B. Attosecond Streak Camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef]
- Miaja-Avila, L.; Lei, C.; Aeschlimann, M.; Gland, J.L.; Murnane, M.M.; Kapteyn, H.C.; Saathoff, G. Laser-Assisted Photoelectric Effect from Surfaces. Phys. Rev. Lett. 2006, 97, 113604. [Google Scholar] [CrossRef]
- Cattaneo, L.; Vos, J.; Lucchini, M.; Gallmann, L.; Cirelli, C.; Keller, U. Comparison of attosecond streaking and RABBITT. Opt. Express 2016, 24, 29060. [Google Scholar] [CrossRef] [PubMed]
- Kasmi, L.; Lucchini, M.; Castiglioni, L.; Kliuiev, P.; Osterwalder, J.; Hengsberger, M.; Gallmann, L.; Krüger, P.; Keller, U. Effective mass effect in attosecond electron transport. Optica 2017, 4, 1492. [Google Scholar] [CrossRef]
- Kazansky, A.K.; Kabachnik, N.M. Theoretical description of atomic photoionization by an attosecond XUV pulse in a strong laser field: effects of rescattering and orbital polarization. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 2163–2177. [Google Scholar] [CrossRef]
- Fleck, J.A.; Morris, J.R.; Feit, M.D. Time-Dependent Propagation of High Energy Laser Beams through the Atmosphere. Appl. Phys. B 1976, 10, 129–160. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A. Solution of the Schrödinger equation by a spectral method II: Vibrational energy levels of triatomic molecules. J. Chem. Phys. 1983, 78, 301–308. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Seah, M.P.; Dench, W.A. Quantitative Electron Spectroscopy of Surfaces: A Standard Data Base for Electron Inelastic Mean Free Paths in Solids. Surf. Interface Anal. 1979, 1, 2–11. [Google Scholar] [CrossRef]
- Guggenmos, A.; Akil, A.; Ossiander, M.; Schäffer, M.; Azzeer, A.M.; Boehm, G.; Amann, M.-C.; Kienberger, R.; Schultze, M.; Kleineberg, U. Attosecond photoelectron streaking with enhanced energy resolution for small-bandgap materials. Opt. Lett. 2016, 41, 3714. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Z.; Carr, A.; Matyba, P.; Szilvási, T.; Emmerich, S.; Piecuch, M.; Keller, M.; Zusin, D.; Eich, S.; et al. Distinguishing attosecond electron–electron scattering and screening in transition metals. Proc. Natl. Acad. Sci. USA 2017, 114, E5300–E5307. [Google Scholar] [CrossRef]
- Jiménez-Galán, Á.; Martín, F.; Argenti, L. Two-photon finite-pulse model for resonant transitions in attosecond experiments. Phys. Rev. A 2016, 93, 023429. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).