Abstract
In this paper, we present a cloud image data protection algorithm with a multilevel encryption scheme and automated-selection mechanism to maintain the privacy of cloud data contents. This algorithm is also useful for the protection of personal or commercial data uploaded to the cloud server for real-time applications, monitoring, and transmission. Fundamental and well-known in cryptography, the confusion–diffusion scheme, as well as an automated-selection mechanism (sliding pixel window) were selected as the main motor of the proposed algorithm to cipher images. First, a sliding pixel window is selected to expedite a two-stepped process, whether in small or big images. The confusion stage was designed to drastically change data from plain image to cipher image. The conversion of pixels from decimal to binary and their vertical and horizontal relocation were performed to help in this stage, not only by randomly moving bits, but also by changing the pixel values when they returned to their corresponding decimal values. Meanwhile, the diffusion stage was designed to destroy all possible existing patterns in the sliding pixel window after the confusion stage. Two hyperchaotic systems, together with a logistic map (multilevel scheme), produce pseudorandom numbers to separately conceal the original data of each subplain image through first- and second-level encryption processes. The two-stepped algorithm was designed to be easily implemented by practitioners. Furthermore, the experimental analysis demonstrates the effectiveness and feasibility of the proposed encryption algorithm after being tested using the benchmark “Lena” image, as well as the “Bruce Lee” image, the latter of which is completely different to the first one, statistically speaking.
1. Introduction
Nowadays, in an online environment where tons of personal data are shared and instantaneously stored in servers or clouds that are distributed all over the globe, it is very difficult for people to maintain control over sensitive information when necessary. Here, we refer to different types of information, such as emails, photos, videos, and audio that are an essential part of our lives. If we cannot control or take care of our data, they can be accessed, stolen, altered, or copied by alien entities in seconds, without our consent.
Thus, data protection has become important to every member of society. Large companies have been caught up in the conflict due to server data leakages that exposes all of a user’s stored information. Even though information is processed and protected in many ways in order to prevent attacks and protect digital assets from being compromised, these processes are often inadequate in keeping them secure. This reality poses an enormous challenge both for privacy and cybersecurity. This is where data encryption comes in.
Encryption helps to protect information by turning readable data into unreadable results. Nowadays, the most popular globally used applications are based on sharing and storing images online. Image encryption has become one of the most critical tools in today’s cyberworld. A digital image is characterized by intrinsic features such as bulk data, high pixel correlation, and redundancy. Therefore, image encryption is an extremely important technology to ensure the security of sensitive information. Different image encryption schemes are outlined in this paper, such as optical transformation [1,2,3,4], cellular automata [5,6,7], DNA coding [8,9,10,11,12], data encryption standard (DES) [13,14,15], advanced encryption standard (AES) [16,17,18,19,20], and Blowfish [21]. However, the last three were mainly designed for textual information rather than digital image information.
In 1989, the British mathematician Matthews introduced the first chaos-based encryption algorithm, where a logistic map was used as a key generator [22]. In fact, chaotic behaviors can be determined by nonlinear dynamic systems, where any tiny initial deviation will be exponentially amplified. Intrinsic properties of chaotic systems, such as ergodicity, sensitive dependence on initial conditions, random like behavior, and the mixing effect, lead to a natural relationship and structural similarity between chaos and cryptography. This is an important milestone for chaos-based encryption technology.
Later, in 1998, Fridrich introduced the first general architecture for a chaos-based image cipher [23] consisting of permutation and diffusion. In the first stage, pixels were permutated by a two-dimensional area-preserving chaotic map. Then, pixel values were modified using a discretized chaotic map in the diffusion procedure. This architecture became the most popular structure and has been adopted in many chaos-based image encryption algorithms. For instance, Chen et al. [24] used a 3D Arnold’s cat map for substitution and employed Chen’s chaotic system for the diffusion process. In [25], an image encryption algorithm with a permutation–diffusion structure was introduced and a tent map used to shuffle the positions of image pixels, and delayed coupled map lattices (DCML) were then employed to confuse the relationship between the plain and cipher image.
Some researchers improved the two-stage structure, presenting a one-stage structure. Wang et al. [26] proposed an image encryption algorithm that combined the permutation and diffusion stages into one stage, where the plain image was divided into blocks that could be permutated as a unit, and another algorithm that could simultaneously perform confusion and diffusion was proposed in [27], but the pixel of the image was the unit in confusion. In addition, a three-stage image encryption structure was developed and introduced; Seyedzadeh et al. [28] used a quantum logistic map to diffuse the relationship of pixels, employed a two-dimensional logistic map to modify the values of diffused pixels, and exploited random circular shift operation to rearrange the bits of each encrypted pixel. Zhu et al. [29] introduced an improved permutation–diffusion architecture, which included three stages: plain pixel-related swapping confusion, diffusion, and plain pixel-related swapping confusion.
However, a ciphertext or cipher image can easily be deciphered by chosen plaintext and ciphertext attacks [30,31,32] if the permutation operation just changes the position of the pixel in the permutation stage, and the pseudorandom sequence generated by the chaotic system is independent of the plaintext and diffusion process. To avoid attackers cracking cryptosystems by using an order from top to bottom and from left to right, a variety of image encryption algorithms using bit-level permutation have been proposed. Xu et al. [33] proposed a novel bit-level image encryption algorithm via chaotic maps, such as a technique that uses piecewise linear chaotic maps (PWLCM) and bit-level permutations to achieve this goal. In [34], Zhu et al. proposed a bit-level permutation scheme for image encryption that is based on both Arnold’s cat and logistic maps. In [35], a new bit-level encryption algorithm was developed based on spatiotemporal nonadjacent coupled map lattices that made it possible for any bit in pixels to break the limit of its bit plane without extra space in the permutation process. The permutation process at the bit level is actually able to simultaneously change the positions and gray values of pixels for high-resolution images; however, this requires more computational resources which naturally increases the iterative times of chaotic systems.
On the other hand, low-dimensional chaotic maps, such as the logistic map, are easy to use and require fewer computational resources. For high security considerations, low-dimensional chaotic systems are rarely applied for ciphering confidential images with high security requirements. In addition, some general methods can decipher these images, such as phase-space reconstruction or nonlinear prediction, but it is difficult to decipher images with high-dimensional chaotic systems. High-dimensional chaotic systems, especially hyperchaotic systems, have a larger key space, better sensitivity, more complex dynamic characteristics, and randomness. Consequently, a hyperchaotic system is especially appropriate for data protection with high security considerations [36,37,38,39,40]. In 2008, Gao and Chen [36] proposed a hyperchaos-based image encryption algorithm using pixel-level permutation; although this algorithm has the advantage of a large key space, Ruouma and Belghith [37] demonstrated that it could not resist chosen plaintext and ciphertext attacks due to the permutation process being at the pixel level. Further, hyperchaos-based image encryption algorithms with DNA encoding and genetic recombination were separately presented by Zhang et al. [38] in 2013, and Wang and Zhang [39] in 2016. Similarly, complex permutation and ciphering processes demand much greater consumption of computational resource in order to satisfy high security requirements.
According to research achievements and valuable experiences from the works listed in this paper, a cloud image data protection algorithm with a multilevel encryption scheme and automated-selection mechanism was developed. The proposed algorithm was designed to work with all image types regardless of their features. The automated-selection mechanism commonly used nowadays, which is a simple sliding window, improves the efficiency when the cryptosystem is used to cipher big images and other types of images not considered by other mechanisms, such as 4K and HD images.
Furthermore, a bit-level permutation process in the confusion stage and a hyperchaos-based ciphering and hierarchical encryption process in the diffusion stage make the current system even more secure. The initial conditions for the confusion and diffusion stages are defined at the beginning of the process. This is to produce large chaos trajectories that eventually become pseudorandom values after the correct iteration of hyperchaotic systems and several chaotic maps. A subsection of the image is chosen by an appropriate automated-selection mechanism to start the encryption process. Then, the process shuffles the image at the bit level via a logistic map in the confusion stage, which not only relocates the bits within the selected subimage, but also changes the pixel values, increasing the permutation efficiency.
Finally, through a combination of two hyperchaotic systems and a second logistic map, the diffusion stage becomes a multilevel encryption scheme that makes patterns much harder to identify, and vastly increases the amount of data needed to analyze in order to break the cipher image. Therefore, the system is highly secure and beneficial to many companies looking for a fast, safe, and efficient way to cipher their images, especially those which are high-resolution.
2. Materials and Methods
In this section, the proposed image encryption and its decryption processes are introduced. The configuration of the main idea is provided in Figure 1, where a classical two-staged cryptosystem is shown:

Figure 1.
Configuration of the interactive image encryption.
- (1)
- In the confusion process, an appropriate slide window size is selected (M × N), which divides the original plain image into several subplain images. After this step, each subplain image can be handled through the confusion and diffusion stages until the whole plain image has been encrypted. Therefore, the first process is the confusion stage, Sub-section where a moving-window shuffling process at the bit level is developed mainly to destroy the correlations of adjacent pixels within the window size.
- (2)
- The second stageSub-section, is the diffusion stage. It uses the same window size as the one assigned in the Sub-section where a multilevel encryption process is administered. Two hyperchaotic systems and a logistic map are applied to cipher the image content twice for more security.
2.1. Confusion Stage—Moving-Window Shuffling Process
One of the important characteristics of an image is the strong correlation between adjacent pixels. Therefore, the main mission of the confusion stage is to destroy the relationship of adjacent pixels by relocating those pixels (bit-level) in the horizontal and vertical directions. However, this consumes much computing time and many resources if all of the relationships of adjacent pixels in a plain image are to be broken at the same time—a huge matrix of new locations has to be generated. As a result, an appropriate size of window M × N was selected in this article to shuffle each subimage content at the bit level, where new limited locations for each bit number could more effectively be produced. The schematic diagram is shown in Figure 2a,b.

Figure 2.
(a) Selected sliding window M × N. (b) From decimal to binary of gray pixel value.
In Figure 2a, an appropriate size of window M × N was selected to further divide the plain image into several subimages, where the window size in this article was set to be 16 × 4 pixels. In order to operate the shuffling process at the bit level, in Figure 2b, we can see that the gray value of each pixel in the selected window is transformed from a decimal number to a binary number (D to B), i.e., the size of the bit-leveled subimage in the selected window was changed to M × N × 8. After finishing the whole shuffling process, the new subimage goes back to the decimal numbers (B to D) and a new gray value for each pixel as well as the low-correlated adjacent pixels could be obtained in the new subimage.
For the shuffling process, the first logistic map is applied to further generate necessary new position matrices in rows and columns for bit-level relocations, which can be described in Equation (1):
where n = 0, 1, …, ∞; zn refers to the state of the first logistic map in each iteration; r is the system parameter which was set to be r = 3.99; and initial condition z0 must be provided by the user at the beginning. The chaotic behavior is shown in Figure 3.

Figure 3.
Chaotic behavior of the logistic map.
- (1)
- For the shuffling process in the row direction, Equation (2) was applied to further convert the state value of the first logistic map in Equation (1) to a new position in each iteration:where zn is the state of the logistic map; Mzi(j) ϵ [1, M] is the new position for each binary number; and j = 1, 2, …, M describes the numbers of elements in each row direction. Mzi is a row vector representing the new position vector where i = 1, 2, …, N × 8 refers to the total number of row vectors. As a result, this repetitive process generates a new position matrix Mb(i,j), which is described in Equation (3). Following the new position matrix Mb to operate the shuffling process in the row direction, a completely new subimage at the bit level can be obtained. The complete flowchart is given in Figure 4.
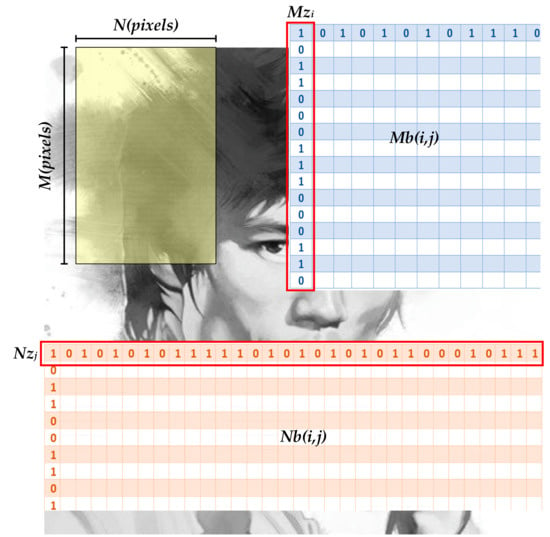 Figure 4. New position matrices of each subimage in row and column directions.
Figure 4. New position matrices of each subimage in row and column directions. - (2)
- For the shuffling process in the column direction, Equation (4) was applied to further convert the state value of the first logistic map in Equation (1) to a new column position:where Nzj(i) ϵ [1, N × 8] is the new position for each binary number and i = 1, 2, …, N × 8 denotes the number of elements in each column direction. Nzj is a column vector representing the new position vector and j = 1, 2, …, M refers to the total number of column vectors. As a consequence, this repetitive process generates a new position matrix, Nb(i,j), which is described in Equation (5). Following the new position matrix Nb, to further finish the shuffling process in the column direction, a completely new bit-level subimage is gained.
At the end of this process, the new subimage at the bit level is converted back to the decimal numbers (B to D), and a new gray value of each pixel and low-correlated adjacent pixels can be obtained in the new subimage. The final result of this new subimage is labeled as S(M,N).
2.2. Diffusion Stage—Multilevel Encryption Scheme
After obtaining the shuffled subimage through Sub-Section 2.1, the multilevel encryption scheme is applied to encrypt this subimage, which raises the security level by simultaneously ciphering the data with two hyperchaotic systems and a logistic map; the proposed encryption scheme is outlined in Figure 5.

Figure 5.
Flowchart of the multilevel encryption scheme.
In Figure 5, we can see that the hyperchaotic systems and the second logistic map are driven by the initial conditions provided before iterating the encryption system, and they then generate chaotic sequences for subimage encryption. In addition, the data generated via the logic map were designed here to equip two considerable functions—the first being the second-level ciphering tool and the other choosing a combination of states given from the two hyperchaotic systems for first-level encryption in each column pixel.
The classical Lorenz system and Chen’s system were considered as the hyperchaotic systems in this paper, and their chaotic sequences with different kinds of possible combinations were applied to provide the random data in this encryption process. The classical Lorenz system can be described as
where x1, x2, x3 are system states; σ, ρ, and β are system parameters; and when σ = 10, ρ = 28, and β = 8/3, the system reveals chaotic behavior as shown in Figure 6a. Further, Chen’s system is represented in Equation (7):
where x4, x5, x6 are system states; a, b, and c are system parameters; and when a = 35, b = 3, and c = 28, chaos attractors are stimulated, which are given in Figure 6a,b.

Figure 6.
Three-dimensional chaotic motion of classical a Lorenz system and Chen’s system.
According to the selected window size of 16 × 4, four pixels of the subimage were chosen to be ciphered in each iteration of the dynamic systems; therefore, four states of the hyperchaotic systems in Equations (6) and (7) are systematically selected for image encryption following the designed combinations of states in Table 1, as given below:

Table 1.
Different state combinations.
In this step, the second logistic map represented by Equation (8), as shown in Figure 5, is applied to select the possible combinations for encryption in Table 1; initial conditions generate a new sequence after iteration using Equation (9). The generated serial numbers are 0–14.
In accordance with the selected combination in Equation (9), the first-level ciphering data generated via the two hyperchaotic systems can be obtained from Equation (10):
where I = 1, 2, 3, …, 6 represent six states, and |xi| returns the absolute value of xi. Floor(xi) returns the value of yi to the nearest integer less than or equal to xi and mod(x,y) returns the remainder after division. Finally, Pi ϵ [0, 255] refers to enciphering values applied to the encryption process.
Further, the second-level ciphering data generated via the second logistic map in Equation (8) can be obtained as follows:
Finally, the encryption operation is the result of XOR among four consecutive pixels, which represents one row of shuffled moving window S(M,N) and the selected combinations states SNn; this step represents the first-level encryption. Second-level encryption is obtained after applying previous cipher data XOR Pi. This stage is represented as follows:
The process needs to be executed several times to encrypt the entire image. Those iterations are performed via a selected 16 × 4 sliding window, and each initial condition is updated with the final result of each interaction.
2.3. Decryption Process
The decryption algorithm is similar to the encryption algorithm, i.e., for an encrypted image, the inverse process must be applied to obtain the plain image. In all stages, the same initial conditions and the same parameters must be used.
3. Experimental Results and Discussion
In this section, the experimental results are provided to show the effectiveness and feasibility of the novel image encryption algorithm. Some plain images were selected to be the experiment examples, and all of them had different sizes; all required initial conditions for the encryption system were created via pseudorandom generators once the process began.
3.1. Experimental Analysis
“Bruce Lee” was …. Once the initial conditions have been created, the moving window is selected to further shuffle the goal image at the bit level. An image where the relationships between adjacent pixels has been disturbed is shown in Figure 7c, with the corresponding histogram shown in Figure 7d. The multilevel encryption scheme was applied to encrypt the whole image and raise security. Then, the cipher image and its histogram can be obtained; here, Figure 7e,f shows the final result and its histogram, respectively.

Figure 7.
(a) Plain image; (b) histogram of the original image; (c) cipher image after shuffling per bit level; (d) image histogram; (e) ciphered image; (f) histogram of the ciphered image.
The famous image “Lena” was also selected, sized 512 × 512; it is shown in Figure 8a, and its respective histogram in Figure 8b. The initial conditions for applying the proposed cryptosystem were provided by a pseudorandom generator, as in the case of the “Bruce Lee” image. Once the shuffling stage was applied, the position of each pixel in addition to the pixel value were changed; the result is shown in Figure 8c, and its corresponding histogram in Figure 8d. Multilevel encryption was applied, and the resultant cipher image and its histogram are illustrated, respectively, in Figure 8e,f.

Figure 8.
(a) Plain image; (b) histogram of the original image; (c) cipher image after shuffling per bit level; (d) image histogram of (c); (e) ciphered image; (f) histogram of the ciphered image.
The histograms is the original and ciphered images were compared, and it can be seen that the histogram of the ciphered image completely differed from the original one in being fairly uniform; this means that our proposed algorithm not only performed well but is also secure and can resist statistical attacks.
3.2. Security Analysis
The goal of applying an encryption algorithm is to obtain an indecipherable result, i.e., a hacker must not be able to recognize the plain image behind the ciphered image; thus, the security analysis in this section demonstrates that the proposed encryption algorithm is highly secure.
3.2.1. Key Space Analysis
The proposed image encryption algorithm uses several initial conditions to reach its goal, which is a cipher image. For this purpose, eight initial conditions were created to be used in two logistic maps and six hyperchaotic systems.
Table 1 shows 15 state combinations from a universe of 1296 possibilities; 15 randomly selected combinations were used in the testing process. This feature allows the precision to be defined as equal to 10−14; thus, the secret key space is at least 15 × 1084 ≈ 2283.
Thus, the secret key space is large enough to resist either exhaustive or brute-force attacks. Initial conditions yield different options for the encryption process, so those conditions can be changed into a new set of credentials in the authorization system.
3.2.2. Key-Sensitivity Test
Every initial condition in this process is derived from a proper pseudorandom generator; then, these data should be the same in the encryption of the plain image as well as the decryption of the cipher image; if the initial conditions are even in a decimal fraction, then the decryption process gives a different image than the original plain image. The following initial conditions organized in Table 2 were generated and used in this document:

Table 2.
Initial conditions derived from user interactivity for encryption.
The result of the cipher image using the previous values is shown in Figure 7e, and its histogram in Figure 7f. In this case, very small change was given in the initial conditions mentioned above, which was applied to decrypt the cipher image for further investigation, as shown in Table 3.

Table 3.
Initial conditions with small change derived from user interactivity for decryption.
The experimental result is shown in Figure 9a,b and Figure 10a,b. As Figure 9 and Figure 10 reveal, the process for decrypting the cipher image with different initial conditions gave a different image from the expected result. This fact occurs even if there is only a tiny change; consequently, the key-sensitivity test demonstrated that the proposed novel image encryption algorithm has a high level of sensitivity to the key.

Figure 9.
Bruce Lee image decryption. (a) Decrypted cipher image with different initial conditions; (b) histogram of (a).

Figure 10.
Lena image decryption. (a) Decrypted cipher image with different initial conditions; (b) histogram of (a).
3.2.3. Correlation Analysis of Two Adjacent Pixels
Correlation is a measurement tool for the relationship between two variables or pixels in an image; in fact, adjacent pixels of an original image are highly correlated in the horizontal, vertical, and diagonal directions [11]. Therefore, correlation in a cipher image should be sufficiently low to demonstrate that the proposed encryption algorithm can resist statistical attacks.
In total, 3000 pairs of adjacent pixels in each direction were randomly chosen from a plain image and a cipher image, so the correlation coefficient of each pair could be calculated using the following formulas [9]:
where x and y are gray values of two adjacent pixels in the image. Figure 11 and Figure 12 show the correlation of two adjacent pixels. The high correlation of adjacent pixels from the original image in three different directions can be observed on the left-hand side in Figure 11 and Figure 12; every dot is located linearly along the diagonal, whereas in the cipher image, every point is scattered on the entire plane. Thus, the correlation between adjacent pixels was reduced after applying the encryption process.
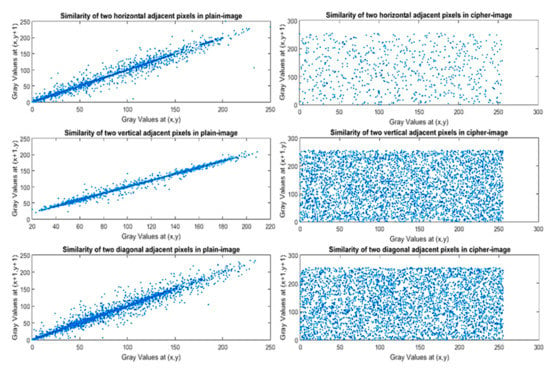
Figure 11.
Correlation of two adjacent pixels in the Lena image.

Figure 12.
Correlation of two adjacent pixels in the Bruce Lee image.
Table 4 indicates the correlation coefficient values. Results showed that the correlation coefficient was very close to zero in the ciphered image, highlighting the fact that the proposed encryption algorithm is secure and that the final result had nonpredictable tendency.

Table 4.
Correlation coefficient values.
Furthermore, we compared our proposed method with other algorithms proposed in the past using the Lena image (256 × 256) as a reference. Table 5 displays the comparison and concludes that the proposed system completely destroyed correlation between pixels. In addition, other larger images were added to the comparison to expand the scope of possibilities regarding the size of an image. Values close to zero showed the current system achieved the main goal in both large and small images.

Table 5.
Comparison results of the correlation coefficient test for the Lena image (256 × 256).
3.2.4. Information Entropy Analysis
Information entropy is the most important measure of randomness. Let m be the source of information; the formula for calculating information entropy can be expressed as follows:
where n is the number of bits that are required to represent symbol mi and p(mi) is the probability of m. The maximum entropy of an 8-bit gray image is equal to 8 when all pixels are equally distributed, which shows that the information is random. If the value is close to 8, it is unlikely for an encrypted image to be decrypted by attackers [11]. Table 6 shows the comparative entropy between the plain and cipher image.

Table 6.
Information-entropy analysis.
Furthermore, comparison results between the proposed method and other algorithms for the Lena image (256 × 256) are illustrated in Table 7. The analysis in Table 7 demonstrates that our algorithm was better than all those presented in the literature since the information entropy analysis results for our method were closest to 8. Large images were also included to demonstrate that the presented method can not only be used with small images but also with large.

Table 7.
Comparison results of information entropy analysis for the Lena image (256 × 256).
4. Conclusions
In this paper, an image data protection algorithm based on a multilevel encryption scheme and automated-selection mechanism was developed to further protect personal and commercial data uploaded to cloud servers for real-time applications, monitoring, and transmission. The main contributions of this paper are summarized as follows: (1) The automated-selection mechanism is crucial for the proposed scheme. The size of the mechanism that chooses the subimage directly affects the system performance and efficiency. Furthermore, thanks to this mechanism, high-resolution images can be easy to cipher, with high-level encryption obtained at the end. The automatic mechanism is also known as the sliding pixel window, which expedites the two-step process, that is, the confusion and diffusion stages. The confusion stage was designed to drastically change data from plain image to cipher image. To help in this stage, pixel conversion from decimal to binary and its vertical and horizontal relocation are performed not only to randomly move bits, but also to change the pixel values when they return to their corresponding decimal values. (2) The diffusion stage was designed to destroy all possible patterns in the sliding pixel window still present after the confusion stage. Two hyperchaotic systems with a logistic map (multilevel scheme) produce pseudorandom numbers to separately conceal the original data of each subplain image in the first- and second-level encryption processes. Security analysis was performed on the final result to demonstrate that the proposed image encryption algorithm makes brute-force attacks infeasible. Another key feature is its high security level. (3) The proposed method can be useful in communication systems, and it can be further improved to be implemented in real time. Different hyperchaotic systems can also be combined and used in the two-stage scheme to improve the encryption algorithm. As future research, a new layer can be added to automatically create suitable initial conditions for correct chaos iteration.
Author Contributions
Conceptualization, S.-Y.L. and C.-S.C.; methodology, S.-Y.L., C.-S.C., M.A.B.H. and L.-M.T.; software, S.-Y.L. and M.A.B.H.; validation, M.A.B.H. and C.-S.C.; formal analysis, S.-Y.L., L.-M.T. and C.-S.C.; investigation, M.A.B.H. and L.-M.T.; resources, S.-Y.L. and L.-M.T.; writing—original draft preparation, M.A.B.H. and S.-Y.L.; writing—review and editing, S.-Y.L., M.A.B.H. and C.-S.C.; visualization, S.-Y.L., M.A.B.H., and L.-M.T.; supervision, S.-Y.L. and C.-S.C.
Funding
This research was funded in part by the Ministry of Science and Technology (MOST 107-2628-E-027- 003-MY3, MOST 108-2221-E-027 -094) and in part by the Institute for Development and Quality, Macao.
Acknowledgments
We deeply appreciate the big support from the Ministry of Science and Technology, National Taipei University of Technology, Taiwan, and the important support from the research team of the Institute for Development and Quality, Macao.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
References
- Li, X.; Meng, X.; Yang, X.; Yin, Y.; Wang, Y.; Peng, X.; He, W.; Dong, G.; Chen, H. Multiple-image encryption based on compressive ghost imaging and coordinate sampling. IEEE Photonics J. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Chen, W. Optical multiple-image encryption using three-dimensional space. IEEE Photonics J. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Yao, S.; Chen, L.; Chang, G.; He, B. A new optical encryption system for image transformation. Opt. Laser Technol. 2017, 97, 234–241. [Google Scholar] [CrossRef]
- Liu, J.; Bai, T.; Shen, X.; Dou, S.; Lin, C.; Cai, J. Parallel encryption for multi-channel images based on an optical joint transform correlator. Opt. Commun. 2017, 396, 174–184. [Google Scholar] [CrossRef]
- Dalhoum, A.; Latif, A.; Mahafzah, B.A.; Awwad, A.A.; Aldhamari, I.; Ortega, A.; Alfonseca, M. Digital image scrambling using 2D cellular automata. IEEE Multimed. 2012, 19, 28–36. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Hei, R.M.H.; Jahan, M.V. Chaos-based image encryption using a hybrid cellular automata and a DNA sequence. In Proceedings of the 2015 International Congress on Technology, Communication and Knowledge (ICTCK) 2015, Mashhad, Iran, 11–12 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 247–252. [Google Scholar]
- Wei, R.; Li, X.; Wang, Q.-H. Double color image encryption scheme based on off-axis holography and maximum length cellular automata. Optik 2017, 145, 407–417. [Google Scholar] [CrossRef]
- Enayatifar, R.; Abdullah, A.H.; Isnin, I.F. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Opt. Lasers Eng. 2014, 56, 83–93. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Zhang, Y.-Q.; Bao, X.-M. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Al-Mashhadi, H.M.; Abduljaleel, I.Q. Color image encryption using chaotic maps, triangular scrambling, with DNA sequences. In Proceedings of the 2017 International Conference on Current Research in Computer Science and Information Technology (ICCIT) 2017, Slemani, Iraq, 26–27 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 93–98. [Google Scholar]
- Liu, H.; Wang, X. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, X.; Han, F. Image encryption algorithm based on hyperchaotic maps and nucleotide sequences database. Comput. Intel. Neurosc. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Hsia, C.H.; Chi, K.Y.; Chen, B.Y. High-quality and high-capacity data hiding based on absolute moment block truncation coding. J. Internet Technol. 2019, 20, 1–10. [Google Scholar]
- Yun-Peng, Z.; Wei, L.; Shui-Ping, C.; Zheng-Jun, Z.; Xuan, N.; Wei-di, D. Digital image encryption algorithm based on chaos and improved DES. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cy bernetics 2009, San Antonio, TX, USA, 11–14 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 474–479. [Google Scholar]
- Gong-bin, Q.; Qing-feng, J.; Shui-sheng, Q. A new image encryption scheme based on DES algorithm and Chua’s circuit. In Proceedings of the 2009 IEEE International Workshop on Imaging Systems and Techniques 2009, Shenzhen, China, 11–12 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 168–172. [Google Scholar]
- Chen, Y.Y.; Hsia, C.H.; Jhong, S.Y.; Lin, H.J. Data hiding method for AMBTC compressed images. J. Ambient Intell. Humanized Comput. 2018, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y. Test and Verification of AES Used for Image Encryption. 3D Res. 2018, 9, 3. [Google Scholar] [CrossRef]
- Dey, S.; Ayyar, S.S.; Subin, S.; Asis, P.A. Sd-ies: An advanced image encryption standard application of different cryptographic modules in a new image encryption system. In Proceedings of the 2013 7th International Conference on Intelligent Systems and Control (ISCO) 2013, Coimbatore, India, 4–5 January 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 285–289. [Google Scholar]
- Zeghid, M.; Machhout, M.; Khriji, L.; Baganne, A.; Tourki, R. A modified AES based algorithm for image encryption. Int. J. Comput. Sci. Eng. 2007, 1, 70–75. [Google Scholar]
- Toughi, S.; Fathi, M.H.; Sekhavat, Y.A. An image encryption scheme based on elliptic curve pseudo random and advanced encryption system. Signal Process. 2017, 141, 217–227. [Google Scholar] [CrossRef]
- Bora, S.; Sen, P.; Pradhan, C. Novel color image encryption technique using Blowfish and Cross Chaos map. In Proceedings of the 2015 International Conference on Communications and Signal Processing (ICCSP) 2015, Melmaruvathur, India, 2–4 April 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 2015, pp. 0879–0883. [Google Scholar]
- Matthews, R. On the derivation of a “chaotic” encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. Int. J. Bifurc. Chaos 1998, 08, 1259–1284. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z.; Fang, J.-A. Image encryption using chaotic coupled map lattices with time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2456–2468. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.-W.; Liao, X.; Chen, G. A new chaos-based fast image encryption algorithm. Appl. Soft Comput. 2011, 11, 514–522. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Liu, H. A new image encryption algorithm based on chaos. Opt. Commun. 2012, 285, 562–566. [Google Scholar] [CrossRef]
- Seyedzadeh, S.M.; Norouzi, B.; Mosavi, M.R.; Mirzakuchaki, S. A novel color image encryption algorithm based on spatial permutation and quantum chaotic map. Nonlinear Dyn. 2015, 81, 511–529. [Google Scholar] [CrossRef]
- Chen, J.-X.; Zhu, Z.-L.; Fu, C.; Yu, H. A fast image encryption scheme with a novel pixel swapping-based confusion approach. Nonlinear Dyn. 2014, 77, 1191–1207. [Google Scholar] [CrossRef]
- Xiao, D.; Liao, X.; Wei, P. Analysis and improvement of a chaos-based image encryption algorithm. Chaos Solitons Fractals 2009, 40, 2191–2199. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. Breaking a novel image encryption scheme based on an improper fractional order chaotic system. Multimed. Tools Appl. 2015, 76, 1817–1826. [Google Scholar] [CrossRef]
- Wang, X.; Guoxiang, H. Cryptanalysis on a novel image encryption method based on total shuffling scheme. Opt. Commun. 2011, 284, 5804–5807. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Color image encryption based on one-time keys and robust chaotic maps. Comput. Math. Appl. 2010, 59, 3320–3327. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, X.-Y. A new image encryption algorithm based on non-adjacent coupled map lattices. Appl. Soft Comput. 2015, 26, 10–20. [Google Scholar] [CrossRef]
- Gao, T.; Chen, Z. A new image encryption algorithm based on hyperchaos. Phys. Lett. A 2008, 372, 394–400. [Google Scholar] [CrossRef]
- Rhouma, R.; Belghith, S. Cryptanalysis of a new image encryption algorithm based on hyperchaos. Phys. Lett. A 2008, 372, 5973–5978. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, L.; Wei, X. A novel image fusion encryption algorithm based on DNA sequence operation and hyperchaotic system. Optik Int. J. Light Electron. Opt. 2013, 124, 3596–3600. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.-L. A novel image encryption algorithm based on genetic recombination and hyperchaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
- Wang, H.Y.; Lin, H.J.; Gao, X.Y.; Cheng, W.H.; Chen, Y.Y. Reversible AMBTC-based data hiding with security improvement by chaotic encryption. IEEE Access 2019, 7, 38337–38347. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An image encryption algorithm based on hyperchaos and dna sequence. Multimed. Tools Appl. 2014, 72, 57–70. [Google Scholar]
- Wang, X.; Qian, W. A fast image encryption algorithm based on only blocks in cipher text. Chin. Phys. B 2014, 23, 030503. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Chen, H. A hyperchaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt. Lasers Eng. 2017, 90, 238–246. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, Y. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt. Lasers Eng. 2015, 66, 10–18. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).