A Reduced-Order Model for the Vibration Analysis of Mistuned Blade–Disc–Shaft Assembly

Abstract

An effective reduced-order model is presented in this paper for the vibration analysis of a mistuned blade–disc–shaft assembly considering the flexibility of the shaft and the rotordynamic effects. For the sake of accurate modeling and quantitative analysis, three-dimensional (3D) finite element models were employed in obtaining the governing equations of motion with the Coriolis force, centrifugal stiffening, and spin softening effects taken into account. Then, an efficient model order reduction technique based on the coordinate projection by normal modes of tuned assembly and cyclic symmetry analysis was developed for mistuned blade–disc–shaft assembly. The criterion of whether one matrix could be incorporated in cyclic symmetry analysis is presented. During the modeling, the mistuning in blade and disc was taken into account and dealt with independently. In mistuning projection, the blade and disc parts were both projected onto their tuned counterparts of the sector model, where the boundary conditions were set to be fixed and free, respectively. Finally, an example of a blade–disc–shaft assembly was employed to validate the effectiveness of the presented method in free and forced vibration analysis.

1. Introduction

Blade–disc–shaft assemblies are the key components of engines and compressors and take an important position in the design of these machines [1]. As the basis for design, developing accurate dynamic models for such assemblies and gaining deep insight into their vibration characteristics are of great significance. For this reason, the vibration issues of blades and rotor systems attracted enormous attention from researchers and engineers, and a huge number of investigations were published in the past few decades [1,2,3,4]. Nevertheless, most of the available investigations concentrated either on the vibration of the blade and disc by neglecting the flexibility of the shaft or on the dynamics of rotor systems by assuming the blade and disc to be rigid and tuned.

Some researchers considered the mutual interactions between bladed discs and shafts and developed several dynamic models for blade–disc–shaft assemblies. Crawley et al. [5] presented a simplified analytical model for rotating a flexible blade-rigid disc-flexible cantilevered shaft system. Okabe et al. [6] addressed an equivalent modeling technique for a blade–shaft system by dividing the system into a shaft plus additional equivalent mass-spring models of blades. Zhang et al. [7] presented a method for dynamic analysis of flexible blade–disc–shaft systems by means of the finite element method and a modal synthesis approach. Huang et al. [8] developed an analytical approach for the coupled shaft torsion and blade bending vibration analysis using the weighted residuals method. Chun et al. [9] proposed an analytical substructure synthesis method for analyzing the coupled free vibrations between shaft and blades. A1-Bedoor [10,11] presented efficient models for coupled shaft-torsional and blade-bending vibration analysis using Lagrange’s equation and the assumed modes method. Ma et al. [12] developed a dynamic model for rotor–blade systems by representing blades as Timoshenko beams and shafts as multiple lumped mass points connected by massless springs. She et al. [13] developed an analytical model for the coupling vibration analysis of a blade–disc–shaft system. In these investigations, the mistuning in blades and discs, which is an inevitable issue due to manufacturing tolerances, material deviations, and in-service wear, tended to be neglected. Regarding this issue, some researchers took mistuning into account. Khader et al. [14] presented a simple analytical model for non-rotating flexible blade-rigid disc-flexible shaft assemblies by representing blade mistuning as frequency deviations. Kim [15] developed a simplistic model for describing the in-plain whirling behavior of a mistuned bladed rotor using complex coordinate transformation and modulation. Li et al. [16] established a dynamic model for a shaft–disc–blade system considering the mistuning in blade length and stagger angle. These investigations provided effective ways for the modeling of blade–disc–shaft assemblies. Nevertheless, the models developed in these investigations were mainly analytical or lumped with, more or less, some simplifications and assumptions. Although such models have the advantages of ease of use, they have limitations in modeling and analysis of complex rotor assemblies, such as those of engines and compressors in practical industrial application.

Three-dimensional (3D) finite element models could overcome these limitations by discretizing the complex assemblies as solid elements, where the detailed geometry can be accurately captured, and the flexibility of all components can be taken into account. Such models were widely employed in the modeling and analysis of bladed discs [17,18,19,20] and complex rotor systems [21,22,23,24]. Nevertheless, the huge number of degrees of freedom (DOFs) in 3D finite element models hinders the computational efficiency in analysis, especially for systems containing random factors, such as mistuning. Hence, a number of model order reduction techniques were developed, including the generalized component mode synthesis methods [25,26,27] and some other effective methods for specific structures, such as the subset of nominal modes (SNM) [28], the fundamental mistuning model (FMM) [29], and the component mode mistuning method (CMM) [30] for mistuned bladed discs. The substructure-based methods are more general approaches for reduced-order modeling. Nevertheless, they are often not that efficient in analyzing mistuned blade discs, as a large number of interface DOFs may be retained, resulting in the model not being concise enough. SNM, FMM, and CMM are more efficient methods, as they were proposed with respect to mistuned bladed discs. In these investigations, however, the shafts were commonly assumed to be rigid and their flexibilities tended to be neglected. For the analysis of mistuned a blade–disc–shaft assembly, the flexibility of the shaft should not be neglected, as it may lead to non-negligible coupling vibration between the shaft and bladed disc. Therefore, an effective model order reduction technique for a mistuned blade–disc–shaft assembly remains to be developed.

In this paper, a reduced-order model for the vibration analysis of mistuned blade–disc–shaft assemblies is presented, where the rotordynamic effects are all taken into account. Firstly, 3D finite element models of blade–disc–shaft assemblies are employed to obtain the governing equations of motion. Then, an efficient model order reduction technique based on the coordinate projection by normal modes of tuned assembly and cyclic symmetry analysis is developed. During the model order reduction, the mistuning in blade and disc is taken into account and dealt with independently. Finally, the effectiveness of the presented method is validated by an example of a blade–disc–shaft assembly. This paper is organized as follows: in Section 2, the governing equations of motion are presented. Section 3 addresses the formulations of model order reduction. Section 4 contains the validation of the presented method. Conclusions are given in Section 5.

2. Equations of Motion

Practical blade–disc–shaft assemblies tend to possess complex geometries, which are hardly modeled by lumped parameter models without several simplifications. Three-dimensional finite element models could accurately describe complex structures without simplifications. As bladed discs tend to be axially symmetric, their governing equations contain periodically time-variant terms if analyzed in inertial frames of reference. Therefore, the rotating frames are employed in this paper. For a 3D finite element model of a mistuned blade–disc–shaft assembly, its governing equation of motion at a constant rotating angular velocity $\mathsf{\Omega }$ has the following general form:

$$M\ddot{u}+\left[C_d+C_c\left(\mathsf{\Omega }\right)\right]\dot{u}+\left[K_e+K_c\left(\mathsf{\Omega }\right)-K_s\left(\mathsf{\Omega }\right)+K_{\delta }\right]u=f,$$

(1)

where $M$, $C_d$, and $K_e$ are the mass, damping, and elastic stiffness matrices of the assembly, $C_c\left(\mathsf{\Omega }\right)$, $K_c\left(\mathsf{\Omega }\right)$, and $K_s\left(\mathsf{\Omega }\right)$ represent the speed-dependent Coriolis, centrifugal stiffening, and spin softening matrices, respectively, $K_{\delta }$ denotes the additional stiffness matrix due to mistuning, $u$ is the vector of response, and $f$ represents the vector of external forces. As the 3D finite element models are employed, the above matrices are obtained via linear assumption. In this paper, the external forces acting on the blades are assumed to be traveling wave excitations, where the forces on the ith blade can be expressed as

$$f_i(t)=B_{0}cos\left(\omega t-{\phi }_i\right),i=1,2,\cdots ,N,$$

(2)

where $B_0$ denotes the forcing amplitude vector, $\omega$ represents the angular frequency of excitation, and $\omega =C\mathsf{\Omega }$, where C is the engine order (EO) of excitation, and ${\phi }_i$ is the interblade phase angle defined as ${\phi }_i=\left(i-1\right)C{\theta }_0$, where ${\theta }_0=2\pi /N$, and N is the number of blades.

3. Reduced-Order Modeling

3.1. Model Order Reduction via Cyclic Symmetry Analysis

Model order reduction techniques are often employed, combined with finite element models, to significantly reduce the computational requirements during analysis. It is much more urgent for mistuned bladed discs, as mistuning is highly random and thousands of mistuning patterns are often needed to study the statistical vibration characteristics. In this paper, the ideas presented in References [28,29,30] are employed and further developed for blade–disc–shaft assemblies. From a general perspective of view, these methods belong to the mode superposition method, whereas the modes used are those of a tuned bladed disc rather than a certain mistuned case. According to these approaches, the normal modes of the tuned blade–disc–shaft assemblies are used as the basis for projecting the mistuned physical model into a modal domain, which can be represented as

$$u={\Phi }_{t}q,$$

(3)

where ${\Phi }_t$ denotes the mode matrix of the tuned assembly in static condition, where the matrices due to rotation are not included during eigenvalue analysis, and $q$ represents the modal coordinate vector. The effectiveness of this coordinate transformation for mistuned blade–disc–shaft assemblies is validated in the next section.

In the vibration analysis of bladed discs, the cyclic symmetry properties are often employed to reduce the computation requirements [31,32]. A tuned blade–disc–shaft assembly is also cyclically symmetric if the shaft is axially symmetric. In the analysis of a rotating blade–disc–shaft assembly, the rotordynamic effects should not be neglected. However, few relative investigations considered these effects. As the rotordynamic matrices are all speed-dependent, the Coriolis matrix is skew-symmetric, and the centrifugal stiffening matrix depends on the stress distributions due to centrifugal forces, whether these matrices can be included in cyclic symmetry analysis should be rigorously verified. It can be proven that one matrix could be incorporated in cyclic symmetry analysis if such a matrix of the sector model has the following relationship with that of its adjacent sector.

$${\stackrel{⌢}{M}}_s={\left[R_s\left({\theta }_0\right)\right]}^{\mathrm{T}}{\stackrel{⌢}{M}}_{s+1}{R}_s\left({\theta }_0\right),$$

(4)

where ${\stackrel{⌢}{M}}_s$ and ${\stackrel{⌢}{M}}_{s+1}$ denote the matrices of sth and (s + 1)th sectors, respectively, and $R_s\left({\theta }_0\right)$ represents a rotation transformation matrix in term of the sector angle.

$$R_s\left({\theta }_0\right)=I_{N_n}\otimes R_e\left({\theta }_0\right),$$

(5)

where $I_{N_n}$ denotes an identity matrix of dimensions $N_n$, where $N_n$ is the number of nodes in a sector model, the symbol $\otimes$ denotes the Kronecker product, and $R_e\left({\theta }_0\right)$ is an elementary matrix. Taking the rotation axial along the z-axis as an example, $R_e\left({\theta }_0\right)$ can be expressed as

$$R_e\left({\theta }_0\right)=\left[\begin{array}{ccc}\cos {\theta }_0& \sin {\theta }_0& 0\\ -\sin {\theta }_0& \cos {\theta }_0& 0\\ 0& 0& 1\end{array}\right].$$

(6)

Detailed proof of this proposition, for brevity, is presented in Appendix A. According to the explanation in Appendix A, the Coriolis, centrifugal stiffening, and spin softening matrices can all be incorporated in cyclic symmetry analysis. In this circumstance, the mode matrix ${\Phi }_t$ represented in terms of cyclically symmetric modes can be used as the projecting basis during model order reduction. Then, ${\Phi }_t$ can be explicitly expressed as

$${\Phi }_t=\left(E\otimes I_{N_s}\right)\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{\Phi }}_h^s\right),$$

(7)

where $E$ denotes the complex Fourier matrix with $e_{mn}=e^{j(m-1)(n-1){\theta }_0}/\sqrt{N}$ for $m,n=1,2,\cdots ,N$, $I_{N_s}$ denotes an identity matrix, ${\tilde{\Phi }}_h^s$ is the mode matrix of hth nodal diameter (ND), and $\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{\Phi }}_h^s\right)$ denotes a pseudo-block diagonal matrix with ${\tilde{\Phi }}_h^s$ in its diagonal. Then, the governing equation in Equation (1) can be reduced by using the coordinate transformation in Equation (3) as

$$\tilde{M}\ddot{q}+\left[{\tilde{C}}_d+{\tilde{C}}_c\left(\mathsf{\Omega }\right)\right]\dot{q}+\left[{\tilde{K}}_e+{\tilde{K}}_c\left(\mathsf{\Omega }\right)-{\tilde{K}}_s\left(\mathsf{\Omega }\right)+{\tilde{K}}_{\delta }\right]q=\tilde{f},$$

(8)

where

$$\begin{array}{l}\tilde{M}=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}{\tilde{M}}^h{\tilde{\Phi }}_h^s\right]\\ {\tilde{C}}_d=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}{\tilde{C}}_d^h{\tilde{\Phi }}_h^s\right]\\ {\tilde{C}}_c=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}{\tilde{C}}_c^h{\tilde{\Phi }}_h^s\right]\\ {\tilde{K}}_e=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}{\tilde{K}}_e^h{\tilde{\Phi }}_h^s\right]\\ {\tilde{K}}_c=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}{\tilde{K}}_c^h{\tilde{\Phi }}_h^s\right]\\ {\tilde{K}}_s=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}{\tilde{K}}_s^h{\tilde{\Phi }}_h^s\right]\\ \tilde{f}=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[{\left({\tilde{\Phi }}_h^s\right)}^{\mathrm{T}}\right]\left(E^{\ast }\otimes I_{N_s}\right)f\end{array},$$

(9)

where

$$\begin{array}{l}{\tilde{M}}^h={\tilde{M}}_2{e}^{j(h-1){\theta }_0}+{\tilde{M}}_1+{\tilde{M}}_3{e}^{-j(h-1){\theta }_0}\\ {\tilde{C}}_d^h={\tilde{C}}_{d,2}{e}^{j(h-1){\theta }_0}+{\tilde{C}}_{d,1}+{\tilde{C}}_{d,3}{e}^{-j(h-1){\theta }_0}\\ {\tilde{C}}_c^h={\tilde{C}}_{c,2}{e}^{j(h-1){\theta }_0}+{\tilde{C}}_{c,1}+{\tilde{C}}_{c,3}{e}^{-j(h-1){\theta }_0}\\ {\tilde{K}}_e^h={\tilde{K}}_{e,2}{e}^{j(h-1){\theta }_0}+{\tilde{K}}_{e,1}+{\tilde{K}}_{e,3}{e}^{-j(h-1){\theta }_0}\\ {\tilde{K}}_c^h={\tilde{K}}_{c,2}{e}^{j(h-1){\theta }_0}+{\tilde{K}}_{c,1}+{\tilde{K}}_{c,3}{e}^{-j(h-1){\theta }_0}\\ {\tilde{K}}_s^h={\tilde{K}}_{s,2}{e}^{j(h-1){\theta }_0}+{\tilde{K}}_{s,1}+{\tilde{K}}_{s,3}{e}^{-j(h-1){\theta }_0}\end{array},$$

(10)

where the subscripts of “1”, “2” and “3” in the above matrices represent the terms in the corresponding block-circulated matrices in Equation (A10) shown in Appendix A.

The reduced-order mistuning matrix ${\tilde{K}}_{\delta }$ is also generated via the coordinate transformation in Equation (3), giving

$${\tilde{K}}_{\delta }={\left({\Phi }_t\right)}^{\mathrm{T}}{K}_{\delta }{\Phi }_t.$$

(11)

In most available investigations, only the mistuning in blades was taken into account. This may partly have been because the blade tends to be more flexible and less structurally coupled than the disc. Actually, mistuning in discs is also inevitable due to manufacturing tolerances and deteriorations during operation. The mistuning in discs may not play that significant a role as blades in the vibration of bladed discs. Nevertheless, it may be non-negligible for blade–disc–shaft assemblies, as the flexibilities in the shaft may lead to significant coupling motions between the shaft and disc. Therefore, the mistuning in blades and discs is considered and dealt with independently in this paper. Then, ${\tilde{K}}_{\delta }$ can be further expanded, without loss in accuracy, into blade and disc parts as

$${\tilde{K}}_{\delta }={\left({\Phi }_t^b\right)}^{\mathrm{T}}{K}_{\delta }^b{\Phi }_t^b+{\left({\Phi }_t^d\right)}^{\mathrm{T}}{K}_{\delta }^d{\Phi }_t^d={\tilde{K}}_{\delta }^b+{\tilde{K}}_{\delta }^d,$$

(12)

where ${\Phi }_t^b$ and ${\Phi }_t^d$ denote the mode matrices corresponding to the blade and the disc parts, respectively, and $K_{\delta }^b$ and $K_{\delta }^d$ represent the corresponding mistuning matrices of the two parts. Despite the simple expressions, ${\tilde{K}}_{\delta }^b$ and ${\tilde{K}}_{\delta }^d$ are difficult to determine, as the mistuning matrices $K_{\delta }^b$ and $K_{\delta }^d$ of a realistic bladed disc are highly random and difficult to measure. For this reason, frequency mistuning models were more often employed in available investigations for mistuning quantization. In this paper, such a model is also used. Detailed deductions on obtaining the reduced-order mistuning matrices ${\tilde{K}}_{\delta }^b$ and ${\tilde{K}}_{\delta }^d$ are presented in the sections below.

3.2. Parametric Projection of Blade Mistuning

The mistuning projection method proposed by Lim et al. [30] is employed in this section to include blade mistuning in the reduced-order model. The core idea of this method is to project the mistuning matrix onto the normal modes of a tuned blade cantilevered at its root. The main procedures of this method are briefly reviewed herein. Firstly, the blade part mode ${\Phi }_t^b$ is represented by cyclically symmetric modes as shown in Equation (7).

$${\Phi }_t^b=\left(E\otimes I_{N_b}\right)\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{\Phi }}_h^b\right),$$

(13)

where ${\tilde{\Phi }}_h^b$ denotes the blade part of ${\tilde{\Phi }}_h^s$, and $I_{N_b}$ is an identity matrix of dimensions $N_b$, where $N_b$ denotes the number of DOFs in a sector model of blade.

Then, the blade part’s cyclically symmetric modes are represented by the normal modes of the tuned blade cantilevered at its root.

$${\tilde{\Phi }}_h^b={\Phi }_{fix}^b{\tilde{p}}_h^b,$$

(14)

where ${\Phi }_{fix}^b$ is the normal mode matrix of the tuned cantilevered blade, and ${\tilde{p}}_h^b$ denotes the participation factor. By the above transformation, ${\Phi }_t^b=\left(I_N\otimes {\Phi }_{fix}^b\right){\tilde{p}}^b$, where ${\tilde{p}}^b=\left(E\otimes I_{N_b}\right)\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{p}}_h^b\right)$. As the blades are not directly coupled, $K_{\delta }^b$ has a block-diagonal form as $K_{\delta }^b=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left(K_{\delta ,h}^b\right)$. Then, the blade part’s reduced-order mistuning matrices ${\tilde{K}}_{\delta }^b$ can be expressed as

$${\tilde{K}}_{\delta }^b={\left({\tilde{p}}^b\right)}^{\mathrm{T}}\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{K}}_{\delta ,h}^b\right){\tilde{p}}^b,$$

(15)

where ${\tilde{K}}_{\delta ,h}^b={\left({\Phi }_{fix}^b\right)}^{\mathrm{T}}{K}_{\delta ,h}^b{\Phi }_{fix}^b$. As ${\tilde{K}}_{\delta ,h}^b$ tends not to be diagonal, it is often approximately processed in frequency mistuning models by keeping only the diagonal elements, which can be represented as

$${\tilde{K}}_{\delta ,h}^b\approx \underset{m=1,2,\cdots ,M}{\mathrm{diag}}\left({\delta }_{h,m}^b{\lambda }_m^b\right),$$

(16)

where M is the number of retained modes of the tuned cantilevered blade, ${\lambda }_m^b$ represents the mth eigenvalue of the tuned cantilevered blade, and ${\delta }_{h,m}^b$ denotes the deviation ratio, which is often set to be a random parameter during analysis.

3.3. Parametric Projection of Disc Mistuning

Unlike the projection of blade mistuning, the coordinates between adjacent sectors of the disc are directly coupled, and the disc mistuning matrix cannot be expressed in block-diagonal form. Therefore, the mistuning projection method in the previous section cannot be directly employed. Nevertheless, the idea of representing the overall modes by normal modes of a relatively simple component and projecting the mistuning matrix onto these normal modes can be utilized. Of course, some modifications to the formulations are needed to account for the coupling issue of the disc model.

Firstly, the disc part mode ${\Phi }_t^d$ is represented by cyclically symmetric modes.

$${\Phi }_t^d=\left(E\otimes I_{N_d}\right)\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{\Phi }}_h^d\right),$$

(17)

where ${\tilde{\Phi }}_h^d$ denotes the disc part of ${\tilde{\Phi }}_h^s$, and $I_{N_d}$ is an identity matrix of dimensions $N_d$, where $N_d$ is the number of DOFs in a sector model of the disc with the left cyclic symmetry surface eliminated.

As mentioned above, the mistuning matrices of adjacent sectors of the disc are crossed and coupled. Proper processes are needed to make the matrix block-diagonal. It can be found that adjacent sector models can be made independent in form by coordinate expansion, where the original and expanded coordinates with respect to the disc model are expressed as

$$u_t^d=\left[\begin{array}{c}{u}_1^d\\ u_2^d\\ ⋮\\ u_s^d\\ ⋮\\ u_N^d\end{array}\right],u_s^d=\left\{\begin{array}{c}{u}_{s,R}^d\\ u_{s,I}^d\end{array}\right\},{\widehat{u}}_t^d=\left[\begin{array}{c}{\widehat{u}}_1^d\\ {\widehat{u}}_2^d\\ ⋮\\ {\widehat{u}}_s^d\\ ⋮\\ {\widehat{u}}_N^d\end{array}\right],{\widehat{u}}_s^d=\left\{\begin{array}{c}{\widehat{u}}_{s,R}^d\\ {\widehat{u}}_{s,I}^d\\ {\widehat{u}}_{s,L}^d\end{array}\right\},$$

(18)

where $u_t^d$ denotes the original coordinate vector with respect to ${\Phi }_t^d$, ${\widehat{u}}_t^d$ is the expanded coordinate, and the subscript “R”, “L” and “I” denote the right and left cyclic boundary DOFs and internal DOFs, respectively. It can also be proven that the disc mistuning matrix $K_{\delta }^d$ can be obtained using an expanded block-diagonal matrix ${\widehat{K}}_{\delta }^d=\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\widehat{K}}_{\delta ,h}^d\right)$, with

$${\tilde{K}}_{\delta }^d={\left({\Phi }_t^d\right)}^{\mathrm{T}}{K}_{\delta }^d{\Phi }_t^d={\left({\widehat{\Phi }}_t^d\right)}^{\mathrm{T}}{\widehat{K}}_{\delta }^d{\widehat{\Phi }}_t^d,$$

(19)

where ${\widehat{\Phi }}_t^d$ denotes the expanded modes with respect to ${\Phi }_t^d$. Detailed deductions on this proposition are presented, for brevity, in Appendix B. Similar to the expression of ${\Phi }_t^d$ in Equation (17), the expanded modes ${\widehat{\Phi }}_t^d$ with respect to ${\widehat{u}}_t^d$ can also be expressed by cyclically symmetric modes.

$${\widehat{\Phi }}_t^d=\left(E\otimes I_{N_d}\right)\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\widehat{\tilde{\Phi }}}_h^d\right),$$

(20)

where ${\widehat{\tilde{\Phi }}}_h^d$ denotes the expanded cyclic modes of ${\tilde{\Phi }}_h^d$, and

$${\tilde{\Phi }}_h^d=\left\{\begin{array}{c}{\tilde{\Phi }}_{h,R}^d\\ {\tilde{\Phi }}_{h,I}^d\end{array}\right\},{\widehat{\tilde{\Phi }}}_h^d=\left\{\begin{array}{c}{\tilde{\Phi }}_{h,R}^d\\ {\tilde{\Phi }}_{h,I}^d\\ {\tilde{\Phi }}_{h,L}^d\end{array}\right\},$$

(21)

where ${\tilde{\Phi }}_{h,L}^d$ is a matrix dependent on ${\tilde{\Phi }}_{h,R}^d$; for hND modes,

$${\tilde{\Phi }}_{h,L}^d=e^{j(h-1){\theta }_0}{R}_d\left({\theta }_0\right){\tilde{\Phi }}_{h,R}^d,$$

(22)

where $R_d\left({\theta }_0\right)$ denotes a rotation transformation matrix, and $R_d\left({\theta }_0\right)=I_{cd}\otimes R_e\left({\theta }_0\right)$, where $I_{cd}$ is an identity matrix of dimensions $N_{cd}$, and $N_{cd}$ is the number of nodes on cyclic symmetry interface.

Then, similar to that shown in Equation (14), the expanded cyclic modes ${\widehat{\tilde{\Phi }}}_h^d$ are represented by the normal modes of the disc component.

$${\widehat{\tilde{\Phi }}}_h^d={\Phi }_{fre}^d{\tilde{p}}_h^d,$$

(23)

where ${\Phi }_{fre}^d$ denotes the normal mode matrix of a tuned sector model of the disc with the left and right interfaces, as well as the adjacent interface between the disc and shaft, being set to be free, and ${\tilde{p}}_h^d$ denotes the participation factor. Herein, the free constraint is employed on the disc–shaft adjacent interface instead of a fixed one, because the latter one may not accurately describe the 1ND coupling modes between shaft and disc, leading to non-negligible errors in forced responses. The employment of free modes avoids such issues and presents satisfactory results in both frequencies and forced responses.

By substituting Equation (22) into the expression of ${\tilde{K}}_{\delta }^d$ and neglecting the non-diagonal terms, the disc part’s reduced-order mistuning matrices ${\tilde{K}}_{\delta }^d$ can be expressed as

$${\tilde{K}}_{\delta }^d\approx {\left({\tilde{p}}^d\right)}^{\mathrm{T}}\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left[\underset{w=1,2,\cdots ,W}{\mathrm{diag}}\left({\delta }_{h,w}^d{\lambda }_w^d\right)\right]{\tilde{p}}^d,$$

(24)

where ${\tilde{p}}^d=\left(E\otimes I_{N_d}\right)\underset{h=1,2,\cdots ,N}{\mathrm{Bdiag}}\left({\tilde{p}}_h^d\right)$, W is the number of retained modes of the disc component, ${\delta }_{h,w}^d$ is the deviation ratio, and ${\lambda }_w^d$ denotes the wth eigenvalue of the tuned disc component.

On this basis, the free and forced vibration of tuned and mistuned blade–disc–shaft assemblies can be analyzed by using the governing equation of motion in Equation (8) and the coordinate transformation in Equation (3). As the mistuning in blade and disc is taken into account, the effects of blade and disc mistuning on the vibration characteristics of blade–disc–shaft assemblies can be investigated.

4. Validation of Reduced-Order Models

Validation of the developed order reduction method is presented in this section. As the accuracy of the reduced-order model in vibration analysis for practical structures relies on the accuracy of its counterpart full-order model, the effectiveness of the developed method can be verified by comparing the results of the reduced-order model with those of the full order model.

Figure 1 illustrates the finite element model of a blade–disc–shaft assembly, which is used as an example in this section, where the DOFs of the whole model and the sector model are equal to 103,563 and 7179, respectively. The whole model contains 18 sectors. The reduced-order model contains 216 DOFs with 12 modes per ND. During the projection of blade and disc mistuning, the retained modes of the cantilevered blade and free disc are 20 and 50, respectively. The excitation is applied at the tip of the blades with an amplitude of 2 N. The structural damping is assumed to be Rayleigh damping and $C_d=\beta K_e$, where $\beta$ is set to 3 × 10⁻⁶ in the subsequent analysis. The material of the blade and disc is titanium alloy, and that of the shaft is steel, where the properties of these materials are listed in Table 1.

Figure 1. The finite element model of a blade–disc–shaft assembly and its sector model.

Table 1. Material properties of the blade, disc, and shaft.

Properties	Blade and Disc	Shaft
Density	7850 kg/m3	4420 kg/m3
Poisson’s ratio	0.3	0.31
Young’s modulus	210 GPa	210 GPa

Generally, the mistuning in the blade and disc is random and hard to measure. Herein, a simpler mistuning model, the commonly used proportional mistuning model, is used to validate the developed method. Small random variations in Young’s modulus are introduced as

$$\{\begin{array}{l}{E}_n^b=\left(1+{\delta }_n^b\right)E_0\\ E_n^d=\left(1+{\delta }_n^d\right)E_0\end{array},n=1,2,\cdots ,N,$$

(25)

where $E_n^b$ and $E_n^d$ denote the Young’s modulus of the nth sector models of the blade and disc, $E_0$ represents the nominal Young’s modulus, and ${\delta }_n^b$ and ${\delta }_n^d$ are random variables representing the small variations. Specifically, the employed proportional mistuning patterns of the blade and disc in the subsequent analysis are listed in Table 2.

Table 2. The mistuning parameters of the blade and disc.

Blade	${\mathit{\delta }}_{\mathit{n}}^{\mathit{b}}(\%)$	Disc Sector	${\mathit{\delta }}_{\mathit{n}}^{\mathit{d}}(\%)$
1	1.351	1	0.675
2	−2.342	2	−0.632
3	1.070	3	1.561
4	1.246	4	−1.614
5	−1.553	5	−0.211
6	1.763	6	−0.412
7	1.447	7	0.921
8	1.009	8	1.026
9	−0.377	9	−1.088
10	−0.070	10	−0.035
11	−2.1667	11	−0.184
12	2.053	12	0.509
13	1.842	13	0.728
14	−0.825	14	0.886
15	−0.421	15	−0.772
16	−3.228	16	0.623
17	3.123	17	0.535
18	−1.272	18	−1.167

Figure 2 illustrates the natural frequencies versus nodal diameters of the tuned blade–disc–shaft assembly in a static condition. Some of the 0ND and 1ND modes are shaft-dominated and not involved in the lines. With this diagram, the excited modes can be easily obtained by comparing the exciting frequency and the natural frequencies.

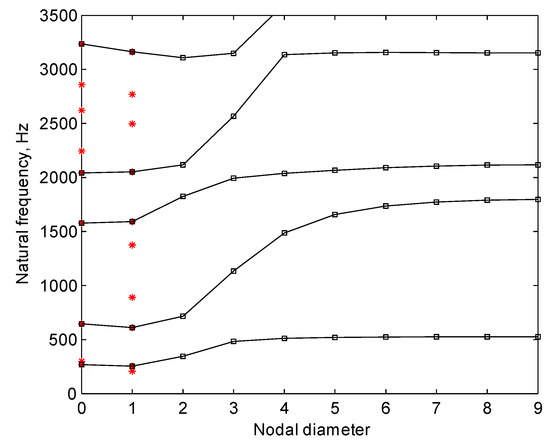
Figure 2. Natural frequencies versus nodal diameters of the tuned blade–disc–shaft assembly in a static condition.

Figure 3 shows the comparisons of the forced responses of the mistuned blade–disc–shaft assembly using the normal modes of the mistuned case and those of its tuned counterpart. The presented results are the responses of the excitation nodes, which are located at the tip of each blade. In the subsequent analysis, the results of these nodes are also employed. It can be seen in the figures that the results agree very well. The maximum relative error in amplitude is less than 0.1%. Therefore, the normal modes of the tuned blade–disc–shaft assembly can accurately represent the modes of mistuned assembly.

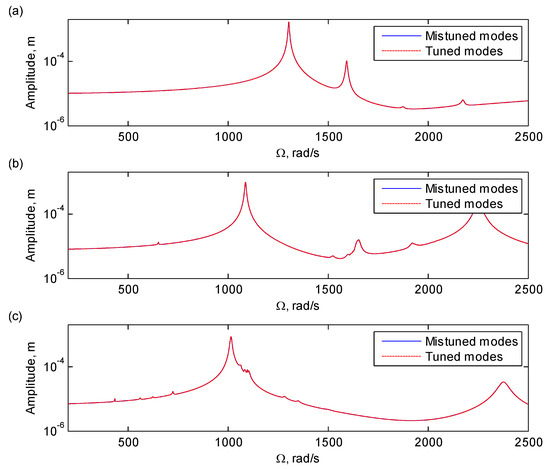
Figure 3. Comparisons of the forced responses of the excitation nodes of the assembly using the normal modes of the mistuned case and those of its tuned counterpart with excitations of (a) one engine order (1EO), (b) 2EO, and (c) 3EO.

Figure 4 shows the comparisons of the first 100 natural frequencies of the tuned assembly using the full-order model and cyclic symmetric sector model. It can be seen in the figure that the two cases agree well, with the maximum relative error in natural frequency being less than 0.01%. Therefore, cyclic symmetry analysis is also feasible for bladed discs mounted on flexible shafts.

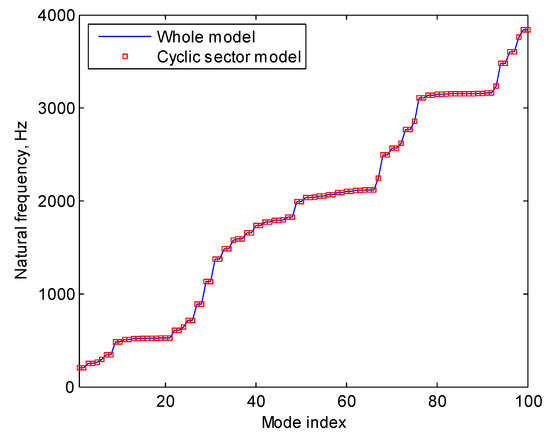
Figure 4. Comparisons on the first 100 natural frequencies of the tuned blade–disc–shaft assembly using the full-order model and cyclic symmetry sector model.

Figure 5 shows the relative errors in eigenvalues of the reduced-order model at different rotating speeds, where the first 20 are included and the mistuning in the blade and disc is considered. It can be seen in the figure that the relative error grows with rotating speed but within a relatively small range. Although the relative errors increase for higher-order eigenvalues, the overall maximum relative error is still less than 0.1% when the rotating speed is less than 2000 rad/s. Thus, the presented model order reduction technique can give accurate results in eigenvalues for a mistuned blade–disc–shaft assembly in spite of the significant reduction in model order.

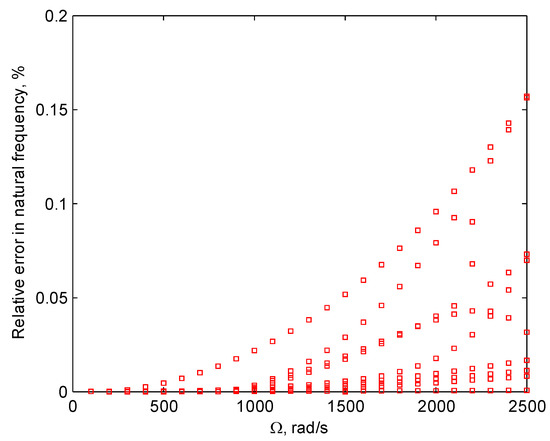
Figure 5. The relative errors in eigenvalues of the reduced-order model of a mistuned blade–disc–shaft assembly at different rotating speeds.

Figure 6 and Figure 7 illustrate the comparisons of forced responses of the assembly between the full-order model (FOM) and reduced-order model (ROM) with mistuning in the blade and disc, respectively, where the 1EO, 2EO, and 3EO excitations are presented. As can be seen in the figures, for both cases of blade and disc mistuning, the two models give quite similar results in the entire speed range with different EOs of excitations. Thus, it can be concluded that the reduced-order model can give quite accurate results in forced responses compared with those of the full-order model.

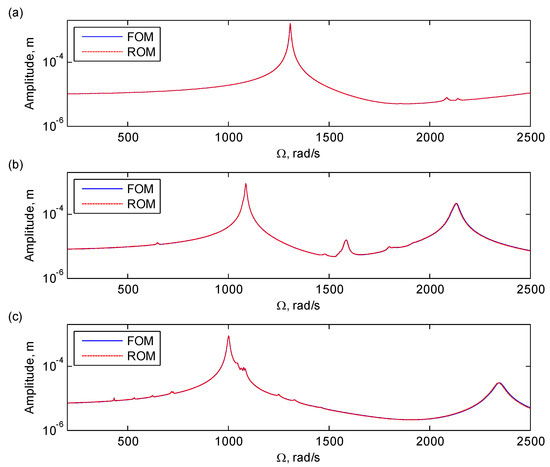
Figure 6. Comparisons of the forced responses of the excitation nodes of the assembly with blade mistuning between the full-order model and reduced-order model with excitations of (a) 1EO, (b) 2EO, and (c) 3EO. The full- and reduced-order models contain 103,563 and 7179 degrees of freedom (DOFs), respectively.

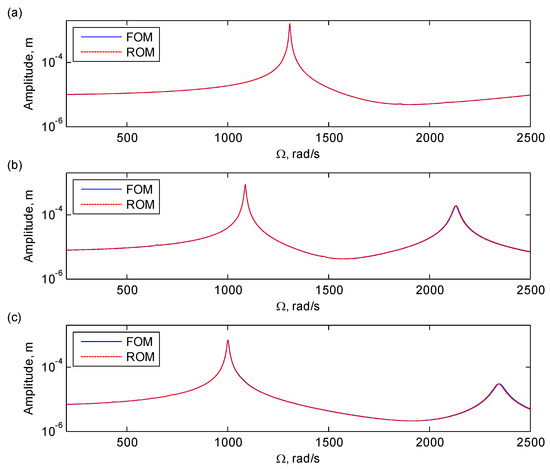
Figure 7. Comparisons of the forced responses of the excitation nodes of the assembly with disc mistuning between the full-order model and reduced-order model with excitations of (a) 1EO, (b) 2EO, and (c) 3EO. The full- and reduced-order models contain 103,563 and 7179 DOFs, respectively.

In order to illustrate the efficiency of the presented method, the computational time of the reduced-order model in computing natural frequencies and forced responses is compared with that of the full-order model, which is listed in Table 3. The specifications of the employed computer during the analysis were as follows: Intel Core i7-8700 central processing unit (CPU) with 3.20 GHz; size and speed of the cache memory = 32 GB and 2666 MHz, respectively; size of the solid-state drive (SSD) hard disk = 512 GB. The presented values are all the averages of 100 analysis cases. It can be seen that the presented model order reduction technique could significantly increase the computational efficiency.

Table 3. Comparison on the computational efficiency between full-order model (FOM) and reduced-order model (ROM).

Analysis Type	FOM (s)	ROM (s)	Ratio
First 100 natural frequencies	31.79	0.135	235
Forced response at a rotating speed	8.94	0.00895	999

Based on the results presented in this section, the effectiveness and efficiency of the presented method can be validated. With this method, the coupling vibrations between bladed disc and shaft, as well as the effects of the shaft’s flexibility on the vibration of a mistuned bladed disc, can be studied. Nevertheless, these issues are not the focus of this paper and can be addressed in further studies.

5. Conclusions

In this paper, an effective reduced-order model was presented for the vibration analysis of a mistuned blade–disc–shaft assembly. Three-dimensional finite element models, which can provide accurate modeling and quantitative analysis for complex structures, were introduced to obtain the governing equations of motion, where the Coriolis force, centrifugal stiffening, and spin softening effects due to rotation were all taken into account. An efficient model order reduction technique, based on the coordinate projection by normal modes of tuned assembly and cyclic symmetry analysis, was developed for a mistuned blade–disc–shaft assembly. As the basis for employing cyclic symmetry analysis, the criterion of whether one matrix could be incorporated in the analysis, as well as rigorous proof, was given. It was shown that the Coriolis, centrifugal stiffening, and spin softening matrices satisfy this criterion and can be converted into block-circulated forms in cyclically symmetric coordinates. In the presented model order reduction method, the mistuning in the blade and disc was taken into account and dealt with independently to reflect the realistic conditions of blade–disc–shaft assemblies. Regarding the coupling issue of the disc mistuning matrix, an effective mistuning projection approach was developed by using coordinate expansion and projecting the mistuning matrix onto a free tuned sector model of the disc. Detailed deductions on the theoretical basis of coordinate expansion were presented. The employed example of a blade–disc–shaft assembly illustrates the effectiveness of the presented method in free and forced vibration analysis in both static and rotating conditions.

As cyclic symmetry analysis was employed in this paper, the presented method required the rotating systems to be cyclically symmetric. In some circumstances, such requirements may not be satisfied due to the anisotropy in supports, such as the anisotropy in bearings and foundations, which may lead to periodically time-variant terms and more complicated vibration characteristics. Then, further development of this method should be done, which was not included in this paper and remains to be conducted in the future.