Mixed-Mode Delamination Growth Prediction in Stiffened CFRP Panels by Means of a Novel Fast Procedure
Abstract
1. Introduction
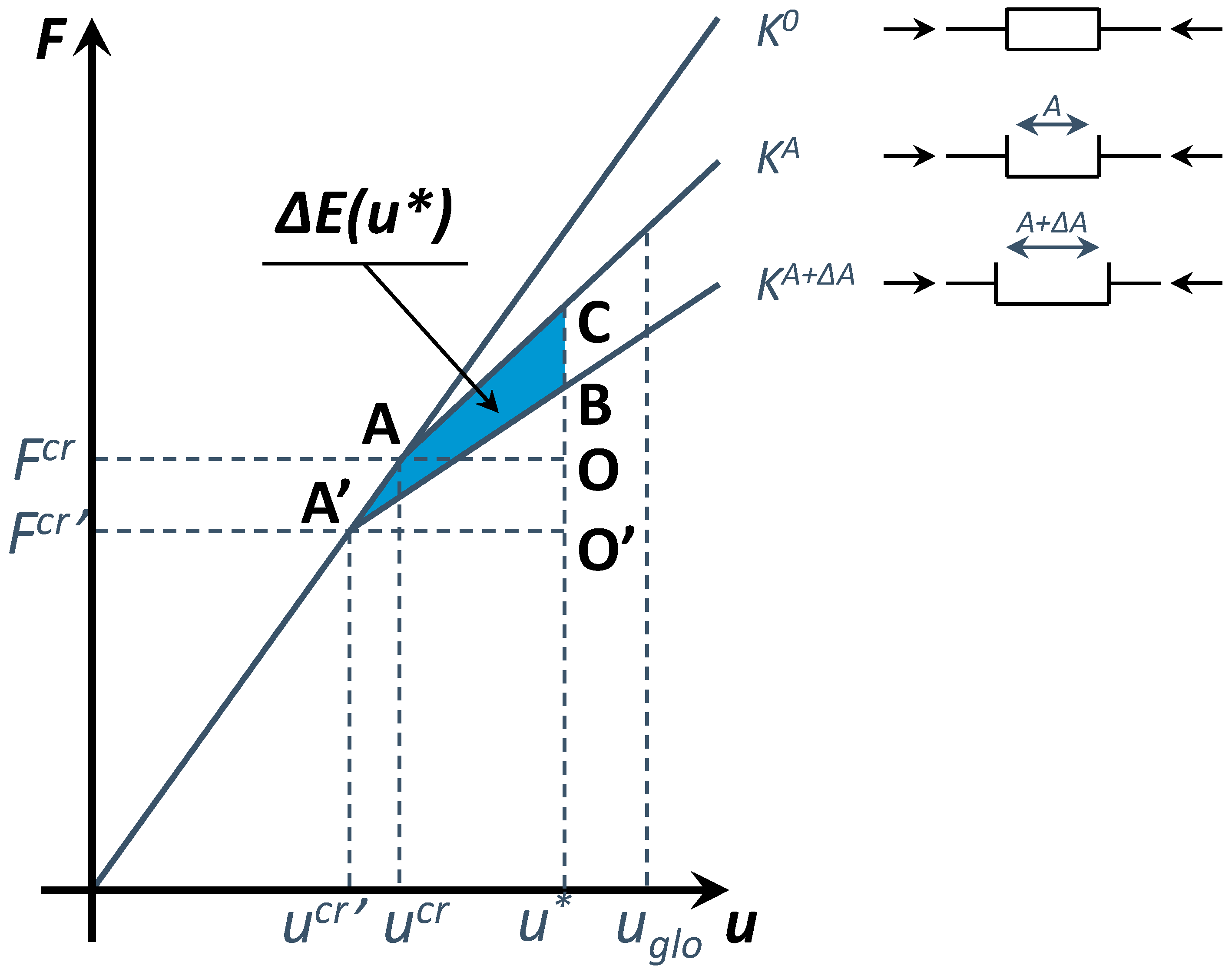
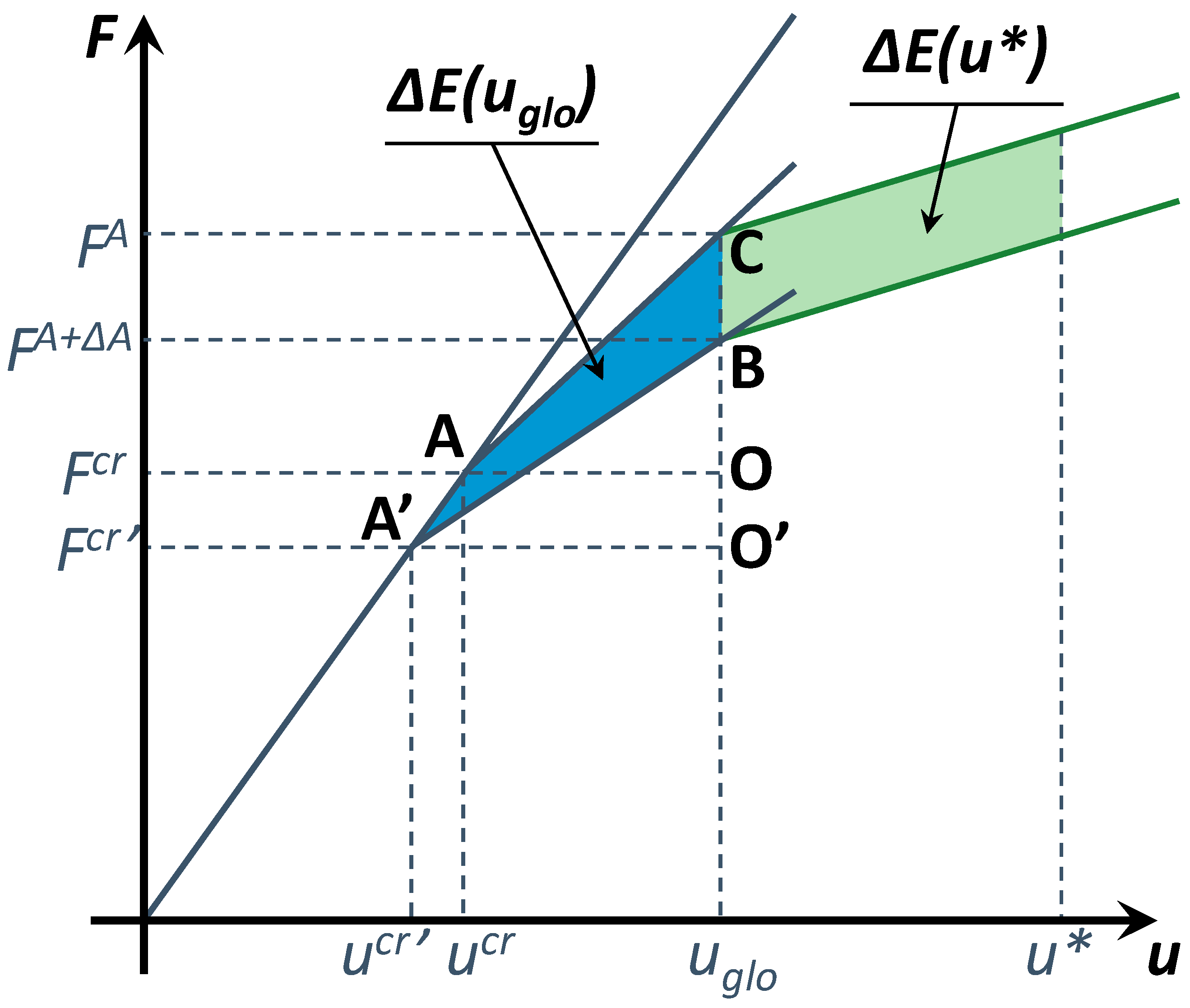
2. Theoretical Background
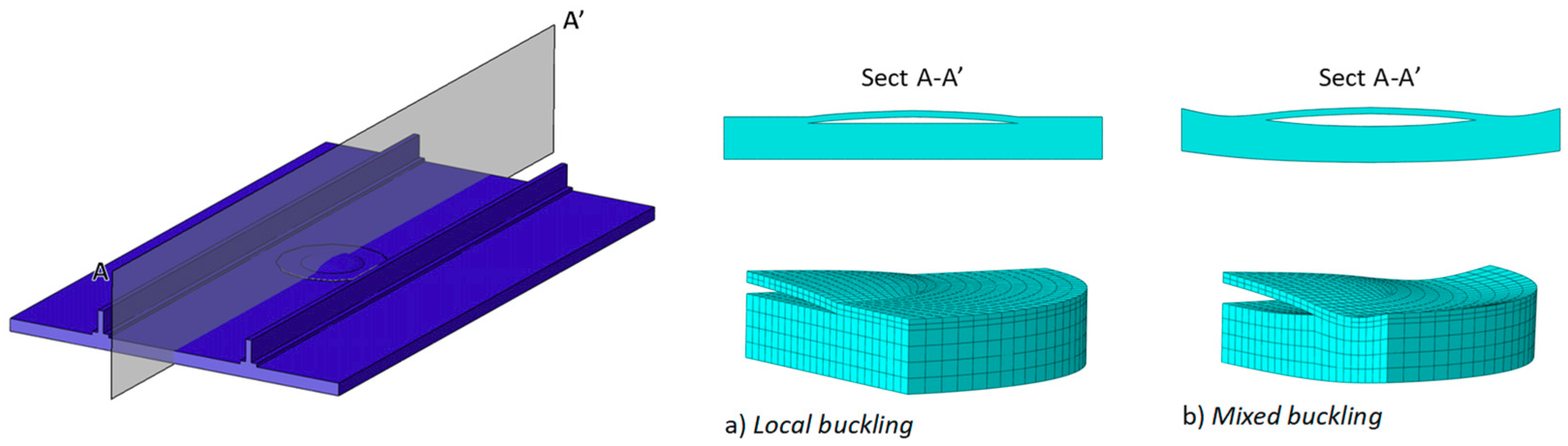
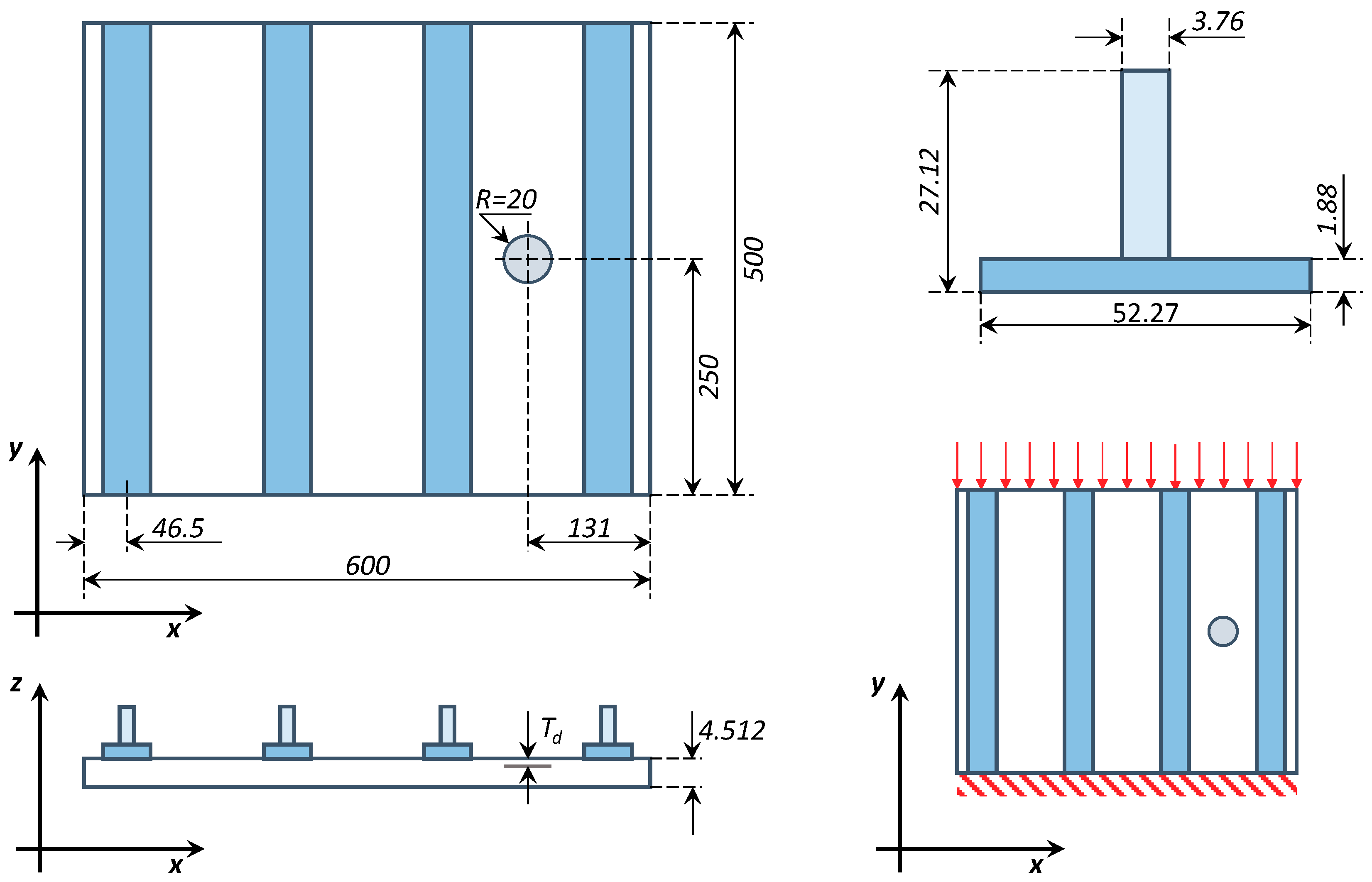
3. Numerical Applications and Discussion
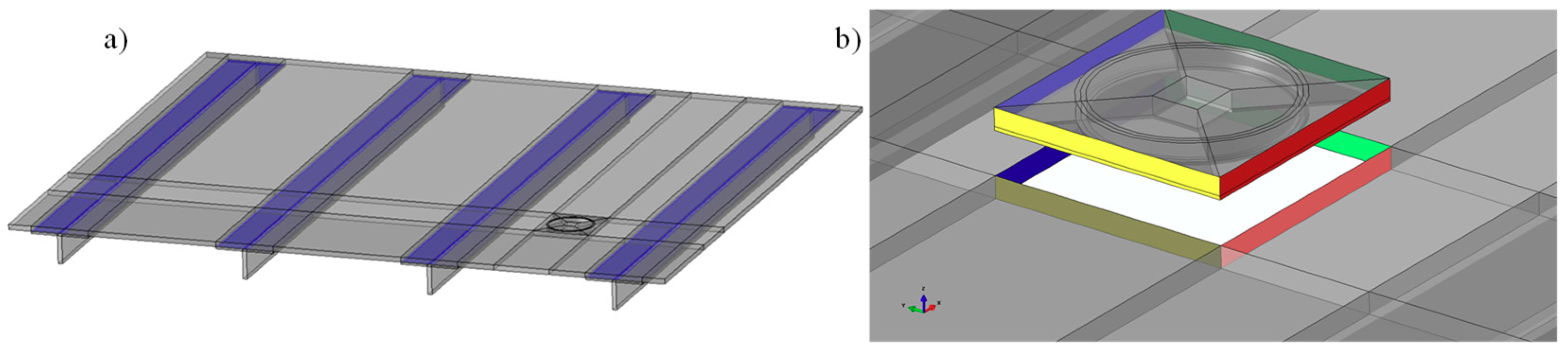
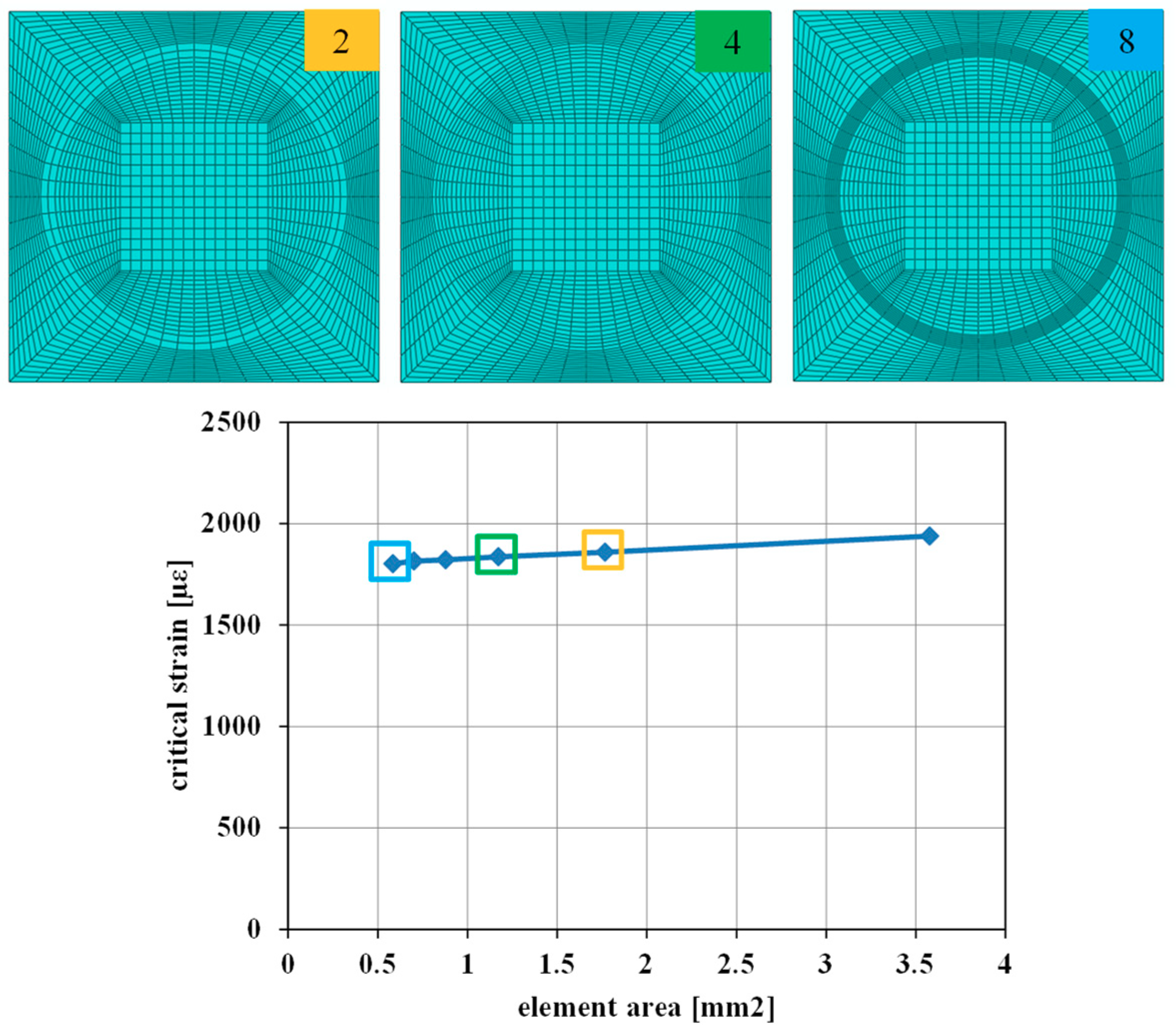
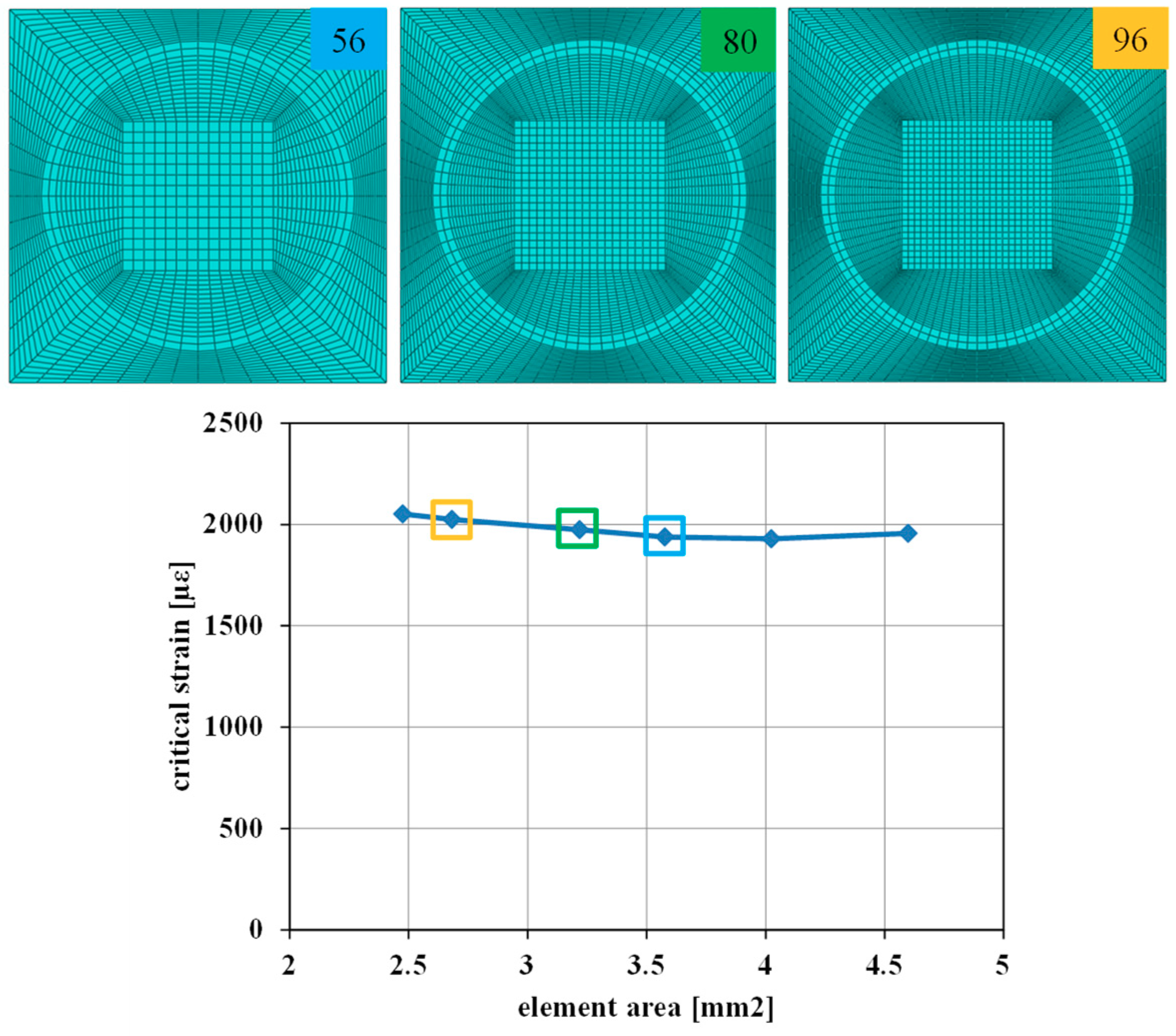
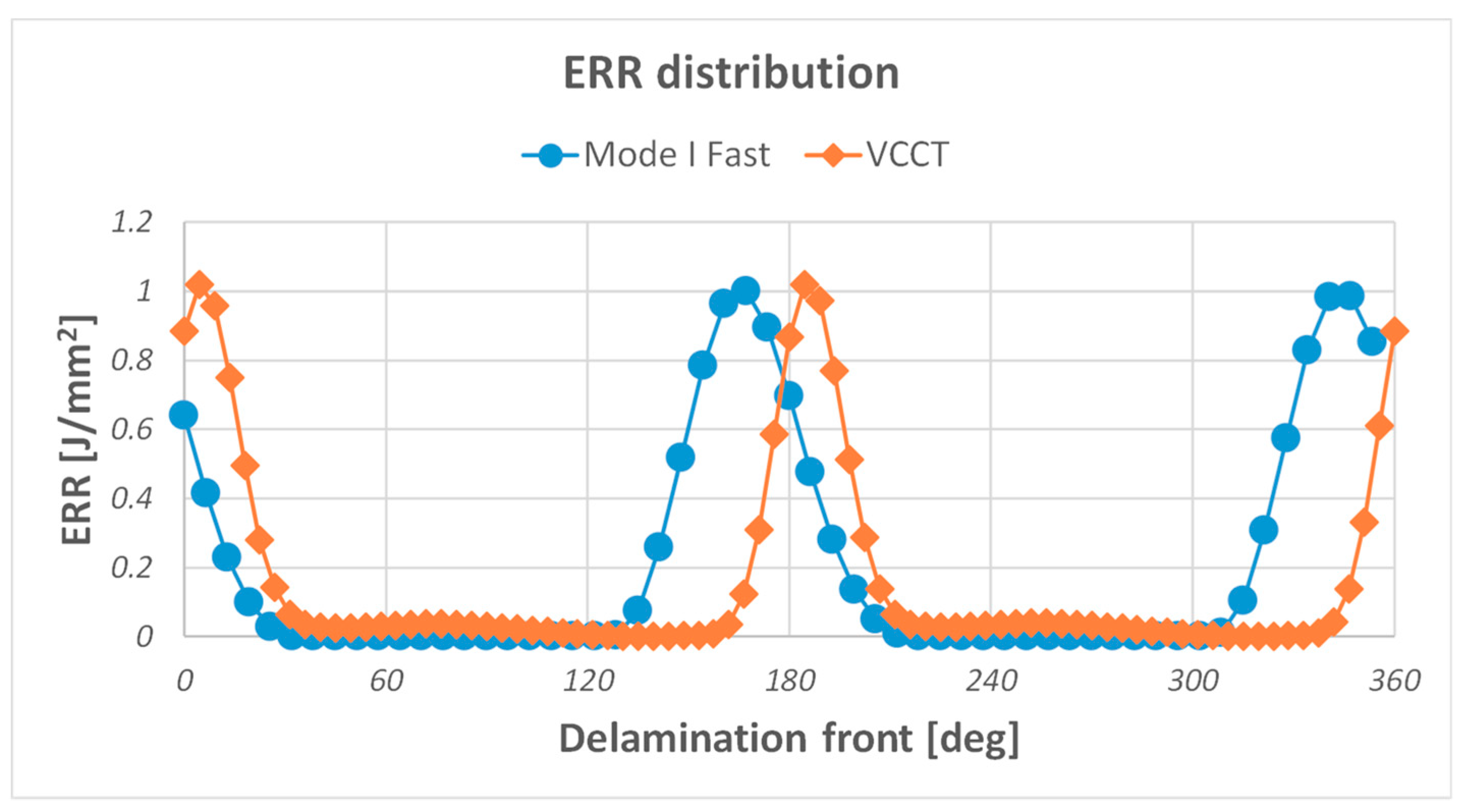
3.1. Test Case 1: Validation and Applicability of the Mode I Fast Procedure
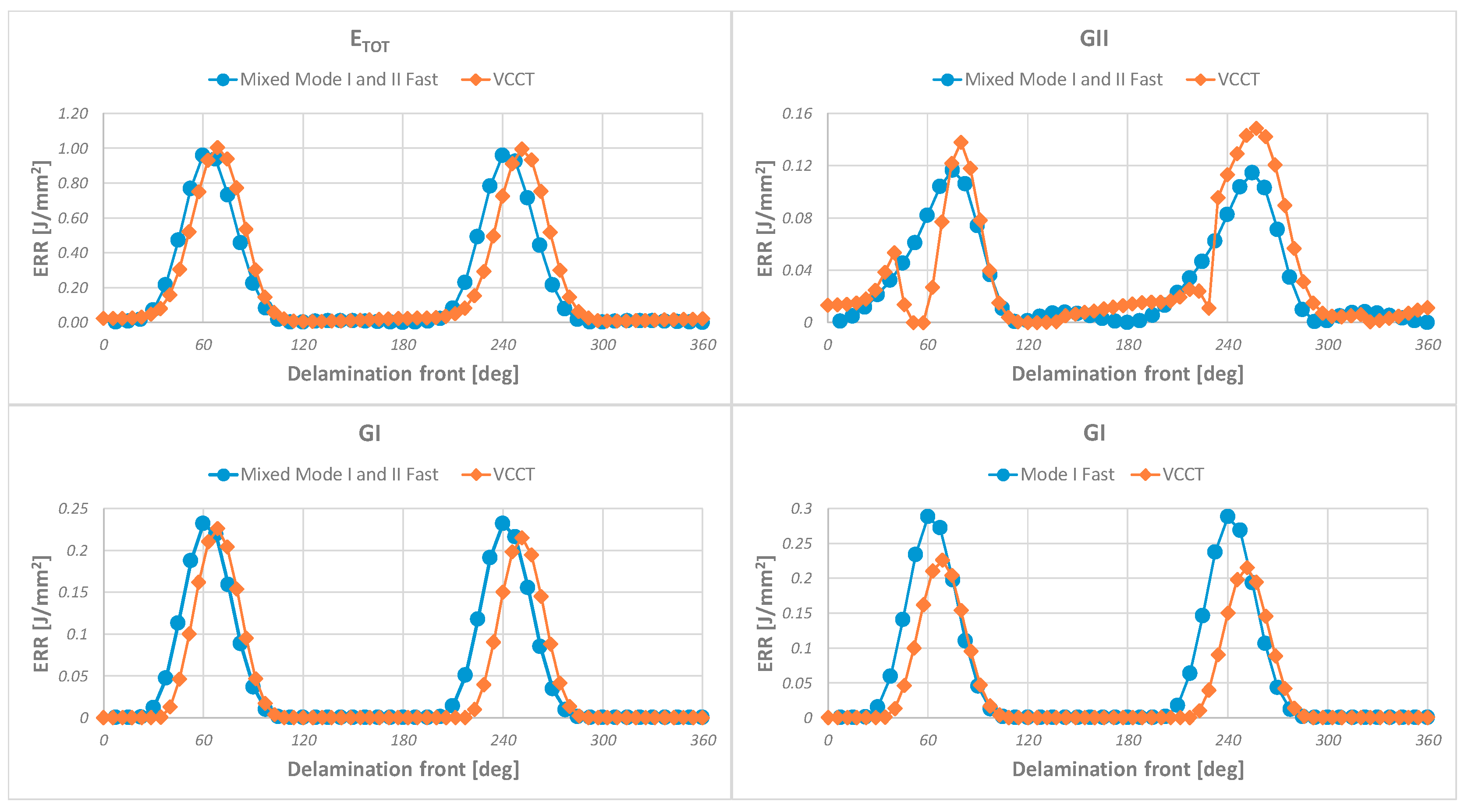
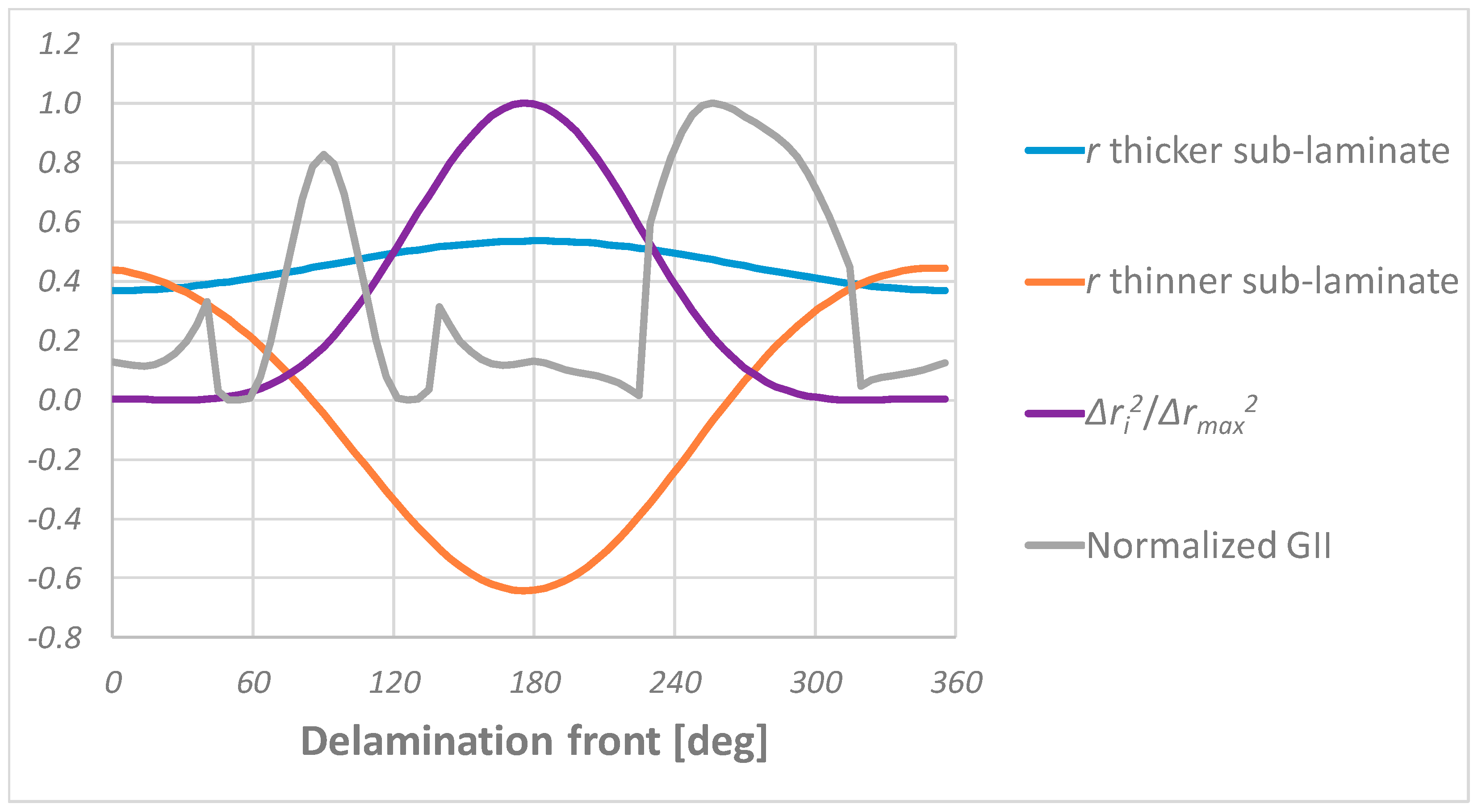
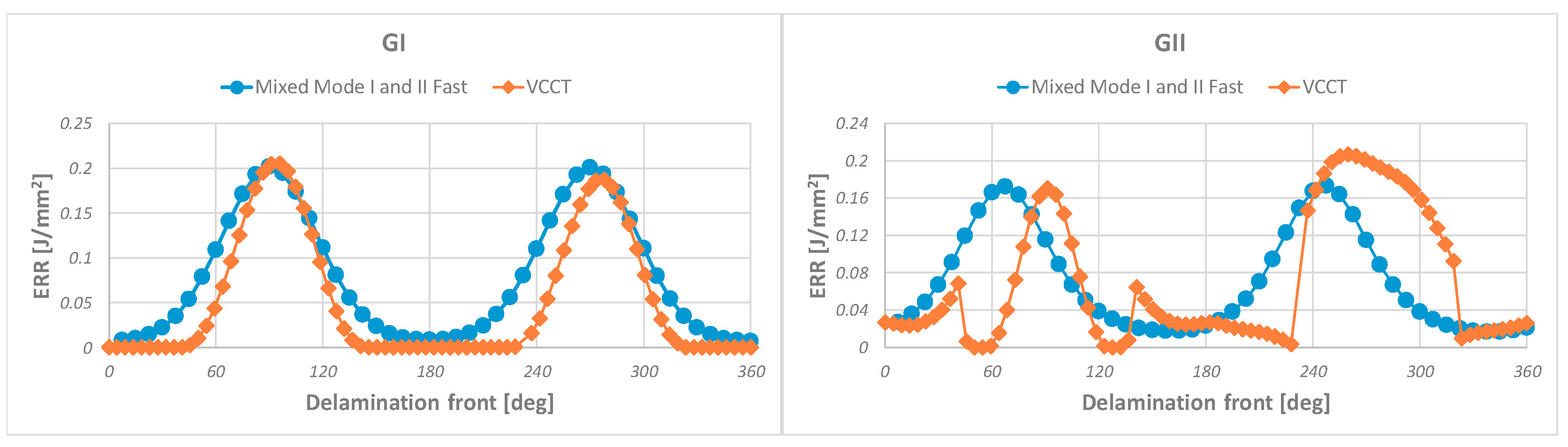
3.2. Test Case 2: Validation and Applicability of the Mixed Mode I and II Fast Procedure
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seon, G.; Makeev, A.; Nikishkov, Y.; Lee, E. Effects of defects on interlaminar tensile fatigue behavior of carbon/epoxy composites. Compos. Sci. Technol. 2013, 89, 194–201. [Google Scholar] [CrossRef]
- Andrews, S.D.; Ochoa, O.O.; Owens, S.D. The Effects of Fastener Hole Defects. J. Compos. Mater. 1993, 27, 2–20. [Google Scholar] [CrossRef]
- Elder, D.J.; Thomson, R.S.; Nguyen, M.Q.; Scott, M.L. Review of delamination predictive methods for low speed impact of composite laminates. Compos. Struct. 2004, 66, 677–683. [Google Scholar] [CrossRef]
- Geubelle, P.H.; Baylor, J.S. Impact-induced delamination of composites: A 2D simulation. Compos. Part B Eng. 1998, 29, 589–602. [Google Scholar] [CrossRef]
- Parlapalli, M.R.; Soh, K.C.; Shu, D.W.; Ma, G. Experimental investigation of delamination buckling of stitched composite laminates. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2024–2033. [Google Scholar] [CrossRef]
- Craven, R.; Iannucci, L.; Olsson, R. Delamination buckling: A finite element study with realistic delamination shapes, multiple delaminations and fibre fracture cracks. Compos. Part A Appl. Sci. Manuf. 2010, 41, 684–692. [Google Scholar] [CrossRef]
- Karihaloo, B.L.; Stang, H. Buckling-driven delamination growth in composite laminates: Guidelines for assessing the threat posed by interlaminar matrix delamination. Compos. Part B Eng. 2008, 39, 386–395. [Google Scholar] [CrossRef]
- Ashizawa, M. Fast Interlaminar Fracture of a Compressively Loaded Composite Containing a Defect. In Proceedings of the Fifth DOD/NASA Conference on Fibrous Composites in Structural Design; Report No. NADC-81096-60; Naval Air Development Center: Warminster, PA, USA, January 1981; pp. 1–1269. [Google Scholar]
- Ramkumar, R.L. Fatigue Degradation in Compressively Loaded Composite Laminates; NASA CR-165681; NASA Langley Research Center: Hampton, VA, USA, 1981.
- Ramkumar, R.L. Performance of a Quantitative Study of Instability-Related Delamination Growth; NASA CR-166046; NASA Langley Research Center: Hampton, VA, USA, 1983.
- Byers, B.A. Behaviour of Damaged Graphite/Epoxy Laminates under Compression Loading; NASA CR-159293; NASA Langley Research Center: Hampton, VA, USA, 1980.
- Chai, H.; Knauss, W.G.; Babcock, C.D. Observation of Damage Growth in Compressively Loaded Laminates. Exp. Mech. 1983, 23, 329–337. [Google Scholar] [CrossRef]
- Shivakumar, K.N.; Whitcomb, J.D. Buckling of a Sublaminate in a Quasi-Isotropic Composite Laminate. J. Compos. Mater. 1985, 19, 2–18. [Google Scholar] [CrossRef]
- Whitcomb, J.D.; Shivakumar, K.N. Strain-Energy Release Rate Analysis of a Laminate with a Postbuckled delamination. In Numerical Methods in Fracture Mechanics; NASA TM-89091; NASA Langley Research Center: Hampton, VA, USA, 1987. [Google Scholar]
- Kim, H.J.; Hong, C.S. Buckling and Postbuckling Behaviour of Composite Laminates with an Embedded Delamination. Compos. Sci. Technol. 1997, 57, 557–564. [Google Scholar] [CrossRef]
- Singh, K.L.; Dattaguru, B.; Ramamurthy, T.S.; Mangalgiri, P.D. Delamination Tolerance Studies in Laminated Composite Panels. Sadhana 2000, 25, 409–422. [Google Scholar] [CrossRef]
- Shahwan, K.; Waas, A.M. Unilateral Buckling of rectangular Plates. Int. J. Solids Struct. 1994, 31, 75–89. [Google Scholar] [CrossRef]
- Shahwan, K.; Waas, A.M. Buckling of Unilaterally Constrained Plates: Application to the Study of Delaminations in Layered Structures. J. Frankl. Inst. 1998, 335, 1009–1039. [Google Scholar] [CrossRef]
- Whitcomb, J.D. Analysis of a Laminate with a Postbuckled Embedded Delamination, Including Contact Effects. J. Compos. Mater. 1992, 26, 1523–1535. [Google Scholar] [CrossRef]
- Whitcomb, J.D. Three Dimensional Analysis of a Postbuckled Embedded Delamination. J. Compos. Mater. 1989, 23, 862–889. [Google Scholar] [CrossRef]
- Köllner, A.; Völlmecke, C. Post-buckling behaviour and delamination growth characteristics of delaminated composite plates. Compos. Struct. 2018, 203, 777–788. [Google Scholar] [CrossRef]
- Kutlu, Z.; Chang, F.-K. Modeling Compression Failure of laminated Composites Containing Multiple Through-the-Width Delaminations. J. Compos. Mater. 1992, 26, 350–387. [Google Scholar] [CrossRef]
- Orifici, A.C.; de Zarate Alberdi, I.O.; Thomson, R.S.; Bayandor, J. Compression and post-buckling damage growth and collapse analysis of flat composite stiffened panels. Compos. Sci. Technol. 2008, 68, 3150–3160. [Google Scholar] [CrossRef]
- Krueger, R. The Virtual Crack Closure Technique: History, Approach and Applications; NASA/CR-2002-211628; ICASE Report; NASA Langley Research Center: Hampton, VA, USA, 2002.
- Liu, P.F.; Hou, S.J.; Chu, J.K.; Hu, X.Y.; Zhou, C.L.; Liu, Y.L.; Zheng, J.Y.; Zhao, A.; Yan, L. Finite element analysis of postbuckling and delamination of composite laminates using virtual crack closure technique. Compos. Struct. 2011, 93, 1549–1560. [Google Scholar] [CrossRef]
- Gudmundson, P. Micromechanically based constitutive models for damage evolution in composite laminates. Int. J. Damage Mech. 2000, 9, 29–39. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Riccio, A.; Linde, P.; Raimondo, A.; Buompane, A.; Sellitto, A. On the use of selective stitching in stiffened composite panels to prevent skin-stringer debonding. Compos. Part B Eng. 2017, 124, 64–75. [Google Scholar] [CrossRef]
- Riccio, A.; Russo, A.; Sellitto, A.; Raimondo, A. Development and application of a numerical procedure for the simulation of the “Fibre Bridging” phenomenon in composite structures. Compos. Struct. 2017, 168, 104–119. [Google Scholar] [CrossRef]
- Hallett, S.R.; Green, B.G.; Jiang, W.G.; Wisnom, M.R. An experimental and numerical investigation into the damage mechanisms in notched composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 613–624. [Google Scholar] [CrossRef]
- Hughes, T.; Cottrell, J.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative numerical methods based on SFEM and IGA for computing stress concentrations in plates with discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Nguyen-Xuan, H. High-order B-splines based finite elements for delamination analysis of laminated composites. Compos. Struct. 2013, 102, 261–275. [Google Scholar] [CrossRef]
- Guo, Y.; Nagy, A.P.; Gürdal, Z. A layerwise theory for laminated composites in the framework of isogeometric analysis. Compos. Struct. 2014, 107, 447–457. [Google Scholar] [CrossRef]
- Dimitri, R.; Zavarise, G. Isogeometric treatment of frictional contact and mixed mode debonding problems. Comput. Mech. 2017, 60, 315–332. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F. Numerical Study of the Mixed-Mode Delamination of Composite Specimens. J. Compos. Sci. 2018, 2, 30. [Google Scholar] [CrossRef]
- Dimitri, R.; Tornabene, F.; Zavarise, G. Analytical and numerical modeling of the mixed-mode delamination process for composite moment-loaded double cantilever beams. Compos. Struct. 2018, 187, 535–553. [Google Scholar] [CrossRef]
- Riccio, A.; Damiano, M. A Fast Numerical Methodology for Delamination Growth Initiation Simulation. In Damage Growth in Aerospace Composites; Springer: Berlin/Heidelberg, Germany, 2015; pp. 199–220. ISBN 978-3-319-04003-5. [Google Scholar]
- Riccio, A.; Damiano, M.; Raimondo, A.; Di Felice, G.; Sellitto, A. A fast numerical procedure for the simulation of inter-laminar damage growth in stiffened composite panels. Compos. Struct. 2016, 145, 203–216. [Google Scholar] [CrossRef]
- Riccio, A.; Zarrelli, M.; Giordano, M. A Linear Numerical Approach to Simulate the Delamination Growth Initiation in Stiffened Composite Panels. J. Compos. Mater. 2010, 44, 1841–1866. [Google Scholar] [CrossRef]
- ABAQUS Manual; Revision 6.5-1; Theory; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2004.
- Sellitto, A.; Borrelli, R.; Caputo, F.; Riccio, A.; Scaramuzzino, F. Methodological approaches for kinematic coupling of non-matching finite element meshes. Procedia Eng. 2011, 10, 421–426. [Google Scholar] [CrossRef][Green Version]




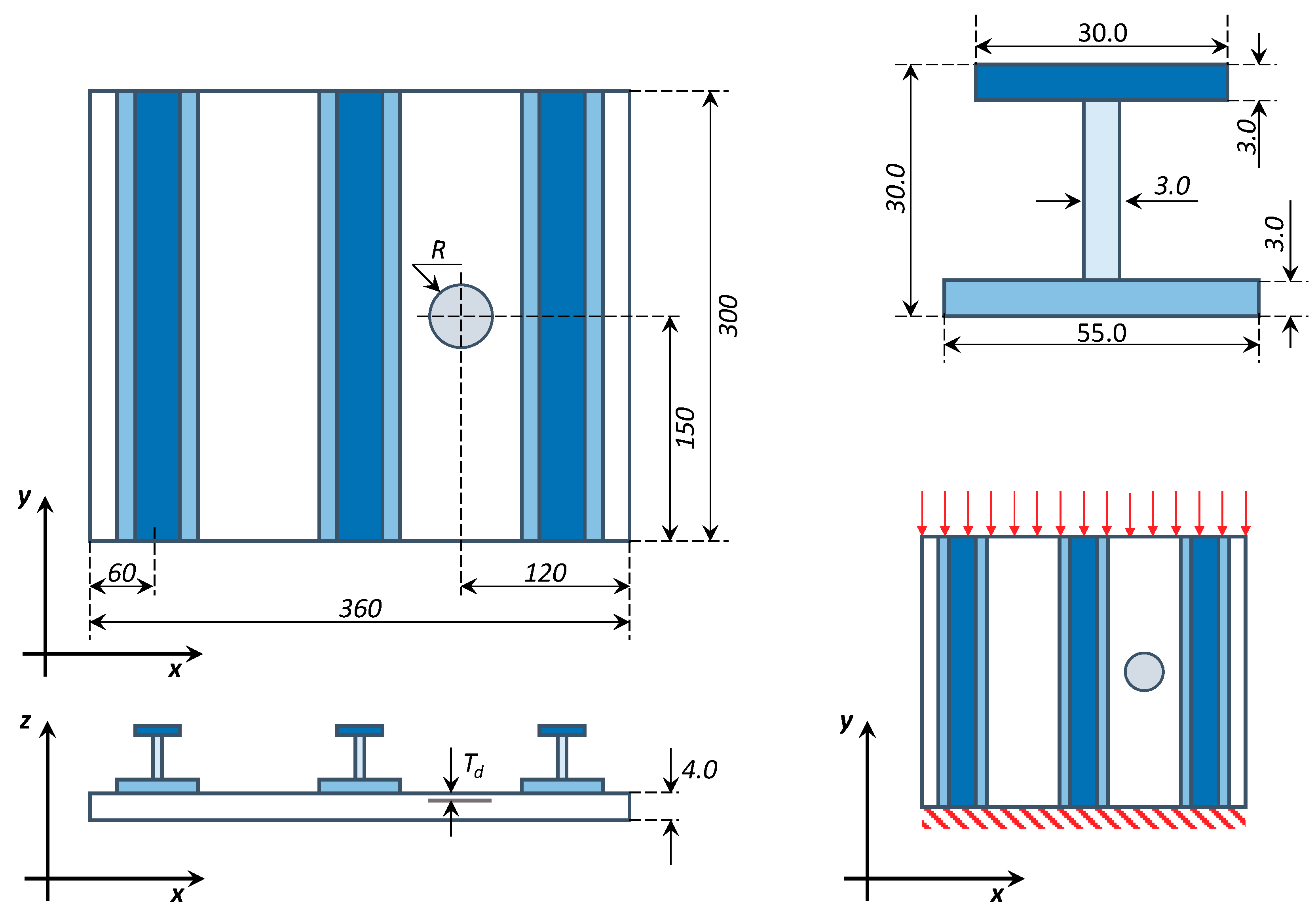
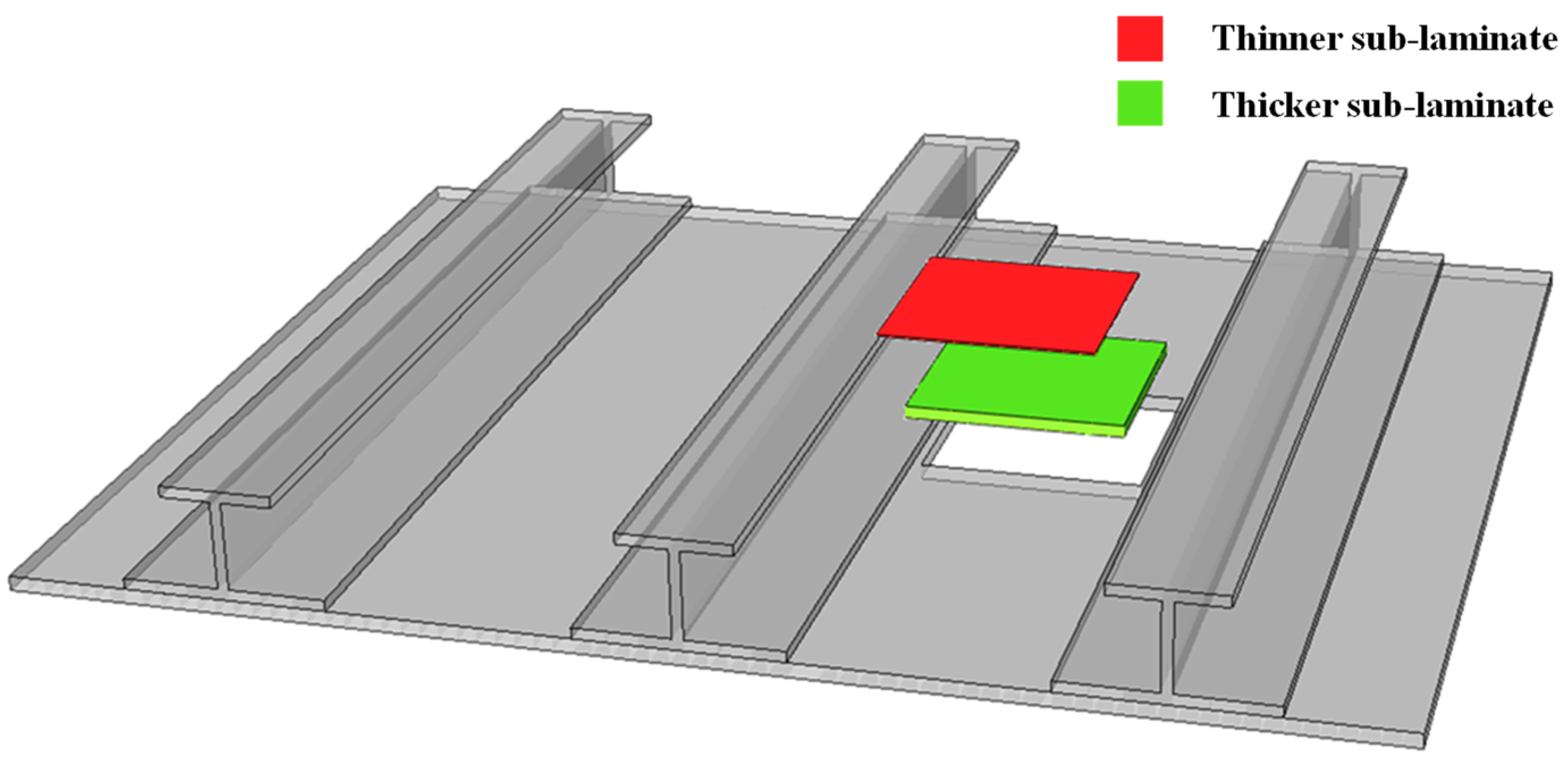


| E1 (GPa) | E2 = E3 (GPa) | G12 = G13 (GPa) | G23 (GPa) | ν12 = ν13 (-) | ν23 (-) | GIC (J/m2) | GIIC (J/m2) | tp (mm) |
|---|---|---|---|---|---|---|---|---|
| 147.0 | 9.0 | 5.0 | 3.0 | 0.3 | 0.42 | 175 | 532 | 0.188 |
| Approach | εbuckling (με) | εdel (με) | Fdel (kN) | Computational Time (s) |
|---|---|---|---|---|
| Fast Procedure | 980.3 | 1700.7 | 366.6 | 295 |
| VCCT | 1024.8 | 1780.0 | 382.9 | 4349 |
| E1 (GPa) | E2 = E3 (GPa) | G12 = G13 (GPa) | G23 (GPa) | ν12 = ν13 (-) | ν23 (-) | GIc (J/m2) | GIIc (J/m2) | tp (mm) |
|---|---|---|---|---|---|---|---|---|
| 155.0 | 8.57 | 7.4 | 4.8 | 0.33 | 0.52 | 280 | 519 | 0.125 |
| Delamination Interface | Delamination Depth | εcr | Error | Analysis Method |
|---|---|---|---|---|
| 4th–5th (90°/+45°) | 12.5% | 2415.33 | VCCT | |
| 2887.44 | 19.5% | Mode I Fast | ||
| 3104.18 | 22.2% | Mixed mode I and II Fast | ||
| 5th–6th (+45°/−45°) | 15.62% | 2678.00 | VCCT | |
| 2645.89 | 1.2% | Mode I Fast | ||
| 2788.06 | 3.9% | Mixed mode I and II Fast | ||
| 6th–7th (−45°/0°) | 18.7% | 3607.00 | VCCT | |
| 3284.56 | 9.8% | Mode I Fast | ||
| 3620.72 | 0.4% | Mixed mode I and II Fast | ||
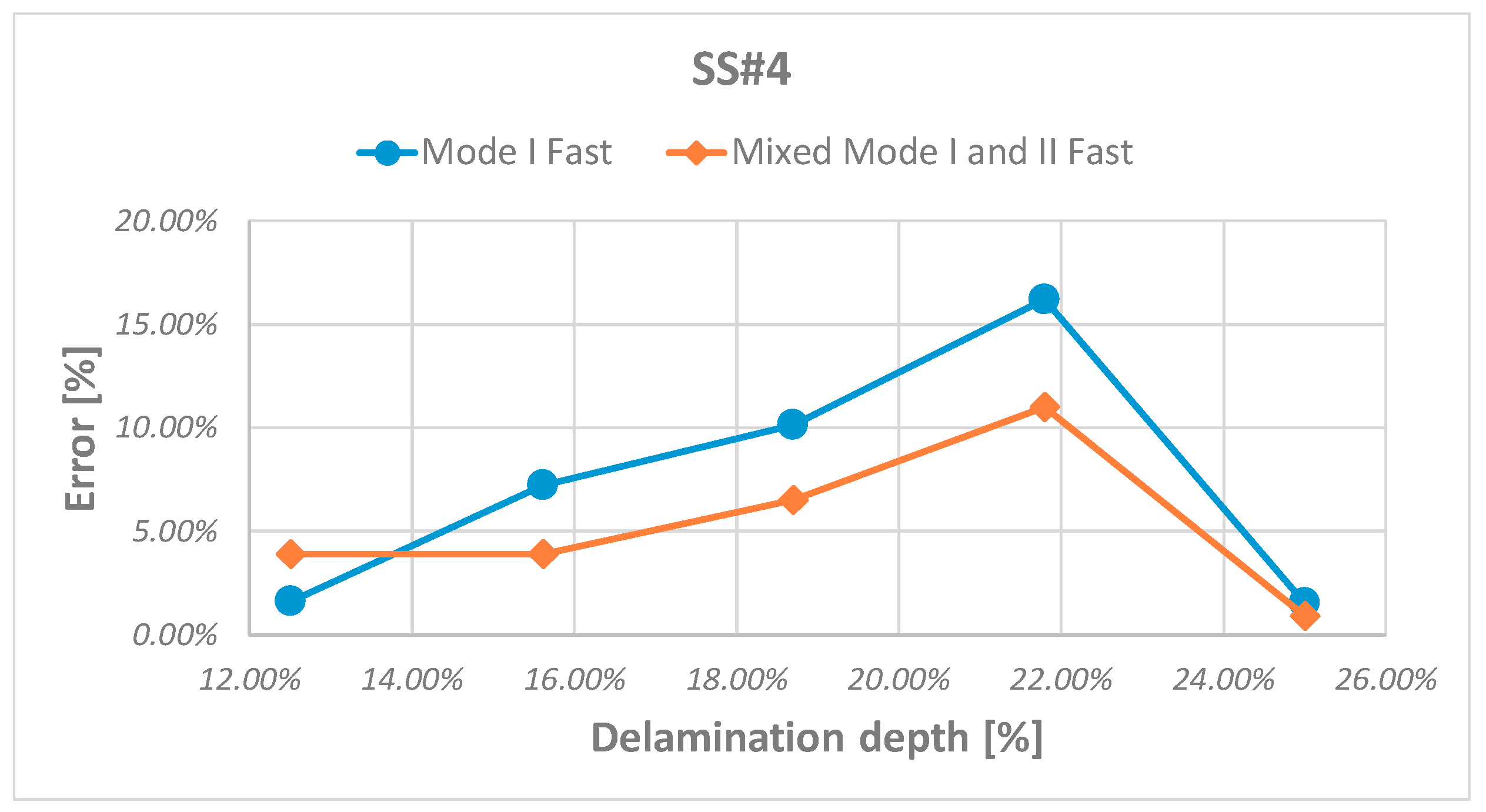
| 7th–8th (0°/90°) | 21.8% | 3938.00 | VCCT | |
| 3266.97 | 20.5% | Mode I Fast | ||
| 3528.79 | 11.6% | Mixed mode I and II Fast | ||
| 8th–9th (90°/+45°) | 25% | 3752.00 | VCCT | |
| 3474.52 | 8.0% | Mode I Fast | ||
| 3602.93 | 4.1% | Mixed mode I and II Fast |
| Delamination Interface | Delamination Depth | εcr | Error | Analysis Method |
|---|---|---|---|---|
| 4th–5th (90°/+45°) | 12.5% | 2890.67 | VCCT | |
| 2843.92 | 1.6% | Mode I Fast | ||
| 3007.27 | 3.9% | Mixed mode I and II Fast | ||
| 5th–6th (+45°/−45°) | 15.62% | 3288.00 | VCCT | |
| 3065.76 | 7.2% | Mode I Fast | ||
| 3165.35 | 3.9% | Mixed mode I and II Fast | ||
| 6th–7th (−45°/0°) | 18.7% | 4804.00 | VCCT | |
| 4361.94 | 10.1% | Mode I Fast | ||
| 4509.78 | 6.5% | Mixed mode I and II Fast | ||
| 7th–8th (0°/90°) | 21.8% | 5500.00 | VCCT | |
| 4734.76 | 16.2% | Mode I Fast | ||
| 4954.13 | 11.0% | Mixed mode I and II Fast | ||
| 8th–9th (90°/+45°) | 25% | 5926.00 | VCCT | |
| 5838.88 | 1.5% | Mode I Fast | ||
| 5874.92 | 0.9% | Mixed mode I and II Fast |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sellitto, A.; Saputo, S.; Damiano, M.; Russo, A.; Riccio, A. Mixed-Mode Delamination Growth Prediction in Stiffened CFRP Panels by Means of a Novel Fast Procedure. Appl. Sci. 2019, 9, 4761. https://doi.org/10.3390/app9224761
Sellitto A, Saputo S, Damiano M, Russo A, Riccio A. Mixed-Mode Delamination Growth Prediction in Stiffened CFRP Panels by Means of a Novel Fast Procedure. Applied Sciences. 2019; 9(22):4761. https://doi.org/10.3390/app9224761
Chicago/Turabian StyleSellitto, Andrea, Salvatore Saputo, Michele Damiano, Angela Russo, and Aniello Riccio. 2019. "Mixed-Mode Delamination Growth Prediction in Stiffened CFRP Panels by Means of a Novel Fast Procedure" Applied Sciences 9, no. 22: 4761. https://doi.org/10.3390/app9224761
APA StyleSellitto, A., Saputo, S., Damiano, M., Russo, A., & Riccio, A. (2019). Mixed-Mode Delamination Growth Prediction in Stiffened CFRP Panels by Means of a Novel Fast Procedure. Applied Sciences, 9(22), 4761. https://doi.org/10.3390/app9224761








