Secure On-Off Transmission in UAV Relay-Assisted mmWave Networks

Abstract

This paper investigates secure transmission in unmanned aerial vehicle (UAV) relay-assisted millimeter wave (mmWave) networks, where the selected UAV relay performs secure transmission in both the on-off and non-on-off schemes. Meanwhile, there are multiple eavesdroppers randomly distributed on the ground and attempting to wiretap the transmission. Leveraging the air-to-ground channel model and the tools of stochastic geometry, the novel expressions of transmit probability (TP) and secrecy outage probability (SOP) are derived in both the on-off and non-on-off transmission schemes with perfect beam alignment. The secrecy performance improvement is demonstrated in the on-off transmission scheme, and we find that there exists an optimal altitude of UAV relays to achieve the best TP. In addition, due to the limitations of UAV carriers, such as its low computational capacity and high mobility, the perfect beam alignment is difficult to achieve in the mmWave networks aided by UAV relays, and the effect of beam alignment error on the secrecy performance is investigated in the considered networks. Analyzing the numerical and simulation results, we find that the SOP will not have obvious deterioration when the beam alignment error is relatively small, and the SOP can be improved by using the antennas with a large number of elements. However, in high beam alignment error regime, the antenna arrays with a smaller number of elements will provide the better SOP.

1. Introduction

Millimeter wave (mmWave) has attracted considerable research attention due to its plentiful available spectrum resources [1,2,3]. Nevertheless, with the high frequencies, mmWave signals are extremely sensitive to the blockage effect, and their path losses are severe. As such, the mmWave communication links are prone to outage, especially in an environment with dense blockage, e.g., a mountainous area. To this end, deploying the unmanned aerial vehicle (UAV) relays in the air has been investigated for performance improvement and disconnection recovery in the mmWave networks [4,5].

Although the performance improvement can be obtained by employing the UAV relays, it also makes the transmission vulnerable to eavesdroppers due to the inherent broadcast of the wireless networks. As such, it is one of the key concerns to provide a secure communication in UAV relay-assisted mmWave networks. In contrast to the conventional upper-layer security methods mainly based on cryptographic protocols [6], physical-layer security has been emerged as a powerful approach to protect information transmission against wiretapping by exploiting the randomness of wireless medium, e.g., noise and interference [7]. Some potential application scenarios and challenges in terms of physical-layer security are presented in [8,9,10,11]. In this paper, we focus on secure on-off transmission in UAV relay-assisted mmWave networks.

1.1. Related Work and Motivation

Cooperative relay has been identified as an effective technique to improve the system performance of mmWave networks, and has attracted considerable attention recently [12,13,14]. To be specific, in [12], the coverage probability of the mmWave networks aided by relay, in which the base stations and relays are modeled under the stochastic geometry framework, has been investigated in both the best path and best relay selection protocols. Deploying the directional antennas at relays helps improve the reliability in the mmWave networks, the maximum achievable rate of the mmWave relay networks has been examined by considering the beamwidth of directional antennas in [13]. In addition, Lin et al. [14] has demonstrated the effects of co-channel interference on outage performance in the mmWave relay networks. Nevertheless, all above mentioned works focus on the mmWave communication networks on the ground.

At present, due to the flexible deployment and the supply of line-of-sight (LOS) links for UAV, operating the UAVs as relays has emerged as a promising way for performance enhancement in wireless communication networks [15,16,17]. Specifically, considering an UAV relay-assisted network, the authors in [15] have studied the channel model and examined the system performance in terms of average rate, outage probability, and bit error rate. In [16], the authors have investigated the conditions of establishing multi-hop single link or multiple dual-hop links by using UAV relays for the purpose of achieving better outage performance. In addition, Chen et al. [17] has demonstrated the effect of the altitude of UAV relay on the reliability performance in the UAV relay-assisted communication networks, then they has explored the optimal altitude of UAV relay for minimum outage probability. However, these works only investigate the performance of UAV relay-assisted networks without secrecy consideration.

Physical-layer security can protect information transmission with lower computation complexity in UAV relay networks [18,19,20]. Considering an UAV relay system, where multiple relays and eavesdroppers exist in the air, the secrecy outage probability (SOP) has been examined in [18]. Meantime, in [19], the average secrecy rate of the UAV relay networks has been studied. Involving the mmWave bands, the related literature is small. In our previous work [20], we have considered an UAV-enabled mmWave communication system, in which a source transmits the signals to a destination via a determined UAV relay, physical-layer security has been studied by using the 3D directional antenna pattern. It is worth mentioning that the on-off transmission [21,22], as an effective measure to guarantee the transmission quality and further enhance physical-layer security, still has not been investigated in UAV relay networks.

On the other hand, the existing works of mmWave communication networks mainly considered that the perfect beam alignment occurs at the legitimate nodes. However, due to the practical limitations, e.g., the limited computational capacity and mobility of transmitters and receivers, the beam alignment error is inevitable in practical mmWave communication scenarios. In [23], the average rate and coverage performance has been examined in the mmWave cellular networks with beam alignment errors, which are modeled as independent Gaussian distributions. Later, Cheng et al. [24] has adopted flat-top model to describe the beam alignment error of directional antenna, and the coverage probability of mmWave cellular networks has been studied. Please note that these works have not clarified that how the beam alignment errors affect the secrecy performance in UAV relay-assisted mmWave networks.

In summary, contrasting to the previous works, the secure communication in the UAV relay-assisted mmWave networks is still an open issue. First, with the aid of UAV relay in the mmWave networks, how to design the on-off transmission scheme to further enhance the physical-layer security is a challenging work. In addition, taking into account the practical limitation in terms of imperfect beam alignment at legitimate nodes, the effects of beam alignment errors on the secrecy performance of UAV relay-assisted mmWave networks still needs to be investigated.

1.2. Contribution

In this paper, we investigate the secure on-off transmission in UAV relay-assisted mmWave networks, and the secrecy performance is examined by considering the beam alignment errors. Our main contributions are summarized as follows:

• Considering a ground mmWave communication networks aided by multiple UAV relays, where multiple eavesdroppers randomly distribute on the ground. More specifically, the locations of UAV relays and eavesdroppers are modeled as independent Poisson Point Processes (PPPs), and the opportunistic relay selection scheme is adopted. Then, the on-off transmission scheme is designed to enhance the secrecy performance of the considered networks, and we find that the lower SOP can be obtained by adopting the higher threshold of data transmission.
• With perfect beam alignment, the new closed-form expressions of transmit probability (TP) and SOP are derived in both the on-off and non-on-off transmission schemes by using the tools of stochastic geometry and Gauss–Chebyshev integration. It is revealed that the TP is not a monotonous function versus the altitude of UAV relays, which means that the best TP can be obtained by properly designing the UAV relays’ altitude. In addition, the secrecy performance has remarkable positive correlations with the transmit power and the number of antenna elements.
• Taking into account the beam alignment error, a typical error model is adopted under the 3D antenna pattern, and the tractable expressions of the SOP are derived. Analyzing the numerical and simulation results, we find that the SOP will not have obvious deterioration with small beam alignment error, and we can enhance the secrecy performance by using the antenna array with large number of elements. However, when the beam alignment error is severe, the antenna array with smaller number of elements provides the lower SOP.

The remainder of this article is organized as follows. The system model is presented in Section 2. In Section 3, we examine the TP and SOP in both the on-off and non-on-off transmission schemes, and the SOPs with beam alignment error are analyzed. Then, the simulation results are shown in Section 4. Finally, we summarize the conclusions in Section 5.

2. System Model

2.1. Network Model

Consider a mmWave UAV system consisting of one source (S), one destination (D), multiple UAV relays and multiple eavesdroppers, as shown in Figure 1. We assume that the direct link from S to D is disconnected since mmWave signals are easy to be blockaded on the ground, and the communication occurs via a selected UAV relay ($R_0$). To be specific, S first sends the messages to $R_0$, and $R_0$ employs the decode-and-forward protocol to forward its received signals to D. Meanwhile, there are multiple ground eavesdroppers randomly distributed around D and out of the coverage area of S, which means that the eavesdroppers only wiretap the transmission from $R_0$ to D, similar to [25,26,27]. In addition, the distribution of UAV relays follows a homogeneous PPP ${\mathsf{\Phi }}_U$ with density ${\lambda }_U$, and we assume that all UAV relays are deployed inside a circular disc with radius Q and at the same altitude H [16,28]. The ground eavesdroppers are modeled as an independent homogeneous PPP ${\mathsf{\Phi }}_E$ with density ${\lambda }_E$.

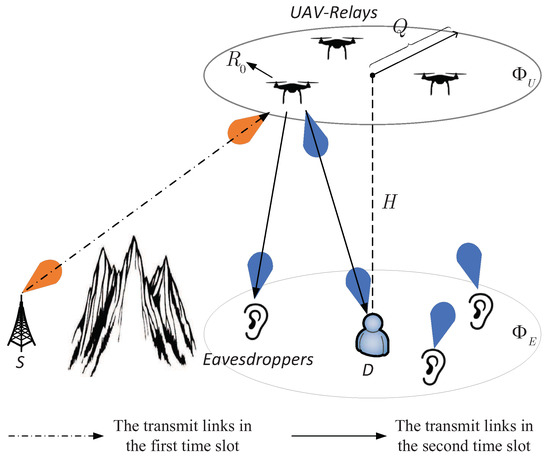
Figure 1. System Model.

For facilitating the analysis, a 3D polar coordinate system is adopted, in which S and D locate at $\left(d_{SD},\pi ,0\right)$ and $\left(0,0,0\right)$ respectively. Then, for the UAV relay $R_x$ at $\left(r,\theta ,H\right)$, the distance from S to $R_x$ and $R_x$ to D are represented as $d_{S{R}_x}=\sqrt{d_{SD}^2+r^2-2r{d}_{SD}cos(\theta -\pi )+H^2}$, and $d_{R_{x}D}=\sqrt{r^2+H^2}$.

2.2. Antenna and Beam Alignment Error Model

To compensate high path loss of mmWave signals, we assume that the directional antenna arrays are deployed at all nodes. A 3D sectorized antenna model is adopted to approximate the antenna gain pattern [28,29], and the diagram is given as Figure 2. More specifically, the antenna gain between node i and j is expressed as $G_{ij}\in \left\{G_M^i{G}_M^j,G_M^i{G}_m^j,G_m^i{G}_M^j,G_m^i{G}_m^j\right\}$ with probability $\left\{P_M^i{P}_M^j,P_M^i{P}_m^j,P_m^i{P}_M^j,P_m^i{P}_m^j\right\}$, where $i,j\in \left\{S,R_0,D,E_e\right\}$ denote the source, the selected UAV relay, the destination or the eavesdropper at location e, $G_M^i\left(G_m^i\right)$ represents the array gain of the main lobe (side lobe) at node i, and $P_M^i\left(P_m^i\right)$ is the probability that the array gain $G_M^i\left(G_m^i\right)$ occurs. In the scenario without beam alignment error, we assume that the legitimate nodes can adjust their antenna orientations and align to each other. Then, for the selected UAV relay $R_0$, the maximum of beam depression angle is calculated as ${\theta }_{max}=2arctan\left(Q/H\right)$, and the probability that the ground eavesdroppers fall in the main lobe of UAV relay can be expressed as $P_M^{R_0}={\theta }_a^R{\theta }_d^R/\pi {\theta }_{max}$, where ${\theta }_a^R$ and ${\theta }_d^R$ are the azimuth angle and depression angle of the UAV relay, respectively. Moreover, the probability that the eavesdropper $E_e$ aligns to the selected UAV relay can be written as $P_M^{E_e}={\theta }_a^E{\theta }_d^E/\left(\pi \left(\pi -{\theta }_d^E\right)\right)$, where ${\theta }_a^E$ and ${\theta }_d^E$ are the azimuth and elevation angles of the eavesdropper. Accordingly, we can obtain $P_m^{R_0}=1-P_M^{R_0}$ and $P_m^{E_e}=1-P_M^{E_e}$.

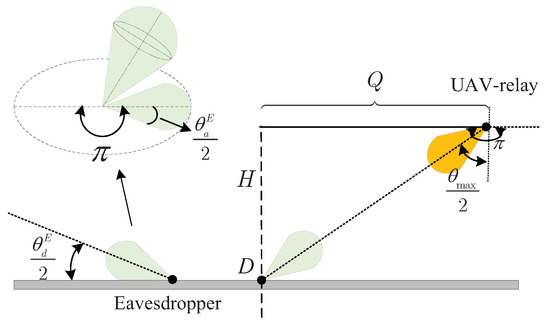
Figure 2. Illation of 3D antenna gain.

We consider that the legitimate nodes S, $R_x$ and D will estimate the angles of arrival and departure, and adjust the antenna steering orientations to obtain the maximum directive gains. However, due to the errors in angles estimations, the beam alignment error is inevitable in practical applications. In this paper, the 3D antenna gain is adopted in which the beam alignment occurs when the main lobe of the antenna array aligns the target in both azimuth and elevation. We denote the beam alignment error in the azimuth (elevation) at node $k\in \left\{S,R_0,D\right\}$ as ${\epsilon }_a^k\left({\epsilon }_d^k\right)$, and the errors are modeled as independent Gaussian-distributed variables with zero mean [23,30]. For simplicity, we assume that the variances of the beam alignment errors in the azimuth and elevation at node k are same, denoting as ${\sigma }_k^2$. Thus, the cumulative distribution functions (CDFs) of $\left|{\epsilon }_a^k\right|$ and $\left|{\epsilon }_d^k\right|$ are expressed as $F_{\left|{\epsilon }_a^k\right|}\left(x\right)=F_{\left|{\epsilon }_d^k\right|}\left(x\right)=erf\left(x/\left(\sqrt{2}{\sigma }_k\right)\right)$, where $erf\left(·\right)$ is the error function.

2.3. Channel Model

Due to the blockage effects, the air-to-ground links can be LOS or non-line-of-sight (NLOS). Similar to [31], the occurrence probabilities of LOS and NLOS are given as $p_L\left(r\right)=1/\left\{1+aexp\left[-b\left(arctan\left(H/r\right)-a\right)\right]\right\}$, and $p_N\left(r\right)=1-p_L\left(r\right)$, where r is the horizontal distance from UAV to the ground node, and a and b are the environment dependent constant values. Moreover, the propagation characteristics for LOS and NLOS links are different in mmWave bands [32,33]. Giving the link of length d, the path loss can be given as $L\left(d\right)=C_j{d}^{-{\alpha }_j}$ for $j\in \left(L,N\right)$, where $C_j={10}^{-{\zeta }_j}$ is the intercept of the link with parameter ${\zeta }_j$, ${\alpha }_j$ is the path loss exponent, and L and N denote that the link is LOS or NLOS. In addition, the small-scale fading for each link is modeled as independent Nakagami-m fading [34]. More specifically, the small-fading channel gain between two nodes follows normalized Gamma random variable, and for a LOS link, it is expressed as ${\left|h_{ij}\right|}^2\sim \mathsf{\Gamma }\left(N_L,1\right)$; for a NLOS link, ${\left|h_{ij}\right|}^2\sim \mathsf{\Gamma }\left(N_N,1\right)$, where $i,j\in \left\{S,R_x,D,E_e\right\}$.

Based on the above assumptions on antenna and channel models, the signal to noise (SNR) at the legitimate receiver is written as

$${\gamma }_{ij}=\frac{P_t{G}_{ij}{\left|h_{ij}\right|}^{2}L\left(d_{ij}\right)}{N_0},i\in \left\{S,R_x\right\},j\in \left\{R_x,D\right\},$$

(1)

where $P_t$ is the transmit power, $R_x\in {\mathsf{\Phi }}_U$ is the available UAV relay at position x, $d_{ij}$ is the distance from node i to j and $N_0$ denotes the noise power. In addition, we focus on the non-colluding eavesdropping case, where all eavesdroppers process the received signals independently. As such, the secrecy performance is dominated by the largest SNR at the most malicious eavesdropper, which is written as

$${\gamma }_E=\underset{E_e\in {\mathsf{\Phi }}_E}{max}\left\{\frac{P_t{G}_{R_0{E}_e}{\left|h_{R_0{E}_e}\right|}^{2}L\left(d_{R_0{E}_e}\right)}{N_0}\right\}.$$

(2)

2.4. Relay Selection and Transmission Scheme

Under the decode-and-forward relaying strategy, we adopt an opportunistic relay selection scheme with two phases. First, we select a set of UAV relays, which can successfully decode the messages received from S. Specifically, for a potential UAV relay $R_x\in {\mathsf{\Phi }}_U$, if the channel capacity between S and $R_x$ is greater than a threshold $C_{th}$, the relay $R_x$ can decode the S’s messages correctly [35,36], and the decoding set is defined as $\hat{\mathsf{\Phi }}=\left\{R_x\in {\mathsf{\Phi }}_U,C_{S{R}_x}>C_{th}\right\}$. After that, the UAV relay $R_0$, which provides the lowest path loss to D, is selected from $\hat{\mathsf{\Phi }}$ to forward the S’s messages to D. To this end, the selected relay offers the minimum length of LOS or NLOS link to D.

Based on the above system model, there are multiple ground eavesdroppers monitoring the transmission of $R_0\to D$ link and attempting to interpret the confidential messages. In order to enhance physical-layer security, the on-off transmission scheme is adopted at $R_0$, as done in [21,22]. More specifically, based on the pilot signals from D, $R_0$ can obtain the channel capacity $C_{R_{0}D}$ of the $R_0\to D$ link. Then $R_0$ performs data transmission only when $C_{R_{0}D}$ is above the threshold $\mu$. In order to highlight the effect of secrecy performance in the on-off transmission scheme, the conventional non-on-off transmission scheme is analyzed in this paper as well, in which the selected UAV relay $R_0$ always transmits the signals after decoding the messages from S.

To further clarify the relay selection and on-off transmission scheme, we also depict the detailed scheduling period of these two processes as Figure 3. The relay selection process contains three parts:

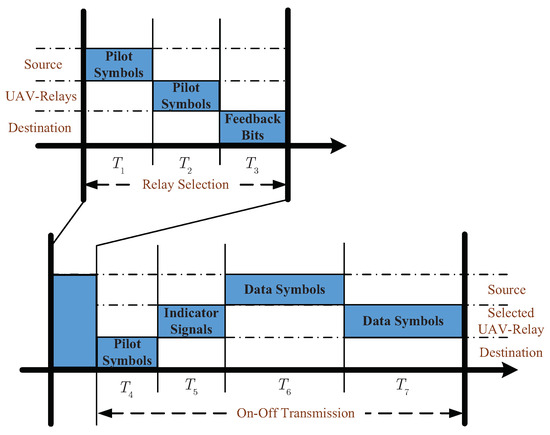
Figure 3. Scheduling period of the relay selection and on-off transmission processes.

$T_1$: S sends the pilot symbols to all UAV relays, and the UAV relays calculate the channel capacities of their links from S, then $\hat{\mathsf{\Phi }}$ can be obtained.

$T_2$: The UAV relays in $\hat{\mathsf{\Phi }}$ transmit the pilot signals to D, then D can find $R_0$.

$T_3$: D responds the selection results to the UAV relays, and the selection process is completed.

After that, the selected UAV relay $R_0$ performs on-off transmission, which is divided into four time slots:

$T_4$: D sends the pilot signals to $R_0$, and $R_0$ calculated the channel capacity $C_{R_{0}D}$.

$T_5$: If the $C_{R_{0}D}>\mu$, $R_0$ sends the indicator signals to S. But when $C_{R_{0}D}\le \mu$, $R_0$ keeps silent and waits the next pilot signals from D.

$T_6$: After S receives the indicator signals, it transmits the date symbols to $R_0$.

$T_7$: $R_0$ forwards the messages to D by using decode-and-forward strategy.

It should be mentioned that there are beam training phases before S and $R_0$ transmit the data symbols [37,38,39], which is not our focus.

3. Secrecy Evaluation

In this section, we first present the probability distribution function (PDF) of the horizontal distance from the selected UAV relay $R_0$ to the destination D. Then, we derive the closed-form expressions of the TP and SOP with and without the on-off transmission strategy. Furthermore, the effect of beam alignment error on the secrecy performance is analyzed.

3.1. Preliminary Analysis

For an UAV relay $R_x$, the probability of including in the decoding set $\hat{\mathsf{\Phi }}$ depends on the distance from S to $R_x$. To be specific, the UAV relay $R_x$ is more likely to be contained in $\hat{\mathsf{\Phi }}$ when it is closed to S. Meantime, the channels between S and $R_x$ with different x are independent, then $\hat{\mathsf{\Phi }}$ can be regarded as an inhomogeneous PPP. The density of the point process is derived as

$$\begin{array}{cc}\hfill \hat{\lambda }\left(x\right)& ={\lambda }_{U}Pr\left(C_{S{R}_x}>C_{th}\right)\hfill \\ & ={\lambda }_{U}Pr\left(\frac{P_t{G}_{S{R}_x}{\left|h_{S{R}_x}\right|}^{2}L\left(d_{S{R}_x}\right)}{N_0}>2^{C_{th}}-1\right)\hfill \\ & ={\lambda }_{U}Pr\left({\left|h_{S{R}_x}\right|}^2>\frac{N_0\left(2^{C_{th}}-1\right)}{P_t{G}_{S{R}_x}L\left(d_{S{R}_x}\right)}\right)\hfill \\ & ={\lambda }_U{\displaystyle \sum _{j\in \left\{L,N\right\}}}{p}_j\left(r\right)\frac{\mathsf{\Gamma }\left(N_j,\frac{N_0\left(2^{C_{th}}-1\right)d_{S{R}_x}^{{\alpha }_j}}{P_t{G}_{S{R}_x}{C}_j}\right)}{\mathsf{\Gamma }\left(N_j\right)}\hfill \end{array}$$

(3)

where r is the horizontal distance from S to $R_x$.

The opportunistic relay selection assumes the selected UAV relay $R_0$, which offer the lowest path loss to D, is selected to forward S’s messages. It is easy to know that $R_0$ is the nearest relay in ${\hat{\mathsf{\Phi }}}_L$ (${\hat{\mathsf{\Phi }}}_N$) from D, where ${\hat{\mathsf{\Phi }}}_L$ (${\hat{\mathsf{\Phi }}}_N$) is the LOS (NLOS) decoding UAV relay set with density $p_L\left(r\right)\hat{\lambda }\left(x\right)$ ($p_N\left(r\right)\hat{\lambda }\left(x\right)$).

Lemma 1.

Denoting the horizontal distance from D to the nearest LOS (NLOS) UAV relay as $r_L$ ($r_N$), the PDF of $r_j$, $j\in \left\{L,N\right\}$ is presented as

$$f_{r_j}\left(r\right)=\sum _{i=1}^T{w}_i^{\left(\theta \right)}r{p}_j\left(r\right)\hat{\lambda }\left(r,{\theta }_i\right)e^{v_j\left(r\right)},$$

(4)

where T is the abscissas of the quadrature by using Gauss–Chebyshev integration, ${\theta }_i=\pi \left(1+cos\frac{\left(2i-1\right)\pi }{2T}\right)$, $w_i^{\left(\theta \right)}=\frac{\pi }{T}\sqrt{{\theta }_i\left(y-{\theta }_i\right)}$, and $v_j\left(r\right)$ is written as

$$v_j\left(r\right)=-\sum _{i,k=1}^T{w}_i^{\left(\theta \right)}{w}_k^{\left(r\right)}{r}_k{p}_j\left(r_k\right)\hat{\lambda }\left(r_{k,}{\theta }_i\right),$$

(5)

where $r_k=\frac{r}{2}\left(1+cos\frac{\left(2k-1\right)\pi }{2T}\right)$, $w_k^{\left(r\right)}=\frac{\pi }{T}\sqrt{r_k\left(y-r_k\right)}$.

Proof. 

See Appendix A. □

Lemma 2.

Giving that the selected UAV relay is LOS, the conditional PDF of $r_L$ is written as

$$g_{r_L}\left(r\right)=\frac{f_{r_L}\left(r\right)}{A_L}{e}^{{\nu }_N\left(max\left(0,\sqrt{{\left(\frac{C_N}{C_L}\right)}^{\frac{2}{{\alpha }_N}}{\left(r^2+H^2\right)}^{\frac{{\alpha }_L}{{\alpha }_N}}-H^2}\right)\right)},$$

(6)

where $A_L$ is the probability that $R_0$ is LOS, and its expression is given as

$$A_L=\sum _{k=0}^T{w}_k^{\left(r\right)}{e}^{{\nu }_N\left(max\left(0,\sqrt{{\left(\frac{C_N}{C_L}\right)}^{\frac{2}{{\alpha }_N}}{\left({r_k}^2+H^2\right)}^{\frac{{\alpha }_L}{{\alpha }_N}}-H^2}\right)\right)}{f}_{r_L}\left(r_k\right).$$

(7)

Proof. 

See Appendix B. □

Similar to (6), giving that the selected UAV relay is NLOS, the conditional PDF of $r_N$ is written as

$$g_{r_N}\left(r\right)=\frac{f_{r_N}\left(r\right)}{A_N}{e}^{{\nu }_L\left(min\left(Q,\sqrt{{\left(\frac{C_L}{C_N}\right)}^{\frac{2}{{\alpha }_L}}{\left(r^2+H^2\right)}^{\frac{{\alpha }_N}{{\alpha }_L}}-H^2}\right)\right)},$$

(8)

where $A_N=1-A_L$ is the probability that $R_0$ is NLOS.

3.2. Performance Analysis with Perfect Beam Alignment

In this subsection, considering the perfect beam alignment between the legitimate transmitter and receiver, the new closed-form expressions for the TP and SOP are derived in the on-off transmission scheme. For comparison, we then consider the conventional non-on-off transmission scheme and present the SOP.

3.2.1. On-Off Transmission Scheme

In this scheme, with the pilot signals from the destination D, the selected UAV relay $R_0$ sends the messages only when the channel capacity $C_{R_{0}D}$ is above a threshold $\mu$. Then, the TP is derived as

$$\begin{array}{cc}\hfill p_{tx}& =Pr\left(C_{R_{0}D}>\mu \left|R_0\in \hat{\mathsf{\Phi }}\right.\right)\hfill \\ & =\frac{Pr\left({\left|h_{R_{0}D}\right|}^2>\frac{N_0\left(2^{\mu }-1\right)}{P_t{G}_{R_{0}D}L\left(d_{R_{0}D}\right)}\right)}{Pr\left(R_0\in \hat{\mathsf{\Phi }}\right)}\hfill \\ & =\frac{{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\int }_0^Q\frac{\mathsf{\Gamma }\left(N_j,\frac{N_0\left(2^{\mu }-1\right)d_{R_{0}D}^{{\alpha }_j}}{P_t{G}_{R_{0}D}{C}_j}\right)}{\mathsf{\Gamma }\left(N_j\right)}{g}_j\left(r\right)dr}{{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\int }_0^Q{g}_j\left(r\right)dr}\hfill \\ & \stackrel{a}{=}\frac{{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\displaystyle \sum _{i=1}^T}{\overline{w}}_i^{\left(r\right)}{\tau }_j\left(\mu ,r_i,H,G_{R_{0}D}\right)g_{r_j}\left(r_i\right)}{{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\displaystyle \sum _{i=1}^T}{\overline{w}}_i^{\left(r\right)}{g}_{r_j}\left(r_i\right)}\hfill \end{array}$$

(9)

where step (a) is due to the Gauss–Chebyshev integration, $r_i=\frac{Q}{2}\left(1+cos\frac{\left(2i-1\right)\pi }{2T}\right)$, ${\overline{w}}_i^{\left(r\right)}=\frac{\pi }{T}\sqrt{r_i\left(Q-r_i\right)}$ and ${\tau }_j\left(\mu ,r_i,H,G_{R_{0}D}\right)$ is written as

$${\tau }_j\left(\mu ,r_i,H,G_{R_{0}D}\right)=\frac{\mathsf{\Gamma }\left(N_j,\frac{N_0\left(2^{\mu }-1\right){\left(r_i^2+H^2\right)}^{\frac{{\alpha }_j}{2}}}{P_t{G}_{R_{0}D}{C}_j}\right)}{\mathsf{\Gamma }\left(N_j\right)}.$$

(10)

The SOP is the probability that the secrecy outage occurs when $R_0$ performs data transmission. As such, the SOP in on-off scheme is derived as

$$\begin{array}{cc}\hfill p_{sop}^{on-off}& =1-Pr\left(C_{R_{0}D}-C_E>C_S\left|\left(C_{R_{0}D}>\mu \left|R_0\in \hat{\mathsf{\Phi }}\right.\right)\right.\right)\hfill \\ & =1-\frac{Pr\left({\gamma }_E<\frac{1+{\gamma }_{R_{0}D}}{C_s}-1,{\gamma }_{R_{0}D}>2^{\mu }-1\right)}{p_{tx}}\hfill \\ & =1-\frac{1}{p_{tx}}{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\int }_0^Q{\int }_{2^{\mu }-1}^{\infty }{g}_j\left(r\right)F_{{\gamma }_E}\left(\frac{1+x}{2^{C_S}}-1\right)f_{{\gamma }_{R_{0}D,j}}\left(x\right)drdx\hfill \\ & \stackrel{b}{\approx }1-\frac{1}{p_{tx}}{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\displaystyle \sum _{i,k=1}^T}{\overline{w}}_i^{\left(r\right)}{w}_k^{\left(x\right)}{g}_j\left(r_i\right)F_{{\gamma }_E}\left(\beta \left(x_k\right)\right)f_{{\gamma }_{R_{0}D,j}}\left(x_k\right),\hfill \end{array}$$

(11)

where $F_{{\gamma }_E}\left(·\right)$ is the CDF of ${\gamma }_E$, $f_{{\gamma }_{R_{0}D,j}}\left(·\right)$ is the PDF of ${\gamma }_{R_{0}D}$ with LOS or NLOS $R_0\to D$ link, $\beta \left(y\right)=\frac{1+y}{C_s}-1$, step (b) is due to the fact that the maximal ${\gamma }_{R_{0}D}$ can be approximated as ${\gamma }_{R_{0}D}^{max}=\frac{5P_t{N}_L{G}_M^{R_0}{G}_M^{D}L\left(H\right)}{N_0}$, and $x_k=\frac{\left({\gamma }_{R_{0}D}^{max}+2^{\mu }-1\right)\left({\gamma }_{R_{0}D}^{max}-2^{\mu }-1\right)}{2}cos\frac{\left(2k-1\right)\pi }{2T}$ and $w_k^{\left(x\right)}=\frac{\pi }{T}\sqrt{\left(x_k-2^{\mu }+1\right)\left({\gamma }_{R_{0}D}^{max}-x_k\right)}$ are the parameters by using Gauss–Chebyshev integration.

We note that (11) is calculated by using the CDF of ${\gamma }_E$ and the PDF of ${\gamma }_{R_{0}D}$ when $R_0\to D$ link is LOS or NLOS. Without loss of generality, we only take into account the eavesdroppers inside a circular area, and the radius is set as Q for simplicity. Then, the CDF of ${\gamma }_E$ is derived as

$$\begin{array}{cc}\hfill F_{{\gamma }_E}\left(x\right)=& Pr\left(\underset{e\in {\mathsf{\Phi }}_E}{max}{\gamma }_{E_e}\le x\right)\hfill \\ & ={\mathrm{E}}_{{\mathsf{\Phi }}_E}\left({\displaystyle \prod _{e\in {\mathsf{\Phi }}_E}}Pr\left({\gamma }_{E_e}\le x\right)\right)\hfill \\ & \stackrel{c}{=}exp\left(-{\lambda }_E{\int }_{R^2}Pr\left({\gamma }_{E_e}>x\right)d{R}^2\right)\hfill \\ & =exp\left(-{\lambda }_E{\displaystyle \sum _{G_{R_{0}E}}}Pr\left(G_{R_{0}E}=V\right){\displaystyle \sum _{j\in \left\{L,N\right\}}}{\mathsf{\Xi }}_j\left(V,x\right)\right),\hfill \end{array}$$

(12)

where step (c) is due to the void probability of PPP, ${\mathsf{\Xi }}_j\left(V,x\right)$ is given as

$$\begin{array}{cc}\hfill {\mathsf{\Xi }}_j\left(V,x\right)=& {\int }_0^{2\pi }{\int }_0^Q{p}_j\left(r\right)Pr\left({\gamma }_{E_e,j}>x\left|{\mathsf{\Phi }}_E^j\right.\right)rdrd\theta \hfill \\ & =\frac{2\pi }{\mathsf{\Gamma }\left(N_j\right)}{\int }_0^Q\mathsf{\Gamma }\left(N_j,\frac{N_{0}x{d}_{R_0{E}_e}^{{\alpha }_j}}{P_{t}V{C}_j}\right)p_j\left(r\right)rdr\hfill \\ & =\frac{2\pi }{\mathsf{\Gamma }\left(N_j\right)}{\displaystyle \sum _{i=1}^T}{\overline{w}}_i^{\left(r\right)}\mathsf{\Gamma }\left(N_j,\frac{N_{0}x{\left(r_i^2+H^2\right)}^{\frac{{\alpha }_j}{2}}}{P_{t}V{C}_j}\right)p_j\left(r_i\right)r_i,\hfill \end{array}$$

(13)

where ${\mathsf{\Phi }}_E^j,j\in \left\{L,N\right\}$ is the set of LOS or NLOS eavesdroppers seen from $R_0$.

Then, the PDF of ${\gamma }_{RD,j}$ is derived as

$$\begin{array}{cc}\hfill f_{{\gamma }_{R_{0}D,j}}\left(x\right)& ={\left[Pr\left({\left|h_{R_{0}D}\right|}^2<\frac{N_{0}x{d}_{R_{0}D}^{{\alpha }_j}}{P_t{G}_{R_{0}D}{C}_j}\right)\right]}^{\prime }\hfill \\ & =\frac{1}{\mathsf{\Gamma }\left(N_j\right)}{\left[\gamma \left(N_j,\frac{N_{0}x{d}_{R_{0}D}^{{\alpha }_j}}{P_t{G}_{R_{0}D}{C}_j}\right)\right]}^{\prime }\hfill \\ & \stackrel{d}{=}\frac{1}{\mathsf{\Gamma }\left(N_j\right)}{\left(\frac{N_{0}x{d}_{R_{0}D}^{{\alpha }_j}}{P_t{G}_{R_{0}D}{C}_j}\right)}^{N_j}{x}^{N_j-1}{e}^{-\frac{N_{0}x{d}_{R_{0}D}^{{\alpha }_j}}{P_t{G}_{R_{0}D}{C}_j}},\hfill \end{array}$$

(14)

where step (d) is due to ([40], Equation (0.410)) and ([40], Equation (8.350.1)).

Finally, we can calculate the SOP in the on-off transmission scheme by substituting (12) and (14) into (11).

Remark 1.

We clarify that the TP in the on-off transmission scheme is affected by the threshold μ, the transmit power $P_t$, the antenna gains of the legitimate links and the altitude of UAV relays H, as indicated by (9). It is worth mentioning that the TP is not a monotonous function of H. Specifically, when H starts to increase, the TP increases due to the larger LOS probability of the $R_0\to D$ link. But if H is large enough, the path loss is severe, which will cause the decrease of TP. Moreover, when $P_t\to \infty$, the TP $p_{tx}\to 1$ according to (9), and the SOP $p_{sop}^{on-off}$ approaches a constant due to the fact that the secrecy capacity $C_{R_{0}D}-C_E$ is mainly affected by the channel states of legitimate and eavesdropping links if $P_t$ is large enough.

3.2.2. Non-On-Off Transmission Scheme

For comparison, we also give the TP and SOP for conventional non-on-off scheme, in which the selected UAV relay $R_0$ always transmits the signals after receiving the messages from S. It is obvious that the TP in non-on-off transmission scheme is $p_{tx}^{non}=1$. And the SOP is derived as

$$\begin{array}{cc}\hfill p_{sop}^{non}& =1-Pr\left({\gamma }_{R_{0}D}>2^{C_s}(1+{\gamma }_E)-1\right)\hfill \\ & =1-{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\displaystyle \sum _i^T}{\overline{w}}_i^{\left(r\right)}{g}_{r_j}\left(r_i\right){\int }_0^{\infty }{\int }_{\overline{\beta }\left(x\right)}^{\infty }{F}_{{\gamma }_{R_{0}D},j}\left(y\right)f_{{\gamma }_E}\left(x\right)dzdy\hfill \\ & \stackrel{e}{=}1-{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\displaystyle \sum _i^T}{\overline{w}}_i^{\left(r\right)}{g}_{r_j}\left(r_i\right){\int }_0^{\infty }{F}_{{\gamma }_E}\left(x\right)f_{{\gamma }_{R_{0}D},j}\left(\overline{\beta }\left(x\right)\right){\overline{\beta }}^{\prime }\left(x\right)dy\hfill \\ & \stackrel{f}{\approx }1-{\displaystyle \sum _{j\in \left\{L,N\right\}}}{A}_j{\displaystyle \sum _{i,k}^T}{\overline{w}}_i^{\left(r\right)}{\overline{w}}_k^{\left(x\right)}{g}_{r_j}\left(r_i\right)F_{{\gamma }_E}\left(x_k\right)f_{{\gamma }_{R_{0}D},j}\left(\overline{\beta }\left({\overline{x}}_k\right)\right){\overline{\beta }}^{\prime }\left({\overline{x}}_k\right),\hfill \end{array}$$

(15)

where $F_{{\gamma }_E}\left(·\right)$ and $f_{{\gamma }_{R_{0}D},j}\left(·\right)$ are given as (12) and (14), step (e) is obtained by using integration by parts, step (f) is due to the maximum ${\gamma }_{R_{0}D}^{max}$ is approximated as ${\gamma }_{R_{0}D}^{max}=\frac{5P_t{N}_L{G}_{R_0}^M{G}_D^{M}L\left(H\right)}{{\sigma }^2}$, ${\overline{w}}_k^{\left(x\right)}=\frac{\pi }{T}\sqrt{{\overline{x}}_k\left({\gamma }_{R_{0}D}^{max}-{\overline{x}}_k\right)}$, ${\overline{x}}_k=\frac{{\gamma }_{R_{0}D}^{max}}{2}\left(1+cos\frac{\left(2k-1\right)\pi }{2T}\right)$, and $\overline{\beta }\left(y\right)=2^{C_s}\left(1+y\right)-1$.

3.3. Performance Analysis with Beam Alignment Error

Based on the antenna model mentioned in Section 2.2, the beam alignment occurs when the orientation of the target node falls in the main lobe of the transmitter’s antenna gain. For the 3D antenna, if the additive beam alignment error is not larger than half of the main-lobe beamwidth in both of the azimuth and elevation, i.e., $\left|{\epsilon }_a^k\right|\le {\theta }_a^k/2$, $\left|{\epsilon }_d^k\right|\le {\theta }_d^k/2$, $k\in \left\{S,R_x,D\right\}$, the beam alignment is deemed to be achieved. Then the probability that node k align its target node is calculated by

$$\begin{array}{cc}\hfill P_A^k& =F_{\left|{\epsilon }_a^k\right|}\left(\frac{{\theta }_a^k}{2}\right)F_{\left|{\epsilon }_d^k\right|}\left(\frac{{\theta }_d^k}{2}\right)\hfill \\ & =erf\left(\frac{{\theta }_a^k}{2\sqrt{2}{\sigma }_k}\right)erf\left(\frac{{\theta }_d^k}{2\sqrt{2}{\sigma }_k}\right).\hfill \end{array}$$

(16)

Since the existence of beam alignment error, the antenna gain between the legitimate nodes i and j, $i,j\in \left\{S,R_0,D\right\}$, which is denoted as $G_{ij}$, can be described as a discrete random variable. As such, the PDF of $G_{ij}$ can be given by

$$\begin{array}{cc}{f}_{G_{ij}}\left(y\right)\hfill & =P_A^i{P}_A^j\delta \left(y-G_M^i{G}_M^j\right)+P_A^i{\overline{P}}_A^j\delta \left(y-G_M^i{G}_m^j\right)\hfill \\ & +{\overline{P}}_A^i{P}_A^j\delta \left(y-G_m^i{G}_M^j\right)+{\overline{P}}_A^i{\overline{P}}_A^j\delta \left(y-G_m^i{G}_m^j\right),\hfill \end{array}$$

(17)

where ${\overline{P}}_A^i=1-P_A^i$ (${\overline{P}}_A^j=1-P_A^j$), and $\delta \left(·\right)$ is the Kronecker delta function.

Let the $p_{sop}^{on-off}\left(y_1,y_2\right)$ and $p_{sop}^{non}\left(y_1,y_2\right)$ be the SOP in the on-off and non-on-off transmission schemes when $G_{S{R}_0}=y_1$ and $G_{R_{0}D}=y_2$. The SOP in the on-off transmission scheme is formulated as

$$\begin{array}{cc}\hfill {\hat{p}}_{sop}^{on-off}& ={\int }_0^{\infty }{\int }_0^{\infty }{p}_{sop}^{on-off}\left(y_1,y_2\right)f_{G_{S{R}_0}}\left(y_1\right)f_{G_{R_{0}D}}\left(y_2\right)d{y}_{1}d{y}_2\hfill \\ & ={\displaystyle \sum _{G_{S{R}_0}}}Pr\left(G_{S{R}_0}=y_1\right){\displaystyle \sum _{G_{R_{0}D}}}Pr\left(G_{R_{0}D}=y_2\right)p_{sop}^{on-off}\left(y_1,y_2\right),\hfill \end{array}$$

(18)

where $G_{ij}$ belongs to $\left\{G_M^i{G}_M^j,G_M^i{G}_m^j,G_m^i{G}_M^j,G_m^i{G}_m^j\right\}$ with probability $\left\{P_A^i{P}_A^j,P_A^i{\overline{P}}_A^j,{\overline{P}}_A^i{P}_A^j,{\overline{P}}_A^i{\overline{P}}_A^j\right\}$ for $i,j\in \left\{S,R_0,D\right\}$. The SOP in the non-on-off scheme is similar to (18), but replacing ${\hat{p}}_{sop}^{on-off}$ and $p_{sop}^{on-off}\left(y_1,y_2\right)$ with ${\hat{p}}_{sop}^{non}$ and $p_{sop}^{non}\left(y_1,y_2\right)$, respectively.

Remark 2.

It can be clarified that the beam alignment probability of node k is affected by the main-lobe beamwidth in both the azimuth and elevation ${\theta }_a^k$, ${\theta }_d^k$ and the beam alignment error ${\sigma }_k$, as indicated by (16). Obviously, the SOPs in both the on-off and non-on-off transmission schemes increase as ${\sigma }_k$ becomes large. This is because that the larger ${\sigma }_k$ degrades the channel qualities of legitimate links. Nevertheless, when the error is relatively small, the SOP would not have a decided change because the main lobe of the transmitter’s antenna still can cover the target nodes. In addition, when ${\sigma }_k$ is severe, the SOP is worse by using the antenna array with larger number of elements due to its lower side-lobe gain and narrow beamwidth.

4. Simulation Results

In this section, some simulation results are provided to show the secrecy performance of UAV relay-assisted mmWave networks under both the on-off and non-on-off transmission schemes, and the impact of beam alignment error is discussed. Monte Carlo simulations are conducted in each figure to verify our numerical results. We consider that the uniform planar square antenna is adopted at each node, the antenna element number of the S, UAV relays, D and eavesdroppers are denoted as $N_l$, $l\in \left\{S,R_x,D,E_e\right\}$, and the main-lobe beamwidth, the antenna gain of the main lobe and side lobe of an N element antenna are given in Table 1. In addition, the mmWave communication operates at carrier frequency 28 GHz, and the simulation parameters are shown in Table 2.

Table 1. 3D Antenna Pattern [29].

Number of antenna elements	N
Main-lobe Beamwidth ${\theta }_a={\theta }_d$	$\sqrt{\frac{N}{3}}$
Main-lobe Gain $G_M$	N
Side-lobe Gain $G_m$	$\frac{\sqrt{N}-\frac{\sqrt{3}}{2\pi }Nsin\left(\frac{\sqrt{3}}{2\sqrt{N}}\right)}{\sqrt{N}-\frac{\sqrt{3}}{2\pi }sin\left(\frac{\sqrt{3}}{2\sqrt{N}}\right)}$

Table 2. Simulation Parameters.

Type	Values
Distance between S and D	800 m
Radius of UAV relay area	$Q=$ 200 m
Number of antenna elements	$N_S=16$, $N_D=N_{E_e}=4$
Blockage parameters	$a=9.6$, $b=0.28$
Path loss parameters	$\begin{array}{c}{\alpha }_L=2,{\zeta }_L=61.4\hfill \\ {\alpha }_N=2.92,{\zeta }_N=72\hfill \end{array}$
Small-scale fading parameters	$N_L=3,N_N=2$
Noise power [23]	$N_0\left(\mathrm{dBm}\right)=-174+10lg\left(BW\right)+NF$
Noise figure	$NF=10\mathrm{dB}$
Bandwidth	$\mathrm{BW}=1\mathrm{GHz}$

Figure 4 shows the TP versus the UAV relays’ altitude H with different $\mu$ and in both the on-off and non-on-off transmission schemes. First, under the on-off transmission scheme, we find that the TP first increases and then decreases as H becomes large. It can be explained that larger H causes higher LOS probability, but if the LOS probability is large enough, the TP is mainly affected by the path loss, which increases as H becomes large. Secondly, the TP increases by decreasing the transmission threshold $\mu$. It demonstrates that we can adjust the TP by changing $\mu$ under on-off transmission scheme. In addition, as $C_{th}$ increases, no matter $\mu$ equals to 4, 4.5, or 5, the TP decreases. The reason is that the selected UAV relay would be closer to S for achieving the decoding process when $C_{th}$ increases, which causes that the path loss of second hop increases.

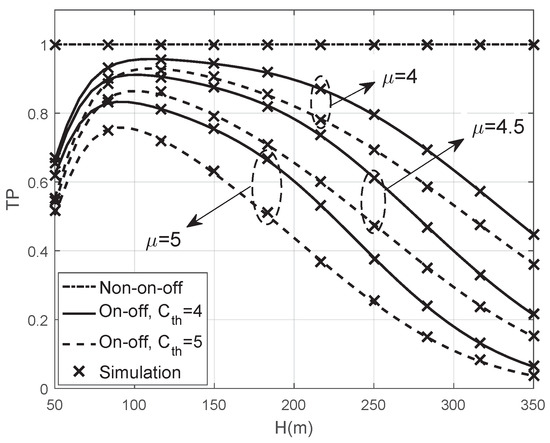
Figure 4. The TP versus the altitude of UAV relay when $P_t=30$ dBm, $N_{R_x}=9$, and ${\lambda }_U=5\times {10}^{-4}$.

In Figure 5, we plot the SOP versus the transmit power $P_t$ for different $N_{R_x}$ and in both the on-off and non-on-off schemes. Observing from Figure 5, the SOP with $N_{R_x}=16$ outperforms the SOP with $N_{R_x}=9$ since the received SNR can be enhanced by adopting the antennas array with large amount of elements. Furthermore, the SOP can be improved in the on-off transmission scheme especially with large $\mu$. This is because that the selected relay performs data transmission only when the channel quality of $R_0\to D$ link beyond $\mu$ in the on-off transmission scheme, and larger $\mu$ means better channel from $R_0$ to D when transmission occurs. It is worth mentioning that the SOP is not a monotonous function of $P_t$ when $\mu$ is large. It can be explained that the improvement of SOP is obvious with large $\mu$ in the low $P_t$ region due to the large gap between legitimate and eavesdropping channel capacities, but the eavesdroppers also benefit from larger $P_t$, as such, the channel capacity gap becomes narrow and then approach a constant as $P_t$ continue increasing.

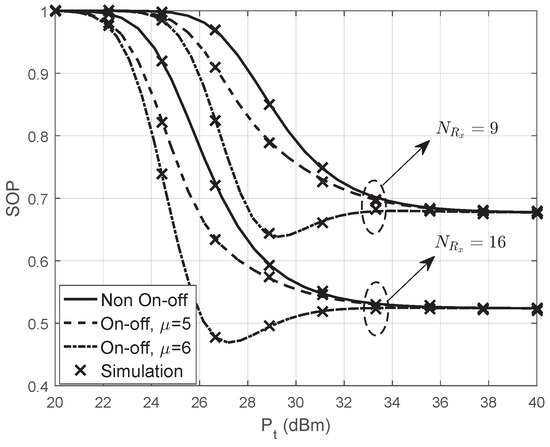
Figure 5. The SOP versus the transmit power $P_t$ when $H=$ 120 m, $C_{th}=4$, $C_s=1$, ${\lambda }_R=1\times {10}^{-3}$, and ${\lambda }_E=2\times {10}^{-3}$.

Figure 6 illustrates the effect of the eavesdropper density ${\lambda }_E$ on the SOP with different beam alignment error ${\sigma }_k$ and in both the on-off and non-on-off transmission schemes. Obviously, with the increasing of ${\lambda }_E$, no matter ${\sigma }_k$ equals to 0°, 8° or 10°, the SOP increases in both two transmission schemes. Besides, the SOP becomes large as ${\sigma }_k$ deteriorates. The reason is that the channel capacities of legitimate links decrease due to the lower channel gain when ${\sigma }_k$ increases. Nevertheless, the SOP in on-off transmission scheme outperforms the SOP in non-on-off transmission scheme. It demonstrates that the secrecy performance in the considered networks can be improved by using the on-off transmission scheme.

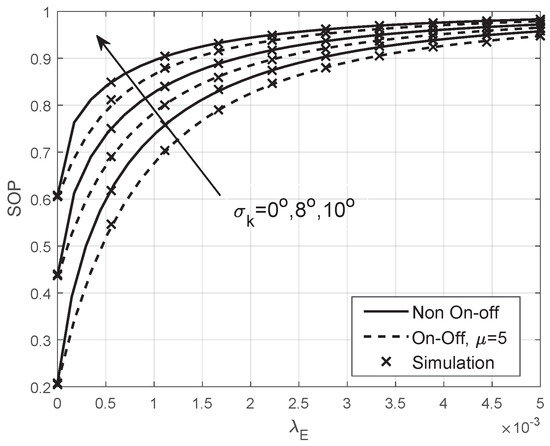
Figure 6. The SOP versus the density of eavesdroppers ${\lambda }_E$ when $P_t=$ 30 dBm, $H=120$, $N_{R_x}=9$, $C_{th}=4$, $C_s=1$, and ${\lambda }_U=5\times {10}^{-4}$.

Figure 7 shows the SOP versus the beam alignment error ${\sigma }_k$ with different $N_{R_x}$ in both the on-off and non-on-off transmission schemes. It can be observed that the SOP increases as ${\sigma }_k$ becomes large. However, we can find that the increase of SOP is not remarkable when ${\sigma }_k$ is relatively small. This is because the target nodes still can fall in the main lobe of the transmit antenna when ${\sigma }_k$ is small. Moreover, it is noteworthy that the SOP can be improved by adopting the on-off transmission scheme, but the improvement is slighter when $N_{R_x}=16$. It can be explained that the channel capacity of $R_x\to D$ link always exceeds $\mu =5$ due to the high antenna gain with $N_{R_x}=16$. In addition, when ${\sigma }_k$ is not too large, the better SOP can be obtained by adopting more antenna elements due to the high antenna gain. However, in the high ${\sigma }_k$ regime, the antenna array with lesser elements will provide better SOP due to its larger beamwidth of the main lobe.

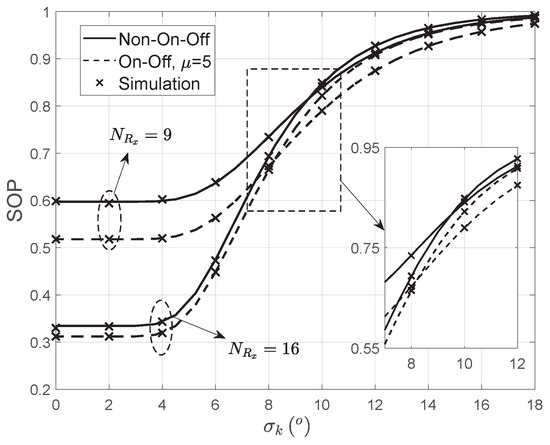
Figure 7. The SOP versus the eavesdropper density ${\lambda }_E$ when $P_t=$ 30 dBm, $H=$ 120 m, $C_{th}=4$, $C_s=1$, ${\lambda }_U=5\times {10}^{-4}$, and ${\lambda }_E=1.5\times {10}^{-3}$.

5. Conclusions

In this paper, we investigate secure transmission in UAV relay-assisted mmWave networks where the beam alignment is achieved or not. The closed-form expressions for TP and SOP in both the on-off and non-on-off transmission schemes are derived by considering the beam alignment error or not. Analyzing the numerical and simulation results, we find that the SOP indeed can be improved by using the on-off transmission scheme, and the SOP can be further decreased by increasing the threshold of data transmission. In addition, the TP is not a monotonous function of the UAV relays’ altitude in the on-off transmission scheme, and there exist an optimal altitude of UAV relay to obtain the best TP. Moreover, the SOP will not deteriorate when the beam alignment error is relatively small, and we can improve the SOP by adopting the antenna with more elements. Nevertheless, in the high alignment error regime, the antenna array with smaller number of elements provides the better SOP.