Abstract
Cylindricity is a kind of three-dimensional form distortion of a cylinder. An accurate in situ measurement of cylindricity is relatively complex because measuring and reconstructing cylindrical profile and evaluating out-of-cylindricity should be involved. Any method of in situ measuring cylindricity must solve a common issue, i.e., to eliminate spindle error motions and carriage error motions during measurement and reconstruction. Thus, error separation techniques have played an important role in in situ cylindricity measurement through multipoint detections. Although several valuable five-point methods for in situ measurement of cylindrical profile have been proposed up to present, namely the parallel scan, spiral scan, and V-block scan, there are obvious differences in many aspects, such as the arrangement of probes, error separation model, reconstruction method, adaptability to service environment, accuracy and reliability in practical application, etc. This paper presents the evaluation of their advantages and disadvantages in theory and the actual measurement based on the standard ISO 12180. Suggestions for best meeting the requirements of modern manufacturing and the most prospective one for industrial applications are also given.
1. Introduction
Large rollers, whose sizes can sometimes reach a diameter of a few meters and a length of several meters, are employed in many heavy industries, e.g., papermaking, automobile, metallurgy, and shipbuilding. Such a roller should be characterized by high form accuracy, because its cylindricity errors would incorporate in the products, such as super calendar papers, roll-to-roll films, piston cylinders, and automobile steel sheets, etc. Using conventional roundness and cylindricity instruments may be impractical due to their large size and mass. Hence, there are increasing needs for accurate measurement of out-of-cylindricity of rollers in order to ensure the surface quality of the products. In situ measurements in production may be a good solution [1,2]. In general, a spindle supports the measured cylinder to rotate and a carriage slides along the longitudinal direction, which are indispensable in the in situ measuring system for the cylindricity. Raw probe signals representing radial deviations of the cylinder are always superposed by the radial error motions of the cylinder, which come from the spindle radial and tilt error motions, and the carriage straightness error motions [1,2,3,4]. Nevertheless, how to fully eliminate the radial error motions of the cylinder and straightness error motions of the carriage in the in situ measuring system is a great challenge [2,5]. Two basic issues are involved here: mathematical modeling of cylindrical profile and mathematical modeling of the measuring system.
1.1. Mathematical Modeling Cylindricity
The parameters and recommendations for measurement of cylindricity are described in the standard ISO 12180 [6]. The cylindrical profile can be considered as three superposed deviations: radial deviations, median line deviations, and cross-section deviations, as shown in Figure 1. Obviously, median line deviations denote out-of-straightness of the median line of a cylinder, and radial deviations and cross-section deviations denote the radius deviation and out-of-roundness of the cross-section, respectively.
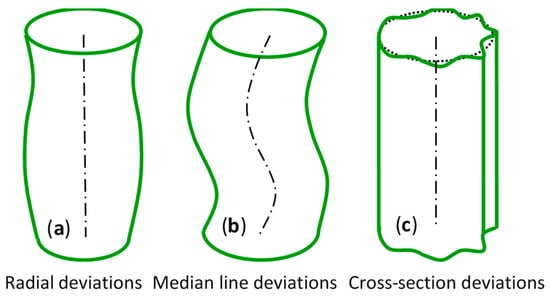
Figure 1.
Components of the cylindricity deviations.
Cylindrical profile is made up of sequential cross-sectional profiles arranged in the axial direction, and each cross-sectional profile can be described as definite periodic signals with a base frequency equal to rotational frequency of the cylinder [5]. Therefore, the cylindrical profile can be described as a Fourier expansion:
where, and are respectively the axial and angular coordinates of the cylindrical profile, and is the radius of the cross-sectional profile. , which denotes the harmonic vector of the cross-sectional profile, can be expressed with the Legendre interpolation, i.e., , and . Substituting and into Equation (1), the cylindrical profile can be rewritten as follows:
Term 2 in Equation (2) belongs to the first harmonic component of the cross-sectional profile. Let and , then, can be characterized as a vector from the rotating center in a cross-section of the cylinder to the least squares center (LSC) of the cross-sectional profile [5,7]. If the linear term about the Z-axis in is canceled, the cylinder as a whole will be tilted and moved, and the cylindrical profile will be not changed. Thus, the mathematical model of the cylindrical profile can be expressed by Equation (3).
where, is the first harmonic component of the cross-sectional profile. Obviously, a median line of the cylindrical profile, as shown Figure 1b, can be fitted through the LSC vectors in sequential cross-sections [5,6,8]. The harmonic component, , represents average radius deviations of sequential cross-sectional profiles, as shown Figure 1a. The sum of the harmonic components, denoted by , represents the out-of-roundness of sequential cross-sectional profiles, as shown Figure 1c.
From Equation (3), a feasible method of measuring and reconstructing a cylindrical profile can be suggested. It is to accurately measure the radius deviations, roundness errors, and LSC vectors of sequential cross-sections. Moreover, the median line is fitted through the LSCs, and cylindrical profile can be reconstructed by assembling the measured radius deviation and out-of-roundness of each cross-section on the fitted median line.
1.2. Mathematical Modeling of the Measuring System
Cylindricity errors are three-dimensional form deviations, and accurate measurement of cylindricity is relatively complex, should include measuring and reconstructing cylindrical profile, and evaluating out-of-cylindricity. Any in situ measuring system must employ several probes mounted onto a carriage to sense the radial deviations of the cylinder while the cylinder is rotating and the carriage is sliding along the longitudinal direction. It is known that rotating of the cylinder or sliding of the carriage have inevitable five degree-of-freedom geometric error motions due to their manufacturing and assembly errors. Therefore, the method of measuring cylindrical profile must be able to eliminate error motions of the cylinder and carriage in data analysis. Error separation techniques (ESTs) have been used in measurement of the form errors, such as straightness, flatness, roundness, and so on. Error separation techniques ensure measurement accuracy by separating form errors and error motions with specific designed setup and special mathematical modeling. In general, the three-point roundness EST [3,4,9] can remove the radial error motions in the cross-section of the cylinder and accurately determine radius deviations and out-of-roundness of the cross-sectional profile of the cylinder [3,5,9]. However, the first harmonic of the cross-sectional profile are inseparable from that of the radial error motions in the cross-section of the cylinder [3,4,5,8,9]. The first harmonic of the cross-sectional profile denotes the vector from rotating center to the LSC of the cross-sectional profile. Median line of the cylinder is a spatial curve that is fitted through the LSCs of sequential cross-sectional profiles [6,8]. Therefore, three-point roundness EST is insufficient to accurately determine a cylindrical profile.
Modeling of a probe sensing the cylindrical profile is particularly foundational for cylindrical profile measurement. Reference [10] built such a measurement model, as shown in Figure 2. is the global coordinate system, in which the cylinder coordinate system and the carriage coordinate system are located. Theoretically, there are ten terms of error motions, including the cylinder’s translational error motions and tilt error motions , as well as the carriage’s straightness error motions and three angular error motions of pitch , yaw , and roll . The vectors of the and in the system are and , respectively. Let the rotation angle of the cylinder be . In the system, the measuring point P locates at , and point P in the system would be offset due to the carriage error motions. If , , and quadratic terms of the errors are omitted, the actual position of point P in the system is:
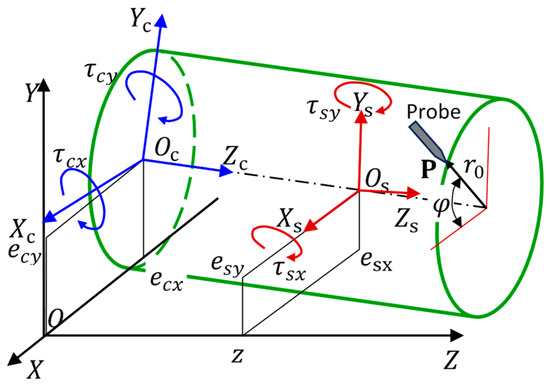
Figure 2.
Probe senses cylindrical profile and error motions [10].
In a similar way, in the system, because of point P’s offsets caused by the error motions of the cylinder, the actual position of point P in the system is:
Obviously, the output of the probe indicates their difference in system:
where, is the cylindrical profile. Equation (4) indicates that output of the probe is a mixture of cylindrical profile and all kinds of error motions in measuring system, in which [], [], [], and [] are the mutual independent error motions. Therefore, the minimum number of the probes in order to fully eliminate the error motions is five [10]. From Figure 2 and Equation (4), the three-point roundness EST [3,4,5,9] arranges three probes in one cross-section of the cylinder, and the error motions [] and [] are sensed by the probe, and can be canceled. If all error motions are expected to be eliminated, a few probes must be arranged in the axial direction to sense the error motions [] and [].
The literature on the subject of in situ measurement of cylindricity is limited. Nyberg [11] proposed the four-point EST for in situ measurement of cylindricity, which combines the concepts of two-point straightness and three-point roundness ESTs. The signals from the three probes were used to calculate radius deviations and out-of-roundness of each cross-sectional profile. Whereas the signals from the two probes placed at the same generatrix in the cylinder were employed to determine out-of-straightness of the generatrix. However, this method sidesteps the problem of accurately determining curved median line profile of the cylinder, although it was successfully verified on a dedicated measuring device by the experiments.
Several valuable five-point ESTs for in situ measurement of cylindrical profile have been reported [8,10,12,13]. They are clearly different in the arrangement of probes, error separation model, reconstruction method, adaptability to service environment, and accuracy of measuring and reconstructing. Related technical notes are presented in the following for comparing and evaluating pros and cons. Suggestions for best meets the requirements of modern manufacturing and the most prospective one for industrial applications will then be made.
2. Error Separation Models for In Situ Measurement of Cylindricity
2.1. Parallel Scan EST
Reference [8] presented a parallel scan EST for measuring cylindrical profile, as shown in Figure 3. Let the cylinder be divided by cross-sections, and the axial distance between each two cross-sections be . Five displacement probes are mounted onto the carriage, which moves along the Z direction. When the carriage is located at the position and the cylinder rotates one revolution, Probes 1–3 sense the mixed radial errors in the cross-section, meanwhile, Probes 4 and 5 sense the X directional mixed errors in the and cross-sections. When data collection is completed, the carriage moves a distance along the Z direction and enters the position. At this moment, Probes 1–3 locates in the cross-section and Probes 4 and 5 locate in the and cross-sections, respectively. Data collection of new revolution will be carried on.
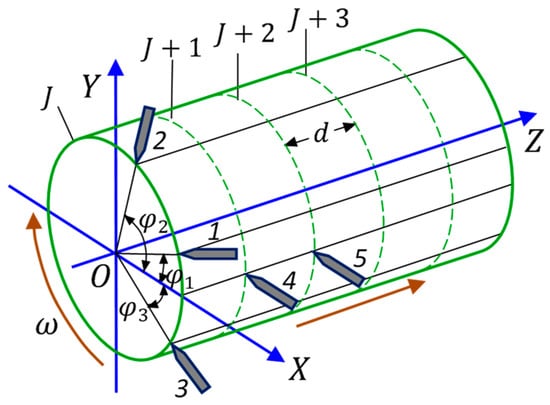
Figure 3.
Schematic of parallel scan EST for measurement of cylindrical profile. The 1–5 are the displacement probes.
When the carriage locates at the position, the cylinder is rotating and Probes 1–5 collects data. It was verified that the harmonic vector of the cross-sectional profile of the cylinder could be detected with the three-point roundness EST [3,4,5,8,9] by the outputs of Probes 1–3, denoted by . Therefore, and , indicating the radius deviation and out-of-roundness of the cross-sectional profile, can be accurately determined. In addition, , indicating the separated result of the X directional error motions in the cross-section of the cylinder, can be obtained by the outputs of Probes 1 and 2, as shown in Ref. [8,14]. The first harmonic vector should be , here, is the discrete Fourier transform operator.
Simultaneously, Probes 4 and 5 sense the X directional mixed errors, including the and cross-sectional profiles, denoted by and , the X directional error motions in the cross-section and the tilt error motion of the cylinder around the Y direction , as well as the X directional straightness deviations of the carriage and yawing , as shown in Figure 2 and Figure 3. From Equation (4), the outputs of Probes 4 and 5, denoted by , are given by
Applying Discrete Fourier transform () to and , we may obtain the harmonic vectors of the outputs of Probes 4 and 5, denoted by and , in which the first harmonic vectors are and , respectively.
is designated as the first harmonic vector of the X directional additional error motions induced by the tilt error motions of the cylinder around the Y-axis. Referencing the sequential three-point straightness EST [5,15], the iterative formulas used to extract , representing the LSC vectors of each cross-sectional profile, ware derived in in Appendix of Reference [14]. When the carriage locates at the first position, let and be equal to “zero”. The first harmonic vector of the cross-sectional profile is extracted by:
The LSC vector of the cross-sectional profile is or , with which a curved median line of the cylinder can be accurately fitted, here, . It is noteworthy that the curved median line fitted through the LSCs of each cross-sectional profile, as a whole, undergoes little movement and inclination because and are all set to “zero”, rather than their truth-values. The correctness of the curved median line profile will not be affected.
Now, by means of the three-point roundness EST and Equation (6), as well as and , indicating the harmonic vectors of the cross-sectional profiles, can be detected accurately. A reconstructed cylindrical profile, denoted by , can be achieved by;
Where, is the inverse discrete Fourier transform operator. Theoretical analysis and numerical validation about this EST have been performed in Reference [8]. The results verify that error motions of the cylinder and carriage are all removed, i.e., full harmonic error separation is realized. The LSCs of each cross-sectional profile of the cylinder are accurately extracted even if the error motions of the cylinder are not repeatable in each rotation. The spatial curved median line of the cylinder is accurately determined by fitting through the LSCs of the sequential cross-sectional profiles. The cylindrical profile conforming to the standard ISO 12180 [6], can then be reconstructed by Equation (7), as shown in Equation (3). The cylindrical form errors, not only cylindricity but also out-of-roundness, generatrix straightness, taper angle, and radius deviation, can be evaluated simultaneously by using the reconstructed cylindrical profile.
2.2. Spiral Scan EST
Reference [10] presented the spiral five-probe arrangement for measurement of cylindrical profile, as shown in Figure 4. Five displacement probes arranged in a spiral scanning-path are mounted onto the carriage, which moves along the Z direction. This system makes it possible to transform the cylindrical profile measurement to the one-dimensional straightness measurement of the spiral profile on the cylinder given that the rotation of the cylinder keeps pace with the movement of the carriage. Let the total number of scanning points per revolution be , and the scanning angular interval should be . When probes move along the spiral line, the variable of the carriage moving along the Z direction is proportional to the variable of the cylinder rotating, i.e., , where, constant is the pitch of the spiral line. The angular positions of Probes 1–5 are with respect to the X direction, and axial positions are , respectively. When the cylinder rotates and the carriage moves synchronously, several error motions come up as shown in Figure 2, including the cylinder’s radial error motions and tilt error motions , as well as the carriage straightness error motions and pitching , yawing . Here, is number of total rotating circle of the spiral line on the cylinder. Let be the spiral line profile on the cylinder. According to Equation (4), the outputs of the five probes, denoted by , can be written as follow:
where, ; are the initial zero-setting values of the probes. Similarly to the three-point straightness EST based on [5,16], the weighted output of Probes 1–5 should be . Let the weighted coefficients be and , and , . The weighted output can be rewritten as: Where, is the weighted initial zero-setting value. Obviously, all error motions of the cylinder and carriage are removed from . Moreover, applying the to and introducing the time-shift theorem, we can obtain the harmonic vectors of the weighted output as follows:
where, . If the transfer function , the harmonic vectors of the spiral line profile on the cylinder are:
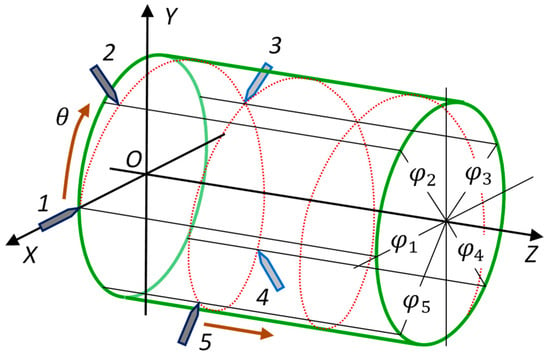
Figure 4.
Schematic of spiral scan EST [10]. The 1–5 are the displacement probes.
According to the properties of the , and . Similar to the parallel scan EST, the initial zero-setting value – of Probes 1–5 is also allocated a value of zero or the nominal radius, which will not affect the spiral line profile on the cylinder. Applying the to , we may obtain , indicating the spiral line profile on the cylinder. A reconstructed cylindrical profile should be:
It’s worth noting that, different from the parallel scan EST, the spiral scan EST measures the one-dimensional straightness of the spiral profile on the cylinder, and reconstructs an integral cylindrical profile. It is difficult to distinguish the radius deviation and out-of-roundness of each cross-section, as well as the profile of the spatial curved median line of the cylinder.
2.3. V-Block Scan EST
Ref. [1,12,13,17] presented the V-block scan EST for measurement of cylindrical profile as shown in Figure 5. An element connecting the two V-blocks functions as guideway, along which a carriage moves. A displacement probe is mounted onto the carriage. When the cylinder driven by the spindle rotates, probe keeps collecting data. At the moment, two V-blocks should contact reliably with the surface of the cylinder, and the measuring system should avoid rotating around and moving in the Z-axis. Because five points are contact with the measured surface during measuring, this system may be regarded as an analogous five-point EST measuring system.
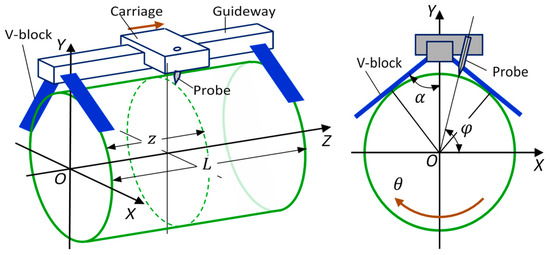
Figure 5.
Schematic of V-block scan EST [1,12,13]. The left shows the measured cylinder in the OXYZ system; the right shows the cross-section of the cylinder in the plane of the V-block.
As shown in Figure 5, the OXYZ system was assumed in such a way that the Z-axis coincides with the axis of the nominal cylinder, and the plane determined by the X- and Y-axes coincide with the plane of the left V-block. The Y-axis is the angular bisector of the V-block. Let the total number of scanning points per revolution be , and the scanning angular interval should be . Let the angular position of the probe be with respect to the X-axis, and the half angle of the V-block be . Because the system rides on the cylinder during measuring, the radial and tilt error motions of the cylinder will have nothing to do with the output of the probe. However, as those two cross-sectional profiles that are contacted by two V-blocks have roundness errors, it would make the measuring system generate the radial and tilt error motions. At this moment, the probe situated in measured cross-section will collect the radial mixed errors, including the cross-sectional profile , the measuring system’s radial error motions in the cross-section where the probe is, as well as the carriage straightness error motions , in the location where the probe is. According to Equation (4), the output of the probe should be:
where, the initial zero-setting value of the probe is omitted due to without impact on accurate measurement. It is worth noting that , indicating the measuring system’s radial error motions in measured cross-section, are caused by the cross-sectional profiles in contacted with the two V-blocks. There are obviously four points on the V-blocks in contact with the cross-sections defined by the plane of the cylinder. If the contacted points are regarded as the virtual probes, output of the virtual probes in the cross-sections should be “zero”. It is obvious that the cross-sectional profiles control the radial error motions of the measuring system in the cross-sections, denoted by .
At this moment, if the carriage moves, and the probe locates in the cross-sections, respectively, the probe collects the radial mixed errors during cylinder rotating. The outputs of the probe should be , as shown in Equation (12). Taking to , we will achieve the harmonic vector of the cross-sectional profiles , as follow.
where, is the transfer function, and are the harmonic vectors of the output of the probe when it locates in the cross-sections. are the harmonic vectors of the disturbances from the carriage straightness error motions when the probe locates in the cross-sections.
If stiffness of the measuring system is sufficient, the radial error motions of the measuring system in measured cross-section, denoted by , should be the linear combination of . Here, their harmonic vectors, denoted by and , can be achieved.
Now, taking to Equation (12), we will obtain the harmonic vector of the output of the probe when it locates in measured cross-section:
Bringing and into Equation (14), we can determine , indicating the harmonic vectors of the measured cross-sectional profile of the cylinder.
where, is the harmonic vector of the output of probe in measured cross-section. is the harmonic vector of the disturbances from the carriage straightness error motions in measured cross-section. A reconstructed cylindrical profile can be achieved by taking to , similarly to Equation (6). However, it is worth noting that Equations (13)–(15) are true if the transfer function , in addition, the disturbances from the carriage straightness error motions will impact the accuracy of the V-block scan EST.
3. Applicative and Comparative Analysis for In Situ Measurement of Cylindricity
Three error separation models for in situ measurement of cylindricity have been investigated as above. Theoretically, they all can be used to measure and reconstruct cylindrical profile. However, their validity and accuracy need to be verified by numerical verifications through experiments so as to further reveal characteristic features as well as main benefits and drawbacks.
3.1. Experimental Verification and Analysis of Parallel Scan EST
An experimental system based on the parallel scan EST was setup as shown in Figure 6. The headstock and tailstock supported the cylinder. The carriage had three parallel sections separated by a distance d = 40 mm. Five inductive displacement probes (TESA GTL 21 DC) were mounted onto the carriage, in which Probes 1–3 were mounted in the left section according to the three-point roundness EST, and Probes 4 and 5 were located in the middle and right sections. An angular encoder (RENISHAW RESM 52, 8192 lines, zero line, 5 subdivisions) was mounted on the rotor in the headstock to control the course of data acquisition so as to obtain uniform sampling on the circumference. The total number of sampling points per revolution N was 1024. In order to avoid the non-first harmonic suppression [3,4,5,8,14] and achieve the large error transfer function , the angular positions of the Probes 1–3 were set respectively as shown in Figure 7. The rotational speed of the cylinder was 1 rpm.

Figure 6.
Photograph of the parallel scan EST experimental system.
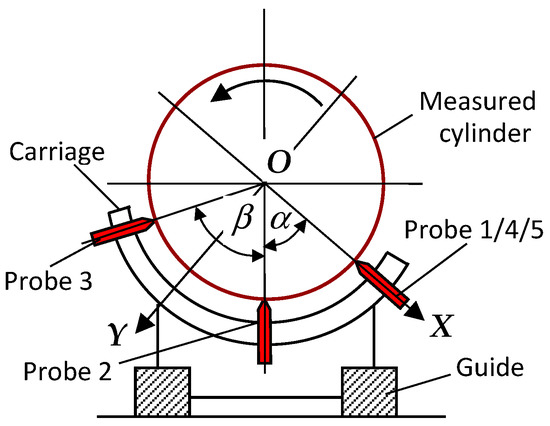
Figure 7.
Angular positions of Probes 1–5.
It can be seen from Figure 3 and Equation (6) that the parallel scan EST is to simultaneously execute the three-point roundness and sequential three-point straightness ESTs [5,8] for the detection of the radius deviation, out-of-roundness, and LSC of each cross-section of the cylinder, respectively. A novelty of the EST is to accurately detect the spatial curved median line of the cylinder and to measure and reconstruct cylindrical profile consistent to the standard ISO 12180 [6]. The key to verifying the validity of the EST is to evaluate the accuracy of the measured curved median line profile of the cylinder. Currently, there is not a mature method to calibrate the curved median line profile, and it is difficult to investigate the error motions of the cylinder. Therefore, we will compare the repeatability of the curved median line profiles to prove the accuracy. In engineering practices, the high repeatability of measurement results will indicate high-precision of the measurements, and also high accuracy to some extent.
Six measurement experiments were conducted on the experimental system for same cylinder shown in Figure 6, the number of the cross-section divided in the cylinder was . A set of software was developed to sequentially control the course of measurements and data collections of Probes 1–5. By calculating Equation (6) with iterative, the LSC vector of the cross-sectional profile of the cylinder was extracted, with which the curved median line profile was fitted in each experiment, as shown in Figure 8. Although the profiles of the curved median line were quite consistent among in the six experiments, the variations of the extracted LSC vector of each cross-sectional profile were significant, being approximately within the range ±2.5 ± 2.5iμm, which cannot be a convincing proof of the accuracy of the parallel scan EST for measuring cylindrical profile.
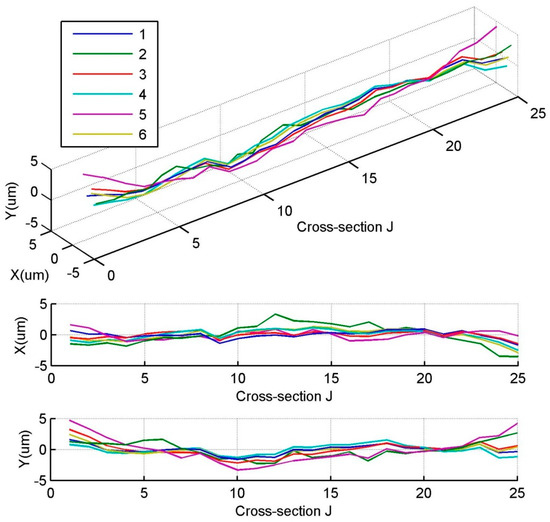
Figure 8.
Median line profiles measured by the parallel five-point EST.
Theoretically, this EST can eliminate the radial and tilt error motions of the cylinder as well as the carriage straightness error motions. Actually, similarly to the sequential three-point straightness EST, the double integration calculations [15] as Equation (6) are executed for detecting the LSC vectors of each cross-sectional profile of the cylinder, which reduces the anti-interference capacity of the EST. Influences of various interferences on detecting the LSC vectors of each cross-section are amplified, which conduct the large variations in the measured median line profiles. In particular, when there are significant systematic interferences in the measuring system, such as inconsistencies in sensitivity and linearity, angular and positional errors of five probes, an obvious distortion of the measured median line profile will occur. Even more, the larger the total number of the cross-section in the cylinder is, the more serious the distortion is.
Comparatively, if the outputs of Probes 1–4 are used to measure and reconstruct the cylindrical profile, this EST will become an integrated EST of the three-point roundness and sequential two-point straightness. Here, the sequential two-point straightness EST [18] is executed for the detection of the LSC vector of each cross-sectional profile of the cylinder. Let us see Equation (6), , which is the first harmonic vector of the additional X directional error motions induced by the tilt error motions of the cylinder around the Y-axis of each position, should be omitted, and the double integration calculations will be avoided. At this moment, the tilt error motions of the cylinder cannot be removed although the influences of various interferences on detecting the LSC vector of each cross-section are weakened. In engineering practices, the tilt error motions of the cylinder are much smaller, particularly in case if the cylinder is long and the rotation speed is low. Figure 9 shows the curved median line profiles measured by the outputs of Probes 1–4. Obviously, the measured profiles are in good consistency in six experiments, and the variation of the extracted LSC vector of each cross-sectional profile is within the range ±1 ± 1iμm, which shows a convincing proof of the accuracy of the parallel scan EST for measuring cylindrical profile.
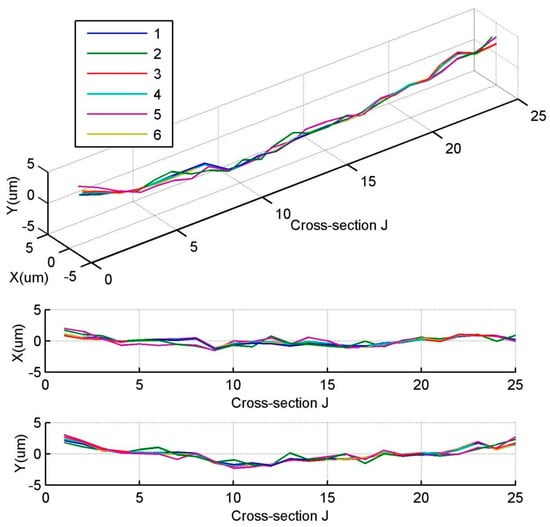
Figure 9.
Median line profiles measured by the parallel four-point EST.
The accuracy of the extracted LSC vectors of sequential cross-sectional profiles by the four-point EST is higher than that extracted by the five-point EST if the tilt error motions of the cylinder are small and negligible. Figure 8 and Figure 9 show that the profiles of the curved median line measured by two parallel ESTs differ slightly, and the conformity of the spatial median line measured by the parallel four-point EST is validated to be higher in the six experiments, which implies that the tilt error motions of the cylinder of the experimental system is small. Therefore, the parallel four-point EST is more suitable for in situ measurement of cylindricity of the large-scale roller, where the tilt error motions of the cylinder are indeed small in case that the cylinder is long and the rotation speed is low. On this basis, the cylindrical profile can be accurately reconstructed by Equation (7).
3.2. Applicative Analysis of Spiral Scan EST
Theoretically, the spiral scan EST for measuring the cylindrical profile must face two basic queries. One is harmonic suppression and the other is the multi-point straightness EST based on . As stated above, Equation (9) would be true if the transfer function was not “zero”. However, when , the transfer function should be:
This means that the harmonic suppression happens in this EST, i.e., the harmonic component of the spiral line profile on the cylinder is unable to exactly be determined. In Reference [10], the partial transfer function was shown as Figure 10.
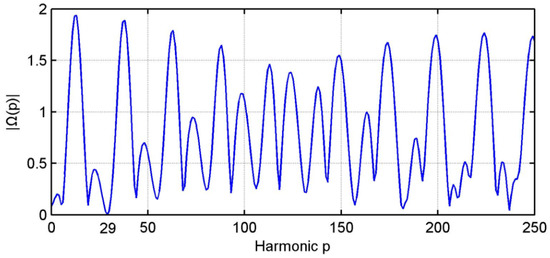
Figure 10.
Transfer function of spiral scan EST. Here, angular position of five probes is 0°, 395°, 838.7°, 1236.5°, 1658.8°, respectively, and pitch of spiral line is . Number of total rotating circles of spiral line is [10].
A numerical validation procedure has been developed in this study to help qualitative and quantitative evaluation of the cylindrical profile obtained by this EST. Whether the harmonic suppression impacts correct detection of spiral line profile on the cylinder should be verified first.
We created a set of given data to describe a virtual spiral line profile on the cylinder. A series of random data was used to simulate the radial error motions of two imaginary rolling bearings that supported the cylinder to rotate so that the different error motions in each revolution were simulated. A series of the other random data was used to simulate the carriage straightness error motions including yaw and pitch. The outputs of five probes were set according to Equation (8), and then, the procedures of reconstructing the spiral line on the cylinder were carried out according to Equations (9)–(11).
As shown in Figure 11, the given spiral line profile on the cylinder only with the median line deviations is similar to Figure 1b. The difference between the measured spiral line profile and given one presents periodicity, which is the harmonic component of the spiral line profile on the cylinder. Such a difference causes the spiral line profile measured by this EST to slightly shift as a whole, yet the profile of the spiral line is not distorted. Therefore, the harmonic suppression of this EST will not impact the accuracy of measuring the spiral line profile.
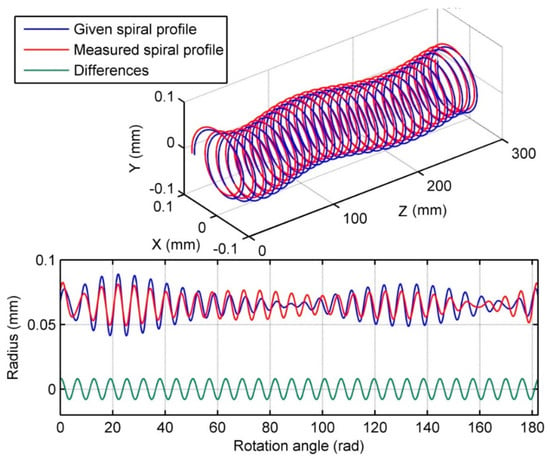
Figure 11.
Comparison of the measured spiral line profile with given one in the case of ideal measurement. Here, angular position of probes is 0°, 395°, 838°, 1236°, 1659°, respectively, and pitch of spiral line is . Number of total rotating circles of spiral line is .
The measured spiral line profile as shown in Figure 11 is based on a kind of “ideal measurement”, i.e., based on an assumption that the straightness profile of the spiral line is closed, because the spiral scan EST is based on in theory. In the case of “ideal measurement” during numerical validations, the sampling of five probes were carried out under the condition that the starting point and ending point of given spiral line profile were connected. However, it is impossible in actual measurements. If the angular distance between Probes 1 and 5 is and the total rotation angle of the cylinder is , Probes 2–4 cannot normally collect data in the angular range from to during actual measurement. Now, how to estimate the output of Probes 2–4 in this angular range would affect the precision of the measured spiral line profile on the cylinder. Here, the outputs of Probes 2–4 in the angular range from to are assigned with the data collected by Probe 1 in the angular range from 0 to so as to best agree with the requirement for closed profile. Figure 12 demonstrates the verified results of this EST in the case of “actual measurement”.
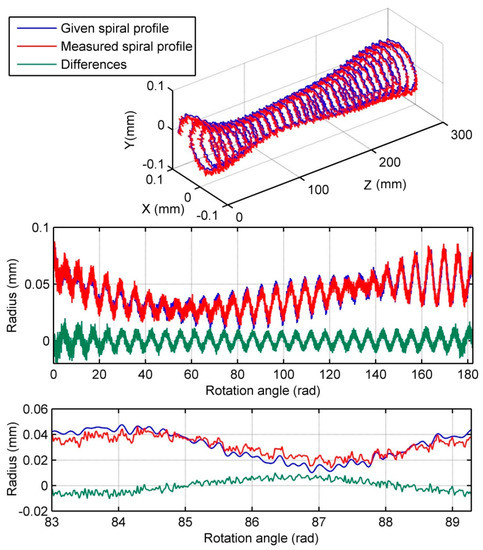
Figure 12.
Comparison of the measured spiral line profile with given one in the case of actual measurement. Here, angular position of probes is 0°, 395°, 838°, 1236°, 1659°, respectively, and pitch of spiral line is . Number of total rotating circles of spiral line is .
From Figure 12, it may be found that the given spiral line profile on the cylinder with the median line deviation, radius deviations and roundness errors, and the measured spiral line profile is almost the same as the given one except for its slight translation. Their differences also present the periodicity of the harmonic. Because the data substitutions of Probes 2–4 introduce some errors, the difference between the measured spiral line profile and given one has the high-frequency components. In addition, the measured spiral line profiles at both ends of the cylinder are deteriorated significantly. However, in engineering practice, we pay attention to low frequency parts of the measured profile, high frequency error in the measured profile can be eliminated by filtering. Therefore, the shortened effective measurement length of the spiral line profile is a weakness of this EST. It is worth noting that the above numerical verification results were obtained under the condition that the radial error motions of two imaginary rolling bearings and carriage error motions were only 20% of the given spiral line profile on the cylinder. If this ratio goes up, the confidence level of the spiral line profile measured by this EST will be greatly decreased.
In Reference [10], a prototype instrument was developed based on the spiral scan EST. Comparing the results of the instrument with that of a commercial roundness measuring machine indicated the feasibility of measuring out-of-roundness, but the instrument seemed to be not able to identify the curved median line profile of the cylinder. In the opinion of the authors of Reference [10], the harmonic suppression issue in this EST was worth in-depth examined. Whereas, they did not touch the issue of the multi-point straightness EST based on .
3.3. Applicative Analysis of V-Block Scan EST
Frist, we should evaluate the validity and accuracy of the V-block scan EST based on the standard ISO 12180 [6]. From Equation (15), we seem to obtain the measured cross-sectional profiles . However, from Equation (13), it can be verified that the transfer function , as shown below.
Therefore, Equations (13) and (15) are not true in this case, the first harmonic suppression occurs in the V-block scan EST. It can be seen that and , which indicate the first and harmonic vectors of the cross-sectional profiles, cannot be accurately extracted. In other word, the LSCs vectors of the cross-sectional profiles are unknowable.
On the basis of routine, and will be set as “zero”. Then, and could be also regarded as “zero” because the radial and tilt error motions of the measuring system are controlled by the cross-sectional profiles. In view of the properties of , there are and in Equation (13). From Equation (15), , which indicate the first and harmonic vectors of the measured cross-sectional profiles of the cylinder, are:
However, and are actually existent and are typical of the LSC vectors of the cross-sectional profiles in contact with two V-blocks. They induce and , indicating the first harmonic vectors of the radial error motions of the measuring system. Substituting and into Equation (14), , which indicate the first and harmonic vectors of the output of the probe, can be rewritten as follow:
Equation above shows that comprises and linear combination of and . However, from Equation (16), the LSC vectors in the measured cross-sections are just based on the line connecting the actual LSCs of the cross-section, i.e., and . Hence, the spatial curved median line fitted by or has a little movement and inclination, based on which the cylindrical profile can be reconstructed accurately even if the suppression of the first harmonic exists.
The non-first harmonic suppression [3,4,5,8,14], which denotes the transfer function , will impact the measurement accuracy of the out-of-roundness of each cross-sectional profile of the cylinder. Whether suppression of the non-first harmonic exists in this EST will depend on the values of angular parameters of and as shown in Figure 5. Digital simulations were performed to verify how to configure parameters of and to avoid the non-first harmonic suppression. Figure 13 demonstrates the relationships between the angular parameters and the harmonic suppression. It may be found that if and , the harmonic suppression occurs. Especially, when , full harmonic suppression will occur. Let total number of scanning points per revolution be and , and , the non-first harmonic suppression of this EST will be avoided provided that , and the greatest common factor of and as well as is 1, e.g., and . Therefore, this measuring system needs to carefully adjust the angular position of the probe so as to avoid the non-first harmonic suppression and get the transfer function as large as possible.
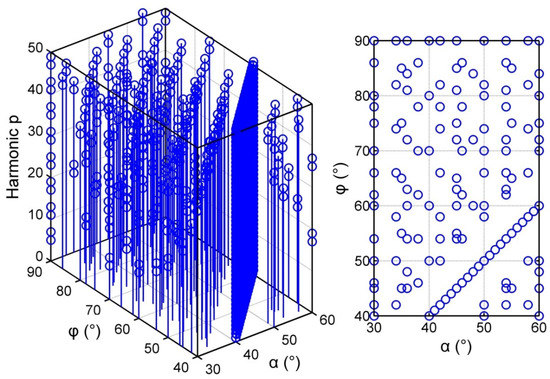
Figure 13.
Non-first harmonic suppressions and the values of angular parameters of and . If transfer function at given and , the harmonic suppression occurs. Here, and , harmonic order .
The harmonic component denotes the radius deviations of the sequential cross-sectional profiles. From Equation (15), measurement accuracy of the radius deviations depends on:
It is known that and come from and , i.e., the carriage straightness error motions in the cross-sections, in other word, the guideway’s slope in the XOZ and YOZ plane. Due to the existence of guideway’s errors at the cross-sections, the reconstructed cylindrical profile would produce a conical form. , indicating the harmonic component of the disturbances from the carriage straightness error motions in the measured cross-section, directly results in the measurement errors in the radius of the reconstructed cylindrical profile, as shown in Figure 1a.
In References [12,13,17], computer simulations of this EST for measurement of cylindrical profile were conducted to assess the non-first harmonic suppression. The results indicate that the 11th harmonic component exists when and were selected. From Figure 13, the harmonic suppression occurs in this case. It is a weakness that the straightness deviations of the guideway affect directly measurement accuracy of the cylindrical profile. It yields the necessity to compensate for the carriage straightness deviations in order to improve the measurement accuracy. In the authors’ opinion, however, the compensation method should not change the fact that guideway’s slopes in XOZ and YOZ planes would make the reconstructed cylindrical profile be a conical form. A measuring system allowing cylindricity measurements by this EST was constructed [12,13,17]. Some potential sources of systematic errors, such as, unequal angles of V-blocks, calibration error of the probe, deflection of the probe axis from its nominal orientation were analyzed. A series of experiments were conducted involving the comparison of measurement results of a group of cylindrical elements. The cylindricity deviation of each sample element was determined with two methods: V-block scan EST and high accurate radial method [19]. The conducted tests showed that the difference lies within the interval ±19% (for a probability level p = 0.95).
4. Conclusions
Three five-point ESTs used for in situ cylindricity measurement were analyzed to determine their characteristic features as well as main benefits and drawbacks.
The following are conclusions drawn about the parallel scan EST:
- Measurement of cylindrical profile was performed with five displacement probes. Outputs from five probes were used to measure radius deviations and roundness deviations of sequential cross-sectional profiles, as well as the LSC vectors of sequential cross-sectional profile, with which spatial curved median line profile of the cylinder was determined. Further, cylindrical profile could be accurately reconstructed by assembling each obtained cross-sectional profile onto the spatial curved median line.
- The completeness of the measurement model in theory is promising. Accurate detection of the spatial curved median line of the cylinder highlights its novelty, and the error motions of the cylinder and carriage in measuring system are fully eliminated.
- Detecting full harmonic components of sequential cross-sectional profiles is dependent on how the three probes in one cross-section are located relative to each other. Therefore, to ensure good anti-interference capability, angular arrangement of the three probes should be carefully selected so as to obtain large transfer function .
- The probes should be strictly calibrated and carefully chosen. Especially, inconsistencies of sensitivity and linearity among five probes should be overcome as much as possible, which is a main factor impacting on the precision of spatial curved median line of the cylinder.
- Accuracy of the method has not been verified by calibration.
- The method is suitable for on-machine measurement of cylindrical profile. Where, the carriage can be mounted onto the tool carriage. Measurement cost is relatively low.
- The parallel four-point scan EST is more suitable for in situ cylindricity measurement of large-scale roller, where the tilt error motions of the cylinder are negligible because the roller is long and the rotation speed is low.
The conclusion about spiral scan EST can be summarized as follows:
- Measurement of cylindrical profile is performed with five displacement probes, which are arranged in a spiral scanning-path. Cylindrical profile measurement is transformed to one-dimensional straightness measurement by the multi-point straightness EST based on .
- The multi-point straightness EST based on is built in an assumption that the straightness profile is end-to-end. The actual spiral profile on the cylinder is impossible to achieve. Therefore, direct adoption of straightness EST based on to measure and reconstruct spiral profile on the cylinder would weaken the theoretical completeness.
- The way to fill a segment of data of Probes 2–4 at the tail end of measurement becomes a crucial factor to determine measurement accuracy. In light of the authors’ experience, if straightness errors of actual spiral profile are significant in the outputs of the probes, it may be a good solution that a segment of data of Probes 2–4 at the tail end of measurement are assigned by the data collected by Probe 1 at the head end of measurement.
- The harmonic suppression of the EST will not impact measurement accuracy of the spiral line profile. It only causes a slight shift of the measured spiral line profile.
- Because a segment of data of Probes 2–4 at the tail end of measurement is uncertain, the accuracy of the measured spiral line profiles at both ends of the cylinder deteriorated significantly. Therefore, the shortened effective measurement length of the spiral line profile is a weakness.
- Accuracy of the method has not been verified by calibration.
- If this EST is employed in situ measurement of cylindricity, motion accuracy of the guideway and spindle should be high.
The conclusions about V-block scan method can be summarized as follows:
- Measurement of cylindrical profile was performed with the measuring system made up of two V-blocks and a displacement probe. During measuring, two cross-sectional profiles that contact two V-blocks control the radial and tilt error motions of the measuring system, yielding repeatable error motions of the measuring system in each revolution. This makes the measured cylindrical profile immune to the error motions of the cylinder.
- Error motions of the cylinder are removed, whereas, the carriage straightness error motions will directly impact the measurement accuracy of cylindrical profile, which would weaken the theoretical completeness.
- Detecting full harmonic components of sequential cross-sectional profiles is dependent on selection angular values of the probe and V-block. Therefore, to ensure good anti-interference capability, angular value of the probe should be carefully selected so as to obtain large transfer function .
- The measurement uncertainty was assessed through statistical testing. The expanded uncertainty reached 19% compared to the results obtained with the highly accurate radial method. This EST was verified in practice using a model test stand, not on a large roller.
- It is a portable system, and is suitable for in situ measurement.
- During measurement, it is crucial to avoid the measuring system rotating around and moving in the Z-axis of the cylinder. How to decrease the impact from straightness deviations of the guideway is crucial to measurement accuracy.
- Compensation for the straightness deviations of the guideway was proposed to improve the measurement accuracy. In the authors’ opinion, however, it may be a good solution to diametrically arrange the second probe in the axial direction of the original probe.
Summing up, the parallel four-point scan technique is recommended for on-machine measurement cylindricity of large rollers, where spindle tilt error motions are negligible. Diametrical arrangement of the second probe in the axial direction of original probe will make the V-block scan EST be the most prospective technique for short roller. However, it is worth noting that, in actual multipoint EST, the main factor of impact on measurement accuracy is the inconsistency of characteristics between multiple displacement probes; therefore, probes should be carefully chosen.
Author Contributions
W.L. and K.F. conceived and investigated; P.H. designed the experimental system and performed the experiments; W.L. simulated, analyzed and wrote; K.F. modified.
Funding
This research was funded by [National Natural Science Foundation of China] grant number [51475132 and 51475133] and [Natural Science Foundation of Anhui Province of China] grant number [1508085ME81].
Acknowledgments
This study has been supported by the National Natural Science Foundation of China (Grant Nos.: 51475132, 51475133) and the Natural Science Foundation of Anhui Province of China (Grant No.: 1508085ME81). The authors would like to thank the other members of the research team for their contributions to this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| EST | Error separation technique |
| LSC | Least squares center |
| DET | Discrete Fourier transform |
| IDET | Inverse discrete Fourier transform |
References
- Stępień, K. In situ measurement of cylindricity—Problems and solutions. Precis. Eng. 2014, 38, 697–701. [Google Scholar] [CrossRef]
- Lee, J.C.; Yuki, S.Y.; Gao, W.; Oh, J.; Park, C.H. Precision evaluation of surface form error of a large-scale roll workpiece on a drum roll lathe. Precis. Eng. 2014, 38, 839–848. [Google Scholar] [CrossRef]
- Ozono, S. On a new method of roundness measurement on the three-point method. Proc. ICPE 1974, 1974, 457–462. [Google Scholar]
- Shi, S.Y.; Lin, J.; Wang, X.F.; Zhao, M. A hybrid three-probe method for measuring the roundness error and the spindle error. Precis. Eng. 2016, 45, 403–413. [Google Scholar] [CrossRef]
- Li, S.Y.; Dai, Y.F.; Xie, X.H. On-Side Measurement and Error Compensation Technology for Precision and Ultra-Precision Machining; University of Defense Science and Technology Press: Changsha, China, 2007; pp. 95–279. ISBN 978-7-81099. (In Chinese) [Google Scholar]
- ISO 12180-1 2011, Annex B: Geometrical Product Specifications (GPS)—Cylindricity—Part 1: Vocabulary and Parameters of Cylindrical Form—Consideration in the Assessment of Deviations from Cylindrical Form (International Organization for Standardization). Available online: https://www.iso.org/obp/ui/#iso:std:iso:12180:-1:ed-1:v1:en (accessed on 16 October 2018).
- Zhang, L.; Zhao, Y.; Ba, L. Research and practice on the on-line measurement of cylindricity error in a grinding machine. Key Eng. Mater. 2008, 359–360, 176–180. [Google Scholar]
- Liu, W.W.; Fan, K.C.; Hu, P.H.; Hu, Y. A parallel error separation method for the on-line measurement and reconstruction of cylindrical profiles. Precis. Eng. 2018, 51, 1–9. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Venkatachalam, B.; Raja, J.; Malburg, M. A note on the three-point method for roundness measurement. Precis. Eng. 2005, 29, 257–260. [Google Scholar] [CrossRef]
- Endo, K.; Gao, W.; Yiyono, S. A new multi-probe arrangement for surface profile measurement of cylinders. JSME Int. J. Ser. C 2003, 46, 1531–1537. [Google Scholar] [CrossRef]
- Nyberg, T.R. Dynamic Macro Topography of Large Slowly Rotating Cylinders (Acta Polytechnica Scandinavica, Mechanical Engineering Series); Finnish Academies Technology: Helsinki, Finland, 1993; Volume 108. [Google Scholar]
- Adamczak, S.; Janecki, D.; Stępień, K. Cylindricity measurement by the V-block method—Theoretical and practical problems. Measurement 2011, 44, 164–173. [Google Scholar] [CrossRef]
- Stępień, K.; Janecki, D.; Adamczak, S. Investigating the influence of selected factors on results of V-block cylindricity measurements. Measurement 2011, 44, 767–777. [Google Scholar] [CrossRef]
- Liu, W.W.; Zeng, H.; Liu, S.L.; Wang, H.T.; Chen, W.Y. Four-point error separation technique for cylindricity. Meas. Sci. Technol. 2018, 29, 075007. [Google Scholar] [CrossRef]
- Gao, W.; Yokoyama, J.; Kojima, H.; Kiyono, S. Precision measurement of cylinder straightness using a scanning multi-system. Precis. Eng. 2002, 26, 279–288. [Google Scholar] [CrossRef]
- Li, C.J.; Li, S.Y.; Yu, J.M. High resolution error separation technique for in-situ straightness measurement of machine tools and workpiece. Mechatronics 1996, 6, 337–347. [Google Scholar] [CrossRef]
- Adamczak, S.; Janecki, D.; Stępień, K. Qualitative and quantitative evaluation of the accuracy of the V-block method of cylindricity measurements. Precis. Eng. 2010, 34, 619–626. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y. Accuracy analysis of time domain two-point and three-point EST linearity. Chin. J. Sci. Instrum. 1998, 19, 106–108. [Google Scholar]
- Dawson, D.J.W. Cylindricity and its measurement. Int. J. Mach. Tools Manuf. 1992, 32, 247–253. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).