Abstract
1,1,1,2,3,3,3-Heptafluoropropane (R227ea) is a good refrigerant that reduces greenhouse effects and ozone depletion. In practical applications, we usually have to know the compressed liquid densities at different temperatures and pressures. However, the measurement requires a series of complex apparatus and operations, wasting too much manpower and resources. To solve these problems, here, Song and Mason equation, support vector machine (SVM), and artificial neural networks (ANNs) were used to develop theoretical and machine learning models, respectively, in order to predict the compressed liquid densities of R227ea with only the inputs of temperatures and pressures. Results show that compared with the Song and Mason equation, appropriate machine learning models trained with precise experimental samples have better predicted results, with lower root mean square errors (RMSEs) (e.g., the RMSE of the SVM trained with data provided by Fedele et al. [1] is 0.11, while the RMSE of the Song and Mason equation is 196.26). Compared to advanced conventional measurements, knowledge-based machine learning models are proved to be more time-saving and user-friendly.
1. Introduction
The increasing problems of greenhouse effect and ozone depletion have drawn people’s great attentions during the past decades [2,3,4,5]. In the field of heating, ventilation, air conditioning, and refrigeration (HVAC and R) [6,7,8], scientists started to use 1,1,1,2,3,3,3-heptafluoropropane (R227ea) [9,10,11] as a substitute in order to replace other refrigerants that are harmful to the ozone (like R114, R12, and R12B1), because R227ea has a zero ozone depletion potential (ODP) [12]. Other applications of R227ea include the production of rigid polyurethane foams and aerosol sprays [11,13]. R227ea has been shown to be crucial in industrial fields and scientific research.
In practical applications, the use of R227ea requires the exact values of the compressed liquid densities under certain values of temperatures and pressures. However, due to the complexity and uncertainty of the density measurement of R227ea, precise values of the density are usually difficult to acquire. To solve this problem, molecular dynamic (MD) simulation methods [14,15,16] have been used for predicting related thermophysical properties of refrigerants. Nevertheless, these simulation methods have high requirements for computers and require long computational times. Additionally, they need accurate forms of potential energy functions. Motivated by these issues, here, as a typical case study, we aim at finding out alternative modeling methods to help acquire precise values of the densities of R227ea.
Acquiring the density by theoretical conclusion is an alternative approach to replace the MD methods. Equation of state is one of the most popular descriptions of theoretical studies that illustrates the relationship between temperature, pressure, and volume for substances. Based on the recognition that the structure of a liquid is determined primarily by the inner repulsive forces, the Song and Mason equation [17] was developed in the 1990s based on the statistical-mechanics perturbation theories [18,19] and proved to be available in calculating the densities of various refrigerants recently [20]. However, limitations of the theoretical methods are also apparent. Firstly, the calculated results of refrigerants are not precise enough. Secondly, previous studies only discussed the single result with a given temperature and pressure [20], neglecting the overall change regulation of the density with the changes of temperature and pressure. To find out a better approach that can precisely acquire the density values of R227ea, here, we first illustrate the three-dimensional change regulation of the density of R227ea with the changes of temperature and pressure using the Song and Mason equation, and also use novel machine learning techniques [21,22,23] to predict the densities of R227ea based on three groups of previous experimental data [1,24,25]. To define the best machine learning methods for the prediction of the densities of R227ea, different models should be evaluated respectively, which is a necessary comparison process in environmental science. In this case study, support vector machine (SVM) and artificial neural networks (ANNs) were developed, respectively, in order to find out the best model for density prediction. ANNs are powerful non-linear fitting methods that developed during decades, which have good prediction results in many environmental related fields [26,27,28,29,30]. However, although ANNs usually give effective prediction performances, there is a risk of over-fitting phenomenon [26] if the best number of hidden nodes are not defined, which also indicates that the data size for model training should be large enough. Additionally, the training of ANNs may require relatively long training times if the numbers of hidden nodes are high or the data size is large. Alternatively, SVM, a new machine learning technique developed during these years, has been proved to be effective in numerical predictions for environmental fields [26,27]. The SVM is usually considered to have better generalization performance, leading to better predicted results in many scientific cases [26]. Furthermore, a proper training of SVM has fewer requirements to the data size, ensuring that it can be used for dealing with many complicated issues. Despite the advantages of ANNs and SVM, for the prediction of compressed liquid density of R227ea, it is hard to define the best models without studies. Therefore, here, ANNs (with different numbers of hidden nodes) and SVM were developed respectively. Comparisons were made among different methodologies in order to find the best models for practical applications.
2. Experimental Section
2.1. Theoretical Equation of State
Based on statistical-mechanical perturbation theories [18,19], Song and Mason [17] developed a theoretical equation of state to analyze convex-molecular fluids, which is shown in Equation (1):
where T is the temperature (K), P is the pressure (bar), ρ is the molar density (kg·m−3), kB is the Boltzmann constant, B2(T) is the second virial coefficient, α(T) is the contribution of the repulsive forces to the second virial coefficient, is the average pair distribution function at contact for equivalent hard convex bodies [20], is the packing fraction. To the convex bodies, can be adopted as follows [17,20]:
where γ1 and γ2 are values to reproduce the precise third and fourth virial coefficients, which can be estimated as [17,20]:
and
In terms of , it holds that
where b is the van der Waals convolume, which can be shown with α [17,20]:
B2(T), α(T) and b(T) can be described in with the temperature of normal boiling point (Tnb) and the density at normal boiling point (ρnb) [17,20]:
and
and
where α1 = −0.086, α2 = 2.3988, , and .
Now that we have Equations (1)–(9) above, the last values we should know are γ, Tnb, and ρnb. γ can be obtained from fitting the experimental results, and Tnb and ρnb can be obtained from standard experimental data. According to previous studies, for R227ea, γ is 0.760 [20], Tnb is 256.65 K [31] and ρnb is 1535.0 kg·m−3 [31]. Now we can only input the values of T (K) and P (bar) to Equation (1) and the calculated density of R227ea can be acquired.
2.2. Support Vector Machine (SVM)
SVM is a powerful machine learning method based on statistical learning theory. On the basis of the limited information of samples, SVM has an extraordinary ability of optimization for improving generalization. The main principle of SVM is to find the optimal hyperplane, a plane that separates all samples with the maximum margin [32,33]. The plane helps improve the predictive ability of the model and reduce the error which occurs occasionally when predicting and classifying. Figure 1 shows the main structure of a SVM [34,35]. The letter “K” represents kernels [36]. As we can see from Figure 1, it is a small subset extracted from the training data by relevant algorithm that consists of the SVM. For practical applications, choosing appropriate kernels and parameters are important for us to acquire better prediction accuracies. However, there is still no existing standard for scientists to choose these parameters. In most cases, the comparison of experimental results, the experiences from copious calculating, and the use of cross-validation that is available in software packages can help us address this problem [34,37,38].

Figure 1.
Main structure of a support vector machine (SVM) [35].
2.3. Artificial Neural Networks (ANNs)
ANNs [39,40,41] are machine learning algorithms with the functions of estimation and approximation based on inputs, which are inspired from the biological neural networks of human brains. Being different from networks with only one or two layers of single direction logic, they use algorithms in control determining and function organizing. The interconnected networks usually consist of neurons that can calculate values from inputs and adapt to different circumstances. Thus, ANNs have powerful capacities in numeric prediction and pattern recognition, which have obtained wide popularity in inferring a function from observation, especially when the object is too complicated to be dealt with by human brains. Figure 2 presents a schematic structure of an ANN for the prediction of compressed liquid density of R227ea, which contains the input layer, hidden layer, and output layer. The input layer consists of two nodes, representing the inputted temperature and pressure, respectively. The output layer is made up of the neuron that represents the density of R227ea.
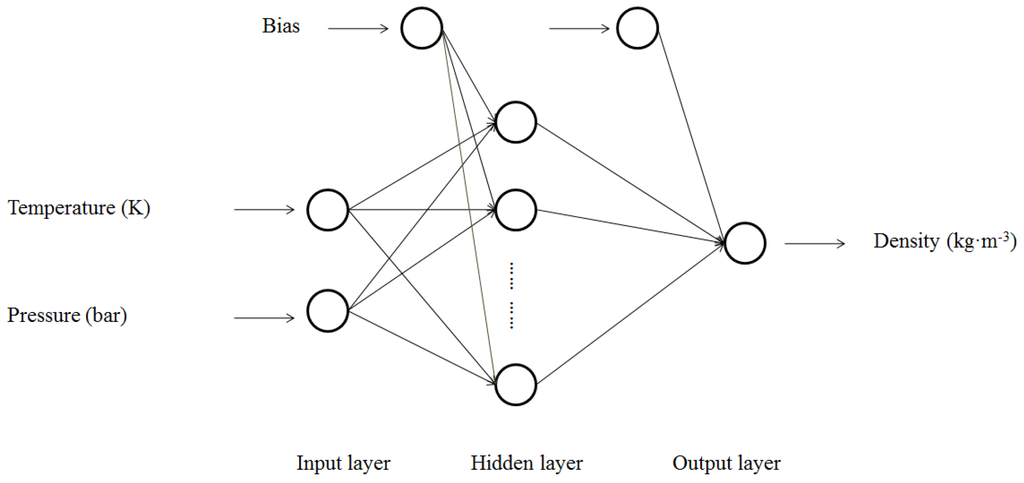
Figure 2.
Schematic structure of an artificial neural network (ANN) for the prediction of compressed liquid densities of 1,1,1,2,3,3,3-heptafluoropropane (R227ea).
3. Results and Discussion
3.1. Model Development
3.1.1. Theoretical Model of the Song and Mason Equation
With the Equations (1)–(9) and related constants, the three-dimensional calculated surface of the compressed liquid density of R227ea can be obtained (Figure 3). To make sufficient comparisons between theoretical calculated values and experimental values, previous experimental results provided by Fedele et al. (with 300 experimental data groups) [1], Ihmels et al. (with 261 experimental data groups) [24], and Klomfar et al. (with 83 experimental data groups) [25], were used for making comparisons in Figure 3. It can be seen that though the experimental data is close to the calculated theoretical surface, the theoretical surface does not highly coincide with all the experimental data. We can see that experimental results provided by Fedele et al. [1] and Ihmels et al. [24] are generally higher than the calculated surface, while the experimental results provided by Klomfar et al. [25] have both higher and lower values than the calculated surface. The root mean square errors (RMSEs) of the theoretical calculated results with the three experimental results are 196.26, 372.54, and 158.54, respectively, which are relatively high and not acceptable to practical applications. However, it should be mentioned that the tendency of the surface is in good agreement with the tendency of the experimental data provided by Fedele et al. [1] and Ihmels et al. [24]. Interestingly, it is obvious to find that when the temperature is close to 100 K, the density would become increasingly high, which has not been reported by experimental results so far.
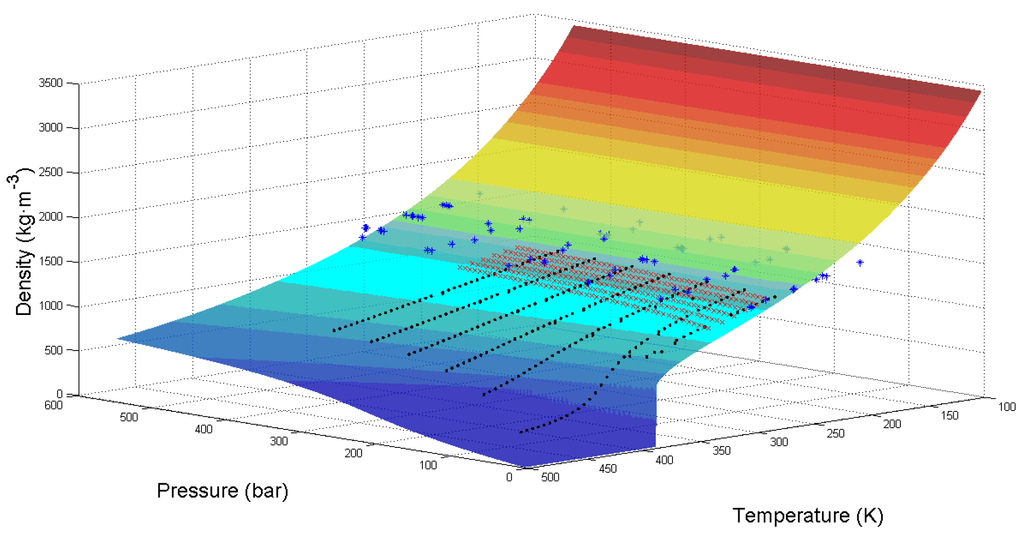
Figure 3.
Theoretical calculated surface and experimental densities of R227ea. The surface represents the theoretical calculated results by Equations (1)–(9); black points represent the experimental results from Fedele et al. [1]; red crosses represent the experimental results from Ihmels et al. [24]; blue asterisks represent the experimental results from Klomfar et al. [25].
3.1.2. Machine Learning Models
To develop predictive models via machine learning, we should first define the independent variables and the dependent variable. With the experimental fact during the practical measurements, the temperature and pressure of R227ea are easy to obtain. Here, we define the temperature (K) and pressure (bar) of the determinant as the independent variables, while the density (kg·m−3) is set as the dependent variable. With the design that users can only input the values of the temperature and pressure to a developed model, we let the machine learning models in our study “learn” the existing data and make precise predictions. The experimental data of Fedele et al. [1], Ihmels et al. [24], and Klomfar et al. [25] were used for model developments respectively. In each model, 80% of the data were set as the training set, while 20% of the data were set as the testing set. The SVMs were developed by Matlab software (Libsvm package [42]) and the ANNs were developed by NeuralTools® software (trial version, Palisade Corporation, NY, USA). General regression neural network (GRNN) [43,44,45] and multilayer feed-forward neural networks (MLFNs) [46,47,48] were chosen as the learning algorithms of ANNs. Numbers of nodes in the hidden layer of MLFNs were set from 2 to 35. In this case study, the number of hidden layer was set as one. Trials of all ANNs were set as 10,000. All these settings of ANNs were set directly in the NeuralTools® software. Linear regression models were also developed for comparisons. To measure the performance of the model and make suitable comparisons, RMSE (for testing), training time, and prediction accuracy (under the tolerance of 30%) were used as indicators that evaluate the models. Model results using experimental data from Fedele et al. [1], Ihmels et al. [24], and Klomfar et al. [25] are shown in Table 1, Table 2, Table 3 and Table 4, respectively. Error analysis results are shown in Figure 4.
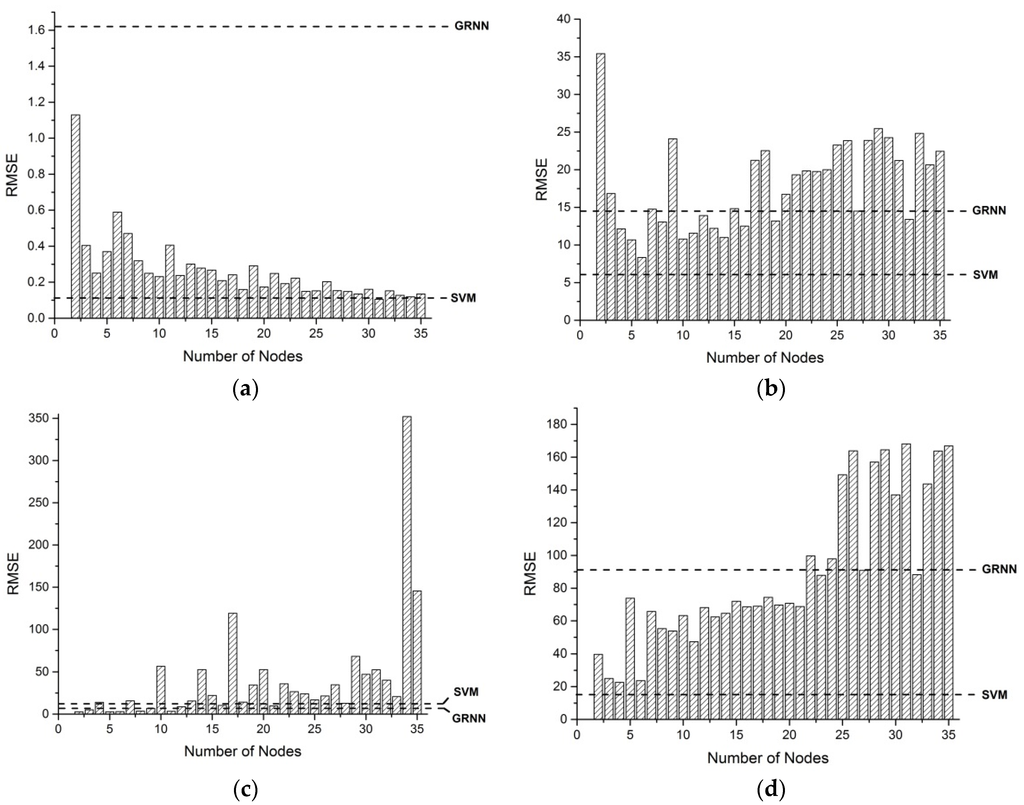
Figure 4.
Root mean square error (RMSE) versus number of nodes of multilayer feed-forward neural networks (MLFNs). Bars represent the RMSEs; black dashed lines represent the RMSEs of general regression neural network (GRNN) and support vector machine (SVM). (a) Machine learning models for data provided by Fedele et al. [1]; (b) machine learning models for data provided by Ihmels et al. [24]; (c) machine learning models for data provided by Klomfar et al. [25]; and (d) machine learning models for data provided by all the three experimental reports [1,24,25].

Table 1.
Prediction models using experimental data by Fedele et al. [1].
| Model Type | RMSE (for Testing) | Training Time | Prediction Accuracy |
|---|---|---|---|
| Linear Regression | 10.90 | 0:00:01 | 85.0% |
| SVM | 0.11 | 0:00:01 | 100% |
| GRNN | 1.62 | 0:00:01 | 100% |
| MLFN 2 Nodes | 1.13 | 0:03:46 | 100% |
| MLFN 3 Nodes | 0.40 | 0:04:52 | 100% |
| MLFN 4 Nodes | 0.25 | 0:06:33 | 100% |
| MLFN 5 Nodes | 0.37 | 0:07:25 | 100% |
| MLFN 6 Nodes | 0.59 | 0:10:38 | 100% |
| MLFN 7 Nodes | 0.47 | 0:13:14 | 100% |
| MLFN 8 Nodes | 0.32 | 0:14:10 | 100% |
| … | … | … | … |
| MLFN 29 Nodes | 0.13 | 2:00:00 | 100% |
| MLFN 30 Nodes | 0.16 | 2:00:00 | 100% |
| MLFN 31 Nodes | 0.10 | 2:00:00 | 100% |
| MLFN 32 Nodes | 0.15 | 2:00:00 | 100% |
| MLFN 33 Nodes | 0.13 | 2:00:00 | 100% |
| MLFN 34 Nodes | 0.12 | 2:00:00 | 100% |
| MLFN 35 Nodes | 0.13 | 2:00:00 | 100% |
Root mean square error (RMSE); Support vector machine (SVM); General regression neural network (GRNN); Multilayer feed-forward neural network (MLFN).

Table 2.
Prediction models using experimental data by Ihmels et al. [24].
| Model Type | RMSE (for Testing) | Training Time | Prediction Accuracy |
|---|---|---|---|
| Linear Regression | 86.33 | 0:00:01 | 63.4% |
| SVM | 6.09 | 0:00:01 | 100% |
| GRNN | 14.77 | 0:00:02 | 96.2% |
| MLFN 2 Nodes | 35.41 | 0:02:18 | 82.7% |
| MLFN 3 Nodes | 16.84 | 0:02:55 | 96.2% |
| MLFN 4 Nodes | 12.14 | 0:03:38 | 96.2% |
| MLFN 5 Nodes | 10.67 | 0:04:33 | 96.2% |
| MLFN 6 Nodes | 8.35 | 0:04:54 | 98.1% |
| MLFN 7 Nodes | 14.77 | 0:06:06 | 96.2% |
| MLFN 8 Nodes | 13.06 | 3:19:52 | 96.2% |
| … | … | … | … |
| MLFN 29 Nodes | 25.46 | 0:31:00 | 90.4% |
| MLFN 30 Nodes | 24.25 | 0:34:31 | 90.4% |
| MLFN 31 Nodes | 21.23 | 0:42:16 | 90.4% |
| MLFN 32 Nodes | 13.40 | 3:38:17 | 96.2% |
| MLFN 33 Nodes | 24.84 | 0:47:06 | 90.4% |
| MLFN 34 Nodes | 20.65 | 0:53:14 | 90.4% |
| MLFN 35 Nodes | 22.46 | 0:58:16 | 90.4% |

Table 3.
Prediction models using experimental data by Klomfar et al. [25].
| Model Type | RMSE (for Testing) | Training Time | Prediction Accuracy |
|---|---|---|---|
| Linear Regression | 15.87 | 0:00:01 | 94.1% |
| SVM | 13.93 | 0:00:01 | 94.1% |
| GRNN | 9.53 | 0:00:01 | 100% |
| MLFN 2 Nodes | 2.72 | 0:01:13 | 100% |
| MLFN 3 Nodes | 5.10 | 0:01:19 | 100% |
| MLFN 4 Nodes | 14.05 | 0:01:36 | 94.1% |
| MLFN 5 Nodes | 2.77 | 0:02:25 | 100% |
| MLFN 6 Nodes | 2.85 | 0:02:31 | 100% |
| MLFN 7 Nodes | 15.72 | 0:03:15 | 94.1% |
| MLFN 8 Nodes | 3.46 | 0:03:40 | 100% |
| … | … | … | … |
| MLFN 29 Nodes | 68.34 | 0:15:03 | 82.4% |
| MLFN 30 Nodes | 47.09 | 0:17:58 | 82.4% |
| MLFN 31 Nodes | 52.60 | 0:22:01 | 82.4% |
| MLFN 32 Nodes | 40.03 | 0:27:46 | 82.4% |
| MLFN 33 Nodes | 20.69 | 0:39:27 | 94.1% |
| MLFN 34 Nodes | 352.01 | 0:56:26 | 11.8% |
| MLFN 35 Nodes | 145.61 | 5:01:57 | 11.8% |
Table 1 and Figure 4a show that the prediction results of machine learning models are generally acceptable, with lower RMSEs than that of linear regression. The SVM and MLFN with 31 nodes (MLFN-31) have the lowest RMSEs (0.11 and 0.10 respectively) and both having the prediction accuracy of 100% (under the tolerance of 30%). However, in our machines, the MLFN-31 requires 2 h for model training, while the SVM only needs about one second, which is also the shortest training time among the results in Table 1. Therefore, the SVM can be defined as the most suitable model for the prediction using the data provided by Fedele et al. [1].
The RMSEs shown in Table 2 and Figure 4b are comparatively higher than those in Table 1. Additionally, in Table 2, the RMSEs and training times of ANNs are comparatively higher than those of the SVM (RMSE: 6.09; training time: 0:00:01). The linear regression has the highest RMSE when testing (86.33). It can be apparently seen that the SVM is the most suitable model for the prediction using the data provided by Ihmels et al. [24].
In Table 3 and Figure 4c, the RMSE of the SVM is relatively higher than those of GRNN and MLFNs with low numbers of nodes. The MLFN with two nodes (MLFN-2) has the lowest RMSE (2.72) and a comparatively good prediction accuracy (100%, under the tolerance of 30%) among all models in Table 3 and, also, the training time of the MLFN-2 is comparatively short (0:01:13). Interestingly, when the numbers of nodes increase to 34 and 35, their corresponding prediction accuracies decrease to only 11.8%. This is because of the over-fitting phenomenon during the training of ANNs when the number of hidden nodes is relatively too high. Therefore, we can define that the MLFN-2 is the most suitable model for the prediction using the data provided by Klomfar et al. [25].

Table 4.
Prediction models using experimental data by all the three experiment reports [1,24,25].
| Model Type | RMSE (for Testing) | Training Time | Prediction Accuracy |
|---|---|---|---|
| Linear Regression | 96.42 | 0:00:01 | 93.0% |
| SVM | 15.79 | 0:00:02 | 99.2% |
| GRNN | 92.33 | 0:00:02 | 93.0% |
| MLFN 2 Nodes | 39.70 | 0:06:50 | 96.1% |
| MLFN 3 Nodes | 25.03 | 0:08:36 | 97.7% |
| MLFN 4 Nodes | 22.65 | 0:10:06 | 99.2% |
| MLFN 5 Nodes | 73.84 | 0:13:49 | 93.0% |
| MLFN 6 Nodes | 23.64 | 0:17:26 | 99.2% |
| MLFN 7 Nodes | 65.74 | 0:14:39 | 93.8% |
| MLFN 8 Nodes | 55.32 | 0:16:18 | 93.8% |
| … | … | … | … |
| MLFN 29 Nodes | 164.54 | 0:52:29 | 89.1% |
| MLFN 30 Nodes | 136.96 | 0:37:38 | 89.8% |
| MLFN 31 Nodes | 168.13 | 0:41:35 | 89.1% |
| MLFN 32 Nodes | 88.25 | 0:50:43 | 93.0% |
| MLFN 33 Nodes | 143.65 | 2:30:12 | 89.8% |
| MLFN 34 Nodes | 163.78 | 1:00:17 | 89.1% |
| MLFN 35 Nodes | 166.92 | 0:44:16 | 89.1% |
Table 4 and Figure 4d show that the SVM has the lowest RMSE (15.79), shortest training time (2 s), and highest prediction accuracy (99.2%). However, it is significant that the best predicted result presented in Table 4 and Figure 4d has a higher RMSE than those in Table 1, Table 2 and Table 3. A possible explanation of this phenomenon is that experimental details in different experiments may generate different deviations when acquiring the compressed liquid density of R227ea because the three groups of data come from three different research groups in different years [1,24,25]. Therefore, the combination of three groups of experimental data may generate additional noise, leading to deviations in training processes and, hence, the tested results have higher RMSEs. However, it should be noted that although the results of the best model here have higher RMSE than those in Table 1, Table 2 and Table 3, these testing results are still acceptable and it is also far more precise than the RMSEs generated by the theoretical equation of state.
3.2. Evaluation of Models
3.2.1. Comparison between Machine Learning Models and the Equation of State
To make comparisons among machine learning models and the theoretical model, we should first compare the RMSEs of different models (Table 5). Results show that the best machine learning models we have chosen in the four experimental groups are all apparently more precise than those results calculated by the Song and Mason equation, with lower RMSEs. The predicted values in the testing sets are generally highly close to their actual values in all the four machine learning models (Figure 5). It should be noted that experimental results provided by Fedele et al. [1] are generally more precise than the other two groups of experimental results [24,25], according to the generalized Tait equation [1,49]. Additionally, the testing RMSE of the SVM for the data provided by Fedele et al. [1] is the lowest during Table 5. One possible reason is that data provided by Fedele et al. [1] may have less experimental errors due to a well-developed measurement method, leading to better training effects, which indicates that data provided by Fedele et al. [1] is a good sample for training in practical predictions.
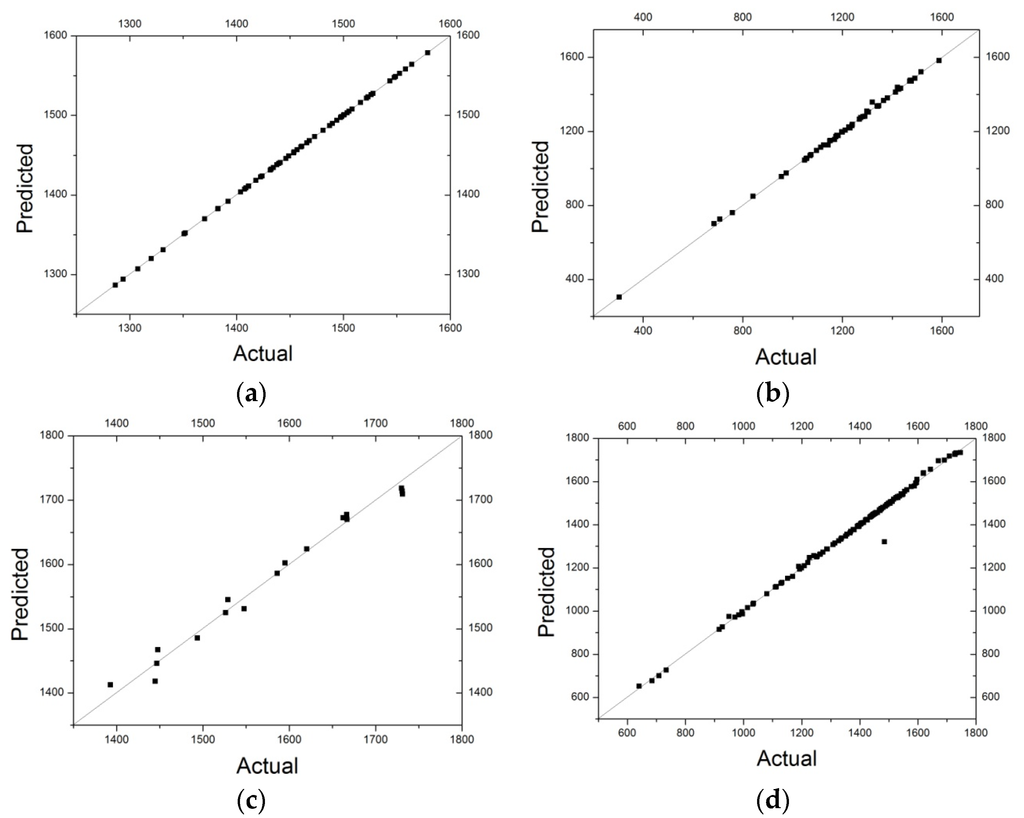
Figure 5.
Predicted values versus actual values in testing processes using machine learning models. (a) The SVM for data provided by Fedele et al. [1]; (b) the SVM for data provided by Ihmels et al. [24]; (c) the MLFN-2 for data provided by Klomfar et al. [25]; and (d) the SVM for data provided by all the three experimental reports [1,24,25].

Table 5.
RMSEs of different models.
| Item | RMSE in Training | RMSE in Testing |
|---|---|---|
| SVM for data provided by Fedele et al. [1] | N/A | 0.11 |
| SVM for data provided by Ihmels et al. [24] | N/A | 6.09 |
| MLFN-2 for data provided by Klomfar et al. [25] | 11.81 | 2.72 |
| SVM for all data [1,24,25] | N/A | 15.79 |
| Theoretical calculation for data provided by Fedele et al. [1] | N/A | 196.26 |
| Theoretical calculation for data provided by Ihmels et al. [24] | N/A | 372.54 |
| Theoretical calculation for data provided by Klomfar et al. [25] | N/A | 158.54 |
3.2.2. Comparison between Conventional Measurement Methods and Machine Learning
Advanced conventional approach for measuring the compressed liquid density of R227ea requires a series of apparatus connecting to be an entire system (Figure 6) [1]. However, the measurement requires time and a series of complex operations, which constraints its applicability. Additionally, the purchase and installation of the apparatus of conventional methods require too much manpower and resources, which indicates that it can only be used for acquiring extremely precise values. In contrast, machine learning models can make precise predictions based on the trained data set and give robust responses with a large number of trained data. Users can only input the new measured data of temperature and pressure and the precise predicted results can be automatically outputted by an appropriate machine learning model. Once the models are developed, new predicted data can be acquired in a very quick way, saving time and manpower. More importantly, it only needs a decent computer and no other apparatus is required anymore.
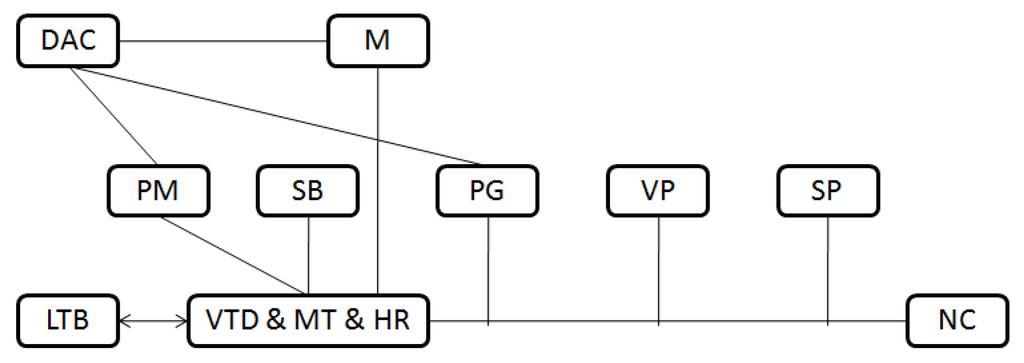
Figure 6.
Apparatus scheme of density measuring for R227ea [1]. VTD represents the vibrating tube densimeter; PM represents the frequency meter; DAC represents the data acquisition and control; MT represents the temperature measurement sensor; M represents the multi-meter; LTB represents the liquid thermostatic bath; HR represents the heating resistance; SB represents the sample bottle; PG represents the pressure gauge; VP represents the vacuum pump; SP represents the syringe pump; NC represents the cylinder.
4. Conclusions
This study is a case study on the prediction of compressed liquid density of refrigerants, using R227ea as a typical example. To precisely acquire the densities of R227ea under different temperatures and pressures, existing measurements require complex apparatus and operations, wasting too much manpower and resources. Therefore, finding a method to predict the compressed liquid density directly is a good way to estimate the numerical values without tedious experiments. To provide a convenient methodology for predictions, a comparative study among different possible models is necessary [26,27,34,35]. Here, we used the Song and Mason equation, SVM, and ANNs to develop theoretical and machine learning models, respectively, for predicting the compressed liquid densities of R227ea. Results show that, compared to the Song and Mason equation, machine learning methods can better generate precise predicted results based on the experimental data. The SVMs are shown to be the best models for predicting the experimental results given by Fedele et al. [1], Ihmels et al. [24], and the combination of all the three experimental results [1,24,25]. The MLFN-2 is shown to be the best model for predicting the experimental results reported by Klomfar et al. [25]. It is also recommended that practical predictions can refer to the model developed with the training of experimental results reported by Fedele et al. [1] due to its more precise experimental results using advanced apparatus. Once a proper model is defined after model training and error analysis (such as the SVM for data provided by Fedele et al. in this case study), we can only input the easily-measured temperature and pressure, and then acquire the compressed liquid density of R227ea directly. Compared to experimental methods, machine learning can “put things right once and for all” with proper experimental data for model training. This study successfully shows that, in practical applications, users can only acquire the temperature and pressure of the measured R227ea and the density can be outputted by the developed appropriate model without additional operations. It should be noted that the target of this study is not to replace the traditional experimental works, but to give an alternative method for scientists and technicians to estimate the values as precise as possible in a limited time.
Author Contributions
Hao Li did the mathematical and modeling works. Xindong Tang simulated the theoretical density surface. Run Wang, Fan Lin, Zhijian Liu and Kewei Cheng joined the discussions and wrote the paper. This work is finished before Hao Li works at The University of Texas at Austin.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fedele, L.; Pernechele, F.; Bobbo, S.; Scattolini, M. Compressed liquid density measurements for 1,1,1,2,3,3,3-heptafluoropropane (R227ea). J. Chem. Eng. Data 2007, 52, 1955–1959. [Google Scholar] [CrossRef]
- Garnett, T. Where are the best opportunities for reducing greenhouse gas emissions in the food system (including the food chain)? Food Policy 2011, 36, 23–23. [Google Scholar] [CrossRef]
- Gholamalizadeh, E.; Kim, M.H. Three-dimensional CFD analysis for simulating the greenhouse effect in solar chimney power plants using a two-band radiation model. Renew. Energy 2014, 63, 498–506. [Google Scholar] [CrossRef]
- Kang, S.M.; Polvani, L.M.; Fyfe, J.C.; Sigmond, M. Impact of polar ozone depletion on subtropical precipitation. Science 2011, 332, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Norval, M.; Lucas, R.M.; Cullen, A.P.; de Gruijl, F.R.; Longstreth, J.; Takizawa, Y.; van der Leun, J.C. The human health effects of ozone depletion and interactions with climate change. Photochem. Photobiol. Sci. 2011, 10, 199–225. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Reddy, A. Optimal control of building HVAC&R systems using complete simulation-based sequential quadratic programming (CSB-SQP). Build. Environ. 2005, 40, 657–669. [Google Scholar]
- T’Joen, C.; Park, Y.; Wang, Q.; Sommers, A.; Han, X.; Jacobi, A. A review on polymer heat exchangers for HVAC&R applications. Int. J. Refrig. 2009, 32, 763–779. [Google Scholar]
- Ladeinde, F.; Nearon, M.D. CFD applications in the HVAC and R industry. Ashrae J. 1997, 39, 44–48. [Google Scholar]
- Yang, Z.; Tian, T.; Wu, X.; Zhai, R.; Feng, B. Miscibility measurement and evaluation for the binary refrigerant mixture isobutane (R600a) + 1,1,1,2,3,3,3-heptafluoropropane (R227ea) with a mineral oil. J. Chem. Eng. Data 2015, 60, 1781–1786. [Google Scholar] [CrossRef]
- Coquelet, C.; Richon, D.; Hong, D.N.; Chareton, A.; Baba-Ahmed, A. Vapour-liquid equilibrium data for the difluoromethane + 1,1,1,2,3,3,3-heptafluoropropane system at temperatures from 283.20 to 343.38 K and pressures up to 4.5 MPa. Int. J. Refrig. 2003, 26, 559–565. [Google Scholar] [CrossRef]
- Fröba, A.P.; Botero, C.; Leipertz, A. Thermal diffusivity, sound speed, viscosity, and surface tension of R227ea (1,1,1,2,3,3,3-heptafluoropropane). Int. J. Thermophys. 2006, 27, 1609–1625. [Google Scholar] [CrossRef]
- Angelino, G.; Invernizzi, C. Experimental investigation on the thermal stability of some new zero ODP refrigerants. Int. J. Refrig. 2003, 26, 51–58. [Google Scholar] [CrossRef]
- Kruecke, W.; Zipfel, L. Foamed Plastic Blowing Agent; Nonflammable, Low Temperature Insulation. U.S. Patent No. 6,080,799, 27 June 2000. [Google Scholar]
- Carlos, V.; Berthold, S.; Johann, F. Molecular dynamics studies for the new refrigerant R152a with simple model potentials. Mol. Phys. Int. J. Interface Chem. Phys. 1989, 68, 1079–1093. [Google Scholar]
- Fermeglia, M.; Pricl, S. A novel approach to thermophysical properties prediction for chloro-fluoro-hydrocarbons. Fluid Phase Equilibria 1999, 166, 21–37. [Google Scholar] [CrossRef]
- Lísal, M.; Budinský, R.; Vacek, V.; Aim, K. Vapor-Liquid equilibria of alternative refrigerants by molecular dynamics simulations. Int. J. Thermophys. 1999, 20, 163–174. [Google Scholar] [CrossRef]
- Song, Y.; Mason, E.A. Equation of state for a fluid of hard convex bodies in any number of dimensions. Phys. Rev. A 1990, 41, 3121–3124. [Google Scholar] [CrossRef] [PubMed]
- Barker, J.A.; Henderson, D. Perturbation theory and equation of state for fluids. II. A successful theory of liquids. J. Chem. Phys. 1967, 47, 4714–4721. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Mozaffari, F. Song and mason equation of state for refrigerants. J. Mex. Chem. Soc. 2014, 58, 235–238. [Google Scholar]
- Bottou, L. From machine learning to machine reasoning. Mach. Learn. 2014, 94, 133–149. [Google Scholar] [CrossRef]
- Domingos, P.A. Few useful things to know about machine learning. Commun. ACM 2012, 55, 78–87. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Ihmels, E.C.; Horstmann, S.; Fischer, K.; Scalabrin, G.; Gmehling, J. Compressed liquid and supercritical densities of 1,1,1,2,3,3,3-heptafluoropropane (R227ea). Int. J. Thermophys. 2002, 23, 1571–1585. [Google Scholar] [CrossRef]
- Klomfar, J.; Hruby, J.; Sÿifner, O. measurements of the (T,p,ρ) behaviour of 1,1,1,2,3,3,3-heptafluoropropane (refrigerant R227ea) in the liquid phase. J. Chem. Thermodyn. 1994, 26, 965–970. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Campilongo, S.; Ficarella, A.; Congedo, P.M. Comparison between wind power prediction models based on wavelet decomposition with Least-Squares Support Vector Machine (LS-SVM) and Artificial Neural Network (ANN). Energies 2014, 7, 5251–5272. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M.; Laforgia, D. Error analysis of hybrid photovoltaic power forecasting models: A case study of mediterranean climate. Energy Convers. Manag. 2015, 100, 117–130. [Google Scholar] [CrossRef]
- Moon, J.W.; Jung, S.K.; Lee, Y.O.; Choi, S. Prediction performance of an artificial neural network model for the amount of cooling energy consumption in hotel rooms. Energies 2015, 8, 8226–8243. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, K.; Li, H.; Zhang, X.; Jin, G.; Cheng, K. Artificial neural networks-based software for measuring heat collection rate and heat loss coefficient of water-in-glass evacuated tube solar water heaters. PLoS ONE 2015, 10, e0143624. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, J.; Wang, K.; Wang, Z. Wind power prediction considering nonlinear atmospheric disturbances. Energies 2015, 8, 475–489. [Google Scholar] [CrossRef]
- Leila, M.A.; Javanmardi, M.; Boushehri, A. An analytical equation of state for some liquid refrigerants. Fluid Phase Equilib. 2005, 236, 237–240. [Google Scholar] [CrossRef]
- Zhong, X.; Li, J.; Dou, H.; Deng, S.; Wang, G.; Jiang, Y.; Wang, Y.; Zhou, Z.; Wang, L.; Yan, F. Fuzzy nonlinear proximal support vector machine for land extraction based on remote sensing image. PLoS ONE 2013, 8, e69434. [Google Scholar] [CrossRef] [PubMed]
- Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum support vector machine for big data classification. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Leng, W.; Zhou, Y.; Chen, F.; Xiu, Z.; Yang, D. Evaluation models for soil nutrient based on support vector machine and artificial neural networks. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, H.; Zhang, X.; Jin, G.; Cheng, K. Novel method for measuring the heat collection rate and heat loss coefficient of water-in-glass evacuated tube solar water heaters based on artificial neural networks and support vector machine. Energies 2015, 8, 8814–8834. [Google Scholar] [CrossRef]
- Kim, D.W.; Lee, K.Y.; Lee, D.; Lee, K.H. A kernel-based subtractive clustering method. Pattern Recognit. Lett. 2005, 26, 879–891. [Google Scholar] [CrossRef]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. Liblinear: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Guo, Q.; Liu, Y. ModEco: An integrated software package for ecological niche modeling. Ecography 2010, 33, 637–642. [Google Scholar] [CrossRef]
- Hopfield, J.J. Artificial neural networks. IEEE Circuits Devices Mag. 1988, 4, 3–10. [Google Scholar] [CrossRef]
- Yegnanarayana, B. Artificial Neural Networks; PHI Learning: New Delhi, India, 2009. [Google Scholar]
- Dayhoff, J.E.; DeLeo, J.M. Artificial neural networks. Cancer 2001, 91, 1615–1635. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 389–396. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Tomandl, D.; Schober, A. A Modified General Regression Neural Network (MGRNN) with new, efficient training algorithms as a robust “black box”-tool for data analysis. Neural Netw. 2001, 14, 1023–1034. [Google Scholar] [CrossRef]
- Specht, D.F. The general regression neural network—Rediscovered. IEEE Trans. Neural Netw. Learn. Syst. 1993, 6, 1033–1034. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Smits, J.; Melssen, W.; Buydens, L.; Kateman, G. Using artificial neural networks for solving chemical problems: Part I. Multi-layer feed-forward networks. Chemom. Intell. Lab. Syst. 1994, 22, 165–189. [Google Scholar] [CrossRef]
- Ilonen, J.; Kamarainen, J.K.; Lampinen, J. Differential evolution training algorithm for feed-forward neural networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar] [CrossRef]
- Thomson, G.H.; Brobst, K.R.; Hankinson, R.W. An improved correlation for densities of compressed liquids and liquid mixtures. AICHE J. 1982, 28, 671–676. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).