Abstract
Visual cryptography encrypts a secret image into two meaningless random images, called shares, such that it can be decrypted by human vision without any calculations. However, there would be problems in alignment when these two shares are staked by hand in practice. Therefore, this paper presents the fault-tolerant schemes of stacking two shares that are acquired from secret image encryption without pixel expansion. The main idea of these schemes is to combine several pixels as a unit and then to encrypt each unit into a specific combination of pixels. Both theoretical analysis and simulation results demonstrate the effectiveness and practicality of the proposed schemes.
1. Introduction
In 1995, Naor and Shamir proposed visual cryptography (VC) (also called visual secret sharing (VSS)), which is a way to encrypt one secret image, such that it can be decoded by human vision without any calculation [1]. The concept is to encrypt a secret image S into two meaningless random images G1 and G2, each called a share (also called sheet, shadow), of which one can be seen as a cipher text, and the other is a key to it. Stacking them is the only way to restore the hidden secret. Random grid-based VSS, invented by Kafri and Keren [2], received more attention in recent years, such as [3,4,5,6,7,8,9]. This method takes each pixel as a grid on the image and applies the concept of random variables to encrypt images.
For VSS, the secret image can be visually reconstructed with shares, printed on transparencies and stacked precisely on an overhead projector. A slight misalignment between the shares could increase the difficulty of identification in image reconstruction. The smaller the size of the shares, the more difficult it will be when you restore the secret image. Therefore, some literature studies this misalignment problem (also called fault-tolerance), such as [8,10,11,12,13,14,15]. Nakajima and Yamaguchi proposed an extended VSS scheme that can enhance the registration tolerance when stacked shares are not aligned perfectly in 2004 [14]. It transfers the secret image into black and white values with the half-tone technique and then encrypts into two random images. The difference from other methods is that one of the random images is larger than the other in a diamond pattern, leading to a certain level of fault tolerance when stacking the shares. In such a pixel expansion-based scheme, the size of the shares and the restored image in their scheme will be 49-times the original secret image. This increases the cost on data restoration and transmission and also makes its implementation inconvenient.
A (k, n)-threshold scheme means that the dealer encrypts secret S into n shares and delivers each to one participant, such that any k (or more) participants can recover the secret by combining their shares, while less than k participants cannot. A (k, n)-threshold VSS scheme is a visual version of the (k, n)-threshold scheme, i.e., stacking any k (or more) shares directly can reconstruct the secret image S. In 2009, Yang et al. considered the misalignment problem in the VSS scheme and designed a misalignment-tolerant VSS scheme based on the trade-off between the usage of big and small blocks to address this misalignment problem [15], called the MTVSS scheme. It is not necessary to align the transparencies precisely. Their scheme can solve the misalignment problem for the (k, n)-threshold VSS scheme. They also propose a useful parameter, CI (correctness index), to represent the quality of the restored image intuitively. However, that scheme also involves pixel expansion. Therefore, this paper is based on Nakajima and Yamaguchi’s idea to design the (2, 2)-threshold visual secret sharing scheme, such that the misalignment problem can be solved without pixel expansion. We shall use the same parameter CI to compare the performance of our schemes to the MTVSS scheme.
The rest of this paper is organized as follows. Section 2 introduces the detailed techniques mentioned above. Section 3 discusses the major findings. In particular, we design four VSS schemes with analysis showing that they achieve better fault tolerance. Section 4 presents the fault tolerance result of various proposed schemes by simulations. Finally, our conclusions are given in Section 5.
2. Experimental Section
2.1. Visual Cryptography Concepts
Different from previous secret sharing scheme techniques, when the shares are stacked, the confidential content can be interpreted with human vision directly. That is, a VC scheme can restore the secret without additional computation. Figure 1 shows the encryption and decryption process model of a VC scheme.
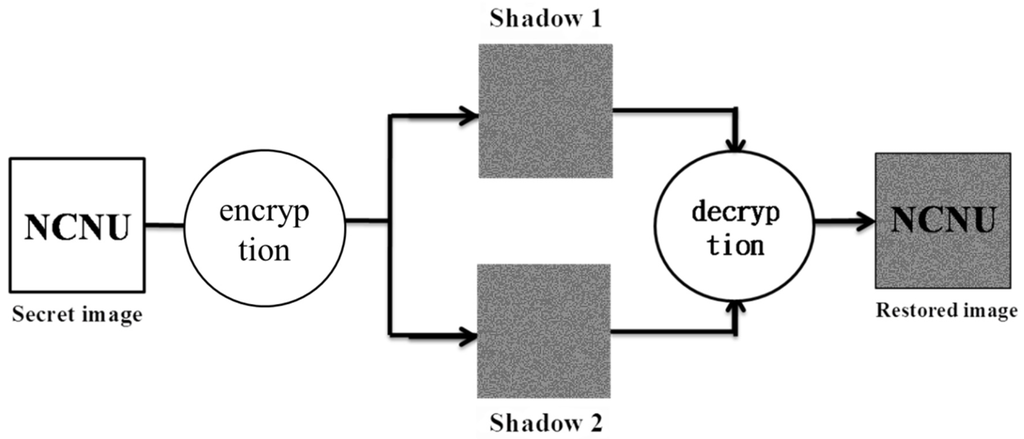
Figure 1.
The visual cryptography (VC) encryption and decryption process model.
In 1995, Naor and Shamir proposed visual cryptography, by introducing a simple and perfectly-secure way that allows secret sharing without any cryptograph computation [1]. To decrypt the secret message, the reader should photocopy each pattern on a separate transparency, align them carefully and project the result with an overhead projector. This basic model can be extended into a visual variant of the k out of n secret sharing problem. The grey level of this combined share is proportional to the Hamming weight H(V) of the “or” m-vector V. A solution to the k out of n visual secret sharing scheme consists of two collections of n × m Boolean matrices C0 and C1. To share a white pixel, the dealer randomly chooses one of the matrices in C0, and to share a black pixel, the dealer randomly chooses one of the matrices in C1, The chosen matrix defines the color of the m subpixels in each one of the n transparencies. The solution is considered valid if the following three conditions are met:
- For any S in C0, the “or” V of any k out of n rows satisfies H(V) ≤ d − a × m.
- For any S in C1, the “or” V of any k out of n rows satisfies H(V) ≥ d.
- For any subset {i1, i2, …, iq} of {1, 2, …, n} with q < k, the two collections of q × m matrices Dt for t ∈ {0, 1} obtained by restricting each n × m matrix in Ct (where t = 0, 1) to row i1, i2, …, iq are indistinguishable in the sense that they contain the same matrices with the same frequencies.
In the above conditions, parameter a means the relative difference between stacked shares that come from a white pixel and a black pixel in the original picture. We would like a to be as large as possible. This scheme is perfectly secure and very easy to implement. However, it causes pixel expansion. That is, the size of the shares and the reconstructed image will be m-times the size of the original secret image, and it deforms the secret image. Therefore, we have the following discussion.
2.2. Random Grid Encryption Algorithm
For understanding the following sections, we have to understand some important notations about the random grid listed in this section in advance. In general, we define S as a secret image with a size of w × h pixels, where w and h are positive integers.
Definition 1.
Let S(i, j) denote a pixel value of the secret image S at position (i, j), defined as:
Actually, 1 is opaque and 0 is transparent when S is printed on a transparency. The opposite value of S(i, j) is denoted as follows.
Definition 2.
Transmittance (T) is defined as the proportion of white pixels to total pixels.
A secret image S is encrypted into two shares G1 and G2. Let ri be a pixel in Gi for i = 1, 2. The resulting value of the overlapped pixels r1 and r2 will be r1 ⊕ r2, where ⊕ stands for the Boolean “or” operation. All results when stacking any two pixels together are shown in Table 1.

Table 1.
Results for stacking two different pixels together.
| r1 | r2 | r1 ⊕ r2 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Kafri and Keren [2] proposed three different encryption algorithms (Algorithm KK1, KK2 and KK3) for halftone images, in which the value of each pixel in a random grid is determined by flipping a coin, i.e., the probability of getting a black or white pixel is the same. Therefore, the transmittance of the random image is 1/2. These algorithms encrypt a secret image S of size w × h into two shares G1 and G2 with the same size. We list these algorithms as follows, where Rand(0/1) is a function with output zero or one randomly and with equal probability.
| Algorithm KK1: |
| Generate a w × h random grid G1 |
| For (i = 0; i < w; i++) |
| For (j = 0; j < h; j++) |
| If (S[i][j] == 0) |
| G2[i][j] = G1[i][j]; |
| else |
| G2[i][j] = 1 − G1[i][j]; |
| Output (G1, G2) |
| Algorithm KK2: |
| Generate a w × h random grid G1 |
| For (i = 0; i < w; i++) |
| For (j = 0; j < h; j++) |
| If (S[i][j] == 0) |
| G2[i][j] = G1[i][j]; |
| else |
| G2[i][j] = Rand(0/1); |
| Output (G1, G2) |
| Algorithm KK3: |
| Generate a w × h random grid G1 |
| For (i = 0; i < w; i++) |
| For (j = 0; j < h; j++) |
| If (S[i][j] == 0) |
| G2[i][j] = Rand(0/1); |
| else |
| G2[i][j] = 1 – G1[i][j]; |
| Output (G1, G2) |
We shall focus on the idea of the Algorithm KK1 in this paper. The analysis of the transmittance of the Algorithm KK1 is show in Table 2. We denote a white pixel by □ and a black pixel by ■ in this paper. Note that using the idea of the Algorithm KK2 or KK3 to construct the following schemes will yield similar results.

Table 2.
The transmittance of the Algorithm KK1.
| S | Probability | G1 | G2 | G1⊕ G2 | T(G1⊕ G2) |
|---|---|---|---|---|---|
| □ | 1/2 | □ | □ | □ | 1/2 |
| 1/2 | ■ | ■ | ■ | ||
| ■ | 1/2 | □ | ■ | ■ | 0 |
| 1/2 | ■ | □ | ■ |
2.3. The Concept of Fault Tolerance
Naor and Shamir proposed an extended visual secret sharing scheme [1] in 1995. When they encrypt the secret image, each pixel on the secret image will be expanded into m subpixels. Nakajima and Yamaguchi proposed an extended visual secret sharing scheme to show that the fault tolerance mechanism can be achieved [14]. They encrypted the secret image into two expanded shares. Each pixel in the secret image will produce a diamond-like 7 × 7 subpixel pattern in the two shares (one is small and the other is big), as shown in Figure 2. Note that their scheme dealed with gray level image, so there is the gray color in Figure 2. Even though there is a slight deviation when stacking, the primary color (black or white) still can be restored. Their design will allow some space for fault tolerance. However, due to the expansion, the size of the restored image will be 49-times the original secret image. Hence, this paper will focus on designing shift-tolerant VSS schemes for black/white secret images without pixel expansion.

Figure 2.
The patterns in Nakajima and Yamaguchi’s scheme [14].
3. Proposed Scheme
The main concept of our algorithm is as follows. First, taking n × n pixels as a unit, the image is divided into several units. In the first generated share, each unit is randomly chosen from the patterns we designed. For the generation of the second share, the number of black and white pixels in each unit on the original secret image needs to be counted individually. This will be used to select the suitable pattern according to the pattern of the first share for the same unit. Run the steps sequentially and repeatedly until the second share is generated. Taking the idea of Nakajima and Yamaguchi’s scheme as a reference [14], we design the special patterns for the main encryption scheme and apply them to the Algorithm KK1 [2]. We design the fault-tolerant VSS schemes by taking n × n pixels as a unit, for n = 3, 4, 5 or 6. The final design of the patterns for encryption schemes when n is 3, 4, 5 and 6 is shown in Table 3, Table 4, Table 5 and Table 6, respectively.
In the following, we analyze the transmittance when two shares are not stacked correctly. Because the pattern of each unit is symmetric, the analysis results are all equal when two units are stacked by shifting one pixel to the right, left, up or down. Here, we only show the result for the n = 4 case where G1 shifts one pixel right. All combinations for such a case when the pixel in the secret image is white or black are shown in Table 7 and Table 8, respectively. The way of stacking has been shown as Figure 3, where the red square represents the stacked position of the unit in G1.

Table 3.
The designed patterns for n = 3.
| Image | G1 | G2 | Stack | Image | G1 | G2 | Stack |
|---|---|---|---|---|---|---|---|
| □ |  |  |  | ■ |  |  |  |
 |  |  |  |  |  |

Table 4.
The designed patterns for n = 4.
| Image | G1 | G2 | Stack | Image | G1 | G2 | Stack |
|---|---|---|---|---|---|---|---|
| □ |  |  |  | ■ |  |  |  |
 |  |  |  |  |  | ||
 |  |  |  |  |  | ||
 |  |  |  |  |  |

Table 5.
The designed patterns for n = 5.
| Image | G1 | G2 | Stack | Image | G1 | G2 | Stack |
|---|---|---|---|---|---|---|---|
| □ |  |  |  | ■ |  |  |  |
 |  |  |  |  |  | ||
 |  |  |  |  |  | ||
 |  |  |  |  |  |

Table 6.
The designed patterns for n = 6.
| Image | G1 | G2 | Stack | Image | G1 | G2 | Stack |
|---|---|---|---|---|---|---|---|
| □ |  |  |  | ■ |  |  |  |
 |  |  |  |  |  | ||
 |  |  |  |  |  | ||
 |  |  |  |  |  |

Figure 3.
Stacked image with one pixel right shifted.

Table 7.
The analysis of stacked units with one pixel shift when the pixel in the secret image is white.
| Image | G1 | G2 | Stack | Image | G1 | G2 | Stack |
|---|---|---|---|---|---|---|---|
| □ |  | 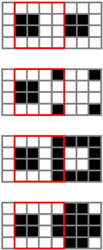 |  | □ |  | 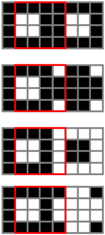 |  |
| □ |  | 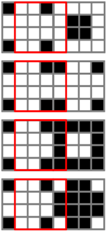 |  | □ |  | 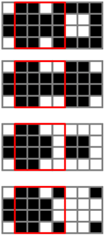 |  |

Table 8.
The analysis of stacked units with one pixel shift when the pixel in the secret image is black.
| Image | G1 | G2 | Stack | Image | G1 | G2 | Stack |
|---|---|---|---|---|---|---|---|
| ■ |  |  |  | ■ |  | 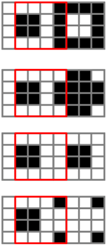 |  |
| ■ |  |  |  | ■ |  |  |  |
In Table 7 and Table 8, each little square represents a pixel, and the red square is the area of the unit in G1 that has been stacked with G2 with one pixel shift. In this case, the ration of the number of white pixels to the total pixels of the stacked unit when the pixel in the secret image is white is (32 + 36 + 8 + 4)/256 = 80/256 = 5/16. Similarly, when the pixel in the secret image is black, this ratio is (16 + 12 + 8 + 12)/256 = 48/256 = 3/16. In summary, Table 9 gives the transmittance analysis for stacking two units for n = 3, 4, 5 or 6. In a perfect stacking, the resulting transmittance for a white secret pixel is 1/2, and because the design of the pattern for a black pixel is accordingly complementary, the resulting transmittance for the black secret pixel is zero. We also analyze the stacking results with different shifts: a one-pixel shift when n is three or four and up to a two-pixel shift when n is five or six. Besides, we also calculate the results for a one-pixel diagonal shift, that is a one-pixel right shift plus a one-pixel down shift. All of the results show that there are differences between the transmittance for the black and white pixels of the stacked image. When the transmittance for a white pixel of a secret image differs from that for a black pixel of a secret image, the original secret image can be recognized. Hence, the following theorem can be concluded.
Theorem 1.
The proposed schemes are the fault-tolerant VSS schemes.
Table 9.
The transmittance analysis for stacking two resulting units.

| 3 × 3 | Stack | Shift 1 pixel |
|---|---|---|
| □ | 1/2 | 7/36 |
| ■ | 0 | 11/36 |

| 4 × 4 | Stack | Shift 1 |
|---|---|---|
| □ | 1/2 | 5/16 |
| ■ | 0 | 3/16 |

| 5 × 5 | Stack | Shift 1 | Shift 2 |
|---|---|---|---|
| □ | 1/2 | 31/100 | 26/100 |
| ■ | 0 | 19/100 | 23/100 |

| 6 × 6 | Stack | Shift 1 | Shift 2 | Shift 3 |
|---|---|---|---|---|
| □ | 1/2 | 50/144 | 42/144 | 38/144 |
| ■ | 0 | 25/144 | 36/144 | 33/144 |

| Diagonal Shift | 4 × 4 | 5 × 5 | 6 × 6 |
|---|---|---|---|
| □ | 381/2048 | 721/3200 | 1189/4608 |
| ■ | 173/2048 | 465/3200 | 422/4608 |
4. Experimental Results
In this section, we evaluate the proposed schemes by simulation, and the experimental results are shown in Figure 4, Figure 5, Figure 6 and Figure 7 for n = 3, 4, 5 and 6, respectively. The secret image we used in the experiment is a halftone image with 300 × 300 pixels. Because there is no pixel expansion, the size of two shares is also 300 × 300 pixels after encryption. Information on the restored image can be identified clearly after stacking these two generated shares perfectly or with a 1-, 2- or 3-pixel shift. It shows that the proposed schemes are effective and that our analysis is valid.
In [15], Yang et al. defined dx as the horizontal deviation (unit: pixel) and CI to measure the difference between the reconstructed images for a given deviation and no deviation. The correctness indices for black and white secret pixels, denoted as CI(B) and CI(W), respectively, are obtained by comparing the secret pixels between the reconstructed images of a deviation dx and no deviation; then, the CI is calculated as the average of all CI(B) and CI(W). For two shares G1 and G2, using the parameter transmittance TB(G1 ⊕ G2) and TW(G1⊕ G2) for the black and white pixels of the secret image, we have:
CI(B) = 1 − 2TB(G1 ⊕ G2), CI(W) = 2TW(G1 ⊕ G2) and CI = (CI(B) + CI(W))/2

Figure 4.
The experimental results for n = 3.

Figure 5.
The experimental results for n = 4.

Figure 6.
The experimental results for n = 5.

Figure 7.
The experimental results for n = 6.
Besides, in their paper, the parameter α2 is used as the ratio of pixel expansion, that is α can be seen as the ratio of pixel expansion in one dimension, and PB is the percentages of the big subpixels in a share.
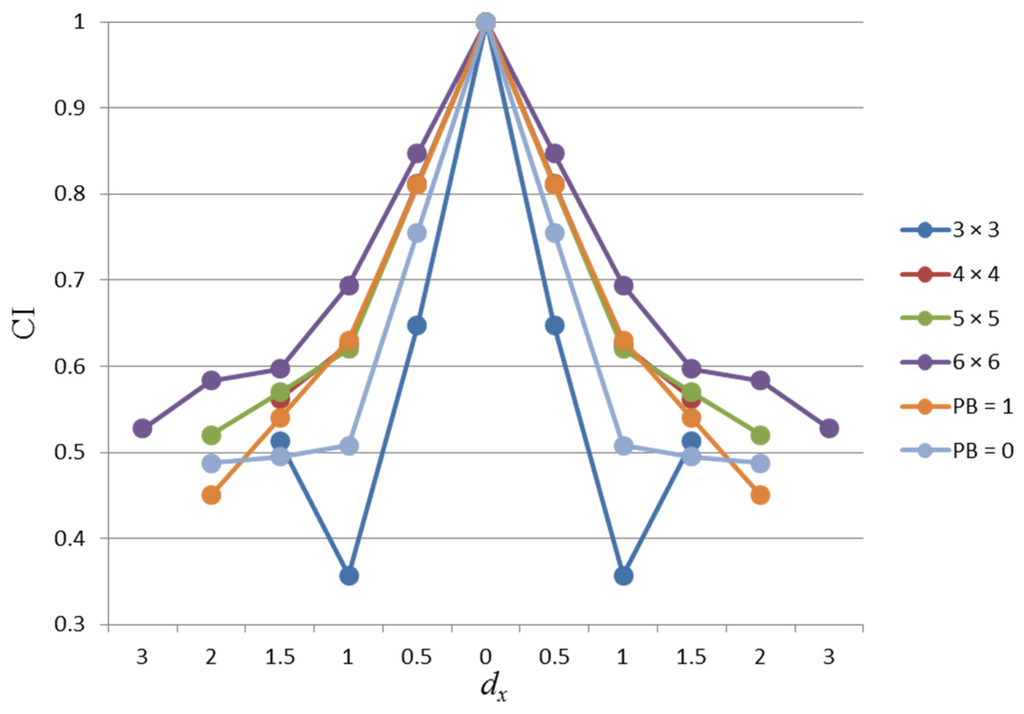
Figure 8.
Comparison of our schemes with the misalignment-tolerant visual secret sharing (MTVSS) scheme for shifting the same pixels. CI, correctness index.
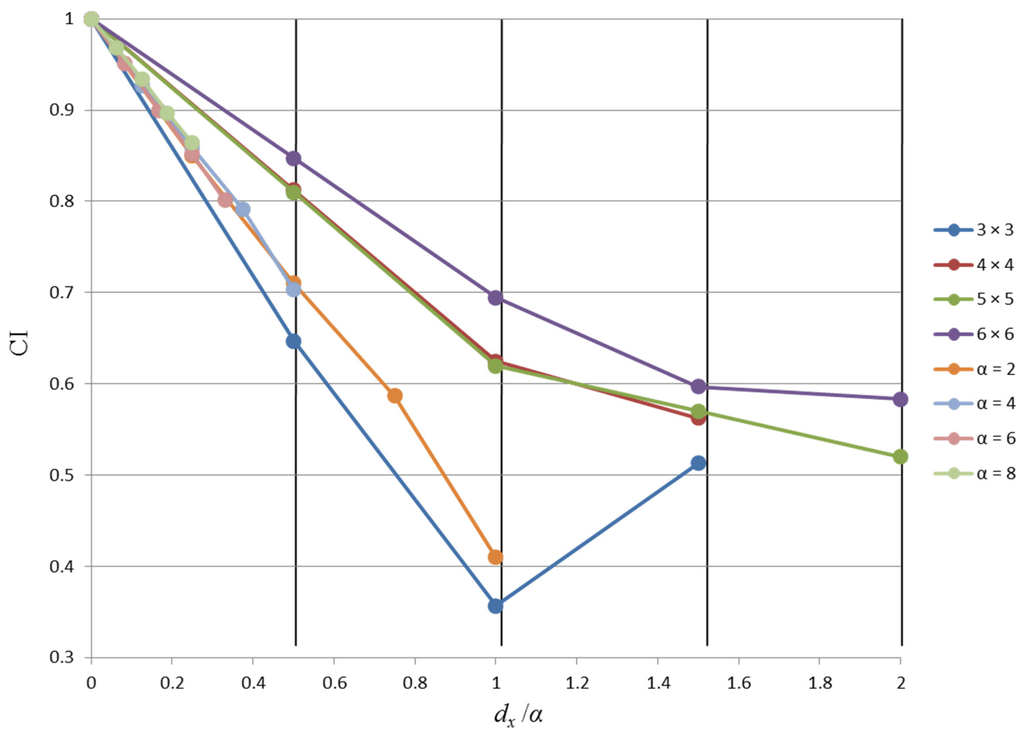
Figure 9.
Comparison of our schemes with MTVSS scheme for shifting the same percentage of the shares.
In the following, we compare the value CI of our schemes to the MTVSS scheme. In Figure 8, we use the result of the MTVSS scheme when α = 2, which means that the pixel expansion of the shares is four-times the secret image. It is not difficult to see that our results are similar to that of PB = 1 in the MTVSS scheme when n is four and five and better when n is six. Figure 9 compares our schemes to the MTVSS scheme for shifting the same percentage of the shares (dx/α). We use the result of the MTVSS scheme when PB = 1 (the best performance among different PBs) for different values of α. One can see that our results are better than the MTVSS scheme when n is bigger than three. In conclusion, both the theoretical analysis and simulation results demonstrate the effectiveness and practicality of our proposed schemes. In Table 10, we list some capabilities of our scheme compared to some previous works.

Table 10.
Comparison of our scheme with the previous works.
| Schemes Capability | Nakajima and Yamaguchi 2004 [14] | Yang et al., 2009 [15] | Our Scheme |
|---|---|---|---|
| Fault-tolerant | Yes | Yes | Yes |
| Without pixel expansion | No | No | Yes |
| By random grid | No | No | Yes |
| Flexible | No | Yes | Yes |
| (k, n)-threshold VSS scheme | No | Yes | No |
5. Conclusions
This paper presents the design of a (2, 2)-threshold visual secret sharing scheme that is fault-tolerant without pixel expansion; the original information can be identified even when we stack the two resulting shares imperfectly. As we know, this paper is the first one to discuss the VSS scheme that can solve the misalignment problem without pixel expansion. That will make the implementation more likely to be realized. For n = 3, the swapping of black and white can be expected in the analysis when we stack the shares with one pixel shift (as shown in Table 9). As for recognizing the graph, the original information still can be identified in this situation. On the other hand, for the purpose of restoring the original image, there will be some space for improvement. In addition, we also expect further study for designing the encryption scheme when n is seven or more. However, the incurred distortion of the graph will be more severe. This challenge will be further studied. Besides, we shall also work on designing a (k, n)-threshold VSS scheme that addresses the misalignment problem without pixel expansion and improving the existing algorithms with a larger transmittance gap between the black and white areas of the resulting stacked image, so that the restored image could be recognized more easily.
Acknowledgments
The authors would like to thank the Ministry of Science and Technology of the Republic of China for financially supporting this research under Contract No. MOST 104-2918-I-260-004.
Author Contributions
All authors discussed the main idea and scientific contribution. Yung-Chang Chen performed the experiments and wrote the first draft. Song Guo contributed in manuscript writing and revisions. Justie Su-Tzu Juan proposed the idea, was supervising computational experiments and analyzed the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Naor, M.; Shamir, A. Visual cryptography. In Proceedings of the Advances in Cryptology, EUROCRYPT’94, Perugia, Italy, 9–12 May 1994; pp. 1–12.
- Kafri, O.; Keren, E. Encryption of pictures and shapes by random grids. Opt. Lett. 1987, 12, 377–379. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.J.-Y.; Juan, J.S.-T. Multi-VSS scheme by shifting random grids. In Proceedings of the World Academy of Science, Engineering and Technology, Tokyo, Japan, 29–30 May 2012; pp. 1277–1283.
- Chen, L.-C. Multi-Secret Images Sharing Schemes. Master’s Thesis, National Chi Nan University, Nantou, Taiwan, 10 July 2014. [Google Scholar]
- Chen, T.-H.; Tsao, K.-H.; Wei, K.-C. Multiple-image encryption by rotating random grids. In Proceedings of the Eighth International Conference on Intelligent Systems Design and Applications, ISDA’08, Kaohsiung, Taiwan, 26–28 November 2008; pp. 252–256.
- Nakajima, M.; Yamaguchi, Y. Extended visual cryptography for natural images. J. WSCG 2002, 10, 303–310. [Google Scholar]
- Shyu, S.J. Image encryption by random grids. Pattern Recognit. 2007, 40, 1014–1031. [Google Scholar] [CrossRef]
- Wang, D.S.; Dong, L.; Li, X. Towards shift tolerant visual secret sharing schemes. IEEE Trans. Inf. Forensics Secur. 2011, 6, 323–337. [Google Scholar] [CrossRef]
- Yan, X.; Wang, S.; Niu, X.; Yang, C.N. Halftone visual cryptography with minimum auxiliary black pixels and uniform image quality. Digit. Signal Process. 2015, 38, 53–65. [Google Scholar] [CrossRef]
- Blundo, C.; Santis, A. Visual cryptography schemes with perfect reconstruction of black pixels. Computer 1998, 22, 449–455. [Google Scholar] [CrossRef]
- Blundo, C.; Bonis, A.; Santis, A. Improved schemes for visual cryptography. Des. Codes Cryptogr. 2001, 24, 255–278. [Google Scholar] [CrossRef]
- Kobara, K.; Imai, H. Limiting the visible space visual secret sharing schemes and their application to human identification. In Proceedings of the International Conference on the Theory and Applications of Cryptology and Information Security: Advances in Cryptology, ASIACRYPT’96, Kyongju, Korea, 3–7 November 1996; pp. 185–195.
- Liu, F.; Wu, C.K.; Lin, X.J. The alignment problem of visual cryptography schemes. Des. Codes Cryptogr. 2009, 50, 215–227. [Google Scholar] [CrossRef]
- Nakajima, M.; Yamaguchi, Y. Enhancing registration tolerance of extended visual cryptography for natural images. J. Electron. Imaging 2004, 13, 654–662. [Google Scholar]
- Yang, C.N.; Peng, A.G.; Chen, T.S. MTVSS: Misalignment tolerant visual secret sharing on resolving alignment difficulty. Signal Process. 2009, 89, 1602–1624. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).