Impact of Population Initialization Strategies on PSO Performance for Job Shop Scheduling Problems

Abstract

Population initialization significantly influences metaheuristic algorithm performance, yet random initialization dominates despite problem-specific needs. This study investigates initialization strategies for the Job Shop Scheduling Problem (JSSP), an NP-hard combinatorial optimization challenge in manufacturing systems, addressing the gap in understanding how different initialization approaches affect solution quality and reliability in constrained discrete problems. The research employs a two-phase experimental design using Particle Swarm Optimization (PSO) on Taillard benchmark instances. Phase 1 evaluates seventeen initialization methods across four categories: random-based, problem-specific heuristics, hybrid methods, and adaptive strategies. Each method is tested through 30 independent runs on six problem instances. Phase 2 develops machine learning-enhanced initialization using variational autoencoders (VAEs) trained on high-quality solutions from successful traditional methods, comparing three VAE variants against conventional approaches. Results show all random-based methods failed completely, while only First-In-First-Out and Most Work Remaining heuristics succeeded consistently among traditional approaches. VAE-based methods achieved 100% solution validity (540/540) versus 97% for traditional methods (349/360), with statistical significance (χ² = 14.27, p < 0.001). The Friedman test confirmed performance differences (χ² = 19.87, p < 0.001, Kendall’s W = 0.828), with VAE methods achieving lower mean ranks and makespan reductions. Despite starting with lower initial diversity, VAE methods exhibited larger diversity increases during optimization, suggesting structured initialization enables more effective exploration than random dispersion.

1. Introduction

Effective scheduling is critical in complex production processes, and time scheduling problems are fundamental in manufacturing systems. The Job Shop Scheduling Problem (JSSP), one of the most challenging scheduling problems, is a highly constrained, combinatorial optimization problem that requires multiple jobs to be processed on specific machines according to predetermined processing sequences. The solution space for this problem is factorial, and obtaining optimal solutions with classical methods is often practically impossible. Therefore, in recent years, metaheuristic algorithms have been widely used to solve NP-hard problems such as JSSP [1].

Nature-inspired metaheuristic algorithms such as Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Artificial Rabbit Optimization (ARO), and Gray Wolf Algorithm (GWO) can yield good results on JSSP; however, their performance varies significantly based on factors such as parameter settings, operator design, and especially initial population quality. Population-based metaheuristic algorithms begin their search process in the solution space with a large number of random individuals. However, how these individuals are generated profoundly affects not only the initial solution quality but also dynamics such as the algorithm’s convergence rate, its ability to maintain diversity, and the probability of being trapped in local minima [2].

Random initialization dominates population generation in metaheuristic algorithms, yet researchers often underestimate its impact on algorithm performance [3]. The initial population critically determines search capability, convergence speed, and solution quality [4,5]. Poor initialization, which generates clustered solutions, leaves search space regions unexplored, while overly scattered populations require excessive iterations to converge. Effective initialization should balance diversity and quality to ensure better exploration coverage [6]. Recent studies investigating alternative strategies suggest advantages under certain conditions [7], yet systematic comparisons across initialization categories remain limited, especially for JSSP.

Solution encoding also affects metaheuristic performance, especially for discrete and combinatorial problems such as JSSP. Encoding schemes must simultaneously represent operation orderings and respect precedence constraints. This study employs continuous random-key encoding with priority-based decoding, enabling PSO compatibility while preserving feasibility. The encoding–initialization interaction, therefore, influences the observed performance differences.

PSO was selected as the optimization framework due to its strong sensitivity to initial population quality. Unlike genetic algorithms, which can partially mitigate poor initialization through crossover and mutation, PSO’s velocity-based update mechanism directly incorporates information from the initial swarm, making its convergence trajectory highly dependent on the initial population. This property makes PSO particularly suitable for isolating the effects of different initialization strategies, which constitute the primary objective of this study. Moreover, the relatively simple structure of PSO compared to GA or ACO enables clearer attribution of performance differences to initialization rather than to complex operator interactions.

Although several NP-hard problems, such as the Traveling Salesman Problem (TSP) and the Knapsack Problem, have been extensively studied in the context of metaheuristic optimization, this study deliberately focuses on the Job Shop Scheduling Problem (JSSP). Unlike TSP or Knapsack, which primarily involve combinatorial ordering or selection decisions, JSSP introduces a highly constrained scheduling structure that simultaneously incorporates precedence constraints, machine capacity constraints, and temporal dependencies. These characteristics make JSSP particularly sensitive to infeasible regions of the search space, and therefore, it is especially suitable for investigating the role of population initialization strategies. Since the objective of this work is to assess how initialization quality affects feasibility, robustness, and convergence behavior in constrained discrete optimization, JSSP provides a more challenging and informative testbed than classical unconstrained or lightly constrained NP-hard problems.

This study demonstrates the impact of different population initialization methods on JSSP through a comprehensive two-phase experimental analysis. In the first phase, four categories of established initialization methods were evaluated: random-based methods (uniform, normal distribution), problem-specific heuristic methods (SPT, LPT, FIFO, and minimal remaining work), hybrid/mixed methods (elite seeding, multi-stage population), and adaptive methods (problem size-based, machine–job ratio adaptations). Each method was tested using a modified PSO-based solver with fixed algorithm parameters across the Taillard JSSP benchmark problems. In the second phase, a variational autoencoder (VAE) was trained on high-quality solutions generated by the best-performing initialization methods from phase one, then evaluated and compared against conventional methods. Each initialization strategy underwent 30 independent runs, with solution quality assessed using multidimensional metrics including validity, initial and final diversity, convergence behavior, and statistical performance measures.

The main contribution of this work lies in a systematic investigation of population initialization strategies for the Job Shop Scheduling Problem (JSSP), demonstrating how domain knowledge can be effectively embedded into metaheuristic initialization. A broad spectrum of initialization techniques is developed and evaluated, ranging from conventional random-based methods to problem-aware approaches that exploit the structural characteristics, precedence constraints, and resource allocation patterns inherent in job shop scheduling. The results underscore the critical role of problem-specific initialization in achieving improved solution quality and robustness for complex combinatorial optimization problems such as JSSP.

Beyond JSSP, related scheduling variants, including Flow Shop Scheduling (FSSP) and Flexible Job Shop Scheduling Problems (FJSP), are also of practical importance. Although these problems are not explicitly examined in the present study, the insights obtained from JSSP—particularly regarding problem-aware initialization, feasibility preservation, and structured diversity control—are expected to be partially transferable. However, due to differences in routing flexibility and machine assignment rules, direct quantitative generalization requires dedicated experimental validation, which is identified as an important direction for future research.

The remainder of this manuscript is structured as follows: Section 2 reviews related work on population initialization in metaheuristic optimization. Section 3 details the JSSP formulation, the PSO algorithm, and the population initialization strategies, including the proposed VAE-based approach. Section 4 presents the experimental studies and comparative results of different initialization methods. Finally, Section 5 discusses the findings and draws concluding remarks.

2. Related Works

Combinatorial optimization problems are characterized by solution spaces that exhibit exponential growth with respect to problem dimensionality. This exponential expansion renders exhaustive enumeration computationally intractable, even for moderately sized problem instances. For the majority of benchmark instances, optimal solutions or tight lower bounds remain unknown [8]. This absence of ground truth necessitates evaluation methodologies based on relative performance metrics rather than absolute optimality gaps [9].

To address these challenges, researchers have developed various optimization methods. Among these approaches, metaheuristic algorithms have gained popularity due to their flexibility and effectiveness. Unlike traditional methods, metaheuristics do not require mathematical models or gradient information about the problem [10]. Instead, they use stochastic search strategies to explore the solution space systematically. These algorithms can handle complex, nonlinear problems and work well even when the problem structure is unknown or poorly understood [11].

The performance of metaheuristic algorithms depends on several factors, with the quality and distribution of the initial population being among the most important considerations [12]. In most studies, populations are generated with uniform random numbers [13]. Such random initialization often leads to clustering and leaves large regions unexplored, which reduces diversity and exploration capability [14]. There are many studies in the literature that aim to improve the performance of algorithms by trying different initialization strategies [15,16,17,18].

Numerous studies have investigated the impact of population initialization strategies on algorithm performance. Maaranen et al. tested 52 benchmark functions and found no consistent advantage of advanced methods over pseudo-random initialization, although quasi-random and stochastic sieve techniques showed benefits in some cases [19]. Li, Liu and Yang evaluated 22 methods across 19 problems and five optimizers. They showed that algorithm performance is sensitive to initialization, but the degree of sensitivity varies [20]. Agushaka et al. confirmed this algorithm-dependent effect using 11 initialization methods on 10 metaheuristics with both classical and CEC2020 functions [14]. Tharwat and Schenck reported no significant performance differences among five initialization approaches in constrained optimization problems [21]. Evidence from these studies suggests that the effect of initialization is context-specific and not universal.

However, some studies have demonstrated clear benefits of advanced initialization techniques. Opposition-based learning methods have shown performance improvements in various metaheuristics [22,23]. Quasi-random sequences like Sobol and Halton have proven particularly effective for high-dimensional problems due to their superior space coverage [24,25]. Latin Hypercube Sampling has also shown advantages, especially for expensive optimization problems. Recent studies have further demonstrated its effectiveness as a population initialization strategy in metaheuristic algorithms, with LHS-based NSGA-III showing superior performance metrics compared to random initialization methods [26]. Similarly, research on novel low-discrepancy sequences has shown promise for initialization strategies. Studies have proposed sequences such as WELL, Knuth, and Torus for population initialization, demonstrating superior convergence and diversity preservation compared to uniform random initialization across multiple metaheuristics, including PSO, DE, and BA [27,28]. These findings indicate that while the benefits of initialization are problem-dependent, carefully designed strategies can yield substantial performance improvements in specific contexts [29]. Advanced hybrid approaches have also been proposed, such as Cluster-Based Population Initialization (CBPI), which combines local search, clustering, and elite selection to create intelligent initial populations that significantly enhance algorithm performance [30]. In addition to benchmark problems, Poikolainen, Neri, and Caraffini evaluated their proposed clustering-based population initialization strategy on a real-world problem within the continuous domain.

Kazimipour, Li and Qin, in their comprehensive review of population initialization techniques, noted that existing studies predominantly relied on benchmark functions rather than real-world problem instances, highlighting a significant gap in the literature [31]. While recent studies have begun exploring initialization techniques for discrete problems [32,33,34], comprehensive comparisons of multiple initialization strategies remain limited. Discrete problems such as scheduling introduce additional complexity. The Job Shop Scheduling Problem (JSSP) involves precedence constraints, machine capacities, and operation sequences. The few studies in this area indicate the potential of heuristic and hybrid strategies. Rules such as Shortest Processing Time (SPT), Longest Processing Time (LPT), First-In-First-Out (FIFO), and remaining work-based heuristics exploit problem-specific features. These problem-specific approaches have shown promise in generating higher-quality initial solutions and improving population diversity [35], yet systematic evaluation across discrete problems remains an underexplored area.

In summary, prior work shows mixed results for continuous optimization and limited evidence for discrete problems. The lack of structured comparisons in JSSP motivates this study. We evaluate a broad set of initialization strategies under a fixed PSO framework and extend the analysis with a generative initialization approach based on variational autoencoders (VAEs).

3. Background Description

This section provides the technical foundation necessary for understanding the experimental methodology and results presented in this study. First, the population initialization methods used in this research are introduced. Then, the Particle Swarm Optimization (PSO) metaheuristic algorithm and its parameters are presented. Finally, the characteristics and encoding scheme of the Job Shop Scheduling Problem (JSSP) are discussed.

3.1. Population Initialization Strategies

Population initialization is a critical yet understudied component of metaheuristic algorithms. It directly impacts convergence behavior and solution quality. While random initialization dominates current practice, emerging evidence suggests that strategic population generation can significantly improve algorithmic performance. This section evaluates various initialization approaches, from traditional random methods to sophisticated techniques developed through machine learning.

3.1.1. Random-Based Methods

Random-based initialization strategies form the baseline approach for population generation in metaheuristic algorithms, offering varying degrees of space coverage and distributional properties. This study evaluates four distinct random-based methods: Random Uniform, which generates initial solutions by sampling each dimension uniformly within the predefined bounds to ensure unbiased full coverage of the search space; Random Normal, which samples individuals from a normal distribution centered at 0.5 with moderate standard deviation to balance exploration with slight centralization while applying boundary constraints; Latin Hypercube Sampling (LHS), which provides stratified coverage by partitioning each dimension into equal intervals and sampling without repetition to achieve more uniform distribution [36]; and Sobol Sequences, which employ low-discrepancy quasi-random sequences to systematically cover the search space, proving particularly effective for higher-dimensional optimization problems where uniform coverage is otherwise challenging to achieve [37].

3.1.2. Problem-Specific Heuristic Methods

Problem-specific heuristic initialization strategies leverage domain knowledge of the Job Shop Scheduling Problem by employing established dispatching rules to construct high-quality initial solutions. This study evaluates six priority-based heuristic methods: Shortest Processing Time (SPT), which assigns higher priorities to operations with shorter processing durations to generate efficient job sequences and minimize mean flow time; Longest Processing Time (LPT), which conversely favors operations with longer processing requirements to explore alternative scheduling characteristics and balance machine workloads; First-In-First-Out (FIFO), which prioritizes operations based on their sequential position in each job’s routing, providing a simple yet effective approach for generating feasible initial schedules; Critical Ratio, which prioritizes operations with smaller critical ratios—calculated as total remaining processing time divided by the number of remaining operations—to mimic urgency-driven scheduling strategies; Most Work Remaining (MWR), which assigns higher priority to operations from jobs with maximum cumulative remaining processing time, aligning with makespan reduction strategies that emphasize resource-intensive jobs; and Least Work Remaining (LWR), which conversely prioritizes jobs with minimal remaining work to accelerate completion of smaller jobs and reduce system congestion [38].

3.1.3. Hybrid/Mixed Methods

Hybrid initialization strategies combine multiple approaches to leverage complementary strengths of different initialization techniques, balancing solution quality with population diversity. This study examines five hybrid configurations: Pure Heuristic Mix, which allocates equal proportions (25% each) of the population to SPT, LPT, FIFO, and Critical Ratio-based heuristics to integrate diverse scheduling perspectives; Quality Diversity Balance, which combines 60% heuristic-based initialization (Pure Heuristic Mix) with 40% Latin Hypercube Sampling to ensure both solution quality and systematic space coverage; Elite Seeding, which generates 20% of the population using the SPT heuristic—known for effectiveness in scheduling contexts—while the remaining 80% employs a mixture of random and heuristic strategies (LHS, normal distribution, and LPT) to enhance population diversity; Staged Population, which implements a stratified approach by allocating 30% to SPT, 30% to LPT, 20% to uniform random sampling and 20% to LHS, thereby achieving a balanced initialization that leverages both heuristic quality and exploratory randomness; and Multi-Level Hybrid, which distributes the population across three tiers—40% heuristic-based strategies, 30% LHS, and 30% normal distribution sampling—to provide robust multi-scale coverage of the solution space.

3.1.4. Adaptive Methods

Adaptive initialization methods dynamically adjust population generation strategies based on problem instance characteristics to optimize the exploration–exploitation trade-off for different problem scales and resource configurations. This study evaluates two adaptive approaches: Problem Size Adaptive, which selects initialization strategies according to total problem complexity measured as the product of jobs and machines (num_jobs × num_machines), employing Quality Diversity Balance with high heuristic ratio (0.8) for small-scale problems (≤300 operations, e.g., ta01, ta11) to emphasize exploitation through high-quality solutions, transitioning to Staged Population for medium-scale instances (301–450 operations, e.g., ta21, ta31) to introduce diversity through phase-wise initialization, and reverting to Quality Diversity Balance with reduced heuristic ratio (0.4) for large-scale problems (>450 operations, e.g., ta41, ta51) to encourage exploration through increased randomness; and Machine-Job Ratio Based, which adapts the initialization strategy according to resource structure reflected by the machine-to-job ratio (num_machines/num_jobs), utilizing Multi-Level Hybrid for balanced or machine-rich systems (ratio ≥ 1.0) to exploit parallelism opportunities, Staged Population for moderate resource pressure scenarios (0.65 ≤ ratio < 1.0) to provide structured yet diverse initialization, and Quality Diversity Balance with moderate heuristic contribution (ratio 0.7) for severe resource pressure conditions (ratio < 0.65) where jobs significantly outnumber machines, thereby maintaining solution diversity while addressing resource contention.

3.1.5. Variational Autoencoder (VAE)

A variational autoencoder (VAE) is a generative model that extends the conventional autoencoder framework by incorporating probabilistic inference. Instead of learning deterministic point estimates in latent space as in classical autoencoders, VAEs learn a continuous probabilistic distribution over the latent space. This design not only allows for accurate reconstruction of the input data but also facilitates the generation of novel samples that closely resemble the original distribution. For each data point in the training set, VAEs produce two separate latent representations: one encoding the mean values (μ) and another encoding the standard deviation parameters (σ), which together define the probability distribution characteristics and uncertainty levels for each dimension in the latent space. The training loss of VAE consists of two components. One of them is reconstruction loss that ensures the decoder accurately reconstructs the input, similar to traditional autoencoders. The other one is the KL divergence loss that regularizes the learned distribution to approximate a prior distribution (typically standard Gaussian), ensuring the latent space maintains desirable structural properties [39]. This probabilistic approach enables VAEs to learn smooth latent state representations and generate new samples by sampling from the learned distribution, making them particularly valuable for optimization applications where diverse, high-quality population initialization is essential.

3.2. Particle Swarm Optimization (PSO)

The PSO algorithm is an effective method used to solve complex problems. The algorithm’s logic is based on the foraging behavior of bird flocks, with each particle representing a point in the solution space. A higher particle count can yield better results, but the computational cost also increases. A fitness function is used to determine how close particles are to the solution. At each iteration, the fitness value of all particles is calculated. The position closest to the solution for a particle is called the personal best value, while the position closest to the solution among all particles is called the global best value. Each particle in the flock has information about its current position and velocity, as well as information about the personal best value, which is the position closest to the solution. When calculating the new particle positions, the personal best and the global best values are used along with the current positions [40].

In the standard PSO algorithm, the entire flock initially explores the search space. Convergence occurs towards the end of the search process. The diversity of the initial population plays a significant role in the success of the PSO algorithm. The speeds of the particles are calculated using the formula given in Equation (1), and their positions are calculated using the formula given in Equation (2):

$$v\_ij(t+1)=w\times v\_ij\left(t\right)+c\_1\times r\_1\times (p\_ij-x\_ij(t\left)\right)+c\_2\times r\_2\times (p\_gj-x\_ij(t\left)\right)$$

(1)

$$x\_ij(t+1)=x\_ij\left(t\right)+v\_ij(t+1)$$

(2)

In Equation (1), v_ij is the velocity value of particle i in dimension j. w is the inertial weight. In PSO, the inertial weight parameter regulates the trade-off between diversification and intensification strategies. When set to large values, it enables particles to explore distant regions of the solution space, while smaller values direct particles toward intensive local optimization around current best positions. The acceleration coefficients c1 and c2 control the influence of personal and global best positions. c1 determines how much the particles will consider their own best solutions, while c2 determines how much they will follow the best solution in the entire swarm. Here, x_ij is the current position of particle i in dimension j. p_ij is the best position found by the same particle in dimension j. p_gj represents the best position found in dimension j in the entire swarm. The calculated speed values are adjusted to remain within the predetermined limits [−v_max, v_max]. This limiting process is necessary to ensure that the specified limits are not exceeded during the search and that the global search does not spiral out of control.

In this experimental study, a modified PSO algorithm was implemented with several enhancements to improve performance on JSSP instances. The algorithm employs a population size of 50 particles and runs for a maximum of 400 iterations. Key PSO parameters include initial inertia weight (w) of 0.9 with linear decay set to 0.4 throughout iterations and cognitive and social acceleration coefficients (c1 and c2) both set to 2.0. Particle velocities are initialized randomly in the range [−0.1, 0.1] and constrained within [−0.5, 0.5] bounds to prevent excessive movement. The algorithm incorporates several performance enhancements: local search is performed on the global best solution every 10 iterations using small perturbations (5% noise) on randomly selected dimensions, a diversity monitoring mechanism reinitializes the worst 30% of particles when population diversity falls below 0.01 after iteration 50, and an intensive final local search applies multiple noise levels (0.01, 0.02, 0.05, 0.1) to further refine the best solution. All particle positions are maintained within [0, 1] bounds corresponding to the random key encoding scheme used for JSSP representation, and convergence is tracked based on achieving 95% of the initial best fitness or a fixed improvement threshold. These PSO parameters and settings remained constant across all experiments to ensure fair comparison between different population initialization methods. Figure 1 illustrates the modified PSO algorithm employed in this study.

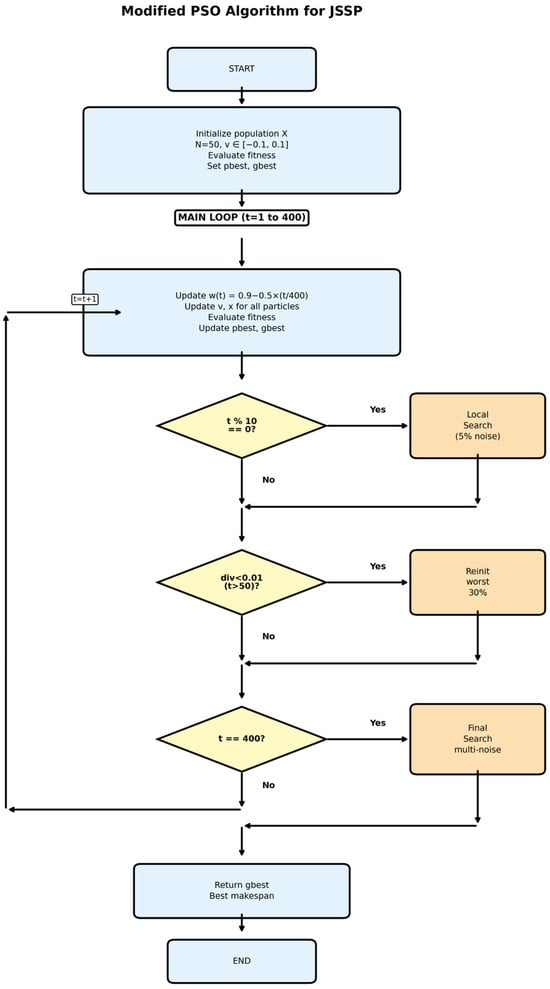
Figure 1. Modified PSO algorithm flowchart for JSSP. Arrows indicate the direction of program execution and control flow between operations.

3.3. Job Shop Scheduling Problem (JSSP)

JSSP is a scheduling problem that determines the order in which a set of jobs ($\mathrm{J}=\left\{j_1,\dots ,j_J\right\}$) will be executed on machines ($M=\{m_1,\dots ,m_M\}$). Each job consists of operations to be performed in a predetermined order. There are several constraints to consider when solving JSSP. 1-Each operation can only be executed on a specific machine and with a specific processing time. 2-A machine can only perform one operation at a time, and the precedence order within each job must be strictly maintained. This problem is NP-hard and is critical in many application areas such as production planning, industrial process management, and resource allocation [41]. The main objective of the problem is to create a schedule that minimizes the completion time $C_{max}$(makespan) of all jobs while balancing machine utilization (Equation (3)).

$${min(C}_{\mathrm{m}\mathrm{a}\mathrm{x}})=\max \left\{C_i\right\},i\in \{1,\dots ,J\}$$

(3)

where $C_i$ denotes the completion time of job $i$.

The JSSP implementation in this study employs a random key encoding scheme combined with a priority-based decoding algorithm. Each solution is represented as a continuous vector of values in the [0, 1] range, where the vector length equals the total number of operations (num_jobs × num_machines). The decoding process converts these random keys into feasible schedules by sorting operations within each job according to their priority values and using a heap-based scheduling algorithm to respect precedence and resource constraints. The system incorporates comprehensive error handling and validation mechanisms, including input validation, boundary checks, and automatic correction of infeasible operations. A caching mechanism (@lru_cache) is implemented to improve computational efficiency during repeated evaluations. The evaluation function performs extensive constraint verification, checking for duplicate operations, precedence violations, machine capacity conflicts, and temporal consistency before calculating the makespan. Constraint-checking and invalidity detection:

$$F(S)=\{\begin{array}{c}makespan\left(S\right),ifSsatisfiesallconstraints\\ {10}^6+\sum _{c\in C}penalty\left(c\right),otherwise\end{array}$$

(4)

where the constraint set C includes the following parameters:

• Operation consistency: Each job–operation pair must appear exactly once in the schedule, ensuring that no operation is duplicated or omitted.

$\forall (j,o):$ no duplicates, valid indices.

• Machine assignment: Every operation must be processed on its correct predefined machine, as specified by the machine-sequence matrix: $\mathrm{machine}\left(j,o\right)=M_{j,o}$
• Processing time validity: The scheduled duration of each operation must exactly match its required processing time.

$$\mathrm{duration}(j,o)=p_{j,o}$$

• Job precedence: The starting time of operation o + 1 must occur after the completion of operation o within the same job.

$${\mathrm{start}}_{j,o+1}\ge {\mathrm{end}}_{j,o}$$

• Machine capacity: No two operations assigned to the same machine may overlap in time.

There should be no overlapping intervals on any machine.

When any constraint is violated, a structured penalty is added:

$$\mathrm{penalty}\left(c\right)\in \left\{\mathrm{5000,7000,8000,9000,10,000,1000}\times \Delta \right\}$$

Invalid solutions are penalized with high fitness values (1 × 10⁶ plus additional penalties) to guide the optimization process away from infeasible regions. The implementation also includes critical path analysis functionality to provide insights into schedule bottlenecks and machine utilization patterns, making it suitable for both optimization and analytical purposes.

4. Experimental Studies and Results

This section presents a comprehensive experimental evaluation of the proposed population initialization methods for the Job Shop Scheduling Problem (JSSP). The experimental design aims to assess the effectiveness, reliability, and scalability of different initialization strategies across various problem scales and characteristics. In the first part of this study, a total of 17 distinct population initialization methods were evaluated and categorized into four groups: random-based methods (4 methods), problem-specific heuristic methods (6 methods), hybrid/mixed methods (5 methods), and adaptive methods (2 methods). For each method, six instances were selected from the Taillard benchmark instances. The instances were chosen from different problem sizes: small-scale problems (ta01: 15 × 15, ta11: 20 × 15), medium-scale problems (ta21: 20 × 20, ta31: 30 × 15), and large-scale problems (ta41: 30 × 20, ta51: 50 × 15).

In the second part of this study, an advanced population initialization strategy based on variational autoencoder (VAE) technology was developed under the heading of machine learning-enhanced initialization. New population individuals were generated from this learned distribution by training multidimensional VAE systems that learned from high-quality solutions obtained from the most successful traditional heuristic methods tested in the first part (FIFO and MWR). Three different VAE-based initialization variants (Pure VAE, VAE Hybrid 60%, VAE Hybrid 40%) were tested, and a comprehensive performance comparison was conducted between traditional heuristic approaches and machine learning-supported population initialization strategies.

Each initialization method was evaluated through 30 independent runs with distinct random seeds to ensure statistical significance and reproducibility. We chose to focus on PSO to ensure controlled experimental conditions and enable in-depth analysis of initialization-algorithm interactions, providing actionable insights for practitioners working on JSSP optimization.

Although the original PSO introduced in 1995 recommended a population size of 20–50 particles, recent research by Piotrowski et al. [42] demonstrated that a range of 50–300 particles provides a safer choice for real-world problems. To balance computational efficiency with solution quality, a population size of 50 was adopted in this study, aligning with widely accepted principles of population-based nature-inspired metaheuristic optimization [43].

To determine an appropriate stopping criterion, preliminary experiments were conducted with different maximum iteration settings. The convergence behavior was analyzed across multiple runs, which indicated that the algorithm achieved substantial convergence within approximately 400 iterations, with negligible performance gains from additional iterations. Consequently, a maximum of 400 iterations was adopted for the main experimental phase to ensure consistent termination conditions while maintaining computational efficiency.

All initial populations generated across different methods were optimized using the same PSO algorithm and evaluated with the same cost function to ensure fair comparison. The tests were conducted on a desktop computer with an Intel(R) Core(TM) i5-12500 3.00 GHz processor and 16 GB of RAM, running the Windows 11 Pro operating system. The project code was written in Python 3.10.12.

Throughout the presentation of experimental results in this study, constraint-violating solutions are designated as INVALID for clear identification and analysis. In the context of Job Shop Scheduling Problems (JSSPs), an INVALID solution refers to a schedule that violates essential problem constraints, rendering it infeasible. Such solutions typically result from incorrect operation sequencing (precedence violations), overlapping assignments on the same machine (capacity conflicts), or decoding failures where a random-key vector cannot be transformed into a valid schedule. To clearly separate valid from invalid schedules during optimization, a large penalty makespan value (typically ≥1,000,000) is assigned to these solutions. Table 1 presents the experimental best, mean, and worst results (makespan) obtained for JSSP instances. In Table 1, results marked as INVALID indicate that all 30 independent runs of a particular population initialization method for a given problem instance produced constraint-violating solutions.

Table 1. Experimental results for JSSP instances (best/mean/worst/std.dev).

Population Initialization Strategies	ta01 (15 × 15)	ta11 (20 × 15)	ta21 (20 × 20)	ta31 (30 × 15)	ta41 (30 × 20)	ta51 (50 × 15)
Random-Based Methods
Random Uniform	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Random Normal	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Latin Hypercube	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Sobol Sequence	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Problem-Specific Heuristic Methods
SPT Heuristic	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
LPT Heuristic	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
FIFO	1548/ 1618/ 1679/ 32.57	1933/ 2074/ 2197/ 51.31	2317/ 2475/ 2804/ 108.85	2381/ 2544/ 2718/ 78.71	2922/ 3074/ 3345/ 93.36	3938/ 4071/ 4273/ 70.54
Critical Ratio	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
MWR	1541/ 1616/ 1739/ 40.18	1926/ 2062/ 2176/ 61.38	2316/ 2466/ 2737/ 88.13	2428/ 2559/ 2777/ 74.62	2982/ 3108/ 3332/ 93.03	3962/ 4074/ 4273/ 73.45
Least Work Remaining	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Hybrid/Mixed Methods
Pure Heuristic Mix	1568/ 1673/ 1802/ 57.46	2028/ 2144/ 2312/ 79.47	2394/ 2509/ 2732/ 102.25	2426/ 2595/ 2803/ 101.25	3002/ 3164/ 3344/ 87.50	3915/ 4198/ 4621/ 168.06
Quality Diversity Balance	1548/ 1646/ 1720/ 43.98	1995/ 2109/ 2270/ 76.67	2415/ 2582/ 2795/ 123.94	2390/ 2656/ 2810/ 106.05	3043/ 3168/ 3335/ 105.22	3969/ 4218/ 4426/ 136.97
Elite Seeding	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Staged Population	INVALID	INVALID	INVALID	INVALID	INVALID	INVALID
Multi-Level Hybrid	1556/ 1681/ 1851/ 76.00	1989/ 2139/ 2304/ 73.24	2350/ 2440/ 2516/ 63.23	2544/ 2722/ 2941/ 124.07	2996/ 3181/ 3397/ 154.78	4012/ 4186/ 4606/ 136.63
Adaptive Methods
Problem Size Adaptive	1564/ 1678/ 1892/ 77.18	1970/ 2107/ 2313/ 87.69	INVALID	INVALID	3053/ 3164/ 3259/ 69.83	4003/ 4197/ 4383/ 117.84
Machine–Job Ratio-Based	1555/ 1663/ 1775/ 55.75	INVALID	2463/ 2536/ 2677/ 71.33	2449/ 2649/ 3053/ 138.47	INVALID	3911/ 4161/ 4344/ 102.92

Experimental results reveal that population initialization strategies exhibit profound and systematic differences in their ability to generate valid solutions across JSSP problem instances of varying complexity. The empirical evidence demonstrates a clear hierarchy of effectiveness, with structured heuristic approaches substantially outperforming both random-based and certain problem-specific methods.

For small-scale problems (ta01: 15 × 15 and ta11: 20 × 15), two initialization strategies emerged as exceptionally robust: FIFO and MWR, both achieving perfect 100% success rates across all experimental runs. This remarkable consistency indicates that initialization strategies grounded in job sequencing logic and workload prioritization principles possess inherent compatibility with the constraint structure of smaller JSSP instances. The FIFO approach, which respects the natural precedence order of operations, and the MWR strategy, which prioritizes jobs with higher computational demands, appear to create initial populations that align well with the optimization landscape of these problems.

As problem complexity increases to medium-scale instances (ta21: 20 × 20 and ta31: 30 × 15), the performance landscape becomes more nuanced and revealing. The FIFO maintains its exceptional reliability, sustaining 100% success rates across both medium-scale problems, thereby establishing itself as the most consistently effective initialization strategy. However, the MWR approach exhibits problem-dependent behavior, achieving 93.3% success on ta21 while recovering to 100% success on ta31. This variation suggests that the effectiveness of workload-based prioritization may be influenced by the specific job-to-machine ratio characteristics of individual problem instances.

The hybrid and mixed methodologies reveal a complex relationship between problem scale and initialization effectiveness. The Pure Heuristic Mix strategy demonstrates significant performance degradation as problem complexity increases: from an excellent 97.1% success rate on ta01, it drops substantially to 46.7% on ta21, before partially recovering to 73.3% on ta31. This non-monotonic behavior suggests that the combination of multiple heuristic principles, while effective for smaller problems, may introduce conflicting guidance as the solution space becomes more complex. Similarly, the Multi-Level Hybrid approach shows variable performance (73.5% on ta01, 16.7% on ta21, 50.0% on ta31), indicating that sophisticated multi-layered initialization strategies may be sensitive to specific problem characteristics rather than simply problem size.

For large-scale problems (ta41: 30 × 20 and ta51: 50 × 15), the performance patterns become even more distinct. The FIFO Heuristic continues its dominance with 100% success rates, reinforcing its position as the most reliable initialization strategy across all problem scales. MWR approach also maintains strong performance with 100% success on both large-scale instances, suggesting that workload-based prioritization scales effectively with problem complexity. However, hybrid approaches show mixed results: while Quality Diversity Balance maintains reasonable performance (around 76–83% success), other hybrid methods like Pure Heuristic Mix show more variable outcomes.

Perhaps the most significant finding is the complete failure of all random-based initialization methods (Random Uniform, Random Normal, Latin Hypercube, Sobol Sequence) across every problem instance tested, regardless of scale or complexity. This universal failure rate of 0% provides compelling evidence that unstructured exploration of the solution space, despite theoretical advantages in terms of diversity and coverage, is fundamentally incompatible with the highly constrained nature of JSSP problems. The constraint satisfaction requirements of JSSP appear to demand initialization strategies that incorporate domain knowledge and respect the underlying problem structure.

Equally noteworthy is the complete failure of certain heuristic strategies, including SPT (Shortest Processing Time), LPT (Longest Processing Time), Critical Ratio, and Least Work Remaining, which achieved 0% success rates across all instances. This suggests that not all scheduling heuristics are equally suitable for population initialization in JSSP optimization. The success of FIFO and MWR, contrasted with the failure of SPT and LPT, indicates that the temporal ordering of operations (FIFO) and aggregate workload considerations (MWR) are more fundamental to generating feasible initial solutions than individual operation duration priorities.

The adaptive methods show interesting but mixed results. The Problem Size Adaptive strategy, designed to adjust initialization behavior based on problem complexity, shows good performance on smaller problems but becomes less reliable on medium-scale instances, suggesting that the adaptation mechanisms may require further refinement. The machine–job ratio-based approach demonstrates variable effectiveness across different problem types, indicating that while the concept of ratio-based adaptation has merit, the specific implementation may need optimization for different problem characteristics.

These findings collectively suggest that successful population initialization for JSSP requires strategies that (1) incorporate fundamental domain knowledge about job sequencing and resource allocation, (2) respect the precedence constraints inherent in manufacturing workflows, (3) maintain consistency across varying problem scales, and (4) avoid the apparent pitfalls of both pure randomization and certain traditional scheduling heuristics. The dominance of FIFO across all problem instances establishes it as a benchmark for effective JSSP population initialization, while the strong performance of MWR provides a complementary approach based on workload distribution principles.

4.1. Machine Learning-Enhanced Initialization

To investigate the effect of informed initialization on JSSP optimization, this study incorporates a machine learning-based approach using a compact variational autoencoder (VAE). Unlike traditional heuristics that rely on fixed dispatching rules, the VAE learns a latent representation of high-quality JSSP solutions and generates new population members by sampling from this learned distribution.

Each solution is encoded as a continuous vector of dimension d = J × M, where J is the number of jobs, and M is the number of machines. Thus, the VAE directly models operation-ordering patterns in the job–machine matrix. Training data were obtained exclusively from the two most reliable heuristic methods identified in earlier evaluations—FIFO and MWR. For each training instance, between 15 and 50 feasible solutions (makespan < 1 × 10⁶) were collected, after which the top 80% elite subset was used to construct the final training dataset. This ensures that the VAE learns the structural characteristics of high-quality schedules rather than noise or infeasible patterns.

To prevent data leakage and ensure a meaningful assessment of generalization, all VAE models were trained only on training instances (TA02, TA12, TA22, TA32, TA42, and TA52), while evaluation was conducted on unseen test instances (TA01, TA11, TA21, TA31, TA41, and TA51). This strict train–test separation allows the analysis to reflect true generalization rather than memorization of training samples. This design explicitly reduces training bias by preventing data leakage and avoiding exposure to inferior or infeasible schedules.

A separate VAE model was trained for each problem dimension. The compact encoder–decoder architecture consists of an input layer of size d = J × M, a hidden layer of 32–128 units (depending on instance size), and a latent space of 4–16 dimensions, automatically selected based on problem scale. The models were trained with the Adam optimizer (learning rate 1 × 10⁻³), using a reconstruction loss combined with a KL divergence term weighted by β = 0.1. Gradient clipping and a ReduceLROnPlateau scheduler were employed for stability, while early stopping prevented overfitting. Model quality was validated through reconstruction-loss convergence (final MSE: 0.0015–0.0045) and a back-testing procedure in which 1000 samples were generated and decoded into schedules. VAE models achieved 100% validity on test instances, while random uniform sampling achieved 0% validity, confirming that learned patterns respect JSSP constraint structure.

During the generation phase, each trained VAE produces new individuals by decoding latent vectors sampled from a standard normal distribution. These samples approximate the distribution of high-quality elite solutions while introducing controlled variability. Three variants were tested: VAE_Pure (100% VAE-generated), VAE_Hybrid_60 (60% VAE + 40% FIFO), and VAE_Hybrid_40 (40% VAE + 60% FIFO), enabling a structured comparison between purely machine learning-driven initialization and mixed strategies. The performance results of these approaches, evaluated on six benchmark instances, are summarized in Table 2.

Table 2. Experimental results for JSSP instances (best/mean/worst/std.dev).

Population Initialization Strategies	ta01 (15 × 15)	ta11 (20 × 15)	ta21 (20 × 20)	ta31 (30 × 15)	ta41 (30 × 20)	ta51 (50 × 15)
VAE_Pure	1527/ 1593/ 1644/ 28.60	1927/ 2001/ 2055/ 33.84	2223/ 2320/ 2390/ 42.57	2389/ 2484/ 2599/ 44.52	2889/ 3001/ 3109/ 52.22	3865/ 3999/ 4147/ 65.42
VAE_Hybrid_60	1524/ 1583/ 1632/ 32.64	1903/ 1994/ 2074/ 39.73	2208/ 2331/ 2416/ 44.93	2365/ 2510/ 2619/ 62.58	2920/ 3012/ 3097/ 44.98	3811/ 4002/ 4088/ 58.88
VAE_Hybrid_40	1500/ 1590/ 1656/ 32.41	1925/ 2017/ 2080/ 37.80	2286/ 2351/ 2441/ 35.44	2416/ 2500/ 2569/ 38.10	2903/ 3023/ 3089/ 48.67	3849/ 4013/ 4179/ 77.25
FIFO	1547/ 1619/ 1702/ 39.13	1964/ 2051/ 2159/ 44.91	2289/ 2480/ 2667/ 89.13	2428/ 2540/ 2689/ 73.52	2958/ 3116/ 3273/ 84.64	3910/ 4080/ 4201/ 67.75
MWR	1571/ 1628/ 1706/ 30.52	2009/ 2070/ 2142/ 37.34	2299/ 2488/ 2726/ 104.23	2406/ 2534/ 2650/ 57.33	2869/ 3094/ 3387/ 96.95	3937/ 4084/ 4305/ 87.95

The experimental results demonstrate that VAE-based methods (VAE_Pure, VAE_Hybrid_60, and VAE_Hybrid_40) consistently produced valid solutions across all test instances, whereas traditional heuristic-based methods (FIFO, MWR) occasionally generated invalid solutions (3.1% of total runs). Figure 2 illustrates the distribution of makespan values obtained by VAE-based and traditional initialization methods across all test instances. The figure highlights that VAE-based approaches consistently produce valid schedules in all experimental runs, whereas traditional heuristic-based methods occasionally fail to generate feasible solutions, particularly on more constrained instances. Moreover, VAE-based methods exhibit more compact performance distributions, indicating higher robustness and reliability compared to FIFO and MWR initialization strategies.

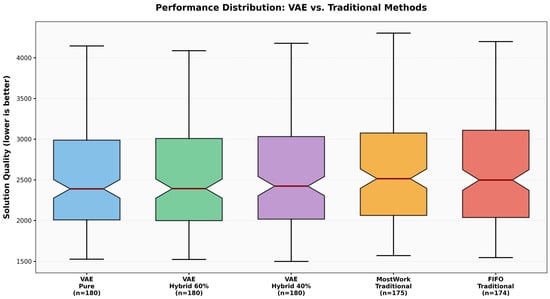
Figure 2. Performance distributions.

The statistics in Table 2 are calculated using only valid solutions. Analysis of average makespan values shows that VAE-based approaches generally achieve lower values, with VAE_Pure performing particularly well on most instances. As expected, makespan values increase with problem size (ta01 to ta51). Additionally, VAE methods demonstrate lower standard deviations, indicating more consistent performance compared to traditional approaches.

A Chi-square test of independence was conducted to examine the relationship between method type and solution validity. The results indicate a significant association between the type of initialization method and solution validity (χ²(1, N = 900) = 14.27, p < 0.001, Cramér’s V = 0.126). VAE-based methods achieved perfect reliability with all 540 experimental runs producing valid solutions (100% success rate), while traditional heuristic-based methods failed in 11 out of 360 attempts (97% success rate). Notably, invalid solutions occurred only in the instances containing 20 machines, suggesting that the difficulty arises not from overall problem size but from the specific constraint structure of 20-machine configurations. Traditional dispatch rules (FIFO and MWR) appear to struggle with the precedence constraint satisfaction in this particular machine configuration, while VAE-based methods successfully learn to navigate these structural complexities. These findings demonstrate the superior robustness and adaptability of machine learning-enhanced initialization compared to conventional heuristics.

The Friedman test on valid solutions across all six instances (χ² = 19.87, p < 0.0005) indicates significant differences among methods’ performances. Kendall’s W (0.828) suggests strong consistency across instances, confirming robust performance differences.

Table 3 presents the post hoc pairwise comparison results using Wilcoxon signed-rank tests with Holm correction. While the Friedman test detected global differences among methods, the small sample size (n = 6 instances) resulted in reduced statistical power for post hoc Wilcoxon tests. The Holm correction further exacerbated this limitation, though the consistent direction of effects (all six VAE vs. Traditional comparisons show raw p = 0.0312) and substantial effect sizes (mean differences ranging from 35 to 84 makespan units) continue to indicate practical significance.

Table 3. Post hoc analysis (Wilcoxon, Holm-adjusted).

Comparison	Wilcoxon p	Holm-Adjusted p	Significant (α = 0.05)	Better (Lower Mean)
VAE_Pure vs. MWR	0.0312	0.3125	No	VAE_Pure
VAE_Pure vs. FIFO	0.0312	0.2812	No	VAE_Pure
VAE_Hybrid_60 vs. MWR	0.0312	0.2500	No	VAE_Hybrid_60
VAE_Hybrid_60 vs. FIFO	0.0312	0.2188	No	VAE_Hybrid_60
VAE_Hybrid_40 vs. FIFO	0.0312	0.1875	No	VAE_Hybrid_40
VAE_Hybrid_40 vs. MWR	0.0312	0.1562	No	VAE_Hybrid_40
VAE_Pure vs. VAE_Hybrid_40	0.0625	0.2500	No	VAE_Pure
VAE_Hybrid_60 vs. VAE_Hybrid_40	0.0938	0.2812	No	VAE_Hybrid_60
VAE_Pure vs. VAE_Hybrid_60	0.3125	0.6250	No	VAE_Pure
FIFO vs. MWR	0.6875	0.6875	No	FIFO

4.2. Population Diversity

Population diversity is a critical performance indicator for evolutionary algorithms and swarm intelligence methods, providing a measure of how effectively an algorithm explores the search space. In combinatorial optimization problems such as JSSP, the diversity of the initial population directly impacts the algorithm’s balance of exploration and exploitation. Low diversity increases the risk of premature convergence, while excessively high diversity can lead to inefficient search. This study analyzes both the initial and final population diversity of different population initialization strategies to examine the search dynamics of VAE-based methods compared to traditional heuristic-based methods. Monitoring population diversity is an important tool for understanding how an algorithm adapts to problem complexity and the relationship between solution quality and search strategy.

The results in Table 4 show clear differences in population diversity dynamics across initialization strategies. VAE-based methods generally start with lower initial diversity compared to traditional heuristics, reflecting the structured nature of their learned representations. Despite this, all VAE variants demonstrate substantial increases in diversity during the search process, indicating effective exploration behavior. In particular, VAE_Pure exhibits consistently strong diversity growth, maintaining a balanced increase across all problem sizes. Hybrid approaches (VAE_Hybrid_60 and VAE_Hybrid_40) produce higher initial diversity, and in several instances—especially ta21, ta31, and ta41—they achieve the largest diversity gains within the VAE group. Traditional heuristic-based strategies (FIFO and MWR) begin with the highest initial diversity values due to their rule-based randomized construction. However, their diversity improvement during the search is more limited, suggesting weaker adaptive exploration capabilities. Overall, VAE-based initialization not only adapts more flexibly to increasing problem complexity but also maintains more dynamic diversity progression, highlighting the advantage of learned solution structures over fixed dispatching rules.

Table 4. Comparative analysis of population diversity dynamics (initial/final/change).

Population Initialization Strategies	ta01 (15 × 15)	ta11 (20 × 15)	ta21 (20 × 20)	ta31 (30 × 15)	ta41 (30 × 20)	ta51 (50 × 15)
VAE_Pure	0.272/ 0.557/ +0.286	0.299/ 0.478/ +0.180	0.346/ 0.603/ +0.256	0.347/ 0.773/ +0.426	0.399/ 0.598/ +0.199	0.384/ 0.664/ +0.280
VAE_Hybrid_60	0.301/ 0.485/ +0.184	0.375/ 0.524/ +0.149	0.415/ 0.782/ +0.367	0.430/ 0.588/ +0.158	0.530/ 0.961/ +0.431	0.500/ 0.728/ +0.228
VAE_Hybrid_40	0.352/ 0.480/ +0.129	0.430/ 0.701/ +0.271	0.495/ 0.838/ +0.343	0.519/ 0.801/ +0.282	0.638/ 0.869/ +0.231	0.633/ 0.879/ +0.246
FIFO	0.394/ 0.519/ +0.125	0.440/ 0.592/ +0.151	0.519/ 0.715/ +0.196	0.593/ 0.778/ +0.185	0.683/ 0.876/ +0.193	0.743/ 0.985/ +0.242
MWR	0.424/ 0.569/ +0.145	0.467/ 0.625/ +0.158	0.543/ 0.718/ +0.175	0.595/ 0.781/ +0.185	0.698/ 0.905/ +0.207	0.843/ 1.071/ +0.228

Figure 3 summarizes the population diversity dynamics across all benchmark instances. VAE-based initialization strategies consistently start with lower initial diversity, reflecting their structured and model-driven generation process. Nevertheless, they exhibit markedly stronger diversity growth during the optimization, indicating more effective adaptive exploration. In contrast, traditional heuristic-based methods (FIFO and MWR) begin with higher initial diversity but show limited diversity evolution, suggesting early structural stagnation. Overall, the graphical analysis confirms that learned initialization enables more dynamic diversity progression than fixed rule-based strategies, particularly as problem size and constraint complexity increase.

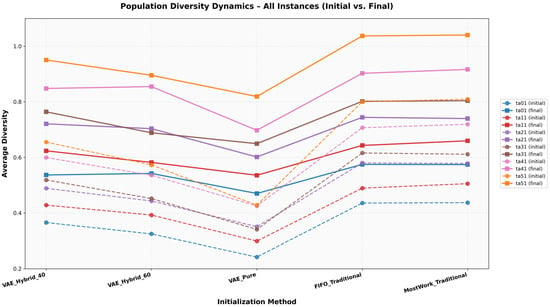
Figure 3. Evolution of population diversity for different initialization strategies. Initial and final diversity values are averaged over 30 independent runs.

5. Conclusions and Discussion

This study investigated the impact of population initialization strategies on PSO performance for the Job Shop Scheduling Problem through a comprehensive two-phase experimental design. In the first phase, 17 distinct initialization methods across four categories (random-based, heuristic-based, hybrid/mixed, and adaptive) were evaluated. In the second phase, machine learning-enhanced initialization using variational autoencoders (VAEs) was developed and compared against the best-performing traditional methods.

5.1. Phase 1: Evaluation of Traditional Initialization Methods

The systematic evaluation of 17 initialization strategies revealed fundamental insights into the requirements for effective JSSP population generation. Random-based methods (Random Uniform, Random Normal, Latin Hypercube, Sobol Sequence) achieved 0% success rates across all problem instances, demonstrating complete incompatibility with constrained discrete optimization problems despite their theoretical advantages in diversity and coverage. Among problem-specific heuristics, only FIFO and MWR succeeded consistently, while SPT, LPT, Critical Ratio, and Least Work Remaining failed entirely (0% success). Hybrid methods showed variable performance: Pure Heuristic Mix achieved 97.1% success on ta01 but degraded to 46.7% on ta21, while Quality Diversity Balance maintained moderate success rates (76–83%) across larger instances. Adaptive methods exhibited instance-dependent behavior, with Problem Size Adaptive achieving good performance on smaller problems but reduced reliability on medium-scale instances. These results establish that successful JSSP initialization requires strategies incorporating domain knowledge about job sequencing and resource allocation while respecting precedence constraints, rather than relying on random exploration or certain traditional scheduling heuristics.

5.2. Phase 2: Machine Learning-Enhanced Initialization

Building on Phase 1 findings, VAE-based initialization methods were trained on solutions from FIFO and MWR heuristics. The experimental results demonstrate significant improvements over traditional approaches. VAE-based methods produced valid solutions in all 540 experimental runs (100% success rate), while traditional heuristic methods achieved valid solutions in 349 out of 360 runs (97% success rate). Statistical analysis confirmed a significant association between method type and solution validity (χ²(1, N = 900) = 14.27, p < 0.001, Cramér’s V = 0.126). Invalid solutions from traditional methods occurred exclusively in 20-machine instances (ta21 and ta41), indicating sensitivity to specific constraint structures that VAE-based methods successfully navigate.

The Friedman test revealed significant performance differences across methods (χ² = 19.87, p < 0.001, Kendall’s W = 0.828). VAE-based methods consistently achieved lower mean ranks (VAE_Pure: 1.50, VAE_Hybrid_60: 1.83, VAE_Hybrid_40: 2.67) compared to traditional methods (FIFO: 4.33, MWR: 4.67) across all six test instances, with mean makespan reductions ranging from 35 to 84 units. While post hoc pairwise comparisons did not achieve statistical significance after Holm correction due to limited sample size (n = 6 instances), the consistent direction of effects and substantial practical differences indicate meaningful performance advantages.

Population diversity analysis revealed a counterintuitive finding: VAE-based methods started with lower initial diversity (0.341–0.511) compared to traditional methods (0.562–0.595), yet exhibited substantially larger diversity increases during optimization (+0.250 to +0.271 vs. +0.182 to +0.183). VAE_Pure, despite having the lowest initial diversity, showed the largest relative increase (1.79×). In contrast, traditional methods started with high initial diversity due to rule-based randomized construction but demonstrated more limited diversity improvement during search. This pattern suggests that structured initialization based on learned solution patterns enables more effective adaptive exploration than broad initial dispersion alone.

The proposed VAE does not simply resample solutions produced by FIFO or MWR heuristics. Instead, it captures their underlying latent structure and generalizes this knowledge to generate novel, previously unseen, and valid schedules.

5.3. Main Findings and Contributions

This research establishes three main findings: (1) Problem-aware initialization incorporating domain knowledge significantly outperforms both random-based and many traditional heuristic approaches for JSSP. (2) Machine learning-enhanced initialization using VAE achieves both higher solution validity (100% vs. 97%) and better makespan performance across diverse problem instances. (3) Effective exploration emerges from structured initialization that enables dynamic diversity growth during optimization, rather than from high initial diversity alone.

These findings contribute to understanding population initialization strategies for combinatorial optimization and demonstrate the value of integrating machine learning techniques into metaheuristic algorithm design. The methodology employed canonical PSO to maintain experimental clarity and ensure that observed performance differences stem from initialization strategies rather than algorithmic modifications.

5.4. Limitations and Future Research Directions

While the present study provides a systematic and controlled analysis of population initialization strategies for the Job Shop Scheduling Problem using a canonical PSO framework, several limitations suggest promising directions for future research. First, the experimental evaluation was deliberately restricted to the standard PSO formulation in order to clearly isolate and attribute performance differences to initialization effects; however, future studies should examine whether the observed trends persist across advanced PSO variants such as adaptive inertia weight PSO, constriction factor PSO, comprehensive learning PSO, and quantum-behaved PSO. Second, although the focus on the classical JSSP enables a rigorous assessment under strict precedence and machine constraints, extending the proposed initialization framework to related scheduling problems, such as Flow Shop and Flexible Job Shop Scheduling Problems, would be valuable to assess generalizability under different routing and flexibility assumptions. Third, the current VAE models were trained using solutions generated by specific high-performing heuristics (FIFO and MWR), and alternative training strategies incorporating solutions from multiple algorithms, semi-supervised learning schemes, or different architectural configurations may further enhance robustness. Additional future directions include extending the framework to multi-objective JSSP formulations, validating scalability on larger industrial-scale instances, and conducting a detailed analysis of computational overhead associated with VAE training and sampling. Collectively, these directions would help establish the broader applicability of machine learning-enhanced initialization strategies across metaheuristic frameworks and complex combinatorial optimization problems.

5.5. Concluding Remarks

This work demonstrates that population initialization represents a critical yet often underestimated component of metaheuristic algorithm design for constrained combinatorial optimization. The findings highlight that effective initialization requires problem-specific knowledge rather than generic diversity-based approaches and that machine learning techniques can successfully capture and generalize this knowledge to produce superior initial populations. By establishing the viability of VAE-based initialization for JSSP and providing a comprehensive evaluation framework, this research contributes to both theoretical understanding and practical application of initialization strategies in scheduling optimization. The insights gained provide a foundation for developing specialized initialization approaches for other manufacturing and production scheduling challenges, ultimately advancing the capabilities of metaheuristic algorithms in solving real-world industrial optimization problems.