Abstract
High-throughput technologies produce large-scale omics datasets, and their integration facilitates biomarker discovery and predictive modeling. However, challenges such as data heterogeneity, high dimensionality, and block-wise missing data complicate the analysis. To address these issues, optimization techniques, including regularization and constraint-based approaches, have been already employed for regression and binary classification problems. Building on these methods, we extended this framework to support multi-class classification. Indeed, applied to a multi-class classification task for breast cancer subtypes, our model achieves accuracy between 73% and 81% under various block-wise missing data scenarios. Additionally, we assess its performance on a regression problem using the exposome dataset, integrating a larger number of omics datasets. Across different missing data scenarios, our model demonstrates a strong correlation (75%) between true and predicted responses. Furthermore, we have updated the bwm R package, which previously supported binary and continuous response types, to also include multi-class response types.
1. Introduction
Recent advances in high-throughput technologies, along with collaborative efforts such as The Cancer Genome Atlas (TCGA) [1], have allowed for the generation of large datasets that include diverse omic profiles and detailed clinical annotations in extensive sample collections. The unprecedented availability of multiple omics data types (e.g., transcriptomics, proteomics, metabolomics) for the same set of samples, a concept widely known as multi-omics, offers a robust platform for investigating molecular mechanisms underlying diseased phenotypes. In machine learning, it is widely recognized that the combination of various omic sources increases predictive model performance and allows for more reliable biomarker discovery, contributing to understanding the characteristics of complex diseases [2]. However, integrating multi-omics data is fraught with challenges [3], such as data heterogeneity, the inherent noise in biological datasets, high dimensionality, and missing data issues.
Multi-omics experiments often encounter missing data problems [4], especially when large portions of data are absent from one or more omics sources, resulting in block-wise missing data. For instance, an examination of sample availability across various experimental strategies in TCGA projects shows a significant imbalance, with RNA-seq and whole-slide imaging samples far exceeding those from other omics such as whole genome or whole exome sequencing. As a result, compiling a sufficiently large dataset with complete information across all omics for each individual is often impractical.
A straightforward solution is to exclude samples with missing values; however, this leads to a significant loss of valuable data. Another approach is to impute missing values, which is a challenging task, especially when the generative process behind the missing data is unknown [4,5]. To overcome this challenge, we adopted an available-case approach, leveraging distinct complete data blocks and avoiding the need for imputation [6]. To support this approach, we extended the functionality of the bmw R package [6], enabling it to handle regression and binary and multi-class classification.
In the following sections, we outline our methodological framework for dealing with block-wise missing data (Section 2), provide the gradient expressions of the loss functions required for multi-class classification (Section 3), and expand upon our previous work in regression and binary classification [6]. Finally, in Section 4, we present two real-world case studies that illustrate the advantages of our approach, while Section 5 and Section 6 contain the discussion and conclusions, respectively.
2. Methods
We take the linear regression model as a starting point that incorporates multiple data sources; let us say S sources. For the i-th source, let denote a data matrix of dimensions , where n is the number of samples and represents the number of variables, with . Furthermore, let be the n-dimensional response vector, where each entry corresponds to the value of a sample. Then, we formulate the model in the following way:
where denotes the noise term, while represents the vector of unknown parameters corresponding to the i-th data source. To enable analysis at both the feature and source levels, we introduce an additional parameter vector (a weight for each source), which incorporates the learned models into the regression setup:
The analysis at the feature level is prominent for deriving meaningful insights from the dataset, understanding the importance of individual features, and taking thoughtful action on data preprocessing and model specification. However, source-level analysis enables the identification of differences between groups, the detection of unique patterns linked to specific sources, and the ability to make data-driven decisions from these findings.
2.1. Block-Wise Missingness and Profiles
In numerous situations, entire blocks of data from specific sources are absent, which means that some samples are completely devoid of features from a particular source. Specifically, the matrix might have rows with completely missing data, and these absent rows can vary between sources . To directly implement feature-level machine learning techniques, one could either exclude all samples from sources with missing data or fill in the missing values using the available data. However, both methods have notable drawbacks. The first approach can significantly decrease the size of the dataset, while the second is heavily dependent on prior knowledge of the reasons behind missing data. Both strategies risk suboptimal outcomes by not addressing the missing block structure in the data.
To retain as much information as possible from the original data, one approach is to partition the dataset into multiple groups, called profiles, based on data availability. As described in [7,8], the concept of a profile is introduced, which allows multiple models to be constructed using only the complete data within each profile. If we consider that each observation has at least one available data source among the S sources in the study, the number of possible missing block patterns is . Each observation is assigned to a profile based on the absence or presence of specific data sources. A binary indicator vector is created for each observation to enable the determination of the profiles, defined as follows:
The data in the indicator vector can be fully expressed by a decimal integer, which will henceforth be called the profile. This profile is obtained by converting the binary vector into a binary number and then translating it into a decimal number. All such profiles are stored in a vector denoted as , with a dimension denoted by . To enhance clarity and facilitate understanding, consider the case with 3 data sources, . Table 1 shows the data availability options for a given sample and their profile number, where 0 indicates that the source is not available and 1 indicates that it is. A particular study will not necessarily present all possible profiles, depending on the experimental circumstances causing the missing data in blocks.

Table 1.
List of profiles. ().
Once we identify the availability of data sources using profiles, we arrange the entire dataset into complete data blocks to extract the maximum information from the available data. To achieve this, for a specific profile m, we group all samples with profile m and those with complete data in all sources defined by profile m, which means source-compatible profiles. As shown in Table 2, we can create numerous blocks with complete data for different sets of sources. For instance, samples in profile 6 are compatible with those in profile 7, allowing us to form a complete data block from sources 1 and 2.

Table 2.
Complete data blocks. ().
Using profiles, we can formulate the model (1) by
where given the profile m, then , , represents the submatrix of the i-th source, is the number of samples that contain m in their profiles, is the weight related to the matrix , and denotes the dimensional vector restricted to that samples. It will be useful to define and to refer to all the model coefficients for the profile m.
Continuing with the previous example, by taking samples in profile and those that have complete data from all sources in that profile, that is, sources 1 and 2, we will obtain the regression matrix . According to Table 2, the matrix will contain the samples of profiles 6 and 7; and, according to Table 1, the samples of profile 6, unlike those of profile 7, have the missing block of source 3. We arrange the samples in matrix such that the initial rows correspond to the smallest profile, followed by rows from increasingly larger profiles, until is complete. This arrangement reveals a box structure in . For example, takes the following form:
We should point out here that since we will consider the model in (2), each weight will multiply the submatrix . For example, although contains missing values, it will not be considered because . We will have
In general, if the source i in is not part of the profile m we assign and so it is not acknowledged for that profile. Naturally, the vector also forms a box-like structure when arranged by rows in the same manner as . In this example,
Thus, in this specific case, the objective is to learn three model coefficients, , , and independently for each data source, as well as the vectors , with , which combine them. Observe that, for the i-th data source, stays the same across profiles, while the component of the vector may vary across each different profile m. Furthermore, to simplify notation, the components related to missing sources are set to zero, instead of specifying vectors of different dimensions (see Table 3).

Table 3.
Vectors of coefficients of the sources along the profiles ().
2.2. Two-Step Optimization Procedure
Our goal is to learn and from the data . To achieve this, we employ the same methodology as in [6] [Section 2.2]. In particular, we apply a two-stage optimization model based on a regularization and constraint approach, which are utilized to enhance model performance, reduce overfitting, and incorporate prior knowledge into the analysis. In fact, in [7,8] the authors introduce the key components required to solve an optimization algorithm based on a unified feature learning model for heterogeneous block-wise missing data, which conducts both feature-level and source-level analysis at the same time. The problem that needs to be solved is as follows:
subject to
Here, can be any convex loss function, including the commonly used least squares loss function, among others. In addition, and are norm functions, which are used to apply regularization techniques and constraints that promote sparsity and control model complexity. Furthermore, serves as the regularization parameter, playing a crucial role in mitigating overfitting by imposing a penalty on the complexity of the model. By controlling the magnitude of the coefficients, helps ensure that the model generalizes well to unseen data, thus improving its predictive performance and stability across different datasets.
The primary components required to compute the parameters and are detailed in [6], Section 2.2, and [9,10,11,12,13,14]. Nevertheless, for the sake of completeness and to enhance clarity for the reader, we include them partially here.
2.2.1. Computing When Is Fixed
When is fixed, the optimal is obtained by solving the following optimization problem:
where the specific form of f is defined by the loss function . For various regularization terms , including penalty functions such as ridge, -norm, and other sparsity-promoting penalties, an efficient optimal solution can be achieved using the -norm projection iteration method, which requires computing . For further details, refer to [6] [Appendix 2].
2.2.2. Computing When Is Fixed
When is fixed, the optimal is determined by solving the following optimization problem:
where the exact expression of g is dictated by the loss function . An efficient optimal solution is derived using the proximal gradient iteration, which requires computing and is well suited for function norms that promote sparse solutions. For additional details, refer to [6] [Appendix 1].
2.2.3. Two-Stage Algorithm
The whole algorithm is depicted as follows (Algorithm 1):
| Algorithm 1 Two-stage iterative solution for and . |
Input: , , , ⟶ Output: Solutions and to (4)
|
The least squares loss function was addressed in [7,8] and the logistic loss function was addressed by the authors in [6]. In the next section, we present a way to incorporate the cross-entropy loss function into this framework, with which to address multi-class classification. We provide the expressions of the functions f in Section 2.2.1 and g in Section 2.2.2 as well as the respective gradients that are necessary for the implementation of the two-step procedure.
3. Multi-Class Classification
In the multi-class case, given a profile m, the model (2) has the vector
where K is the number of classes and is the number of samples associated with the profile m. Furthermore, for each source j, we have the coefficient matrix:
where , , are column vectors of dimension . In a multi-class classification task, the log soft-max loss function
is applied, where is 1 if , and 0 otherwise. Incorporating this loss function, the minimization problem (4) takes the form
subject to . The implementation of Algorithm 1 provides the explicit formulation of functions and gradients involved in the two steps detailed in Section 2.2.1 and Section 2.2.2. We next proceed to obtain these formulations.
3.1. Computing When Is Fixed
According to Section 2.2.1, we minimize using the -norm projection iteration method, for which we only need to compute its gradient. In that case, we have that the function f is
and the gradient is given by
for and .
3.2. Computing When Is Fixed
According to Section 2.2.2, we need to minimize , which is of the form
To minimize g, we apply the proximal gradient iteration method, which requires computing its gradient, given by
for , , and indicates whether j is included in the profile m.
4. Results
In this section, we analyze breast cancer data obtained from The Cancer Genome Atlas (TCGA), emphasizing the use of multi-omics data, including mRNA, miRNA, and DNAm, as detailed in Section 4.1. Our research employs a detailed dataset of 528 samples, each featuring 1000 genomic attributes per omic, utilizing cross-entropy loss to address a multi-class classification challenge.
Furthermore, we investigate the exposome data from the ISGlobal Exposome 2021 Data Challenge project, which examines the connections between environmental exposures and human health, as described in Section 4.2. This dataset presents a regression challenge, aiming to predict the z-score body mass index for children based on diverse environmental factors.
In both instances, we systematically introduce missing data blocks to evaluate their effect on model performance, exploring scenarios with varying levels of missing data. The results highlight the robustness of our model, maintaining high accuracy across different missing data scenarios, and outperforming profile-free approaches. This analysis builds upon previous work where also other multi-omics datasets were considered [6], with the goal of assessing the model’s performance independently and in comparison to other techniques, rather than solely focusing on the consequences of omics data dimensionality, while incorporating the model’s new multi-class capability.
4.1. Breast Cancer Data
The breast cancer patient data were sourced from The Cancer Genome Atlas (TCGA) [1]. We utilized multi-omics data (mRNA, miRNA, and DNAm) as described in [15], accessible via https://github.com/hyr0771/DiffRS-net (accessed date 16 February 2025). This dataset includes four breast cancer subtypes, Basal-like (Basal), Her2-enriched (Her2), Luminal A (LumA), and Luminal B (LumB), which are recognized as the most consistently identified subtypes of human breast cancer [16]. The main characteristics of these subtypes are determined by the expression levels of the estrogen receptor (ER), progesterone receptor (PR), human epidermal growth factor receptor 2 (HER2), and the proliferation marker Ki67 [16,17]. The dataset comprises 528 samples with 1000 genomic features per omic. Relevant features were selected in [15] to reduce omics dimensionality, placing us in a typical omics scenario where n is less than p.
Sample distribution by cancer subtype is as follows: Basal 87, Her2 31, LumA 284, and LumB 126. We employed cross-entropy loss to model the cancer subtype, incorporating the regularization hyperparameter and the norm function to prevent overfitting, particularly in classes with smaller sample sizes like Her2. Regularization helps by penalizing overly complex models, thereby ensuring that the model generalizes well to unseen data and maintains robust performance across different scenarios. To evaluate the effect of missing data blocks, we intentionally introduced random instances where some lacked expression or methylation data, ensuring the missing block structure affected all omics. We systematically assessed the impact by examining scenarios with different percentages of samples having missing blocks, specifically at rates of 5%, 10%, 20%, and 30% (see Figure 1). In each scenario, the dataset was divided into training and testing subsets, with proportions of 2/3 and 1/3, respectively. The model was then trained on the training set and its performance evaluated on the test set.
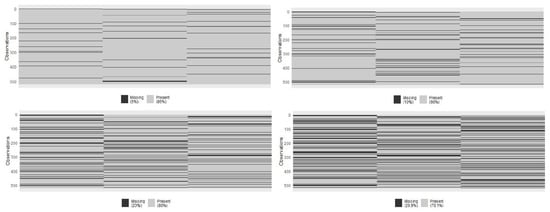
Figure 1.
Block-wise missing scenarios in Breast cancer data.
In Table 4, we show the performance in the different block-wise missing data scenarios. The accuracy remains high around 80%; only in the 30% scenario does it fall below 75%. Both class specificity and Negative Predictive Value remain high in all classes and in all scenarios. The rest of the metrics (Sensitivity, Positive Predictive Value, and F1) show different behavior depending on the class. In the Basal and LumA classes, the metrics reach high values, worsening as the percentage of missing data increases. The metrics in the Her2 and LumB classes show worse behavior. The Her2 class is the least abundant. This is more evident in the test set, where there are only eight samples. Although in the 5% scenario the F1 metric is acceptable, it does not remain that way in the other scenarios. A different situation appears to be that of the LumB class, which is quite abundant. Classification errors are observed between the LumA and LumB classes, erroneously assigning samples of LumB to LumA. As is well known in biomedicine, these cancer subtypes have weak separation from molecular biomarkers, as highlighted in [16,17,18].

Table 4.
Performance metrics in block-wise missing scenarios in breast cancer data. Accuracy and per class Sensitivity (Sen), Specificity (Spc), Positive Predictive Value (PPV), Negative Predictive Value (NPV), and F1.
In Figure 2, we compare the accuracies between profile-free approaches and our profile-based approach. Profile-free approaches integrate omics applying the model 1 where training data are the subset of available complete observations or all observations where missing data were imputed by the k-nn rule. We highlight that our method outperforms both alternative methods in all scenarios.
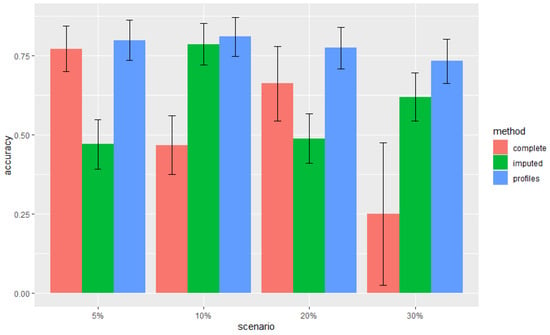
Figure 2.
Breast cancer data. Comparison of accuracy between the three approaches in the different missing block scenarios: complete (only available complete observations were included), imputed (missing data were imputed and all observations were included), profiles (our method). The 95% confidence intervals are shown.
4.2. Exposome Data
The exposome data belong to the ISGlobal Exposome 2021 Data Challenge project [19], which is an initiative aimed at exploring the relationship between environmental exposures and human health. The dataset is publicly available on the same website as the Data Challenge (https://github.com/isglobal-exposomeHub/ExposomeDataChallenge2021/, accessed date 16 February 2025). The dataset used in this study is the exposomeNA dataset, which contains exposome data with missing values. In this study, we focused on numerical variables, keeping all 1301 samples and a total of 176 numerical variables, which were categorized into five blocks based on their characteristics: Covariates (7), Chemical exposures (94), Indoor air (5), Lifestyles (6), and Outdoor exposures (64). The target variable for our regression model is the z-score body mass index for children aged 6–11 years, standardized by sex and age, and optimized using the mean squared error loss. Overall, our model comprises 176 variables organized into five blocks.
Similarly to the breast cancer dataset, missing data in blocks were randomly introduced to evaluate their impact on the performance of the regression model. Missing blocks were generated at rates of 5%, 10%, 20%, 30%, 40%, and 50% (see Figure 3). For each different scenario, the dataset was divided into training (2/3) and test (1/3) subsets. The model was trained using the training data and evaluated in the test set to assess its performance.

Figure 3.
Block-wise missing scenarios in exposome data.
To evaluate performance, we used the root mean square error (RMSE), the mean absolute error (MAE), and the Pearson correlation coefficient between true and predicted responses as evaluation metrics (see Table 5 and Figure 4). Performance remained competitive across all metrics and scenarios, with only a slight decrease observed for high percentages (30% or more) of missing data across blocks. Notably, the Pearson correlation was statistically significant (p-value < 2.2 × 10−16) in all scenarios.

Table 5.
Performance metrics in exposome data. RMSE, MAE, correlation.
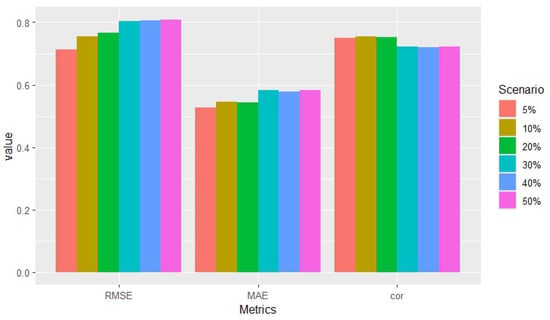
Figure 4.
Metrics across block-wise missing scenarios in exposome data.
To illustrate the distribution of the true values and their predictions across the six scenarios, Figure 5 presents their scatter plots. As expected, based on the metric values, particularly the correlation, there is no significant difference in the distribution of the point clouds among the scenarios. The red line represents the bisector.
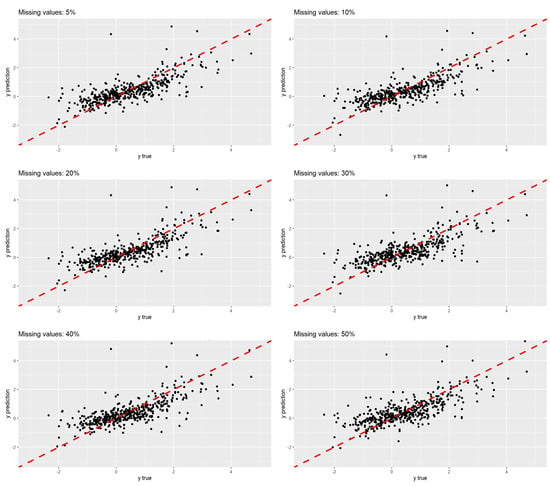
Figure 5.
Scatter plots of predicted values versus true values in several block-wise missing scenarios in exposome data.
5. Discussion
In this study, we adopted the methodological approach outlined in [6] and expanded it to accommodate multi-class classification. We introduced an efficient method for estimating feature and source parameters by alternating between regularization and constraint penalties, which has been implemented in the bwm R package, accessible at https://github.com/sergibaena-miret/Block-Wise-Missing, accessed date 16 February 2025.
To showcase the effectiveness of the two-stage algorithm in managing block-wise missing data in omics studies, we applied it to two multi-omics datasets: breast cancer [15] and exposome data [19].
The breast cancer dataset serves as a case study where the cross-entropy loss is crucial, as the outcome variable to predict is the cancer subtype (Basal, Her2, LumA, and LumB). The predictors in this dataset are divided into three blocks: mRNA, miRNA, and DNAm. This dataset allowed us to assess the effectiveness of our approach in handling various scenarios of block-wise missing data. The metrics used indicated satisfactory performance across all cases. However, in instances where a significant portion of blocks were missing (around 30%), accuracy metrics showed a slight decrease in performance. One strategy for dealing with missing data is to exclude observations with missing data from the analysis, which is clearly inefficient. In this context, we emphasize the comparison between our profile-based approach and the strategy relying solely on complete data. The profile-based approach has proven superior in all scenarios.
On the other hand, the exposome dataset is used as a case study in which the mean squared error is applied as the loss function since the target variable to be predicted is a numerical variable: the z-score body mass index at 6–11 years. The dataset consists of five blocks: Covariates, Chemical exposures, Indoor air, Lifestyles, and Outdoor exposures. Just like the breast cancer dataset, the exposome dataset assesses the performance of our approach using the same block-wise missing scenarios as those in the breast cancer dataset. The metrics applied demonstrate competitive performance in all scenarios. Although performance showed a slight decrease in the scenario with the highest percentage (30% or more) of missing blocks.
Despite these good results, scalability issues could be a concern. The presence of various profiles increases computational complexity, and even with modern computing power, processing high-dimensional data can be time-consuming. This is particularly relevant as the size and complexity of omics datasets continue to grow. Future work should focus on optimizing the algorithm for scalability, potentially through parallel computing or more efficient data handling techniques, to ensure its applicability to larger datasets without compromising performance.
Additionally, sensitivity analysis was performed to assess the model’s robustness by varying the proportions of missingness across different percentages of missing data. Cross-validation was also conducted in [6] for binary classification and regression approaches. Future research should include comprehensive sensitivity analyses to further explore the model’s reliability and robustness under diverse conditions, such as different random seeds and varying noise levels, while continuing to compare its performance to other approaches such as imputation or the removal of missing data, to ensure its effectiveness and adaptability in handling incomplete datasets.
Finally, even if some discussions on different multi-omics datasets have been carried out in [6], we recognize the importance of extending this discussion to other multi-omics data domains for the validation of our model rather than on breast cancer and exposome datasets. Future work should also focus on exploring the model’s adaptability and performance across a broader range of multi-omics datasets, such as those related to neurological disorders, cardiovascular diseases, or metabolic conditions. This would not only demonstrate the model’s versatility but also highlight its potential to uncover insights in diverse biological contexts. Additionally, collaborating with domain experts in these areas could offer valuable insights into tailoring the model to specific research questions and data characteristics.
6. Conclusions
In this research, we addressed the methodological framework introduced in [6] to tackle multi-class classification challenges in the context of block-wise missing data. Our two-stage approach, implemented in the bwm R package, proved effective across two real-world multi-omics datasets: breast cancer and exposome data.
For the breast cancer dataset, our approach maintained high classification performance, with accuracy around 80% in most scenarios. However, as the proportion of missing blocks increased, we observed a decline in performance, particularly for the Her2 and LumB subtypes. The misclassification between LumA and LumB aligns with known biological challenges, as these subtypes share molecular similarities [18].
In the exposome dataset, our method effectively handled missing values while predicting children’s BMI z-scores. The structured partitioning of exposure blocks provided a robust way to assess environmental influences on health, reinforcing the importance of multi-source integration in exposome studies.
Despite these promising results, our approach presents some limitations. When missing data exceeded 30%, performance deterioration became evident, particularly for underrepresented classes. Future work should explore adaptive imputation strategies or uncertainty quantification techniques to mitigate these effects. Additionally, further benchmarking against other missing data strategies could provide deeper insights into the method’s comparative strengths and weaknesses.
Overall, this study underscores the potential of structured missing-data handling in multi-omics research, providing a scalable and interpretable approach for complex biological and environmental datasets.
Author Contributions
S.B.-M.: Software, Formal analysis, Writing, F.R.: Conceptualization, Writing, Data analysis, A.S.: Supervision, E.V.: Conceptualization, Writing, Data analysis. All authors have read and agreed to the published version of the manuscript.
Funding
Our research group has public funding (Ministerio de Ciencia, Innovación y Universidades, PID2023-148013OB-C22/AEI DOI:10.13039/501100011033) which finances all the group’s production, including but not limited to this work.
Data Availability Statement
All relevant data can be downloaded from public repositories. Breast cancer data repository: https://github.com/hyr0771/DiffRS-net (accessed date 16 February 2025), Exposome repository: https://github.com/isglobal-exposomeHub/ExposomeDataChallenge2021/ (accessed date 16 February 2025).
Acknowledgments
We are grateful to everyone at the TCGA Consortium and ISGlobal Exposome 2021 Data Challenge.
Conflicts of Interest
The authors have declared that no competing interests exist.
References
- The Cancer Genome Atlas Research Network; Weinstein, J.N.; Collisson, E.A.; Mills, G.B.; Shaw, K.R.; Ozenberger, B.A.; Ellrott, K.; Shmulevich, I.; Sander, C.; Stuart, J.M. The cancer genome atlas pan-cancer analysis project. Nat. Genet. 2013, 10, 1113–1120. [Google Scholar]
- Chierici, M.; Bussola, N.; Marcolini, A.; Francescatto, M.; Zandonà, A.; Trastulla, L.; Agostinelli, C.; Jurman, G.; Furlanello, C. Integrative network fusion: A multi-omics approach in molecular profiling. Front. Oncol. 2020, 10, 1065. [Google Scholar] [CrossRef]
- Picard, M.; Scott-Boyer, M.P.; Bodein, A.; Périn, O.; Droit, A. Integration strategies of multi-omics data for machine learning analysis. Comput. Struct. Biotechnol. J. 2021, 19, 3735–3746. [Google Scholar] [CrossRef]
- Flores, J.E.; Claborne, D.M.; Weller, Z.D.; Webb-Robertson, B.J.M.; Waters, K.M.; Bramer, L.M. Missing data in multi-omics integration: Recent advances through artificial intelligence. Front. Artif. Intell. 2023, 6, 1098308. [Google Scholar]
- Song, M.; Greenbaum, J.; Luttrell, I.V.J.; Zhou, W.; Wu, C.; Shen, H.; Gong, P.; Zhang, C.; Deng, H.W. A review of integrative imputation for multi-omics datasets. Front. Genet. 2020, 11, 570255. [Google Scholar]
- Baena-Miret, S.; Reverter, F.; Vegas, E. A framework for block-wise missing data in multi-omics. PLoS ONE 2024, 7, e0307482. [Google Scholar] [CrossRef] [PubMed]
- Xiang, S.; Yuan, L.; Fan, W.; Wang, Y.; Thompson, P.M.; Ye, J. Multi-Source Learning with Block-Wise Missing Data for Alzheimer’s Disease Prediction. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’13, Chicago, IL, USA, 11–14 August 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 185–193. Available online: https://doi.org/10.1145/2487575.2487594 (accessed on 4 December 2024).
- Xiang, S.; Yuan, L.; Fan, W.; Wang, Y.; Thompson, P.M.; Ye, J. Bi-level multi-source learning for heterogeneous block-wise missing data. Neuroimage 2014, 102, 192–206. [Google Scholar] [PubMed]
- Ceng, L.; Ansari, Q.; Yao, J.C. Some iterative methods for finding fixed point and for solving constrained convex minimization problems. Nonlinear Anal. Theory Methods Appl. 2011, 74, 5286–5302. [Google Scholar] [CrossRef]
- Levitin, E.S.; Polyak, B. Constrained Minimization Methods. Ussr Comput. Math. Math. Phys. 1966, 6, 1–50. [Google Scholar] [CrossRef]
- Balashova, S.D.; Plaksii, Z.T. Projection-iteration methods for solving constrained minimization problems. J. Math Sci. 1993, 66, 2231–2235. [Google Scholar]
- Berg, E.V.; Schmidt, M.; Friedlander, M.P.; Murphy, K. Group sparsity via linear-time projection. UBC—Department of Computer Science. 2008. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=b41400ffcef0a54c9dd734b1241a94d675bb6f1b (accessed on 4 December 2024).
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. Siam J. Imaging Sci. 2009, 2, 183–202. [Google Scholar]
- Nesterov, Y. Gradient methods for minimizing composite functions. Math. Program. 2013, 140, 1436–4646. [Google Scholar] [CrossRef]
- Zeng, P.; Huang, C.; Huang, Y. DiffRS-net: A Novel Framework for Classifying Breast Cancer Subtypes on Multi-Omics Data. Appl. Sci. 2024, 7, 2728. [Google Scholar]
- Therese, S.; Robert, T.; Joel, P.; Trevor, H.; Stephen, M.J.; Andrew, N.; Shibing, D.; Hilde, J.; Robert, P.; Stephanie, G.; et al. Repeated observation of breast tumor subtypes in independent gene expression data sets. Proc. Natl. Acad. Sci. USA 2003, 14, 8418–8423. [Google Scholar]
- Perou, C.M.; Sørlie, T.; Eisen, M.B.; Van De Rijn, M.; Jeffrey, S.S.; Rees, C.A.; Pollack, J.R.; Ross, D.T.; Johnsen, H.; Akslen, L.A.; et al. Molecular portraits of human breast tumours. Nature 2000, 6797, 747–752. [Google Scholar]
- Singh, A.; Shannon, C.P.; Gautier, B.; Rohart, F.; Vacher, M.; Tebbutt, S.J.; Lê Cao, K.A. DIABLO: An integrative approach for identifying key molecular drivers from multi-omics assays. Bioinformatics 2019, 17, 3055–3062. [Google Scholar]
- Maitre, L.; Guimbaud, J.B.; Warembourg, C.; Güil-Oumrait, N.; Petrone, P.M.; Chadeau-Hyam, M.; Vrijheid, M.; Basagaña, X.; Gonzalez, J.R.; The Exposome Data Challenge Participant Consortium. State-of-the-art methods for exposure-health studies: Results from the exposome data challenge event. Environ. Int. 2022, 168, 107422. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).