Abstract
Given an untrimmed video and a natural language query, the video temporal grounding task aims to accurately locate the target segment within the video. Functioning as a critical conduit between computer vision and natural language processing, this task holds profound importance in advancing video comprehension. Current research predominantly centers on enhancing the performance of individual models, thereby overlooking the extensive possibilities afforded by multi-model synergy. While knowledge flow methods have been adopted for multi-model and cross-modal collaborative learning, several critical concerns persist, including the unidirectional transfer of knowledge, low-quality pseudo-label generation, and gradient conflicts inherent in cooperative training. To address these issues, this research proposes a Multi-Model Collaborative Learning (MMCL) framework. By incorporating a bidirectional knowledge transfer paradigm, the MMCL framework empowers models to engage in collaborative learning through the interchange of pseudo-labels. Concurrently, the mechanism for generating pseudo-labels is optimized using the CLIP model’s prior knowledge, bolstering both the accuracy and coherence of these labels while efficiently discarding extraneous temporal fragments. The framework also integrates an iterative training algorithm for multi-model collaboration, mitigating gradient conflicts through alternate optimization and achieving a dynamic balance between collaborative and independent learning. Empirical evaluations across multiple benchmark datasets indicate that the MMCL framework markedly elevates the performance of video temporal grounding models, exceeding existing state-of-the-art approaches in terms of mIoU and Rank@1. Concurrently, the framework accommodates both homogeneous and heterogeneous model configurations, demonstrating its broad versatility and adaptability. This investigation furnishes an effective avenue for multi-model collaborative learning in video temporal grounding, bolstering efficient knowledge dissemination and charting novel pathways in the domain of video comprehension.
1. Introduction
Video Temporal Grounding (VTG) seeks to accurately pinpoint the corresponding time segment in an untrimmed video based on natural language queries [1]. As a pivotal task at the intersection of computer vision and natural language processing, VTG lays the groundwork for a variety of downstream video comprehension tasks, such as video dialogue systems [2], video relationship detection [3,4,5], and video question answering systems [6,7,8]. The majority of traditional VTG strategies concentrate on refining a single model, typified by the Span-based Model and the 2D-Map Model shown in Figure 1, both of which display distinct advantages and limitations in particular contexts [9]. The Span-based Model explicitly forecasts the probabilistic distribution of a target interval’s start and end points, showcasing commendable capabilities in delineating precise temporal boundaries. Nevertheless, given its dependence on localized feature extraction, it exhibits a diminished aptitude for holistic semantic context modeling, thereby restricting its effectiveness in handling semantically intricate videos [10,11]. In comparison, the 2D-Map Model devises a two-dimensional temporal mapping, partitioning the entire video span into a 2D matrix in which every element corresponds to a prospective temporal clip. Operating within a two-dimensional framework, this model maximizes the score region, thereby adeptly capturing the contextual interplay among temporal segments. However, the expansive search space for candidate clips renders its computational overhead substantial, ultimately undermining boundary prediction precision [12,13,14].
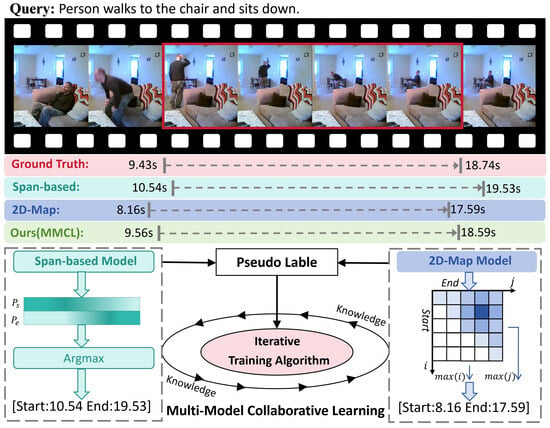
Figure 1.
An illustration of localizing a temporal moment in an untrimmed video using a language query. The 2D-MAP Model and the Span-based Model employ pseudo-labels to facilitate knowledge transfer and achieve collaborative learning across models. Leveraging an iterative training algorithm, they strike a dynamic balance between collaborative learning and independent optimization.
Despite the impressive performance of these models in specific settings, their independent optimization strategies fail to fully exploit the complementary nature among models, disregarding the potential for collaborative learning and thereby limiting further performance enhancement. In recent years, knowledge flow, which encompasses knowledge distillation and transfer, has increasingly become a critical strategy for achieving multi-model cooperative optimization in VTG endeavors. Through the supervised transfer of extensive knowledge from large-scale models to more compact ones, knowledge distillation empowers lightweight models to attain robust performance under constrained computational budgets [9,15,16]. By leveraging cross-modal alignment and data exchange, knowledge transfer fortifies the synergy between visual and textual representations, facilitating effective multimodal co-modeling [17,18]. Nevertheless, existing work often restricts knowledge flow to a unidirectional paradigm, such as transferring insights from larger models to smaller counterparts or employing simplistic cross-modal alignments. Such approaches generate pseudo-labels of limited quality and are prone to gradient conflicts in multi-model collaboration [19,20], thus failing to fully harness the potential of bidirectional cooperative learning and dynamic knowledge sharing. These shortcomings have emerged as a key bottleneck restricting further advancements in VTG performance.
To solve the aforementioned deficiencies, this study introduces a Multi-Model Collaborative Learning (MMCL) framework, illustrated in Figure 1. Within this framework, a bidirectional collaborative learning paradigm is instituted across multiple models, yielding significant enhancements in the performance of video temporal grounding. Concretely, to surmount the constraints of one-way knowledge transfer, the MMCL architecture adopts a bidirectional knowledge transmission scheme. Through an equitable exchange of pseudo-labels across different models, predictions from Model A furnish pseudo-supervision for Model B, while Model B’s output similarly informs Model A. This bidirectional collaboration mechanism fully leverages the complementary learning capacities among models, compensates for the limitations of one-way knowledge flow, and further capitalizes on each model’s strengths in boundary prediction and context modeling. To bolster the fidelity of pseudo-labels, the MMCL framework introduces a CLIP-guided pseudo-label generator. Leveraging the CLIP [21] model’s cross-modal priors, this module calculates the similarity between the video and the query text to provide precise temporal constraints for the pseudo-label generator, thereby reducing noise while enhancing temporal accuracy and semantic consistency of the pseudo-labels. Moreover, to counteract gradient clashes within multi-model collaborative learning, the MMCL framework embeds an iterative training algorithm. During each optimization cycle, one model’s parameters remain static while the other model’s supervision and transfer objectives are refined. This alternating optimization tactic substantially alleviates gradient contention among models and ensures their respective optimization autonomy. Through adaptive calibration of consistency thresholds and transfer loss coefficients, the framework achieves a nuanced balance between cooperative learning and autonomous optimization, culminating in superior overall performance.
Experimental results show that the proposed MMCL framework exhibits pronounced strengths and robust versatility in video temporal grounding. Its inherent adaptability makes the MMCL framework suitable for both heterogeneous and homogeneous model collaboration contexts, where it consistently yields appreciable performance gains. From a theoretical perspective, this study broadens the applicability of knowledge transfer and collaborative learning, addressing limitations in pseudo-label quality and model collaboration mechanisms, while offering an efficient and flexible solution for video temporal grounding. The key contributions of this work are enumerated as follows:
- We propose a multi-model collaborative learning framework employing a bidirectional knowledge transfer scheme to foster cooperative learning across distinct models, thus transcending the confines of isolated model optimization and amplifying cross-model complementarity.
- We design a CLIP-guided pseudo-label generator that harnesses CLIP’s cross-modal priors to optimize pseudo-label generation, improving their quality and robustness, and bolstering the accuracy of knowledge transfer.
- We present an iterative multi-model training algorithm that alternately freezes and optimizes model parameters to effectively mitigate gradient conflicts, safeguard the balance between cooperative and independent optimization, and further boost training stability and model performance.
- Experimental findings reveal that our method effectively enhance the performance of various baseline methods for video temporal grounding. By incorporating both the VSLNet [22] and 2D-TAN [23] baseline models, performance on multiple datasets surpasses current mainstream approaches.
2. Related Work
2.1. Video Temporal Grounding
Video Temporal Grounding (VTG) involves aligning temporal video segments with natural language queries, and existing methods predominantly fall into two categories: Span-based Models and 2D-MAP Models. Span-based Models, such as VSLNet [22], frame the VTG task as a span-based question-answering problem, where video segments serve as context, the target temporal fragment as the answer span, and the linguistic query as the question. These models excel at accurately detecting temporal boundaries and efficiently localizing target segments through boundary regression techniques. However, their focus on explicit boundary prediction often limits their ability to capture broader semantic contexts and handle long-duration interactions, making them less effective in complex video scenarios [10,11]. In contrast, 2D-MAP Models encode all potential start-end intervals as elements of a two-dimensional matrix, refining high-scoring regions to locate the desired temporal segment [9]. The 2D-TAN model [23], for example, constructs a temporal map to model contextual interactions among video segments, offering robust capabilities in modeling context and segment dependencies [24]. Despite their strengths, these models may struggle with boundary prediction accuracy in densely overlapping temporal segments, particularly under intricate temporal distributions [12,13,14]. While both approaches offer distinct advantages, their independent optimization limits the potential of leveraging their complementary strengths, highlighting the need for a collaborative learning framework like MMCL to integrate these methodologies effectively.
2.2. Knowledge Flow in Video Temporal Grounding
The utilization of knowledge flow in multimodal tasks is gaining momentum, predicated on the concept of disseminating knowledge across different models or modalities to augment collective model capability [25]. Present investigations can be bifurcated into two principal streams: knowledge distillation and knowledge transfer. Via knowledge distillation, the expertise of a large model is conferred upon a more compact model, ensuring the latter maintains commendable performance while remaining computationally efficient [26]. By integrating both local and global modality information and applying distillation techniques, Bao et al. improved the feature representation of video understanding models, thereby achieving greater accuracy in temporal localization tasks [16]. Other works leverage the robust representational capacity of large language models (LLMs) to generate weakly supervised pseudo-labels via distillation, thereby offering a novel optimization pathway for VTG tasks [15]. Furthermore, Liang et al. introduced a distillation approach employing multiple teacher models to collectively steer the student model’s learning, significantly boosting temporal localization accuracy for VTG [9]. Diverging from the principles of knowledge distillation, knowledge transfer focuses on facilitating cross-modal information exchanges that foster cooperative learning among distinct modalities. Weng et al. proposed a vision-prompted knowledge transfer method that integrates visual and textual modality features, significantly enhancing multimodal reasoning in video question answering tasks [17]. Wu et al. devised a dynamic knowledge transfer mechanism that enables cross-modal knowledge sharing between visual and textual predictors, effectively bolstering temporal localization and answer generation in video question answering tasks [18]. Although existing knowledge flow methods moderately improve model performance, most studies are confined to unidirectional knowledge transfer (e.g., from large to small models) or cross-modal knowledge migration, failing to fully explore the potential of bidirectional cooperative learning and thus limiting the depth and breadth of knowledge sharing. Additionally, the phenomenon of gradient contention within multi-model collaborative learning undercuts the advantages of coordinated optimization, thus imposing further limitations on knowledge-sharing efficacy and holistic performance improvements.
2.3. Pseudo-Label in Video Temporal Grounding
Pseudo-labels are extensively utilized in video temporal grounding tasks, fundamentally relying on model-generated predictions to form surrogate supervision signals. Such an approach bolsters performance in weakly or semi-supervised settings, while likewise demonstrating considerable viability in low-resource or unsupervised domains [27]. Xu et al. proposed a pseudo-label generation method based on predictive confidence, where high-confidence time segments are filtered for training via a confidence threshold [28]. Nevertheless, this approach remains vulnerable to threshold selection, risking the exclusion of valuable segments or the inclusion of suboptimal ones [29]. An alternative tactic is to utilize the model’s predicted temporal segments as pseudo-labels outright, for instance, leveraging initial predictions as pseudo supervision in weakly supervised video localization [30]. Yet the fidelity of such pseudo-labels is wholly determined by the initial model’s predictive prowess, impeding effective mitigation of noisy segments [30]. While these methods may excel in particular scenarios, pseudo-label quality generally hinges on the accuracy of the underlying model predictions [31]. Inferior pseudo-labels can erode the efficacy of model training and inject noise into the learning procedure, thereby impeding potential gains in performance [32]. Moreover, existing methods lack explicit constraints on the pseudo-label generation range, making it difficult for the model to filter out irrelevant or low-confidence segments.
3. Methodology
In this study, we introduce an MMCL framework tailored for video temporal grounding. The overall architecture of MMCL is illustrated in Figure 2.

Figure 2.
Overview of the proposed Multi-Model Collaborative Learning (MMCL) architecture. The framework comprises: (1) two general models; (2) a CLIP-guided module; (3) a pseudo-label generator; (4) an iterative training algorithm.
3.1. Problem Formulation
The objective of video temporal grounding is to identify the optimal time segment M, consistent with the query’s semantics, given an untrimmed video V of duration L and a natural language query Q. In this task, the video V is denoted by a frame sequence , where represents the i-th frame of the video and T is the total number of frames; the natural language query comprises the j-th word of the query, with W being the total number of words. Presently, mainstream approaches to video temporal grounding typically employ a multimodal fusion paradigm, mapping both the video V and the query Q into a unified shared feature space X. Within the feature space X, the model learns the probability distribution of the time range, predicting the start and end times of the target segment to ensure high semantic consistency with the query.
3.2. General Model
The base architecture of the MMCL framework encompasses a feature extractor, a cross-modal fusion module, and a visual predictor. To address various model requirements under the MMCL framework, the basic model unifies the structure of video temporal grounding architectures, enabling effective multi-model cooperation. The feature extractor obtains features from the input video V and the natural language query Q, encoding both into high-dimensional representations used by the subsequent cross-modal fusion component to model their semantic interconnections. The video is partitioned into N equally spaced segments, each of duration . A pretrained visual model (e.g., 3D ConvNet [33] or CNN [34]) extracts the visual features for each segment, denoted as follows:
Here, is the dimensionality of the video features, and k signifies the current model. The query is processed by a pretrained linguistic model (e.g., GloVe [35] or BERT [36]) to obtain features, denoted by the following:
In this case, represents the dimensional size of the query feature vector. The aforementioned extracted features are subsequently passed to the Cross-Modal Fusion module. The Cross-Modal Fusion module combines the video features and the query features to generate the multimodal fused representation , formally given by the following:
In this formulation, signifies the dimensional scale of the fused feature space. The Cross-Modal Fusion module effectively captures the interactive information between video segments and the query semantics, providing high-quality multimodal representations to the visual prediction module. Under the MMCL framework, each model maintains its native multimodal processing approach while leveraging pseudo-labels to learn from the strengths of the other model. MMCL acts as a flexible collaborative layer that supports diverse architectural choices and fosters model synergy. By using pseudo-labels as soft supervision signals, MMCL facilitates knowledge transfer without altering the inherent multimodal interaction strategies of each model, allowing, for example, the 2D-TAN model to learn fine-grained boundary prediction from VSLNet in fast-changing scenarios, and vice versa. The visual predictor estimates the target time range from the fused features , with the output format varying by model architecture. Span-based models yield 1D probability distributions for the start and end time points, expressed as follows:
Meanwhile, 2D-MAP-based models output a two-dimensional temporal probability matrix, represented by the following:
One dimension i of the matrix corresponds to the start boundary, and the other dimension j to the end boundary, with . Each element in the matrix represents the probability that the video segment begins at index i and ends at index j.
3.3. Pseudo-Label Generator
3.3.1. CLIP-Guided Module
The CLIP-Guided Module leverages the cross-modal alignment capability of the CLIP model between video frames and textual queries, providing a coarse-grained temporal constraint for pseudo-label generation to ensure semantic consistency. The overall process can be broken down into three distinct stages:
(1) Semantic Vector Extraction
The input video V is uniformly sampled into frames across its total length L, represented by . Every frame is paired with a timestamp , where . For each frame f, the CLIP model’s visual encoder yields its semantic vector , formulated as follows:
Concurrently, the query Q is passed through CLIP’s text encoder to obtain its textual representation:
(2) Computing Similarities
To gauge the semantic congruence between and , we calculate their cosine similarity. The calculation is as follows:
In this formulation, , with higher values signifying greater semantic harmony between Q and frame . The sequence of similarity scores for the frames is denoted by .
(3) Generating the Constrained Interval
Drawing on the similarity sequence S, a threshold is utilized to filter relevant frames by their time span. First, all frames with are identified, and their minimum and maximum indices, and , are determined according to Equation (9).
Subsequently, these frame indices are mapped to actual temporal boundaries: . Finally, denotes the coarse-grained temporal interval guided by the CLIP model, which constrains pseudo-label generation.
3.3.2. Pseudo-Labels Generation
In the process of pseudo-label generation, we utilize the coarse-grained temporal interval provided by the CLIP model and apply normalization to constrain the range of pseudo-label creation, thereby ensuring semantic consistency and producing pseudo-labels that align with semantic priors. The generation of pseudo-labels depends on the prediction format of different models. Below, we separately describe the pseudo-label generation processes for Span-based models and 2D-MAP models.
(1) Pseudo-Labels Generation for Span-based Models
As stated in Section 3.2, a Span-based model (such as VSLNet) produces probability distributions and corresponding to the start and end times, respectively. The original probability distributions are normalized over the entire video span , which contains a substantial number of query-irrelevant time segments. To enhance semantic consistency, it is necessary to constrain and re-normalize these distributions based on the temporal window provided by CLIP. Following restriction of these probability distributions to the selected interval, the normalized forms and are specified as follows:
The normalization step guarantees that the distributions remain confined to semantically pertinent intervals, thereby narrowing the pseudo-label search domain and fortifying semantic coherence. Upon finalizing the normalization, the pseudo-label boundaries and emerge by identifying the indices that maximize the normalized probability distributions, formally expressed as follows:
Subsequently, the indices are mapped to pseudo-labels by Equation (13).
(2) Pseudo-Labels Generation for 2D-MAP Models
Under the 2D-MAP model, the pseudo-labels derive from a 2D temporal probability matrix , with i and j designating the start and end indices, respectively, and adhering to . For , elements within the CLIP-guided temporal window are retained, while probabilities outside this range are set to zero. The remaining elements are then normalized to ensure the sum is one. The definition of the normalized probability matrix is as follows:
Subsequently, the highest-probability entry in pinpoints the start and end indices of the pseudo-labels:
Lastly, Equation (16) translates these indices into the pseudo-labels .
By following the procedure above, we leverage CLIP’s semantic guidance to generate high-quality pseudo-labels, thus offering reliable supervisory signals for training.
3.4. Mutual Knowledge Transfer
At the heart of the MMCL framework is the harnessing of inter-model knowledge exchange and cooperative optimization, capitalizing on each model’s complementary capabilities to boost collective outcomes. Within this framework, pseudo-label generation and loss function design constitute the essential elements for enabling collaborative learning. Pseudo-label generation (detailed in Section 3.3) furnishes high-quality supervisory signals for cross-model knowledge migration, while the loss function employs a suitable optimization strategy to effectively merge single-model learning with inter-model collaboration. Accordingly, we construct the comprehensive loss function as a weighted amalgamation of supervision loss and transfer loss, satisfying both each model’s need for accurate learning and the bidirectional knowledge exchange among multiple models. In the supervised learning stage, the supervision loss steers Models A and B to refine their performance using genuine labels as guidance. Formally, it is specified as follows:
Here, and denote the predictions of Model A and Model B, respectively; stands for ground truth; and refers to the particular form of the loss function, which varies depending on the model category. The role of the supervision loss is to align and more tightly with , providing direct supervised feedback to each model. In the knowledge transfer phase, the transfer loss drives collaborative learning between models by optimizing the pseudo-labels produced by the counterpart model, and leverages those pseudo-labels as indirect supervision signals to achieve cross-model knowledge transfer. Specifically, Model A’s transfer loss uses the pseudo-labels produced by Model B, aligning them with A’s predictions to encourage Model A to learn B’s predictive characteristics. Analogously, Model B’s transfer loss imposes knowledge constraints on Model B via , nudging its optimization objective toward Model A’s predictions. The transfer loss is defined as follows:
Building upon the aforementioned supervision and transfer objectives, the MMCL framework accomplishes multi-model cooperative learning through a weighted synthesis of these losses. The aggregate loss function is given by the following:
Here, and serve as hyperparameters governing the balance between transfer losses. With this scheme, every model benefits from solitary supervision-driven optimization toward ground-truth labels and, in parallel, participates in inter-model knowledge exchange facilitated by the transfer losses.
3.5. Iterative Training Algorithm
Within the MMCL framework, the core aim of the loss optimization strategy is to foster coherent predictions among models, yet preserve each model’s autonomy in its individual optimization processes. To accomplish this, we introduce an iterative training algorithm that blends consistency evaluation with dynamic loss tuning, thereby enabling inter-model knowledge exchange and collective enhancement. In this section, we elaborate on the loss function’s optimization strategy from three perspectives: consistency assessment, dynamic loss adjustment, and algorithmic implementation.
3.5.1. Consistency Assessment
Within the realm of multi-model collaborative learning, the temporal intervals forecasted by various models can at times diverge, resulting in inconsistency. To assess and quantify this inconsistency, we introduce the Intersection over Union (IoU) as a measure of consistency. Concretely, IoU is calculated by dividing the intersection of the two predicted time spans by their union, expressed as follows:
In this context, and , respectively, signify the predicted time intervals for Model A and Model B. On the basis of the IoU value, we define an IoU threshold to gauge the degree of concordance between the models’ predictions. When , the alignment between the two models’ predictions is relatively strong, prompting a decrease in the transfer loss weight. Conversely, if , the predictions are deemed inconsistent, warranting an increase in the transfer loss weight so as to guide both models’ results toward consistency. By quantifying the degree of consistency, the MMCL framework can dynamically adjust inter-model learning intensity, ensuring the effectiveness of collaborative learning. Consistency evaluation offers a dynamic adjustment signal that directly influences the adaptive loss adjustment procedure (see Section 3.5.2), guiding transfer loss weighting and providing a basis for iterative training.
3.5.2. Dynamic Loss Adjustment
To balance the independent optimization of each model with the consistency of cross-model predictions in collaborative learning, we devise a dynamic loss adjustment strategy founded on IoU. Building on top of the supervision and transfer losses, we incorporate a dynamic weighting factor (refer to Equation (21)) to regulate the influence of transfer loss on the total loss. The definition of the dynamic factor is as follows:
Here, is a parameter that governs the attenuation of the transfer loss under high consistency conditions. The total loss function after dynamic adjustment can be expressed as follows:
In this expression, and are the intrinsic weights for the transfer loss, and the factor modulates the strength of cross-model transfer in accordance with IoU. Under conditions of strong predictive alignment, the framework grants each model greater latitude for autonomous optimization, whereas lower alignment triggers a heavier emphasis on cross-model knowledge exchange, thereby bolstering model concordance. Leveraging this strategy, the MMCL framework deftly orchestrates the magnitudes of both supervision and transfer losses, securing an optimal trade-off between inter-model knowledge sharing and standalone optimization.
3.5.3. Algorithmic Realization
In the course of knowledge dissemination, inter-model gradients can impede one another, thereby curtailing each model’s capacity to learn independently. This phenomenon, known as gradient contention, occurs when gradients produced by different models or tasks conflict with each other, leading to ineffective optimization. Specifically, when gradients push shared model parameters in opposing directions, they may neutralize each other’s effect, hindering both models’ learning processes. To preclude gradient contention across models and, at the same time, enable effective knowledge transmission and reinforce each model’s autonomy in optimization, we devise an iterative training algorithm. This algorithm partitions loss optimization into several phases and carries them out in a sequentially alternating fashion. Initially, the procedure optimizes Model A’s supervised loss while holding Model B’s parameters static, thus allowing Model A to refine its performance under the supervision of true labels; subsequently, it optimizes Model B’s supervised loss while freezing Model A’s parameters. Thereafter, the framework employs the transfer losses and to impose knowledge constraints on Models A and B, respectively, using pseudo-labels to guide inter-model refinement. See Algorithm 1 for details. This staggered iterative update scheme safeguards each model’s independent feature learning, using pseudo-labels to facilitate a more adaptable form of collaboration. In the end, after repeated iterations, the predictions from both models increasingly align, culminating in a synergistic improvement in overall performance. This algorithm deftly circumvents gradient contention while bolstering both models’ learning capabilities and operational robustness.
| Algorithm 1: Dynamic Loss Adjustment with IoU-based Weighting |
 |
4. Experiments
4.1. Datasets
To evaluate the performance of our proposed MMCL, we conduct experiments on three challenging video temporal grounding datasets:
Charades-STA [1] consists of videos portraying routine activities, sourced from the Charades dataset [37]. It encompasses 6672 videos, 16,128 annotations, and 11,767 temporal moments. The uneven distribution of clip lengths and a high degree of overlap place considerable demands on local feature modeling. Of the annotated moments, 12,408 are allocated for training and 3720 for testing.
ActivityNet Caption [38] was initially constructed for dense video captioning. It comprises around 20,000 YouTube videos with diverse contents, averaging 120 s in length. The dataset features semantic variety and broad domains, placing higher demands on the multimodal representation capability of models. Following the experimental setup in [22,23], val1 is used as the validation set and val2 as the test set, containing 37,421 and 17,505 annotated temporal moments for training and testing, respectively. Currently, this is the largest dataset in this task.
TACoS [39] is a video temporal grounding dataset focusing on kitchen scenarios, derived from the MPII Cooking Composite Activities dataset [39]. It comprises 127 videos with annotated time segments, totaling over 18 h in duration. The dataset features a large number of consecutive actions, with dense temporal distributions and a high overlap ratio, posing greater challenges for boundary-based models. Following [22,23], 10,146, 4589, and 4083 temporal annotations are used for training, validation, and testing, respectively.
4.2. Baselines
We employ VSLNet [22] and 2D-TAN [23] as two baseline networks in the framework, representing the typical Span-based and 2D-MAP models, respectively. Both have publicly available source code, and we train and evaluate the MMCL framework on the three datasets described in Section 4.1.
4.3. Implementation Details
4.3.1. Evaluation Metrics
Following existing video grounding works, we evaluate the performance on two main metrics:
mIoU: This metric measures the mean Intersection over Union (IoU) between the model’s predicted intervals and the reference intervals. By averaging the IoU values over the entire test set, it reflects the overall localization accuracy of the model and effectively evaluates the precision of temporal segment predictions.
Recall: We adopt “” as the evaluation metrics, following [1]. The “” represents the percentage of language queries having at least one result whose IoU between predictions with ground-truth is larger than m. In our experiments, we reported the results of and .
4.3.2. Experimental Settings
For each baseline method, VSLNet follows the configurations reported in their original paper, adopting the C3D-feature version of VSLNet. As for 2D-TAN, the components of the framework likewise follow the same parameters as presented in its original documentation. The hyperparameters and (refer to Section 3.4) regulate the weighting for the transfer losses and . Based on validation tuning, we choose and to strike a balance between supervision and transfer objectives in model optimization. The IoU threshold (see Section 3.5) evaluates predictive alignment between models, set at 0.5 to maintain a reasonable level of discriminatory power. The factor (see Section 3.5), responsible for dynamically modulating weights, is fixed at 0.8 to attenuate the transfer loss under scenarios of high model consistency. The number of video frames in the CLIP-Guided Module (see Section 3.3.1) is set to 32 to balance semantic representational power and computational efficiency. The similarity threshold (see Section 3.3.1) is set to 0.4, filtering out highly relevant frames to generate a more precise guiding temporal range. The learning rates and are both set to 0.0001, and the number of iterative optimization cycles K (see Algorithm 1) is set to 10.
4.4. Training and Inference
This subsection provides an examination of how the MMCL framework performs throughout both training and inference stages. Figure 3 juxtaposes the framework’s outcomes in loss optimization, test accuracy, signal learning, and noise memorization.

Figure 3.
Comparison between single-model learning and multi-model collaborative learning in terms of training loss, test accuracy, signal learning, and noise memorization.
Observing the training loss curve reveals that MMCL demonstrates a noticeably swifter reduction in loss compared with the baseline model. In addition, as training epochs progress, the loss steadily converges to a more stable, lower plateau. This expedited convergence owes much to the framework’s bidirectional knowledge transfer design, which allows the two models to exchange learned representations and leverage pseudo-labels as supplementary supervisory signals, thus steering clear of local optima. In the testing phase, the cooperative learning facilitated by the MMCL framework markedly enhances the accuracy of both models. Especially during the final training iterations, VLSNet’s contextual reasoning and 2D-TAN’s temporal boundary localization both become more refined, indicating that this collaborative mechanism can successfully broaden each model’s performance ceiling. The signal learning trajectory reveals that the MMCL framework incrementally fortifies the cooperative models’ capacity to capture relevant signals, subsequently stabilizing and outperforming any single-model baselines. CLIP’s guidance mechanism, leveraging semantic priors to refine pseudo-labels’ precision and coherence, plays a key role in these gains. The juxtaposition of noise memorization curves offers additional evidence of the efficacy of CLIP-guided pseudo-labels. By more effectively suppressing spurious or low-fidelity time segments, the MMCL framework supplies purer supervisory signals for training.
4.5. Comparison with State-of-the-Arts
4.5.1. Comparative Methods
We compare our proposed MMCL with state-of-the-art video temporal grounding methods on three public datasets. These methods can be grouped into two categories:
(1) Span-based Models: CTRL [1], ROLE [40], ACL [41], SM-RL [42], ExCL [43], DRN [44], CBLN [45], PS-VTG [28], D3G [46], PFU [47], TGN [48], ABLR-af [49], ABLR-aw [49], ACRN [50], VSLNet [22], MRTNet(VSLNet) [51];
(2) 2D-MAP Models: SAP [52], QSPN [53], DEBUG [54], MAN [55], GDP [56], CI-MHA [57], CMIN [58], 2D-TAN [23], MMN [59], MRTNet(2D-TAN) [51]
4.5.2. Quantitative Analysis
The outcomes on the three benchmarks, as reported in Table 1, Table 2 and Table 3, indicate that our MMCL framework significantly enhances the baseline models’ performance.

Table 1.
Performance comparison with the state-of-the-art models on Charades-STA dataset.

Table 2.
Performance comparison with the state-of-the art models on ActivityNet Caption dataset.

Table 3.
Performance comparison with the state-of-the-art models on TACoS dataset.
Summarizing the results in Table 1, Table 2 and Table 3, we see that on the Charades-STA dataset, 2D-TAN underperforms VSLNet mainly because its 2D-MAP mechanism struggles with short segments and high-overlap video scenarios, whereas VSLNet’s boundary-classification approach allows more precise modeling of short-segment boundaries. After incorporating the MMCL framework, 2D-TAN learns the semantic modeling capability of VSLNet’s boundary-classification approach, improving its mIoU to and achieving a relative improvement of , demonstrating that the MMCL framework effectively compensates for 2D-TAN’s shortcomings in modeling short segments. By contrast, on the TACoS dataset, VSLNet underperforms 2D-TAN because its span-based structure finds it difficult to handle the dense and uneven segment distribution of TACoS, while 2D-TAN’s 2D-MAP mechanism is better suited for complex temporal-relationship modeling. After integrating the MMCL framework, VSLNet acquires long-segment relational modeling and temporal context-capturing abilities from 2D-TAN, raising its mIoU to and yielding a relative improvement. These results demonstrate that the MMCL framework, through knowledge transfer and collaborative learning, significantly improves both models’ performance on the datasets where they originally fared poorly.
From the results in Table 2, both models achieve improved performance on the ActivityNet Caption dataset. With its semantic modeling advantage, VSLNet achieves an mIoU of on this dataset. However, by learning richer temporal relationship modeling from 2D-TAN through the MMCL framework, its mIoU rises to , a relative improvement of . Similarly, by sharing knowledge with VLSNet, 2D-TAN advances its mIoU from to , achieving a relative improvement.
In sum, through cross-model knowledge sharing and joint learning, the MMCL framework allows the two baseline models to mutually address their shortcomings and amplify their respective advantages. On TACoS, VLSNet reaps the benefits of 2D-TAN’s temporal relationship modeling; on Charades-STA, 2D-TAN inherits stronger boundary-modeling capabilities from VLSNet. This reciprocal learning and knowledge transfer characteristic endows the MMCL framework with robust adaptability across different task scenarios. Moreover, relative to other competing methods and MRTNet, the MMCL framework achieves superior results on all metrics in each of the three datasets, offering additional validation of its efficacy.
4.6. Performance of Isomorphic Models
Even under identical model architectures, the random sampling of training data and mini-batch dynamics induce divergent biases in temporal segments, feature representations, or modality alignment. Such discrepancies lay the groundwork for knowledge transfer between structurally identical models. To assess the MMCL framework’s efficacy and potential constraints in same-architecture collaborative learning, we designate 2D-TAN as both Model A and Model B and conduct experiments on the Charades-STA dataset, employing the hyperparameters outlined in Section 4.3.2. According to Figure 4, the models utilizing the MMCL framework demonstrate a degree of performance enhancement relative to the baseline model. This finding suggests that even with a uniform model design, differences in data inputs and the stochastic nature of feature learning give rise to variations in predictive outcomes. The MMCL framework capitalizes on these variations for inter-model knowledge transfer, thereby achieving a synergistic boost in overall performance.

Figure 4.
Performance comparison of isomorphic models on the Charades-STA dataset under the MMCL framework.
4.7. Ablation Studies
In an effort to streamline the experimental design, the following ablation studies are carried out on the Charades-STA dataset, leveraging VSLNet and 2D-TAN as baseline architectures.
4.7.1. Loss Function
To evaluate the effectiveness of each component in the proposed loss function, we conduct a series of tests with different loss settings, as shown in Table 4.

Table 4.
Performance comparison of MMCL with different losses on Charades-STA dataset.
Supervision loss ( and ) underpins the independent optimization of each model; removing this component forces the affected model to depend predominantly on transfer loss and pseudo-labels for training. As an example, omitting strips Model A of its capacity for standalone optimization, resulting in a notable performance drop. Concurrently, the pseudo-labels transferred to Model B deteriorate in quality, undermining the efficacy of knowledge transfer. However, since Model B still retains , its performance decline is relatively limited. Similarly, removing leads to a significant reduction in Model B’s performance, especially when capturing strict boundaries (e.g., ). Model A is also affected by the degraded quality of pseudo-labels, but to a lesser extent, as it still depends on . Excluding the transfer losses ( and ) disrupts the inter-model knowledge-sharing mechanism. Removing prevents Model A from assimilating supplementary insights from Model B, leading to a performance dip. Model B, retaining and its corresponding supervisory signals, suffers only marginal setbacks. Conversely, removing robs Model B of its ability to acquire knowledge from Model A, causing a significant performance drop, whereas Model A’s performance sees only a minor decline since it can still rely on its own supervision signals for independent optimization.
4.7.2. Hyperparameters of and
From Equation (22) in Section 3.5.2, it is evident that the base weights and for the transfer loss exert a direct influence on the strength of inter-model knowledge transfer. In this study, we hold constant while varying the fundamental weights and . Referring to Figure 5, once and approximate 0.5, knowledge transfer finds an equilibrium that enables mutual learning and leads to superior overall performance. When and remain small, the force of knowledge transfer lessens, causing each model to rely heavily on its own supervision and thereby producing results akin to the baseline model. This situation suggests that inter-model cooperation is curtailed, and it becomes challenging to compensate for the limitations inherent in a solitary model. If and are severely skewed (e.g., is much larger than or vice versa), knowledge transfer adopts a one-sided flow, resulting in asymmetrical performance. Conversely, if and are both sizable, the frequency of knowledge transfer escalates, injecting abundant “noise” that hampers the model’s ability to distinguish useful supervisory cues from extraneous transfer signals, ultimately diminishing cooperative gains. Taken together, properly tuning and is essential for upholding equilibrium and moderation in inter-model knowledge sharing; doing so maximizes each model’s unique advantages while averting skewed transfer or excessive disruption that might undermine overall performance.
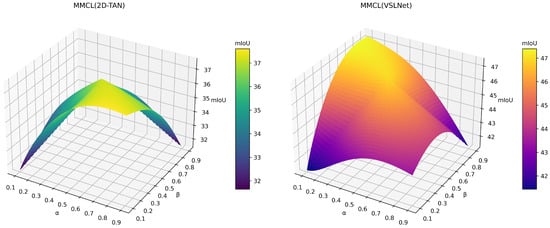
Figure 5.
Effect of transfer-loss weights ( and ) on model performance.
4.7.3. Hyperparameters of and
The hyperparameters and , which govern the dynamic adjustment of transfer loss (see Section 3.5.2), play key roles in determining recall, precision, and overall inter-model cooperation. In this study, and remain fixed at 0.5, while performance metrics are gathered for various pairs (see Figure 6). As the consistency threshold, measures the degree of similarity in the models’ predictions. A relatively small defines consistency more leniently, capturing a greater number of predictions and thereby boosting recall, yet at the risk of admitting low-quality knowledge flow that can erode precision. By contrast, a larger imposes tighter consistency requirements, fostering higher precision but limiting collaborative interactions between models and thereby diminishing recall. Experimental findings suggest that a suitably moderate strikes an effective compromise between shared knowledge transfer and independent optimization. Meanwhile, the dynamic factor dictates the degree of transfer-loss attenuation when models exhibit high consistency. A larger enables models to lean more on their internal supervision signals, thus bolstering precision. Conversely, a smaller strengthens cross-model knowledge sharing, likely improving recall at the expense of reduced independence in optimization. Under lenient consistency requirements (e.g., ), the influence of and on recall is minimal, producing relatively stable performance. This suggests that collaborative knowledge exchange reliably enhances the model’s overall recall capability. Under more balanced consistency thresholds (e.g., ), the models grow increasingly sensitive to variations in and , making prudent parameter choices pivotal for balancing recall and precision. Under stringent consistency metrics (e.g., ), the models display the highest sensitivity to and , and moderate in combination with a mid-to-high yields peak performance during collaborative learning. In summary, and jointly manage the trade-off between recall and precision and, by dynamically calibrating the strength of knowledge transfer, serve as key levers for enhancing the overall efficacy of cooperative learning.

Figure 6.
Effect of the consistency threshold () and the dynamic adjustment factor () on model performance.
4.7.4. Effectiveness Analysis of the CLIP-Guided Module
In the CLIP-guided module, both the number of sampled video frames and the similarity threshold play a key role in determining the quality of pseudo-labels, thereby shaping the outcomes of inter-model knowledge transfer as well as final performance. In this subsection, we separately discuss the impact of varying the number of video frames and the similarity threshold on the MMCL framework, with the corresponding results presented in Figure 7. First, holding the similarity threshold constant at , we gradually raise the number of sampled frames. As depicted in Figure 7a, the model’s performance (mIoU) progressively increases alongside the number of frames. This indicates that a higher frame count enriches the temporal scope and contextual fidelity of the pseudo-labels, effectively expanding the reservoir of knowledge they convey. Nevertheless, upon reaching 64 frames, performance gains level off or marginally drop because incorporating excessive frames does not translate into significant feature benefits but rather introduces unwarranted noise and squanders computational overhead. Subsequently, keeping constant, we adjust the similarity threshold to gauge how performance responds. As illustrated in Figure 7b, the model’s performance follows a nonlinear trajectory in response to variations in the similarity threshold . A too-low threshold incorporates excessive low-grade segments in the pseudo-labels, weakening their utility in guiding optimization. Conversely, a too-stringent threshold narrows the scope of pseudo-labels, hindering the capture of the video’s broader context and thereby stifling collaborative improvement. In comparison, a moderate threshold () attains an equilibrium between filtering out noise and retaining adequate coverage, yielding pseudo-labels of superior quality for facilitating knowledge transfer. In sum, judiciously determining the number of frames and the similarity threshold is vital for producing robust pseudo-labels, thereby proving indispensable for successful inter-model knowledge transfer and performance enhancement.

Figure 7.
Effect of the number of video frames and the similarity threshold on performance in the CLIP-guided module.
4.7.5. Qualitative Analysis
Figure 8 shows qualitative results of MMCL(VSLNet) on the Charades-STA dataset and MMCL(2D-TAN) on the TACoS dataset. From the examples, we can observe that in the Charades-STA dataset, which features short action intervals with rapidly shifting boundaries, MMCL(VSLNet) demonstrates heightened temporal sensitivity and refined boundary delineation under CLIP guidance. As for the TACoS dataset, known for its longer action durations, MMCL(2D-TAN) demonstrates greater boundary-capturing precision under CLIP guidance. In the absence of CLIP guidance, the model frequently yields more expansive time spans than the actual annotations, hindering its ability to precisely identify the critical moments aligned with the query. This result reaffirms the crucial function of the CLIP-guided module in refining pseudo-label accuracy.

Figure 8.
Qualitative results of MMCL(VSLNet) and MMCL(2D-TAN).
4.8. Case Study
The case study evaluates the MMCL (Multi-Model Collaborative Learning) framework’s ability to harness the complementary strengths of VSLNet and 2D-TAN models across various video temporal grounding scenarios, including short and long videos, complex temporal relationships, and fast-changing scenes.
In scenarios with short videos (Figure 9, left), where precise boundary detection is critical, MMCL improved 2D-TAN’s performance by allowing it to learn from VSLNet’s accuracy in temporal boundary prediction. Conversely, in long video scenarios (Figure 9, right), which require a broader temporal context, MMCL enhanced VSLNet’s performance by incorporating 2D-TAN’s strength in extended temporal modeling. This demonstrates the framework’s capacity to facilitate effective mutual learning between models with distinct advantages. In Figure 10, the performance on “difficult” samples was examined through complex temporal scenarios and fast-changing scenes. Difficult samples in our study refer to scenarios that require a deep understanding of extended temporal dependencies or rapid visual changes. The task demands not only temporal segmentation but also an understanding of the sequential order of events. VSLNet, typically challenged by such scenarios, showed notable improvement under the MMCL framework, demonstrating enhanced temporal reasoning by leveraging 2D-TAN’s strengths. Conversely, in fast-changing scenarios like the BMX race video, which required precise alignment between fast-paced visual cues and the query, MMCL (2D-TAN) showed a significant performance gain. This result indicates that 2D-TAN, through bidirectional knowledge transfer, learned from VSLNet’s dynamic attention mechanism, which is particularly effective in fast-changing environments.

Figure 9.
Performance of MMCL framework in short vs. long video scenarios.

Figure 10.
MMCL framework in fast-changing vs. complex temporal scenarios.
In specific challenging samples (Figure 11 and Figure 12), the standalone models struggled with accurate predictions, whereas the MMCL-enhanced models succeeded. The MMCL (2D-TAN) model adapted better to fast-changing scenarios by learning from VSLNet’s strengths, while MMCL (VSLNet) demonstrated improved performance in complex temporal scenarios by leveraging 2D-TAN’s proficiency in modeling long-range temporal dependencies. These results confirm that the MMCL framework not only preserves each model’s inherent strengths but also facilitates adaptive knowledge transfer, leading to improved performance on difficult samples and demonstrating the intended collaborative learning effect.

Figure 11.
Improved temporal grounding in fast-changing scenarios with MMCL (2D-TAN).

Figure 12.
Enhanced performance in complex temporal scenarios with MMCL (VSLNet).
5. Conclusions
In this work, we proposed a Multi-Model Collaborative Learning (MMCL) framework that achieves efficient collaboration among multiple models through bidirectional knowledge transfer, a CLIP-guided pseudo-label generation mechanism, and an iterative training algorithm. Extensive evaluations across three benchmark datasets confirm that MMCL surpasses conventional baselines. Furthermore, the MMCL framework is highly versatile and can be employed in both isomorphic and heterogeneous model configurations, thus providing a novel paradigm for multi-model collaboration. While our current study focused on well-established datasets such as Charades-STA, ActivityNet Captions, and TACoS, we recognize the value of validating the MMCL framework on more recently released datasets, such as TVR and QVHighlight. These datasets introduce unique challenges, including longer video durations, more complex queries, and multi-view video sources. Exploring these datasets in future work will allow us to assess the generalization ability of MMCL under more diverse and evolving conditions. Even so, opportunities remain to enhance the framework’s computational overhead and training efficiency. Future work will concentrate on devising a more compact architecture and real-time optimizations, broadening the applicability of the framework in diverse real-world contexts.
Author Contributions
Conceptualization, X.G. and J.W.; methodology, Y.T., X.G. and B.L.; software, Y.T. and B.L.; validation, Y.T. and B.L.; formal analysis, Y.T.; investigation, Y.T. and B.L.; resources, X.G. and J.W.; data curation, Y.T. and B.L.; writing—original draft preparation: Y.T. and B.L.; writing—review and editing: Y.T. and X.G.; visualization, Y.T.; supervision, X.G. and J.W.; project administration, X.G. and J.W.; funding acquisition, X.G. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Guangdong Province (No. 2023A1515010673), in part by the Shenzhen Science and Technology Innovation Bureau key project (No. JSGG20220831110400001, No. CJGJZD20230724093303007, KJZD20240903101259001), in part by Shenzhen Medical Research Fund (No. D2404001), in part by Shenzhen Engineering Laboratory for Diagnosis & Treatment Key Technologies of Interventional Surgical Robots (XMHT20220104009), and the Key Laboratory of Biomedical Imaging Science and System, CAS, for the Research platform support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to restrictions in the data use agreement with the data provider.
Acknowledgments
The authors would like to thank all individuals and institutions who contributed to this research through technical support, administrative assistance, and valuable discussions. Their support is greatly appreciated.
Conflicts of Interest
There are no potential competing interests in our paper. All authors have seen the manuscript and approved to submit it to your journal. We confirm that the content of the manuscript has not been published or submitted for publication elsewhere.
References
- Gao, J.; Sun, C.; Yang, Z.; Nevatia, R. TALL: Temporal Activity Localization via Language Query. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Chu, Y.W.; Lin, K.Y.; Hsu, C.C.; Ku, L.W. End-to-End Recurrent Cross-Modality Attention for Video Dialogue. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 2456–2464. [Google Scholar] [CrossRef]
- Ji, W.; Li, Y.; Wei, M.; Shang, X.; Xiao, J.; Ren, T.; Chua, T.S. VidVRD 2021: The Third Grand Challenge on Video Relation Detection. In Proceedings of the 29th ACM International Conference on Multimedia, MM ’21, Chengdu, China, 20–24 October 2021; pp. 4779–4783. [Google Scholar] [CrossRef]
- Shang, X.; Li, Y.; Xiao, J.; Ji, W.; Chua, T.S. Video Visual Relation Detection via Iterative Inference. In Proceedings of the 29th ACM International Conference on Multimedia, MM ’21, Chengdu, China, 20–24 October 2021; pp. 3654–3663. [Google Scholar] [CrossRef]
- Shang, X.; Ren, T.; Guo, J.; Zhang, H.; Chua, T.S. Video Visual Relation Detection. In Proceedings of the 25th ACM International Conference on Multimedia, MM ’17, Mountain View, CA, USA, 23–27 October 2017; pp. 1300–1308. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xiao, J.; Ji, W.; Chua, T.S. Invariant Grounding for Video Question Answering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Los Alamitos, CA, USA, 19–24 June 2022; pp. 2928–2937. [Google Scholar]
- Xiao, J.; Yao, A.; Liu, Z.; Li, Y.; Ji, W.; Chua, T.S. Video as Conditional Graph Hierarchy for Multi-Granular Question Answering. In Proceedings of the AAAI Conference on Artificial Intelligence, Online Conference, 22 February–1 March 2022; Volume 36, pp. 2804–2812. [Google Scholar] [CrossRef]
- Li, S.; Li, B.; Sun, B.; Weng, Y. Towards Visual-Prompt Temporal Answer Grounding in Instructional Video. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 8836–8853. [Google Scholar] [CrossRef] [PubMed]
- Liang, R.; Yang, Y.; Lu, H.; Li, L. Efficient Temporal Sentence Grounding in Videos with Multi-Teacher Knowledge Distillation. arXiv 2014, arXiv:2308.03725. [Google Scholar]
- Lan, X.; Yuan, Y.; Wang, X.; Wang, Z.; Zhu, W. A Survey on Temporal Sentence Grounding in Videos. ACM Trans. Multimed. Comput. Commun. Appl. 2023, 19, 1–33. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Chen, M.; Zhang, Y.; Feng, R.; Gao, S. SPTNET: Span-based Prompt Tuning for Video Grounding. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023; pp. 2807–2812. [Google Scholar] [CrossRef]
- Ding, X.; Wang, N.; Zhang, S.; Huang, Z.; Li, X.; Tang, M.; Liu, T.; Gao, X. Exploring Language Hierarchy for Video Grounding. IEEE Trans. Image Process. 2022, 31, 4693–4706. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, K.; Li, J.; Chen, G.; Wang, M.; Guo, D. Dual-path temporal map optimization for make-up temporal video grounding. Multimed. Syst. 2024, 30, 140. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Jia, J.; Liu, S.; Ding, K. Text-Visual Prompting for Efficient 2D Temporal Video Grounding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 14794–14804. [Google Scholar]
- Bao, P.; Shao, Z.; Yang, W.; Ng, B.P.; Er, M.H.; Kot, A.C. Omnipotent Distillation with LLMs for Weakly-Supervised Natural Language Video Localization: When Divergence Meets Consistency. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 747–755. [Google Scholar] [CrossRef]
- Bao, P.; Xia, Y.; Yang, W.; Ng, B.P.; Er, M.H.; Kot, A.C. Local-Global Multi-Modal Distillation for Weakly-Supervised Temporal Video Grounding. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 738–746. [Google Scholar] [CrossRef]
- Weng, Y.; Li, B. Visual Answer Localization with Cross-Modal Mutual Knowledge Transfer. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, Y.; Wei, X.Y.; Li, Q. PolySmart @ TRECVid 2024 Medical Video Question Answering. arXiv 2024, arXiv:2412.15514. [Google Scholar]
- Shi, G.; Li, Q.; Zhang, W.; Chen, J.; Wu, X.M. Recon: Reducing Conflicting Gradients from the Root for Multi-Task Learning. arXiv 2023, arXiv:2302.11289. [Google Scholar]
- Liu, B.; Liu, X.; Jin, X.; Stone, P.; Liu, Q. Conflict-Averse Gradient Descent for Multi-task learning. In Proceedings of the Advances in Neural Information Processing Systems, Red Hook, NY, USA, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 18878–18890. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models From Natural Language Supervision. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; Meila, M., Zhang, T., Eds.; Volume 139, pp. 8748–8763. [Google Scholar]
- Zhang, H.; Sun, A.; Jing, W.; Zhou, J.T. Span-based Localizing Network for Natural Language Video Localization. arXiv 2020, arXiv:2004.13931. [Google Scholar]
- Zhang, S.; Peng, H.; Fu, J.; Luo, J. Learning 2D Temporal Adjacent Networks for Moment Localization with Natural Language. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12870–12877. [Google Scholar] [CrossRef]
- Zhang, S.; Peng, H.; Fu, J.; Lu, Y.; Luo, J. Multi-Scale 2D Temporal Adjacency Networks for Moment Localization With Natural Language. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 9073–9087. [Google Scholar] [CrossRef] [PubMed]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Hinton, G. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Zheng, M.; Gong, S.; Jin, H.; Peng, Y.; Liu, Y. Generating Structured Pseudo Labels for Noise-resistant Zero-shot Video Sentence Localization. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Toronto, ON, Canada, 9–14 July 2023; Rogers, A., Boyd-Graber, J., Okazaki, N., Eds.; pp. 14197–14209. [Google Scholar] [CrossRef]
- Xu, Z.; Wei, K.; Yang, X.; Deng, C. Point-Supervised Video Temporal Grounding. IEEE Trans. Multimed. 2023, 25, 6121–6131. [Google Scholar] [CrossRef]
- Xu, Y.; Wei, F.; Sun, X.; Yang, C.; Shen, Y.; Dai, B.; Zhou, B.; Lin, S. Cross-Model Pseudo-Labeling for Semi-Supervised Action Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, Louisiana, 21–24 June 2022; pp. 2959–2968. [Google Scholar]
- Jiang, X.; Xu, X.; Zhang, J.; Shen, F.; Cao, Z.; Shen, H.T. Semi-Supervised Video Paragraph Grounding With Contrastive Encoder. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 21–24 June 2022; pp. 2466–2475. [Google Scholar]
- Luo, F.; Chen, S.; Chen, J.; Wu, Z.; Jiang, Y.G. Self-Supervised Learning for Semi-Supervised Temporal Language Grounding. IEEE Trans. Multimed. 2023, 25, 7747–7757. [Google Scholar] [CrossRef]
- Piao, Y.; Lu, C.; Zhang, M.; Lu, H. Semi-Supervised Video Salient Object Detection Based on Uncertainty-Guided Pseudo Labels. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 5614–5627. [Google Scholar]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning Spatiotemporal Features With 3D Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Alaparthi, S.; Mishra, M. Bidirectional Encoder Representations from Transformers (BERT): A sentiment analysis odyssey. arXiv 2020, arXiv:2007.01127. [Google Scholar]
- Sigurdsson, G.A.; Varol, G.; Wang, X.; Farhadi, A.; Laptev, I.; Gupta, A. Hollywood in homes: Crowdsourcing data collection for activity understanding. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 510–526. [Google Scholar]
- Caba Heilbron, F.; Escorcia, V.; Ghanem, B.; Carlos Niebles, J. ActivityNet: A Large-Scale Video Benchmark for Human Activity Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Regneri, M.; Rohrbach, M.; Wetzel, D.; Thater, S.; Schiele, B.; Pinkal, M. Grounding Action Descriptions in Videos. Trans. Assoc. Comput. Linguist. 2013, 1, 25–36. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Nie, L.; Tian, Q.; Chen, B.; Chua, T.S. Cross-modal Moment Localization in Videos. In Proceedings of the 26th ACM International Conference on Multimedia, MM ’18, Seoul, Republic of Korea, 22–26 October 2018; pp. 843–851. [Google Scholar] [CrossRef]
- Ge, R.; Gao, J.; Chen, K.; Nevatia, R. MAC: Mining Activity Concepts for Language-Based Temporal Localization. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 245–253. [Google Scholar] [CrossRef]
- Wang, W.; Huang, Y.; Wang, L. Language-Driven Temporal Activity Localization: A Semantic Matching Reinforcement Learning Model. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Ghosh, S.; Agarwal, A.; Parekh, Z.; Hauptmann, A. ExCL: Extractive Clip Localization Using Natural Language Descriptions. arXiv 2019, arXiv:1904.02755. [Google Scholar]
- Zeng, R.; Xu, H.; Huang, W.; Chen, P.; Tan, M.; Gan, C. Dense Regression Network for Video Grounding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Liu, D.; Qu, X.; Dong, J.; Zhou, P.; Cheng, Y.; Wei, W.; Xu, Z.; Xie, Y. Context-Aware Biaffine Localizing Network for Temporal Sentence Grounding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 11235–11244. [Google Scholar]
- Li, H.; Shu, X.; He, S.; Qiao, R.; Wen, W.; Guo, T.; Gan, B.; Sun, X. D3G: Exploring Gaussian Prior for Temporal Sentence Grounding with Glance Annotation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 13734–13746. [Google Scholar]
- Ju, C.; Wang, H.; Liu, J.; Ma, C.; Zhang, Y.; Zhao, P.; Chang, J.; Tian, Q. Constraint and Union for Partially-Supervised Temporal Sentence Grounding. arXiv 2023, arXiv:2302.09850. [Google Scholar]
- Chen, J.; Chen, X.; Ma, L.; Jie, Z.; Chua, T.S. Temporally Grounding Natural Sentence in Video. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; Riloff, E., Chiang, D., Hockenmaier, J., Tsujii, J., Eds.; pp. 162–171. [Google Scholar] [CrossRef]
- Yuan, Y.; Mei, T.; Zhu, W. To Find Where You Talk: Temporal Sentence Localization in Video with Attention Based Location Regression. In Proceedings of the 2019 AAAI Conference on Artificial Intelligence, Hilton Hawaiian Village, Honolulu, HI, USA, 27 January–1 February 2019; pp. 9159–9166. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Nie, L.; He, X.; Chen, B.; Chua, T.S. Attentive Moment Retrieval in Videos. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, SIGIR ’18, Ann Arbor, MI, USA, 8–12 July 2018; pp. 15–24. [Google Scholar] [CrossRef]
- Ji, W.; Qin, Y.; Chen, L.; Wei, Y.; Wu, Y.; Zimmermann, R. Mrtnet: Multi-Resolution Temporal Network for Video Sentence Grounding. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 2770–2774. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, Y.G. Semantic Proposal for Activity Localization in Videos via Sentence Query. In Proceedings of the AAAI Conference on Artificial Intelligence, Hilton Hawaiian Village, Honolulu, HI, USA, 27 January–1 February 2019; pp. 8199–8206. [Google Scholar] [CrossRef]
- Xu, H.; He, K.; Plummer, B.A.; Sigal, L.; Sclaroff, S.; Saenko, K. Multilevel Language and Vision Integration for Text-to-Clip Retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 9062–9069. [Google Scholar] [CrossRef]
- Lu, C.; Chen, L.; Tan, C.; Li, X.; Xiao, J. DEBUG: A Dense Bottom-Up Grounding Approach for Natural Language Video Localization. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 7 November 2019; Inui, K., Jiang, J., Ng, V., Wan, X., Eds.; pp. 5144–5153. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, X.; Wang, X.; Wang, Y.F.; Davis, L.S. MAN: Moment Alignment Network for Natural Language Moment Retrieval via Iterative Graph Adjustment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Chen, L.; Lu, C.; Tang, S.; Xiao, J.; Zhang, D.; Tan, C.; Li, X. Rethinking the Bottom-Up Framework for Query-Based Video Localization. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 10551–10558. [Google Scholar] [CrossRef]
- Yu, X.; Malmir, M.; He, X.; Chen, J.; Wang, T.; Wu, Y.; Liu, Y.; Liu, Y. Cross Interaction Network for Natural Language Guided Video Moment Retrieval. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR ’21, Virtual, 11–15 July 2021; pp. 1860–1864. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, Z.; Zhao, Z.; Xiao, Z. Cross-Modal Interaction Networks for Query-Based Moment Retrieval in Videos. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR ’19, Paris, France, 21–25 July 2019; pp. 655–664. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Wu, T.; Li, T.; Wu, G. Negative Sample Matters: A Renaissance of Metric Learning for Temporal Grounding. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 22 February–1 March 2022; pp. 2613–2623. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, A.; Jing, W.; Zhen, L.; Zhou, J.T.; Goh, S.M.R. Parallel Attention Network with Sequence Matching for Video Grounding. In Proceedings of the Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021, Online Event, 1–6 August 2021; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).