Differential Privacy in Federated Learning: An Evolutionary Game Analysis

Abstract

This paper examines federated learning, a decentralized machine learning paradigm, focusing on privacy challenges. We introduce differential privacy mechanisms to protect privacy and quantify their impact on global model performance. Using evolutionary game theory, we establish a framework to analyze strategy dynamics and define utilities for different strategies based on Gaussian noise powers and training iterations. A differential privacy federated learning model (DPFLM) is analyzed within this framework. A key contribution is the thorough existence and stability analysis, identifying evolutionarily stable strategies (ESSs) and confirming their stability through simulations. This research provides theoretical insights for enhancing privacy protection in federated learning systems.

1. Introduction

In the era of the information age, the generation and accumulation of data is accelerating at an unprecedented rate. However, this vast amount of data is often fragmented across various locations and managed by multiple entities. Traditionally, analyzing such dispersed data has relied heavily on centralized processing, which requires the aggregation of data from various locations. As concerns over data security and privacy continue to grow, conventional approaches have become increasingly inadequate, often resulting in significant privacy leakages [1]. Specifically, when private data are used for model training, the trained models may inadvertently disclose sensitive information through their behavior or structure [2,3,4].

In recent years, federated learning (FL) has emerged as a novel machine learning (ML) paradigm, gradually gaining traction. The core idea of federated learning is to enable multiple clients to collaboratively train a shared machine learning model while keeping their data decentralized and locally stored. Although federated learning can protect client privacy to some extent, significant challenges remain. For example, Shokri et al. [5] introduced membership inference attacks, highlighting a significant privacy vulnerability within federated learning. In response to such challenges, recent studies have increasingly turned to advanced cryptographic tools, such as secure multi-party computation and differential privacy, to enhance privacy protection in federated learning [6]. For instance, Wei et al. [7] investigated the trade-off between convergence performance and differential privacy protection in federated learning under a unified noise scale. Hu et al. [8] examined the relationship between model accuracy and privacy protection with a uniform noise scale. Geyer et al. [9] studied the relationship between privacy loss and model performance. However, despite significant progress in addressing privacy concerns in federated learning, many critical questions remain open for exploration. For instance, while existing studies have highlighted the importance of privacy protection through techniques such as secure multi-party computation and differential privacy, there is still a need for more comprehensive frameworks to quantify privacy leakage and to understand the impact of privacy preferences on model performance. This gap underscores the ongoing and evolving nature of privacy protection in federated learning, making it a highly relevant and active area of research.

Game theory, particularly evolutionary game theory, provides a powerful framework for analyzing the strategic behavior of participants in federated learning systems. Traditional game theory focuses on systematically analyzing competitors to choose the best strategy for maximizing personal benefits [10]. In contrast, evolutionary game theory [11,12,13] emphasizes the evolution of strategies and changes at the population level. It is widely used for analyzing interactions between groups. In the context of federated learning, evolutionary game theory can effectively model the dynamic behavior of clients as they balance the trade-off between privacy protection and model performance. Clients aim to maximize their utility by selecting strategies that protect their privacy while still contributing to the global model’s accuracy. The concept of population share in evolutionary game theory can be used to reflect the proportion of clients adopting different strategies over time, capturing the evolving dynamics of client behavior [14]. Recently, incentive allocation mechanisms in evolutionary game theory have garnered academic attention [15,16,17]. A well-designed incentive mechanism can shape the behavioral patterns of the group during evolutionary games, reduce the selfish behavior of individuals, and thereby enhance group stability. Previous studies [18,19,20] have applied game theory ideas using various models but have not considered the impact of individual strategies on overall incentives.

In reality, individual strategy choices play a crucial role in determining the performance of the global model in federated learning and have a direct impact on the actual overall incentives. Given the decentralized nature of federated learning, where each client has the autonomy to choose strategies that balance privacy protection and model performance, understanding these choices and their collective impact is essential. Traditional game theory, while powerful, often focuses on individual strategy optimization and may not fully capture the dynamic and evolving nature of client behavior in federated settings. In contrast, evolutionary game theory provides a more comprehensive framework to analyze how individual strategies evolve over time and how these changes affect the overall system dynamics. This study leverages the strengths of evolutionary game theory to address the challenges posed by individual strategy choices in federated learning and makes several key contributions:

• Evolutionary game theory analysis: We employ evolutionary game theory to analyze the differential privacy protection problem in federated learning. Unlike traditional game theory, which focuses on individual strategy choices, our approach examines the dynamics of population shares, capturing how the collective behavior of participants evolves over time. This perspective provides a novel framework for understanding the interplay between privacy preferences and system performance.
• Impact of differential privacy mechanisms: We quantify the impact of differential privacy mechanisms on global model performance and reflect these impacts in the incentive pool. Additionally, we characterize privacy leakage to understand its effects on user utility, providing a comprehensive analysis of the trade-offs between privacy protection and model performance.
• Differential privacy federated learning model (DPFLM): We constructed DPFLM, a robust model that integrates differential privacy into federated learning. We also propose an algorithm to compute the utility of each strategy, enabling systematic analysis of the incentives associated with different privacy mechanisms.
• Existence and stability analysis: We conducted a thorough analysis of the existence of solutions in evolutionary game theory. For the two-strategy case, we derived closed-form results for the evolutionarily stable strategies (ESSs). For more general cases, we validate our theoretical findings through extensive simulations, demonstrating the practical applicability of our approach.

2. Related Work and Preliminaries

2.1. Gaussian Mechanism Differential Privacy in Federated Learning

The differential privacy (DP) mechanism is a privacy-preserving method designed to protect individual datums while still allowing meaningful statistical information to be extracted [21,22]. The core principle of differential privacy involves adding a controlled amount of noise during the computation of statistical information or data analysis. This noise obscures the contributions of individual data points, thereby preventing privacy breaches that target specific individuals.

Traditionally, differential privacy has been applied to centralized data at a trusted data center, where a trusted third party administers differential privacy measures and releases the processed data. This approach, known as centralized differential privacy, relies on a trusted third party data collector to ensure that the original data are not disclosed. However, identifying a truly trustworthy third-party data collector is challenging in real-world scenarios. This challenge has led to the development of localized differential privacy, which decentralizes the privacy-preserving process and assigns it to each data-owning user. This approach reduces the potential risk of privacy leakage. The localized differential privacy data processing framework is illustrated in Figure 1.

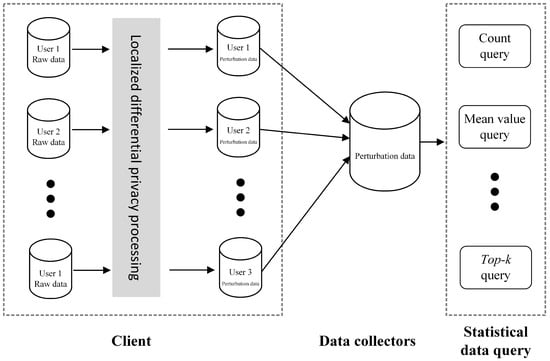
Figure 1. Localized differential privacy data processing framework.

In Figure 1, the clients correspond to the participants in federated learning, with their raw data being the model’s post-training parameters. The data collector corresponds to the server, which aggregates and queries statistical data to form the global model. From the perspective of implementing differential privacy mechanisms for numerical data, there are two main approaches: Gaussian differential privacy and Bayesian differential privacy. While Bayesian differential privacy is suitable for smaller data samples, it has drawbacks such as high computational costs and the need for prior information [23,24]. In contrast, the Gaussian mechanism for differential privacy has low computational costs [25] and is easy to implement, making it ideal for handling real-time data and large-scale datasets [26]. Although the accuracy of Gaussian differential privacy is generally lower than that of Bayesian differential privacy, certain algorithms can enhance the accuracy of models using Gaussian mechanisms for differential privacy. For instance, in the work by Chuanxin et al. [27], the accuracy was improved threefold using the proposed Noisy-FL algorithm.

In this paper, we adopt the definition of $(\epsilon ,\delta )$-DP, as presented in [28], which is given by

$$\mathrm{Pr}\left[\mathcal{M}\left(\mathcal{D}\in \mathcal{O}\right)\right]\le e^{\epsilon }\mathrm{Pr}\left[\mathcal{M}\left({\mathcal{D}}^{\prime }\in \mathcal{O}\right)\right]+\delta ,$$

(1)

where $\mathcal{D}$ is the original dataset, and ${\mathcal{D}}^{\prime }$ is a dataset that differs from $\mathcal{D}$ by only a single data point. To be precise, ${\mathcal{D}}^{\prime }$ is considered a neighboring dataset to $\mathcal{D}$ if ${\mathcal{D}}^{\prime }$ can be obtained from $\mathcal{D}$ by either adding, removing, or modifying a single record. $\mathcal{O}$ represents the set of possible output results. $\epsilon$ is the privacy budget, which controls the degree of privacy leakage. $\delta$ is the additional privacy budget, which controls the upper bound on the probability of privacy leakage. $\mathcal{M}$ represents the application of a randomized perturbation algorithm in differential privacy. According to (1), a smaller value of $\epsilon$ implies that more noise is added, making it difficult to distinguish between the datasets $\mathcal{D}$ and ${\mathcal{D}}^{\prime }$. This results in stronger privacy protection. In other words, when two datasets, $\mathcal{D}$ and ${\mathcal{D}}^{\prime }$, with minor differences are perturbed by the randomized algorithm, $\mathcal{M}$, the resulting output dataset, $\mathcal{O}$, should have minimal differences. These differences are controlled by $\epsilon$. The smaller the $\epsilon$, the stronger the privacy protection. The implementation of differential privacy is illustrated in Figure 2.

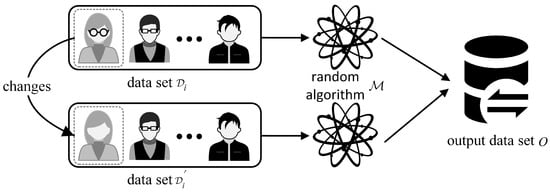
Figure 2. Implementation of differential privacy.

In this study, different clients have different privacy budgets. This is because different clients may handle datasets with varying levels of sensitivity. For instance, some clients might possess highly sensitive personal data, while others deal with less sensitive information. Furthermore, clients may have different privacy requirements based on their specific contexts, regulations, or agreements. Since we implement a Gaussian mechanism, this translates to different powers of Gaussian noise. According to [29], during the Tth round of aggregation, the relationship between Gaussian noise power and privacy budget can be expressed as $\sigma =\Delta \sqrt{2Tlog(1.25/\delta )}/\epsilon$, where $\Delta ={max}_{\mathcal{D},{\mathcal{D}}^{\prime }}\left|\right|\mathcal{O}\left(\mathcal{D}\right)-\mathcal{O}\left({\mathcal{D}}^{\prime }\right)\left|\right|$. When the range of gradient updates is limited, we can always find a finite constant, C, such that $\Delta =2C/D$. Then, we can obtain

$$\sigma ={\displaystyle \frac{2C\sqrt{2Tlog(1.25/\delta )}}{D\epsilon }}.$$

(2)

The equation calculates the standard deviation, $\sigma$, of the Gaussian noise, which is computed based on each client’s privacy budget. This calculation is based on their dataset size, D, the global training round number, T, the pre-defined privacy failure probability, $\delta$, and the gradient clipping threshold, C. This calculated $\sigma$ value is then used within the Gaussian mechanism to add noise to the gradient updates uploaded by that client, ensuring differential privacy protection.

2.2. Incentive Mechanisms in Federated Learning

In federated learning (FL), clients are rational actors who face critical challenges, such as potential privacy leakage risks, when participating in collaborative model training. These inherent costs create disincentives for client participation, leading to situations where a subset of clients may be reluctant to engage in the collaborative learning process. To address this fundamental challenge, the implementation of incentive mechanisms becomes essential. Specifically, a rationally structured incentive scheme can reward clients commensurate with their contributions, thereby motivating them to tolerate associated costs and actively participate in FL frameworks. Such mechanisms aim to align individual rationality with collective learning objectives by balancing computational costs, privacy risks, and model performance.

Significant research efforts have been devoted to developing optimized solutions from diverse perspectives. For instance, Muhammad et al. [30] proposed a reputation-rating algorithm to evaluate client trustworthiness, thereby enhancing global model performance through rigorous credibility assessment. Wang et al. [31] introduced a fair and robust federated learning (FRFL) framework, leveraging contract theory principles to design a client selection mechanism that mitigates free-riding behaviors while ensuring reliability. Weng et al. [32] developed DeepChain, a blockchain-enabled deep learning architecture that utilizes value-driven incentives to align client behaviors with collaborative objectives through cryptographic commitments. However, these seminal publications predominantly overlook the critical aspect of inter-client strategic interactions. As federated learning fundamentally constitutes an iterative multi-round process, it inherently embodies evolutionary game-theoretic characteristics, where clients dynamically adapt their training strategies in response to environmental feedback (e.g., reward distributions and peer behaviors). Evolutionary game theory provides essential analytical tools, such as replicator dynamics equations and evolutionarily stable strategies, which enable the establishment of a realistic behavioral modeling framework tailored to FL ecosystems. This paradigm captures continuous strategy evolution through population-level adaptation mechanisms, transcending the limitations of conventional static game models. For example, Zou et al. [33] constructed an evolutionary game model to analyze the long-term strategies of device participation in training, considering the resource heterogeneity of mobile devices. Their study revealed the driving mechanism of decision evolution in balancing resource constraints and benefits. In a decentralized setting, Cheng et al. [34] proposed a blockchain-based federated learning (BCFL) game framework. Through a two-stage “node selection-data sharing” strategy game, they demonstrated how blockchain transparency facilitates trust-building among participants and derived the conditions for cooperative benefit allocation under Nash equilibrium. Regarding the stability of complex federated networks, Hammoud et al. [35] designed a cloud federation formation model that integrates genetic algorithms with evolutionary games. Their findings proved that multi-round strategy adjustments can converge to a federated topology optimized for quality of service (QoS). In terms of security defense, Abou et al. [36] incorporated the probability of IIoT network attacks into the game payoff function and proposed the FedGame model. This model leverages evolutionary stable strategies (ESSs) to filter out collaborative alliances capable of resisting malicious node interference. These studies offer a systematic framework for designing incentive mechanisms in federated learning across multiple dimensions, including resource allocation, trust-building, topology optimization, and security defense. Hence, in this paper, we focus on evolutionary game analysis in federated learning to address these challenges and improve client participation and collaboration.

3. System Model and Evolutionary Game Formulation

3.1. System Model

We consider a differential privacy federated learning model comprising I clients, denoted by $P_1,\dots ,P_I$, and a central server. When the server initiates a training task, it assigns the task to the clients and offers incentives to those who participate. Clients, in turn, decide whether to engage in the training task and, if so, employ differential privacy mechanisms to protect the privacy of their local data. Specifically, they select appropriate numbers of local iterations, $E_i$, and add Gaussian noise with power ${\sigma }_i$ during model training and parameter uploading. The federated learning system model is illustrated in Figure 3.

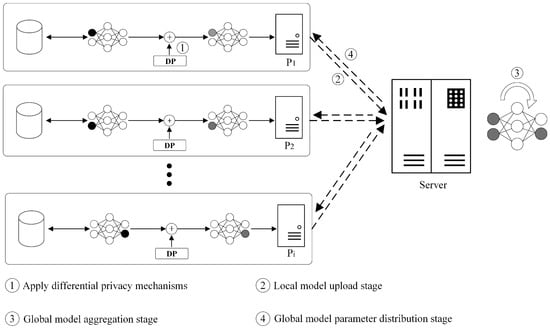
Figure 3. Federated learning system model.

To analyze this model within the framework of evolutionary game theory, we define the following components:

• Players: The players in this game are the clients, denoted by $P_1,\dots ,P_I$.
• Strategies: The nth strategy available to a player can be expressed as $S_n=(E_n,{\sigma }_n)$, where $E_n$ is the number of local iterations per round, and ${\sigma }_n^2$ is the Gaussian noise power. We assume there are N strategies in total, denoted by $S_1,\dots ,S_N$. Here, ‘strategies’ represent the different combinations of local iterations and Gaussian noise power that a client can choose. These strategies are formulated based on the practical application of differential privacy in FL. Different noise powers represent varying levels of privacy protection, with higher noise offering stronger privacy but potentially impacting model accuracy and, thus, the incentive pool. The number of local iterations also influences both model contribution and potential privacy leakage. These strategies are relevant to clients because they directly control the trade-off between their privacy protection and their potential utility. Clients with different privacy preferences or data sensitivity levels might choose different strategies.
• Population share: The population share represents the proportion of clients choosing a particular strategy within the strategy space. Let $x_n\in \mathbf{X}$ denote the proportion of the population that selects strategy $S_n$, and it satisfies ${\sum }_{n=1}^N{x}_n=1$.
• Utility: The utility for each client is determined by their net income, which is the difference between the payoff obtained from the server and the training costs incurred. The utility for selecting strategy $S_n$ at time t is denoted by $U_n\left(t\right)$. For simplicity, this is subsequently abbreviated as $U_n$.

In the framework of evolutionary game theory, each player can maximize their utility by adjusting their own strategy. The selection of strategies by clients is of significant importance because it directly impacts the trade-off between utility and privacy. An optimal strategy aims to maximize client utility while adhering to privacy constraints. For instance, a client prioritizing incentives above all else might choose a strategy that introduces minimal or no noise to their data. Although this could potentially maximize their contribution to an incentive pool, it would simultaneously lead to a substantial increase in privacy leakage, potentially undermining the overall privacy guarantees of the system. Conversely, if all clients were to adopt overly conservative strategies by adding excessive noise, the aggregated model would suffer from poor training quality, resulting in a diminished incentive pool and, ultimately, reduced utility for all clients. Therefore, the strategic selection of privacy mechanisms is crucial to achieving a delicate equilibrium, enabling clients to derive meaningful utility from participation while simultaneously ensuring robust privacy protection. In essence, effective strategy selection is key to balancing client incentives with the fundamental requirement of privacy preservation within the system. As the game progresses, players’ strategies will continuously evolve, making this process a dynamic adjustment. Overall, the population shares of different strategies will also change over time. The notations are summarized in Table 1.

Table 1. List of notations.

Notation	Meaning
$P_i$	Player i
$E_n$	Number of iterations for strategy n
${\sigma }_n^2$	Gaussian noise power for strategy n
I	Number of players
N	Number of strategies
A	Basic incentive for participating in training
$x_n$	Proportion of the population selecting strategy $S_n$
$U_n\left(t\right)$	Utility function of $S_n$ at time t
$Q_E$	Size of the incentive pool

3.2. Utility Function

The utility function in our model accounts for the impact of differential privacy on the training model. Specifically, the utility for each client is determined based on the upper bounds of convergence for both the global and local loss functions, as well as the strategies selected.

3.2.1. Incentive Pool

When clients conduct model training and employ differential privacy mechanisms, they upload their local model parameters to the server. The server then aggregates these parameters from all participants to generate a global model. The upper bound of convergence for the global loss function is used to estimate the algorithm’s convergence rate, thereby quantifying the impact of Gaussian noise and the number of iterations on model performance. The size of the incentive pool is determined based on the model’s performance. Drawing inspiration from [29], we express the global loss function $L_g$ as follows:

$$L_g={\displaystyle \frac{\mathsf{\Theta }}{c\eta TG}}+{\displaystyle \frac{5{\eta }^2{l}^2({\sigma }_L^{2}G+6{\sigma }_G^2{G}^2)}{c}}+{\displaystyle \frac{d^2}{c{\eta }^2{N}^2{G}^2}}\sum _{n=1}^N({\sigma }_n^2·I·x_n)$$

(3)

Here, $\mathsf{\Theta }$ represents the difference between the initial loss and the optimal loss. c is a constant. $\eta$ is the model learning rate. T is the number of global updates. G is the number of global iterations. l is the Lipschitz constant. ${\sigma }_L^2$ bounds the variance of the stochastic gradients at each client, and ${\sigma }_G^2$ bounds the difference between the gradient of a single client and the global one. From Equation (3), we observe that the larger the Gaussian noise added by the clients, the larger the loss, implying a slower convergence rate for the global model. Consequently, the size of the incentive pool is given by

$$Q_E={\displaystyle \frac{r}{L_g}},$$

(4)

where r is a constant determined by the server.

3.2.2. Payoff, Cost, and Utility

The incentive pool is shared among all clients. Since the noise added by the clients affects the performance of the model, and the larger the noise, the worse the performance of the local model, the payoff should be lower for clients with larger noise power. We assume that the client with noise power ${\sigma }_n^2$ should receive a payoff proportional to ${\displaystyle \frac{1}{{\sigma }_n}}$. Given that the size of the incentive pool is $Q_E$, using normalization, the payoff for choosing noise power ${\sigma }_n^2$, denoted by $p_n$, is given by

$$p_n=Q_E·{\displaystyle \frac{\frac{1}{{\sigma }_n}}{I·{\sum }_{i=1}^N\frac{x_i}{{\sigma }_i}}}+A,$$

(5)

where A represents the basic reward granted by the server to participants for their involvement in the training process. We observe that the payoffs, $p_1,\dots ,p_N$, are determined by the population shares $x_1,\dots ,x_n$.

The cost arises from the impact of Gaussian noise on privacy leakage for each client. Most current studies measure privacy leakage through experiments, which, however, requires access to user data, contradicting the original intention of privacy protection. Liu et al. [29] conducted research on the theoretical measurement of privacy leakage, making it possible to theoretically quantify privacy leakage and apply it to various scenarios and datasets. Motivated by their results, we express the cost of strategy, $S_n$, $c_n$, as

$$c_n={\displaystyle \frac{{\eta }^2{E}_n^2}{2{\sigma }_n^2}}.$$

(6)

Here, $\eta$ is the model learning rate. We emphasize that more local iterations make the model more suitable for the local dataset, increasing the likelihood of data leakage.

Summarizing the above, the utility for selecting strategy $S_n$ can be expressed as

$$U_n=p_n-c_n=Q_E·{\displaystyle \frac{\frac{1}{{\sigma }_n}}{I·{\sum }_{i=1}^N\frac{x_i}{{\sigma }_i}}}+A-{\displaystyle \frac{{\eta }^2{E}_n^2}{2{\sigma }_n^2}}.$$

(7)

Notice that $U_n$ is a function of $x_1,\dots ,x_n$. The following Algorithm 1 summarizes the calculation of the utility.

Algorithm 1 Utility Calculation Algorithm.

1: Input: Selected strategy profile $S_n$, other federated learning parameters 2: Output: The utility for selecting strategy $S_n$, $U_n$ 3: Initialize the input parameters. 4: Based on the overall noise and the number of iterations, use the global loss function, calculate the result of $Q_E$ according to Equations (3) and (4). 5: Based on the strategies chosen, calculate the payoff and cost using Equations (5) and (6). 6: Calculate the utility for selecting strategy $S_n$, $U_n$, using Equation (7).

3.3. Replicator Dynamics

Replicator dynamics (RDs) is a widely used model that describes how strategies evolve over time in evolutionary game theory. It is primarily applied to study the dynamic processes of strategy selection and evolution [37]. Therefore, this study employs replicator dynamics to analyze the dynamic process of strategy selection and evolution in our federated learning system.

The utility for selecting strategy $S_n$ is given by Equation (7), and the average utility of the clients involved in the training can be given by the following expression:

$$\overline{U}={\displaystyle \frac{1}{N}}\sum _{n=1}^N{U}_n{x}_n$$

(8)

In each federated learning task, clients can freely choose their strategies to maximize their utilities. Since the utility is related to the population share, clients cannot simply select the strategy with the minimum noise to achieve the largest size of the incentive pool. Based on the above analysis, the replicator dynamics equation for clients can be expressed as

$${\dot{x}}_n\left(t\right)\triangleq {\varphi }_n\left(x_1\left(t\right),\dots ,x_N\left(t\right)\right)=\Delta x_n\left(t\right)\left[U_n\left(t\right)-\overline{U}\left(t\right)\right],\forall n\in N.$$

(9)

Here, $\Delta$ represents the positive learning rate, which controls the speed at which the clients adapt to different strategies. Based on replicator dynamics, when the utility of a client is lower than the average, it will adjust its strategy to obtain a higher utility. Often, at the end of the game, an equilibrium point will be reached.

4. Game Analysis

In this section, we investigate the existence and stability of the replicator dynamics described by Equation (9). Regarding existence, we demonstrate that the game has at least one stable point (equilibrium). Regarding stability, we show that once the game reaches equilibrium, it can return to the equilibrium state even if disturbed. First, we prove the boundedness of Equation (9) in Lemma 1.

Lemma 1.

For all $n,v\in \{1,\dots ,N\}$, the first-order derivative of ${\varphi }_n(x_1,\dots ,x_N)$ with respect to $x_v\left(t\right)$ is bounded.

Proof of Lemma 1.

For ease of calculation, we omit t in the proof. Then, the coefficients of the first, second, and third terms in Equation (3) are constants. The sum of the first and second terms is denoted by B, and the coefficient of the third term is denoted by C. Thus, Equation (3) can be rewritten as

$$L_g=B+C·\sum _{i=1}^N({\sigma }_n^2·I·x_i)$$

(10)

The derivative of ${\varphi }_n(x_1,\dots ,x_N)$ with respect to $x_v$ can be given as follows:

$${\displaystyle \frac{d{\varphi }_n(x_1,\dots ,x_N)}{d{x}_v}}=\Delta \left[{\displaystyle \frac{d{x}_n}{x_v}}\left(U_n-\overline{U}\right)+x_n\left({\displaystyle \frac{d{U}_n}{d{x}_v}}-{\displaystyle \frac{d\overline{U}}{d{x}_v}}\right)\right].$$

(11)

This equation represents the partial derivative of the replicator dynamics equation ${\varphi }_n(x_1,\dots ,x_N)$ with respect to the population share of strategy v, denoted as $x_v$. It is derived using the product rule of differentiation. Specifically, considering ${\varphi }_n$ as a product of two terms, $\Delta x_n$ and $(U_n-\overline{U})$, its derivative with respect to $x_v$ is given by ${\displaystyle \frac{d{\varphi }_n}{d{x}_v}}={\displaystyle \frac{d(\Delta x_n)}{d{x}_v}}(U_n-\overline{U})+(\Delta x_n){\displaystyle \frac{d(U_n-\overline{U})}{d{x}_v}}$. To simplify the notation, we define

$$G(x_1,\dots ,x_N)=\sum _{i=1}^N({\sigma }_n^2·I·x_i),H(x_1,\dots ,x_N)=I·\sum _{i=1}^N{\displaystyle \frac{x_i}{{\sigma }_i}}.$$

(12)

Thus, we can obtain

$${\displaystyle \frac{d{U}_n}{d{x}_v}}={\displaystyle \frac{-r·\frac{dG(x_1,\dots ,x_N)}{d{x}_v}}{{\left[B+c·G(x_1,\dots ,x_N)\right]}^2}}·{\displaystyle \frac{1}{{\sigma }_{n}H(x_1,\dots ,x_N)}}+{\displaystyle \frac{r}{B+c·G(x_1,\dots ,x_N)}}·{\displaystyle \frac{\frac{dH(x_1,\dots ,x_N)}{d{x}_v}}{{\sigma }_{n}H{(x_1,\dots ,x_N)}^2}}.$$

(13)

Since ${\displaystyle \frac{dG(x_1,\dots ,x_N)}{d{x}_v}}={\sigma }_v^2·I$, ${\displaystyle \frac{dH(x_1,\dots ,x_N)}{d{x}_v}}={\displaystyle \frac{I}{{\sigma }_v}}$, we can obtain that $\left|{\displaystyle \frac{d{U}_n}{d{x}_v}}\right|$ is bounded. Hence, $\left|{\displaystyle \frac{d{\varphi }_n(x_1,\dots ,x_N)}{d{x}_v}}\right|$ is also bounded. □

Then, we can prove that the solution of (9) exists.

Theorem 1.

For all $n\in \{1,\dots ,N\}$, the solution of (9) exists.

Proof of Theorem 1.

From Lemma 1, we can obtain that $\left|{\displaystyle \frac{d{\varphi }_n(x_1,\dots ,x_N)}{d{x}_v}}\right|$ is bounded. In addition, it is straightforward to see that ${\varphi }_n(x_1,\dots ,x_N)$ and ${\displaystyle \frac{d{\varphi }_n(x_1,\dots ,x_N)}{d{x}_v}}$ are both continuous. Therefore, ${\varphi }_n(x_1,\dots ,x_N)$ satisfies the Lipschitz condition with respect to $x_1,\dots ,x_N$. According to the Picard-Lindelöf theorem, for any given initial conditions, the system of differential equations has a unique solution in the region under consideration. □

Now, we analyze the stability of this evolutionary game. We begin with the definition of Nash equilibrium.

Definition 1.

The population state ${\mathit{x}}^{*}=[x_1^{*},\dots ,x_N^{*}]$ is called a Nash equilibrium of the game if for all feasible states $\mathit{x}=[x_1,\dots ,x_N]$ in the population, the inequality ${(\mathit{x}-{\mathit{x}}^{*})}^T\mathsf{\varphi }\left({\mathit{x}}^{*}\right)\le 0$ holds, where $\mathsf{\varphi }\left({\mathit{x}}^{*}\right)=[{\varphi }_1\left({\mathit{x}}^{*}\right),\dots ,{\varphi }_N\left({\mathit{x}}^{*}\right)]$ [38].

In simpler terms, a Nash equilibrium is a fixed point of the ordinary differential equation, i.e.,

$$\forall n\in \mathcal{N},{\dot{x}}_n\left(t\right)=0.$$

Suppose there exists another population state, ${\mathit{x}}^{\prime }$, that attempts to invade the state ${\mathit{x}}^{*}$ by attracting a fraction of players $\lambda \in (0,1)$. If the following condition holds for all $\lambda \in (0,1)$, then ${\mathit{x}}^{*}$ is an evolutionarily stable strategy (ESS). The definition is given as follows.

Definition 2.

If there exists a neighborhood $\mathcal{B}\in \mathcal{X}$ such that

$${(\mathit{x}-{\mathit{x}}^{*})}^T\mathsf{\varphi }\left({\mathit{x}}^{*}\right)=0,{({\mathit{x}}^{*}-\mathit{x})}^T\mathsf{\varphi }\left(\mathit{x}\right)\ge 0,\forall x\in \mathcal{B}$$

then the population state ${\mathit{x}}^{*}$ is an ESS of the game.

In practice, when N is very large, it is difficult to find a closed-form solution for ${\mathit{x}}^{*}$. Thus, we study the case of two strategies ($N=2$) to illustrate stability in the game. Other cases can also be analyzed using a similar method, but due to the complexity of the calculations, they are not listed in this paper. In the numerical simulation section, cases with more than two strategies are still considered. Taking two strategies as an example, the share of choosing strategy 1 is $x_1$, and the share of choosing strategy 2 is $x_2$. Based on the replicator dynamics and the constraint conditions, the following equations can be listed:

$$\left\{\begin{array}{c}\Delta x_1\left(U_1-\overline{U}\right)=0,\hfill \\ \Delta x_2\left(U_2-\overline{U}\right)=0,\hfill \\ x_1+x_2=1.\hfill \end{array}\right.$$

(14)

The utility for selecting strategy $S_1$, $U_1$ can be expressed as

$$U_1={\displaystyle \frac{r}{B+C·\left({\sigma }_1^{2}I{x}_1+{\sigma }_2^{2}I{x}_2\right)}}·{\displaystyle \frac{1}{{\sigma }_1^{2}I\left(\frac{x_1}{{\sigma }_1}+\frac{x_2}{{\sigma }_2}\right)}}-{\displaystyle \frac{{\eta }^2{E}_1^2}{2{\sigma }_1^2}}+A$$

(15)

When I is sufficiently large, the influence of B on $U_1$ can be ignored, and we let

$$a={\displaystyle \frac{r}{C{I}^2}},b_1={\displaystyle \frac{{\eta }^2{E}_1^2}{2{\sigma }_1^2}},b_2={\displaystyle \frac{{\eta }^2{E}_2^2}{2{\sigma }_2^2}}.$$

(16)

By substituting the above into Equation (15), we obtain the simplified expression of $U_1$ as follows:

$$U_1={\displaystyle \frac{a}{\left({\sigma }_1^2{x}_1+{\sigma }_2^2{x}_2\right)·\left(\frac{x_1}{{\sigma }_1}+\frac{x_2}{{\sigma }_2}\right){\sigma }_1}}-b_1+A.$$

(17)

By substituting Equation (17) into Equation (14), we obtain that

$$x_1^{*}\in \left\{{\displaystyle \frac{{\sigma }_1^2-{\sigma }_2^2-{\sigma }_1{\sigma }_2-\beta }{2\left({\sigma }_1^2-{\sigma }_2^2\right)}},0,1,{\displaystyle \frac{{\sigma }_1^2-{\sigma }_2^2-{\sigma }_1{\sigma }_2+\beta }{2\left({\sigma }_1^2-{\sigma }_2^2\right)}}\right\},$$

(18)

where

$$\begin{array}{ccc}\hfill \beta & =& \left(\right(4a{\sigma }_1^2-4a{\sigma }_2^2+b_1{\sigma }_1^4+b_1{\sigma }_2^4-b_2{\sigma }_1^4-b_2{\sigma }_2^4+2b_1{\sigma }_1{\sigma }_2^3+2b_1{\sigma }_1^3{\sigma }_2-2b_2{\sigma }_1{\sigma }_2^3-2b_2{\sigma }_1^3{\sigma }_2\hfill \\ & +& 3b_1{\sigma }_1^2{\sigma }_2^2-3b_2{\sigma }_1^2{\sigma }_2^2)/(b_1-b_2){)}^{0.5}.\hfill \end{array}$$

(19)

Thus, $x_2^{*}=1-x_1^{*}$, and in all solutions, we should have $x_1^{*}\in [0,1]$.

Further, we will study the evolutionary stability of four fixed points. In the cases of $x_1^{*}=0$ and $x_1^{*}=1$, the shares of the two strategies are $(0,1)$ and $(1,0)$, respectively. In these two cases, the forms are similar. Therefore, we only need to check the case of $x_1^{*}=0$.

The ordinary differential equation in Equation (9) asymptotically stabilizes to an ESS when the replicator dynamics are continuous in time. If the Jacobian matrix of the ordinary differential equation is negative definite at the steady state, then the point is asymptotically stable. The Jacobian matrix of the ordinary differential equations for this two-strategy case can be given as

$$J\triangleq \left(\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{\partial {\varphi }_1(x_1,x_2)}{\partial x_1}}& {\displaystyle \frac{\partial {\varphi }_1(x_1,x_2)}{\partial x_2}}\\ {\displaystyle \frac{\partial {\varphi }_2(x_1,x_2)}{\partial x_1}}& {\displaystyle \frac{\partial {\varphi }_2(x_1,x_2)}{\partial x_2}}\end{array}\right){|}_{x_1=x_1^{*},x_2=1-x_1^{*}}$$

(20)

To simplify the calculation process and make the final result simpler, we assume $I\to +\infty$ so that

$$\underset{I\to \infty }{lim}a=\underset{I\to \infty }{lim}{\displaystyle \frac{r}{CI}}=0.$$

(21)

By substituting $a=0$ into Equation (20), we can obtain that

$$J=\left(\begin{array}{cc}2b_1{x}_1-b_1+b_2{x}_2& b_2{x}_1\\ b_1{x}_2& b_1{x}_1-b_2+2b_2{x}_2\end{array}\right).$$

(22)

Then, we can obtain the following:

• When $x_1^{*}={\displaystyle \frac{{\sigma }_1^2-{\sigma }_2^2-{\sigma }_1{\sigma }_2-\beta }{2({\sigma }_1^2-{\sigma }_2^2)}}$ is an ESS, then the following inequalities must be satisfied:

  $$\left\{\begin{array}{c}det\left(J_{11}\right)={\displaystyle \frac{(2b_1-b_2)\gamma }{2({\sigma }_1^2-{\sigma }_2^2)}}+b_1<0,\hfill \\ det\left(J\right)={\displaystyle \frac{(b_1-b_2)({\sigma }_1^2-{\sigma }_2^2+\gamma )(2b_1{\sigma }_1^2-2b_1{\sigma }_2^2+b_1\gamma -b_2\gamma )}{2{({\sigma }_1^2-{\sigma }_2^2)}^2}}>0\hfill \end{array}\right.,$$

  (23)

  where ${\gamma =\beta |}_{a=0}+{\sigma }_1{\sigma }_2-{\sigma }_1^2+{\sigma }_2^2$.
• When $x_1^{*}={\displaystyle \frac{{\sigma }_1^2-{\sigma }_2^2-{\sigma }_1{\sigma }_2+\beta }{2({\sigma }_1^2-{\sigma }_2^2)}}$ is an ESS, then the following inequalities must be satisfied:

  $$\left\{\begin{array}{c}det\left(J_{11}\right)={\displaystyle \frac{(b_2-2b_1)\gamma }{2({\sigma }_1^2-{\sigma }_2^2)}}+b_1<0,\hfill \\ det\left(J\right)={\displaystyle \frac{(b_1-b_2)({\sigma }_2^2-{\sigma }_1^2+\gamma )(2b_1{\sigma }_2^2-2b_1{\sigma }_1^2+b_1\gamma -b_2\gamma )}{2{({\sigma }_1^2-{\sigma }_2^2)}^2}}>0\hfill \end{array}\right..$$

  (24)
• When $x_1^{*}=1$ or $x_1^{*}=0$, the condition that the Jacobian matrix of the ordinary differential equation is negative definite cannot be satisfied. Taking $x_1^{*}=0$ as an example, the following two conditions need to be satisfied:

  $$b_2-b_1<0,b_2^2-b_1{b}_2>0.$$

  (25)
  However, since $b_1$ and $b_2$ are both greater than 0, there is no solution that satisfies the conditions. Therefore, $x_1^{*}=1$ or $x_1^{*}=0$ are not stable points.

5. Numerical Results

In this section, we present numerical results to further substantiate our analysis and provide additional insights.

5.1. Utilities

In this subsection, we investigate the impact of different Gaussian noise powers on the utilities of various strategies in federated learning scenarios. Specifically, we analyze both two-strategy and four-strategy scenarios to understand how varying levels of noise affect the overall utility of the participating clients.

5.1.1. Two-Strategy Scenario

We first consider the model under a two-strategy scenario, with simulations examining the impact of varying Gaussian noise powers on the utilities. The parameters are set as follows: $a=10$, $b_1=0.02$, and $b_2=0.02$. The basic incentive for training is set as $A=5$, with a fixed population share of $[0.5,0.5]$. Additionally, ${\sigma }_1$ is held constant at $0.1$, while the initial value of ${\sigma }_2$ is set at $0.1$ and incremented by $0.02$ up to $2.5$. The values of $U_1$ and $U_2$ are observed in the left figure of Figure 4.

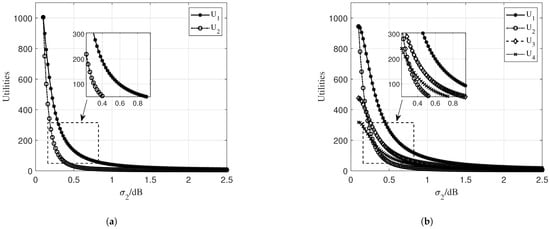
Figure 4. Utilities for different scenarios: (a) Two-strategy scenario. (b) Four-strategy scenario.

As shown in the left figure of Figure 4, the utilities of the two parties are initially identical. However, as ${\sigma }_2$ increases, the utilities of both parties begin to decrease, with a more pronounced impact on $U_2$. This decline occurs because the continuous addition of Gaussian noise to $S_2$ affects the accuracy of model training, which, in turn, influences the size of the total incentive pool, ultimately leading to a reduction in the utilities of both parties.

5.1.2. Four-Strategy Scenario

In the right figure of Figure 4, we consider a scenario with four strategies. The parameters are set as $a=10$, $b_1=0.02$, $b_2=0.02$, ${\sigma }_1=0.1$, ${\sigma }_2=0.1$, ${\sigma }_3=0.2$, and ${\sigma }_4=0.3$. The shares are set to $[0.25,0.25,0.25,0.25]$, and the basic incentive for training is $A=5$. Throughout the simulation, the values of ${\sigma }_1$, ${\sigma }_3$, and ${\sigma }_4$ remain constant. We start with an initial value of ${\sigma }_2=0.1$ and increment it by $0.02$ up to $2.5$. By examining the utilities of different strategies, as shown in the figure, it is clear that the greater the Gaussian noise added to $S_2$, the lower the utilities.

Overall, the results demonstrate that the utility of each strategy is significantly influenced by the level of Gaussian noise added during the training process. As the noise increases, the utility of the strategies decreases, highlighting the trade-off between privacy protection and model performance.

5.2. Stability Analysis

In this section, we conduct a comprehensive stability analysis to verify the theoretical results presented in the previous section. Through numerical simulations, we examine the stability of the system under different scenarios, including two-strategy, four-strategy, and eight-strategy cases. The goal is to demonstrate that the system converges to an ESS under various initial conditions and parameter settings.

Two-Strategy Scenario

We begin with a two-strategy scenario, where the system’s stability is analyzed under varying Gaussian noise powers. The parameters are set as follows: $I=80,000$, $N=2$, ${\sigma }_1=0.1$, $E_1=100$, ${\sigma }_2=1.1$, $E_2=695$, $\eta =0.0002$, and $A=5$. Additional parameters include $a=0.02$, $b_1=0.008$, $b_2=0.004$, and initial shares $[0.4,0.6]$. The evolution of shares and utilities is shown in Figure 5.

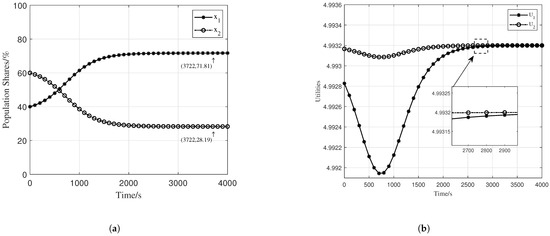
Figure 5. Population shares and utilities for two-strategy scenario (Equation (23) holds): (a) Population shares. (b) Utilities.

The Jacobian matrix satisfies Equation (23), indicating that it is negative definite. The equilibrium point is calculated as $x^{*}=[0.7181,0.2813]$. This implies that regardless of the initial shares, the system will eventually converge to this ESS. As shown in Figure 5, when the initial conditions satisfy Equation (23), the simulation results are consistent with the analytical results, thereby confirming the correctness of our previous analysis. From the right figure of Figure 5, we observe that when the system converges to the ESS, the utilities no longer change.

To further validate the stability analysis, we conducted a simulation for the second case where Equation (24) is satisfied. The number of clients is still set as $I=80,000$. For Strategy $S_1$, the Gaussian noise is set to ${\sigma }_1=0.4$ with $E_1=1265$ iterations. For Strategy $S_2$, the Gaussian noise is ${\sigma }_2=1.1$ with $E_2=778$ iterations. The learning rate is $\eta =0.0002$, and the basic incentive for training is still set as $A=5$. Other parameters are set as $a=0.1$, $b_1=0.2$, and $b_2=0.01$. The initial shares for selecting strategies were set to $[0.4,0.6]$. In this scenario, the Jacobian matrix satisfies Equation (24), indicating that it is negative definite. Through computation, we obtained the equilibrium point $x^{*}=[0.2180,0.7820]$.

As shown in the left figure of Figure 6, when the initial conditions satisfy Equation (24), the simulation results are consistent with the computed results, thereby verifying our analysis. From the right figure of Figure 6, it is evident that when the system converges to the ESS, the utilities no longer change.

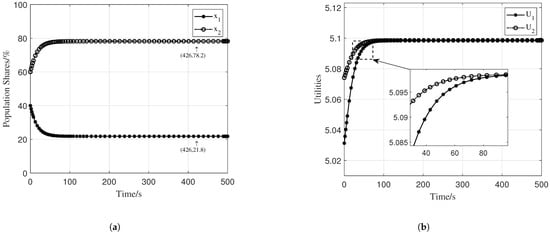
Figure 6. Population shares and utilities for two-strategy scenario (Equation (24) holds): (a) Population shares. (b) Utilities.

5.3. Beyond Two-Strategy Scenario

Next, we consider a four-strategy scenario to further validate the stability analysis. The parameters are set as $a=0.01$, $b_1=0.03551$, $b_2=0.0256$, $b_3=0.0164$, and $b_4=0.025$. The values of ${\sigma }_1$ to ${\sigma }_4$ form an arithmetic sequence starting at $0.21$ with a common difference of $0.01$. The initial shares for selecting strategies were set to $[0.4,0.1,0.15,0.35]$. The numerical simulation results for this four-strategy scenario are shown in Figure 7. The equilibrium point is calculated as $x^{*}=[0.604,0.246,0.148,0.002]$. The simulation result demonstrates that the system also reaches an evolutionarily stable strategy in the case of the four-strategy scenario.

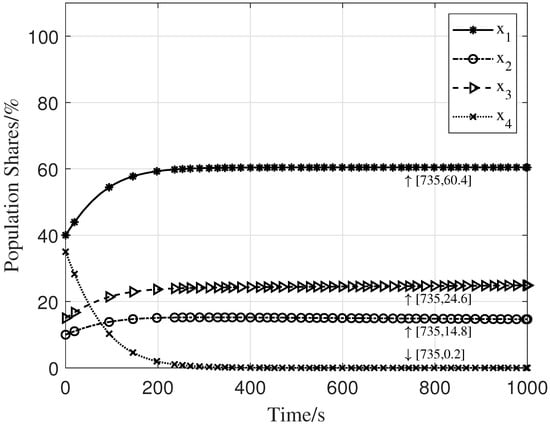
Figure 7. Population shares for four-strategy scenario.

Finally, we extend the stability analysis to an eight-strategy scenario. The parameters are set as $a=0.0009$, $b_1=0.007\times {10}^{-5}$, $b_2=1\times {10}^{-5}$, $b_3=1\times {10}^{-5}$, $b_4=1\times {10}^{-5}$, $b_5=0.002$, $b_6=0.0011$, $b_7=0.003$, and $b_8=0.0031$. The values of ${\sigma }_1$ to ${\sigma }_8$ form an arithmetic sequence starting at $0.05$ with a common difference of $0.001$. The initial shares for selecting strategies are set to $[0.18,0.08,0.11,0.16,0.105,0.1,0.19,0.0705]$. The simulation results for this eight-strategy scenario are shown in Figure 8. The equilibrium point is $x^{*}=[0.6817,0.3105,x_3,\dots ,x_8]$, where $x_3$ to $x_8$ are all $9.75\times {10}^{-4}$. This simulation result demonstrates that the system also reaches an evolutionarily stable strategy in the eight-strategy case.

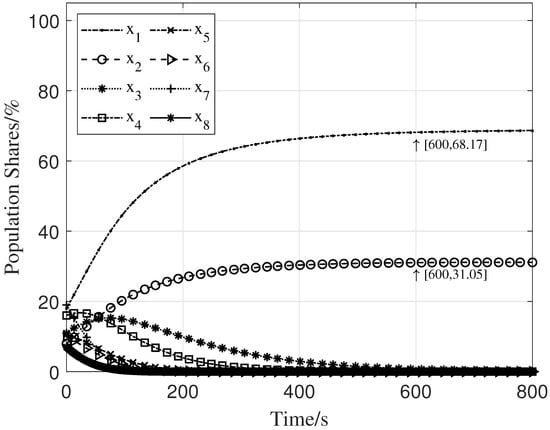
Figure 8. Population shares for eight-strategy scenario.

These results further confirm that the system reaches an evolutionarily stable strategy, even with a larger number of strategies.

6. Conclusions

This study integrates the differential privacy afforded by the Gaussian mechanism into federated learning, employing both global loss functions and privacy leakage metrics to quantify the added noise. This approach helps to create a more realistic modeling scenario. We propose an incentive allocation algorithm tailored to the DPFLM framework. This algorithm is designed to consider the noise levels introduced by each client. It also takes into account the number of iterations. Crucially, our DPFLM, analyzed through the lens of evolutionary game theory, provides a valuable framework to understand and address the critical challenges of privacy and incentive design in federated learning.

Through theoretical analysis, particularly focusing on a two-strategy scenario, we derive detailed analytical results regarding the ESS. This analysis demonstrates how clients, acting strategically, balance their privacy concerns with the desire for incentives and how the system can evolve towards a stable equilibrium of privacy strategies. Extensive simulations across two-, four-, and eight-strategy scenarios further validate our theoretical findings and demonstrate the practical applicability of our approach in diverse settings. Our model supports federated learning by offering a framework to analyze the privacy-utility trade-off, providing insights into the dynamic evolution of client privacy strategies, and informing the design of effective incentive mechanisms that promote both client participation and privacy protection.

For future work, we suggest exploring the incorporation of additional factors, such as propagation delay and dataset size, which could significantly influence the model’s behavior. Furthermore, integrating federated learning with other advanced deep learning techniques could provide valuable insights into the impact of these factors and open up new avenues for research.