Bio-Inspired Traffic Pattern Generation for Multi-AMR Systems

Featured Application

This work addresses the challenge of improving AMR traffic flow in industrial settings by automatically generating optimized movement constraints, offering a scalable solution for modern warehouses and smart factories seeking to improve their intralogistics efficiency.

Abstract

In intralogistics, autonomous mobile robots (AMRs) operate without predefined paths, leading to complex traffic patterns and potential conflicts that impact system efficiency. This paper proposes a bio-inspired optimization method for autonomously generating spatial movement constraints for autonomous mobile robots (AMRs). Unlike traditional multi-agent pathfinding (MAPF) approaches, which focus on temporal coordination, our approach proactively reduces conflicts by adapting a weighted directed grid graph to improve traffic flow. This is achieved through four mechanisms inspired by ant colony systems: (1) a movement reward that decreases the weight of traversed edges, similar to pheromone deposition, (2) a delay penalty that increases edge weights along delayed paths, (3) a collision penalty that increases weights at conflict locations, and (4) an evaporation mechanism that prevents premature convergence to suboptimal solutions. Compared to the existing approaches, the proposed approach addresses the entire intralogistic problem, including plant layout, task distribution, release and dispatching algorithms, and fleet size. Its autonomous movement rule generation and low computational complexity make it well suited for dynamic intralogistic environments. Validated through physics-based simulations in Gazebo across three scenarios, a standard MAPF benchmark, and two industrial environments, the movement constraints generated using the proposed method improved the system throughput by up to 10% compared to unconstrained navigation and up to 4% compared to expert-designed solutions while reducing the need for conflict-resolution interventions.

1. Introduction

Setting up efficient multi-robot systems in industrial environments presents a complex challenge. In industrial settings, this requires careful consideration of numerous interconnected parameters, such as plant layout, task distribution, dispatching, and pathfinding algorithms [1]. These parameters form a web of dependencies where adjustments to one aspect often necessitate changes in others to maintain the overall system efficiency and performance [2,3]. The specific characteristics of each intralogistic problem demand strategically developed movement constraints to prevent collisions, deadlocks, and congestion—common challenges that impact system performance in warehouse and manufacturing environments [4,5].

While various terms are used in the literature to describe movement rules for mobile robots, this paper focuses on movement constraints and spatial rules that influence robot navigation decisions, implemented through costmaps in the form of weighted directed grid graphs. This implementation provides more flexibility than traditional roadmaps (physical or virtual predefined paths) while maintaining structured traffic patterns.

Traditionally, intralogistic automation has relied on Autonomous Guided Vehicles (AGVs), which require predefined paths marked by magnetic tapes or similar guidance systems. These roadmaps must be carefully designed by human experts with a deep understanding of system operations [6]. While effective, this manual design process can be extremely time-consuming, leading to increased research interest in automated approaches that can accelerate the process and improve the solution quality [7,8,9,10].

In recent years, autonomous mobile robots (AMRs) have emerged as a flexible alternative to AGVs, offering the ability to navigate anywhere within the workspace [11]. However, this increased flexibility does not automatically translate to higher efficiency. In narrow corridors or aisles, unrestricted AMR movement can lead to congestion and reduced throughput [12]. Similarly, in high-density storage areas, the lack of structured movement can result in inefficient navigation and increased collision risks [13]. Thus, while AMRs do not require physical guidance infrastructure, they still benefit from structured movement patterns that help to prevent or resolve conflicts efficiently.

To address these challenges while maintaining AMRs’ inherent flexibility, we propose an approach based on ant colony optimization (ACO) for the automated generation of movement constraints. The method utilizes a weighted, directed grid graph where the edge weights are dynamically adjusted according to real-time performance metrics. The approach combines offline costmap generation through simulation-based optimization with subsequent integration into path planning systems. During simulation, the algorithm explores the workspace under various operational conditions, utilizing digital pheromones to represent traversal costs, congestion levels, and collision risks. These pheromone distributions are aggregated into precomputed costmaps that provide a foundation for global path planning. The resulting costmaps can be integrated with established planning algorithms such as A*, effectively guiding robots toward more efficient collective movement patterns.

The optimization algorithm implements four mechanisms derived from ant colony systems. These include movement rewards that reinforce successful paths, delay penalties that modify weights based on task completion times, collision penalties that adjust weights in conflict areas, and an evaporation mechanism that prevents convergence to suboptimal solutions. In contrast to existing approaches that consider only the physical layout, our method incorporates key intralogistic system parameters including fleet size, task distribution patterns, dispatching algorithms, and operational constraints. This systematic approach enables the generation of movement constraints optimized for specific applications, thereby reducing robot conflicts and improving system performance.

To validate and demonstrate the effectiveness of this approach, we present a comprehensive study organized as follows. Section 2 presents the related work, focusing on the movement constraint generation method. Section 3 describes the proposed bio-inspired optimization method, including the discrete-time grid graph simulation and the detailed mechanisms of the optimization algorithm. The implementation of these movement constraints in the ROS2 Nav2 navigation stack is also presented. In Section 4, we validate our approach on three distinct scenarios: a standard multi-agent pathfinding (MAPF) benchmark layout and two real industrial environments using both event-based and physics-based simulations. The solutions are evaluated based on collision reduction and system throughput. Section 5 concludes the paper with the key findings and future research directions.

2. Related Work

Movement constraints (roadmaps and costmaps) that guide path planning algorithms can fundamentally shape traffic patterns and multi-robot system performance. This is achieved by proactively reducing collisions, i.e., adapting the environment’s movement constraints to prevent collisions before they occur (e.g., introducing one-way traffic and roundabouts). This section examines approaches for generating and optimizing such movement constraints, focusing on cost-based coordination methods and bio-inspired optimization strategies.

The optimization of movement strategies for large robot fleets has undergone significant developments in recent years. Kleiner et al. [14] introduced the Adaptive Road Map Optimization (ARMO) approach, which uses linear programming to optimize roadmaps in response to environmental changes and varying transportation demands. While ARMO is computationally efficient and adapts well to dynamic environments, it fails to provide a backup solution when the required throughput exceeds the network capacity. Building on this work, Digani et al. [7] and later Beinschob et al. [8] developed semi-automated approaches for industrial AGV systems that maximize coverage, connectivity, and redundancy through medial axis transformation and intelligent road direction assignment. These methods excel in corridor identification and intersection creation but require significant manual tuning. Stenzel et al. [6,10] also focused on redundancy and robustness measures of roadmaps, proposing an automated roadmap creation approach that is able to utilize as much space as possible. The main disadvantage of redundancy-focused approaches is that they create many unnecessary paths, leading to low road utilization. Additionally, these approaches tend to have high computational costs [9], making them less suitable for constantly changing environments.

Further advances in roadmap generation came through the Optimized Directed Roadmap Graph (ODRM) approach by Henkel and Toussaint [15]. Their method leverages the inherent collision-avoidance properties of directed graphs for point agents, using stochastic gradient descent to optimize both vertex positions and edge directions. This optimization leads to emergent properties such as edges parallel to walls and patterns resembling two-lane streets or roundabouts. A complementary approach by Uttendorf et al. [9] combines mathematical pathfinding with human expertise through fuzzy logic. Their expert system, based on modified Bellman–Ford and A* algorithms, incorporates domain knowledge about path crossings, merging, obstacle avoidance, and directional preferences through a fuzzy inference system. While this approach benefits from human expertise, significant setup effort is required, including formatting inputs and defining constraints, making it economically viable only for complex scenarios. Its solutions are also influenced by the order of connections in the transport matrix, which can introduce biases unless multiple iterations are tested, increasing computational costs. While expert knowledge can be incorporated through fuzzy rules, modifying or extending them requires expertise in fuzzy logic and direct code adjustments, making the approach less accessible to non-experts.

Another promising approach to global path planning and generation of roadmaps is reinforcement learning (RL). Kozjek et al. [16] proposed an RL approach for the precomputation of routes for large AMR fleets, while Kim and Kim [17] combined multi-agent RL with a graph neural network. Recent work by Choi et al. [18] demonstrated RL’s potential for holistic optimization of factory layouts and AGV paths, achieving improvements in throughput, logistics movement distance, and fleet size reduction through a multilayered approach. Several researchers have extended RL approaches to address specific challenges in AGV coordination. Chen et al. [19] combined ACO with deep RL to handle multi-objective optimization and improve robustness against uncertainties, and Zhang et al. [20] developed an improved Q-learning approach for load balancing and traffic flow optimization using macroscopic fundamental diagrams. Furthermore, Hu et al. [21] proposed a multi-agent deep deterministic policy gradient method for conflict-free path planning in container terminals, incorporating both centralized learning and distributed execution to coordinate multiple AGVs. However, these RL approaches face significant challenges in real-world deployment: they require extensive training data and computational resources, scale poorly with increasing fleet sizes, and primarily focus on individual path planning rather than generating system-wide movement rules. When optimizing for multiple objectives like throughput, energy efficiency, and collision avoidance, these methods often require prohibitively long training times and struggle to generalize across different environmental configurations.

Because of their ability to handle complex dynamic environments and lower computational complexity, bio-inspired optimization strategies, such as Particle Swarm Optimization (PSO), Genetic Algorithms (GAs), and ACO, have gained a great deal of interest in robotic navigation. Even though the optimal solution is not guaranteed, these approaches are able to find sufficiently good solutions in a reasonable amount of time [22]. PSO approaches are inspired by the behavior of flocks of birds and have previously shown promise in tackling path planning [23,24,25] and task allocation [26]. GA approaches are based on the principles of natural selection, crossover, and mutation and have also been used for path planning problems for decades [22]. They have been used to generate optimal paths for robots in both static [27] and dynamic environments [28].

For generating efficient movement strategies, ACO algorithms, inspired by the foraging behavior of ants, have shown particular promise through their evolution of weighted path structures. A simple ACO algorithm for traffic flow improvement was demonstrated in [29], where directed weighted edges in a gridmap are iteratively optimized. The basic ACO approach was enhanced through various techniques to improve its performance. Tao et al. [30] combined ACO with fuzzy control to address convergence speed issues, using critical obstacle influence factors and dynamic parameter adjustment to optimize single-robot path planning. Kulatunga et al. [31] applied ACO to simultaneous task allocation and path planning for AGVs, demonstrating its effectiveness in dynamic environments. Garcia et al. [32] and Purian et al. [33] explored pheromone-based weight adaptation to balance path length with other constraints, such as safety and energy efficiency. Similarly, Gan et al. [34] enhanced traditional ACO through time-varying pheromone distribution and optimized update strategies, although primarily focusing on single-robot applications. In traffic management applications, Bedi et al. [35] showed how ACO principles can dynamically adjust path costs to avoid congestion. Jansen and Sturtevant [36] introduced the idea of direction maps, which provide information about previous movements of agents and lead to implicit cooperation during movement and planning. This approach proved to be cheaper and more robust compared to explicit planning approaches.

Despite these advances, several key limitations persist across the existing approaches. Traditional optimization methods like ARMO and expert systems require significant manual tuning and struggle with dynamic environments. While RL approaches show promise for holistic optimization, they face fundamental challenges in sample efficiency and computational scalability when dealing with large fleet sizes and multiple competing objectives. Bio-inspired methods, although computationally efficient, have primarily focused on single-agent path planning rather than generating system-wide movement constraints. Table 1 classifies the reviewed approaches for costmap/roadmap optimization in multi-robot systems, highlighting the key features of each method. The classification shows that, while several approaches address specific aspects of roadmap generation and optimization, few methods address all the desired features simultaneously. In particular, most approaches either focus on AGVs rather than AMRs, neglect weighted graph representations that are critical for traffic balancing, or lack the computational efficiency needed for practical deployment. Furthermore, many methods do not consider the entire system holistically, focusing only on the graph structure without accounting for the task distribution, fleet size, and actual movement patterns. Our proposed approach aims to address these limitations by combining the strengths of bio-inspired optimization with a holistic consideration of the complete AMR-based intralogistic system.

Table 1. Classification of approaches for costmap/roadmap optimization in multi-robot systems.

Category	Subcategory	References	Features
			Robot Type	Conflict Focus	Directed Graph	Weighted Graph	System Holistic	Comp. Efficient
Graph Optimization	Graph-metric	[7,8]	AGV	✓	✓
		[6,10]	AGV	✓
	System-metric	[14]	AGV	✓	✓	✓	✓	✓
		[15]	AMR	✓	✓		✓
		[9]	AGV	✓	✓	✓	✓
RL	Multi-agent	[16]		✓
		[17]		✓		✓
		[18]	AGV	✓
		[20,21]	AGV	✓		✓
Bio-inspired	PSO	[23,24,25,26]						✓
	GA	[27,28]						✓
	ACO	[19]	AGV	✓		✓
		[30,32,33,34]				✓		✓
		[31,35]	AGV			✓		✓
		[36]			✓			✓
		[37]	AGV	✓	✓	✓		✓
	Our approach		AMR	✓	✓	✓	✓	✓

✓: Feature is present.

In our previous work [37], we developed an ACO-inspired algorithm that autonomously generates roadmaps for AGVs by considering the full set of problem characteristics. Combined with Safe Interval Path Planning (SIPP), the method proved to be highly effective: the generated roadmaps achieved up to 15% higher throughput compared to the solutions presented in the literature. This paper significantly upgrades the previously proposed ACO algorithm and extends these concepts to multi-AMR systems, focusing on spatial movement constraints that proactively reduce conflicts without requiring temporal coordination.

3. Methodology

Our approach extends the ACO framework to address the specific challenges of multi-robot transport systems. The core innovation lies in adapting ACO’s pheromone-based pathfinding to handle collision avoidance and delay minimization in dynamic environments. The algorithm continuously modifies edge weights in a grid graph based on robot movements, collisions, and task performance, effectively creating an emergent coordination system for multiple AMRs.

3.1. Environment Representation and Problem Formulation

The environment is represented as a weighted grid graph $\mathcal{G}=(V,E,w)$, where vertices V correspond to traversable locations and directed edges $E\subseteq V\times V$ connect adjacent vertices. The weight function $w:E\to [ϵ,1-ϵ]$ assigns positive real values to edges, representing the cost of moving along that edge, where $ϵ$ is a small positive constant that prevents numerical issues at the boundaries. The weights correspond to the concentration of pheromones on the edges in the ACO framework, influencing the path planning decisions of the AMRs, with lower weights indicating more favorable paths. Tasks are defined as tuples $T=(p_{\mathrm{pickup}},p_{\mathrm{dropoff}},t_{\mathrm{due}})$ specifying a pickup location, a dropoff location, and a due time. New tasks are generated as existing ones are completed and are assigned to the nearest available AMR.

The optimization objective is to determine the optimal weight configuration $w^{*}={\left\{w_e^{*}\right\}}_{e\in E}$ that maximizes system throughput $\mathsf{\Theta }$, defined as the number of tasks completed per unit time:

$$\underset{w}{argmax}\mathsf{\Theta }\left(w\right);w_e\in [ϵ,1-ϵ]\forall e\in E$$

(1)

In this framework, system throughput $\mathsf{\Theta }\left(w\right)$ is a composite metric reflecting the effectiveness of AMR operations under the edge weight configuration w. While individual weights influence the immediate routing decisions of AMRs, their collective configuration shapes the emergent behavior of the entire system. The optimization problem presents a substantial search space due to the continuous nature of the weights and the combinatorial nature of weight configurations. Furthermore, the emergent nature of the optimization metric necessitates an optimization approach capable of refining complex behaviors over time.

Given the complexity of the search space, traditional optimization methods such as gradient descent or linear programming are not well suited for the problem. In contrast, the proposed bio-inspired approach offers several advantages, including scalability in terms of layout size and number of vehicles, adaptability to continuous task execution, and computational efficiency through parallelism.

3.2. Bio-Inspired Coordination Mechanisms

In our framework, each AMR acts as an “ant” executing transport tasks. Paths are planned using a modified A* algorithm that favors straight-line movements by adding small penalties for direction changes. The costmap guiding AMR navigation evolves through the following four bio-inspired mechanisms that continuously update edge weights:

Movement rewards (pheromone deposition): Similar to pheromone trails in natural ant colonies, successful movements reinforce paths by reducing their costs:

$$\Delta w_e=-r_m$$

(2)

where $r_m$ is the movement reward factor. The mechanism encourages the reuse of paths.

Collision handling: When AMRs encounter conflicts, the system applies both temporal delays and spatial penalties:

$$t_{collision}=t_p·n_{conflict}$$

(3)

where $t_p$ is the base penalty duration and $n_{conflict}$ is the number of AMRs involved. In addition, the edges that lead to the collision are penalized to prevent the AMRs from taking these paths in the future:

$$\Delta w_e=p_c·\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{regular}\mathrm{collision}\hfill \\ {\alpha }_s\hfill & \mathrm{if}\mathrm{side}\mathrm{collision}\hfill \end{array}\right.$$

(4)

where $p_c$ is the collision penalty factor and ${\alpha }_s\in [0,1]$ is the side collision multiplier, which can be adjusted to reduce the penalty for side collisions. This reflects that merging into the existing traffic flow is less disruptive than head-on collisions.

Delay feedback: The third mechanism takes into account the delay by reducing costs when the task is completed on time and increasing costs when collisions and resulting delays occur. When a task is completed, all edges in its path are updated based on the delay:

$$\Delta w_e={\alpha }_d·(t_{completion}-t_{due})$$

(5)

where ${\alpha }_d$ is the delay factor and $(t_{completion}-t_{due})$ is the task’s delay. This mechanism reinforces paths without delays and helps to avoid future conflicts by discouraging AMRs from using recently contested paths.

Pheromone evaporation: The evaporation mechanism is designed to prevent the system from over-relying on recently adjusted edge weights that may have been affected by temporary conditions such as transient congestion or short-lived obstacles. By gradually resetting the value of each weight to its initial value $w_{init}$, the system ensures that the influence of past events diminishes over time. The edge weights gradually return to their initial value $w_{init}$ through

$$\Delta w_e=-\lambda (w_e-w_{init})$$

(6)

where $\lambda$ is the evaporation rate. This prevents the system from becoming trapped in suboptimal patterns.

Weight update implementation: The effectiveness of the bio-inspired mechanisms depends critically on how weight modifications are implemented. A key challenge is maintaining edge weights within meaningful bounds ([$ϵ$, 1$-ϵ$]) while ensuring that repeated modifications do not lead to saturation or numerical instability. To address this, we employ a log-ratio transformation for all weight updates:

$$w_{new}={\displaystyle \frac{e^{ln(w_{old}/(1-w_{old}))+\Delta w}}{1+e^{ln(w_{old}/(1-w_{old}))+\Delta w}}}$$

(7)

where $w_{new}$ is the updated edge weight, $w_{old}$ is the current edge weight, and $\Delta w$ represents the weight modification determined by the various mechanisms. This transformation naturally bounds weights between 0 and 1 while preserving relative differences in magnitudes of the modifications. It enables smooth, continuous updates without abrupt changes. All previously described mechanisms (movement rewards, collision penalties, delay feedback, and evaporation) express their modifications as $\Delta w$ values, which are then applied through this transformation. This unified approach to weight updates ensures that the different mechanisms work harmoniously, creating a robust and stable adaptation system that maintains its responsiveness throughout extended operation periods.

Figure 1 illustrates the coordination process with three AMRs executing assigned tasks simultaneously. Figure 1a displays their movement paths, highlighting a collision between two robots near the end of their routes. The subsequent figures demonstrate the sequential application of our bio-inspired mechanisms: initial movements decrease path costs (Figure 1b), collision locations are assigned higher costs (Figure 1c), paths are then reinforced or penalized based on the resulting delays (due to the collisions, shown in Figure 1d), and, finally, evaporation gradually returns costs toward the neutral value of 0.5 (Figure 1e). For clarity, neutral costs are omitted from the figure.

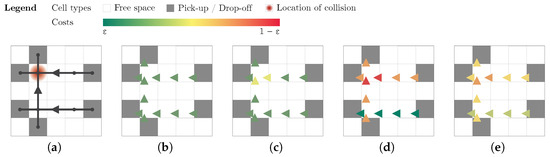
Figure 1. Illustration of the bio-inspired mechanisms. (a) AMR movements and the corresponding weights after applying (b) movement rewards (pheromone deposition), (c) collision handling, (d) delay feedback, and (e) pheromone evaporation.

Algorithm implementation: Building on these weight modification mechanisms, the complete algorithm, presented in Algorithm 1, operates continuously during system runtime. For each AMR, it combines path planning with real-time adaptation of the environment representation. The algorithm processes new tasks as they arrive, plans and executes movements for each AMR, and updates edge weights based on system feedback. This continuous adaptation creates emergent behavior where the system learns to avoid congestion and minimize delays while maintaining efficient paths.

The algorithm maintains a balance between exploitation of known good paths (through movement rewards) and exploration of alternatives (through evaporation). This core ACO-inspired behavior is enhanced with mechanisms specifically designed for multi-robot coordination. Immediate collision avoidance is achieved through dynamic weight penalties that redistribute traffic away from congested areas, while the delay feedback mechanism serves a dual purpose: it both optimizes task execution times and reinforces the avoidance of potentially problematic paths where delays might occur due to congestion or frequent conflicts. Together, these mechanisms create an adaptive system that learns to anticipate and prevent delays by steering AMRs towards efficient conflict-free paths.

Algorithm 1 Bio-inspired cost optimization

1: Initialize grid graph $\mathcal{G}=(V,E,w)$ with neutral weights 2: while simulation running do 3:    Handle new task arrivals and assignments 4:    for each AMR $a\in A$ do 5:          Plan path using modified A* on $\mathcal{G}$ 6:          Move according to plan 7:          if movement successful then 8:                   Apply movement reward to traversed edge 9:          else if collision occurred then 10:              Apply collision penalty 11:              Delay involved AMRs 12:          end if 13:          if task completed then 14:              Apply delay-based penalties/rewards 15:          end if 16:    end for 17:    Apply evaporation to all edge weights 18: end while

3.3. Implementation and Parameters

A discrete-event simulator was developed to evaluate and optimize the proposed approach. The simulator handles all key events, including the arrival of the tasks, assignments, robot movements, and collision detection. Event processing is optimized for performance to enable fast evaluation over many iterations, which facilitates parameter tuning and algorithmic refinements. The simulation tracks the state of all AMRs, active tasks, and edge weights, updating them according to the mechanisms described above when events occur.

The optimization process operates through three sequential phases, each emphasizing different aspects of the movement strategy. All edge weights are bounded between 0 and 1 and represent normalized movement costs that directly influence A* path planning. The weights are initialized at 0.5 to allow both positive preferences (weights below 0.5) and avoidance patterns (weights above 0.5) to develop. To ensure a stable and gradual evolution of the weights, the modification factors ($r_m$, $p_c$, ${\alpha }_s$, ${\alpha }_d$, and $\lambda$) are set several orders of magnitude smaller than the weights themselves, typically around ${10}^{-3}$. This allows the system to accumulate meaningful patterns over many iterations without sudden destabilizing changes.

The parameters for each phase are shown in Table 2.

Table 2. Optimization parameters by phase.

Parameter	Phase 1	Phase 2	Phase 3
Movement reward ($r_m$)	0.001	0	0.002
Collision penalty ($p_c$)	0.007	0.003	0
Side collision factor (${\alpha }_s$)	0.7	0.7	-
Delay factor (${\alpha }_d$)	0	0.002	0
Evaporation rate ($\lambda$)	0.015	0.010	0.020
Duration (iterations)	100,000	50,000	50,000

In Phase 1, the focus is on collision avoidance and the formation of basic traffic patterns with aggressive collision penalties. Phase 2 focuses on optimizing the timing of tasks by introducing delay penalties while reducing collision sensitivity. In the final phase, movement patterns are refined through increased movement rewards and evaporation, allowing for smoother traffic flow. The effectiveness of the optimization depends on the balance between these mechanisms. Strong collision penalties in the early phases establish basic safety patterns, while the emphasis on movement rewards and evaporation in the later phases allows these patterns to adapt to changing conditions. The delay factor helps to maintain efficient task completion without compromising the emergent traffic patterns. An analysis of the optimization parameters as well as stability and convergence is presented next through an illustrative example.

3.4. Illustrative Example

To illustrate the key mechanisms of the optimization process, we present a simplified $4\times 4$ test scenario, shown in Figure 2. The environment contains four AMRs with pickup and dropoff stations positioned in the corners.

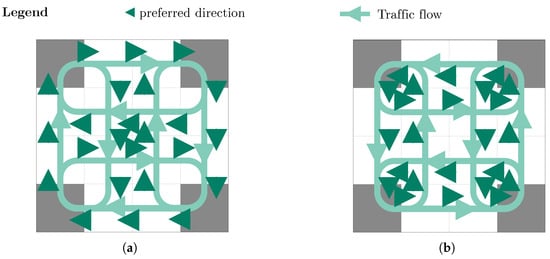
Figure 2. Solutions to the test problem: (a) first solution and (b) second solution.

For each generated task T, the due time $t_{due}$ is set to $d+3$, where d is the minimum path length for the AMR to complete the task. This buffer of 3 time units provides some flexibility in conflict resolution while maintaining pressure on the system to optimize routes. The collision penalty parameter $t_p$ is set to 6 units, which creates a significant incentive for the optimization process to develop conflict-avoiding movement patterns.

The optimization process results in two symmetrical solutions, shown in Figure 2a,b, demonstrating how different movement patterns can evolve under the same optimization parameters due to the stochastic nature of the process. Both solutions generate inner and outer rings, preferring movements in opposite directions.

The temporal evolution of movement patterns during the optimization process can be observed through successive snapshots taken every 20,000 iterations, as shown in Figure 3. For clarity, only costs lower than the neutral value of 0.5 are displayed. During the first 100,000 iterations, an inner roundabout pattern emerges through the combined effect of the movement reward mechanism and the collision penalty. The latter is particularly important in penalizing the initial shortest routes along the outer edges of the environment, where head-on collisions are most likely to occur. This naturally leads to the formation of a central circular pattern that provides conflict-free paths between stations. Between iterations 100,000 and 150,000, the delay penalty becomes the dominant factor, driving the propagation of costs outward from the established inner ring. In this phase, the organized movement pattern is effectively extended to the outer regions of the environment. In the final phase of optimization (iterations 150,000 to 200,000), the established movement patterns are reinforced through continued application of the movement reward mechanism, while the evaporation mechanism evaporates the rest.

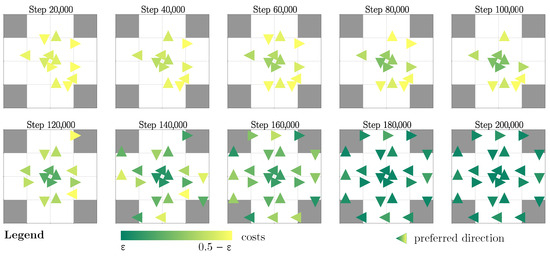
Figure 3. The emergence of the resulting movement patterns.

Further experiments with modified parameters reveal how different conditions influence the emerging movement patterns. When only a single AMR operates in the environment, the optimization generates bidirectional paths that directly connect pickup and dropoff stations, as shown in Figure 4a. Without the need to avoid conflicts, the system naturally converges to these shortest paths between stations. The importance of the collision penalty mechanism becomes evident when it is disabled, as illustrated in Figure 4b, which shows the optimization results using 4 AMRs. In this case, the movement reward mechanism alone leads to the formation of a single-direction outer ring, where the direction (clockwise or counterclockwise) is randomly determined in the early stages of optimization and subsequently reinforced through positive feedback. If, instead, additional tasks are introduced between the top two stations, creating higher traffic demand along the top row, a distinct hybrid pattern emerges (Figure 4c). A bidirectional path is formed between these frequently connected stations, demonstrating the algorithm’s ability to adapt to non-uniform task distribution patterns.

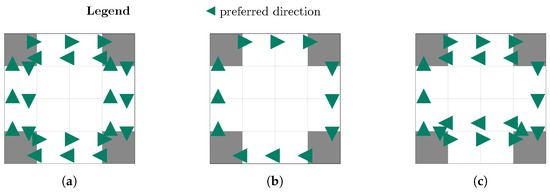
Figure 4. Additional test scenarios demonstrating the impact of different parameters on the emerging movement patterns: (a) solution with a single AMR, (b) solution without collision penalty, and (c) solution with additional tasks.

A sensitivity analysis was performed by varying key parameters, specifically the collision penalty $p_c$ in Phase 1 and the delay factor ${\alpha }_d$ in Phase 2. As illustrated in Figure 5, alternative parameter values can sometimes achieve similar performance levels. However, the default parameter configuration converges more reliably to the optimal solution.

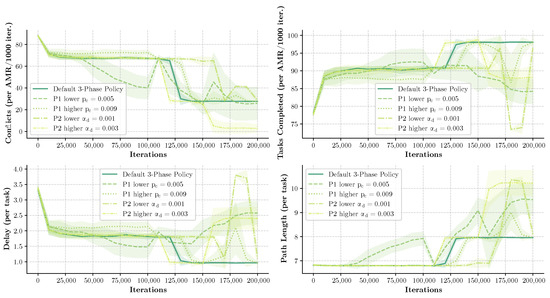
Figure 5. Sensitivity analysis of key parameters by phase.

Figure 6 compares the performance of the default algorithm with a variant where Phase 1 is omitted (i.e., without the initial 100,000 optimization iterations). Without Phase 1, the algorithm primarily relies on Phase 2 to determine the movement directions, followed by Phase 3, which reinforces them. The results show that both system performance (e.g., throughput) and stability, as measured by the standard deviation of performance metrics, decrease significantly without Phase 1. This shows how important the initial phase is for establishing basic collision avoidance strategies before throughput is optimized in subsequent phases.

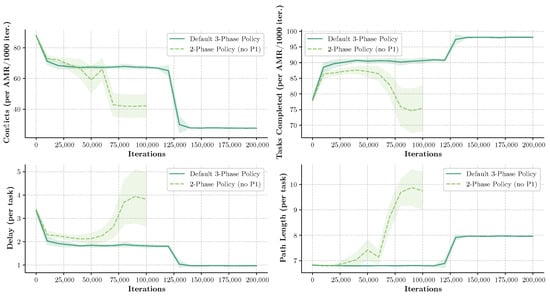
Figure 6. Comparison of algorithm performance when Phase 1 is removed, means and standard deviations.

This simple yet illustrative example demonstrates several important strengths of the proposed optimization approach. From the test scenarios, we can clearly observe how the algorithm consistently generates coherent movement patterns that adapt to different operating conditions and system parameters. The emergence of roundabouts, bidirectional corridors, and hybrid solutions shows that the method can discover suitable movement constraints without requiring explicit programming of these patterns.

The results are particularly notable in their consistency. While the stochastic nature of the process can lead to different specific solutions, as shown in the original two variants, the generated patterns invariably reflect the underlying system requirements. For example, when traffic is concentrated between specific stations, the algorithm reliably develops more direct routes between these points while maintaining efficient circulation patterns for the remaining traffic. Similarly, the degradation to simple bidirectional paths in the single-AMR case and the emergence of unidirectional flow when collision avoidance is not prioritized demonstrate that the optimization process responds logically to changes in system parameters.

3.5. ROS2 Implementation

ROS, recently upgraded to ROS2, is a set of software libraries and tools for the development of robotic applications [38]. One of the key systems within ROS2 is Nav2, a comprehensive modular and easily reconfigurable navigation stack that facilitates the seamless integration of diverse sensors, planners, and controllers. The top-level component of Nav2 is the Behavior Tree Navigator, which activates and tracks the progress of the three task-specific asynchronous servers, i.e., the Recovery Server, the Controller Server, and the Planner Server [39]. Each of these task-specific servers operates as an ROS2 node that provides algorithm plugins in the form of dynamically loaded libraries at runtime.

Global path planning is usually formulated as a graph search problem to find the shortest path from the starting point to the goal destination [40]. Computing the global path for a robot is a task of the planner server, more precisely the global planner. It seeks to find the optimal sequences of valid configurations to determine a route through an environment [41]. The algorithms for global path planning are usually extensions of Dijkstra’s algorithm that try to find the path with minimum cost. Since the A* algorithm was used for generation of bio-inspired grid graphs, we tested our approach by comparing A* that works on non-optimized cost maps to A* that calculates the least cost path based on the obtained optimized costmaps. For this purpose, a new Nav2 global planner plugin was developed. For local planning and conflict resolution in a dynamic environment, the Model Predictive Path Integral (MPPI) controller [42], a successor of Timed Elastic Band (TEB) and pure path tracking MPC controllers, was used.

To simulate the robots and test the developed plugin, Gazebo [43], a 3D rigid body simulator, was used. It provides the necessary interfaces for physics-based simulations in realistic environments. The robot used for the simulations was the Turtlebot3 Waffle, a two-wheeled robot equipped with a 360 Laser Distance Sensor LDS-01. For this robot, a physical model and interface packages are already provided by ROS2. We chose Turtlebots 3 for our Gazebo simulations because they provide a standardized, well-documented platform that captures the essential kinematic and motion planning challenges of differential-drive robots, commonly employed in warehouse logistics. Their widespread use in robotics research also allows for better reproducibility and comparison with other approaches.

4. Case Studies

To validate our approach, we tested the optimization algorithm on three distinct environments: a standard MAPF benchmark layout featuring connected rooms and two real industrial scenarios from manufacturing facilities. For the industrial scenarios, we compared our results with solutions from human experts to evaluate their performance against traditional manual design approaches. These cases were chosen to demonstrate the effectiveness of the method across different scales and levels of complexity, from academic benchmarks to real-world applications.

Given the unique nature of our approach, which focuses on spatial optimization through movement constraints rather than temporal coordination as in traditional MAPF, a direct comparison with the existing benchmarks is challenging. While MAPF benchmarks typically evaluate collision avoidance and temporal efficiency, our method addresses the spatial distribution of robot traffic and the associated costs. Therefore, we evaluated our approach in two ways: first by comparing it to human expert solutions in real industrial scenarios and second by measuring the improvement over standard A* pathfinding without directional constraints. This evaluation methodology enables demonstrating both the practical value in real-world settings and the quantitative benefits of our spatial optimization approach.

The expert solutions were designed by industry practitioners who were provided the layout, number of robots, and task descriptions, including frequencies and pickup/delivery locations. The experts manually drew their preferred directions on paper, which were then translated into low directed costs for comparison with our automated approach. While expert-designed solutions benefit from human intuition and experience, they face several inherent limitations. Experts typically rely on simple rules and visual heuristics, making it difficult to optimize for complex interactions between multiple robots. They tend to favor symmetric patterns that are easier to conceptualize but may not be optimal. Additionally, it is difficult for experts to take into account the specifics of an intralogistic problem such as specific task frequencies between stations.

The evaluation process included both quick assessments and comprehensive validations to ensure the robustness of our optimization algorithm. First, we used the optimization algorithm to generate movement constraints for each environment using the event-based simulator. The solutions were then evaluated within the same environment. We then performed a thorough validation of the optimized movement constraints using physics-based simulations in Gazebo. In this stage, the constraints were implemented through our custom Nav2 global planner plugin, which enabled a detailed examination of the algorithm’s performance in a more realistic simulation environment.

All the optimizations were performed with the same parameter settings as described in Section 3, with the only variation being the number of AMRs, which was adjusted according to the specific requirements of each environment. This consistency helps to demonstrate the robustness of the method across different scenarios while also illustrating how the resulting movement patterns naturally adapt to the unique characteristics of each layout.

4.1. MAPF Benchmark: Rooms’ Layout

The rooms’ layout represents a standard benchmark from the MAPF literature [44], consisting of multiple connected rooms separated by narrow corridors. This layout is particularly challenging due to its bottlenecks and potential for deadlocks in the doorways. The environment contains sixteen rooms connected by narrow corridors, five pickup and five dropoff stations distributed across the rooms, and corridors wide enough for only one AMR at a time. The optimization process for five AMRs resulted in several notable movement patterns, namely one-way traffic flows through certain corridors as shown in Figure 7.

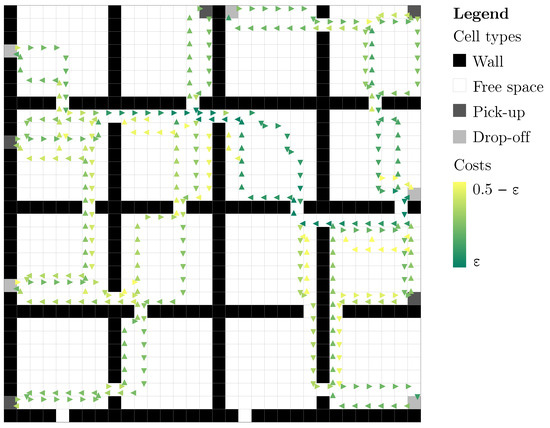
Figure 7. The solution to the rooms’ layout, obtained through the presented algorithm.

4.2. Industrial Scenario A

The first industrial scenario represents a real manufacturing facility designed for two automated forklifts. The layout features input buffers (pickup stations) in the bottom left area and dropoff stations in the top right, with several intermediate buffer locations distributed throughout the space. Figure 8 shows two solutions, one designed by an expert and another generated algorithmically. The most notable difference is in the bottom left area, where the expert chose two-way traffic along the sides of the layout, while the algorithmic solution features two downwards paths and an upwards one through the center. Another notable difference is that the experts could only provide preferred directions for each cell; therefore, the costs are either low (green arrow) or neutral (everywhere else).

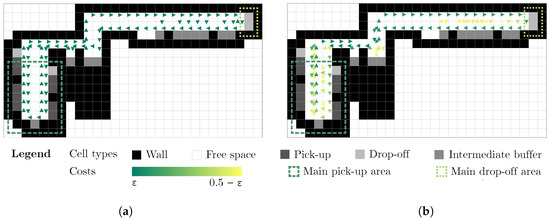
Figure 8. The (a) expert and (b) algorithmic solutions for industrial scenario A. Pickups in light, intermediate buffers in medium, and dropoffs in dark blue.

4.3. Industrial Scenario B

The second industrial scenario depicts another manufacturing facility designed for five automated forklifts. The layout is characterized by a vertical material flow, with pickups at the top, processing units on the right—each with their own pickups and dropoffs—and final dropoffs in the bottom left, along with scattered intermediate buffers. Figure 9 shows the expert and algorithmic solutions. The algorithmic solution features significantly more one-way movement patterns.

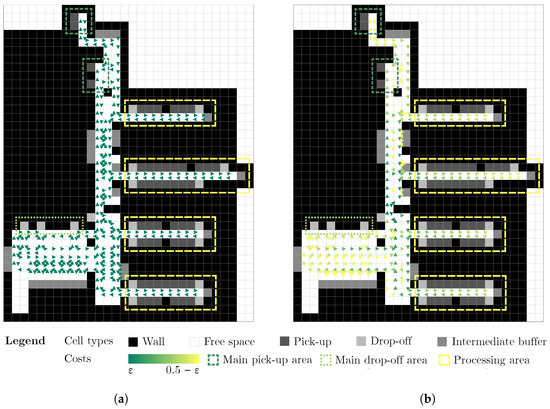
Figure 9. The (a) expert and (b) algorithmic solutions for industrial scenario B.

4.4. Evaluation in the Event-Based Simulator

Although the event-based simulator was primarily used for optimization, its computational efficiency also makes it valuable for rapid evaluation of different movement strategies. We leveraged this capability to perform detailed performance comparisons across multiple metrics. For each scenario, key operational aspects were evaluated through simulations running for 10,000 iterations (ticks of simulated time) with 10 repetitions to ensure statistical significance. The evaluation tracked the number of conflicts (collisions requiring recovery), tasks completed, percentage of tasks completed within their due time, average delay per task, and total path length traveled by all the AMRs.

In the rooms scenario (Table 3), our approach performed significantly better across all the metrics compared to unweighted pathfinding. Conflicts decreased by 41.9% (7.50 vs. 12.90), whereas task completion improved by 10.7% (9.12 vs. 8.24). On-time task completion increased substantially from 63.4% to 85.0%. The average delay per task dropped by 68.9% (2.34 vs. 7.52), with only a minimal increase in path length (90.98 vs. 88.44).

Table 3. Rooms’ results.

Metric	Unweighted	Ours
Conflicts (per AMR/1000 iter.)	12.90 ± 0.48	7.50 ± 0.44
Tasks Completed (per AMR/1000 iter.)	8.24 ± 0.18	9.12 ± 0.20
Tasks in Time (%)	63.39 ± 2.33	84.99 ± 2.38
Delay (per task)	7.52 ± 0.69	2.34 ± 0.35
Path Length (per task)	88.44 ± 0.90	90.98 ± 0.98

In industrial scenario A (Table 4), our method showed statistically significant improvements over both the unweighted and expert approaches. Conflicts were significantly reduced to 3.55 ± 0.25 compared to the unweighted (6.85 ± 0.35, $p<0.05$) and expert (3.85 ± 0.40, $p<0.05$) solutions. The task completion rate was highest at 22.70 ± 0.25, significantly higher than the expert (20.05 ± 0.35) and unweighted (22.05 ± 0.35) solutions. On-time task completion reached 76.6%, with the lowest average delay being 0.47 units. This was achieved with only a modest increase in path length compared to unweighted routing (39.62 vs. 37.84).

Table 4. Scenario A results.

Metric	Unweighted	Expert	Ours
Conflicts (per AMR/1000 iter.)	6.85 ± 0.35	3.85 ± 0.40	3.55 ± 0.25
Tasks Completed (per AMR/1000 iter.)	22.05 ± 0.35	20.05 ± 0.35	22.70 ± 0.25
Tasks in Time (%)	65.40 ± 3.04	73.99 ± 2.06	76.64 ± 2.44
Delay (per task)	1.37 ± 0.14	0.59 ± 0.11	0.47 ± 0.09
Path Length (per task)	37.84 ± 0.34	44.72 ± 0.42	39.62 ± 0.27

The more complex industrial scenario B (Table 5) demonstrated statistically significant improvements across the key metrics. Conflicts decreased significantly by 20.3% compared to the expert solution (14.64 ± 0.40 vs. 18.38 ± 0.96) and by 30.8% compared to unweighted (21.16 ± 0.60). Task completion showed significant improvement to 14.36 ± 0.22 tasks versus the expert (12.98 ± 0.44) and unweighted (12.42 ± 0.28) solutions. On-time delivery reached 85.72%, significantly higher than the expert (77.15%) and unweighted (68.39%) solutions. Average delay was reduced to 2.54 units while maintaining path lengths comparable to the expert solution.

Table 5. Scenario B results.

Metric	Unweighted	Expert	Ours
Conflicts (per AMR/1000 iter.)	21.16 ± 0.60	18.38 ± 0.96	14.64 ± 0.40
Tasks Completed (per AMR/1000 iter.)	12.42 ± 0.28	12.98 ± 0.44	14.36 ± 0.22
Tasks in Time (%)	68.39 ± 2.43	77.15 ± 3.28	85.72 ± 1.34
Delay (per task)	6.17 ± 0.37	4.37 ± 0.55	2.54 ± 0.29
Path Length (per task)	45.69 ± 0.90	47.69 ± 1.37	47.52 ± 0.53

Across all the evaluated scenarios, our bio-inspired optimization approach consistently demonstrated substantial reductions in conflicts and delays while enhancing task completion rates and punctuality. As shown in Figure 10, the system achieves a steady improvement in punctuality—a critical metric for industrial applications—throughout the 200,000 iteration optimization process. The minimal increases in path lengths indicate that the algorithm effectively balances the trade-offs between minimizing traversal distances and enhancing overall system performance.

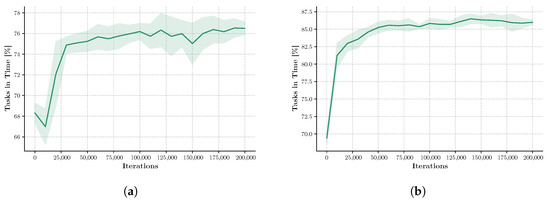
Figure 10. Analysis of punctuality for industrial scenarios: (a) scenario A and (b) scenario B.

4.5. Gazebo Simulations

We validated our approach using physics-based simulations in Gazebo. The simulations were executed in the simulator (Figure 11a,b), using the environments built based on the three example maps (obstacles represented as walls), and visualized using RViz (Figure 11c).

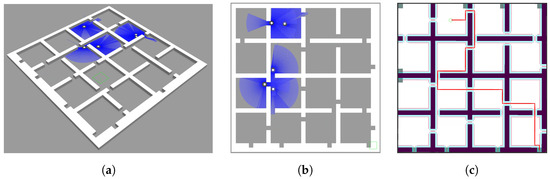
Figure 11. Simulation in ROS2/Gazebo: (a) 3D view of the rooms’ layout, (b) top-down view, and (c) RViZ view.

The duration of the simulation was 1 h of simulated time. We compared the throughput of A* that works on non-optimized costmaps with A* that works on costmaps generated by the proposed bio-inspired algorithm. This comparison is motivated by several factors. Firstly, A* is widely regarded as a benchmark algorithm in path planning due to its efficiency and optimality guarantees. Secondly, since our bio-inspired method uses A* as its underlying pathfinding algorithm, A* serves as the most appropriate baseline for comparison. This allows us to isolate and evaluate the specific improvements introduced by our bio-inspired weight optimization. Additionally, A* is widely used in many robotic navigation systems, including the ROS2 Nav2 stack, making it a practical and relevant comparison point for real-world applications.

4.6. Results

We evaluated our bio-inspired movement constraints against unweighted map and expert-designed solutions by measuring the total number of completed tasks and distinguishing between tasks completed with and without recovery actions due to conflicts such as near-collisions during one-hour simulations. The results are shown in Figure 12.

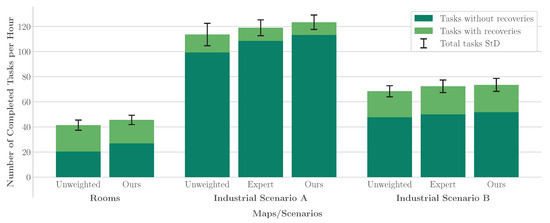
Figure 12. Performance comparison across scenarios. Bars show tasks completed with and without recovery actions; whiskers indicate the standard deviation of total task completions.

In the rooms scenario, our algorithmic solution improved the efficiency as fewer recovery actions were needed (18.7 ± 2.21 vs. 20.9 ± 2.02 for the unweighted map) while more tasks were completed overall (45.6 ± 3.72 vs. 41.4 ± 4.03). The higher proportion of tasks without recovery actions (26.9 ± 4.12 vs. 20.5 ± 4.50) indicates more effective traffic management.

For industrial scenario A, our approach showed a significant improvement, with more tasks completed (123.4 ± 5.72) than both the unweighted map (113.6 ± 8.95) and expert solutions (119.0 ± 6.32). Notably, fewer recovery interventions were required (10.1 ± 2.96 vs. 14.2 ± 2.94 for the unweighted map and 10.4 ± 2.50 for the expert solution), indicating more efficient movement patterns.

In the more complex industrial scenario B, which involves five AMRs, our solution achieved higher throughput (73.5 ± 5.15 tasks) compared to the unweighted map (68.4 ± 4.45) and expert solutions (72.4 ± 4.99). The recovery interventions were comparable across all the approaches (21.7 ± 2.95 for our algorithmic solution, 20.7 ± 2.95 for the unweighted map, and 22.3 ± 2.50 for the expert solution), suggesting that some baseline level of conflict resolution may be unavoidable in complex environments.

These results show that our bio-inspired constraints consistently improve system performance, particularly in scenarios with clear traffic patterns. The method effectively reduces the number of recovery actions while maintaining or improving throughput across different environmental complexities.

5. Conclusions

This study presents a bio-inspired approach for the autonomous generation of movement constraints in multi-AMR systems, demonstrating how an optimization mechanism based on four basic principles—movement rewards, collision penalties, delay feedback, and evaporation—can effectively improve system performance. It was shown that spatial constraints can proactively reduce the number of conflict situations without temporal coordination.

The efficiency of the proposed method was validated through both event-based and physics-based simulations. The solutions obtained with our method consistently outperformed both unconstrained navigation and expert-designed solutions. Significant improvements in system performance were observed in several test scenarios, including standard MAPF benchmarks and real industrial environments.

Compared to other existing approaches, our method offers several advantages. First, the method integrates complete system characteristics, including layout, fleet size, task distribution, and dispatching algorithms, into the optimization process and tailors the solution to the specific intralogistics problem. The existing approaches usually only take into account the layout. Second, the method can successfully handle complex spatial constraints (e.g., narrow corridors), which reduces the need for recovery actions while ensuring high throughput. Third, solution generation is very fast and typically requires only a few minutes, even for complex layouts. If the system parameters change (increased demand, different material flow, fleet size, etc.), the movement constraints can be adapted quickly and without manual redesign.

The adaptability and low computational complexity of the proposed approach provide flexibility that traditional design approaches lack, making it particularly practical for dynamic real-world applications. The successful integration with the ROS2 Nav2 stack through a custom global planner plugin also demonstrates the practical applicability of the approach in standard robotics frameworks.

However, there are some limitations of the proposed method that should be considered. We have shown that conflict situations with other vehicles can be proactively reduced through spatial constraints, but the performance advantages diminish in extremely dense traffic situations, where temporal coordination becomes essential. For real-world deployment, our approach could be integrated with state-of-the-art scheduling algorithms to jointly address spatial and temporal coordination. This can lead to additional improvements in system efficiency.

Another limitation of the proposed method is that it assumes static obstacles, while the resolution of conflicts with dynamic obstacles is left to the local planner. It also does not incorporate real-time adaptability mechanisms to adjust movement constraints dynamically based on observed traffic fluctuations.

To enhance real-world applicability, several future directions should be explored. First, the optimization algorithm should be extended to incorporate dynamic parameter adjustment, enabling more effective adaptation to varying traffic densities and patterns. Second, integrating reinforcement learning techniques could further enhance the adaptability of movement constraints in response to real-time operational conditions. A hybrid approach combining bio-inspired heuristics with learning-based methods may offer a robust solution for balancing proactive spatial constraint generation with real-time adaptability. Finally, additional validation in real industrial settings would help to verify the effectiveness of the method under actual operating conditions. This includes evaluating how the approach scales with larger fleets, interacts with dynamic obstacles such as human workers, and integrates with industrial fleet management systems. Addressing these aspects would help to bridge the gap between theoretical performance gains and real-world deployment.