Overview of Target Normal Sheath Acceleration Experiments and Diagnostics at SPARC_LAB

Abstract

The interaction of an ultra-short, high-power laser pulse with a solid target, in the so-called Target Normal Sheath Acceleration (TNSA) configuration, produces particles in the MeV range. Fast electrons can escape from the target after the interaction, inducing electrostatic fields on the order of TV/m close to the target surface. These fields accelerate MeV protons and heavy ions at the rear of the target, allowing them to escape. The complete process is difficult to probe, as it occurs on the sub-ps timescale. At the INFN-LNF SPARC_LAB test facility, single-shot diagnostics such as the Electro-Optic Sampling (EOS) are being developed and tested for time-resolved direct measurements of the produced electrons and associated longitudinal electric fields. Electrons are the core of the process, and their properties determine the following production of positive charge particles and electromagnetic radiation. Different target geometries and materials are being investigated to analyze the enhancement of fast electron emission and the correlation with positive charge production. Simultaneous observations of electron and proton beams have been performed using two diagnostic lines, the EOS for electrons and a time-of-flight (TOF) detector for protons. This work provides an overview of the previous experiments performed at SPARC_LAB dedicated to the TNSA characterization.

1. Introduction

Currently, high-power, ultra-short laser systems—reaching powers up to the multi-petawatt (PW) [1] level—are available via Chirped Pulse Amplification (CPA) technology [2]. These systems are employed in a wide range of experimental fields, including materials science, laboratory astrophysics [3], and particle acceleration [4,5,6,7]. In particular, the interaction between an ultra-short (fs), ultra-intense ($I>{10}^{18}$ W/cm²) laser pulses [8,9], and a solid target has enabled the development of electron, proton, and ion sources via the Target Normal Sheath Acceleration (TNSA) mechanism. The ionic particle beams produced exhibit remarkable characteristics that make them ideal for several applications [10,11], such as hadron therapy in cancer treatment [12,13]. The proton and ion beams generated contain a high number of particles and are accelerated to energies in the multi-MeV range [14,15]. They have ps-scale durations, low emittance, and are laminar [7]; their production is closely linked to the electrons accelerated during the initial stages of the TNSA.

The process involves the interaction of the laser pulse with a solid target, such as a thin foil (ranging from a few to several hundreds µm). The laser pulse can successfully transfer energy to relativistic electrons, primarily through ponderomotive mechanisms, such as the JxB process [16]. These so-called “hot” electrons are generated at the front surface and propagate into the target bulk, attempting to escape from the rear side into the vacuum. Among them, the most energetic manage to escape (fast electrons), leaving behind an unbalanced positive charge on the target, which generates a strong quasi-static electric potential (TV/m), responsible for ionization of atoms at the target back side [7]. This leads to the ion acceleration to energies on the order of tens of MeV [17,18,19]. The electric field also confines the remaining part of the electronic cloud to the target rear surface at a distance of the order of the Debye length [20].

The mechanism is complex and involves the generation of electromagnetic pulses (EMPs) [21]. The spectrum of this radiation depends on the laser intensity [22] and consists of two components. The first one is in the GHz domain [23,24,25] and it originates from the neutralization of return currents flowing within the target to balance the induced positive charge. The second component is an ultra-short (tens of ps) THz pulse [26,27], which is linked to the current associated with fast electrons. These phenomena occur on extremely short timescales, making experimental investigation particularly challenging.

The temporal evolution of electrons and electromagnetic fields generated during the interaction can be directly investigated using Electro-Optic Sampling (EOS) diagnostics. This was demonstrated at the SPARC_LAB test facility of INFN-LNF [28], where, for the first time in this context, single-shot measurements with femtosecond resolution were performed on both fast electrons and electromagnetic pulses produced by the interaction of the 200 TW FLAME laser system [29] with a solid target. This diagnostic enabled a detailed investigation of the relationship between the target geometry and key properties of the generated electron bunches, such as charge, energy, and duration.

For proton beam characterization, a diamond-based time-of-flight (TOF) detector was implemented [30]. All measurements were also analyzed as a function of the available laser beam parameters. In this review, we provide the experimental results carried out at SPARC_LAB regarding the fast electron characterization, the electron–proton beam correlation, and the EMPs detection.

2. Experimental Setup

The experiments were performed at the SPARC_LAB test facility with the FLAME laser. The system is a 200 TW Ti–Sapphire laser-based on Chirped Pulse Amplification (CPA) technology, delivering up to 6 J energy and 30 fs at 800 nm (at the final cryo-amplifier output). The beam is transported to the interaction chamber after temporal compression and optimized using two acousto-optic modulators (Fastlite MAZZLER and DAZZLER), with a total energy transport efficiency of 70%. This system section operates in a high-vacuum environment (∼${10}^{-6}$ mbar) to prevent self-focusing effects and to minimize contamination during the experiments. The high temporal contrast ratio is ${10}^{-6}$ at ps-level and <${10}^{-9}$ at ns-scale.

The setup in the experimental area is shown in Figure 1; the laser beam is focused on the target to reach high interaction intensities using a gold-coated, 15-degree Off-Axis Parabolic (OAP) mirror (f/10) with a focal length of 1 m. In these experiments, the laser spot is optimized by a Shack–Hartmann wavefront sensor and by a deformable mirror to remove aberrations after the CPA chain and to have the maximum energy in the laser focal spot. The latter had a diameter of 25 µm Full Width Half Maximum (FWHM).

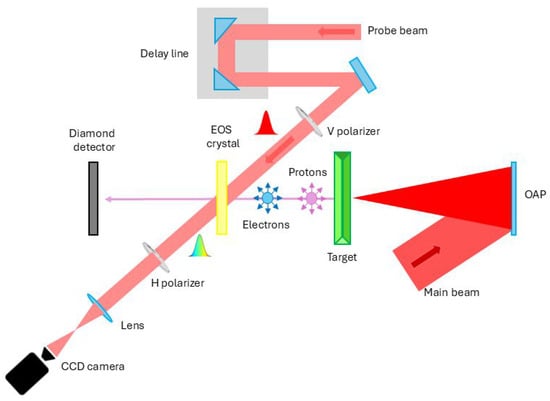
Figure 1. Sketch of the experimental setup. The FLAME laser is focused by a parabolic mirror (OAP) on the solid target; then an electro-optic sampling crystal, coupled with a probe laser beam, is used for electron and EMP diagnostics and to temporally scan the interaction by the delay line. The signal is detected by a CCD camera. A time-of-flight (TOF) diamond detector has been installed for proton diagnostics.

Different solid targets were tested, varying thickness, geometry, and materials to investigate their effect on the energy gain of the accelerated ions. The main configuration employed a stainless steel sharp target such as a commercial razor blade [31]. Subsequently, planar and tipped targets were tested, including the aluminum foil and a needle-shaped tip [32]. A sapphire target was also tested [33]; it was 400 µm thick, uncoated, and had a resistivity ranging from ${10}^{16}\Omega ·$ cm at $25°$ to ${10}^6\Omega ·$ cm at $100°$.

In the laser system, the probe beam is split from the beamline after the second amplifier to operate at low energy (some tens of mJ) with a temporal compression down to 35–40 fs, in addition to ensuring a jitter-free synchronization. It has a transverse spot size of 6 mm (FWHM), and it follows a specific transport line to the experimental area.

The two beams are synchronized in the interaction chamber via an optical delay line by means of an $\alpha$-cut BBO crystal. The latter is installed on a holder together with the ZnTe crystal, 1 mm above the target. The synchronization is achieved by looking for the second harmonic generation (SHG) signal produced in the crystal. The light emitted from the SHG determines the overlap time, which is our reference time. After that, the delay line is adjusted to synchronize the probe beam with respect to the emitted electrons or electromagnetic pulses to generate a detectable signal on the CCD camera. The diagnostics of the interaction chamber (Figure 1) are described in detail in the following section.

3. Diagnostics

3.1. EOS Detector

The Electro-Optic Sampling is one of the diagnostic techniques implemented during the experimental campaigns [31,32,33,34,35,36,37] on laser–solid target interactions at SPARC_LAB. It is a single-shot diagnostic that employs a $10\times 10$ mm² ZnTe 500 µm-thick crystal, cut along the (110)-plane, to obtain time-resolved measurements of the properties of fast electrons produced during the interaction, enabling the investigation of the temporal evolution of the TNSA process. The EOS resolution is determined by the probe beam duration, the type of electro-optic (EO) crystal, and its thickness; for our experimental conditions, the system achieves a temporal resolution on the order of 100 fs.

The setup is shown in Figure 2: the probe beam from the FLAME laser system impinges on the crystal at an angle ${\theta }_i$ of $28°$, with a spot diameter of approximately 6 mm (FWHM). Thanks to the spatial encoding technique [38], the temporal profile of the electrons emitted from the target is mapped onto the transverse profile of the laser beam. The equation that relates the longitudinal coordinate of the bunch $t_i$ to the transverse coordinate of the laser $x_i$ is $t_i=x_{i}sin{\theta }_i/c$, with c being the speed of light. A temporal window of about 10 ps was obtained under these conditions.

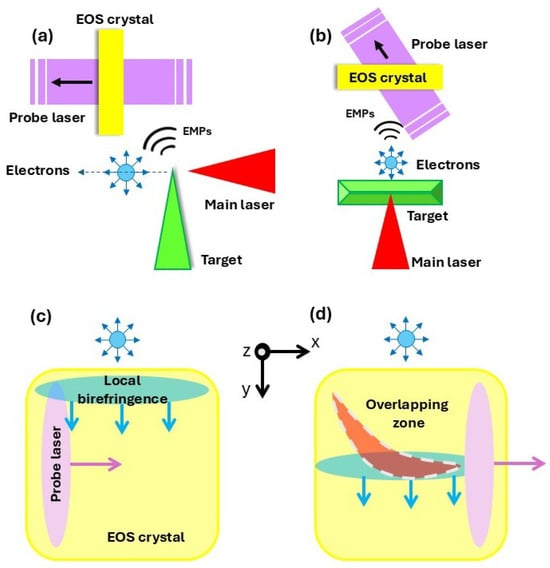
Figure 2. EOS experimental setup: Side and top view (a,b) for the electron and EMPs detection. The bunch travel normally and below the crystal surface, while the probe laser crosses the crystal with an incident angle. (c,d) Working principle of the diagnostics: the electron Coulomb field or the electromagnetic pulses induce a birefringence (blue region) in the crystal, which shifts downwards while the electric field penetrates in the crystal. The laser beam (pink region) crosses the sample and its polarization is rotated. Picture (d) shows the signal (red region) created by the overlap; it is flipped in both directions due to the imaging lens used in the setup.

The electric field generated by the electron bunch $E_b\left(t\right)$ induces a localized birefringence in the crystal, which in turn induces a modulation in the polarization of the probe beam with a relative phase shift of

$$\Gamma \left(t\right)={\displaystyle \frac{\pi n_0^{3}d}{{\lambda }_L}}{r}_{41}{E}_b\left(t\right)\sqrt{1+3co{s}^2\alpha }$$

(1)

where d is the crystal thickness, $n_0$ is the optical refractive index calculated in ${\lambda }_L$ (laser central wavelength), $r_{41}$ is the electro-optic coefficient, and $\alpha$ is the angle between $E_b$ and the crystallographic X-axis of the crystal. A polarizer, placed downstream of the crystal and oriented orthogonally to the initial polarization of the probe, converts this polarization modulation into intensity variation that can be easily detected by a CCD (dynamic range 68 dB, 12 MHz, full frame). Therefore, the intensity signal output detected by the CCD is $I_{out}=I_{laser}si{n}^2(\Gamma /2)$ where $I_{laser}$ is the probe laser intensity. In the absence of EO-induced phase retardation, no light is transmitted through the analyzer. A temporal calibration of the CCD pixels was possible due to the spatial encoding setup: $\Delta t_{pixel}=(\Delta x_{pixel}/c)·sin{\theta }_i\approx$ 15 fs where $\Delta x_{pixel}$ is the pixel size.

This approach allows for a direct mapping of the electric field generated by the electrons, which is proportional to the bunch charge. The intensity of the resulting signal can therefore be used to estimate the charge. Additionally, the signal width corresponds to the temporal duration of the electron bunch, also providing a temporal length direct measurement.

Moreover, the EOS diagnostics can also be employed as a Time-Of-Flight (TOF) [38] detector by measuring the temporal delay of the signal with respect to a known reference. Then, from the particle time of flight ${\Delta }_{t_{TOF}}$, the particle velocity can be determined $v=d/{\Delta }_{t_{TOF}}$ and consequently so can its energy $E=m_e{c}^2/(\sqrt{1-{(v/c)}^2)}$, with $m_e{c}^2$, enabling a time-resolved energy measurement. This provides a distinct advantage over conventional, time-integrated diagnostics such as magnetic spectrometers.

This diagnostic was also used to detect the electromagnetic pulses generated during the laser–solid target interaction. By varying the delay of the probe beam with respect to the emission of the pulses, it is possible to reconstruct their temporal evolution. Also in this case, the local birefringence of the crystal changes as the electromagnetic field passes through. Section 4.2 provides the details and the related analysis.

3.2. Time-of-Flight Detector

The Time-Of-Flight diamond detector is another diagnostic tool used in experimental campaigns for detecting the accelerated ion and proton beams produced during the TNSA process [39,40]. This device, whose structure is shown in Figure 3, has a surface and interdigital geometry with multiple electrodes in the active area. These electrodes are spaced by 20 µm, allowing us to achieve a temporal resolution of 800 ps, which is higher than that of standard commercial detectors. In addition to excellent temporal resolution, it provides a high energy resolution up to 3% for MeV-range ion bunches at 105 cm between the detector and the source. The detector thickness determines the maximum energy measurable. Diamond detectors are insensitive to visible light but can detect particles with energies above the band gap threshold.

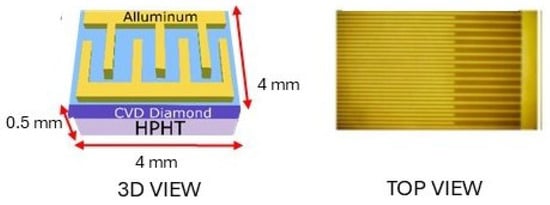
Figure 3. Schematic layout of the TOF detector geometry. The layer structure in 3D view and the surface Al interdigitated electrodes on the top view. Active area of the detector was $2$ mm², the metal fingers were processed to 20 µm in width, and the electrodes are spaced by 20 µm.

The detector is biased at −150 V and equipped with a custom-designed high-frequency bias-tee to separate the direct current (DC) signal from the alternating current (AC) signal, the latter resulting from electron–hole pairs generated by the energy deposited in the diamond by charged particles. The detector is susceptible to interference from EMPs, which act as a noise source and have remarkable effects on the diagnostics electronical components. Several precautions were adopted to minimize the EMP coupling with the detector and to have a high signal-to-noise ratio. For example, in the adopted setup, the diamond detector was mounted at the end of a 65-cm-long pipe (connected to the interaction chamber) with an internal radius of 20 mm, which acts as a cylindrical waveguide with a cutoff frequency of 4.3 GHz. A detailed study on the properties, implementation, and optimization of this diamond detector is thoroughly described in the reference [41].

4. Experimental Results

4.1. Fast Electrons

The first experimental campaigns conducted at FLAME led to the direct and time-resolved detection of fast electrons [31]. These measurements were performed with sub-picoseconds temporal resolution using EOS diagnostics, which allowed precise characterization of the charge, temporal duration, and mean energy.

In the first experiment, the target was a stainless steel wedged razor blade (1-µm-thick) on which the main laser beam was focused with a maximum energy of 2 J in the interaction chamber. Figure 4 shows a typical single-shot EOS image acquired by the CCD (a), displaying the signal induced by the fast electron bunch. The signal exhibits a curved and non-uniform structure; the first effect is caused by the superposition direction of the signal on the crystal, while the latter arises from the non-uniform transverse profile of the probe beam and surface inhomogeneities on the ZnTe crystal. The EOS signal intensity is proportional to the bunch charge, which was ∼2 nC. The temporal profile was retrieved by averaging a series of line-outs taken along the time axis (white arrows in Figure 4a) and the bunch duration is 310 fs (FWHM), as shown in Figure 4b.

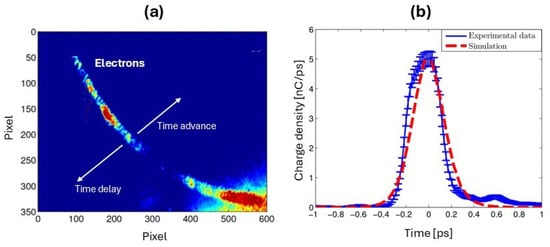
Figure 4. EOS signal of fast electrons (a) and corresponding temporal profile of the electron bunch in the snapshot (b). A series of line-outs were performed along the time direction (white arrows), and the profile is obtained from the average of these line-outs. The error bars are the standard deviation of the average; the experimental results (blue points) are compared with a numerical simulation in MATLAB (Version R2015b, The MathWorks, Inc.) environment of the temporal profile (red dashed line).

After this analysis, different target geometries were tested to investigate how the shape of the irradiated surface affects fast electron emission. Previous studies [42,43] have shown that structured targets can lead to increased final ion energies, mainly due to enhanced electrostatic field. In our experiment, we aimed to verify whether increasing the curvature of the surface irradiated by the laser results in a higher number of emitted electrons.

4.1.1. Different Target Shapes

Snapshots with the EOS signal for different target shapes are shown in Figure 5.

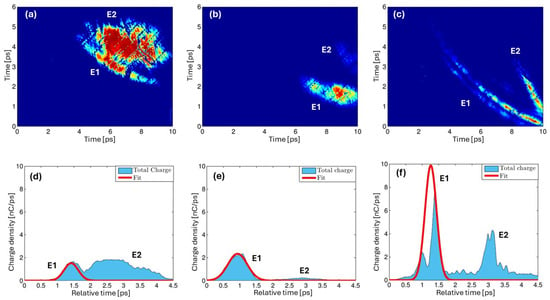
Figure 5. Fast electrons bunches with different target geometries: (a) planar, (b) wedged, and (c) tipped targets. The charges of the bunches are 1.2 nC (E1) and 3 nC (E2) for (d); 2 nC (E1) and 0.3 nC (E2) for (e), and 7 nC (E1) and 3 nC (E2) for (f). Longitudinal charge profiles of the snapshots fitted by a Gaussian function (red line) are shown in the bottom plots [32].

Two distinct electron bunches are visible in Figure 5a for the interaction of 2 J of laser beam with a planar target, a 10 µm-thick aluminum foil. The first bunch (E1) carries a charge of approximately 1.2 nC with a mean energy of 7 MeV, while the second bunch (E2), significantly broader, has a charge of about 3 nC and a lower energy of 1 MeV. The blue regions represent the total charge of the EOS snapshots, while the B1 charges are extrapolated by the Gaussian envelopes. The mean energy of these electrons was determined by measuring their time of flight to the detector, and the temporal length was retrieved directly from the EOS trace, together with the bunch charge and the electric field. The corresponding longitudinal charge profile of this snapshot is shown in Figure 5d where the relative time between the two bunches was measured to be 1.5 ps.

The wedged target was a commercial razor blade and data are shown in Figure 5b; the first electron bunch (E1) exhibits increased charge, around 2 nC, while maintaining a similar energy of 7 MeV. The second bunch (E2) is 0.3 nC with a delay of 2 ps to the first.

Finally, Figure 5c presents the results obtained using a needle tip target. In this configuration, the first bunch (E1) reaches a higher energy of 12 MeV and a significant number of particles of 7 nC, which induce a strong birefringence in the crystal. Here too, a second electron bunch (E2) is clearly visible, carrying an estimated charge of about 3 nC. Numerical simulations of EOS output in MATLAB environment are well described and reported in [32].

4.1.2. Different Target Materials

Additional experiments were conducted to characterize fast electron emission from targets with varying material composition and thickness, consistently using the same diagnostic techniques [33,36]. This approach enabled the acquisition of experimental evidence supporting scaling laws that describe the phenomenon as a function of the laser energy incident on the target (from 0.4 J to 4 J) and the target material.

The materials under comparison were stainless steel (wedged metallic target) and sapphire (dielectric). The two targets have different thicknesses; the laser is focused on the tip of the first one, which is 5-µm-thick, while in the second case, the target has a thickness of 400 µm. Different materials strongly affects charge confinement and hot-electron transport. Sapphire exhibits extremely high resistivity under ambient conditions, which prevents lateral charge dissipation on ultrafast timescales and leads to a stronger and longer-lived sheath field that inhibits electron refluxing. In contrast, the metallic target rapidly neutralizes surface charge due to its high conductivity, resulting in a weaker sheath field and enhanced hot-electron refluxing [44]. This difference obviously affects the process and the parameters of the accelerated electrons. Below, the results of a scan of the metallic target thickness are also reported in detail, showing how the charge, the duration of the electron bunch, and the electric field vary as function of the thickness.The charge $Q_{fast}$ [nC] and the peak electric field ${\Sigma }_{fast}$ [MV/m] of the hot electron bunches were retrieved from the EOS signal’s amplitude and spatial extent. The Figure 6 shows two plots (a) for the wedged-metallic target and (b) for the dielectric target, displaying the results of the charge values and electric field peak as a function of the laser energy delivered to the target (measured r.m.s. value).

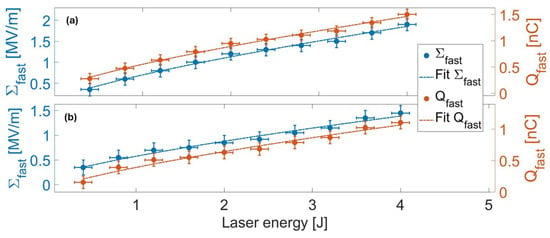
Figure 6. Plots of the fast electrons charge (red points) and of the peak electric field (blue points) as function of the laser energy. (a) Experimental data for the wedged-metallic target and (b) for the dielectric target [33].

Each point is the average value over 10 shots, with vertical error bars corresponding to the standard deviation. As shown, both parameters exhibit a positive correlation with laser energy, consistent with the expectation that higher intensities enhance charge extraction and thus increase the resulting electric field.The experimental data were fitted by power functions; the results for the metallic target are

$$\begin{array}{cc}\hfill Q_{fast,M}=(0.50\pm 0.03)E_L^{(0.746\pm 0.02)}+(0.06\pm 0.04)& \hfill \\ \hfill {\Sigma }_{fast,M}=(0.63\pm 0.04)E_L^{(0.746\pm 0.02)}+(0.07\pm 0.04)\end{array}$$

(2)

and for the dielectric target are

$$\begin{array}{cc}\hfill Q_{fast,D}=(0.37\pm 0.04)E_L^{0.749\pm 0.02)}+(0.03\pm 0.02)& \hfill \\ \hfill {\Sigma }_{fast,D}=(0.44\pm 0.04)E_L^{(0.748\pm 0.02)}+(0.11\pm 0.04).\end{array}$$

(3)

An analytic scaling law, derived in [33] and based on theoretical models [45,46,47,48,49], was used to support the experimental results: $Q_{fast},{\Sigma }_{fast}\propto E^{3/4}$ from a minimum energy value of 0.4 J.

We also retrieved the temporal duration of these fast electron bunches as a function of the laser energy, as shown in Figure 7, and fitted the data with a power function

$$\begin{array}{cc}\hfill {\tau }_{fast,M}=(-1.3\pm 0.4)E_L^{(0.7\pm 0.1)}+(3.9\pm 0.4)& \hfill \\ \hfill {\tau }_{fast,D}=(-0.5\pm 0.15)E_L^{(1\pm 0.15)}+(3.9\pm 0.3)\end{array}$$

(4)

respectively, for the metallic and dielectric target.

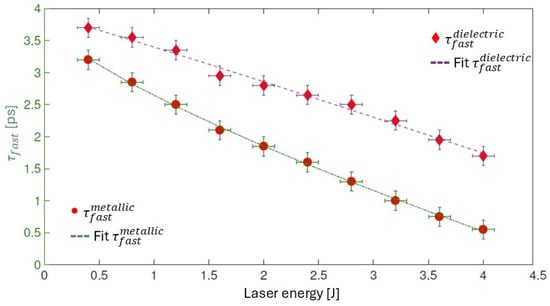
Figure 7. Plots of the fast electrons temporal length as a function of the laser energy for the metallic target (circles and green dashed line) and for the dielectric target (diamonds and purple dashed line) [33].

The scaling laws describing the bunch temporal duration are quite different: with the metallic target, the temporal length decreases more significantly as the laser energy increases compared to the dielectric target. In general, at lower laser energy, the electrons are less relativistic, and the temporal duration increases due to the velocity spread of the bunch. Additionally, the barrier potential acts as a velocity filter. Conversely, at higher laser energies, relativistic electrons are emitted with a smaller velocity spread, resulting in a temporally shorter bunch, and the strong potential continues to act as a high-velocity pass filter.

Thereafter, the electron parameters were also measured changing the thickness of the metallic target; its geometry is shown in Figure 8a, where the wedge angle is $\theta \sim (17°\pm 3°)$ and the tip has a thickness of 5 µm.

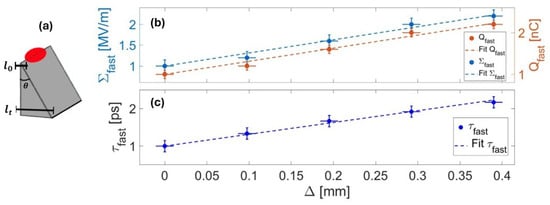
Figure 8. Experimental data for the thickness scan.(a) Sketch of the target geometry. (b) (Blue circles) Peak electric field and (red circles) charge of the accelerated electrons as a function of the increase $\Delta$ in target thickness. (c) (Blue circles) Temporal duration of the electron bunches as a function of the increase $\Delta$ in target thickness. The thickness error bars are related to the slit resolution [33].

The laser was focused at the maximum energy (∼4 J) at different heights on the target, thereby changing the thickness. Figure 8b shows the experimental data for the charge and the electric field of the fast electrons. The x-axis is defined as $\Delta =l_t-l_0$, i.e., the increase in thickness relative to the tip $l_0$, where $\Delta =0$. We observed that, as the layer thickness increases, the number of extracted electrons also increases, resulting in higher bunch charge and a stronger electric field. The experimental data were well described by the following empirical linear law:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\Sigma }_{fast}}{{\Sigma }_0}}=1+(3.15\pm 0.35)\Delta \end{array}$$

(5)

$$\begin{array}{c}\hfill {\displaystyle \frac{Q_{fast}}{Q_0}}=1+(3.15\pm 0.35)\Delta \end{array}$$

(6)

where ${\Sigma }_0$ and $Q_0$ are retrieved from Figure 6 for the $\Delta =0$ configuration.

Figure 8c shows the bunch temporal duration as a function of the target thickness. As the latter increases, the ${\tau }_{fast}$ lengthens due to the space charge effect caused by the increase in charge. The empirical law describing the bunch duration parameter as a function of $\Delta$ is

$$\begin{array}{c}\hfill {\displaystyle \frac{{\tau }_{fast}}{{\tau }_0}}=1+(3.1\pm 0.2)\Delta \end{array}$$

(7)

where ${\tau }_0$ was retrieved experimentally from Figure 7 when the laser is focused on the target tip. This behavior highlights the dependence of the temporal duration on the charge and how the space charge effect ($\propto Q/{\gamma }^2)$ dominates for low energy electrons. More details based on theoretical models [44,50] about the temporal evolution of the fast electrons are reported in [36], where a simplified scalar model called the Electron Ballistic Code (EBC) have been developed. In Figure 9, the simulated temporal bunch profiles are compared with the experimental data for different laser energies ( ranging from 0.4 J to 2 J) on a 10 µm-thick aluminum foil target.

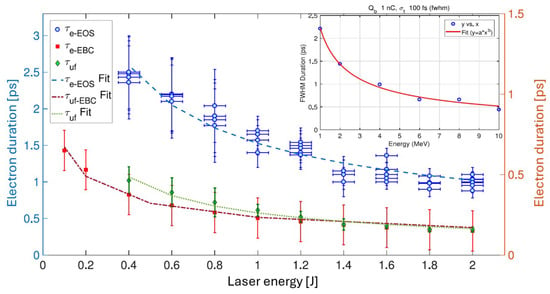
Figure 9. The temporal electron bunch duration for different laser energy. The experimental data in blue circles (with respect to the blue axis on the left) and the simulated data in red squares (with respect to the red axis on the right). The green points (with respect to the right axis) are the deconvoluted experimental data after the application of the EOS calibration value in the plot on the top-right [36].

The plot compares the experimental results (in blue on left axis) with those obtained from simulations (in red on right axis). However, the simulated results do not account for the response of the EOS diagnostics at different electron beam energies. Therefore, the experimental data have been deconvoluted (green point on the right axis) using the calibration curve shown in the inset. As expected, the beam duration decreases with increasing laser energy and at higher laser energies the data are in perfect agreement with theoretical values. On the other hand, the difference between the experimental data and theoretical values increases at lower laser energies. One explanation is that, at lower laser energies, the electrons are less energetic and in the propagation the space charge forces cannot be neglected. However, these effects are not included in our model, which was well described in [36]. For the simulation, N = 5$e^3$ points were used for the energy discretization and the maximum energy was $E_m=20T_h$, where $T_h$ is the temperature which describes the particles energy distribution. For our experimental condition $T_h=0.51(\sqrt{1+a_0^2}-1)$, where $1.5<a_0<4$ is the normalized vector potential of the laser beam.

4.2. Electromagnetic Pulses

In addition to electron and ion bunches, the high-intensity laser–target interaction also generates electromagnetic pulses. Studying the characteristics of these pulses provides a more comprehensive understanding of the interaction process. At FLAME, it was possible to detect and analyze these EMPs using EOS diagnostics (setup in Figure 2), including the temporal duration, peak electric field, and time evolution of the emitted pulses [34].

The target was a commercial blade with a varying thickness: 0.7 µm at the edge and 6 µm at the center, with an opening angle of 17° ± 3°. The same EOS encoding method used for fast electron detection was applied to analyze the EMP signals, but in this case, the probe laser is systematically delayed or advanced relative to the EMP signal to reconstruct its temporal profile.

In the acquired EOS images (Figure 10), the probe laser travels through the crystal from left to right; the latter is always 1 mm downstream and above the target. The horizontal extent of the detected signal reflects the physical size of the radiation source on the target. By increasing the delay of the probe $\Delta t_0$ relative to the EMP, the signal shifts to the left side of the snapshot, revealing the temporal evolution of the field and providing information on the expansion velocity of the emitting area on the target surface. The vertical width corresponds instead to the temporal duration of the pulse. Different shots with 2 J laser pulse on 0.7 µm target are shown in Figure 10, where the probe delay was increased by 2.5 ps; instead, the x-axis is the probe arrival time at the crystal associated to each pixel. As the delay increases, the signal intensity varies, reflecting the changing charge density on the target, the source of the EMPs. However, the temporal duration of the individual pulses remains constant throughout the observed time window of 15 ps. The average duration of the detected radiation in Figure 10 was (6 ± 1) ps (FWHM). Beyond this time interval, the EMPs become too weak to be detected by the EOS detector. The observed propagation velocity was (0.94 ± 0.03)c and the result is in agreement with previous works [23,51].

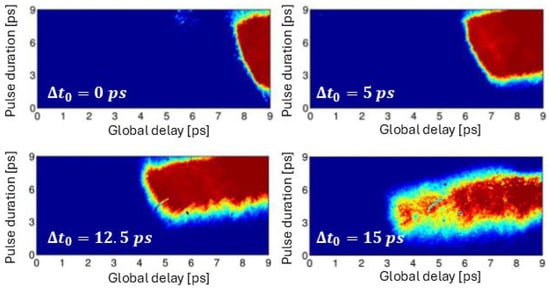
Figure 10. EMPs signal on EOS diagnostics obtained at different delays of the probe beam $\Delta t_0$ [34].

Figure 11a shows the field amplitude (log scale) as a function of time for different levels of laser energy focused on the target (10%, 50%, 100%). An increase in the field strength is observed with increasing laser energy, reaching a maximum of 0.8 MV/m. The temporal duration also changes, ranging from 5 ps to 7.1 ps (FWHM), and the pulses decay exponentially over time [52], as shown by the fits in the plot. The plot (b) presents the peak field as a function of laser energy described by a power law $E_T=(0.20\pm 0.03)E_L^{(0.30\pm 0.06)}$. The field enhancement is relatively modest compared to the corresponding increase in laser energy.

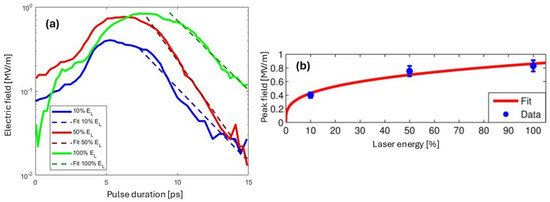
Figure 11. The radiation pulse profile $E_T$ (a) is retrieved from the vertical thickness of the signal from EOS diagnostics at different laser energies. The duration is about 5 ps (at 10 %), 5.7 ps (at 50%) and 7.1 ps (at 100%). (b) The peak amplitudes of $E_T$ are a function of the laser energy [34].

Several shots were also performed, allowing simultaneous and direct detection, via EOS diagnostics, of both the emitted electrons and EMPs. In Figure 12, two EOS signals are reported. In these acquisitions, the laser was focused (at 2 J) on the target tip of 0.7 µm (a) and (at 1 J) on the target bulb of 6 µm (b). In Figure 12a, two distinct bunches with different energies and charges are visible; the first one (the most intense) on the bottom left represents the fast electrons (narrow tilted shape). It carries 2 nC with a mean energy of 7 MeV and a temporal duration of 400 ps (FWHM). The second one is less intense and has a broader structure; it reaches the crystal with a 2 ps delay relative to the first and carries 0.3 nC of charge with 0.6 MeV of energy.

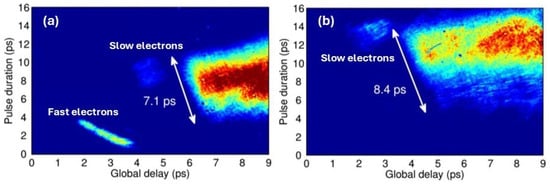
Figure 12. (a) Single-shot picture obtained with the EOS detector when the laser is focused on the 0.7 µm-thick target at full energy. Two electron bunches are detected simultaneously with the EMPs. (b) Single-shot picture at 1 J laser energy, focused on the target bulk (6 µm), with the probe laser delayed by 4 ps. One slow electron bunch and EMPs are detected [34].

In Figure 12b, the probe laser is delayed of 4 ps, the EMP signal shifts to the left, and the fastest bunch is no longer visible because it falls outside the diagnostics time window. Moreover, the temporal duration of the EMP increases since, through changing the target thickness and laser energy, the amount of energy involved in the interaction changes. This clearly demonstrates that the process dynamics are linked to the laser energy deposition as reported in the results in Figure 11. Simulations were carried out to support these results, and a time-resolved analysis of the interaction process was done by the 2D PIC code TURBOWAVE [53]. The simulations are described in detail in [34].

Some investigations with other techniques, such as the proton probing [54], have enabled the analysis of the dependence of EMP pulse amplitudes on laser parameters, confirming their correlation with both the incident beam energy and its temporal duration. Furthermore, the net charges associated with the propagating electromagnetic pulses have also been studied in detail as a function of the laser intensity.

4.3. Proton Beams

The diamond TOF detector was used to characterize ion beams accelerated by the quasi-static electric field at the rear side of the target. This diagnostic system allowed the retrieval of the proton bunches’ kinetic energy.The experimental setup is described in Section 2. A typical signal acquired by the oscilloscope is shown in Figure 13, in this experimental case, the laser pulse is focused on a 5-µm-thick stainless steel target with an intensity of ${10}^{19}$ W/cm². Two distinct peaks can be observed in the picture, occurring at different times: the first, less intense, is associated with X-rays and fast electrons, while the second, more visible, corresponds to the proton bunch.

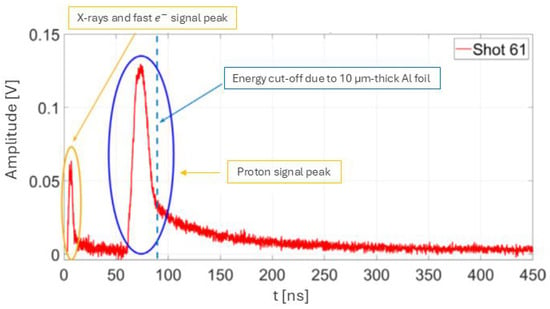
Figure 13. Signal provided by the TOF detector and oscilloscope: the first peak on the left is associated with X-rays and electrons; the second peak is associated with proton bunches accelerated in the TNSA process [35].

The time delay between the two signals is defined as $\Delta t$ and it is measured with respect to the first peak rising front. Therefore, the proton beam energy is calculated by $E_{ion}=m_{ion}{c}^2(\gamma -1)$, where $m_{ions}$ is the ion rest mass and $\gamma =1/\sqrt{1-{\beta }^2}$ is the Lorentz relativistic factor. The factor $\beta =L/\left(c(\Delta t+t_0)\right)$ is defined by the distance between the TOF detector and the target $L=$105 cm and the time of flight of the X-rays from the source to the detector $t_0=$ 3.3 ns.

To shield the TOF from electromagnetic radiation and target debris, a 10-micron-thick Al foil was placed in front of it. The energy attenuation introduced by the filter was evaluated through MonteCarlo simulations using the SRIM code [55], as reported in [35].

The oscilloscope signal is presented as a reference for the proton energy analysis in the following section. Under these experimental conditions, it shows a maximum proton energy of 1.37 MeV, representing one of the first preliminary results obtained with this diagnostic tool.

4.4. Electron–Proton Beams Correlation

Since ion generation and acceleration are closely linked to electron beam production in the early stages of the TNSA mechanism, analyzing the correlation between these two particle types is of fundamental importance. For this reason, we performed simultaneous time-resolved measurements of both protons and electrons, using the available diagnostics [35,37,56].

First, parametric scans were performed by varying the laser pulse duration (from 30 to 300 fs) and the focal spot size (diameter at $1/e^2$ from 30 to 120 µm) while keeping the laser energy constant at 2 J on a 10-micron-thick Al foil as target [56]. Then, the laser was set at 30 fs with a waist of 15 µm, changing the energy on the target from (0.5 to 2 J). The goal was to measure the evolution of the maximum proton energy and the properties of the fast electron bunch (charge and temporal duration). While the relevant literature on this topic is extensive, previous works reported a scaling law for the maximum proton energy [57,58,59], and for our target thickness and laser pulse duration, the expected values are of few MeV.

In Figure 14, we present some experimental results. On the left (a–c), we show the measured electron bunch charge and duration, along with the maximum proton energy, as a function of the laser pulse duration. On the right (b–d), the same quantities are plotted with respect to the laser focal spot size. As expected, the characteristics of the fast electrons depend on the laser intensity on the target, which in turn varies with both the pulse duration and the focal spot area. Furthermore, as already reported in previous works [57], the proton energy shows weak dependence on the laser pulse duration while being more strongly influenced by the spot size and the total energy delivered to the target.

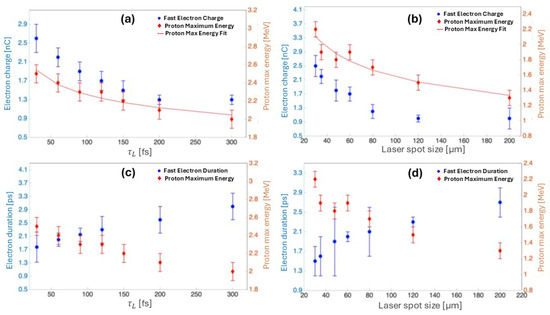
Figure 14. Experimental data of the simultaneous detection of electron and proton beams. (a,c) Plot of the electron beam charge, electron beam duration, and proton maximum energy as function of the laser temporal length. (b,d) Plot of the electron beam charge, electron beam duration, and proton maximum energy as function of the laser spot size [37].

Focusing first on the temporal scan in Figure 14a,c: the electron bunch charge $q_e$ decreases as the pulse duration increases, while the bunch duration ${\tau }_e$ increases linearly. This behavior is consistent with the reduced intensity for longer pulses, leading to less energetic electrons with broader temporal distribution. In this configuration, the maximum proton energy follows a power law scaling as

$$E_{max}^p\left[\mathrm{MeV}\right]=(3.5\pm 0.4){\tau }_L{\left[\mathrm{fs}\right]}^{(-0.09\pm 0.03)}.$$

(8)

In (b,d) for the laser spot size scan, the ${\tau }_e$ still follows a linear increase and $q_e$ decreases for the reduced laser intensity on the target. The maximum proton energy exhibits a faster decrease with larger laser spot size $r_L$, following a power law scaling as

$$E_{max}^p\left[\mathrm{MeV}\right]=(4.8\pm 0.2)r_L{\left[\mu \mathrm{m}\right]}^{(-0.25\pm 0.09)}.$$

(9)

Considering the laser intensity definition $I_L=E_L/\left(\pi r_L^2{\tau }_L\right)$, the proton energy behavior can be expressed as $E_{max}^p\propto I_L^{(-0.1\pm 0.04)}$. Overall, the maximum measured proton energy was (2.9 ± 0.1) MeV with an electron bunch carrying ∼ (1.8 ± 0.4) nC.

The correlation between electrons and protons was also analyzed as a function of the laser energy, keeping the pulse duration and spot size constant. The experimental results reported in Figure 15 were supported also by numerical simulations carried out with the EBC [36], which allowed to determine the potential barrier which is responsible for the proton acceleration and also the fast electron bunch duration, showing an excellent agreement with the experimental data. Figure 15a shows the trend of the electron charge and the maximum proton energy as the laser energy increases. The relation between the maximum proton energy and the laser energy was

$$E_{max}^p\left[\mathrm{MeV}\right]=(1.84\pm 0.09)E_L{\left[\mathrm{J}\right]}^{(0.56\pm 0.12)}.$$

(10)

The results show a general trend in agreement with what has been reported in the literature in previous studies [57,60,61].

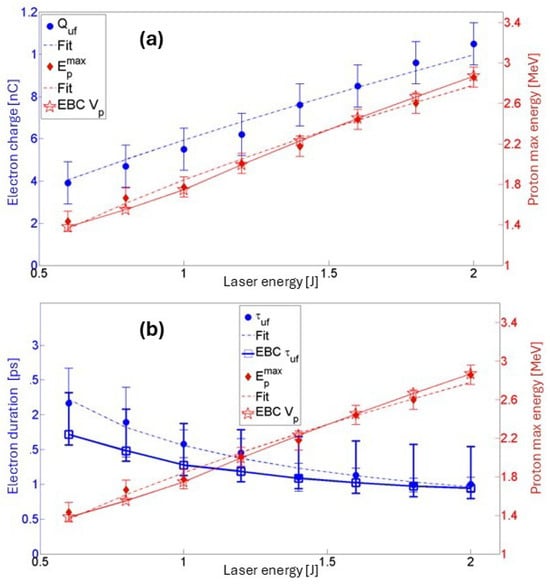
Figure 15. Experimental data of the simultaneous detection of electron and proton beams. (a) Plot of the electron beam charge (blue) and proton maximum energy (red) for different laser energies. For lower laser energy, there is a reduction in both the emitted electron charge and the potential on the target, leading to a lower signal-to-noise ratio and larger error bars. (b) Plot of the electron beam duration (blue) and proton maximum energy (red) for different laser energies [56].

The plot in Figure 15b presents the experimental data for the electron bunch duration and the proton energy, again as a function of $E_L$ and compared with simulations. The following function describes the evolution of ${\tau }_{fast}$

$${\tau }_{fast}\left[\mathrm{ps}\right]=(1.56\pm 0.07)E_L{\left[\mathrm{J}\right]}^{(-0.7\pm 0.1)}.$$

(11)

In the last Figure 16, the maximum proton energy as a function of the fast electron charge (orange data) and duration (green data) is shown, where the bars represent the statistical error. The experimental data are described by

$$\begin{array}{cc}\hfill E_{max}^p\left[\mathrm{MeV}\right]=(2.7\pm 0.2)Q_{fast}{\left[\mathrm{nC}\right]}^{(0.6\pm 0.1)}& \hfill \\ \hfill E_{max}^p\left[\mathrm{MeV}\right]=(2.8\pm 0.1){\tau }_{fast}{\left[\mathrm{ps}\right]}^{(-0.9\pm 0.2)}.\end{array}$$

(12)

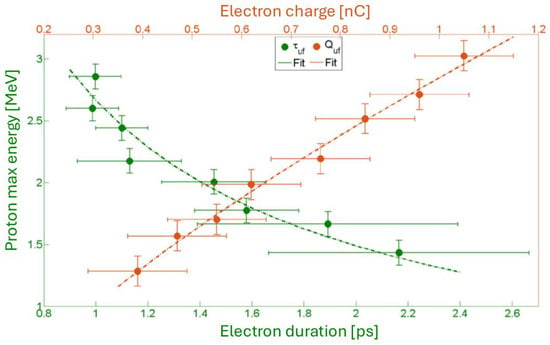
Figure 16. Experimental data of proton maximum energy as a function of the electron beam duration (green) and charge (orange) [56].

5. Conclusions

This paper reviews the experiments carried out at the SPARC_LAB facility at the National Laboratories of Frascati-INFN, investigating laser–solid target interactions in the TNSA configuration. The diagnostics used to characterize the process are initially presented in detail, with particular emphasis on the detection of electron bunches, electromagnetic pulses, and accelerated proton beams in different experimental setups.

The EOS diagnostics enabled, for the first time, the direct, time-resolved, and simultaneous single-shot detection of both electrons and EMPs, with unprecedented resolution better than 100 fs. The electron beam properties were analyzed for different target shapes and materials, as well as for various laser parameters, allowing the reconstruction of the target charging dynamics. These results demonstrated an increase in the charge and energy of fast electrons for sharp-structured targets, and the production of more charged and shorter electron bunches as the laser energy increased.

The analysis of the EMPs proved to be a complementary diagnostic to electron and ion measurements, offering deeper insight into the TNSA acceleration mechanism.

In the last experimental campaigns, the correlation between the maximum energy of the accelerated protons and the fast electrons was investigated. The results showed that the proton energy increases with the charge extracted by fast electrons as a direct consequence of a stronger potential on the target’s rear surface. Therefore, the initial conditions, such as the laser parameters and target geometries, determine the proton acceleration process. This analysis demonstrated that it is possible to predict the proton energy spectrum based on the characterization of fast electrons. All the analyses were supported by numerical simulations, some of which are reported in previous works.