Dynamic Response of Droop-Controlled Grid-Forming Inverters Under Varying Grid Impedances for Enhanced Stability in Microgrids

Abstract

The fast-growing integration of renewable energy sources into the utility grids jeopardizes the system’s performance and stability at risk. Particularly, the increasing tendency of power electronics converters in the current renewables-based power generation and their integration to utility grids through long sub-sea cables compromises the grid strength and amplifies the risk of system instability during disturbances. To sustain grid stability and ensure effective regulation during transients, grid-following (GFL) and grid-forming (GFM) control approaches have been extensively proposed for power systems with inverter-based resources (IBRs). The former approach is solely based on a phase-locked loop (PLL) to track the phase angle of grid voltage, which reduces the system stability margin, particularly in weak-grid scenarios. Consequently, grid-forming control is increasingly recognized for its ability to maintain stability and ensure reliable operation under weak-grid conditions. Droop control is one of the most widely used grid-forming control strategies owing to its capability to emulate the behavior of synchronous machines, achieve autonomous power sharing, and ensure stable voltage and frequency regulation even under varying grid conditions. This paper aims to evaluate the impact of grid impedance and its characteristics (i.e., resistive or inductive grid impedance) on the dynamic performance of a droop control GFM grid-connected converter. To that end, first, a detailed MATLAB/Simulink model of a voltage source converter implementing the proposed droop-based GFM control is developed. Then, the overall system will be validated by performing on distinct case studies including weak and stiff power grids with inductive, resistive and nonlinear impedances in response to various grid disturbances.

1. Introduction

In recent years, enormous efforts have been made to shift the power system industry from conventional non-renewable generation to renewable-based generation. Among renewable resources, wind and photovoltaic (PV) are gaining more attention, globally, due to their low environmental impact, declining costs, and abundant availability, to name but a few. As illustrated in Figure 1, future power systems are expected to become increasingly inverter-dominated, rather than relying on conventional synchronous generators. Unlike traditional generation systems, distributed generation units (DGs) are interfaced with load centers and the utility grid through power electronics converters, usually called interfacing converters [1]. These converters control and regulate the active and reactive power delivered to utilities. They provide fast response and robust control; however, they lack the inherent provision of inertial and reactive power support during system disturbances, which are crucial for maintaining grid stability.

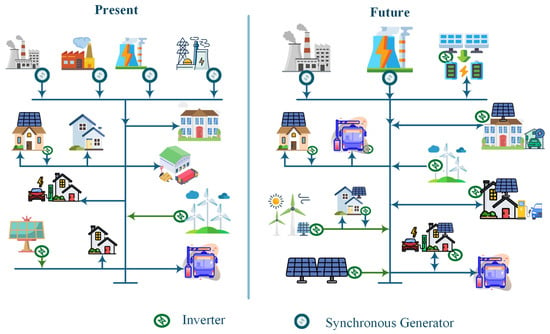
Figure 1. An illustration of fast-growing trend toward the IBRs integration.

In addition, conventional power systems mostly rely on synchronous machines, having a rigid synchronization with each other, to support the system voltage and frequency stability by means of exciters and governor control, respectively. During various grid disturbances, such as load variation and faults, the frequency of the conventional power system is maintained within permissible limits through the mechanical inertia of the machine. In contrast, the IBRs connected to the power grid follow the grid frequency by using phase-locked loop (PLL) controllers, hence the name grid-following (GFL), for maintaining the system operation and stability [2]. Notably, a GFL-based IBR cannot maintain voltage or frequency during grid disconnection, limiting its ability to operate in stand-alone mode [3]. Particularly, the voltage control at PCC for GFL converters becomes a challenging issue when they are connected to utility grids by means of high-impedance lines such as offshore wind power plants [4]. Therefore, the growing penetration of IBRs and the gradual phase-out of conventional generators consequently fragile potential of the power grid to deal with abrupt perturbation. As an alternative, GFM control has been extensively studied and implemented in academia and industry, respectively, as it replicates essential synchronous generator characteristics, including virtual inertia, damping, and droop response [5].

Although grid-following (GFL) and grid-forming (GFM) converters differ in control structure and dynamic behavior, their primary objective is the same: to regulate active and reactive power injection while respecting system voltage and current limits [5]. Their responses during grid disturbances, however, are fundamentally different. As shown in Figure 2, a GFL converter behaves like a current source, maintaining a constant current phasor I_g, which results in variations in the converter output voltage phasor Vc (Figure 2a, right). In contrast, a GFM converter operates as a voltage source behind a low series impedance, keeping its voltage phasor constant while the current phasor varies (Figure 2b, right). The magnitude of these variations depends on the disturbance characteristics and grid stiffness, highlighting the importance of converter type for maintaining stability under weak-grid or sudden perturbation scenarios [6].

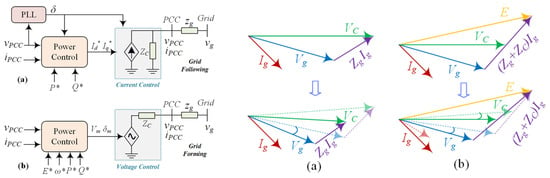
Figure 2. Simplified representation of power converters control: (a,b) (left) GFL and GFM control; (a,b) (right) GFL and GFM (phasor).

Various studies have investigated droop-based grid-forming control strategies, each addressing specific aspects of system performance, as summarized in Table 1. Classification approaches have been proposed to distinguish control variants based on PLL integration [7] and control loop architecture [8], while advanced controllers including fractional-order PI [9] and power angle-frequency droop [10] have been developed to enhance transient response and stability margins. Modeling techniques for large-scale system analysis [11] and impedance-based stability assessment [12] have also been established. However, these studies primarily focus on steady-state operation or specific fault scenarios without comprehensively addressing the dynamic performance during mode transitions under varying grid impedances. Additional research has examined harmonic interactions [13], feeder impedance compensation [14], global stability conditions [15], and oscillation suppression in hybrid systems [16]. Comparative analyses between different control approaches [17] have highlighted trade-offs in implementation complexity and dynamic performance.

Beyond droop control strategies, the broader context of grid-connected converter performance under varying grid strengths has been extensively studied. In [18], the effects of grid strength and impedance parameters on the power transfer capability of grid-connected converters employing the GFL approach are examined, showing that a high short-circuit ratio (SCR) coupled with a low R/X ratio enhance the system’s power transfer capability. Similarly, ref. [19] provides a thorough insight into the performance of GFM IBR under various grid operating conditions. The study mainly focuses on the comparison of various existing GFM control approaches with attention to large-signal stability. However, the authors do not consider the effect of high IBR penetration on system stability. Moreover, research in [20] provides an assessment study on grid strength in terms of small-signal stability for 100% IBR with GFL and GFM control. Authors in [21] provide a comparative study of single-loop and multi-loop droop control GFM approach and their impact on the dynamic performance of the converter. Another research in [10] analyzes the performance of droop and oscillator-based GFM converters in response to terminal voltage, transient stability, and harmonics compensation in the converter’s output current. It is revealed that droop control is superior in harmonic current suppression due to the definite time-scale separation of control loops, while the oscillator-based GFM approach is easy to implement due to fewer number of sensors requirements. However, these works mostly focused on either the GFL approach or virtual synchronous generator (VSG)-based GFM control. Moreover, most of the authors in the reported research works focused on droop control for GFM converters for different objectives such as seamless transition, damping oscillations, and load sharing between parallel converters.

Despite these valuable contributions, the existing literature lacks a systematic investigation of droop-based GFM inverter behavior during islanded-to-grid-connected transitions combined with short transient faults (50–500 μs) and varying grid impedance characteristics (SCR and X/R ratios), particularly under nonlinear loading conditions. The impact of grid strength and its characteristics on the dynamic performance of droop-based GFM converters needs to be further investigated to evaluate the performance under various grid disturbances, particularly changes in SCR and X/R ratio, short transient faults, mode transitions, and nonlinear load conditions.

To address this gap in knowledge, this paper models a grid-connected converter employing droop-based GFM control as a case study. Comprehensive guidelines for developing various control loops of the proposed converter are provided. Then, the dynamic performance of the droop-controlled GFM inverter is evaluated under distinct grid operating conditions with varying impedances, including islanded-to-grid-connected transitions, transient faults of 50–500 μs duration, and operation under nonlinear loads with varying SCR and X/R ratios.

The main contributions of this work are summarized as follows.

• A comprehensive modeling and control framework for droop-based grid-forming converters is developed with detailed implementation guidelines for all control loops.
• Dynamic performance of the proposed GFM converter is thoroughly investigated and discussed during distinct cases of grid strength and the mode of operation (i.e., islanded or grid-connected) through MATLAB/Simulink (R2024-b) simulations.
• The inverter’s performance during short transient faults (50–500 μs) and under nonlinear loads is analyzed, including voltage and current responses and total harmonic distortion (THD).

The rest of this paper is organized as follows: Section 2 presents the configuration and control design of the droop-based GFM converter. Section 3 discusses the simulation results and performance evaluation under various operating conditions. Finally, Section 4 concludes the paper with key findings and future research directions.

Table 1. Comparative summary of droop-based GFM control research: analysis methods and identified gaps.

Reference	Control Approach	Analysis Method	Grid Condition	Fault/Disturbance	Key Metric	Key Limitations
[7]	PLL-integrated droop	Time-domain simulation, pole map	Single-terminal HVDC	Ideal DC Bus	Power regulation accuracy, virtual inertia	No mode transition, fixed impedance
[8]	Single/multi-loop droop	Small-signal stability analysis	Microgrid	N/A	Stability boundary, damping ratio	Steady-state stability, no transient faults
[9]	FOPI droop	Monte Carlo optimization, ISE/ISCO	Transmission system	Unbalanced load, line fault	Error reduction (65–83%)	Specific faults, no impedance variation
[22]	Basic (P-f, Q-V) droop	Positive-sequence EMT comparison	Transmission (IEEE 39-bus)	Three-phase fault	Computational efficiency, accuracy	Transmission-level focus, no μs faults
[13]	Droop with harmonic control	Multiple-harmonic DPM, eigenvalue	Two-inverters network	DC offset, 2nd harmonic, unbalance	Eigenvalue migration, damping	No impedance variation study
[14]	Robust V-I droop	MIMO stability, disturbance observer	Islanded microgrid	Feeder impedance uncertainty, nonlinear load	PCC voltage THD, power-sharing error	No rapid impedance change
[10]	Power angle-frequency droop	Transient stability, HIL validation	Grid-connected inverter	Voltage dip (20–80%)	Stability margin, recovery time	No X/R ratio impact, no mode transition
[15]	Complex droop (dVOC)	Lyapunov stability, full-order dynamics	Grid-connected inverter	Grid interruption	ROA, transient stability conditions	Theoretical focus, no SCR analysis
[12]	Droop with AIM	Impedance modeling (αβ-frame)	Grid-connected inverter	Load change, grid impedance variation	Frequency coupling bandwidth	Steady-state validation only
[16]	Adaptive droop	ISCR-based stability, eigenvalue	Hybrid GFM-GFL	Wideband oscillation	Oscillation damping, frequency range	No short-duration faults
This Work	GFM Droop	Time domain, THD, mode transition	Islanded/grid-connected	Transient faults, nonlinear load, impedance variation	Voltage/current THD, frequency deviation, recovery time	Comprehensive dynamic analysis addressing identified gaps

Table 1. Comparative summary of droop-based GFM control research: analysis methods and identified gaps.

Reference	Control Approach	Analysis Method	Grid Condition	Fault/Disturbance	Key Metric	Key Limitations
[7]	PLL-integrated droop	Time-domain simulation, pole map	Single-terminal HVDC	Ideal DC Bus	Power regulation accuracy, virtual inertia	No mode transition, fixed impedance
[8]	Single/multi-loop droop	Small-signal stability analysis	Microgrid	N/A	Stability boundary, damping ratio	Steady-state stability, no transient faults
[9]	FOPI droop	Monte Carlo optimization, ISE/ISCO	Transmission system	Unbalanced load, line fault	Error reduction (65–83%)	Specific faults, no impedance variation
[22]	Basic (P-f, Q-V) droop	Positive-sequence EMT comparison	Transmission (IEEE 39-bus)	Three-phase fault	Computational efficiency, accuracy	Transmission-level focus, no μs faults
[13]	Droop with harmonic control	Multiple-harmonic DPM, eigenvalue	Two-inverters network	DC offset, 2nd harmonic, unbalance	Eigenvalue migration, damping	No impedance variation study
[14]	Robust V-I droop	MIMO stability, disturbance observer	Islanded microgrid	Feeder impedance uncertainty, nonlinear load	PCC voltage THD, power-sharing error	No rapid impedance change
[10]	Power angle-frequency droop	Transient stability, HIL validation	Grid-connected inverter	Voltage dip (20–80%)	Stability margin, recovery time	No X/R ratio impact, no mode transition
[15]	Complex droop (dVOC)	Lyapunov stability, full-order dynamics	Grid-connected inverter	Grid interruption	ROA, transient stability conditions	Theoretical focus, no SCR analysis
[12]	Droop with AIM	Impedance modeling (αβ-frame)	Grid-connected inverter	Load change, grid impedance variation	Frequency coupling bandwidth	Steady-state validation only
[16]	Adaptive droop	ISCR-based stability, eigenvalue	Hybrid GFM-GFL	Wideband oscillation	Oscillation damping, frequency range	No short-duration faults
This Work	GFM Droop	Time domain, THD, mode transition	Islanded/grid-connected	Transient faults, nonlinear load, impedance variation	Voltage/current THD, frequency deviation, recovery time	Comprehensive dynamic analysis addressing identified gaps

2. Configuration and Control of Proposed GFM Converter

2.1. Description of the System Under Study

A single-line diagram of the electrical network considered in this work is shown in Figure 3. The system consists of a grid-forming (GFM) voltage source converter supplying a local PQ load rated at 2 kW and 2 kVAr, as well as a distributed PQ load of the same rating connected through a low-voltage distribution feeder. These loads are interfaced with a 230 V, 50 Hz utility grid. The converter employs an LC output filter represented by L_f and C_f, which shapes the inverter voltage and attenuates switching harmonics. The utility grid is modeled as an ideal voltage v_g in series with an equivalent impedance (Z_g = R_g + jX_g). The AC bus voltage is expressed by v_pcc which is the point of common coupling (PCC), and v_c represents the converter output voltage. The grid and inverter output currents are represented by i_g and i_o, respectively.

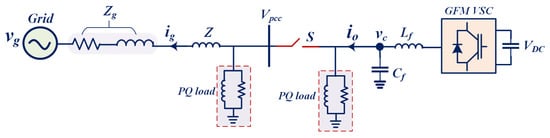
Figure 3. Single-line diagram of the power system under study.

The operating mode of the converter depends on the status of switch S. When switch S is open, the inverter operates in stand-alone (islanded) mode, supplying power solely to the local load. In this situation, both the frequency and the magnitude of the PCC voltage are dictated by the GFM control strategy and the dynamic characteristics of the connected load. Conversely, when switch S is closed, the system transitions to grid-connected mode, and the converter output voltage v_c must match the grid voltage v_g in magnitude, phase, and frequency.

During severe grid disturbances, such as voltage sags, faults, or instability events, it is common practice to intentionally disconnect the VSC from the grid to prevent excessive currents and ensure uninterrupted operation for the local load. Once the grid returns to normal conditions, the magnitude and frequency of v_g and v_c may differ significantly. If switch S is closed under these mismatched conditions, the resulting transient power exchange may lead to substantial inrush currents and trigger converter overcurrent protection. To prevent such undesirable events, IEEE Std. 1547-2018 [23] mandates strict synchronization limits for voltage magnitude, frequency deviation, and phase angle difference before reconnection of distributed energy resources. Thus, prior to reclosing S, the converter voltage v_c must be synchronized with the grid voltage v_g to ensure a smooth transition back to grid-connected operation.

The overall structure of the adopted control framework is illustrated in Figure 4. The hierarchical control architecture includes primary droop control, inner voltage and current regulation loops, a secondary control layer that restores deviations in voltage amplitude and frequency, and a tertiary control layer that determines real and reactive power exchange with the grid. The control scheme is implemented in the αβ reference frame to facilitate the use of proportional–resonant (PR) controllers, which provide infinite gain at the fundamental frequency and ensure zero steady-state tracking error [24].

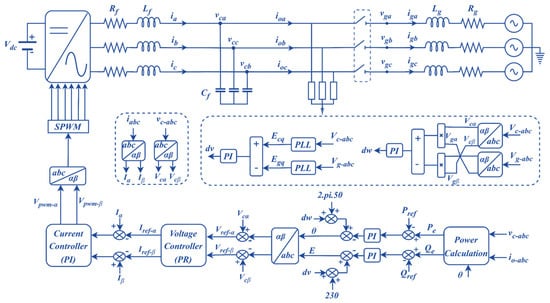
Figure 4. Overall control structure of the proposed droop-based GFM inverter.

2.2. Power Controller

The v_αβ and i_αβ components are used to obtain the instantaneous values of active and reactive power, p and q, as expressed in (1). To eliminate the high frequency ripples, the obtained values of p and q are passed through low pass filters with cutoff frequency ω_c, yielding the average values $P_e$ and $Q_e$ as given in (2):

$$\left\{\begin{array}{c}p=\left(v_{\alpha }{i}_{\alpha }+v_{\beta }{i}_{\beta }\right)\\ q=\left(v_{\beta }{i}_{\alpha }-v_{\alpha }{i}_{\beta }\right)\end{array}\right.$$

(1)

$$P_e, Q_e={\displaystyle \frac{{\omega }_c}{s+{\omega }_c}}. \left(p,q\right)$$

(2)

Here, $v_{\alpha \beta }$ and $i_{\alpha \beta }$ denote the capacitor voltage and output current, while p and q represent the instantaneous active and reactive power, respectively.

2.3. Droop Controller

In this work, a dynamic-compensated droop-based primary outer control is employed to determine the reference values for the phase angle θ and voltage magnitude V. These references, obtained from the outer loop, subsequently fed to the inner voltage and current control loops which synthesize the converter’s terminal voltage reference. While conventional droop control relies solely on proportional relationships in the active power–frequency (P-f) and reactive power–voltage (Q-V) characteristics, the adopted scheme enhances this structure by incorporating derivative terms to improve transient response and oscillation damping, and an integral term in the Q-V loop to eliminate steady-state reactive power errors. This modification enables more accurate voltage and frequency regulation under rapid power variations and strengthens stability in weak-grid scenario.

The enhanced P-f and Q-V droop characteristics are expressed in (3) and (4), respectively. The corresponding block diagram of the adopted outer control loop is shown in Figure 5. In the proposed structure, the P-f droop determines the phase angle deviation, while the Q-V droop governs the amplitude of the terminal voltage, both benefiting from the added dynamic compensation.

$$\omega ={\omega }_{ref}+k_{pp}.\left(P_{ref}-P_e\right)+m_d.{\displaystyle \frac{dP}{dt}}$$

(3)

$$V=V_{ref}+(k_{pq}+{\displaystyle \frac{K_{qi}}{s}}).\left(Q_{ref}-Q_e\right)+n_d.{\displaystyle \frac{dQ}{dt}}$$

(4)

where ω and V are the measured angular frequency and amplitude of the inverter output voltage, V_ref, and ω_ref are the rated angular frequency and output voltage, $P_e$ and $Q_e$ are the measured active and reactive power obtained from the power calculation block as described in Equation (7), P_ref and Q_ref are the active and reactive power references, respectively.

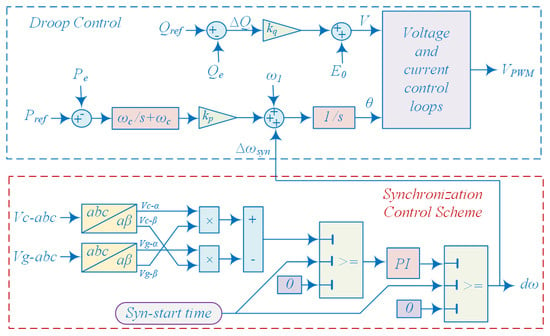
Figure 5. Control block diagram of GFM converter with synchronization control loop.

2.4. Synchronization Control Loop

The control block diagram of the synchronization control process adopted in this research is depicted in Figure 5, enclosed in the red lines. This control mechanism is activated at t = 1 s to synchronize the converter voltage v_c with the grid voltage v_g before closing the switch S to connect to the grid. It can be noted from Figure 5 that the phase difference between v_c and v_g is obtained by cross product of such vectors and comparing their result with zero, and the error is applied to the PI controller. The output of PI controller, ∆ω, is added to the active power control loop to determine the reference angular frequency ω of the voltage. Therefore, the phase angle θ_c of the converter voltage is equal to the phase angle θ_g of grid voltage, in steady-state operation, after synchronization is achieved.

During the synchronization process, prior to switch S closing, the control law of the active power loop can be drawn as

$$∆\omega =\left(k_{ps}+{\displaystyle \frac{k_{is}}{s}}\right)\left[V_{g\alpha }.V_{c\beta }-V_{g\beta }.V_{c\alpha }\right]$$

(5)

Here, $V_{g\alpha } ,V_{g\beta }$ and $V_{c\alpha } , V_{c\beta }$ are the magnitude of grid and converter’s output voltage in alpha–beta reference frame, respectively. The error between two voltage phases is fed to the PI controller to reduce the phase error and provide a control signal ∆ω to the converter to control its phase and frequency. The proportional and integral gains of the PI controller are represented by k_ps and k_is (k_ps = 5 × 10⁻⁵, k_is = 0.001), respectively.

It is important to note that the synchronization control loop is enabled only during the synchronization process, and it is disabled as soon as the synchronization is fulfilled. The synchronization process is obtained by using the alpha–beta components of the grid and the converter voltage variables v_c and v_g. Therefore, the synchronization process is fulfilled when (6) is satisfied.

$$\sin ({\theta }_g-{\theta }_c)=0$$

(6)

The effectiveness of the adopted synchronization scheme can be observed from the simulation waveform in Figure 6. Before t = 1 s, the VSC operates in stand-alone mode to supply the power to the local PQ load. However, the output frequency of the converter deviates from the grid frequency, which can be observed from the phase angle difference between v_c and v_g. To synchronize the two voltages, the synchronization scheme is activated at t = 1 s which regulates such phase difference to zero around t = 1.5 s.

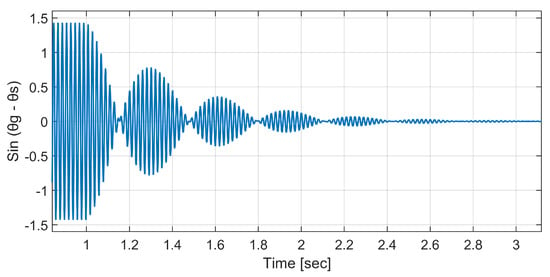
Figure 6. Phase difference between V_g and V_c during transition from IS to GC mode.

2.5. Inner Voltage and Current Control Loop

The inner control loop consists of two cascaded voltage and current control loops as presented in Figure 7, which are responsible for controlling the converter terminal voltage and the reference current injected by the converter, respectively. The two cascaded controllers are represented by a block diagram as shown in Figure 8, where the voltage control loop incorporates the PR controller while the current control loop uses the PI controller. A detailed model of the internal control loops has been presented by [25,26]. The closed-loop transfer function of the current loop is given as follows:

$$T_i\left(s\right)={\displaystyle \frac{I_c\left(s\right)}{I_{ref}\left(s\right)}}={\displaystyle \frac{G_I\left(s\right) K_{PWM}}{Ls+r+G_I\left(s\right) K_{PWM}}}$$

(7)

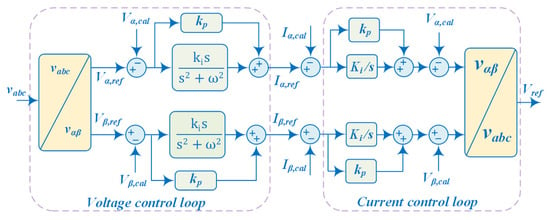
Figure 7. Inner voltage current control loops.

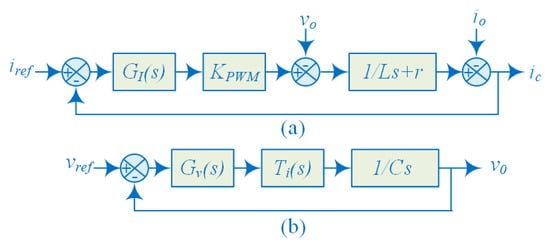
Figure 8. Block diagram of inner loops: (a) current control loop; (b) voltage control loop.

If $G_I\left(s\right)=k_{pi}$,

$$T_i\left(s\right)={\displaystyle \frac{I_c\left(s\right)}{I_{ref}\left(s\right)}}={\displaystyle \frac{k_{pi} K_{PWM}}{Ls+r+k_{pi} K_{PWM}}}$$

(8)

$$\left|T_i\left(s\right)\right|={\displaystyle \frac{k_{pi} K_{PWM}}{\sqrt{{\omega }^2{L}^2+{\left(k_{pi}{K}_{PWM}+r\right)}^2}}}$$

(9)

Taking the switching frequency of 10 kHz, the cutoff frequency ω_c of the current loop is set to $f_{ib}={\displaystyle \frac{1}{5}}{f}_s=2000 \mathrm{Hz}.$ Then, the $k_{pi}$ value is calculated based on the bandwidth (${\omega }_c=-3 \mathrm{dB}$).

Similarly, the closed-loop transfer function of voltage control, as shown in Figure 8, is given as follows:

$$T_v\left(s\right)={\displaystyle \frac{G_v\left(s\right)T_i\left(s\right)}{Cs+G_v\left(s\right)T_i\left(s\right)}}$$

(10)

Putting $G_v\left(s\right)=k_{pv}+{\displaystyle \frac{k_{iv}s}{s^2+{\omega }_0^2}}$, Equation (10) can be modified as follows:

$$T_v\left(s\right)={\displaystyle \frac{B_2{s}^2+B_{1}s+B_0}{A_4{s}^4+A_3{s}^3+ A_2{s}^2+A_{1}s + A_0}}$$

(11)

where $B_2=k_{pv}{k}_{pi}{K}_{PWM}$; $B_1=k_{iv}{k}_{pi}{K}_{PWM}$; $B_0=A_0=k_{pv}{k}_{pi}{K}_{PWM}{\omega }_0^2$; $A_4=CL$; $A_3=C{k}_{pi}{K}_{PWM}$; $A_2=k_{pv}{k}_{pi}{K}_{PWM}+CL{\omega }_0^2$; $A_1=C{k}_{pi}{K}_{PWM}{\omega }_0^2+k_{iv}{k}_{pi}{K}_{PWM}$.

Bode plots of the designed current and voltage control loops are reported in Figure 9. It is worth noting that the current loop exhibits a bandwidth of approximately 4 kHz with a phase margin of about 75°, ensuring fast and stable current regulation. In contrast, the voltage loop has a bandwidth of around 800 Hz with a phase margin of approximately 50°. This design ensures that the current loop bandwidth is significantly higher than the voltage loop bandwidth (about five times larger), which is a standard requirement for cascaded control structures. The sufficient gain and phase margins in both loops confirm the robustness and stability of the controller design.

Figure 9. Bode plots of inner loops: (a) current control loop; (b) voltage control loop.

2.6. Secondary Control

The secondary control aims to compensate for the frequency and voltage deviations introduced by the droop control due to abrupt changes in load or power generation. Therefore, the secondary control adjusts the frequency and voltage deviations within the permissible limit defined by a particular grid code. The adopted voltage and frequency restoration compensator can be derived as follows [27]:

$$\delta \omega =k_{pF}\left({\omega }_{ref}-\omega \right)+k_{iF}\int \left({\omega }_{ref}-\omega \right)dt+∆{\omega }_s$$

(12)

$$\delta E=k_{pE}\left(E_{ref}-E\right)+k_{iE}\int \left(E_{ref}-E\right)dt$$

(13)

where $k_{pF}$, $k_{iF}$, $k_{pE}$, and $k_{iE}$ are the control parameters of the secondary control compensator, it is worth noting that $∆{\omega }_s$ is the synchronization term which is equal to zero in the absence of grid.

2.7. Tertiary Control

The tertiary control is adopted to control the active and reactive power flow between the GFM converter and utility grid by measuring the P_e and Q_e and comparing them with their reference values P_ref and Q_ref, as expressed in (14) and (15).

$${\omega }_{ref}=\left(K_{pP}+{\displaystyle \frac{K_{iP}}{s}}\right).\left(P_{ref}-P_e\right)$$

(14)

$$E_{ref}=\left(K_{pQ}+{\displaystyle \frac{K_{iQ}}{s}}\right).\left(Q_{ref}-Q_e\right)$$

(15)

The set point of frequency and voltage amplitude is generated by tertiary when the converter is in On-grid mode, while the control remains inactive in Off-grid mode, and these reference values in the secondary are selected appropriately.

3. Simulation Results and Discussion

To demonstrate the effectiveness of the adopted control scheme shown in Figure 3 and Figure 4, a comprehensive simulation model of a 10 kVA grid-connected inverter is developed in Matlab/Simulink environment. Detailed simulations are performed to systematically evaluate the dynamic performance of the droop-based GFM control under diverse operating conditions. The key system and control parameters are listed in Table 2. Initially, a strong power grid with SCR = 7 is considered to establish baseline performance in both islanded and grid-connected modes. Step changes in active and reactive power references are applied to assess reference-tracking capability and transient response. To evaluate fault ride-through performance, three-phase to ground faults with durations of 50 µs, 100 µs, 350 µs, and 500 µs are applied at the point of common coupling. Power quality assessment under nonlinear loading conditions is conducted using a three-phase diode rectifier with resistive–inductive load. Subsequently, to investigate performance sensitivity to grid strength, extensive simulations are performed across varying SCRs (3, 7) and X/R ratios (1, 3, 7) during islanded-to-grid-connected mode transitions.

Table 2. Parameters of the system under study.

Parameters	Symbol	Value	Parameters	Symbol	Value
Grid Parameters			Inverter Parameters
Grid voltage	Vg	230 V	Rated power	S	10 × 103 VA
Grid frequency	f	50 Hz	DC side voltage	Vdc	650 V
Grid inductance	Lg	1.8 × 10−3 H	Filter inductance	Lf	1.8 × 10−3 H
Grid resistance	Rg	0.1 Ω	Filter capacitance	Cf	9 × 10−6 F
Switching frequency	fs	10 × 103 Hz	Filter resistance	Rf	0.02 Ω
GFM Control Parameters
Voltage controller (PR) gains	Kpv, Kiv	0.03, 93.839	P-f droop gain	Kpp	0.05 ω/Pref p.u
Current controller (PI) gains	Kpi, Kii	0.04, 0	Q-V droop gain	Kpq	0.10 V0/Qref p.u
Secondary Control Parameters			Tertiary Control Parameters
kpF, kiF	0.005, 0.1		kpP, kiP	0.007, 9.8
kpE, kiE	0.001, 0.11		kpQ, kiQ	0.0025, 13

3.1. Performance Evaluation in Islanded and Grid-Connected Mode of Operation

Simulations are performed in this section to evaluate the performance of the adopted droop-based GFM converter in islanded (IS) and grid-connected (GC) operation modes. The simulation waveform of the grid voltage and current, converter output voltage and current, active and reactive power, frequency, and synchronization error are presented in Figure 10 and Figure 11. It can be noted from the figures that initially the inverter supplies a local load of 2 kW and 1 kVAr while operating in islanded mode. A synchronization control scheme presented in [28] is adopted to synchronize the grid and converter voltage before closing the switch S to integrate the converter into the grid. It is obvious that before t = 1 s, the frequency of the grid and converter voltages deviated from each other, which can be realized from the synchronization error reported in Figure 11 (right, a). The synchronization scheme is activated at t = 1 s to synchronize the converter voltage with grid voltage, where the synchronization error is regulated to be less than ±5V at around t = 1.5 s.

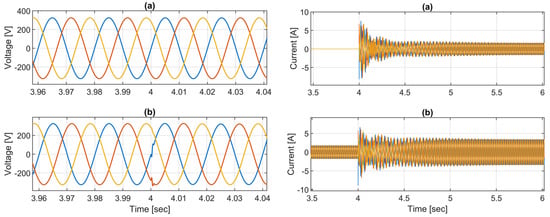
Figure 10. System response during transition from IS to GC mode: (a,b) (left) grid voltage and converter output voltage; (a,b) (right) grid current and converter output current.

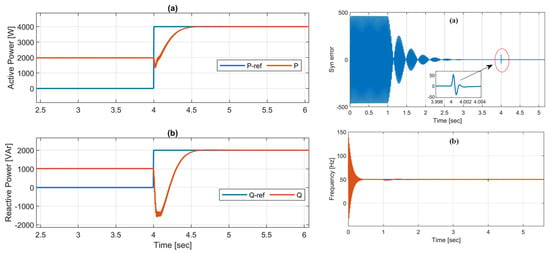
Figure 11. System response during transition from IS to GC mode: (a,b) (left) active and reactive power; (a,b) (right) synchronization error and frequency measured at PCC.

Once the synchronization is ensured, the grid with a 2 kW and 1 kVAr PQ distributed load connects by closing the switch at t = 4 s. It can be seen from the active and reactive power plots that after t = 4 s the converter supplies 4 kW and 2 kVAr to the two PQ loads (2 kW and 1 kVAr each). The simulations reveal that the system works well, where the converter has the competence to synchronize with the grid and maintain a constant output voltage in either mode of operation, i.e., islanded and grid-connected. The grid and converter voltage are balanced and constant in magnitude. Moreover, the simulation results show that the adopted GFM control algorithm works effectively to adjust voltage and frequency according to the changes in active and reactive power references.

3.2. Change in Power Set Point

In this part of the simulations, the response of the implemented control algorithm in tracking the reference signals has been evaluated by applying a step change in the active and reactive power set points. At t = 10 s, a sudden increment of 2 kW and 1 kVAr happens in the generation; therefore, the active power of generation rises from 4 kW to 6 kW, and reactive power is 3 kVAr, where the surplus power (2 kW and 1 kVAr) is injected into the grid. The active and reactive power outputs of the GFM converter are depicted in Figure 12. It is worth noting that the outer power control loop has a strong ability to trace the reference signals during transients. Moreover, the grid voltage under αβ axis and frequency measured at PCC for the proposed control algorithm are presented in Figure 12 and Figure 13. It can be observed from the figures that the adopted GFM control can work well, and the voltage loop can track the given αβ references.

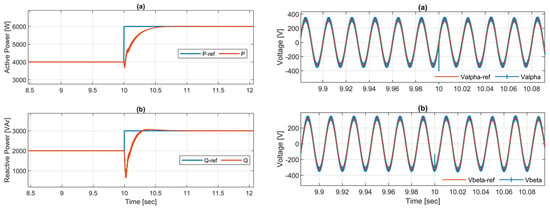
Figure 12. System response during a step change in power: (a,b) (left) active power and reactive power; (a,b) (right) reference and measured voltages in alpha–beta frame.

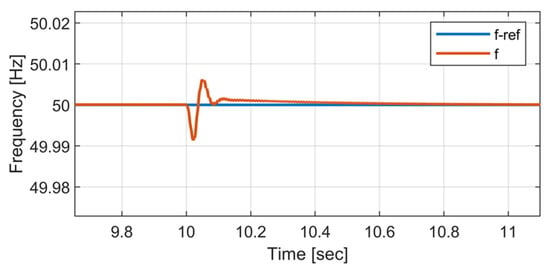
Figure 13. System frequency measured at PCC.

3.3. Power Quality Analysis with Nonlinear Load

To evaluate the power quality performance of the proposed grid-connected inverter system under nonlinear impedance conditions, a detailed harmonic analysis was carried out for both currents and voltages at key system nodes—namely, the grid side, inverter output, and load terminals as shown in Figure 14. A 2-kW nonlinear load (diode rectifier supplying a resistive load) was connected at the PCC. This configuration caused the load current to exhibit significant waveform distortion due to the rectification process, thereby injecting current harmonics into the system.

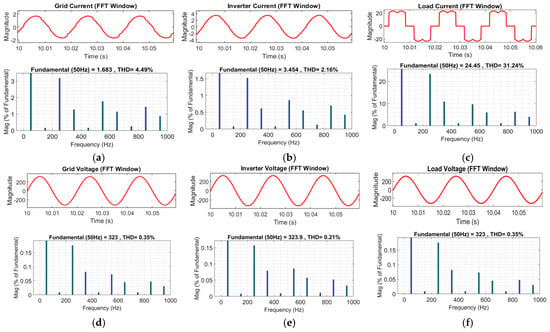
Figure 14. FFT-based THD analysis of grid-connected inverter under nonlinear load: (a) grid current, (b) inverter output current, (c) load current, (d) grid voltage, (e) inverter output voltage, and (f) load voltage.

The Fast Fourier Transform (FFT) analysis was performed to quantify the total harmonic distortion (THD) in the time-domain waveforms of the grid current, inverter output current, and load current, as well as their corresponding voltages.

• The load current showed the highest THD (≈31%), confirming the highly nonlinear nature of the connected load.
• The inverter output current exhibited a considerably lower THD (≈2%), indicating that the inverter’s control and filter effectively mitigated most harmonic components before feeding into the grid.
• The grid current maintained a moderate THD level (≈4%), demonstrating that the inverter successfully prevented significant harmonic injection into the grid.

Similarly, voltage waveforms at all three nodes were analyzed to assess the inverter’s impact on voltage quality. The grid voltage, inverter output voltage, and load voltage all maintained THD levels below 0.5%, well within IEEE Std. 519-2014 limits [29], indicating that the inverter effectively regulated its terminal voltage and did not distort the grid voltage.

Moreover, Figure 15 illustrates the variation in THD with load from 1 kW to 6 kW. As the load increases, the THD of inverter and grid currents rises due to higher harmonic injection from the nonlinear load, whereas the load current THD remains nearly constant. The voltage THD remains below 1% for all cases, confirming compliance with IEEE 519 standards.

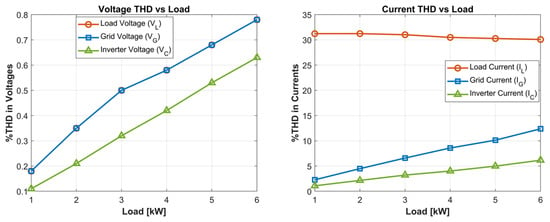
Figure 15. Variation in voltage and current THD with variation in nonlinear load.

Overall, the results confirm that the proposed inverter system provides excellent harmonic performance, even under nonlinear loading, by maintaining both current and voltage THD well within acceptable limits. This validates the inverter’s capability for grid-friendly operation and harmonic suppression, which are critical for modern renewable and power-electronic-dominated grids.

3.4. Change in SCR and X/R Ratio

The impedance of the grid and connecting lines has a significant impact on the dynamic performance of grid-connected converters. The strength of the grid is usually measured by SCR which is inversely proportional to the grid impedance as described [30]:

$$SCR={\displaystyle \frac{P_{sc}}{P_{DC rated}}}= {\displaystyle \frac{V_g^2}{Z_g.P_{DC rated}}}$$

(16)

where P_sc represents the grid short-circuit power; P_DC-rated is the rated power of the connected converter; V_g and Z_g are grid voltage and impedance, respectively. It is worth noting that the higher the grid impedance, the lower the SCR value and the less the grid strength, and vice versa. Moreover, with a given SCR value, the X/R ratio is another important factor to be considered in the converter performance.

Voltage source converters connected to weak power grids are highly sensitive to changes in active and reactive power injection and/or absorption. In a particular case of a weak grid with severe disturbance, the converter may lose synchronization and disconnect from the grid. In this subsection, the performance of the proposed converter is evaluated for various cases of grid strength, as detailed in Table 3, during the transition from islanded to grid-connected mode of operation.

Table 3. Summary of the selected grid and line impedance parameters.

Parameters	SCR = 7			SCR = 3
	X/R = 1	X/R = 3	X/R = 7	X/R = 1	X/R = 3	X/R = 7
Grid resistance (Rg)	0.534 Ω	0.239 Ω	0.107 Ω	1.246 Ω	0.557 Ω	0.249 Ω
Grid inductance (Lg)	1.7 × 10−3 H	2.3 × 10−3 H	2.4 × 10−3 H	3.96 × 10−3 H	5.32 × 10−3 H	5.54 × 10−3H
Line inductance (Ll)	1.8 × 10−3 H	1.8 × 10−3 H	1.8 × 10−3 H	1.8 × 10−3 H	1.8 × 10−3 H	1.8 × 10−3 H

In the first case, simulation results are obtained for the strong grid with SCR = 7 and the X/R ratio is selected as 1, 3, and 7. The key performance indicators during the transition from islanded to grid-connected mode, at t = 4 s, are shown in Figure 16. As shown in the figures, in predominantly resistive networks (X/R = 1), active power flow follows $P=V_c{V}_{g}cos\delta /R$, creating stronger P-V coupling that manifests as larger voltage fluctuations in subplot c (≈309 V minimum) and more pronounced active power oscillations in subplot a. Conversely, in inductive networks (X/R = 7), the relationship $P=V_c{V}_{g}sin\delta /X$ and $Q=V_c\left(V_c-V_{g}cos\delta \right)/X$ predominates, resulting in improved voltage stability (≈311 V minimum) and smoother power transitions. The reactive power transients (subplot b) exhibit approximately 3500 VAr peak-to-peak variation, with X/R = 7 showing superior damping coefficient due to the natural energy storage characteristics of inductive networks. The frequency deviation in subplot g (reaching 50.08 Hz), where network impedance affects the synchronizing coefficient, resulting in smaller frequency excursions for higher X/R ratios. The converter current in (subplot f) demonstrates the relationship I ≈ P/V, with X/R ratio influencing the power–angle relationship and consequently the transient current characteristics.

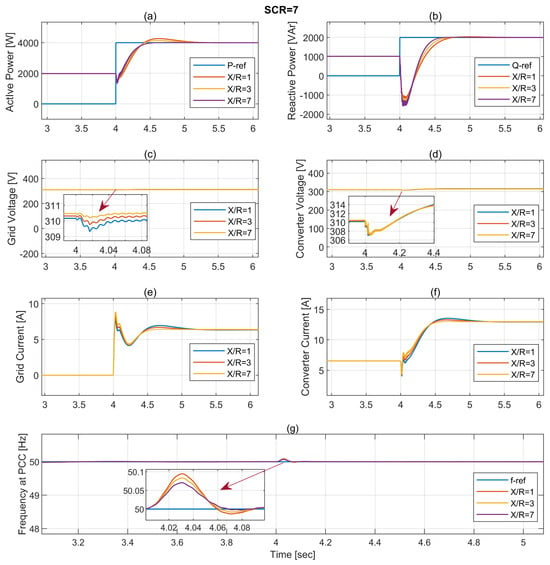
Figure 16. System response during transition with respect to SCR = 7 and X/R = 1, 3, and 7: (a) active power; (b) reactive power; (c) grid voltage; (d) converter voltage; (e) grid current; (f) converter output current; (g) frequency at PCC.

Similarly, in the second case, simulation results are obtained for the weak grid with SCR = 3, and the X/R ratio is selected as 1, 3, and 7. As shown in Figure 17, the reduced short-circuit ratio significantly impacts system dynamics across all metrics. Active power transition (subplot a) exhibits a more pronounced initial power dip compared to the SCR = 7 case, with P-V coupling producing more distinctive differences between X/R ratios. The reactive power response (subplot b) shows deeper negative excursions (exceeding 500 VAr) and slower recovery, validating the mathematical relationship $Q=V_c\left(V_c-V_{g}cos\delta \right)/X$ where lower SCR amplifies voltage sensitivity. Most notably, grid and converter voltage profiles (subplots c and d) reveal substantially deeper voltage sags (reaching approximately 304 V for X/R = 1 versus 308 V for X/R = 7), representing a ~2% deeper voltage depression than in the stronger grid case. This aligns with voltage sensitivity factor theory, where ∂V/∂Q increases with decreasing SCR. The transient grid current (subplot e) exhibits more pronounced oscillatory behavior with higher peak currents, while converter current dynamics (subplot f) demonstrate slower convergence to steady state. The frequency excursions (subplot g) reach approximately 50.1 Hz—slightly higher than in the SCR = 7 case, where lower SCR effectively reduces the system’s ability to resist frequency deviations.

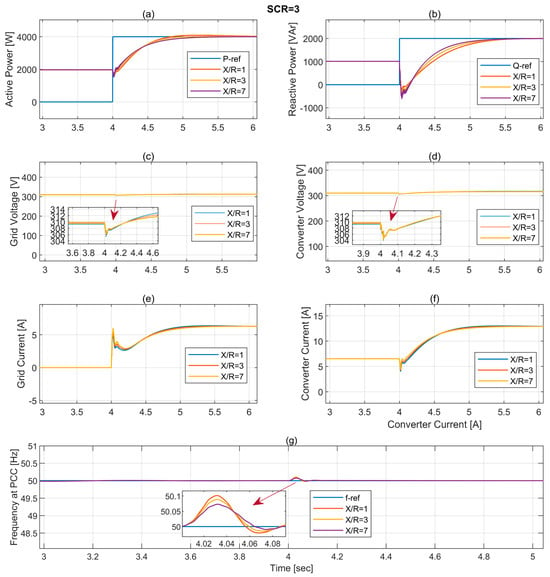
Figure 17. System response during transition with respect to SCR = 3 and X/R = 1, 3, and 7: (a) active power; (b) reactive power; (c) grid voltage; (d) converter voltage; (e) grid current; (f) converter output current; (g) frequency at PCC.

The key performance indicators observed in various cases of grid strength and its impedance characteristics are summarized in Table 4. To sum up, the weaker grid case (SCR = 3) consistently demonstrates more pronounced transient behavior across all measured parameters: deeper voltage sags (approximately 4% deeper than with SCR = 7), larger reactive power excursions, more significant frequency deviations, and prolonged settling times. The impact of X/R ratio variations becomes more consequential in weaker grids, with X/R = 1 exhibiting substantially degraded performance compared to X/R = 7, particularly in voltage recovery and reactive power stabilization.

Table 4. Summary of key performance indicators under varying grid SCR and X/R conditions.

Case	SCR	X/R	Active Power Deviation (W)	Reactive Power Excursion (VAr)	Min Grid Voltage (V)	Min Converter Voltage (V)	Max Grid Current (A)	Max Converter Current (A)	Peak Frequency Deviation (Hz)	Active Power Settling Time (s)
1	7	1	1500	−1500	309	306	8.0	13.5	0.08	0.50
2	7	3	1600	−1400	310	307	7.8	13.3	0.07	0.48
3	7	7	1700	−1300	311	308	7.6	13.1	0.06	0.55
4	3	1	1800	−550	304	302	5.5	13.0	0.10	0.65
5	3	3	1850	−500	306	304	5.3	12.8	0.09	0.60
6	3	7	1900	−450	308	305	5.2	12.6	0.08	0.55

To analyze the impact of grid impedance variations on the small-signal stability of the droop-based GFM inverter, a linearized state-space model was derived from the active power–frequency and reactive power–voltage droop equations. The state vector was defined as

$$x={\left[\begin{array}{cccc}\delta & \omega & V& \xi \end{array}\right]}^T,$$

(17)

where $\delta$ is the power angle, $\omega$ is the angular frequency deviation, V is magnitude of the terminal voltage, and $\xi$ is the integral state associated with the Q-V control loop. The resulting small-signal model can be expressed as follows:

$$\dot{x}=Ax, A=\left[\begin{array}{cc}\begin{array}{cc}0& 1\\ -k_{pp}{V}_g^2& -D\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}-k_{pq}/L_g& k_{qi}\\ -1/L_g& 0\end{array}\end{array}\right]$$

(18)

The grid impedance was parameterized by the short-circuit ratio (SCR) and X/R ratio, such that both grid strength and impedance characteristics are reflected in the eigenvalue analysis.

Figure 18 shows the eigenvalue trajectories for two representative grid strengths (SCR = 7 and SCR = 3) under a continuous sweep of X/R from 1 to 7. For SCR = 7, eigenvalues remain well-damped in the left half-plane, confirming fast dynamics and robust stability. In contrast, for SCR = 3, eigenvalues shift closer to the imaginary axis as X/R increases, indicating weaker damping and lightly oscillatory modes. These results confirm that both grid strength and impedance characteristics significantly affect the dynamic performance of droop-controlled GFM inverters.

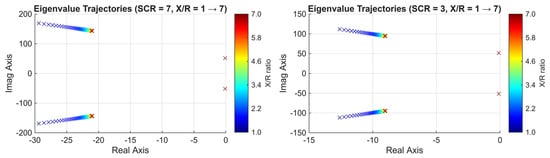
Figure 18. Eigenvalue trajectories of the system under varying grid impedances and X/R ratio.

Overall, all eigenvalues remain in the left half-plane across the investigated range of SCR and X/R, confirming that the droop-controlled GFM inverter remains stable under all considered grid conditions, with stability margins that depend on grid strength and impedance ratio.

3.5. Performance of the System Under Transient Faults

The dynamic response of the inverter under three-phase fault conditions with varying durations (50 µs, 100 µs, 350 µs, and 500 µs) is presented in Figure 19, where the fault is applied at t = 10 s at the PCC. The results reveal a strong correlation between fault duration and the severity of system disturbances. Notably, the 50 µs fault produces negligible impact on all monitored parameters, with voltage, current, active power, reactive power, and frequency maintaining near steady-state values throughout the fault event. This suggests that the inverter control system response time is significantly longer than 50 µs, effectively filtering out such ultra-short transients. In contrast, as fault duration increases to 100 µs and beyond, the inverter begins to exhibit measurable responses. For the 100 µs fault, mild voltage sag and current spike are observed, though recovery is rapid and well-damped. The most significant disturbances occur during the 350 µs and 500 µs faults, where the PCC voltage drops sharply to approximately 323–324 V from the nominal 328 V, accompanied by substantial current spikes reaching up to 10 A (compared to 7.5 A nominal). Active power exhibits sharp spikes exceeding 2300 W followed by temporary dips before recovery, while reactive power surges to approximately 2100 VAR, demonstrating the inverter’s grid-support capability during voltage disturbances. The frequency response shows pronounced oscillations of ±1.5 Hz, reflecting the power–frequency coupling inherent in droop-based control. Post-fault recovery demonstrates damped oscillatory behavior with stabilization times proportional to fault duration, ranging from 100 ms for the 100 µs fault to 400 ms for the 500 µs fault, while maintaining synchronization throughout all events. These results indicate that fault duration acts as a critical threshold parameter, with faults below 50–100 µs being effectively transparent to the control system, validating the robustness of the droop-based grid-forming control for practical grid applications.

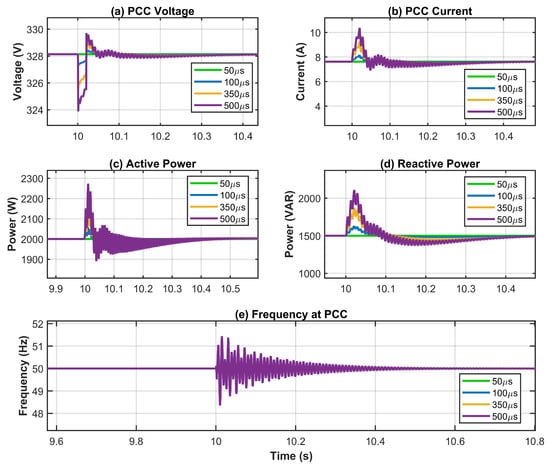
Figure 19. Performance of the system under three-phase short-circuit fault with varying duration (50–500 µs).

4. Conclusions

The fast-growing penetration of renewable energy sources in modern power systems affects grid strength and presents significant stability challenges. This work provides important insights into droop-controlled grid-forming (GFM) converters and the impact of grid impedance (SCR) and its characteristics (X/R ratio) on the dynamic performance of inverter-based power systems. Following an extensive literature review that identified critical research gaps in existing GFM control studies, a detailed case study is conducted to evaluate the dynamic performance of the droop-based GFM converter under diverse and challenging operating conditions, including varying grid impedances, mode transitions, transient faults, and nonlinear loads.

The study reveals that the proposed GFM approach exhibits superior reference-tracking capabilities during sudden changes in active and reactive power set points and maintains stable voltage and frequency in both grid-connected and autonomous modes. Simulation results quantify the influence of grid strength (SCR) and impedance angle (X/R ratio) on system performance: scenarios with SCR = 3 show greater deviations in all KPIs compared to SCR = 7 cases, while higher X/R ratios consistently improve performance metrics—reducing voltage sags by up to 2.3%, decreasing frequency deviations by approximately 25%, and accelerating settling times by 15–22%. These improvements are particularly critical in weak-grid conditions.

To complement the dynamic performance analysis, a linearized small-signal stability study with eigenvalue trajectories and Bode plots of the inner voltage and current loops have been included, demonstrating system stability and providing guidance for controller bandwidth selection. Transient fault analysis under three-phase to ground faults (50–500 µs) reveals critical threshold behavior: faults below 50–100 µs produce negligible impact, while longer durations trigger proportional responses with voltage sags reaching 5 V, current spikes up to 10 A, and power transients exceeding 15%. Recovery times range from 100 ms (100 µs fault) to 400 ms (500 µs fault), with the droop control maintaining synchronization throughout all events, demonstrating robust fault ride-through capability.

Performance under nonlinear loads (three-phase diode rectifier) shows voltage THD below 1% and current THD below 5%, remaining within IEEE 519 limits despite harmonic injections. These findings offer valuable design guidelines for inverter control systems in evolving power networks, especially in weak-grid applications, where accurate impedance characterization is essential for stable operation. The robustness and scalability of the proposed scheme for large-scale microgrids, supported by detailed stability analysis, will be explored in future studies.