Improved Metaball Discrete Element Method with Robust Contact Algorithm for General-Shaped Particles with Rounded Features

Abstract

Particle shape is a critical factor governing the macroscopic behavior of granular materials. While the Discrete Element Method (DEM) has proven to be a powerful tool for modeling these materials, the accurate representation of particles with realistic geometries remains a significant challenge. Numerous shape description techniques have been developed to address this, including sphere-clustering, polyhedral, spheropolyhedral, and superquadric approaches. However, these methods often introduce artificial surface roughness or are limited to highly regular geometries, particularly when modeling general-shaped particles with rounded features. The proposed method reformulates collision detection in the Metaball Discrete Element Method (MDEM) as a constrained optimization problem, ensuring stable and physically consistent contact handling. Validation results show excellent agreement with analytical solutions and significantly improved robustness over unconstrained MDEM approaches. Finally, the model is applied to analyze the effects of particle shape on compaction and segregation, demonstrating that the proposed MDEM effectively captures the influence of complex shapes on macroscopic behavior and offers strong potential for engineering and scientific applications.

1. Introduction

Irregularly shaped particles with rounded features are ubiquitous in geotechnical and industrial engineering [1,2,3]. Typical examples include natural soils, river pebbles, and rocks, with industrial counterparts ranging from pharmaceutical pills to agricultural seeds [4,5,6,7]. Particle shape governs macroscopic behaviors such as packing density, shear strength, flowability, and segregation. It does so by modulating contact topology, force-chain stability, rotational resistance, and local kinematics [4,8]. Therefore, accurately representing particle shape is essential for predicting granular material behavior. This is crucial in fields like geotechnics, pharmaceutical manufacturing, and agricultural processing.

Modeling irregularly shaped particles poses unique challenges due to their discontinuous nature and highly heterogeneous microstructure [9,10]. Classical continuum numerical methods assume that materials completely fill the space, and their behaviors are described by constitutive laws, which are typically expressed as differential equations relating macroscopic field variables like stress and strain [11]. However, these methods struggle to capture grain-scale interactions, especially when particle shapes are irregular [12]. As an alternative, the Discrete Element Method (DEM) has emerged as a powerful tool for simulating granular systems from a bottom-up perspective. In the DEM, each particle is tracked individually and allowed to interact via collisions and contact forces. As a result, complex macroscopic phenomena can emerge naturally from the collective dynamics of many particles [13]. With the rapid increase in computational power, the DEM has become increasingly popular in geotechnical, pharmaceutical, and agricultural applications for both static and dynamic behaviors [14].

A critical issue in DEM simulations is how to represent the geometry of individual particles. The simplest and most common idealization uses spheres (or circles in 2D), for which contact detection and force evaluation are exceptionally efficient [15]. However, real particles are often non-spherical, and particle shape can have a pronounced effect on bulk material behavior [3,4]. Several experimental and numerical studies demonstrate that using spheres can lead to simulation results that are misleading, predicting physical behaviors that are fundamentally different from those observed in reality. For instance, Soltanbeigi et al. [16] emphasized that the fundamental physics of torque and force transmission in spherical particles differs markedly from that of particles with explicitly modeled shapes. Similarly, Yang et al. [17] studied the creep and stress relaxation behaviors of granular materials, which a single spherical shape parameter cannot capture.

Over the past decades, a variety of shape description techniques have been proposed to incorporate realistic particle geometries into the DEM. Zhao and Zhao [18] recently provided a comprehensive review on shape descriptors, where the advantages and drawbacks of existing methods are discussed in detail. These methods can be broadly categorized into three classes [18,19]:

(1)

Primitive-clumped methods: A straightforward strategy is sphere clumping, where complex shapes are approximated by rigidly bonding multiple simple spheres into a single composite particle [20]. Contact detection between clumps is then reduced to a series of sphere–sphere interactions, preserving the computational advantages of spherical primitives [21]. However, this method introduces artificial surface roughness originating from the constituent spheres, which does not exist in the actual particle geometry. Furthermore, accurately approximating irregular shapes often requires hundreds of spheres per particle, greatly increasing the number of potential contact checks and the memory footprint [22].

(2)

Mesh-based methods: Another common approach represents particles as polygonal (2D) or polyhedral (3D) meshes. Such models can capture irregular geometries, including flat facets, sharp edges, and vertices, and are particularly suited for reproducing shapes obtained from scanned real grains [23]. Nonetheless, non-smooth geometries pose significant challenges for contact detection, as computing overlaps or forces between two arbitrarily oriented polyhedra is computationally expensive. Moreover, coarse mesh representations introduce artificial angularity unless extremely fine discretization is used, which again increases the computational cost [24,25,26]. To mitigate the numerical instability of pure polyhedral models while retaining geometric fidelity, the spheropolyhedron technique was developed. This approach generates smoothed shapes by computing the Minkowski sum of a base polyhedron and a sphere with a specified radius. Collisions between two spheropolyhedra can then be handled via interactions between their dilated boundaries, often reducing contact detection to simpler distance queries instead of costly polyhedron–polyhedron intersection checks [27,28]. The main limitation of Minkowski sum-based shapes is that the computational cost and complexity grow with the number of facets in the base polygon or polyhedron.

(3)

Analytical surface methods: Another class of shape representation uses analytic implicit or parametric surfaces to describe irregularly shaped particles [29]. Among these, the superquadric approach defines smooth convex shapes using analytical equations with a small number of parameters [30]. The advantage of superquadric shapes is that their surfaces are smooth and differentiable, which can facilitate analytic contact calculations. However, the diversity of shapes representable by a single superquadric is limited; classical superquadrics cannot easily capture non-symmetrical features [31]. To address this limitation, Zhao et al. [32] extended the concept and proposed a poly-superellipsoid method, in which each particle’s surface is composed of multiple superellipsoid patches. This allows for the representation of non-centrosymmetric and more complex convex geometries while retaining surface smoothness. Beyond superquadric-based models, several other analytical shape descriptors have been investigated. Potential particle methods define convex shapes via a single implicit mathematical function, although extending this approach to fully general 3D geometries remains challenging [33]. Fourier series-based methods describe particle boundaries using a Fourier expansion. This provides a smooth mathematical representation of arbitrarily complex planar shapes and can simplify the contact calculations by working in the space of Fourier coefficients [34]. The level-set DEM (LS-DEM) represents particle surfaces using a signed distance function, which provides geometric flexibility but requires substantial memory to store the level-set field [35,36]. Shi et al. [37] recently introduced a GPU-accelerated LS-DEM for particles with complex shapes, where a significant increase in speed is observed. More recently, the Metaball Discrete Element Method (MDEM) was introduced, where irregular particle shapes are represented using metaball functions. Contact detection is formulated as an unconstrained optimization problem, where the sum of the two metaball scalar fields is minimized. This can cause convergence toward non-physical minima when particles are far apart, leading to potential instability [38,39]. While this approach offers high geometric fidelity, the lack of constraints can negatively impact computational efficiency.

In this study, we propose and validate an improved MDEM framework incorporating a Lagrange multiplier formulation, specifically tailored for general particles with rounded features. The aim is to achieve a balance between high shape fidelity and computational efficiency. Compared with a superquadric DEM, the proposed model can describe rounded shapes with no symmetry requirement, and it is more computationally efficient than level-set DEM when dealing with convex particles (see Figure 1). The remainder of this paper is organized as follows: Section 2 introduces the mathematical formulation of the proposed shape representation and its contact detection algorithm. Section 3 presents validation studies, comparing the method’s accuracy against analytical solutions and experimental benchmark data. Section 4 demonstrates the application of the method to a complex engineering problem, showcasing its capabilities and offering new insights into the behavior of granular materials with rounded particles. Section 5 summarizes the main findings.

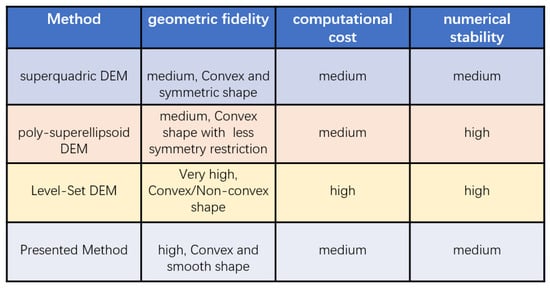
Figure 1. Comparison between different shape descriptors in the DEM.

2. Metaball Discrete Element Method

2.1. Discrete Element Method

The DEM is a numerical technique that explicitly resolves the translational and rotational motions of individual particles [15,40]. The translational dynamics are governed by Newton’s second law, while rotational motion is described by the angular momentum conservation equation:

$$\left\{\begin{array}{c}{m}_i{\mathit{a}}_i=m_i\mathit{g}+{\displaystyle \sum _{j=1}^N}{\mathit{F}}_{ij}^c+{\mathit{F}}_i^e,\hfill \\ {\displaystyle \frac{d}{dt}}\left({\mathbf{I}}_i{\mathit{\omega }}_i\right)={\displaystyle \sum _{j=1}^N}{\mathit{T}}_{ij}^c+{\mathit{T}}_i^e,\hfill \end{array}\right.$$

(1)

where $m_i$, ${\mathbf{I}}_i$, ${\mathit{a}}_i$, and ${\mathit{\omega }}_i$ represent its mass, inertia tensor, translational acceleration, and angular velocity, respectively. The force on the particle is the sum of gravity $m_i\mathit{g}$, external forces ${\mathit{F}}_i^e$, and contact forces $\sum {\mathit{F}}_{ij}^c$ from neighboring particles. Similarly, the torque is composed of external torques ${\mathit{T}}_i^e$ and contact-induced torques $\sum {\mathit{T}}_{ij}^c$. It should be noted that the rotational dynamics are practically solved by applying Euler’s equation within the particle’s body-fixed reference frame [40,41].

A key component of the DEM is the contact forces ${\mathit{F}}_{ij}^c$ and torques ${\mathit{T}}_{ij}^c$. Among the various available models, the linear spring–dashpot formulation proposed by Cundall and Strack [42] is one of the most widely adopted. In this model, the normal contact force between particles i and j is given by

$$F_n^c=k_n\delta +{\eta }_n({\mathit{v}}_{\mathit{j}}-{\mathit{v}}_{\mathit{i}})·\mathit{n},$$

(2)

where $k_n$ and ${\eta }_n$ are the stiffness and damping coefficients in the normal direction, while $\mathit{n}$ is the unit vector connecting the particle centers. The tangential contact force $F_t^c$ follows Coulomb’s friction criterion, $F_t^c\le {\mu }_s{F}_n^c$, and is evaluated as

$$\left\{\begin{array}{cc}{F}_t^c\hfill & =min({\mu }_s{F}_n^c,F_{t0}^c),\hfill \\ F_{t0}^c\hfill & =\Vert -k_t\mathit{\xi }-{\eta }_t\left(({\mathit{v}}_{\mathit{j}}-{\mathit{v}}_{\mathit{i}})·\mathit{t}\right)\Vert ,\hfill \end{array}\right.$$

(3)

where ${\mu }_s$ is the static friction coefficient; $k_t$ and ${\eta }_t$ are the tangential stiffness and damping coefficient, respectively; $\mathit{t}$ is the unit tangential vector; and $\mathit{\xi }$ is the tangential displacement vector determined from the relative tangential motion. $F_t^{c_0}$ represents the initial trial tangential force before enforcing the Coulomb friction criterion. For time integration, the governing equations of motion are numerically integrated using the second-order Velocity Verlet algorithm [13].

2.2. Metaball Function

Many particle shapes can be represented by implicit surfaces, which are mathematically defined by implicit functions. Metaballs are a specific type of implicit surface [38]. The metaball function used in this study is defined as

$$M\left(\mathit{x}\right)=\sum _{i=0}^{n-1}{\displaystyle \frac{k_i}{{\Vert \mathit{x}-{\mathit{x}}_{\mathit{i}}\Vert }^2}}=1$$

(4)

In this equation, ${\mathit{x}}_{\mathit{i}}$ is the i-th control point, collectively forming the skeleton of the shape. $k_i$ is the corresponding weight that controls the influence range of ${\mathit{x}}_{\mathit{i}}$, and n is the total number of control points. For instance, a sphere is a special case described by Equation (4) with a single control point at its center, where the radius is equal to $\sqrt{k_0}$. The particle surface is implicitly defined by $M\left(\mathit{x}\right)=1$. One key advantage of Equation (4) is the lack of restrictions on the selection of control points, with weights able to take any non-negative value. This flexibility allows metaball functions to describe a wide variety of complex shapes.

A 2D metaball particle and its control points are illustrated in Figure 2, which illustrates the influence of control point weights on shape boundaries, showing how varying weights alter the resulting particle geometry. The contour plot of the scalar field, $M\left(\mathit{x}\right)$, highlights a key property: the area enclosed by an isosurface ($M\left(\mathit{x}\right)=C$) increases as the threshold value, C, decreases. This property will be used to handle collisions between metaballs in the next section.

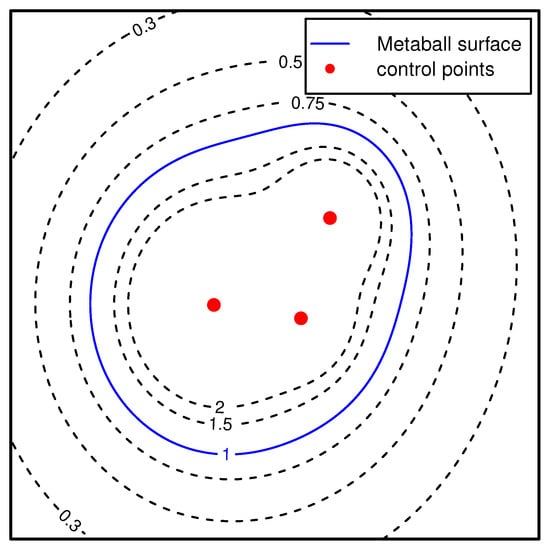
Figure 2. Two-dimensional graphic illustration of a metaball particle and its control points. The dash lines refer to Equation (4) with different values.

2.3. Collision of Two Metaballs

Collision detection between two metaballs requires determining the contact point, contact normal, and overlap. Instead of a purely geometric approach, this can be formulated as an optimization problem using the analytical metaball expression (Equation (4)). However, since small overlaps are permitted in the DEM, the minimum distance can become negative upon particle contact, undermining stability and accuracy. To mitigate this issues, we adopt a spherometaball strategy inspired by the spheropolyhedra method. A spherometaball is the Minkowski sum of an eroded metaball and a sphere of radius $R_s$ (Figure 3). With overlaps small relative to $R_s$, the eroded metaballs remain non-intersecting, reducing collision detection to sphere–sphere interactions [39]. The remaining task is to compute the closest points between the eroded metaballs, a non-trivial problem for implicit surfaces.

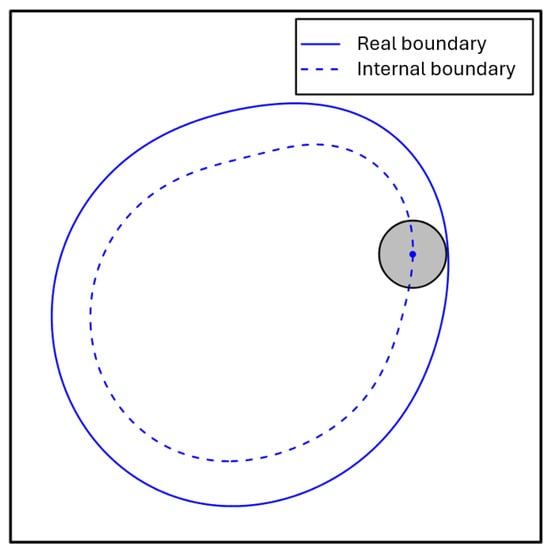
Figure 3. An illustration of a spherometaball The solid and dash lines refer to the original metaball and the internal metaball. The original metaball is approximated by the Minkowski sum of the internal metaball and a sphere.

The original Metaball DEM takes advantage of the following observation: the metaball function naturally depends on distance; instead of solving the closest-point problem directly, a point that locally minimizes ${\mathit{M}}_i\left(x\right)+{\mathit{M}}_j\left(x\right)$ is found by the Newton–Raphson method, and the closest points are approximated by a Taylor expansion. Although the original Metaball DEM performs well when initialized appropriately for iterations, it suffers from several drawbacks. First, the global minimum differs from the desired local minimum, where $\mathit{x}$ goes to infinity. ${\mathit{M}}_i\left(x\right)+{\mathit{M}}_j\left(x\right)$ achieves its global minimum, which is obviously not useful for finding the closest points. Unfortunately, the Newton–Raphson method can converge towards this solution with an improper initial guess. Although this problem can be solved by using a backup scheme with a better initial guess, it is time-consuming and problem-dependent, which makes the scheme less robust. Secondly, when evaluating the closest points, the original Metaball DEM assumes that the closest points are not far away from the local minimum, which is only true when the gap between two particles is small. On the other hand, when the gap is large, the first-order Taylor expansion may introduce a significant error. To overcome these limitations, we introduce an improved scheme where the closest points are found directly. Since there is no intersection between two Metaballs, finding the closest point on Metaball j to Metaball i is equivalent to solving the following constrained optimization problem:

$$\begin{array}{cc}\hfill & maximize{M}_i\left(\mathit{x}\right)\hfill \\ \hfill & subjectto{M}_j\left(\mathit{x}\right)=1\hfill \end{array}$$

(5)

It is worth mentioning that Equation (5) is equivalent to minimizing the distance to particle i since $M\left(\mathit{x}\right)$ increases with decreasing distance to the particle surface.

Equation (5) formulates contact detection as a constrained optimization problem, where the objective is to find the point on one metaball surface that maximizes the distance field of the other, ensuring non-overlapping and stable contact representations. It can be solved by the Lagrange Multiplier method, where the constrained optimization is converted into unconstrained optimization. The Lagrangian $\mathcal{L}(\mathit{x},\lambda )$ is defined as

$$\mathcal{L}(\mathit{x},\lambda )=M_i\left(\mathit{x}\right)+\lambda (M_j\left(\mathit{x}\right)-1)$$

(6)

where $\lambda$ is the Lagrange multiplier. If the maximum of Equation (6) exists, all its partial derivatives should be zero. Thus we can define following residual function:

$$\mathit{f}(\mathit{x},\lambda )=\left[\begin{array}{c}\nabla M_i\left(\mathit{x}\right)+\lambda \nabla M_j\left(\mathit{x}\right)\\ M_j\left(\mathit{x}\right)-1\end{array}\right]=\mathbf{0}$$

(7)

Equation (7) is a nonlinear equation, and its analytical solution is very difficult to find. Similar to the original Metaball DEM, we solve Equation (7) efficiently by the Newton–Raphson method. The derivative of Equation (7) (Jacobian) is given as

$$\mathit{J}(\mathit{x},\lambda )=\left[\begin{array}{cc}{\nabla }^2{M}_i\left(\mathit{x}\right)+\lambda {\nabla }^2{M}_j\left(\mathit{x}\right)& \nabla M_j\left(\mathit{x}\right)\\ \nabla M_j{\left(\mathit{x}\right)}^{\top }& 0\end{array}\right]$$

(8)

The second row corresponds to the derivative of the constraint function $M_j\left(x\right)=1$, ensuring that the optimization remains on the metaball surface. The bottom-right element is zero since the constraint equation is independent of the Lagrange multiplier $\lambda$.

For each iteration, the closest point ($\mathit{x}$) and $\lambda$ are updated as

$$\left[\begin{array}{c}{\mathit{x}}_{k+1}\\ {\lambda }_{k+1}\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_k\\ {\lambda }_k\end{array}\right]-\alpha {\mathit{J}}^{-1}\mathit{f}$$

(9)

where $\alpha$ is a damping coefficient for the Newton–Raphson method to avoid oscillations. Its value is set to 1 as the default in this study.

It is well known that the initial point of the Newton–Raphson method significantly influences stability and the convergence rate. Two strategies are used to choose a proper initial point: (1) After a potential collision (a pair of particles) is detected, the previous local minimum point is used as the initial point (${\mathit{x}}_0$). If this potential collision already exists at the previous time step, ${\lambda }_0$ is handled in the same manner. Since the displacements of particles are small during one time step, the previous local minimum point is most likely close to the solution of Equation (7) at the current time step. (2) If the previous local minimum point does not exist, the surface mesh is used to find a proper initial guess by looping over all the surface vertices of particle j and to find the vertex with the maximum $M_i\left({\mathit{V}}_j\right)$ as ${\mathit{x}}_0$, with ${\lambda }_0=1\times {10}^{-5}$. The flowchart shown in Figure 2 of the proposal metaball–metaball contact algorithm can be found in Algorithm 1. It improves robustness by reformulating collision detection as a constrained optimization problem, which ensures more accurate and stable contact handling, especially for particles with complex geometries.

It is worth mentioning that, in some extreme cases, the Newton–Raphson method may still fail to converge even with a carefully chosen initial guess. Thus, we introduce a backup strategy to further improve accuracy. If convergence fails, the damping coefficient $\alpha$ is reduced by a factor of 2, and the initial guess is reset. We intentionally avoid more advanced stabilization techniques, such as the line search, because the undamped Newton–Raphson method already succeeds in most practical scenarios. The additional computational cost of such methods is unnecessary for our applications, where the proposed backup strategy suffices to handle rare convergence failures. This same stabilization approach is consistently applied wherever the Newton–Raphson method is used in this work.

Algorithm 1 Metaball constrained optimization

Require:  Initial guess ${\mathit{x}}_0\in {\mathbb{R}}^3$, ${\lambda }_0\in \mathbb{R}$ Require:  Metaball functions $M_i\left(\mathit{x}\right)$, $M_j\left(\mathit{x}\right)$ with gradients and Hessians Require:  Convergence tolerance $ϵ$, max iterations $K_{max}$ 1: $(\mathit{x},\lambda )\leftarrow ({\mathit{x}}_0,{\lambda }_0)$                   ▹ Initialize as in Equation (5) 2: $\mathrm{residual}\leftarrow \infty$   While (residual $>\epsilon$ and $k<K_{max}$) do 3: Compute $M_j\left(\mathit{x}\right)$, $\nabla M_j\left(\mathit{x}\right)$, ${\nabla }^2{M}_j\left(\mathit{x}\right)$ 4: Compute $M_i\left(\mathit{x}\right)$, $\nabla M_i\left(\mathit{x}\right)$, ${\nabla }^2{M}_i\left(\mathit{x}\right)$ 5: $\mathit{f}\leftarrow \mathrm{Equation}\left(7\right)$                        ▹ Residual vector 6: $\mathrm{new}\_\mathrm{residual}\leftarrow \parallel \mathit{f}\parallel$ 7: if$\mathrm{new}\_\mathrm{residual}<ϵ$or$|\mathrm{residual}-\mathrm{new}\_\mathrm{residual}|<{10}^{-12 }$then 8:        break 9: end if 10: $\mathit{J}\leftarrow \mathrm{Equation}\left(8\right)$                         ▹ Jacobian matrix 11: $\left[\begin{array}{c}{\mathit{x}}_{k+1}\\ {\lambda }_{k+1}\end{array}\right]\leftarrow \mathrm{Equation}(9)$                        ▹ Newton step 12: return$\mathit{x}$                         ▹ Solution to Equation (5)

For the closest point on particle i, the above algorithm is still applicable in principle; however, it is not the best solution in terms of efficiency. Instead, we can leverage the fact that $\nabla M_i\left({\mathit{x}}_{ci}\right)$ is parallel with $\nabla M_j\left({\mathit{x}}_{cj}\right)$, where ${\mathit{x}}_{ci}$ and ${\mathit{x}}_{cj}$ are the closet points. Thus, we have

$${\mathit{x}}_{ci}={\mathit{x}}_{cj}+t\nabla M_j\left({\mathit{x}}_{cj}\right)$$

(10)

Here, t denotes the signed distance along the normal vector, representing the separation between the two closest points.

It can be combined with $M_i\left({\mathit{x}}_{ci}\right)=1$ to yield

$$M_i\left({\mathit{x}}_{cj}+t\nabla M_j({\mathit{x}}_{cj})\right)=1$$

(11)

where the only unknown is t. Equation (11) is also solved by the Newton–Raphson method when the initial condition is set to $t_0=0$.

Finally, the overlap $\delta$, contact direction $\mathit{n}$, and contact point ${\mathit{x}}_{cp}$ are defined as

$$\left\{\begin{array}{cc}\hfill & \delta =R_{si}+R_{sj}-\Vert {\mathit{x}}_{ci}-{\mathit{x}}_{cj}\Vert \hfill \\ \hfill & \mathit{n}={\displaystyle \frac{{\mathit{x}}_{ci}-{\mathit{x}}_{cj}}{\Vert {\mathit{x}}_{ci}-{\mathit{x}}_{cj}\Vert }}\hfill \\ \hfill & {\mathit{x}}_{cp}={\mathit{x}}_{ci}+(R_{si}-0.5\delta )\mathit{n}\hfill \end{array}\right.$$

(12)

The collision between a sphere and a metaball can be handled similarly by converting the sphere to a metaball: use the sphere mass centre as the only control point and set its weight as the square of the radius.

2.4. Collision of the Metaball and Plane

It is common to use planes as boundaries in DEM simulations; the collisions between the metaball and the plane are handled similarly as metaball collisions. Here the question is how to find the closest points between the metaball and the plane. As Figure 4 shows, it is equal to finding a point on the metaball with a normal that is perpendicular to the plane and pointing towards the inside of the plane. Thus, we can formulate the following equations:

$$\left\{\begin{array}{cc}\hfill \nabla M\left(\mathit{x}\right)& =\lambda {\mathit{n}}_w,\hfill \\ \hfill M\left(\mathit{x}\right)& =1,\hfill \end{array}\right.$$

(13)

where ${\mathit{n}}_w$ is the normal direction of the plane. $\lambda$ serves as the Lagrange multiplier, ensuring that the metaball surface normal is parallel to the plane normal. Equation (13) can be solved by the Newton–Raphson Method as well. Similar to the collision of metaballs, the previous solution is used as the initial point if this potential collision already exists at the previous time step. Otherwise, the initial point is determined by finding the surface vertices on the metaball with the shortest distance to the plane.

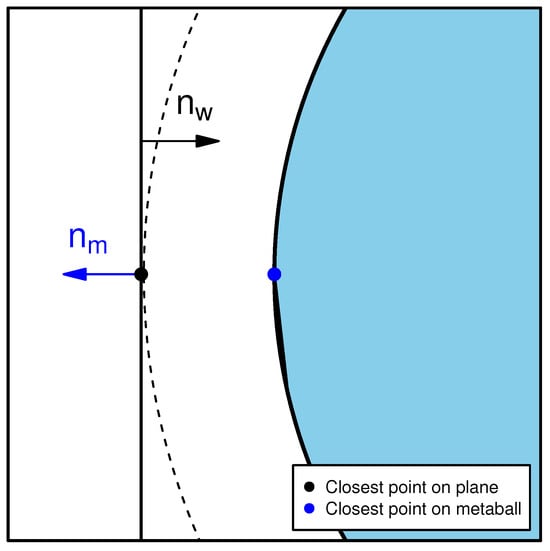
Figure 4. Collision between the metaball and the plane. The coordinate is rotated to make sure that the norm of plane ${\mathit{n}}_w$ is perpendicular to the x-axis. The problem is transformed to find a point on the plane where its norm (${\mathit{n}}_m$) to the metaball is perpendicular to ${\mathit{n}}_w$.

Once the closest point on metaball ${\mathit{x}}_{cm}$ is determined, the corresponding closest point on plane ${\mathit{x}}_{cw}$ is found by projecting ${\mathit{x}}_{cm}$ to the plane, and the overlap $\delta$, contact direction $\mathit{n}$, and contact point ${\mathit{x}}_{cp}$ are defined as

$$\left\{\begin{array}{cc}\hfill & \delta =R_{sm}+R_{sw}-\Vert {\mathit{x}}_{cm}-{\mathit{x}}_{cw}\Vert \hfill \\ \hfill & \mathit{n}={\displaystyle \frac{{\mathit{x}}_{cm}-{\mathit{x}}_{cw}}{\Vert {\mathit{x}}_{cm}-{\mathit{x}}_{cw}\Vert }}\hfill \\ \hfill & {\mathit{x}}_{cp}={\mathit{x}}_{cw}+0.5\delta \mathit{n}\hfill \end{array}\right.$$

(14)

2.5. Collision Detection

The collision detection process in the DEM takes a considerable part of the total computational costs. By replacing metaballs with their circumscribed spheres, the classical Linked Cell Method can be used for the coarse contact detection phase, as shown in Figure 5. The domain is divided into cubic cells, and particles are hashed into cells. Collision detection is only conducted for particles that are within the same cell or near neighboring cells. A potential collision can be found when the overlap of circumscribed spheres is larger than zero. The cell size is determined by the largest circumscribed spheres in the system.

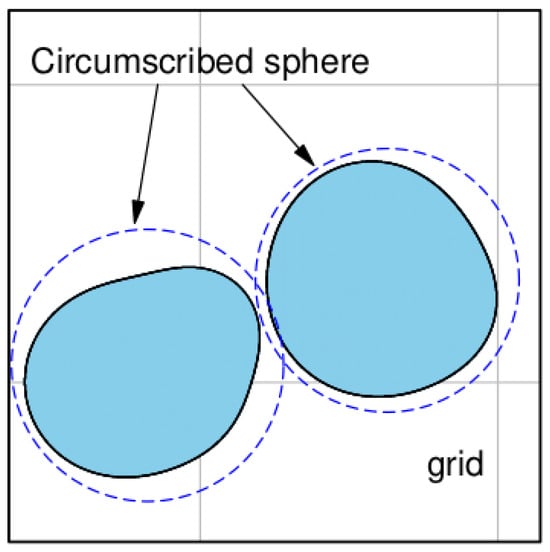
Figure 5. Contact detection between two metaballs. The circumscribed spheres (blue dashed lines) are sorted into cells (gray). A potential collision can be found if the overlap of circumscribed spheres is larger than zero.

3. Validations

To validate the proposed algorithm for metaball–metaball interactions, we conduct simulations of the collision between two metaballs. The particle shape is shown in Figure 6, where three control points are used, which form a triangle. The particle density is $3\times {10}^3$$\mathrm{kg}/{\mathrm{m}}^3$. The spherical radius is $R_s=2\times {10}^{-4}$$\mathrm{m}$, and the time step is set to $dt=1\times {10}^{-5}$$\mathrm{s}$. Two metaballs are placed with a small gap along the x direction, and they are assigned opposite velocities with a magnitude of $0.1$$\mathrm{m}/\mathrm{s}$. The normal stiffness coefficient is $k_n=1\times {10}^7$$\mathrm{N}/\mathrm{m}$, and the rotational degree of freedom is removed. Figure 7 shows the kinetic energy as a function of time, where the kinetic energy is normalized by the initial kinetic energy, and time is normalized by the total simulated time. Different damping coefficients (${\eta }_n$) are used to model energy loss due to contact. Kinetic energy is conserved during the collision without damping. With an increasing damping coefficient, the energy loss due to the contact is also correctly captured in the model.

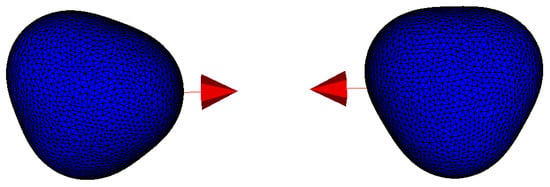
Figure 6. Particle shape used in the simulation of two metaball contacts. The red arrows show the initial velocity.

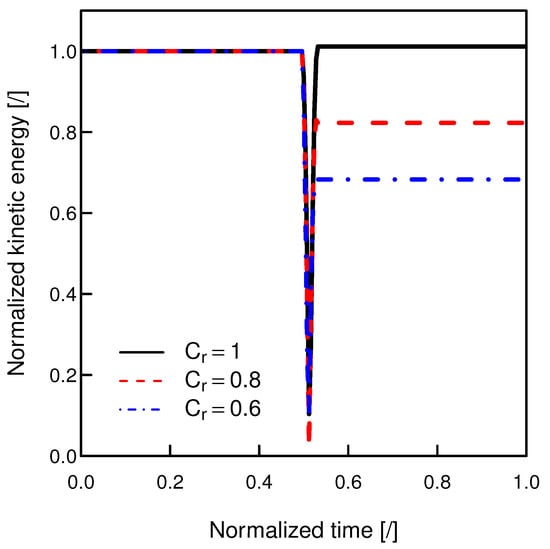
Figure 7. Energy as a function of time during the collision between two metaballs with different damping coefficients.

To validate the correctness of the proposed algorithm for metaball–plane interactions, as well as the friction model, simulations of a metaball sliding on a plane are conducted. The simulations consist of two stages: First, the metaball is free falling from a certain height under gravity with no other constraints. Once the kinetic energy of the metaball reaches zero due to damping, its degree of freedom for rotation is removed to prevent rolling. Then, different initial velocities ($0.1,0.2,0.3,$ and $0.4$$\mathrm{m}/\mathrm{s}$) along the x-axis are assigned to the metaball. The friction coefficient is set to $0.2$, and other model parameters used in the simulations remain the same as in the simulations of the collision between two metaballs. Figure 8 shows the final displacement as a function of the initial velocity. The simulated final displacements agree excellently with the theoretical predictions, and the RMSE is less than $1\times {10}^{-7}$, demonstrating the correctness of the proposed algorithm for metaball–plane interactions as well as our DEM implementation.

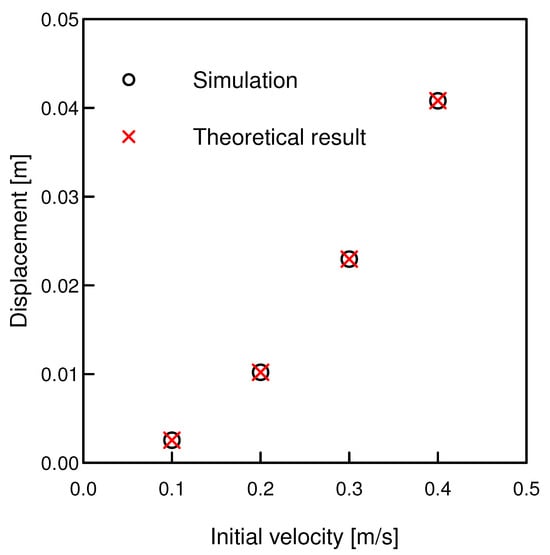
Figure 8. Final displacement as a function of the initial velocity of sliding between the metaball and the plane.

4. Numerical Examples

This section presents two numerical examples designed to evaluate the capability of the proposed method and to demonstrate the influence of particle shape on bulk mechanical behavior. The examples are as follows: (1) the packing and uniaxial compression of granular assemblies and (2) the segmentation of complex particle aggregates.

Across all simulations, a consistent set of microscopic parameters is employed to ensure a valid comparison between cases. The contact normal and tangential stiffness are set to $k_n=1\times {10}^7$$\mathrm{N}/\mathrm{m}$ and $k_n=1\times {10}^5$$\mathrm{N}/\mathrm{m}$, respectively, while the normal and tangential damping coefficients are calculated from the coefficient of restitution, which is set to $0.8$. These parameters were calibrated through a series of simulations to ensure physically realistic behavior, and they are held constant for all subsequent tests involving the same material.

4.1. Packing and Uniaxial Compression of Granular Assemblies

To investigate the influence of particle morphology, this simulation compares the behavior of two distinct particle types: irregular metaballs and spheres. The irregular metaballs are defined by three control points that form a triangle, as illustrated in Figure 9, with a characteristic spacing of $1.5\times {10}^{-3}$ m. For spheres, a single control point is placed at the center, and the square root of its weight factor defines the radius. Both particle types are modeled with identical volumes to ensure a direct comparison. All mechanical parameters are kept the same for both sphere and metaball particles.

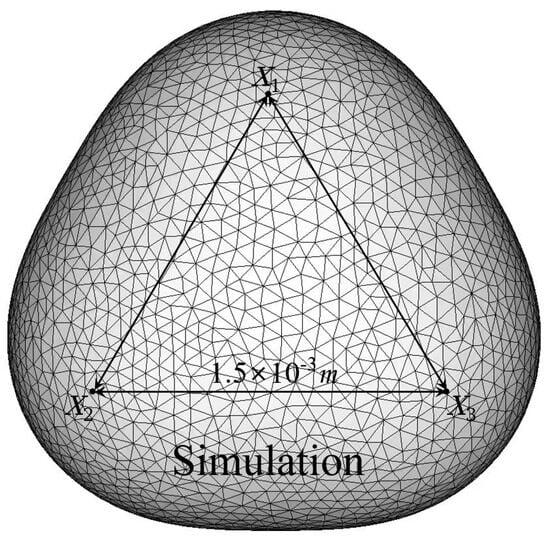
Figure 9. Illustration of the metaball-based particle shape defined by its control points.

The simulation procedure consists of three main stages: packing, adding a top lid, and compression. Initially, 1500 particles of a single type (either metaballs or spheres) are generated at random positions and orientations within a rectangular container with dimensions of $0.4 \mathrm{m}\times 0.4 \mathrm{m}\times 2.5 \mathrm{m}$. The particles are then allowed to settle under gravity until the system reaches a quasi-static state, forming a stable initial packing. Once the particle bed is stable, a flat and rigid lid is positioned on top of the granular assembly, and it is constrained to move only in the z direction. Gravity is applied to the top lid, and gravity is removed from the particles. Once equilibrium is reached, this wall is then driven downward at a constant velocity of $0.01 \mathrm{m}/\mathrm{s}$ to apply uniaxial compression to the sample.

Figure 10 presents the vertical stress evolution for irregular and spherical assemblies, respectively. The stress on the top wall is obtained from contact forces acting on the boundaries. A comparison of these results reveals a significant influence of particle shape on the macroscopic mechanical response of the granular system. The most clear observation is the dramatic difference in the magnitude of the measured stress: the stress in the spherical particle is approximately two orders of magnitude greater than that observed in the assembly with irregular particles.

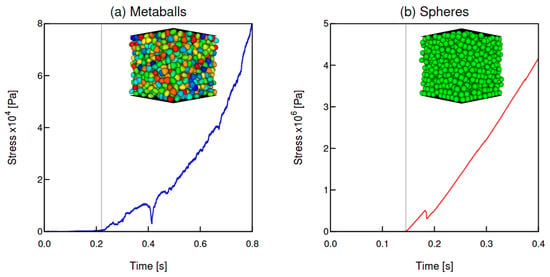
Figure 10. Stress evolution during 1D compression for sphere and metaball samples.

For spheres, compression begins at $t\approx 0.15$ s, and stress increases almost linearly until the peak is reached. This smooth response reflects dense sphere packing, where load is transmitted through a stable network of point contacts. Deformation occurs mainly by sliding and rolling, producing gradual compaction and stiffening. Minor fluctuations are linked to localized slip events, but the overall behavior remains homogeneous and stable.

In contrast, the irregular assembly shows a markedly different response. Compression starts later ($t\approx 0.25$ s) and produces a nonlinear, serrated stress curve with sharp rises and abrupt drops. This stick–slip behavior arises from mechanical interlocking and fragile force chains. Angular particles inhibit sliding and rotation, forming rigid but unstable load-bearing chains. Under increasing strain, these chains buckle and collapse, releasing stress abruptly. The system then reorganizes, and the process repeats, yielding the characteristic jagged response and limiting the bulk strength.

The two-order-of-magnitude contrast highlights the critical role of particle morphology. While spherical assemblies sustain high pressures via uniform contact networks and elastic deformation, irregular particles rely on unstable force chains that dissipate energy through recurrent structural collapses, resulting in a much softer bulk response.

To further investigate the micro-structural origins of the observed mechanical behavior, the distribution of the coordination number, Z, was analyzed for both particle systems after the packing stage. The coordination number is defined as the number of particles in direct contact with a given particle. Figure 11 presents the probability density functions for both the spherical and irregular polygonal (metaball) particle assemblies after initial packing.

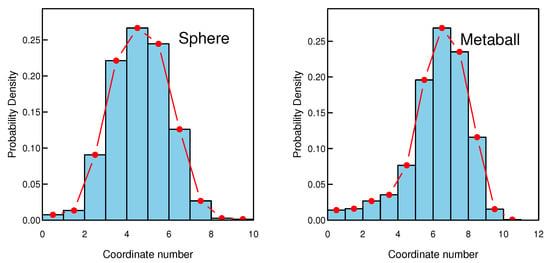
Figure 11. Distribution of the coordinate number for sphere and metaball samples.

For the spherical assembly, the coordination number distribution is centered around a mean of $Z\approx 5$, spanning symmetrically from $Z=1$ to $Z=8$, which is consistent with typical values for randomly packed spherical particles. This structure facilitates particle rearrangement through rolling and sliding, contributing to the homogeneous compression behavior observed previously. In contrast, the irregular particles exhibit a higher coordination number, with both the peak and mean around $Z\approx 7$. The distribution also exhibits a noticeable positive skew, with a tail extending towards higher coordination numbers ($Z>8$). This asymmetry suggests that the angular geometry facilitates highly interlocked local configurations where some particles achieve an exceptionally large number of contacts. This significant increase in overall particle connectivity is a direct consequence of the particle’s shape, leading to a more robustly interlocked fabric. This higher degree of interlocking restricts particle mobility, preventing easy rearrangement and giving rise to the formation and subsequent collapse of strong force chains, which explains the stick–slip stress response and the overall lower bulk strength of the assembly.

To further investigate the micro-mechanics, we examined the probability density distributions of normal and shear contact forces at the beginning of compression (Figure 12 and Figure 13). Across both systems, normal forces (order ${10}^{-2}$ N) exceed shear forces (order ${10}^{-3}$ N) by roughly one order of magnitude, confirming that load transmission is dominated by normal contacts.

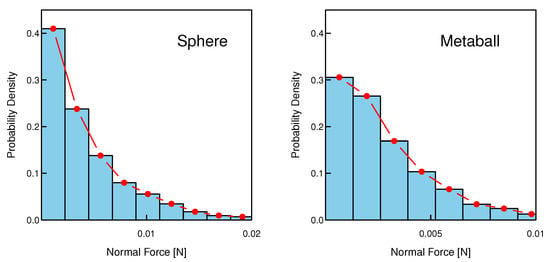
Figure 12. Distribution of normal contact force for sphere and metaball samples.

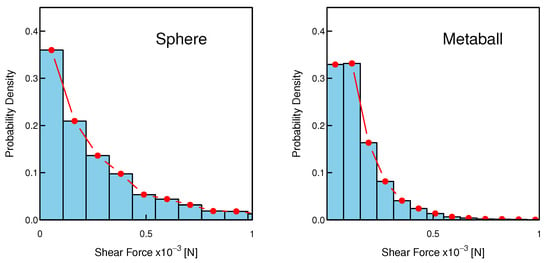
Figure 13. Distribution of shear contact force for sphere and metaball samples.

The normal force distributions for both particle types exhibit a characteristic exponential-like decay, indicating that the contact network is dominated by a large number of weak contacts, with a small fraction of contacts carrying significantly larger loads. However, the influence of particle shape is evident in both the magnitude and the decay rate. For the sphere assembly, the distribution has a longer tail, extending to much higher forces (up to $0.02$ N), and it decays more rapidly. In contrast, the distribution for the irregular particles has a lower maximum force (below $0.01$ N), which indicates that the force chains in the interlocked system with irregular particles are weaker and less prevalent than the robust chains formed by the spheres. A similar trend is observed in the shear force distributions. Although the overall magnitude of shear forces is comparable between the two systems, the decay rate for the irregular particles is marginally faster than that for the spheres. These results imply that the interlocking nature of the non-spherical particles creates a more constrained contact environment where the mobilization of large tangential forces is less probable.

Overall, the most significant difference between the sphere and metaball assemblies is the stress evolution under the same compression condition. It is reasonable to believe that the close-packing density of metaballs should be higher than that of spheres, which leads to more space for metaballs to reorient instead of accumulating stress.

4.2. Segregation of Complex Particle Aggregates

This numerical experiment examines the influence of particle shape on size-induced segregation. Two simulations are conducted, each involving a bidisperse mixture of large and small particles. The small particles are identical in both cases, while the large particles differ in shape: either perfect spheres or irregular particles generated via the metaball method. To ensure a valid comparison, the large spheres and metaballs are assigned equal volumes, which are $6.147$ times larger than the small particles.

The initial setup is identical for both cases. A total of 100 large and 4500 small particles are randomly distributed within a rectangular volume, creating a well-mixed initial state. Fixed small spheres form a rough bottom to provide friction, which will later introduce a velocity gradient along the z direction. Periodic boundary conditions are applied to the horizontal direction. The system is then released from rest and allowed to fall under gravity, settling into a stable packed column. Once the granular column has reached a quasi-static state, a shear flow is induced by adjusting the direction of gravity by an inclining angle of ${25}^{\circ }$. The final spatial distributions after packing, as well as the evolution of segregation patterns during the shearing phase, are then analyzed and compared between the two cases to elucidate the role of large particle non-sphericity in segregation.

The evolution of segregation for systems with large spherical and irregular particles is shown in Figure 14 and Figure 15, respectively. These snapshots highlight the distinct segregation dynamics that arise from the combined effects of particle shape, gravity-driven deposition, and subsequent shear. In general, large particles gradually rise to the top, regardless of the shape of the particles. This observation implies that the size difference is the primary impact factor for segregation.

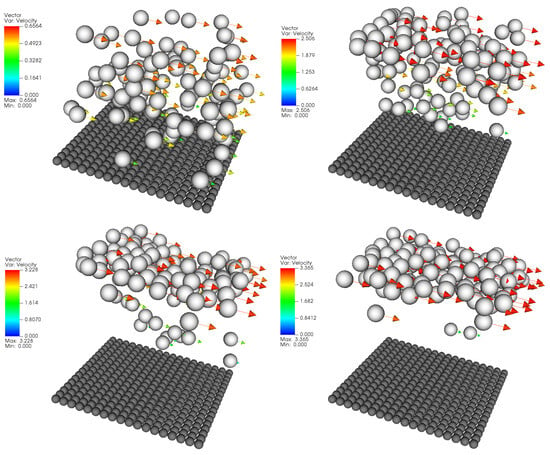
Figure 14. Snapshots of the segregation process for the system with large spheres at 10, 75, 120, and 195 $\mathrm{s}$.

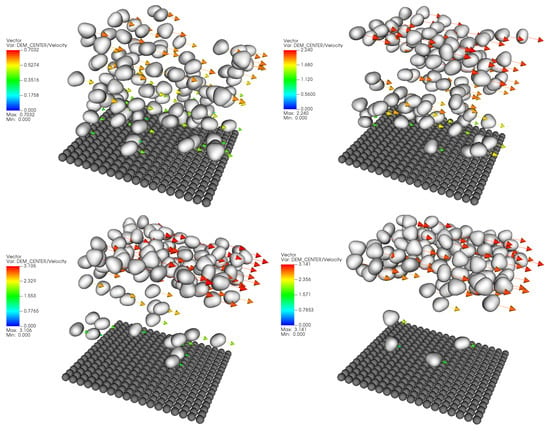
Figure 15. Snapshots of the segregation process for the system with large metaballs at 10, 75, 120, and 195 $\mathrm{s}$.

For the bidisperse system with large spheres (Figure 14), the initial mixed cluster of large and small particles becomes randomly distributed during deposition. When shear begins, the angle of the channel induces internal flow within the packing. The large spheres exhibit strong rebound and kinetic activity, often bouncing at the surface rather than penetrating the column, which promotes their accumulation near the free surface. As shear continues, this separation intensifies. The smooth surfaces of the spheres facilitate downward percolation of small particles, which readily fill the underlying voids, leaving the large spheres almost entirely segregated from the top layer.

A qualitatively similar process occurs for large irregular particles (Figure 15). During deposition, irregular metaball particles and small particles are randomly mixed. Once shear begins, smaller particles percolate downward through voids, gradually forcing larger irregular particles upward. Although their angular geometry dissipates more energy during collisions than spheres, it does not prevent the upward migration of large particles. By $t=120$ s, a distinct stratified state emerges, with most of the large irregular particles concentrated at the free surface. This outcome demonstrates that particle non-sphericity modifies the dynamics but does not fundamentally alter the final segregation pattern, which remains similar to that of spherical particles.

To provide a quantitative basis for the observations, the segregation process was analyzed by tracking the time evolution of the average vertical position (z-coordinate) for the large particles. Figure 16 plots the average height for both the large spheres and the large irregular metaballs as a function of time during the shearing stage.

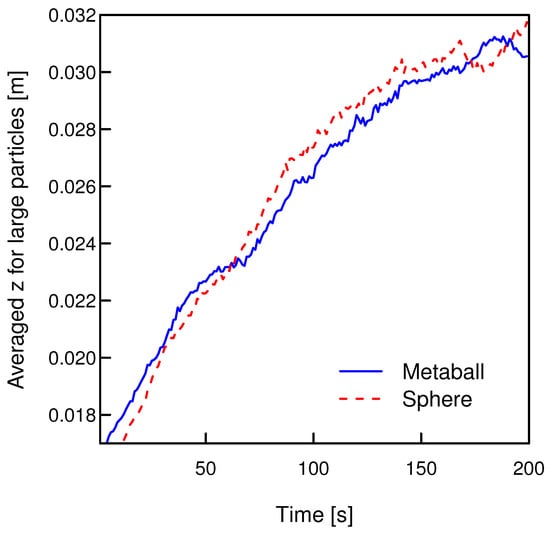
Figure 16. Time evolution of the averaged height for large spheres and metaballs during segregation.

A clear upward trend is observed for both particle types, confirming the segregation behavior suggested by the snapshots. Starting from an initial average height of approximately 0.018 $\mathrm{m}$, both the spheres and the metaballs, driven by the shear, steadily migrate towards the free surface of the granular bed. This upward movement continues for approximately 100 s with constant segregation velocity; then, the segregation velocity gradually decreases with time. At around 200 $\mathrm{s}$, the large particles have risen as high as possible within the assembly, and a stable stratified layer has formed at the top.

It is clear that the segregation dynamics of the two differently shaped particles share great similarity; the curves for the spheres (red dashed line) and the metaballs (blue solid line) are closely matched throughout the entire process. This indicates that both the overall rate of segregation and the final extent of segregation are nearly identical. This strongly supports the conclusion that the size difference between the particles is the dominant mechanism driving the segregation behavior, overwhelming the secondary effects of particle shape.

To analyze the particle spatial distribution during segregation, we further examined the standard deviation of the vertical position (z-coordinate) for the large particles, as plotted in Figure 17. The time evolution of the standard deviation reveals two different stages of the segregation process. Initially, during the first 75 s of shearing, the standard deviation for both systems increases from approximately 0.0075 m to a peak of about 0.0085 m. This initial phase represents the fluidization of the granular bed. The applied shear mobilizes the particles, breaking down the initial packed structure and transiently increasing vertical dispersion before the size-based segregation mechanism becomes dominant. Therefore, although large particles are still moving upward, the standard deviation increases due to the dilation of samples.

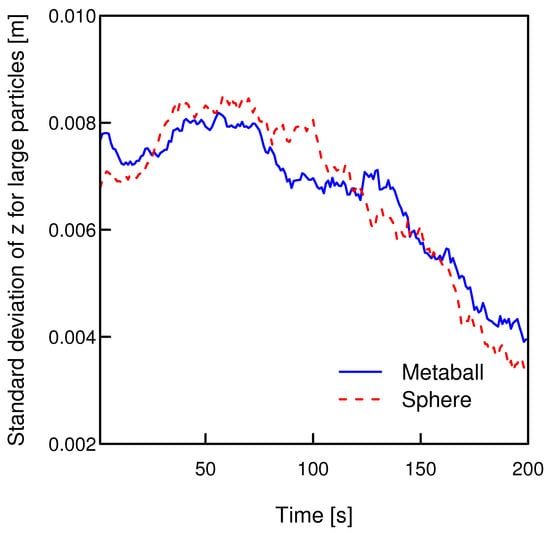
Figure 17. Time evolution of the standard deviation for large spheres and metaballs during segregation.

Following this peak, a prolonged phase of decay is observed. During this period, the standard deviation for both spheres and metaballs steadily decreases. This monotonic decrease is the quantitative signature of the segregation process. As the large particles migrate upwards and coalesce at the free surface, their vertical spread within the assembly is significantly reduced. The final low value of the standard deviation confirms the formation of a highly segregated layer of large particles, which is consistent with the visual evidence from the snapshots. Moreover, the comparison between the spherical and irregular particles yields great similarity.

In terms of efficiency, the simulation time for both spheres or irregular particles is almost identical; it takes around 13.6 min wall time to execute a 200 $\mathrm{s}$ simulation. The same simulations are also conducted with the original MDEM, and it is found that the simulation time difference between the proposed model and the original one is negligible since both models solve optimization problems related to the contact. The same conclusion can be drawn for the average iteration number; the proposed model takes 3.23 iterations on average, whereas the average number of iteration is 3.45 for the original MDEM.

5. Concluding Remarks

In this study, we present an improved Metaball Discrete Element Method for simulating granular materials composed of non-spherical particles with rounded features. The primary innovation of this work lies in the reformulation of the contact algorithm. By treating the finding for the closest points between two particle surfaces as a constrained optimization problem solved with a robust Lagrange multiplier method, we have overcome the stability and convergence issues inherent in the original scheme. This enhancement, combined with a spherometaball strategy and efficient initial guess procedures, has resulted in a more robust, accurate, and computationally efficient framework for handling non-spherical particle shapes with round features. The method’s fundamental correctness was validated through benchmark tests, including particle–particle collisions and particle–plane sliding, which showed excellent agreement with theoretical predictions.

The capabilities of the improved MDEM were subsequently demonstrated through two comprehensive numerical examples that explored the profound influence of particle shape on macroscopic granular behavior. In the uniaxial compression example, the model successfully captured the different mechanical responses of irregular versus spherical particles. It is found that particle shape differences can lead to a two-order-of-magnitude difference in bulk stress and distinct stress–strain characteristics. The analysis of micro-structural properties confirmed the link between macroscopic behavior and particle-scale mechanisms, demonstrating the method’s high fidelity. The proposed model is further applied to size-induced segregations. Simulations revealed that size difference was the dominant factor, leading to a similar final segregated state for both large spherical and irregular particles. Nevertheless, the model was sensitive enough to capture subtle dynamic differences in their migration paths.

In conclusion, this model generalizes the application of the DEM to any convex round particle while improving numerical stability, signifying a significant advancement over previous approaches. The presented findings demonstrated the model’s promise as a robust numerical tool for exploring the effects of complex particle morphology in three dimensions, with broad relevance to engineering and science.