Many-Objective Edge Computing Server Deployment Optimization for Vehicle Road Cooperation

Abstract

In the Internet of Vehicles (IoV), vehicles need to process a large amount of perception data to support tasks such as road navigation and autonomous driving. However, their computational resources are limited. Therefore, it is necessary to explore the combination of vehicle–road cooperation with edge computing. Roadside units (RSUs) can provide data access services for vehicles, and deploying edge servers on RSUs can improve the data processing capability in IoV environments and ensure the sustainability of vehicle communications, thus supporting complex traffic scenarios more effectively. In this work, we study the deployment of RSUs in vehicle–road cooperative systems. To balance the deployment cost of RSUs and the quality of service (QoS) of vehicle users, we propose an RSU deployment optimization model with six objectives, including time delay, energy consumption and security when vehicles offload their tasks to RSUs, as well as load balancing and the number and communication coverage area of RSUs. In addition, we propose a Wasserstein generative adversarial network (WGAN)-based Two_Arch2 (WGTwo_Arch2) to solve this many-objective optimization problem to better ensure the diversity and convergence of the solutions. In addition, a polynomial variation strategy based on Lecy’s flight mechanism and a diversity archive selection strategy with an adaptive Lp-norm are also proposed to balance the exploratory and exploitative capabilities of the algorithm. The effectiveness of the proposed algorithm WGTwo_Arch2 for 6-objective RSU deployment optimization is verified by comparisons with five different algorithms.

1. Introduction

In recent years, with the rapid development of new generation communication technologies such as 5G and 6G, the number of vehicles connected to the Internet of Vehicles (IoV) and the amount of data for in-vehicle applications have increased [1]. However, vehicles have limited computing power and storage to perform many computational tasks, requiring them to offload tasks to servers for processing. Cloud servers can provide powerful computational services. However, they are physically far away from vehicle users and incompatible with latency-sensitive tasks. Unlike traditional cloud processing, edge computing effectively reduces network latency, saves energy in vehicle transmissions by processing data locally, and reduces the risk of cybersecurity attacks when data are in the cloud. As an infrastructure in the IoV, roadside units (RSUs) are fixed devices installed near roads that have stronger communication and computation capabilities than vehicles do. RSUs provide wide-coverage network access for vehicles [2] and play a key role in vehicle–road cooperation [3]. In IoV, edge servers are usually deployed on RSUs to provide various real-time services for vehicles. Intelligent vehicles in real-world scenarios can provide a variety of intelligent services. For example, vehicle control and road traffic-type services require high real-time performance to improve road safety and avoid hazardous situations, and entertainment and media-type services require continuous data streams to maintain a better service experience [4], whereas RSUs are costly to install and maintain, and large-scale deployments can impose expensive overheads on operators. Therefore, the RSU deployment problem is modeled as a multiobjective optimization problem, aiming to balance between conflicting user service quality and deployment cost, which is more suitable for practical application scenarios.

Vehicle–road cooperation systems rely primarily on wireless communication; however, when the wireless transmission range is limited, RSUs can provide access services only to vehicles within the communication area. To reduce the energy consumption and time delay of vehicles, in this study, task computation in vehicles is not considered. Instead, the tasks are offloaded to edge or cloud servers to provide satisfactory quality of service (QoS) for users. In addition, considering vehicle mobility, the time required to complete computational tasks may necessitate data transmissions across multiple RSUs during task execution [5]. Then, it is necessary to backhaul the data in the form of wireless multihop communication between multiple RSUs. However, this process can easily be used by attackers to steal sensitive information, thus exposing vehicle users to security threats. Therefore, the ability to ensure the privacy of vehicle users is a key factor affecting the QoS. Existing security algorithms typically rely on encryption for ensuring data privacy. However, the extensive encryption/decryption process leads to severe latency and energy consumption, which is a key challenge for resource-limited vehicles. In this study, instead of using security techniques such as encryption and authentication, the probability of eavesdropping during multihop transmission is used as an optimization objective to secure the network while minimizing latency and energy consumption. Providing higher QoS to more vehicles is the fundamental purpose of deploying RSUs. Therefore, the coverage area is also an important measure used to evaluate the QoS provided by the network. To fully utilize the computational potential of edge computing so that vehicle requests should be processed in RSUs as much as possible, in this study, the number of vehicles covered by RSUs is used as an objective to measure RSU coverage. In addition, RSUs are expensive to install and maintain. When RSUs are not load balanced, the prolonged high loads on certain servers can lead to overheating and hardware failure, whereas idle RSUs lead to resource waste. Therefore, this paper introduces the concept of maximizing the load balance of RSUs to reduce the maintenance cost and maximize the operator’s investment. Most studies maximize the QoS within a limited budget [4,6,7]. Previous RSU deployment optimization studies usually consider deployment cost, coverage area, time delay, or energy consumption as a measure of QoS [8,9,10], but few consider factors such as transmission security and load balancing; therefore, in this paper, we construct a six-objective RSU deployment optimization model including network delay and energy consumption, network transmission security, load balancing, deployment cost, and coverage area.

The RSU deployment strategy has been shown to be an NP-hard problem [1,11]. The evolutionary algorithm (EA) is a population-based stochastic optimization algorithm inspired by the law of natural evolution that does not easily fall into local optimal solutions when solving NP-hard problems and has good performance in non-differentiable non-convex and multi-objective optimization problems [12,13,14,15]. However, when the number of objectives to be optimized increases, the convergence speed and diversity of traditional multi-objective evolutionary algorithms decrease. Therefore, when solving many-objective optimization problems (the number of objectives is greater than 3), the overall optimization often leads to many locally optimal solutions during the search process as the dimensionality of the decision variables grows rapidly, which not only prevents the algorithms from finding the globally optimal solution but may also trigger premature convergence or even stagnation. To address this challenge effectively, Wang et al. [12] proposed the Two_Arch2 algorithm for solving many-objective optimization problems. The algorithm preserves the diversity and convergence of candidate solutions by maintaining two different archives, each with a specific selection and updating strategy. The algorithm performs well in terms of convergence, diversity, and complexity. In addition, by learning sufficiently from high-quality datasets, deep neural networks exhibit strong feature representation and non-linear fitting capabilities. Data generation methods based on deep generative adversarial network (GAN) models have shown extremely superior performance in learning complex high-dimensional data distributions. The traditional GAN [16] is a generative and discriminative gaming process through which adversarial training ultimately leads to the generation of high-quality synthetic data. Wasserstein-GAN (WGAN) [17] is an improved GAN model that introduces the Wasserstein distance as an optimization objective to train generators and discriminators in a more stable and interpretable way. Therefore, this paper introduces the WGAN-based Two_Arch2 algorithm (WGTwo_Arch2), which uses a WGAN-based population initialization strategy and population mating selection strategy to improve the diversity of solutions in the population, as well as a polynomial mutation strategy based on Levy’s flight mechanism and a diversity archive updating strategy based on the adaptive Lp-norm to increase the exploration efficiency and global convergence of the algorithm.

This study focuses on the MaOP algorithm and its application to the problem of deploying RSUs in edge computing-based vehicle-road cooperation. The main contributions of this study are as follows:

• A six-objective optimization model incorporating time delay, energy consumption, security, load balancing, and number and communication coverage areas is proposed for the RSU deployment optimization problem.
• The WGTwo_Arch2 algorithm is proposed to optimize the many-objective deployment model of RSUs. To enhance the algorithm’s ability to identify diverse solutions, Kent chaotic mapping data is applied to train the WGAN to generate random individuals covering the entire distribution space during the population initialization process, making the initial population distribution more uniform. A mating selection strategy based on the WGAN is designed to generate more diverse solutions for offspring generation.
• To improve the global search ability and convergence speed of the algorithm when dealing with many-objective problems, a polynomial variation strategy based on the Levy flight mechanism is proposed. The stochastic wandering mechanism of the Levy flight is used to generate variation probabilities, enabling better exploration of the global search space. An adaptive Lp-norm-based strategy for updating diversity archives is proposed to control exploration and exploitation. Finally, the effectiveness of the proposed algorithm in solving the RSU many-objective deployment optimization problem is experimentally verified.

The remainder of this paper is arranged as follows. The related work is given in Section 2. The architecture of the vehicle-road cooperation system based on RSUs and the RSU deployment optimization model are presented in Section 3.1. The proposed WGTwo_Arch2 algorithm is described in Section 3.2. Section 4 provides the experimental comparison results and analysis. In Section 5, we discuss the limitations of this work and future research directions. Finally, Section 6 summarizes this article.

2. Related Work

2.1. Large-Scale Many-Objective Optimization Problem (LSMaOP)

Multi-objective optimization problems (MOPs) involve several conflicting objective functions that need to be optimized simultaneously to obtain a set of satisfactory solutions, which can be described as follows:

$$\begin{array}{cc}\hfill \mathrm{Minimize}F\left(X\right)& \hfill =\left\{f_1\left(X\right), f_2\left(X\right),\dots ,f_m\left(X\right)\right\}\\ \mathrm{s}.\mathrm{t}.X\hfill & \hfill =\left(x_1,x_2,\dots ,x_n\right)\in \mathrm{\Omega }\end{array}$$

(1)

where there are n dimensions of decision variables and m objective functions, in the decision space $\mathrm{\Omega }$, individual X contains n dimensions of decision variables. When the number of decision variables is greater than or equal to 1000 and the number of objective functions is greater than 3, the multi-objective optimization problem is classified as a large-scale many-objective optimization problem. The decision space $\mathrm{\Omega }$ is the set of all possible decision variables in a multi-objective optimization problem, which contains the individuals $x_1$, $x_2$. The first solution $x_1$ is said to dominate the second solution $x_2$ if solution $x_1$ outperforms solution $x_2$ on all the objective functions or is better on at least one of the objective functions and is at least non-inferior to solution $x_2$ on the others. A Pareto-optimal solution is one in which there is no other solution in the decision space that is superior to it on all objective functions. That is, a Pareto optimal solution is non-dominated, and a set of Pareto optimal solutions together form a Pareto Optimal Set (PS).

2.2. Two_Arch2 Algorithm

The Two_Arch algorithm divides the set of non-dominated solutions into two archives: the convergence archive (CA) and the diversity archive (DA). The CA and DA operate under different update rules due to their different objectives (convergence and diversity, respectively). If a new candidate individual is a non-dominated member of the population, i.e., no individual in the two archives can dominate it and the candidate can dominate the other individuals in the two archives, the candidate enters the CA, and the dominated individual is removed. If the candidate individual cannot dominate any other individual and is not dominated by any archived individual, it enters the DA. In the Two_Arch algorithm, the sizes of CA and DA are variable. However, the total number of individuals in both archives is kept constant. If the total archive size is exceeded, the Euclidean distance from an individual in the DA to an individual in the CA is calculated. Then, the individual with the shortest Euclidean distance in the DA is removed. This process is repeated until the total archive size is restored. The Two_Arch2 algorithm effectively improves the update strategies of the CA and DA on the basis of the two archives of the original Two_Arch algorithm. It introduces the $I_{\epsilon +}$ metric [14] in the CA to accelerate convergence toward the true Pareto front (PF), while leveraging the Pareto advantage to increase the diversity of the population in the DA. Specifically, the sizes of the CA and DA are fixed individually. If the CA exceeds the fixed size, the quality indicator $I_{\epsilon +}$ guides selection, and the solution with the smallest $I_{\epsilon +}$ loss is removed. If the DA exceeds the fixed size, the solution with the largest or smallest objective value is removed first, and then the DA is updated using the similarity metric that is based on the Lp-norm (p < 1) distance until the fixed size is restored. In addition, during the offspring generation process, crossover operations are performed in the CA and DA, but only mutation operations are performed in the CA, and finally, the DA with better diversity is output. Algorithm 1 shows the pseudo-code of the the Two_Arch2.

Algorithm 1: The Two-Archive2 Algorithm

2.3. Research Status of RSU Deployment Optimization

With the rapid development of the IoV, achieving low time delay and high security have become important requirements for many electronic devices. By applying edge computing to vehicle–road cooperation, it becomes possible to provide stable access services for vehicles, minimize the distance and time delay of data transmission, and reduce the risk of cybersecurity attacks on the data in the cloud, ensuring that the vehicles can access networks stably and quickly to obtain the required services. This is highly important for improving the user experience and ensuring service continuity.

RSU deployment is considered a multi-objective optimization problem that has been studied by some scholars using EAs. For example, Ning et al. [2] proposed an energy-efficient scheduling (MEES) scheme based on heuristic algorithms supporting MEC to minimize the energy consumption of RSUs under task delay constraints. Considering the mobility of vehicles in the IoV, Talpur et al. [8] proposed a deep reinforcement learning-based dynamic service placement (DRLD-SP) framework to minimize the maximum edge resource usage and service latency. Chen et al. [18] solved the joint optimization problem of user coverage and reliability for edge application placement (EAP-CR) by using integer planning techniques. Lin et al. [9] constructed a multi-objective RSU deployment model (MORD) to minimize the data transmission delay, data transmission loss rate, RSU-aware overlap region and communication overhead of RSUs and maximize the average RSU coverage. They applied the non-dominated sorting genetic algorithm II (NSGA-II) [19] to solve the proposed MORD optimization problem. However, these five objectives were merged into two objective functions, and energy consumption and mobility were not considered. Fan et al. [1] proposed a task offloading scheme for heterogeneous cellular networks that combines 5G base stations with 4G base stations and applied the linear relaxation improved branch-and-bound algorithm (BBA) to minimize two objectives, total delay and energy consumption, to identify the optimal task offloading and resource allocation scheme, thus improving the user experience. Chaudhary et al. [11] minimized power consumption and maximized the model secrecy capability using mixed integer non-linear programming (MINLP) and proposed a lightweight resilient key exchange authentication protocol to mitigate the various IoV security threats. Zhang et al. [10] maximized RSU coverage with minimum deployment cost and constructed a multi-objective model using an enhanced MOQPSO algorithm. Massobrio et al. [4] optimized two objectives, QoS and RSU deployment cost, for vehicular ad hoc networks using an improved NSGA-II evolutionary algorithm to solve for the optimal location and type of RSU. The transmitted data rate and the end-to-end delay were utilized as QoS measures. Nikookaran et al. [6] considered minimizing the capital expenditure (CAPEX) installation/opening costs and long-term energy operating (OPEX) costs of RSUs and proposed the minimum cost route clustering algorithm to solve the integer linear program problem to detect RSU locations. Kumrai et al. [20] applied EAs to optimize the communication coverage area as well as the number of RSUs. Wang et al. [21] proposed a multi-objective differential evolution algorithm-based discrete elite orientation (MODE-deg) to optimize the number and coverage area of RSUs. Guerna et al. [22] proposed a new genetic intersection-coverage algorithm (GICA) based on the priority concept to optimize the number of and coverage of RSUs. Wu et al. [23] proposed a capacity maximization placement scheme for RSUs in which vehicles can communicate with RSUs either directly or through multiple hops. An integer linear programming model was developed to maximize the aggregate throughput in the network. By considering high traffic density and low traffic density scenarios, Yu et al. [7] established an optimization model for RSU deployment with the objectives of data transmission delay and RSU coverage and constructed a model using EA. Ghosh et al. [24] proposed the memetic framework-based optimal RSU deployment (MFRD) algorithm to maximize the coverage area of each RSU and minimize the overlap between the coverage areas of neighboring RSUs. Considering the problem that a fixed coverage distance cannot adapt to diverse V2R scenarios, Huo et al. [3] assumed that RSUs have different transmit powers, performed coverage analysis of RSUs on the basis of the packet delivery ratio model to obtain the coverage distance, and used the total coverage time as the evaluation metric for the QoS, considering the purchase and installation costs. Finally, the NSGA-II was applied to solve this RSU multi-objective deployment optimization problem to improve the QoS and reduce the deployment cost. Lu et al. [25] proposed a deep reinforcement learning-based ES placement policy (DESP) to maximize coverage and workload balancing and minimize the average latency. Shen et al. [26] proposed a dynamic ES placement method (DEP), which models the DEP as the optimization problem with the reconstruction cost, network delay, and load balancing as the objectives and the threshold of the number of ESs and the edge coverage as the constraints. The non-dominated sorting genetic algorithm III (NSGA-III) [27] was applied to optimize the location and the number of ESs.

3. Methods

3.1. System Model and Problem Formulation

In this section, we introduce the architecture of an edge computing-based vehicle-road cooperation. Within this framework, RSUs equipped with edge servers play a central role by providing services to IoV devices. RSUs are not only responsible for storing massive amounts of data but also for analyzing and processing these data in depth to ensure that IoV devices can obtain accurate and timely service support. Therefore, to optimize the overall system performance, we propose a many-objective RSU deployment optimization model, which integrally considers six objectives, including the time delay, energy consumption, and security of vehicle offloading tasks, as well as load balancing, deployment cost, and coverage area of RSUs.

3.1.1. The Vehicle-Road Cooperation System for RSU-Based Deployment

The architecture of the edge computing-based vehicle-road cooperation is shown in Figure 1. It is assumed that vehicles and RSUs carrying edge servers are randomly distributed on a unidirectional road with a distance of 3 km. The RSUs are distributed along the road, and each RSU covers a communication area where vehicles can offload their computational tasks via a wireless local area network (WLAN). The RSUs are connected to each other via a 5G core network. Assume that there are m edge computing servers in the system and that these m RSUs are arranged in order from left to right as $E=\left\{e_1,e_2,\dots ,e_m\right\}$. The system includes n ($n=50$) vehicles, denoted by $V=\left\{v_1,v_2,\dots ,v_n\right\}$. It is assumed that each vehicle has a task to process and offload to the nearest edge server or to a cloud server for processing. In addition, assume that each vehicle $v_n$ has a computationally intensive task $Z_n=\left(b_n,d_n\right)$ [21], where $b_n$ denotes the size of the input data (in bits) for this task, which is randomly set to the size of [400, 600] (in kbits). $d_n$ denotes the total number of CPU cycles required to complete the computational task, which is randomly set to [900, 1100] (in megacycles). The number of CPU cycles $d_n$ is positively correlated with the task size $b_n$.

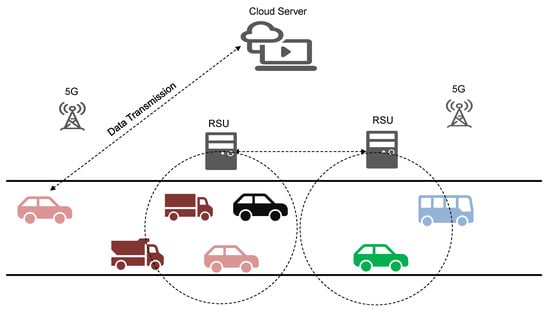
Figure 1. Vehicle–road cooperation based on edge-computing.

During a certain period, vehicles simultaneously send task processing requests to RSUs. The offloading decision of user $v_n$ is denoted by $x_n^i$; if $i\le 1\le m$, then user $v_n$ offloads the task to the edge server $e_m$, and the vehicle users assigned to $e_m$ are denoted by the set $E{S}_m=\left\{v_1,v_2,\dots ,v_k\right\}$($0\le k\le n$) according to the priority (i.e., $v_1$ is the first to be processed). The data that arrives at RSUs with priority are processed first, and the queuing priority can be known according to the transmission delay. In addition, the RSU has limited computing power and cannot serve all the user task requests it receives. The queuing time strongly affects the service experience of the vehicle user. If the queuing time of the vehicle user is greater than the time of transmission of the vehicle to the cloud server (i.e., $T_n^{\mathrm{Que}}>T_n^{\mathrm{cloud}}$), the vehicle task is directly offloaded to the cloud server. The maximum wireless communication range of the RSU is assumed to be d (d = 250 m). If there is no RSU within this distance, the vehicle offloads the task directly to the cloud server, and the vehicle offloaded to the cloud server is denoted as $CL=\left\{v_1,v_2,\dots ,v_c\right\}$($0\le c\le n$). In addition, owing to the mobility of the vehicle, the vehicle’s original location (denoted by $v_o$) and destination location (denoted by $v_d$) affect the selection of the computational task offloading method [22]. Assuming that the vehicle is moving in one direction along the road at a constant speed, the destination position $v_d^n$ is calculated from the initial position $v_o^n$ of vehicle $v_n$ and its speed v:

$$v_d^n=v_o^n+\left(T_n^t+T_n^{Que}+T_n^c\right)·v$$

(2)

Assuming that $v_o$ and $v_d$ are in the same RSU coverage area d, $v_o$ should offload the computational data to this RSU $e_i$ for processing via wireless communication technology. At the end of the computation process, the data can be returned from $e_i$ to the vehicle located at $v_d$. Assuming that the original and destination positions of the vehicle are within two RSUs $e_i$ and $e_j$, respectively, the task is offloaded to the nearest RSU $e_i$ that is connected to the $v_o$, and after the processing is completed, $e_i$ transmits the data through multiple hops to $e_j$, which in turn transmits the processed data to the vehicle.

After processing the task, the RSU must transmit the processed data back to the vehicle. It determines whether the vehicle is still in the transmission range of RSU $e_m$ after $T_n^t+T_{qc}$ time. If the vehicle is still in the transmission range, the data are directly transmitted back. Alternatively, if the vehicle is in the transmission range of another RSU $e_q$, $e_m$ is transmitted to $e_q$ via a multihop. Finally, if the vehicle is not in the transmission range of any of the RSUs, the processed data are sent via a multihop to the nearest RSU to the vehicle, and when the vehicle passes through the transmission range of that RSU, the data are transmitted back to the vehicle. Transmission between the RSUs is performed via a wireless backhaul link.

3.1.2. The RSUs Deployment Optimization Model

In this section, we focus on the optimization problem of RSU deployment in edge computing-based vehicle-road cooperation system. In this scenario, RSUs play a crucial role in that they not only reduce the computational burden of vehicular devices but also effectively scale down the transmission delay and guarantee real-time performance for high-bandwidth applications. Therefore, a six-objective optimization model that comprehensively considers total delay, energy consumption, security, load balancing, deployment cost, and coverage is constructed. The details are as follows:

1.

Total delay

In computationally intensive applications, the output data of a computation are often significantly smaller than the input data. Therefore, the time required to return the computation results to the vehicle is negligible. If the vehicle transmits data to an RSU for processing, the user’s time delay mainly consists of the transmission delay, queuing delay, and computation delay of the data in the RSU. If the vehicle transmits data to the cloud server for processing, the queuing time and the computation processing time are negligible because the cloud server has sufficient computational resources, and only the transmission delay needs to be considered.

The time delay of the vehicle transmits data to an RSU: when vehicle $v_n$ transmits task $Z_n$ to RSU $e_m$, the transmission delay is generated at this time as follows:

$$T_n^t={\displaystyle \frac{b_n}{{\lambda }_{n,m}}}$$

(3)

where ${\lambda }_{n,m}$ denotes the transmission rate (in bps) obtained by vehicle user $v_n$ when it offloads the task to RSU $e_m$:

$${\lambda }_{n,m}=W\times {log}_2\left(1+{\displaystyle \frac{p_n{\rho }_0{l}_{n,m}^{-\beta }}{{\delta }_0^2+{\sum }_{v_i\in E{S}_m·and{v}_i\ne v_n}{p}_i{\rho }_0{l}_{i,m}^{-\beta }}}\right)$$

(4)

where W is the channel bandwidth, which is set to 5 MHz. The transmission power $p_n$ of the vehicle determines the strength of the signal sent by the vehicle, and the transmit power and idle power are set to 500 mW and 100 mW, respectively. The small-scale fading coefficient ${\rho }_0$ accounts for the rapid variation in the signal over short distances due to multipath effects, etc. The distance between vehicle user n and base station m is expressed as $l(n,m)$, and $\beta$ denotes the path loss coefficient (a constant), which is set to 3. ${\delta }_0^2$ denotes the noise power spectral density, which is set to ${10}^{-9}\mathrm{W}$ [28].

The vehicle’s queuing delay in the RSUs: The vehicles in the set $E{S}_m$ transmit messages to $e_m$ at the same time and wait in line to be processed. The waiting time of vehicle $v_n$ ($n>1$) in $e_m$ is computed as follows:

$$T_n^{\mathrm{Que}}=\left\{\begin{array}{cc}\hfill T_{n-1}^t+T_{n-1}^c+T_{n-1}^{Que}-T_n^t,& T_{n-1}^t+T_{n-1}^c+T_{n-1}^{Que}>T_n^t\hfill \\ \hfill 0,& T_{n-1}^t+T_{n-1}^c+T_{n-1}^{Que}\le T_n^t\hfill \end{array}\right.$$

(5)

The vehicle’s computation delay in the RSU: When a task arrives at the RSU, the RSU processes it, assuming that the computational power of the RSU is $F_{e}s$, which is set to 5 GHz. The average computation time for all the vehicles in the system is

$$T_n^c={\displaystyle \frac{d_n}{F_{es}}}$$

(6)

The vehicle’s transmission delay in the cloud server: The time delay of the vehicle user $v_n$ who is processing the task in the cloud server can be calculated as

$$T_n^{\mathrm{cloud}}={\displaystyle \frac{b_n}{{\lambda }_{n,\mathrm{cloud}}}}$$

(7)

Therefore, the average time delay for all vehicles is

$$\overline{T}={\displaystyle \frac{{\sum }_{j=1}^m{\sum }_{v_i\in E{S}_j}{T}_i^t+T_i^c+T_i^{Que}+{\sum }_{i\in CL}{T}_i^{cloud}}{n}}$$

(8)

The objective function for minimizing the time delay can be normalized and expressed as

$$min{f}_{\mathrm{delay}}=-{\displaystyle \frac{1}{\overline{T}}}$$

(9)

2.

Energy consumption of vehicles

When user $v_n$ transmits task $Z_n$ to RSU $e_m$, the transmission energy consumption is

$$E_n^{es}=p_n{T}_n^t={\displaystyle \frac{p_n{b}_n}{R_{n,m}}}$$

(10)

where $p_n$ is set to 500 mW. The transmission energy consumption when user $v_n$ transmits task $Z_n$ to the cloud server is as follows:

$$E_n^{\mathrm{cloud}}={\displaystyle \frac{p_n{b}_n}{R_{n,\mathrm{cloud}}}}$$

(11)

When the RSU processes the task of user $v_n$, user $v_n$ is in the idle state, and the idle energy consumption of the vehicle can be calculated as follows:

$$E_n^c=p_{\mathrm{idle}}{T}_n^c={\displaystyle \frac{p_{\mathrm{idle}}{d}_n}{F_{es}}}$$

(12)

where $p_{\mathrm{idle}}$ is the power consumption in the idle state, which is set to 100 mW. The cloud server has sufficient computational resources to process the task very quickly, so the idle energy consumption of the vehicle assigned to the cloud server is ignored, and only the transmission energy is consumed. In the last step, user $v_n$ downloads the output data from the server. Since the size of the output data is much smaller than the size of the input data, the latency and energy consumption in this phase are intentionally ignored. The total energy consumption of the vehicle is defined as

$$V_{\mathrm{total}}=\left\{\begin{array}{cc}\hfill E_n^{es}+E_n^c,& \mathrm{RSU}\hfill \\ \hfill E_n^{\mathrm{cloud}},& \mathrm{Cloud}\hfill \end{array}\right.$$

(13)

The average energy consumption objective function for all vehicles is

$$E_{\mathrm{total}}={\displaystyle \frac{{\sum }_{j=1}^m{\sum }_{v_i\in E{S}_j}{E}_n^{es}+E_n^c+{\sum }_{i\in CL}{E}_i^{\mathrm{cloud}}}{n}}$$

(14)

The objective function for minimizing energy consumption can be normalized and expressed as:

$$min{f}_{\mathrm{ene}}=-{\displaystyle \frac{1}{E_{\mathrm{total}}}}$$

(15)

3.

Security

Secure transmission is a key metric of QoS and is used to measure the probability of successful transmission. RSUs return data via multiple hops. Assuming that the probability that the link between two RSUs in the network is eavesdropped (i.e., transmitted packets may be intercepted) is $p_d$, the probability of successful forwarding between RSUs between each hop is $1-p_d$. When the number of hops in the path increases, the cumulative probability of successful eavesdropping on the end-to-end overall link will rise significantly, leading to a marked decline in the overall security of the path with more hops. In addition, a greater number of RSUs through which the data packets pass not only increases the delay but also means that the failure of any RSU in the path will cause the entire path becoming unavailable, thereby reducing the reliability of data transmission. Therefore, the number of RSU hops passed through when returning data is used as a measure of security. If the vehicle’s original and destination locations are within two RSUs $e_m$ and $e_i$, respectively, and j RSUs need to be passed between $e_m$ and $e_i$, the probability that $e_m$ forward the data successfully to vehicle $v_n$ is as follows:

$$p_n^m={\left(1-p_d\right)}^{j+1}$$

(16)

where $p_d={10}^{-9}$.

Therefore, the average safe forwarding rate for all vehicles is denoted as:

$$V_{\sec }={\displaystyle \frac{{\sum }_{j=1}^m{\sum }_{v_i\in E{S}_j}{p}_i^J}{{\sum }_{j=1}^m{\sum }_{v_i\in E{S}_j}1}}$$

(17)

The minimization objective function is expressed as follows:

$$min{f}_{\sec }=1-V_{\sec }$$

(18)

4.

Load balancing of RSUs

Load balancing improves both the availability of RSUs, by optimizing their resource allocation, and the reliability of the network by effectively handling congestion and failure events. The average load of the RSUs is denoted as

$$\overline{C}={\displaystyle \frac{{\sum }_{i=1}^m\left|E{S}_i\right|}{m}}$$

(19)

The vehicles covered by each RSU should be the same as possible. When an excessive number of vehicles are connected to certain RSUs, it often results in in a greater level of interference in vehicle data transmission. This also leads to stress overload in busy task RSUs and resource waste in idle RSUs. The standard deviation of the RSU load is used to denote the balanced load among them:

$$Std=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^m{\left(\left|E{S}_i\right|-\left|\overline{C}\right|\right)}^2}{m}}}$$

(20)

The balanced load of the RSUs is normalized and expressed as a minimization objective function:

$${minf}_{\mathrm{load}}=1-{\displaystyle \frac{1}{1+std}}$$

(21)

5.

Cost of deploying RSUs

The RSU cost is related mainly to the number of RSUs, so the minimized RSU cost is denoted as

$$min{f}_{\mathrm{cost}}={\displaystyle \frac{N}{12}}$$

(22)

6.

Coverage area of RSUs

The more vehicles that RSUs can communicate with, the greater the coverage of the car network. Therefore, the coverage should be maximized and denoted as

$$Cov={\displaystyle \frac{{\sum }_{i=1}^m\left|E{S}_i\right|}{n}}$$

(23)

The objective function is expressed as follows:

$$min{f}_{cov}=1-Cov$$

(24)

7.

Six-objective optimization model

In summary, we construct a six-objective optimization model. That is, minimize total delay, energy consumption, balanced load, and deployment cost, and maximize security and coverage. The six-objective optimization model based on RSUs deployment is shown below:

$$min\left\{f_{\mathrm{delay}}, f_{\mathrm{ene}}, f_{\sec }, f_{\mathrm{load}}, f_{\mathrm{cost}}, f_{\mathrm{cov}}\right\}$$

(25)

3.2. The Proposed WGTwo_Arch2 Approach

This section presents the solution framework for the six-objective optimization model proposed in Section 3. This approach is based on the Two_Arch2 algorithm. The proposed WGAN-based population initialization strategy and mating selection strategy, Levy distribution-based polynomial variation strategy and adaptive Lp-norm diversity archive updating strategy are first introduced, and then the proposed improvements are incorporated into the Two_Arch2 optimization framework to form the WGTwo_Arch2 algorithm. The pseudocode is shown in Algorithm 2. Finally, the superiority of WGTwo_Arch2 is verified by analyzing the experimental results through the objective function value and performance evaluation metrics.

Algorithm 2: Population initialization strategy based on WGAN

3.2.1. WGAN-Based Population Initialization Strategy and Mating Selection Strategy

GANs [26] mainly consist of a generator and a discriminator. The generator receives random noise vectors and generates new samples similar to the real data through an inverse convolutional network. The discriminator is a binary classifier that extracts features of the input data on the basis of a convolutional network, aiming at distinguishing whether the input samples are generated data or real data. The generator and discriminator are trained in an alternating adversarial game process, where the competition between the generator and the discriminator leads to an equilibrium process as the training progresses. Once training is complete, the generator can be used to generate high-quality synthetic data such that the discriminator cannot effectively distinguish between true and false data. The Jensen–Shannon (JS) scatter or Kullback–Leibler (KL) scatter used by traditional GANs as a loss function is as follows:

$$D_{\mathrm{loss}}=-{\displaystyle \frac{1}{m}}\sum _{i=1}^m\left[log\left(D\left(x^{\left(i\right)}\right)\right)+log\left(1-D\left(G\left(z^{\left(i\right)}\right)\right)\right)\right]$$

(26)

$$G_{\mathrm{loss}}=-{\displaystyle \frac{1}{m}}\sum _{i=1}^{m}log\left(D\left(G\left(z^{\left(i\right)}\right)\right)\right)$$

(27)

where $D_{loss}$ is the discriminator loss, $G_{loss}$ is the generator loss, $D\left(x\right)$ denotes the judgment probability of the discriminator on a real sample, and $\mathrm{D}\left(\mathrm{G}\right(\mathrm{z}\left)\right)$ denotes the judgment probability on a generated sample. With respect to the original loss function, problems such as training instability exist. The WGAN [27] introduces the Wasserstein distance as a loss function to improve the stability of the gradient, providing a better measure of the difference between the two distributions and makes it easier to generate high-quality data samples:

$$W{D}_{\mathrm{loss}}=-\left(E_{x\sim p_{\mathrm{data}}}\left[\mathrm{D}\left(\mathrm{x}\right)\right]-E_{z\sim p_z}\left[\mathrm{D}\left(\mathrm{G}\left(\mathrm{z}\right)\right)\right]\right)$$

(28)

$$W{G}_{\mathrm{loss}}=-E_{z\sim p_z}\left[\mathrm{D}\left(\mathrm{G}\left(\mathrm{z}\right)\right)\right]$$

(29)

where $W{D}_{\mathrm{loss}}$ is the discriminator loss, i.e., maximizing the difference between the real sample and the generated sample, $W{G}_{\mathrm{loss}}$ is the generator loss, i.e., minimizing the Wasserstein distance between the generated sample and the real sample, $D\left(x\right)$ denotes the judgment probability of the discriminator on the real sample, and $\mathrm{D}\left(\mathrm{G}\right(\mathrm{z}\left)\right)$ denotes the judgement probability on the generated sample. In the Two_Arch2 algorithm, the initial population is generated through randomization. However, this may lead to a non-uniform distribution of the initial population, thus reducing the population diversity and introducing high levels of uncertainty into the optimization process. The chaotic system is described as a non-linear, stochastic-like deterministic bounded system that is neither periodic nor convergent and is highly sensitive to its initial parameters and conditions. Owing to its regularity, stochasticity, ergodicity and unpredictability, chaos is regarded as a reliable source of stochasticity that provides a more efficient search strategy for heuristic optimization algorithms than traditional random sequences do. The Kent chaotic map is a type of non-linear chaotic mapping with a wireless number of mapping folding, which has good traversability, uniformity and randomness and can effectively prevent the algorithm from falling into local extremes. The Kent map is used to generates the solution sequence:

$$x_{i+1}=\left\{\begin{array}{cc}{\displaystyle \frac{x_i}{a}},& 0\le x_i\le a\\ {\displaystyle \frac{1-x_i}{1-a}},& a<x_i<1\end{array}\right.$$

(30)

where a is a control parameter, $a\in (0,1)$, which is set to a value of 0.4. The range of its chaotic orbital state values is (0, 1). Therefore, the population initialization formula is

$$x_{i+1}=\left\{\begin{array}{c}{\displaystyle \frac{x_i}{a}}\times \left({\mathrm{value}}_{\mathrm{high}}-{\mathrm{value}}_{\mathrm{low}}\right)+{\mathrm{value}}_{\mathrm{low}}\\ {\displaystyle \frac{1-x_i}{1-a}}\times \left({\mathrm{value}}_{\mathrm{high}}-{\mathrm{value}}_{\mathrm{low}}\right)+{\mathrm{value}}_{\mathrm{high}}\end{array}\right.$$

(31)

where value_high and value_low are the maximum and minimum values of the decision variables, respectively.

In the population initialization stage, we abandon the traditional random initialization method. Firstly, we use the Kent chaotic map to generate an initial sequence with good traversal and non-repetitiveness, providing high-quality initial training data for WGAN. Subsequently, we use the trained WGAN model to generate the initial population. The generated initial individuals are not only random but also cover the “remote” areas in the entire distribution space that are ignored by traditional methods, enhancing the global diversity of the population and effectively avoiding the algorithm from prematurely falling into a local optimal region. The pseudocode is shown in Algorithm 2.

Mating selection is employed to produce the next generation by selecting certain individuals from the CA and DA for crossover and mutation. An effective mating selection strategy for a population is crucial for maintaining the genetic diversity of the population and driving the search process toward the Pareto optimal frontier. In the Two_Arch2 algorithm, a random selection strategy and a Pareto dominance selection strategy are utilized to select individuals for offspring generation. To increase the diversity of the solutions, we propose a Pareto dominance selection strategy based on the WGAN, i.e., we use the non-dominated solutions in the CA to train the generator and discriminator of the WGAN, and the WGAN-generated individuals are selected for mating. Therefore, during the evolutionary process, in addition to mating selection from the current population, WGAN is regularly used to generate new individuals to participate in the generation of offspring. This breaks the possible “inbreeding” of the population in the later stage of evolution. It is crucial for maintaining the wide distribution of the Pareto Front solution set, especially in handling many-objective problems, effectively preventing the population from contracting to a small segment of the front. Therefore, the new solutions generated by WGAN may be located in areas that the current population has not explored but have high potential, thereby helping the algorithm escape from local Pareto optimality and move towards the global Pareto optimal front to promote convergence. The pseudocode is shown in Algorithm 3.

Algorithm 3: The mating selection strategy based on WGAN

Input: CA,DA,Population size N;  Output: ParentC, ParentM;  1 ParentM ← N individuals randomly selected from CA;  2 ParentC ← N/2 individuals randomly selected from DA;  3 NonDominate ← N/2 individuals randomly selected from CA;  4 Training generators and discriminators of WGAN using non-dominated solutions;  5 ParentC ← N/2 solutions are generated using WGAN;  6 return ParentC and ParentM;

3.2.2. Polynomial Variation Strategy Based on the Levy Distribution

Variation operations are an important way for individuals in a population to explore the solution space. Polynomial variation is a probability-based variation operation that generates new individuals by randomly perturbing individual genes, effectively introducing diverse individuals and improving the global search ability of the algorithm. The Two_Arch2 algorithm enables better searches for the optimal solution by polynomially varying the individuals. Specifically, chromosomal variation is achieved by first randomly generating a variation parameter u, randomly selecting an individual for a particular gene, and then summing the variation value with the value of that gene. The parameters of polynomial variation include the variation probability, perturbation size, and perturbation index. Among them, the mutation probability determines the probability of each individual being mutated, the perturbation size determines the size of the perturbation, and the perturbation index determines the direction of the perturbation. The mutation formula is as follows:

$$x_t^{\prime }=\left\{\begin{array}{cc}\hfill x_t+\left(u_t-l_t\right){\left[2r+(1-2r){\left({\displaystyle \frac{u_t-x_t}{u_t-l_t}}\right)}^{d+1}\right]}^{{\displaystyle \frac{1}{d+1}}-1},& \hfill r\le 0.5\\ \hfill x_t+\left(u_t-l_t\right)\left[1-{\left[2(1-r)+2(r-0.5){\left({\displaystyle \frac{x_t-l_t}{u_t-l_t}}\right)}^{d+1}\right]}^{{\displaystyle \frac{1}{d+1}}}\right],& r>0.5\hfill \end{array}\right.$$

(32)

where $x_t$ denotes a randomly selected locus, $x_t^{\prime }$ denotes the mutated locus, and r denotes a random number uniformly distributed in the interval (0, 1). d denotes the probability of mutation, and $u_t$ and $l_t$ denote the upper and lower bounds of the variable, respectively.

To avoid blindly applying variation operations, the variation parameter r in polynomial variation is randomly generated. A polynomial variation strategy based on the Levy distribution is adopted to reasonably determine the variation range of the population. We adopt the random walk characteristics of Levy flight to dynamically control the mutation step size. Compared with a fixed mutation probability, Levy flight has the features of both small-scale local search and large-scale long-distance leaps. The “long jumps” in Levy flight enable the algorithm to explore unknown regions far from the current population, which is crucial for enhancing global search capabilities and discovering potential optimal solutions. Meanwhile, the “short jumps” allow the algorithm to conduct fine exploitation after identifying promising areas. This self-balancing characteristic of “exploration” and “exploitation” ensures that the algorithm conducts guided random search in a relatively large population, maintaining diversity without sacrificing convergence speed. Therefore, generating the variational parameter r from the Levy flight strategy not only increases the search region of the solution but also enhances the algorithm’s ability to search for the solution. This strategy enables the algorithm to avoid falling into local optima, thus increasing its probability of finding the global optimum solution. The formula for generating the variational parameter r using the Levy flight strategy is as follows:

$$\sigma ={\left({\displaystyle \frac{\Gamma (1+\beta )sin(\pi \beta /2)}{\pi \beta \Gamma \left(\right(1+\beta )/2)}}\times {\displaystyle \frac{2^{(\beta -1)/2}}{\beta }}\right)}^{1/\beta }$$

(33)

$$u=norm(0,\sigma )$$

(34)

$$v=norm(0,1)$$

(35)

$$r={\displaystyle \frac{u}{{\left|\nu \right|}^{1/\beta }}}$$

(36)

where $\Gamma$ is the gamma function, $\beta$ is the shape parameter of the step size distribution with a value of 1.5, and u and v denote the standard normal distributions $N\left(0,{\sigma }^2\right)$ and $N(0,1)$ of random numbers, respectively.

3.2.3. Diversity Archive Update Based on the Adaptive Lp-Norm

The DA in Two_Arch2 complements the CA, which guides the population to converge to the PF. In contrast, the DA focuses on maintaining the diversity of the population, and its update is based on the Pareto dominance strategy. However, unlike traditional algorithms that use the crowding distance as a criterion for environment selection, the DA uses the Lp-norm-based distance as a similarity measure between solutions, prioritizing the retention of solutions in sparse regions. The setting of p can affect the evaluation of diversity and thus the distribution of solutions in the target space. In the original DA update strategy, p is set to 1/m (m is the number of objects). Although the distance based on the Lp-norm can largely improve the diversity of the algorithm, it is not conducive to the utilization of its own characteristics if it is used indiscriminately for all individuals in each iteration. Therefore, in this paper, the value of p is dynamically adjusted on the basis of the number of iterations. Therefore, the algorithm has a better global search ability to cover the potentially optimal region at the early stage of optimization and focuses on local depth-seeking at the later stage to achieve a wide distribution of the solution set and ensure the balance between exploration and exploitation of the algorithm, with the following formula:

$$p={\displaystyle \frac{1}{1+e^{p\times \frac{t}{T}}}}$$

(37)

where T is the maximum number of iterations and t is the current number of iterations.

4. Experimental Evaluation

This section first describes the parameter settings of the edge computing-based vehicle–road cooperation architecture. Then, a comparison of the proposed algorithm with MaOEA-IGD [29], TiGE2 [30], hpaEA [31], Two_Arch2 [12], and NSGA-III [27] on the basis of the values of hypervolume (HV) metric and the six optimization objectives proposed in this section.

4.1. Experimental Parameter Settings

Assuming that there are 50 vehicles on a one-way road with a range of 3 km, we set up experiments with 1 to 12 RSUs. We use four optimization algorithms to solve the RSU deployment optimization problem. Each algorithm is run 20 times, and the objective function is evaluated 100,000 times. The other experimental parameters are shown in Table 1.

Table 1. Parameter settings.

Symbol	Description	Value
n	the maximum number of RSUs	12
m	the number of the vehicles	50
W	channel bandwidth	5 MHz
$b_n$	the size of the input data	[400, 600] kbits
$d_n$	the required total number of CPU cycles	[900, 1100] megacycles
$p_n$	vehicle transmission power	500 mW
$p_{i}dle$	vehicle transmission power	100 mW
${\rho }_0$	small-scale fading coefficient	${10}^{-5}$
$\beta$	Path loss coefficient	3
d	the maximum communication range	250 m
${\delta }_0^2$	the noise power spectral density	${10}^{-9}$ W
$p_d$	Probability of being eavesdropped	${10}^{-9}$
$maxFE$	Maximum evaluation times	100,000

4.2. Comparison and Analysis of Experimental Results

The variability in the number of RSUs deployed is analyzed on the basis of the set of Pareto optimal solutions obtained. Figure 2 presents a visualization of the experimental results for the the six algorithms on each optimization objective (the smaller the objective value is, the better the optimization). As shown in Figure 2a,b,d, the performance of the solution obtained by the improved algorithm WGTwo_Arch2 is significantly better than that of the remaining five algorithms on three objectives, time delay, energy consumption and security. The performance of the six algorithms under the load balancing and coverage area objective is shown in Figure 2c,e, where the WGTwo_Arch2 algorithm is optimized after MaOEA-IGD. However, MaOEA-IGD can only find solution sets with RSU numbers less than 9, which has significant shortcomings in terms of diversity. In summary, the WGTwo_Arch2 algorithm demonstrates superior performance in solving the many-objective deployment optimization problem for RSUs in the IoV, achieving low latency, effectively reducing the energy overhead of the system and ensuring the security of data transmission.

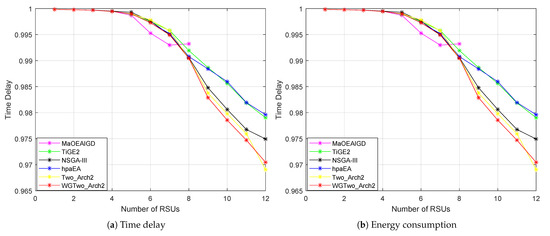
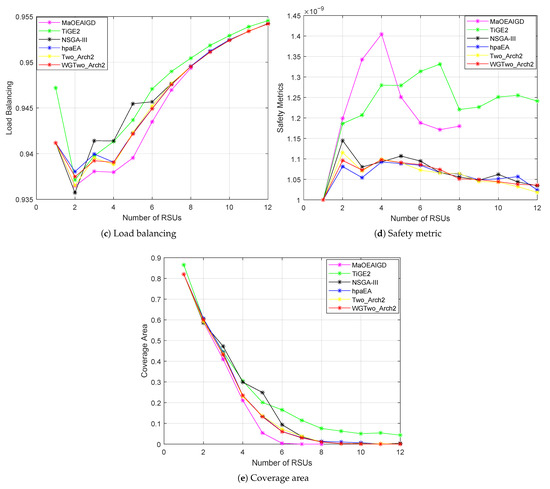
Figure 2. Comparison of average objective values between WGTwo_Arch2 and other algorithms.

4.3. Comparison of HV Indicator Values

The HV, as a comprehensive evaluation metric, can be used to assess the performance of algorithm-generated PFs effectively in terms of diversity and convergence. This metric quantifies the performance of an algorithm by calculating the volume of the space enclosed by the PFs with respect to a predefined reference point. This reference point is usually set as the point of minimum value in each target direction, which serves as a benchmark for evaluation. If a larger value of HV is obtained during the calculation process, then the algorithm usually performs better in terms of convergence and diversity. The HV is calculated via the following equation:

$$HV(ps,ref)=VOL\left\{\bigcup _{f\in ps}\left[f_1,f_1^{ref}\right]\times \dots \times \left[f_m,f_m^{ref}\right]\right\}$$

(38)

where $ps$ denotes the set of optimal solutions obtained by the algorithm, which contains solutions that perform well under multiple objective functions. $ref$ is the set reference point, which is usually chosen as the minimum value point in each objective direction as the benchmark for calculating the hypervolume. m denotes the number of objectives, which determines the dimensions of the objective space that need to be accounted for during HV calculation. In this paper, the proposed algorithm is compared with the other five algorithms in terms of the HV term. The number of evaluations is set to 100,000, and each algorithm is tested independently over 20 runs. The final HV value is computed as the average of these 20 runs. As shown in Table 2 and Figure 3, the HV metric value of the WGTwo_Arch2 algorithm is the largest, indicating its superior performance in solving the many-objective RSU deployment optimization problem.

Table 2. HV index values.

Algorithm	HV
WGTwo_Arch2	$1.384\times {10}^{-3}$
Two_Arch2	$1.282\times {10}^{-3}$
NSGA-III	$1.240\times {10}^{-3}$
hpaEA	$1.243\times {10}^{-3}$
TiGE2	$1.297\times {10}^{-3}$
MaOEA-IGD	$1.037\times {10}^{-3}$

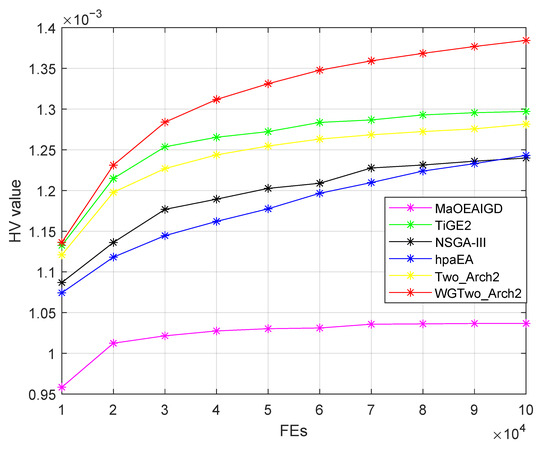
Figure 3. The HV value evolutionary curves of algorithms for the six-objective optimization model.

Based on the HV values obtained from 20 experiments, the mean and standard deviation 95% confidence intervals of six algorithms were calculated as follows: For WGTwo_Arch2, the confidence interval of the mean is (0.001372, 0.001392) and the standard deviation is (0.0000160, 0.0000307). For Two_Arch2, the 95% confidence interval of the mean is (0.001264, 0.001306) and the standard deviation is (0.0000339, 0.0000651). For hpaEA, the 95% confidence interval of the mean is (0.001199, 0.001248) and the standard deviation is (0.0000404, 0.0000777). For NSGA-III, the 95% confidence interval of the mean is (0.001216, 0.001260) and the standard deviation is (0.0000364, 0.0000700). For MaOEA-IGD, the 95% confidence interval of the mean is (0.001009, 0.001065) and the standard deviation is (0.0000459, 0.0000880). For TiGE2, the 95% confidence interval of the mean is (0.001284, 0.001310) and the standard deviation is (0.0000214, 0.0000412). The larger the HV value, the better the comprehensive performance of the algorithm in solving practical application problems. Among them, the mean of WGTwo_Arch2 is higher than that of other algorithms and its interval is the narrowest, indicating that the average performance of WGTwo_Arch2 is better. In addition, the standard deviation interval of WGTwo_Arch2 is the smallest, indicating that this algorithm has the most stable performance.

4.4. Time Complexity Analysis

Assuming the population size is N, the decision variables are D and the number of objective functions is m. In WGTwo_Arch2, the Kent chaos mapping and WGAN are applied to generate N individuals with m objectives, with time complexities of $O\left(mN\right)$ and $O\left(mNd\right)$ respectively, where d represents the complexity of the generator network (such as the number of layers and neurons per layer). In the mating selection strategy, WGAN is employed to generate individuals with a time complexity of $O\left(mNd\right)$. Then, updating the CA based on indicator selection with time complexity of $O\left(N^2\right)$, updating the DA involves performing non-dominant sorting and diversity maintenance based on the Lp norm, so the time complexity is $max\left\{O\left(N^2{log}^{m-2}N\right),O\left(m{N}^2\right)\right\}$. Therefore, the total complexity of WGTwo_Arch2 is $max\left\{O\left(N^2{log}^{m-2}N\right),O\left(m{N}^2\right),O\left(mNd\right)\right\}$. The comparison of computational complexity with other algorithms is shown in Table 3.

Table 3. Computational complexity of compared algorithms.

Algorithm	Computational Complexity
WGTwo_Arch2	$max\left\{O\left(N^2{log}^{m-2}N\right),O\left(m{N}^2\right),O\left(mNd\right)\right\}$
Two_Arch2	$max\left\{O\left(N^2{log}^{m-2}N\right),O\left(m{N}^2\right)\right\}$
NSGA-III	$max\left\{O\left(N^2{log}^{m-2}N\right),O\left(m{N}^2\right)\right\}$
hpaEA	$O\left(N{log}^{m-1}N+m{N}^2+m^{3}N\right)$
TiGE2	$O\left(m{N}^2+(J+K)N\right)$
MaOEA-IGD	$O\left(t{N}^3\right)$

5. Discussion

This paper focuses on the deployment optimization of RSUs in edge computing-based cooperative vehicle-infrastructure systems. A many-objective deployment optimization model for RSUs is established and a corresponding algorithm named WGTwo_Arch2 is proposed. Experimental results demonstrate that the proposed algorithm exhibits good optimization performance on the constructed model. However, there are still certain limitations in terms of model construction and algorithm design. Firstly, the constructed RSU deployment optimization model is a simplified model, which fails to fully reflect the complex traffic conditions in reality, thus limiting the applicability and credibility of the model in actual road networks. In future research, we will focus on incorporating more realistic road condition parameters (such as real-time traffic density, vehicle speed distribution and communication load) or directly integrating real traffic flow data to enhance the practicality and generalization ability of the model. Secondly, although the WGTwo_Arch2 algorithm performs well in the currently experimental scenarios, its scalability in handling larger-scale problems has not been verified. For example, when the number of RSUs increases significantly, the road range expands, or the scale of vehicle nodes grows, further investigation is needed to determine whether the algorithm can still maintain good convergence speed and solution diversity. In addition, whether the algorithm is applicable to other types of many-objective optimization problems (such as task offloading and resource allocation) also needs to be explored.

6. Conclusions

Efficient IoV networks require optimal RSU deployment for a given road layout, which can reduce network latency and improve data transmission efficiency. However, deploying and maintaining RSUs is costly. Therefore, maximizing the QoS with a limited budget is a major challenge. In this paper, we describe the RSU deployment problem in edge computing-based vehicle–road cooperation and model it as a deployment optimization problem with multiple objectives. To evaluate the performance of the system architecture comprehensively, a six-objective optimization model is constructed that integrates several key factors, such as time delay, energy consumption, security, load balancing, deployment cost and coverage area. The WGTwo_Arch2 algorithm is subsequently proposed by incorporating the WGAN-based population initialization strategy and mating selection strategy, the Kent map-based population initialization strategy, the polynomial variation strategy based on the Levy distribution, and the diversity archive updating strategy based on the adaptive Lp norm into the Two_Arch2 framework. The execution process and pseudocode of the proposed enhancements are detailed. Finally, by comparing the objective function values and performance evaluation indices, it is verified that the WGTwo_Arch2 algorithm clearly outperforms the other algorithms in several aspects.