Excavation-Induced Disturbance in Natural Structured Clay: In-Situ Tests and Numerical Analyses

Abstract

Deep excavation in natural structured clay causes disturbance to the surrounding soil, which damages the soil structure and results in soil strength reduction. This study investigates excavation-induced disturbance in natural clay based on a case of subway station excavation. A series of piezocone tests was performed adjacent to the diaphragm wall before and after excavation to determine the disturbance degree based on cone tip resistance. The stress and deformation variations in soil were also obtained via numerical simulations, and the mechanisms of excavation-induced disturbance were proposed based on the numerical simulation results. The results showed that excavation caused a decrease in the cone tip resistance, and the disturbance degree of soil determined by cone tip resistance ranged from 0% to 50%. At identical locations, the disturbance degree of soil increased with excavation depth. The main reason for excavation disturbance is the increase in shear stress. Therefore, shear strain can serve as an indicator of the degree of disturbance, and the relationship between disturbance degree and shear strain can be expressed by a power function. The degree of soil disturbance is affected not only by the magnitude of the diaphragm wall horizontal displacement but also by its deformation distribution pattern.

1. Introduction

Natural sedimentary clays possess inherent structure. Construction activities in such structured clays induce significant disturbance to soil, altering their mechanical properties. Existing research demonstrates that after disturbance, key soil parameters including the yield stress [1,2,3], undrained shear strength [4,5], compression index [6,7], and small-strain shear modulus [8] decrease, while the recompression index [9] and damping ratio [10,11] increase. These changes may lead to increased settlement of the soil surrounding the excavation and pose risks to the safety of adjacent structures [12]. Therefore, it is important to investigate the disturbances induced by excavation in natural clay.

Due to alterations in the mechanical properties of soil after disturbance, numerous researchers have developed methods to assess the degree of soil disturbance based on laboratory tests [13]. For instance, Nagaraj et al. [14] evaluated the degree of disturbance using the change rate of yield stress before and after disturbance. Tanaka [15] determined the degree of disturbance using the change in suction before and after disturbance. Donohue et al. [16] assessed the degree of disturbance based on changes in shear wave velocity before and after disturbance. However, since processes such as sampling, transportation, storage, and specimen preparation inevitably induce disturbance [17,18,19], laboratory tests cannot accurately evaluate the degree of disturbance caused by construction activities. Suzuki et al. [20] estimated the zone of excavation disturbance around tunnels using resistivity and acoustic tomography. Bellmunt et al. [21] adopted time-lapse cross-hole electrical resistivity tomography to monitor the effects of an urban tunnel excavation on surrounding soil. Xu et al. [22] conducted cone penetration tests (CPT) and vane shear tests on the soil above the tunnel before and after shield tunneling. The results indicated that the cone tip resistance and undrained shear strength of the soil above the tunnel decreased after shield construction. Chen et al. [23] employed cone penetration testing to investigate the change in cone tip resistance of the soil at the bottom of the excavation and established a calculation method for the degree of soil disturbance based on cone tip resistance. Gao et al. [24,25] performed cone penetration tests and cross-hole seismic testing on the soil surrounding the shield tunnel before and after tunneling. Li et al. [26] utilized cone penetration testing and the disturbance degree calculation method defined by Chen et al. [23] to calculate the degree of disturbance in the soil adjacent to an excavation in Ningbo.

Previous studies primarily focused on utilizing cone penetration tests (CPT) to evaluate the disturbance degree and extent of disturbance zone induced by shield tunneling, with relatively limited investigation to disturbance caused by the excavation. More importantly, most existing studies have only inferred the disturbance degree from CPT results, without systematically analyzing the underlying mechanisms, distribution patterns, or influencing factors of excavation-induced soil disturbance. Consequently, a comprehensive understanding of how excavation affects the mechanical and structural integrity of surrounding soft soils remains insufficient.

In this paper, excavation-induced disturbance in natural sedimentary clay is investigated based on a case of subway station excavation. Piezocone tests were performed before and after excavation to quantify the disturbance degree based on variations in cone tip resistance. Complementary numerical simulations were conducted to capture soil stress and deformation variations during the excavation process. The combined experimental and numerical analyses revealed the mechanisms governing excavation-induced disturbance and established a quantitative relationship between disturbance degree and shear strain. Furthermore, the spatial distribution of soil disturbance and its key influencing factors were identified and characterized. These findings, which were largely absent from existing literature, provide novel insights into the problem of soil disturbance during excavation. By filling a critical knowledge gap, this study delivers invaluable results for both academic understanding and engineering practice, particularly for the design and construction of excavation projects in soft clay strata. The results not only enhance the theoretical framework for interpreting soil behavior under excavation-induced stress changes but also offer practical guidance for minimizing disturbance effects in geotechnical engineering applications.

2. In Situ Tests Before and After Excavation

2.1. Case Description

The test area is located in Nanjing, Jiangsu Province, China. The examined excavation is a subway station of Line 9, as shown in Figure 1. The excavation is oriented north–south with a total length of 257.5 m, comprising a subway station and two launching shafts for shield tunneling. The subway station has a width of 18.1 m and an excavation depth of 18.37 m, while the launching shafts are 22.2 m in width and 19.42 m in depth. Located in the urban area, the excavation is adjacent to buildings and roads, including low-rise masonry structures and high-rise reinforced concrete frame buildings. The minimum distance between the excavation and adjacent structure is 10 m.

To mitigate impacts on traffic, the station was excavated using the semi-top-down method. The typical cross-section of the excavation is shown in Figure 2. The retaining system comprises diaphragm walls and struts. The diaphragm walls are 800 mm in thickness and extend to a depth of 46.7 m. Four levels of struts were adopted for the station excavation. The uppermost strut is concrete strut with a cross-sectional area of 800 mm × 1200 mm, which also serves as cover slab beams. The spacing of the concrete strut ranges from 5.5 m to 6.6 m. The concrete cap beam was used to connect all the concrete struts. The remaining three levels of struts were steel tube struts with an outer diameter of 800 mm and wall thickness of 16 mm. The spacing of the steel strut ranges from 2 m to 4 m. For the steel struts, the servo system was employed to minimize the horizontal movement of the diaphragm wall and prevent the steel struts from failure. The servo steel struts were connected to the steel plates embedded in the diaphragm wall to provide horizontal reaction force. The excavation base was reinforced with deep mixing piles arranged in a staggered grid pattern, forming improved zones measuring 3 m in both width and depth.

After the installation of the concrete supports, excavation at the profile under investigation in this study started on 5 April 2023. The first excavation phase to the depth of 8.4 m lasted for 26 days, after which the first level of steel struts was installed. Subsequently, the second excavation phase was carried out, reaching the depth of 12 m over a period of 13 days, followed by the installation of the second level of steel struts. The third phase then involved excavation to the depth of 15.5 m, which took 17 days and was followed by the installation of the third level of steel struts. Finally, the final excavation phase to a depth of 18.37 m, along with the pouring of the concrete base slab, was completed over 42 days. The entire excavation process thus spanned a total of 104 days.

2.2. Geotechnical Conditions

The subway station is situated within the Yangtze River floodplain. The geological formation of the strata primarily consists of Holocene middle-late period sediments, according to the code for investigation of geotechnical engineering [27]. The representative geotechnical profile is presented in Figure 2. From the top to the bottom of the profile, the soils encountered are fill, mucky silty clay, and moderately weathered sandstone. The groundwater is phreatic water with the water table approximately 1.5 m below ground surface.

To evaluate the physical and mechanical properties of subsoils, borehole sampling was conducted at the construction site followed by a series of laboratory test. The laboratory tests consisted of basic tests for unit weight and water content, oedometer test for constrained modulus, simple direct shear test for cohesion and friction angle, and unconfined compressive strength test for sensitivity. The mean values of the soil parameters obtained from laboratory testing are presented in

Table 1. Physical and mechanical parameters of soil and rock.

Soil	St	ω (%)	γ (kN/m3)	e	IL	Ip	Es (MPa)	${\mathit{c}}_{\mathbf{cq}}^{\prime }$ (kPa)	${\mathit{\phi }}_{\mathbf{cq}}^{\prime }$ (°)
Fill	-	34.3	18.2	0.98	0.82	15.0	3.74	18.9	9.0
Mucky silty clay	4.5	36.0	17.9	1.04	1.08	14.1	3.57	13.3	13.0
Sandstone	-	-	25.3	-	-	-	-	-	38.4

Notes: ω = Water content, γ = Unit weight, e = Void ratio, I_L = Liquidity index, I_p = Plasticity index, E_s = Constrained modulus, $c_{\mathrm{cq}}^{\prime }$ = Effective cohesion from direct shear test, ${\phi }_{\mathrm{cq}}^{\prime }$ = Effective friction angle from direct shear test.

. The results indicate that the thick mucky silty clay layer at this site is characterized by low strength and high sensitivity, which implies it is sensitive to excavation disturbance.

2.3. Instrumentation and Piezocone Test Before and After Excavation

Inclinometers and settlement markers were employed to monitor horizontal displacement of the diaphragm walls and ground surface settlement during excavation. The locations of the monitoring section discussed in this study are presented in Figure 1, while the instrument layout is presented in Figure 3. Inclinometers were embedded within the diaphragm walls, extending 40 m below the ground surface. Four settlement markers were installed at lateral offsets of 2 m, 7 m, 12 m, and 22 m from the diaphragm wall to monitor surface settlement.

Moreover, piezocone testing (CPTU) was conducted at the monitoring section to investigate the variations in soil cone tip resistance before and after excavation. Figure 3 illustrates the CPTU sounding locations. Three CPTU soundings were selected at lateral offsets of 4 m (CPTU-1), 7 m (CPTU-2), and 10 m (CPTU-3) from the diaphragm walls. Before excavation, piezocone tests were performed to obtain the cone tip resistance of undisturbed soils. Post-excavation piezocone tests were performed when the excavation depth was 8 m and 18.37 m, respectively. Therefore, three piezocone tests were conducted at each of the following excavation stages: before excavation began, at 8 m depth, and at 18 m depth.

The standard piezocone was employed in the tests. The apex angle and cross-sectional area of the cone are 60° and 10 cm², respectively. The pore pressure filter element was positioned at the cone shoulder. During the test, penetration rate was maintained at 20 mm/s. The CPTU soundings extended to approximately 20 m below the ground surface, exceeding the excavation depth.

2.4. Evaluation of Soil Disturbance After Excavation

Figure 4 presents cone tip resistance q_t profiles before and after excavation. The numeral suffix in the legend of each figure denotes the excavation depth during the CPTU test. The numeral 0 indicates the CPTU tests were conducted before excavation, numeral 1 indicates the excavation depth was 8 m, and numeral 2 indicates the excavation depth was 18.37 m. The soil profile exhibits relatively uniform distribution, with q_t values below 1 MPa. Due to the effects of overburden stress, the cone tip resistance q_t increases with depth. Overall, there was an obvious decrease in cone tip resistance q_t after excavation. The magnitude of reduction increases with excavation depth. Further, deeper soil exhibits greater reductions in cone tip resistance q_t.

Soil disturbance degree can be quantified through variations in cone tip resistance. Chen et al. [23] and Li et al. [26] defined the disturbance degree (SDD) as the rate of change in net cone tip resistance q_net (q_net = q_t − σ_v0), expressed as:

$$\mathrm{SDD}={\displaystyle \frac{q_{\mathrm{net}}-q_{\mathrm{net},\mathrm{d}}}{q_{\mathrm{net}}}}={\displaystyle \frac{\left(q_{\mathrm{t}}-{\sigma }_{\mathrm{v}0}\right)-\left(q_{\mathrm{t}}-{\sigma }_{\mathrm{v}0,\mathrm{d}}\right)}{\left(q_{\mathrm{t}}-{\sigma }_{\mathrm{v}0,\mathrm{d}}\right)}}$$

(1)

where the subscript d represents the parameters after excavation; σ_v0 is the total overburden stress.

The disturbance degree (SDD) after excavation is presented in Figure 5. It is evident that soils within the CPTU range were affected by the excavation-induced disturbance, exhibiting disturbance degrees predominantly ranging from 0 to 50%. At identical locations, the disturbance degree increased with excavation depth. Within individual CPTU boreholes, disturbance degree first decreased and then increased with depth.

3. Numerical Analyses

3.1. Numerical Model of the Excavation

3.1.1. Finite Element Model, Mesh, and Boundary Conditions

Variations in stress and strain of soil were another excavation-induced disturbance effect. Numerical simulations were used to obtain the stress and strain variations in soil behind the diaphragm wall. To accurately capture soil deformation, horizontal displacements of the diaphragm walls at different excavation depths were imposed as boundary conditions to model the excavation process. The numerical model is based on the CPTU test section, which is located 127.5 m from the corner of excavation and exceeds five times the excavation depth [28,29]. Thus, plane strain analysis yields the same results as those computed by three-dimensional simulations. Considering the symmetry and computational efficiency, two plane strain models were established using PLAXIS 2D 2017 software [30], as shown in Figure 6. To mitigate boundary effects, the model was set to 100 m in width and 50 m in height. The two models simulated excavation depths of 8 m and 18.37 m, respectively.

Figure 6 also presents the mesh of the finite element model. The soil was modeled by the 15-noded triangular elements, and mesh refinement was adopted for the elements near the diaphragm walls. The FE model was composed of 4327 elements and 35,368 nodes.

Before the excavation simulation, a mesh independence verification was conducted to demonstrate that the simulation results are independent of mesh density. Five mesh configurations were employed, ranging from very coarse, coarse, medium, to fine and very fine. The very fine mesh configuration was used for the excavation simulation. The maximum surface settlement behind the diaphragm wall was chosen as the indicator to investigate the relationship between numerical simulation results and mesh density. Figure 7 illustrates the distribution of maximum surface settlement under different mesh densities. It can be observed that the maximum surface settlement decreases with increasing mesh density, and a minimum of fine mesh is required to achieve mesh-independent results. Hence, the mesh density adopted in this study is sufficient to obtain accurate simulation results.

The left boundary was constrained in the perpendicular direction, and the bottom boundary was constrained both horizontally and vertically. The top boundary is free to move. Along the right boundary, horizontal displacements of the diaphragm walls were prescribed as boundary conditions, while horizontal fixity was imposed on the remainder of the boundary.

Horizontal displacements of the diaphragm walls during CPTU tests are presented in Figure 8. The wall displacements were monitored by inclinometers with vertical measurement intervals of 0.5 m. In the numerical model, linear interpolation was applied between measurement points to facilitate segmented input of wall displacements. As shown in Figure 8, the diaphragm wall exhibits a parabolic deformation pattern, with maximum horizontal displacement occurring 3.13 m below the final excavation level.

3.1.2. Material Models and Input Parameters

The subsoils primarily comprise fill, mucky silty clay, and weathered sandstone. The mechanical behavior of fill and sandstone was modeled using the Mohr-Coulomb model, while the Hardening soil small strain (HSS) model was adopted to simulate the mechanical behavior of mucky silty clay. The most significant feature of the HSS model is the modeling of soil stiffness degradation within the small-strain range, which is essential for excavation analysis [31]. Two types of hardening processes—namely, shear hardening and compression hardening—are introduced to describe the nonlinear soil behavior. The deviatoric yield surface f_dev with a non-associated flow rule is used to explain the plastic strains induced by deviatoric loading:

$$f_{\mathrm{dev}}={\displaystyle \frac{q_{\mathrm{a}}}{E_{50}}}{\displaystyle \frac{q}{q_{\mathrm{a}}-q}}-{\displaystyle \frac{2q}{E_{\mathrm{ur}}}}-{\gamma }^{\mathrm{p}},q=q_{\mathrm{f}}/R_{\mathrm{f}}$$

(2)

where γ^p is plastic shear strain, which controls the expanding of the deviatoric yield surface, q is the deviatoric stress, q_a and q_f are the asymptotic and ultimate deviatoric stress, R_f is the failure ratio, E₅₀ is the secant Young’s modulus at 50% of the ultimate deviatoric stress, E_ur is the unloading–reloading secant Young’s modulus.

The cap yield surface f_cap with associated flow rule is employed to model the plastic strains originating from isotropic loading:

$$f_{\mathrm{cap}}={\displaystyle \frac{{\tilde{q}}^2}{{\alpha }^2}}+p{\prime }^2-p_{\mathrm{p}}^2,\tilde{q}={\sigma }_1^{\prime }+\left(\delta -1\right){\sigma }_2^{\prime }-\delta {\sigma }_3^{\prime }$$

(3)

where α is an auxiliary model parameter that relates to the coefficient of earth pressure at rest, q is a special stress measure for deviatoric stresses, δ = (3 + sin φ′)/(3 − sin φ′), p_p is the isotropic preconsolidation stress.

The Mohr–Coulomb strength criteria control the ultimate limit state. The small strain behavior is described by the Hardin–Drnevich relationship. Detailed descriptions of the HSS model can be found in the original publication [32].

The soil constitutive model parameters were derived from laboratory tests and in situ tests [33].

Table 2. Soil parameters of the constitutive models.

Soil	γ (kN/m3)	E′ (MPa)	ν′	c′ (kPa)	φ′ (°)
Fill	18.2	10	0.3	0.1	30
Sandstone	25.3	500	0.3	2000	0.1
Mucky silty clay	γ (kN/m3)	$E_{50}^{\mathrm{ref}}$	$E_{\mathrm{oed}}^{\mathrm{ref}}$	$E_{\mathrm{ur}}^{\mathrm{ref}}$	c′ (kPa)
	17.9	3.6	2.3	13.8	0.1
	φ′ (°)	$G_0^{\mathrm{ref}}$ (MPa)	γ0.7 (10−4)	m	νur
	26	56	1.7	1	0.2

Notes: E′ = Elastic modulus of Mohr–Coulomb model, ν′ = Poisson’s ratio, c′ = Effective cohesion, φ′ = Effective friction angle, $E_{50}^{\mathrm{ref}}$ = Secant modulus from triaxial compression tests, $E_{\mathrm{oed}}^{\mathrm{ref}}$ = Tangent modulus from one-dimensional compression tests, $E_{\mathrm{ur}}^{\mathrm{ref}}$ = Unloading and reloading modulus from triaxial compression tests, $G_0^{\mathrm{ref}}$ = Shear modulus at small strain, γ_0.7 = threshold shear strain, m = Power for the stress-level dependency of stiffness, ν_ur = Poisson’s ratio for unloading–reloading.

summarizes the values of soil constitutive model parameters.

The diaphragm walls were simulated using a linear elastic constitutive model with a thickness of 0.8 m, Young’s modulus of 30 GPa, and Poisson’s ratio of 0.15. The diaphragm walls were “wished” into place for all analyses. Thus, installation of the wall caused no stress changes or displacements in the surrounding soil. Interface elements were incorporated between the walls and surrounding soil to simulate wall-soil interaction.

3.1.3. Steps for Numerical Simulation

The groundwater of the excavation site is phreatic water in fill and mucky clay layers, with an initial water table at 1.5 m below ground surface. Because the diaphragm walls were inserted into the sandstone, the hydraulic connection inside and outside the excavation was cut off. Consequently, the groundwater table outside the excavation remained unchanged, and a constant groundwater table was maintained in numerical simulations. The initial stress conditions were generated via K₀ loading incorporating soil unit weight γ_s and overconsolidation ratio OCR. The undrained elasto-plastic analysis was adopted for the numerical simulations. The main simulation steps are as follows:

• Establishing initial stress fields through K₀ loading.
• Activating diaphragm walls and wall-soil interfaces.
• Resetting displacements induced by wall construction, then imposing horizontal wall displacements when the excavation depth was 8 m, and executing undrained elasto-plastic analysis.
• Imposing horizontal wall displacements when the excavation depth was 18.37 m, and executing undrained elasto-plastic analysis.

3.1.4. Model Validation

Figure 9 compares the measured ground settlements with numerical simulation results. For all excavation stages, the simulated values demonstrate good agreement with field measurements. It should be noted that the model slightly underestimates settlements at specific monitoring points when the excavation depth is 19.37 m. This may be attributed to partial dissipation of negative excess pore water pressure induced by excavation unloading, which is not accounted for in the undrained numerical simulation. Overall, the established numerical model accurately predicts excavation-induced ground settlement and can be further utilized for analyzing stress and strain variations in subsoils.

3.2. Soil Stress and Deformation Variations

To investigate the evolution of stress–strain states in soils adjacent to the excavation before and after construction, the excavation-affected zone and representative soil elements within it were selected for analysis. Figure 10 illustrates the excavation-affected zone and distribution of representative elements. According to the numerical simulation results, the surface settlement extends approximately 40 m from the diaphragm wall and the soil horizontal deformation also extends 40 m below the ground surface. Therefore, the analysis of stress–strain behavior of soil within this zone is sufficient. Furthermore, representative soil elements were selected at 5 m depth intervals throughout the CPTU sounding depth to characterize the development of stress–strain paths of soils.

Figure 11 presents the effective mean stress p′- deviator stress q paths of typical soil elements adjacent to the excavation. It can be observed that after excavation, the effective mean stress p′ of these soil elements remained constant or decreased slightly, while the deviatoric stress q increased. This p′-q stress path evolution indicates that the excavation is under undrained excavation conditions. Under undrained conditions, the excavation-induced unloading reduced total stresses in the surrounding soils. The total stress reduction predominantly transformed into the negative pore water pressure, thereby maintaining or slightly decreasing effective mean stress p′.

Figure 12 presents the deformation of soils adjacent to the excavation. Horizontal displacements at lateral offsets of 5, 10, 20, and 30 m from the diaphragm wall, and vertical displacements at depths of 5, 10, 20, 30, and 35 m are also plotted. The gray dashed line indicates the pre-excavation soil position, serving as the datum line. The solid black line represents the horizontal displacement profile, where leftward deflection relative to the datum line denotes displacement toward the excavation, with deflection magnitude corresponding to displacement magnitude. The black dashed line depicts the vertical displacement profile, with downward deflection from the datum line indicating settlement, where deflection magnitude similarly correlates with settlement magnitude.

As shown in Figure 12, soil settlement occurs within a specific depth below the ground surface, defining this area as the settlement zone. Shallow soils within this zone exhibit trough-shaped settlement distribution. Settlement decreases with increasing depth, while the location of maximum settlement progressively shifts closer to the diaphragm wall. At a critical depth, the deformation pattern transitions from trough-shaped to triangular distribution, with maximum settlement occurring at the diaphragm wall. Below the settlement zone, soil heave occurs with a triangular distribution pattern. The soil heave decreases proportionally with distance from the diaphragm wall.

Figure 12 further reveals that soils adjacent to the diaphragm wall exhibit horizontal displacement patterns analogous to the deformation profile of the diaphragm wall. With increasing distance from the wall, the displacement pattern progressively transitions to a cantilever-type distribution, with the maximum horizontal displacement occurring at the ground surface. At the ground surface, the horizontal displacements increase initially and then decrease with increasing distance from the diaphragm wall, forming a trough-shaped horizontal displacement distribution.

Figure 13 illustrates the shear strain distribution within the soil adjacent to the excavation. Due to the non-uniform deformation of the diaphragm wall, the displacement of the soil in the middle section of the wall exceeds that near the top and bottom of the wall. The resulting relative displacement between these zones induces the soil arching effect. The location of the maximum diaphragm wall deformation corresponds to the trapdoor in Terzaghi’s soil arching experiment [34,35]. Shear planes develop on either side of this trapdoor. The soil adjacent to these shear planes is subjected to shearing, leading to increased shear strain and deviatoric stress. When the trapdoor deformation becomes sufficiently large, the shear strain in the soil near the shear planes is close to the failure shear strain, and the soil reaches the failure state.

4. Discussion

Natural sedimentary clays have inherent structure, characterized by a specific fabric (arrangement of soil particles) and bonding (cementation between soil particles). Due to the effects of structure, natural clays exhibit distinct mechanical properties compared to remolded clays; for instance, at the same stress level, natural clays typically have a higher void ratio and higher strength than remolded clays. The additional load applied to natural structured clays is the primary cause of disturbance. When the load exceeds the yield stress of natural structured clays, the structure gradually degrades [36,37]. The mechanical behavior of disturbed structured clays lies between remolded clay and natural structured clay. Figure 14 illustrates the change in undrained shear strength of structured clay after disturbance. The undrained shear strength of the intact structured clay is denoted as S_u0. Disturbance destroys the soil structure, resulting in a reduction in undrained shear strength of clay. The undrained shear strength of the disturbed structured clay is denoted as S_ud. Structural degradation primarily affects the peak strength of clay. When the shear strain causes the structure of the clay to be completely destroyed, the effective stress paths of both intact and disturbed soils ultimately converge at the Critical State Line (CSL).

When additional load is applied to soil, the load is carried by both the soil skeleton and the pore water. According to the principle of effective stress, the applied load is equal to the sum of the effective stress and the pore water pressure. The effective stress is sustained by the soil skeleton, while the excess pore water pressure is carried by the pore water. Further, the effective stress acting on the soil skeleton is carried by cementation and friction between soil particles. At low levels of applied load, the effective stress is primarily carried by interparticle cementation, and the soil porosity is relatively high. As the effective stress increases, cementation bonds between clay particles are progressively broken, leading to degradation of the soil structure and a progressive reduction in soil porosity.

Excavation in saturated natural clay is typically rapid and completed within a short timeframe. Consequently, the soil around the excavation can be considered to be in an undrained state during excavation. Under the undrained conditions, the stress changes in the soil induced by excavation are decomposed into changes in mean stress and deviatoric stress. According to the principle of effective stress, the mean stress change is predominantly carried by the pore water pressure, generating negative excess pore water pressure. Therefore, the soil structure will not be influenced by variations in mean stress. Since pore water cannot sustain shear stress, the deviatoric stress is carried by the soil skeleton, and the soil structure will degrade due to the deviatoric stress. Based on the above analysis, under undrained excavation conditions, the direct cause of soil disturbance is the shear stress experienced by the soil. Consequently, soil shear strain is associated with both the degree of soil disturbance and mechanical properties of soil.

Figure 15 presents the relationship between the disturbance degree (SDD) determined by the piezocone tests and the soil shear strain γ_s determined by numerical simulations. It is observed that the disturbance degree increases with an increase in shear strain. The relationship between disturbance degree and shear strain can be expressed by a power function with the coefficient of determination of 0.79:

$$\mathrm{SDD}=25.4{\gamma }_{\mathrm{s}}^{0.33}\times 100\%$$

(4)

Gao et al. [25] reported a similar relationship, which can be approximately divided into two parts: when γ_s ranged from 0 to 2‰, SDD was linearly related to γ_s; i.e., SDD = 330 × γ_s. When γ_s ranged from 2‰ to 14‰, SDD could be expressed as SDD = 30 × γ_s + 60. It can be observed that the disturbance degree increases with increasing shear strain. For identical shear strain levels, the disturbance degree calculated using the formula proposed by Gao et al. [25] is higher than that calculated by the formula proposed in this paper. This discrepancy may be attributed to differences in the structural strength of the soil corresponding to each formulation.

Equation (4) establishes a relationship between soil deformation and the degree of disturbance. Based on this relationship, engineers can more conveniently determine the soil disturbance degree from its deformation, rather than relying on in situ testing. Soil deformation is readily measurable and computable, whereas in situ testing is costly and time-consuming.

Equation (4) indicates that for the same location of the soil, the increase in shear strain is the cause of the increase in disturbance. This finding explains why soil disturbance initially decreases and then increases with depth. According to Figure 13, the displacement of the soil in the middle section of the diaphragm wall exceeds that near the top and bottom of the diaphragm wall. Consequently, two shear planes develop, as illustrated in Figure 13. The soil adjacent to these shear planes experiences higher shear strains. Hence, taking CPTU-1-2 as an example, the degree of soil disturbance decreases within the depth of 5 to 10 m. When the depth exceeds 10 m, the soil disturbance increases with depth. This phenomenon indicates that the degree of soil disturbance is determined not only by the magnitude of the diaphragm wall horizontal displacement but also by its deformation distribution pattern. Although the horizontal displacement of the diaphragm wall increases within the depth of 5 to 10 m, the degree of soil disturbance decreases.

5. Conclusions

This study investigates excavation-induced soil disturbance based on a subway station excavation. The piezocone tests were performed to determine the disturbance of soil around the excavation, and the mechanisms of excavation-induced disturbance were proposed based on the numerical simulations of the excavation. The following conclusions could be drawn:

• Excavation-induced disturbance caused a decrease in the cone tip resistance. The disturbance degree of soil determined by cone tip resistance ranged from 0% to 50%.
• At identical locations, the disturbance degree of soil increased with excavation depth. Within the same CPTU boreholes, the disturbance degree firstly decreased and then increased with depth.
• The degree of soil disturbance is affected not only by the magnitude of the diaphragm wall horizontal displacement but also by its deformation distribution pattern. Although the horizontal displacement of the diaphragm wall increases with depth at shallow depths, the soil disturbance decreases, which is due to the formation of shear planes.
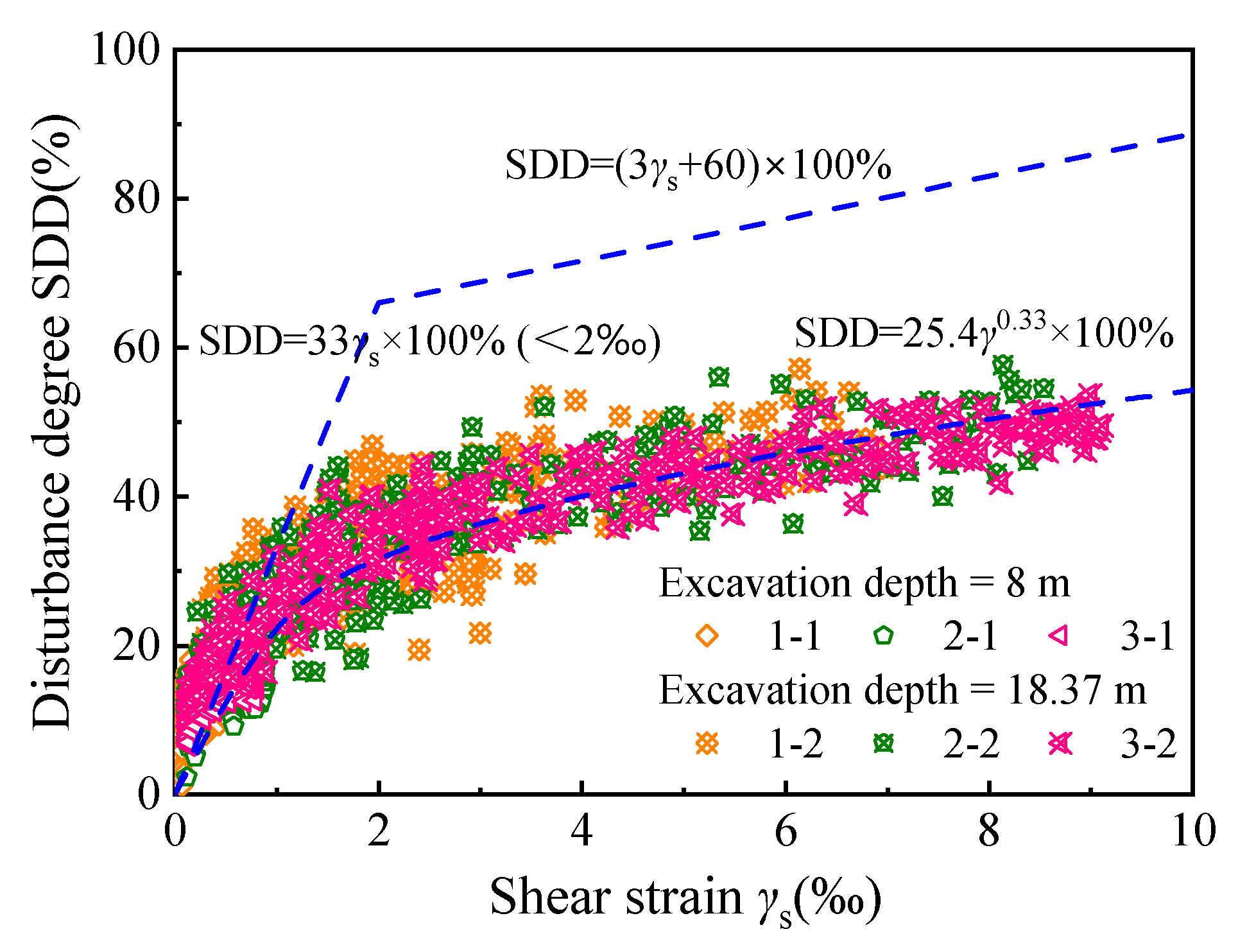
• The reason for excavation disturbance is the increase in shear stress caused by excavation. Consequently, soil shear strain can be associated with the disturbance degree of soil. Based on the numerical simulation and piezocone test results, it was found that the relationship between disturbance degree and shear strain can be expressed by a power function.