Assessment of the Impact of k-ε and k-ω Turbulence Models on the Compatibility of CFD Simulations with PIV Measurements for Flow Through a Measuring Orifice

Abstract

The article presents the results of flow investigations downstream of a standard and slotted orifice plate, obtained using both experimental measurements with the Particle Image Velocimetry (PIV) method and numerical calculations performed in a CFD environment. The aim of the study was a detailed analysis of the velocity field structure and an evaluation of the prediction accuracy of different turbulence models in relation to experimental data. The study employed models from the k-ε and k-ω groups, which were compared in terms of their agreement with measurement results in various flow regions. The study demonstrated that no single turbulence model guarantees optimal results across the entire investigated domain. Model selection should therefore be adapted to the analyzed flow region k-ω models in the vicinity of the orifice and k-ε models in the developed flow region. The findings have significant practical implications for the engineering of orifice flow meters, enabling a more informed use of CFD methods in the design and validation of industrial measurement systems.

1. Introduction

Accurate measurement of fluid flow in closed pipes has a crucial role in many industries, such as energy, chemical, food, and pharmaceutical [1,2]. Due to the high variability of the physicochemical properties of liquids, there is no universal measurement method. Therefore, in practice, it is necessary to individually adapt the technique to the process conditions and search for new, more accurate solutions [3].

In industrial applications where extreme conditions occur (high temperatures, aggressive media, large pipe diameters), differential pressure flow meters such as orifices and Venturi tubes are very often used. Orifice flow meters are widely described in ISO 5167-1:2022 [4,5]. In thermal power plants, where steam reaches high temperatures and pressures, electronic flow meters can be damaged, while orifice devices can prove to be reliable. Similarly, in the chemical and petrochemical industries, devices with electronic components are excluded, and flow meters made of special materials become the only option [6]. In the case of mechanically contaminated or multiphase media (e.g., crude oil with water and gas), electronic sensors may be unreliable, while orifices remain functional. Also, for very large pipe diameters (DN ≥ 1000), mass flow meters and electromagnetic flow meters are expensive and difficult to construct, and orifice plates remain a practical solution. In billing applications, such as natural gas measurement, ISO 5167 provides not only a technical but also a legal basis [7], while other technologies require additional certification [8]. Furthermore, in environments with strong vibrations (e.g., turbines), Coriolis flow meters can give false readings, and orifices, due to the lack of moving parts, show much greater mechanical resistance [5].

Due to their wide application and importance in extreme conditions, orifices are constantly being improved in terms of design. The literature contains solutions for modifying the flow opening in an orifice, in which the centrally located round opening has been replaced, for example, with slots [9,10] or multiple round openings [11,12]. In [13], the authors presented the results of experimental studies in which they compared the pressure drop behind fractal orifices.

Hall and Holste were the pioneers in conceptualizing the slotted plate, which was subsequently implemented at the Dansby power plant in Texas to achieve the pressure drop necessary for gas sampling and analysis [14].

Kumar, Wong, and Bing [15] conducted numerical studies to examine the behavior of fluid flow through different hole shapes (rectangular and circular, β = 0.40) in a slotted orifice. The tests were conducted in a horizontal system, and the tested medium was wet gas. In numerical studies, they used the k-ε turbulence model standard. The analyses showed that although the shape of the openings (circular vs. rectangular) does not significantly affect the pressure difference, rectangular slots allow for better pressure recovery.

In article [11], the authors focused on the metrological analysis of a four-hole measuring orifice (module m = 0.25) installed in a 50 mm diameter pipeline. The study included detailed numerical simulations (CFD) using k-ε-realizable and k-ω-BSL turbulence models, and validation of these models by comparison with experimental results. The tests were carried out in the Reynolds number range from 4200 to 19,000, in the area of developing turbulent flow. The analysis showed that the k-ω BSL 2M model better describes the flow at smaller pressure differences Δp, while k-ε realizable 2M gives better agreement with the experiment for larger Δp values. The differences between the models were small—the maximum difference was 3.36%, and the deviations from the experiment did not exceed 1.82% for k-ε realizable and 1.54% for k-ω BSL. The simulation results also indicated the possibility of using shortened straight sections (2D) before and after the orifice, which is of great practical importance in industrial installations with limited installation space. It was observed that a very short zone of flow discontinuity forms behind the orifice, after which the flow quickly stabilizes and the resulting vortices transition into parallel, steady flows. The conclusions confirmed that multi-orifice flow meters have more favorable metrological properties than centric orifices, including a more stable discharge coefficient (approx. 2% higher at Re > 10,000).

Tomaszewski et al. [16] presented an analysis of flow through six-hole orifice flow meters (MHO) and compared it with a standard single-hole orifice (SHO). The main objective of the study was to investigate the relationship between mass flow and pressure drop and to assess the influence of orifice geometry on the flow coefficient. The authors also analyzed the resistance to flow disturbances generated by an obstruction in the pipeline. The research was conducted experimentally on humid air in a 100 mm diameter channel, testing four variants of MHO multi-hole orifice geometry and single-hole orifices (SHO) with the same restriction coefficients (0.5164–0.7). The researchers performed numerical simulations (CFD) with a realizable k-ε turbulence model to visualize flow patterns and predict pressure drops. The results showed that the flow coefficient for the tested MHOs was similar to the values obtained for SHOs. Multi-hole orifices with lower restriction coefficients showed slightly better resistance to flow disturbances than conventional SHOs, although these differences decreased for higher restriction coefficients. The introduction of an obstacle always led to a decrease in the measured pressure drop and an increase in the calculated flow coefficient. The results of numerical simulations correlated with experimental data in terms of the effect of the obstacle on the pressure drop, confirming the usefulness of CFD tools for predicting this phenomenon.

In the article [17], the authors compared the prediction performance of turbulence models: standard k-ε and realizable k-ε, Launder & Sharma k-ε, and SST k-ω, in simulations of cavitation flows through a nozzle. They analyzed the impact of different turbulence models, comparing the results with experimental data in order to select the best model for accurate simulation of cavitation flow. The authors point out that there is no universal model that works best in all scenarios—their results indicate that realizable k-ε may be more adequate where cavitation phenomena and large variable gradients dominate. Although the analyzed case concerns cavitation flow, it is also important to compare and select an appropriate turbulence model to describe flow in areas with high gradients.

The paper [18] presents the results of research aimed at experimental validation and CFD simulation of two-phase water-air flow through an orifice. The research was conducted for two-phase flow with a Reynolds number ranging from 700 to 11,000 and an air volume fraction ranging from 10% to 45%. Computational fluid dynamics (CFD) with various turbulence models was used to simulate the orifice flow meter under two-phase flow conditions. The Euler-Euler multiphase model, which treats all phases as continuous, was used for modeling, which is appropriate when the volume fraction exceeds 10%. It was found that the k-epsilon RNG turbulence model gave the most accurate results compared to experimental data. This is due to the fact that the k-epsilon RNG model takes into account the uniform distribution of disturbances along the central axis of the flow and assumes similarity in the distribution of disturbance-related quantities in this region. When comparing the average errors with the laboratory results, the k-epsilon RNG model showed an average error of 1.5%, while the standard k-epsilon had 2.1%, k-omega SST 8.2%, and k-omega STN 10.2%. The simulation showed that the maximum two-phase flow velocity along the axis in front of the flow meter was 0.4 m/s, increased to 0.75 m/s after passing through the orifice, and then gradually decreased, which is a result of friction effects and energy losses.

The study [19] analyzed flow fields generated by a synthetic stream using particle imaging velocimetry (PIV). Flow parameters such as velocity, turbulent kinetic energy (TKE), and vorticity were compared at a Reynolds number Re = 5000 and dimensionless stroke lengths L₀ = 2 and 10. Three-hole shapes with the same equivalent diameter (circular, square, and slit) were considered. It was found that as the stroke length increases, the maximum average velocity decreases, but this velocity remains at a higher level at a greater distance for L₀ = 10 than for L₀ = 2. For circular and square holes, the velocity and TKE distributions along the axis decreased more slowly than for the slot hole, where the flow area was locally narrowed and then widened. The values in close proximity to the hole (x/d < 4) were higher at shorter stroke (L₀ = 2), which results from the higher operating frequency and shorter time between successive pulses. Despite the higher velocity, the flow for L₀ = 2 was more orderly and characterized by a lower level of turbulence.

Phenomena related to flow through openings with different geometries have also been studied using experimental methods, including particle imaging velocimetry (PIV). An example of such research is the publication by Zhi-ping Guo et al. [20]. The researchers studied in detail the turbulence characteristics of cavitation flow behind circular plates with multiple holes. The aim of the study was to experimentally understand the mechanisms of combating pathogenic microorganisms using hydrodynamic cavitation. To this end, the researchers used a self-developed hydrodynamic cavitation device and PIV technique to measure longitudinal velocity, turbulence intensity, and Reynolds stress, as well as high-speed photography to observe cavitation flow regimes. The experimental results showed that an increase in the number of holes caused an increase in flow velocity, turbulence, and Reynolds stress, which promoted a stronger shearing effect and more effective destruction of microorganisms. The staggered hole arrangement generated higher values of the tested parameters than the checkerboard-type arrangement, as well as a higher density of cavitation clouds. The results obtained represent a significant contribution to the development of disinfection methods based on the phenomenon of cavitation.

In article [21], Xu Jing-lei and co-authors presented experimental studies of the transient characteristics of a synthetic jet generated by a circular hole. The main objective of the work was to investigate the detailed flow field structure in different phases of the jet cycle, which is important for its applications in active flow control. The study used the phase-synchronized PIV method, which enabled the visualization and analysis of the evolution of vortices, saddle points, and changes in velocity and cross-sectional profiles of the jet. The experiment was conducted using a piston actuator with a variable depth hole (1.5 mm, 2 mm, and 3.5 mm), which allowed the influence of geometry on the flow structure to be assessed. It was shown that, over time, the dimensionless distance between the vortex core and the peak axial velocity increased, and the saddle point moved downstream in accordance with the piston cycle. The velocity profiles exhibited self-similarity in both the instantaneous and averaged fields. It was shown that an increase in the depth of the hole resulted in higher values of axial velocity, mass flow, and momentum, as well as their shift along the flow axis.

Recent studies highlight the growing use of the Particle Image Velocimetry (PIV) technique for liquid flow visualization in channels and pipes, not only in advanced research but also in educational laboratory setups. Brazhenko et al. [22] demonstrated a low-cost DIY PIV system for investigating Poiseuille flow, confirming the method’s accuracy and accessibility even for basic experimental conditions.

In response to the growing industry requirements, increasingly advanced design solutions for measuring elements, such as orifice plates and multi-hole plates, are being developed. Their geometry is subject to intensive optimization in order to reduce pressure losses, improve flow stability, and increase the repeatability and reliability of measurement results. Minimizing flow disturbances behind the measuring element is particularly important because it affects both the accuracy of the measurement and the efficiency of the entire system.

Research into flow behavior in the region of throttling elements increasingly combines experimental and computational methods. To measure the actual velocity field, techniques such as PIV are used, which allow for obtaining a detailed, spatial image of the flow structure under real conditions.

In contrast, numerical calculations within CFD enable flow simulation for various design variants and operating conditions, which significantly reduces the time and cost of optimization. CFD methods allow, among other things, prediction of assembly errors, especially in the case of strongly rotating flow. CFD enables the study of flow meter responses under operating conditions and the analysis of phenomena leading to measurement errors, provided that boundary conditions are defined, a mesh is prepared, and a turbulence model is selected. Simulation results are most useful when the sources of error are well understood and can be verified against experimental data, and with increasing computing power and validation progress, CFD will be increasingly used to evaluate and analyze the use of orifices in flow measurement.

The combination of both methods (PIV and CFD) allows not only for the validation of numerical models, but also for the identification of areas where turbulence models such as k-ε or k-ω better or worse reproduce the phenomena observed in the experiment.

In CFD simulations, the accuracy of flow phenomenon representation largely depends on the turbulence model used. In the case of flows behind throttling elements, such as orifices, we encounter strong velocity gradients, recirculation areas, and directional variability of the stream. In order to accurately represent these phenomena, two-equation models such as k-ε (standard and realizable) and k-ω (including Baseline modifications) are primarily used in engineering practice. Comparing the results obtained with these models with experimental PIV data allows us to determine which model best represents the nature of the flow behind the orifice at a given measurement point. Analysis of error values, such as Root Mean Square Error (RMSE), percentage error (%error) and Mean Absolute Percentage Error (MAPE), allows for a quantitative assessment of the quality of numerical predictions in relation to actual measurements.

The aim of this work is to compare the results of flow velocity measurements obtained using the PIV method with the results of CFD simulations performed using various turbulence models (standard k-ε, realizable k-ε, k-ω, and k-ω BSL), and then to assess which of the models best represents the actual flow behind the orifice in the pipeline.

The novelty of this work lies in the combined CFD–PIV analysis of both standard and slotted orifice plates, providing a direct quantitative comparison of RANS turbulence models under two distinct geometrical configurations of metering elements.

2. Materials and Methods

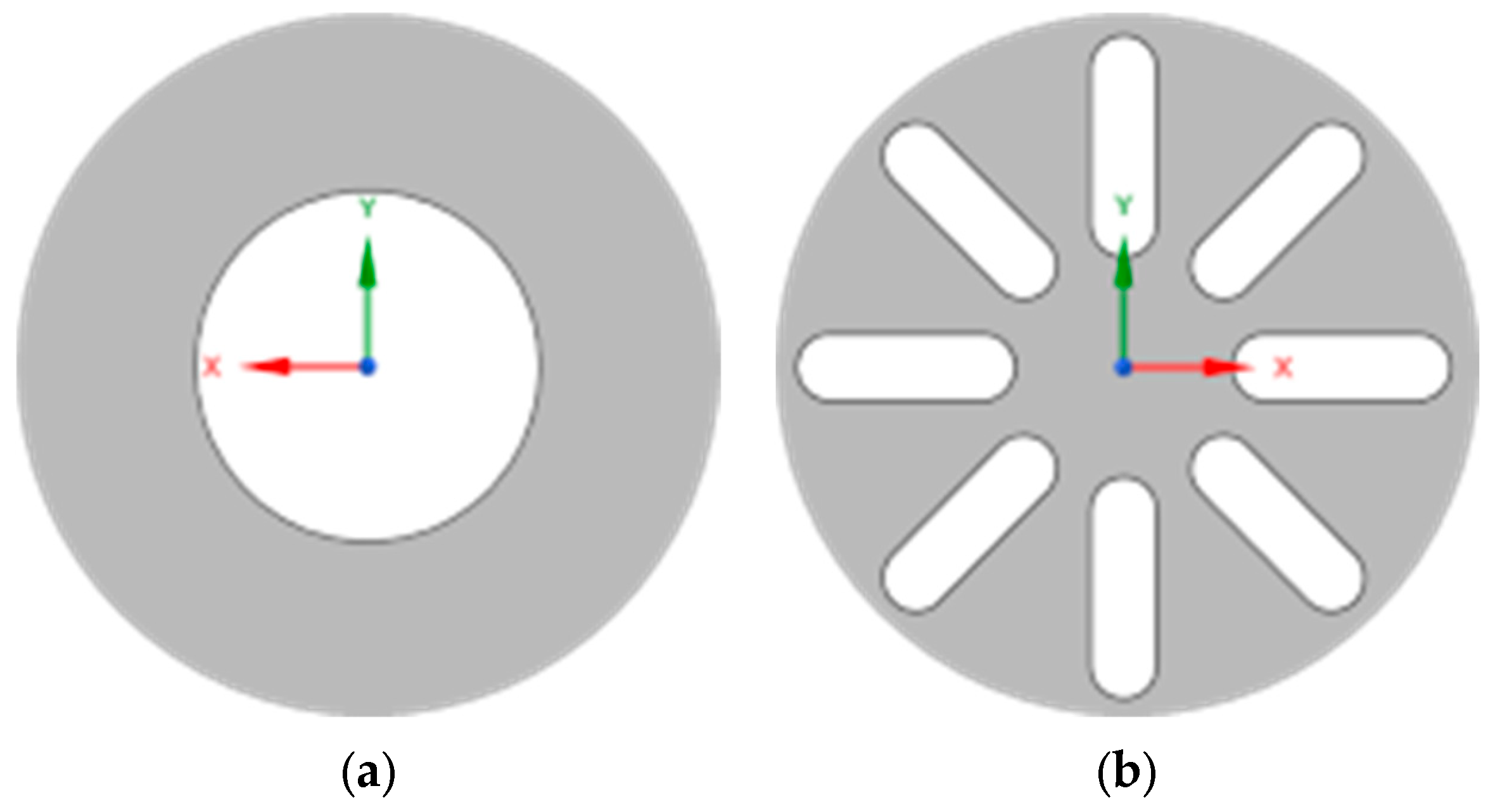
Two measuring orifices were tested: a standard orifice and a slotted orifice. Both orifices were designed to maintain an identical restriction ratio β = 0.5. The diagram and characteristic dimensions of the tested orifices are presented in Figure 1 and Table 1.

Figure 1. Schematic of the tested orifices: (a) standard, (b) slotted.

Table 1. Characteristic dimensions of measuring orifices.

		Orifice
		Standard (STD)	Slotted (ST)
Pipeline diameter [m]		0.05	0.05
Hole diameter [m]		0.025	-
Slot [m]	Width	-	0.00235
	Length	-	0.0108
β ratio		0.5	0.5

The measurements were taken at equal intervals along the length of the pipeline, ranging from 0.005 to 0.25 m.

2.1. Experimental Research (PIV)

The PIV method is an experimental measurement technique used to determine the velocity of fluid flow. It involves tracking the displacement of small particle tracers, called markers, which are introduced into the fluid being studied. Laser light is most often used to visualize the movement of these particles, illuminating a selected flow plane. Changes in the position of the markers over time are recorded with a video camera. Unlike traditional methods, which measure velocity at a single point, the PIV method allows simultaneous measurement of velocity across the entire flow field. This provides a complete picture of the flow dynamics, which is particularly valuable when studying turbulent phenomena and visualizing jets and vortices. The study analyzed velocity components in the horizontal (u) and vertical (v) directions.

The experimental studies were conducted in a closed system, the diagram of which is shown in Figure 2.

Figure 2. Schematic diagram of the test stand, 1—camera, 2—laser, 3—pipe, 4—orifice, 5—rectangular liquid tank, 6—circulating liquid inlet, 7—circulating liquid outlet, 8—light sheet.

The test stand consisted of a pipe system with an internal diameter of 0.05 m and a measuring section 1.6 m long. A measuring orifice was installed in the pipe to function as a throttling element. The working fluid circulated in a closed circuit and was pumped by two Grundfos CR5-7 pumps (Grundfos Holding A/S, Bjerringbro, Denmark). The flow rate was monitored by an ENKO EM-005C electromagnetic flowmeter (ENKO S.C., Kielce, Poland) and regulated by shut-off valves. The PIV (Particle Image Velocimetry) method was used to determine the velocity field, using PMMA-RhB-FRAK-SC57-01 markers (Dantec Dynamics A/S 16-18, Tonsbakken DK-2740, Skovlunde, Denmark). Their type and concentration were selected on the basis of preliminary tests, in accordance with the requirements of the method [23]. The measurement was performed for two streams with velocities of 0.283 m/s and 0.424 m/s.

The images were recorded using a Dantec Dynamics FlowSense EO-4M CCD camera (Dantec Dynamics A/S 16-18, Tonsbakken DK-2740, Skovlunde, Denmark), positioned perpendicular to the pipeline axis, at the orifice installation site. The PIV measurements were carried out in a two-dimensional (2D) plane perpendicular to the pipe axis. The dimension of the analyzed section was approximately 0.2 × 0.05 m. The length is measured from the location of the orifices, and the height corresponds to the cross-section of the tube. The images were recorded in double frame mode, with an acquisition frequency of 10 Hz and an interval between pulses of 500 µs. For each measurement series, 1000 images were taken. The measurement area was illuminated with a Dantec Dynamics DualPower TR Nd:YAG pulsed laser (Dantec Dynamics A/S 16-18, Tonsbakken DK-2740, Skovlunde, Denmark).

The uncertainty of the PIV measurements, estimated from repeated series and calibration accuracy, was approximately ±2.5%

For the purposes of generalizing the results, dimensionless parameters were used, i.e., r/R, v/V.

To assess the accuracy of the turbulence model in reproducing the velocity distribution, error measures were calculated: root mean square error (RMSE), percentage error (%error), and mean absolute percentage error (MAPE).

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{\sum {\left({\mathrm{v}}_{\mathrm{C}\mathrm{F}\mathrm{D}}-{\mathrm{v}}_{\mathrm{P}\mathrm{I}\mathrm{V}}\right)}^2}{\mathrm{n}}}}$$

(1)

$$\%\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}={\displaystyle \frac{{\overline{\mathrm{V}}}_{\mathrm{C}\mathrm{F}\mathrm{D}}-{\overline{\mathrm{V}}}_{\mathrm{P}\mathrm{I}\mathrm{V}}}{{\overline{\mathrm{V}}}_{\mathrm{P}\mathrm{I}\mathrm{V}}}}\times 100\%$$

(2)

${\overline{\mathrm{V}}}_{\mathrm{C}\mathrm{F}\mathrm{D}}$, ${\overline{\mathrm{V}}}_{\mathrm{P}\mathrm{I}\mathrm{V}}$—average velocity from the CFD and from PIV

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{\mathrm{N}}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}\left|\%\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\right|$$

(3)

2.2. Numerical Research (CFD)

The numerical flow modeling procedure consisted of three stages. The CFD simulations were performed in a three-dimensional (3D) domain reproducing the experimental pipe geometry. The computational domain included the orifice plate and straight pipe sections consistent with the experimental setup. Boundary conditions were set as a uniform velocity inlet (0.283 m/s or 0.424 m/s), a pressure outlet (0 Pa gauge), and no-slip walls. The first was to develop the computational geometry, followed by its discretization, i.e., dividing the area into smaller elements. The simulation used the finite volume method, which involves controlling the volume and transforming differential equations into algebraic equations that can be solved numerically. Discretization is crucial because it affects both the calculation time and the accuracy of the results; the greater the number of grid elements, the more accurate the results, but excessive grid density increases the calculation time without significantly improving the quality of the results.

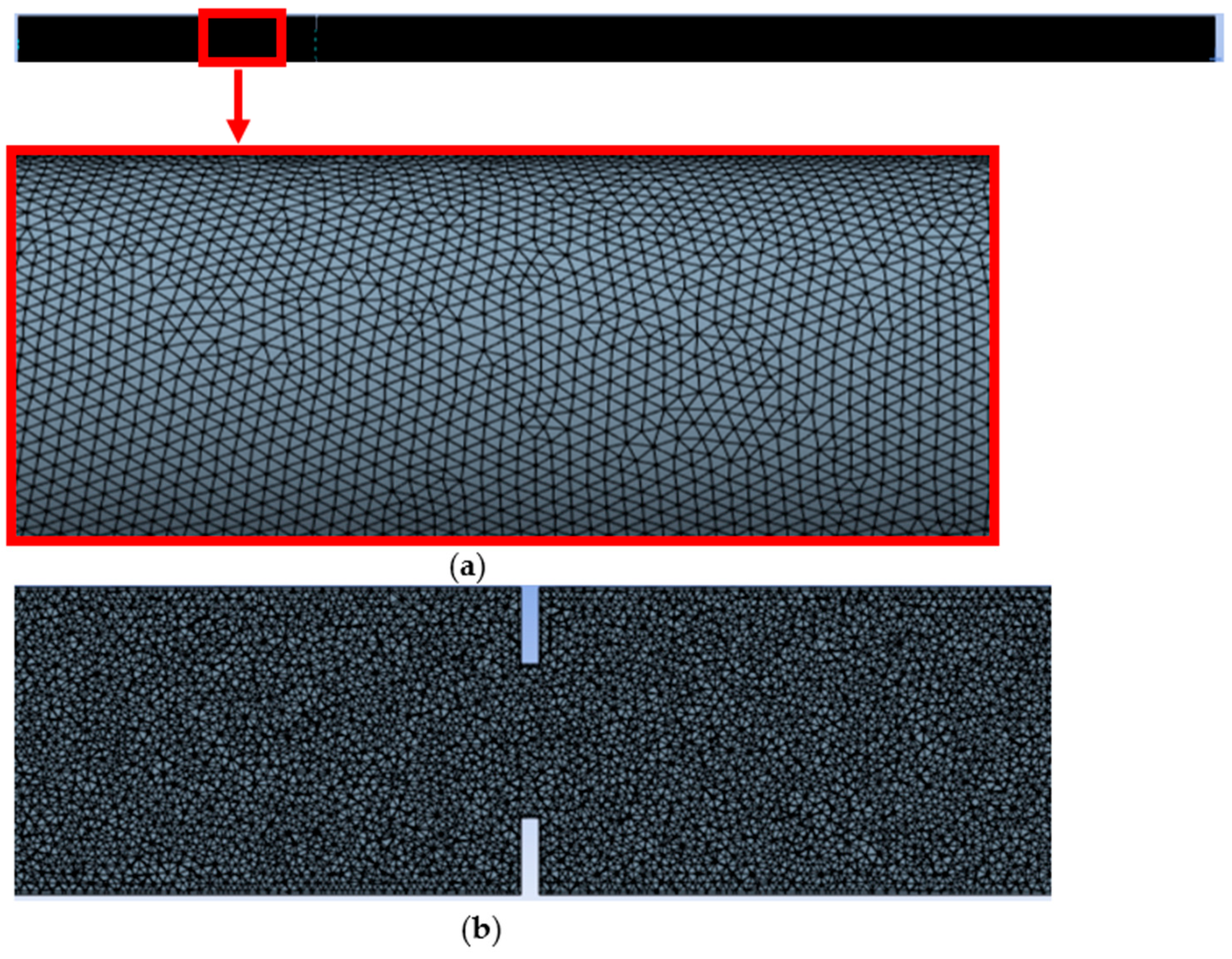
Before performing the actual calculations, tests were carried out to determine the impact of mesh density on the calculation results, by performing simulations for meshes with different numbers of elements. The results of the analysis of the impact of the number of mesh elements on the resulting pressure difference across the orifice are presented graphically in Figure 3.

Figure 3. The effect of the number of mesh elements on the pressure difference.

Analysis of Figure 3 shows that as the number of mesh elements increased, differential pressure also increased, but after reaching a certain level, these values began to stabilize. This means that further increases in mesh density were not necessary. These changes did not significantly affect the velocity profile or pressure distribution, but they did significantly increase the calculation time. Subsequent simulations were performed for a mesh consisting of 5,791,501 elements.

The computational grid was verified to ensure adequate quality before performing the simulations. The average skewness was 0.1972 and the average orthogonal quality was 0.8012, confirming good mesh regularity and numerical stability.

The numerical solution was carried out using a pressure-based solver operating in the steady-state mode. Spatial discretization of the momentum and turbulence equations employed the second-order upwind scheme, while pressure–velocity coupling was performed using the SIMPLE algorithm. The convergence criterion for all equations was set to 10⁻⁵.

Figure 4 shows the computational mesh used in the study. An unstructured mesh was used.

Figure 4. Unstructured mesh, (a) local view of the computational mesh, (b) cross-sectional view of the computational mesh inside the area close to the orifice plate.

Numerical calculations were performed using four different turbulence models: the standard k-ε model, the k-ε realizable model, as well as the k-ω and k-ω BSL models. Each of these models is characterized by a different approach to describing turbulent phenomena and has its own advantages and limitations in the context of different types of flows. The aim of the analysis was to compare the simulation results obtained for each model with data from experimental studies in order to determine which model best reflects the actual flow behavior and ensures the highest consistency of numerical results with the experiment.

First, the standard k-ε model was used for flow modeling. It is a classic two-equation turbulence model based on equations for turbulent kinetic energy (k) and its dissipation (ε). This model allows turbulent fluid motion to be described using the averaged Navier–Stokes equations (RANS). The model assumes isotropy of turbulence and works best in steady flows with high Reynolds numbers, especially away from walls. It is relatively simple and fast to compute but may have limited accuracy for flows with strong pressure gradients or large stream separation. The motion of an incompressible fluid is described by the following equations:

Governing equations for incompressible fluid flow.

Basic equations governing turbulent flow, averaged over time:

Continuity equation:

$$\nabla ·\overline{\mathrm{u}}=0$$

(4)

Equation of movement (averaged Navier–Stokes equations (RANS)):

$${\displaystyle \frac{\partial {\overline{\mathrm{u}}}_{\mathrm{i}}}{\partial \mathrm{t}}}+{\overline{\mathrm{u}}}_{\mathrm{j}}{\displaystyle \frac{\partial {\overline{\mathrm{u}}}_{\mathrm{i}}}{{\partial \mathrm{x}}_{\mathrm{j}}}}=-{\displaystyle \frac{1}{\mathsf{\rho }}}{\displaystyle \frac{\partial \overline{\mathrm{p}}}{\partial {\mathrm{x}}_{\mathrm{i}}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\nu }+{\mathsf{\nu }}_{\mathrm{t}}\right)\left({\displaystyle \frac{\partial {\overline{\mathrm{u}}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}}+{\displaystyle \frac{\partial {\overline{\mathrm{u}}}_{\mathrm{j}}}{{\partial \mathrm{x}}_{\mathrm{i}}}}\right)\right]$$

(5)

where

• ${\overline{\mathrm{u}}}_{\mathrm{i}}$—average speed in the direction of i;

• $\overline{\mathrm{p}}$—average pressure;
• ρ—fluid density;
• ν—kinematic viscosity;
• ν_t—turbulent viscosity.

The k-ε model closes the RANS equations, providing formulas for ν_t and additional transport equations for turbulence.

In the k-ε model, turbulent viscosity is defined as:

$${\mathsf{\nu }}_{\mathrm{t}}={\mathrm{C}}_{\mathsf{\mu }}{\displaystyle \frac{{\mathrm{k}}^2}{\mathsf{\epsilon }}}$$

(6)

C_µ ≈ 0.09.

Transport equation for kinetic energy of turbulence k:

$${\displaystyle \frac{\partial \mathrm{k}}{\partial \mathrm{t}}}+{\overline{\mathrm{u}}}_{\mathrm{j}}{\displaystyle \frac{\partial \mathrm{k}}{{\partial \mathrm{x}}_{\mathrm{j}}}}={\mathrm{P}}_{\mathrm{k}}-\mathsf{\epsilon }+\left[\left(\mathsf{\nu }+{\displaystyle \frac{{\mathsf{\nu }}_{\mathrm{t}}}{{\mathsf{\sigma }}_{\mathrm{k}}}}\right){\displaystyle \frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]$$

(7)

Transport equation for dissipation ε:

$${\displaystyle \frac{\partial \mathsf{\epsilon }}{\partial \mathrm{t}}}+{\overline{\mathrm{u}}}_{\mathrm{j}}{\displaystyle \frac{\partial \mathsf{\epsilon }}{{\partial \mathrm{x}}_{\mathrm{j}}}}={\mathrm{C}}_{1\mathsf{\epsilon }}{\displaystyle \frac{\mathsf{\epsilon }}{\mathrm{k}}}{\mathrm{P}}_{\mathrm{k}}-{\mathrm{C}}_{2\mathsf{\epsilon }}{\displaystyle \frac{{\mathsf{\epsilon }}^2}{\mathrm{k}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\nu }+{\displaystyle \frac{{\mathsf{\nu }}_{\mathrm{t}}}{{\mathsf{\sigma }}_{\mathsf{\epsilon }}}}\right){\displaystyle \frac{\partial \mathsf{\epsilon }}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]$$

(8)

The second turbulence model that was analyzed is k-ε realizable. This model is a modified version of the k-ε model, which introduces an improved equation for ε and a modified turbulent viscosity function. It is more accurate than the standard model for flows with bends, strong stretching, large velocity gradients, and recirculation. It works well in analyses of flow behind obstructions.

In the k-epsilon model, realizable turbulent viscosity is defined similarly to the standard model, but C is a function of local flow properties, which provides better prediction at high strains.

The transport equation for kinetic energy of turbulence k is similar to that in the standard model.

Transport equation for dissipation ε:

$${\displaystyle \frac{\partial \mathsf{\epsilon }}{\partial \mathrm{t}}}+{\overline{\mathrm{u}}}_{\mathrm{j}}{\displaystyle \frac{\partial \mathsf{\epsilon }}{{\partial \mathrm{x}}_{\mathrm{j}}}}=\mathsf{\rho }{\mathrm{C}}_1\mathrm{S}\mathsf{\epsilon }-\mathsf{\rho }{\mathrm{C}}_2{\displaystyle \frac{{\mathsf{\epsilon }}^2}{\mathrm{k}+\sqrt{\mathsf{\nu }\mathsf{\epsilon }}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\nu }+{\displaystyle \frac{{\mathsf{\nu }}_{\mathrm{t}}}{{\mathsf{\sigma }}_{\mathsf{\epsilon }}}}\right){\displaystyle \frac{\partial \mathsf{\epsilon }}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]$$

(9)

where

S—stream deformation tensor module

$$\mathrm{S}=\sqrt{2{\mathrm{S}}_{\mathrm{i}\mathrm{j}}{\mathrm{S}}_{\mathrm{i}\mathrm{j}}}, {\mathrm{S}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial {\overline{\mathrm{u}}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}}}+{\displaystyle \frac{\partial {\overline{\mathrm{u}}}_{\mathrm{j}}}{{\partial \mathrm{x}}_{\mathrm{i}}}}\right)$$

The two other models that were analyzed were the k-ω model and the BLS model.

The k-omega standard model is based on kinetic energy of turbulence (k) and turbulence dissipation rate (ω). In fluid mechanics, this model is used to describe turbulence in flows, which is particularly sensitive to conditions close to the wall and performs well in boundary layers without the need for wall functions. This makes it suitable for modeling wall flows and laminar-turbulent transitions. However, it may be less numerically stable in areas far from walls if the boundary conditions are not properly selected. The k-omega model is a RANS model.

In the momentum equation, turbulent viscosity is described as:

$${\mathsf{\nu }}_{\mathrm{t}}={\displaystyle \frac{\mathrm{k}}{\mathsf{\omega }}}$$

Equation for kinetic energy of turbulence k:

$${\displaystyle \frac{\partial \mathrm{k}}{\partial \mathrm{t}}}+{\overline{\mathrm{u}}}_{\mathrm{j}}{\displaystyle \frac{\partial \mathrm{k}}{{\partial \mathrm{x}}_{\mathrm{j}}}}={\mathrm{P}}_{\mathrm{k}}-\mathsf{\beta }*\mathrm{k}\mathsf{\omega }+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\nu }+{\mathsf{\sigma }}_{\mathrm{k}}{\mathsf{\nu }}_{\mathrm{t}}\right){\displaystyle \frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]$$

(10)

For ω:

$${\displaystyle \frac{\partial \mathsf{\omega }}{\partial \mathrm{t}}}+{\overline{\mathrm{u}}}_{\mathrm{j}}{\displaystyle \frac{\partial \mathsf{\omega }}{{\partial \mathrm{x}}_{\mathrm{j}}}}=\mathsf{\alpha }{\displaystyle \frac{\mathsf{\omega }}{\mathrm{k}}}{\mathrm{P}}_{\mathrm{k}}-\mathsf{\beta }{\mathsf{\omega }}^2+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\nu }+{\mathsf{\sigma }}_{\mathrm{k}}{\mathsf{\nu }}_{\mathrm{t}}\right){\displaystyle \frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]$$

(11)

• P_k = ν_yS_ijS_ij
• Typical model constants:
• A ≈ 0.556, β = 0.075, β* = 0.09, σ_k = 2.0, σ_ω = 2.0

The last model analyzed was the BSL (Baseline) model, which is an extension of the standard k-ω model. Near walls, it behaves like the k-ω model (with accurate mapping of the wall boundary layer), while in the rest of the domain it switches to the k-ε model. This maintains the stability of calculations and accuracy both near walls and in free flow zones. It is a compromise between the simplicity of the RANS model and the need for more accurate representation of actual flow.

BSL equations are similar to standard k-ω equations, but with the addition of a transition function and corresponding modifications to model constants.

Equation for kinetic energy of turbulence k:

$${\displaystyle \frac{\partial \left(\mathsf{\rho }\mathrm{k}\right)}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \left(\mathsf{\rho }{\overline{\mathrm{u}}}_{\mathrm{j}}\mathrm{k}\right)}{{\partial \mathrm{x}}_{\mathrm{j}}}}=\mathrm{P}-\mathsf{\beta }*\mathsf{\rho }\mathrm{k}\mathsf{\omega }+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\mu }+{\mathsf{\sigma }}_{\mathrm{k}}{\mathsf{\mu }}_{\mathrm{t}}\right){\displaystyle \frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]$$

(12)

For ω:

$${\displaystyle \frac{\partial \left(\mathsf{\rho }\mathsf{\omega }\right)}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \left(\mathsf{\rho }{\overline{\mathrm{u}}}_{\mathrm{j}}\mathsf{\omega }\right)}{{\partial \mathrm{x}}_{\mathrm{j}}}}={\displaystyle \frac{\mathsf{\gamma }}{{\mathsf{\nu }}_{\mathrm{t}}}}\mathrm{P}-\mathsf{\beta }\mathsf{\rho }{\mathsf{\omega }}^2+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[\left(\mathsf{\mu }+{\mathsf{\sigma }}_{\mathsf{\omega }}{\mathsf{\mu }}_{\mathrm{t}}\right){\displaystyle \frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]+2(1-{\mathrm{F}}_1){\displaystyle \frac{\mathsf{\rho }{\mathsf{\sigma }}_{\mathsf{\omega }2}}{\mathsf{\omega }}}{\displaystyle \frac{\partial \mathrm{k}}{\partial {\mathrm{x}}_{\mathrm{j}}}}{\displaystyle \frac{\partial \mathsf{\omega }}{\partial {\mathrm{x}}_{\mathrm{j}}}}$$

(13)

The constants of the model are mixed according to the F1 function (Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications), thanks to which the model is reduced to standard k-ω near the wall and retains the properties of k-ε in the distant field.

3. Results and Discussion

The results of experimental tests and numerical simulations of flow behind a measuring orifice in a pipeline are presented and discussed below. Laboratory measurements were performed using the PIV method, while calculations were performed using various turbulence models available within the CFD method, including: standard k-ε, realizable k-ε, k-ω, and k-ω BLS models.

The results were presented in the form of velocity field visualizations, graphs, and tables. For each case, basic error indicators were calculated: RMSE, %error, MAPE which enabled a quantitative assessment of the fit of CFD models to PIV data. The discussion includes an interpretation of the differences between the various turbulence models, taking into account their theoretical characteristics and potential sources of measurement and numerical errors.

The velocity maps for an inlet flow velocity of 0.283 m/s are presented below for both the standard and slotted orifices. The velocity fields shown refer to the individual turbulence models used.

The tables below show velocity maps for flow velocities of 0.283 m/s and 0.424 m/s for both standard and slotted orifices. The velocity fields shown refer to the individual turbulence models used.

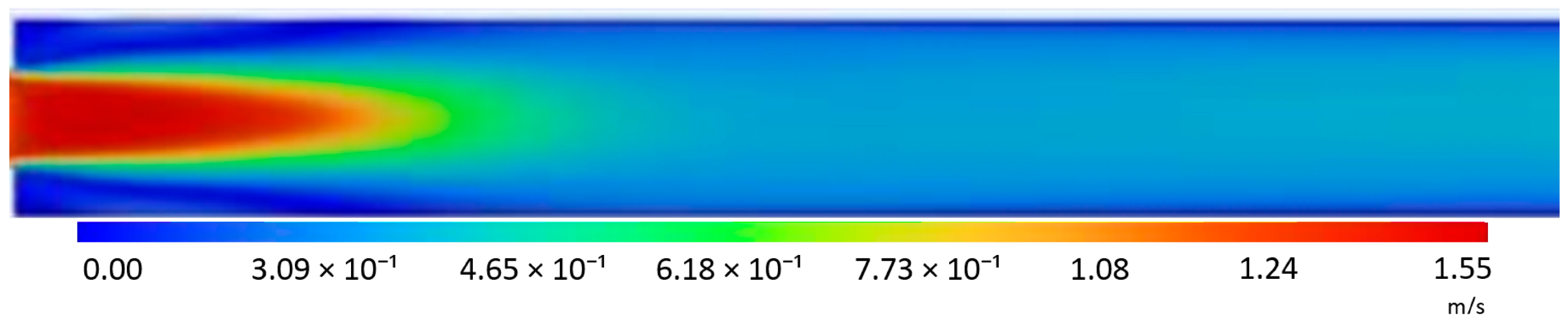
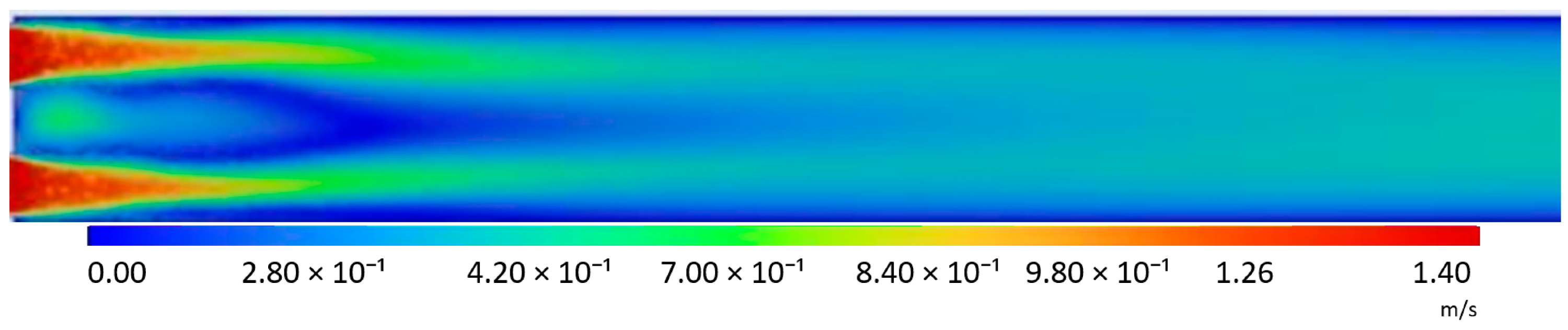
The Table 2 presents figures comparing velocity field distributions obtained from the PIV experiment and numerical simulations using four different turbulence models (k-ε standard, k-ε realizable, k-ω, and k-ω BSL) for flow through a standard orifice at a reference velocity of 0.283 m/s.

Table 2. Velocity maps for standard orifice plates for inlet flow velocities of 0.283 m/s.

Method	Standard Orifice, Velocity: 0.283 m/s
PIV
k-ε standard
k-ε realizable
k-ω
k-ω BSL

Experimental results (PIV) indicate a clearly developed recirculation zone behind the throat, covering an area with a high velocity gradient, where both reverse flow areas (negative values) and local velocity maxima in the axis of symmetry occur. Strong differences in the velocity field are characteristic, confirming the high complexity of the flow in this area.

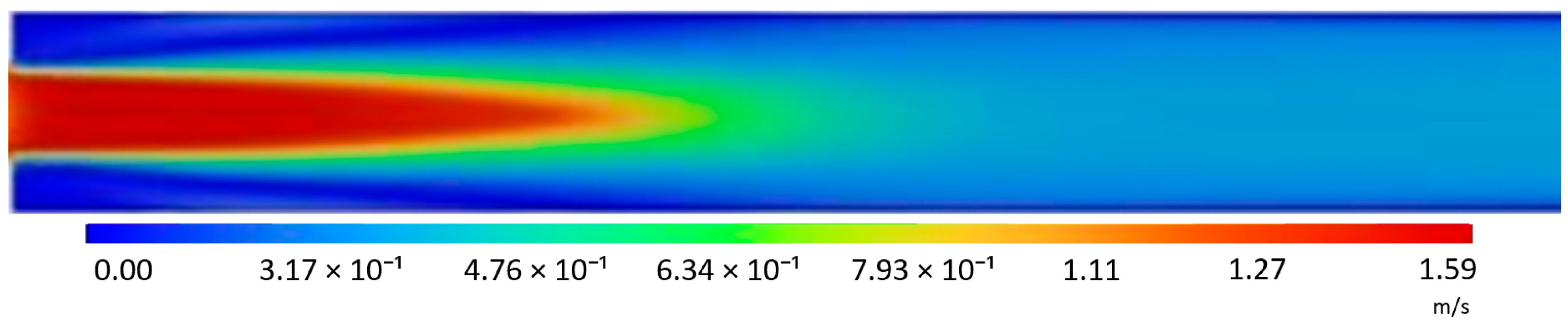
The results of numerical calculations also indicate a clearly developed recirculation zone behind the throat and maximum velocities in the axis of symmetry, but depending on the turbulence model used, these distributions differ significantly. For the k-epsilon standard model used, the maximum velocity values are approximately 1.55 m/s. The flow is smoother. The k-ε realizable model reflects the presence of an area of increased velocity just behind the orifice, an area of characteristic recirculation zone. Too rapid velocity decay causes the stream in the axis to be shorter compared to the standard model. The k-ω model presents a more extended high-velocity zone in the duct axis, while also indicating a slightly greater variation in the flow field compared to the k-ε models. The maximum values are approximately 1.59 m/s. The k-ω BLS (Baseline) model has a significantly shorter length of the high-velocity zone in the pipeline axis compared to k-ω. The maximum values are 1.59 m/s.

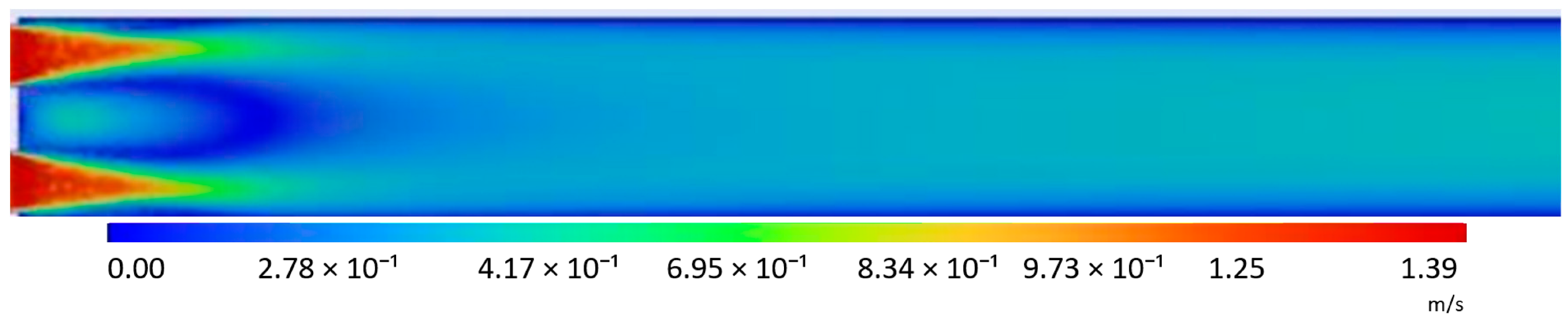
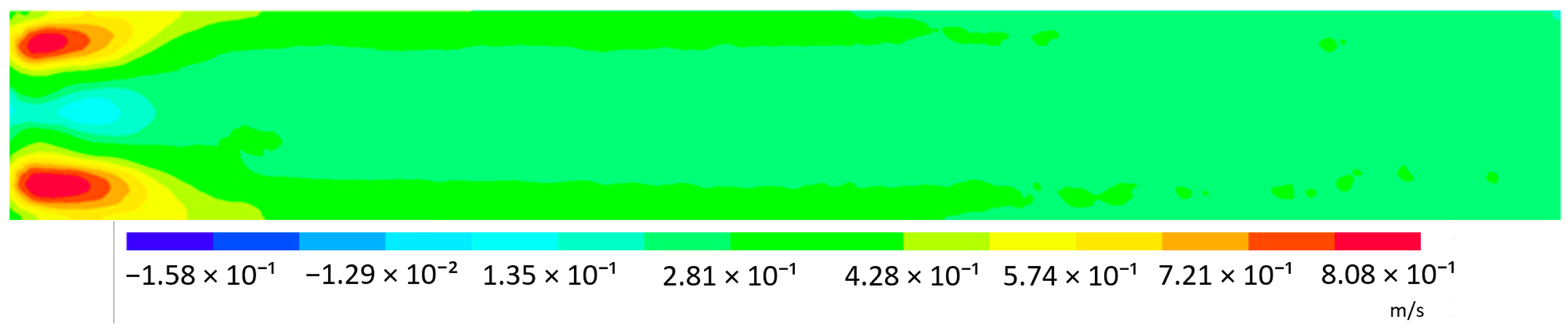
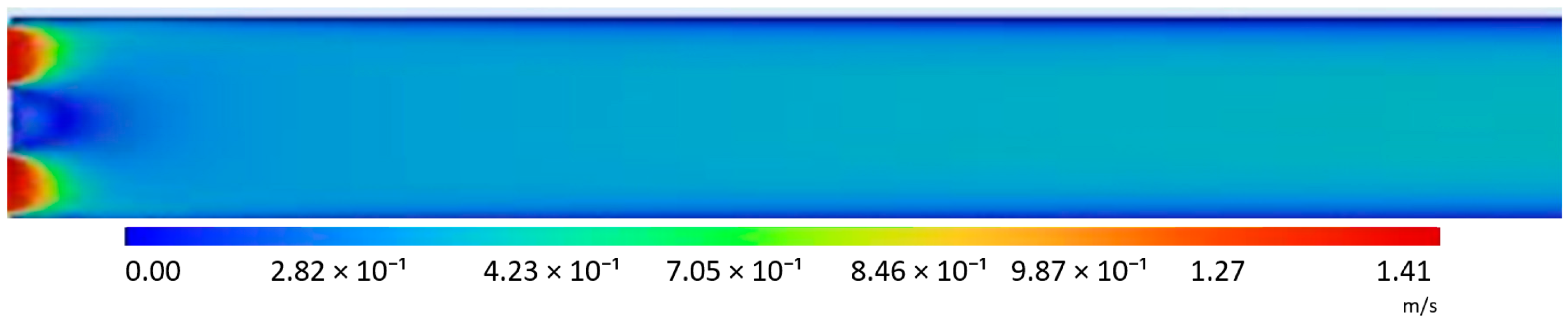
A similar analysis was performed for the slotted orifice. Table 3 shows velocity maps for the slotted orifice at an inlet velocity of 0.283 m/s. PIV experimental studies show a double-ridge flow structure typical for this geometry: local velocity concentrations just behind each slot and areas of rapid outflow towards the duct axis. The color scale shows maxima of ~0.8 m/s (from the PIV panel), and in small areas there is also a signal of opposite sign (slightly negative values close to zero), indicating local disturbances or low-amplitude reverse flows. The velocity fields obtained by analyzing the simulation of the jet are similar to those obtained in the experiment. The standard k-ε model generates output jets that are formed similarly to those in PIV. High-velocity zones dissipate quickly.

Table 3. Velocity maps for slotted orifice plates for inlet flow velocities of 0.283 m/s.

Method	Slotted Orifice, Velocity: 0.283 m/s
PIV
k-ε standard
k-ε realizable
k-ω
k-ω BLS

On the model map, the maximum velocity values are higher than in PIV (maxima of approximately 1.36 m/s). The realizable version retains a slightly more concentrated form of vortices than the k-ε standard, with separate arcs visible behind the gaps, but they are still shorter. The predictions by the model are similar to the k-ε standard (approx. 1.41 m/s), which is still significantly higher than in the measurement. The k-ω model shows features similar to the PIV field, with more distinct separation and elongation of the jets, wider shear layers, and a more distinct transition zone between the jet and the surroundings. The maxima in the model field are also oversized (approximately 1.40 m/s), but the distribution is less homogeneous than in the k-ε versions, thanks to which local morphologies (e.g., “arcs” and places of rapid mixing) are better captured. The BLS k-ω model shows behavior similar to the basic k-ω: it maintains a distinct structure and relatively extended shear layers. The maxima and overall velocity scale are comparable to k-ω (approx. 1.39 m/s). The difference is a slightly different width of the streams and the rate of dispersion, which indicates sensitivity to the default parameters of the model.

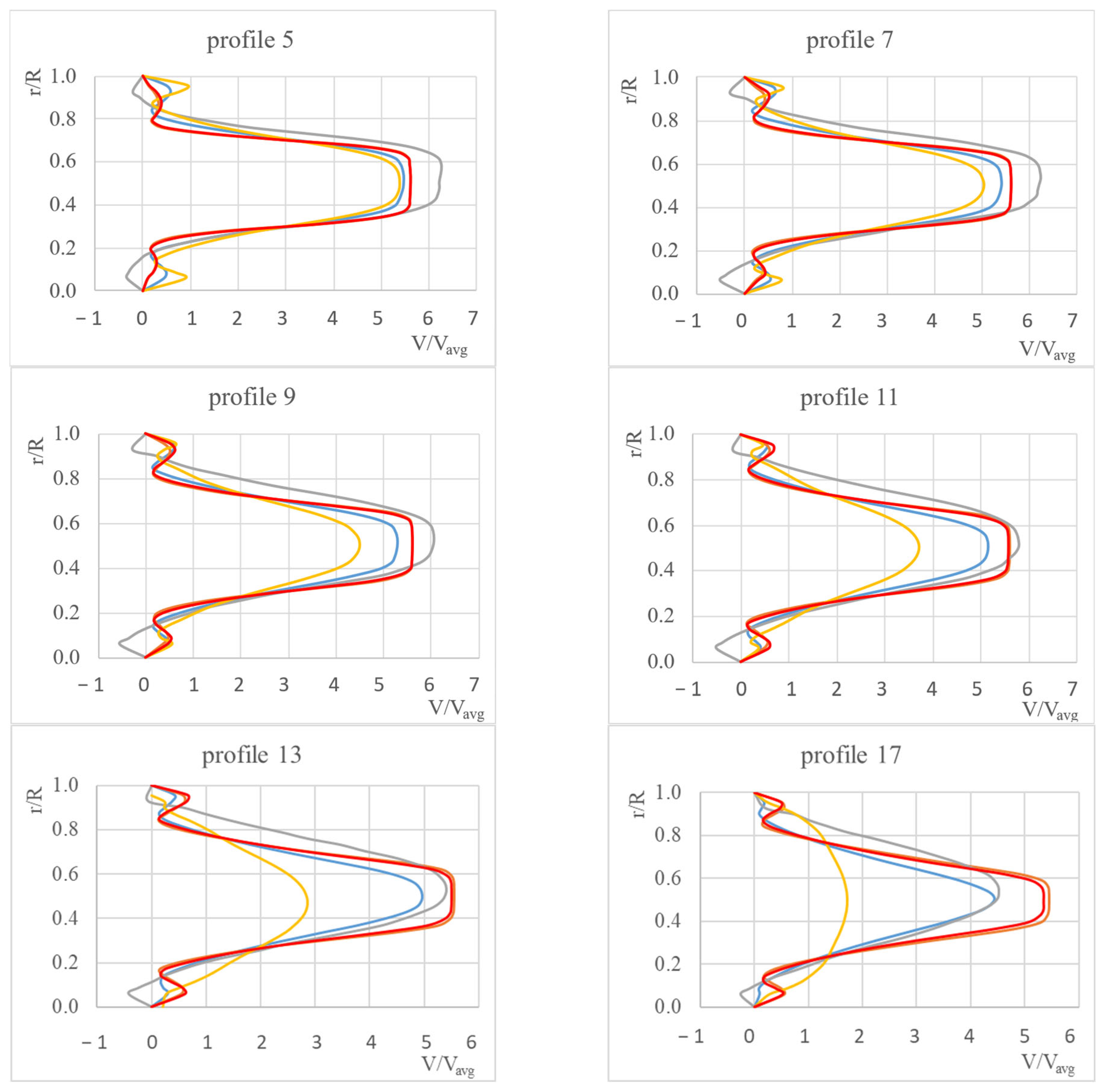
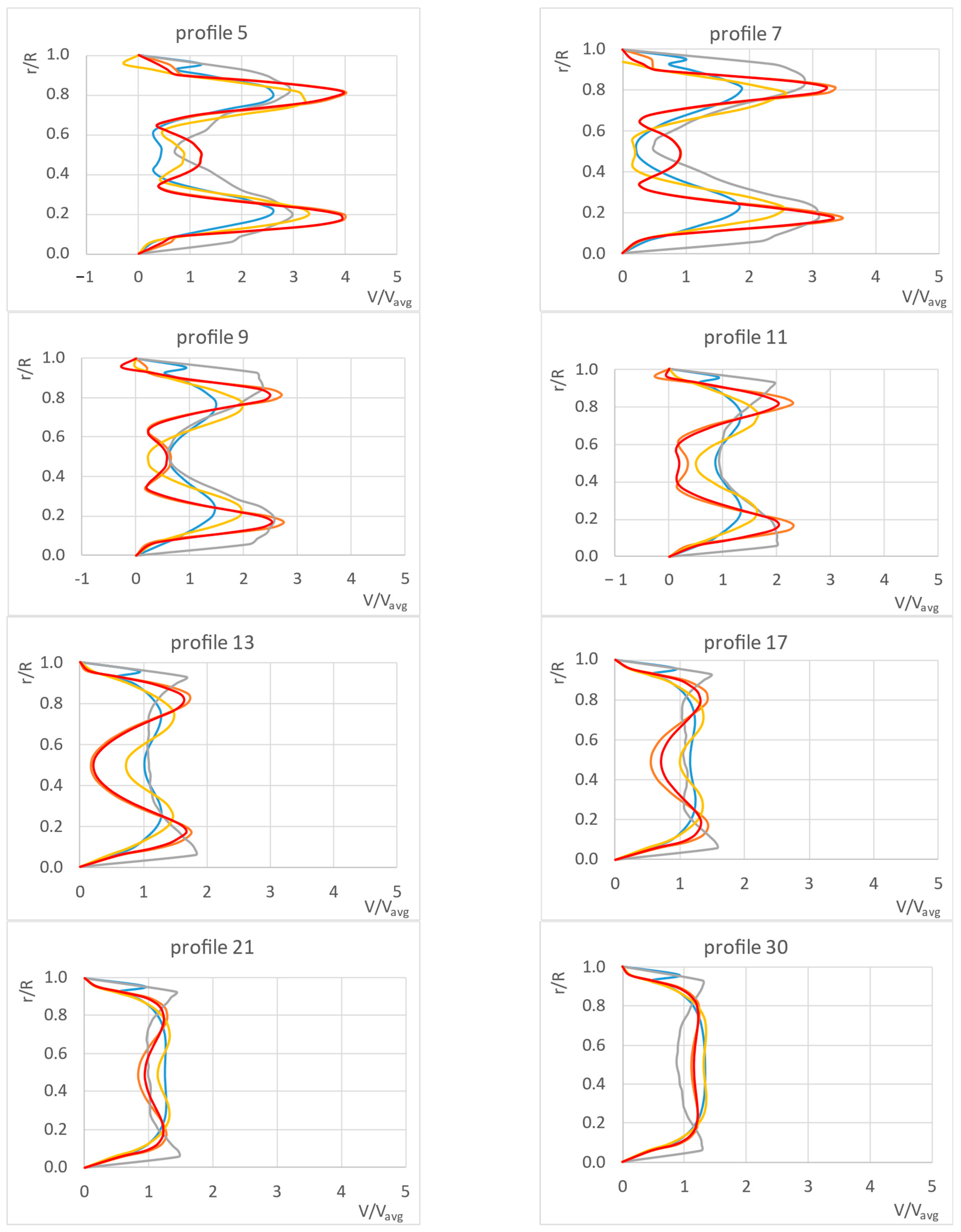
Another element that was analyzed was the velocity profiles at specific distances from the orifice. Due to the number of profiles obtained in the experiment, nine profiles were selected that reflect the flow pattern. The results of the tests for the standard orifice plate, for selected profiles, for speeds of 0.283 m/s and 0.424 m/s are presented below.

The set of velocity profiles shown in the Figure 5 compares experimental data obtained using the PIV method with the results of numerical calculations for four turbulence models: standard k-ε, realizable k-ε, k-ω, and k-ω BSL. Each graph represents a separate measurement profile in which the velocity distribution was analyzed as a function of the radial position r/R, with the velocity values normalized to the average flow velocity V/V_avg. The PIV data serve as a reference point for assessing the accuracy of numerical models.

Figure 5. Comparison of velocity profiles for a standard orifice in selected profiles for an inlet velocity of 0.283 m/s.

Analyzing the above figures, it can be seen that the highest apparent velocities occur in the pipeline axis and range from 6.2 for PIV to 5.3–5.6 depending on the turbulence model used. Near the walls, the velocity drops to 0. In the zone closest to the throat (profiles 5–7), PIV and CFD measurements show a characteristic narrow core of the flow, with high axial velocity and a drop towards the walls, where the effects of recirculation and shear layers are noticeable. In this regard, differences between RANS models and experimental results can be observed. However, when comparing turbulence models, the differences in profile 5 are minor, while in profile 7 the differences between them are clearly visible. In the case of k-omega models, a flattened jet front can be seen. In both cases, an underestimation of the maximum in the V/V_avg axis can be observed.

In the flow development zone (profiles 9–13), the core gradually widens, which in PIV translates into a flattening of the profile and equalization of wall velocities. Significant differences appear between individual numerical models. The k-omega models show the greatest consistency between simulation and PIV studies. With regard to maximum apparent velocities, the differences between calculations and experiments are within the range of 5–7%. The k-epsilon realizable model shows the least consistency, with differences between the model and the experiment for this area ranging from 21–47%.

In the further zone (profiles 17–21), the flow approaches fully developed, and the differences between the models are significant. The flow velocity in the experiment decreases, and the stream begins to stabilize. In this zone, the standard k-epsilon model shows the best agreement between CFD and PIV, with differences in peak values between simulations and experiments ranging from 0.5% to 10%. The k-epsilon realizable model continues to show the greatest differences between CFD and PIV.

A similar analysis was performed on velocity profiles at an inlet velocity of 0.424 m/s. The trend remained similar to that observed at lower inlet velocities.

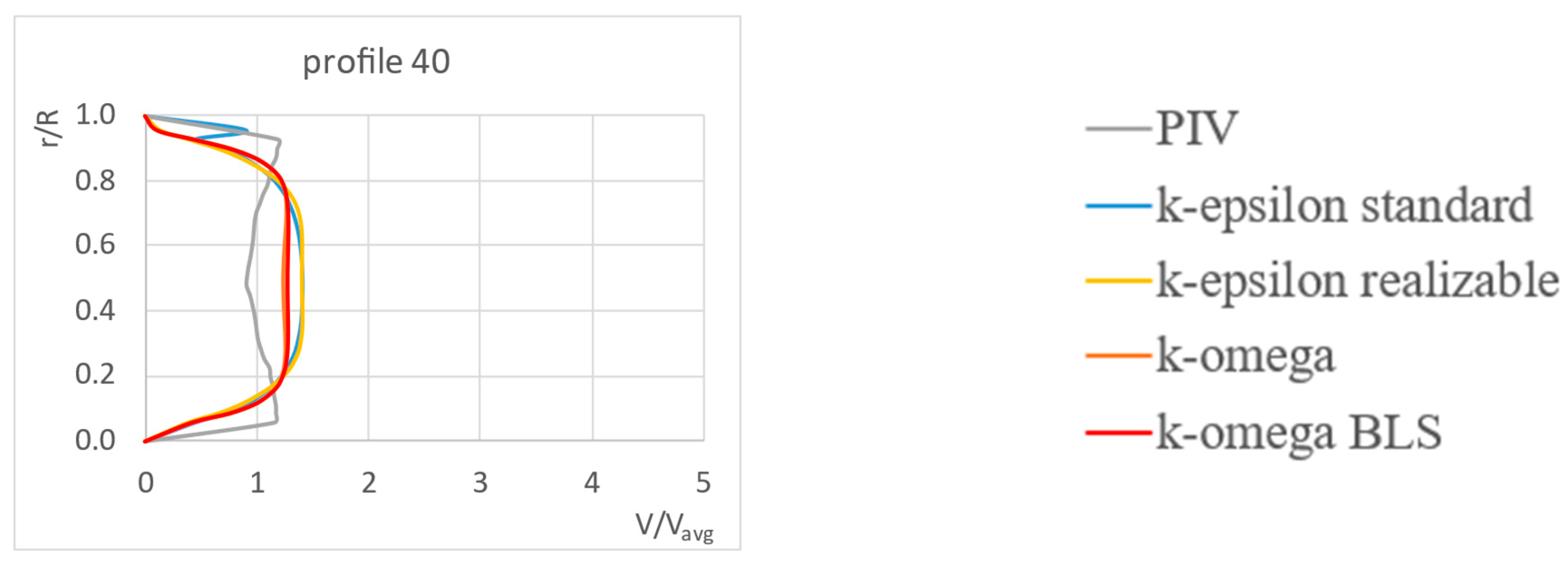
The velocity profiles for the slotted orifice at a velocity of 0.283 m/s are shown below.

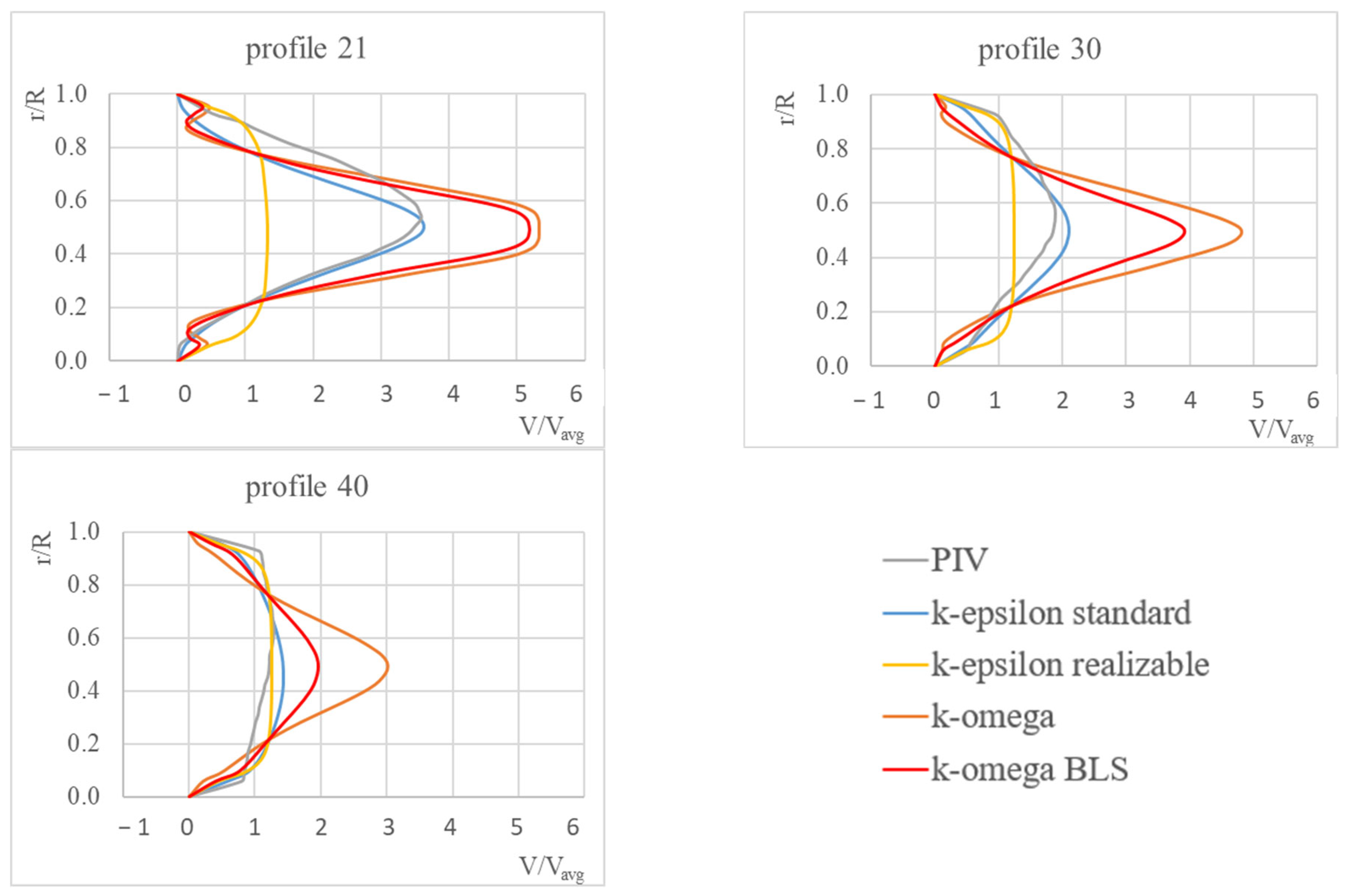
A similar analysis was performed for the slotted orifice. As presented in Figure 6, below is a comparative analysis of velocity profiles at selected points along the pipeline. The detailed analysis concerns an inlet velocity of 0.283 m/s.

Figure 6. Comparison of velocity profiles for a slotted orifice in selected profiles for an inlet velocity of 0.283 m/s.

Analyzing (profiles 5–7) we can see that the initial flow zone exhibits the most complex velocity profile structures. PIV and CFD data indicate the presence of a distinct double hump, i.e., two local maxima. In profiles 5–7, both peaks are clearly marked. In profile 5, the standard k-ε model shows the closest similarity between the simulation velocity distribution and the experiment. In profile 7, there is a clear difference between the two distributions; at this point, the maximum peaks from the PIV data are similar to the k-ω model, the velocity distribution in the BLS variant performs slightly better, maintaining the position of local maxima. However, looking at the minimum apparent velocity values, the k-ω models deviate significantly from the distribution from the experiments; in this part, the nature of the velocity distribution is better reflected by the k-ε model (both standard and realizable).

In profile 9, a progressive stabilization of flow is observed; in both CFD and PIV, the maximum apparent velocities decrease and reach a value below 3. The k-ω models reproduce the dominant maximum more reliably, while the k-ε models differ significantly from the experimental data. In profile 11, the velocity profile (PIV) shows flow asymmetry, with peaks differing from each other. The k-ε model accurately reflects the nature of the velocity distribution, but the maximum velocities still differ from those obtained experimentally. In the case of the other models, two distinct peaks with maximum apparent velocities in the range of 2.5 and a peak with a minimum apparent velocity close to 0 are still observed, while for the experiment this value is approximately 2 and 1, respectively. In further profiles, a clear stabilization of the apparent velocity can already be seen for PIV and the standard k-ε model. All turbulence models are approaching the PIV measurements in their predictions, but the k-ε distributions still show a wider “flattening” in the fast flow zone, while k-ω maintain better sharpness and maximum location. From profile0 21 flow is already significantly stabilized, and differences between models and measurements are limited. All models correctly reproduce the main maximum and minimum, although in the case of PIV the maximum values occur closer to the walls, while the simulation results show these values shifted slightly towards the pipeline axis. The velocity profiles are almost fully consistent with each other and with PIV, indicating that the dominant turbulent structures have been dispersed and the flow has taken on a predictable quasi-steady character. In this zone, the influence of the turbulence model selection on the average velocity profile is already minimal.

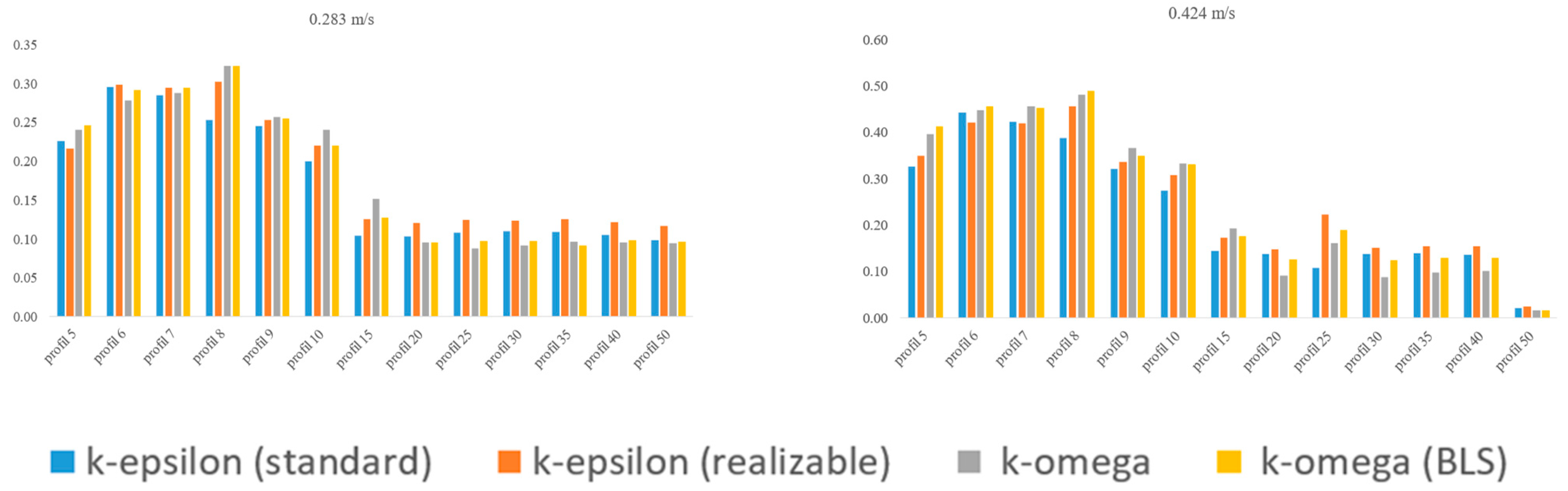
In order to quantitatively assess the agreement between CFD simulations and PIV experimental results, the root mean square error (RMSE) values were calculated. This metric allows the differences between predicted and measured velocity profiles to be captured in a single value, but due to the squaring of deviations, it emphasizes local discrepancies more strongly.

The figure shows the results of these analyses.

When analyzing the Figure 7 for a speed of 0.283 m/s, it can be seen that the average RMSE values clearly indicate that the best agreement with the experiment was obtained for the standard k-ε model, whose average error was 0.168. This model was also characterized by a very stable distribution of values along the tested section—the minimum RMSE reached 0.06 (profile 35–40), and the maximum did not exceed 0.27 (profile 10). The higher RMSE observed for profile 10 may be due to the presence of strong recirculation interactions and a shear layer immediately below the throat of the hole, where velocity gradients and local instability are most pronounced. In this zone, the transient vortex structures captured by PIV may not be fully represented in steady-state CFD predictions, leading to a local increase in discrepancies. These results suggest that the standard k-ε model is characterized by a good balance between the accuracy of mapping the acceleration area behind the nozzle and the description of further flow stabilization.

Figure 7. The root mean square error, standard orifice.

A completely different picture was obtained for the k-ε realizable model, which showed by far the highest error values. The average RMSE for this model reached 0.248, and the maximum value was as high as 0.47 in profile 15, i.e., in the zone of intense obstacle interaction with the flow structure. This result confirms earlier qualitative observations that this model tends to over-disperse turbulent energy, leading to significant deviations from the values measured in areas with strong velocity gradients.

The k-ω and k-ω BSL models achieved intermediate results. The average RMSE values were 0.271 and 0.225, respectively, with both models exhibiting slightly different error characteristics. The k-ω model achieved relatively high maximum RMSE values—up to 0.41 (profile 30)—which indicates its limited ability to map flow stabilization in the further part of the pipe. The k-ω BSL model, on the other hand, showed a more even distribution of values, with a maximum RMSE of 0.34 and a minimum of 0.06 (profile 50). It can therefore be concluded that the BSL variant is more stable and slightly better suited to the measurement results than the classic k-ω model.

As with lower speeds, the root mean square error (RMSE) allows us to determine which of the turbulence models used best represents the flow measured by PIV in a standard orifice flow.

The average RMSE values indicate that the most favorable results were obtained for the standard k-ε model, whose average error was 0.26, with extreme values ranging from 0.04 (profile 35) to 0.44 (profile 15). This model was characterized by relatively low error values in the further part of the duct (profiles 30–50), which confirms its ability to correctly map the flow stabilization process.

The k-ε realizable model achieved an average RMSE of 0.315, with a maximum error value of 0.53 (profile 15). Its distribution was characterized by systematically higher values than in the case of the standard model, especially in the zone of intense turbulence (profiles 9–20). Although the RMSE values decreased in the further profiles, this model still showed greater discrepancies from the measurements compared to the standard k-ε model.

Significantly higher errors were generated by the k-ω model, whose average RMSE was 0.424—the highest among all the models analyzed. Its maximum values reached as high as 0.67 (profile 25), which clearly indicates a limited ability to map the flow behind the orifice at higher inlet velocities. It is worth noting that the error values remained elevated also in the further part of the duct, which suggests that this model has difficulty capturing the flow stabilization process. The limited stabilization predicted by the k-ω model can be attributed to its formulation, in which the specific dissipation rate (ω) equation enhances the transport of turbulent kinetic energy from near-wall regions into the core flow. As a result, turbulence intensity remains elevated and decays more slowly, causing the flow to require a longer distance to reach a fully developed state.

The k-ω BSL model showed an average RMSE of 0.333, with values ranging from 0.09 (profile 50) to 0.55 (profile 25). These results place it between the k-ε realizable model and the classic k-ω model. BSL provided a relatively good fit in the initial and final profiles, but in the middle area (profiles 20–30), the error values were clearly overestimated.

A similar analysis was performed on the slotted orifice. For lower flow velocities, the RMSE distribution was characterized by relatively low values, indicating good agreement between the models and the experimentally measured waveform, as shown in Figure 8. The best fit was again achieved by the k-ε standard model, with a mean RMSE of 0.174, with a maximum value of 0.30 (profile 6). This model maintained low errors further downstream (profiles 15–50), where the RMSE decreased to 0.10–0.11.

Figure 8. The root mean square error, slotted orifice.

The k-ε realizable model had a slightly higher mean RMSE (0.188), but the differences from the standard model were minor. The highest values occurred in the initial profiles, and in the final cross-sections of the pipe, the errors decreased to 0.12–0.13.

The k-ω and k-ω BSL models produced very similar results (mean RMSE of 0.181 and 0.181, respectively). In the initial profiles (6–8) the RMSE values reached 0.28–0.32, while in the subsequent profiles (20–50) they remained at the level of 0.09–0.10, which indicates a correct representation of the flow stabilization process.

At higher flow speeds, the RMSE values increased, confirming the greater difficulty of numerical models in representing more dynamic structures behind the orifice.

The standard k-ε model achieved an average RMSE of 0.231, with a maximum of 0.44 (profile 6). It was characterized by a significant decrease in values in subsequent profiles—down to 0.02 in profile 50—indicating high prediction stability in the region of stabilized flow. The realizable k-ε model achieved an average RMSE of 0.258, with maximum values reaching 0.46 (profile 8). As with the lower velocity, the error distribution was higher than that of the standard model, but with a tendency to decrease in subsequent profiles (down to 0.03 in profile 50).

The k-ω model had an average RMSE of 0.255, with maximum values reaching 0.48 (profile 8). In the initial sections, the differences from the reference data were significantly greater, but further along the conduit, the error steadily decreased, reaching minimum values of 0.02–0.10.

The BSL k-ω model achieved an average RMSE of 0.258, with a maximum error of 0.49 (profile 8). This model’s results were very similar to the classic k-ω model, although in the middle section of the conduit (profiles 20–30), the RMSE values remained slightly higher than those of the standard model.

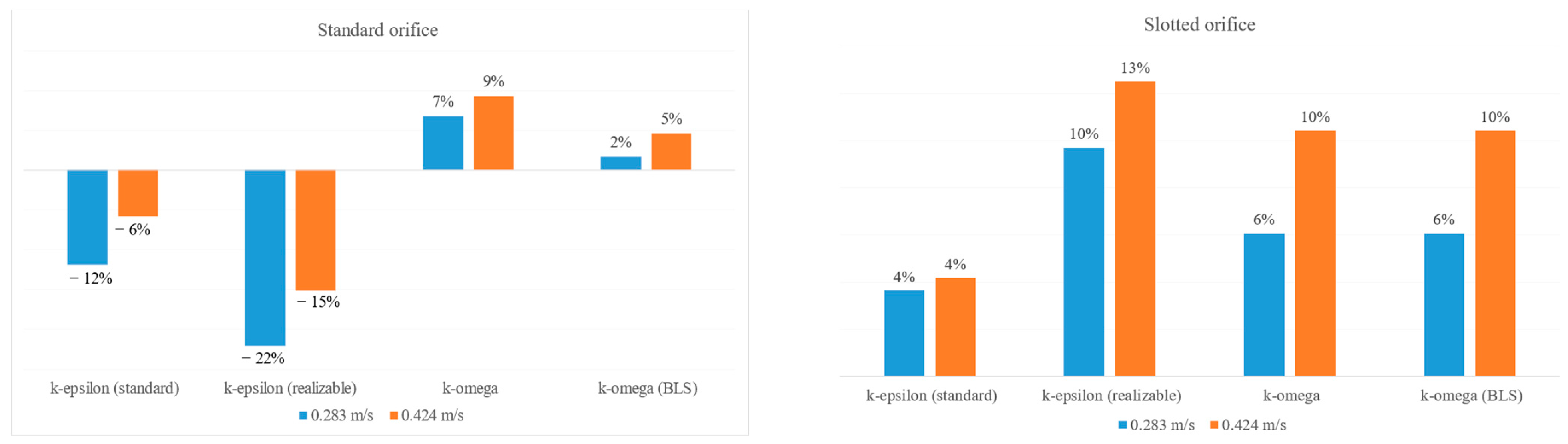
To quantitatively assess the agreement between the numerical and experimental results, we calculated the relative error (error%) and mean absolute percentage error (MAPE). The former allows us to determine the direction of the deviation (systematic over- or underestimation of the PIV velocity relative to the measured value), while the MAPE describes the average magnitude of the differences in percentage terms, regardless of their sign. The following tables and graphs present detailed values of these indices for individual turbulence models and geometric configurations.

Percentage error analysis reveals clear relationships between orifice geometry, inlet velocity value and the behavior of individual turbulence models, as shown in Figure 9.

Figure 9. Percentage error for standard orifice and slotted orifice, for two different velocities (0.283 m/s and 0.424 m/s).

For the standard orifice, models based on k-ε assumptions show a negative error (tendency to underestimate the measurement): the standard variant gives about −12% at 0.283 m/s and −6% at 0.424 m/s, while the realizable variant underestimates even more (about −22% and −15%). The k-ω models show the opposite tendency—they predict values usually higher than the measurement (positive error): the classic k-ω ≈ +7% and +9%, while the BSL variant limits this overestimation to levels of about +2% and +5%. This pattern indicates that in the flow through a standard orifice, the k-ε (especially realizable) most likely over-models mixing and dissipation, leading to a flattening and underestimation of the flow peak, while the k-ω (especially without blending) tends to maintain sharper velocity structures and consequently overestimates them; the BSL variant, thanks to the adaptive combination of the k-ω and k-ε formulations, better compensates for this over-modeling.

For the slotted orifice, a different pattern of errors is observed: all models exhibit positive errors (predictions above the measured values), but their magnitude depends on the model and velocity. The k-ε (standard) model remains the closest to the measurements (ca. +4% at both velocities), the k-ε realizable overestimates more (≈+10% and +13%), while the k-ω and k-ω BSL give moderate overestimates (≈+6% and +10% and +6% and +10%, respectively). An increase in velocity generally intensifies the discrepancies (especially visible for the realizable and k-ω), suggesting a nonlinear sensitivity of the models to the intensity of separation and mixing phenomena; at the same time, the geometric distribution of the flow through the slots changes the nature of the field (less strong, more diffuse contraction than in the standard orifice), which translates into a change in the sign and magnitude of the error relative to the model.

From the point of view of practical applications, these results indicate that the choice of model depends on the geometry: for a standard orifice, the most balanced predictions are given by k-ω BSL (the smallest absolute error), while for a slotted orifice, the best agreement is given by k-ε standard; the k-ε realizable model most often generates the largest deviations and requires caution in the interpretation of results in the region of strong gradients.

Mean absolute percentage error (MAPE) values indicate significant differences in prediction quality between individual turbulence models. The lowest errors were obtained for the k-omega BLS model (5.706%) and the k-epsilon standard model (6.370%), confirming their greater stability and better flow representation compared to other models. The classic k-omega model exhibited a slightly higher error (8.140%), suggesting a tendency to overestimate local velocity values in some areas. The k-epsilon realizable model performed by far the worst (14.837%), with an error more than twice that of the best models, confirming previous observations regarding its limited ability to correctly represent strong velocity gradients and stream separation effects. The results clearly indicate that, of the models analyzed, the k-omega BLS and the classic k-epsilon standard provide the best flow prediction accuracy, while the realizable model should be used with caution.

4. Conclusions

Experimental studies using the PIV technique and numerical CFD calculations enabled a detailed analysis of the flow structure downstream of a standard orifice. Comparison of the results showed that both experimental and numerical methods reliably reproduce hydrodynamic phenomena, but differences in accuracy depended on the turbulence model used and the distance from the throttling element.

In the zone immediately downstream of the orifice (profiles 5–7), the best agreement with experimental measurements was achieved by models from the k-ω family, particularly the k-ω BSL model, which better reproduced recirculation and the flow structure. In the transition region (profiles 9–13), the k-ω BSL model maintained stable predictions, while in the further steady-state zone (profiles 20 and beyond), the most accurate results were obtained using the k-ε standard model.

Error analysis (RMSE, MAPE, and %error) confirmed that none of the turbulence models was optimal across the entire domain studied. The choice of the appropriate model should therefore depend on the nature of the analyzed flow region—k-ω models for near-field zones and k-ε models for steady-state flow zones.

It should also be emphasized that the presented results are obtained under certain numerical assumptions, such as steady-state flow, specific boundary conditions, and a fixed computational mesh. These factors may contribute to quantitative discrepancies between numerical and experimental data, although the observed trends remain consistent. Future studies will include transient analyses and mesh refinement to further verify the robustness of the observed trends.

The presented results further emphasize the practical importance of selecting a turbulence model based on both geometry and flow area, especially in configurations with slotted plates, which remain not much researched in this area.

The obtained results have significant practical implications, as they enable informed adaptation of the CFD model to a specific engineering case, minimizing errors in the prediction of pressure drop, turbulence development, and velocity distribution. Consequently, they can contribute to more accurate design and calibration of orifice flowmeters used in industrial installations.

In summary, when selecting a turbulence model for CFD simulation of flow through orifices or other throttling elements, the dominant flow characteristics in the region being analyzed should be considered. The results of this study indicate that k-ω models, particularly the k-ω BSL variant, perform best in regions with strong velocity gradients, recirculation, and near-wall phenomena, while the standard k-ε model provides the highest accuracy in steady and fully developed flow regions where turbulence is isotropic. The obtained results can provide a practical guide for engineers and researchers to facilitate the selection of an appropriate turbulence model in similar industrial applications.