Deep Hybrid AI Models Applied to Predict, Model, and Forecast the Next Upcoming Periods of Ozone in Craiova City

Abstract

Artificial intelligence (AI) plays an important role in analyzing air quality, providing new insights that enable informed environmental policy decisions at the local level based on air pollution modeling and forecasting. The aim of this study is to analyze various hybrid AI methods to predict, model, and anticipate hourly ground-level ozone concentrations. Ground-level ozone concentrations impact human health and the environment. The data used in this study was downloaded from the website of the Romanian Agency for Environmental Protection and spans five years (2020–2024). The dataset comprises two categories of data: (i) seven meteorological parameters, including temperature (T), relative humidity, precipitation, air pressure, solar brightness, wind direction, and velocity; (ii) twenty air pollutants, including two types of particulate matter, carbon monoxide, sulfur dioxide, ground-level ozone, three types of nitrogen oxide, ammonia, six volatile organic compounds, and five toxic elements. The study follows a six-stage approach: (1) data preprocessing is conducted to identify and address anomalies, outliers, and missing values, while ozone trends are analyzed; (2) correlations between ozone concentrations and other variables are examined, considering only non-missing values; (3) data splitting is carried out in training and testing sets; (4) a total of 27 hybrid AI-based algorithms are applied to determine the optimal predictive model for ozone concentration based on related variables; (5) fifty feature selection methods are applied to find the most relevant predictors for predicting ozone concentration; (6) a novel deep NARMAX model is employed to model and anticipate hourly ozone levels in Craiova. Using a set of statistical metrics, the results of the models are assessed. This research provides a novel perspective on the robustness of the predictive performance of the proposed model.

1. Introduction

Air pollution refers to the presence of harmful substances in the Earth’s atmosphere, often resulting from human activities such as industrial processes, transportation, and energy production [1]. These pollutants encompass a range of substances, including particulate matter (PM); nitrogen oxide (NO_x); sulfur dioxide (SO₂); carbon monoxide (CO); toxic elements like lead (Pb), nickel (Ni), arsenic (As), cadmium (Cd), and radon (Nt); and volatile organic compounds (VOCs) like benzene (C₆H₆), ethylbenzene (C₈H₁₀), three isomers of xylene (o-, m- and p-xylene), and toluene (C₈H₁₀) [2]. The significance of air pollution lies in its ability to compromise air quality, leading to adverse effects on human health, ecosystems, and climate safety [3].

Urban environments are characterized by a concentration of diverse activities that contribute to air pollution [4]. The most significant sources include industrial emissions, road traffic, power plants, construction activities, and residential heating [5]. Understanding the specific sources of air pollutants is vital for every urban area to develop targeted strategies to mitigate pollution levels [6].

The consequences of air pollution are far-reaching and impact the health of urban populations [3]. Exposure to pollutants has been linked to respiratory and cardiovascular diseases, exacerbation of existing health conditions, and an increased risk of premature mortality [7]. Furthermore, air pollution adversely affects the environment, leading to soil and water contamination, acid rain, and damage to vegetation [8].

Air quality forecasting plays a pivotal role in managing and mitigating the adverse impacts of air pollution on human health and the environment [9]. Over the years, various AI-based approaches have been utilized to predict and anticipate air quality levels, with statistical models, machine learning (ML) and deep learning (DL) models, and hybrid models emerging as key techniques [10]. An overview of various AI methods and algorithms applied to tasks in chemical engineering, such as regression, classification, clustering, dimensionality reduction, prediction, and forecasting, can be found in [11]. Table 1 provides a detailed review of different AI approaches, outlining their strengths and limitations in the context of air pollution and air quality forecasting.

Table 1. Various AI-based methods employed (or methods that can be employed) in the context of air pollution/quality.

Category	Model/Method	Key Features	Primary Application(s)	Advantages	Limitations	Reference
Statistical models	Hidden Markov model (HMM)	Models and predicts state transitions in machine operations	Failure state prediction.	It is well suited for modeling sequential data such as time series sensor readings, making them effective for predicting state transitions in machinery	Assume independence of observations given the hidden state, which may not always hold true in complex systems	[12]
	Autoregressive (AR) model	Time series forecasting	Models time series based on its own past values; linear dependence.	Simple, interpretable, suitable for stationary data	Limited to linear relationships, assumes stationarity	[13]
	Autoregressive integrated moving average (ARIMA)	Forecasting, economic and industrial time series	Combines AR and MA models with differencing for non-stationary data.	Effective for non-stationary data, well established	Requires parameter tuning, assumes linearity	[14]
	Autoregressive moving average (ARMA)	Stationary time series forecasting	Combines AR and MA components to model time series with past values and errors.	Captures both trend and cycle, useful for stationary series	Not suitable for non-stationary data	[15]
	Autoregressive moving average with exogenous inputs (ARIMAX)	Forecasting with external variables	Extends ARIMA by including exogenous (external) variables.	Incorporates additional influencing factors, flexible	Complex model fitting data preprocessing is needed	[16]
	Seasonal ARIMA (SARIMA)	Seasonal time series forecasting	ARIMA model with seasonal components for periodic data.	Good for data with clear seasonality	Complex parameter tuning, longer training time	[17]
	Nonlinear autoregressive moving average with exogenous inputs (NARMAX)	Complex system modeling, process forecasting	Extends ARMA with nonlinear dynamics and exogenous inputs.	Modeling nonlinear relationships, robust for dynamic systems	Complex to implement, computationally intensive	[4]
	Vector autoregression (VAR)	Multivariate time series forecasting	Modeling interdependencies among multiple time series variables.	Captures relationships between series, effective for macroeconomic data	Assumes all series are stationary, complex modeling	[18]
	Nonlinear Autoregressive neural network (NARNN)	Nonlinear time series forecasting	Uses neural network architecture for autoregressive forecasting tasks.	Captures complex, nonlinear relationships	Requires extensive data and computational resources	[19]
Machine learning	Artificial neural networks (ANN)	Regression, classification, pattern recognition	Composed of layers of interconnected neurons, it can model complex, nonlinear relationships.	High accuracy, flexible modeling	Computationally intensive, requires large datasets	[20]
	Decision tree (DT)	Classification, regression, feature selection	Hierarchical structure with nodes representing decisions/tests on features; interpretable results.	Simple, interpretable, handles both numerical/categorical data	Prone to overfitting	[21]
	Support vector machine (SVM)	Classification, regression, detecting anomalies	Separates classes with a hyperplane, maximizing margin; kernel functions extend to nonlinear boundaries.	Effective for high-dimensional data	Sensitive to parameter selection and scaling	[22]
	Extreme learning machine (ELM)	Fast neural network training, regression	A single hidden layer consists of random weights in the hidden layer for faster training.	Quick training time, straightforward implementation	Less flexible in architecture	[23]
	Extreme gradient boosting (XGBoost)	Classification, regression, ensemble learning	Builds decision trees sequentially, correcting previous errors; uses gradient descent optimization.	High efficiency, strong performance in competitions	It can be complex to tune	[24]
	Random forest (RF)	Classification, regression, anomaly detection	Ensemble decision trees trained on different data subsets; combined results for improved accuracy.	Robust against overfitting, handles large datasets	Large ensembles can be resource-intensive	[25]
	Tree bagger (TB)	Ensemble learning, boosting, classification	Ensemble of decision trees trained with bootstrapping; combines predictions for a final output.	Reduces overfitting, reliable performance	Not ideal for very high-dimensional data	[26]
	Generalized linear regression model (GLRM)	Regression, predictive modeling	Extension of linear regression with a link function for handling non-normally distributed data.	Useful for complex distributions	Assumes linear predictor relationships	[27]
	Gaussian process regression (GPR)	Non-parametric regression	Models output as a distribution over functions, providing a probabilistic prediction.	Provides uncertainty estimates	Computationally expensive for large datasets	[28]
	Linear regression (LR)	Basic regression	Models the relationship as a linear equation between dependent and independent variables.	Simple, interpretable, easy to implement	Limited to linear relationships	[29]
	Generalized additive model (GAM)	Regression, nonlinear modeling	Extends GLRMs with additive, nonlinear effects for each predictor.	Flexibility in nonlinear relationships	Computationally more complex than linear regression	[30]
	Kernelized ridge regression model (KRRM)	Nonlinear regression	Combines ridge regression regularization with a kernel trick for nonlinear transformations.	Good for nonlinear relationships, mitigates overfitting	Kernel choice is critical	[31]
	Linear ridge regression (LRR)	Linear regression with regularization	Adds a penalty to linear regression coefficients to reduce multicollinearity issues.	Reduces overfitting, simple solution	Limited to linear solutions	[32]
	K-nearest neighbors (KNN)	Classification, regression	Instance-based learning finds the majority class among k-nearest data points.	Simple, non-parametric, easy to implement	Computationally expensive for large datasets, sensitive to feature scaling	[33]
	Bayesian linear regression (BayesLR)	Classification, text analysis	A probabilistic classifier based on Bayes’ theorem with strong independence assumptions.	Fast, works well with small datasets	Assumes feature independence, which can be unrealistic	[33]
	Gradient boosting machine (GBM)	Classification, regression, ensemble learning	Sequentially builds decision trees to minimize prediction errors through gradient descent.	High accuracy, adaptable to different data types	Sensitive to overfitting, requires careful tuning	[34]
	Bayesian network (BN)	Probabilistic inference, diagnosis, decision support	Graphical model representing relationships between variables using probabilities.	Handles uncertainty well, interpretable	Computationally intensive for large networks	[35]
Deep learning	Recurrent neural networks (RNNs)	Sequential data modeling for time series patterns	Predicting RUL and anomaly detection in sensor data.	They are designed to process sequential data such as time series sensor readings, making them effective for maintenance forecasting	Training RNNs is computationally expensive, especially for large datasets.	[36]
	Long short-term memory (LSTM)	Advanced RNN for long-term dependencies in time series	Time series forecasting.	Effective for both short-term and long-term predictions, making them highly applicable for RUL estimation and fault detection	It is computationally intensive and requires significant training time compared to simpler models	[37]
	LSTM-based recurrent neural networks (LSTM-RNNs)	Time series prediction, sequence modeling	Incorporates memory cells for sequential data and cyclic connections in the network.	Good for sequential tasks, language modeling	Training can be slow, vanishing gradient problem	[38]
	Convolutional neural networks (CNNs)	Image and video analysis	Applies convolutional layers for automatic feature extraction in spatial data.	Effective for high-dimensional image data	Requires large amounts of data and high computational power	[39]
	Feedforward neural network (FNN)	- Unidirectional flow of information (no cycles) - Consists of input, hidden, and output layers - Typically trained using backpropagation	- Pattern recognition. - Function approximation. - Classification and regression tasks.	- Simple and easy to implement - Effective for structured data	- Prone to overfitting if too complex - Cannot model temporal dependencies	[40]
	Deep neural network (DNN)	- Multiple hidden layers (deep architecture) - Nonlinear activation functions - Trained using backpropagation with optimization techniques	- Image and speech recognition. - Natural language processing. - Complex pattern recognition.	- Can model complex relationships in data - High capacity for learning	- Requires large amounts of data and computational power - Prone to vanishing/exploding gradient problems	[41]
	Residual neural network (ResNet)	- Introduces skip (residual) connections to bypass layers - Reduces vanishing gradient issues - Can have very deep architectures	- Computer vision (image classification, object detection). - Speech recognition. - Time series forecasting.	- Allows training of very deep networks - Mitigates vanishing gradient problem - Improves accuracy in deep learning tasks	- Higher computational cost - Requires careful tuning of architecture	[42]
	Fully connected neural network (FCNN)	- Every neuron in one layer is connected to every neuron in the next layer - Uses dense layers without specialized structures like convolution or recurrence	- General purpose modeling. - Classification and regression. - Feature extraction.	- Simple and widely applicable - Works well for structured data	- Computationally expensive for large inputs - Prone to overfitting due to large number of parameters	[43]
	Reinforcement learning models (RL)	Robotics, optimization, game AI	Learned through trial and error, receiving rewards for actions in an environment.	Adaptable, can learn complex tasks	Training can be time-consuming and data-hungry	[44]
	Autoencoders	Learns compressed representations for anomaly detection	Anomaly detection.	It can effectively reduce the dimensionality of high-dimensional sensor data, simplifying analysis	Are highly sensitive to the quality and variability of training data, which may lead to false positives/negatives	[45]
	Transformer models	Handles long-term dependencies in time-series data	Advanced time series analysis.	Can capture long-term dependencies in time series data	Requires significant computational resources, especially for large datasets	[46,47]
	Physics-informed models	Integrates domain knowledge with AI for improved predictions	Complex mechanical systems modeling.	Incorporate physical laws and domain knowledge, improving prediction accuracy and interpretability	Developing physics-informed models requires significant domain knowledge, which can limit their accessibility	[48]
Hybrid models	LSTM + ARIMA	Combines deep learning with statistical methods for improved predictions	Long-term forecasting.	Combines LSTM’s ability to model nonlinear and long-term dependencies with ARIMA’s strength in handling linear and short-term trends	Requires careful preprocessing to align both models’ requirements such as stationarity for ARIMA and scaled data for LSTM	[49]
	Autoencoders + clustering	Detects and classifies anomalies	Anomaly detection and classification.	Autoencoders identify anomalies by reconstructing normal behavior, while clustering classifies these anomalies into meaningful categories	Combining autoencoders with clustering increases computational overhead during both training and inference	[50]
Feature engineering	K-means clustering	Elbow plot is used for unsupervised anomaly detection. Segmentation of data into clusters	Partitions data into K clusters based on distance to centroids. Identifying abnormal operating conditions.	Simple, efficient, and widely used for large datasets	Sensitive to initialization, assumes spherical clusters	[51]
	Average silhouette plot	Silhouette analysis is used to evaluate the quality of clusters	Measures how similar an object is to its cluster compared to other clusters.	Helps in choosing the optimal cluster count	Less informative for very complex clustering structures
	Hierarchical clustering	Dendrogram is used to understand data structure, hierarchical clustering	Creates nested clusters by merging or splitting data points.	Does not require pre-specifying the number of clusters, visual hierarchy	Computationally intensive for large datasets, sensitive to linkage method
	DBSCAN	Detects dense clusters for anomalies	Clustering operational anomalies.	Effectively identifies and handles noise or outliers, which are common in maintenance data	Performance is highly sensitive to the choice of epsilon and minimum points, which may require trial-and-error tuning	[52]
	PCA, t-SNE	Dimensionality reduction techniques	Reducing data complexity for (PdM) models.	Reduces the complexity of high-dimensional data while retaining most of the variance.	Requires proper scaling of input data for meaningful results
	SHAP, LIME	Key feature identification methods	Selecting critical variables like vibration, temperature, etc.	Both work with any machine learning model, making them versatile for predictive maintenance applications	Both methods can be computationally expensive, especially for complex models and large datasets

In the literature, there are a few studies on air pollution that were developed for Craiova city. These studies are based on various approaches (statistical or based on artificial intelligence). In [53], the authors conducted a statistical comparison of the main pollutants (PMs, NO_x, and SO₂) for two consecutive years, emphasizing the air pollution episodes according to the limits established by the European Environmental Agency (EEA). The ground-level ozone issue was addressed merely as a tangential outcome of rising NO_x levels. Another study [54] examines the natural and anthropogenic causes of some pollutants (NO_x, SO₂, CO, CO₂, and O₃) in urban agglomerations of Romania. In [55], the authors focused on two datasets covering eight months of data about PM_2.5 concentration. The datasets for Craiova were provided by a community-based sensor network (uRADMonitor) and the Romanian Agency for Environmental Protection. The researchers pinpointed the PM_2.5 pollution episodes and highlighted the advantage of using two complementary sensor networks without considering ozone pollution. In [56], the authors showed how the uRADMonitor was built. The uRADMonitor is a community-based sensor network that is used to monitor air quality in urban areas, where in Romania there are 630 low-cost sensors connected to the network. The data provided by this independent network was compared with the data provided by the Romanian Agency for Environmental Protection network (148 automatic air quality monitoring fixed stations and 11 mobile stations). Based on a one-year dataset, the researchers studied PM₁₀ pollution levels in the five largest urban areas in Romania by utilizing five annual statistical indicators recommended by the EEA. It is emphasized again that the key advantage of the independent networks is their ability to generate a considerable volume of open-source data with a high level of granularity (every minute or even every thirty seconds) in contrast to the official network, which produces data at every hour. The disadvantages are associated with the various techniques for measurement and sensor calibration. In [57], the authors calculated the linear Pearson correlation coefficients between PM₁₀ levels and meteorological parameters using data from thirteen identical sensors located in different areas of Craiova. They also compared the values provided by those thirteen sensors for PM₁₀ and PM_2.5 concentrations with World Health Organization (WHO) recommendations identifying the air pollution episodes. Based on hierarchical regression analysis, the researchers analyzed the correlations between meteorological parameters and particulate matter concentrations [58]. In an educational context (Erasmus+ project, 2021-1-RO01-KA220-HED-000030286), the authors compared air quality in three cities (Craiova, Banska Bystrica, Adana) from three different countries (Romania, Turkey, and Slovakia). The conclusion of this research showed that results are affected by location, even if the authors used identical sensors. A significant statistical study for ozone in Craiova [59], based on one year of data with high granulation (one minute), and applying a dual-method approach (SPSS and Phyton), found a strong positive correlation between ozone concentration and temperature and significant negative correlations with relative humidity, PM concentrations, NO₂, and CO. The authors used the T-test to check if the ozone weekday weekend effect might be observed in Craiova. The result was negative. Also, the researchers did not identify exceedances in the recommendations of the WHO and the limits imposed by the EEA for ground-level ozone concentration.

Furthermore, using ML, DL, or hybrid approaches, there is also a set of studies for air pollution prediction and forecast, e.g., based on a four-year dataset (2009–2014) concerning air pollution recorded by four air quality monitoring stations that belong to the National Environmental Agency. In [60], the authors applied hybrid statistics and artificial intelligence techniques, such as feedforward neural networks (FANNs) and wavelet–feedforward neural networks (WFANNs), to time series of four air pollutants (PM_2.5, PM₁₀, NO₂, and O₃). They investigated when FANN and WFANN can be used successfully as air pollution prediction tools. Another study [4] proposed a combination of hybrid models, such as input variable selection (IVS), machine learning (ML), and a regression method, aiming to predict, model, and forecast the daily Air Quality Index and particulate matter concentrations. The authors considered a two-year dataset (one-minute granulation) collected by one low-cost sensor that comprised three meteorological parameters (T, P, RH) and seven air pollutants (PM₁, PM_2.5, PM₁₀, O₃, VOC, CH₂O, CO₂). It was observed that combining feature selection methods with the decision tree (DT), least square regression (LSR), and nonlinear autoregressive moving average model (NARMAX) significantly improved prediction, forecasting of PM concentrations, and AQI accuracy. Based on Craiova’s weather features, the authors of another study [61] have proven that photovoltaics are a viable solution to reduce air pollution in a busy city like Craiova. The implications of air pollution for photovoltaic systems using six random forest models are newly investigated. The Shapley additive explanations technique was applied to interpret the decision-making model. In [5], a daily time series of ozone and fine particulate matter (PM) concentrations was forecasted using a meta-hybrid deep NARMAX (nonlinear autoregressive moving average with exogenous inputs) model. The dataset of three years contained the following: (i) data at each minute for meteorological parameters (T, P, RH) and air pollutant concentrations (PMs, O₃, CO₂, VOCs, formaldehyde CH₂O), (ii) hourly data on wind direction, wind speed, and sun brightness provided by the National Meteorological Administration.

The current understanding and forecasting of air quality in this urban area (Craiova, Romania) face several limitations:

-

Short-term forecasting: most existing models focus on short-term predictions, providing only a limited number of future values per air pollutant.

-

Absence of certain variables: existing research often lacks comprehensive studies that incorporate all relevant variables for air pollutant prediction and forecasting.

-

Model limitations: many models are constrained by the specific location and dataset used, making them difficult to generalize in other areas.

-

Model selection: in some cases, models are chosen and applied without a thorough assessment or justification for their selection.

-

Statistical evaluation: some studies rely on a narrow set of statistical metrics and indices, limiting the robustness of model accuracy assessments.

This research aims to overcome these limitations by exploring the use of various hybrid AI methods to predict, model, and forecast hourly ground-level ozone (O₃) concentrations. The dataset consists of 27 measured variables, categorized into meteorological parameters like temperature (T), air pressure (P), relative humidity (RH), precipitation, sun brightness, wind direction and speed, and air pollutants (PM_2.5; PM₁₀; CO; SO₂; O₃; NO; NO₂; NOₓ; NH₃; VOCs; Nt; VOCs like benzene (C₆H₆), toluene (C₇H₈), ethylbenzene (C₈H₁₀), and m-, o-, and p-xylene; and toxic elements like Pb, Cd, Ni, and As). The methodology is an approach in four stages. First, data preprocessing is performed to detect and correct anomalies, outliers, and missing values, while ground-level ozone trends in Craiova are analyzed over recent years. In the second stage, correlations between ozone concentrations and other variables are examined, considering only complete data (non-missing values and variables). In the third stage, various hybrid AI algorithms were assessed to determine the optimal predictive model for ozone concentrations. In the last stage of this approach, a novel deep NARMAX model is employed to model and forecast hourly ozone levels in Craiova.

This paper is organized into five sections. Section 2 briefly presents the climatic features of the area of interest, air quality monitoring stations that were selected for this study, and the dataset. Mainly, this section focuses on data preprocessing, correlation analysis, and the temporal trends of variables within the dataset. Section 3 provides a brief review of the AI-based models used. It also outlines the evaluation criteria and the overall study framework. Section 4 presents the results and discussion. Finally, Section 5 concludes the paper with the main findings and a brief overview of future challenges and perspectives.

2. Data Description

2.1. Area of Interest and Climate Description

This research is focused on Craiova, a city which is located in the Oltenia Plain (part of the Romanian Plain) which is the key economic, historical, and cultural hub in the southwestern part of Romania. Craiova has 243,765 inhabitants (according to the 2022 census conducted by the National Institute of Statistics). The ongoing growth of this city also has negative impacts, including air pollution caused by rising traffic and the use of a heating system based on an old thermal power station, construction zones, and industrial activity. The city has 285 hectares green spaces in neighborhoods (according to the Air Quality Plan for Craiova (2020–2024)). Unfortunately, the trend is shifting towards a reduction in green areas to make way for the development of residential neighborhoods.

Craiova has a transitional temperate continental climate specific to the Romanian Plain, with sub-Mediterranean influences due to its position in southwestern Romania. The inhabitants of this city enjoy four seasons. The altitude is 100–120 m. Winters are cold (the average temperature in January is −2.4 °C, but absolute minimal temperatures can decrease below −25 °C in arctic invasion situations), and summers are hot (the average temperature in July is over 22 °C) with frequent heatwaves (absolute maximum temperatures may exceed 40 °C). Over the last three decades, the tendency is to have longer and hotter summers and milder winters. Also, more snowy days are recorded during early spring [62,63]. The average annual precipitation varies between 570 and 645 mm. Craiova enjoys about 2200–2250 h of sunshine per year. The highest frequency of winds is from the east and west (42%), followed by the northeast (34%), and the south, southeast, and southwest (24%). Active atmospheric dynamics are a climatic feature of this area. The atmospheric calm in the cold period of the year is characterized by significant temperature inversions and by fog. Using data from the MODIS satellite (land surface temperature and land cover type), five heat islands were identified in the paved areas of the city [64].

2.2. Air Quality Monitoring Stations and the Dataset

The source of the hourly open-source dataset is the Romanian Agency for Environmental Protection’s website (https://www.calitateaer.ro/). The dataset spans five years (1 January 2020–31 December 2024) and contains two categories of data: (i) seven meteorological parameters and (ii) thirteen air pollutants. Figure 1 shows the distribution of the four stations for air quality monitoring (DJ-1, DJ-2, DJ-3, and DJ-5) in Craiova.

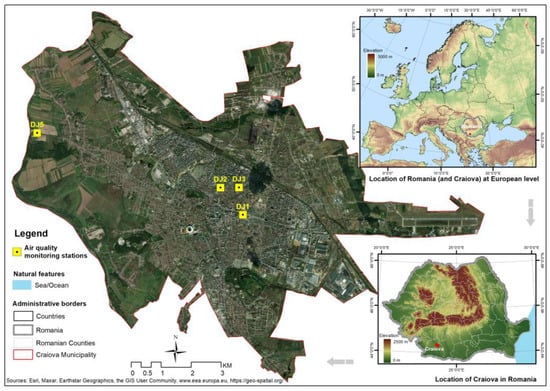
Figure 1. Distribution of the stations for air pollution monitoring in Craiova.

Table 2 indicates the geographical coordinates of the stations, type, location, and parameters that each station measures. In general, a traffic station assesses the influence of traffic on air quality and has a representative radius of 10–100 m. The industrial station evaluates the influence of industrial activities on air quality and has a representative radius of 100 m −1 km. Urban and suburban stations have a representative radius of 1–5 km.

Table 2. Features of the stations from Craiova.

Station ID	Coordinates (Latitute, Longitude, Altitude)	Type	Location	Measured Parameters
DJ 1	44.3266373; 23.7967072; 113.00	Traffic	Calea Bucuresti	C6H6, CO, C8H10, m-, o- and p-Xylene, NO2, NO, NOx, PM10, SO2, C7H8
DJ 2	44.3266373; 23.7967072; 113.00	Urban background	City Hall, A.I. Cuza Street	T; P; RH; wind direction and velocity; precipitations; sun brightness; C6H6; CO; NO; NO2; NOx; SO2; C7H8; PM2.5; PM10; SO2; m-, o- and p-xylene
DJ 3	44.3267708; 23.8044415; 83.00	Mixed (industrial and traffic)	Maria Tanase Street	NH3, NO, NO2, NOx, Ni, O3, PM10, SO2
DJ 5	44.3422203; 23.7197227; 85.00	Suburban background	Breasta Water Station	CO, NO, NO2, NOx, O3, PM10, SO2

The measurement method for sulfur dioxide concentration is UV fluorescence (ISO/FDIS 10498). The chemo-luminescence method helps to measure nitric oxide, nitrogen dioxide, and other nitrogen oxides’ concentrations in the air (ISO 7996/1985). The gravimetric method (according to EN 12341) is a standard method to measure PM_2.5 and PM₁₀ concentrations. The carbon monoxide concentration in the air is determined using the non-dispersive infrared spectrometric method. Lead is determined by atomic absorption spectroscopy (ISO 9855/1993). Ground-level ozone concentration is measured based on an electrochemical method.

Table 3 presents all variables that were taken into consideration in this research. The variables are split into inputs (predictors) and the target variable (one output). There are two aims in the following: (1) to find out the correlation between variables and (2) to recognize the most significant predictors for accurately predicting, modeling, and forecasting ozone concentrations. As can be easily observed in Table 3, there are seventeen input variables and only one output variable, ozone concentration.

Table 3. The considered predictor variables and output.

Variable’s Number	Index	Parameter	Unit
Variable 1	$u_1$	Benzene (C6H6)	μg/m3
Variable 2	$u_2$	Carbon monoxide (CO)	μg/m3
Variable 3	$u_3$	Ethylbenzene (C6H5CH2CH3 or C8H10)	μg/m3
Variable 4	$u_4$	m-Xylene (C6H4(CH3)2)	μg/m3
Variable 6	$u_5$	Nitric monoxide (NO)	μg/m3
Variable 6	$u_6$	Nitrogen dioxide (NO2)	μg/m3
Variable 7	$u_7$	Oxides of nitrogen (NOx)	μg/m3
Variable 8	$u_8$	o-xylene (C6H4(CH3)2)	μg/m3
Variable 9	$u_9$	p-xylene (C6H4(CH3)2)	μg/m3
Variable 10	$u_{10}$	Precipitations	mm
Variable 11	$u_{11}$	Relative humidity (RH)	%
Variable 12	$u_{12}$	Sulfur dioxide (SO2)	μg/m3
Variable 13	$u_{13}$	Solar brightness	W/m2
Variable 14	$u_{14}$	Temperature (T)	°C
Variable 15	$u_{15}$	Toluene (C6H5CH3 or C8H10)	μg/m3
Variable 16	$u_{16}$	Wind direction	grN
Variable 17	$u_{17}$	Wind velocity	m/s
Output 1	$y$	Ozone (O3)	μg/m3

2.3. Data Pre-Processing

Figure 2 presents the raw hourly data used in this study before preprocessing. The objective is to assess data continuity, verify the availability of all collected variables, and identify suitable variables for the next stage, where more continuous data will be selected to analyze correlations between O₃ and other variables, ultimately aiding in the development of optimal AI-based models for ozone prediction and forecasting in Craiova. As observed, certain variables exhibit discontinuities, while some, such as Ni and NH₃, lack recorded values entirely. Notably, meteorological variables appear to be continuous, with minimal missing data. In contrast, air pollutant data contain several gaps. Specifically, O₃, NO, NO₂, NO_x, CO, C₆H₆, C₈H₁₀, three isomers of xylene (m-, o-, p-xylene), and C₇H₈ are available for the period between 1 January 2020 and 18 April 2022. A second dataset, covering PM₁₀ and PM_2.5, spans from 18 February 2022 to 24 September 2024. A visualization of the evolution in time of pollutant concentrations effectively highlights missing and discontinuous variables by referencing the presence of NaN values in the ozone dataset. Based on this analysis, variables such as As, Cd, Ni, Pb, NH₃, Nt, P, PM_2.5, and PM₁₀ are excluded from further analyses due to their significant data gaps.

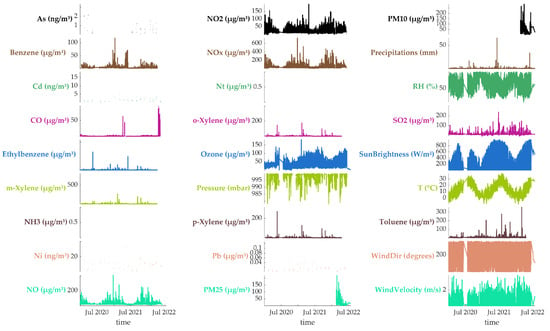
Figure 2. A visualization of data (including missing values) used in this work.

Figure 3 illustrates the percentage of missing data for each variable in the dataset. As previously mentioned, NH₃ and Nt have 100% missing values, indicating no recorded data. Additionally, As, Cd, Ni, and Pb are almost entirely absent, with more than 90% missing values. Meteorological variables exhibit near-complete continuity, with missing data percentages below 3%. In contrast, pollutant variables show significant gaps, with approximately 50% missing values.

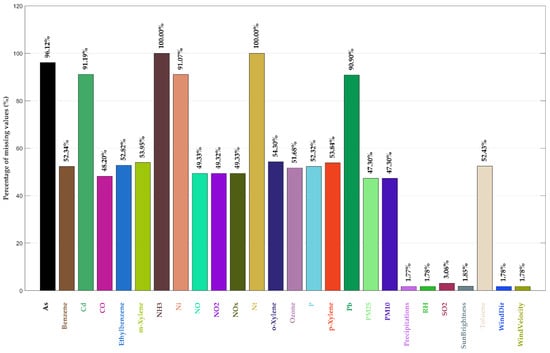
Figure 3. Percentage of the missing values in the data used in this work.

Figure 4 illustrates the distribution of ozone concentrations against the selected variables, excluding missing values. This visualization includes ozone data alongside meteorological parameters and pollutant variables. The main goal of this analysis is to investigate the correlations between ozone levels and the considered variables. The results suggest that ozone concentrations tend to decrease with lower temperatures and sun brightness while increasing with higher relative humidity (RH) and elevated NO, NO₂, and NOₓ levels. However, no clear correlation is observed between the ozone and the remaining variables. Additionally, the plot highlights specific periods with notably high ozone concentrations, providing valuable insights for further analysis.

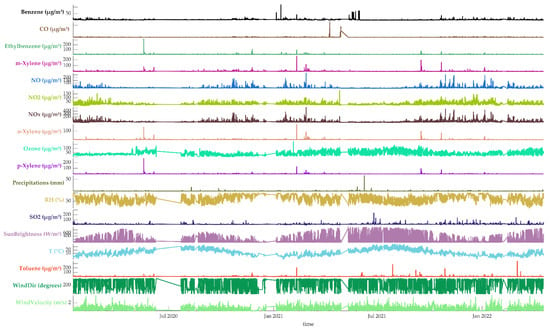
Figure 4. Ozone versus the selected variables, excluding missing values.

Furthermore, Figure 5 illustrates the correlation strength among all selected variables. The highest correlation is observed between ozone and relative humidity (inverse correlation, r = −0.54), followed by sun brightness (r = 0.43), NO₂ (inverse correlation, r = −0.41), temperature (r = 0.40), and NO_x (inverse correlation, r = 22120.39). A moderate correlation is noted between ozone and NO (inverse correlation, r = −0.30), wind velocity (r = 0.27), and benzene (inverse correlation, r = −0.21). A weaker correlation is found with m-xylene (inverse correlation, r = −0.17), toluene (inverse correlation, r = −0.15), o-xylene (inverse correlation, r = −0.13), and p-xylene (inverse correlation, r = −0.10). However, no significant correlation is identified between ozone and the remaining variables. We may conclude that key variables like temperature and sunlight drive ozone formation, while humidity and pollutants may suppress it.

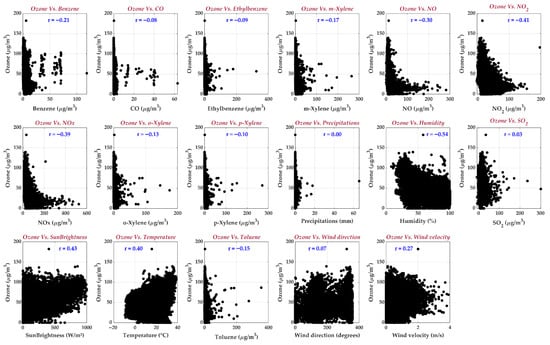
Figure 5. Matrix of correlation: ozone versus the selected variables.

Figure 6 provides a comprehensive analysis of seasonal ozone trends, outliers, and correlations with other variables, including seasonality and monthly variations.

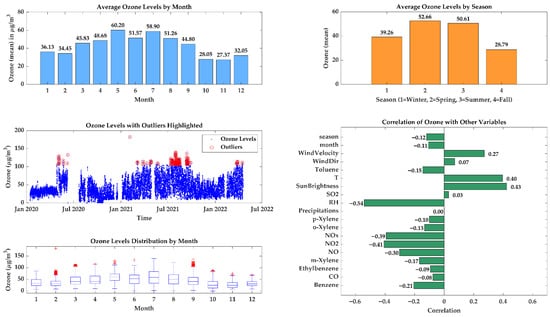
Figure 6. Ozone trends visualization.

-

Monthly trends (first subplot): this plot illustrates average ozone concentrations for each month. Higher ozone levels are observed during summer months (June, July, and August) due to increased solar radiation and higher temperatures, which enhance photochemical reactions. Conversely, lower ozone concentrations are recorded in winter months (December and January) due to reduced sunlight and colder temperatures.

-

Seasonal trends (second subplot): a bar chart aggregates monthly ozone data into four seasons (winter, spring, summer, and fall). The highest ozone levels are observed in summer (season 3), driven by higher temperatures and intense sunlight. In contrast, the lowest ozone levels occur in winter (season 1), when photochemical activity is minimal.

-

Outlier detection (third subplot): a scatter plot highlights extreme ozone values (outliers) over time. Outliers, marked in red, may indicate pollution spikes, measurement errors, or unusual meteorological conditions. The overall time series exhibits periodic fluctuations, likely influenced by daily and seasonal cycles.

-

Correlation analysis (fourth subplot): a horizontal bar chart presents the correlation strength between ozone and other variables. Positive correlations are found with temperature and sun brightness, suggesting that ozone levels increase with higher temperatures and solar radiation. Negative correlations appear with variables like relative humidity, indicating that higher moisture content can suppress ozone formation.

-

Ozone distribution by month (fifth subplot): a box plot displays the distribution of ozone concentrations for each month, capturing medians, quartiles, and outliers. The summer months exhibit a wider range of ozone values, likely due to higher photochemical activity, whereas winter months display more stable and lower concentrations.

3. Materials and Methods

The materials and methods should be described with sufficient details to allow others to replicate and build on the published results. Please note that the publication of your manuscript implies that you must make all materials, data, computer code, and protocols associated with the publication available to readers. Please disclose at the submission stage any restrictions on the availability of materials or information. New methods and protocols should be described in detail while well-established methods can be briefly described and appropriately cited.

3.1. AI-Based Models Employed

The AI-based models that are used to predict, model, and forecast ozone concentrations for future times are investigated in the following section. The models that were chosen include statistical AI-based models designed for time series forecasting, machine learning (ML) and deep learning (DL) models specifically suited for prediction chores, and feature engineering techniques used for dimensionality reduction.

Twenty-three ML and DL models are chosen, used, and contrasted for prediction chores. They are presented in detail in Table 1. To determine the optimal set of predictor variables that can improve the prediction accuracy of the best-performing model, the model obtained in this stage was combined with feature selection approaches. Table A1 offers a summary of the FS approaches used here (see Appendix A). Fifty FS methods are used in all.

Moreover, the next phase uses the most suitable statistical models for multi-step-ahead forecasting and modeling of ozone levels, utilizing past data and the latest observations of related predictor variables. A deep nonlinear system identification technique is employed, utilizing a deep nonlinear autoregressive moving average model with exogenous inputs (Deep-NARMAX). This model characterizes a discrete-time nonlinear system with input u and output y, as described by Equation (1). To forecast the upcoming time step t, the model uses historical ozone concentration values at t − 1, t − 2, t − 3, etc., as provided by Equation (2). The most pertinent predictor variable is subjected to a similar procedure, which forecasts its future value based on its past values. Ozone levels for upcoming time frames are iteratively predicted using these predicted values, with the procedure being repeated for succeeding time steps, as described in Section 3.2.

$$\left\{\begin{array}{c}x\left(\mathrm{t}+1\right)=f\left(\mathrm{x}\left(\mathrm{t}\right),\mathrm{u}\left(\mathrm{t}\right),\mathrm{w}\left(\mathrm{t}\right)\right)\\ y\left(\mathrm{t}\right)=h\left(\mathrm{x}\left(\mathrm{t}\right),\mathrm{e}\left(\mathrm{t}\right)\right) \end{array}\right.$$

(1)

where w is the process noise (the weight), and e is the measurement noise (the error).

$$\mathrm{y}\left(\mathrm{t}\right)=\mathrm{F}\left(\mathrm{y}\left(\mathrm{t}-1\right),\dots ,\mathrm{y}\left(\mathrm{t}-\mathrm{n}\right),\mathrm{u}\left(\mathrm{t}\right),\dots ,\mathrm{u}\left(\mathrm{t}-\mathrm{k}\right),\mathrm{e}\left(\mathrm{t}-1\right),\dots ,\mathrm{e}\left(\mathrm{t}-\mathrm{r}\right)\right)+\mathrm{e}\left(\mathrm{t}\right)$$

(2)

where y(t) is the output variable at time t, u(t) is the combination of the predictor variables involved at time t, and e(t) is the model’s error term. Model function F is a nonlinear function that depends on the past values of the output and variable inputs. The previous equation can be presented in another version, in the context of linear models (Equation (3)).

$$\mathrm{y}\left(\mathrm{t}\right)={\mathrm{\theta }}_1\mathrm{y}\left(\mathrm{t}-1\right)+{\mathrm{\theta }}_2\mathrm{y}\left(\mathrm{t}-\mathrm{n}\right)+{\mathrm{\theta }}_3\mathrm{u}\left(\mathrm{t}-1\right)+{\mathrm{\theta }}_4\mathrm{u}\left(\mathrm{t}-\mathrm{k}\right)+{\mathrm{\theta }}_5\mathrm{e}\left(\mathrm{t}-1\right)+{\mathrm{\theta }}_6\mathrm{e}\left(\mathrm{t}-\mathrm{r}\right)$$

(3)

where ${\mathrm{\theta }}_1$, ${\mathrm{\theta }}_2$, ${\mathrm{\theta }}_3$, ${\mathrm{\theta }}_4$, ${\mathrm{\theta }}_5$, and ${\mathrm{\theta }}_6$ are the coefficients of the model, which are determined based on input and output data.

Equations (1) and (2) represent the general formulation of nonlinear dynamic systems used in AI-based modeling. Equation (1) corresponds to the state-space form, while Equation (2) expresses the functional dependency used by models such as NARX and NARMAX. This formulation bridges the gap between theoretical dynamic modeling and data-driven learning frameworks adopted in this study.

To improve clarity, we emphasize the following:

• Equation (1) serves as a conceptual framework connecting AI models with classical system identification theory.
• Equation (2) expresses the functional mapping structure that data-driven models (e.g., NARX, NARMAX) learn during training.
• The innovation lies in integrating this general dynamic representation with AI-based learning and hybrid feature selection to improve model generalization and interpretability.

3.2. Evaluation Criteria and Statistical Indices

A method for assessing the performance of obtained outcomes was proposed by the authors in [65], introducing a performance score (φ) that indicates the effectiveness of a considered model. This performance score offers a consistent way to evaluate the precision and dependability of the model in forecasting and predicting ozone levels. Equation (4) provides the mathematical expression of the score φ. Poorer model performance is indicated by higher values of φ. Equations (5)–(10) reflect the metrics used in Equation (4): mean bias error (MBE), root mean square error (RMSE), t-statistic (TS) and standard deviation (σ), coefficient of determination (R²), Willmott’s Index of Agreement (WIA), and slope of best-fit line (SBF). Equations (11) and (12) provide the standard deviation (σ) and mean absolute percentage error (MAPE), which can be used for further investigation.

It is important to mention that the statistical indicators employed here are categorized into two groups: dispersion (error-based) and overall performance (correlation-based). For dispersion indicators such as MBE, RMSE, and Sd, the best rank corresponds to values closer to zero, whereas for overall performance indicators such as R², the best rank corresponds to values closer to one. This section offers a precise description of the experimental results, their interpretation, and inferred experimental conclusions.

$$\mathrm{\phi }=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{M}\mathrm{B}\mathrm{E}\right)+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}\right)+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{T}\mathrm{S}\right)+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{R}}^2\right)+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{W}\mathrm{I}\mathrm{A}\right)+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathrm{S}\mathrm{B}\mathrm{F}\right)$$

(4)

$$\mathrm{M}\mathrm{B}\mathrm{E}={\displaystyle \frac{1}{\mathrm{K}}}\sum \left({\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}\right)$$

(5)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\left({\displaystyle \frac{1}{\mathrm{K}}}\sum {\left({\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}\right)}^2\right)}^{{\displaystyle \frac{1}{2}}}$$

(6)

$$\mathrm{T}\mathrm{S}={\left[{\displaystyle \frac{\left(\mathrm{K}-1\right){\mathrm{M}\mathrm{B}\mathrm{E}}^2}{\left({\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}^2-{\mathrm{M}\mathrm{B}\mathrm{E}}^2\right)}}\right]}^{{\displaystyle \frac{1}{2}}}$$

(7)

$${\mathrm{R}}^2=1-{\displaystyle \frac{\sum {\left({\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}\right)}^2}{\sum {\left({\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}-\overline{{\mathrm{v}}_{\mathrm{m}}}\right)}^2}}$$

(8)

$$\mathrm{S}\mathrm{B}\mathrm{F}={\displaystyle \frac{\left[\sum \left({\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-\overline{{\mathrm{H}}_{\mathrm{p}}}\right)\left({\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}-\overline{{\mathrm{v}}_{\mathrm{m}}}\right)\right]}{\sum {\left({\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}-\overline{{\mathrm{v}}_{\mathrm{m}}}\right)}^2}}$$

(9)

$$\mathrm{W}\mathrm{I}\mathrm{A}=1-{\displaystyle \frac{\left[\sum {\left({\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}\right)}^2\right]}{\sum {\left[\left|{\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-\overline{{\mathrm{v}}_{\mathrm{m}}}\right|+\left|{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}-\overline{{\mathrm{v}}_{\mathrm{m}}}\right|\right]}^2}}$$

(10)

$$\mathrm{\sigma }={\left[{\displaystyle \frac{\mathrm{K}\left({\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}^2-{\mathrm{M}\mathrm{B}\mathrm{E}}^2\right)}{\left(\mathrm{K}-1\right)}}\right]}^{{\displaystyle \frac{1}{2}}}$$

(11)

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{100}{\mathrm{K}}}\sum \left|{\displaystyle \frac{\left({\mathrm{v}}_{\mathrm{p}}^{\mathrm{i}}-{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}\right)}{{\mathrm{v}}_{\mathrm{m}}^{\mathrm{i}}}}\right|$$

(12)

K represents the total number of measurements, and parameters ${\mathrm{v}}_{\mathrm{p}}^{\mathrm{I}}$, ${\mathrm{v}}_{\mathrm{m}}^{\mathrm{I}}$, and $\overline{\mathrm{v}}$ correspond to the ith predicted value, ith measured value, and mean value of ozone.

3.3. Methodology

For precise ozone concentration forecasting, we apply a methodology in six stages that combines data preprocessing, correlation analysis, model selection, feature selection, model training, and final deployment. Each stage is explained in detail in the following section:

1. Data preprocessing is carried out in three steps: (i) min–max scaling is utilized for normalization in order to improve model convergence and stability. (ii) Z-scores are utilized for outlier detection. (iii) The k-nearest neighbors (k-NN) method is utilized to identify the anomalies and to exclude anomalous data points.

2. Correlation analysis and trend exploration follows two steps: (i) the correlation between ozone concentrations and the other variables is analyzed. (ii) The trends in ozone levels are visualized to achieve insights into temporal patterns.

3. Data splitting. To assess the performance of each model, the dataset is divided into training (70%) and testing (30%) sets.

4. Model selection. To determine the best-performing model for ozone prediction, the performance of 23 ML and DL models is evaluated.

5. Feature selection is carried out in two steps: (i) to increase prediction accuracy, the efficacy of 50 feature selection strategies is assessed. (ii) Based on this evaluation, the best models and most relevant predictor variables are chosen.

6. Multi-step-ahead forecasting with Deep-NARMAX: (i) Future ozone levels are forecasted using a deep-NARMAX model. (ii) Historical ozone data and other relevant variables are used to determine and refine the optimal mathematical formulation for ozone value forecasting.

4. Results and Discussion

4.1. Best-Performing Model for Ozone Prediction

Figure 7 compares ML and DL models for predicting ozone concentration during the training and testing phases. The top three models in the training phase are DT, treebag, and ELM, while in the testing phase, the leading models are RF, treebag, and xGBoost. Based on R² values, treebag emerges as the best-performing model in both stages, exceeding the confidence threshold of 0.95 in training and achieving approximately 0.89 in testing. Additionally, its MAPE values remain close to zero, demonstrating a strong agreement between measured and predicted ozone concentrations. These findings suggest that these ML models outperform other ML and DL models in hourly ozone prediction. To further improve prediction accuracy in the testing phase, we assessed the hybridization performance of RF, treebag, and xGBoost.

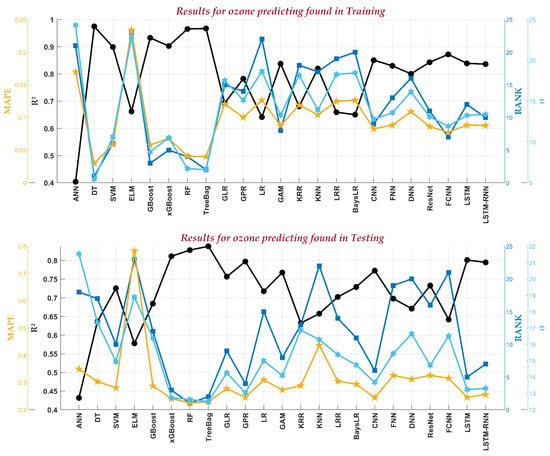
Figure 7. A comparison of ML and DL for predicting ozone concentration in the training and testing stages.

Figure 8 presents the statistical results of this hybridization, showcasing seven possible ozone prediction models derived from the three top-performing ML models. As illustrated, the RF–treebag hybrid model outperforms the others, achieving the highest prediction accuracy. The corresponding statistical metrics in the testing phase are R² = 0.96615, MBE = 0.002468 μg/m³, RMSE = 6.2576 μg/m³, MAPE = 0.087766 μg/m³, and σ = 6.2582 μg/m³, demonstrating its effectiveness in enhancing ozone concentration prediction.

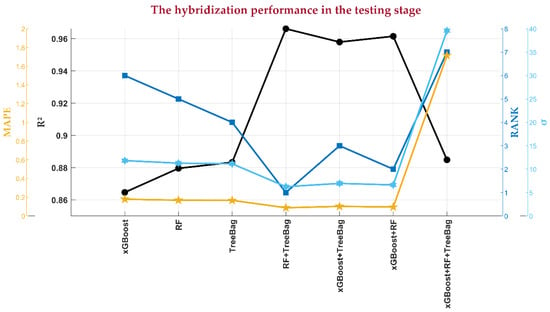
Figure 8. A comparison the top-performing and hybrid top-performing models for predicting ozone concentration in the training and testing stages.

Furthermore, for the top-performing RF–treeBag hybrid model, Figure 9 presents the predicted versus measured ozone concentrations through a time series plot, error distribution, and scatter plot. These visualizations provide insights into the model’s accuracy, error patterns, and the correlation between predicted and observed values, further validating its effectiveness in ozone concentration prediction. In the subsequent phase, the hybrid RF–treebag model is utilized to enhance the accuracy of the most effective feature selection technique, identifying the optimal set of predictors for predicting ozone concentrations.

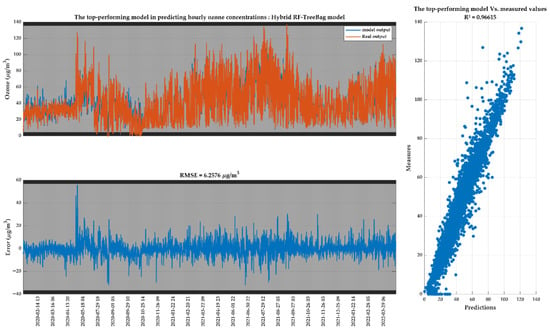
Figure 9. The top-performing model for predicting ozone concentration Vs. measured values.

Figure 10 shows the optimal set of predictors for predicting ozone concentrations displayed by each FS technique studied.

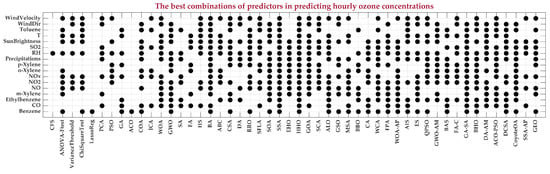
Figure 10. The best combinations of predictors in predicting hourly ozone concentrations.

Figure 11 presents the statistical analysis results for the best feature combinations identified by each of the 50 FS techniques. The highest prediction accuracy is achieved using the GEO model, which identifies the most relevant predictors for ozone concentration as benzene, m-xylene, NO, NO_x, p-xylene, precipitation, RH, SO₂, sun brightness, toluene, and wind velocity. The corresponding statistical metrics in the training phase are R² = 0.9554, MBE = −0.01419 μg/m³, RMSE = 7.3224 μg/m³, MAPE = 0.0458 μg/m³, and σ = 7.3227 μg/m³, and in the testing phase, the corresponding statistical metrics are R² = 0.95656, MBE = 0.043114 μg/m³, RMSE = 7.2145 μg/m³, MAPE = 0.10317 μg/m³, and σ = 7.2151 μg/m³. In contrast, other FS techniques showed minimal correlation and weak predictive accuracy for ozone concentration.

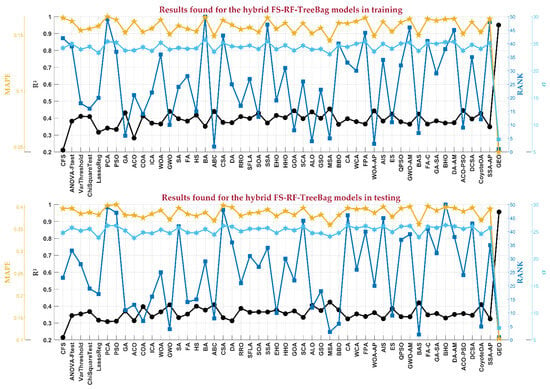
Figure 11. A comparison of FS techniques in predicting ozone concentration in the training and testing stages.

4.2. Best-Performing Model for Ozone Forecasting

Finding and evaluating the most accurate Deep-NARMAX model for ozone level forecasting is the main goal of this subsection. To accurately forecast future ozone levels, the Deep-NARMAX approach used in this study investigates various historical data configurations for ozone and other relevant variables. The following tuning parameters are part of the model initialization: (1) range of time lags for the output variable (nu = [1 5]); (2) range of time lags for the input variables (ny = [1 5]); (3) range of time lags for the error term (ne = [1 5]); (4) maximum time lag among variables (p_temp = max([nu, ny])); (5) nonlinearity degree of the model (degree = 2); (6) maximum length of the potential model terms (term_len = 5); (7) gate weight threshold for feature selection (threshold = 0.7).

The top-performing Deep-NARMAX model for multi-step-ahead forecasting of hourly ozone concentrations is illustrated in Figure 12. This figure presents the forecasted ozone concentrations and the corresponding forecast errors, as well as RMSE and R² values. The most accurate forecasting model is based on the following key predictors: ozone concentration at time (t − 1), solar brightness ($u_{13}$) at time (t − 5), and wind direction ($u_{16}$) and nitrogen dioxide NO₂ ($u_6$) at time (t − 4). The statistical evaluation of this model demonstrates strong predictive performance, with low dispersion in error metrics and an R² value approaching 0.95, aligning with the confidence level threshold. These results confirm that the proposed Deep-NARMAX model is a reliable and efficient approach for forecasting ozone concentrations with high accuracy. The statistical analysis is given by Table 4.

$$\begin{gathered} y\left(t\right)=0.96753y\left(t-1\right)+0.061099u_6\left(t-4\right)-0.013305u_{13}\left(t-5\right)+0.0043781u_{16}\left(t-4\right) \\ +1.0001{.10}^{-5}{u}_{13}^2(t-5) \end{gathered}$$

(13)

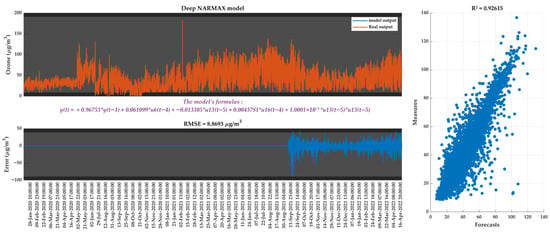
Figure 12. Multi-step-ahead time series forecasting of ozone concentrations using the Deep-NARMAX model.

Table 4. A statistical performance analysis.

Model	R	MBE	MAE	RMSE	MAPE	σ	Rank
Deep-NARMAX	0.92615	0.035727	5.8357	8.8693	0.03528	8.8695	1

5. Conclusions

In this study, an advanced deep AI-based approach was implemented to predict, model, and forecast ozone concentrations. The results demonstrated high accuracy in both prediction and forecasting of ground-level ozone concentrations.

5.1. Key Conclusions

• Among 27 ML and DL models evaluated, the hybrid RF–treebag model emerged as the top-performing model for predicting hourly ozone concentrations in both training and testing. This model achieved excellent results in the testing stage, with R² = 0.96615, MBE = 0.002468 μg/m³, RMSE = 6.2576 μg/m³, MAPE = 0.087766 μg/m³, and σ = 6.2582 μg/m³.
• From 50 FS techniques assessed, the GEO technique was identified as the best feature selection method, providing the most effective predictor combination for ozone concentration prediction. The analysis indicated that the most relevant predictors for ozone concentration are C₆H₆, isomers of xylene, NO, NO_x, precipitation, RH, SO₂, sun brightness, C₇H₈, and wind velocity. When coupled with the hybrid RF–treebag model, this approach yielded strong predictive accuracy, with R² = 0.95656, MBE = 0.043114 μg/m³, RMSE = 7.2145 μg/m³, MAPE = 0.10317 μg/m³, and σ = 7.2151 μg/m³.
• A novel Deep-NARMAX model was successfully developed for forecasting and modeling future ozone concentrations. The model relies on key predictors, including ozone concentration at time (t − 1), sun brightness at time (t − 1), and month at time (t − 2). Its statistical evaluation confirmed robust predictive performance, achieving R² = 0.93614, MBE = −0.26051 μg/m³, RMSE = 8.279 μg/m³, MAPE = 0.032824 μg/m³, and σ = 8.2752 μg/m³.

5.2. Challenges

• There is no long-term research on the hybrid ML-DL approach on ground-level ozone based on the dataset supplied by the Romanian Agency for Environmental Protection (member of the EEA network). The amount of missing data in the Romanian Agency for Environmental Agency network has to be clarified and effectively understood.
• No study compares the quality of the data from different open sources about air pollution (independent low-cost sensor networks, the EEA network, and satellite data), eventually complementing the information from different data sources to complement data missing from one dataset.
• Improvement of the techniques of prediction and forecasting in air pollution allow decision-makers to select the best solutions for the benefit of their local communities.

5.3. Limitations

The main limitations of this research include the percentage of missing data from the Romanian Agency for Environmental Protection, the frequency of the dataset (hourly), the small number of air quality monitoring stations (four), and the uneven distribution of the stations in Craiova.

5.4. Perspectives

Using the datasets provided by satellites and comparing them with the results from independent networks and the network that belongs to the National Environmental Agency might help better comprehend ozone pollution locally. There are satellites that provide data about ozone concentration: NASA satellites (AURA and Terra and Aqua), European Space Agency satellites (Sentinel-5 Precursor, Envisat), NOAA Satellites (Suomi NPP and NOAA-20, GOES), Japanese satellites (GOSAT), Russian satellites (Meteor-M Series), Canadian satellites (SCISAT-1), Indian satellites (INSAT-3D and INSAT-3DR).