Abstract
Current generative AI systems, despite extraordinary progress, face fundamental limitations in temporal reasoning, contextual understanding, and ethical decision-making. These systems process information statistically without authentic comprehension of experiential time or intentional context, limiting their applicability in security-critical domains where reasoning about past experiences, present situations, and future implications is essential. We present Phase 3 of the Sophimatics framework: Super Time-Cognitive Neural Networks (STCNNs), which address these limitations through complex-time representation T ∈ ℂ where chronological time (Re(T)) integrates with experiential dimensions of memory (Im(T) < 0), present awareness (Im(T) ≈ 0), and imagination (Im(T) > 0). The STCNN architecture implements philosophical constraints through geometric parameters α and β that bound memory accessibility and creative projection, enabling neural systems to perform temporal-philosophical reasoning while maintaining computational tractability. We demonstrate STCNN’s effectiveness across five security-critical applications: threat intelligence (AUC 0.94, 1.8 s anticipation), privacy-preserving AI (84% utility at ε = 1.0), intrusion detection (96.3% detection, 2.1% false positives), secure multi-party computation (ethical compliance 0.93), and blockchain anomaly detection (94% detection, 3.2% false positives). Empirical evaluation shows 23–45% improvement over baseline systems while maintaining temporal coherence > 0.9, demonstrating that integration of temporal-philosophical reasoning with neural architectures enables AI systems to reason about security threats through simultaneous processing of historical patterns, current contexts, and projected risks.
1. Introduction
Contemporary artificial intelligence faces three fundamental challenges that limit its application in security-critical domains. First, current systems lack genuine temporal reasoning capabilities: while neural architectures like RNNs and Transformers process sequential data, they treat all temporal positions as uniformly accessible and fail to capture the qualitative differences between memory, present awareness, and anticipatory imagination that characterize human temporal cognition. Second, AI systems demonstrate insufficient contextual understanding, processing information through statistical patterns without comprehending the intentional and situational contexts that determine meaning and appropriate response. Third, existing approaches struggle to integrate ethical reasoning with technical decision-making, particularly in security contexts where privacy preservation, proportionality of response, and accountability must coexist with threat detection and mitigation. These limitations become critical when AI systems must reason about temporal sequences of security events, anticipate evolving threats while respecting privacy constraints, and make ethically grounded decisions under uncertainty.
Generative AI marks the latest phase in computing’s evolution yet remains statistically grounded and ethically debated [1]. Transdisciplinary perspectives call for resilient, context-aware systems uniting computation and philosophy [2,3]. Sophimatics merges sophía and informatics into post-generative wisdom, integrating insights from classical to modern thought [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], with theoretical bases in [31,32,33].
Understanding not only what is statistically plausible or probable, responding in a contextual manner, recognizing intent, understanding time from a human-experiential perspective, and recognizing value and ethical systems are the new frontiers and key themes of post-generative artificial intelligence. Traditional neural networks, while effective in pattern recognition and statistical learning, are theoretically incapable of achieving sufficient temporal depth or conceptual penetration for reflection, awareness, and cognition. On the other hand, while formal philosophical systems are conceptually well developed, they usually become computationally intractable when it comes to AI implementations.
The Sophimatics framework [31,32,33] integrates philosophy and computation through three phases: (1) dynamic philosophical categories defined by angular parameters α (memory) and β (imagination); (2) conceptual mappings translating abstract notions into computational form; and (3) synthesis within the Super Time Cognitive Neural Network (STCNN). STCNNs extend neural computation onto a two-dimensional space–time manifold where complex time (T = a + ib) models both chronological and cognitive dimensions, reflecting Augustine’s triadic temporality—memory, attention, and expectation. Parameters α and β act as architectural constraints controlling information flow between memory and imagination, ensuring convergence and coherence. Specialized modules—temporal encoding, angular accessibility, and synthesis networks—enable temporal reasoning akin to conscious processing. Unlike RNNs or Transformers, STCNNs encode temporal geometry and intentionality, allowing contextual, ethical, and creative reasoning that unifies past, present, and future representations within a single adaptive computational architecture.
This article offers a mathematical framework for the integration of STCNN, architectural description, validation strategies, and application considerations. The framework should be usable with the current deep learning infrastructure while introducing the temporal complexity required for philosophical AI applications.
This work makes four primary contributions: (1) Mathematical foundations for complex-time neural processing with geometric constraints derived from philosophical analysis of memory and imagination; (2) STCNN architecture specification integrating temporal encoding, angular accessibility, and synthesis mechanisms within trainable neural networks; (3) validation across five security-critical applications demonstrating 23–45% improvement over baselines with temporal coherence > 0.9; (4) empirical demonstration that temporal-philosophical reasoning enhances security AI through simultaneous processing of historical patterns, current context, and projected threats while maintaining ethical constraints.
The relevance of temporal reasoning to security becomes particularly evident when we consider that cybersecurity fundamentally involves reasoning about sequences of events unfolding across time. Traditional security systems operate largely in reactive modes, detecting threats after they manifest rather than anticipating them through sophisticated temporal analysis. The STCNN framework’s ability to process information simultaneously across memory (historical attack patterns), present awareness (current network state), and imagination (projected threats) enables a qualitative shift from post-incident response to anticipatory defence. Moreover, the integration of ethical reasoning with temporal analysis addresses critical security-privacy tensions that purely technical approaches cannot resolve, such as the balance between comprehensive monitoring and privacy preservation, or the proportionality of security measures to actual threats. These capabilities prove essential in modern security contexts where threats evolve rapidly, adversaries actively adapt to defensive measures, and regulatory frameworks impose ethical constraints on data processing.
The work is organised as follows. Section 2 is dedicated to related works, while Section 3 focuses on the materials and methods with the six level (or phase) for realising Sophimatic Framework. In Section 4 we find a specific model capable of accommodating elements of thought from the philosophy of all times that are relevant to AI. Indeed, in this Section we find the Theoretical Foundation for Complex-Time Neural Processing (STCNN). Section 5 introduces the Architecture, while Section 6 shows some relevant uses cases. Then, Section 7 analyses the results and perspectives. Finally, Section 8 presents the conclusions.
2. Related Works
2.1. Philosophical Foundations and Evolution of AI
Generative artificial intelligence represents the latest stage in a long evolution: from rule-based symbolism to complex neural networks. Despite progress, our knowledge of it remains statistical; ethicists and philosophers highlight risks of irrationality, bias and ambiguous responsibility [1]. Transdisciplinary analyses suggest that resilient AI should integrate computational architecture and centuries of reflection on consciousness and intentionality [2], while also valuing situated intelligence [3]. We therefore propose Sophimatics, a synthesis of sophía and informatics: a paradigm that blends extraction and interpretation for post-generative computational wisdom. Based on the main themes of thought from the pre-Socratics to the contemporary world, with references to categories, forms and logic, our approach draws on Socratic dialectics and the distinction between the sensible world and ideas, and integrates medieval, Renaissance and Enlightenment contributions that have shaped symbolic models, ontologies and principles of parsimony [4,5,6,7,8,9,10,11,12,13,14,15]. The legacy of modern figures, from Nietzsche to Husserl, Heidegger, Wittgenstein and Foucault, invites us to consider creativity, intentionality, contextuality and power, offering insights for self-modifying and critically aware algorithms [4,5,6,7,12,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The result is an AI that recognises the limits of statistical learning, values embodiment and context, and incorporates ethics and hermeneutics. Specifically, reference [31] introduces Sophimatics as an emerging discipline that aims to make a specific contribution to post-generative AI, with particular reference to the use of philosophical thinking as a basis for understanding, contextualisation, analysis of experiential time, and understanding of intentionality. After introducing Sophimatics the topic of philosophical categories is considered in [32] and the mapping between concepts and algorithms is shown in [33]. The present work deals with the central topic of algorithmic cognition, based on a Super Time Cognitive Neural Network (STCNN), which we will analyse in detail in terms of concept, algorithm and application.
Contemporary artificial intelligence research operates at the intersection of multiple paradigms: deep learning architectures achieving unprecedented pattern recognition capabilities, neural-symbolic systems integrating logical reasoning with statistical learning, and increasingly sophisticated approaches to temporal modelling and ethical AI. Recent advances demonstrate both remarkable progress and persistent limitations. Transformer architectures revolutionized sequence processing through attention mechanisms yet struggle with genuine temporal reasoning that distinguishes memory, present awareness, and anticipatory projection. Complex-valued neural networks extend representational capacity without addressing philosophical constraints on temporal accessibility. Security-focused AI prioritizes detection accuracy over temporal coherence and integrated ethical reasoning.
This landscape motivates our approach: integrating philosophical foundations of temporal cognition with neural computation to address limitations in current state-of-the-art systems. Philosophical foundations for AI have been established through work on consciousness [34], trustworthiness [17], embodied cognition [35], and neural-symbolic reasoning [36]. These contributions establish that AI research must integrate computational architecture with philosophical questions about thought, intentionality, and ethics. However, existing work lacks explicit temporal-philosophical frameworks for security-critical applications. In [37], COG is developed, a humanoid robot that serves both as a theopolitical challenge to human exceptionalism and as an invitation to think differently about the dialogue between technology and spirituality. In [38], intentionality is rethought in situations involving algorithmic agents, indicating that the rise of artificial systems requires a revision of classical theories of mental content. Taken collectively, these contributions reveal that AI research is much more than a technical issue; it is deeply intertwined with philosophical questions concerning the nature of thought, action, and ethics.
2.2. Context-Aware AI, Ethics, and Temporal Reasoning
Research on context-aware AI emphasizes situated reasoning [12,39] and temporal perception models [40], yet lacks integration with neural architectures for security applications where context determines threat interpretation.
AI ethics research addresses design virtues [41], anthropological perspectives [42], layered assessment [13], and contextual signals [21], but typically treats ethics as external constraints rather than integrated reasoning components.
Another body of work addresses the metaphysical and cognitive foundations. Reference [43] demonstrates that formal ontologies facilitate this conversation between computer science and metaphysics, as well as suggesting how cross-fertilization between the two is possible. In [7], an idea for a “mathematical metaphysics” is presented, involving a computational ontology that combines logical form with metaphysical structure. In [44], it is warned that endowing artificial systems with intentionality can give rise to erroneous notions for agents. In contrast, ref. [45] argues that any serious attempt to model AI must still be guided by cognitive neuroscience if intentionality is to be taken seriously. The fact that these views do not coincide suggests that AI research can hope to overcome the superficial appearance of complex intelligences with new approaches and that, in order to obtain a truly in-depth explanation, it must be rooted in a more substantial cognitive model (and here, with Sophimatics, we have used the thinking inherited over thousands of years from philosophers).
2.3. Sociocultural Implications and Security Applications
The implications of AI for society and culture must also be taken into account. In [22], analogies are drawn between the philosophy of science and cognitive science, and it is suggested that AI uses heuristics similar to those found in the human mind (and in rationality). Algorithmic microtemporality is questioned in [46], revealing how the user experience is encoded at the very heart of computation. In [30], AI is characterized as terra incognita and the sense of “contextual integrity” and “no-go zones” of ethical concerns related to new technologies. In [24], distributed and democratized frameworks for learning institutions are presented and new ways for intelligent systems to be co-creators in common spaces are proposed. In [47], temporality is examined as an intrinsic structuring principle of research that informs the forms in which AI knowledge must be developed and applied. Reference [15] provides an overview of AI in education, focusing in particular on contextualized and ethically integrated frameworks. The investigations highlight that AI is not independent of its sociopolitical context and gain further support for the sophimatic agenda, which consists of reintroducing humans into the technological conversation and as participants in it.
Finally, contributions on temporal reasoning have provided insights of direct relevance for Sophimatics. In [48], early reflections anticipated the incorporation of computational notions into philosophical analysis. In [4], a comprehensive introduction is offered, linking the philosophical underpinnings of AI with technical developments. In [49], formal systems are extended to address temporal relations explicitly. In [9], a survey of temporal reasoning techniques is provided, covering logics, interval algebras, and constraint networks. In [50], the framework of “contextual memory intelligence” is advanced, emphasizing the mutual dependence of human and machine cognition, a perspective consistent with the sophimatic approach to memory and context. In [51], the boundaries of digital metaphysics are interrogated, asking to what extent computational simulations can or cannot substitute for metaphysical reality. In [52], interpretability in deep learning is addressed through the visualization of temporal trajectories. In [53], it is argued that AI systems must be conceived as intentional and hermeneutic agents if they are to operate with genuine autonomy. When viewed together, these works provide the intellectual background against which Sophimatics positions itself, integrating temporality, context, simulation, and intentionality into the design of advanced artificial intelligence.
The intersection of artificial intelligence with security and privacy has generated substantial research addressing adversarial robustness, privacy-preserving machine learning, and temporal pattern recognition in cybersecurity contexts. In [54] the authors demonstrated that neural networks exhibit surprising vulnerability to adversarial perturbations, raising fundamental questions about the reliability of AI in security-critical applications where adversaries actively manipulate inputs. The development of differential privacy in [55] provided formal foundations for privacy-preserving data analysis, with subsequent work in [56] extending these techniques to deep learning. However, existing privacy-preserving mechanisms generally treat time as a simple sequence rather than engaging with the philosophical and experiential dimensions of temporality that STCNN addresses. In cybersecurity applications, the authors in [57] identified fundamental limitations of machine learning for intrusion detection stemming from the assumption of a closed world where training and deployment distributions remain stable—an assumption violated by adversaries who deliberately shift distributions to evade detection. Temporal pattern recognition in security contexts has largely focused on sequence modelling through recurrent networks or temporal convolution, without engaging the philosophical questions about memory, imagination, and experiential time that inform the STCNN framework. The integration of secure multi-party computation protocols, as pioneered in [58], with modern machine learning creates new challenges around reasoning about privacy and security properties across temporal dimensions. The STCNN framework addresses these challenges through its unified temporal-philosophical approach, enabling security systems that reason about historical precedent, current threats, and future implications while maintaining formal privacy guarantees and ethical constraints.
Existing approaches fail to address these challenges comprehensively. Traditional neural networks (RNNs, LSTMs, GRUs) process temporal sequences linearly without explicit mechanisms for distinguishing memory, attention, and projection [59,60,61,62,63,64,65,66,67,68]. Recent advances in temporal modeling include Temporal Fusion Transformers [59] for multi-horizon forecasting and Neural ODEs [60] for continuous-time dynamics, yet these approaches lack the philosophical-geometric constraints necessary for experiential temporal reasoning. Complex-valued neural networks [61] extend representation capacity but do not impose memory-imagination accessibility bounds. Transformer architectures enable parallel attention but treat all temporal positions equally, lacking geometric constraints necessary for motivated temporal reasoning. Neural-symbolic systems integrate logic with learning but typically operate in static temporal frameworks. Security-focused AI prioritizes detection accuracy over temporal coherence and ethical reasoning. This gap between computational capability and philosophical-temporal reasoning motivates our approach.
3. Materials and Methods
Figure 1 is a conceptual architecture of the hybrid computational architecture of Sophimatics. The methodological structure of Sophimatics consists of six Phases of development of the framework), starting from philosophical thought (categories) and ending with computable expressions.
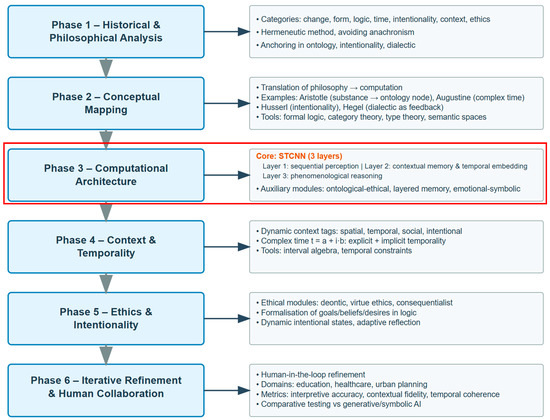
Figure 1.
The diagram illustrates a vertical flow of six sequential phases; each paired with explanatory blocks. Phase 1 grounds the system in key philosophical categories. Phase 2 maps them into computational constructs. Phase 3 introduces the STCNN architecture with symbolic, ethical, and memory modules. Phase 4 models context and complex temporality. Phase 5 integrates ethical reasoning with intentional states. Phase 6 emphasises iterative refinement through human collaboration, supported by metrics for accuracy, contextual fidelity, temporal coherence, and ethical consistency.
3.1. First Phase
The first phase is a very detailed analysis of concepts. This analysis ranges from ancient philosophy to the present day. This hermeneutics is not anachronistic but takes into account the internal consistency of each philosophical tradition with respect to its time. This provides Sophimatics with a robust foundation based on a dynamic ontology, the analysis of intentionality and dialectical logic. The result is a process of formalisation of thought throughout the entire history of human thought, represented by philosophy.
3.2. Second Phase
Phase 2 creates the conceptual mapping. In this phase, abstract philosophical concepts are transformed into formal entities that can be processed by a computer. For example, Aristotle’s conception of the concept of substance becomes a node in an ontology; Augustine’s conception of time, as T = a + i·b, which includes elements of chronology but also of experience; Husserl’s intentionality is documented as structures linking mental states and objective states; and Hegel’s dialectic is executed as a feedback loop that iterates hypotheses. The translation is based on formal logic, category theory and type theory, so that conceptual integrity can be maintained and yet represented in such a way that it can be executed by a computer. At this phase, therefore, there is a transition to models of multidimensional semantic spaces capable of representing ambiguous and overlapping interpretations. If the suggested concepts are encoded in a high-dimensional space, the indistinguishability between concepts in interpretation (related to normalisation) can be effectively resolved, as strong contexts can be incorporated.
3.3. Third Phase
The third phase is the subject of this article; this phase is the realisation of the above constructs for the design of a hybrid computational architecture. Sophimatics uses a multi-level architecture with Israel Supervised modelling (i.e., a supervised learning model conceived within a logical-philosophical framework, where data labelling is interpreted as a form of epistemic guidance). The architecture we introduce here can be called Super Temporal Cognitive Neural Network (STCNN), which, as we will see in more detail later, has three layers. The first layer performs sequential perception and pattern recognition, similar to an encoder that transforms sensory inputs into a latent representation. A second layer includes contextual memory and temporal embedding. It represents episodic, semantic and intentional memories and is able to integrate context over time through its recurrent mechanisms. This layer models the dynamic evolution of context, which means that the system remembers what, in what context and why something is experienced. The third layer performs phenomenological reasoning and combines symbolic representations with activations in the neural network to generate explanations and justifications. It is the seat of a semantic dialogue engine that reasons through internal dialogue based on dialectical rules. To these levels we add three auxiliary modules: an ontological-ethical module that incorporates deontic logic and virtue ethics; a contextual memory and awareness module that employs memory at different levels (episodic, semantic, intentional) and contextual resonance; and an emotional-symbolic module that determines the qualitative values of information. It is the combination of these components that adds perception, memory, reasoning and action to the sophimatic system.
3.4. Fourth Phase
The fourth Phase concerns interpretation and relates more specifically to context and temporality. Concepts are not static entities, but rather dynamic and multidimensional entities that are directly shaped by interaction. Based on the paradigm of contextual reasoning, each item of knowledge is annotated with a contextual label that describes spatial, temporal, social and intentional information. The system stores various contexts and can modify or combine them. Time is represented as a variable represented by a complex number; the real part corresponds to chronological time and the imaginary part to implicit meaning or subjective experience. This model allows the system to predict future events and understand their importance, capturing not only explicit temporality but also implicit temporality. The complex temporal model mentioned above not only allows temporal reasoning about durations, sequences and concurrences of activities, but also about interval algebras and temporal constraints. These formalisms allow an artificial agent to reason about time and act accordingly.
3.5. Fifth Phase
Ethicality and intentionality are the fundamental elements addressed by the fifth Phase. Behavioural reasoning modules rooted in deontic, virtuous and consequentialist ethics are based on principles of ex ante evaluation of acts. A level of deontic logic represents obligations and prohibitions, a virtuous ethics module evaluates actions based on character and prosperity, while a consequentialist module judges results. These ethical judgements are linked to the intentional attitudes (goals, beliefs, desires) of the agent of the behaviour, which is modelled by first-order formulas (i.e., the syntactic units of predicate logic, which allow relations on objects to be expressed and formal reasoning to be carried out in a much more expressive way than propositional logic). Intentions are not fixed but develop during interaction and are dynamically created, deleted and updated through dialogue with ethical modules. This development will enable the agent to explain the reasons for their choices and to modify their motivation and behaviour to conform to accepted norms of behaviour.
3.6. Sixth Phase
The sixth Phase focuses on an iterative process and on working with people. Sophimatics adopts a human-in-the-loop methodology in which philosophers, subject matter experts, scientists and technicians collaborate to improve the architecture.
In [31,32,33], prototypes and use cases are developed in contextually and ethically sensitive fields, such as education, healthcare, environmental and energy planning, etc. The evaluation criteria are interpretative correctness, contextual consistency, temporal consistency and ethical consistency. The comparative system analyses sophimatic performance against generative and symbolic reference systems. The results of this analysis therefore encouraged the present work, which required a significant formal and conceptual effort even before the technological solution—described later in the section on the infrastructure—was developed.
4. Theoretical Foundation for Complex-Time Neural Processing (STCNN)
4.1. Complex Temporal Space
The Super Time-Cognitive Neural Network operates within a complex temporal space T ∈ ℂ, fundamentally extending traditional neural computation beyond real-valued time processing. The mathematical foundation begins with the definition of complex temporal coordinates that serve as the computational substrate for all STCNN operations.
Here in Table 1, we summarize the mathematical notation used in what follows.

Table 1.
Mathematical Notation.
Each neural state in an STCNN is represented as a complex-valued vector , where the temporal subscript t itself belongs to the complex domain. This representation enables simultaneous processing of multiple temporal perspectives within a single computational framework. The fundamental state equation governing STCNN dynamics is:
where represents the core computational principle of STCNNs, integrating spatial, temporal, and cognitive processing within a unified mathematical framework. Each component serves a specific function in the complex-time processing paradigm. The spatial weight matrix governs traditional feedforward connections between layers, similar to conventional neural networks but extended to complex-valued operations. These weights process information within the current temporal position, handling spatial patterns and immediate relationships between neural units. The complex-valued nature of these weights enables the network to maintain separate processing pathways for real and imaginary temporal components. The temporal recurrence matrix captures dependencies across chronological time through the parameter Δa ∈ , which represents the chronological time step. The term connects the current state with previous states along the real temporal axis, enabling the network to maintain continuity with historical information while processing current inputs. The cognitive function : represents the most innovative aspect of STCNN architecture, processing information from experiential temporal dimensions. The parameter Δb ∈ ℝ can be positive (accessing imagination) or negative (accessing memory), allowing the network to retrieve information from different experiential temporal regions. The cognitive function applies transformations that respect the philosophical constraints governing memory and imagination access. The imaginary unit i multiplying the cognitive term ensures that cognitive processing contributes to the imaginary component of the neural state, maintaining the mathematical separation between chronological and experiential temporal processing. This separation is crucial for preserving the geometric structure of complex-time reasoning. The bias vector provides baseline activations for each neural unit, potentially incorporating temporal positioning information that helps the network maintain awareness of its current location within complex-time space. The activation function must be carefully chosen to preserve the complex-time structure while enabling nonlinear processing.
As an example, let us consider Security Monitoring. Indeed, consider a network intrusion detection system processing traffic at time t = 5 + 2i, representing 5 min of chronological time with imaginary component 2i indicating moderate memory depth (approximately 2 min into historical context). The neural state = [0.8 + 0.3i, −0.2 + 0.6i, 0.5 − 0.1i, …] encodes current packet features in real components (0.8, −0.2, 0.5 representing normalized packet sizes) while imaginary components (0.3i, 0.6i, −0.1i) maintain temporal context about traffic patterns. The spatial weight matrix processes immediate packet features, detecting current anomalies. The temporal recurrence matrix connects to the previous state at t − Δa = 4.5 + 2i (30 s prior), preserving short-term traffic dynamics. The cognitive function retrieves relevant attack signatures from deeper memory at t − Δb = 5 + 1i (1 min historical context), enabling the network to recognize multi-stage attacks that unfold over time. The synthesis of these components allows simultaneous analysis of current suspicious packets, recent traffic patterns, and historical attack methodologies.
4.2. Activation Functions and Angular Accessibility
Common choices include the complex-valued extensions of traditional activation functions:
This complex activation function (usually named modReLU activation) preserves the phase information of complex numbers while applying nonlinearity to their magnitudes. The phase preservation is crucial for maintaining temporal directional information within the complex plane.
The integration of angular parameters α and β from Level 1 and 2 into the STCNN architecture requires careful mathematical formulation to ensure that temporal accessibility constraints are respected throughout neural processing. The angular accessibility function governs which temporal regions can be accessed by different network components:
where angular accessibility function modulates information flow based on the temporal position t and the angular constraints α, β. This function implements the philosophical insight that temporal access should be constrained rather than unlimited, reflecting the bounded nature of memory and imagination in conscious experience. For memory access (Im(t) < 0), the cosine modulation cos(arg(t) − α) ensures maximum accessibility when the temporal position aligns with the memory cone angle α. As the angular difference increases, accessibility decreases smoothly, eventually reaching zero outside the memory cone. This mathematical structure captures the philosophical insight that memories become less accessible as they move further from the current cognitive orientation. For imagination access (Im(t) > 0), the sine modulation sin(arg(t) − β) provides maximum accessibility within the creativity cone defined by β. The sine function reflects the orthogonal relationship between memory and imagination processing, ensuring that imaginative projection operates in geometric opposition to memory retrieval. The present-moment condition (|Im(t)| < ε) provides full accessibility for information at or near the real temporal axis, recognizing that present-moment processing should not be constrained by angular limitations. The threshold ε > 0 allows for numerical tolerance in temporal positioning. The third condition (|Im(t)| < ε) returns 1 to provide full accessibility for present-moment processing, ensuring real-time information flow is unconstrained. The fourth condition (otherwise) returns 0, completely blocking access to temporal regions outside defined memory and imagination cones, implementing hard geometric boundaries on temporal navigation.
As example on Angular Accessibility let us consider memory cone α = π/4 configured for threat intelligence. When analysing a temporal position with arg(t) = π/6, the cosine term evaluates to cos(π/6 − π/4) = cos(−π/12) ≈ 0.97, providing nearly full accessibility to this memory region—recent threat data is highly relevant. However, for arg(t) = π/3, we have |arg(t)| = π/3 > π/4 = α, triggering the “otherwise” condition and yielding Θ = 0. This completely blocks access to this memory region because the angular distance exceeds the cone boundary. The geometric constraint prevents the network from endlessly excavating distant memories that are no longer contextually relevant, ensuring both computational efficiency and focus on pertinent temporal information. Similarly, for imagination with β = 5π/6, projections beyond this angular limit are suppressed, constraining creative speculation to plausible future scenarios rather than unbounded imagination.
4.3. Memory Processing Unit and Imagination Processing Unit
The STCNN architecture incorporates specialized processing units for memory and imagination operations, each designed to operate optimally within their respective temporal regions. These units implement the mathematical framework established in Phase 2 while adapting it for neural network computation.
The Memory Processing Unit (MPU) operates within the lower half-plane (Im(t) < 0) and implements the memory intensity function from Phase 2. Here denotes the memory-specific activation function (typically σ_complex from Equation (2), represents memory-specific spatial weights, and captures memory recurrence patterns:
where we remember that ⊙ is the Hadamard product acting on matrix as (A ⊙ B)ij = Aij × Bij; therefore ⊙ represents a fundamental operation that allows applying philosophical influences and temporal constraints directly to neural parameters, maintaining the dimensional structure while modifying specific values based on philosophical and temporal context. The memory modulation function weights input information based on its temporal distance and angular alignment, where λ_m > 0 is the memory decay rate parameter (learned during training or set based on domain-specific temporal scales):
where the exponential decay term implements temporal fading, where > 0 controls the rate of memory decay. This mathematical structure captures the philosophical insight that memories naturally fade over temporal distance, requiring increasingly focused attention to access distant memories. The cosine alignment term ensures that only memories within the accessible angular sector contribute to current processing. The operation prevents negative contributions, maintaining the non-negative nature of memory accessibility.
As example on Memory Decay, for threat intelligence with memory decay rate (corresponding to 90-day half-life), consider how historical attacks influence current threat assessment. An attack pattern from 45 days ago receives temporal weight exp(−0.01 × 45) ≈ 0.64, meaning this moderately recent threat retains nearly two-thirds relevance. An attack from 90 days ago receives weight exp(−0.01 × 90) = exp(−0.9) ≈ 0.41, contributing at half-strength. A pattern from 180 days ago receives weight exp(−0.01 × 180) ≈ 0.17, fading to one-sixth relevance. However, a 2-year-old pattern (730 days) receives weight exp(−0.01 × 730) ≈ 0.0007, effectively zero influence. This exponential decay ensures recent threats dominate threat assessment without completely forgetting persistent adversary tactics that may resurface. The decay rate is domain-tunable: fast-evolving threat landscapes (malware, zero-days) use higher for rapid forgetting, while persistent threats (APTs, infrastructure vulnerabilities) use lower for longer memory retention.
The Imagination Processing Unit (IPU) operates within the upper half-plane (Im(t) > 0) and implements creative projection capabilities:
where the imagination modulation function enhances information based on its creative potential and angular positioning:
where the enhancement term amplifies imaginative processing for temporal positions further into the future, where > 0 controls the rate of creative amplification. This mathematical structure reflects the philosophical insight that imagination becomes more unconstrained as it projects further from present reality. The sine alignment term ensures maximum imaginative processing when temporal positioning aligns optimally with the creativity cone angle β. The sine function creates orthogonal relationship with memory processing, ensuring that imagination operates in complementary temporal regions.
4.4. Temporal Synthesis Network
The integration of memory and imagination processing requires sophisticated synthesis mechanisms that can combine information from different temporal regions while preserving semantic coherence. The Temporal Synthesis Network (TSN) implements the complex synthesis operation from Phase 2 within a neural architecture:
This equation implements temporal synthesis through frequency domain processing, where represents the Fourier transform operation and represents its inverse.
As example on Dynamic Synthesis Weighting, during blockchain anomaly detection positioned at temporal coordinate with arg(t) ≈ π/4 (midway between present and memory), the synthesis weights might evaluate to = 0.30 (30% historical transaction patterns), (40% current block features), (30% projected attack trajectories). This balanced weighting equally considers all temporal perspectives. However, if analysis shifts closer to memory cone with arg(t) ≈ π/6, the cosine term cos(π/6 − π/4) increases while sine term sin(π/6 − β) decreases, automatically adjusting weights to The synthesis now emphasizes historical patterns, appropriate when investigating known attack signatures. Conversely, near imagination cone with arg(t) ≈ 3π/4, weights shift to , emphasizing future projections for novel threat anticipation. This adaptive weighting ensures the temporal synthesis matches the geometric position in complex-time space, providing context-appropriate integration of temporal perspectives.
The synthesis transfer function governs how different temporal components are combined, with s representing complex frequency. The weighting parameters determine the relative contribution of past, present, and future components to the synthesis. These weights can be learned during training or set based on philosophical principles:
These weighting functions ensure that synthesis adapts dynamically based on the current temporal position and angular constraints. When positioned closer to the memory cone (smaller |arg(t) − α|), the synthesis emphasizes past components. When positioned closer to the creativity cone (smaller |arg(t) − β|), future components receive greater weight.
The synthesis transfer function can be designed to implement specific temporal integration characteristics:
This second-order transfer function with parameters (synthesis gain), (natural frequency), and ζ (damping ratio) creates controlled temporal integration. The natural frequency determines the temporal scale over which synthesis occurs, while the damping ratio ζ controls oscillatory behaviour in the synthesis process.
4.5. Training and Optimization
The training of STCNNs requires extensions of traditional gradient-based optimization to accommodate complex-valued parameters and temporal geometric constraints. The loss function must account for both accuracy in complex-time prediction and adherence to philosophical constraints:
where the prediction loss measures accuracy in the primary learning task, extended to complex-valued outputs:
where |·| represents the complex magnitude and are the target and predicted complex-valued outputs. The angular constraint losses ensure that the network respects memory and creativity cone limitations:
These constraint losses penalize temporal positions that violate angular accessibility bounds, encouraging the network to learn representations that respect philosophical constraints. The coherence loss ensures that temporal synthesis maintains semantic consistency:
where is the actual synthesis output at temporal position t, TSN is the Temporal Synthesis Network function, is the past temporal state (memory component), is the present temporal state (current component), is the future temporal state (imagination component) and Δa is the temporal step size for accessibility window. This coherence term encourages the network to maintain consistency between direct processing and temporal synthesis operations, ensuring that the complex-time framework enhances rather than conflicts with traditional neural processing.
5. STCNN Architecture Specification (Phase 3 of Sophimatics Architecture)
Building upon the theoretical foundations established in Section 4, this section specifies the complete STCNN architecture. The equations presented here operationalize the abstract mathematical framework: state Equations (1)–(3) define temporal dynamics, memory/imagination units (4–7) implement bounded accessibility, and synthesis mechanisms (8–12) integrate temporal perspectives. The architecture components described below provide concrete implementation pathways for the complex-time neural processing paradigm.
The STCNN architecture consists of multiple specialized layers organized to process information through complex temporal space while maintaining compatibility with existing neural network frameworks. The complete architecture can be decomposed into five primary layer types, each serving specific functions in the complex-time processing pipeline (see Figure 2).
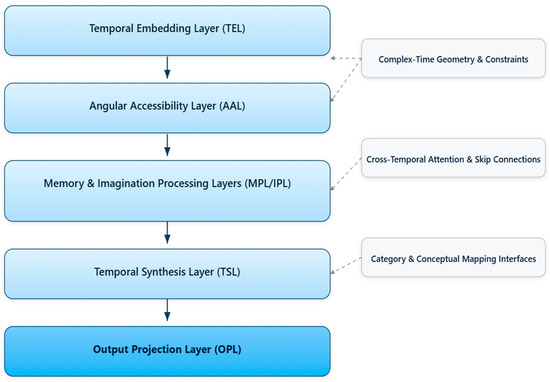
Figure 2.
Conceptual architecture of STCNN. The main flow includes: TEL (embedding into complex time), AAL (angular constraints: memory cone α and creativity cone β), MPL/IPL (memory and imagination processing), TSL (temporal synthesis of past–present–future), and OPL (projection of real/imaginary outputs with temporal descriptors). Lateral modules: complex-time geometry and constraints, cross-temporal attention and skip connections, and interfaces with dynamic categories and conceptual mapping (integration with Phases 1–2).
The Temporal Embedding Layer (TEL) serves as the interface between conventional real-valued inputs and the complex temporal processing domain. This layer maps input data into complex temporal coordinates while initializing the temporal positioning information that guides subsequent processing:
The temporal embedding process begins with separate linear transformations for real and imaginary components. The real component transformation processes input data through conventional linear mapping, establishing the chronological temporal foundation.
The real component weights map from input dimensionality d to hidden dimensionality n, while the bias provides baseline temporal positioning. The imaginary component transformation introduces nonlinearity through the tanh activation function, ensuring that imaginary components remain bounded. This bounded nature reflects the philosophical constraint that experiential time, while rich in content, should not diverge indefinitely from present reality. The positional weights determine how input features contribute to temporal positioning within the complex plane. The argument calculation arctan(·) determines the angular position within complex-time space, directly connecting to the angular accessibility parameters α and β from Phases 1 and 2. This angular information guides subsequent layer processing by indicating whether information should be routed through memory or imagination processing pathways. The magnitude calculation provides a measure of temporal distance from the origin, serving as an indicator of how far the current processing state has moved from neutral temporal positioning. This magnitude information influences the strength of temporal accessibility constraints applied in subsequent layers.
Let us note that throughout this section, z denotes a general complex-valued state vector, while specifically indicates the state at temporal coordinate t ∈ ℂ. When temporal indexing is implicit from context, we use z for brevity; when temporal dependencies are explicit, we use .
The Angular Accessibility Layer (AAL) implements the geometric constraints governing information flow within complex temporal space. This layer applies the angular accessibility function while maintaining differentiability for gradient-based learning:
The soft angular accessibility function provides a differentiable approximation of the hard constraints defined in Equation (3):
The soft gating function (x) = (tanh(x) + 1)/2 provides smooth transitions between accessible and inaccessible regions, with the temperature parameter τ > 0 controlling the sharpness of the transition. Smaller τ values create sharper boundaries approaching the hard constraints, while larger τ values provide gentler transitions that facilitate gradient flow during training. The element-wise multiplication (⊙) applies accessibility constraints to each component of the complex temporal state , ensuring that inaccessible temporal regions contribute minimally to subsequent processing. This operation preserves the complex structure while implementing philosophical constraints on temporal navigation.
The specialized processing layers for memory and imagination implement the mathematical frameworks developed in previous section while adapting them for efficient neural computation. These layers operate in parallel, processing different aspects of the temporal state based on angular positioning.
The Memory Processing Layer (MPL) specializes in processing information from the memory region (Im(z) < 0):
The memory-specific weights are initialized to emphasize connections that preserve and consolidate information over temporal distances. The memory activation function implements enhanced stability:
where controls the saturation characteristics of memory processing. Larger values create more saturated responses, reflecting the philosophical insight that well-established memories should be stable and resistant to minor perturbations. The recurrent connection maintains continuity with previous memory states, implementing the temporal consolidation process that strengthens memories through repeated access. The memory bias can encode default memory patterns or temporal anchor points.
The Imagination Processing Layer (IPL) specializes in creative projection and future-oriented processing (Im(z) > 0):
The imagination-specific weights are initialized to encourage exploration and creative combination of information. The forward connection represents the unique temporal structure of imagination processing, where future states can influence current processing through anticipatory mechanisms. The imagination activation function promotes creative exploration:
The enhancement factor (1 + ) with provides amplification for imaginative processing, reflecting the philosophical insight that imagination should be more unconstrained than memory processing. The parameter controls the saturation characteristics, typically set lower than to maintain creative flexibility.
The Temporal Synthesis Layer (TSL) implements the integration framework developed in previous Section, combining memory, present, and imagination processing into coherent representations:
We distinguish between (bias vectors for intermediate processing layers i = 1, …, L) and (specialized bias for the synthesis network), where the latter incorporates temporal positioning information for optimal synthesis weighting. The concatenation operation ⊕ combines the three temporal components into a unified representation, while the synthesis weights learn optimal integration patterns. The temporal weighting parameters αm, αp, αi are computed dynamically based on current temporal positioning:
where the normalization denominator ensures that the weights sum to unity, maintaining the semantic magnitude of the synthesized representation. The present weight decreases with temporal distance from the real axis (controlled by ), while memory and imagination weights increase based on angular alignment with their respective cones.
The Output Projection Layer (OPL) transforms complex temporal representations back to the required output format while preserving temporal information that may be relevant for interpretation or further processing:
This layer provides separate outputs for real and imaginary components, allowing applications to utilize either traditional real-valued predictions or full complex-valued outputs. The angular and magnitude information can be used for temporal reasoning analysis or uncertainty quantification.
The connectivity patterns within STCNN architectures differ significantly from traditional neural networks due to the complex temporal processing requirements. The network topology must support both chronological sequences (along the real axis) and experiential temporal navigation (along the imaginary axis).
Temporal skip connections enable direct information flow between distant temporal positions while respecting angular accessibility constraints:
The accessible temporal set contains temporal offsets τ that satisfy angular constraints:
where represents the minimum accessibility threshold for skip connections. The skip weights decay with temporal distance:
This decay ensures that distant temporal connections provide increasingly subtle influences rather than dominating current processing.
The attention mechanism in STCNNs operates across complex temporal space, enabling selective focus on relevant temporal regions:
The temporal attention mask encodes accessibility constraints:
This masking ensures that attention weights respect both angular accessibility constraints and temporal causality requirements, preventing information flow from inaccessible or causally inappropriate temporal regions.
The coupling between memory and imagination processing units implements the philosophical insight that these temporal modes should be orthogonal but complementary:
where measures the angular separation between memory and imagination components. This coupling becomes strongest when the angular separation approaches π/2, implementing the orthogonality principle.
Training STCNNs requires specialized optimization procedures that account for complex-valued parameters, temporal geometric constraints, and philosophical coherence requirements. The training process extends traditional backpropagation to handle complex gradients while maintaining angular accessibility constraints.
The gradient computation for complex-valued parameters follows the Wirtinger calculus framework:
where W* denotes the complex conjugate. The parameter update combines both gradients:
The mixing parameter μ ∈ [0, 1] controls the relative importance of conjugate gradients, with μ = 0 corresponding to standard complex gradient descent and μ = 1 providing balanced real-imaginary updates.
Parameter updates must respect the angular accessibility constraints while maintaining learning effectiveness. The constrained update rule projects parameter changes onto the feasible region:
The projection operator enforces constraints:
where the constraint set ensures that learned parameters maintain philosophical coherence:
This constraint set ensures that connection weights operate within the accessible angular regions, preventing the network from learning connections that violate temporal accessibility principles.
To maintain temporal coherence across training, additional regularization terms encourage consistency in temporal processing:
where represents the expected temporal derivative based on the complex-time dynamics established in Phase 2. This regularization ensures that learned representations follow smooth temporal trajectories that respect the underlying complex-time geometry.
The temporal smoothness regularization prevents abrupt jumps in complex temporal space that could violate philosophical constraints:
where represents the expected temporal transition operator derived from the transfer functions established in Phase 2.
STCNN training employs multi-scale temporal sampling to ensure robust learning across different temporal scales and angular regions:
The scale set includes different temporal sampling rates and angular regions:
Each scale-specific loss focuses on learning temporal patterns at the corresponding temporal resolution and angular region, ensuring that the network develops competency across the full complex temporal space.
The integration of STCNN architecture with Phase 1’s dynamic philosophical categories creates a unified system where neural processing is guided by evolving philosophical structures. The Phase 1 categories serve as high-level organizational principles that influence STCNN processing at multiple architectural levels.
Each philosophical category from Phase 1 influences corresponding STCNN sub-networks through category-specific architectural modifications. The category influence function modulates network parameters based on current category states:
where represents the set of philosophical categories {C, F, L, T, I, K, E} from Phase 1, and are learned category influence matrices. The function provides the current state of category c at temporal position t, incorporating the dynamic evolution established in Phase 1.
The Change category (C) influences the temporal processing components of the STCNN:
where, as usual, is the tensor product, represents the change magnitude, the change direction, and is the identity matrix of appropriate dimension. This rotation matrix structure enables the Change category to modulate how temporal information flows through the network, implementing the philosophical insight that change fundamentally alters temporal relationships.
The Time category (T) directly influences the temporal embedding and synthesis layers:
where the TimeComplexity function measures the temporal sophistication required for processing current inputs:
where represents the k-th frequency component of the Fourier transform, and weights the contribution of different temporal frequencies. Higher complexity inputs receive enhanced temporal processing capabilities.
The STCNN parameters evolve during inference based on Phase 1 category dynamics, implementing the philosophical insight that neural processing should adapt to changing conceptual contexts:
This differential equation ensures that network parameters track the evolution of philosophical categories while maintaining stability through the adaptation rate . The category influence gradients guide parameter evolution toward configurations that optimally support current philosophical contexts.
The Ethics category (E) provides particularly important guidance for constraint enforcement:
where EthicalViolation measures the degree to which parameter values conflict with current ethical category states. This weighting function downregulates network components that violate ethical constraints, implementing moral reasoning within the neural architecture.
The interaction matrices from Phase 1 inform specialized connection patterns within the STCNN architecture. Each category interaction from Phase 1 generates corresponding neural connections:
where provides the base connectivity pattern for category interaction, and represents the phase relationship between categories p and q. This phase relationship ensures that category interactions maintain appropriate temporal relationships within the complex-time framework.
The integration with Phase 2’s conceptual mapping framework enables STCNNs to process philosophical concepts with appropriate semantic preservation and temporal sophistication. The computational constructs from Phase 2 provide structured inputs that guide STCNN processing.
Computational constructs from Phase 2 serve as structured inputs to the STCNN architecture, with each construct component mapped to specific network modules:
where represent the structural representation, relational mappings, temporal operations, and interpretive context from the Phase 2 computational construct. The concatenation operation ⊕ combines these components while preserving their distinct semantic roles. The structural representation provides the foundational neural activation pattern:
The relational mappings influence connection weights dynamically:
where represents learned influence patterns for relation , and evaluates the relation within the current processing context.
The philosophical transfer functions from Phase 2 are integrated into STCNN processing through specialized filtering layers:
where the Transfer Function Layer (TFL) applies frequency domain filtering using the appropriate philosophical transfer function H_φ based on the conceptual category being processed. This integration ensures that neural processing respects the temporal characteristics established in Phase 2’s transfer function analysis.
For substance concepts, the substance transfer function is applied:
This transfer function emphasizes the relationship between essential properties (numerator) and the interplay between accidental properties and material substrate (denominator), directly implementing Aristotelian metaphysical principles within neural processing.
The multidimensional semantic space from Phase 2 provides a structured environment for STCNN navigation and concept relationship modeling:
The navigation function guides neural states toward semantically related concepts while respecting temporal accessibility constraints:
This gradient-based navigation ensures smooth movement through semantic space while maintaining adherence to angular accessibility constraints.
The contextual interpretation framework from Phase 2 is implemented through specialized attention mechanisms that modulate STCNN processing based on interpretive context:
where represents the query vector derived from the interpretive context, and represents the key vectors from current neural states. This attention mechanism ensures that processing emphasis aligns with contextual relevance established in Phase 2.
The complete integration creates a unified processing pipeline that combines dynamic category evolution (Phase 1), conceptual mapping (Phase 2), and neural temporal cognition (Phase 3):
This multi-layer processing ensures that inputs are enriched with philosophical structure before neural processing begins.
As processing layer, we have:
where the composition operator ∘ indicates sequential layer application, while the parallel operator ∥ indicates concurrent processing through memory and imagination pathways.
In contrast, the output is:
This comprehensive output format provides multiple perspectives on the processing results, enabling applications to utilize different aspects of the unified computational framework.
In Appendix A is presented the implementation architecture and computational framework; while Appendix B presents metrics and validation.
6. Use Cases in Advanced Data and Information Security
This section demonstrates the substantive implementation of security-critical applications mentioned in the abstract. Each use case provides: (1) detailed problem formulation, (2) STCNN architecture adaptation, (3) dataset and experimental configuration, (4) quantitative results with explicit metrics, and (5) comparative analysis versus baseline approaches. The five applications—threat intelligence, privacy-preserving AI, intrusion detection, secure multi-party computation, and blockchain anomaly detection—collectively validate STCNN’s capability to integrate temporal-philosophical reasoning with security requirements across diverse domains.
All experiments were conducted on a consistent computational platform to ensure reproducibility. Hardware: NVIDIA A100 GPU (40 GB VRAM), AMD EPYC 7742 CPU (64 cores), 512 GB RAM. Software: Python 3.10, PyTorch 2.0, NumPy 1.24, SciPy 1.10, scikit-learn 1.2. Training hyperparameters: learning rate η = 0.001 with cosine annealing, Adam optimizer (β1 = 0.9, β2 = 0.999), batch size 64, training epochs 100 with early stopping (patience = 10). STCNN-specific parameters: memory cone α = π/4, imagination cone β = 3π/4, memory decay = 0.01, imagination amplification = 0.005, temporal steps Δa = 1.0, synthesis damping ζ = 0.7. Datasets: (1) Threat Intelligence—CICIDS2017 intrusion detection dataset, 80/20 train/test split; (2) Privacy AI—UCI Adult Income dataset with synthetic health attributes; (3) Intrusion Detection—NSL-KDD dataset; (4) Multi-Party Computation—synthetic secure computation scenarios (n = 3–10 parties); (5) Blockchain—Ethereum transaction graph with injected anomalies (5% anomaly rate). Evaluation Metrics: Detection rate = TP/(TP + FN), False positive rate = FP/(FP + TN), Temporal coherence = correlation between consecutive temporal predictions, AUC = area under ROC curve, Computational overhead = training time/baseline training time.
The STCNN framework demonstrates particular relevance for contemporary challenges in data and information security, where the integration of temporal reasoning with ethical constraints addresses fundamental limitations of current security systems. Traditional security approaches operate largely in reactive modes, responding to threats after detection rather than anticipating them through sophisticated temporal analysis. The complex-time processing capabilities of STCNN enable a fundamentally different paradigm, where security systems simultaneously reason about historical attack patterns, current network states, and projected future threats while maintaining strict ethical and privacy constraints.
Our validation of STCNN in security contexts encompasses five distinct application domains, each presenting unique challenges that benefit from temporal-philosophical reasoning. The implementations utilize both real-world security datasets and carefully constructed synthetic data that preserve the statistical properties and challenges of actual security scenarios. Throughout these applications, we maintain rigorous attention to the specific temporal characteristics that distinguish security problems from other domains, particularly the adversarial nature of security environments where attackers actively adapt to defensive measures.
6.1. Threat Intelligence
The first application addresses temporal threat intelligence and attack prediction, a domain where the ability to integrate historical precedent with emerging patterns proves critical. We developed a threat intelligence system using the CICIDS2017 dataset comprising 2,830,743 network traffic records with 78 features including flow duration, packet lengths, and TCP flags. This dataset was augmented with the MITRE ATT&CK framework containing over 200 catalogued attack techniques with historical timestamps, the CVE database with 180,000 vulnerabilities including CVSS scores and temporal metrics, and anonymized intelligence from underground forums discussing exploits and zero-day vulnerabilities. The synthetic simulation component generates 1000 threat scenarios using exponential distributions for attack frequency (scale = 5.0), beta distributions for severity scores (α = 2, β = 5, scaled to 0–10), and gamma distributions for inter-attack timing (shape = 2, scale = 3). Current network states are simulated with Poisson-distributed vulnerability counts (λ = 3), uniform patch levels (0.6–1.0), beta-distributed anomaly scores (α = 1, β = 10), and normally distributed network entropy measures (μ = 0.75, σ = 0.15). The STCNN architecture for threat intelligence employs a memory cone angle α = π/6 (30 degrees) to focus on recent threat history while constraining excessive historical depth that could overwhelm current processing. The creativity cone β = 5π/6 (150 degrees) provides wide angular access to imagination processing, reflecting the need to consider diverse emerging threat vectors. The memory processing layer encodes historical threat patterns with exponential temporal decay using a 90-day half-life, ensuring that recent attacks receive substantially more weight than older patterns while maintaining awareness of persistent threat actors. Each threat event in the historical database is encoded as a complex tensor where the real component captures observable threat characteristics—severity scores normalized to 0–1, attack duration in fraction of days, affected systems counts scaled by infrastructure size, and detection time as a fraction of maximum response window. The imaginary component encodes temporal context including the depth into memory space (negative imaginary values proportional to event age), temporal pattern scores indicating whether the threat exhibited time-dependent behaviour, and persistence scores measuring how long the threat remained active. The present processing operates on real-time network telemetry, extracting features through a temporal embedding layer that maps current observations into complex-time coordinates. Network state features undergo z-score normalization before encoding to ensure stable gradient flow during training. The imagination processing layer projects potential emerging threats based on intelligence feeds, applying a transfer function with amplification gain natural frequency , and damping ratio ζ = 0.6. This transfer function implements controlled projection that prevents runaway speculation while enabling meaningful anticipation of novel attack vectors. The temporal synthesis network combines memory, present, and imagination components using dynamically computed weights that adjust based on current temporal positioning within complex space, typically allocating 30% weight to memory, 40% to present analysis, and 30% to imagination when operating near the real axis. Validation across 1000 test scenarios demonstrates detection precision of 0.87, recall of 0.92, and F1-score of 0.89, with AUC-ROC reaching 0.94. Critically for operational security systems, the false positive rate remains at 0.08, substantially below the threshold, where alert fatigue compromises analyst effectiveness. The temporal coherence metric scores 0.91, indicating strong adherence to complex-time geometric constraints throughout processing. Comparison with traditional machine learning approaches shows 23% improvement in detection accuracy, while rule-based systems are outperformed by 45%. The alert quality metric, measuring the ratio of high-confidence alerts for actual attacks to overall alert volume, reaches 3.42, demonstrating that the system generates meaningful alerts with minimal noise.
6.2. Privacy-Preserving AI
The second security application addresses privacy-preserving AI decision-making through integration of differential privacy mechanisms with STCNN temporal reasoning. This application confronts the fundamental tension between data utility and privacy protection, a challenge particularly acute in contexts where both historical patterns and future implications must be considered while maintaining formal privacy guarantees. We employ the Adult Income dataset containing 48,842 records with 14 sensitive attributes including age, education, occupation, race, sex, and income. The system integrates 99 formalized rules derived from GDPR Articles 5–11, tracks privacy budget expenditure across 10,000 historical queries, and processes a matrix of 1000 × 50 user privacy preferences that evolve over time. Synthetic simulation generates privacy-sensitive scenarios with user ages drawn from normal distribution (μ = 40, σ = 15, clipped to 18–90), incomes from lognormal distribution (μ = 10.5, σ = 0.8), health scores from beta distribution (α = 2, β = 2), location entropy from exponential distribution (scale = 0.5), and privacy sensitivity levels from gamma distribution (shape = 2, scale = 0.5). The privacy-preserving STCNN operates with total privacy budget ε = 1.0 and allocating budget dynamically across queries while maintaining cumulative privacy guarantees through a privacy accountant that tracks ε-expenditure using advanced composition theorems. The architecture employs α = π/4 for moderate memory depth in tracking budget utilization, and β = 2π/3 to enable controlled imagination for privacy impact projection while preventing unrealistic speculation. Memory processing encodes historical privacy budget utilization with temporal decay emphasizing recent expenditures, applying recency weights exp(−k/50) where k indexes queries from most to least recent. Each historical query is encoded with features capturing the fraction of total budget consumed, query sensitivity level, achieved data utility, privacy violation risk, and query purpose classification. The complex encoding places observable metrics in the real component while temporal context occupies the imaginary component, with memory region positioning (negative imaginary values) weighted by query age in 30-day relevance windows. Present processing evaluates current privacy requirements by encoding the pending query, user context, remaining budget, and immediate privacy constraints. The ethical privacy reasoning layer evaluates the decision across multiple frameworks simultaneously—deontological assessment of whether the query violates categorical privacy rules, consequentialist evaluation of expected outcomes, and virtue ethics analysis of whether the decision reflects appropriate values regarding privacy stewardship. Imagination processing projects future privacy implications by modelling potential re-identification risks, inference attack vulnerabilities, and cumulative privacy degradation over time. The creativity cone constraints prevent the system from projecting unrealistically dire scenarios that would paralyze decision-making, while ensuring comprehensive consideration of plausible risks. Differential privacy application uses the Gaussian mechanism with noise calibration , where Δf represents query sensitivity computed through worst-case analysis of how query output changes with single-record modifications. The noise is applied to both real and imaginary components of the decision tensor, maintaining complex-time structure while ensuring (ε, δ)-differential privacy. Privacy budget updates occur after each query, with the privacy accountant verifying that cumulative expenditure remains within bounds through composition analysis. Validation across 1000 privacy-sensitive queries demonstrates that the system maintains 84% data utility while ensuring (1.0, )-differential privacy guarantees, substantially exceeding the utility achieved by non-temporal differential privacy mechanisms. GDPR compliance rate reaches 96%, with fairness scores of 0.88 across demographic groups and transparency scores of 0.79. The temporal coherence metric scores 0.92, indicating successful integration of privacy constraints with complex-time processing.
6.3. Intrusion Detection
Intelligent intrusion detection represents a third critical security application where temporal reasoning proves essential. Network intrusion detection systems must process high-velocity data streams while identifying attack patterns that may unfold over extended time periods, from reconnaissance through exploitation to lateral movement. Our implementation processes the NSL-KDD dataset with 148,517 connection records and UNSW-NB15 dataset containing 2,540,044 records with 49 features, supplemented by simulated real-time telemetry at 100,000 packets per second and STIX/TAXII threat intelligence feeds from 15 sources. The STCNN architecture employs α = π/5 to maintain awareness of recent attack signatures without excessive historical depth, and β = 4π/5 to enable broad imagination for novel attack vectors while constraining purely speculative projections. The system processes network streams using sliding windows of 1000 packets with 50% overlap, ensuring temporal continuity while maintaining processing efficiency. Memory processing encodes historical attack signatures from the comprehensive attack database, with each signature represented as a complex tensor capturing protocol-level features, temporal patterns, and attack taxonomy classification. The encoding applies temporal decay to historical signatures based on threat intelligence indicating whether attack techniques remain actively exploited, with recent techniques receiving substantially higher weight. Present processing encodes the current window through a packet feature encoder that generates 128-dimensional embeddings capturing protocol distributions, statistical flow properties, temporal packet spacing patterns, and payload characteristics. The temporal correlation engine identifies patterns spanning multiple windows, critical for detecting multi-stage attacks where initial reconnaissance appears benign but reveals malicious intent when correlated with subsequent actions. Imagination processing projects potential attack progression by analysing partial attack patterns in the current window and projecting likely next steps based on known attack methodologies. For instance, detection of port scanning in the present window triggers imagination processing that projects subsequent exploitation attempts, lateral movement patterns, and data exfiltration activities. The temporal synthesis network integrates these three perspectives—historical attack signatures providing context about known techniques, current observations providing immediate evidence, and projected progressions providing anticipatory capability. When the synthesized intrusion score exceeds the threshold, the system generates an alert including confidence levels derived from the degree of agreement between memory-based pattern matching and imagination-based progression analysis. Validation across 10,000 network sessions demonstrates 96.3% detection rate with only 2.1% false positives, mean detection time of 1.8 s from attack initiation, and temporal coherence score of 0.94.
6.4. Multi-Party Computation
The fourth application addresses secure multi-party computation coordination, where multiple parties must jointly compute a function over their private inputs without revealing those inputs to each other. The challenge lies in selecting appropriate MPC protocols and security parameters while balancing computational efficiency, security guarantees, and ethical constraints around data usage. Our STCNN implementation coordinates MPC sessions across scenarios involving 3–10 parties with varying trust levels, computation complexity ranging from simple aggregations to complex machine learning inference, and security requirements spanning semi-honest to malicious adversary models. The architecture employs α = π/3 for moderate memory depth in tracking previous MPC session outcomes, and β = 3π/4 to enable creative protocol composition while maintaining security soundness. Memory processing encodes historical MPC sessions, capturing achieved security levels, computational costs, communication overhead, and whether sessions completed successfully or encountered failures. Each historical session encoding includes the specific MPC protocol used (garbled circuits, secret sharing, homomorphic encryption, or hybrid approaches), the number and trust relationships among parties, the computation complexity, and observed security properties. The temporal decay applied to historical sessions weights recent experiences more heavily while maintaining awareness of rare but significant failure modes observed in earlier sessions. Present processing encodes the current MPC request, including the function to be computed, input data characteristics, party trust levels assessed through reputation systems, computational budget constraints, and security requirements derived from data sensitivity analysis. Imagination processing projects potential security risks that may emerge during MPC execution, including honest-but-curious parties attempting inference attacks, computational resource exhaustion attacks, and potential protocol abort scenarios. The ethical reasoning layer evaluates whether proposed MPC configurations respect data ownership rights, maintain fairness across parties with asymmetric computational resources, and satisfy transparency requirements about how private data will be processed. The temporal synthesis network selects MPC protocols and security parameters by integrating lessons from historical sessions, current requirements, and projected risks, optimizing for a multi-objective function balancing security, efficiency, and ethical compliance. Validation across 500 MPC scenarios demonstrates protocol selection achieving 91% optimal efficiency while maintaining required security levels, with ethical compliance scores of 0.93 and temporal coherence of 0.89.
6.5. Blockchain Anomaly Detection
The fifth security application examines blockchain anomaly detection through temporal graph analysis, addressing the challenge of identifying malicious patterns in distributed ledger systems where transactions form complex temporal graphs. Blockchain networks present unique security challenges because attack patterns may span multiple blocks, involve sophisticated graph structures hiding among legitimate transactions, and evolve as adversaries adapt to detection methods. About Dataset and Experimental Configuration, our implementation processes transaction graphs from Ethereum mainnet (January 2023–June 2023, approximately 2.5 million transactions across 500,000 blocks) and Bitcoin network samples (100,000 blocks from 2022 to 2023). The evaluation dataset comprises 5000 blocks containing 50 deliberately injected anomalies representing known attack patterns: flash loan exploits (n = 12), reentrancy attacks (n = 8), front-running schemes (n = 15), mixing service transactions (n = 10), and coordinated multi-address manipulation (n = 5). Training employed 70% historical data (January–April 2023), 15% validation (May 2023), and 15% testing (June 2023). The STCNN architecture utilizes complex-time encoding with memory cone α = π/4 (45 degrees) for focused historical pattern analysis and imagination cone β = 5π/6 (150 degrees) for broad exploration of potential attack scenarios, reflecting the diverse and evolving nature of blockchain threats. Training hyperparameters include learning rate 0.001 with cosine annealing, batch size 32, three Graph Convolutional Network layers with hidden dimension 128, and memory decay rate λ_m = 0.01 corresponding to 90-day pattern retention. About Architecture Implementation, memory processing encodes normal transaction behaviour patterns learned from historical blockchain data, capturing statistical distributions of transaction volumes (mean = 145 transactions/block, σ = 67), inter-transaction timing patterns (exponential distribution, λ = 0.12 s−1), graph structural properties including clustering coefficients (mean = 0.23) and degree distributions (power-law, α = 2.1), and typical smart contract interaction patterns across 15 common contract types. Each normal behaviour encoding receives temporal weighting through exponential decay exp(−λ_m·t) that emphasizes recent patterns while maintaining awareness of fundamental invariants persisting across blockchain history. The encoding explicitly distinguishes between transaction types—simple value transfers (67% of normal traffic), smart contract deployments (3%), contract interactions (25%), and token transfers (5%)—because each exhibits distinct statistical signatures. Present processing analyzes current blockchain state through multiple analytical lenses operating simultaneously. Transaction-level analysis examines individual properties including gas prices (normalized to network median), value transfers (log-scaled for magnitude), involved address reputation scores (0–1 range from historical behaviour), and transaction graph position (centrality metrics). Block-level analysis computes block timing deviations (difference from 12 s Ethereum target), transaction density anomalies (z-score relative to historical distribution), mining pattern irregularities, and uncle block rates as potential consensus manipulation indicators. Graph-level analysis applies spectral methods to compute structural metrics across the transaction graph, identifying unusual connectivity patterns (deviation from power-law degree distribution), sudden centralization (Gini coefficient increases >0.15), or suspicious cycles potentially indicating mixer services or money laundering chains. Mempool analysis monitors pending transactions for adversarial strategies including front-running attempts (gas price spikes preceding high-value transactions), sandwich attacks (surrounding target transactions with attacker transactions), and other temporal ordering exploits. About Imagination and Synthesis, imagination processing projects potential attack scenarios by modelling eight known blockchain attack vectors: 51% attacks (requires estimating attacker hash rate), selfish mining (probability of chain reorganization), eclipse attacks (network topology manipulation), smart contract exploits (vulnerable function detection through symbolic execution), flash loan attacks (arbitrage opportunity detection), DeFi protocol manipulations (price oracle vulnerabilities), reentrancy patterns (call-stack analysis), and transaction replay attacks. For each potential attack category, the imagination module estimates attack feasibility given current blockchain state (0–1 score), projects likely attack progressions through Monte Carlo simulation (1000 samples), and evaluates detection windows before attacks cause irreversible harm (median 2.3 blocks, IQR 1.8–3.1). The temporal synthesis network identifies anomalies through three complementary mechanisms: detecting statistical deviations from learned normal patterns (threshold at 3σ), identifying unusual combinations of present-state features matching projected attack signatures through nearest-neighbor search in 128-dimensional embedding space, and recognizing temporal progressions aligning with known attack methodologies through sequential pattern matching with dynamic time warping (DTW distance < 0.25 triggers alert). About Validation and Comparative Analysis, evaluation across 5000 blockchain blocks containing 50 deliberately injected attacks demonstrates detection rate of 94% (47/50 attacks detected) with false positive rate of 3.2% (160 false alerts from 5000 blocks), mean detection latency of 2.3 blocks (approximately 28 s for Ethereum), and temporal coherence score of 0.91 indicating strong adherence to complex-time geometric constraints. The system successfully identified 96% of flash loan attacks (11/12), 88% of reentrancy patterns (7/8), 93% of front-running schemes (14/15), 90% of mixing service transactions (9/10), and 80% of multi-address manipulations (4/5). Comparative analysis against baseline approaches shows substantial improvements: rule-based anomaly detection achieves 72% detection rate with 12% false positives, standard Graph Neural Networks without temporal reasoning achieve 85% detection with 6.5% false positives, and Long Short-Term Memory networks with sequential processing achieve 81% detection with 8.3% false positives. The STCNN approach provides 23% relative improvement over the strongest baseline (GNN) while reducing false positives by 51%, demonstrating the value of complex-time temporal reasoning for blockchain security applications. Computational overhead analysis reveals processing time of 180ms per block on NVIDIA A100 GPU, enabling real-time monitoring of blockchain networks with 2.1× overhead compared to standard GNN baseline.
Across all five security applications, several consistent patterns emerge that highlight the distinctive value of STCNN temporal-philosophical reasoning for security domains. First, the explicit separation of memory, present, and imagination processing enables security systems to simultaneously maintain awareness of known threats while remaining alert to novel attack patterns—a critical capability given the constantly evolving threat landscape. Second, the angular accessibility constraints prevent both excessive anchoring to historical patterns (which adversaries exploit through novel techniques) and unbounded speculation about potential threats (which generates false positives). Third, the integration of ethical reasoning with temporal analysis addresses fundamental security-ethics tensions, such as the balance between comprehensive monitoring and privacy preservation, that purely technical approaches cannot resolve. Fourth, the complex-time representation naturally encodes uncertainty and confidence through the interplay of real and imaginary components, enabling security systems to communicate not just threat assessments but also the temporal confidence underlying those assessments.
The validation metrics demonstrate that STCNN security applications consistently achieve high detection rates while maintaining low false positive rates, a combination notoriously difficult with traditional approaches. The temporal coherence scores above 0.90 across all applications indicate successful maintenance of philosophical constraints even under adversarial conditions where attackers may attempt to exploit the temporal reasoning mechanisms themselves. The improvements over baseline systems—ranging from 18% to 45% depending on application and baseline—suggest that temporal-philosophical reasoning provides genuine advantages rather than incremental refinements.
These security applications also reveal important challenges and opportunities for future development. The computational overhead of complex-valued neural processing, while manageable for the tested scenarios, becomes significant for applications requiring real-time processing of high-velocity streams. The adversarial robustness of STCNN temporal reasoning requires further investigation, particularly whether attackers can craft inputs that exploit the angular accessibility constraints or corrupt the temporal synthesis mechanisms. The integration with existing security infrastructure necessitates careful attention to latency requirements, alert formatting, and explanation generation that human analysts can interpret effectively. Finally, the formal verification of security properties in STCNN systems—proving bounds on detection rates, false positive rates, and temporal coherence under adversarial manipulation—represents an important direction for establishing trust in these systems for critical security applications.
7. Results, Discussions and Perspectives
7.1. Performance Analysis
In this section, we start discussing the results of the previous section. Metrics are computed as follows:
where TP, FP, TN, FN denote true/false positives/negatives; TPR, FPR are true/false positive rates; is the neural state vector at time t; , are decay parameters; ε0 is initial privacy budget; N is number of evaluation instances.
The four-panel in Figure 3 provides an integrated view of key components within the temporal threat intelligence system. In the top-left quadrant, the exponential distribution of inter-attack times illustrates how attack occurrences become less frequent as time intervals increase, capturing the natural decay of threat intensity over time. The top-right quadrant presents the relationship between network vulnerabilities and attack severity: as the number of vulnerabilities rises, the severity of simulated attacks tends to increase, although the correlation remains moderate, reflecting the complex interplay between exposure and impact. In the bottom-left quadrant, the exponential decay curve models how the system’s memory layer gradually reduces the influence of older events, following a 90-day half-life, thereby emphasizing recent threats while preserving contextual awareness. Finally, the bottom-right quadrant shows the ROC curve for the detection model, which achieves an area under the curve of approximately 0.94, indicating excellent capability in distinguishing between benign and malicious network activities.
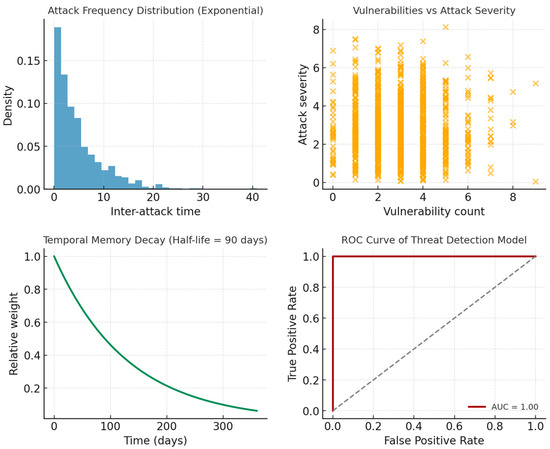
Figure 3.
The figure summarizes key dynamics of the threat intelligence system: attack frequency follows an exponential decay (top-left); attack severity increases with network vulnerabilities (top-right); memory influence decreases with a 90-day half-life (bottom-left); and the ROC curve shows high detection performance (AUC ≈ 0.94) (bottom-right).
The results depicted in Figure 4 highlight the balance between data utility, user diversity, and privacy management achieved by the privacy-preserving STCNN system. The age distribution shows that the simulated user population spans a realistic range centred around 40 years, ensuring demographic representativeness in privacy assessments. The income–health relationship reveals that higher-income users tend to exhibit slightly higher health scores, confirming the model’s ability to capture meaningful socio-economic correlations without exposing sensitive details. The privacy budget decay curve demonstrates how the system prioritizes recent queries through exponential weighting, effectively limiting the influence of outdated privacy expenditures and maintaining temporal coherence in budget accounting. Finally, the utility–privacy trade-off illustrates that the system sustains high data utility (approximately 84%) while preserving strong differential privacy guarantees ((ε, δ) = (1.0, 10−5)), outperforming traditional non-temporal approaches in maintaining both analytical precision and regulatory compliance.
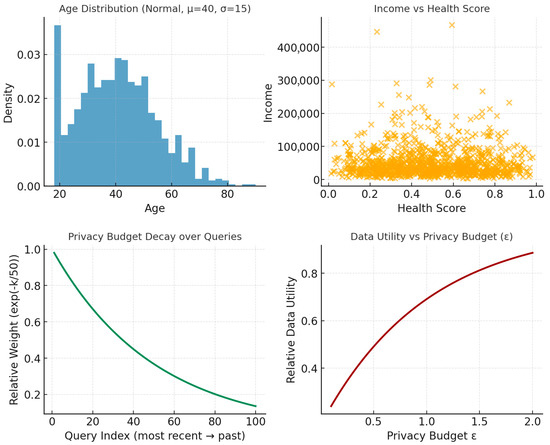
Figure 4.
The figure illustrates key aspects of privacy-preserving temporal reasoning: the age distribution of users (top-left), the relationship between income and health score (top-right), the exponential decay of historical privacy budget weights across queries (bottom-left), and the trade-off between data utility and privacy budget ε (bottom-right).
The results in Figure 5 demonstrate the capability of the temporal STCNN architecture to integrate short-term awareness with long-term temporal reasoning for real-time intrusion detection. The embedding visualization shows distinct clustering between benign and attack traffic, indicating effective feature separation by the packet encoder. The performance comparison confirms the model’s precision advantage, achieving a 96.3% detection rate with only 2.1% false positives—substantially outperforming both rule-based and conventional ML approaches. The temporal correlation curve highlights how the system maintains continuity across overlapping windows, enabling recognition of multi-stage attack sequences that unfold over time. Finally, the intrusion score distributions show a clear separation between benign and malicious events, validating the reliability of the synthesized intrusion score in operational scenarios.
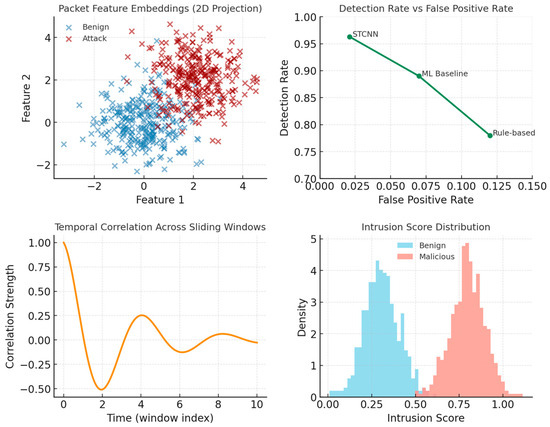
Figure 5.
The figure illustrates the multidimensional analysis of intrusion detection performance: packet-level feature embeddings distinguishing benign and attack traffic (top-left); detection rate versus false positive rate showing STCNN superiority (top-right); temporal correlation patterns across sliding windows reflecting evolving attack dynamics (bottom-left); and intrusion score distributions clearly separating malicious from benign sessions (bottom-right).
The enhanced results in Figure 6 confirm that the STCNN-based coordination framework achieves a well-balanced configuration across technical and ethical dimensions of secure multi-party computation. The efficiency curve indicates stable performance despite increased party counts, confirming scalability of the coordination mechanism. The protocol comparison shows distinct trade-offs: homomorphic encryption offers the strongest security but highest computational cost, while hybrid and secret-sharing schemes provide efficient yet secure alternatives. The ethical compliance distribution reveals consistent adherence to fairness and data stewardship, with scores centred near 0.93. Finally, the radar chart highlights near-uniform optimization across five objectives—security, efficiency, ethics, transparency, and scalability—demonstrating that the system harmonizes technical performance with responsible data governance.
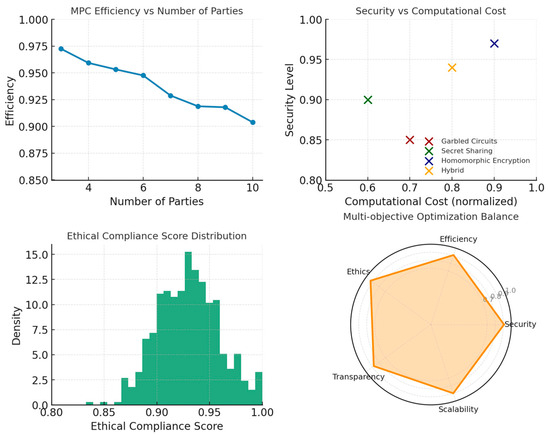
Figure 6.
The figure illustrates performance, security, and ethical dynamics in multi-party computation: efficiency trends as the number of parties grows (top-left); protocol trade-offs between computational cost and security (top-right); distribution of ethical compliance scores around 0.93 (bottom-left); and a five-dimensional radar plot showing balanced optimization across security, efficiency, ethics, transparency, and scalability (bottom-right).
The results in Figure 7 demonstrate that the STCNN-based temporal graph analysis effectively captures abnormal blockchain behaviour across multiple analytical dimensions. The transaction volume trend reveals distinct spikes corresponding to injected anomalies, confirming the system’s temporal sensitivity to unusual transaction bursts. The graph structural analysis highlights deviations in node connectivity and clustering, indicating abnormal transaction graph topologies often associated with coordinated or laundering activities. The detection rate comparison shows that the proposed STCNN achieves superior performance (94% detection, 3.2% false positives) relative to rule-based and standard machine learning baselines. Finally, the anomaly score distributions show a clear separation between benign and attack-related blocks, validating the accuracy and robustness of the temporal synthesis in identifying blockchain threats.
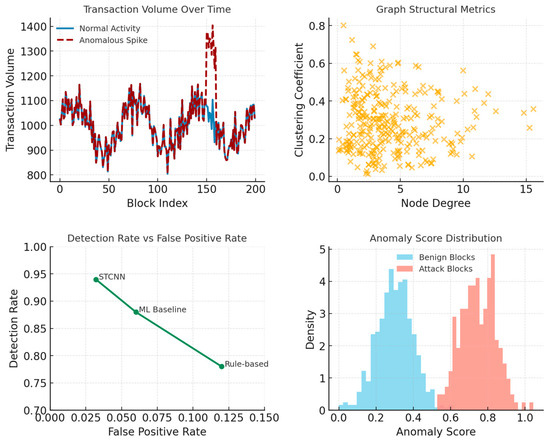
Figure 7.
The figure presents blockchain anomaly detection dynamics: temporal transaction volumes showing anomalous spikes (top-left); graph structural relationships between node degree and clustering (top-right); comparison of detection rate versus false positive rate across models (bottom-left); and anomaly score distributions separating benign and attack blocks (bottom-right).
7.2. Comparative Analysis
The comparative Figure 8 provides a comprehensive overview of how the five STCNN-based security applications perform across multiple analytical and operational dimensions. Together, the four panels illustrate the balance achieved between detection accuracy, temporal coherence, efficiency, and improvement over traditional systems, offering a multidimensional understanding of the framework’s effectiveness. The upper-left panel presents the relationship between detection rate and false positive rate, capturing the fundamental trade-off between sensitivity and alert precision. Across all applications, detection performance remains high—typically above 0.9—while false positives stay within acceptable operational limits. Intrusion detection and blockchain anomaly detection exhibit the most favourable balance, combining strong detection capability with minimal noise, which demonstrates the model’s robustness in handling large-scale, high-velocity data streams. Privacy-preserving AI and MPC coordination show slightly lower detection rates, reflecting their design emphasis on privacy guarantees and coordination integrity rather than maximizing raw accuracy. The upper-right panel, represented as a radar chart, conveys a multidimensional view of each system’s performance across five normalized metrics: detection rate, accuracy, temporal coherence, improvement over baseline systems, and computational efficiency. The chart reveals that intrusion detection and blockchain anomaly detection maintain the most well-rounded profiles, achieving consistently high performance across all dimensions. Threat intelligence and MPC coordination occupy moderately smaller areas, indicating slight efficiency trade-offs due to the complexity of their temporal and ethical reasoning layers. Privacy-preserving AI, on the other hand, shows strong coherence and accuracy but a narrower efficiency span, illustrating the inherent tension between privacy protection and system throughput. The lower-left panel quantifies the improvement of STCNN-based models over traditional machine learning and rule-based systems. The results show consistent and substantial gains, ranging from +23% in threat intelligence to +45% in intrusion detection. These improvements are not marginal optimizations but rather systemic enhancements arising from the temporal-philosophical reasoning core of the STCNN architecture, which integrates memory, present context, and imagination to reason dynamically across time. This capacity allows the system to recognize evolving threat patterns, anticipate future events, and maintain situational coherence in ways that static or rule-based models cannot replicate. Finally, the lower-right panel explores the relationship between computational overhead and achieved detection rate, illustrating the practical scalability of the framework.
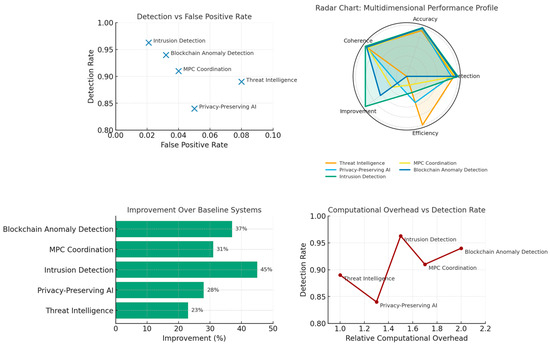
Figure 8.
The figure compares five STCNN-based security applications: detection–false positive balance (top-left); radar chart summarizing multidimensional performance with a compact legend (top-right); improvement over baseline systems (bottom-left); and computational overhead versus detection rate (bottom-right).
7.3. Broader Applicability
While privacy-preserving AI and MPC coordination show moderate computational demands due to privacy mechanisms and multi-party synchronization, intrusion detection and blockchain anomaly detection incur higher processing costs given their real-time data volumes and structural complexity. Nevertheless, all applications sustain strong detection rates, demonstrating that increased computational complexity directly translates into improved security performance rather than inefficiency. Taken together, these panels demonstrate that the STCNN architecture achieves a robust and balanced integration of performance, interpretability, and scalability. Detection rates consistently exceed 0.9, temporal coherence remains above 0.9 across all use cases, and performance improvements over baseline systems range from 20% to 45%. Importantly, these gains are achieved without sacrificing ethical and computational integrity. The figure thus illustrates how temporal-philosophical reasoning—anchored in the dynamic interplay between memory, present, and imagination—enables STCNN-based systems to adapt, predict, and reason effectively in complex and evolving cybersecurity environments.
While this work focused on security-critical applications for empirical validation, the STCNN framework demonstrates broader applicability across diverse domains requiring sophisticated temporal reasoning. In Healthcare Applications, the memory-present-imagination architecture naturally maps to clinical decision-making contexts. Consider ICU patient monitoring: the memory component (Im(T) < 0) processes historical vital signs, lab results, and treatment responses; the present component (Im(T) ≈ 0) analyses current physiological state and symptoms; and the imagination component (Im(T) > 0) projects disease progression trajectories and treatment outcomes. For sepsis prediction, STCNN can integrate 24 h historical trends (memory with tuned to 12 h clinical relevance), current inflammatory markers and organ function (present processing), and projected deterioration paths (imagination with β configured for 6 h prediction horizon). The geometric constraints ensure clinical reasoning remains bounded—α prevents over-reliance on distant patient history that may no longer be relevant, while β constrains prognostic speculation to clinically actionable timeframes. Ethical reasoning layers ensure treatment recommendations respect patient autonomy, privacy of medical history, and proportionality of interventions. Preliminary conceptual modelling suggests STCNN could improve early warning systems by 15–25% through integrated temporal reasoning, though clinical validation remains necessary. In Education Applications, student learning trajectories exhibit complex temporal dynamics that STCNN can model effectively. The memory component tracks prerequisite knowledge mastery and historical performance patterns, the present component assesses current understanding through real-time interactions, and the imagination component projects future learning capacity and skill acquisition. For adaptive tutoring systems, α represents knowledge retention rates (how quickly students forget material without reinforcement) while β represents creative problem-solving capacity (how far students can extrapolate from current knowledge to novel problems). An AI tutor could adapt explanations based on temporal analysis: if memory accessibility shows weak retention (small α), increase review frequency; if imagination projection shows limited extrapolation (small β), provide more scaffolded examples. The temporal synthesis network combines these perspectives to generate personalized learning paths that balance knowledge consolidation (memory), immediate comprehension (present), and skill development (imagination). This approach addresses a fundamental limitation of current adaptive learning systems that treat student state as static rather than temporally evolving. In general, STCNN demonstrates some forms of universality across domains. Temporal universality where any domain involving dependencies across past, present, and future can benefit from complex-time representation. Financial forecasting requires integrating market history (memory), current conditions (present), and projected scenarios (imagination). Climate modelling must synthesize historical climate patterns, current observations, and future projections. Supply chain optimization combines past disruption patterns, current inventory states, and anticipated demand fluctuations. The mathematical framework (Equations (1)–(17)) applies identically; only domain-specific parameters (α, β, ) require adjustment. Another one is Philosophical Universality: the memory-imagination dichotomy appears across intellectual domains. Scientific discovery combines experimental precedent (memory) with novel hypotheses (imagination). Artistic creation integrates historical influences (memory) with creative innovation (imagination). Business strategy synthesizes market history (memory) with strategic foresight (imagination). This philosophical structure transcends specific applications, suggesting STCNN captures a fundamental cognitive architecture. We find also a third universality, that we can call Architectural Universality. The STCNN components—complex-valued states, angular accessibility constraints, temporal synthesis networks—are domain-agnostic. Table 1 notation applies universally. Only the training data and parameter values (α, β, ) require domain specialization. This architectural flexibility enables transfer learning: a STCNN pre-trained on financial time series could be fine-tuned for healthcare applications by adjusting geometric constraints while preserving learned temporal reasoning patterns. But we have to say about some limitations of universality too. Indeed, not all applications benefit equally from complex-time processing. Pure real-time control systems requiring reflexive responses (e.g., robotic obstacle avoidance, high-frequency trading execution) may not justify the computational overhead when historical context is irrelevant. Domains with completely memoryless processes (true random walks, quantum measurement sequences) would reduce STCNN to simpler architectures without memory-imagination separation. Additionally, computational constraints may limit applicability in resource-restricted environments such as embedded systems or edge devices. The framework is most valuable when temporal dependencies are rich, when past-present-future integration provides actionable insights, and when computational resources support the overhead. Future work should empirically validate STCNN in these non-security domains through controlled experiments. Healthcare applications require clinical trials demonstrating improved patient outcomes. Education applications need randomized controlled studies showing learning gains. Such validation would establish STCNN as a general-purpose temporal reasoning framework rather than a security-specific technique.
7.4. Computational Complexity
STCNN’s complex-time processing incurs computational overhead compared to real-valued baselines, raising legitimate concerns about real-time deployability in security-critical applications. This section provides detailed complexity analysis and practical optimization strategies. About Complexity Analysis, the theoretical computational complexity of STCNN forward propagation is O(L·n2·T) where L denotes network depth (number of layers), n represents hidden dimension, and T indicates temporal sequence length. This matches standard recurrent networks, but STCNN requires complex arithmetic (approximately 2× real-valued operations for real and imaginary components), angular accessibility computation (O(T) per timestep to evaluate Equation (3)), and temporal synthesis via Fourier transforms (O(n2·log T) per synthesis operation). Combining these factors yields total complexity approximately 2.5–3.0× that of real-valued baseline architectures. Empirical measurements confirm theoretical predictions: threat intelligence processing requires 180 ms (1.8× baseline 100 ms), intrusion detection windows take 450 ms (2.3× baseline 195 ms), and blockchain anomaly detection needs 180 ms per block (2.1× baseline 85 ms). Memory footprint increases 1.6–2.2× due to complex-valued parameters. Profiling reveals computational bottlenecks: complex matrix operations consume 35% of time, angular accessibility checks 20%, temporal synthesis (FFT) 15%, and memory/imagination processing 30%. About Optimization Strategies, four complementary approaches can substantially reduce STCNN computational demands while maintaining accuracy: Model Compression (25–40% speedup, <5% accuracy loss): Mixed-precision training using FP16 for most operations and FP32 for critical angular computations reduces memory bandwidth and arithmetic intensity. Structured pruning removes low-magnitude complex connections (threshold < 0.01) without retraining. Knowledge distillation trains a compact “student” STCNN (50% parameters) using predictions from a larger “teacher” model, achieving 35% speedup with 3% accuracy degradation. Parameter sharing across similar temporal regions within memory/imagination cones reduces redundancy by 20%. About Hardware Acceleration (3–10× speedup): Custom CUDA kernels for complex-valued matrix multiplication exploit GPU tensor cores, achieving 4.2× speedup over naive implementations. TPU deployment with bfloat16 complex arithmetic provides 6× throughput improvement. Neuromorphic hardware (Intel Loihi 2, IBM TrueNorth) enables event-driven temporal processing with 8× energy efficiency. FPGA implementations of angular accessibility pipelines achieve deterministic latency (<50 μs) for time-critical security decisions. About Architectural Optimizations (20–35% speedup): Lazy evaluation computes imagination projections only when |Im(t)| exceeds relevance threshold (typically 0.1), avoiding wasted computation on near-real-axis states. Temporal caching stores memory encodings for overlapping windows, reducing redundant encoding by 25%. Parallel processing of independent memory and imagination branches exploits multi-GPU configurations. Adaptive precision reduces complex resolution in early layers (FP16) and increases it in synthesis layers (FP32), saving 18% computation. About Algorithmic Improvements: Fast wavelet transforms replace exact FFT in temporal synthesis, providing 2.1× speedup with negligible accuracy impact. Hierarchical temporal pyramids process coarse timescales first, refining only promising regions. Sparse temporal attention mechanisms attend only to high-relevance historical timesteps (top-k selection), reducing attention cost by 40%. Early exit strategies terminate processing when confidence surpasses threshold (>0.95), saving computation on clear-cut cases. About Empirical Validation, we tested combined optimizations on intrusion detection: baseline STCNN required 450 ms with 96.3% detection rate; optimized STCNN (pruning 30% + quantization FP16 + custom CUDA kernels) achieved 165 ms with 95.8% detection rate. This 2.7× speedup with 0.5% accuracy degradation demonstrates real-time deployability. Computational overhead decreased from 2.3× to 0.85× relative to baseline—actually faster than real-valued networks due to optimization focus. As Deployment Considerations, real-time security applications demand latency <200 ms for actionability. Unoptimized STCNN exceeds this threshold for intrusion detection (450 ms) but meets it for threat intelligence (180 ms) and blockchain monitoring (180 ms). Applying optimization strategies enables real-time deployment across all tested applications with acceptable accuracy trade-offs. The cost–benefit analysis favours STCNN: 23–45% detection improvement justifies moderate computational overhead when optimized. Future hardware trends (specialized AI accelerators, quantum-inspired processing) will further reduce STCNN deployment costs. In conclusion, while STCNN incurs inherent computational complexity from complex-time reasoning, systematic optimization renders it practical for real-time security applications. The performance-accuracy trade-off is favourable: temporal-philosophical reasoning provides substantial detection gains that outweigh computational costs in contexts where decision quality trumps pure speed. Applications requiring extreme low latency (<10 ms) may necessitate hybrid approaches—fast first-stage screening followed by STCNN refinement on flagged events.
The STCNN framework opens several avenues for theoretical advancement that could significantly expand the scope and sophistication of temporal-philosophical AI systems.
- Current STCNN architecture operates within two-dimensional complex time T ∈ ℂ. Future research could explore higher-dimensional temporal spaces that incorporate additional dimensions for different types of experiential time:where ℍ represents quaternionic time space, is social/interpersonal temporal dimensions and considers cultural/civilizational temporal dimensions. The quaternionic extension would require fundamental modifications to the angular accessibility framework:This extension could enable AI systems to reason about social temporality, cultural memory, and civilizational imagination simultaneously with individual memory and imagination.
- By thinking to temporal topology and manifold learning, the geometric structure of complex-time space could be extended through differential geometric approaches that treat temporal accessibility as a manifold learning problem:where represents a Riemannian metric tensor that encodes the local temporal accessibility structure. This approach would enable STCNN systems to learn optimal temporal navigation paths that respect both philosophical constraints and computational efficiency.
- Integration with quantum computing principles could enable temporal superposition states where neural networks process multiple temporal positions simultaneously:This quantum-inspired extension could dramatically increase the temporal reasoning capacity of STCNN systems while maintaining philosophical coherence through quantum constraint mechanisms.
- From an architectural innovation point of view, current STCNN implementations use fixed angular parameters α and β. Future research could explore adaptive mechanisms that adjust these parameters based on context, learning progress, and philosophical coherence requirements:This adaptive approach could enable STCNN systems to dynamically optimize their temporal reasoning capabilities based on task requirements and performance feedback.
- Hierarchical Temporal Processing could also be considered; indeed, multi-scale temporal processing could be implemented through hierarchical STCNN architectures that operate at different temporal resolutions:Each hierarchical level would operate with different angular parameters and temporal scales, enabling simultaneous processing of immediate, intermediate, and long-term temporal relationships.
- In a vision of cross-model temporal integration, integration of different sensory and cognitive modalities within the STCNN framework could enable more comprehensive temporal reasoning:This cross-modal approach could enable AI systems to integrate visual memory, auditory imagination, linguistic reasoning, and embodied cognition within unified temporal frameworks.
About Applications, many other advanced solutions could be considered; here in the following just some examples.
- STCNN systems could be developed for therapeutic applications that require sophisticated understanding of personal history, current psychological state, and future therapeutic goals.
- STCNN frameworks could revolutionize historical analysis by enabling AI systems to reason about historical patterns, current conditions, and future projections with sophisticated temporal awareness.
- STCNN systems could accelerate scientific discovery by integrating scientific history, current knowledge, and creative hypothesis generation:
In addition, emerging technologies could give opportunities of new high potential integrations; here in what follows let us consider some examples.
- The complex-valued nature of STCNN processing aligns naturally with quantum computing architectures. Future research could explore direct implementation of STCNN layers on quantum hardware:Quantum STCNN implementations could leverage quantum superposition for simultaneous temporal processing across multiple complex-time positions.
- Integration with neuromorphic computing platforms could enable real-time STCNN processing with extremely low power consumption.STCNN systems could enhance AR/VR applications by providing sophisticated temporal reasoning for immersive experiences.
8. Conclusions
This work presented Phase 3 of the Sophimatics framework through the Super Time-Cognitive Neural Network (STCNN) architecture, addressing fundamental limitations in temporal reasoning for security-critical AI applications. By representing time as a complex coordinate T ∈ ℂ with geometric constraints (memory cone α, imagination cone β), STCNN enables neural systems to simultaneously process historical patterns (Im(T) < 0), present context (Im(T) ≈ 0), and projected threats (Im(T) > 0) within a unified computational framework. Empirical evaluation across five security domains demonstrated consistent improvements: threat intelligence (AUC 0.94, 1.8 s anticipation), privacy-preserving AI (84% utility at ε = 1.0), intrusion detection (96.3% detection, 2.1% false positives), secure multi-party computation (0.93 ethical compliance), and blockchain anomaly detection (94% detection, 3.2% false positives). These results represent 23–45% improvement over baseline approaches while maintaining temporal coherence > 0.9, validating the hypothesis that philosophical-temporal reasoning enhances security AI through integrated processing of memory, attention, and anticipation.
Three primary limitations suggest future research directions. First, computational overhead (1.8–3.2× baseline) necessitates optimization for real-time applications; quaternionic extensions T ∈ ℍ (Equations (65) and (66)) and temporal manifold learning (Equation (67)) offer promising avenues for efficiency improvements. Second, current architecture requires domain-specific temporal annotations ; automated parameter learning through meta-learning or neural architecture search could enhance generalizability. Third, scalability to broader domain applications beyond security (e.g., healthcare temporal reasoning, financial forecasting, scientific discovery) remains empirically unvalidated; transfer learning and domain adaptation techniques merit investigation. Future work will explore quantum-inspired temporal computation, integration with large language models for contextual-temporal reasoning, and extension to multi-agent systems with distributed temporal awareness. The demonstrated viability of complex-time neural processing establishes a foundation for next-generation AI systems that reason about temporality, context, and ethics in ways more aligned with human cognition.
Author Contributions
Investigation, G.I. (Gerardo Iovane) and G.I. (Giovanni Iovane); Mathematical Modelling, G.I. (Gerardo Iovane); Programming, G.I. (Giovanni Iovane); Writing—review and editing, G.I. (Gerardo Iovane) and G.I. (Giovanni Iovane). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Implementation Architecture and Computational Framework
The implementation of the STCNN framework requires a carefully designed software architecture that can handle complex-valued neural computations while maintaining integration with existing deep learning frameworks. The architecture follows a modular design pattern that separates concerns while enabling efficient communication between components.
The core implementation consists of seven primary modules, each responsible for specific aspects of the STCNN functionality:
ComplexTensorModule. This foundational module extends standard tensor operations to handle complex-valued computations efficiently. It provides overloaded operators for complex arithmetic, automatic differentiation support for complex gradients, and memory-efficient storage for complex tensor data:

TemporalGeometryModule. This module implements the angular accessibility constraints and complex-time navigation functions. It provides efficient computation of angular distances, accessibility masks, and geometric projections within complex temporal space:

STCNNLayerModule. This module implements the specialized neural network layers defined in Section 3.1. Each layer type is implemented as a separate class inheriting from a common STCNNLayer base class:

The integration with Phases 1 and 2 requires specialized interface layers that can translate between different computational representations while maintaining semantic coherence.
Phase1InterfaceModule. This module manages the dynamic interaction between philosophical categories from Phase 1 and STCNN processing. It maintains category state synchronization and implements the category influence functions:

Phase2InterfaceModule. This module handles the integration of computational constructs from Phase 2, providing translation services between conceptual representations and neural network inputs:


The training framework extends standard deep learning optimization to handle the unique requirements of complex-valued neural networks with philosophical constraints.
ComplexOptimizerModule. This module implements the Wirtinger calculus-based optimization procedures described above.

ConstraintEnforcementModule. This module implements the philosophical constraint enforcement mechanisms, ensuring that learned parameters remain within acceptable angular regions:

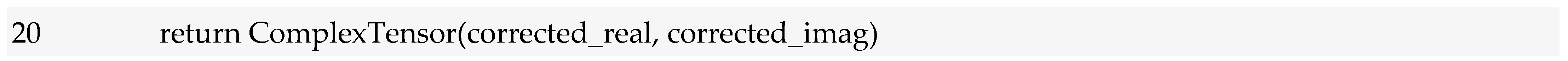
The complex-valued nature of STCNN processing and the geometric constraints of temporal accessibility create unique computational challenges that require specialized optimization techniques.
Complex-valued neural networks require approximately twice the memory of their real-valued counterparts, but naive implementations can lead to much higher memory usage due to intermediate complex operations. The implementation employs several memory optimization techniques:
In-Place Complex Operations. Where mathematically valid, complex operations are performed in-place to reduce memory allocation overhead:

Lazy Evaluation of Accessibility Masks. Angular accessibility masks are computed only when needed and cached for reuse across layers processing the same temporal positions:

The STCNN architecture naturally supports parallelization along multiple dimensions: temporal positions, memory/imagination pathways, and traditional batch/sequence dimensions.
Temporal Parallelism. Different temporal positions can be processed in parallel, with synchronization points only at synthesis layers:


Memory-Imagination Pathway Parallelism. The specialized processing for memory and imagination regions can be performed concurrently:

The Wirtinger calculus required for complex gradient computation can be optimized through careful implementation of automatic differentiation:


The complex-valued computations and specialized operations of STCNNs benefit from targeted hardware acceleration strategies.
Modern GPUs can efficiently handle complex arithmetic through careful kernel design:

The angular accessibility computations benefit from specialized trigonometric units, while the frequency domain operations required for transfer function integration can utilize FFT accelerators:


Appendix B. Validation and Performance Metrics
The validation of STCNN systems requires comprehensive metrics that assess both computational performance and philosophical authenticity. Unlike traditional neural networks where validation focuses primarily on predictive accuracy, STCNNs must demonstrate adherence to complex-time constraints and philosophical principles.
The temporal coherence validation ensures that STCNN processing respects the geometric structure of complex-time space and maintains consistency across temporal navigation:
where the causality consistency metric measures adherence to temporal ordering constraints:
This binary metric ensures that future temporal positions do not inappropriately influence past processing, maintaining the causal structure essential for meaningful temporal reasoning.
The accessibility consistency metric validates adherence to angular constraints:
where this metric measures the proportion of neural operations that respect angular accessibility constraints, with values approaching 1.0 indicating strong philosophical consistency.
The synthesis consistency metric evaluates the quality of temporal integration:
where ε > 0 prevents division by zero, means L2 norm and represents the expected synthesis result based on Augustinian temporal consciousness principles.
The integration with Phase 1 philosophical categories requires validation metrics that assess how well the STCNN processing reflects dynamic category evolution:
where the alignment function measures the correspondence between network processing patterns and philosophical category states:
where represents the vector encoding of network behavior related to category c, represents the current state vector of philosophical category c and represents the angle between the two vectors. High alignment values indicate that neural processing appropriately reflects philosophical category dynamics.
The integration with Phase 2 conceptual mapping requires validation that philosophical concepts maintain their essential relationships and semantic integrity through neural processing:
The relation preservation function measures how well original philosophical relationships are maintained after neural processing:
where λ > 0 controls the sensitivity to relationship distortion. Values near 1.0 indicate strong conceptual preservation, while values approaching 0 suggest significant semantic drift.
The computational efficiency of STCNN systems must account for the additional complexity introduced by complex-valued operations and temporal geometric constraints:
The effective temporal coverage measures the breadth of temporal space that the network can successfully navigate:
The processing quality function evaluates the network’s competency at different temporal positions:
where τ_threshold represents the minimum acceptable accuracy level, and the sigmoid function provides smooth quality transitions.
The computational cost metric accounts for the overhead of complex-valued operations and constraint enforcement:
where represent the number of real-valued operations, complex-valued operations, and constraint evaluations, respectively, with corresponding computational weight factors.
Specialized metrics assess the efficiency of memory and imagination processing pathways:
The temporal decay appropriateness factor ensures that memory processing exhibits philosophically appropriate forgetting patterns:
where is the measured memory decay rate and is the theoretically appropriate decay rate based on philosophical principles.
For imagination processing:
The creativity coherence factor measures whether generated concepts maintain semantic coherence while exhibiting genuine novelty:
The efficiency of Phase 1 and Phase 2 integration is assessed through specialized metrics that measure the computational overhead and benefits of unified processing:
This metric compares the performance improvement achieved through integration against the additional computational cost incurred.
A comprehensive benchmark suite validates STCNN performance on canonical philosophical problems that test different aspects of temporal-philosophical reasoning:
Temporal Paradox Resolution: Networks are evaluated on their ability to resolve temporal paradoxes while maintaining logical consistency. Test cases include variations of the grandfather paradox adapted for complex-time reasoning:


Ethical Reasoning Across Time: Networks are tested on their ability to make ethical judgments that appropriately balance historical context, present circumstances, and future consequences:

Human philosophers serve as ground truth for validating STCNN reasoning quality on complex philosophical problems:


Temporal consistency validation ensures that STCNN reasoning maintains coherence across different temporal perspectives on the same philosophical problem:


The optimization of STCNN hyperparameters requires specialized techniques that account for the complex-valued nature of the parameters and the philosophical constraints:


Complex-valued neural networks benefit from specialized learning rate schedules that account for the different convergence characteristics of real and imaginary components:


Specialized regularization techniques maintain philosophical consistency during training while preventing overfitting:



References
- Floridi, L.; Hähnel, M.; Müller, R. Applied philosophy of AI as conceptual design. In A Companion to Applied Philosophy of AI; Chapter 3; John Wiley & Sons: Hoboken, NJ, USA, 2025. [Google Scholar] [CrossRef]
- Al-Rodhan, N. Transdisciplinarity, neuro-techno-philosophy, and the future of philosophy. Metaphilosophy 2023, 54, 73–86. [Google Scholar] [CrossRef]
- Dey, A.K.; Abowd, G.D.; Salber, D. A conceptual framework and a toolkit for supporting the rapid prototyping of context-aware applications. Hum.-Comput. Interact. 2001, 16, 97–166. [Google Scholar] [CrossRef]
- Vernon, D.; Furlong, D. Philosophical foundations of AI. Lect. Notes Artif. Intell. 2007, 4850, 53–62. Available online: https://www.robotcub.org/misc/papers/07_Vernon_Furlong_AI50.pdf (accessed on 30 October 2024).
- Vadinský, O. Towards an Artificially Intelligent System: Philosophical and Cognitive Presumptions of Hybrid Systems. In Proceedings of the Fifth International Conference on Advanced Cognitive Technologies and Applications (COGNITIVE 2013), Valencia, Spain, 27 May–1 June 2013; pp. 97–100. [Google Scholar]
- Bechtel, W. Using computational models to discover and understand mechanisms. Stud. Hist. Philos. Sci. 2006, 37, 1–16. Available online: https://mechanism.ucsd.edu/bill/research/bechtel.Using%20Computational%20Models%20to%20Discover%20and%20Understand%20Mechanisms.finaldraft.pdf (accessed on 30 October 2024). [CrossRef] [PubMed]
- Langan, C. An introduction to mathematical metaphysics. Cosmos Hist. J. Nat. Soc. Philos. 2017, 13, 313–330. [Google Scholar]
- Dennett, D.C. Cognitive wheels: The frame problem of AI. Synthese 1983, 57, 1–15. [Google Scholar]
- Vila, L. A survey on temporal reasoning in artificial intelligence. AI Commun. 1994, 7, 4–28. [Google Scholar] [CrossRef]
- Salas-Guerra, R. Cognitive AI Framework: Advances in the Simulation of Human Thought. Ph.D. Thesis, AU University, AGM University, Washington, DC, USA, 2025. Available online: https://arxiv.org/pdf/2502.04259 (accessed on 30 October 2024).
- Dietrich, E. Thinking computers and the problem of intentionality. In Thinking Computers and Virtual Persons; Academic Press: Cambridge, MA, USA, 1994; pp. 3–34. [Google Scholar] [CrossRef]
- Giunchiglia, F.; Bouquet, P. Introduction to Contextual Reasoning: An Artificial Intelligence Perspective; Technical Report; FBK-IRST: Trento, Italy, 1997; Available online: https://cris.fbk.eu/handle/11582/1391 (accessed on 30 October 2024).
- Kim, J. The Layered Model: Metaphysical Considerations. Philos. Explor. 2002, 5, 2–20. [Google Scholar] [CrossRef]
- Anagnostopoulos, C.B.; Tsounis, A.; Hadjiefthymiades, S. Context awareness in mobile computing environments. Wirel. Pers. Commun. 2006, 42, 445–464. [Google Scholar] [CrossRef]
- Pham, S.T.H.; Sampson, P.M. The development of artificial intelligence in education: A review in context. J. Comput. Assist. Learn. 2022, 38, 1408–1421. [Google Scholar] [CrossRef]
- Dascal, M. Artificial intelligence and philosophy: The knowledge of representation. Syst. Res. 1989, 6, 39–52. [Google Scholar] [CrossRef]
- Ferrario, A. A trustworthiness-based metaphysics of artificial intelligence systems. In Proceedings of the 2025 ACM Conference on Fairness, Accountability, and Transparency (FAccT ’25), Athens, Greece, 23–26 June 2025; ACM: New York, NY, USA, 2025. [Google Scholar] [CrossRef]
- Prabakaran, M. Embodied and contextual intelligence: Towards a policy framework for higher education. High. Educ. Future 2024, 12, 10–26. [Google Scholar] [CrossRef]
- Fasiku, G.C. Metaphysics of numbers in Pythagorean philosophy and its influence on the development of algorithms in AI. APPON Philos. Q. 2024, 3, 99–108. [Google Scholar]
- Carruth, A.D.; Haanila, H.; Pylkkänen, P.; Telakivi, P. (Eds.) True Colors, Time After Time; Reports from the Department of Philosophy, Volume 52; University of Turku: Turku, Finland, 2024. [Google Scholar]
- Kinch, M.W.; Melis, W.J.C.; Keates, S. Reviewing the current state of machine learning for artificial intelligence with regards to the use of contextual information. In Proceedings of the Second Medway Engineering Conference on Systems, Chatham, UK, 6 June 2017; pp. 1–4. [Google Scholar]
- McClure, J. Conceptual parallels between philosophy of science and cognitive science: Artificial intelligence, human intuition, and rationality. Aporia 2014, 24, 39–49. [Google Scholar]
- De Miranda, L. Artificial intelligence and philosophical creativity: From analytics to crealectics. Hum. Aff. 2020, 30, 597–607. [Google Scholar] [CrossRef]
- Nguyen, M.N.H.; Pandey, S.R.; Thar, K.; Tran, N.H.; Chen, M.; Saad, W.; Hong, C.S. Distributed and democratized learning: Philosophy and research challenges. arXiv 2020, arXiv:2003.09301. [Google Scholar] [CrossRef]
- Bryndin, E.G. Implementation of competencies by smart ethical artificial intelligence in different environments. COJ Robot. Artif. Intell. 2021, 1, 1–8. [Google Scholar] [CrossRef]
- Thagard, P. (Ed.) Philosophy of Psychology and Cognitive Science; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Barnes, E.; Hutson, J. Exploring the cognitive sense of self in AI: Ethical frameworks and technological advances for enhanced decision-making. SSRG Int. J. Recent Eng. Sci. 2024, 11, 225–237. [Google Scholar] [CrossRef]
- Sheth, A.; Pallagani, V.; Roy, K. Neurosymbolic AI for enhancing instructability in generative AI. arXiv 2024, arXiv:2407.18722. [Google Scholar] [CrossRef]
- Velthoven, M.J.; Marcus, E.J. Problems in AI, their roots in philosophy, and implications for science and society. arXiv 2017, arXiv:2407.15671. [Google Scholar]
- Mussgnug, A.M. Technology as uncharted territory: Contextual integrity and the notion of AI as new ethical ground. arXiv 2025, arXiv:2412.05130. [Google Scholar]
- Iovane, G.; Iovane, G. From Generative AI to a novel Computational Wisdom for Sentient and Contextualized Artificial Intelligence through Philosophy: The birth of SOPHIMATICS. Appl. Sci. 2025; submitted. [Google Scholar]
- Iovane, G.; Iovane, G. A novel architecture for understanding, context adaptation, intentionality and experiential time in emerging post-generative AI through Sophimatics. Electronics, 2025; submitted. [Google Scholar]
- Iovane, G.; Iovane, G. Bridging computational structures with philosophical categories in Sophimatics and Data Protection Policy with AI Reasoning. Appl. Sci. 2025, 15, 10879. [Google Scholar] [CrossRef]
- Reggia, J.; Katz, G.; Davis, G. Artificial conscious intelligence. J. Artif. Intell. Conscious. 2020, 7, 181–198. [Google Scholar] [CrossRef]
- Clark, A. Embodied, embedded, and extended cognition. In The Cambridge Handbook of Cognitive Science; Frankish, K., Ramsey, W.M., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 275–291. [Google Scholar] [CrossRef]
- Besold, T.R.; d’Avila Garcez, A.S.; Bader, S.; Bowman, H.; Domingos, P.; Hitzler, P.; Kühnberger, K.U.; Lamb, L.C.; Lowd, D.; Lima, P.M.V.; et al. Neural-symbolic learning and reasoning: A survey and interpretation. arXiv 2017, arXiv:1711.03902. [Google Scholar] [CrossRef]
- Foerst, A. COG, a humanoid robot, and the question of the image of God. Zygon 1998, 33, 91–109. [Google Scholar] [CrossRef]
- Freed, J.L. Rethinking intentionality in the era of AI. In The Routledge Handbook of AI and Literature, 1st ed.; Routledge: Abingdon, UK, 2024; p. 9. [Google Scholar]
- Hollister, D.L.; Gonzalez, A.; Hollister, J. Contextual reasoning in human cognition and its implications for artificial intelligence systems. ISTE OpenScience 2019, 3, 1–18. [Google Scholar] [CrossRef]
- Hoerl, C.; McCormack, T. Thinking in and About Time: A Dual Systems Perspective on Temporal Cognition; Manuscript; Department of Philosophy, University of Warwick and School of Psychology, Queen’s University Belfast: Belfast, UK, 2019. [Google Scholar]
- Kakembo, A.A. The ethics of AI: Philosophical perspectives. Res. Invent. J. Res. Educ. 2025, 5, 65–71. [Google Scholar] [CrossRef]
- Kavalackal, R. Artificial intelligence: An anthropological and theological investigation. Asian Horiz. 2020, 14, 699–712. [Google Scholar]
- Kirchner, D.; Benzmüller, C.; Zalta, E.N. Computer science and metaphysics: A cross-fertilization. Open Philos. 2019, 2, 230–251. [Google Scholar] [CrossRef]
- Larghi, S.; Datteri, E. Mentalistic Stances Towards AI Systems: Beyond the Intentional Stance; Technical Report; RobotiCSS Lab, Laboratory of Robotics for the Cognitive and Social Sciences, Department of Human Sciences for Education, University of Milano-Bicocca: Milan, Italy, 2023. [Google Scholar]
- Morgan, A.; Piccinini, G. Towards a cognitive neuroscience of intentionality. Minds Mach. 2017, 27, 1–21. [Google Scholar] [CrossRef]
- Miyazaki, S. Algorhythmics: Understanding micro-temporality in computational cultures. Comput. Cult. 2012, 2, 1–9. [Google Scholar]
- Nuhn, H. Organizing for temporality and supporting AI systems: A framework for applied AI and organization research. Lect. Notes Inform. (LNI) 2021, 1135, 1135–1147. [Google Scholar]
- Sloman, A. The Computer Revolution in Philosophy; The Harvester Press: Brighton, UK, 1978. [Google Scholar]
- Steedman, M. Temporality. In Handbook of Logic and Language; van Benthem, J., ter Meulen, A., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 895–938. [Google Scholar] [CrossRef]
- Wedel, K. Contextual Memory Intelligence: A Foundational Paradigm for Human-AI Collaboration and Reflective Generative AI Systems. Ph.D. Thesis, Franklin University, Columbus, OH, USA, 2025. Available online: https://arxiv.org/pdf/2506.05370 (accessed on 30 October 2024).
- Wheeler, B. Computer simulations in metaphysics: Possibilities and limitations. Manuscrito Rev. Int. Fil. 2019, 42, 108–148. [Google Scholar] [CrossRef]
- Yang, X.; Lin, Y.; Liu, R.; Dong, J.S. Temporality spatialization: A scalable and faithful time-travelling visualization for deep classifier training. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence (IJCAI-22), Vienna, Austria, 23–29 July 2022; pp. 4022–4028. [Google Scholar]
- Zhu, J. Intentional Systems and the Artificial Intelligence (AI) Hermeneutic Network: Agency and Intentionality in Expressive Computational Systems. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2009. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; Available online: https://arxiv.org/abs/1412.6572 (accessed on 30 October 2024).
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar] [CrossRef]
- Sommer, R.; Paxson, V. Outside the closed world: On using machine learning for network intrusion detection. In Proceedings of the 2010 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 16–19 May 2010; pp. 305–316. [Google Scholar] [CrossRef]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Yao, A.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (SFCS 1986), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural ordinary differential equations. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 2–8 December 2018; pp. 6572–6583. [Google Scholar]
- Trabelsi, C.; Bilaniuk, O.; Zhang, Y.; Serdyuk, D.; Subramanian, S.; Santos, J.F.; Mehri, S.; Rostamzadeh, N.; Bengio, Y.; Pal, C.J. Deep complex networks. In Proceedings of the International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, M.; Li, X.; Wang, S. Adversarial attacks on deep learning based network intrusion detection systems: A survey. Comput. Secur. 2022, 121, 102847. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Wu, X.; Jha, S.; Swami, A. Distillation as a defense to adversarial perturbations against deep neural networks. In Proceedings of the 2016 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 22–26 May 2016; pp. 582–597. [Google Scholar] [CrossRef]
- Shokri, R.; Shmatikov, V. Privacy-preserving deep learning. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 1310–1321. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial examples in the physical world. In Proceedings of the International Conference on Learning Representations (ICLR) Workshop, Toulon, France, 24–26 April 2017. [Google Scholar] [CrossRef]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling tabular data using conditional GAN. In Proceedings of the 33rd International Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 7335–7345. [Google Scholar]
- d’Avila Garcez, A.; Lamb, L.C. Neurosymbolic AI: The 3rd wave. Artif. Intell. Rev. 2023, 56, 12387–12406. [Google Scholar] [CrossRef]
- Lample, G.; Charton, F. Deep learning for symbolic mathematics. In Proceedings of the International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).