Electricity Package Recommendation Integrating Improved Density Peaks Clustering and Fuzzy Group Decision-Making
Abstract
1. Introduction
2. Methods
2.1. Multi-Attribute Customer Decision-Making System Establish
2.1.1. Establishment of User Profiling and Labeling System
2.1.2. Similar User Identification Based on IDPC
2.2. Electricity Tariff Satisfaction Evaluation Based on Dynamic Fuzzy Group Decision
2.2.1. Integration of Heterogeneous User Evaluation Information Based on Trapezoidal Fuzzy Numbers
2.2.2. Determination of Group Decision Weights Based on Dynamic Assignment
- 1.
- Determination of User Weights Based on the Minimum Proximity Method.
- 2.
- Determination of Attribute Weights Based on the Maximum Deviation Method.
- 3.
- Determination of Time Weights Based on Subjective–Objective Integration.
2.2.3. Comprehensive Evaluation of Package Satisfaction Based on MCRM
2.3. Package Recommendation Based on Satisfaction of Similar User Groups
3. Results
3.1. Introduction to the Arithmetic Example
3.2. Analysis of User Clustering Results
3.3. Performance Evaluation of the Electricity Package Recommendation Method
3.3.1. Quantitative Assessment and Effectiveness Analysis of Recommendation Results
3.3.2. Comparison with Simulated Actual Choices
- Users sensitive to contract flexibility tend to prefer packages with shorter contract periods.
- When price differences are small, users pay more attention to the freedom of contract adjustments.
- Users with high quarterly electricity consumption are particularly sensitive to incentive discounts.
- The quality of value-added services has a greater impact on individual decision-making than minor price fluctuations (within ±0.05 CNY/kWh).
- Users with high load volatility value stability-related services, whereas users with low load volatility tend to prioritize cost-optimization services.
3.4. Algorithmic Complexity Analysis
3.5. Performance Comparison of Different Methods
3.5.1. Comparison of Clustering Algorithm Performance
3.5.2. Comparison of Recommendation Strategies
- Method 1: This method only uses group utility values as the evaluation criterion.
- Method 2: This method has no user clustering; recommendations are based directly on the average evaluations of all users.
- Method 3: This method employs equal weighting and does not differentiate attribute priorities dynamically.
- The comparison of Spearman correlation coefficients between these three methods and the proposed method is illustrated in Figure 7.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Set of electricity retail packages | |
| Set of evaluation attributes | |
| Set of all users | |
| The -th similar user group | |
| Learning factors for the PSO algorithm | |
| Cut-off distance for the DPC algorithm | |
| Quarterly electricity consumption of user | |
| Quarterly consumption volatility of user | |
| Quarterly load factor of user | |
| Average peak load ratio of user | |
| Average valley load ratio of user | |
| Inertia weight for the PSO algorithm | |
| Profile vector of user | |
| Trapezoidal fuzzy evaluation value | |
| Weight of user within a group | |
| Weight of evaluation attribute | |
| Weight of time period | |
| Fuzzy positive and negative ideal solutions for attribute | |
| Comprehensive compromise value of package in period | |
| Final comprehensive compromise value of package | |
| Individual regret value of package in period | |
| Group utility value of package in period | |
| Relative distance of user | |
| Local density of user |
References
- Wang, L. International Energy Agency: The outline of an “electrified world” is gradually becoming clear. China Energy News, 4 November 2024. [Google Scholar]
- Fotis, G.; Maris, T.I.; Mladenov, V. Risks, Obstacles and Challenges of the Electrical Energy Transition in Europe: Greece as a Case Study. Sustainability 2025, 17, 5325. [Google Scholar] [CrossRef]
- Anderson, E.; Ferris, M.; Philpott, A.; Anitescu, M.; Cramton, P.; Geng, S.; Green, R.; Homem-de-Mello, T.; Huber, O.; Leclère, V.; et al. Ten Challenges for Mathematical Modeling of the Green-Energy Transition. Curr. Sustain./Renew. Energy Rep. 2025, 12, 26. [Google Scholar] [CrossRef]
- Wang, M.; He, Y.; Lu, Y. Experience and enlightenment of retail electricity price package system design in Japan’s electricity market. J. North China Electr. Power Univ. (Soc. Sci. Ed.) 2021, 1, 48–55. [Google Scholar]
- Tokyo Electric Power Company Holdings, Inc. Available online: https://www.tepco.co.jp (accessed on 25 July 2025).
- Ye, Y.; He, Y.; Chen, F.; Liu, P. Development experience and enlightenment of retail electricity price package system in the UK. Electr. Power Demand Side Manag. 2020, 22, 97–100. [Google Scholar]
- Office of Gas and Electricity Markets (Ofgem). Available online: https://www.ofgem.gov.uk (accessed on 25 July 2025).
- He, Y.; Chen, F.; Ye, Y.; Liu, P.; Gao, X. Experience and enlightenment of retail electricity price packages in the Australian market. Smart Power 2019, 47, 19−23+28. [Google Scholar]
- iSelect. Available online: https://www.iselect.com.au/energy/ (accessed on 25 July 2025).
- Wang, X.; Liu, C.; Wu, B.; Wang, W.; Sun, Y.; Peng, J.; Liu, X.; Zhang, K. Design strategy of electricity purchase and sale combination package based on the characteristics of electricity prosumers in power system. Processes 2024, 12, 2836. [Google Scholar] [CrossRef]
- Han, X. Research on Demand-Side Electricity Retail Operation Strategies Adapting to the New Electricity Market. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2023. [Google Scholar]
- Yang, T. Research on Electricity Sales Strategy for Users Participating in Ancillary Services. Master’s Thesis, Southeast University, Nanjing, China, 2023. [Google Scholar]
- Li, T. Research on Differentiated Pricing of Electricity Retail Packages. Master’s Thesis, North China Electric Power University, Beijing, China, 2023. [Google Scholar]
- Anvari, M.; Proedrou, E.; Schäfer, B.; Beck, C.; Kantz, H.; Timme, M. Data-driven load profiles and the dynamics of residential electricity consumption. Nat. Commun. 2022, 13, 4593. [Google Scholar] [CrossRef]
- Jin, L.; Spurlock, A.; Borgeson, S.; Fredman, D.; Hans, L.; Patel, S.; Todd-Blick, A. Load Shape Clustering Using Residential Smart Meter Data: A Technical Memorandum; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2016. [Google Scholar]
- Ma, Y.; Li, Q.; Chen, H.; Zhang, Z.; Lin, Z.; Yang, L. Recommendation method for electricity retail plan based on BLAP clustering and multigranular hesitant fuzzy sets. Autom. Electr. Power Syst. 2023, 47, 96–104. [Google Scholar]
- Yang, J.; Wang, G.; Pang, Z. Research on issues related to density peak clustering. J. Nanjing Univ. (Nat. Sci.) 2017, 53, 791–801. [Google Scholar]
- Gao, Z.; Du, K. Improved research based on particle swarm optimization algorithm. Value Eng. 2025, 44, 101–103. [Google Scholar]
- Aranganayagi, S.; Thangevel, K. Clustering categorical data using silhouette coefficient as a relocating measure. In Proceedings of the International Conference on Computational Intelligence and Multimedia Applications (ICCIMA 2007), Sivakasi, India, 13–15 December 2007; pp. 13–17. [Google Scholar]
- Jiang, L.; Liang, J.; Liu, X.; Xu, X. Research on the calculation method of flow through a control gate based on the PSO-SVM model. J. Yellow River Conserv. Technol. Inst. 2023, 35, 6–10. [Google Scholar]
- Wu, Y. Research on Multi-Attribute Group Decision-Making Method Based on Extended Triangular Fuzzy Numbers. Master’s Thesis, Xi’an Technological University, Xi’an, China, 2025. [Google Scholar]
- Zhang, L.; Ni, J. Order priority of interval intuitionistic fuzzy numbers and its application in group evaluation. Math. Pract. Theory 2023, 53, 223–231. [Google Scholar]
- Jin, W. Research on Multi-Attribute Decision-Making Methods Under Multi-Granularity Hesitant Fuzzy Language. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2024. [Google Scholar]
- Fei, T. Research on Multi-Attribute Group Decision-Making Method Based on Probabilistic Interval-Valued Hesitant Fuzzy Information. Master’s Thesis, Sichuan Normal University, Chengdu, China, 2025. [Google Scholar]
- Qi, C. Hybrid multi-attribute group decision-making method based on trapezoidal fuzzy MULTIMOORA. Stat. Decis. 2019, 35, 41–45. [Google Scholar]
- Chen, Y.; Xiao, H.; Xiong, C. Research on objective weighting method based on entropy function and maximizing deviation. Hoist. Convey. Mach. 2020, 7, 75–79. [Google Scholar]
- Zhang, S.; Zhang, M.; Chi, G. Scientific and technological evaluation model based on entropy weight method and its empirical research. Manag. J. 2010, 7, 34–42. [Google Scholar]
- Kishor, A.; Singh, A.K.; Pal, N.R. Orness measure of OWA operators: A new approach. IEEE Trans. Fuzzy Syst. 2014, 22, 1039–1045. [Google Scholar] [CrossRef]
- Yang, W.; Wu, Y. A new improvement method to avoid rank reversal in VIKOR. IEEE Access 2020, 8, 21261–21271. [Google Scholar] [CrossRef]
- Lin, P.; Dong, C.; Liu, P. Dynamic hybrid multi-attribute group decision making method based on trapezoidal fuzzy numbers. J. Hebei Univ. (Nat. Sci. Ed.) 2024, 44, 337–345. [Google Scholar]
- Bao, H.; Li, H.; Liu, T.; Ke, Q.; Zhang, J. A multi-attribute decision-making method for green product design based on P-hesitant fuzzy sets and VIKOR. Comput. Integr. Manuf. Syst. 2024, 30, 3492–3501. [Google Scholar]
- Yang, J.; Li, L. VIKOR method for dynamic disturbing fuzzy multi-attribute decision making. J. Neijiang Norm. Univ. 2024, 39, 32–38. [Google Scholar]
- Wang, B.; Yang, F.; Zhang, S. A method of electricity consumption behaviour clustering and pricing packages based on data mining. Inf. Syst. Signal Process. J. 2020, 5, 18–23. [Google Scholar] [CrossRef]
- Yu, D.; Xu, Y. A VIKOR-based method for group decision making with interval type-2 fuzzy numbers. Appl. Soft Comput. 2018, 63, 152–167. [Google Scholar]
- Jeong, H.C.; Jang, M.; Kim, T.; Joo, S.-K. Clustering of load profiles of residential customers using extreme points and demographic characteristics. Electronics 2021, 10, 290. [Google Scholar] [CrossRef]
- Cen, S.; Yoo, J.H.; Lim, C.G. Electricity pattern analysis by clustering domestic load profiles using discrete wavelet transform. Energies 2022, 15, 1350. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, J.; Guo, X. User behavior clustering and electricity package recommendation based on improved fuzzy c-means. IEEE Access 2019, 7, 124356–124365. [Google Scholar]

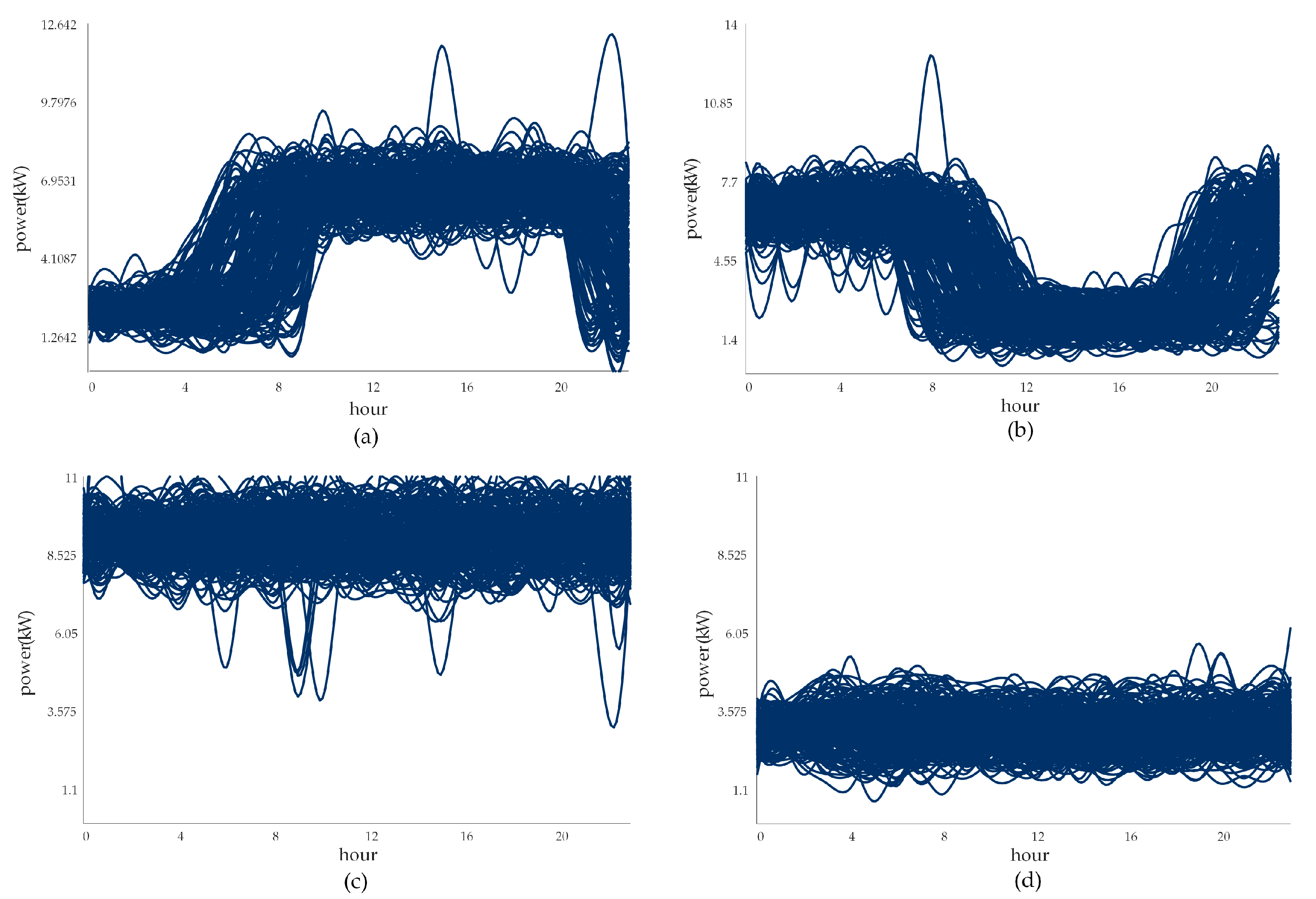


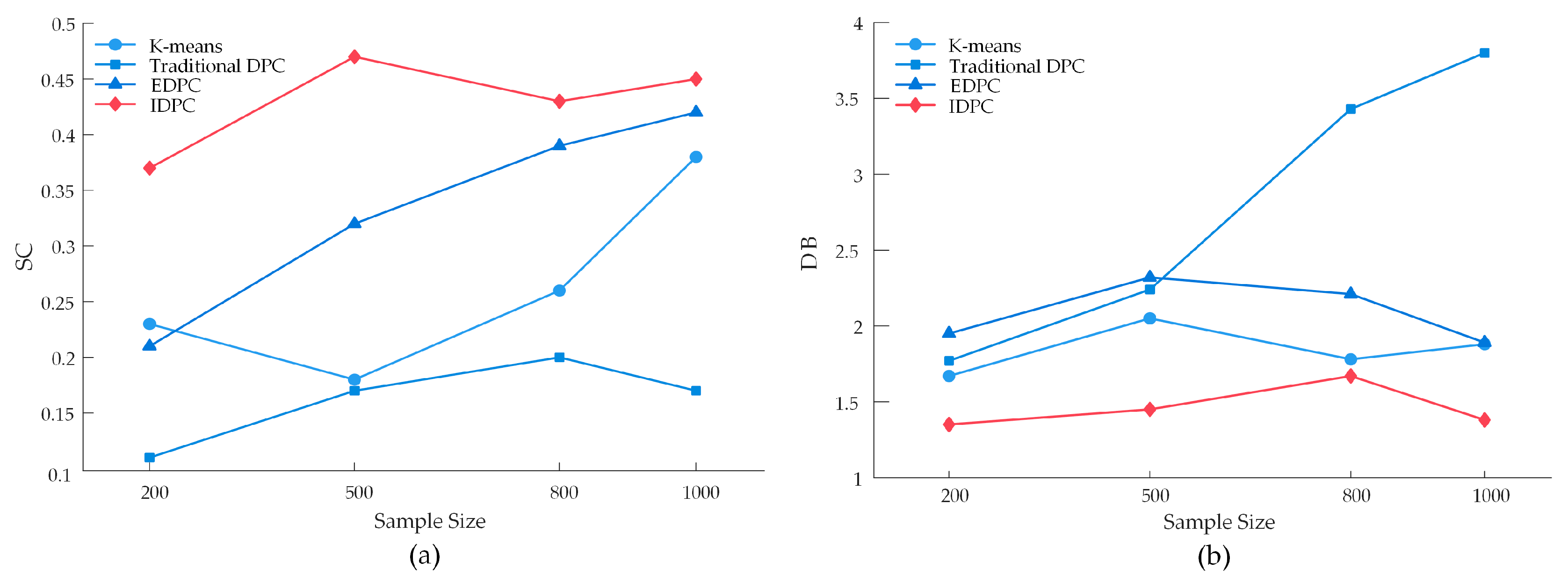
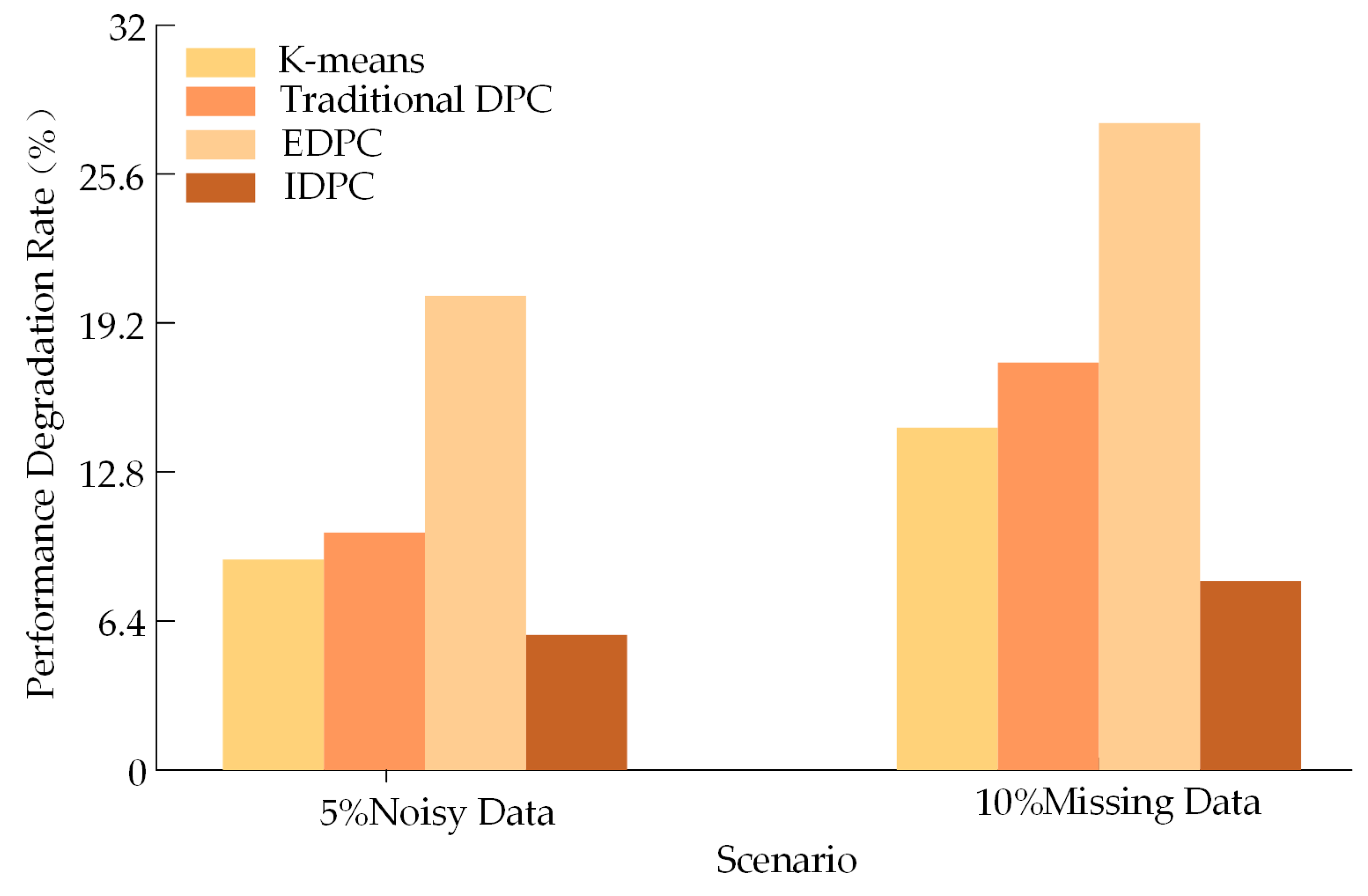
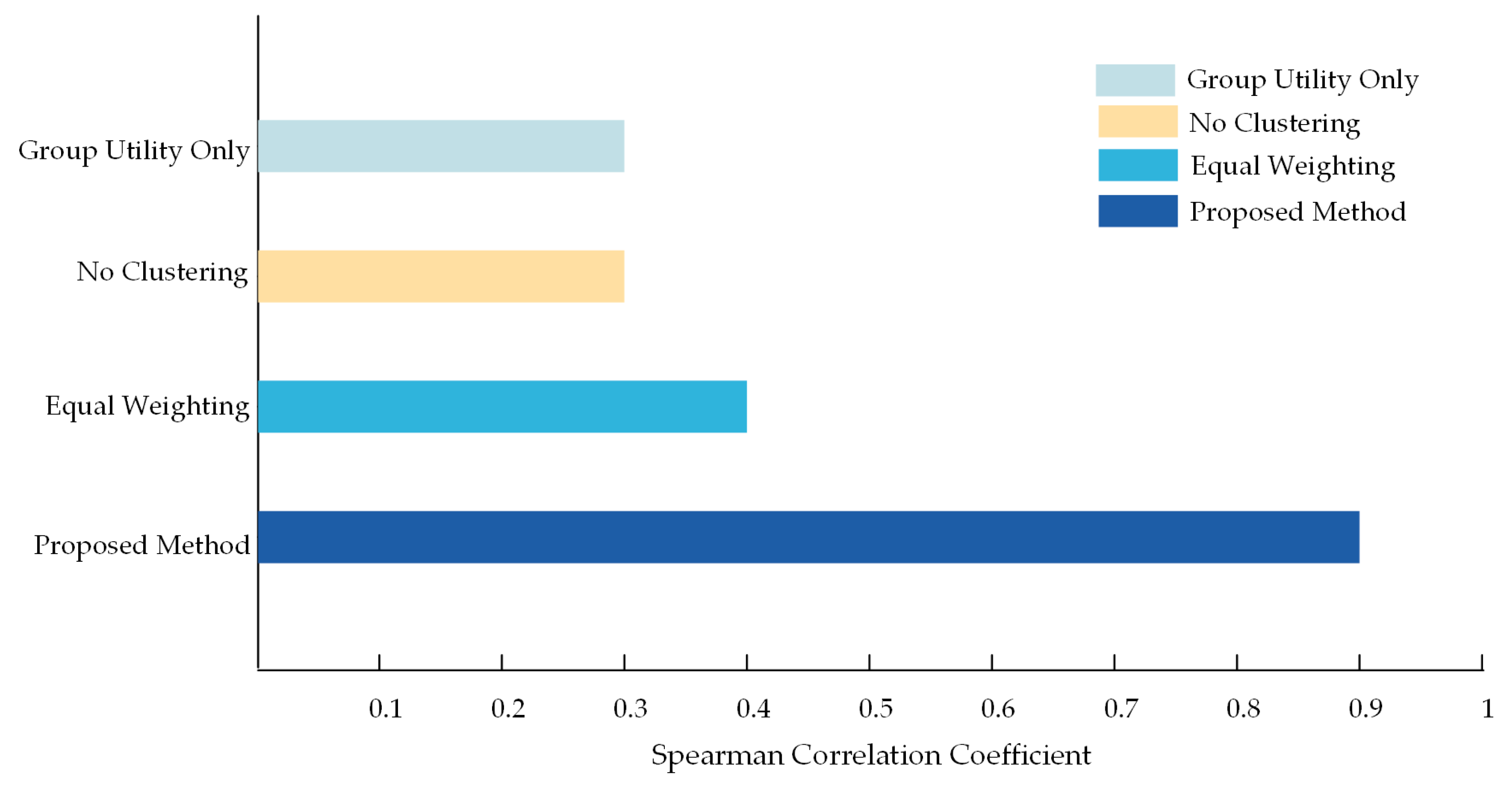
| Label | Definition | Physical Calculation Formula |
|---|---|---|
| Quarterly Electricity Consumption | Total energy consumption within a quarter | |
| Quarterly Consumption Volatility | Ratio of the standard deviation to the mean of the monthly average consumption within a quarter | |
| Quarterly Load Factor | Mean ratio of the average load to the maximum load within a quarter | |
| Average Peak Load Ratio | Mean ratio of the average peak-period load to the daily average load | |
| Average Valley Load Ratio | Mean ratio of the average valley-period load to the daily average load |
| Information Type | Original Form | Corresponding Trapezoidal Fuzzy Number |
|---|---|---|
| Real Number | ||
| Interval Number | ||
| Triangular Fuzzy Number | ||
| Intuitionistic Fuzzy Number | ||
| Interval Intuitionistic Fuzzy Number | ||
| Hesitant Fuzzy Linguistic Term | ||
| Binary Semantic |
| Package | Price/(CNY·(kW·h)−1) | Green Electricity Ratio (%) | Contract Flexibility | Value-Added Services | Incentive Discount (%) |
|---|---|---|---|---|---|
| A1 | 0.65 (0–200 kW·h) | 20 | Fixed for 1 year | Basic maintenance | 5 |
| 0.58 (201–500 kW·h) | |||||
| 0.55 (>501 kW·h) | |||||
| A2 | 0.65 (Peak: 8:00–22:00) | 65 | Fixed for 1 year | Quarterly inspection | 10 |
| 0.78 (Off-peak: 22:00–8:00) | |||||
| A3 | 0.72 (0–150 kW·h) | 35 | Flexible on demand | Basic maintenance | 10 |
| 0.70 (151–400 kW·h) | |||||
| 0.68 (>401 kW·h) | |||||
| A4 | 0.74 (Peak: 8:00–22:00) | 45 | Fixed for 6 months | Full-cycle maintenance | 12 |
| 0.62 (Off-peak: 22:00–8:00) | |||||
| A5 | 0.78 (0–150 kW·h) | 35 | Fixed for 1 year | Quarterly inspection | 15 |
| 0.65 (151–400 kW·h) | |||||
| 0.50 (>401 kW·h) |
| Rank | Package ID | Group Utility Value (S) | Individual Regret Value (R) | Compromise Value (Q) |
|---|---|---|---|---|
| 1 | A4 | 0.423 | 0.209 | 0.030 |
| 2 | A5 | 0.385 | 0.319 | 0.209 |
| 3 | A2 | 0.417 | 0.343 | 0.277 |
| 4 | A3 | 0.690 | 0.336 | 0.490 |
| 5 | A1 | 0.983 | 0.472 | 1.000 |
| Package ID | Model-Recommended Ranking | Simulated Actual Ranking |
|---|---|---|
| A4 | 1 | 1 |
| A5 | 2 | 2 |
| A2 | 3 | 4 |
| A3 | 4 | 3 |
| A1 | 5 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Zhou, Y.; Ma, Y. Electricity Package Recommendation Integrating Improved Density Peaks Clustering and Fuzzy Group Decision-Making. Appl. Sci. 2025, 15, 11875. https://doi.org/10.3390/app152211875
Jiang X, Zhou Y, Ma Y. Electricity Package Recommendation Integrating Improved Density Peaks Clustering and Fuzzy Group Decision-Making. Applied Sciences. 2025; 15(22):11875. https://doi.org/10.3390/app152211875
Chicago/Turabian StyleJiang, Xinyi, Yuxuan Zhou, and Yuanqian Ma. 2025. "Electricity Package Recommendation Integrating Improved Density Peaks Clustering and Fuzzy Group Decision-Making" Applied Sciences 15, no. 22: 11875. https://doi.org/10.3390/app152211875
APA StyleJiang, X., Zhou, Y., & Ma, Y. (2025). Electricity Package Recommendation Integrating Improved Density Peaks Clustering and Fuzzy Group Decision-Making. Applied Sciences, 15(22), 11875. https://doi.org/10.3390/app152211875





