Development of Deployable Reflector Antenna for the SAR Satellite: Part 4—Thermal Analysis-Assumed Orbital Environment Using Well-Correlated Antenna Assembly Model Based on Thermal Balance Test
Abstract
1. Introduction
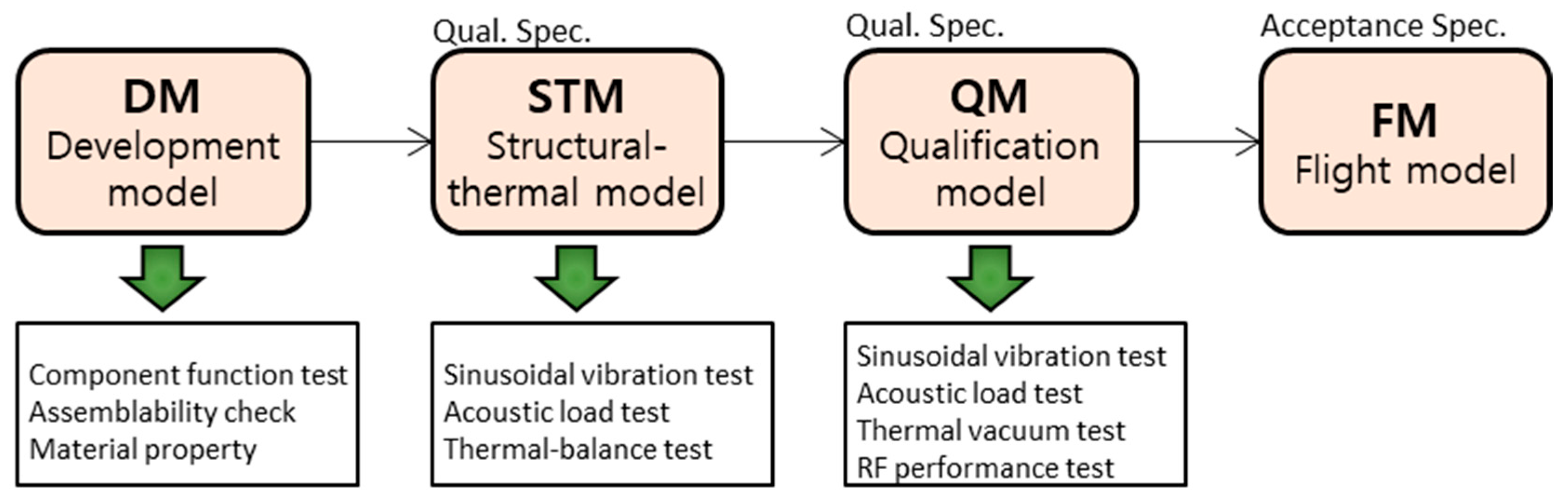
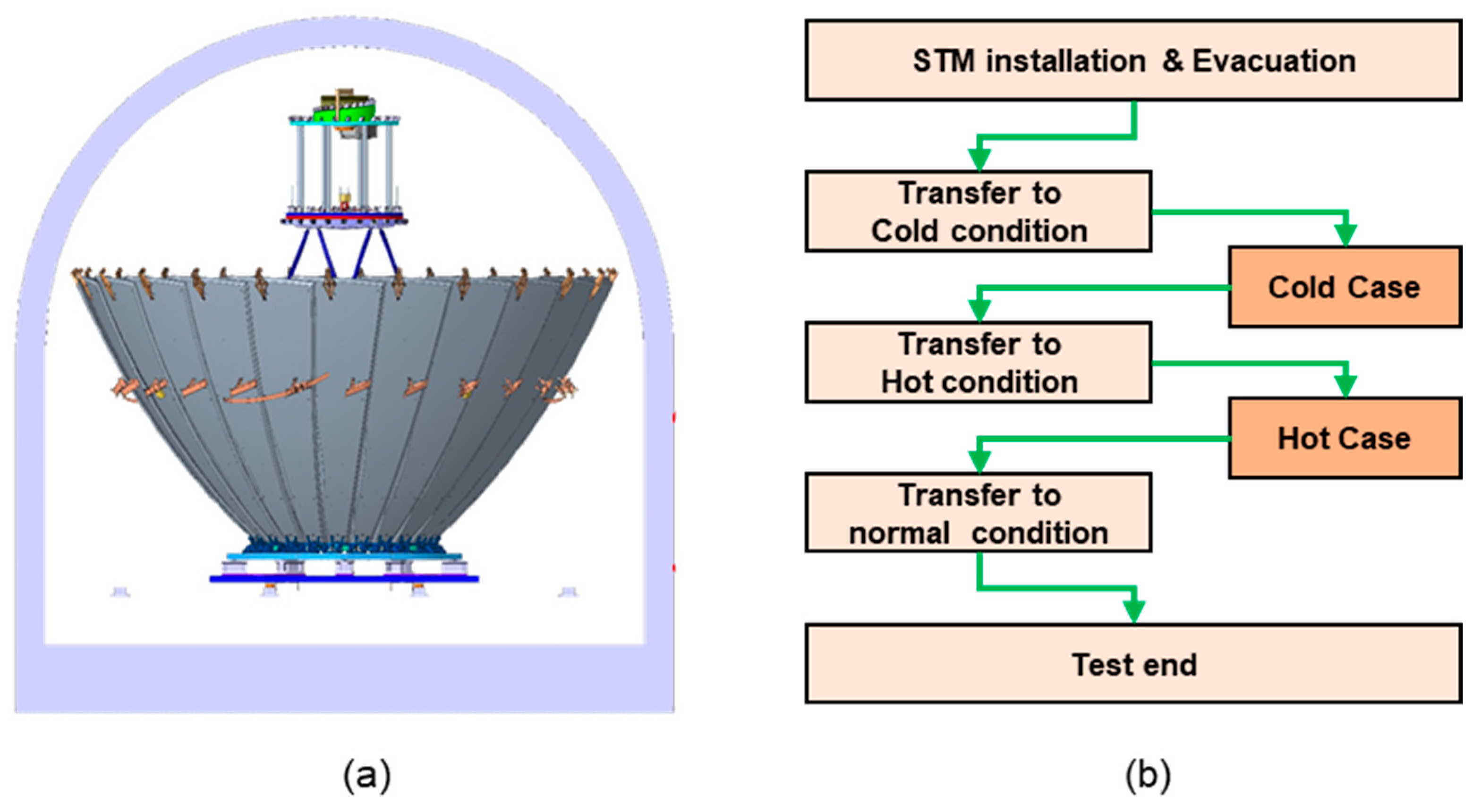
2. Thermal Balance Test of the Deployable Reflector Antenna on STM Phase
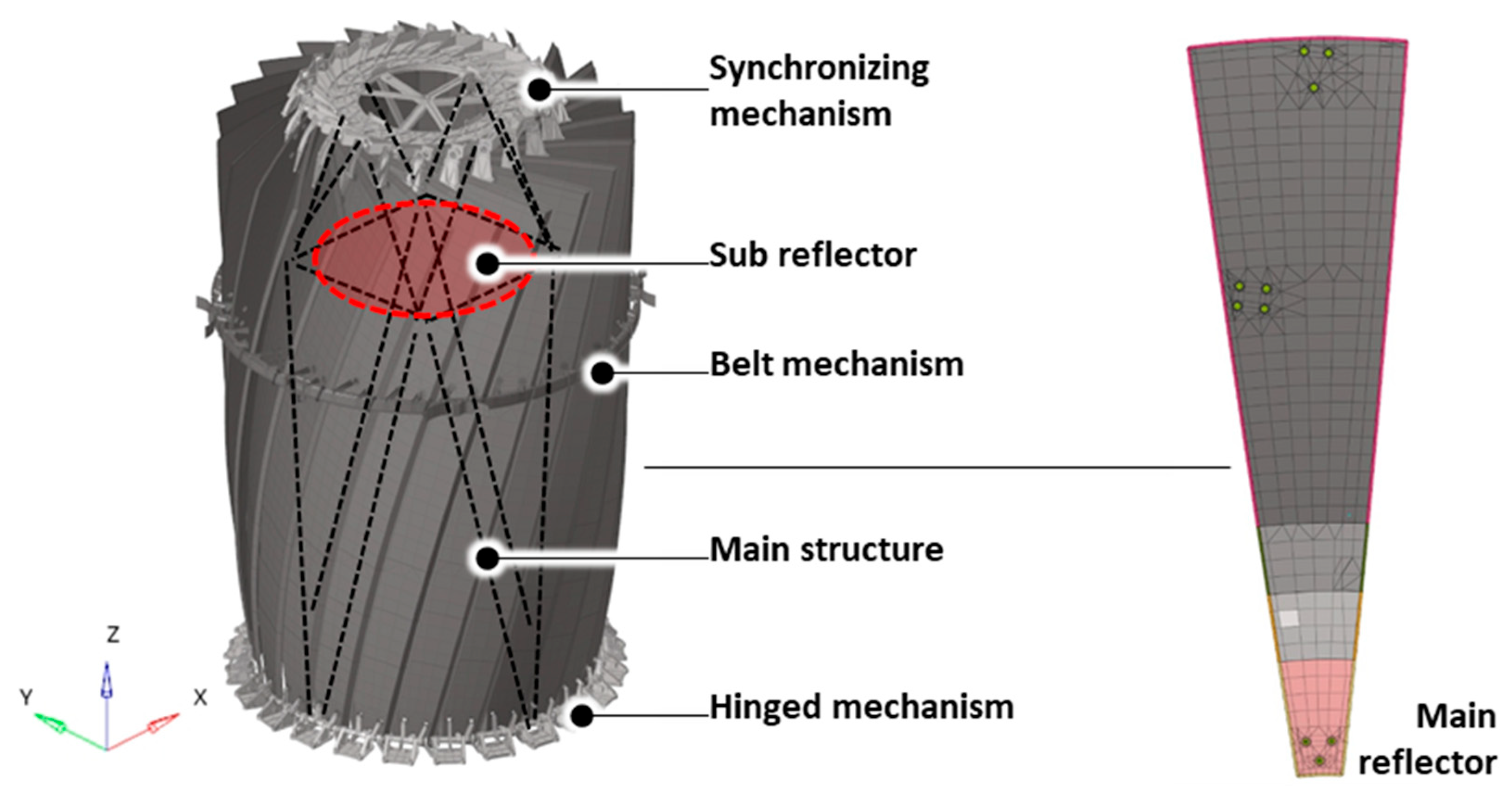
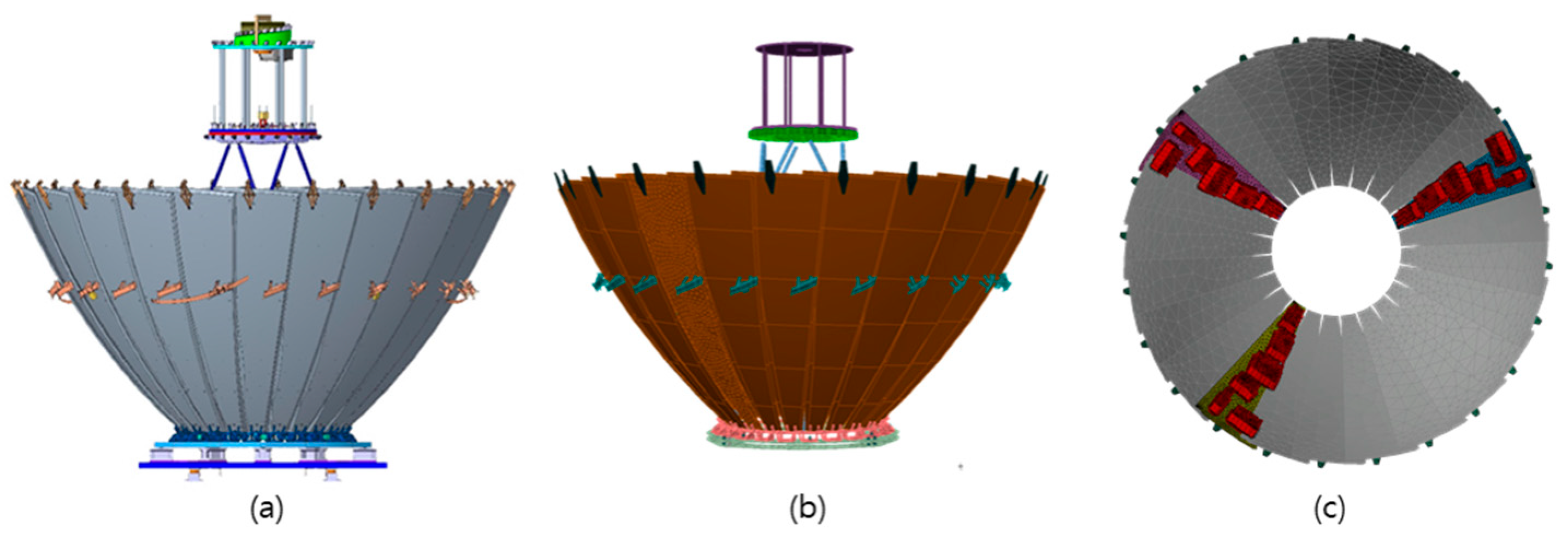
2.1. Configuration of the Deployable Reflector Antenna STM
2.2. Thermal Mathematical Model for the Thermal Balance Test
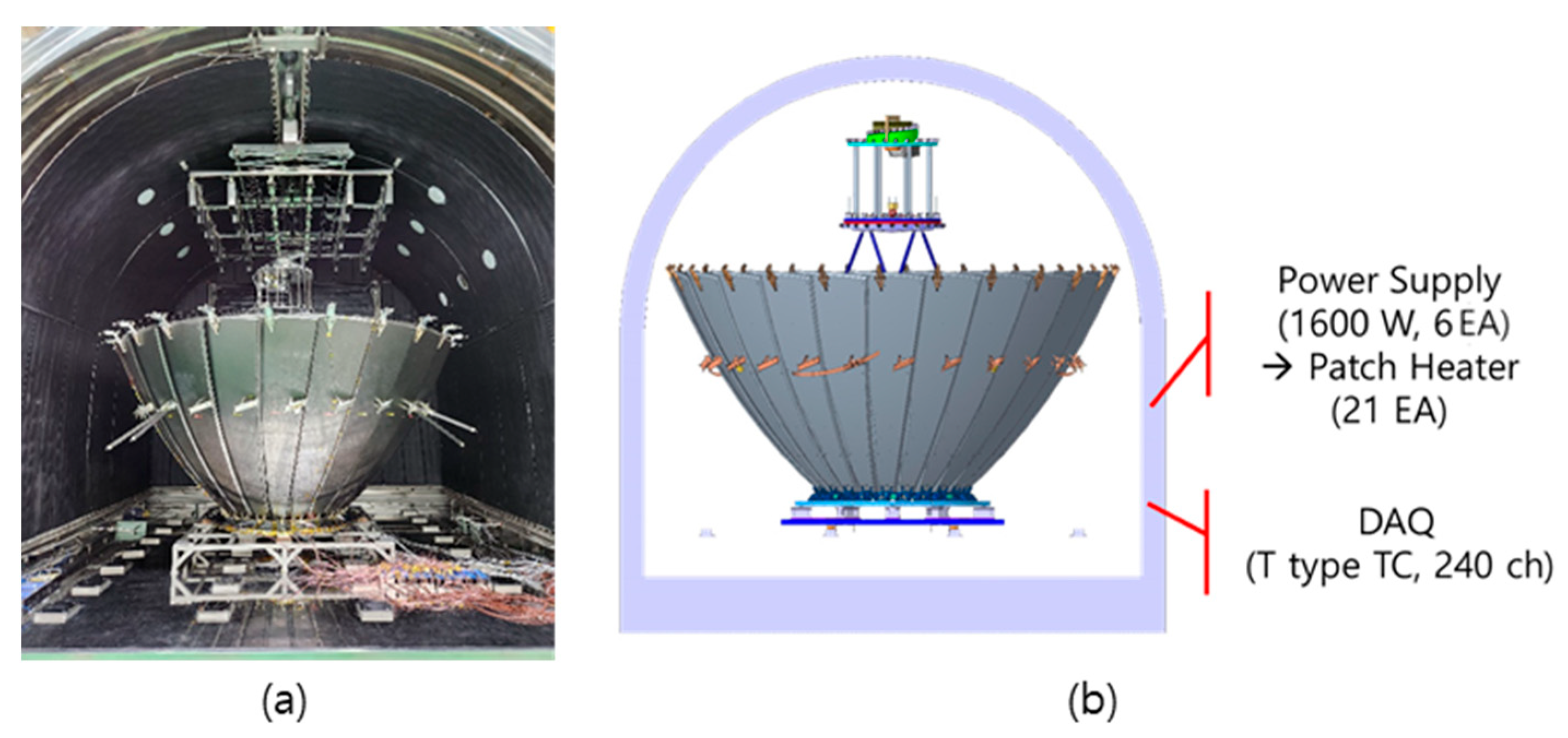
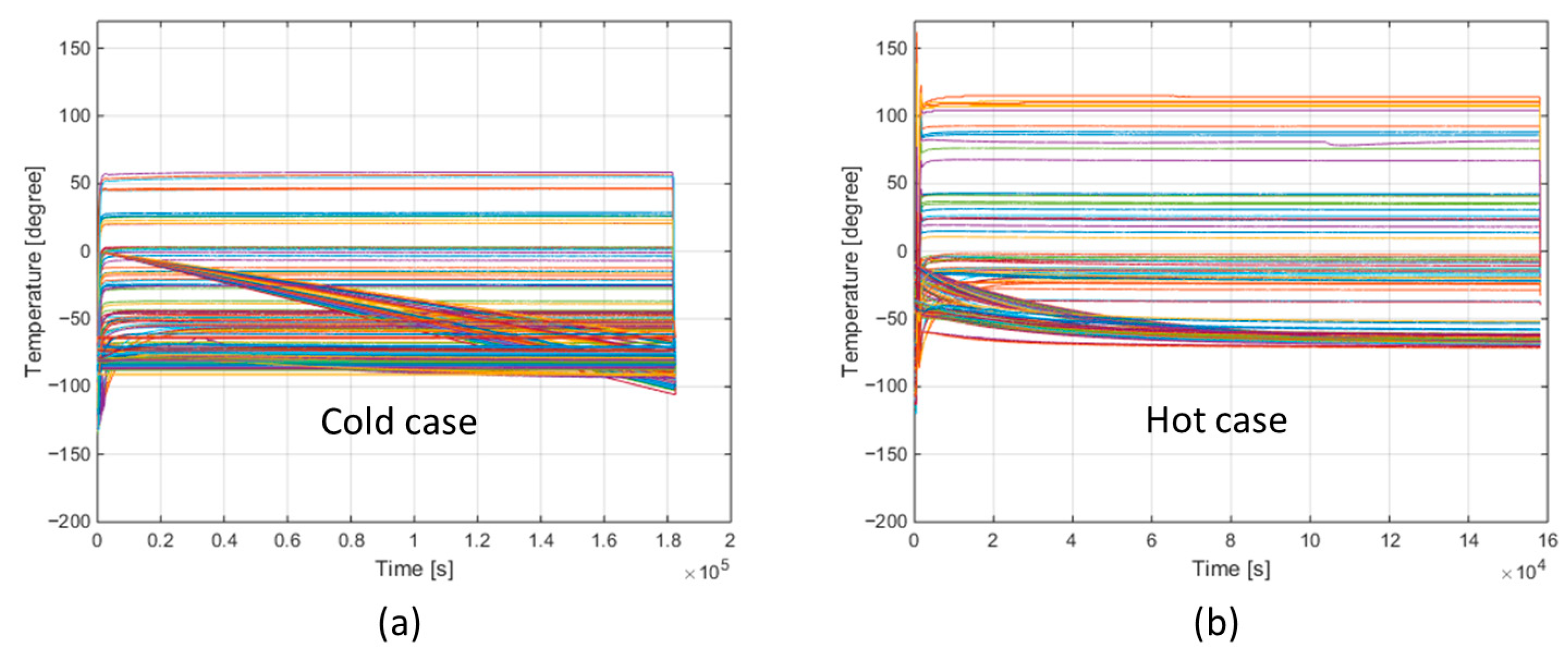
2.3. Thermal Balance Test
3. Thermal Mathematical Model Correlation and Thermal Analysis Assumed Orbital Environment
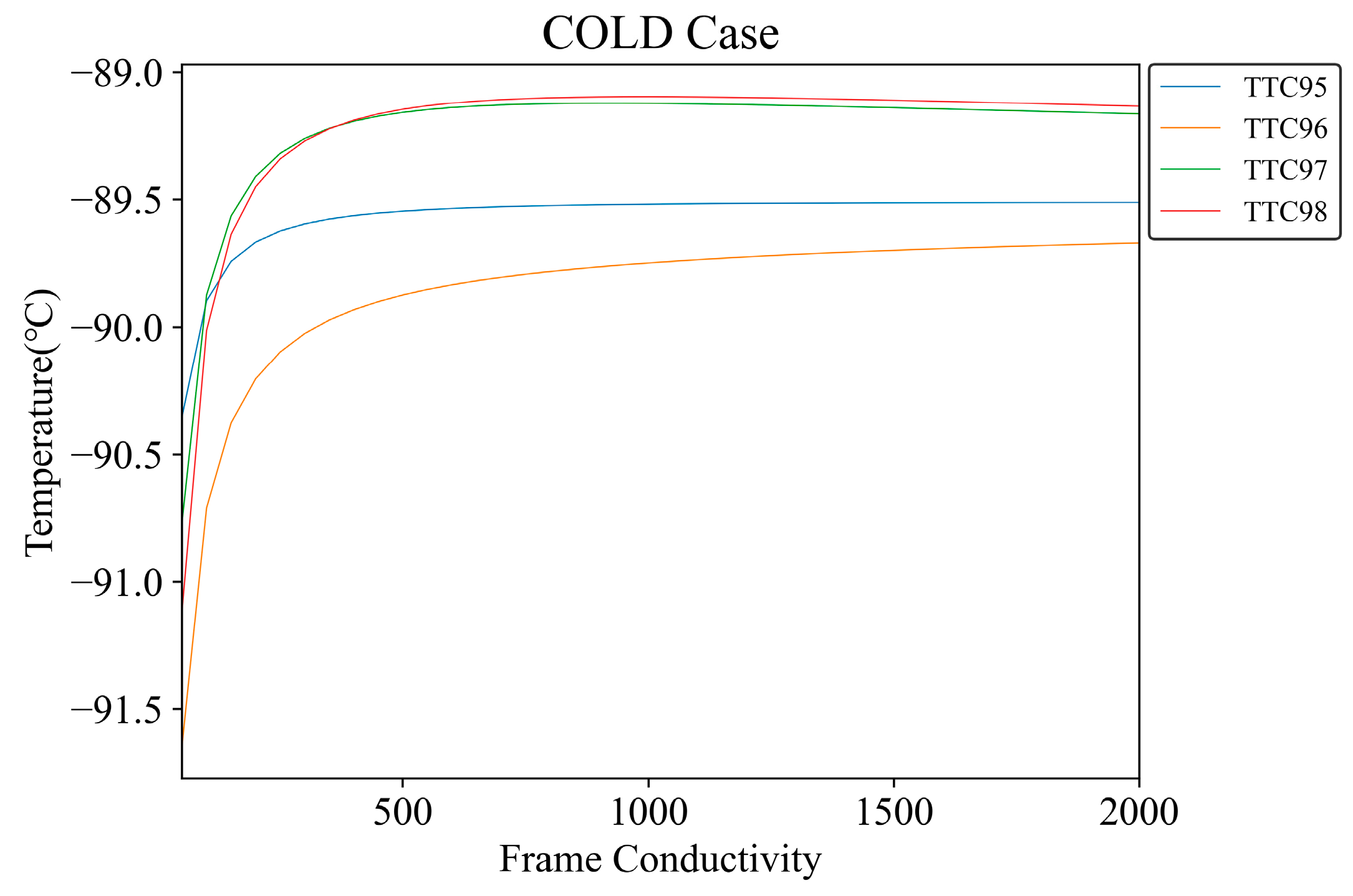
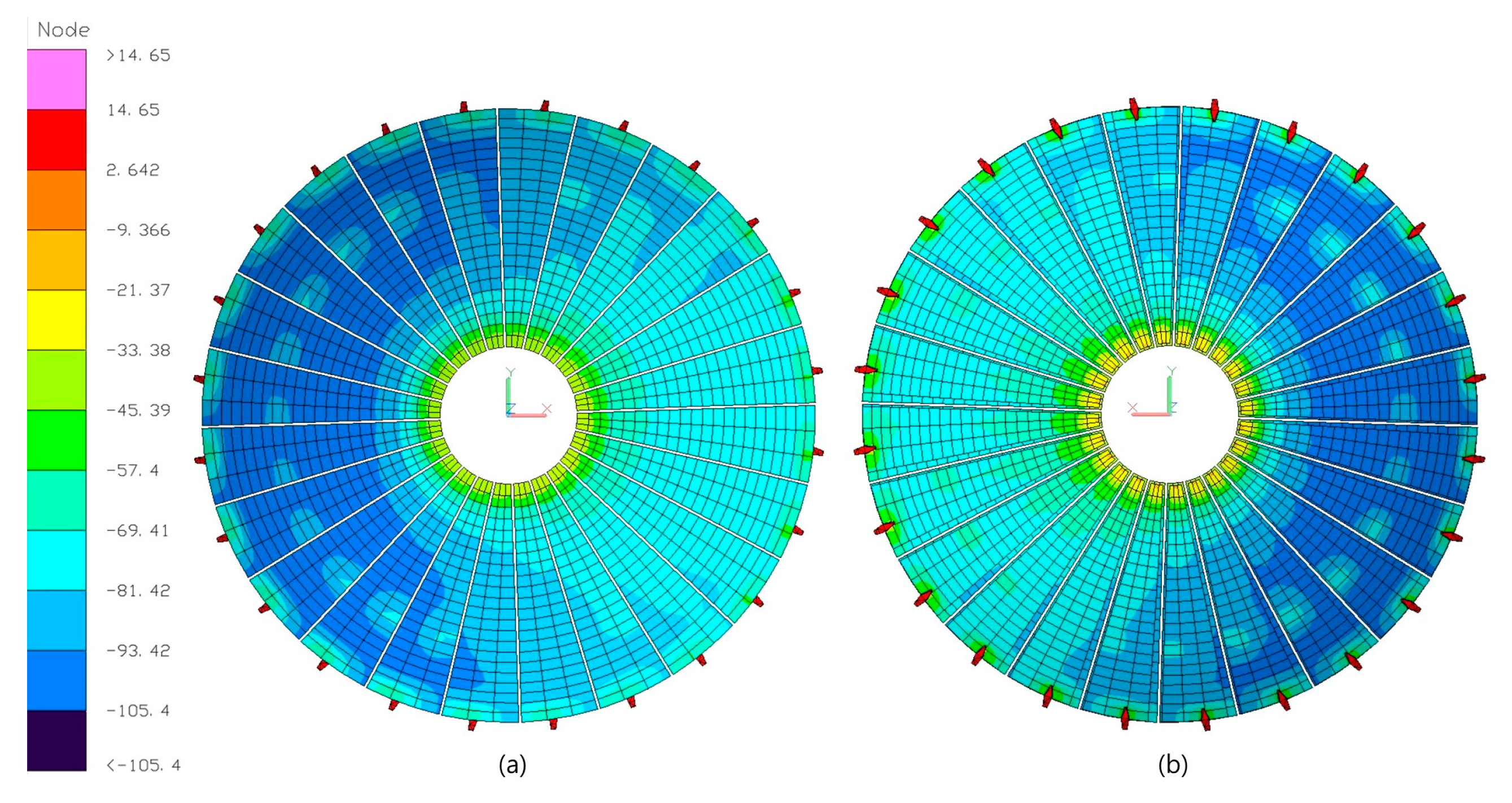
3.1. Thermal Mathematical Model Correlation
3.2. Thermal Analysis-Assumed Orbital Environment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Singh, P.; Diwakar, M.; Shankar, A.; Shree, R.; Kumar, M. A Review on SAR Image and its Despeckling. Arch. Comput. Methods Eng. 2021, 28, 4633–4653. [Google Scholar] [CrossRef]
- Castelletti, D.; Farquharson, G.; Stringham, C.; Duersch, M.; Eddy, D. Capella Space First Operational SAR Satellite. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Brussels, Belgium, 2021. [Google Scholar]
- Wijker, J. Random Vibrations in Spacecraft Structures Design: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 165. [Google Scholar]
- ECSS-E-ST-10-03C; ECSS Standard: Testing (31 May 2022). European Consortium for Space Standards: Noordwijk, The Netherlands, 2022. Available online: https://ecss.nl/standard/ecss-e-st-10-03c-rev-1-testing-31-may-2022/ (accessed on 30 July 2023).
- Howard, E.M. Faster, Better, Cheaper: Low-Cost Innovation in the U.S. Space Program; The Johns Hopkins University Press: Baltimore, MD, USA, 2003. [Google Scholar]
- Kim, H.; Kim, D.G.; Do, R.H.; Koo, K.R.; Yu, Y. Development of Deployable Reflector Antenna for the SAR-Satellite: Part 1. Design and Analysis of the Main Reflector Using Honeycomb Sandwich Composite Structure. Appl. Sci. 2024, 14, 1590. [Google Scholar] [CrossRef]
- Kim, D.G.; Kim, H.; Kim, D.Y.; Do, R.H.; Koo, K.R.; Yu, Y. Development of a Deployable Reflector Antenna for the Synthetic Aperture Radar Satellite, Part 2: Manufacturing and Qualification of the Main Reflector Using a Honeycomb Sandwich Composite Structure. Appl. Sci. 2024, 14, 11273. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.G.; Do, R.H.; Koo, K.R.; Yu, Y. Development of Deployable Reflector Antenna for the SAR-Satellite, Part 3: Environmental Test of Structural-Thermal Model. Appl. Sci. 2025, 15, 1436. [Google Scholar] [CrossRef]
- Hengeveld, D.; Moulton, J.; Tobin, D.; Vasas, R.; Nelson, E.; Liu, A.; Peabody, H. Reduced-order modeling for spacecraft thermal-structural applications. In Proceedings of the International Conference on Environmental Systems, St. Paul, MN, USA, 10–14 July 2022. No. ICES-2022-110. [Google Scholar]
- Hengeveld, D.; Biskner, A. Enhanced data exploration through Reduced-order models. In Proceedings of the 47th International Conference on Environmental Systems, Charleston, SC, USA, 16–20 July 2017. [Google Scholar]
- Hengeveld, D.; Moulton, J. Automatic creation of reduced-order models using Thermal Desktop. In Proceedings of the 48th International Conference on Environmental Systems, Albuquerque, NM, USA, 8–12 July 2018. [Google Scholar]
- Perellón, M.; Alvarez, R.; Petrini, P.; Sauer, A.; Dolce, S. Sentinel 1–spacecraft and SAR antenna thermal design, analysis, verification and flight performances. In Proceedings of the 45th International Conference on Environmental Systems (ICES), Bellevue, WA, USA, 12–16 July 2015. [Google Scholar]
- Park, T.Y.; Kim, S.Y.; Jung, H.Y.; Lee, J.E.; Yun, J.H.; Oh, H.U. Thermal design and analysis of unfurlable CFRP skin-based parabolic reflector for spaceborne SAR antenna. Int. J. Aeronaut. Space Sci. 2021, 22, 433–444. [Google Scholar] [CrossRef]
- Arora, J.S. Introduction to Optimum Design; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]



| H/W | Material Property [Thermo-Physical] | Conductivity [W/m/K] | Density [kg/m3] | Specific Heat [J/kg/K] |
|---|---|---|---|---|
| HM | Al-6061 T6 | 167 | 2700 | 896 |
| BM | ||||
| SM | ||||
| Subreflector | ||||
| Main reflector-SM bracket | ||||
| Main reflector | Main reflector | correlation target | 1700 | 830 |
| Baseplate | Baseplate | correlation target | 1900 | 732 |
| Lower strut | Strut | 210 | 1850 | 800 |
| Upper strut | ||||
| Frame | Frame | 155.6 | 1900 | 732 |
| H/W | Material Property [Optical] | Absorptivity (α) | Emissivity (ε) | α/ε |
|---|---|---|---|---|
| HM | Alodine | 0.350 | 0.100 | 3.500 |
| BM | ||||
| SM | ||||
| Subreflector | ||||
| Main reflector-SM bracket | ||||
| Main reflector | Main reflector | 0.910 | 0.800 | 1.138 |
| Baseplate | Baseplate | 0.920 | 0.746 | 1.233 |
| Lower strut | MLI | 0.040 | 0.005 | 8.000 |
| Upper strut | ||||
| Frame |
| Contact | Cold Case | Hot Case | |
|---|---|---|---|
| From | To | [W/K] | |
| Baseplate | HM | correlation target | |
| Baseplate | Lower strut | 0.076 | |
| HM | Main reflector | correlation target | |
| Lower strut | Frame | 0.076 | |
| Frame | Upper strut | 0.076 | |
| Frame | Subreflector | 0.002 | |
| Upper strut | SM | 0.308 | |
| SM | Wire holder | 7.402 | |
| Wire holder | Main reflector-SM Brk. | 0.018 | |
| Main reflector | Main reflector-SM Brk. | correlation target | |
| Main reflector | BM | correlation target | |
| Test Conditions | Qualification |
|---|---|
| Number of cycles | 1 |
| Temperature stabilization | 1 °C/5 h |
| Shroud temperature | <−180 °C |
| Vacuum level | <1 × 10−5 mbar |
| Temperature tolerance | ±1 °C |
| Material | Conductivity | Initial Value | Bounded Condition | Final Value (Cold/Hot) | |
|---|---|---|---|---|---|
| Lower Limit | Upper Limit | ||||
| Main reflector | In Plane [W/m/K] | a | a | 25 a | 14.2 a/17.8 a |
| Out Plane [W/m2/K] | b | b | 25 b | 10.9 b/17.9 b | |
| Baseplate | In Plane [W/m/K] | c | c | 25 c | 10.4 c/20.5 c |
| Out Plane [W/m2/K] | d | d | 10 d | 4.5 d/4.7 d | |
| Contact Pair | Heat Conduction Coefficient | Initial Value | Bounded Condition | Final Value (Clod/Hot) | ||
|---|---|---|---|---|---|---|
| From | To | Lower Limit | Upper Limit | |||
| Baseplate | HM | [W/K] | e | e | 25 e | 18.4 e/20.5 e |
| HM | Main reflector | [W/K] | f | f | 25 f | 2.7 f/3.1 f |
| Main reflector | Main reflector-SM Brk. | [W/K] | g | g | 25 g | g/g |
| Main reflector | BM | [W/K] | h | h | 25 h | 3.7 h/3.7 h |
| Material Property [Thermo-Physical] | Cold Case | Hot Case | ||
|---|---|---|---|---|
| k [W/m/K] | h [W/m2/K] | k [W/m/K] | h [W/m2/K] | |
| Main reflector | 14.2 a | 10.9 b | 17.8 a | 17.9 b |
| Baseplate | 10.4 c | 4.5 d | 20.5 c | 4.7 d |
| Contact Pair | Cold Case | Hot Case | |
|---|---|---|---|
| From | To | h [W/K] | |
| Baseplate | HM | 18.4 e | 20.5 e |
| Main reflector | HM | 2.7 f | 3.1 f |
| Main reflector | Main reflector-SM Brk. | g | g |
| Main reflector | BM | 3.7 h | 3.7 h |
| H/W | Material Property [Thermo-Physical] | Conductivity [W/m/K] | Density [kg/m3] | Specific Heat [J/kg/K] |
|---|---|---|---|---|
| HM | A-6061 T6 | 167 | 2700 | 896 |
| HRBM | ||||
| SM | ||||
| Subreflector | ||||
| Main reflector-SM bracket | ||||
| Main reflector | Main reflector | (a) | 28 (b) | 1420 (b) |
| Baseplate | Baseplate | (a) | 32 (b) | 904 (b) |
| Lower strut | Strut | 210 | 1850 | 800 |
| Upper strut | ||||
| Frame | Frame | 155.6 | 1900 | 732 |
| MLI | MLI | (c) | 350 | 860 |
| Temperature [°C] | Conductivity [W/m/K] |
|---|---|
| −150 | 2.95 × 10−5 |
| −100 | 3.36× 10−5 |
| −50 | 5.04 × 10−5 |
| 0 | 7.36 × 10−5 |
| 50 | 10.6 × 10−5 |
| 75 | 12.6 × 10−5 |
| 100 | 15 × 10−5 |
| H/W | Material Property [Optical] | Absorptivity (α) | Emissivity (ε) | α/ε |
|---|---|---|---|---|
| HM | Alodine | 0.350 | 0.100 | 3.500 |
| HRBM | ||||
| SM | ||||
| Subreflector | ||||
| Main reflector-SM bracket | ||||
| Main reflector | Main reflector | 0.910 | 0.800 | 1.138 |
| Baseplate | Baseplate | 0.920 | 0.746 | 1.233 |
| Lower strut | MLI | 0.040 | 0.005 | 8.000 |
| Upper strut | ||||
| Frame | ||||
| Solar Panel(in/out) | Solar Panel | 0.940/0.920 | 0.880/0.800 | 1.068/1.150 |
| FAA Module | White Trim | 0.400 | 0.800 | 0.500 |
| FAA Module | Black Paint | 0.900 | 0.920 | 0.978 |
| FAA Housing |
| Component | Operating Temperature | Predict Temperature | Pass/Fail | |||
|---|---|---|---|---|---|---|
| Min [°C] | Max [°C] | Min [°C] | Max [°C] | Min [°C] | Max [°C] | |
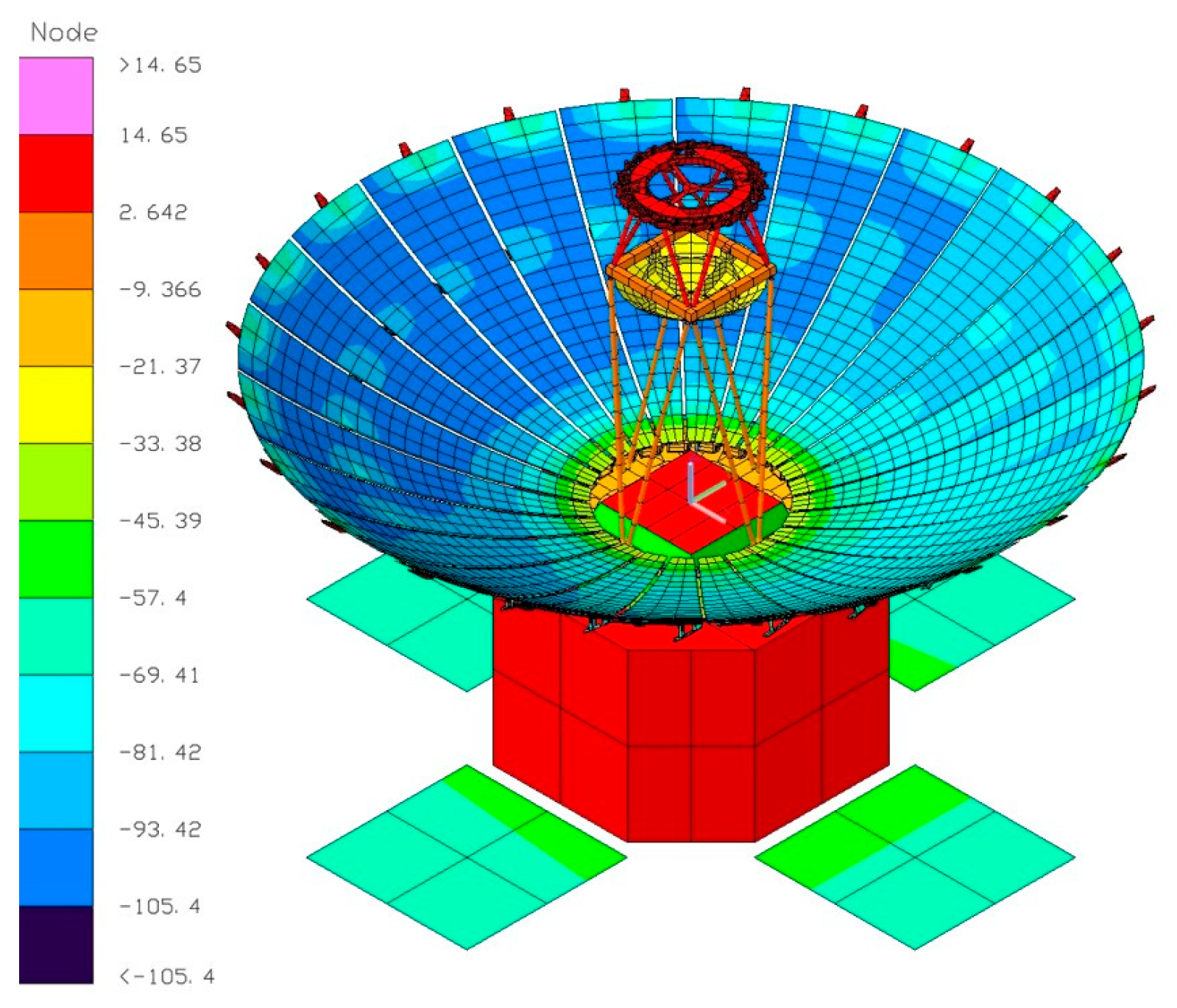
| Main reflector | a | a + 300 | −105.43 | 109.69 | PASS | PASS |
| Strut | b | b + 260 | −12.86 | 6.51 | PASS | PASS |
| Subreflector | c | c + 330 | −30.84 | −7.17 | PASS | PASS |
| SM | d | d + 220 | 5.37 | 6.93 | PASS | PASS |
| HM | e | e + 65 | −12.99 | −0.42 | PASS | PASS |
| Baseplate | f | f + 300 | −12.86 | −0.32 | PASS | PASS |
| Component | Operating Temperature | Predict Temperature | Pass/Fail | |||
|---|---|---|---|---|---|---|
| Min [°C] | Max [°C] | Min [°C] | Max [°C] | Min [°C] | Max [°C] | |
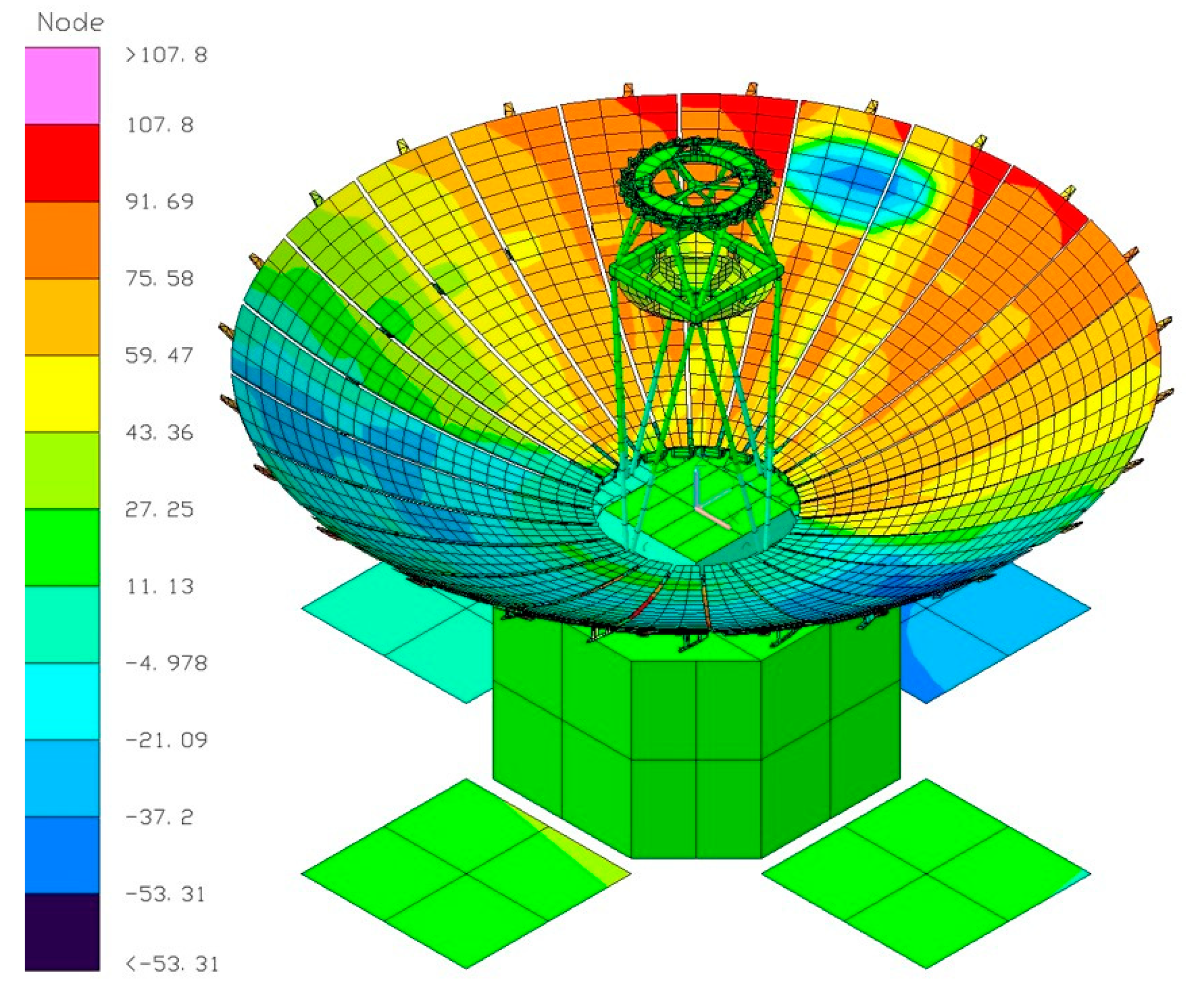
| Main reflector | a | a + 300 | −80.70 | 108.12 | PASS | PASS |
| Strut | b | b + 260 | 2.47 | 19.31 | PASS | PASS |
| Subreflector | c | c + 330 | −1.84 | 66.45 | PASS | PASS |
| SM | d | d + 220 | 18.20 | 18.87 | PASS | PASS |
| HM | e | e + 65 | 2.31 | 16.43 | PASS | PASS |
| Baseplate | f | f + 300 | 2.47 | 17.96 | PASS | PASS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, R.-H.; Kim, H.-G.; Kim, D.-G.; Koo, K.-R. Development of Deployable Reflector Antenna for the SAR Satellite: Part 4—Thermal Analysis-Assumed Orbital Environment Using Well-Correlated Antenna Assembly Model Based on Thermal Balance Test. Appl. Sci. 2025, 15, 11766. https://doi.org/10.3390/app152111766
Do R-H, Kim H-G, Kim D-G, Koo K-R. Development of Deployable Reflector Antenna for the SAR Satellite: Part 4—Thermal Analysis-Assumed Orbital Environment Using Well-Correlated Antenna Assembly Model Based on Thermal Balance Test. Applied Sciences. 2025; 15(21):11766. https://doi.org/10.3390/app152111766
Chicago/Turabian StyleDo, Ryoon-Ho, Hyun-Guk Kim, Dong-Geon Kim, and Kyung-Rae Koo. 2025. "Development of Deployable Reflector Antenna for the SAR Satellite: Part 4—Thermal Analysis-Assumed Orbital Environment Using Well-Correlated Antenna Assembly Model Based on Thermal Balance Test" Applied Sciences 15, no. 21: 11766. https://doi.org/10.3390/app152111766
APA StyleDo, R.-H., Kim, H.-G., Kim, D.-G., & Koo, K.-R. (2025). Development of Deployable Reflector Antenna for the SAR Satellite: Part 4—Thermal Analysis-Assumed Orbital Environment Using Well-Correlated Antenna Assembly Model Based on Thermal Balance Test. Applied Sciences, 15(21), 11766. https://doi.org/10.3390/app152111766







