Abstract
This article focuses on the problem of building a real-world predictive maintenance system for hydraulic piston pumps. Particular attention is given to the issue of limited data availability regarding the failure state of systems with a damaged valve plate. The main objective of this work was to analyze the impact of imbalanced data on the quality of the failure prediction system. Several data balancing techniques, including oversampling, undersampling, and combined methods, were evaluated to overcome the limitations. The dataset used for evaluation includes recordings from eleven sensors, such as pressure, flow, and temperature, registered at various points in the hydraulic system. It also includes data from three additional vibration sensors. The experiments were conducted with imbalance ratios ranging from 0.5% to a fully balanced dataset. The results indicate that two methods, Borderline SMOTE and SMOTE+Tomek Links, dominate. These methods allowed the system to achieve the highest performance on a completely new dataset with different levels of damaged valve plates, for the balance rate larger than three percent. Furthermore, for balance rates below one percent, the use of data balancing methods may adversely affect the model. Finally, our results indicate the limitations of the use of cross-validation procedures when assessing data balancing methods.
1. Introduction
In recent years, the integration of artificial intelligence and machine learning into industrial operations has revolutionized how companies manage their assets. A primary focus of this transformation is predictive maintenance, a strategy that utilizes advanced analytics to detect impending component failures by continuously monitoring operational data [1]. The ability to forecast equipment issues before they occur is critical to minimizing downtime and maximizing productivity.
The industrial landscape is heavily dependent on the performance and reliability of hydraulic systems, which are foundational to heavy machinery in sectors such as metal processing, construction, and mining. The failure of a hydraulic component, such as a piston pump, can severely compromise the stability of a production process. The economic impact of such events often far outweighs the cost of the component itself. A notable example is the failure of a pump in a coal mine’s long-wall shearer, where a component worth hundreds of euros led to an estimated economic loss in the range of hundreds of thousands of euros.
One of the causes of failure is, for example, contamination of the working fluid (oil). This is often due to improper maintenance (e.g., a lack of or delayed filter replacement) or improper filling of oil tanks (oil not at the required purity level, errors in start-up procedures, etc.). Another factor accelerating wear or failure is the fact that many hydraulic systems are still built without sensors monitoring oil temperature. As a result, the oil overheats, which has many unfavorable consequences. First, at elevated temperatures, the kinematic viscosity of the oil becomes approximately two times lower compared to its nominal viscosity. For ISO VG 46 oil, whose nominal viscosity at 40 °C is 46 cSt, at 60 °C its kinematic viscosity is approximately 20 cSt. As a result, in heavily loaded systems, this can lead to the degrading phenomenon of cavitation in pump components.
This stark imbalance between component cost and failure cost powerfully demonstrates the immense value of accurate predictive failure models.
One of the main challenges for the large-scale implementation of machine learning methods in industrial settings is the availability of training data that adequately describes both normal (operational) and failure states. While collecting data from an operational system under normal conditions is typically straightforward, obtaining sufficient data representing actual failure events is rarely accessible or common. This asymmetry in class distribution presents a major difficulty for the training process. Specifically, the training data is highly imbalanced, characterized by a dominating majority class (the normal state) and only a few available samples representing the minority class (the failure state). Such an imbalanced distribution makes machine learning models challenging to train and prone to inaccurate classification.
In this work, we evaluate various methods designed to overcome these difficulties in building an accurate model for recognizing valve plate failures in a piston pump. As discussed in detail in the following section, numerous approaches exist to handle imbalanced classification [2]. Among these, data-level methods are particularly important. These methods offer the advantage of easily extending current classification systems by introducing an additional preprocessing step, thus avoiding direct modification of the already operational classification algorithm. Therefore, our research focuses specifically on this family of techniques.
This work serves as a direct continuation of our previous research presented in [3], which established a foundational understanding of the system. In that prior study, we evaluated several prediction methods and analyzed the necessity of flow, temperature, and pressure sensors required to achieve high prediction accuracy. Crucially, however, our previous work addressed a balanced classification problem, a scenario that is not representative of real-world pump operating conditions.
The existing literature concerning imbalanced classification for failure prediction methods often provides only a general overview of popular techniques [2]. Furthermore, although many methods and approaches have been developed for piston pump failure prediction, none of them specifically address the problem of imbalanced classification while accounting for the nonlinearities and dynamic characteristics typical of these devices.
Therefore, this study aims to address this critical gap by investigating the factors influencing prediction performance under imbalanced conditions. Specifically, this research is dedicated to answering the following research questions:
- How does the amount of pump failure data (i.e., the imbalance rate) influence prediction performance?
- Which data-level balancing method is most suitable for dealing with unbalanced classification in the context of valve plate failure prediction?
- What are the inherent limitations associated with the use of data-level balancing methods?
- How do data-level strategies influence the knowledge extracted from the data compared to the knowledge extracted from a fully balanced dataset?
All analyses are conducted on data collected under laboratory conditions for a piston pump. Four states were simulated: one normal state and three failure states with different levels of valve plate degradation. In addition to classical sensors for pressure, temperature, and flow, the collected data includes basic vibration sensor data, such as vibration speed (in accordance with the ISO 20816-3 standard [4]).
The remainder of the manuscript is organized as follows. First, we present the current state of the art in piston pump failure prediction and in dealing with imbalanced data. Section 3 then describes the experimental setup, including the data collection procedure, the machine learning pipeline, and the metrics used. Finally, in Section 4, the obtained results are presented and discussed. The last section, Section 5, summarizes our findings and outlines future research directions.
2. Related Work
This research addresses two independent aspects: the problem of piston pump predictive maintenance and the issue of imbalanced classification. Each of these topics is considered separately below, with a focus on recent progress in each respective field.
2.1. Imbalanced Data Classification
The problem of building effective prediction models for imbalanced data is a long-standing challenge in machine learning, and numerous methods have been developed to address it. These approaches can be broadly classified into three main categories [2]:
- 1.
- Data-Level Methods The first group of methods focuses on direct modification of the dataset before it is used to train a model. These techniques can be further divided into three sub-groups: undersampling, oversampling, and hybrid methods.
- UndersamplingUndersampling techniques aim to reduce the number of samples in the majority class to match the number of samples in the minority class. While simple random undersampling involves the random removal of majority samples, more sophisticated methods have been developed to make the process more strategic. These methods are typically based on nearest neighbor analysis. Among the most popular are the Edited Nearest Neighbor (ENN) algorithm [5] and the Tomek Links algorithm [6]. The ENN algorithm does not guarantee a perfectly balanced dataset, but it effectively removes noisy and border samples. It works by examining each majority class sample and marking it for removal if it is incorrectly classified by its k nearest neighbors from the entire training set. Tomek Links operates differently, also eliminating border samples from the majority class. It begins by identifying “Tomek Links,” which are pairs of samples from two opposite classes that are each other’s nearest neighbors (e.g., A is the nearest neighbor of B, and B is the nearest neighbor of A). After identifying such links, all majority class samples involved are removed, thereby cleaning the border between the classes. These methods have also served as a foundation for other techniques, such as RIUS [7], which focuses on retaining the most relevant majority samples while discarding the rest.
- OversamplingThese methods focus on increasing the number of samples in the minority classes. This can be achieved naively by sampling with replacement until a desired number of samples is reached. However, many more intelligent methods have been developed, most notably the SMOTE family of algorithms [8]. The basic concept behind SMOTE involves generating new synthetic samples by randomly selecting a minority class sample (sample A), then randomly selecting one of its k nearest neighbors (sample B) from the same class, and placing the new sample at a random position on the line segment connecting A and B. The SMOTE family has undergone rapid development, with advancements such as Borderline SMOTE [9,10], k-means SMOTE [11], and SMOTE with approximate nearest neighbors [12], which all focus on generating samples in crucial border areas. Another popular oversampling method is based on Adaptive Synthetic Sampling (ADASYN) [13,14]. The idea behind ADASYN is to shift the learning algorithm’s focus toward difficult minority instances that lie near the decision boundary. It works similarly to SMOTE but first identifies these hard-to-classify minority samples, and then generates a greater number of new samples to strengthen their representation.
- Hybrid MethodsHybrid methods combine oversampling and undersampling, often by applying these two processing steps sequentially. Examples include SMOTE with Tomek Links [15] or SMOTE with ENN [16], as well as combinations with other undersampling methods.
- 2.
- Algorithm-Level Methods This group consists of algorithm-level modifications that make the learning model more sensitive to the minority class without physically altering the dataset itself. The most standard approach within this category is cost-sensitive learning, which utilizes class weights or instance weights within the cost function minimized during model training. Many popular models provide direct parameters for this purpose. For instance, models such as XGBoost [17], LightGBM [15], and Support Vector Machines (SVMs) [18] allow users to prioritize the minority class by adjusting class weights or modifying the cost function. These instance weights can be set statically or allowed to evolve dynamically during the training process. Some authors propose the use of meta-models that create an additional internal sub-model to learn how to adapt sample weights, as suggested by Shu et al. [19]. Another example of algorithm-level modification is gradient adaptation, where gradients—instead of sample weights—are re-scaled proportionally to the class imbalance [20]. This technique allows for a proportional update of the neuron weights during training, effectively biasing the learning process towards the minority class.
- 3.
- Ensemble Methods Ensemble methods build prediction models by combining multiple submodels into a single, robust model. Each submodel is trained on balanced or nearly balanced data. A popular member of this group is the Bagging-Based Ensemble where each submodel is trained on a downsampled minority class [21]. A good example of this method is the Balanced Random Forest algorithm. This method adapts the standard Random Forest by building a training set for each tree in the forest through balanced undersampling and oversampling, ensuring each individual tree is trained on a more balanced subset of the data [22]. Additionally, Boosting-Based Ensembles, such as AdaBoost [23] or XGBoost [17], often inherently handle imbalanced data by re-weighting training samples as explained in the previous paragraph.
2.2. Machine Learning in Failure Prediction
Machine learning techniques are still developing in many fields, including predicting failures in power hydraulic devices. In addition to classic classification methods such as KNN and decision trees, simple and deep neural networks are also used.
The literature compares classic machine learning algorithms, including SVM, KNN, and gradient boosted trees [24].
Nevertheless many authors have emphasized artificial neural networks (ANNs), multilayer perceptrons (MLPs), or convolutional neural networks (CNNs). Article [25] describes an example of using a neural network, particularly a convolutional neural network. Another approach, also based on the use of a convolutional neural network, is described in [26,27]. In the presented research, pressure, vibration, and acoustic signals are used as input data for prediction. In [28], the researchers describe a deep learning method that uses a Bayesian optimization (BO) algorithm to find the best model hyperparameters. In this paper, the vibration signal of a piston pump is used as a data source. CWT preprocesses the signal, and then a preliminary CNN model is prepared. Finally, a Gaussian-based BO was used to prepare an adaptive CNN model (CNN-BO). Another solution, based on the use of RBF neural networks combined with noise filtering algorithms and vibration diagnostics, is presented in [29].
However, we see that classic machine learning algorithms are dominating techniques in this area. Examples of using a modified KNN algorithm, combined with the just-in-time learning (JITL) principle, can be found to determine the remaining useful life (RUL) [30]. This method was applied to hydraulic pumps, taking into account pressure measurements. The authors of [29,31] also use the term RUL in conjunction with a Bayesian regularized radial basis function neural network (Trainbr-RBFNN) when studying an external gear pump, or modified auto-associative kernel regression (MAAKR) and monotonicity-constrained particle filtering (MCPF) while working with a piston pump. Remaining useful life is also studied in [32] using the autoregressive integrated moving average (ARIMA) forecasting method. The subject of the study was a reciprocating pump, for which leak volume was considered an important parameter for predicting the remaining service life. Another publication [33] describes the application of a method based on empirical wavelet transform (EWT), principal component analysis (PCA), and extreme learning machine (ELM) to analyze vibration sensor data.
Hybrid approaches are also presented. One of hybrid predictive maintenance models was proposed in [34]. This paper focuses on a solution that combines improved complete empirical mode decomposition with adaptive noise (ICEEMDAN), principal component analysis (PCA), and a least squares support vector machine (LSSVM). The model is optimized by combining the coupled simulated annealing and Nelder–Mead simplex optimization algorithms (ICEEMDAN-PCA-LSSVM). The proposed technique was compared with three established methods [linear discriminant analysis (LDA), support vector machine (SVM), and artificial neural network (ANN)] with multiclass classification capabilities.
In another paper [35] presenting research on axial piston pumps, a transfer learning method for fault severity recognition was proposed. This method is based on adversarial discriminative domain adaptation combined with a convolutional neural network (CNN). Similarly to [28], this paper also describes research using the vibration signal as data for ML techniques.
Finally, article [36] provides a review of the recent literature, where the authors present condition monitoring systems based on various machine learning (ML) techniques.
The fields of imbalanced classification and pump failure prediction have largely developed independently. To the best of the authors’ knowledge, the specific challenge of tackling imbalanced classification in piston pump failure prediction has not been directly covered in the existing literature. However, many researchers have addressed imbalanced classification in various other areas of fault diagnosis or predictive maintenance.
For instance, in [15], the authors evaluated SMOTE, Tomek Links, and a combined SMOTE+Tomek Links approach alongside three popular classification methods (kNN, Naive Bayes, and SVM) for condition monitoring of a wound-rotor induction generator. Their results indicated that the combination of SMOTE+Tomek Links with kNN yielded the best performance. Another study concerning fault diagnostics with imbalanced data was presented in [37], where the authors proposed integrating SMOTE with the Easy Ensemble algorithm. This combined solution was evaluated on two distinct datasets related to wind turbine failure forecasting, and the results demonstrated that the proposed method outperformed all other techniques when using XGBoost as the base classifier. More recent research concerning class imbalance in predictive maintenance within the automotive industry was presented in [38]. The authors compared various techniques, including basic SMOTE, cost-sensitive learning, and ensemble methods, finding that the integration of multiple imbalance-handling techniques delivered superior performance. The only study identified that uses oversampling techniques specifically in the context of hydraulic pumps is [39], where the authors applied the SMOTE technique for the life estimation of a hydraulic pump. However, this work focused on remaining useful life estimation (RUL) using accumulated damage theory rather than addressing a classification problem.
3. Experiment Setup
The experimental design was structured into three distinct stages, each addressing an independent research objective.
The first stage was designed to demonstrate the impact of class imbalance on prediction performance. Experiments were conducted with varying imbalance rates, where we evaluate how the number of available samples from the failure state influences classification performance. The obtained results establish a lower bound for the second stage of experiments, where a dataset balancing mechanism was employed to improve prediction performance. The second stage is dedicated to a comparative analysis of various data-level modification methods. We analyze the impact of different undersampling, oversampling, and hybrid methods on prediction performance. The final stage focuses on an analysis of the model’s internal structure and how the behavior of particular models changes when faced with insufficient data. This last step is analyzed by assessing feature importance analysis.
Below, we provide a detailed description of all elements used in the experiments.
3.1. Test Bench
To obtain data for training and testing the predictive models, a laboratory environment was built based on a variable displacement piston pump. An HSP10VO45DFR pump with a nominal displacement of 45 cm3/rev. was used. Pumps of this type are often used in industrial and mobile hydraulic systems. A detailed description of the test stand construction is presented in [3], and here only a simplified model is presented showing the hydraulic diagram Figure 1 explaining which parameters were recorded.
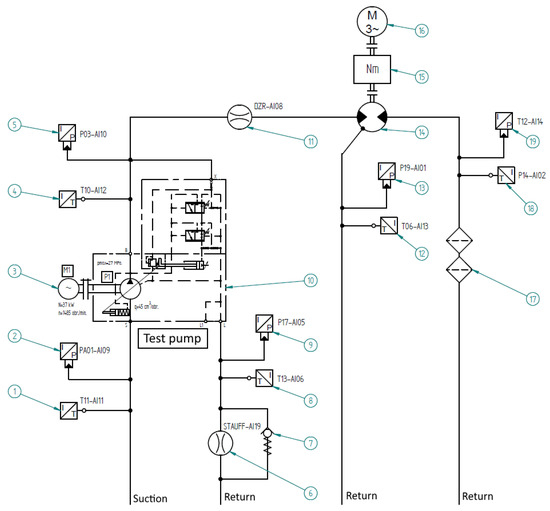
Figure 1.
Hydraulic diagram of the test bench.
In addition to the process sensors used in the previous stage of research, which enabled the measurement of parameters such as pressure, flow, and temperature, vibrations were also measured using vibration diagnostic sensors. During the tests, a set of three VSA001 sensors was used, along with a dedicated VSE100 measuring transducer from IFM. The measurement set measures vibration velocity in accordance with the ISO 20816-3 standard. The sensors were placed at three points on the pump along each of the geometric axes:
- Sensor 1 horizontally, perpendicular to the pump shaft;
- Sensor 2 vertically, perpendicular to the pump shaft;
- Sensor 3 along the pump shaft.
The visualization of the placement of the vibration sensors is shown in Figure 2.

Figure 2.
Experimental setup photo showing the pump and the visualized locations of the vibrodiagnostic sensors.
The complete list of sensors is presented in Table 1.

Table 1.
List of sensors used in the experiments.
Measurement data were collected using two different acquisition systems. Pressure, flow, and temperature data were acquired by a dedicated computer system at a sampling rate of approximately 40 samples/s. Data from the vibration sensors were recorded by a separate computer running IFM VES004 v2.33.00 software at a sampling rate of 1 sample/s. Both acquisition systems also recorded the real-time sample. Next, data from all sensors were synchronized in the time domain at a sampling rate of 1 sample/s. The measurements were conducted at varying oil temperatures. The oil was heated from room temperature to reach its operating temperature at around 40 °C, cooled down, and the data recording process was repeated to ensure full coverage of the input feature space. The data collection process was conducted at three distinct stages of pump operation. First, pump operation was recorded in a normal state (Operational Test, OT). Following this, three different levels of valve plate damage were recorded (Under Test, UT1, UT2, and UT3). To ensure that the recorded signals were not influenced by any assembly or disassembly operations, the OT recordings were performed in two separate cycles: once before and once after the UT damage recordings. Finally, to avoid information leak of the constructed machine learning system the minimum and maximum suction oil temperature were determined for each data set. This parameter serves as a reference point (background) for the remaining data and should therefore be the same for all pump states. Thus, each data set was limited to a common range of 21 °C to 40 °C. Only records with torque values > 19 Nm and <221 Nm were selected to exclude start-up states and prepare the test bench for the actual tests. Finally, duplicate records and NaN values were removed. Summary of final records number obtained is presented in Table 2.

Table 2.
Preprocessed Dataset Records.
3.2. Datasets Used in the Experiments
For the ML model evaluation stage, three datasets were created. One training dataset called and two test sets and . To construct these datasets, the OT data were divided into two parts based on the heating cycle. The first part of the OT data was combined with the UT1 set to form Dataset 1 (the training set). The second part was then used to create the two test sets: it was combined with the UT2 set to form Dataset 2 and with the UT3 set to form Dataset 3. For the training and test datasets, data were collected after the oil had cooled down. This approach ensured that the process information captured a wide range of oil suction temperatures in the suction line.
Next, all datasets were randomly sampled to achieve fully balanced settings such that balance ratio or . Next, imbalance conditions were introduced to to simulate the conditions under which we have limited data collected in the failure operating conditions. The imbalance was obtained by sampling down the failure state such that . Here, each state was obtained by subsampling the previous BR state, starting from . The obtained datasets are available in Table 3.

Table 3.
Datasets used in the experiments.
3.3. Model Evaluation Method
As detailed in the previous section, the experiments utilized three distinct datasets. was employed for the training and hyperparameter optimization of the prediction models, while and were used to validate model performance on new data exhibiting different levels of valve plate degradation. A consistent data processing pipeline was employed across all experiments.
First, using , each model was optimized and tuned to achieve the highest predictive performance. This model optimization was conducted via a grid search coupled with a 10-fold cross-validation procedure used to assess performance. Within each cross-validation fold, the data processing pipeline consisted of several key steps. The data was first standardized to a zero mean and unit standard deviation. Standardization parameters (mean and standard deviation) were computed solely from the training fold and then applied to both the training and testing folds. Subsequently, if required, a data-balancing algorithm was executed on the training fold. The preprocessed training fold was then used to train the model. The trained model was applied to the corresponding testing fold, and the results from all folds were averaged to obtain the final performance metrics. The pipeline of the cross-validation procedure is shown in Figure 3.

Figure 3.
Data processing pipeline including cross-validation test used in the experiments for parameter optimization and performance assessment on .
These steps enabled the identification of the optimal hyperparameters for the prediction model. The specific parameters used in the experiments are detailed in the following section.
After identifying the optimal model, it was retrained on and subsequently evaluated on and . This final training procedure also consisted of the same data processing steps: standardization, data balancing, and then model training on the entirety of . The resulting model was then applied to and , as shown in Figure 4.
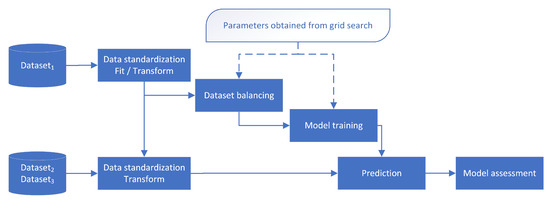
Figure 4.
Data processing pipeline used to assess the performance on and using the model trained on .
3.4. Methods Used in the Experiments
The initial results presented in [3] indicate that the best-performing model was a neural network. However, given that the underlying dataset has been updated—notably with the inclusion of new features, particularly from vibration sensors—the model selection process was repeated. The detailed evaluation procedure is provided in Section 3.5, aiming to identify a robust reference model for the remaining experiments.
The models compared in this selection stage were the k-Nearest Neighbor (kNN) classifier, Random Forest (RF), Gradient Boosted Trees, and the Multilayer Perceptron (MLP) neural network. The specific parameters utilized during the model evaluation are listed in Table 4.

Table 4.
Set of parameters used for the evaluation of the prediction models.
It was also determined that models typically employed for time series prediction, such as Recurrent Neural Networks (e.g., LSTMs or GRUs), would not be evaluated. This decision was made to actively mitigate the risk of information leakage stemming from the sinusoidal characteristic of the load applied during the data collection process. Since the sinusoidal load covers the full continuous range of recorded input features, even minor inaccuracies or negligible changes in load characteristics between experiments could lead to an overestimation of the model’s performance. Therefore, only the feature values recorded within a given single time stamp were used as a set of input features. Furthermore, previous work described in [3] already demonstrated that evaluating the influence of small historical window sizes provided no substantial gain in performance, while simultaneously increasing the computational complexity.
The initial results presented in [3] indicated that the best-performing model was a neural network, but since the dataset has changed and new features were added, in particular the vibration sensors, the process of model selection was repeated. The details of the evaluation procedure are provided in Section 3.5. In this stage the reference model was identified and was used in the remaining experiments. In this comparison the k-Nearest Neighbor classifier, Random Forest, Gradient Boosted Trees, and the Multilayer Neural Network were used. The parameters used for the model evaluation are presented in Table 4.
It was also decided not to evaluate models typically used for time series prediction, such as recurrent neural networks (e.g., LSTMs or GRU). The decision was made to avoid information leak caused by the characteristics of the load used during the data collection process. Here, the load has a sinusoidal form, allowing to cover full range of continuous space of recorded input features. Inaccuracy and small changes in load characteristics between the experiments may cause overestimation of the results; therefore, only values recorded within a given time stamp were used for the training step. Additionally, the influence of small historical window sizes was evaluated in [3] indicated no gain in performance, rather causing an increase in computational complexity.
Among the strategies for mitigating class imbalance, we employed data-level algorithms for data balancing methods. The selection of this family was motivated by its high versatility and general applicability. Data-level algorithms, for instance, can be seamlessly integrated with any prediction model and do not necessitate any internal modification of the classifier, unlike algorithm-level approaches or ensemble methods that usually require altering the model’s cost function or structure, or require the use of sample weight modification during training.
The following data balancing methods were evaluated in our experiments. Given that these methods were also fine-tuned, the specific parameters used for each are also provided:
- Undersampling
- ENN, ;
- Tomek Links.
- Oversampling
- SMOTE, ;
- Borderline-SMOTE, , ;
- ADASYN, .
- Hybrid
- SMOTE+ENN, , ;
- SMOTE+Tomek Links, .
3.5. Basic Analysis
In the initial stage of the experiments, no dataset balancing methods were applied. This stage was designed to verify two primary aspects: first, to identify the best-performing model for subsequent use as the reference classifier, and second, to evaluate the prediction performance of this reference classifier across various dataset balance rates (BRs).
- Part 1: Classifier Selection and Optimization
In the first part of this stage, four families of classifiers were evaluated and optimized: the k-Nearest Neighbor (kNN) classifier, Random Forest (RF), Gradient Boosted Trees, and the Multilayer Perceptron (MLP) neural network. All models were optimized on using a cross-validation procedure to identify the best configuration. Subsequently, the identified best models were trained on the entire and then applied to the distinct datasets, and . A comprehensive set of the evaluated parameters is provided in Table 4.
- Part 2: Performance Evaluation under Skewed Distribution
The second part of this stage was designed to provide insights into the performance degradation caused by skewed class distributions. The results from this section also serve to establish a lower bound for the prediction performance, against which the effectiveness of the balancing mechanisms applied in the second experimental stage can be compared.
In these experiments, the failure class of was randomly subsampled to achieve different levels of balance rates (BRs). The obtained performance was recorded by evaluating the reference model on using a cross-validation procedure. Furthermore, the model trained on was also evaluated on the fully balanced datasets, and , allowing for a clear identification of the performance drop attributable to the skewed training data distribution.
3.6. Dataset Balancing Model Comparison
The second stage of the experiments was dedicated to evaluating the impact of various dataset balancing methods on the performance of the final prediction model. Here, the best model from the balanced was used as the base classifier. This decision is justified because balancing methods are intended to produce a fully balanced dataset; therefore, a model with a structure identical to the one obtained on the balanced dataset should also yield the highest performance.
In these experiments, a grid search procedure was again employed to select the optimal dataset balancer hyperparameters for a fixed neural network. All methods presented in Section 3.4 were evaluated, and the resulting classifier was assessed on and . Similarly to the previous stage, the experiments were repeated for each balance ratio.
This stage provided an additional benefit by offering information on how different methods behave across various imbalance rates. This is particularly important for the practical implementation of the system, where a user can choose the appropriate balancing method based on the data’s imbalance rate. To assess the overall performance, we used F1-score, balanced accuracy, and the Matthews correlation coefficient. The summary of the data sampling methods was obtained using the Balancer Area Under the Curve metric, which calculates the area under the BR–F1-score curve. The details of the metrics used in the experiments are provided in Section 3.7.
The final stage of the experiments evaluated the stability of the prediction models, which may be influenced by data imbalance and the data balancing method used. To assess model stability, we performed a feature importance analysis. The underlying assumption of this research was that a model trained on a balanced dataset should extract the same knowledge as a model trained on the original, full dataset with . Therefore, an effective data balancing method should ensure that the feature importance remains as similar as possible to that obtained from the original dataset. Significant changes in feature importance suggest a modification in the knowledge extracted by the model, which can adversely affect its overall performance.
For this analysis, we used a permutation-based method to evaluate feature importance. This technique works by permuting the values of a given feature and then measuring the subsequent drop in the model’s predictive performance. This process is repeated multiple times, and the average drop in performance serves as an indicator of that feature’s importance. This method is advantageous because it keeps the feature space constant while preserving the individual feature distributions, as only the values are shuffled across the data samples. To quantify the similarity in feature importance between the original and balanced datasets, we used Pearson’s correlation coefficient (CC), which was chosen for its robustness against constant components or biases in the importance scores.
3.7. Metrics Used for Model Evaluation
Given the imbalanced nature of the prediction problems, classical prediction accuracy is not a suitable measure of performance. Therefore, for model evaluation, we employed more robust metrics: balanced accuracy (BAcc), the F1-score (F1), and the Matthews correlation coefficient (MCC), along with our own proposal of a new performance measure called BAUC.
- F1-macro
The F1-score is the harmonic mean of precision and recall, defined as:
where:
- Precision is the number of true positives divided by the total number of predicted positives. It answers the question: “Of all the instances predicted as positive, how many were truly positive?”
- Recall is the number of true positives divided by the number of true positives plus false negatives. It answers the question: “Of all the instances that were truly positive, how many did the model correctly identify?”
Since the standard F1-score is calculated for a single positive class, we used the F1-macro version in our experiments. The F1-macro score is calculated as the average of the F1-scores determined for each class independently. In our two-class case, this means the F1-score is calculated twice: once assuming the Normal class is positive and once assuming the Failure class is positive. The final F1-macro value is obtained as:
- Balanced accuracy
Balanced accuracy is a popular measure for evaluating performance in imbalanced problems. It is calculated independently as the mean recall for each class, thereby providing a class-balanced measure of performance.
- Matthews Correlation Coefficient
The Matthews correlation coefficient (MCC) is another measure often used to evaluate performance in imbalanced classification. This measure directly utilizes all elements of the confusion matrix and is calculated using the formula
where:
- TP (True Positives) = Correctly predicted positive instances.
- TN (True Negatives) = Correctly predicted negative instances.
- FP (False Positives) = Incorrectly predicted positive instances (Type I Error).
- FN (False Negatives) = Incorrectly predicted negative instances (Type II Error).
It is important to note that the MCC measure is defined within the range of −1 to +1, where +1 represents a perfect prediction, 0 indicates a prediction no better than random guessing, and −1 signifies a perfect inverse prediction (always misclassifying).
- BAUC metric
Additionally, to provide an overall comparison of the data balancing methods, we propose a new metric called the Balancer Area Under the Curve (BAUC). The purpose of this metric is to summarize the performance of individual data balancing methods across a range of imbalanced rates. The BAUC metric is calculated as the area under the curve defined by the imbalanced rate and the corresponding performance score. We computed the area using Simpson’s 1/3 rule (Equation (5)) as it offers a more accurate approximation than the trapezoidal rule by employing a polynomial fit rather than a linear one.
where .
The concept of the BAUC metric is illustrated in Figure 5.
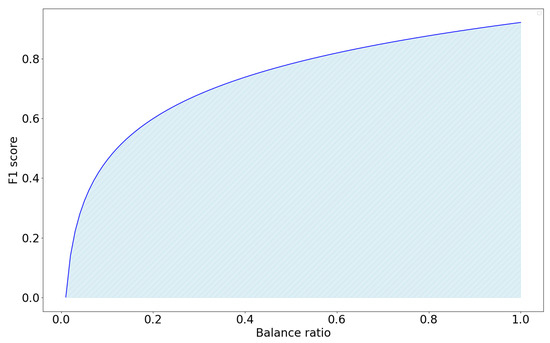
Figure 5.
An example of performance metric.
A perfect BAUC value approaches 1, which indicates that a data balancing method can achieve a performance F1-score of 1 regardless of the data’s imbalance rate.
3.8. Tools Used in the Experiments
The experiments were implemented in Python 3.11 using the Scikit-learn library [40], which was employed for cross-validation tasks and classification models. Data balancing methods were adopted from the Imbalanced-learn library [41]. The experiments were executed on a computer server equipped with two AMD EPYC 7200 processor, and 1 TB of RAM. The scripts and datasets used to conduct the experiments are publicly available at [42].
4. Results and Discussion
4.1. The Influence of Data Imbalance on Model’s Prediction Performance
The initial stage of the experiments involved a two-fold approach: first, comparison and optimization of the prediction models to achieve the highest prediction performance; and second, an analysis of how imbalanced data affects the model’s predictive performance.
The results of the first stage of the analysis are presented in Table 5. This table identifies the best-performing model obtained for each of the four classifier families evaluated on the fully balanced dataset; namely, kNN, Random Forest, Gradient Boosted Trees, and the MLP neural network.

Table 5.
Comparison of the prediction performance obtained by the best performing models trained on and evaluated using a cross-validation procedure on and two test sets and .
The results indicate that the highest prediction performance was achieved by the MLP neural network, specifically a configuration consisting of two hidden layers with 40 and 20 neurons, respectively. According to the cross-validation test, the second best-performing model was kNN, followed by Gradient Boosted Trees, with the Random Forest model ranking fourth.
This best-performing MLP configuration was subsequently evaluated on and . For both of these additional datasets, the MLP network again yielded the highest performance. Specifically, on , the second-best model was Gradient Boosted Trees, followed by kNN and Random Forest, mirroring the rank order obtained during the cross-validation procedure. However, on , the second-best model was Random Forest, followed by Gradient Boosted Trees, with kNN achieving the lowest performance. The consistency of these results across all datasets indicates the dominating performance properties of the MLP network, which was consequently selected and utilized as the reference model for all subsequent studies.
As anticipated, Figure 6 demonstrates that the model’s predictive performance decreases as the balance ratio (BR) drops. This dependency appears to be highly nonlinear, even logarithmic. These results underscore the importance of employing data balancing methods to mitigate the performance degradation that occurs in the presence of imbalanced data.
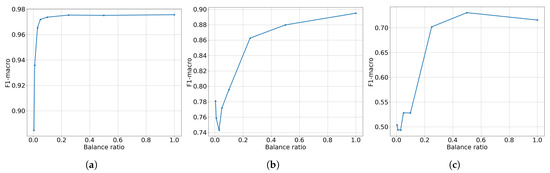
Figure 6.
The influence of the balance ratio on the prediction performance (F1-score). (a) Results on , (b) results on , (c) results on .
A notable difference can be observed between the evaluation characteristics presented in Figure 6a–c. In Figure 6a, which shows results for , the values represent the mean performance obtained from a cross-validation procedure. Due to the presence of similar samples in the data recording procedure, the predictive performance is very high. It is also important to note that the test sets within this cross-validation procedure are imbalanced. This can lead to an inaccurate performance assessment because the minority class is underrepresented, causing inappropriate prediction performance. Here, the predictive performance begins to drop for and shows almost no degradation above this point.
The results from and are significantly more informative, as both of these datasets are balanced. For (Figure 6b), the predictive performance begins to drop at a of , falling from nearly to . Even worse results are obtained for (Figure 6c), where the performance drops from to . Notably, while the drop in performance for both datasets begins for a , there is a surprising, albeit insignificant, increase in performance at a of . In general, both Figure 6b,c exhibit a similar shape but on different performance scales.
4.2. Comparison of Data Balancing Methods
The results obtained in the previous section indicate a clear performance drop as the data balance ratio decreases. The primary question that arises is how data balancing methods can improve performance under these conditions. A comparison of all evaluated methods is shown in Figure 7, with separate plots for each of the three datasets. The detailed results are presented in Appendix A.
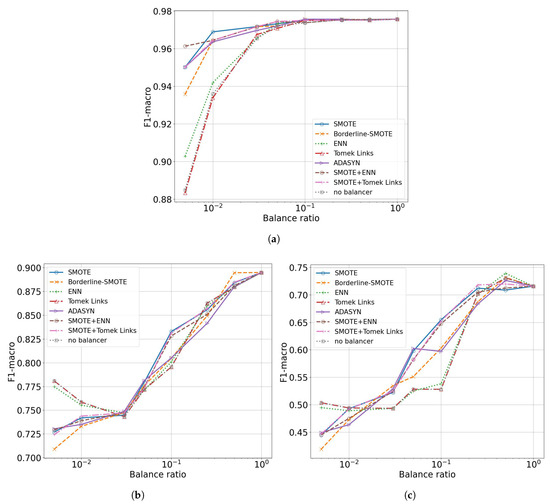
Figure 7.
Relationship between model performance and the data balance ratio obtained when the model was trained on for a given balance rate and evaluated on: (a) (cross-validation procedure), (b) , and (c) .
It is important to note that for , the results were obtained using a cross-validation procedure. In contrast, for and , the models were trained on at a given balance rate and then applied to these two datasets. In the figures, the x-axis is presented on a logarithmic scale to better illustrate the models’ behavior at the lowest balance rates, where the number of samples for each class is significantly different.
4.2.1. Performance on
The results for indicate that all oversampling and hybrid methods—in particular, Borderline SMOTE, ADASYN, SMOTE+Tomek Links, SMOTE+ENN, and standard SMOTE—provide significant benefits to the overall model performance. The downsampling methods, on the other hand, do not have a significant impact. Among the downsampling techniques, only ENN for the lowest balance rates resulted in an accuracy increase of 2 percentage points. On the other hand, the largest impact of the use of data balancing was obtained at a balance rate of , where an F1-score of nearly was achieved with the use of SMOTE-ENN, compared to with no data-balancing technique.
The overall comparison, including all balance ratios, was evaluated using the Balancer Area Under Curve (BAUC) metric, which measures the area under the balance rate vs. F1-score curve. Further details on this metric are provided in Section 3.7. The final ranking based on this metric is shown in Figure 8a. These results indicate that standard SMOTE outperforms all other methods, with a small performance difference when compared to Borderline SMOTE. A subsequent performance drop is observed for the following methods, with SMOTE+ENN occupying the third position. The two worst-performing methods are the no balancer solution and the Tomek Links downsampling method, with Tomek Links performing even worse than no balancing at all.
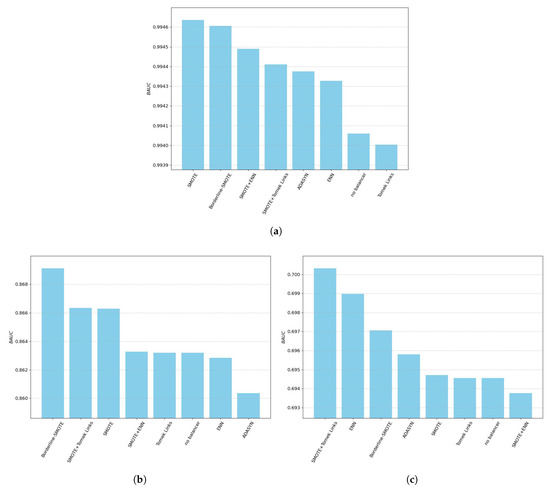
Figure 8.
Visualization of the BAUC metrics obtained for each data balancing method for each of the datasets: (a) . (b) . (c) .
4.2.2. Performance on and
The situation changes for and . At the highest balance rates, all methods behave similarly, and balancing does not provide any significant benefits. The performance simply oscillates without a single dominating method. However, when the balance rate drops to , SMOTE, SMOTE+Tomek Links, and SMOTE+ENN begin to perform significantly better than the competitors, leading to substantial performance gains. The gain is approximately 4 percentage points for and 12 percentage points for . Finally, at balance ratios of , all balancing methods behave similarly. At the lowest balance rates, the simple no balancer and ENN methods even begin to outperform the oversampling and hybrid methods by up to 5 percentage points.
The source of this behavior is discussed in detail in the following subsection.
An overall comparison using the BAUC metric for and is shown in Figure 8b,c. A notable difference in the order of the top-performing models is observed here. Borderline SMOTE and SMOTE–Tomek Links now lead the rankings. The detailed results for all datasets, including the obtained BAUC metrics, are presented in Table 6. This table also shows the ranks assigned to each model, with a rank of 1 indicating the best-performing solution and a rank of 8 for the worst. The final column contains the average rank across all evaluated datasets. According to this average rank, Borderline SMOTE is the best-performing model, followed by SMOTE+Tomek Links and the classical SMOTE algorithm. The worst results were obtained for no balancer and the pure Tomek Links downsampling algorithm.

Table 6.
Average models ranking with BAUC scores.
4.2.3. Discussion
One of the most surprising results is the increase in performance of the no balancer solution at the lowest balance rates. This phenomenon stems from the severe underrepresentation of the minority class in highly imbalanced datasets, which significantly alters the distribution of particular input variables. This phenomenon is visualized in Figure 9, which shows box plots for each input variable of the minority class for different balance rates.
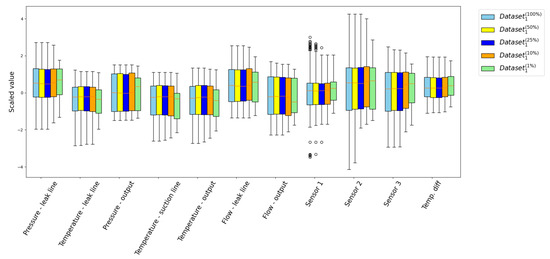
Figure 9.
Visualization of the input variable distributions using box plots for balance rates in the range . The figure shows that the distribution of the input variables for is noticeably different from the others, while for the remaining balance rates, the distributions are very similar.
As seen in Figure 9, for all input variables and for balance rates in the range , the distribution of each variable remains largely unchanged, with the median and the first and third quartiles showing only insignificant differences. In contrast, at , the changes are significant. We do not present results for smaller balance ratios, as their variables are simply subsampled from the variable set of the next higher balance ratio, so the situation gets even worse.
This change in distribution particularly influences variables such as Pressure–leak line, where the median increases. All temperatures (leak line, output, and suction line) also show a significant decrease in both the median and the interquartile range. Additionally, the Flows variables exhibit distinct first and third quartiles. A very significant change is also observed for vibration Sensor 2 and Sensor 3, where the first and third quartiles are notably altered.
These changes collectively influence the model training process by violating the I.I.D. (Independent and Identically Distributed) principle. For , this phenomenon is not observed because the model’s performance is evaluated on the imbalanced dataset using a standard cross-validation (CV) procedure. Therefore, when the balancer adds new samples, they all belong to the modified distribution. Since the test set within the CV is subsampled from the same training set, no significant change in performance is observed.
On the other hand, in and , where the original distribution is fixed, oversampling methods do not provide any benefits and may even worsen the results. This is because oversampling adds new samples into a space where the model already has data, which can exacerbate boundary effects. This, in turn, degrades the model’s performance in subspaces that fall outside the original minority class distribution. Therefore, when considering the use of balancing methods, it is important to collect enough data to cover the entire feature space and use the balancing methods with care.
4.3. Feature Importance Analysis
The final set of experiments addresses the problem of model stability as the dataset size decreases. As described in Section 3.5, stability was measured using feature importances extracted from the model, assuming a fully balanced training scenario.
The obtained results are presented in Figure 10. An analysis of the bar plots shows that the Flow–leak line variable remains the most important across all experiments. Similarly, the Pressure output typically maintains its position as the second most important variable, but only for . When the balance rate decreases further, Sensor 1 starts to dominate over Pressure output. The remaining features are less important, and their order of importance changes.
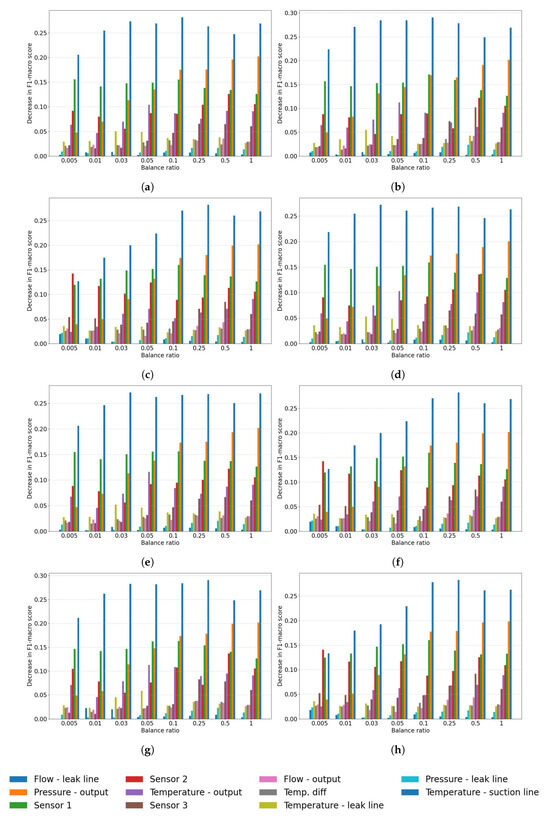
Figure 10.
Feature importance depending on balancing models for . (a) SMOTE. (b) ADASYN. (c) No balancer. (d) SMOTE+ENN. (e) SMOTE+Tomek Links. (f) Tomek Links. (g) Borderline SMOTE. (h) ENN.
An overall comparison is shown in Figure 11. This figure presents the Pearson’s correlation coefficient (CC) calculated between the feature importances obtained from a reference model (trained on the full dataset) and those from a model trained on a balanced dataset. A high correlation value indicates that the feature importances of the balanced models are similar to those of the reference model. Conversely, when the feature importance changes significantly, the CC score begins to drop.
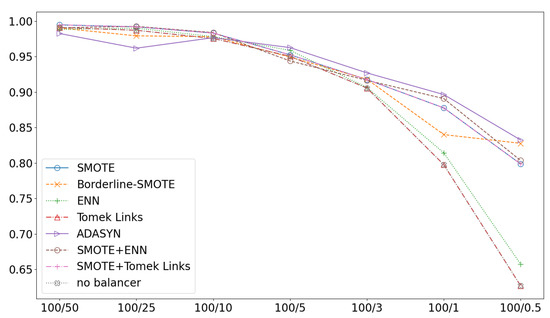
Figure 11.
Pearson correlation of balance ratio factors.
The results indicate that for larger balance ratios, specifically in the range , the feature importances behave similarly across all models. This suggests that the extracted knowledge remains largely consistent within this range of imbalance. The only notable exception is ADASYN, which yields significantly lower correlation values (approximately 0.97) compared to the average of 0.99 observed for other methods. This phenomenon may be attributed to the fact that ADASYN focuses on generating synthetic data for hard-to-classify samples located near the decision boundary. This targeted generation likely modifies the underlying distribution of the input data, potentially resulting in changes to the internal model structure.
For balance rates smaller than 5%, the correlation begins to drop. Initially, for and , all models show a similar decrease in their CC scores. However, at lower rates, the CC score drops significantly for ENN, Tomek Links, and the no balancer solution, reaching 0.67, 0.63, and 0.63, respectively. In contrast, the remaining methods show a more gradual decrease in correlation. This suggests that the oversampling and hybrid methods attempt to preserve the data distribution, even as it changes, which in turn means the original knowledge is no longer fully preserved. This leads to CC scores of around 0.83 for these methods for .
5. Conclusions
This research investigates the applicability and effectiveness of data balancing methods for building predictive maintenance systems, specifically for valve plate failure prediction. The study was designed to simulate a real-world scenario in which a limited amount of failure state data is available for model training. We evaluated seven state-of-the-art balancing methods and compared them against a baseline solution without any balancing.
The results indicate that the use of data-balancing methods has several important limitations and implications:
- The assessment of data balancing methods using a standard cross-validation procedure should be interpreted with caution. The results can be misleading, especially when dealing with extremely low balance rates, as the test set may not accurately represent the data distribution of the entire space in which the model may operate. This phenomenon is observed through the differing shapes of the balance rate plots obtained for compared to the remaining balanced sets, and .
- The lowest effective balance ratio at which data balancing methods provided benefits ranged from 5% to 1%. While for , the methods did not yield significant gains at 1%, for , the performance improvement remained substantial.
- For the lowest balance ratios (), the use of data balancing methods proved detrimental to the models, leading to a decrease in overall prediction performance, making them inapplicable in real-life systems.
- The use of data balancing methods, particularly oversampling and hybrid, causes small changes to the knowledge extracted from the data. When the balance ratio decreases, the oversampling methods are unable to preserve the true data distribution, leading to a gradual decrease in performance. That is observed in a decrease in the feature importance correlation plot.
- It is essential to collect a sufficient amount of training data to ensure full coverage of the feature space; otherwise, the resulting model is highly susceptible to bias. This finding directly implies the necessity of collecting a certain minimum number of training samples representing the minority (failure) state. Within the constraints of the conducted experiments, this minimum threshold was identified as approximately 130 samples, corresponding to a balance ratio of .
In summary, the best-performing models were Borderline SMOTE, followed closely by SMOTE + Tomek Links. Based on these results, we recommend utilizing these two hybrid data-level methods when developing a commercial-grade predictive maintenance system for valve plate failure prediction.
Further research is planned to extend the collected dataset to include other types of failures, such as plunger failure, allowing for the investigation of coincidence and interaction effects among multiple simultaneous failure types, as well as the collection of data from multiple pumps. Furthermore, we intend to investigate the impact of other algorithmic approaches for handling data imbalance problems, specifically in the context of extremely small minority class sizes, by comparing other approaches against the best data-level methods identified in the current experiments.
Author Contributions
Conceptualization, M.R. and M.B.; methodology, M.B. and M.R.; software, M.R. and M.B.; validation, M.B. and M.R.; formal analysis, M.B.; investigation, M.R. and M.B.; resources, M.R.; data curation, M.R.; writing—original draft preparation, M.B. and M.R.; writing—review and editing, M.B.; visualization, M.R.; supervision, M.B.; project administration, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry of Science and Higher Education, grant number 11/040/SDW22/030, and the Silesian University of Technology, grant number BK-227/RM4/2025.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets and scripts used to run experiments are available on GitHub: https://github.com/mblachnik/2025_Data_balancers_pumps (accessed on 16 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Detailed Performance Metrics
Appendix A.1. Dataset1
Performance metrics obtained for for different data balancing methods and for different balance ratios.
| Balance Ratio | |||||||||
| Model | Metric | 0.005 | 0.01 | 0.03 | 0.05 | 0.1 | 0.25 | 0.5 | 1.0 |
| F1-macro | 0.9309 | 0.9632 | 0.9681 | 0.9793 | 0.9711 | 0.9735 | 0.9755 | 0.9757 | |
| ADASYN | BACC | 0.8309 | 0.9518 | 0.9622 | 0.9734 | 0.9613 | 0.9667 | 0.9738 | 0.9736 |
| MCC | 0.7036 | 0.9104 | 0.9304 | 0.9532 | 0.9272 | 0.9390 | 0.9541 | 0.9539 | |
| F1-macro | 0.9059 | 0.9496 | 0.9668 | 0.9784 | 0.9714 | 0.9743 | 0.9757 | 0.9758 | |
| Borderline SMOTE | BACC | 0.8096 | 0.9411 | 0.9600 | 0.9731 | 0.9624 | 0.9680 | 0.9739 | 0.9736 |
| MCC | 0.6772 | 0.8961 | 0.9260 | 0.9525 | 0.9306 | 0.9424 | 0.9542 | 0.9539 | |
| F1-macro | 0.8650 | 0.9191 | 0.9436 | 0.9598 | 0.9684 | 0.9747 | 0.9750 | 0.9750 | |
| Edited Neares tNeighbours | BACC | 0.7561 | 0.9074 | 0.9449 | 0.9625 | 0.9651 | 0.9684 | 0.9733 | 0.9736 |
| MCC | 0.5403 | 0.8455 | 0.9004 | 0.9330 | 0.9367 | 0.9431 | 0.9538 | 0.9538 | |
| F1-macro | 0.8485 | 0.9161 | 0.9438 | 0.9592 | 0.9678 | 0.9746 | 0.9750 | 0.9750 | |
| No balancer | BACC | 0.7456 | 0.9048 | 0.9440 | 0.9619 | 0.9645 | 0.9685 | 0.9732 | 0.9736 |
| MCC | 0.5194 | 0.8427 | 0.8988 | 0.9318 | 0.9357 | 0.9429 | 0.9535 | 0.9538 | |
| F1-macro | 0.9369 | 0.9618 | 0.9699 | 0.9794 | 0.9712 | 0.9740 | 0.9757 | 0.9758 | |
| SMOTE | BACC | 0.8309 | 0.9502 | 0.9638 | 0.9739 | 0.9616 | 0.9677 | 0.9741 | 0.9736 |
| MCC | 0.7117 | 0.9082 | 0.9331 | 0.9537 | 0.9274 | 0.9388 | 0.9544 | 0.9539 | |
| F1-macro | 0.9558 | 0.9634 | 0.9678 | 0.9749 | 0.9732 | 0.9738 | 0.9755 | 0.9757 | |
| SMOTE ENN | BACC | 0.8506 | 0.9519 | 0.9629 | 0.9711 | 0.9648 | 0.9662 | 0.9737 | 0.9736 |
| MCC | 0.7539 | 0.9102 | 0.9282 | 0.9453 | 0.9347 | 0.9360 | 0.9541 | 0.9539 | |
| F1-macro | 0.9309 | 0.9622 | 0.9690 | 0.9792 | 0.9713 | 0.9741 | 0.9757 | 0.9758 | |
| SMOTETomek | BACC | 0.8309 | 0.9513 | 0.9632 | 0.9738 | 0.9618 | 0.9677 | 0.9741 | 0.9736 |
| MCC | 0.7036 | 0.9096 | 0.9322 | 0.9536 | 0.9276 | 0.9389 | 0.9544 | 0.9539 | |
| F1-macro | 0.8309 | 0.9368 | 0.9648 | 0.9774 | 0.9721 | 0.9739 | 0.9756 | 0.9757 | |
| TomekLinks | BACC | 0.7252 | 0.8715 | 0.9303 | 0.9473 | 0.9540 | 0.9690 | 0.9734 | 0.9736 |
| MCC | 0.5664 | 0.7296 | 0.8942 | 0.9310 | 0.9397 | 0.9438 | 0.9540 | 0.9539 | |
Appendix A.2. Dataset2
Performance metrics obtained for for different data balancing methods and for different balance rates.
| Balance Ratio | |||||||||
| Model | Metric | 0.005 | 0.01 | 0.03 | 0.05 | 0.1 | 0.25 | 0.5 | 1.0 |
| F1-macro | 0.7346 | 0.7396 | 0.7488 | 0.7791 | 0.8125 | 0.8416 | 0.8659 | 0.8950 | |
| ADASYN | BACC | 0.6860 | 0.6929 | 0.6966 | 0.7297 | 0.7743 | 0.8126 | 0.8453 | 0.8840 |
| MCC | 0.3998 | 0.4133 | 0.4323 | 0.5137 | 0.6007 | 0.6720 | 0.7254 | 0.7854 | |
| F1-macro | 0.7035 | 0.7356 | 0.7517 | 0.7783 | 0.8028 | 0.8529 | 0.8947 | 0.8950 | |
| Borderline SMOTE | BACC | 0.6747 | 0.6872 | 0.6981 | 0.7283 | 0.7634 | 0.8278 | 0.8826 | 0.8840 |
| MCC | 0.3563 | 0.4023 | 0.4392 | 0.5116 | 0.5746 | 0.6975 | 0.7864 | 0.7854 | |
| F1-macro | 0.7748 | 0.7553 | 0.7472 | 0.7712 | 0.8009 | 0.8600 | 0.8796 | 0.8950 | |
| Edited Nearest Neighbours | BACC | 0.7518 | 0.7220 | 0.7066 | 0.7322 | 0.7747 | 0.8377 | 0.8634 | 0.8840 |
| MCC | 0.5145 | 0.4614 | 0.4363 | 0.4939 | 0.5694 | 0.7125 | 0.7549 | 0.7854 | |
| F1-macro | 0.7809 | 0.7586 | 0.7431 | 0.7718 | 0.7956 | 0.8627 | 0.8797 | 0.8950 | |
| No balancer | BACC | 0.7613 | 0.7265 | 0.6997 | 0.7321 | 0.7686 | 0.8412 | 0.8635 | 0.8840 |
| MCC | 0.5312 | 0.4700 | 0.4244 | 0.4951 | 0.5570 | 0.7184 | 0.7550 | 0.7854 | |
| F1-macro | 0.7209 | 0.7419 | 0.7471 | 0.7719 | 0.8329 | 0.8568 | 0.8847 | 0.8950 | |
| SMOTE | BACC | 0.6668 | 0.6959 | 0.6948 | 0.7224 | 0.8029 | 0.8332 | 0.8699 | 0.8840 |
| MCC | 0.3619 | 0.4194 | 0.4280 | 0.4937 | 0.6492 | 0.7056 | 0.7654 | 0.7854 | |
| F1-macro | 0.7227 | 0.7423 | 0.7472 | 0.7745 | 0.8283 | 0.8507 | 0.8811 | 0.8950 | |
| SMOTEENN | BACC | 0.6697 | 0.6969 | 0.6947 | 0.7245 | 0.7981 | 0.8256 | 0.8654 | 0.8840 |
| MCC | 0.3673 | 0.4208 | 0.4281 | 0.5009 | 0.6370 | 0.6917 | 0.7577 | 0.7854 | |
| F1-macro | 0.7209 | 0.7419 | 0.7471 | 0.7719 | 0.8329 | 0.8568 | 0.8847 | 0.8950 | |
| SMOTE Tomek | BACC | 0.6668 | 0.6959 | 0.6948 | 0.7224 | 0.8029 | 0.8332 | 0.8699 | 0.8840 |
| MCC | 0.3619 | 0.4194 | 0.4280 | 0.4937 | 0.6492 | 0.7056 | 0.7654 | 0.7854 | |
| F1-macro | 0.7809 | 0.7586 | 0.7431 | 0.7718 | 0.7956 | 0.8627 | 0.8797 | 0.8950 | |
| Tomek Links | BACC | 0.7613 | 0.7265 | 0.6997 | 0.7321 | 0.7686 | 0.8412 | 0.8635 | 0.8840 |
| MCC | 0.5312 | 0.4700 | 0.4244 | 0.4951 | 0.5570 | 0.7184 | 0.7550 | 0.7854 | |
Appendix A.3. Dataset3
Performance metrics obtained for for different data balancing methods and for different balance rates.
| Balance Ratio | |||||||||
| Model | Metric | 0.005 | 0.01 | 0.03 | 0.05 | 0.1 | 0.25 | 0.5 | 1.0 |
| F1-macro | 0.4584 | 0.4675 | 0.5287 | 0.5591 | 0.6063 | 0.6832 | 0.7166 | 0.7156 | |
| ADASYN | BACC | 0.4740 | 0.4835 | 0.5159 | 0.5428 | 0.5963 | 0.6702 | 0.7113 | 0.7297 |
| MCC | −0.0520 | −0.0330 | 0.0319 | 0.0858 | 0.1928 | 0.3416 | 0.4229 | 0.4616 | |
| F1-macro | 0.3450 | 0.4817 | 0.5338 | 0.5655 | 0.5943 | 0.6903 | 0.7700 | 0.7156 | |
| Borderline SMOTE | BACC | 0.4371 | 0.4894 | 0.5175 | 0.5464 | 0.5856 | 0.6825 | 0.7695 | 0.7297 |
| MCC | −0.1310 | −0.0211 | 0.0351 | 0.0932 | 0.1713 | 0.3655 | 0.5390 | 0.4616 | |
| F1-macro | 0.4947 | 0.4890 | 0.4933 | 0.5249 | 0.5382 | 0.7015 | 0.7390 | 0.7156 | |
| Edited Nearest Neighbours | BACC | 0.5468 | 0.5218 | 0.5111 | 0.5369 | 0.5714 | 0.6962 | 0.7368 | 0.7297 |
| MCC | 0.0956 | 0.0440 | 0.0222 | 0.0739 | 0.1442 | 0.3927 | 0.4736 | 0.4616 | |
| F1-macro | 0.5036 | 0.4941 | 0.4933 | 0.5282 | 0.5280 | 0.7019 | 0.7305 | 0.7156 | |
| No balancer | BACC | 0.5596 | 0.5275 | 0.5059 | 0.5378 | 0.5629 | 0.6980 | 0.7302 | 0.7297 |
| MCC | 0.1223 | 0.0556 | 0.0118 | 0.0756 | 0.1271 | 0.3960 | 0.4603 | 0.4616 | |
| F1-macro | 0.4514 | 0.4927 | 0.5241 | 0.5754 | 0.6546 | 0.7179 | 0.7195 | 0.7156 | |
| SMOTE | BACC | 0.4590 | 0.5010 | 0.5125 | 0.5546 | 0.6465 | 0.7071 | 0.7245 | 0.7297 |
| MCC | −0.0821 | 0.0021 | 0.0250 | 0.1096 | 0.2934 | 0.4155 | 0.4492 | 0.4616 | |
| F1-macro | 0.4461 | 0.4815 | 0.5242 | 0.5678 | 0.6475 | 0.6913 | 0.7122 | 0.7156 | |
| SMOTEENN | BACC | 0.4577 | 0.4950 | 0.5121 | 0.5481 | 0.6408 | 0.6832 | 0.7170 | 0.7297 |
| MCC | −0.0846 | −0.0101 | 0.0243 | 0.0967 | 0.2818 | 0.3670 | 0.4343 | 0.4616 | |
| F1-macro | 0.4514 | 0.4927 | 0.5241 | 0.5754 | 0.6546 | 0.7179 | 0.7195 | 0.7156 | |
| SMOTETomek | BACC | 0.4590 | 0.5010 | 0.5125 | 0.5546 | 0.6465 | 0.7071 | 0.7245 | 0.7297 |
| MCC | −0.0821 | 0.0021 | 0.0250 | 0.1096 | 0.2934 | 0.4155 | 0.4492 | 0.4616 | |
| F1-macro | 0.5036 | 0.4941 | 0.4933 | 0.5282 | 0.5280 | 0.7019 | 0.7305 | 0.7156 | |
| Tomek Links | BACC | 0.5596 | 0.5275 | 0.5059 | 0.5378 | 0.5629 | 0.6980 | 0.7302 | 0.7297 |
| MCC | 0.1223 | 0.0556 | 0.0118 | 0.0756 | 0.1271 | 0.3960 | 0.4603 | 0.4616 | |
References
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.d.P.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Kaur, H.; Pannu, H.S.; Malhi, A.K. A systematic review on imbalanced data challenges in machine learning: Applications and solutions. ACM Comput. Surv. (CSUR) 2019, 52, 1–36. [Google Scholar] [CrossRef]
- Rojek, M.; Blachnik, M. A Dataset and a Comparison of Classification Methods for Valve Plate Fault Prediction of Piston Pump. Appl. Sci. 2024, 14, 7183. [Google Scholar] [CrossRef]
- ISO 20816-3:2024; Measurement and Evaluation of Machine Vibration—Part 3: Industrial Machine Sets—Guidance for Evaluation of Vibration When Machine Is Running. International Organization for Standardization: Geneva, Switzerland, 2024.
- Wilson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 2007, SMC-2, 408–421. [Google Scholar] [CrossRef]
- Tomek, I. Two modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, 6, 769–772. [Google Scholar]
- Hoyos-Osorio, J.; Alvarez-Meza, A.; Daza-Santacoloma, G.; Orozco-Gutierrez, A.; Castellanos-Dominguez, G. Relevant information undersampling to support imbalanced data classification. Neurocomputing 2021, 436, 136–146. [Google Scholar] [CrossRef]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Advances in Intelligent Computing, Proceedings of the International Conference on Intelligent Computing, Hefei, China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Sun, Y.; Que, H.; Cai, Q.; Zhao, J.; Li, J.; Kong, Z.; Wang, S. Borderline smote algorithm and feature selection-based network anomalies detection strategy. Energies 2022, 15, 4751. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Juez-Gil, M.; Arnaiz-Gonzalez, A.; Rodriguez, J.J.; Lopez-Nozal, C.; Garcia-Osorio, C. Approx-SMOTE: Fast SMOTE for big data on apache spark. Neurocomputing 2021, 464, 432–437. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Tekkali, C.G.; Natarajan, K. An advancement in AdaSyn for imbalanced learning: An application to fraud detection in digital transactions. J. Intell. Fuzzy Syst. 2024, 46, 11381–11396. [Google Scholar] [CrossRef]
- Swana, E.F.; Doorsamy, W.; Bokoro, P. Tomek link and SMOTE approaches for machine fault classification with an imbalanced dataset. Sensors 2022, 22, 3246. [Google Scholar] [CrossRef]
- Nizam-Ozogur, H.; Orman, Z. A heuristic-based hybrid sampling method using a combination of SMOTE and ENN for imbalanced health data. Expert Syst. 2024, 41, e13596. [Google Scholar] [CrossRef]
- Wang, C.; Deng, C.; Wang, S. Imbalance-XGBoost: Leveraging weighted and focal losses for binary label-imbalanced classification with XGBoost. Pattern Recognit. Lett. 2020, 136, 190–197. [Google Scholar] [CrossRef]
- Yang, C.Y.; Yang, J.S.; Wang, J.J. Margin calibration in SVM class-imbalanced learning. Neurocomputing 2009, 73, 397–411. [Google Scholar] [CrossRef]
- Shu, J.; Xie, Q.; Yi, L.; Zhao, Q.; Zhou, S.; Xu, Z.; Meng, D. Meta-weight-net: Learning an explicit mapping for sample weighting. Adv. Neural Inf. Process. Syst. 2019, 32, 1919–1930. [Google Scholar] [CrossRef]
- Zhou, H.; Yin, H.; Deng, X.; Huang, Y. Online Harmonizing Gradient Descent for Imbalanced Data Streams One-Pass Classification. In Proceedings of the IJCAI, Macao, China, 19–25 August 2023; pp. 2468–2475. [Google Scholar]
- Liu, X.Y.; Zhou, Z.H. Ensemble methods for class imbalance learning. In Imbalanced Learning: Foundations, Algorithms, and Applications; Wiley: Hoboken, NJ, USA, 2013; pp. 61–82. [Google Scholar]
- More, A.; Rana, D.P. Review of random forest classification techniques to resolve data imbalance. In Proceedings of the 2017 1st International Conference on Intelligent Systems and Information Management (ICISIM), Aurangabad, India, 5–6 October 2017; pp. 72–78. [Google Scholar]
- Seiffert, C.; Khoshgoftaar, T.M.; Van Hulse, J.; Napolitano, A. RUSBoost: A hybrid approach to alleviating class imbalance. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2009, 40, 185–197. [Google Scholar] [CrossRef]
- Bykov, A.; Voronov, V.; Voronova, L. Machine learning methods applying for hydraulic system states classification. In Proceedings of the 2019 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 20–21 March 2019; pp. 1–4. [Google Scholar]
- Tang, S.; Zhu, Y.; Yuan, S. A novel adaptive convolutional neural network for fault diagnosis of hydraulic piston pump with acoustic images. Adv. Eng. Inform. 2022, 52, 101554. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. An improved convolutional neural network with an adaptable learning rate towards multi-signal fault diagnosis of hydraulic piston pump. Adv. Eng. Inform. 2021, 50, 101406. [Google Scholar] [CrossRef]
- Tang, S.; Khoo, B.C.; Zhu, Y.; Lim, K.M.; Yuan, S. A light deep adaptive framework toward fault diagnosis of a hydraulic piston pump. Appl. Acoust. 2024, 217, 109807. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Trans. 2022, 129, 555–563. [Google Scholar] [CrossRef]
- Guo, R.; Li, Y.; Zhao, L.; Zhao, J.; Gao, D. Remaining useful life prediction based on the Bayesian regularized radial basis function neural network for an external gear pump. IEEE Access 2020, 8, 107498–107509. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Zhang, S.; Xue, D.; Zhang, S. Research on prediction method of hydraulic pump remaining useful life based on KPCA and JITL. Appl. Sci. 2021, 11, 9389. [Google Scholar] [CrossRef]
- Yu, H.; Li, H. Pump remaining useful life prediction based on multi-source fusion and monotonicity-constrained particle filtering. Mech. Syst. Signal Process. 2022, 170, 108851. [Google Scholar] [CrossRef]
- Sharma, A.K.; Punj, P.; Kumar, N.; Das, A.K.; Kumar, A. Lifetime prediction of a hydraulic pump using ARIMA model. Arab. J. Sci. Eng. 2024, 49, 1713–1725. [Google Scholar] [CrossRef]
- Ding, Y.; Ma, L.; Wang, C.; Tao, L. An EWT-PCA and extreme learning machine based diagnosis approach for hydraulic pump. IFAC-PapersOnLine 2020, 53, 43–47. [Google Scholar] [CrossRef]
- Buabeng, A.; Simons, A.; Frempong, N.K.; Ziggah, Y.Y. Hybrid intelligent predictive maintenance model for multiclass fault classification. Soft Comput. 2024, 28, 8749–8770. [Google Scholar] [CrossRef]
- Shao, Y.; Chao, Q.; Xia, P.; Liu, C. Fault severity recognition in axial piston pumps using attention-based adversarial discriminative domain adaptation neural network. Phys. Scr. 2024, 99, 056009. [Google Scholar] [CrossRef]
- Surucu, O.; Gadsden, S.A.; Yawney, J. Condition monitoring using machine learning: A review of theory, applications, and recent advances. Expert Syst. Appl. 2023, 221, 119738. [Google Scholar] [CrossRef]
- Wu, Z.; Lin, W.; Ji, Y. An integrated ensemble learning model for imbalanced fault diagnostics and prognostics. IEEE Access 2018, 6, 8394–8402. [Google Scholar] [CrossRef]
- Mahale, Y.; Kolhar, S.; More, A.S. Enhancing predictive maintenance in automotive industry: Addressing class imbalance using advanced machine learning techniques. Discov. Appl. Sci. 2025, 7, 1–21. [Google Scholar] [CrossRef]
- Geng, Y.; Wang, S.; Zhang, C. Life estimation based on unbalanced data for hydraulic pump. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 796–801. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Marcin, R.; Marcin, B. Research Scripts. Available online: https://github.com/mblachnik/2025_Data_balancers_pumps (accessed on 16 September 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).