Single Image-Based Reflection Removal via Dual-Stream Multi-Column Reversible Encoding

Abstract

Reflection removal from a single image is an ill-posed problem due to the inherent ambiguity in separating transmission and reflection components from a single composite observation. In this paper, we address this challenge by introducing a reversible feature encoding strategy combined with a simplified dual-stream decoding structure. In particular, the reversible NAFNet encoder enables us to retain all feature information throughout the encoding process while avoiding memory overhead, an aspect that is crucial for separating overlapping structures. In place of complex gated mechanisms, the proposed dual-stream decoder leverages shared encoder features and skip connections, thus enabling implicit bidirectional information flow between transmission and reflection streams. Although our model adopts a lightweight structure and omits attention modules, it achieves competitive results on standard reflection removal benchmarks, indicating that efficient and interpretable designs can match or surpass more complex counterparts.

1. Introduction

In the rapidly evolving fields of computational photography and computer vision, removing reflections from single images has emerged as a critical research problem. This task holds significant practical value for enhancing image quality in diverse applications, including object recognition, scene reconstruction, and augmented reality [1,2,3]. As illustrated in Figure 1, reflections primarily occur when images are captured through transparent media such as glass, typically resulting in a composite image that merges the desired transmission of the scene behind the glass with an undesired, mirror-like reflection.

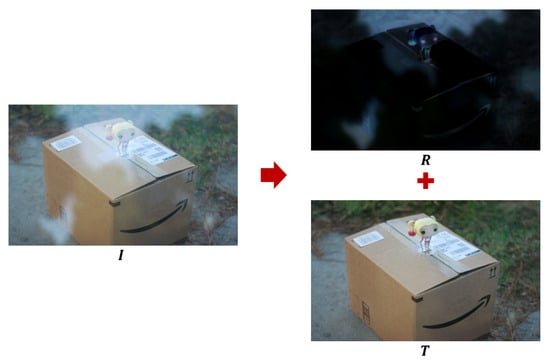
Figure 1. The captured image $\mathbf{I}$, which includes reflections, is composed of the unwanted reflected image $\mathbf{R}$ and the desired image $\mathbf{T}$.

Mathematically, this composite image can be expressed [4], represented as

$$\begin{array}{c}\hfill \mathbf{I}=\mathbf{T}+\mathbf{R},\end{array}$$

(1)

where $\mathbf{I}\in {\mathbb{R}}^{m\times n}$ represents the observed image in 2D space, $\mathbf{T}\in {\mathbb{R}}^{m\times n}$ is the transmission layer (background), and $\mathbf{R}\in {\mathbb{R}}^{m\times n}$ is the reflection layer. This decomposition is inherently ill-posed due to the infinite number of possible combinations of $\mathbf{T}$ and $\mathbf{R}$ that satisfy Equation (1).

To more accurately model real-world complexities, the equation can be extended [5,6], represented as

$$\begin{array}{c}\hfill \mathbf{I}=\alpha ·\mathbf{T}+\beta ·\mathbf{R},\alpha ,\beta \in \mathbb{R},\end{array}$$

(2)

where $\alpha ,\beta$ are scalar attenuation factors that represent the relative strengths of the transmission and reflection layers. Here, the operator “·” denotes scalar multiplication applied element-wise to all pixels of the image.

Further refinement introduces an alpha-matting map [7], represented as

$$\begin{array}{c}\hfill \mathbf{I}=\mathit{\alpha }·\mathbf{T}+\left(\mathbf{1}-\mathit{\alpha }\right)·\mathbf{R},\end{array}$$

(3)

where $\alpha \in {\mathbb{R}}^{m\times n}$ denotes the weight of the transmission layer at each pixel, and $(1-\alpha )$ is the complementary weight for the reflection layer. The · again represents scalar multiplication.

Although these refinements improve the realism of the mathematical model, they also increase computational complexity. To generalize further, residual terms can be added [8], represented as

$$\begin{array}{c}\hfill \mathbf{I}=\mathbf{T}+\mathbf{R}+\varphi (\mathbf{T},\mathbf{R}),\end{array}$$

(4)

where $\mathbf{T}$ and $\mathbf{R}$ denote the estimated transmission and reflection layers, respectively. Equality in Equation (4) indicates that the estimated layers can be expressed as the sum of the ground-truth layers $\mathbf{T}$ and $\mathbf{R}$ and an additional residual term. Here, $\varphi (\mathbf{T},\mathbf{R})$ represents additional residual interactions between $\mathbf{T}$ and $\mathbf{R}$, capturing nonlinear dependencies or interference effects that are not modeled by simple additive composition. While we introduce the generalized remainder term $\varphi (T,R)$ in Equation (4) to acknowledge real-world nonlinear interactions (e.g., saturation, scattering, ambient interference) that are not captured by a simple additive model, we do not explicitly model $\varphi (T,R)$ with a dedicated module or loss in this work. Instead, its effects are implicitly accounted for through the reconstruction consistency $I\approx \widehat{T}+\widehat{R}$ and complementary objectives (perceptual and exclusion losses), which encourage faithful layer formation and decorrelation. This keeps the framework lightweight and practical while retaining a formulation that is general enough to cover non-ideal phenomena.

The mathematical formulation of reflection removal has become more precise and detailed; the separation of $\mathbf{T}$ and $\mathbf{R}$ remains a challenging problem, motivating the development of robust and efficient algorithms for single-image reflection removal. Although considerable progress has been made with modeling and learning-based techniques, several fundamental limitations persist in existing methods.

First, most deep learning models employ a single-stream architecture that processes input images holistically, without explicitly separating the transmission and reflection layers [9,10]. While these models can generate visually convincing outputs, they frequently mix layer-specific features, making it challenging to suppress strong reflections or retain delicate background details.

Second, dual-stream architectures such as the DSRNet model by Hu and Guo [8] have sought to overcome this limitation through interaction modules connecting the transmission and reflection streams. However, these interaction mechanisms can sometimes create bottlenecks in information flow, leading to unstable training dynamics and performance degradation, especially in scenes with complex reflection patterns [11].

Third, most existing methods rely on residual or attention-based backbones that do not possess inherent invertibility. This results in the accumulation of information loss in deeper layers, which is problematic for reflection removal tasks that require both the preservation and disentanglement of fine details from each layer.

To address these issues, we propose a reflection removal framework that combines a reversible network backbone with a lightweight dual-stream decoder. Our main contributions are as follows:

• We adapt the reversible NAFNet encoder—originally proposed for image restoration [12]—to the reflection removal setting. The invertible residual design aims to preserve feature information during encoding and can support memory-efficient training via activation recomputation.
• We adopt a dual-stream decoder without heavy attention or gating modules. Shared encoder features are propagated via skip connections to two parallel branches corresponding to transmission and reflection, providing simple cross-stream interaction while keeping the decoder compact.

Prior work has explored reversible encoders and dual-stream decoders separately. Here, we study their combination for single-image reflection removal and describe design choices that seek to reduce cumulative feature loss while retaining training stability. We present evidence under the evaluated settings and discuss limitations.

Our approach is simple and resource-efficient, achieving promising performance on benchmarks by enabling bidirectional feature exchange via skip connections without complex attention or gating mechanisms.

The remainder of this paper is organized as follows: Section 2 reviews related work in classical, multi-image, and single-image reflection removal. Section 3 presents the proposed reversible dual-stream architecture in detail. Section 4 reports experimental results on public datasets and compares performance with prior methods. Finally, Section 5 concludes the paper and discusses future directions.

2. Related Work

2.1. Traditional (Non-Learning-Based) Reflection Removal

Traditional methods for reflection removal rely on physical modeling and handcrafted priors to address the inherent ill-posedness of the problem. A widely used image formation model posits that the observed image $\mathbf{I}\in {\mathbb{R}}^{m\times n}$ is the linear sum of a transmitted layer $\mathbf{T}\in {\mathbb{R}}^{m\times n}$ (background) and a reflected layer $\mathbf{R}\in {\mathbb{R}}^{m\times n}$ (foreground), with potential attenuation or blur affecting $\mathbf{R}$ [13]. Early approaches often required multiple input images or user-provided annotations to resolve the ambiguity. For example, multiple images of the same scene could be captured under varying conditions—such as different orientations of a polarization filter or flash/no-flash pairs—to facilitate layer separation [14,15]. When such additional modalities are available, physics-based priors (e.g., polarization cues or lighting variations) can be leveraged to assist in layer separation. However, in practice, acquiring multiple well-aligned images or accurate user-provided masks is often infeasible, which has motivated increasing interest in single-image methods that exploit visual priors.

Because single-image reflection removal is inherently ill-posed, traditional approaches typically impose strong assumptions in the gradient or frequency domains of the constituent layers. A common assumption is that unwanted reflections exhibit lower sharpness or smoother textures than the underlying background. For instance, Li and Brown [13] formulated an energy minimization problem encouraging the reflection layer to have smooth, attenuated gradients and the transmission layer to have sparse, in-focus gradients. Similarly, Wan et al. [15] computed per-pixel depth-of-field to distinguish reflection edges from background edges, based on the observation that reflections are often more blurred; these edge maps then guided a constrained optimization to recover both layers. Other methods have exploited specific phenomena such as “ghosting” artifacts: Shih et al. [16] modeled the doubled, shifted reflections caused by thick glass and applied a deblurring-based algorithm to separate the ghosted layers. Low-rank priors have also been explored; for example, Han and Sim [17] framed reflection removal as a low-rank matrix completion problem, assuming that the reflection layer lies in a lower-rank subspace that can be separated from the background.

While these handcrafted-prior methods can be effective in controlled settings, their performance often degrades on real-world images containing complex reflection patterns. Moreover, their optimization procedures are typically computationally expensive, limiting their practical applicability.

2.2. Multi-Image Reflection Removal

Using multiple images or exposures of the same scene can substantially reduce the ambiguity in reflection removal. Many studies exploit differences in reflection appearance across images to facilitate the separation of the transmission and reflection layers. A common approach employs polarization: capturing images with varying polarizer angles changes the relative intensities of the reflected and transmitted components, enabling separation using polarization physics [14]. Another strategy leverages controlled lighting; for example, capturing both flash and no-flash images can help suppress or remove specular reflections by isolating the reflection component under one lighting condition.

Some methods utilize slight viewpoint or camera movements; as the camera shifts, reflections on glass surfaces exhibit motion patterns distinct from the background, making them easier to separate. Sirinukulwattana et al. [18] exploited a stereo disparity cue from two images to identify and smooth the reflection layer while preserving the sharp transmitted layer. In general, multi-view or burst-photography approaches impose that true background features maintain consistent motion across frames, whereas reflection features violate this consistency. For example, Xue et al. [19] presented an optimization method that iteratively separates layers by exploiting differences in their optical flow fields across a short video sequence. Other approaches enforce cross-image consistency or apply low-rank constraints; for instance, some methods achieve layer separation by sparsely decomposing motion components or applying rank and structural priors to the background across several images.

These multi-image methods often yield strong performance because the additional observations provide constraints that make the problem more tractable. In recent years, learning-based multi-image approaches have also been proposed. For example, Liu et al. [20] designed a CNN that processes a short sequence captured by a moving camera; by alternating between estimating optical flow for each layer and reconstructing the layers with a deep network, they leverage motion parallax cues to disentangle reflections from the background.

Both model-based and learning-based multi-image approaches consistently demonstrate that multiple observations substantially enhance the quality of reflection removal. Nevertheless, such methods require controlled capture environments or access to video sequences, which are not always available. This limitation continues to drive research into effective single-image reflection removal techniques.

2.3. Single-Image Reflection Removal with Deep Learning

In recent years, data-driven approaches based on deep learning have greatly advanced single-image reflection removal by automatically learning relevant priors from large datasets. Early deep learning methods formulated reflection removal as a layer separation problem and trained models using synthetic datasets. Fan et al. [21] developed one of the first CNN-based systems that directly mapped a reflected input image to a clean background output. To train their model, they created composite images by overlaying natural images with blurred reflections, simulating the defocus effect of out-of-focus reflections. Their two-stage architecture first predicted an intrinsic edge map to locate strong background structures, which then guided the final reconstruction of the transmission layer. This demonstrated the feasibility of end-to-end reflection removal, but results could be over-smoothed when reflections were sharp or dominant.

Subsequent works improved quality by introducing better training losses and network designs. A notable example is Zhang et al. [9], who trained a deep network with a combination of perceptual loss, adversarial loss, and exclusion loss to enforce separation of layers. The perceptual loss (computed using a pre-trained VGG network) encourages the output to match the ground-truth background in high-level feature space, while the exclusion loss penalizes correlations between the gradient maps of the estimated reflection and transmission layers. By leveraging both low-level cues (through exclusion of overlapping edges) and high-level fidelity (through perceptual similarity), their method produced significantly clearer background restorations than earlier approaches.

Other researchers incorporated domain knowledge into network architectures. Wan et al. [5] proposed a multi-scale concurrent network that explicitly predicts the reflection layer’s gradient profile alongside the image itself, integrating gradient inference with image reconstruction in a unified framework. They also employed perceptual feature loss to improve visual realism. These deep learning methods decisively outperformed classical approaches, particularly on complex real-world images where handcrafted priors often fail.

Recent research has continued to advance single-image reflection removal, focusing on robust training and network refinement. One challenge is the scarcity of real-world training pairs containing both reflection-free and reflected images. To address this, Wen et al. [7] went beyond linearity by synthesizing more realistic reflection images that include non-linear phenomena such as saturation and environmental effects, and they trained a cascaded network on this data to better generalize to real reflections. Wei et al. [10] introduced a method that leverages misaligned real photos—where the same scene with and without reflections are not perfectly registered—by using an alignment-invariant loss function during training. This strategy, implemented in the ERRNet model, expanded the diversity of real-world training examples and improved robustness to misalignment.

At the same time, network architectures have evolved toward more iterative and interpretable designs. For example, the Iterative Boosting framework (IBCLN) by Li et al. [22] uses a cascaded refinement scheme in which the network progressively refines the estimated transmission and reflection layers over multiple stages, allowing them to boost each other’s prediction quality. By alternately refining the residual reflection and background—using memory units to retain information between iterations—the cascade architecture achieves excellent performance in various benchmarks. Recently, an approach using a diffusion-based generation model has also appeared. L-DiffER improved the restoration of the low-transmission reflection section by using text descriptions of scenes and reflections as positive and negative prompts, respectively, and securing generation fidelity with altruistic condition definition and multi-condition construction [23].

To summarize, most modern approaches for single-image reflection removal employ deep convolutional networks trained on tailored data with custom loss formulations. They have led to significant improvements in both the quantitative (PSNR/SSIM) and qualitative (visual quality) performance compared to previous methods, resulting in clearer and more realistic output images. Continued research aims to enhance these networks for more difficult scenarios (such as severe reflections); nevertheless, recent advances have clearly positioned deep learning as the dominant approach in single-image reflection removal.

Single-image reflection removal is inherently challenged by the overlap between the background ($\mathbf{T}$) and the reflection ($\mathbf{R}$). Unlike generic restoration tasks (e.g., denoising, deblurring), where information loss primarily reduces overall sharpness, even slight feature collapse in reflection removal directly confuses layer membership, since $\mathbf{T}$ and $\mathbf{R}$ often share edges and textures. This makes preserving fine-scale details particularly crucial for stable disentanglement. To address this, we adopt an invertible coupling encoder. By splitting features into two partitions and designing them to be exactly recoverable in the reverse direction, the encoder suppresses cumulative loss in intermediate representations. This guarantees that overlapping cues (edges, textures) remain intact, preventing the decoder from irrecoverably mixing $\mathbf{T}$ and $\mathbf{R}$. The preserved features also ensure that the dual-stream decoder’s mutual gating (MuGI) has reliable evidence for cross-suppression and cross-enhancement; without such preservation, MuGI could suppress or enhance features on the wrong branch due to missing cues, leading to unstable separation.

Meanwhile, the decoder retains a symmetric backbone but specializes the branches: ($\mathbf{DecT}$) predicts the residual reflection component ($\Delta \mathbf{T}$) to be removed and produces ($\widehat{\mathbf{T}}=\mathbf{I}-\Delta \mathbf{T}$), whereas ($\mathbf{DecR}$) directly reconstructs ($\widehat{\mathbf{R}}$). This design ensures complementary decomposition of the two layers. Compared to prior dual-stream approaches such as DSRNet [8] and IBCLN [22], which rely on heavy gating or cascaded refinement, our decoder adopts a simpler mutual-gating strategy without attention-heavy modules. Similarly, unlike RDNet [11], which applies invertibility to generic image restoration but not to layer separation, our framework specifically integrates a reversible encoder with a dual-stream design to preserve overlapping features while enabling stable disentanglement. This deliberate combination of an invertible encoder and a mutually gated decoder is motivated by the observation that non-invertible backbones accumulate information loss at deeper layers. By contrast, invertibility jointly secures feature preservation and stable $\mathbf{T}/\mathbf{R}$ disentanglement, as corroborated by the improved PSNR/SSIM of the dual-stream + invertible encoder configuration (Table 2).

3. Methodology

3.1. Overall Architecture

The proposed reflection removal framework employs a dual-stream design to simultaneously recover both the clean (transmission) and reflection layers from a single image. The overall architecture is inspired by the dual-branch framework presented in Hu and Guo [8], but augmented with a reversible network backbone to preserve information flow [24]. As shown in Figure 2, the network employs a multiscale encoder to process the input, followed by parallel decoding streams to reconstruct the transmission ($\mathbf{T}$) and reflection ($\mathbf{R}$) images.

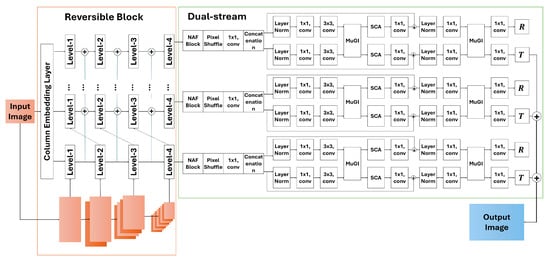
Figure 2. Overview of the proposed network architecture. The model consists of a reversible encoder block (left, orange box) and a dual-stream decoder (right, green box). The input image is first processed by a Column Embedding Layer, which converts the input into overlapping patch embeddings via a $7\times 7$ convolution. These embeddings are processed through multi-scale reversible coupling across four levels in the encoder. The dual-stream decoder reconstructs the transmission ($\mathbf{T}$) and reflection ($\mathbf{R}$) layers in parallel, leveraging multi-level features and interaction modules (NAF, MuGI, SCA, etc.). Stage-wise predictions are aggregated to form the final output.

Specifically, the input image is projected by a Column Embedding Layer using a $7\times 7$ convolution with stride 2, effectively partitioning the input into overlapping patches suitable for multi-column processing. The embedded features serve as the initial input to the reversible encoder.

To address the limitations of fixed gating patterns in earlier dual-stream networks, our encoder incorporates reversible architectures (described in detail below) to maintain information integrity during feature extraction [11,24]. The encoder generates deep feature representations that are shared across both streams, allowing the transmission and reflection decoders to exploit the same low-level features. Each decoder branch then specializes in reconstructing one layer ($\mathbf{T}$ or $\mathbf{R}$) from these features. By passing encoder features via skip connections to each decoder, the model ensures that both transmission and reflection streams incorporate detailed semantic information at multiple scales.

We also add a global residual connection for the transmission layer. Specifically, the network predicts a residual image, which, when added to the input, yields the clean transmission estimate. This residual learning strategy accelerates convergence by focusing the network on predicting the reflection component to remove.

The architecture can be executed in a cascaded fashion for progressively refined results—multiple reversible columns (stages) produce intermediate $\mathbf{T}$ and $\mathbf{R}$ estimates, which are supervised during training and ultimately aggregated into the final output from the last stage. Specifically, we set $N=4$ for the number of cascaded columns, enabling multi-level refinement; outputs from preceding stages are used to inform later ones, with each stage producing $({\mathbf{T}}^k,{\mathbf{R}}^k)$.

Unlike prior approaches that adopt either a reversible backbone or a dual-stream decoder in isolation, our architecture deliberately combines both components. This is motivated by the observation that non-reversible backbones inevitably accumulate information loss in deeper layers, while heavily gated dual-stream networks often suffer from unstable training dynamics. By unifying a reversible NAFNet encoder with a MuGI-based dual-stream decoder, we achieve a complementary balance.

3.2. Reversible NAFBlock

The basic structure of a NAFBlock, shown in Figure 3, consists of a depthwise convolution, a SimpleGate operator, a Simplified Channel Attention (SCA) module, and a pointwise convolution. Each component plays a distinct role in efficient feature transformation. The depthwise convolution processes each channel independently to extract spatial features while significantly reducing computational cost compared to a standard convolution. The SimpleGate mechanism splits the feature channels into two parts $(U,V)$ and applies element-wise gating $U\odot \sigma \left(V\right)$, where $\sigma (·)$ is the sigmoid activation function, and ⊙ denotes element-wise multiplication. This operation enables selective information flow without relying on computationally expensive attention mechanisms. The SCA module computes a lightweight channel-wise importance vector $\mathrm{SCA}\left(\mathbf{Z}\right)\in {\mathbb{R}}^C$ to rescale features, thereby enhancing informative channels and suppressing less relevant ones. Finally, the pointwise convolution performs a $1\times 1$ convolution to mix information across channels, integrating the spatially processed features from the depthwise stage.

Figure 3. Structure of a NAFBlock used in the reversible encoder. Each block consists of a depthwise convolution, a SimpleGate with Simplified Channel Attention (SCA), and a pointwise convolution. This lightweight design enables efficient feature transformation while preserving important channel information.

To ensure invertibility, we organize NAFBlocks into Reversible Blocks (Figure 4), which implement the coupling structure described in Equations (9) and (10). Let the input feature be denoted as $\mathbf{X}\in {\mathbb{R}}^{m\times n}$, where m represents the spatial dimension and n denotes the channel dimension. As illustrated in the figure, the input feature $\mathbf{X}$ is first split channel-wise into two halves, ${\mathbf{X}}_a$ and ${\mathbf{X}}_b$. In the forward pass, ${\mathbf{X}}_a$ is updated by adding the output of a transformation function $F(·)$ applied to ${\mathbf{X}}_b$, yielding ${\mathbf{Y}}_a={\mathbf{X}}_a+F\left({\mathbf{X}}_b\right)$. Next, ${\mathbf{X}}_b$ is updated by adding the output of another transformation function $G(·)$ applied to ${\mathbf{Y}}_a$, resulting in ${\mathbf{Y}}_b={\mathbf{X}}_b+G\left({\mathbf{Y}}_a\right)$. Here, $F(·)$ and $G(·)$ are sub-networks composed of stacked NAFBlocks, where F focuses on transforming the second half’s features using context from the first half, and G transforms the first half using context from the updated second half. This bi-directional coupling allows continuous feature interaction between both partitions.

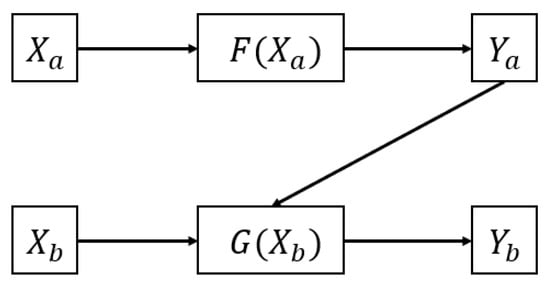
Figure 4. Forward flow of a Reversible Block (RevBlock). The input features are split into two halves, ${\mathbf{X}}_a$ and ${\mathbf{X}}_b$, and processed through coupled transformations $F(·)$ and $G(·)$ to produce ${\mathbf{Y}}_a$ and ${\mathbf{Y}}_b$. Here, F updates ${\mathbf{X}}_a$ based on ${\mathbf{X}}_b$’s context, while G updates ${\mathbf{X}}_b$ based on the newly computed ${\mathbf{Y}}_a$. This coupling enables invertibility, allowing exact recovery of the input from the output via Equation (10).

The key property of this structure is that it is exactly invertible: given ${\mathbf{Y}}_a$ and ${\mathbf{Y}}_b$, we can recover the original inputs by computing ${\mathbf{X}}_b={\mathbf{Y}}_b-G\left({\mathbf{Y}}_a\right)$ and then ${\mathbf{X}}_a={\mathbf{Y}}_a-F\left({\mathbf{X}}_b\right)$. This coupling mechanism ensures that no information is lost during forward propagation, allowing all intermediate activations to be recomputed on-the-fly during backpropagation for memory efficiency.

Figure 4 provides a more detailed schematic of this process. The input tensor is divided into two equal channel groups. Function F processes ${\mathbf{X}}_b$ to generate an update for ${\mathbf{X}}_a$, while function G processes the updated ${\mathbf{Y}}_a$ to update ${\mathbf{X}}_b$. Because F and G are each constructed from NAFBlocks, they include depthwise convolution, SimpleGate, and SCA, enabling both local spatial refinement and channel-wise feature reweighting in each coupling step. This ensures that each half of the feature map is conditioned on the other, which strengthens cross-partition dependency modeling.

Unlike previous approaches that use computationally intensive self-attention layers, NAFBlocks employ simple gating and lightweight attention mechanisms, significantly reducing computational costs without sacrificing performance. Formally, within an NAFBlock the input feature $\mathbf{X}$ is first normalized and passed through two convolutions, represented as

$${\mathbf{X}}_1={\mathrm{Conv}}_1\left(\mathrm{Norm}\left(\mathbf{X}\right)\right),{\mathbf{X}}_2={\mathrm{Conv}}_2\left({\mathbf{X}}_1\right),$$

(5)

where $\mathbf{X}\in {\mathbb{R}}^{C\times H\times W}$ is the input tensor, ${\mathrm{Conv}}_k$ denotes a convolutional layer, and $\mathrm{Norm}(·)$ is a normalization function.

A channel-split gating then produces two halves $(\mathbf{U},\mathbf{V})$ and combines them by

$$(\mathbf{U},\mathbf{V})=\mathrm{split}\left({\mathbf{X}}_2\right),\mathbf{Z}=\mathbf{U}\odot \sigma \left(\mathbf{V}\right),$$

(6)

The result $\mathbf{Z}$ is scaled by SCA and transformed, represented as

$${\mathbf{Z}}^{\prime }={\mathrm{Conv}}_3\left(\mathbf{Z}\odot \mathrm{SCA}\left(\mathbf{Z}\right)\right),$$

(7)

where $\mathrm{SCA}(·)$ returns a per-channel scaling vector.

Finally, a two-step residual addition is applied, represented as

$$\mathbf{Y}=\mathbf{X}+\beta {\mathbf{Z}}^{\prime },{\mathbf{Y}}_{\mathrm{out}}=\mathbf{Y}+\gamma ·\mathrm{FN}\left(\mathbf{Y}\right),$$

(8)

where $\beta ,\gamma \in \mathbb{R}$ are learnable scalars and $\mathrm{FN}(·)$ is a small feed-forward network (two $1\times 1$ convolutions with a SimpleGate in between).

To ensure reversibility, we adopt the design principle of invertible residual networks [24]. Specifically, we arrange NAFBlocks in coupled pairs such that the input to each reversible unit can be split and reconstructed from its output. Let $\mathbf{X}=[{\mathbf{X}}_a,{\mathbf{X}}_b]$ be the split input feature. The forward transformation is defined as

$${\mathbf{Y}}_a={\mathbf{X}}_a+F\left({\mathbf{X}}_b\right),{\mathbf{Y}}_b={\mathbf{X}}_b+G\left({\mathbf{Y}}_a\right),$$

(9)

where F and G are sub-networks made of stacked NAFBlocks.

This transformation is information-lossless and can be inverted as:

$${\mathbf{X}}_b={\mathbf{Y}}_b-G\left({\mathbf{Y}}_a\right),{\mathbf{X}}_a={\mathbf{Y}}_a-F\left({\mathbf{X}}_b\right).$$

(10)

During training, this reversible architecture enables memory-efficient backpropagation by recomputing intermediate activations on-the-fly [11].

The decoder branches, corresponding to transmission (DecT) and reflection (DecR), consist of stacked NAFBlocks followed by upsampling operations. Here, DecT denotes the decoder branch dedicated to reconstructing the transmission layer $\widehat{\mathbf{T}}$, and DecR denotes the branch for reconstructing the reflection layer $\widehat{\mathbf{R}}$. Each decoder block receives shared encoder features and skip connections from corresponding encoder stages to preserve spatial detail.

The decoding process in each stage involves the following:

1

$1\times 1$ convolution to project the features (reduce or expand the number of channels to match the target dimension).

2

A stack of NAFBlocks for feature transformation.

3

An upsampling module, implemented via bilinear interpolation or sub-pixel convolution to increase the spatial resolution.

4

A final convolution layer to generate either $\widehat{\mathbf{T}}$ or $\widehat{R}$.

In the transmission branch (DecT), the network predicts a residual image $\Delta \mathbf{T}$ that represents the estimated reflection content to be removed from the input image. This residual is subtracted from the input image $\mathbf{I}$ to obtain the final clean transmission estimate

$$\widehat{\mathbf{T}}=\mathbf{I}-\Delta \mathbf{T}.$$

In the reflection branch (DecR), the network directly reconstructs the reflection layer $\widehat{\mathbf{R}}$. This symmetric yet specialized design ensures that both streams focus on their respective targets while sharing structural information through skip connections, effectively disentangling overlapping features from the input image.

3.3. Dual-Stream Fusion Layer

We employ a dual-stream architecture to regulate the flow and separation of information between the transmission and reflection layers. In the DSRNet design by Hu and Guo [8], mutually gated blocks are utilized to facilitate feature exchange between streams. In our design, we explicitly adopt a Mutually-Gated Interaction (MuGI) block, which performs cross-gating between the transmission and reflection features.

Once encoding is complete, we divide the feature representation into two streams for parallel decoding into transmission and reflection outputs. At each decoder layer, the intermediate transmission feature $\mathbf{T}$ and reflection feature $\mathbf{R}$ are modulated by gating functions that exchange information between the two streams:

$$\begin{array}{cc}\hfill \widehat{\mathbf{T}}& ={\mathcal{G}}_1\left(\mathbf{T}\right)\odot {\mathcal{G}}_2\left(\mathbf{R}\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \widehat{\mathbf{R}}& ={\mathcal{G}}_1\left(\mathbf{R}\right)\odot {\mathcal{G}}_2\left(\mathbf{T}\right),\hfill \end{array}$$

(12)

where ⊙ denotes element-wise multiplication. This ensures complementary behavior: if an edge is enhanced in the transmission stream, it is suppressed in the reflection stream, and vice versa.

The Mutually-Gated Interaction (MuGI) block, as depicted in Figure 5, enables explicit feature exchange between the transmission and reflection streams. Here, $\mathbf{T}$ denotes the feature map of the transmission stream, and $\mathbf{R}$ denotes the feature map of the reflection stream, where C, H, and W are the number of channels, height, and width, respectively. Each stream’s features ($\mathbf{T}$ and $\mathbf{R}$) are processed through two gating functions, ${\mathcal{G}}_1(·)$ and ${\mathcal{G}}_2(·)$. Unlike additive fusion, these functions generate gating maps that are multiplied across streams, ensuring that $\widehat{\mathbf{T}}$ is modulated by information from $\mathbf{R}$, and $\widehat{\mathbf{R}}$ by information from $\mathbf{T}$. The cross-connections in the figure illustrate how the network mutually enhances or suppresses features between the two streams, enabling complementary learning for more robust and interpretable layer separation.

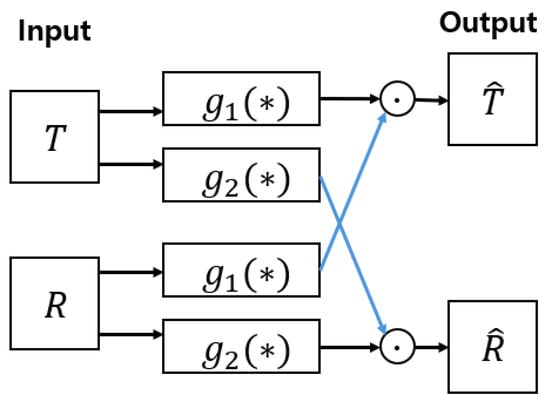
Figure 5. Structure of the Mutually-Gated Interaction (MuGI) block. * denotes the function’s input. Transmission features ($\mathbf{T}$) and reflection features ($\mathbf{R}$) are processed through two gating functions (${\mathcal{G}}_1$ and ${\mathcal{G}}_2$). The outputs are mutually modulated by cross-stream gating, i.e., $\widehat{\mathbf{T}}={\mathcal{G}}_1\left(\mathbf{T}\right)\odot {\mathcal{G}}_2\left(\mathbf{R}\right)$ and $\widehat{\mathbf{R}}={\mathcal{G}}_1\left(\mathbf{R}\right)\odot {\mathcal{G}}_2\left(\mathbf{T}\right)$, enabling complementary learning for robust layer separation.

Empirically, we found that this cross-gated interaction, combined with shared encoder features and skip connections, was sufficient to achieve high separation quality without the need for heavy attention modules. This approach also avoids the risk of information bottlenecks observed in heavily gated models like DSRNet [8], while keeping the dual decoder lightweight and maintaining effective bidirectional feature communication.

3.4. Loss Function Design

To guide the network in decomposing the input image $\mathbf{I}$ into transmission ($\mathbf{T}$) and reflection ($\mathbf{R}$) layers, we define a total loss function composed of multiple complementary objectives. Here, $\mathbf{I}$ denotes the input RGB image, $\mathbf{T}$ and $\mathbf{R}$ are the ground-truth transmission and reflection images, and $\widehat{\mathbf{T}}$ and $\widehat{\mathbf{R}}$ are their corresponding predicted outputs. H and W are the image height and width.

Each loss term is formulated to enforce a different aspect of decomposition quality.

Content Loss: The content loss enforces pixel-level accuracy by minimizing the $L_1$ norm between the predicted and ground truth layers, represented as

$${\mathcal{L}}_{\mathrm{pix}}^{\mathbf{T}}=|\widehat{\mathbf{T}}-\mathbf{T}{|}_1,{\mathcal{L}}_{\mathrm{pix}}^{\mathbf{R}}={|\widehat{\mathbf{R}}-\mathbf{R}|}_1,$$

(13)

where ${|·|}_1$ denotes the element-wise $L_1$ norm over all pixels. This loss ensures correct reconstruction of color and texture at the pixel level.

Gradient Loss: To improve edge sharpness, especially in the transmission layer, we include a first-order image gradient loss, represented as

$${\mathcal{L}}_{\mathrm{grad}}^{\mathbf{T}}=|{\nabla }_x\widehat{\mathbf{T}}-{\nabla }_x\mathbf{T}{|}_1+{|{\nabla }_y\widehat{\mathbf{T}}-{\nabla }_y\mathbf{T}|}_1.$$

(14)

Here, ${\nabla }_x$ and ${\nabla }_y$ denote horizontal and vertical gradient operators, respectively. This term promotes consistency in image edges and reduces blur.

Perceptual Loss: Following Zhang et al. [9], we apply a perceptual loss based on the VGG-19 network to capture high-level semantics and textures, represented as

$${\mathcal{L}}_{\mathrm{perc}}^{\mathbf{T}}=\sum _{\ell }{|{\mathbf{\Phi }}_{\ell }\left(\widehat{\mathbf{T}}\right)-{\mathbf{\Phi }}_{\ell }\left(\mathbf{T}\right)|}_1.$$

(15)

Here, ${\mathbf{\Phi }}_{\ell }(·)$ denotes the feature map extracted from the ℓ-th layer of a pretrained VGG-19 model. This loss enhances perceptual realism by ensuring that reconstructed images resemble natural scenes in feature space.

Exclusion Loss: Also inspired by Zhang et al. [9], the exclusion loss encourages disjoint structural information between $\widehat{\mathbf{T}}$ and $\widehat{\mathbf{R}}$, represented as

$${\mathcal{L}}_{\mathrm{excl}}=\sum _{i,j}\left(\left|{\partial }_x{\widehat{\mathbf{T}}}_{ij}·{\partial }_x{\widehat{\mathbf{R}}}_{ij}\right|+\left|{\partial }_y{\widehat{\mathbf{T}}}_{ij}·{\partial }_y{\widehat{\mathbf{R}}}_{ij}\right|\right),$$

(16)

where ${\partial }_x$ and ${\partial }_y$ denote partial derivatives with respect to the horizontal and vertical directions, $(i,j)$ are pixel coordinates, and · represents element-wise multiplication. This term penalizes overlapping gradients in both layers, promoting better separation.

Reconstruction Loss: To ensure that the predicted layers recombine into the input image, we apply a reconstruction consistency loss, represented as

$${\mathcal{L}}_{\mathrm{rec}}={|\widehat{\mathbf{T}}+\widehat{\mathbf{R}}-\mathbf{I}|}_2^2.$$

(17)

Here, ${|·|}_2$ denotes the Euclidean ($L_2$) norm over all pixels. This enforces the physical constraint that $\mathbf{I}=\widehat{\mathbf{T}}+\widehat{\mathbf{R}}$, aligning with the image formation model.

Total Loss: All terms are linearly combined with weights, represented as

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{pix}}^{\mathbf{T}}+\alpha {\mathcal{L}}_{\mathrm{pix}}^{\mathbf{R}}+\beta {\mathcal{L}}_{\mathrm{perc}}^{\mathbf{T}}+\gamma {\mathcal{L}}_{\mathrm{excl}}+\delta {\mathcal{L}}_{\mathrm{rec}}.$$

(18)

Here, $\alpha$, $\beta$, $\gamma$ and $\delta$ are scalar hyperparameters that control the relative weight of each loss term. In this study, $\alpha$ = 1.0, $\beta$ = 0.1, $\gamma$ = 0.05, and $\delta$ = 1.0 were set to adjust the relative weights of loss items.

4. Experimental Results

4.1. Implementation Details

We implemented our model in PyTorch version 2.5.1 [25] and trained it for 50 epochs on an RTX 3050 GPU (NVIDIA Corporation, Santa Clara, CA, USA) using the Adam optimizer [26]. The initial learning rate was set to $1\times {10}^{-4}$, decaying via a multi-step scheduler at 60% and 85% of the total epochs. The batch size was set to 4, and Automatic Mixed Precision (AMP) was optionally enabled depending on the computing environment. We employed early stopping by monitoring the validation PSNR at the end of each epoch, with a patience of 5 epochs. Training was halted if validation PSNR did not improve for five consecutive epochs. All reported results are from the checkpoint that achieved the best validation PSNR. SSIM was also computed as a reference metric but not used as a selection criterion.

To enable fair comparison with prior work, training and evaluation followed two widely used data settings. The first setting, adopted in [27,28], consists of 90 real image pairs from [9] and 7643 synthetic pairs generated from the PASCAL VOC dataset [29]. The second setting, following [8,30], additionally includes 200 real image pairs from [22]. Synthetic data were generated according to the physical model proposed in DSRNet [8]. Within each training source, the validation set was split using a hold-out strategy based on a predefined validation ratio, and hyperparameter tuning was performed exclusively on the validation set. The original input resolution was preserved during training, but reflect padding (to multiples of 8) was applied to the image borders for computational stability. After inference, restored images were cropped back to their original resolution for evaluation. We report Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) as evaluation metrics.

4.2. Qualitative Evaluation

We first assess the visual quality of our reflection removal results in comparison with existing methods. Figure 6, Figure 7 and Figure 8 present representative samples from the SolidObject, Postcard, and Real20 test sets, respectively. The proposed reversible NAFNet + dual-stream model consistently produces background images with markedly reduced residual reflections compared to prior approaches. In contrast, several baseline methods exhibit either visible residual reflections or distortion in the recovered background. For example, the method of Zhang et al. [9] leaves faint ghosting artifacts in the Postcard example, whereas our method yields a clean background reconstruction. Similarly, traditional architectures may fail to suppress reflections entirely—leaving semi-transparent artifacts—or may over-remove important background structures by misclassifying them as reflections [21].

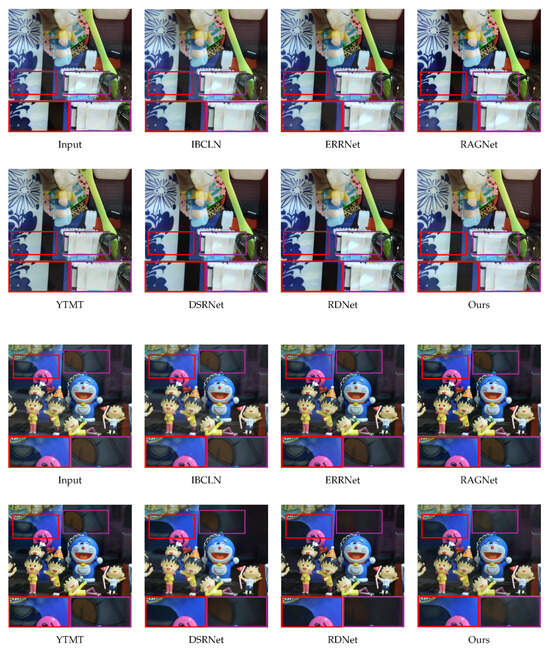
Figure 6. Qualitative comparison on Solid datasets. The red and purple squares are enlarged sections where reflection removal has been applied.

Figure 7. Qualitative comparison on the Postcard dataset. The red and purple squares are enlarged sections where reflection removal has been applied.

Figure 8. Qualitative comparison on Real datasets. The red and blue squares are enlarged sections where reflection removal has been applied.

As shown in the top row of Figure 6 and the bottom row of Figure 8, our method demonstrates superior results compared to other models. In addition, in Figure 7 and other examples, the reflection separation quality is comparable to that of competing approaches. These results indicate that our method performs well on standard benchmarks and generalizes robustly to unconstrained real-world conditions.

4.3. Quantitative Evaluation

We further evaluate our method on three benchmark datasets: Postcard, Real20 and SolidObject using peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) as quantitative metrics. In this paper, all results from comparative methods were cited from the original papers (published/official repositories), and no retraining was performed. Table 1 reports a comparison between our method and several state-of-the-art baselines. On average, this model achieved competitive SSIM values, but the PSNR score was relatively low. This is interpreted as a result of high structural similarity but slightly lower pixel accuracy because the loss function is designed to emphasize structural and perceptual consistency (gradient, perception loss) rather than pixel-level accuracy. While our approach does not perform well on every dataset, it demonstrates satisfactory performance on average.

Table 1. Quantitative results of various methods on three real-world benchmark datasets. The best results are highlighted in bold, and the second-best results are underlined.

Method	Real20		Objects		Postcard		Average
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Zhang et al. [9]	16.81	0.797	22.55	0.788	22.68	0.856	20.68	0.814
ERRNet [10]	22.89	0.803	24.87	0.896	22.04	0.876	23.27	0.858
IBCLN [22]	21.86	0.762	24.87	0.893	23.39	0.875	23.37	0.843
RAGNet [28]	22.95	0.793	26.15	0.903	23.67	0.879	24.26	0.858
YTMT [27]	23.26	0.806	24.87	0.896	22.91	0.884	23.68	0.862
DSRNet [8]	24.23	0.820	26.28	0.914	24.56	0.908	25.02	0.881
RDNet [11]	24.43	0.835	25.76	0.905	25.95	0.920	25.38	0.887
Ours	23.24	0.848	25.88	0.913	24.96	0.902	24.69	0.888

4.4. Ablation Study

To verify the effectiveness of each architectural component, we conduct an ablation study by comparing four variants of our model: (i) single-stream + plain encoder, (ii) dual-stream + plain encoder, (iii) single-stream + reversible encoder, and (iv) dual-stream + reversible encoder (our full model). The -RevEnc variants replace the reversible encoder with a standard non-reversible encoder, while the -DualStream variants remove the dual-stream decoder and adopt a single-stream decoder. Quantitative results on the Postcard test set are summarized in Table 2, showing that the dual-stream reversible configuration achieves the best PSNR and SSIM, while the lighter plain encoder models provide higher computational efficiency at the cost of image quality.

Table 2. Ablation study on architectural variants of our reflection removal network. Comparison between dual- vs. single-stream decoders and reversible vs. plain encoders. Metrics are averaged over the validation set. Best results are highlighted in bold.

Configuration	Params (M)	GFLOPs	Latency	Throughput	PSNR	SSIM
Single-Stream + Plain	15.19	208.14	10.39	385.13	22.90	0.796
Dual-Stream + Plain	16.24	259.68	28.61	139.81	23.59	0.860
Single-Stream + Rev.	42.33	594.69	44.45	89.99	23.63	0.863
Dual-Stream + Rev.	43.38	1009.72	69.09	57.89	24.69	0.888

Table 2. Ablation study on architectural variants of our reflection removal network. Comparison between dual- vs. single-stream decoders and reversible vs. plain encoders. Metrics are averaged over the validation set. Best results are highlighted in bold.

Configuration	Params (M)	GFLOPs	Latency	Throughput	PSNR	SSIM
Single-Stream + Plain	15.19	208.14	10.39	385.13	22.90	0.796
Dual-Stream + Plain	16.24	259.68	28.61	139.81	23.59	0.860
Single-Stream + Rev.	42.33	594.69	44.45	89.99	23.63	0.863
Dual-Stream + Rev.	43.38	1009.72	69.09	57.89	24.69	0.888

5. Conclusions

In this work, we addressed the challenging task of single-image reflection removal by proposing an efficient and interpretable framework that integrates a reversible encoder with a simplified dual-stream decoder. Unlike prior methods that rely heavily on attention modules or gated blocks, our design suggests that promising performance can be achieved under the evaluated settings while maintaining low complexity through careful architectural choices.

The novelty of our study lies in the purposeful integration of a reversible encoder with a dual-stream decoder. Rather than claiming universal superiority, we study this combination and provide initial evidence that it may help balance feature preservation with training stability under the evaluated settings. We discuss design choices that seek to reduce cumulative feature loss while keeping the training dynamics stable.

Specifically, we employed a reversible NAFNet encoder, originally developed for general image restoration, and adapted it to reflection removal. Its invertible residual structure preserves feature information during encoding and can enable memory-efficient training via activation recomputation.

On the decoding side, our dual-stream design omits explicit attention or gating mechanisms. Instead, we propagate shared encoder features to both transmission and reflection branches via skip connections, enabling simple bidirectional interaction while keeping the decoder compact. This differentiates our method from dual-stream architectures that depend on heavy gating or attention, which can reduce computational overhead while maintaining training stability.

Experiments on public benchmarks yield reliable quantitative and qualitative results and demonstrate robustness in real-world cases without requiring any test-time adjustments. Overall, this work highlights the reversible dual-stream architecture as a promising direction for efficient and high-quality reflection cancellation. Nevertheless, the limitation of this work is that by prioritizing structural similarity, pixel-wise accuracy (e.g., PSNR) is relatively low. In future work, we plan to expand towards improving pixel-level accuracy while maintaining structural consistency through improvements in loss functions, self-supervised learning, and data augmentation techniques. In addition, we will extend our model and evaluation and explore more challenging scenarios, including complex illumination, motion blur, and surface irregularities, as well as self-supervised learning strategies.