Comparative Analysis and Validation of LSTM and GRU Models for Predicting Annual Mean Sea Level in the East Sea: A Case Study of Ulleungdo Island
Abstract
1. Introduction
1.1. Motivation and Objectives
1.2. Related Works
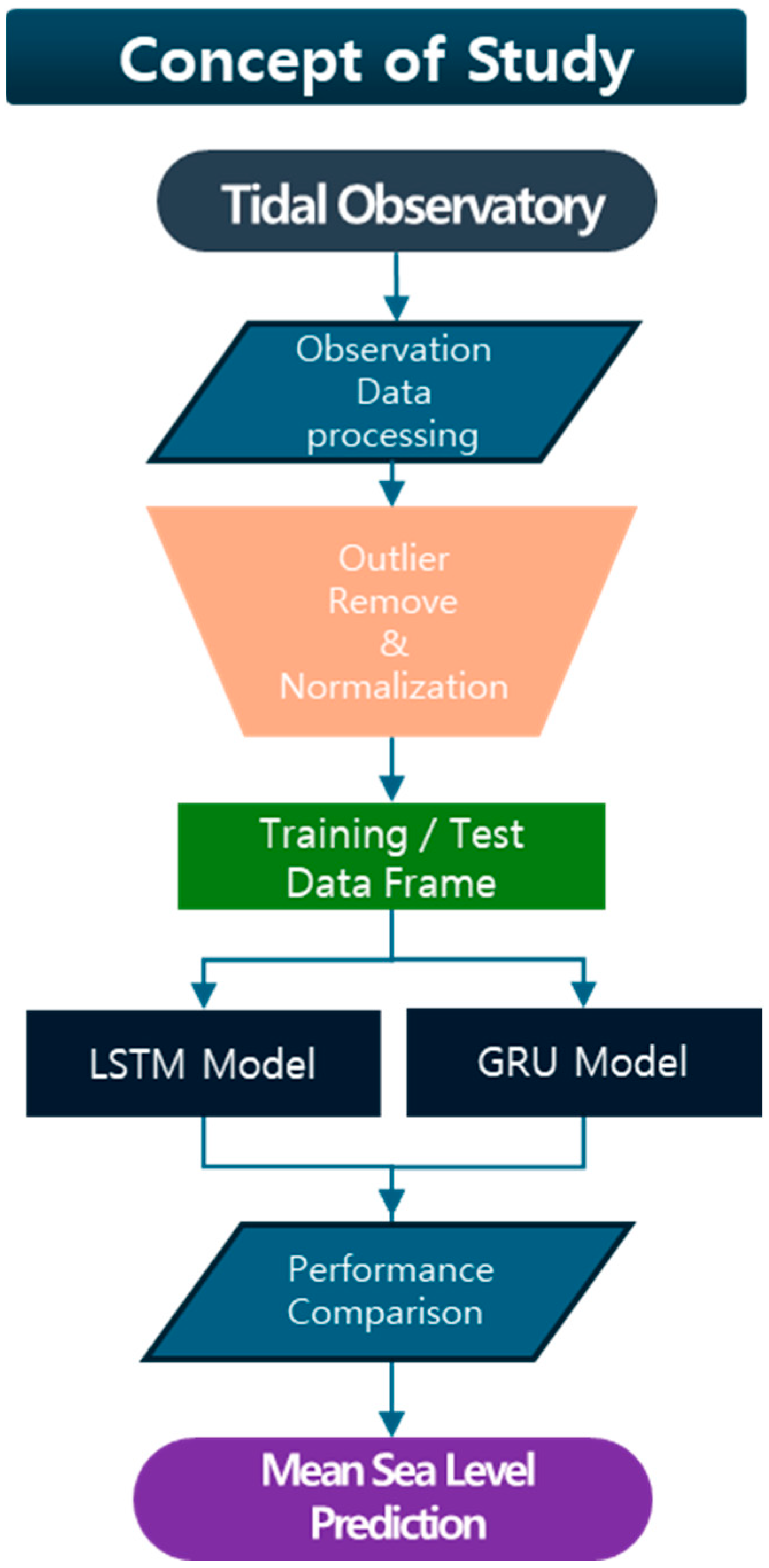
2. Materials and Methods
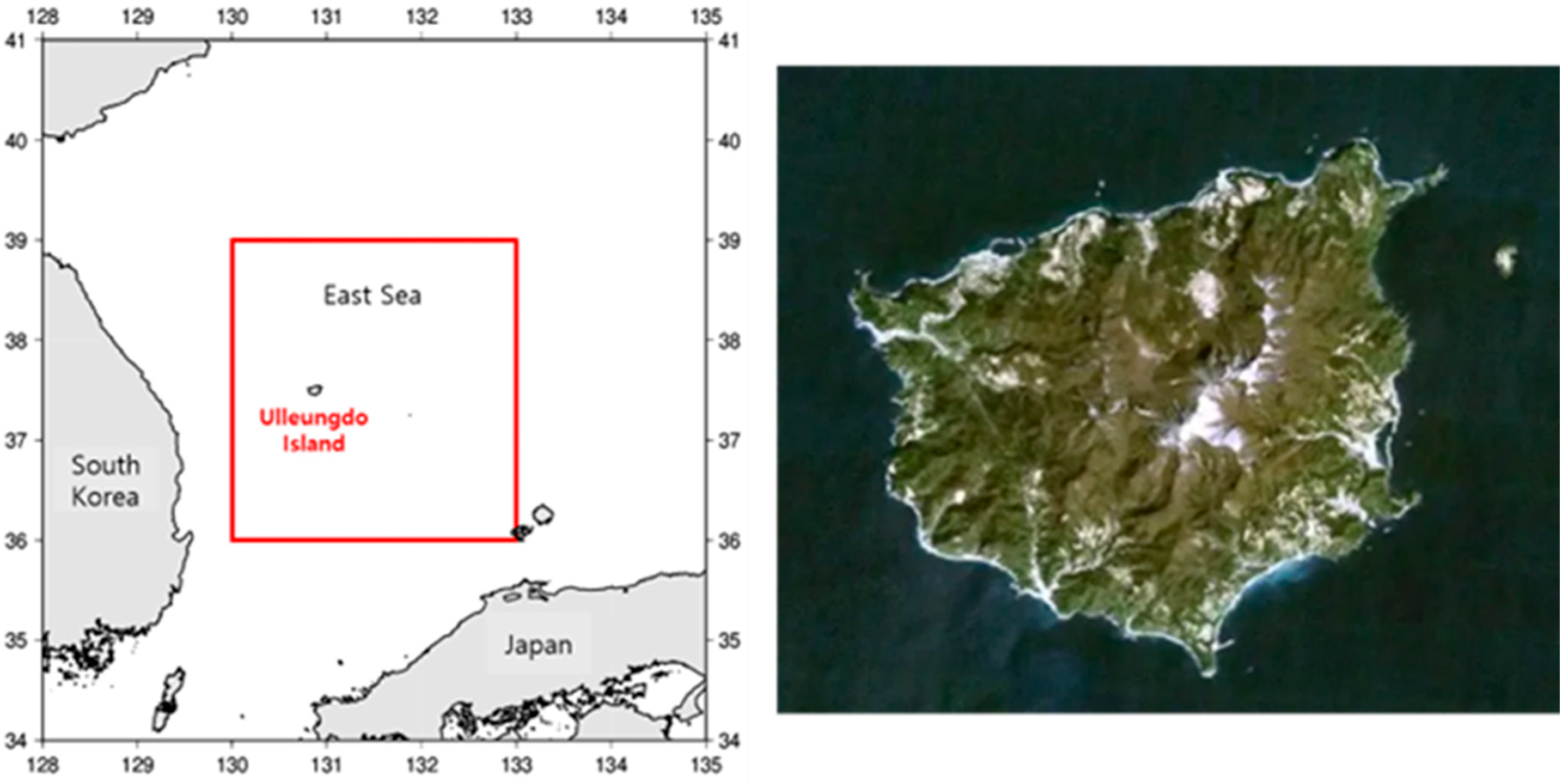
2.1. Study Area
2.2. Deep Learning Algorithm
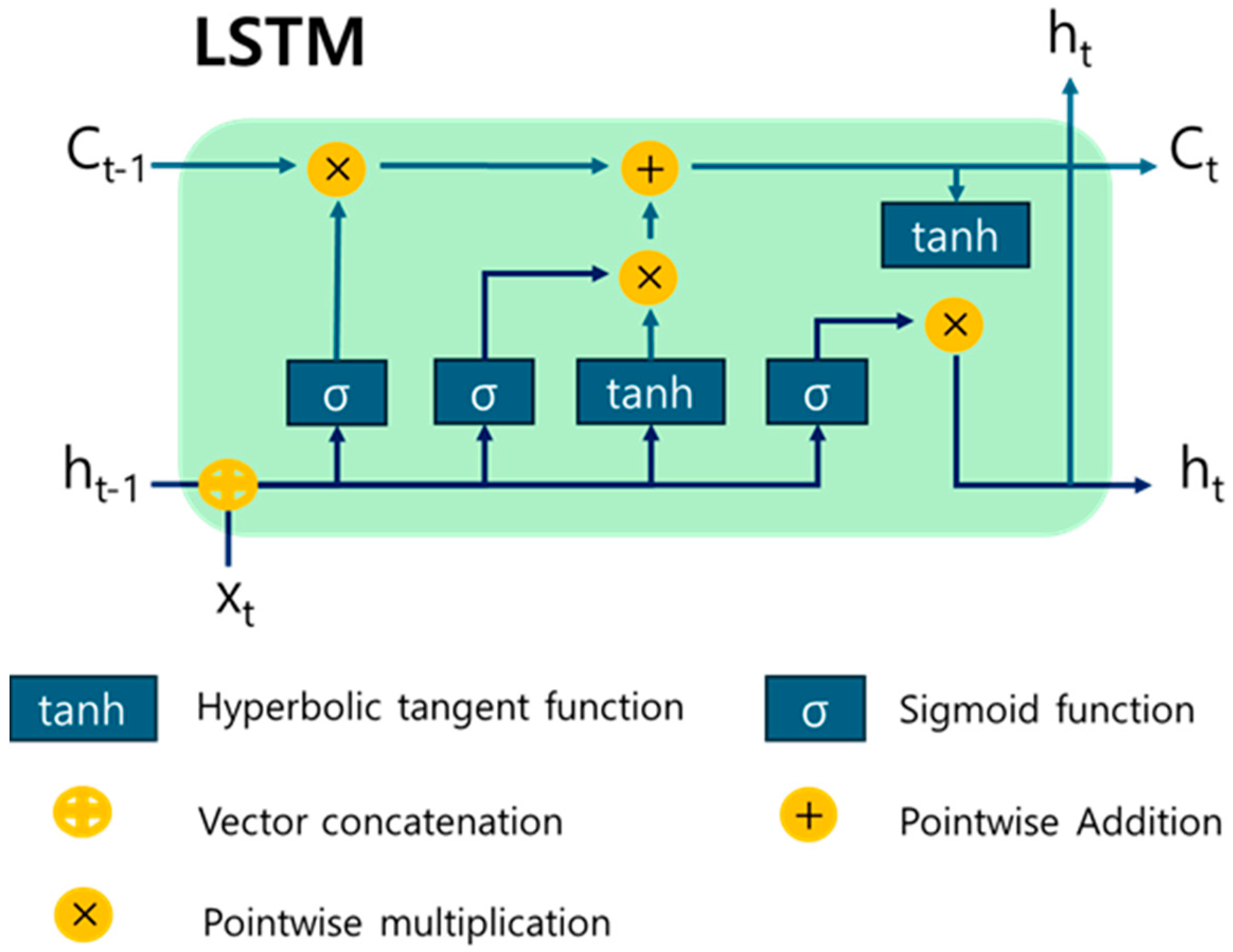
2.2.1. Long Short-Term Memory (LSTM) Networks for Sequential Data Prediction
- Forget gate: Decides which past information to retain.
- Input gate: Determines which new information to incorporate.
- Output gate: Controls how much information from the cell state is passed to the next layer or time step.
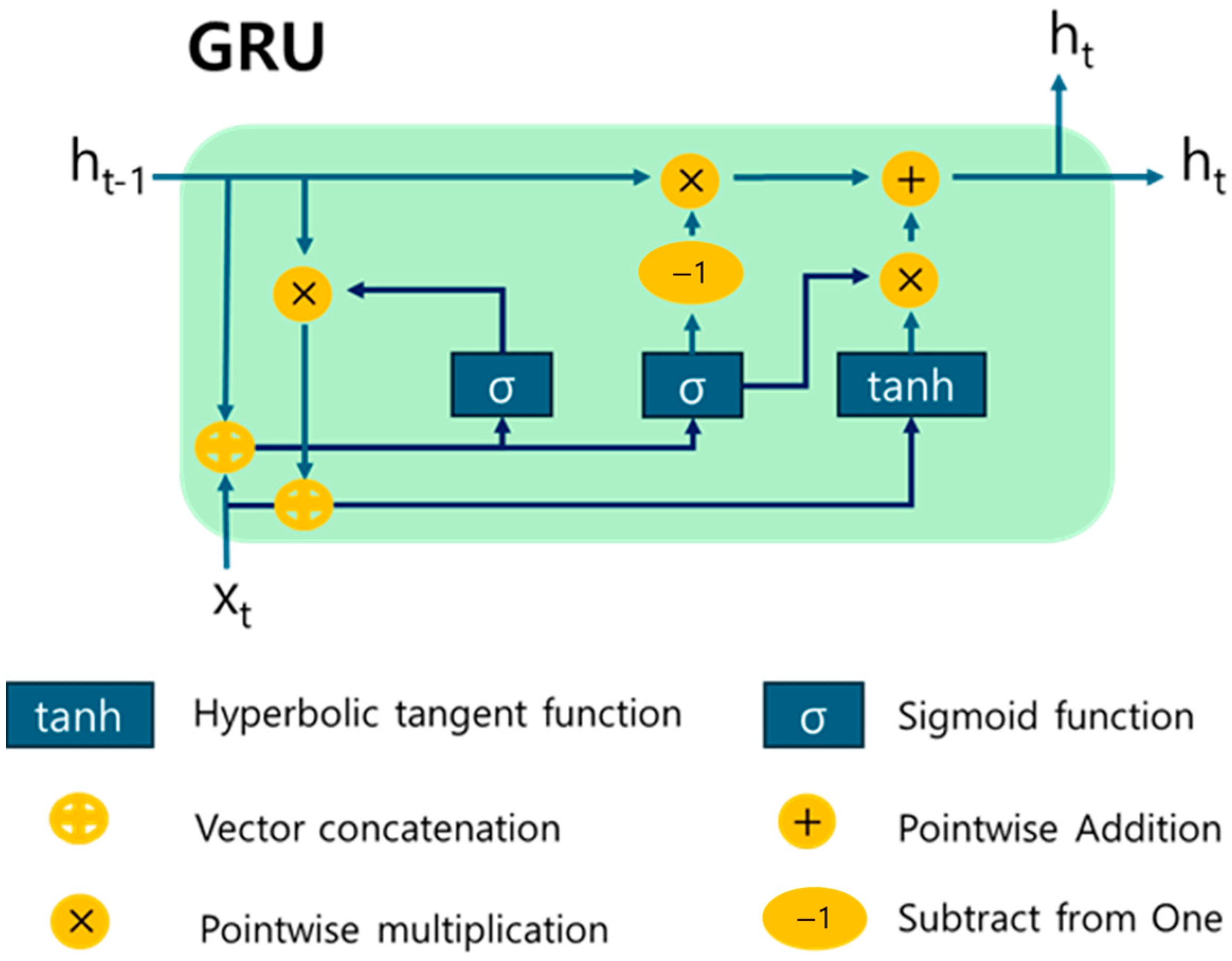
2.2.2. Gated Recurrent Unit for Sequential Learning
- Update gate: balances new information and past memory to determine the final output.
- Reset gate: controls how much previous information is ignored when processing new input.
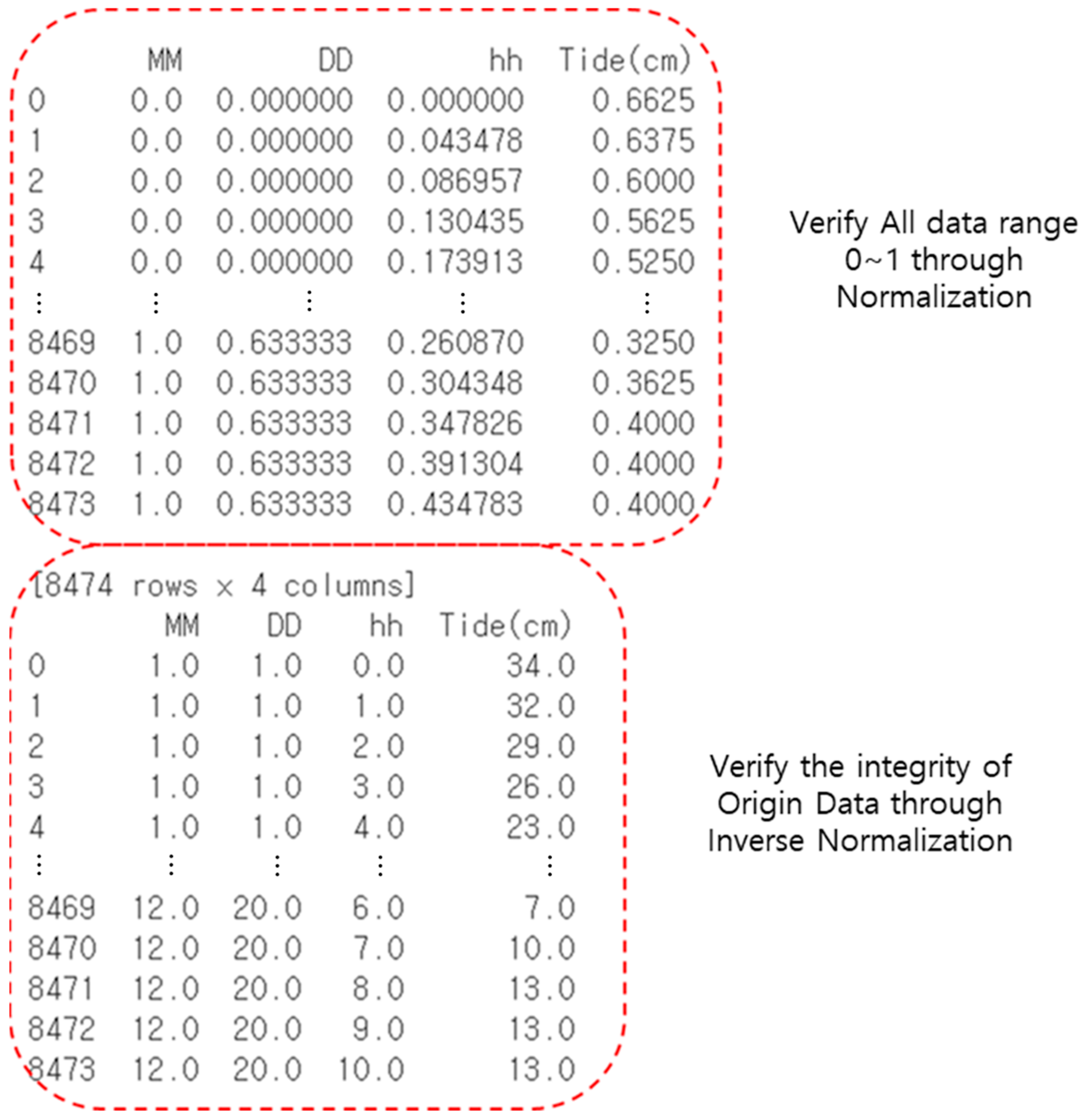
2.2.3. Normalization and Data Structuring for Training
2.2.4. Prediction Model Set Up
2.3. Model Performance Test
- represents the actual value;
- represents the predicted value;
- is the number of data points.
- represents the actual value,
- represents the predicted value,
- is the number of data points, and
3. Results
3.1. Data Preprocessing
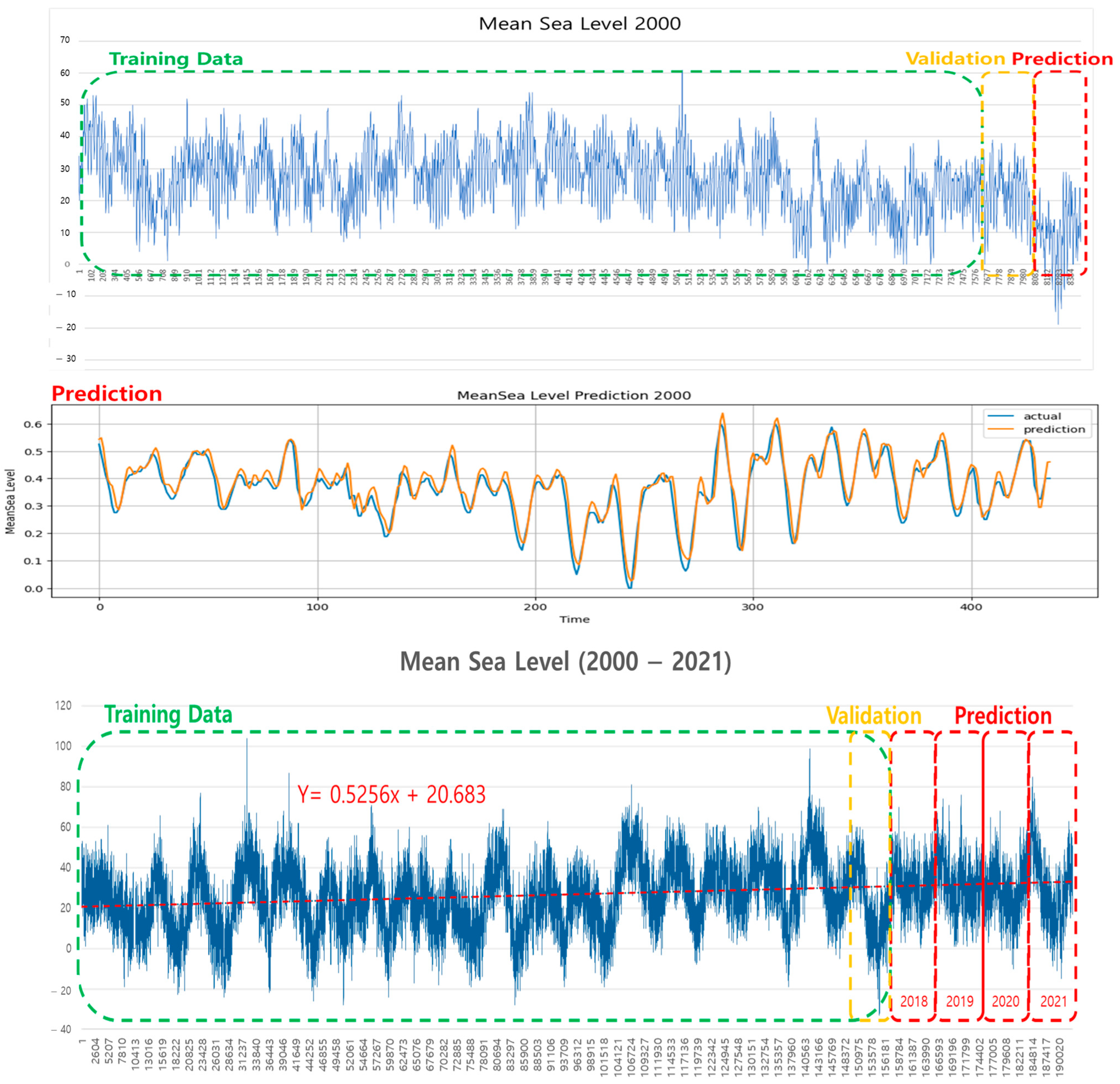
3.2. Performance Evaluation and Prediction Using the GRU Model
3.3. Statistical Analysis of Predicted Values
4. Discussion
4.1. Strengths of the Study
4.2. Limitations and Areas for Improvement
4.3. Future Research Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Raj, N.; Brown, J. Prediction of Mean Sea Level with GNSS-VLM Correction Using a Hybrid Deep Learning Model in Australia. Remote Sens. 2023, 15, 2881. [Google Scholar] [CrossRef]
- Raj, N. Prediction of Sea Level with Vertical Land Movement Correction Using Deep Learning. Mathematics 2022, 10, 4533. [Google Scholar] [CrossRef]
- Rus, M.; Mihanović, H.; Ličer, M.; Kristan, M. HIDRA3: A Deep-Learning Model for Multipoint Ensemble Sea Level Forecasting in the Presence of Tide Gauge Sensor Failures. Geosci. Model Dev. 2025, 18, 605–620. [Google Scholar] [CrossRef]
- Hassan, K.M.d.A. Predicting Future Global Sea Level Rise From Climate Change Variables Using Deep Learning. Int. J. Comput. Digit. Syst. 2023, 13, 829–836. [Google Scholar] [CrossRef]
- Liu, J.; Jin, B.; Wang, L.; Xu, L. Sea Surface Height Prediction With Deep Learning Based on Attention Mechanism. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Song, T.; Han, N.; Zhu, Y.; Li, Z.; Li, Y.; Li, S.; Peng, S. Application of Deep Learning Technique to the Sea Surface Height Prediction in the South China Sea. Acta Oceanol. Sin. 2021, 40, 68–76. [Google Scholar] [CrossRef]
- Bahari, N.A.A.B.S.; Ahmed, A.N.; Chong, K.L.; Lai, V.; Huang, Y.F.; Koo, C.H.; Ng, J.L.; El-Shafie, A. Predicting Sea Level Rise Using Artificial Intelligence: A Review. Arch. Comput. Methods Eng. 2023, 30, 4045–4062. [Google Scholar] [CrossRef]
- Hassanpour, H.; Corbett, B.; Mhaskar, P. Artificial Neural Network-Based Model Predictive Control Using Correlated Data. Ind. Eng. Chem. Res. 2022, 61, 3075–3090. [Google Scholar] [CrossRef]
- Bao, Y.; Mohammadpour Velni, J. A Hybrid Neural Network Approach for Adaptive Scenario-Based Model Predictive Control in the LPV Framework. IEEE Control Syst. Lett. 2023, 7, 1921–1926. [Google Scholar] [CrossRef]
- Abaza, B.F.; Gheorghita, V. Artificial Neural Network Framework for Hybrid Control and Monitoring in Turning Operations. Appl. Sci. 2025, 15, 3499. [Google Scholar] [CrossRef]
- Choi, Y.J.; Park, B.R.; Hyun, J.Y.; Moon, J.W. Development of an Adaptive Artificial Neural Network Model and Optimal Control Algorithm for a Data Center Cyber–Physical System. Build. Environ. 2022, 210, 108704. [Google Scholar] [CrossRef]
- Wang, D.; Shen, Z.J.; Yin, X.; Tang, S.; Liu, X.; Zhang, C.; Wang, J.; Rodriguez, J.; Norambuena, M. Model Predictive Control Using Artificial Neural Network for Power Converters. IEEE Trans. Ind. Electron. 2022, 69, 3689–3699. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar] [CrossRef]
- Kanagachidambaresan, G.R.; Ruwali, A.; Banerjee, D.; Prakash, K.B. Recurrent Neural Network. In Programming with TensorFlow; Prakash, K.B., Kanagachidambaresan, G.R., Eds.; EAI/Springer Innovations in Communication and Computing; Springer International Publishing: Cham, Switzerland, 2021; pp. 53–61. ISBN 978-3-030-57076-7. [Google Scholar]
- White, L.; Togneri, R.; Liu, W.; Bennamoun, M. Recurrent Neural Networks for Sequential Processing. In Neural Representations of Natural Language; Studies in Computational Intelligence; Springer: Singapore, 2019; Volume 783, pp. 23–36. ISBN 978-981-13-0061-5. [Google Scholar]
- Donkers, T.; Loepp, B.; Ziegler, J. Sequential User-Based Recurrent Neural Network Recommendations. In Proceedings of the Proceedings of the Eleventh ACM Conference on Recommender Systems, Como, Italy, 27 August 2017; ACM: New York, NY, USA, 2017; pp. 152–160. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Lindemann, B.; Müller, T.; Vietz, H.; Jazdi, N.; Weyrich, M. A Survey on Long Short-Term Memory Networks for Time Series Prediction. Procedia CIRP 2021, 99, 650–655. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Dumre, P.; Bhattarai, S.; Shashikala, H.K. Optimizing Linear Regression Models: A Comparative Study of Error Metrics. In Proceedings of the 2024 4th International Conference on Technological Advancements in Computational Sciences (ICTACS), Tashkent, Uzbekistan, 13 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1856–1861. [Google Scholar]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Airlangga, G. A Comparative Analysis of Machine Learning Models for Predicting Student Performance: Evaluating the Impact of Stacking and Traditional Methods. Brilliance 2024, 4, 491–499. [Google Scholar] [CrossRef]
- Jain, P.; Sahoo, P.K.; Khaleel, A.D.; Al-Gburi, A.J.A. Enhanced Prediction of Metamaterial Antenna Parameters Using Advanced Machine Learning Regression Models. Prog. Electromagn. Res. C 2024, 146, 1–12. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kim, J.-H.; Luo, J.-J. Deep Learning for Multi-Year ENSO Forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, R.-H. A Self-Attention–Based Neural Network for Three-Dimensional Multivariate Modeling and Its Skillful ENSO Predictions. Sci. Adv. 2023, 9, eadf2827. [Google Scholar] [CrossRef]
- Mu, B.; Cui, Y.; Yuan, S.; Qin, B. Incorporating Heat Budget Dynamics in a Transformer-Based Deep Learning Model for Skillful ENSO Prediction. npj Clim. Atmos. Sci. 2024, 7, 208. [Google Scholar] [CrossRef]
- Wang, H.; Hu, S.; Guan, C.; Li, X. The Role of Sea Surface Salinity in ENSO Forecasting in the 21st Century. npj Clim. Atmos. Sci. 2024, 7, 206. [Google Scholar] [CrossRef]
- Wang, G.-G.; Cheng, H.; Zhang, Y.; Yu, H. ENSO Analysis and Prediction Using Deep Learning: A Review. Neurocomputing 2023, 520, 216–229. [Google Scholar] [CrossRef]
- Sun, M.; Chen, L.; Li, T.; Luo, J. CNN-Based ENSO Forecasts With a Focus on SSTA Zonal Pattern and Physical Interpretation. Geophys. Res. Lett. 2023, 50, e2023GL105175. [Google Scholar] [CrossRef]
- Palanisamy Vadivel, S.K.; Kim, D.; Jung, J.; Cho, Y.-K.; Han, K.-J. Monitoring the Vertical Land Motion of Tide Gauges and Its Impact on Relative Sea Level Changes in Korean Peninsula Using Sequential SBAS-InSAR Time-Series Analysis. Remote Sens. 2020, 13, 18. [Google Scholar] [CrossRef]
- Palanisamy Vadivel, S.K.; Kim, D.; Jung, J.; Cho, Y.-K. Multi-Temporal Spaceborne InSAR Technique to Compensate Vertical Land Motion in Sea Level Change Records: A Case Study of Tide Gauges in Korean Peninsula. In Proceedings of the 22nd EGU General Assembly, Online, 4–8 May 2020. [Google Scholar]
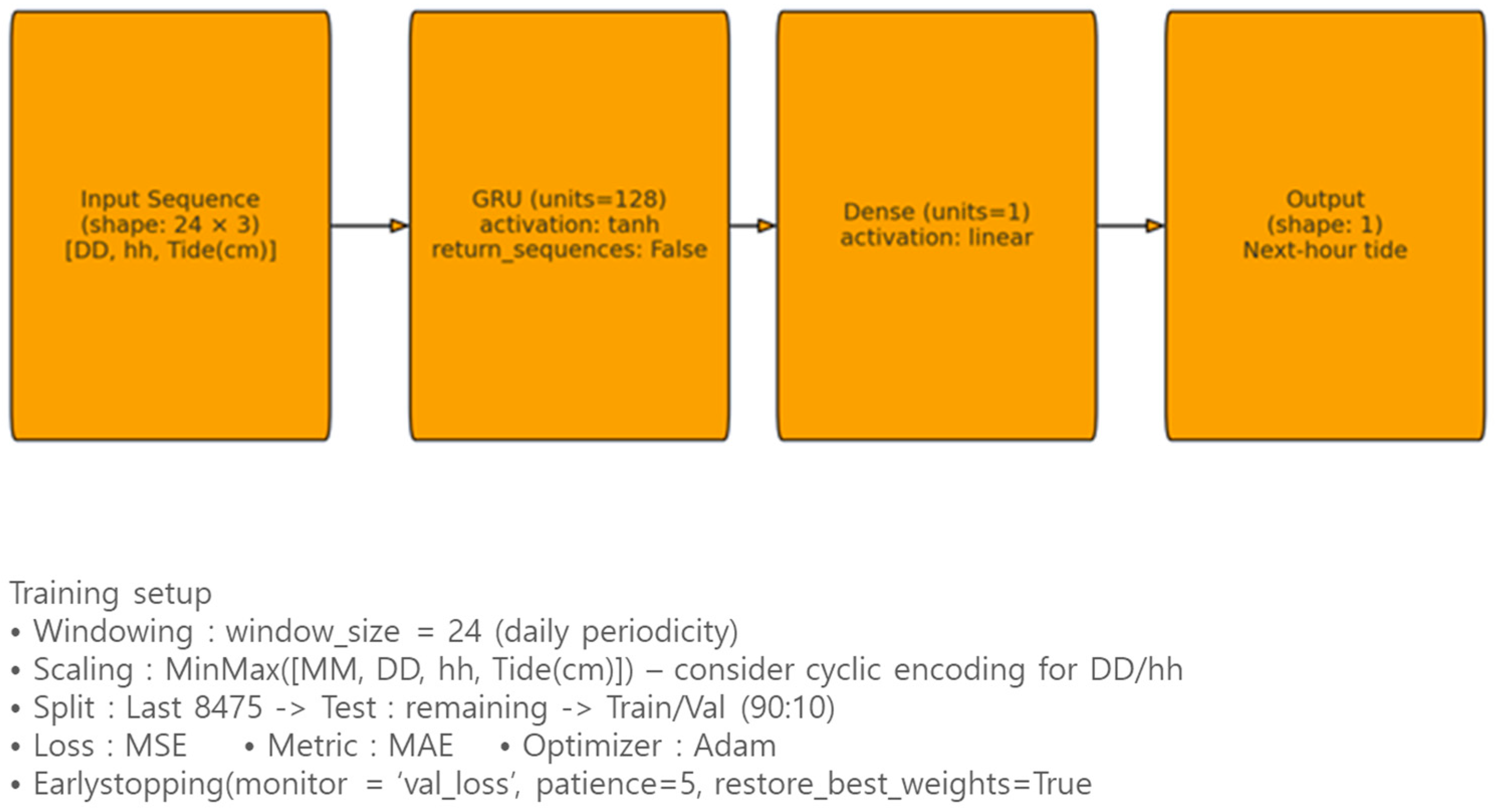
| Category | HyperParameters | Values/Setting | Description |
|---|---|---|---|
| Data Preprocessing | Scale_cols | ‘MM’, ‘DD’, ‘hh’, Tide(cm)’ | Columns scaled using MinMaxScaler |
| window_size | 24 | Number of time steps in the input sequence (24 h) | |
| feature_cols | ‘DD’, ‘hh’, Tide(cm)’ | Input features for the model | |
| label_cols | Tide(cm) | Target variable (output) | |
| Model Architecture | LSTM/GRU | 128 | Number of units in the LSTM/GRU layer |
| LSTM/GRU activation | ‘tanh’ | Activation function of the GRU layer | |
| Dense activation | ‘linear’ | Activation function of the output layer | |
| Training | Loss function | ‘mse’ | Loss function (Mean Squared Error) |
| Optimizer | ‘adam’ | Optimizer used for training | |
| Metrics | [‘mse’] | Metrics used to evaluate model performance | |
| Epochs | 10 | Maximum number of training epochs | |
| Batch size | 128 | Number of samples per gradient update | |
| Evaluation | MAE | Calculated | Mean Absolute Error on test set |
| MSE | Calculated | Mean Squared Error on test set | |
| RMSE | Calculated | Root Mean Squared Error on test set | |
| R2 | Calculated | Coefficient of determination on test set |
| RMSE (cm) LSTM | RMSE (cm) GRU | R2 LSTM | R2 GRU | |
|---|---|---|---|---|
| 2000 | 0.0305483 | 0.0382224 | 0.93871251 | 0.91795243 |
| 2001 | 0.0267737 | 0.0235437 | 0.94683073 | 0.95923109 |
| 2002 | 0.0198661 | 0.0195591 | 0.93804817 | 0.94926756 |
| 2003 | 0.0238027 | 0.0154562 | 0.94382575 | 0.96688104 |
| 2004 | 0.0280277 | 0.0194604 | 0.94051736 | 0.95867230 |
| 2005 | 0.0332199 | 0.0241424 | 0.91831683 | 0.92986552 |
| 2006 | 0.0183807 | 0.0198762 | 0.94254776 | 0.95349526 |
| 2007 | 0.0187517 | 0.0185590 | 0.93361393 | 0.94880581 |
| 2008 | 0.0223006 | 0.0262448 | 0.93683214 | 0.93822615 |
| 2009 | 0.0221001 | 0.0166219 | 0.94755805 | 0.95272318 |
| 2010 | 0.0278998 | 0.0170530 | 0.93773657 | 0.95130882 |
| 2011 | 0.0190270 | 0.0208902 | 0.95512379 | 0.94951727 |
| 2012 | 0.0269434 | 0.0189083 | 0.94039562 | 0.95751103 |
| 2013 | 0.0203827 | 0.0192146 | 0.95065621 | 0.95301725 |
| 2014 | 0.0225711 | 0.0195938 | 0.94250673 | 0.95012517 |
| 2015 | 0.0182813 | 0.0217119 | 0.95178142 | 0.940106614 |
| 2016 | 0.0353317 | 0.0286314 | 0.93108283 | 0.93818435 |
| 2017 | 0.0234526 | 0.0196174 | 0.96127031 | 0.94774695 |
| 2018 | 0.0382011 | 0.0159021 | 0.91667517 | 0.96028611 |
| Average | 0.0243295 | 0.0215793 | 0.94073961 | 0.94857567 |
| Year | Min | Max | Mean | SD | RMSE (cm) | R2 |
|---|---|---|---|---|---|---|
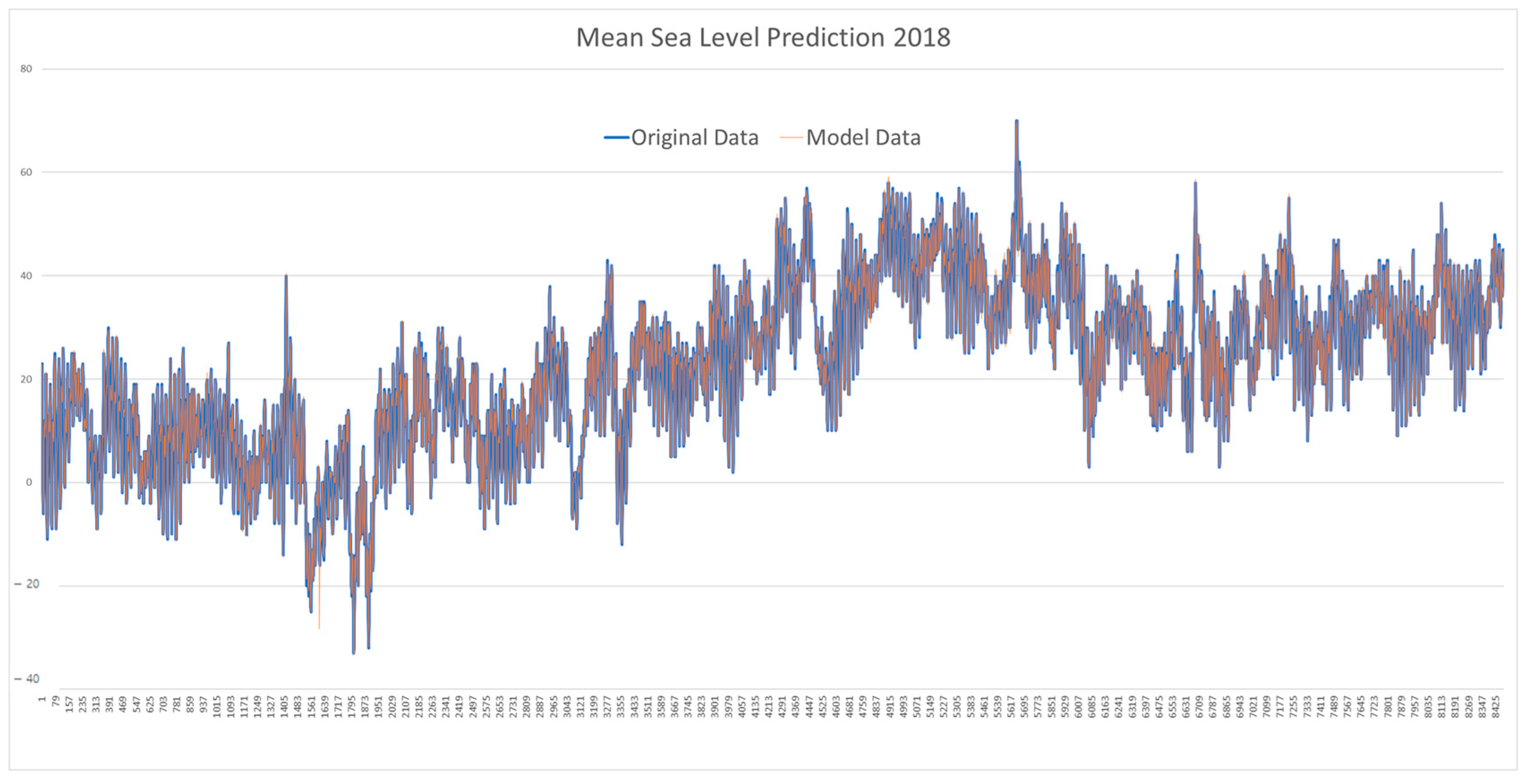
| 2018 | −33.4218968 | 70.13188955 | 22.79023389 | 15.5509162 | 0.451515716 | 0.947321561 |
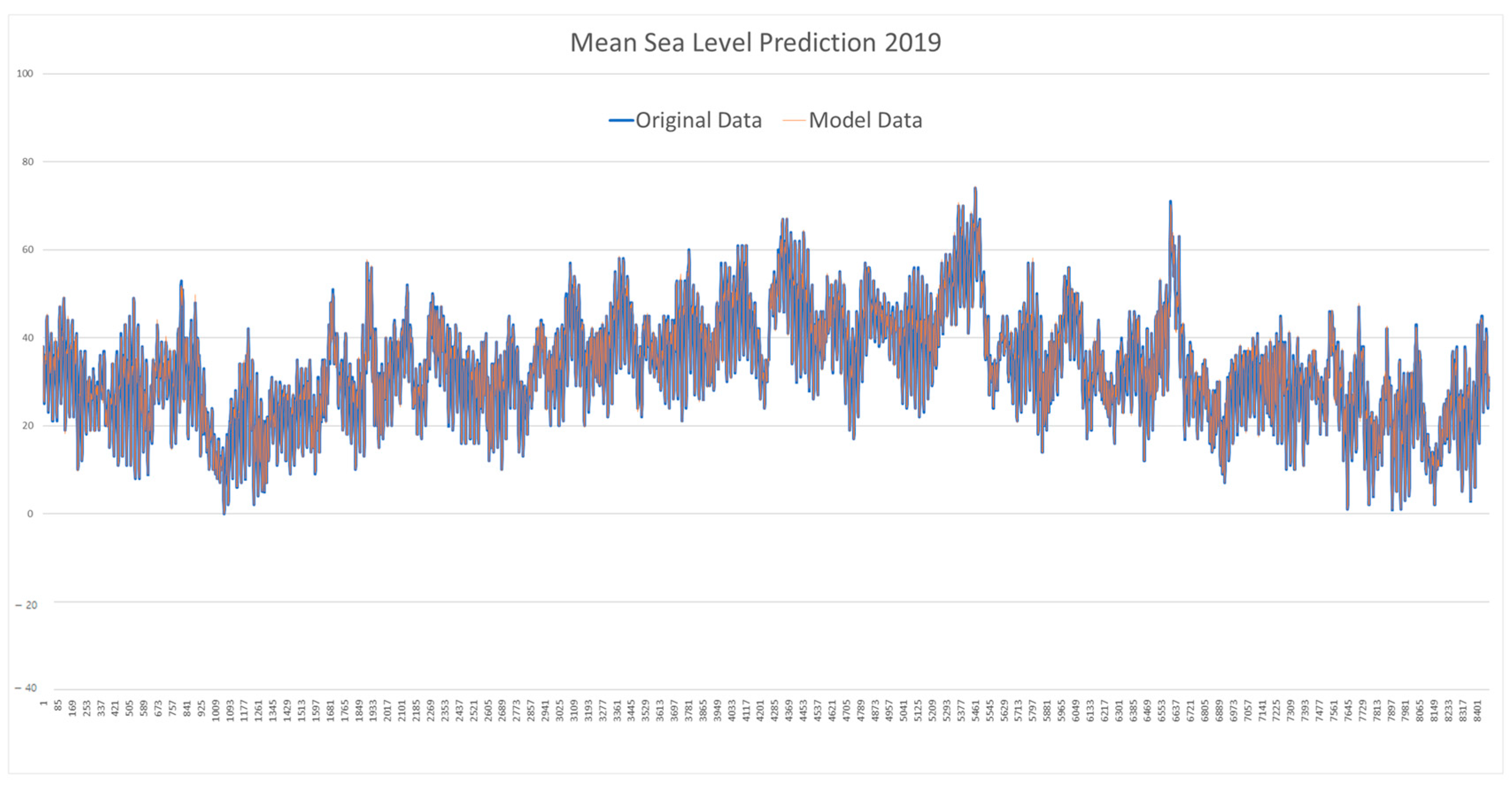
| 2019 | 0 | 74.42184979 | 33.18118768 | 11.76926402 | 0.424361879 | 0.956375532 |
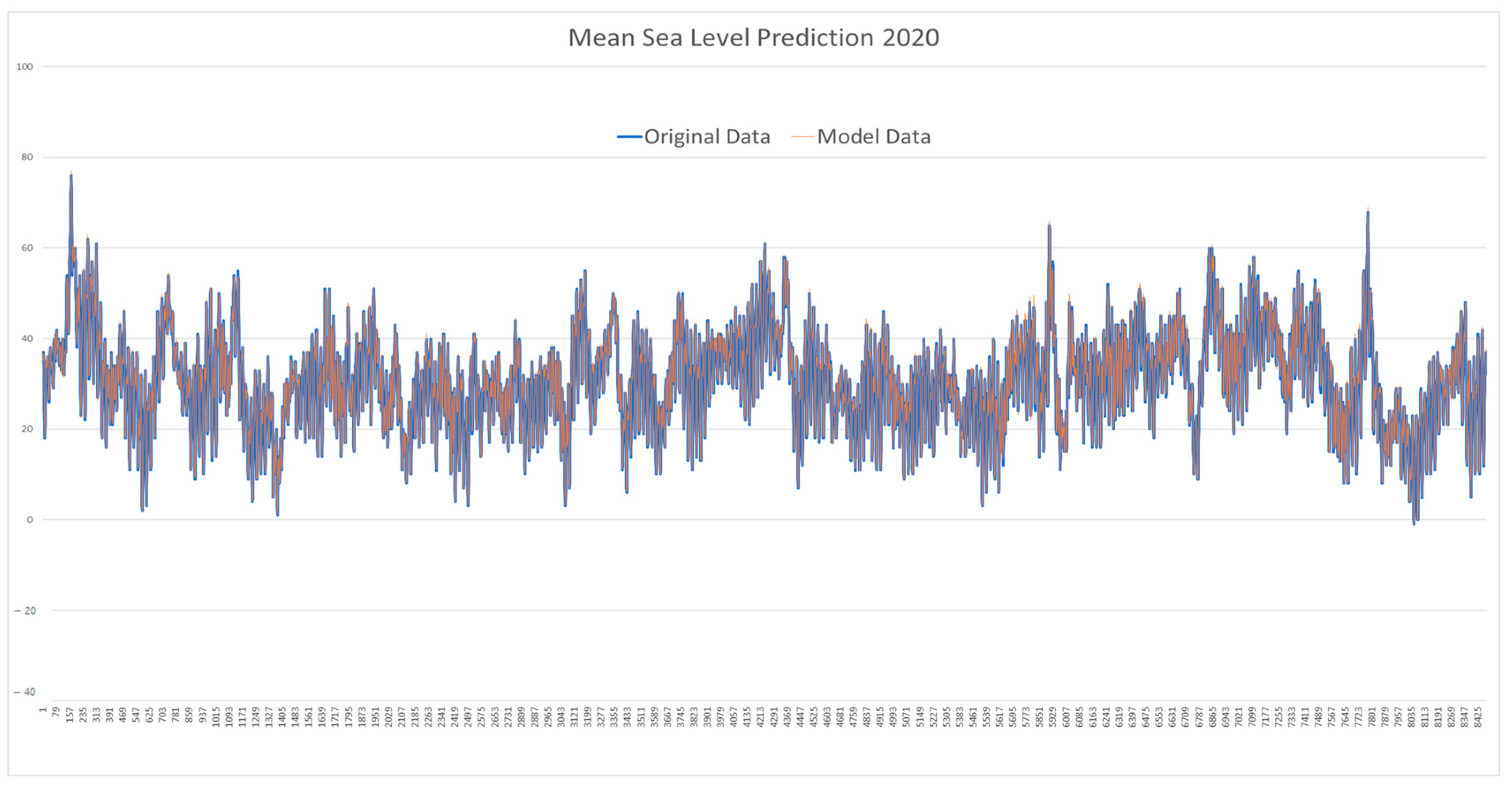
| 2020 | −1.00044944 | 77.07113945 | 31.22588493 | 10.41988822 | 0.472818855 | 0.940678283 |
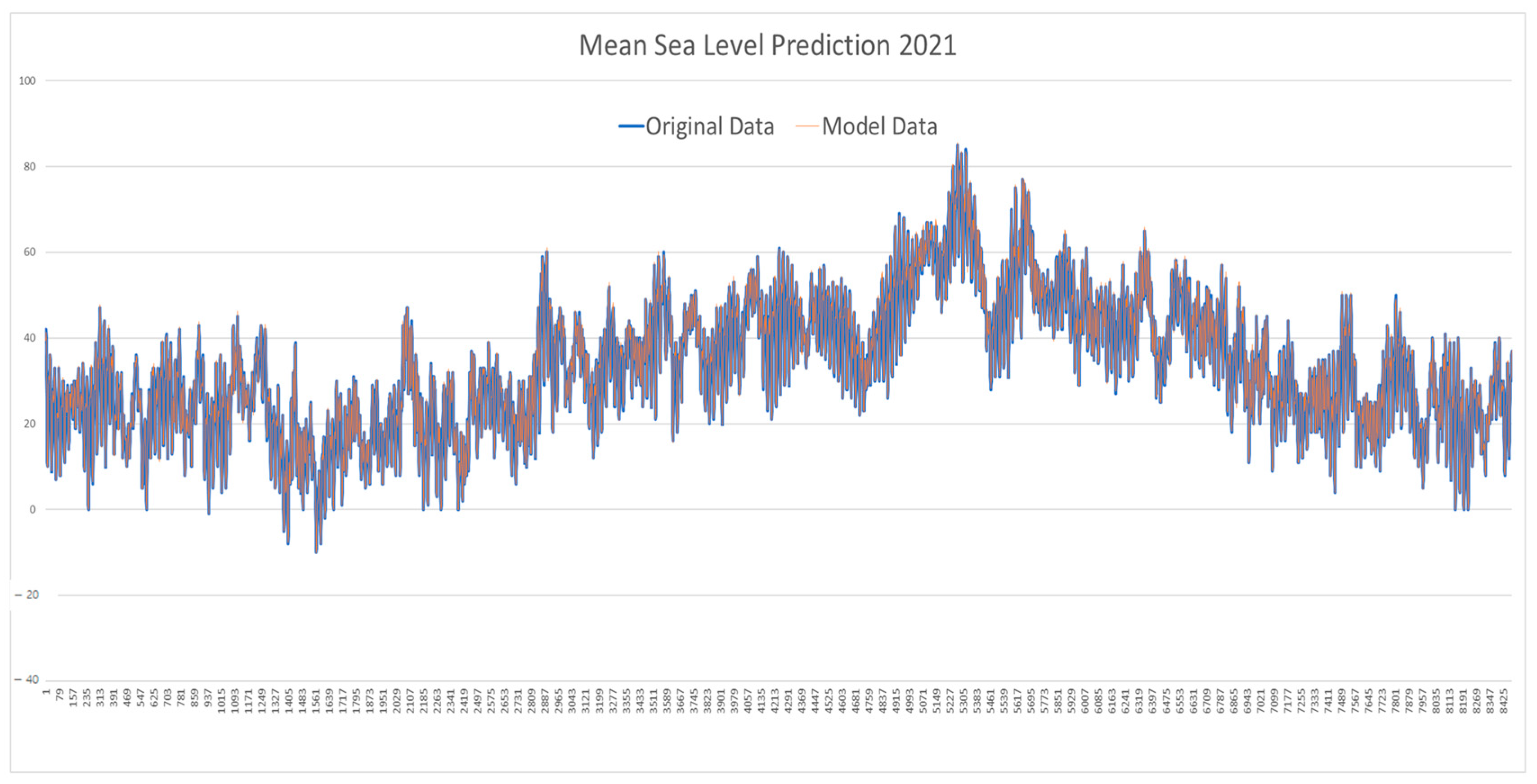
| 2021 | −10.0351062 | 85.55377282 | 33.61195034 | 15.06894462 | 0.437674301 | 0.958148283 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.-Y.; Yun, H.-S.; Yoon, H.-M.; Lee, S.-J. Comparative Analysis and Validation of LSTM and GRU Models for Predicting Annual Mean Sea Level in the East Sea: A Case Study of Ulleungdo Island. Appl. Sci. 2025, 15, 11067. https://doi.org/10.3390/app152011067
Kim T-Y, Yun H-S, Yoon H-M, Lee S-J. Comparative Analysis and Validation of LSTM and GRU Models for Predicting Annual Mean Sea Level in the East Sea: A Case Study of Ulleungdo Island. Applied Sciences. 2025; 15(20):11067. https://doi.org/10.3390/app152011067
Chicago/Turabian StyleKim, Tae-Yun, Hong-Sik Yun, Hyung-Mi Yoon, and Seung-Jun Lee. 2025. "Comparative Analysis and Validation of LSTM and GRU Models for Predicting Annual Mean Sea Level in the East Sea: A Case Study of Ulleungdo Island" Applied Sciences 15, no. 20: 11067. https://doi.org/10.3390/app152011067
APA StyleKim, T.-Y., Yun, H.-S., Yoon, H.-M., & Lee, S.-J. (2025). Comparative Analysis and Validation of LSTM and GRU Models for Predicting Annual Mean Sea Level in the East Sea: A Case Study of Ulleungdo Island. Applied Sciences, 15(20), 11067. https://doi.org/10.3390/app152011067







