Inverse Procedure to Initial Parameter Estimation for Air-Dropped Packages Using Neural Networks
Abstract
1. Introduction
1.1. Introduction to Cargo Airdrop Processes
- Accuracy defining the drop zone, dependent on data from navigation systems (GPS, GLONASS, INS),
- Maneuverability, mainly dependent on the aerodynamics of the capsule, but also on the structural strength (acting g-forces),
- Achievable range, which allows for dropping the cargo from a safe distance, thereby minimizing potential losses while maintaining safety conditions,
- Achievable object speed, which in turn minimizes the time required to deliver the airdropped cargo,
- Flight profile, which allows for low-altitude flight,
- Weather conditions, mainly those whose effects cannot be predicted (atmospheric turbulence, wind shear, and gusts),
- All kinds of human factors, such as pilot or operator skills, or their availability.
1.2. Types of Airdrop Systems
- Non-precision cargo airdrop systems
- ○
- They are characterized by low accuracy, meaning the cargo does not always land at the intended point,
- ○
- Most commonly used during good visibility,
- ○
- These systems require a low altitude and typically involve flying over the drop zone, which is not always possible and carries a high risk of mission failure, as well as danger to the pilot and aircraft.
- Precision cargo airdrop systems
- ○
- Work on guided airdrop systems began in the early 1960s, utilizing a modified parabolic parachute [6],
- ○
- Equipped with Autonomous Guidance Units (AGU), whose elements include: a computer for calculating flight trajectory, communication devices with antennas, a GPS receiver, temperature and pressure sensors, LIDAR radar, devices controlling steering lines, and an operating panel,
- ○
- They use appropriate devices that detect the wind profile and speed,
- ○
- They allow for airdropping cargo from altitudes of over 9000 m with a drop accuracy of 25 to 150 m [7],
- ○
- They utilize advanced software (Launch Acceptability Region, LAR) that calculates the area from which a drop can be made to ensure the cargo hits the target,
- ○
- Joint Precision Airdrop System, which is designed for conducting precise airdrops from high altitudes and comes in a wide range of versions depending on cargo weight (from 90 kg to 4500 kg). Equipped with a wing-type gliding parachute, it has the ability to fly in any direction regardless of wind and to change flight direction at any moment [8].
- Guided parachutes/parafoils
- ○
- They are equipped with Autonomous Guidance Units (AGU), that allow for a change in flight trajectory, including: adjusting the course mid-flight, avoiding obstacles, and precise maneuvering to reach the designated drop point,
- ○
- They have the ability to be dropped from higher altitudes and greater distances from the drop point,
- ○
- Ram-air parachutes (wing-type) are characterized by their maneuverability and ability to fly in any direction,
- ○
- Round parachutes (modified) are less maneuverable than ram-air, but have the advantage of being cheaper to produce; they are used in systems like AGAS, where pneumatic muscle actuators are used for steering,
- ○
- The parachute’s smart guidance System Joint Precision Airdrop System (JPADS) autonomously calculates the correct drop point. To do this, it uses data from global positioning, weather models, and advanced mathematical operations, allowing it to reach the target on its own based on the received coordinates.
1.3. Safety in Airdrop Operations
1.4. Forecasting the Drop Zone and Determining the Impact Point
1.5. Application of Neural Networks in Airdrop Research
1.6. Forward and Inverse Neural Models for Airdrop Dynamics
1.7. Scope of the Present Study
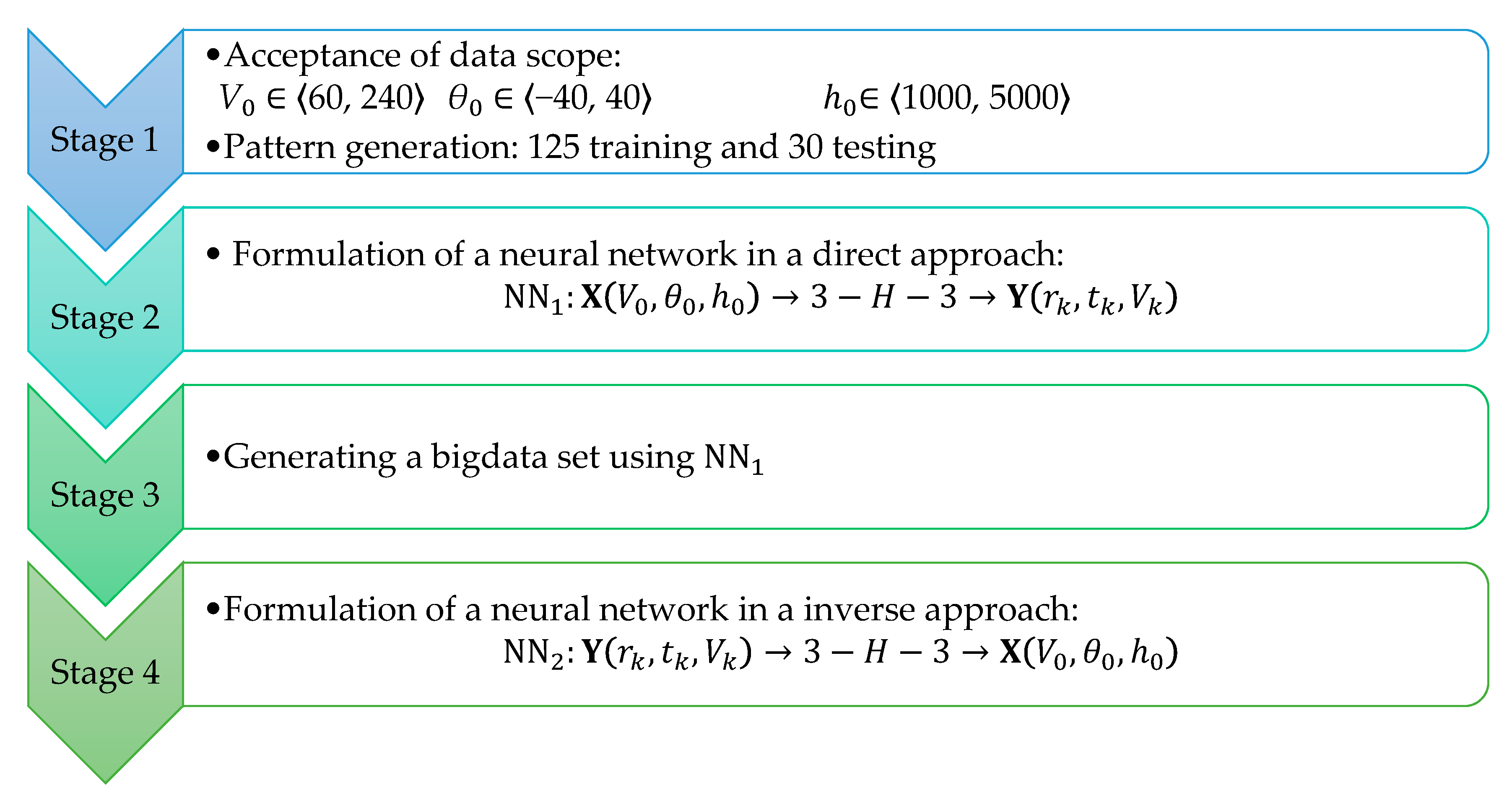
2. Research Assumptions and Methods
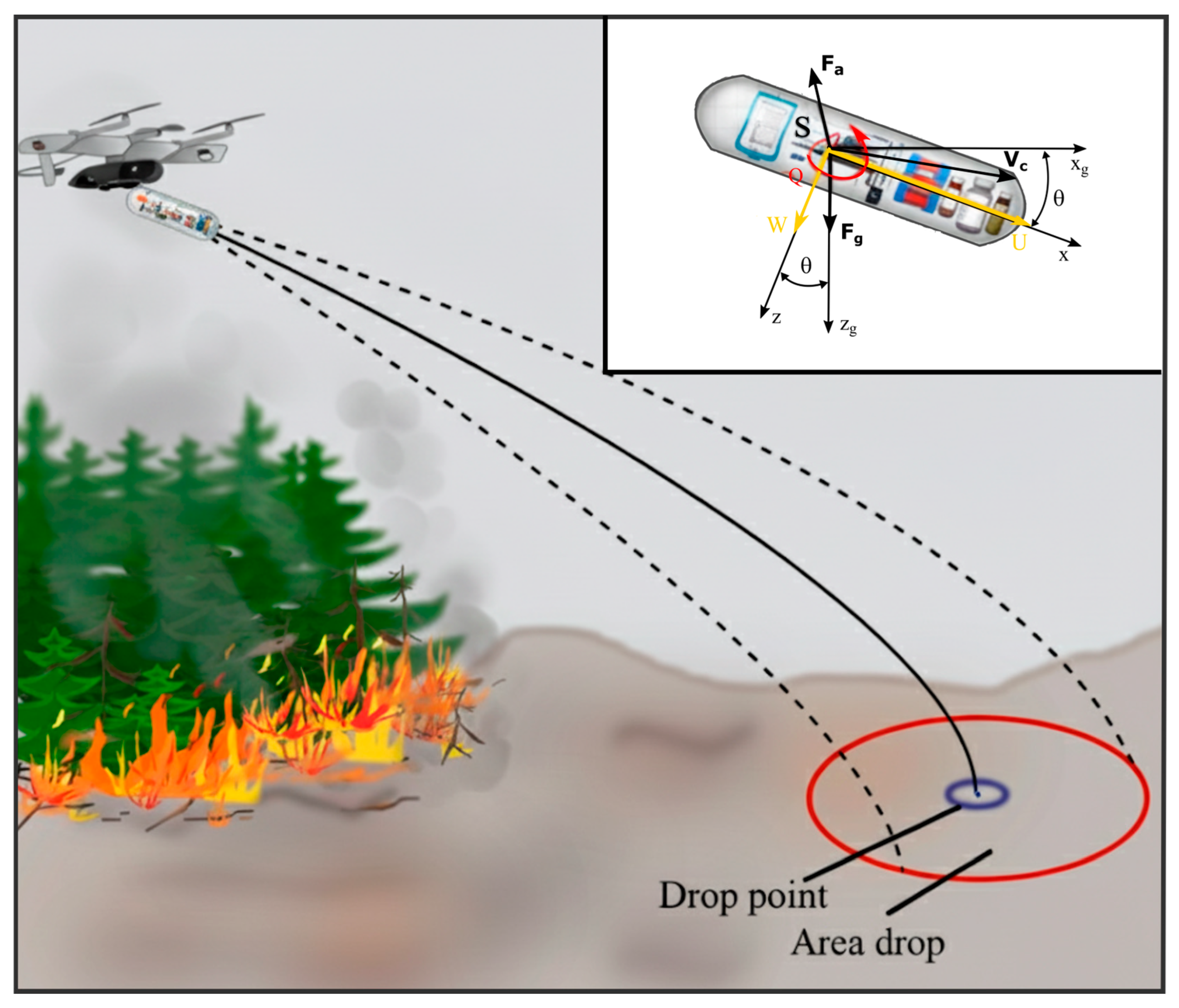
2.1. Stage 1: Flight Assumptions and Capsule’s Mathematical Model
- Reduced air resistance—this advantage is extremely important because it minimizes friction and air turbulence around the capsule, allowing for faster and more controlled descent,
- Improved precision and trajectory prediction—aerodynamically shaped capsules are less susceptible to the influence of crosswinds and other atmospheric disturbances. Their flight path is more stable and easier to predict, which increases the chances of a precise airdrop,
- Increased stability during descent—allows the capsule to maintain a constant orientation in flight, reducing the risk of uncontrolled spinning, swaying, or tumbling. This is particularly important to avoid cargo damage,
- Reduced loads on the capsule’s structure and its contents. Laminar airflow around an aerodynamic shape minimizes the dynamic forces acting on the capsule, which reduces the risk of damage to its structure and contents, especially sensitive items such as precision measuring equipment or shock-sensitive packaged medications,
- More stable parachute opening and deployment if one is used. In the presented research, the use of a parachute was not considered. The capsule is dropped directly, e.g., from an airplane or an unmanned aerial vehicle,
- Additionally, if an increased descent speed is desired when rapid cargo delivery is a priority.
- The capsule is a rigid solid, made of resistant materials that are not easily damaged,
- The mass of the capsule does not change with time,
- The capsule is an axisymmetric solid,
- The planes of geometric, mass, and aerodynamic symmetry are the planes ,
- There is no wind speed.
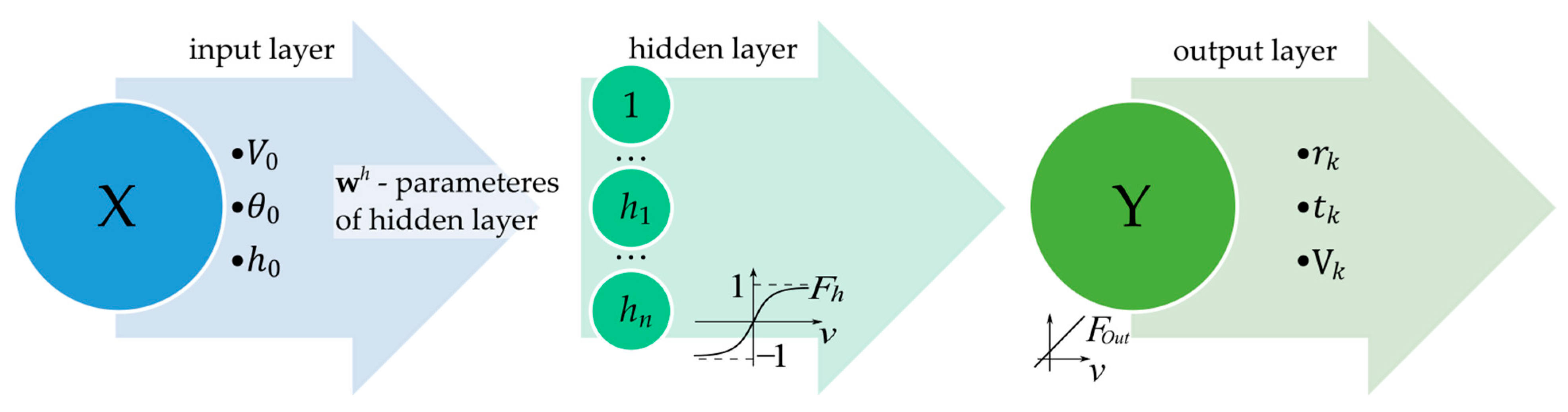
2.2. Stage 2: Simple Neural Network:NN1 in a Direct Approach
2.3. Stage 3: Generating a Big Dataset Using
2.4. Stage 4: Formulation of a Neural Network in an Inverse Approach NN2
3. Results
- Case 1—deterministic verification: in this scenario, all input variables of the network (range, flight time, and final velocity) are taken from the reference dataset (Stage 1), and the outputs generated by NN2 (V0.NN, θ0.NN, h0.NN) are compared to the corresponding values from the reference set to assess their accuracy. The errors are calculated by comparing the original data (Stage 1) with the outputs of the neural network NN2.
- Case 2—verification using random datasets: the input data for the network are sampled from predefined intervals based on a discrete uniform distribution. The results obtained from NN2 are verified by analyzing the final parameters after conducting simulations using the estimated initial conditions.
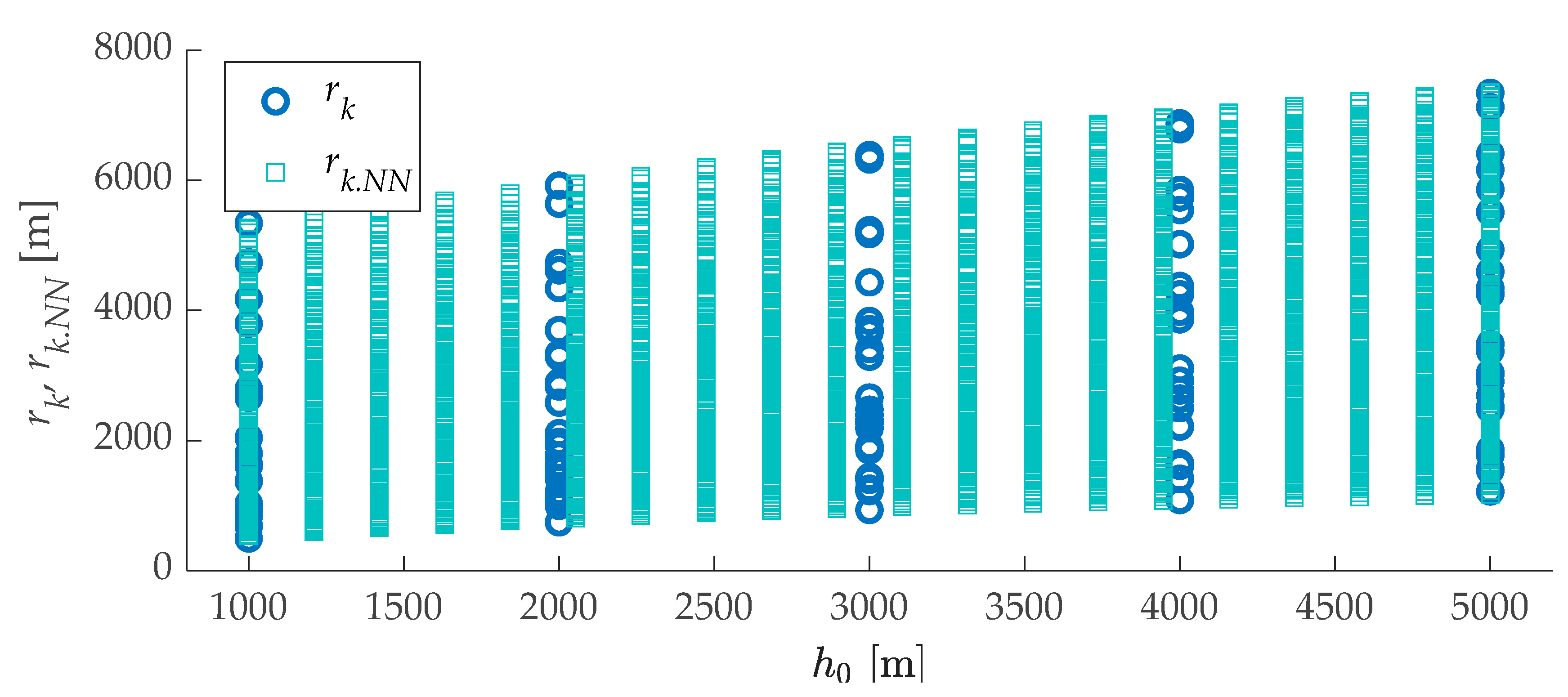
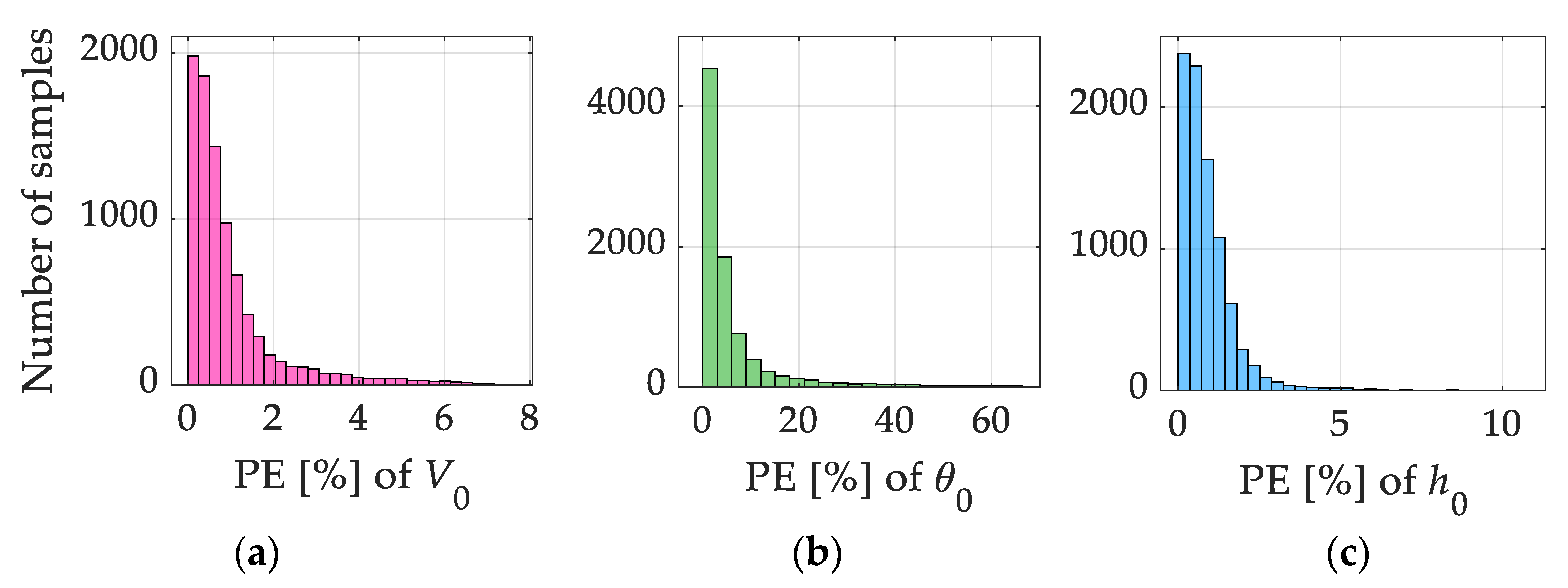
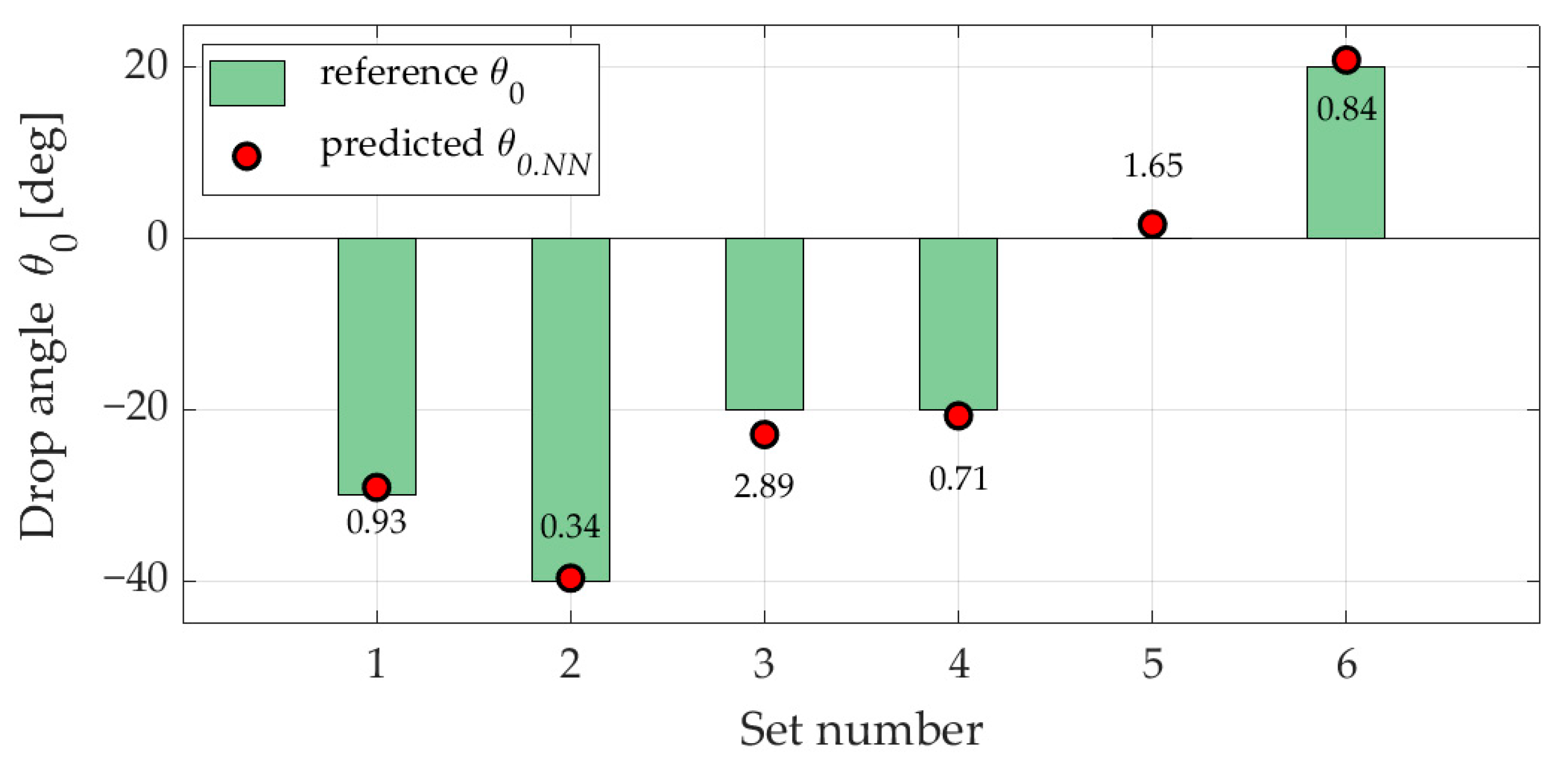
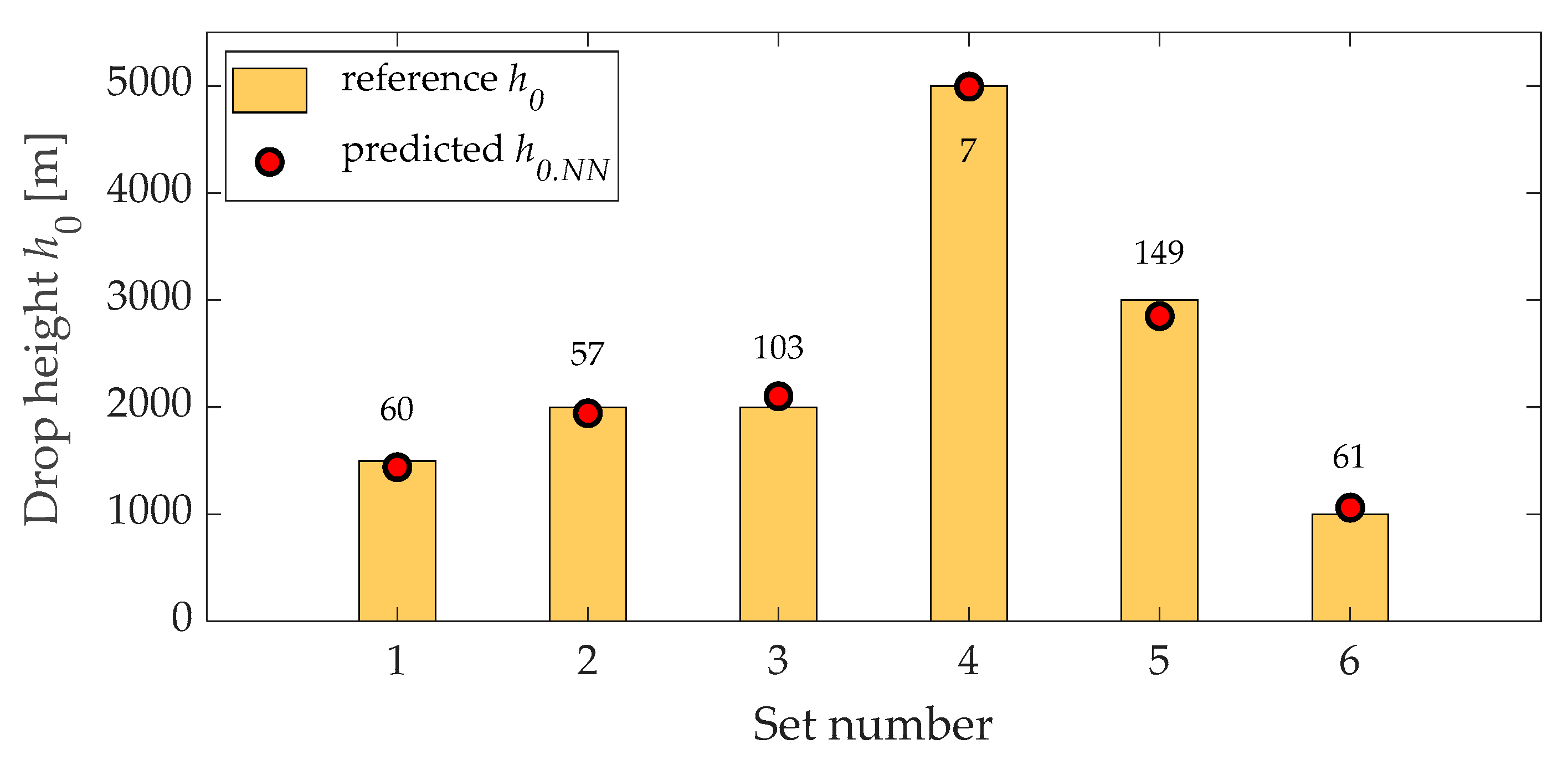
3.1. Case 1
3.2. Case 2
- rk.rand ∈ ⟨492, 7347⟩ [m],
- tk.rand ∈ ⟨5, 53⟩ [s],
- Vk.rand ∈ ⟨145, 292⟩ [m/s].
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGU | Autonomous Guidance Unit; |
| APER-DDQN | Adaptive Priority Experience Replay Deep Double Q-Network; |
| BN | Bayesian Network; |
| BPNN | Backpropagation Neural Network; |
| CARP | Calculated Aerial Release Point; |
| DDQN | Deep Double Q-Network; |
| GA | Genetic Algorithm; |
| GLONASS | Globalnaya Navigatsionnaya Sputnikovaya Sistema (Global Navigation Satellite System); |
| GNSS | Global Navigation Satellite System; |
| GPS | Global Positioning System; |
| INS | Inertial Navigation System; |
| JPADS | Joint Precision Airdrop System; |
| KE | Kane’s Equation (model equation mentioned); |
| LIDAR | Light Detection and Ranging, |
| MLP | Multilayer Perceptron; |
| MPE | Mean Percent Error; |
| MSE | Mean Squared Error; |
| NN1 | Neural Network (direct analysis) |
| NN2 | Neural Network (inverse analysis) |
| NNs | Neural Networks; |
| PADS | Precision Airdrop Systems; |
| PDT | Parent-Divorcing Technique; |
| PER | Prioritized Experience Replay; |
| RFI | Radio Frequency Interference; |
| SLAM | Simultaneous Localization and Mapping; |
| STPA-BN | System-Theoretic Process Analysis-Bayesian Network; |
| UAF | Universal Activation Function; |
| UAV | Unmanned Aerial Vehicle; |
| WSHA | Whale-Swarm Hybrid Algorithm; |
| List of Symbols | |
| α | Angle of attack |
| αt | Nutation angle |
| CaN | Coefficient of the aerodynamic normal force |
| CaNr | Coefficient of the aerodynamic damping force |
| CaX | Coefficient of the aerodynamic axial force |
| CaX0 | Zero pitch coefficient |
| CaXα2 | Pitch drag coefficient |
| Cm | Coefficient of the aerodynamic tilting moment |
| Cq | Coefficient of the damping tilting moment |
| d | Diameter of the capsule body |
| FaX | Axial aerodynamic force |
| FaN | Normal force |
| Fh(⋅) | Activation function of the hidden layer |
| Fout(⋅) | Activation function of the output layer |
| Fx | Sum of all external forces along body axes |
| Fx | Resultant force along x body axis |
| Fz | Sum of all external forces along body axes |
| Fz | Resultant force along z body axis |
| g | Acceleration of gravity |
| H | Number of neurons in the hidden layer |
| h0 | Initial height |
| I | Moment of inertia matrix |
| Iy | Moment of inertia about the pitch axis |
| m | Capsule mass |
| M | Total pitching moment acting on the capsule |
| Mc | Sum of all external moments, expressed in the capsule body frame |
| Ω | Angular velocity vector of the body frame with respect to the inertial frame, also expressed in body coordinates |
| p, P | Pairs of data |
| ρ | Air density |
| Q | Component of the angular velocity vector of the capsule body |
| rk | Range |
| Sb | Characteristic surface (cross-sectional area of the capsule) |
| θ0 | Initial angle of pitch / angle of release |
| tk | Flight time |
| U | Component of the velocity vector of the capsule in relation to the air in the boundary system Sxyz (along x-axis) |
| V0 | Initial velocity |
| Vc | Velocity of the capsule, expressed in body coordinates |
| Vk | Impact velocity |
| W | Component of the velocity vector of the capsule in relation to the air in the boundary system Sxyz (along z-axis) |
| w, b | Set of neural network parameters (weights and biases) |
| X | Input vector (e.g., control parameters, material parameters) |
| xg | x-coordinate of the initial point |
| xk | x-coordinate of the end point (cargo drop) |
| Y | Output vector (e.g., observed system response, simulation result) |
| yi(p) | Reference data |
| zg | z-coordinate of the initial point |
| zk | z-coordinate of the end point (cargo drop) |
| ti(p) | Computed values |
References
- Wu, Q.; Wu, H.; Jiang, Z.; Tan, L.; Yang, Y.; Yan, S. Multi-objective optimization and driving mechanism design for controllable wings of underwater gliders. Ocean Eng. 2023, 286, 115534. [Google Scholar] [CrossRef]
- Li, G.; Cao, Y.; Wang, M. Modeling and Analysis of a Generic Internal Cargo Airdrop System for a Tandem Helicopter. Appl. Sci. 2021, 11, 5109. [Google Scholar] [CrossRef]
- Xu, B.; Chen, J. Review of modeling and control during transport airdrop process. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416678142. [Google Scholar] [CrossRef]
- Basnet, S.; Toroody, A.B.; Chaal, M.; Lahtinen, J.; Bolbot, V.; Banda, O.A.V. Risk analysis methodology using STPA-based Bayesian network-applied to remote pilotage operation. Ocean Eng. 2023, 270, 113569. [Google Scholar] [CrossRef]
- Xu, J.; Tian, W.; Kan, L.; Chen, Y. Safety Assessment of Transport Aircraft Heavy Equipment Airdrop: An Improved STPA-BN Mechanism. IEEE Access 2022, 10, 87522–87534. [Google Scholar] [CrossRef]
- Kane, R.; Dicken, M.T.; Buehler, R.C. A Homing Parachute System Technical Report; Sandia Corporation: Albuquerque, NM, USA, 1961. [Google Scholar]
- Wegereef, J.W. Precision airdrop system. Aircr. Eng. Aerosp. Technol. Int. J. 2007, 79, 12–17. [Google Scholar] [CrossRef]
- Jóźwiak, A.; Kurzawiński, S. The concept of using the Joint Precision Airdrop System in the process of supply in combat actions. Mil. Logist. Syst. 2019, 51, 27–42. [Google Scholar] [CrossRef]
- Mathisen, S.H.; Grindheim, V.; Johansen, T.A. Approach Methods for Autonomous Precision Aerial Drop from a Small Unmanned Aerial Vehicle. IFAC-PapersOnLine 2017, 50, 3566–3573. [Google Scholar] [CrossRef]
- Lu, J.; Zou, T.; Jiang, X. A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots. Sensors 2022, 22, 8909. [Google Scholar] [CrossRef]
- Dever, C.; Dyer, T.; Hamilton, L.; Lommel, P.; Mohiuddin, S.; Reiter, A.; Singh, N.; Truax, R.; Wholey, L.; Bergeron, K.; et al. Guided-Airdrop Vision-Based Navigation. In Proceedings of the 24th AIAA Aerodynamic Decelerator Systems Technology Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Felux, M.; Fol, P.; Figuet, B.; Waltert, M.; Olive, X. Impacts of Global Navigation Satellite System Jamming on Aviation. Navigation 2023, 71, navi.657. [Google Scholar] [CrossRef]
- Mateos-Ramirez, P.; Gomez-Avila, J.; Villaseñor, C.; Arana-Daniel, N. Visual Odometry in GPS-Denied Zones for Fixed-Wing Unmanned Aerial Vehicle with Reduced Accumulative Error Based on Satellite Imagery. Appl. Sci. 2024, 14, 7420. [Google Scholar] [CrossRef]
- Li, D.; Zhang, F.; Feng, J.; Wang, Z.; Fan, J.; Li, Y.; Li, J.; Yang, T. LD-SLAM: A Robust and Accurate GNSS-Aided Multi-Map Method for Long-Distance Visual SLAM. Remote Sens. 2023, 15, 4442. [Google Scholar] [CrossRef]
- Pramod, A.; Shankaranarayanan, H.; Raj, A.A. A Precision Airdrop System for Cargo Loads Delivery Applications. In Proceedings of the International Conference on System, Computation, Automation and Networking (ICSCAN), Puducherry, India, 30–31 July 2021. [Google Scholar] [CrossRef]
- Cheng, W.; Yang, C.; Ke, P. Landing Reliability Assessment of Airdrop System Based on Vine-Bayesian Network. Int. J. Aerosp. Eng. 2023, 23, 1773841. [Google Scholar] [CrossRef]
- Siwek, M.; Baranowski, L.; Ładyżyńska-Kozdraś, E. The Application and Optimisation of a Neural Network PID Controller for Trajectory Tracking Using UAVs. Sensors 2024, 24, 8072. [Google Scholar] [CrossRef] [PubMed]
- Yong, L.; Qidan, Z.; Ahsan, E. Quadcopter Trajectory Tracking Based on Model Predictive Path Integral Control and Neural Network. Drones 2025, 9, 9. [Google Scholar] [CrossRef]
- Hertz, J.; Krogh, A.; Palmer, R. Introduction to the Theory of Neural Computation, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Haykin, S. Neural Networks-A Comprehensive Foundation; Prentice Hall: New York, NY, USA, 1999. [Google Scholar]
- Truong Pham, D.; Xing, L. Neural Networks for Identification, Prediction and Control, 1st ed.; Springer: London, UK, 2012. [Google Scholar]
- ParaZero’s DropAir: Precision Airdrop for Contested Environments. Available online: https://www.autonomyglobal.co/parazeros-dropair-precision-airdrop-for-contested-environments/ (accessed on 10 August 2025).
- Xu, R.; Yu, G. Research on intelligent control technology for enhancing precision airdrop system autonomy. In Proceedings of the International Conference on Machine Learning and Computer Application (ICMLCA), Hangzhou, China, 27–29 October 2023. [Google Scholar]
- Wang, Y.; Yang, C.; Yang, H. Neural network-based simulation and prediction of precise airdrop trajectory planning. Aerosp. Sci. Technol. 2022, 120, 107302. [Google Scholar] [CrossRef]
- Ouyang, Y.; Wang, X.; Hu, R.; Xu, H. APER-DDQN: UAV Precise Airdrop Method Based on Deep Reinforcement Learning. IEEE Access 2022, 10, 50878–50891. [Google Scholar] [CrossRef]
- Li, K.; Zhang, K.; Zhang, Z.; Liu, Z.; Hua, S.; He, J. A UAV Maneuver Decision-Making Algorithm for Autonomous Airdrop Based on Deep Reinforcement Learning. Sensors 2021, 21, 2233. [Google Scholar] [CrossRef]
- Wei, Z.; Shao, Z. Precision landing of autonomous parafoil system via deep reinforcement learning. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024. [Google Scholar] [CrossRef]
- Qi, C.; Min, Z.; Yanhua, J.; Min, Y. Multi-Objective Cooperative Paths Planning for Multiple Parafoils System Using a Genetic Algorithm. J. Aerosp. Technol. Manag. 2019, 11, e0419. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.L.; Zhu, E.L.; Chen, Z.Q.; He, Y.P. Genetic algorithm based homing trajectory planning of parafoil system with constraints. J. Cent. South Univ. Technol. 2017, 48, 404–410. [Google Scholar] [CrossRef]
- Zhang, A.; Xu, H.; Bi, W.; Xu, S. Adaptive mutant particle swarm optimization based precise cargo airdrop of unmanned aerial vehicles. Appl. Soft Comput. 2022, 130, 109657. [Google Scholar] [CrossRef]
- Wu, Y.; Wei, Z.; Liu, H.; Qi, J.; Su, X.; Yang, J.; Wu, Q. Advanced UAV Material Transportation and Precision Delivery Utilizing the Whale-Swarm Hybrid Algorithm (WSHA) and APCR-YOLOv8 Model. Appl. Sci. 2024, 14, 6621. [Google Scholar] [CrossRef]
- Aster, R.; Borchers, B.; Thurber, C. Parameter Estimation and Inverse Problems; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Bolzon, G.; Maier, G.; Panico, M. Material Model Calibration by Indentation, Imprint Mapping and Inverse Analysis. Int. J. Solids Struct. 2004, 41, 2957–2975. [Google Scholar] [CrossRef]
- Potrzeszcz-Sut, B.; Dudzik, A. The Application of a Hybrid Method for the Identification of Elastic–Plastic Material Parameters. Materials 2022, 15, 4139. [Google Scholar] [CrossRef] [PubMed]
- Potrzeszcz-Sut, B.; Pabisek, E. ANN Constitutive Material Model in the Shakedown Analysis of an Aluminum Structure. Comput. Assist. Methods Eng. Sci. 2017, 21, 49–58. [Google Scholar] [CrossRef]
- Etkin, B. Dynamics of Atmosphere Flight; John Wiley & Sons, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Blakelock, J.H. Automatic Control of Aircraft and Missiles; John Wiley & Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Kowaleczko, G.; Klemba, T.; Pietraszek, M. Stability of a Bomb with a Wind-Stabilised-Seeker. Probl. Mechatron. Armament Aviat. Saf. 2022, 13, 43–66. [Google Scholar] [CrossRef]
- Baranowski, L.; Frant, M. Calculation of aerodynamic characteristics of flying objects using Prodas and Fluent software. Mechanik 2017, 7, 591–593. [Google Scholar] [CrossRef]
- Grzyb, M.; Koruba, Z. Comparative Analysis of the Guided Bomb Flight Control System for Different Initial Conditions. Meas. Autom. Robot. 2024, 3, 41–52. [Google Scholar] [CrossRef]
- Humennyi, A.; Oleynick, S.; Malashta, P.; Pidlisnyi, O.; Aleinikov, V. Construction of a ballistic model of the motion of uncontrolled cargo during its autonomous high-precision drop from a fixed-wing unmanned aerial vehicle. Appl. Mech. 2024, 5, 25–33. [Google Scholar] [CrossRef]
- Yuen, B.; Tu Hoang, M.; Dong, X.; Lu, T. Universal Activation Function for Machine Learning. Sci. Rep. 2021, 11, 18757. [Google Scholar] [CrossRef] [PubMed]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley: New York, NY, USA, 1968; Volume 1, 2. [Google Scholar]

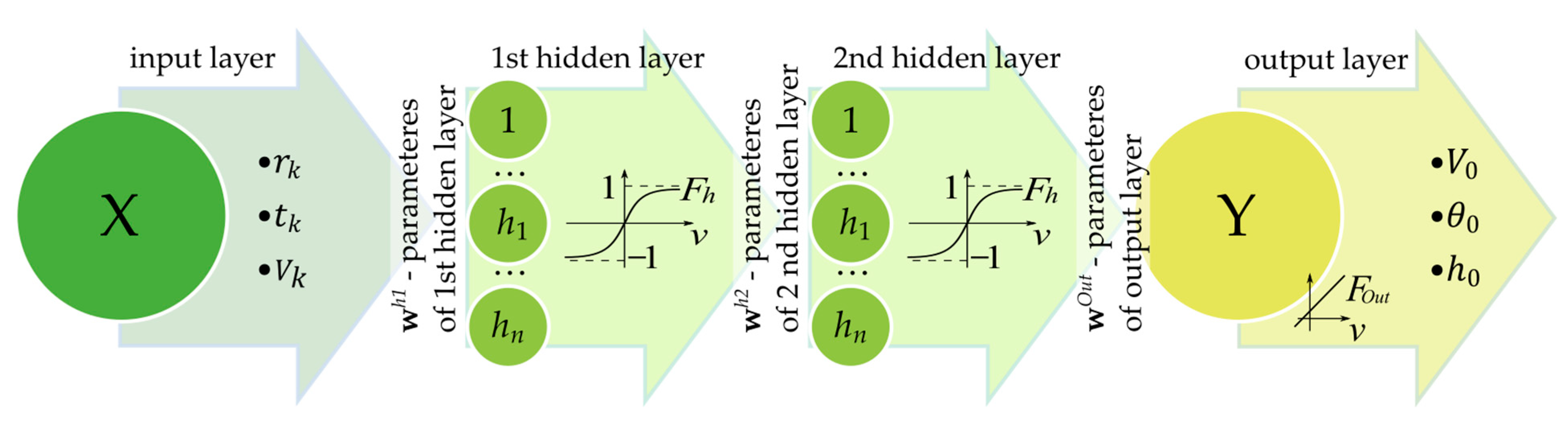


| Adopted Values | Range | Computed Values | Range |
|---|---|---|---|
| [m/s] | [m] | ||
| [deg] | [s] | ||
| [m] | [m/s] |
| Values | Range | Scale Factor | New Range |
|---|---|---|---|
| [m/s] | ⟨60, 240⟩ | 252.0 | |
| [deg] | ⟨−40, 40⟩ | 42.0 | |
| [m] | ⟨1000, 5000⟩ | 5250.0 | |
| [m] | ⟨492.8, 734.4⟩ | 7713.7 | |
| [s] | ⟨5.75, 52.68⟩ | 55.3 | |
| [m/s] | ⟨145.62, 291.38⟩ | 305.9 |
| Learning Phase | Testing Phase | |||
|---|---|---|---|---|
| Values | MPE [%] | MSE | MPE [%] | MSE |
| [m] | 2.03 | 0.0000560 | 2.01 | 0.0000518 |
| [s] | 1.14 | 0.0000331 | 1.30 | 0.0324275 |
| [m/s] | 0.68 | 0.0000421 | 0.63 | 0.1926063 |
| Learning Phase | |||
|---|---|---|---|
| Values | MPE [%] | maxPE [%] | MSE |
| [m/s] | 0.96 | 7.67 | 0.00002 |
| [deg] | 2.68 | 75.01 | 0.00006 |
| [m] | 0.88 | 10.62 | 0.00001 |
| Set No. | Variable (A) V0 [m/s] θ0 [deg] h0 [m] | Stage 1 Output Input to Stage 4 rk [m] tk [s] Vk [m/s] | Stage 4 Output (B) V0.NN[m/s] θ0.NN [deg] h0.NN [m] | Percent Error (A−B) [%] |
|---|---|---|---|---|
| 1 (7) | 150.00 | 1450.20 | 150.05 | 0.03 |
| −30.00 | 11.89 | −29.07 | 3.10 | |
| 1500.00 | 207.85 | 1440.27 | 3.98 | |
| 2 (39) | 150.00 | 1413.30 | 150.93 | 0.62 |
| −40.00 | 13.23 | −39.66 | 0.85 | |
| 2000.00 | 223.83 | 1943.17 | 2.84 | |
| 3 (59) | 100.00 | 1538.50 | 101.43 | 1.43 |
| −20.00 | 17.61 | −22.89 | 14.47 | |
| 2000.00 | 202.70 | 2102.53 | 5.13 | |
| 4 (77) | 240.00 | 4934.00 | 236.01 | 1.66 |
| −20.00 | 27.83 | −20.71 | 3.53 | |
| 5000.00 | 285.84 | 4992.56 | 0.15 | |
| 5 (95) | 200.00 | 4432.50 | 203.75 | 1.88 |
| 0 | 26.25 | 1.65 | - | |
| 3000.00 | 252.51 | 2851.01 | 4.97 | |
| 6 (123) | 240.00 | 4738.80 | 231.50 | 3.54 |
| 20.00 | 24.86 | 20.84 | 4.19 | |
| 1000.00 | 219.08 | 1061.39 | 6.14 |
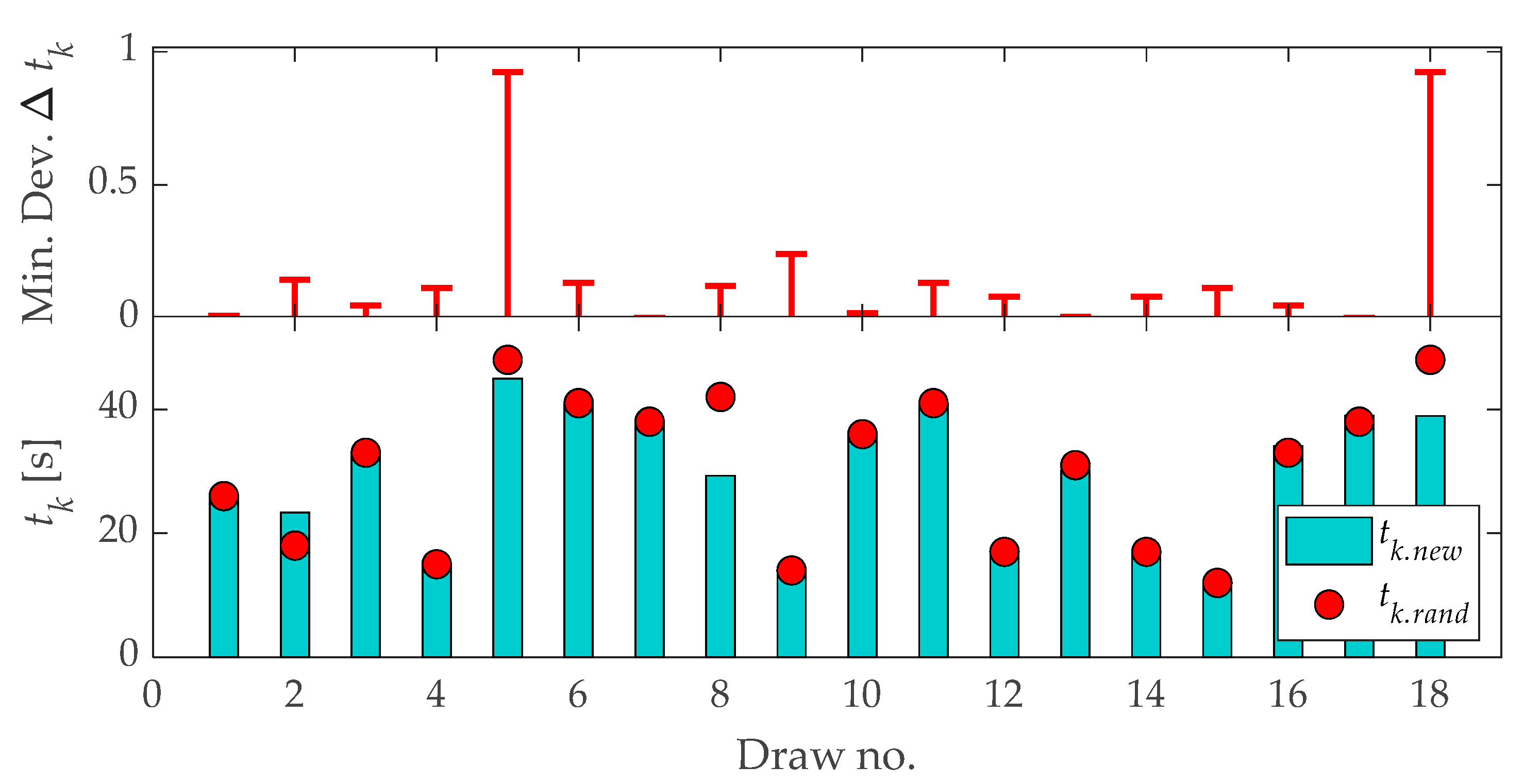
| Draw No. | Input to Stage 4 (C): rk.rand [m] | Stage 1 Result (D): rk.new [m] | Percent Error (C−D) [%] | Absolute Error (C−D) [m] | Min. Dev. of Δrk [m] |
|---|---|---|---|---|---|
| 1 | 4213.00 | 4205.10 | 0.19 | 7.90 | 35.30 |
| 2 | 2692.00 | 2569.70 | 4.76 | 122.30 | 4.10 |
| 3 | 3504.00 | 3436.00 | 1.98 | 68.00 | 17.40 |
| 4 | 2257.00 | 2319.0 | 2.67 | 62.00 | 7.20 |
| 5 | 3567.00 | 3907.30 | 8.71 | 340.30 | 80.40 |
| 6 | 2966.00 | 3064.90 | 3.23 | 98.90 | 44.00 |
| 7 | 3353.00 | 3344.80 | 0.25 | 8.20 | 21.00 |
| 8 | 1925.00 | 2108.80 | 8.72 | 183.80 | 6.00 |
| 9 | 755.00 | 797.27 | 5.30 | 42.27 | 11.37 |
| 10 | 3067.00 | 3132.80 | 2.10 | 65.80 | 24.80 |
| 11 | 6647.00 | 6731.70 | 1.26 | 84.67 | 139.90 |
| 12 | 3309.00 | 3238.90 | 2.16 | 70.10 | 11.50 |
| 13 | 2636.00 | 2460.00 | 7.15 | 176.00 | 1.30 |
| 14 | 705.00 | 776.87 | 9.25 | 71.87 | 12.99 |
| 15 | 1453.00 | 1431.80 | 1.48 | 21.20 | 2.80 |
| 16 | 5191.00 | 5185.10 | 0.11 | 5.90 | 6.90 |
| 17 | 5921.00 | 5988.70 | 1.13 | 67.70 | 0.50 |
| 18 | 6334.00 | 5597.10 | 13.17 | 736.90 | 11.70 |
| Draw No. | Input to Stage 4 (C): tk.rand [s] | Stage 1 Result (D): tk.new [s] | Percent Error (C−D) [%] | Absolute Error (C−D) [s] | Min. Dev. of Δtk [s] |
|---|---|---|---|---|---|
| 1 | 26.00 | 25.86 | 0.54 | 0.14 | 0.010 |
| 2 | 18.00 | 23.35 | 22.91 | 5.35 | 0.145 |
| 3 | 33.00 | 33.11 | 0.33 | 0.11 | 0.048 |
| 4 | 15.00 | 15.00 | 0 | 0 | 0.114 |
| 5 | 48.00 | 44.94 | 6.81 | 3.06 | 0.924 |
| 6 | 41.00 | 41.13 | 0.32 | 0.13 | 0.133 |
| 7 | 38.00 | 37.65 | 0.93 | 0.35 | 0.001 |
| 8 | 42.00 | 29.28 | 43.44 | 12.72 | 0.121 |
| 9 | 14.00 | 14.26 | 1.82 | 0.26 | 0.241 |
| 10 | 36.00 | 36.37 | 1.02 | 0.37 | 0.018 |
| 11 | 41.00 | 40.96 | 0.10 | 0.04 | 0.133 |
| 12 | 17.00 | 16.45 | 3.34 | 0.55 | 0.080 |
| 13 | 31.00 | 30.20 | 2.65 | 0.80 | 0.005 |
| 14 | 17.00 | 17.23 | 1.33 | 0.23 | 0.080 |
| 15 | 12.00 | 11.90 | 0.84 | 0.10 | 0.114 |
| 16 | 33.00 | 34.05 | 3.08 | 1.05 | 0.048 |
| 17 | 38.00 | 38.99 | 2.54 | 0.99 | 0.001 |
| 18 | 48.00 | 38.93 | 23.30 | 9.07 | 0.924 |
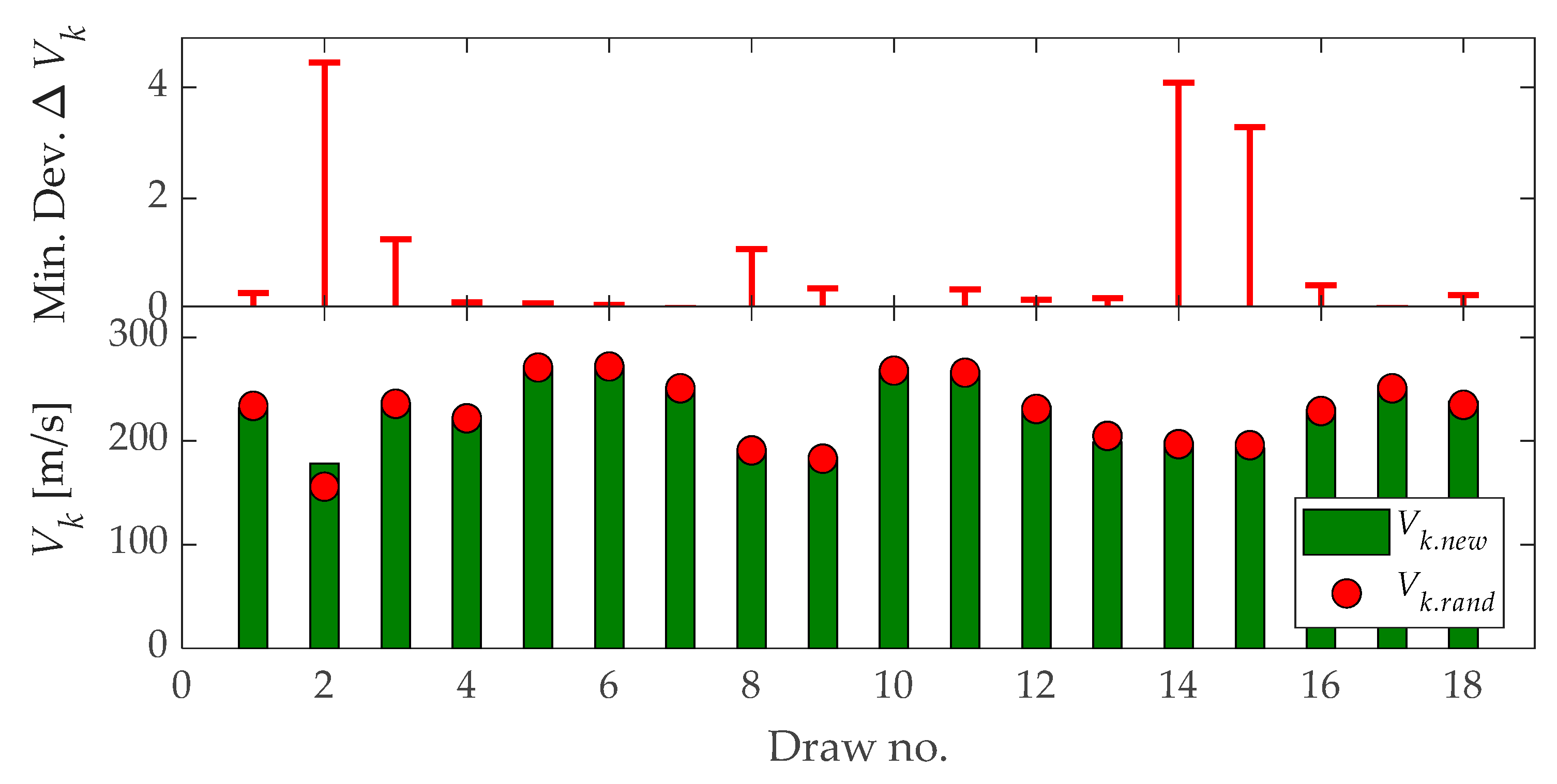
| Draw No. | Input to Stage 4 (C): Vk.rand [m/s] | Stage 1 Result (D): Vk.new [m/s] | Percent Error (C−D) [%] | Absolute Error (C−D) [m/s] | Min. Dev. of ΔVk [m/s] |
|---|---|---|---|---|---|
| 1 | 234.00 | 231.88 | 0.91 | 2.12 | 0.30 |
| 2 | 156.00 | 178.19 | 12.45 | 22.19 | 4.45 |
| 3 | 236.00 | 235.15 | 0.36 | 0.85 | 1.27 |
| 4 | 222.00 | 220.97 | 0.47 | 1.03 | 0.13 |
| 5 | 271.00 | 270.37 | 0.23 | 0.63 | 0.11 |
| 6 | 272.00 | 272.33 | 0.12 | 0.33 | 0.09 |
| 7 | 251.00 | 248.95 | 0.82 | 2.05 | 0.03 |
| 8 | 191.00 | 191.81 | 0.42 | 0.81 | 1.09 |
| 9 | 183.00 | 184.06 | 0.58 | 1.06 | 0.38 |
| 10 | 268.00 | 268.18 | 0.07 | 0.18 | 0.02 |
| 11 | 266.00 | 267.33 | 0.50 | 1.33 | 0.36 |
| 12 | 231.00 | 233.47 | 1.06 | 2.47 | 0.18 |
| 13 | 205.00 | 199.00 | 3.02 | 6.00 | 0.21 |
| 14 | 197.00 | 198.95 | 0.98 | 1.95 | 4.09 |
| 15 | 196.00 | 192.70 | 1.71 | 3.30 | 3.28 |
| 16 | 229.00 | 228.33 | 0.29 | 0.67 | 0.44 |
| 17 | 251.00 | 252.26 | 0.50 | 1.26 | 0.03 |
| 18 | 235.00 | 238.14 | 1.32 | 3.14 | 0.27 |
| Draw No. | V0.NN [m/s] | θ0.NN [°] | h0.NN [m] |
|---|---|---|---|
| 1 | 192.53 | 11.22 | 2126.03 |
| 2 | 140.17 | 30.44 | 1000.00 |
| 3 | 138.71 | 30.62 | 2816.64 |
| 4 | 174.76 | −15.08 | 1663.18 |
| 5 | 153.44 | 46.80 | 4399.42 |
| 6 | 108.77 | 36.14 | 4993.07 |
| 7 | 133.79 | 39.46 | 3442.67 |
| 8 | 119.64 | 48.61 | 1540.09 |
| 9 | 78.36 | −41.24 | 1656.65 |
| 10 | 105.05 | 16.01 | 4797.22 |
| 11 | 237.73 | 26.25 | 3582.56 |
| 12 | 222.36 | −4.50 | 1480.92 |
| 13 | 130.14 | 45.96 | 1610.60 |
| 14 | 66.26 | −43.64 | 2127.58 |
| 15 | 138.07 | −22.62 | 1263.42 |
| 16 | 220.27 | 33.28 | 1625.57 |
| 17 | 226.62 | 31.75 | 2703.74 |
| 18 | 231.41 | 39.59 | 1847.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Potrzeszcz-Sut, B.; Grzyb, M. Inverse Procedure to Initial Parameter Estimation for Air-Dropped Packages Using Neural Networks. Appl. Sci. 2025, 15, 10422. https://doi.org/10.3390/app151910422
Potrzeszcz-Sut B, Grzyb M. Inverse Procedure to Initial Parameter Estimation for Air-Dropped Packages Using Neural Networks. Applied Sciences. 2025; 15(19):10422. https://doi.org/10.3390/app151910422
Chicago/Turabian StylePotrzeszcz-Sut, Beata, and Marta Grzyb. 2025. "Inverse Procedure to Initial Parameter Estimation for Air-Dropped Packages Using Neural Networks" Applied Sciences 15, no. 19: 10422. https://doi.org/10.3390/app151910422
APA StylePotrzeszcz-Sut, B., & Grzyb, M. (2025). Inverse Procedure to Initial Parameter Estimation for Air-Dropped Packages Using Neural Networks. Applied Sciences, 15(19), 10422. https://doi.org/10.3390/app151910422







