Abstract
Multi-task learning (MTL) has emerged as a promising paradigm in machine learning, which enables models to generalize better by sharing representations and learning strategies across tasks. However, it may struggle to tune parameters that equally benefit all tasks. To solve this problem, a multi-task parallel model (MTPM) is proposed based on the fuzzy neural networks (FNNs) and the joint gradient descent algorithm (JGDA) that simultaneously optimizes the parameters across parallel tasks. First, an MTPM is constructed using the FNN to extract the interaction features and the specificity features from multiple related tasks. In this model, the shared neurons and specific neurons are embedded into individual FNN rather than single-type neurons, which avoids the conflict of the correlation between tasks and the independence of each task. Second, a JGDA is proposed to achieve the analytical optimization of parameters in the proposed model, including the shared parameters and the specific parameters. The potential correlations between different tasks and the specificity of each task can be shaped to balance knowledge sharing and independent learning. Third, an adaptive learning rate strategy is designed to further improve the model’s performance. In this strategy, the global learning rate (GLR) and task-specific learning rate (SLR) are managed separately, which can improve the model performance by coordinating the training process of different tasks. Finally, the experimental results show that the method proposed in this paper outperforms the traditional method in terms of MTL effects. Compared to single-task benchmark experiments, the model proposed in this paper achieves an average RMSE improvement of 24.2% across three application scenarios, which demonstrates its effectiveness and practicality.
1. Introduction
Machine learning has been increasingly interested in solving practical problems through mathematical modeling, such as image classification [1,2,3], speech recognition [4,5,6,7], and biomedical analysis [8,9]. FNNs have been considered a promising machine learning method for solving practical problems due to their ability to approximate nonlinear functions [10]. As the complexity and the number of tasks increase, higher demands are placed on the training performance of FNNs. However, isolated single-task learning frameworks may ignore empirical information from other tasks, which leads to learning resource expenditure. Therefore, it is a crucial challenge to build an MTL model that can integrate across-task knowledge and optimize learning efficiency.
To solve the modeling task in the multi-task scenario, there has been a large amount of research devoted to developing efficient models. MTL has been proposed to improve generalization by the joint training of multiple related tasks. Wu and Lisser proposed a multi-branch MTL framework to solve multiple nonlinear problems in parallel [11]. In this framework, the physics-informed neural network was utilized to model a task in each branch, which can solve MTL problems by training multiple models simultaneously. Liao et al. proposed a MTL model that added task gates to control the flow of information between tasks [12]. A dynamic weighting strategy was designed to link two network models to train the detection task and the classification task simultaneously. Ding et al. proposed a MTL fuzzy multivariate controller based on FNNs [13]. The model structure was adjusted by calculating neuron similarity through a self-organizing mechanism. These multiple independent single-task models require separate model training for each task, which is computationally expensive. Moreover, Zhao et al. designed a feature-constrained MTL method, which consisted of multiple LASSO models [14]. In this method, the feature-constrained mechanism was used to capture the shared features across tasks. The results showed that LASSO with shared information achieved good performance in multi-task prediction. Chen et al. proposed a multi-model MTL model to obtain data relevance by merging multiple data modalities [15]. Multiple sub-models were merged and shared network layers to predict both hospitalization time and mortality. Xu et al. proposed a long-term and short-term memory autoencoder MTL model [16]. A cascade-parallel architecture was used to facilitate the sharing of relevant information across different tasks. Tian et al. proposed a framework with a shared feature learning layer that decomposed the task into interrelated subtasks [17]. The task-sharing layer was further optimized with the self-attention mechanism, which improved the efficiency of capturing temporal dependencies. However, the model that relies on task sharing may ignore inter-task independence, which inevitably leads to task-specific negative transfer.
In terms of constructing a multitasking learning model, the corresponding optimization algorithms must update the parameters of the model. Wang et al. proposed a similarity measurement method for assignment of task weights in deep belief networks [18]. The weights were adaptively adjusted based on iterative loss variation to balance the training process for each task. Then, Li et al. proposed a confidence-weighted learning algorithm to update the weights by minimizing the Kullback–Leibler divergence of the old and new weight distributions [19]. This approach stabilized the information retained in each round and the previous rounds, which enhanced the classification performance. Wang et al. designed a principled loss function based on homoskedastic uncertainty weighting and the Laplace distribution [20]. The weighting parameters of each subtask were updated synchronously during the learning process of the multi-task model, which promoted the simultaneous convergence of each subtask. However, the task effect imbalance cannot be avoided by optimizing loss function weighting, which leads to the optimization of some tasks being neglected. To alleviate the negative effects between tasks, Wu et al. proposed a multi-task genetic algorithm [21]. The method estimated the deviation between two tasks and eliminated it in the chromosome transfer so that the optimal solutions of the two tasks are approached. Chen et al. proposed an inter-task knowledge transfer algorithm based on transfer rank, which improved the probability of positive inter-task transfer by calculating the transfer rank [22]. Mao et al. proposed a mirror gradient lift algorithm to regularize the task variance [23]. The regularization parameters were required to be updated before updating the parameters in each iteration. However, the parallel training of different tasks may lead to different optimization directions, which may cause gradient conflicts to degrade the performance of the model. Liu et al. [24] proposed a conflict-free gradient update mechanism that ensures the simultaneous descent of each loss term during optimization by constructing an update direction with the positive dot product of the gradients of all loss terms. However, it involves all task gradients and pseudo-inverse operations, which are computationally redundant in multi-task scenarios.
Although the gradient descent algorithm has been proven to be an effective method for resolving multitasking learning, it still has the challenge of determining the learning rate strategy that maintains the convergence speed and accuracy of the multi-task model. Huang et al. proposed an adaptive adjustment strategy, which designed multi-scale modulation coefficients to dynamically modulate optimization trajectories during the training process [25]. Luo et al. developed an iteration-adaptive learning rate scheduler, which gradually decays the learning rate in a manner inversely proportional to the increasing training step [26]. However, the above methods fail to reconcile gradient profiles across tasks dynamically in MTL. Zhai et al. proposed an adaptive independent learning rate strategy [27]. The corresponding learning rate strategies were configured for different types of parameters, which were determined by the learning rate and gradient information of the previous round. Duchi et al. proposed an adaptive learning rate optimization method [28], where the learning rate was individually adjusted for each parameter based on historical gradient information. These methods mitigate the inadequacy of the uniform learning rate in accommodating all dimensions while incurring a considerable computational cost. Jeong et al. developed an adaptive learning rate from an exponential moving average of the loss rate [29]. While this method reduced the computational burden, it was a scalar GLR. However, the gradient scale and the difficulty of parameter optimization may differ significantly for different tasks. A globally uniform learning rate strategy cannot be adapted to the learning requirements of various tasks, which may lead to slow convergence.
Based on the above analysis, this paper proposes a multi-task parallel model based on a joint gradient descent algorithm (MTPM-JGDA) to improve the generalization ability by information utilization. The main contributions of this paper are as follows:
- (1)
- A multi-task parallel model with FNNs is established, including a task-sharing structure and a task-independent structure. The shared structure is the sharing of some neurons in the hidden layer to obtain the relevant information between tasks. The independent structure is composed of independent neurons for holding the individual task-specific characteristics.
- (2)
- A joint gradient descent algorithm is proposed to update the parameters of the MTPM. In this algorithm, a gradient correction discriminant strategy is designed to resolve the task gradient direction conflict problem, which utilizes the gradient cosine value to evaluate the difference in the gradient direction. Then it guides the optimization of the shared parameters and the specific parameters through gradient correction.
- (3)
- An adaptive learning rate strategy is proposed to separate the GLR from the SLR to balance the multi-task training speed. The GLR is related to the task-shared parameter gradient for updating the shared parameters, while the SLR depends on the task error variation associated with training results.
The main content of this paper is as follows: Section 2 gives a brief description of the FNN model used in the MTPM. Section 3 describes the model of the MTPM, the JGDA, and the adaptive learning rate strategy. Section 4 demonstrates the convergence of the proposed method. Section 5 conducts three multi-task experiments using the multi-tasking model and compares the prediction results with those of other methods. Finally, Section 6 concludes this article.
2. Preliminaries
2.1. MTL
MTL is a machine learning method that utilizes the relationship between tasks to solve multiple tasks simultaneously. In general, the network structure is shared in the multi-task model through the hard parameter mechanism or soft parameter sharing mechanism [30].
The hard parameter sharing mechanism is to share the entire bottom hidden layer among all tasks [31], and the shared layer is required to capture all common shared features. The model output is
where x is the input vector, h(·) is the shared layer output function, θs is the shared layer parameter, θt is the parameter of the tth task, and Ht(·) is the output function of the tth task.
The soft parameter-sharing mechanism has a specific module for each task and exploits the shared knowledge through information fusion between independent modules [32]. The model output can be expressed by
where gt,k(·) is the tth task gating network, E(·) is the task information fusion component, and k is the number of fusion modules.
However, the above mechanisms are prone to negative migration in low-correlation tasks, which leads to performance degradation and becomes a key bottleneck in the practical application of MTL.
2.2. Fuzzy Neural Network
To construct a multi-task model, a multiple-input multiple-output (MIMO) FNN is introduced, and its network structure is shown in Figure 1.
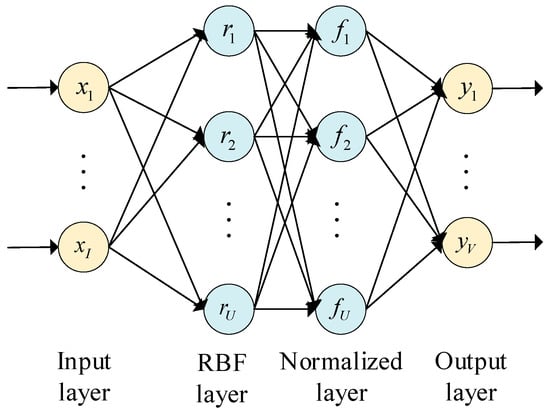
Figure 1.
The architecture multi-input multi-output FNN.
The network consists of four layers and is described as follows:
Input layer: there are I neurons, which are defined by
where x is the input vector and xi is the input of the ith neuron.
RBF layer: there are U neurons, and every neuron is a radial basis function (RBF) form with
where ru is the output of the uth neuron, cin is the center of the RBF connecting the ith neuron to the uth neuron, σiu is the width of the RBF connecting the ith neuron to the uth neuron, and e is a natural constant.
Normalized layer: There are U neurons, the output of the uth neuron is
Output layer: The output is
where each element of W is a weight connection between the normalization layer and the output layer, f is the matrix consisting of the output of the normalization layer, f = [f1, f2,…, fU].
V is the number of network outputs. When V = 1, the network is a single-output structure, which is used for the prediction or recognition task of a single indicator, at this time W ∈ ℝU×1, which can be denoted by
When V ≥ 2, the network is a multi-output structure, which can be used for the prediction or recognition task of multiple indicators. At this time W ∈ ℝU×V, which can be expressed by
The training objective function of the neural network is shown in Equation (7):
where ek = yk − ŷk, k denotes the current iteration number, yk is the kth desired output, ŷk is the kth actual output, and the training objective is achieved by making the loss function as small as possible.
The multi-input, single-output FNN is used to independently train a single task, which ignores the correlation information between the tasks. With the growing number of tasks, the workload of adjusting the structure and parameters of FNNs will increase. Multi-task joint training can increase the sample information from other tasks to make connections between different tasks and improve the model’s performance. In contrast, MIMO neural networks are trained together with the same parameters, which are fully shared between the tasks. This model structure cannot take into account the independent information of each task simultaneously, which leads to uneven effects of the tasks.
3. Multi-Task Modeling Approach Based on JGDA
The MTPM is composed using multiple FNNs, the JGDA is proposed as the model parameter training method, and an adaptive learning rate strategy is incorporated into the algorithm to enhance the convergence speed of the model.
3.1. MTPM
The MTPM consists of the FNN, as shown in Figure 2. The proposed model utilizes the correlation between tasks by partially sharing the network structure between each task. The red neurons represent the shared neurons. The parameters of the neurons of this model are updated in the way shown below the figure, where the different parameters of each task are updated following the corresponding learning method. The adaptive learning rate strategy is completed by the cooperation of the GLR and the SLR.
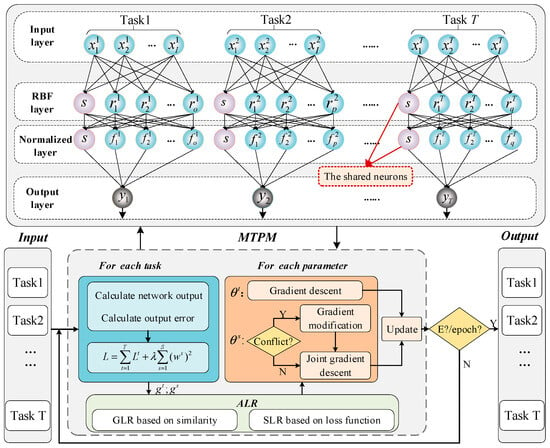
Figure 2.
Multi-task parallel model architecture.
The MTPM also consists of four layers. Let the number of tasks be T, and the layers of the model are shown below:
Input layer: the number of neurons in this layer is I × T, each task inputs I features, and the input vector is
where is the ith input of the tth task.
RBF layer: this layer consists of the task-specific neuron section and the shared neuron section. The outputs are
where is the output of the nth task-specific neuron for the tth task, Nt is the number of tth task-specific neurons, is the output of the mth shared neuron for the tth task, and M is the number of shared neurons.
Normalized layer: this layer consists of two parts, and the output is
where is the output of the nth task-specific neuron for the tth task and is the output of the mth shared neuron for the tth task.
Output layer: the number of neurons in this layer is equal to the tasks, and the output of the tth task is
where is the weight of the nth task-specific neuron for the tth task and is the weight of the mth shared neuron.
3.2. JGDA
3.2.1. Multi-Task Parameter Update Method
The MTPM involves the issues of parameter updating for multiple tasks, which needs to ensure the optimization of the objective function for multiple tasks simultaneously during task training to meet the training performance of each task. The JGDA proposed is employed to train networks for multiple tasks concurrently, which fully utilizes the correlation between tasks and also retains the independence of the tasks. The training objective in a single-task FNN is to make the loss function as small as possible, while multiple tasks correspond to multiple loss functions.
The training objective for multiple tasks can be expressed by
where Lt(θs, θt), t = 1, 2,…,T, T is the number of tasks, and Lt is its corresponding loss function with respect to θs and θt. θs is the shared part of the parameter that indicates the similarity between multiple tasks, θt is the specific part of the parameter that indicates the independence between multiple tasks, and the parameter includes neural network training process c, σ, and w.
The loss function satisfies a monotonically decreasing function during training with
where k denotes the iteration number, Lk is the loss function value at the kth iteration, and are the current shared and specific parameters, respectively, Lk+1 is the loss function after the parameters are updated, and and are the updated shared and specific parameter representations, respectively. Because the loss function in the JGDA belongs to the binary primary function, when calculating the direction of the tth task-specific parameter descent gradient, the task-specific parameter gradient derivation is sufficient.
The specific parameters θt in the training process of the neural network include the center ct and width σt of the Gaussian function, and the weights wt from the normalization layer to the output layer. The gradient of each specific parameter is calculated as follows:
where A is the RBF layer output summation.
The specific parameters of the tth task are updated by
To compute the direction of the falling gradient of the shared parameter for the tth task, it is sufficient to derive the gradient of the shared parameter, denoted by
The shared parameters θs include cs, σs, and ws, and the gradient of each shared parameter is calculated with
The shared parameters for the tth task are updated by
where η is the learning rate for updating the shared parameters, and αt is the task weight corresponding to the tth task.
Thus, the problem of updating the gradient of a shared parameter is
Meanwhile, in the multi-task model, L2 regularization is added to avoid over-dependence between tasks and reduce task information conflicts. By penalizing the shared neuron weights, the model keeps the weights in balance to enhance the generalization. The loss function of the multi-task model is expressed by
where L is the total loss, Lt is for the tth task,
is the shared weight. λ is the regularization coefficient, and the strength of regularization can be controlled by adjusting λ. A smaller λ will allow the model to focus more on task-specific learning, while a larger λ will promote weight sharing between tasks.
3.2.2. Joint Gradient Method
The proposed JGDA has been proven to be able to solve the multi-task parallelism problem by the following analytical procedure. As shown in Figure 3, the gradients of multiple tasks suffer from gradient interference when computing shared gradients during parameter updating. In this paper, an example of gradient modification with two tasks is shown in Figure 3a. From a one-dimensional point of view, the difference in the magnitude of the gradients of the two tasks leads to conflicting tasks. If the gradient value of task 1 is larger than that of task 2, it may result in the network focusing more on the training of task 1, and the model performance decreases. Alternatively, the angle between the gradients of the two tasks may be obtuse from a two-dimensional perspective. This results in interference between the gradient components of the two training models, which leads to degradation of model performance. In this case, it is assumed that the gradients of the two tasks can be offset from each other in some directions to make the model training optimal. However, as shown in the right panel of Figure 3a, the two task gradient conflicts cannot be completely offset. To address this potential problem, this paper proposed a method to update the shared gradients.
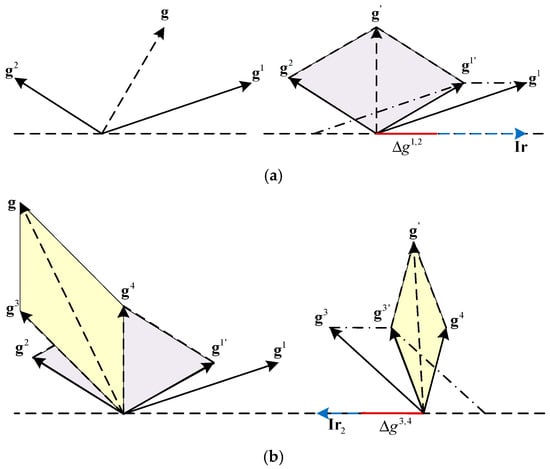
Figure 3.
Schematic of gradient modification. (a) Gradient modification for two tasks. (b) Gradient modification for multiple tasks.
To simplify the description, the shared parameter gradient of the first task is denoted as g1 = ∂L1(θs,θ1)/∂θ1, and the shared parameter gradient of the second task is denoted as g2 = ∂L2(θs,θ2)/∂θ2. According to Figure 3, ϕ is the angle between g1 and g2.
When cosϕ ≥ 0, there is no gradient interference problem; when cosϕ < 0 there is a gradient interference problem. Ir is the interference direction of the two gradients, Ir = g1 − g2, ϕ1 and ϕ2 are the angles between the two gradients and the interference direction, respectively, and the cosine of the angle is calculated as follows:
Then, the gradient difference between the two gradients in the direction of the gradient interference is
where g1cosϕ1 is the interference gradient component of the gradient of task 1 in the interference direction and g2cosϕ2 is the interference gradient component of the gradient of task 2 in the interference direction. The gradient difference is displayed as shown in Δg1,2 of Figure 3a.
The gradient of task 1 is modified with the resulting gradient difference:
The modified gradient is shown as g1′ in Figure 3a. Similarly, when considering more tasks, multiple gradients are modified in order of strongest to weakest correlation since the multi-task model leverages inter-task correlation to train learning. For example, of the three tasks, the two tasks with more relevance are modified first. g1 and g2 are modified to obtain a shared gradient denoted as g4, and then the gradient is modified for g4 and g3 of task three. The modification method is the same as the gradient modification of the two tasks: find the gradient interference direction Ir2 = g3 − g4 between g4 and g3, calculate the cosine value of the angle between g4 and g3 and Ir2, respectively, and then modify the g3 method as in Equation (33). The modification process and method are shown in Figure 3b.
The shared parameter update also requires α, which is the corresponding weight of the shared parameter gradient for each task. First, determine which metrics need to be predicted for each by selecting the desired output data as the comparison sequence, denoted Xt(o) = {Xt(1), Xt(2),…, Xt(O)}, t = 1, 2,…, T, and the input data for the metrics that need to be predicted as the reference sequence, denoted Yi(o) = {Yi(1), Yi(2),…, Yi(O)}, i = 1,2,…, I, where o is used to specify the sequence, O is the length of the sequence, and I is the dimensionality of the reference sequence.
To avoid the influence of different dimensions on the analysis results, the dataset is
The gray correlation coefficient with the comparison sequence xt(o) and reference sequence yi(o) is calculated by
Denote Δt(o) = |xi(o) − yt(o)|, then the equation can be rewritten as
where ρ ∈ (0,1) is the resolution coefficient, ρ = 0.5 [33].
Equations (35) and (36) are the degree of correlation between the comparison sequence and the reference sequence, while the gradient weight for the task in this paper is the degree of importance of the reference sequences. Therefore, the average of the correlation coefficients of each reference sequence is
The α of the reference sequence is calculated to obtain the task gradient weights with
3.3. Adaptive Learning Rate Strategy
In the MTPM-JGDA, the GLR and the SLR are designed to update the shared and task-specific parameters, respectively. As Figure 4a gives two examples of similar task gradients, Figure 4b shows how the task learning rate varies with gradient similarity.
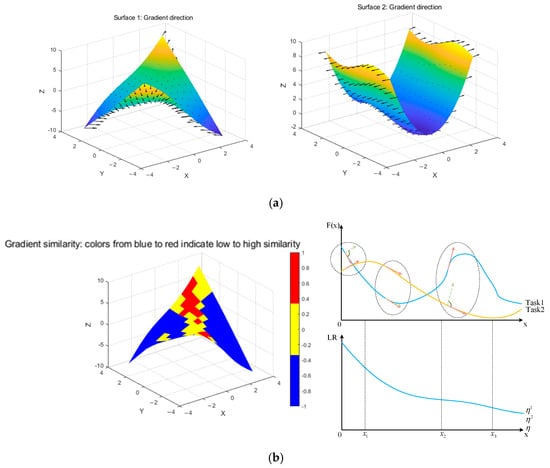
Figure 4.
Adaptive learning rate strategy. (a) Task and gradient directions: schematized as two surface functions, Z1 = sin(X) × cos(Y) + X × Y; Z2 = cos(X) × sin(Y) + X2, the arrow indicates the direction of the gradient. (b) Schematic illustration of task gradient similarity and corresponding partial learning rate changes.
The GLR is adjusted by the gradient similarity matrix with
where stj is the gradient similarity matrix between the tasks, which is computed by cosine similarity, η0 is the initial learning rate, related to the SLR, ηt is the tth SLR, and ε is set to 1 to enable the equation to hold. Gt is the cumulative gradient of the tth task, which is computed by
where is the cumulative gradient shared by all shared parameters in the shared structure l for task t, and G is the cumulative gradient of all tasks for the shared parameters. The ratio of C is equivalent to the degree of contribution of task t across all tasks relative to the shared parameters. By balancing the role of the cumulative gradient across tasks, it avoids gradient vanishing and stabilizes the training process. Combined with the consideration of the parameter update method in the previous Equation (27), the final shared parameter update method is
The SLR is used to update each task-specific parameter. It is adjusted according to the trend of the loss function
where τ is a unit increment that can be considered as a fixed step size. Combine with Equation (22) to calculate a specific parameter update.
By dynamically adjusting the SLR and GLR, it can prevent certain tasks from being too dominant in the learning process in MTPM-JGDA. It effectively balances the influence between tasks and the update rate of shared parameters and promotes better convergence of the model. Finally, the proposed JGDA is shown in Algorithm 1.
| Algorithm 1. The proposed JGDA. | |
| Input: K: maximum iterations. θ: shared parameters θs, tth task-specific parameters θt. 1. Initialization Initialize the parameters θ(c,σ,w),the GLR η and the SLR ηt. 2. Parameters learning process for k = 1:K for o = 1:O for p = 1:P | |
| Calculate the outputs of RBF layer. | %Equations (11) and (12) |
| Own the output of normalized layer. | %Equations (13) and (14) |
| Calculate the output of output layer. | %Equation (15) |
| Evaluate the error. | |
| end | |
| Calculate task-specific parameter gradient. | %Equation (18) |
| Calculate shared parameter gradient. | %Equation (23) |
| for u,v ∈ T | |
| if gu × gv< 0 | |
| Calculate interference direction Ir. | |
| Calculate the gradient difference Δgu,v. | %Equation (32) |
| Obtain the modified gradient gu′. | %Equation (33) |
| end if | |
| Calculate weight of tasks αu, αv. | %Equation (38) |
| end | |
| end | |
| Calculate the GLR. | %Equation (39) |
| Calculate the SLR. | %Equation (46) |
| end | |
| Calculate shared parameter update. | %Equation (44) |
| Calculate task-specific parameter update. | %Equation (45) |
| end | |
4. Convergence Discussion
In this section, a convergence analysis of the gradient correction in the proposed JGDA is presented. The results show that multiple tasks can be trained simultaneously by exploiting the correlation between them, and the trained model still converges with gradient correction.
In the JGDA, Δg1,2 is used to correct the gradient of g1. The angle between the corrected gradients g1 and g2 is acute, cos(g1,g2) ≥ 0, which reduces the factor of gradient interference between tasks. It is next shown that the correction of gradient interference ensures the convergence of the model. Define the loss function for each of the two tasks as L1:Rn → R, L2:Rn → R, and the objective function for the whole model is L(θ) = L1(θ) + L2(θ), where g1 = ∇L1(θ), g2 = ∇L2(θ).
The proof of the effectiveness of gradient correction in a JGDA is shown below. If the objective functions of the tasks are all differentiable and convex, assume that the gradient is continuous and η satisfies η ≤ (1/(g)2), then the gradient-corrected JGDA converges to the optimal value L(θ′).
Proof: According to the assumptions, g1 and g2 are denoted as the gradients of task 1 and task 2, respectively. Ir is the direction of the interference, Ir = g1 − g2, and the condition for the occurrence of gradient conflict is that the angle between two gradients is obtuse. There are two possibilities for whether there is gradient interference during model training. When there is no gradient interference, i.e., cos(g1, g2) ≥ 0, iterate using the JGDA with a step size η ≤ (1/(g)2). If there is a problem of gradient interference, i.e., cos(g1, g2) < 0, iterate by modifying the gradient.
Since the objective function L(θ) is continuously differentiable, L is expanded to quadratic at θ using Taylor’s formula with
Then, gradient correction is used to update θ′ using θ′ = θ − ηg′ = θ − η(g1 + g2) = θ − η(g1 − Δg1,2×Ir/||Ir|| + g2) to replace θ′ in Equation (47). The equation can be written as
Since η ≤ (1/(g)2), it is to obtain by
Combining the inequalities above, the final result is
Therefore, based on the derived results, it can be concluded that the total objective function of the model exhibits a decreasing trend after parameter updates, which continues to decrease after multiple iterations. It can be concluded from the extrapolation results that the JGDA using the gradient correction is able to guarantee the reduction in the objective function at each iteration during training. The effectiveness of gradient correction in the JGDA is proven.
Then, it is shown that the training model still converges when gradient modifications are made for tasks of three tasks or more. The gradient modification at multiple tasks is modified sequentially. At three tasks, the shared gradient after the modification of the first two tasks is redefined as g4 = g1′ + g2, and the gradient modification on g4 and g3. The direction of gradient interference between them is Ir2, and the gradient difference in the direction of gradient interference is defined as Δg4,3, with the modified g1′ = g3 − Δg4,3*Ir2/|| Ir2||. The final gradient and g are changed accordingly.
The proof is carried out using the Taylor expansion (47), and the process updates θ′ using the gradient correction, θ′ = θ − ηg′ = θ − η(g1′ + g2 + g3) = θ − η(g1 − Δg1,2×Ir/||Ir|| + g2 + g3 − Δg4,3 × Ir2/||Ir2||). Then θ′ is put into the expansion with
Because g = g1 + g2 + g3, since g4 = g1′ + g2 = g1 − Δg1,2×Ir/||Ir|| + g2, further simplifying the above equation, it has
Since the assumption holds under the condition that η ≤ (1/(g)2), it has
And with || g + g1 + g2 ||2 < g (g + g1 + g2), it can eventually be obtained by
It can be inferred that not only does the loss function of the multi-task model converge for two tasks, but the model also achieves convergence when multiple tasks are involved. This demonstrates that after gradient modification, the multi-task model based on the joint gradient modification algorithm retains the capability for each task to achieve the desired results.
5. Experimental Studies
In this section, three multi-task experiments are conducted on the JDGA proposed, and the effectiveness of the proposed algorithm is demonstrated by comparing the results with other algorithms. The first two of these experiments are for two tasks, and the third experiment is for three tasks. The three experiments are wind energy forecasting, ship fuel consumption forecasting, and multi-site air quality forecasting. The data from different turbines within a wind farm exhibit both shared patterns stemming from common weather systems and individual variations due to their geographic locations and mechanical wear levels. The main engine fuel consumption and auxiliary engine fuel consumption of ships share the same underlying physical mechanisms, such as ship resistance and propulsion efficiency. The air quality at adjacent stations is also influenced by related weather and temperature effects. Therefore, these multi-task scenarios were used to demonstrate that the proposed algorithm can solve multi-task problems.
The experiments verify the effectiveness of the method in this paper by comparing the multi-task model based on the JGDA with the single-task model of the gradient descent algorithm. The superiority of the JGDA is also verified by comparing it with PCGrad [34], Gradvac [35], and GradNorm [36] for the multi-task model. The testing environment of the proposed method includes Windows 10 Home Edition 64-bit operating system and MATLAB R2022a platform. The root mean square error (RMSE) and the mean absolute error (MAE) are chosen to evaluate the model prediction performance. The calculation formula is shown below:
where yo is the true value of the oth data, ŷo is the model-predicted value of the oth data, and O is the number of predicted points. In this study, MAE focuses on quantifying the absolute error loss in the predicted values, while RMSE is more sensitive to the effect of anomalous predicted values. Data from each experiment are obtained through more than 10 experiments, and the data presented are the mean and standard deviation of three experiments.
5.1. The Experimental Results of the Wind Energy Prediction
This experiment validates the effectiveness of the proposed model through wind energy prediction experiments on two tasks. The dataset is the Data Science for Wind Energy dataset, an online public dataset [37]. The chosen dataset is the Wind Farm Dataset1, collected every 10 min. It consists of data from 6 wind turbines, and every two files collect the data at the same time, for example, WT1 and WT2, WT3 and WT4, and WT5 and WT6. In this study, the data were averaged for every six 10 min periods, and the data were resampled at 1 h intervals. The proposed MTL-JGDA is compared with other benchmark models using Wind Turbine1 and Wind Turbine2, i.e., WT1 and WT2, in Dataset1. Experiment 1 sets up two tasks, both of which are wind energy data measured by wind turbines. The variable x for both turbines is sensor measurements from the same meteorological mast, so there is a correlation between the two tasks. The experimental data is selected for a certain 20 days as a test set, the first 10 days as a validation set, and the rest of the data as a training set. The test set contains approximately 480 samples, while the training set contains approximately 6000 samples. The total number of iterations is 100, and the number of hidden layer-specific neurons for both tasks is N1 = 7 and N2 = 7, respectively, where two neurons are selected as the shared neuron for each task. The initial values of the parameters are taken randomly from [0, 1].
The experiment validates the effectiveness of the model by comparing the single-task model prediction with the multi-task model prediction. Figure 5 and Figure 6 are the optimum prediction results for task 1 for WT1 data and task 2 for WT2 data, respectively, which include the prediction results and prediction errors. The results in the figures show that the MTPM-JGDA is able to achieve the prediction results. The error metrics of the two models in Experiment 1 are listed in Table 1. In fact, with the single-task model as the benchmark model, the prediction effect of the multi-task model with other algorithms is improved to different degrees. Nevertheless, numerical comparisons show that the proposed JGDA is significantly superior to the predictions of the other methods. Specifically, the proposed multi-task model (mean RMSE = 6.735) aligns with the results reported in [38] on this dataset (RMSE = 7.058), which indicates that multi-task learning is a highly effective approach for performance enhancement. The reduced mean RMSE achieved by the model proposed in this paper further validates the effectiveness and superiority of the proposed method.
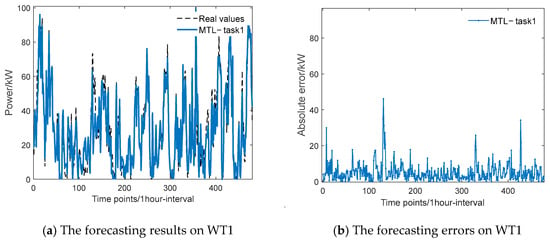
Figure 5.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 10% of the entire WT1 dataset.
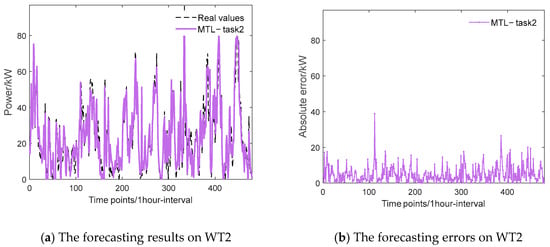
Figure 6.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 10% of the entire WT2 dataset.

Table 1.
Comparison of wind energy prediction numerical results.
In comparison to the single-task model specifically, the MTPM-JGDA decreases the testing RMSE by 34.85% and 36.63% in two tasks, respectively, and decreases the testing MAE by 37.37% and 44.11%, respectively. To demonstrate the effectiveness of the proposed adaptive learning rate strategy, ablation experiments are designed. Compared with task 1 in MTL-JGDA with a fixed learning rate, the training RMSE of MTL-JGDA with an adaptive learning rate is larger by 0.150, while the testing RMSE is significantly improved by 0.613, which indicates that the adaptive learning rate is better able to avoid overfitting.
To verify the statistical significance of performance differences, a paired t-test was conducted between the MTL-JGDA and STL-FNN baseline models based on the absolute error of 480 samples in the test set. The results indicate that the proposed model achieves highly significant performance improvements in both wind turbine power forecasting tasks (WT1: t(479) ≈ 15.2, p < 0.001; WT2: t(479) ≈ 14.7, p < 0.001). This strongly demonstrates that the observed RMSE reduction is not attributable to random factors but rather stems from the inherent superiority of the model’s performance.
5.2. The Experimental Results of Ship Fuel Consumption Prediction
This experiment verifies the validity of the model by predicting the fuel consumption of the main engine and auxiliary engine of the ship. The dataset is the sensor data of three different fishing boats for a period of one month, which is a public dataset [39]. This dataset includes the fuel consumption of the main engine and auxiliary engine, and the factors affecting the fuel consumption. The original dataset is sampled every minute for the sensors. This experiment averages every 15 datasets and resamples them at 15 min intervals. Engine inlet and outlet flow and temperature are selected as the main influencing factors as the model input, and engine fuel consumption is selected as the output. Sensor data from a fishing vessel in the selected dataset, and both tasks are to predict engine fuel data for the vessel. Experiment 2 is set as two tasks using fuel consumption data from two different engines on the same ship, so the two tasks have a certain correlation. After removing outliers from the experimental datasets, 100 datasets are chosen as the test set, and the first 1700 datasets are chosen as the training set. The total number of iterations is 400, and the number of neurons specific to the hidden layer for both tasks is N1 = 6, N2 = 6, respectively, where one neuron is taken as the shared neuron for each task. The initial values of the parameters are taken randomly from [0, 1].
Experiment 2 further validates the generalization of the MTPM-JGDA. Figure 7 and Figure 8 show the fuel consumption prediction results for the main engine and auxiliary engine, respectively. Among them, Figure 7a shows the fuel consumption of the main engine, and Figure 6b shows the fuel consumption prediction error of the main engine. Similarly, Figure 8a shows the fuel consumption prediction results for the auxiliary engine, and Figure 8b shows the fuel consumption prediction errors for the auxiliary engine. As can be seen from the degree of fit of the prediction results in the figure, the proposed method is able to accurately predict two related tasks at the same time.
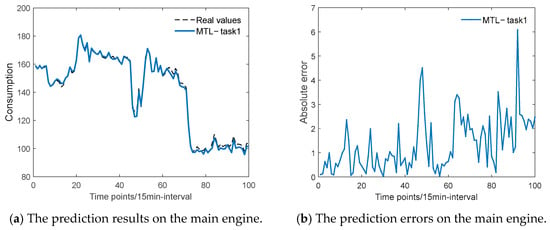
Figure 7.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 6% of the entire main engine dataset.
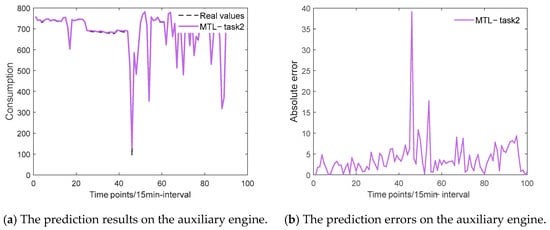
Figure 8.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 6% of the entire main auxiliary engine.
Table 2 lists the error indexes of the two tasks in experiment 2. It can be seen that the performance of the multi-task model is better in the two evaluation indices of RMSE and MAE. Comparing MTL-GradNorm and the benchmark model, although the RMSE is optimized in task 1, task 2 increases the error instead. In contrast, the model proposed in this paper improves the prediction results in both tasks. Specifically, the error performance of the two indicators of task 1 on the multi-task model decreased by 60.74% and 63.78% compared with that of the single-task model, while the error performance of task 2 decreased by 62.52% and 61.10%, respectively. Although the MTL-JGDA with an adaptive learning rate is not good enough for the training error on task 2, it still outperforms the fixed learning rate in terms of testing error.

Table 2.
Comparison of ship fuel consumption prediction numerical results.
Meanwhile, the effectiveness of task 1 stands out significantly when compared to other multi-task learning models such as MTL-PCGrad and MTL-GradNorm, which highlights the advantages of the JGDA in resolving gradient conflicts between tasks. Crucially, the simultaneous improvement in test results for both tasks demonstrates that the JGDA successfully achieves positive information sharing across tasks. In the ship fuel consumption prediction experiment, a paired t-test was conducted based on the absolute error of 100 test samples. Main engine fuel consumption prediction: t(99) ≈ 16.8, p < 0.001; auxiliary engine fuel consumption prediction: t(99) ≈ 13.5, p < 0.001. The results reaffirm that the performance advantages of MTL-JGDA exhibit extremely high statistical significance.
5.3. The Experimental Results of Multi-Site Quality Prediction
This experiment verifies the validity of the MTPM-JGDA through PM2.5 concentration prediction at multiple sites. Using the public dataset, Beijing Multi-Site Air Quality [40]. This dataset includes air pollutant data and meteorological data about PM2.5 from multiple sites in Beijing with a sampling interval of 1 h. The data from three of these stations were selected for this experiment, two of which are close to each other, and the other is farther away. The dataset is processed to remove the missing corresponding data. Several factors that have a strong influence on PM2.5 are selected as inputs, and PM2.5 concentrations are used as outputs. All of these sites are located in Beijing and have some correlation. After preprocessing the data, the first 400 datasets are selected for the test set, and the first 6400 datasets for the training set. The total number of iterations is 200, and the number of neurons specific to the hidden layer for the three tasks is N1 = 6, N2 = 5, and N3 = 5, respectively, where one neuron is used as a shared neuron for each task. The initial values of the parameters are taken randomly from [0, 1].
Experiment 3 verifies the effectiveness of the model by comparing the single-task model with the multi-task model. Figure 9, Figure 10 and Figure 11 show the experimental prediction results of PM2.5 at three sites, Tiantan, Huairou, and Changping, respectively. Each set of figures contains two subplots: (a) PM2.5 prediction results at the site (b) PM2.5 prediction errors at the site. It can be seen that the predictions for all three tasks remain equally well-fitted. Table 3 shows the error comparison between the single-task model and the multi-task model for each task of experiment 3. For specific comparisons, task 1 has reduced 7.42% and 9.35% on two error evaluation indexes than the single-task model; task 2 has decreased 21.73% and 18.39%; and task 3 has reduced 14.63% and 27.92%. It is worth noting that task 3 has a smaller training RMSE in the single-task model but is not as effective as the multi-task model in testing the MAE. This suggests that the multi-task model has a higher prediction accuracy with a relatively small mean error.
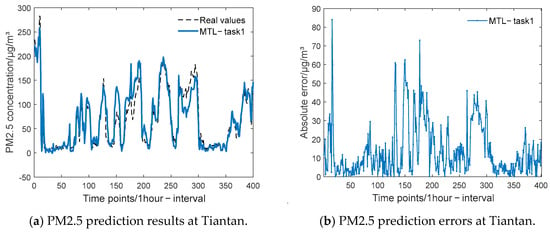
Figure 9.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 6% of the entire Tiantan dataset.
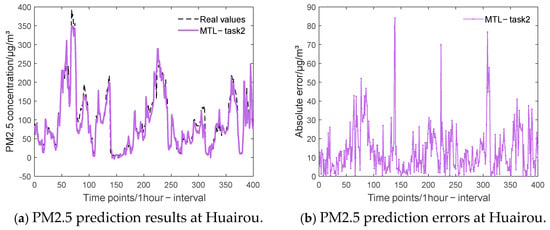
Figure 10.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 6% of the entire Huairou dataset.
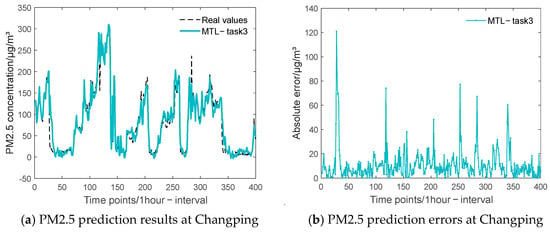
Figure 11.
Forecasting results (a) and errors (b) of the MTL model on the test set, which comprises the last 6% of the entire Changping dataset.

Table 3.
Comparison of multi-site quality prediction numerical results.
Comparing the fixed learning rate with the adaptive version of MTL-JGDA reveals that the adaptive mechanism delivers comprehensive and significant performance improvements at both task 2 and task 3. For example, the adaptive version reduces the test RMSE from 19.689 to 17.827 and the MAE from 14.335 to 13.368 at task 2. This clearly demonstrates that the mechanism enhances prediction accuracy and strengthens the model’s generalization capability, which makes its output results more reliable.
It is evident from the comparison of the error results that the prediction performance of the multi-task models is significantly enhanced. In this experiment, the MTL-JGDA achieved statistically significant performance improvements at task 1 (t(399) ≈ 8.1, p < 0.01) and task 2 (t(399) ≈ 5.4, p < 0.01). Although minor performance fluctuations were observed, the differences were not statistically significant (t(399) ≈ −1.2, p = 0.23). On the one hand, this demonstrates that the model can effectively capture shared information across sites to enhance prediction accuracy for most sites. On the other hand, it also indicates that the model does not cause significant performance degradation at sites where performance is already approaching its upper limit.
6. Conclusions
In this paper, an MTPM is constructed, a JGDA is proposed, and an adaptive learning rate is designed for the multi-task modeling approach. The constructed model structure has a shared part that utilizes the correlated empirical information between multiple tasks, which can be used to process multiple related tasks simultaneously. The proposed algorithm is used to update the parameters of the shared structure part of the model, which utilizes the correlation of tasks to weight the respective task gradients. To consider the problem of the gradient influence of multiple gradients, new shared gradients are obtained by gradient modification. An adaptive learning rate strategy is introduced in the algorithm design to enable the step size to be automatically adjusted and improve the convergence speed of the model. Moreover, this paper proves the theoretical convergence of the proposed algorithm and applies it to three example studies. The validity of the MTPM-JGDA is proved through comparison with the single-task model, and the superiority of the proposed algorithm is demonstrated through comparison with other algorithms. Specifically, compared to single-task learning, the proposed model achieves an average reduction of approximately 35% in RMSE and 38% in MAE on the test set. This substantial performance improvement fully demonstrates the effectiveness of the core idea of leveraging the JGDA mechanism to extract shared information across tasks.
Since the proposed MTPM-JGDA exploits the first-order gradient method, the parameter search capability is limited. The proposed algorithm cannot fully utilize the higher-order information of the objective function. Future research will be devoted to studying the higher-order gradient method, which can further improve the predictive performance and efficiency of the model.
Author Contributions
Methodology, Y.Y.; Validation, X.W.; Investigation, X.W. and Y.Y.; Data curation, X.W. and Y.Z.; Writing—original draft, Y.Z. and Y.Y.; Project administration, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by National Science Foundation of China under Grants 62422301, 62125301 and 92467205, National Key Research and Development Project under Grants 2022YFB3305800-05, Beijing Nova Program under Grant Z211100002121073, and Youth Beijing Scholar under Grant No. 037.
Informed Consent Statement
This article does not contain studies with human participants or animals. Statement of informed consent is not applicable since the manuscript does not contain any patient data.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the protection of data privacy and intellectual property rights.
Conflicts of Interest
All the authors declare that they have no competing financial interests or personal relationships that could influence the work reported in this paper.
References
- Yang, Y.; Tang, X.; Zhang, X.; Ma, J.; Liu, F.; Jia, X.; Jiao, L. Semi-supervised multiscale dynamic graph convolution network for hyperspectral image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 6806–6820. [Google Scholar] [CrossRef]
- Hong, Q.; Lin, L.; Li, Z.; Li, Q.; Yao, J.; Wu, Q.; Liu, K.; Tian, J. A distance transformation deep forest framework with hybrid-feature fusion for cxr image classification. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 14633–14644. [Google Scholar] [CrossRef]
- Abdar, M.; Fahami, M.A.; Rundo, L.; Radeva, P.; Frangi, A.F.; Acharya, U.R.; Khosravi, A.; Lam, H.-K.; Jung, A.; Nahavandi, S. Hercules: Deep hierarchical attentive multilevel fusion model with uncertainty quantification for medical image classification. IEEE Trans. Ind. Inform. 2022, 19, 274–285. [Google Scholar] [CrossRef]
- Shahamiri, S.R. Speech vision: An end-to-end deep learning-based dysarthric automatic speech recognition system. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 852–861. [Google Scholar] [CrossRef]
- Kim, M.; Kim, H.-I.; Ro, Y.M. Prompt tuning of deep neural networks for speaker-adaptive visual speech recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 1042–1055. [Google Scholar] [CrossRef] [PubMed]
- Jalayer, R.; Jalayer, M.; Baniasadi, A. A Review on Sound Source Localization in Robotics: Focusing on Deep Learning Methods. Appl. Sci. 2025, 15, 9354. [Google Scholar] [CrossRef]
- Gómez-Sirvent, J.L.; de la Rosa, F.L.; Sánchez-Reolid, D.; Sánchez-Reolid, R.; Fernández-Caballero, A. Small Language Models for Speech Emotion Recognition in Text and Audio Modalities. Appl. Sci. 2025, 15, 7730. [Google Scholar] [CrossRef]
- He, X.; Tang, Y.; Yu, B.; Li, S.; Ren, Y. Joint Extraction of Biomedical Events Based on Dynamic Path Planning Strategy and Hybrid Neural Network. IEEE/ACM Trans. Comput. Biol. Bioinform. 2024, 21, 2064–2075. [Google Scholar] [CrossRef]
- Lan, W.; Tang, Z.; Liu, M.; Chen, Q.; Peng, W.; Chen, Y.-P.P.; Pan, Y. The Large Language Models on Biomedical Data Analysis: A Survey. IEEE J. Biomed. Health Inform. 2025, 29, 4486–4497. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, Y.; Chang, Y.-C.; Lin, C.-T. Robust Fuzzy Neural Network with an Adaptive Inference Engine. IEEE Trans. Cybern. 2024, 54, 3275–3285. [Google Scholar] [CrossRef]
- Wu, D.; Lisser, A. Parallel solution of nonlinear projection equations in a multitask learning framework. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 3490–3503. [Google Scholar] [CrossRef]
- Liao, Q.; Chai, H.; Han, H.; Zhang, X.; Wang, X.; Xia, W.; Ding, Y. An integrated multi-task model for fake news detection. IEEE Trans. Knowl. Data Eng. 2021, 34, 5154–5165. [Google Scholar] [CrossRef]
- Ding, H.; Qiao, J.; Huang, W.; Yu, T. Cooperative event-triggered fuzzy-neural multivariable control with multitask learning for municipal solid waste incineration process. IEEE Trans. Ind. Inform. 2023, 20, 765–774. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, Q.; Ye, J.; Chen, F.; Lu, C.-T.; Ramakrishnan, N. feature constrained multi-task learning models for spatiotemporal event forecasting. IEEE Trans. Knowl. Data Eng. 2017, 29, 1059–1072. [Google Scholar] [CrossRef]
- Chen, J.; Li, Q.; Liu, F.; Wen, Y. M3T-LM: A multi-modal multi-task learning model for jointly predicting patient length of stay and mortality. Comput. Biol. Med. 2024, 183, 109237. [Google Scholar] [CrossRef]
- Xu, X.; Yoneda, M. Multitask air-quality prediction based on LSTM-autoencoder model. IEEE Trans. Cybern. 2019, 51, 2577–2586. [Google Scholar] [CrossRef]
- Tian, T.; Raj, A.; Xavier, B.M.; Zhang, Y.; Wu, F.-Y.; Yang, K. A multi-task learning framework for underwater acoustic channel prediction: Performance analysis on real-world data. IEEE Trans. Wirel. Commun. 2024, 23, 15930–15944. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, B.; Liu, K.; Shen, M.; Niu, M.; Han, L. A new multitask learning method for tool wear condition and part surface quality prediction. IEEE Trans. Ind. Inform. 2020, 17, 6023–6033. [Google Scholar] [CrossRef]
- Li, G.; Hoi, S.C.H.; Chang, K.; Liu, W.; Jain, R. Collaborative online multitask learning. IEEE Trans. Knowl. Data Eng. 2013, 26, 1866–1876. [Google Scholar] [CrossRef]
- Wang, J.; Lin, L.; Teng, Z.; Zhang, Y. Multitask learning based on improved uncertainty weighted loss for multi-parameter meteorological data prediction. Atmosphere 2022, 13, 989. [Google Scholar] [CrossRef]
- Wu, D.; Tan, X. Multitasking genetic algorithm (MTGA) for fuzzy system optimization. IEEE Trans. Fuzzy Syst. 2020, 28, 1050–1061. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.-L.; Gu, F.; Tan, K.C. A multiobjective multitask optimization algorithm using transfer rank. IEEE Trans. Evol. Comput. 2022, 27, 237–250. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, Z.; Liu, W.; Lin, X.; Hu, W. Task variance regularized multi-task learning. IEEE Trans. Knowl. Data Eng. 2022, 35, 8615–8629. [Google Scholar] [CrossRef]
- Liu, Q.; Chu, M.; Thuerey, N. Config: Towards conflict-free training of physics informed neural networks. arXiv 2024, arXiv:2408.11104. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Zhang, S.; Pang, J. Optimization of electric vehicle sound package based on LSTM with an adaptive learning rate forest and multiple-level multiple-object method. Mech. Syst. Signal Process. 2023, 187, 109932. [Google Scholar] [CrossRef]
- Luo, L.; Xiong, Y.; Liu, Y.; Sun, X. Adaptive gradient methods with dynamic bound of learning rate. arXiv 2019, arXiv:1902.09843. [Google Scholar] [CrossRef]
- Zhai, X.; Qiao, F.; Ma, Y.; Lu, H. A novel fault diagnosis method under dynamic working conditions based on a CNN with an adaptive learning rate. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. Available online: http://jmlr.org/papers/v12/duchi11a.html (accessed on 1 July 2011).
- Jeong, J.J.; Koo, G. AdaLo: Adaptive learning rate optimizer with loss for classification. Inf. Sci. 2025, 690, 121607. [Google Scholar] [CrossRef]
- Ruder, S. An overview of multi-task learning in deep neural networks. arXiv 2017, arXiv:1706.05098. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Sun, J.; Qi, D. Flow prediction in spatio-temporal networks based on multitask deep learning. IEEE Trans. Knowl. Data Eng. 2019, 32, 468–478. [Google Scholar] [CrossRef]
- Bahrampour, S.; Nasrabadi, N.M.; Ray, A.; Jenkins, W.K. Multimodal task-driven dictionary learning for image classification. IEEE Trans. Image Process. 2015, 25, 24–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.-K.; Zhang, Q.; Chong, H.-Y.; Wang, X. Integrated supplier selection framework in a resilient construction supply chain: An approach via analytic hierarchy process (AHP) and grey relational analysis (GRA). Sustainability 2017, 9, 289. [Google Scholar] [CrossRef]
- Yu, T.; Kumar, S.; Gupta, A.; Levine, S.; Hausman, K.; Finn, C. Gradient surgery for multi-task learning. Adv. Neural Inf. Pro-cess. Syst. 2020, 33, 5824–5836. [Google Scholar] [CrossRef]
- Chen, Z.; Badrinarayanan, V.; Lee, C.Y.; Rabinovich, A. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks. arXiv 2018, arXiv:1711.02257. [Google Scholar] [CrossRef]
- Wang, Z.; Tsvetkov, Y.; Firat, O.; Cao, Y. Gradient vaccine: Investigating and improving multi-task optimization in mas-sively multilingual models. arXiv 2020, arXiv:2010.05874. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, K.; Zhang, S.; Zhang, Z. Wind power forecasting: A hybrid forecasting model and multi-task learning-based framework. Energy 2023, 278, 127864. [Google Scholar] [CrossRef]
- Liu, R.; Chen, L.; Hu, W.; Huang, Q. Short-term load forecasting based on LSTNet in power system. Int. Trans. Electr. Energy Syst. 2021, 31, e13164. [Google Scholar] [CrossRef]
- Ilias, L.; Kapsalis, P.; Mouzakitis, S.; Askounis, D. A multitask learning framework for predicting ship fuel oil consumption. IEEE Access 2023, 11, 132576–132589. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, B.; Dong, A.; He, J.; Xu, Z.; Chen, S.X. Cautionary tales on air-quality improvement in Beijing. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170457. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).