Figure 1.
Separable screw: (a) entity diagram; (b) schematic diagram.
Figure 1.
Separable screw: (a) entity diagram; (b) schematic diagram.
Figure 2.
(a) Traditional extrusion screw; (b) optimized separation screw; (c) optimized split pin screw.
Figure 2.
(a) Traditional extrusion screw; (b) optimized separation screw; (c) optimized split pin screw.
Figure 3.
Traditional screw solid modeling and finite element mesh generation: (a) finite element model of the screw; (b) finite element mesh generation.
Figure 3.
Traditional screw solid modeling and finite element mesh generation: (a) finite element model of the screw; (b) finite element mesh generation.
Figure 4.
Mesh quality evaluation diagram of conventional screws.
Figure 4.
Mesh quality evaluation diagram of conventional screws.
Figure 5.
Traditional screw equivalent stress diagram.
Figure 5.
Traditional screw equivalent stress diagram.
Figure 6.
Traditional screw deformation cloud diagram under load.
Figure 6.
Traditional screw deformation cloud diagram under load.
Figure 7.
Separation-type screw and separation-type pin screw equivalent stress diagrams: (a) separation-type screw equivalent stress diagram; (b) separation-type pin bolt equivalent stress diagram.
Figure 7.
Separation-type screw and separation-type pin screw equivalent stress diagrams: (a) separation-type screw equivalent stress diagram; (b) separation-type pin bolt equivalent stress diagram.
Figure 8.
Deformation maps of the separated screw and the separated pin screw under load: (a) separation-type screw deformation cloud map; (b) separate-type pin screw deformation cloud map.
Figure 8.
Deformation maps of the separated screw and the separated pin screw under load: (a) separation-type screw deformation cloud map; (b) separate-type pin screw deformation cloud map.
Figure 9.
The pressure distribution cloud maps in the flow channel under different screw speeds for the conventional screw (the figures from top to bottom represent the outer flow channel cloud map and the axial cross-section cloud map of the flow channel) are shown as follows: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 9.
The pressure distribution cloud maps in the flow channel under different screw speeds for the conventional screw (the figures from top to bottom represent the outer flow channel cloud map and the axial cross-section cloud map of the flow channel) are shown as follows: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 10.
The pressure distribution cloud maps in the flow channel under different screw speeds for the separating screw (the figures from right to left represent the outer flow channel cloud map and the axial cross-section cloud map of the flow channel) are shown as follows: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 10.
The pressure distribution cloud maps in the flow channel under different screw speeds for the separating screw (the figures from right to left represent the outer flow channel cloud map and the axial cross-section cloud map of the flow channel) are shown as follows: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 11.
The pressure distribution cloud maps in the flow channel under different screw speeds for the separating pin screw are shown as follows: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 11.
The pressure distribution cloud maps in the flow channel under different screw speeds for the separating pin screw are shown as follows: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 12.
Shear rate distribution cloud maps under different screw speeds: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 12.
Shear rate distribution cloud maps under different screw speeds: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 13.
Shear rate distribution cloud maps under different rotational speeds of the separating screw: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 13.
Shear rate distribution cloud maps under different rotational speeds of the separating screw: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 14.
Shear rate distribution cloud maps under different rotational speeds of the separating pin screw: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 14.
Shear rate distribution cloud maps under different rotational speeds of the separating pin screw: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 15.
The cloud diagram of the viscosity field distribution under traditional screws of different rotational speeds: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 15.
The cloud diagram of the viscosity field distribution under traditional screws of different rotational speeds: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 16.
Viscosity field distribution cloud maps under different rotational speeds for barrier screws: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 16.
Viscosity field distribution cloud maps under different rotational speeds for barrier screws: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 17.
Viscosity distribution of different-speed separation-type pin screw flow channels: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 17.
Viscosity distribution of different-speed separation-type pin screw flow channels: (a) screw speed of 10 rpm; (b) screw speed of 15 rpm; (c) screw speed of 20 rpm.
Figure 18.
Printed test specimens of pure PLA and 20% CF/PLA composites: (a) tensile test specimens; (b) bending test specimens.
Figure 18.
Printed test specimens of pure PLA and 20% CF/PLA composites: (a) tensile test specimens; (b) bending test specimens.
Figure 19.
Experimental platform for mechanical property testing: (a) diagram of tensile testing experiment; (b) diagram of compressive testing experiment.
Figure 19.
Experimental platform for mechanical property testing: (a) diagram of tensile testing experiment; (b) diagram of compressive testing experiment.
Figure 20.
Average mixing degree of different pin structural parameters.
Figure 20.
Average mixing degree of different pin structural parameters.
Figure 21.
Comparison of mixing degrees between the optimal average mixing degree combination and the optimal orthogonal mixing degree combination.
Figure 21.
Comparison of mixing degrees between the optimal average mixing degree combination and the optimal orthogonal mixing degree combination.
Figure 22.
Comparison of pressure differences among different combinations of pin structural parameters.
Figure 22.
Comparison of pressure differences among different combinations of pin structural parameters.
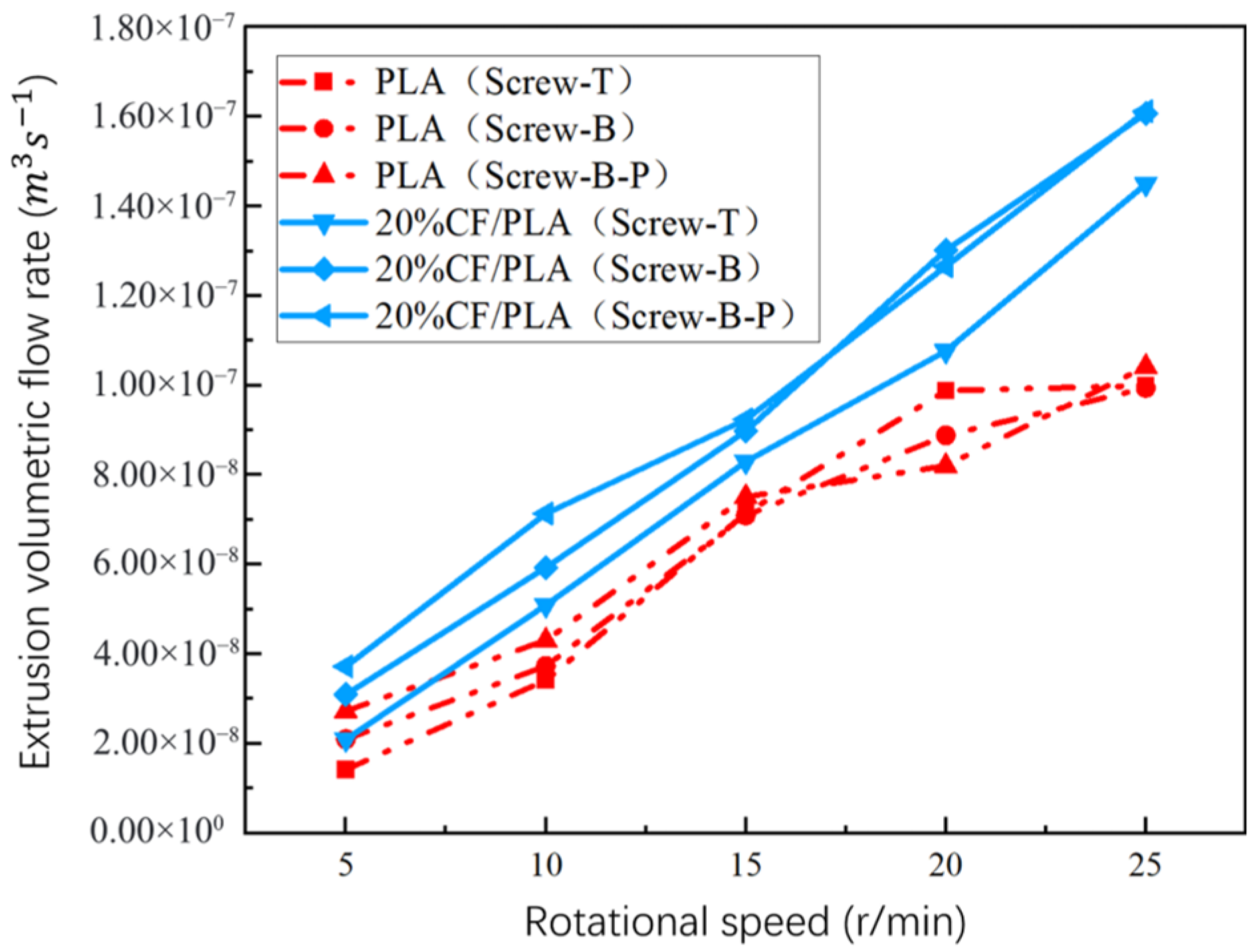
Figure 23.
Comparison chart of extrusion volume flow rates of pure PLA and 20% CF/PLA composite under three different screw types and rotational speeds.
Figure 23.
Comparison chart of extrusion volume flow rates of pure PLA and 20% CF/PLA composite under three different screw types and rotational speeds.
Figure 24.
Bar charts of tensile strength and elastic modulus of samples printed with different extrusion screws: (a) tensile strength; (b) elastic modulus.
Figure 24.
Bar charts of tensile strength and elastic modulus of samples printed with different extrusion screws: (a) tensile strength; (b) elastic modulus.
Figure 25.
Bar charts of flexural strength and flexural modulus of samples printed with different extrusion screws: (a) flexural strength; (b) flexural modulus.
Figure 25.
Bar charts of flexural strength and flexural modulus of samples printed with different extrusion screws: (a) flexural strength; (b) flexural modulus.
Table 1.
Explanation of Formula Symbols and Meanings.
Table 1.
Explanation of Formula Symbols and Meanings.
| k: Parameters determined by cutting tools | : Width of main thread ridge (mm) | : Thread lead angle (°) | : Width of the separating flight |
| : Liquid volume fraction in the solid bed | : Quantity of output | : Yield influence coefficient | D: Screw diameter (mm) |
| : Screw rotational speed (r/min) | : Pitch of the screw (mm) | : Helix angle of the screw (°) | : Outer diameter of the screw (mm) |
| : Yield limit (Pa) | : Safety factor | : Shear stress generated by the torque | C: Ratio of the screw cooling water bore diameter to the root diameter |
| : Moment of inertia (kg·m2) | : Angular acceleration (rad/s2) | : Combined mass of the screw and material (kg) | V: Worn volume (mm3) |
| : Normal load (N) | L: Sliding distance (m) | H: Material Vickers hardness (MPa) | : Density (Kg/m3) |
| : Time (s) | : Velocity vector components in the x directions (m/s) | : velocity vector components in the y directions (m/s) | : Velocity vector components in the z directions (m/s) |
| : Static pressure (Pa) | : Density (Kg/m3) | : Volume force of the microelement in the x direction (N) | : Volume force of the microelement in the y direction (N) |
| : Volume force of the microelement in the z direction (N) | : The relationship between the melt viscosity and temperature of composite materials | : The relationship between the shear rate and temperature of composite materials | : Zero-shear viscosity |
Table 2.
The optimized structural parameters of the split-type screw.
Table 2.
The optimized structural parameters of the split-type screw.
| Parameters | Numerical Value | Parameters | Numerical Value |
|---|
| Aspect ratio L/D | 20 | Lead
| 12.5 mm |
| Barrel diameter
| 16.2 mm | Feed section
| 36 mm |
| Outer diameter of the screw
| 16 mm | Metering section
| 36 mm |
| The width of the spiral rib
| 1.6 mm | Total screw length L | 144 mm |
| Screw–barrel clearance
| 0.1 mm | Feed section channel depth
| 4 mm |
| Pitch angle of the screw
| 14° | Metering section channel depth
| 2 mm |
Table 3.
Physical property parameters of 38CrMoAlA.
Table 3.
Physical property parameters of 38CrMoAlA.
| Property | Numerical Value | Unit |
|---|
| Density | 7850 | |
| Young’s modulus | 200–210 | GPa |
| Poisson’s ratio | 0.3 | - |
| Yield strength | 833.6 | MPa |
| Allowable stress | 557 | MPa |
| Tensile strength | 980 | MPa |
| Safety factor | 2.5~3 | - |
Table 4.
The number of elements and nodes in mesh generation.
Table 4.
The number of elements and nodes in mesh generation.
| Screw Type | Number of Elements | Number of Nodes |
|---|
| Traditional screw | 36,339 | 65,293 |
| Separable screw | 339,652 | 485,887 |
| Separable pin screw | 342,684 | 492,059 |
Table 5.
The rheological parameters of the 20% CF/PLA composite material.
Table 5.
The rheological parameters of the 20% CF/PLA composite material.
| /(Pa·s) | /(Pa·s) | /s | | |
|---|
| | 0.0124 | 0.39 | 0.50 |
Table 6.
20% CF/PLA Material Parameter Table.
Table 6.
20% CF/PLA Material Parameter Table.
| Component | Materials | Density (kg/m3) | Specific Heat Capacity (J/(kg·°C))
| Thermal Conductivity (W/m·K) |
|---|
| Composite materials | 20%CF/PLA | 1300 | 1400 | 0.5 |
| Screw | 38CrMoAlA | 7850 | 460 | 50 |
Table 7.
The basic structural parameters and boundary conditions table of the calculation model.
Table 7.
The basic structural parameters and boundary conditions table of the calculation model.
| Boundary Conditions | Fluid Boundary Conditions | Thermal Boundary Condition |
|---|
| Inlet | 0 | 453.15 K |
| Outlet | 0 | Outflow |
| Inner wall | ω = 1.047, 1.5708, 2.094 rad/s | Insulated |
| Outer wall | 0 | 453.15 K |
| Screw | 10, 15, 20 rpm | - |
Table 8.
The boundary conditions of the calculation model for basic structural parameters.
Table 8.
The boundary conditions of the calculation model for basic structural parameters.
| Boundary Conditions | Flow Conditions | Mixed Conditions |
|---|
| Inlet | 0 | Inflow |
| Outlet | 0 | Outflow |
| Inner wall | 0 | Non-penetrable |
| Outer wall | 0 | Non-penetrable |
| Screw | = 20 rpm | = 20 rpm |
Table 9.
Structural parameters of extrusion screw pin.
Table 9.
Structural parameters of extrusion screw pin.
| Classification | Diameter of the Pin (d/mm)
| Pin Height (h/mm) | Pin Spacing (e/mm) | Axial Angle of the Pin (θ/°) |
|---|
| 1 | 1.5 | 1.4 | 6 | 60 |
| 2 | 2 | 1.6 | 8 | 45 |
| 3 | 2.5 | 1.8 | 10 | 36 |
Table 10.
Orthogonal experimental design for the extrusion screw pin structure.
Table 10.
Orthogonal experimental design for the extrusion screw pin structure.
| Group Number | Diameter of the Pin (d/mm)
| Pin Height (h/mm) | Pin Spacing (e/mm) | Axial Angle of the Pin (θ/°) |
|---|
| 1 | 1.5 | 1.4 | 6 | 60 |
| 2 | 1.5 | 1.6 | 8 | 45 |
| 3 | 1.5 | 1.8 | 10 | 36 |
| 4 | 2 | 1.4 | 8 | 36 |
| 5 | 2 | 1.6 | 10 | 60 |
| 6 | 2 | 1.8 | 6 | 45 |
| 7 | 2.5 | 1.4 | 10 | 45 |
| 8 | 2.5 | 1.6 | 6 | 36 |
| 9 | 2.5 | 1.8 | 8 | 60 |
Table 11.
The degree of integration of the pin structure under different combinations of process parameters.
Table 11.
The degree of integration of the pin structure under different combinations of process parameters.
| Group Number | Degree of Mixture |
|---|
| 1 | 0.601 |
| 2 | 0.824 |
| 3 | 0.613 |
| 4 | 0.817 |
| 5 | 0.912 |
| 6 | 0.841 |
| 7 | 0.657 |
| 8 | 0.749 |
| 9 | 0.489 |
Table 12.
The average mixture degree of various pin structure parameters.
Table 12.
The average mixture degree of various pin structure parameters.
| Parameters | Evaluation Indicators | The Average Values Under Different Combination Levels of the Three Parameters | Range |
|---|
| Level 1 | Level 2 | Level 3 | |
|---|
| Diameter of the pin d | Degree of mixture | 0.679 | 0.857 | 0.632 | 0.225 |
| Pin height h | 0.692 | 0.828 | 0.648 | 0.180 |
| Pin spacing e | 0.730 | 0.710 | 0.727 | 0.020 |
| Axial angle of the pin θ | 0.726 | 0.774 | 0.667 | 0.107 |
Table 13.
Comparison of Different Screw Performance.
Table 13.
Comparison of Different Screw Performance.
| Screw Type | Core Function | Characteristics | Limitations |
|---|
| Traditional three-section small screw | Basic conveying, compression, and melting | Simple structure and convenient manufacturing. | Poor mixing effect, large pressure fluctuation, and unsuitability for high-filled composites |
| General-purpose screw | Basic plasticization and conveying, suitable for general extrusion processing | Simple structure, low compression ratio, and high output | At high rotational speeds, the melt is uneven, prone to cold slug and temperature instability, and cannot handle high-filled or high-viscosity materials. |
| Barrier screw | The barrier structure separates the melt from unmelted solids to ensure complete plasticization | A secondary thread is introduced in the compression section to form a melt channel and a solid channel, resulting in high melt quality and good temperature uniformity | The barrier structure increases the surface area, leading to excessive shear heat and energy consumption at high rotational speeds, thus requiring additional cooling |
| Fractal screw | Multi-channel design improves melt uniformity and energy efficiency | The channels in the feeding section, transition section, and metering section are different, and adiabatic decompression is used to control temperature and improve melt consistency | Poor design of the transition section leads to large pressure fluctuations, poor melt consistency, complex structure, and high manufacturing cost |
| Double screw | Independent adjustment of screw speed allows flexible control of shear intensity and residence time, resulting in wide material applicability | The screw is composed of multiple elements, which can be flexibly configured according to material characteristics | Difficult to manufacture and assemble, insufficient torque at high rotational speeds, limited maximum rotational speed, and small printing volume |
| Separating-pin screw | Integration of solid–liquid separation and efficient mixing. | It balances pressure stability and mixing uniformity with a reliable structure, achieving high performance at low rotational speeds | Its manufacturing is slightly more complex than that of traditional screws |