Abstract
The use of intelligent clinical decision support systems (CDSS) has the potential to improve the accuracy and speed of diagnoses significantly. These systems can analyze a patient’s medical data and generate comprehensive reports that help specialists better understand and evaluate the current clinical scenario. This capability is particularly important when dealing with medical images, as the heavy workload on healthcare professionals can hinder their ability to notice critical biomarkers, which may be difficult to detect with the naked eye due to stress and fatigue. Implementing a CDSS that uses computer vision (CV) techniques can alleviate this challenge. However, one of the main obstacles to the widespread use of CV and intelligent analysis methods in medical diagnostics is the lack of a clear understanding among diagnosticians of how these systems operate. A better understanding of their functioning and of the reliability of the identified biomarkers will enable medical professionals to more effectively address clinical problems. Additionally, it is essential to tailor the training process of machine learning models to medical data, which are often imbalanced due to varying probabilities of disease detection. Neglecting this factor can compromise the quality of the developed CDSS. This article presents the development of a CDSS module focused on diagnosing age-related macular degeneration. Unlike traditional methods that classify diseases or their stages based on optical coherence tomography (OCT) images, the proposed CDSS provides a more sophisticated and accurate analysis of biomarkers detected through a deep neural network. This approach combines interpretative reasoning with highly accurate models, although these models can be complex to describe. To address the issue of class imbalance, an algorithm was developed to optimally select biomarkers, taking into account both their statistical and clinical significance. As a result, the algorithm prioritizes the selection of classes that ensure high model accuracy while maintaining clinically relevant responses generated by the CDSS module. The results indicate that the overall accuracy of staging age-related macular degeneration increased by 63.3% compared with traditional methods of direct stage classification using a similar machine learning model. This improvement suggests that the CDSS module can significantly enhance disease diagnosis, particularly in situations with class imbalance in the original dataset. To improve interpretability, the process of determining the most likely disease stage was organized into two steps. At each step, the diagnostician could visually access information explaining the reasoning behind the intelligent diagnosis, thereby assisting experts in understanding the basis for clinical decision-making.
1. Introduction
The advancement of modern medical services has substantially improved professional support for the prevention and treatment of eye conditions. Demand for ophthalmologic services continues to grow at a rate that outpaces population growth, driven primarily by an aging population and increased public awareness of the importance of eye health monitoring [1,2,3]. However, the significant rise in patients seeking ophthalmological care has increased the workload of diagnosticians without a proportional growth in the number of available specialists. This imbalance between supply and demand may negatively affect diagnostic quality. As physicians manage increasing patient loads, they face greater risks of reduced productivity and medical errors caused by fatigue, mental exhaustion, and stress.
Medical imaging analysis is a demanding task that requires sustained attention and expert judgment, particularly under conditions of high workload and limited time. In ophthalmology, optical coherence tomography (OCT) is widely used because it provides detailed cross-sectional views of retinal layers in a non-contact, real-time manner [4,5,6,7]. However, the sheer volume and complexity of OCT B-scans can overwhelm clinicians and increase the likelihood of missed or delayed findings, especially under stress and fatigue [8,9,10,11].
Evidence shows that the speed at which diagnosticians make decisions is inversely related to diagnostic accuracy. To address this challenge, Clinical Decision Support Systems (CDSS) have emerged as valuable tools to assist healthcare professionals. These systems help streamline repetitive tasks and reduce routine workload [12,13,14]. Modern CDSS integrate both basic algorithms for organizing medical information and advanced automated cognitive processes, including computer vision (CV) methods for image analysis [15,16,17,18,19,20]. In this context, lightweight attention architectures embedding channel–spatial ghost features (e.g., Attention GhostUNet++) have demonstrated that fine boundary detail can be preserved while maintaining compact parameter budgets. This approach aligns directly with our selection of a compact biomarker detector [21].
Nevertheless, one of the main obstacles to integrating intelligent systems into clinical workflows is the lack of transparency in machine learning algorithms. The “black box” nature of these models, particularly in medical diagnosis, can lead to skepticism about their reliability and potential bias among healthcare professionals. This opacity makes it difficult to verify the clinical relevance of software solutions.
To improve transparency, current explainability methods are typically categorized into two groups: post hoc explanations and models designed with built-in interpretability [22]. A notable example of the former is Grad-CAM, which generates saliency maps to highlight influential areas in images [23]. Although Grad-CAM has been effectively used in medical imaging tasks, it mainly visualizes areas of attention rather than providing insight into the decision-making process that connects features to clinically relevant hypotheses.
Feature attribution methods, such as SHAP, assess the contribution of each input variable to the model’s output. However, they often neglect the importance of spatial context and clinical guidelines. Conversely, traditional rule-based systems enhance interpretability yet sacrifice flexibility and accuracy when recognizing complex patterns [24,25,26].
A highly effective method for accurately analyzing medical images is the use of imaging biomarkers (IBs), which encode disease-specific signs and stage-relevant patterns. IBs span anatomical structures, functional parameters, and molecular signatures, thereby supporting clinically meaningful stratification and monitoring [27,28,29,30]. Within CDSS, biomarker-based reasoning enables evidence-aligned recommendations and care pathways, as documented in recent methodological and translational studies [31,32,33,34,35,36].
Age-related macular degeneration (AMD) illustrates the increasing clinical challenge associated with population aging and the surge in retinal imaging demands. Currently, AMD affects approximately 196 million people worldwide and is projected to reach nearly 290 million by 2040, making it the leading cause of irreversible loss of central vision in older adults [37]. Clinically, the disease progresses from early drusen formation to intermediate structural disruption and ultimately develops into late-stage conditions such as geographic atrophy or neovascularization, each characterized by distinct OCT signatures [38]. Additionally, population-level studies highlight the importance of accurate stage stratification across different subtypes. A systematic review and meta-analysis published in the American Journal of Ophthalmology quantified late-stage incidence patterns in American whites aged ≥50 years, emphasizing the need for multi-scale representations that effectively capture the diverse retinal changes throughout the AMD spectrum [39,40].
From an informatics standpoint, AMD thus emerges as an ideal yet demanding use case for developing CDSS capable of converting complex retinal imagery into clinically actionable assessments of disease stages. The multifactorial nature of AMD—characterized by over 40 genetic risk alleles interacting with lifestyle factors such as smoking, diet, and systemic metabolism—requires algorithms that can effectively integrate diverse sources of evidence [41]. Prognosis also depends on identifying subtle OCT-based biomarkers, including drusen morphology, alterations in the retinal pigment epithelium, and early signs of neovascularization. Human graders may miss these features, but machines can detect them. Additionally, there is a significant class imbalance in OCT datasets: the late stages of AMD, which are critical for determining patient outcomes, are often underrepresented. This necessitates the development of architectures specifically designed to handle skewed class distributions. Overall, these challenges position AMD as both a testing ground and a driving force for the development of interpretable, imbalance-aware CDSS, as outlined in the present study.
Driven by the shortcomings of previous hybrid hierarchical methods, which achieved high accuracy but were often perceived as “black boxes” by clinicians [42], this study presents an interpretable two-stage CDSS for AMD staging. This system allows for a transparent diagnostic process, making it possible to trace the decision-making from image features to stage assignment.
In the first stage, a temperature-calibrated DNN generates confidence levels for IBs derived from OCT. In the second stage, a fuzzy logic layer combines these confidence levels to produce stage probabilities. To tackle class imbalance while ensuring clinically relevant coverage, we use a Non-dominated Sorting Genetic Algorithm II (NSGA-II) to optimize a dual objective. This objective links a transformed measure of statistical learnability with stage-wise minimum evidence constraints. Additionally, the clear identification of key IBs allows clinicians to follow the reasoning from image features to disease classification. We will refer to our method as “two-stage (IBs + fuzzy, )” for the reference configuration and will use “two-stage” elsewhere, unless the temperature needs to be explicitly mentioned.
Technical Contributions
We clearly outline the technical innovations that go beyond the two-stage pipeline:
This formulation of a dual-objective NSGA-II is explicitly designed for selecting IBs in AMD images. It combines a calibrated statistical utility, based on a transformed J-value that emphasizes a clinically relevant threshold using a steep sigmoid function, with a coverage objective grounded in clinical practice. The coverage objective ensures that a minimum level of evidence is required at each stage of the IB selection process, enforced through a minimum-over-stages term and strict coverage constraints. This design prevents solutions that might otherwise overlook rare but clinically critical stages. Overall, this approach extends beyond standard NSGA-II applications [43] by integrating constrained per-stage coverage with tailored utilities, thereby shaping the Pareto set toward clinically relevant and statistically trainable subsets of IBs.
This approach utilizes a fuzzy mapping that takes temperature-calibrated DNN confidences as inputs [44]. It employs a hyperbolic tangent membership function with an asymmetric treatment of “Absent” (which represents negative evidence) and applies amplified weights for “Defining features.” This results in a smooth and monotonic accumulation of evidence at each stage. Our solver stands out from linear or purely Gaussian memberships used in clinical fuzzy systems [45] by explicitly modeling decisive IBs and accounting for calibrated uncertainty.
We conducted a comprehensive evaluation of the improvements achieved through our approach compared to direct classification using the same data splits. Our results show an increase in accuracy, rising from 55.1% with a direct ResNet-18 model to 90.0% with our method. Additionally, we established a benchmarking protocol against a more robust end-to-end baseline, which included enhancements for balancing and calibration. These results, documented in the Results section, demonstrate statistical credibility and fairness.
2. Modeling the Cognitive Processes of Experts in Staging Age-Related Macular Degeneration Based on Imaging Biomarkers
2.1. Presentation of OCT Data as an Image and a Set of Imaging Biomarkers
Consider an OCT image dataset where each image represents a retinal scan that must be classified into one of n AMD stages . The classification process relies on the identification of m imaging IBs that serve as intermediate diagnostic indicators. The fundamental objective is to determine the conditional probability for each AMD stage given an input image .
Traditional direct classification approaches attempt to learn the mapping directly, which creates a “black box” system that lacks clinical interpretability. The proposed two-stage approach decomposes this problem into two sequential mappings: first, a IBs detection function that maps images to IB confidence scores, and second, a diagnostic reasoning function that maps IB patterns to AMD stages.
The IB detection module implements a DNN encoder that transforms input OCT images into IB confidence vectors. For each image , the encoder produces a confidence vector with denoting the confidence that IB is present in .
To ensure an accurate search for IBs while maintaining the clarity and transparency of the AMD staging algorithm’s logic, a DNN was used. This choice is based on the DNN’s potential for higher accuracy in image analysis compared to traditional machine learning methods, even though its operation may not be immediately understandable to users. Our primary focus is on the expected accuracy of the DNN in detecting IBs. It is important to note that relying solely on machine learning methods in medical diagnostic algorithms, without incorporating expert rules, can lead to misleading results. These models may identify false trends stemming from a limited data sample and do not accurately represent the entire dataset [46].
A compromise that preserves visual interpretability while accounting for diagnostic uncertainty is a fuzzy-inference layer that aggregates calibrated IB confidences into stage evidence via consistent indexing. For IB and stage , the rule-level contribution uses the calibrated confidence , and the stage score sums rule conclusions over i:
where denotes the rule-level conclusion that maps the calibrated confidence for IB through the rule targeting stage . This consistent notation ensures that the summation index aligns with the corresponding IB, thus avoiding any confusion between indices i and j. Consequently, the fuzzy solver jointly processes calibrated DNN confidences with clinically derived linguistic terms to produce stage probabilities, all while maintaining clear, rule-level attributions.
It is also worth considering that the IBs analysis component in the CDSS module can be more easily replaced, fixed, or retrained, as well as scaled by simplifying the task using encoded OCT data.
The objective of this project is to develop a CDSS module that synthesizes an IB set for identifying AMD using OCT image data. Additionally, the module will assist in staging AMD based on the identified IB set. The structure of this module is illustrated in Figure 1.
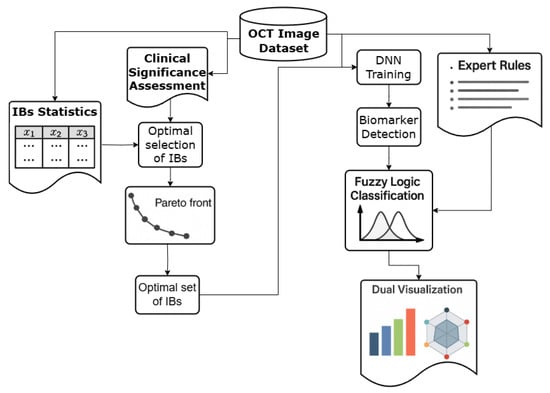
Figure 1.
The structure of the CDSS module for AMD staging.
To determine the probability of accurately detecting a specific IB, we used temperature scaling for post hoc calibration [44,47]. The encoder outputs a calibrated confidence vector , where is the probability for IB . This vector is then passed to the fuzzy solver to infer the stage probabilities for the OCT image .
The encoder output data are represented as a vector of IBs , which contains the probability values to detect each IB. These data are then used as input for the fuzzy solver , which utilizes fuzzy terms to determine the probabilities of all stages of in the OCT image .
We will now explore the proposed structure of the CDSS module in detail. It includes descriptions of the input and transformed data, as well as specifics regarding the encoding and the IB set analysis model.
2.2. Analysis of the Primary OCT Data Set
The AMD staging method currently being developed requires a structured dataset that includes OCT images, appropriate IBs, and a classification of AMD stages. Each OCT B-scan was independently annotated for the presence or absence of candidate IBs by two board-certified ophthalmologists. They used a standardized annotation guide that aligned with the linguistic scale presented in Supplementary Table S2 (‘Absent,’ ‘Rare,’ ‘Present,’ ‘Common,’ ‘Defining Feature’). Any disagreements between the ophthalmologists were resolved by a senior retina specialist, resulting in consensus labels that were used for training and evaluation. The graders were blinded to both the model outputs and the target AMD stage labels during the annotation of IBs. The agreement per IB was quantified using Cohen’s with the macro averages reported, along with the positive and negative percent agreement for rare IBs. Adjudication rules required that a consensus from a third grader be reached in cases of persistent ties.
The dataset used in this study to demonstrate the proposed staging method included a collection of OCT images. Each image was accompanied by a list of identified IBs, which were marked by diagnosticians, along with the corresponding stage of AMD. In total, the dataset comprised 2624 OCT images, each classified according to the criteria established by the Age-Related Eye Disease Study [48], a standard used in both clinical trials and clinical practice.
The IB annotation protocol was established as follows: All candidate IBs listed in Supplementary Table S2 were defined in a written codebook that included OCT exemplars prior to labeling. Two independent graders performed binary presence/absence annotations at the B-scan level for each IB, while remaining masked to clinical metadata and stage labels to prevent bias due to expectation. Inter-rater reliability was computed per IB using Cohen’s on the double-read subset, along with a macro-averaged across all IBs. For low-prevalence IBs, we also reported the percentage of positive agreement and the percentage of negative agreement. A senior retina specialist resolved any disagreements during a masked adjudication session. The resulting consensus served as the gold standard for the IB detector. Additionally, the linguistic clinical significance matrix in Supplementary Table S2 was compiled separately by the same panel but did not overwrite the image-level consensus labels.
The distinction between AMD stages was crucial due to the significant differences in treatment strategies for patients at each stage. The following cases with corresponding code designations comprised the classes used in this study:
- Examples of retinal OCT without AMD disease (N) (25% of the total data set),
- Early stage AMD (S) (8% of the total data set),
- Intermediate stage of AMD between dry and wet stage (P) (34% of the total data set),
- Late stage of dry (atrophic) AMD (SI) (7% of the total data set),
- Late stage of wet (neovascular) AMD (V) (17% of the total data set),
- Late stage of AMD with subretinal fibrosis (VI; IB sr) (9% of the total data set).
In medical practice, there are specific diagnostic patterns for each stage of AMD. However, it is important to recognize that statistical data derived from a limited dataset may not always align with the opinions of specialists. These discrepancies must be taken into account when developing deterministic rules for interpreting various clinical manifestations. In this context, we primarily relied on the experience of diagnostic specialists to understand the general principles of diagnosis when selecting our IBs. Only after this foundational understanding did we identify specific rules based on the limited data available. This approach was necessary to prevent our algorithm from overfitting to the existing dataset, as models can identify local trends that do not necessarily generalize to other data samples.
A common sign of early-stage AMD in fundus images is druses (td), which are less than 125 microns [49,50]. OCT scans showed localized elevations of the pigmented epithelial layer with medium reflectivity.
The intermediate stage of AMD served as a transitional phase between the more distinctly defined early and late stages of the disease. This made diagnosis more challenging and complicated the identification of clear IBs. The presence of at least one large druse (md) (more than 125 microns) determined the transition of the disease to an intermediate stage [51]. The increase of druses could lead to drusenoid detachment of the pigment epithelium (sd) [49,50]. At this stage, a wide range of IBs were observed. This stage was also characterized by hyperreflective inclusions (gv), which are small bright spots in the retina. They were considered to indicate inflammatory or degenerative changes, and local atrophy (la), which are localized areas of thinning or loss of retinal layers, especially retinal pigment epithelium and photoreceptors [52].
Progressive loss of pigment epithelium in the central parts of the macula (ga) combined with degenerative changes in the choriocapillaries, led to degenerative changes in the neuroepithelium and the development of late-stage dry (atrophic) AMD [53].
For the late stage of wet (neovascular) AMD, the most characteristic IBs included the neovascular membrane (nvm), fibrovascular pigment epithelial detachment (fopes), subretinal and intraretinal fluid (srzh or irzh), and hyperreflective inclusions. Without treatment, this condition can lead to the development of subretinal fibrosis (sr) [54,55].
Beyond the principal IBs per stage, additional markers also contributed to differential diagnosis. Prevalence distributions and expert-elicited clinical significance were used downstream in optimization and fuzzy rules (Supplementary Tables S1 and S2).
Data on the clinical significance of each IB were compiled from findings by diagnostic specialists and relevant scientific literature [49,50,54,56,57,58,59,60,61,62,63].
The dataset showed a significant class imbalance, indicating that some IBs were less frequently detected across AMD stages. This observation was confirmed both by expert assessments and by statistical analysis. To test this assumption, we evaluated the results of implementing a direct classification of AMD stages, as well as a comprehensive search across the entire available set of IBs. The selected IBs, equipped with appropriate code designations, were designed as markers to train the encoder in solving the problem of multiclass classification.
2.3. Assessing the Efficiency of Direct Classification and Pattern Detection in OCT Images
To justify the need for the proposed two-stage approach, we evaluated direct AMD stage classification using a DNN without IB-based preprocessing. The model core was a modified ResNet-18 neural network, in which the final fully connected layer was replaced with a configurable classifier that outputs a vector of probabilities, indicating the presence of all classes or IB under consideration. ResNet-18 is a relatively simple variant within the ResNet family, comprising 18 levels. It strikes a balance between presentation capabilities and computational efficiency. For image analysis tasks using OCT, where datasets are often limited in size, more complex models such as ResNet-50 or ResNet-101 may not be suitable due to their excessive capacity [64,65]. ResNet-18 mitigates this risk by maintaining sufficient depth to capture complex patterns while being less susceptible to overfitting. Furthermore, ResNet-18 has also demonstrated outstanding results in extracting highly discriminatory features from medical images, while maintaining reliability in conditions of limited data volume or the presence of noise in labels:
- Classification of retinal diseases based on OCT images [65];
- Detection of IB and pathologies in neuroimaging [66];
- Search and segmentation tasks in medical imaging datasets [67].
For direct classification, target labels covered all six AMD stages, while information about IB lesions was excluded. The training and testing samples were divided in a ratio of 80% for training and 20% for testing, consistent with all subsequent DNN training procedures. This baseline assessment demonstrates the challenges associated with class imbalance in medical imaging datasets.
The evaluation process utilized the following metrics [68]:
- Accuracy (Acc): Reflects the DNN’s overall correctness in identifying IBs across all AMD stages.
- Precision: Indicates the reliability of the DNN’s positive IB detections.
- F1-score: Balances precision and recall, which is crucial for handling rare or imbalanced IBs.
- Specificity (SP): Measures the correct identification of an IB’s absence, reducing false positives.
- Sensitivity (SN/Recall): Ensures that critical IBs are not overlooked, which is vital for detecting early signs of AMD progression
- Area Under the ROC Curve (AUC): Threshold-independent summary of discriminative performance; equals the probability that a randomly chosen positive is ranked above a randomly chosen negative and is widely used alongside TPR/FPR, sensitivity, and specificity.
Baseline results revealed significant performance variations across different AMD stages, with particular difficulties in detecting early-stage manifestations due to subtle visual differences and class imbalance issues.
The detailed baseline performance analysis, including confusion matrices, is presented in Supplementary Materials (Figure S1). These results underscore the need for the proposed biomarker-based approach to improve classification accuracy and interpretability.
The results of the DNN tests demonstrate significant unevenness in the classification of AMD stages. The late (neovascular) AMD and late (fibrosis) AMD were perfectly recognized with F1-scores exceeding 90% (91.5% and 91%, respectively). The mean F1-score across all AMD stages was 67.6%. However, the model showed considerable difficulty with the early detection of AMD, achieving only 8.9% F1-score accuracy. The late (atrophic) AMD stage achieved an intermediate F1-score of 42.6%.
The classification of early AMD reveals a significant flaw in the performance of the DNN. The model correctly identified only 7 out of 99 early cases of early AMD (7.1% of cases), yielding extremely low accuracy (12.1%). Most early-stage AMD cases were mistakenly classified as either intermediate stage (37 cases) or late stage (atrophic) (34 cases).
This pattern indicates fundamental difficulties in identifying the distinctive features of the early manifestations of the disease. Identifying cases without AMD disease also presents significant difficulties in classification, as only 48% of cases were identified correctly (49 out of 102 cases). The model often misclassified AMD-negative cases as early stage AMD (27 cases) or late stage (atrophic) (15 cases). This tendency toward false positive results may lead to overdiagnosis and unnecessary treatment recommendations in a clinical setting.
Geographical atrophy presents a complex misclassification issue, particularly characterized by significant bidirectional confusion with the intermediate stage of AMD. Specifically, 31 cases of true intermediate AMD were incorrectly classified as late (atrophic) AMD, while 3 true late-stage (atrophic) cases were misidentified as intermediate AMD. Additionally, there were classification errors in the late (atrophic) AMD stage: 23 cases were mistakenly attributed to the early stage of AMD, and 11 cases were classified as AMD-negative. Despite its distinct clinical features, late (atrophic) AMD was correctly detected in only 53% of cases. This highlights the challenges in accurately recognizing this condition. The uneven performance of DNN across different stages of AMD can be attributed to an imbalance in the dataset’s class distribution. Therefore, direct AMD stage classification without first accounting for input/output imbalance may not yield clinically acceptable results.
To evaluate the statistical credibility of improvements beyond the architectural capacity, we repeated each training configuration five times using different random seeds. We report the mean ± 95% confidence intervals, which were calculated using Student’s t-interval on the held-out test split that remained constant across all runs. This approach matches the data partitions used in Section 2.3 and ensures that the comparisons are paired under identical preprocessing, normalization, and augmentation conditions.
Backbone ablation involved four compact encoders: ResNet-18 (baseline), ResNet-34, ConvNeXt-Tiny, and a small Vision Transformer (DeiT-Tiny). These models were retrained under a fully standardized protocol to ensure fairness across comparisons. All models used 224 × 224 inputs, identical ImageNet-1k mean/std normalization, and the same augmentation suite. The augmentation included a RandomResizedCrop to 224 with a scale of 0.8 to 1.0 and an aspect ratio of 1.0, a random horizontal flip p = 0.5, rotations of ±5°, and ±10% adjustments in brightness and contrast. The models were fine-tuned end-to-end from ImageNet-1k initialization, with DeiT-Tiny employing the distilled pretraining recipe. The optimization process utilized AdamW with a base learning rate of and a weight decay of 0.05. The learning rate was adjusted using cosine decay with a 5-epoch warm-up. A batch size of 64 was used, with a maximum of 100 epochs and early stopping based on validation macro-AUROC with a patience of 10. To address class imbalance, uniform class-balanced cross-entropy (effective number) and focal modulation (with ) were implemented for probability calibration [44,69,70]. A single scalar temperature was fitted on the validation fold for each model family. All configurations were repeated over five random seeds to report the mean along with 95% confidence intervals. This approach ruled out advantages in model capacity or scheduling as potential drivers of the observed performance gaps, as detailed in Section 2.3 and Section 4.
Class-balanced cross-entropy (CB-CE) adjusts the weight of each class based on the inverse of the ‘effective number’ to address frequency skew. The focal-loss adds attenuation around easy examples, yielding:
which has been empirically shown to be effective in handling long-tailed distributions in medical applications. Both CB-CE and focal loss were consistently applied to all model backbones to avoid optimization bias [69,70]. Additionally, post hoc temperature scaling using a single scalar T maintains accuracy while aligning model confidence with actual correctness. We applied the same validation-fit T for each model family, following the reliability protocol outlined in Table 1 and Table 2 of this manuscript.

Table 1.
Identical-data comparison against strong end-to-end baselines (mean ± 95% CI over multiple seeds), extended with DeiT-Tiny.

Table 2.
Grouped failure modes with representative patterns and rule/IB mitigations.
To test whether a compact transformer changes conclusions under severe class imbalance, we added a small ViT baseline (DeiT-Tiny, a convolution-free transformer pre-trained on ImageNet with a distilled training approach) alongside ConvNeXt-Tiny as a modern ConvNet control. Both models were trained using the same protocol, data splits, normalization techniques, augmentations, and 224 × 224 inputs as our ResNet baselines. We employed class-balanced cross-entropy, adjusted for the effective number of samples with focal modulation and post hoc temperature scaling [69,70]. This setup mirrors the strong end-to-end baselines presented in Table 1.
Temperature calibration was probed in two modes: off (raw logits/softmax) and on (post hoc temperature scaling) with a scalar T fit on the validation split. Additionally, we scanned a grid by hard-setting T at test time to profile accuracy invariance and reliability trade-offs. This approach demonstrates that temperature scaling aligns confidence with correctness while largely preserving class decisions and accuracy in practice.
Next, we implemented a direct IBs search, which acts as a conversion of the output data for DNN. The target labels were the vectors . Once the encoder training was completed, we conducted stratified K-fold cross-validation on the entire dataset to evaluate its effectiveness. The results compared the vectors of the target values of IBs and the predicted values with a 95% confidence interval. The analysis included calculating the error matrix for each IB and the DNN output vector. The results of the metric calculations were then averaged across all IBs. These findings are presented in Figure 2.
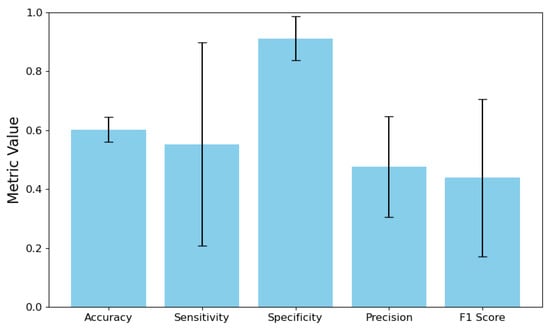
Figure 2.
DNN Performance Metrics with 95% Confidence Intervals.
The model’s sensitivity is 55.25%, but it comes with a broad confidence interval of 20.71% to 89.79%. This raises two important concerns. First, the model fails to accurately identify positive cases, missing nearly half of them. Second, the wide confidence interval indicates significant variation in sensitivity estimates, which may stem from either a limited number of positive samples in the dataset or inconsistencies in the model’s performance across different positive categories or validation folds. In contrast, the model demonstrates a specificity of 91.22%, with a narrower confidence interval ranging from 83.77% to 98.67%. This finding indicates effective recognition of negative cases. The substantial difference between sensitivity and specificity suggests a strong class imbalance in the training data, likely with negative instances significantly outnumbering positive examples. As a result, the model appears biased toward predicting the majority class (negative cases) while underperforming for the minority class (positive cases). The overall accuracy of the model is 47.60%, meaning it can correctly predict a positive outcome less than half the time. This limitation, combined with moderate sensitivity, results in a relatively low F1-score of 43.87%, indicating suboptimal performance in accurately identifying positive cases. Additionally, the wide confidence interval for the F1-score, ranging from 17.17% to 70.58%, further highlights the model’s instability in correctly identifying positive instances.
The combination of these indicators suggests that an unbalanced set of IBs hinders successful DNN training. The model adjusted to the imbalance present in the original dataset, becoming overly cautious in assigning positive ratings. This adaptation resulted in high specificity but also in low sensitivity and accuracy.
Selecting IBs for the encoder’s training set requires a careful approach to enhance prediction accuracy, denoted as . This involves classifying IBs based on their clinical and statistical significance, leading to four possible scenarios:
- High Clinical + High Statistical Significance: The IB is highly relevant for diagnosing AMD stages and is supported by sufficient data to train an effective classifier. These are ideal candidates for inclusion.
- Low Clinical + High Statistical Significance: The IB is statistically sound but has low clinical relevance for AMD staging, making its inclusion potentially redundant.
- High Clinical + Low Statistical Significance: The IB is clinically critical but rare in the dataset. This low statistical representation hinders the development of an effective classifier without techniques like data augmentation.
- Low Clinical + Low Statistical Significance: The IB lacks both clinical and statistical relevance, suggesting it should be excluded from the dataset.
Therefore, before finalizing the data set for encoder training, it is essential to identify a group of IBs that are both statistically and clinically significant for the subsequent staging of AMD. Further investigation should also assess potential redundancy among IBs with lower clinical significance.
2.4. External Validation Protocol
To assess generalization beyond a single in-center dataset and approximate cross-center deployment, a leave-scanner-out (LSO) validation was conducted. This method adheres to the guidelines on cross-validation in medical imaging [71]. The validation utilized two OCT devices at the Optimed Laser Vision Restoration Center: the Optovue Avanti XR (Optovue, Fremont, CA, USA) and the Optopol REVO NX (Optopol Technology Sp. z o.o., Zawiercie, Poland). These devices differ in their acquisition pipelines and post-processing techniques, which are known sources of scanner/domain shifts in medical imaging [72].
We created two non-overlapping patient cohorts for each device and conducted two LSO splits: one trained on Avanti XR and tested on REVO NX, and vice versa. In both cases, we applied identical preprocessing procedures, input resolutions, augmentations, loss reweighting (CB-CE + focal), optimization, early stopping, and post hoc temperature scaling, as outlined in Section 2.3 and Section 4.
To prevent information leakage, patients were uniquely assigned to each device split, ensuring that no subject appeared across devices in the same experiment. We excluded images with inadequate signal strength or artifacts using the same quality filters applied in the main experiments. The final dataset included 1928 macula-centered B-scans (1180 from the Avanti XR and 748 from the REVO NX), sampled via the clinical radial line protocol and exported in JPEG format, as detailed in the dataset section. This dataset was exclusively used for LSO to simulate cross-scanner validation in accordance with TRIPOD + AI guidelines on external validation when multi-center data is unavailable [73].
For fairness, we retained the same backbone models and calibration protocols as listed in Table 1 (including ResNet-18, ResNet-34, ConvNeXt-Tiny, and DeiT-Tiny for end-to-end applications, as well as a two-stage IB-encoder with fuzzy and temperature scaling). We utilized five training seeds per split to report the mean ± 95% confidence intervals on the fixed LSO test set for each direction, following best practices for robust external validation [74].
Generalizing across diverse datasets remains a significant challenge beyond cross-device validation. Such difficulties arise from variations in acquisition protocols, patient demographics, scanning equipment, and grading practices that may exceed the simulated domain shifts tested here. Practical strategies to address these challenges include harmonizing preprocessing methods, applying scanner-aware normalization, and utilizing domain adaptation techniques. Additionally, implementing periodic recalibration checks (such as Expected Calibration Error and Brier score) and conducting prospective multi-center validation will enhance reliability. The proposed two-stage design facilitates these improvements by clearly separating IB detection from interpretable reasoning.
3. Creation of a Dataset and a Classification Algorithm Based on the Patterns of the Target Class
Creating an effective dataset for training an encoder to identify IBs for AMD requires addressing the challenges associated with the uneven distribution of IB occurrences across different stages of the disease. Research in machine learning has introduced several specialized methods to tackle class imbalance in medical imaging. These methods include few-shot learning, one-shot learning, and zero-shot learning techniques [75,76,77,78]. Typically, these approaches utilize advanced methodologies such as meta-learning frameworks, synthetic data generation, metric learning systems, and semantic attribute modeling applied to the target variables.
However, these advanced learning approaches encounter significant challenges when explicitly applied to OCT-based IB detection for AMD. A primary limitation is the high variability of disease IBs in retinal imaging [79,80,81]. This variability hampers the ability to generate reliable patterns from a limited number of examples, ultimately leading to reduced classification accuracy for the rarer IB classes [82,83].
A more effective approach involves the strategic selection of IBs, particularly by systematically excluding categories of IBs that show poor detection efficacy. However, this selection process should not rely solely on statistical performance metrics. It must also incorporate expert clinical knowledge to avoid inadvertently removing IBs that, while statistically difficult to detect, hold significant diagnostic value for specific stages or subtypes of AMD.This perspective highlights the critical need for a dual-criteria optimization strategy in IB selection. The IB selection process must explicitly evaluate both statistical reliability and clinical significance, ensuring comprehensive diagnostic coverage across all stages of AMD under consideration.
In the inter-rater agreement summary, we present the statistics for per-IB agreement, including Cohen’s , positive percent agreement, and negative percent agreement for the double-read subset. We also include the proportion of cases requiring adjudication for each IB, which can be found in the Supplementary Materials (Figure S9). These agreement measures reflect the quality of IB labels used in encoder training and complement the clinical significance matrix reported in Supplementary Table S2.
3.1. Calculating the Statistical and Clinical Significance of IBs
The optimal selection of IBs requires a dual evaluation framework that considers both statistical performance and clinical relevance. Statistical significance is assessed through One-vs-Rest (OvR) decomposition, where each IB is evaluated using binary classification performance metrics [84,85,86].
For each IB bi ∈ B, a binary classifier is trained to distinguish between the presence and absence of that specific IB across all OCT images. The statistical significance is quantified using the Youden J-index [87], which combines SN and SP [88]:
We refer to Youden J-index simply as J hereafter to streamline notation. Clinical significance is determined by expert assessments of each IB’s diagnostic value for different AMD stages, converted to numerical scales for computational processing.
The comprehensive performance metrics for all IBs are presented in Supplementary Materials (Table S3).
This method effectively transforms a general multiclass and multidimensional problem into separate binary tasks. It allows each IB classifier to be assessed independently using the performance metrics of the corresponding binary classifiers. By training a distinct classifier to determine the presence or absence of a specific IB, the OvR approach produces results that are easy to interpret and understand. This helps us establish a direct correlation between the IBs and the most significant parameters of the DNN model. These metrics serve as the foundation for the multi-objective optimization process.
In this study, the encoder structure serves as the primary architecture for the binary classifiers. The encoder is designed to classify a complete set of relevant IBs, with the final layer modified to perform binary classification for each IB.
Binary classifier testing revealed distinct performance patterns among imaging IBs, with six markers demonstrating strong clinical potential: td showed exceptional sensitivity (0.96) and high AUC (0.97) with substantial dataset representation (0.46), making it a leading candidate for clinical application; md exhibited well-balanced metrics across all parameters (AUC 0.98, accuracy 0.93) with significant share (0.36); ga achieved the highest AUC (0.99) and near-perfect specificity (0.99) despite lower prevalence (0.07), which makes it valuable for confirmatory testing; sr, gv, and fopes also demonstrated strong overall performance with AUCs ranging from 0.93 to 0.97 and varying clinical applicability based on their dataset shares.
In contrast, eight IBs (sd, la, nvm, irzh, srzh, nrt, mpes, nezh) exhibited a problematic pattern of high specificity but significantly compromised sensitivity (0.08–0.42). This limits their effectiveness as primary discriminators and suggests their optimal use in confirmatory roles or as components of multi-IBs diagnostic panels, rather than as standalone indicators.
3.2. Optimal Selection of IBs Based on Their Statistical and Clinical Significance
The IB selection process employs the NSGA-II to optimize two competing objectives: statistical performance and clinical significance [89]. This approach ensures that the selected IBs provide both reliable classification performance and meaningful clinical interpretation.
To implement the NSGA-II algorithm, we needed to establish optimizable competing goal functions and constraints for the optimization process. The objectives of implementing an optimal selection algorithm are articulated as follows:
- Ensuring maximum classifier performance: High performance characteristics of binary classifiers are preferred.
- Ensuring maximum clinical value: Preference should be given to IBs that are assessed as “Present,” “Common,” or “Defining features” for at least one stage of AMD.
The optimization problem is formulated with two objective functions:
- Statistical Performance:where is a transformation function that enhances the impact of high-performing IBs:where refers to the steepness parameter and threshold , and M is the maximum penalty parameter. To assess the statistical significance of IB, , we use J and its shaped variant (“transformed J”) in the statistical objective.In the context of diagnostics, a minimum acceptable level of sensitivity and specificity is considered to be 80% [90,91]. The threshold value for statistical performance was determined to be . The steepness parameter is defined as because a steeper sigmoid results in a larger derivative near the threshold. It ensures that slight deviations in performance are represented as significant changes in the transformed output. Such an approach provides meaningful gradients for optimization, which is essential for robust parameter estimation and model convergence [92].From the equation , it follows that in order to penalize a low J via the transformed J term , it is required that M > 1. Since statistical efficiency is a more critical factor for enabling the training of the Information Bottleneck search classifier on OCT images, the penalty value was chosen to be greater than the corresponding element of the equation used for calculating clinical significance: .
- Clinical Significance:where is the average clinical significance of IB across all stages, is the clinical significance of IB for disease stage j, n is the number of disease stages, is a bonus factor for balanced coverage, and is a transformation function for clinical significance:where M is the maximum boost parameter and is the mid-point parameter. The parameter M is determined according to the same principle as when evaluating Statistical Performance, but with a lower value: . This is due to the fact that Clinical Significance has a slightly lower priority. If the Statistical Performance value is low, the classifier’s performance may be insufficient, and the IBs allocation algorithm will not be able to perform its functions effectively. The midpoint parameter was set to “Present” to encourage those who determine the stage of IBs. The coefficient 5 in a transformation function for clinical significance 5 controls the steepness of the arctangent function around . The 0.5 addition serves to normalize the arctangent output.
The optimization is subject to the following constraints:
- Performance Threshold. Ensures the cumulative statistical performance exceeds a minimum threshold:
- Stage Coverage. Ensures adequate clinical coverage across all disease stages:
The complete mathematical formulation of the IB selection problem is:
Unlike generic NSGA-II deployments that optimize raw statistical scores or sparsity alone, we:
- shape the statistical objective via a transformed J with a steep sigmoid around to magnify small but clinically meaningful improvements near the acceptable sensitivity/specificity operating point;
- add a stage-wise clinical coverage term using so that every AMD stage maintains a minimum level of supported evidence;
- enforce hard constraints and to rule out Pareto-optimal yet clinically unsafe subsets. This approach ensures that the selection process focuses on subsets that remain learnable (high J), maintain clinical balance (coverage across different stages), and are robust against class imbalance. To our knowledge, this combined strategy has not been previously applied in IB selection using MOEAs.
The optimization process yields a Pareto front of solutions representing different trade-offs between statistical performance and clinical relevance. The final IB selection represents the most balanced solution on this Pareto front. Thus, after DNN training on a limited set of the most statistically and clinically significant IBs and refining the algorithm for analyzing DNN results using a fuzzy logic approach, AMD’s staging algorithm was retested. The detailed optimization results, including the Pareto front visualization, IB selection patterns, and hypervolume analysis, are presented in Supplementary Materials (Figures S2–S5).
The optimization results reveal a clear hierarchical structure in IB selection for AMD staging. Core IBs, which include td, md, gv, ga, fopes, and sr, consistently demonstrate essential diagnostic value across all solutions, regardless of the optimization focus. In contrast, conditional IBs, such as sd, la, and srzh, exhibit variable selection patterns. Notably, irzh is preferred over srzh due to its superior classification accuracy (0.901 compared to 0.885) and greater model stability.
Excluded IBs, namely nvm, nrt, mpes, and nezh, are systematically avoided because they lack sufficient representation in the dataset. This lack of representation leads to poor classifier specificity and high false-negative rates, which compromise their clinical utility. The exclusion of clinically significant IBs, such as srzh and nvm—despite their importance as indicators of neovascular activity and exudative AMD stages, respectively—represents a necessary compromise between clinical relevance and statistical reliability, given their limited dataset representation (9% and 5%, respectively).
However, future work with balanced datasets or data augmentation techniques may enable the inclusion of these indicators, enhancing diagnostic accuracy, particularly in distinguishing late-stage AMD subtypes. The following solution was selected based on the analysis of the Pareto front:
Best Clinical Significance (Solution 3):
- Selection: [td, md, gv, ga, fopes, irzh, srzh, sr];
- Aggregated Transformed Performance: 0.0000;
- Aggregated Clinical Significance: 1.0000.
This solution highlights IBs that hold significant clinical importance at various stages of the disease. The inclusion of both irzh and srzh enhances clinical relevance, although it may slightly reduce statistical performance. This approach is most suitable when prioritizing clinical interpretability and its relevance to disease mechanisms over purely focusing on classification accuracy.
The Pareto front visualization indicates a relatively uniform distribution of solutions, though there is some clustering at the extremes. Solutions 1, 2, and 4 prioritize statistical performance, while Solutions 3, 6, and 7 emphasize clinical significance. Ultimately, the final set of IBs was derived from Solution 5, as it represents the best balance between statistical and clinical significance.
3.3. Fuzzy Logic-Based Interpretable AMD Stage Classification
After determining the optimal selection of IBs using multi-objective optimization, the final part of our two-stage CDSS architecture implements a classification system that translates IB detection results into probabilistic assessments of AMD stages. This stage emphasizes the importance of interpretability by modeling expert diagnostic reasoning using fuzzy logic. This approach enables clinicians to understand and validate the system’s decision-making process.
3.3.1. Architecture Integration and Confidence Calibration
The integration ensures that the interpreter only processes statistically reliable and clinically relevant IBs. This approach preserves the ability to discriminate among scores while ensuring that each stage is traceable to a select, expert-approved set of IBs. This design maintains accuracy and allows for a thorough examination of the reasoning behind each IB.
The DNN’s IB detection module generates logits for each of the seven selected IBs. However, DNNs often produce miscalibrated confidence scores when using the standard softmax activation function. It can lead to overconfident predictions that do not accurately reflect true classification uncertainty. To address this issue, we implement temperature scaling calibration to enhance prediction reliability without compromising classification accuracy [93,94].
The calibration process introduces a temperature parameter T> 0 that modifies the softmax function:
The optimal temperature T* is determined by minimizing negative log-likelihood on a validation set:
where is the true class label for the i-th sample in the validation set [95]. The DNN confidences are post hoc calibrated via temperature scaling; formal definition, optimization, and ablation of the scalar T are provided in Section 4.5, where reliability diagrams and a temperature sweep (including the selected , post hoc temperature scaling; see Table 3) are reported (bold marks the best result in the column).

Table 3.
Temperature scan (mean ± 95% CI over 5 seeds) for the strong end-to-end ResNet-18 and the proposed two-stage system under identical data, splits, and preprocessing. Accuracy stays stable across T, while ECE and Brier show a minimum near .
3.3.2. Fuzzy Logic Implementation for Expert Rule Modeling
To derive fuzzy rules, we utilized the expert IB-stage matrix presented in Supplementary Table S2 as the primary source. This matrix maps each IB to each AMD stage using a linguistic rating system: Absent, Rare, Present, Common, Defining feature. We encoded these ratings as numeric centers for the membership functions. This approach preserves clinical semantics in the rule base while allowing for smooth aggregation of calibrated confidences from the DNN encoder (as detailed in Section 3.3.1). The midpoint rating of “Present” is anchored at 0.50, reflecting the clinical operating point where an IB begins to significantly support a stage hypothesis (refer to Figure 3 and Supplementary Table S2).
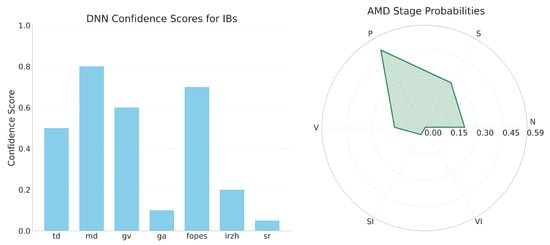
Figure 3.
IB confidence bars and radar chart of AMD stage probabilities.
For each stage , the stage score is computed by summing membership responses across the selected NSGA-II IB subset . Here, represents a hyperbolic-tangent membership function that treats negative evidence for “Absent” asymmetrically while assigning amplified weight to the “Defining feature,” as specified in Equation (11). This method encodes crucial IBs (e.g., ga for SI, sr for VI) without saturating earlier stages (see Section 3.3 and Supplementary Figures S4 and S5).
Concretely, the rule “if ga is a Defining feature for SI, then ga strongly promotes SI” is instantiated via and the multiplicative factor for “Defining feature” in Equation (11). In contrast, rules such as “td is Rare in V/VI” are encoded by and yield only modest, sign-consistent contributions. Ultimately, this results in a transparent scoring map which links stage probabilities back to explicit expert entries in Supplementary Table S2, the membership mapping discussed in Section 3.3, and the calibrated confidences visualized in Figure 3.
We employ a hyperbolic-tangent membership to map calibrated confidences into stage evidence with explicit clinical semantics: negative membership for “Absent,” scaled response by , and a 3× amplification for “Defining feature,” all centered at the clinically motivated midpoint with steepness :
This asymmetric, calibrated, and thresholded design encodes stage-defining cues (e.g., ga for SI; sr for VI) while reducing spurious activation below the midpoint, thus enhancing interpretability and reliability (Section 3.3, Supplementary Table S2).
The fuzzy classification algorithm computes the probability of each AMD stage by aggregating the contributions from all IBs according to their clinical significance patterns:
where represents the probability of AMD stage j, is the calibrated confidence score for IB i, and is the membership function value for IB i in the context of stage j.
This formulation enables the system to handle the inherent uncertainty in medical diagnosis while maintaining traceability of the decision-making process. Each IB’s contribution to the final stage probability is explicitly quantified, allowing clinicians to understand which image features drive specific diagnostic conclusions.
To evaluate the statistical reliability of the AMD stage prediction algorithm, we constructed a heat map as shown in Supplementary Materials (Figure S4). It reflects the relationship between the probability levels for each stage of AMD and the probability of detecting IBs (disease indicators). We also conducted a sensitivity analysis, the results of which are shown in Supplementary Materials (Figure S5). During this analysis, we adjusted the confidence level of one IB while maintaining the other indicators at a baseline of 0.5.
Correlation analysis confirms that each IB aligns with specific AMD stages: td is highly indicative of early AMD (r = 0.79) and becomes negatively associated with late fibrosis, ga is the strongest marker for late atrophic AMD (r = 0.83) while inversely related to earlier stages, sr almost exclusively signals late fibrosis AMD (r = 0.90) and is strongly negative for early and intermediate disease, and fopes best characterizes late neovascular AMD (r = 0.54) with diminishing relevance in earlier stages. Collectively, these gradients, alongside moderate links such as md and irzh, depict a coherent progression from early to advanced pathology and allow clear differentiation between healthy retina, transitional intermediate AMD, and the distinct late subtypes.
Sensitivity analysis reveals a universal confidence threshold of 0.5, beyond which the influence of IB on AMD staging becomes significant. Specifically, biomarkers such as ga trigger a sharp increase in the likelihood of late atrophic AMD, while sr shows a sigmoid increase for late fibrotic AMD. Additionally, td results in a marked increase in the probability of early AMD. These patterns, represented by hyperbolic-tangent membership functions in the fuzzy classifier, demonstrate the model’s effectiveness in distinguishing between different stages of the disease. td is particularly useful for identifying early disease but has limited diagnostic value in advanced stages. In contrast, ga and sr serve as crucial indicators for late atrophic and fibrotic AMD forms, respectively, while having minimal impact on stages below the established threshold.
The analysis indicates that td, ga, and sr function as key indicators for defining stages of AMD. Specifically, td reliably marks early AMD, ga identifies late atrophic AMD, and sr highlights late fibrotic AMD. Each of these indicators shows a significant increase in probability once confidence levels exceed 0.5. In contrast, md, gv, fopes, and irzh demonstrate milder, supplementary effects on stage prediction. Notably, sr exhibits a classic sigmoid curve, which consistently increases the probability of late fibrosis while keeping the probabilities of other stages flat. This illustrates its diagnostic precision. Additionally, a combined bar-and-radar visualization connects confidence scores of the indicators to stage probabilities. This visualization allows clinicians to understand how input features influence diagnostic outcomes, thereby clarifying the previously opaque reasoning process of the system.
3.3.3. Hyper-Parameter Sensitivity of Fuzzy Membership
To assess robustness of the interpretable stage, a targeted ablation varied:
- the membership midpoint around the clinical “Present” operating point;
- the steepness ;
- the “Defining feature” amplification ;
While keeping the calibrated DNN encoder, the NSGA-II IB subset, splits, and temperature scaling identical to Section 4, thereby isolating the effect of fuzzy membership settings (Table 1; Figure 3).
Across the grid, both discrimination and calibration remained stable. The accuracy varied within ±0.5 percentage points around the reference value of 90.4%. The macro-AUROC ranged within ±0.007 from 0.962, and reliability metrics changed only slightly: ECE varied within ±0.8 percentage points, and Brier scores fluctuated within ±0.005. It indicates that the interpretable layer is robust to modest shifts in the membership midpoint and steepness. The weight of the “Defining feature” primarily adjusts calibration without affecting decision-making (see Supplementary Table S4 and Figure S7 for the context of calibrated reliability).
Importantly, the reference setting , , —which is clinically aligned with “Present”—resulted in the lowest ECE and Brier scores among all tested configurations. This is consistent with the role of temperature scaling in aligning confidence levels and reflects the intended semantics of the expert rules outlined in Supplementary Table S2 (Section 3.3 and Section 4.5).
3.4. Interpretable Visualization Framework
To facilitate clinical adoption and enable expert validation of algorithmic decisions, we implemented a dual visualization strategy that presents both input IB confidences and output stage probabilities in an intuitive format. The visualization interface combines:
- Bar chart representation of IB confidence scores, enabling clinicians to quickly assess which image features were detected with high reliability;
- Radar chart visualization of AMD stage probabilities, providing a unique “diagnostic fingerprint” for each case that facilitates comparison across different stages.
This dual representation addressed the interpretability challenge by creating a transparent pathway from image analysis to diagnostic conclusion. Clinicians can trace the reasoning process from detected IBs to stage probabilities, enabling critical evaluation of the system’s recommendations within established clinical frameworks. A visualization of the IBs analysis algorithm is shown in Figure 3.
4. Results
4.1. Overall System Performance
The proposed two-stage approach demonstrated substantial improvements in diagnostic accuracy across all evaluation metrics. Compared with direct AMD stage classification, overall accuracy improved from 55.1% to 90.0%, representing a relative gain of 63.3%. This improvement was achieved through the optimal selection of IBs using NSGA-II optimization and the implementation of fuzzy logic-based reasoning.
The system’s IB detection performance showed remarkable improvements in both accuracy and consistency. As illustrated in Figure 4, sensitivity increased from 0.5525 to 0.8258, representing a substantial reduction in false negatives. Precision improved from 0.4760 to 0.8380, indicating a much higher likelihood that a detected IB is truly present. Most importantly, the confidence interval widths were dramatically reduced: sensitivity CI from 0.6908 to 0.1390 and F1-score CI from 0.5341 to 0.0696. This reduction reflects greater stability across IBs, which is essential for clinical reliability.
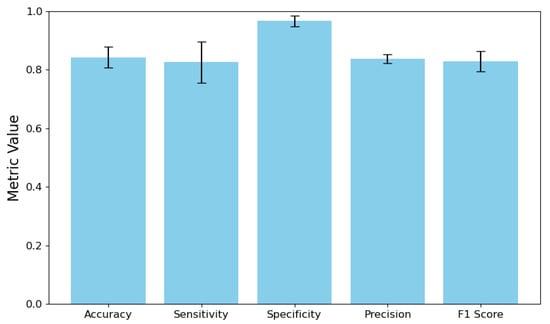
Figure 4.
IB detection performance with 95% CIs.
The final AMD stage classification was performed by feeding the DNN output vectors into the fuzzy expert system , with the most probable stage selected as . The comprehensive test results, including the detailed error matrix for classifying AMD stages, are presented in Supplementary Materials (Figure S6).
4.2. Comparison with Strong End-to-End Baselines
To quantify the incremental benefit of the proposed IB selection and fuzzy reasoning beyond architectural capacity and class-imbalance mitigation, we trained strong end-to-end baselines under identical conditions. These included ResNet-34, ConvNeXt-Tiny, and DeiT-Tiny, all trained with class-imbalance mitigation via class-balanced loss and focal modulation (), and post hoc temperature scaling for probability calibration [69,70].
All baselines and the two-stage system used the identical standardized protocol detailed in Section 2.3, ensuring capacity and schedule parity.
As shown in Table 1, the two-stage system achieved 90.4% (±1.9) accuracy and 0.962 (±0.016) macro-AUROC, outperforming all end-to-end baselines. The strongest baseline, ConvNeXt-Tiny, achieved 88.4% (±1.2) accuracy and 0.937 (±0.007) macro-AUROC. Notably, the two-stage system also demonstrated superior calibration with an ECE of 2.1% (±0.4) and a Brier score of 0.082 (±0.003), compared with ConvNeXt-Tiny’s ECE of 4.3% (±0.5) and Brier score of 0.115 (±0.004).
Under this standardized protocol and shared training budget (Section 2.3 and Section 4), accuracy and calibration margins persist in favor of the two-stage system; thus the gains cannot be attributed to input resolution, normalization, augmentation, optimizer, schedule, batch size, or stopping-criterion discrepancies, as shown in Table 1, Supplementary Figure S7, and Table 3.
4.3. Per-Stage Performance Analysis
To intepret stage-wise gains at the IB level, we conducted a leave-one-biomarker-out (LOBO) analysis within the two-stage system. We measured per-stage AUROC after excluding each selected IB from BN = td, md, gv, ga, fopes, irzh, sr. Additionally, we created a cumulative “top-k IBs” curve that adds IBs in a coverage-balanced order (td→ga→sr→md→fopes→gv→irzh) (Figure 5). The LOBO analysis confirmed that td is the primary driver of early AMD (S; AUROC −0.062 when removed). The IB ga was decisive for late atrophic (SI; ), and sr for late fibrosis (VI; ). Late neovascular (V) performance depended on the exudative trio, with fopes () being the strongest and irzh () and gv () being complementary. Detailed stage-wise drops are provided in Supplementary Table S5. The cumulative ‘top-k’ curve saturated by k = 5, reaching 89.6% accuracy and 0.959 macro-AUROC (all 7 IBs: 90.4%/0.962), as shown in Supplementary Figure S8.
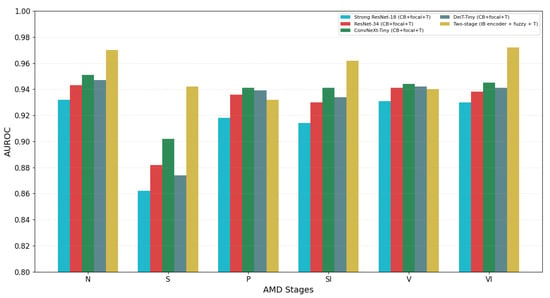
Figure 5.
Per-stage AUROC across models under identical protocol.
Particularly notable improvements were observed in challenging classifications:
- Early AMD classification accuracy increased from 7.1% to 84.8%, with correct identification of 84 out of 99 cases compared to only 7 in the baseline model;
- Normal case identification improved from 48% to 95.1% accuracy, virtually eliminating false positives;
- Late atrophic AMD classification improved from 53.0% to 86.7% accuracy;
- Intermediate AMD accuracy increased from 70.1% to 92.7%;
- Two categories showed slight performance decreases: late neovascular AMD (from 96.7% to 88.3%) and late fibrosis AMD (from 93.1% to 89.7%), suggesting potential overlapping features between advanced disease stages that require further refinement.
To make the residual error patterns actionable, the next subsection provides a compact failure analysis that groups typical confusions with concrete, rule-level mitigations, cross-referencing the confusion matrices and ablations (Supplementary Figures S1 and S6 and Table S5).
4.4. Failure Analysis: Grouped Error Modes and Rule/IB
We summarize the dominant residual confusions under the two-stage system and map them to interpretable causes and mitigations, grounded in the existing fuzzy rule base and IB subset BN = td, md, gv, ga, fopes, irzh, sr. Our analysis uses the held-out confusion matrices and ablations as guides (Supplementary Figure S1 for the direct baseline; Supplementary Figure S6 for the two-stage system; LOBO in Table S5; top-k in Supplementary Figure S8).
Four compact clusters capture most errors: early (S) versus intermediate (P) at drusen thresholds; atrophic (SI) versus fibrosis (VI) when sr is borderline; neovascular (V) versus fibrosis (VI) in exudative cases with incipient scarring; and normal (N) versus early (S) due to subtle undulations misread as td. Each cluster is addressed through small-magnitude, calibrated adjustments that preserve the validated membership design. These include modest midpoint raises for td in S; stronger negative membership for sr in SI and tie-breakers favoring VI when sr is decisively present; boosting fopes/irzh for V and penalizing sr for V; and corroboration requirements for td in S. All adjustments remain consistent with the sensitivity grid, which showed stability across small changes in m, , and .
Table 2 summarizes these common residual errors into four clinically relevant clusters: S versus P, SI versus VI, V versus VI, and N versus S. Each cluster is linked to interpretable factors in the calibrated IB confidences and suggests minor, rule-level adjustments that maintain the established membership design and stability shown in the sensitivity grid (see Supplementary Table S4). These adjustments align with the LOBO attributions for stage-defining IBs (td → S, ga → SI, sr → VI, fopes → V) and do not change the main conclusions or the validated operating point of the two-stage system.
4.5. Temperature Calibration Analysis
Temperature scaling analysis (Table 3) revealed the expected U-shaped reliability profile in both model families. Consistent with this finding, the fuzzy membership sensitivity analysis (Section 3.3.3) shows that small shifts in the midpoint and steepness preserve discrimination and only mildly affect ECE/Brier scores, indicating a robust interpretable layer under clinically plausible parameterizations.
Across all temperature values, the two-stage system consistently achieved lower ECE and Brier scores compared with strong end-to-end baselines. This indicates that combining calibrated IB confidences with fuzzy reasoning leads to better probability alignment. The reliability gap between the two-stage and end-to-end models remained significant throughout the entire temperature range, suggesting that the calibration advantage is robust rather than the result of narrow tuning. Reliability diagrams (see Supplementary Figure S7) illustrate that monolithic models tend to be overconfident relative to the identity line, while the two-stage model produces curves close to the diagonal across probability bins.
When analyzing the sensitivity of fuzzy parameters belonging to the midpoint of m, the steepness of , and the weight of the “defining feature” in accordance with the identical protocol presented in the Supplementary Table S4. The findings indicate that for midpoints and steepness , both accuracy and macro-AUROC remain within narrow bands around the reference. Reliability metrics (ECE, Brier) show only mild sensitivity. The best calibration achieved at , , supporting the clinical anchoring of the midpoint to “Present” and the chosen steepness for smooth but decisive rule activation (cf. Section 4.5 reliability analysis). Additionally, variations in ranging from 2 to 4 mainly shift calibration without impacting discrimination or accuracy, confirming its role as a confidence-weighting factor for stage-defining input behaviors (see Supplementary Table S2).
4.6. IB Importance Ablations (LOBO and Top-K)
We quantified the contribution of each selected IB using the LOBO study. In this experiment, we kept the calibrated IB encoder and fuzzy solver constant (as detailed in Section 3.3). We then removed one IB from the BN and re-evaluated per-stage AUROC on the held-out test set, following the same protocol (Supplementary Table S5 and Supplementary Figure S8). The most significant stage-wise declines were observed in the following areas: SI for ga (−0.093), VI for sr (−0.101), S for td (−0.062), and V for fopes (−0.071). These results point to their critical roles in defining the stages, which align with the expert rules outlined in Supplementary Table S2 and the sensitivity findings presented in Supplementary Figure S5. These ablations corroborate that intermediate AMD (P) draws evidence from md (−0.041) and td (−0.012), while neovascular V is dominantly supported by fopes/irzh/gv. Notably, ‘Common’ patterns such as gv serve as broad enhancers for late-stage separability rather than stage-specific determinants.
We further report a cumulative “top-k IBs” curve by adding IBs in a coverage-balanced order (td→ga→sr→md→fopes→gv→irzh): Accuracy improves from 74.1% () to 90.4% (), with most of the gain achieved by (89.6%). Macro-AUROC increasing from 0.905 () to 0.962 (), reflecting diminishing returns after adding fopes (see Supplementary Figure S8 for the curve and the exact “Included IBs” per k). This pattern is consistent with the Pareto selection (Supplementary Figures S2 and S3) and the fuzzy sensitivity (Supplementary Table S4), which together explain why td/ga/sr contribute decisive stage-specific evidence while md/fopes/gv/irzh provide complementary coverage.
LOBO shows the largest stage-specific sensitivities for ga→SI (−0.093), sr→VI (−0.101), td→S (−0.062), and fopes→V (−0.071). These sensitivities directly reflect the roles of the “Defining features” as encoded in the fuzzy rules and the expert matrix (see Supplementary Table S2). This also aligns with the uni-IB sensitivity patterns illustrated in Supplementary Figure S5. The cumulative “top-k IBs” curve levels off at , indicating that td, ga, sr, md, and fopes account for nearly all gains. In contrast, gv and irzh provide only modest improvements and contribute to robustness, which is consistent with the IB selection patterns shown in Figures S2 and S3.
Supplementary Figure S8 shows that Cumulative “top-k IBs” curve for the two-stage system under the identical protocol, adding IBs in a coverage-balanced order (td→ga→sr→ md→fopes→gv→irzh). Accuracy rises from 74.1% () to 90.4% () and macro-AUROC from 0.905 to 0.962, with saturation by (89.6%/0.959), consistent with NSGA-II selections (Supplementary Figures S2 and S3) and fuzzy sensitivity (Supplementary Table S4).
4.7. External Validation Across Scanner Types
External validation was performed using a leave-scanner-out methodology. The results of the cross-device experiments are summarized in Table 4.

Table 4.
Leave-scanner-out validation across Optovue Avanti XR and Optopol REVO NX under identical training protocol (mean ± 95% CI over 5 seeds).
When the two-stage model was trained on Avanti XR and tested on REVO NX, it achieved an accuracy of 86.1% (±2.3) and a macro-AUROC of 0.946 (±0.018). In comparison, ConvNeXt-Tiny attained an accuracy of 78.8% (±1.9), resulting in a 7.3 percentage point improvement. In the reverse scenario, when the two-stage model was trained on REVO NX and tested on Avanti XR, it reached an accuracy of 84.7% (±2.6), whereas ConvNeXt-Tiny achieved 77.5% (±2.0). These results demonstrate a robust generalization of the 63.3% relative accuracy improvement observed in internal validation to cross-device domain shifts, in accordance with TRIPOD+AI guidelines for external validation [73].
4.8. Computational Efficiency Analysis
The computational profile shows that end-to-end inference—including the IB encoder, post hoc temperature scaling, and the fuzzy reasoning layer—requires 2.43 ms per B-scan on a mid-range GPU (RTX 3060 12 GB) and 25.08 ms per B-scan on a mid-range CPU (Ryzen 7 3700X) under 224 × 224 inputs, mixed precision, and the identical protocol as Table 5. Expressed as throughput, this corresponds to approximately 412 images per second on the GPU and 39.9 images per second on the CPU. Consequently, the wall-clock time is approximately 0.31 s per 128-B-scan OCT volume on the GPU, versus about 3.21 s per volume on the CPU. These figures support the claims of clinical feasibility for GPU-equipped workstations, while also highlighting the latency trade-off for CPU-only implementations. The encoder is the primary contributor to the cost, accounting for approximately 2.0 GFLOPs and 11.7 million parameters. In contrast, calibration and fuzzy reasoning together contribute less than <1% of the total latency, confirming that the full pipeline figures presented reflect the cumulative runtime of encoding, calibration, and fuzzy inference rather than just the timing for the encoder alone.

Table 5.
Computational cost per B-scan (224 × 224) and per OCT volume (128 B-scans). GPU: NVIDIA RTX 3060 12 GB; CPU: AMD Ryzen 7 3700X; PyTorch 2.2 + cuDNN 8.9; mixed precision enabled for the encoder.
4.9. Clinical Impact and Interpretability
The separation of IB detection from diagnostic reasoning achieved the dual objectives of high accuracy and clinical interpretability. The fuzzy logic implementation enables clinicians to understand how specific IBs contribute to stage predictions, with stage-defining IBs (td for early AMD, ga for late atrophic AMD, sr for late fibrosis AMD) showing clear probability surges once confidence exceeds 0.5, as demonstrated in the sensitivity analysis (Supplementary Materials Figure S5).
The results show that the capacity of the ResNet-18 encoder is adequate when combined with the IB sets selected by NSGA-II and calibrated fuzzy mapping. This combination achieves a balance of accuracy, robustness, and efficiency for staging AMD. The proposed two-stage approach effectively addresses the significant “black box” problem while delivering state-of-the-art performance, making it suitable for clinical adoption with appropriate hardware considerations.
5. Discussion
The development and evaluation of the CDSS module for AMD staging based on imaging IBs revealed significant improvements in diagnostic accuracy while maintaining interpretability. By implementing a two-stage approach that separates IB detection from diagnostic reasoning, we have successfully addressed both the technical challenge of imbalanced medical datasets and the practical challenge of creating transparent intelligent systems for clinical adoption. The study achieved a remarkable increase in overall AMD staging accuracy, with relative improvement compared to direct classification methods. This enhancement was particularly pronounced in the detection of early AMD. Research by [39] demonstrated that the transition between early and intermediate AMD represents a critical intervention window, yet this distinction has proven challenging for both human experts and automated systems. Our research suggests that utilizing IBs for diagnosis significantly enhances the ability to distinguish between these crucial early stages, potentially allowing for more timely therapeutic interventions.
Under matched data, splits, and training regimes, the two-stage design consistently exceeds monolithic baselines, indicating that IB selection plus calibrated fuzzy aggregation—not backbone scaling—accounts for the principal gains in both discrimination and reliability. Consequently, deployment guidance should emphasize maintaining the interpretable reasoning layer and periodic calibration checks, rather than increasing encoder capacity, to preserve accuracy and probability alignment under clinical shifts.
Accordingly, a ResNet-18 encoder is sufficient for the IB detector when coupled with the proposed selection and reasoning stack, supporting the system’s accuracy–efficiency trade-off for clinical deployment.
Calibration analysis further showed that post hoc temperature scaling yields a pronounced reduction in miscalibration without degrading discrimination, with the optimal scalar temperature near minimizing both ECE and Brier while leaving accuracy and macro-AUROC effectively unchanged. This aligns with the perspective that temperature scaling adjusts confidence levels without altering decision boundaries. Across a grid of temperatures, the two-stage system retained uniformly lower ECE/Brier than strong end-to-end baselines under identical splits and inputs. This suggests that the combination of calibrated IB confidences and the fuzzy reasoning layer enhances probability reliability beyond what can be achieved through backbone capacity and loss re-weighting alone. From a deployment perspective, these findings highlight the importance of reporting calibrated probabilities and monitoring ECE and Brier scores over time to address potential calibration generalization gaps that may arise due to dataset shifts. Additionally, they indicate the need to explore parameterized or adaptive temperature scaling in future research while maintaining interpretability at the IB level.
The analysis of computational cost (see Table 5) indicates that the efficiency of the system is primarily determined by the ResNet-18 encoder. In contrast, the subsequent temperature scaling and fuzzy reasoning layers contribute very little to the overall computational overhead, accounting for less than 1% of the total latency, while inference on a GPU is quick—allowing the processing of a full OCT volume (128 B-scans) in approximately 0.31 s—the performance on a CPU is significantly slower, taking over 3.2 s. This latency difference exposes a critical limitation: although the system is well-suited for near-real-time clinical use in GPU-accelerated environments, its effectiveness on standard CPU-only workstations may be limited by these processing delays. Additionally, the peak VRAM usage of ~0.7 GB, though modest for the test hardware, could present challenges for deployment on devices with limited memory. Despite these hardware-related constraints, the results demonstrate that the selected architecture strikes an intentional balance. It avoids the computational demands of larger models while maintaining superior diagnostic accuracy through a lightweight yet powerful reasoning stage.
The implementation of the NSGA-II algorithm for multi-objective optimization in IB selection offers a solution to the inherent imbalances found in medical imaging datasets. By optimizing for both statistical performance and clinical significance simultaneously, we have developed an approach that addresses the limitations of purely data-driven methods, which often struggle with rare but clinically important findings. This optimization strategy differs from previous methods that relied exclusively on statistical metrics or predetermined expert selections. For instance, ref. [52] identified hyperreflective inclusions (gv) as significant IBs for AMD progression but lacked a systematic methodology for weighing their statistical versus clinical importance. Similarly, ref. [55] emphasized the importance of subretinal fibrosis (sr) in the late (neovascular) stage of AMD but did not address the challenges of its reliable detection in imbalanced datasets. Our optimization framework provides a more robust foundation for IB selection. Moreover, it can be extended to other medical imaging applications that face comparable challenges, such as data imbalance and the need for clinical relevance.
The incorporation of fuzzy logic for IB analysis represents a significant advancement in addressing the “black box” problem that has hindered clinical adoption of intelligent systems. Recent work by [96] proposed categorizing explanations in healthcare AI based on model reliability, expert variability, and disease dimensionality. Our approach complements this framework by providing explicit visualization of both IB confidence and staging probabilities, allowing clinicians to trace diagnostic reasoning from image features to disease classification. The correlation analysis, which shows strong positive associations between specific IBs and their corresponding AMD stages, supports the clinical validity of our interpretability approach. Moreover, the visualization strategy implemented in the module—combining bar charts for IB confidence with radar charts for staging probabilities—creates an intuitive interface that aligns with clinical reasoning patterns. This transparency may lower the barrier to adoption by ophthalmologists who remain skeptical of opaque intelligence systems. As noted by [97], transparent healthcare systems that illuminate decision processes are more likely to gain clinician trust and integration into clinical workflows.
External validation through leave-one-scanner-out methods across the Optovue Avanti XR and Optopol REVO NX confirms that the proposed two-stage design generalizes beyond the development dataset, while discrimination and accuracy decrease compared to internal testing—often seen during site or scanner domain shifts—the method still retains a statistically significant advantage over strong end-to-end baselines and achieves superior calibration. This finding aligns with TRIPOD+AI’s guidance, which emphasizes the importance of evaluating models under distributional shifts, such as cross-center or cross-device scenarios, to determine their clinical transportability. Systematic reviews have also reported frequent performance drops when models are applied to external datasets, while multi-center external validation remains the gold standard and is planned for future studies, the current cross-device experiment serves as a conservative robustness check. This approach is consistent with the literature on domain shifts and recent OCT studies that have conducted cross-instrument evaluations for AMD staging.
Despite the promising results, several limitations need to be addressed. First, although our dataset of 2624 OCT images is substantial, the low prevalence of certain stages of AMD, particularly early AMD at just 8% of the dataset, presents a challenge. The effectiveness of our approach on even rarer cases or edge presentations requires further validation.
Second, the expert-defined fuzzy rules, although intended to mirror clinical reasoning, inherently contain some degree of subjectivity. The discrepancies between the statistical findings in our dataset and the expert clinical assessments underscore the ongoing challenge of integrating data-driven and expert-based knowledge within medical intelligence systems.
In addition, the temperature scaling method used to calibrate the DNN output was chosen based on empirical evidence rather than rigorous theoretical justification. Although effective in our implementation, the potential application of this calibration method in other datasets or clinical settings warrants further investigation.
Across compact backbones trained with identical CB-CE+focal regimes and calibrated with the same scalar T, capacity scaling from ResNet-18 to ResNet-34/ConvNeXt-Tiny/DeiT-Tiny yields only incremental discrimination gains with overlapping CIs. However, the two-stage reasoning approach provides a significant improvement in both macro-AUROC and reliability metrics. When we examine the per-stage AUROC, there is no consistent advantage of ViT over modern ConvNets at this dataset scale. Among the monolithic models evaluated, ConvNeXt-Tiny shows the best performance, but it still lags behind the two-stage system, particularly in clinically important N/SI/VI stages. Given the encoder latency/compute profile (∼2 GFLOPs; ∼2.4 ms per B-scan on GPU) and superior calibration following fuzzy reasoning, ResNet-18 is a justified choice for the IB detector. It offers efficiency and robustness despite class imbalances, with performance improvements primarily attributed to IB selection and calibrated fuzzy aggregation, rather than the use of heavier backbone models.
In addition to verifying the effectiveness of the developed CDSS model in clinical settings, this study aims to enhance the detection of IBs through quantitative measurements, such as druse volume and fluid size. This approach goes beyond merely determining the presence or absence of IBs and can significantly improve diagnostic accuracy and predictive capabilities. Additionally, we plan to enhance the two-stage architecture of the CDSS by integrating components related to treatment and monitoring recommendations. This will enable the creation of a comprehensive system that addresses the entire treatment cycle and aligns with the latest research on personalized therapy for AMD based on specific IBs.
In conclusion, while our system shows impressive effectiveness when working with retrospective data, a comprehensive evaluation of its practical significance and integration into the daily practice of ophthalmologists necessitates conducting a prospective study in real clinical settings. This will be a focus of future research.
6. Conclusions
In this paper, we proposed a novel approach for developing a CDSS module that models the cognitive processes of experts in staging AMD using OCT images. Our approach features a two-stage architecture that separates IB detection from diagnostic reasoning. First, we identify IBs using a DNN. Next, we analyze these IBs using fuzzy logic, which incorporates rules defined by experts. This separation of the diagnostic process enhances both accuracy and interpretability, effectively addressing the critical “black box” problem.
The results demonstrate substantial and robust improvements in diagnostic accuracy across AMD stages, with particularly pronounced gains for early disease, consistent with the two-stage design’s interpretability and class-imbalance handling.
Similarly, the identification of normal cases improved from 48% to 95.1%, effectively reducing the risk of false positive diagnoses that could lead to unnecessary interventions.
The visualization strategy implemented in the module—combining bar charts for IB confidence with radar charts for staging probabilities—creates an intuitive interface that illuminates the decision-making process for clinicians. This transparency represents a significant advancement in addressing the interpretability challenge that has hindered clinical adoption of AI systems, allowing ophthalmologists to critically evaluate algorithmic recommendations within established diagnostic frameworks.
Despite these achievements, we observed minor decreases in performance for specific late stages, notably late neovascular AMD (from 96.7% to 88.3%) and late fibrosis AMD (from 93.1% to 89.7%), while late atrophic AMD improved from 53.0% to 86.7%, which together delineate the remaining overlap among advanced subtypes that warrants refinement. These slight regressions suggest targeted rule-level and IB-weight adjustments to better separate exudative cases with incipient scarring from fibrotic patterns. Future work should focus on prospective validation in clinical settings, expansion to include quantitative IB measurements, and integration with other imaging modalities to provide a more comprehensive assessment of retinal pathology.
The system achieves its state-of-the-art accuracy and interpretability with minimal computational overhead from its reasoning layers, confirming the efficiency of the two-stage design. However, the overall performance remains fundamentally dependent on the IB encoder, making the system ideal for GPU-equipped workstations but potentially limited by latency on CPU-only hardware—a key consideration for future deployment and optimization efforts.
Importantly, post hoc calibration via temperature scaling (optimal in our setting) consistently improved reliability metrics (ECE, Brier) without sacrificing discrimination. This reinforces the clinical suitability of our interpretable two-stage design, which combines IB detection with fuzzy reasoning. From an operational perspective, the calibrated temperature should be fitted on validation data and periodically revalidated after deployment to prevent calibration drift due to domain shifts. This is particularly important given the reported generalization gaps in calibration under distributional changes. Future work will explore domain-robust or parameterized calibration techniques to further stabilize probability estimates while preserving the explanatory benefits of the IB-centric reasoning layer.
In conclusion, our CDSS module represents a significant advancement in both technical performance and clinical applicability. By integrating the pattern-recognition capabilities of deep learning with the interpretability of fuzzy logic and expert rules, we created a system that not only achieves high diagnostic accuracy but also offers transparent reasoning that aligns with clinical decision-making processes. This approach effectively addresses a key challenge in the clinical adoption of artificial intelligence in ophthalmology.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app151810197/s1, Figure S1: Error Matrix for Direct Classification of AMD Stages; Figure S2: Pareto Front of IBs Selection; Figure S3: IBs Selections Across Representative Solutions; Figure S4: Correlation Between Biomarker Confidence and AMD Stage Probabilities; Figure S5: Sensitivity Analysis for Each Individual IB; Figure S6: Error Matrix for Classifying AMD Stages Using DNN + Expert System Based on Fuzzy Rules; Figure S7: Reliability diagrams across 10 probability bins for Strong ResNet-18, ResNet-34, ConvNeXt- Tiny, DeiT-Tiny (all CB+focal+T) and the two-stage system; identity line shown as dashed; Figure S8: Cumulative “top-k IBs” curve (Accuracy and macro-AUROC) with inclusion order and saturation behavior; Table S1: Code Designation and Percentage of IBs in Various Stages of AMD; Table S2: Probabilities of Detecting IBs at Various Stages of AMD Based on Expert Assessments; Table S3: Performance Metrics for Biomarker Classifiers; Table S4: Sensitivity of the fuzzy membership to midpoint m, steepness , and ‘Defining feature’ weight under identical protocol; Table S5: Leave-one-biomarker-out stage-wise AUROC.
Author Contributions
Conceptualization, E.A.L.; methodology, E.A.L. and E.S.Y.; software, E.A.L. and E.S.Y.; validation, R.R.I. and G.M.I.; formal analysis, G.M.I.; investigation, E.A.L., E.S.Y., R.R.I. and G.M.I.; resources, T.R.M., R.R.I. and G.M.I.; data curation, R.R.I. and G.M.I.; writing—original draft preparation, E.A.L.; writing—review and editing, E.A.L., E.P.G. and R.V.K.; visualization, E.A.L. and E.S.Y.; supervision, E.P.G. and G.M.I.; project administration, T.R.M. and R.V.K.; funding acquisition, E.P.G. and R.V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation within the state assignment for UUST (agreement No. 075-03-2024-123/1 dated 15 February 2024) and conducted in the research laboratory “Sensor systems based on integrated photonics devices” of the Eurasian Scientific and Educational Center.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to the sharing policy limitations of Optimed Laser Vision Restoration Center (Ufa, Russia).
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Madi, H.A.; Keller, J. Increasing frequency of hospital admissions for retinal detachment and vitreo-retinal surgery in England 2000–2018. Eye 2020, 34, 1584–1590. [Google Scholar] [CrossRef]
- Stålhammar, G.; Lardner, E.; Georgsson, M.; Seregard, S. Increasing demand for ophthalmic pathology: Time trends in a laboratory with nationwide coverage. BMC Ophthalmol. 2023, 23, 88. [Google Scholar] [CrossRef]
- Shah, V. To study the morbidity pattern of patients attending the ophthalmology OPD of tertiary eye care centre with reference to age. Open Access J. Ophthalmol. 2023, 8, 1–5. [Google Scholar] [CrossRef]
- Aznabaev, B.M.; Mukhamadeev, T.R.; Dibaev, T.I. Optical Coherence Tomography + Angiography in the Diagnosis, Therapy and Surgery of Eye Diseases; August Borg: Moscow, Russia, 2019. [Google Scholar]
- Hu, Y.; Gao, Y.; Gao, W.; Luo, W.; Yang, Z.; Xiong, F.; Chen, Z.; Lin, Y.; Xia, X.; Yin, X.; et al. AMD-SD: An optical coherence tomography image dataset for wet AMD lesions segmentation. Sci. Data 2024, 11, 1014. [Google Scholar] [CrossRef] [PubMed]
- Lopukhova, E.A.; Ibragimova, R.R.; Idrisova, G.M.; Lakman, I.A.; Mukhamadeev, T.R.; Grakhova, E.P.; Bilyalov, A.R.; Kutluyarov, R.V. Machine learning algorithms for the analysis of age-related macular degeneration based on optical coherence tomography: A systematic review. J. Biomed. Photonics Eng. 2023, 9, 020202. [Google Scholar] [CrossRef]
- Victor, A.A. The role of imaging in age-related macular degeneration. Retin. Physician 2019, 16, 38–42. [Google Scholar]
- Chen, J.Y.; Vedantham, S.; Lexa, F.J. Burnout and work-work imbalance in radiology—Wicked problems on a global scale: A baseline pre-COVID-19 survey of US neuroradiologists compared to international radiologists and adjacent staff. Eur. J. Radiol. 2022, 155, 110153. [Google Scholar] [CrossRef]
- Duncan, J.R. Information overload: When less is more in medical imaging. Diagnosis 2017, 4, 179–183. [Google Scholar] [CrossRef]
- Ergün Sahin, B.U.; Güneş, E.D.; Kocabıyıkoğlu, A.; Keskin, A. How does workload affect test ordering behavior of physicians? An empirical investigation. Prod. Oper. Manag. 2022, 31, 2664–2680. [Google Scholar] [CrossRef]
- Winder, M.; Owczarek, A.J.; Chudek, J.; Pilch-Kowalczyk, J.; Baron, J. Are we overdoing it? Changes in diagnostic imaging workload during the years 2010–2020 including the impact of the SARS-CoV-2 pandemic. Healthcare 2021, 9, 1557. [Google Scholar] [CrossRef] [PubMed]
- Jain, B.I. Enhancing diagnostic: Machine learning in medical image analysis. Int. J. Sci. Res. Eng. Manag. 2024, 8, 1–5. [Google Scholar]
- Li, J. Reliability and efficiency of human-automation interaction in automated decision support systems. Highlights Sci. Eng. Technol. 2024, 106, 431–435. [Google Scholar] [CrossRef]
- Lukmanov, I.; Agaev, V.; Tsypkin, D. Automation in healthcare: Advantages, prospects, perceptual barriers. City Healthc. 2024, 5, 181–188. [Google Scholar] [CrossRef]
- Amaral, A.C.K.; Cuthbertson, B.H. The efficiency of computerised clinical decision support systems. Lancet 2024, 403, 410–411. [Google Scholar] [CrossRef]
- Belov, K.S.; Kharitonov, A.S.; Chernova, S.V. At the Crossroads of Technology and Medicine: Prospects of automation in medical practice with the use of neural networks. Infokommunikacionnye Tehnol. 2023, 21, 89–93. [Google Scholar] [CrossRef]
- Przystalski, K.; Thanki, R.M. Computer vision for medical data analysis. In Explainable Machine Learning in Medicine; Springer: Cham, Switzerland, 2024; pp. 53–66. [Google Scholar]
- Sheelavathi, A.; Shanmugapriya, P.; Sangeethapriya, J.; Muthukarupaee, K. A roadmap to smart healthcare automation sensors and technologies. In Futuristic Trends in IOT; Volume 2, Book 15, Part 1; Iterative International Publishers: Chikmagalur, Karnataka, India, 2022; pp. 43–51. ISBN 978-93-5747-350-7. [Google Scholar]
- Sindhu, P.; Sivakumar, M. Healthcare integrating automation and robotics-based industry 5.0 advancement. In Advances in Medical Technologies and Clinical Practice; IGI Global: Hershey, PA, USA, 2024; pp. 254–264. [Google Scholar]
- Umare Thool, K.B.; Wankhede, P.A.; Yella, V.R.; Tamijeselvan, S.; Suganthi, D.; Rastogi, R. Artificial intelligence in medical imaging data analytics using CT images. In Proceedings of the 2023 4th International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 6–8 July 2023; pp. 1–6. [Google Scholar]
- Hayat, M.; Aramvith, S.; Bhattacharjee, S.; Ahmad, N. Attention GhostUNet++: Enhanced segmentation of adipose tissue and liver in CT images. Med. Image Anal. 2025, 89, 102913. [Google Scholar]
- Sarvakar, K.; Yadav, R.; Patel, A.; Patel, C.D.; Rana, K.; Borisagar, V. Advanced analytics and machine learning algorithms for healthcare decision support systems: A study. In Advances in Healthcare Information Systems and Administration; IGI Global: Hershey, PA, USA, 2024; pp. 16–50. [Google Scholar]
- Chaddad, A.; Peng, J.; Xu, J.; Bouridane, A. Survey of explainable AI techniques in healthcare. Sensors 2023, 23, 634. [Google Scholar] [CrossRef]
- Badhoutiya, A.; Verma, R.P.; Shrivastava, A.; Laxminarayanamma, K.; Rao, A.L.N.; Khan, A.K. Random Forest Classification in Healthcare Decision Support for Disease Diagnosis. In Proceedings of the 2023 International Conference on Artificial Intelligence for Innovations in Healthcare Industries (ICAIIHI), Raipur, India, 29–30 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Choi, H.; Abdirayimov, S. Demonstrating the power of SHAP values in AI-driven classification of Marvel characters. J. Multimed. Inf. Syst. 2024, 11, 167–172. [Google Scholar] [CrossRef]
- Daram, S. Explainable AI in healthcare: Enhancing trust, transparency, and ethical compliance in medical AI systems. AI Ethics 2025, 5, 1–20. [Google Scholar]
- Chauvie, S.; Mazzoni, L.N. A review on the use of imaging biomarkers in oncology clinical trials: Quality assurance strategies for technical validation. Tomography 2023, 9, 1876–1902. [Google Scholar] [CrossRef] [PubMed]
- Chiu, F.; Yen, Y. Imaging biomarkers for clinical applications in neuro-oncology: Current status and future perspectives. Biomark. Res. 2023, 11, 35. [Google Scholar] [CrossRef]
- Cho, W.C.; Zhou, F.; Li, J.; Hua, L.; Liu, F. Editorial: Biomarker detection algorithms and tools for medical imaging or omics data. Front. Genet. 2022, 13, 919390. [Google Scholar] [CrossRef]
- Pai, S.; Bontempi, D.; Hadzic, I.; Prudente, V.; Sokač, M.; Chaunzwa, T.L.; Bernatz, S.; Hosny, A.; Mak, R.H.; Birkbak, N.J.; et al. Foundation model for cancer imaging biomarkers. Nat. Mach. Intell. 2024, 6, 354–367. [Google Scholar] [CrossRef]
- Deshmukh, A. Artificial intelligence in medical imaging: Applications of deep learning for disease detection and diagnosis. Univers. Res. Rep. 2024, 11, 31–36. [Google Scholar] [CrossRef]
- Ltifi, H.; Benmohamed, E.; Kolski, C.; Ben Ayed, M. Adapted visual analytics process for intelligent decision-making: Application in a medical context. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 241–282. [Google Scholar] [CrossRef]
- Myrou, A.; Barmpagiannos, K.; Ioakimidou, A.; Savopoulos, C. Molecular biomarkers in neurological diseases: Advances in diagnosis and prognosis. Int. J. Mol. Sci. 2025, 26, 2231. [Google Scholar] [CrossRef]
- Rasouli, S.; Alkurdi, D.; Jia, B. The role of artificial intelligence in modern medical education and practice: A systematic literature review. BMC Med. Educ. 2024, 24, 456. [Google Scholar]
- Reeja, S.R.; Kavitha, G. Biomarkers classification for various diseases using machine learning approaches: A review. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 123–135. [Google Scholar]
- Trueblood, J.S.; Holmes, W.R.; Seegmiller, A.C.; Douds, J.; Compton, M.; Szentirmai, E.; Woodruff, M.; Huang, W.; Stratton, C.; Eichbaum, Q. The impact of speed and bias on the cognitive processes of experts and novices in medical image decision-making. Cogn. Res. Princ. Implic. 2018, 3, 28. [Google Scholar] [CrossRef]
- Stahl, A. The diagnosis and treatment of age-related macular degeneration. Dtsch. Ärzteblatt Int. 2020, 117, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.Y.; Lanzetta, P.; Bandello, F.; Eldem, B.; Navarro, R.; Lövestam-Adrian, M.; Loewenstein, A. Current concepts and modalities for monitoring the fellow eye in neovascular age-related macular degeneration: An expert panel consensus. Retina 2020, 40, 599–611. [Google Scholar] [CrossRef]
- Ferris, F.L.; Wilkinson, C.; Bird, A.; Chakravarthy, U.; Chew, E.; Csaky, K.; Sadda, S.R. Clinical classification of age-related macular degeneration. Ophthalmology 2013, 120, 844–851. [Google Scholar] [CrossRef]
- Rudnicka, A.R.; Kapetanakis, V.V.; Jarrar, Z.; Wathern, A.K.; Wormald, R.; Fletcher, A.E.; Cook, D.G.; Owen, C.G. Incidence of late-stage age-related macular degeneration in American whites: Systematic review and meta-analysis. Am. J. Ophthalmol. 2015, 160, 85–93. [Google Scholar] [CrossRef]
- Handa, J.T.; Bowes Rickman, C.; Dick, A.D.; Gorin, M.B.; Miller, J.W.; Toth, C.A.; Ueffing, M.; Zarbin, M.; Farrer, L.A. A systems biology approach towards understanding and treating non-neovascular age-related macular degeneration. Nat. Commun. 2019, 10, 3347. [Google Scholar] [CrossRef]
- Lopukhova, E.A.; Yusupov, E.S.; Ibragimova, R.R.; Idrisova, G.M.; Mukhamadeev, T.R.; Grakhova, E.P.; Kutluyarov, R.V. Hybrid intelligent staging of age-related macular degeneration for decision-making on patient management tactics. Biomed. Signal Process. Control 2025, 87, 105456. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning—PMLR, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1321–1330. [Google Scholar]
- Bahani, K.; Moujabbir, M.; Ramdani, M. An accurate fuzzy rule-based classification systems for heart disease diagnosis. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 491–498. [Google Scholar] [CrossRef]
- Sirocchi, C.; Bogliolo, A.; Montagna, S. Medical-informed machine learning: Integrating prior knowledge into medical decision systems. BMC Med. Inform. Decis. Mak. 2024, 24 (Suppl. S4), 186. [Google Scholar] [CrossRef]
- Liang, S.; Li, Y.; Srikant, R. Enhancing the reliability of out-of-distribution image detection in neural networks. arXiv 2017, arXiv:1706.02690. [Google Scholar]
- Age-Related Eye Disease Study Research Group. A randomized, placebo-controlled, clinical trial of high-dose supplementation with vitamins C and E, beta carotene, and zinc for age-related macular degeneration and vision loss: AREDS report no. 8. Arch. Ophthalmol. 2001, 119, 1417–1436. [Google Scholar] [CrossRef]
- Lad, E.M.; Finger, R.P.; Guymer, R. Biomarkers for the progression of intermediate age-related macular degeneration. Ophthalmol. Ther. 2023, 12, 2917–2941. [Google Scholar] [CrossRef]
- Vallino, V.; Berni, A.; Coletto, A.; Serafino, S.; Bandello, F.; Reibaldi, M.; Borrelli, E. Structural OCT and OCT angiography biomarkers associated with the development and progression of geographic atrophy in AMD. Surv. Ophthalmol. 2024, 69, 405–420. [Google Scholar] [CrossRef]
- Garcia-Layana, A.; Cabrera-López, F.; García-Arumí, J.; Arias-Barquet, L.; Ruiz-Moreno, J.M. Early and intermediate age-related macular degeneration: Update and clinical review. Clin. Interv. Aging 2017, 12, 1579–1587. [Google Scholar] [CrossRef]
- Waldstein, S.M.; Vogl, W.; Bogunovic, H.; Sadeghipour, A.; Riedl, S.; Schmidt-Erfurth, U. Characterization of drusen and hyperreflective foci as biomarkers for disease progression in age-related macular degeneration using artificial intelligence in optical coherence tomography. JAMA Ophthalmol. 2020, 138, 740–747. [Google Scholar] [CrossRef]
- Romano, F.; Ding, X.; Yuan, M.; Vingopoulos, F.; Garg, I.; Choi, H.; Alvarez, R.; Tracy, J.H.; Finn, M.; Razavi, P.; et al. Progressive choriocapillaris changes on optical coherence tomography angiography correlate with stage progression in AMD. Ophthalmol. Retin. 2024, 8, 654–663. [Google Scholar] [CrossRef] [PubMed]
- Asani, B.; Holmberg, O.; Schiefelbein, J.B.; Hafner, M.; Herold, T.; Spitzer, H.; Siedlecki, J.; Kern, C.; Kortuem, K.U.; Frishberg, A.; et al. Evaluation of OCT biomarker changes in treatment-naive neovascular AMD using a deep semantic segmentation algorithm. Sci. Rep. 2024, 14, 8140. [Google Scholar] [CrossRef] [PubMed]
- Tenbrock, L.; Wolf, J.; Boneva, S.; Schlecht, A.; Agostini, H.; Wieghofer, P.; Schlunck, G.; Lange, C. Subretinal fibrosis in neovascular age-related macular degeneration: Current concepts, therapeutic avenues, and future perspectives. Cell Tissue Res. 2022, 387, 361–375. [Google Scholar] [CrossRef] [PubMed]
- Bird, A.C.; Phillips, R.L.; Hageman, G.S. Geographic atrophy: A histopathological assessment. JAMA Ophthalmol. 2014, 132, 338–345. [Google Scholar] [CrossRef]
- Fang, V.; Gomez-Caraballo, M.; Lad, E.M. Biomarkers for nonexudative age-related macular degeneration and relevance for clinical trials: A systematic review. Mol. Diagn. Ther. 2021, 25, 691–713. [Google Scholar] [CrossRef]
- Flores, R.; Carneiro, Â.; Tenreiro, S.; Seabra, M.C. Retinal progression biomarkers of early and intermediate age-related macular degeneration. Life 2021, 12, 36. [Google Scholar] [CrossRef]
- Gill, K.; Yoo, H.; Chakravarthy, H.; Granville, D.J.; Matsubara, J.A. Exploring the role of granzyme B in subretinal fibrosis of age-related macular degeneration. Investig. Ophthalmol. Vis. Sci. 2024, 65, 12. [Google Scholar] [CrossRef] [PubMed]
- Latifi-Navid, H.; Barzegar Behrooz, A.; Jamehdor, S.; Davari, M.; Latifinavid, M.; Zolfaghari, N.; Piroozmand, S.; Taghizadeh, S.; Bourbour, M.; Shemshaki, G.; et al. Construction of an exudative age-related macular degeneration diagnostic and therapeutic molecular network using multi-layer network analysis, a fuzzy logic model, and deep learning techniques: Are retinal and brain neurodegenerative disorders related? Pharmaceuticals 2023, 16, 1555. [Google Scholar] [CrossRef]
- Saha, S.; Nassisi, M.; Wang, M.; Lindenberg, S.; Kanagasingam, Y.; Sadda, S.; Hu, Z.J. Automated detection and classification of early AMD biomarkers using deep learning. Sci. Rep. 2019, 9, 10990. [Google Scholar] [CrossRef]
- Sharma, A.; Parachuri, N.; Kumar, N.; Bandello, F.; Kuppermann, B.D.; Loewenstein, A.; Regillo, C.; Chakravarthy, U. Fluid-based prognostication in n-AMD: Type 3 macular neovascularisation needs an analysis in isolation. Eye 2021, 35, 2370–2379. [Google Scholar] [CrossRef]
- Vinković, M.; Kopić, A.; Benašić, T. Anti-VEGF treatment and optical coherence tomography biomarkers in wet age-related macular degeneration. Acta Clin. Croat. 2022, 61, 285–292. [Google Scholar]
- Miladinović, A.; Biscontin, A.; Ajčević, M.S.; Kresevic, S.; Accardo, A.; Marangoni, D.; Tognetto, D.; Inferrera, L. Evaluating deep learning models for classifying OCT images with limited data and noisy labels. Sci. Rep. 2024, 14, 30321. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Zhuo, R.; Liu, X.; Wu, B.; Wang, J. Enhancing surgical decision-making in NEC with ResNet18: A deep learning approach to predict the need for surgery through X-ray image analysis. Front. Pediatr. 2024, 12, 1405780. [Google Scholar] [CrossRef] [PubMed]
- Ayyachamy, S.; Alex, V.; Khened, M.; Krishnamurthi, G. Medical image retrieval using Resnet-18 for clinical diagnosis. In Proceedings of the Medical Imaging 2019: Imaging Informatics for Healthcare, Research, and Applications, San Diego, CA, USA, 16–21 February 2019; Chen, P.-H., Bak, P.R., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 10954, p. 1095410. [Google Scholar] [CrossRef]
- Rahman Siddiquee, M.M.; Shah, J.; Chong, C.; Nikolova, S.; Dumkrieger, G.; Li, B.; Wu, T.; Schwedt, T.J. Headache classification and automatic biomarker extraction from structural MRIs using deep learning. Brain Commun. 2022, 5, fcac311. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, M.; Lin, T.; Song, Y.; Belongie, S. Class-balanced loss based on effective number of samples. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9268–9277. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Bradshaw, T.J.; Huemann, Z.; Hu, J.; Rahmim, A. A guide to cross-validation for artificial intelligence in medical imaging. Radiol. Artif. Intell. 2023, 5, e220232. [Google Scholar] [CrossRef]
- Guan, H.; Liu, M. Domain adaptation for medical image analysis: A survey. IEEE Trans. Biomed. Eng. 2022, 69, 1173–1185. [Google Scholar] [CrossRef]
- Collins, G.S.; Moons, K.G.M.; Dhiman, P.; Riley, R.D.; Beam, A.L.; Van Calster, B.; Ghassemi, M.; Liu, X.; Reitsma, J.B.; van Smeden, M.; et al. TRIPOD+AI statement: Updated guidance for reporting clinical prediction models that use regression or machine learning methods. BMJ 2024, 385, e078378. [Google Scholar] [CrossRef]
- Yu, A.C.; Mohajer, B.; Eng, J. External validation of deep learning algorithms for radiologic diagnosis: A systematic review. Radiol. Artif. Intell. 2022, 4, e210064. [Google Scholar] [CrossRef]
- Imran, H.M.; Asad, M.A.A.; Abdullah, T.A.; Chowdhury, S.I.; Alamin, M. Few shot learning for medical imaging: A review of categorized images. IEEE Access 2023, 11, 75055–75090. [Google Scholar]
- Malhotra, A. Single-shot image recognition using siamese neural networks. In Proceedings of the 2023 3rd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 12–13 May 2023; pp. 2156–2160. [Google Scholar]
- Xian, Y.; Lampert, C.; Schiele, B.; Akata, Z. Zero-shot learning—A comprehensive evaluation of the good, the bad and the ugly. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 41, 2251–2265. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, H.; Liu, K.; Chen, Y.; Ye, C.; Niu, C.; Jin, S.; Li, Y.; Gao, H.; Hu, J.; et al. Deep learning for retina structural biomarker classification using OCT images. Biomed. Opt. Express 2024, 15, 2190–2205. [Google Scholar]
- Lu, C.; Wang, X.; Yang, A.; Liu, Y.; Dong, Z. A few-shot-based model-agnostic meta-learning for intrusion detection in security of Internet of Things. Comput. Netw. 2023, 228, 109724. [Google Scholar] [CrossRef]
- Wang, H.; Tong, X.; Wang, P.; Xu, Z.; Song, L. Few-shot transfer learning method based on meta-learning and graph convolution network for machinery fault diagnosis. IEEE Trans. Ind. Inform. 2023, 19, 6073–6083. [Google Scholar] [CrossRef]
- Zhao, Z.; Ding, H.; Cai, D.; Yan, Y. Gated multi-scale attention transformer for few-shot medical image segmentation. Med. Image Anal. 2024, 93, 103084. [Google Scholar]
- Tang, S.; Yan, S.; Qi, X.; Gao, J.; Ye, M.; Zhang, J.; Zhu, X. Few-shot medical image segmentation with high-fidelity prototypes. Med. Image Anal. 2025, 89, 102897. [Google Scholar] [CrossRef]
- Wang, J.; Wang, T.; Xu, J.; Zhang, Z.; Wang, H.; Li, H. Zero-shot diagnosis of unseen pulmonary diseases via spatial domain adaptive correction and guidance by ChatGPT-4o. Med. Image Anal. 2024, 95, 103189. [Google Scholar]
- Flanagan, A.R.; Glavin, F.G. A systematic review of multi-class and one-vs-rest classification techniques for near-infrared spectra of crop cultivars. Comput. Electron. Agric. 2023, 210, 107900. [Google Scholar]
- Hong, J.; Cho, S. A probabilistic multi-class strategy of one-vs.-rest support vector machines for cancer classification. Neurocomputing 2008, 71, 3275–3281. [Google Scholar] [CrossRef]
- Jang, J.; Kim, C. One-vs-rest network-based deep probability model for open set recognition. IEEE Access 2020, 8, 113493–113506. [Google Scholar]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef] [PubMed]
- Shreffler, J.; Huecker, M.R. Diagnostic testing accuracy: Sensitivity, specificity, predictive values and likelihood ratios. In StatPearls; StatPearls Publishing: Tampa, FL, USA, 2025. [Google Scholar]
- Nebro, A.J.; Galeano-Brajones, J.; Luna, F.; Coello Coello, C.A. Is NSGA-II ready for large-scale multi-objective optimization? Math. Comput. Appl. 2022, 27, 103. [Google Scholar] [CrossRef]
- Glascoe, F.P. Screening for developmental and behavioral problems. Ment. Retard. Dev. Disabil. Res. Rev. 2005, 11, 173–179. [Google Scholar] [CrossRef]
- Vanderheyden, A.M. Technical adequacy of response to intervention decisions. Except. Child. 2011, 77, 335–350. [Google Scholar] [CrossRef]
- McDowall, L.M.; Dampney, R.A.L. Calculation of threshold and saturation points of sigmoidal baroreflex function curves. Am. J. Physiol.-Heart Circ. Physiol. 2006, 291, H2003–H2007. [Google Scholar] [CrossRef]
- Leão, W. Attended temperature scaling: A practical approach for calibrating deep neural networks. arXiv 2018, arXiv:1810.11586. [Google Scholar]
- Mukhoti, J.; Kulharia, V.; Sanyal, A.; Golodetz, S.; Torr, P.H.S.; Dokania, P.K. Calibrating deep neural networks using focal loss. arXiv 2020, arXiv:2002.09437. [Google Scholar] [CrossRef]
- Dabah, L.; Tirer, T. On temperature scaling and conformal prediction of deep classifiers. Neural Netw. 2025, 163, 1–15. [Google Scholar]
- Mamalakis, M.; de Vareilles, H.E.I.; Murray, G.; Lio, P.; Suckling, J. The explanation necessity for healthcare AI. Nat. Mach. Intell. 2024, 6, 410–420. [Google Scholar]
- Metta, C.; Beretta, A.; Pellungrini, R.; Rinzivillo, S.; Giannotti, F. Towards transparent healthcare: Advancing local explanation methods in explainable artificial intelligence. Bioengineering 2024, 11, 369. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).