Abstract
This study uses a U-shaped aqueduct structure in a specific irrigation area as the research object to examine the damage patterns of large-span elevated U-shaped aqueduct structures under seismic action. A single-span aqueduct model that integrates fluid–structure interaction is created with the finite element program ANSYS. The incremental dynamic analysis approach is utilized to perform nonlinear dynamic time–history assessments for three types of bearings—plate rubber bearings, pot rubber bearings and lead-core rubber bearings—under conditions of an empty condition, a half-full condition and a design water level. Seismic fragility curves for the bearings and piers subjected to transverse seismic stress are developed using capacity–demand ratio models and specified damage limit states. The findings demonstrate that the likelihood of aqueduct components being damaged increases substantially as seismic intensity increases, with bearings failing before piers. Under the conditions of empty, half-full and design water levels, the structural mass increases as a result of higher water levels. This alters the dynamic response characteristics and increases the likelihood of failure in a variety of damage states. The probability of plate rubber bearings experiencing minor damage exceedance increases from 11.75% to 61.6% as the water level rises from vacant to design conditions. Lead-core rubber bearings provide better seismic isolation than plate rubber bearings and pot rubber bearings. This greatly lowers the aqueduct structure’s displacement response and damage likelihood. Under design water level circumstances, the chance of mild damage to lead rubber bearings is 8.64%, at a peak ground acceleration of 0.4 g. The damage probabilities for the pot rubber bearings and the plate rubber bearings are 80.68% and 97.45%, respectively. The research findings establish a theoretical foundation for the seismic design and damage evaluation of aqueduct structures in places with high seismic activity, ensuring the stable operation of water transfer projects and sustainable water resource utilization, presenting considerable technical applicability.
1. Introduction
The irregular geographical and temporal allocation of water resources is a significant factor contributing to water shortage in dry parts of China. Many inter-basin water transfer projects have been set up across the country to help with the problems that come with not having enough water and to encourage long-term growth in these areas [1]. Among them, aqueducts play an important part as crucial hydraulic structures within such projects. They perform numerous purposes, including water diversion, conveyance and distribution, which helps to ensure that water transfer systems continue to work in a steady manner [2]. However, numerous critical water transfer projects are required to traverse high-seismic-intensity regions, which present obstacles due to intricate geological conditions [3]. Aqueducts have inadequate seismic performance during intense earthquakes due to structural attributes, such as a high center of gravity and unequal stiffness distribution, rendering them susceptible to damage and resulting in complex and expensive post-earthquake repairs. Consequently, examining the seismic performance of aqueduct constructions has considerable theoretical and practical significance [4,5,6]. Although these studies provide the theoretical groundwork for aqueducts to safely operate, they often overlook many failure dangers that might occur under complex earthquake situations [7]. Seismic fragility theory assesses the risk of structural collapse using probabilistic approaches by measuring the probability that a structure would attain or surpass a defined damage state at varying levels of seismic [8,9,10]. The performance of seismic fragility analysis on aqueduct structures provides essential theoretical foundations for the improvement of their seismic design and the development of effective post-earthquake repair strategies. The safety and resilience of water transfer projects in regions with significant seismic activity are, therefore, improved as a result of this.
Seismic fragility analysis, which is a fundamental component of performance-based earthquake engineering, has been used widely for hydraulic structures due to the fact that it efficiently estimates the possibility of structural damage at various degrees of seismic intensity [11,12,13]. At present, comprehensive studies about the seismic fragility of aqueduct structures have been conducted. Certain academics [14,15] used the OpenSees platform to create finite element model of a double-trough aqueduct body by amalgamating a fiber beam–column element model with a stochastic concrete damage constitutive relationship. A probabilistic analysis of the dynamic response of the structure under composite random excitations was conducted in accordance with the probability density evolution theory. The research revealed that the response probability distribution of the structure displays considerable random fluctuations, characterized by a high coefficient of variation, resulting in a marked reduction in reliability indices and an escalation in failure risk. In order to address the complexity of seismic occurrences, Du et al. [16] investigated the impact that mainshock–aftershock sequences have on the seismic fragility of bent-frame aqueduct constructions. According to the results, the mainshock significantly increased the probability of structural collapse, and the subsequent aftershocks further worsened damage to the aqueduct piers, which resulted in a reduction in the seismic performance of the piers. Additionally, acknowledging the geographical diversity of ground movements, Zhang et al. [17] evaluated the seismic fragility of large-span aqueduct structures subjected to near-fault (NFP) and far-field (FF) ground motions. The investigation demonstrated that NFP ground movements, distinguished by substantial velocity pulses and extended-period components, markedly elevated bearing displacements and pier-top drifts, leading to a structural damage risk exceeding 30% compared to FF motions. In order to achieve a higher degree of accuracy in seismic fragility analysis, Zhang [18] constructed system fragility curves and included the Copula function into the fragility assessment of aqueduct structures in order to obtain a better degree of accuracy in seismic fragility analysis. This was conducted in order to improve the accuracy of seismic fragility analysis. In compared to the first-order boundary approach, this Copula-based methodology offers more accurate forecasts of the likelihood of failure and represents a significant improvement in the modeling of system fragility curves. Furthermore, Ma et al. [19] optimized the traditional Probabilistic Capacity Method (PCM) by introducing correction parameters to more accurately account for the correlation among aqueduct structural components. Compared with the conventional second-order boundary method, the proposed G-PCM method is capable of directly providing precise estimates of system failure probability, rather than relying on interval-based approximations. Nonetheless, current research on the fragility of aqueducts predominantly points out bent-type constructions, with scant investigation into the seismic fragility of large-span elevated U-shaped aqueducts [20,21,22]. Additionally, the majority of research focusses on the likelihood of damage to aqueduct piers during seismic activity, with sparse attention given to the influence of water level fluctuations on the likelihood of bearings failure in various earthquake scenarios.
This study investigates a large-span elevated U-shaped aqueduct that is located inside an irrigation area. With the help of ANSYS software (https://www.ansys.com/, accessed on 4 August 2025), a finite element model of a single-span aqueduct was built. This model included the interaction between the fluid and the structure. Employing the incremental dynamic analysis approach, a nonlinear dynamic time–history analysis was performed on aqueduct structures with plate rubber bearings, pot rubber bearings and lead-core rubber bearings to develop seismic fragility curves for various bearing types. A comparative analysis of the failure probability of various bearings and thin-walled hollow piers under varying water level circumstances was conducted, offering a theoretical foundation for the seismic risk assessment and design of large-span elevated U-shaped aqueduct structures, promoting sustainable water resource utilization and contributing to sustainable development goals.
2. Research Framework and Methodology
A seven-stage procedural framework for the seismic fragility study of large-span elevated U-shaped aqueduct structures is presented in this research. Figure 1 illustrates this framework. A detailed description of the methodology and the logical evolution of each step is provided by the framework.
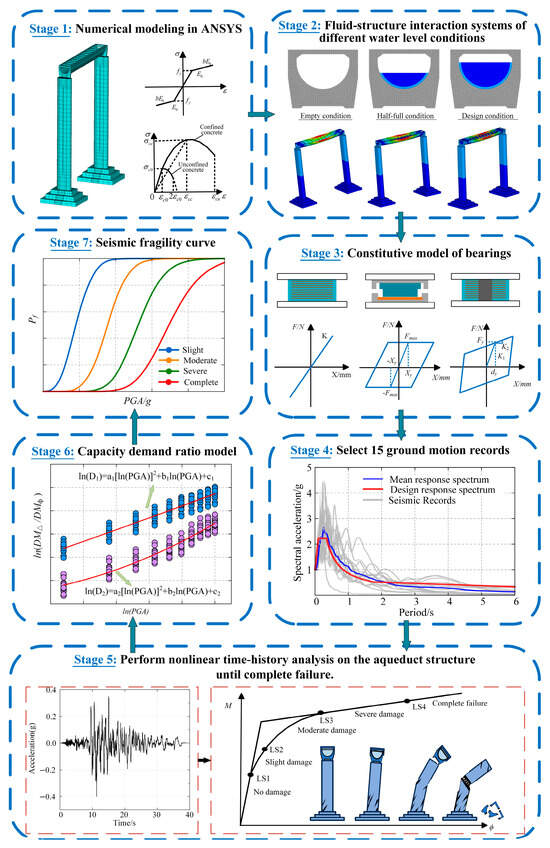
Figure 1.
Flowchart of seismic fragility analysis for aqueduct structures.
Stage 1: The study employed ANSYS software to create a refined finite element model of a large-span elevated U-shaped aqueduct structure. The finite element model defined the geometric parameters, material properties and boundary constraints. The computational precision and accuracy of the model were guaranteed by thoroughly considering the mechanical properties of concrete in both confined and unconfined conditions.
Stage 2: Utilizing the finite element model created in the first phase, fluid–structure interaction systems are constructed for three distinct situations, namely, an empty condition, a condition that is only half full and a design water level. The seismic fragility of the aqueduct structure is evaluated via the use of numerical simulations in order to determine the impact that different water level conditions have on the structure.
Stage 3: In order to improve the model precision in simulating bearing behavior during seismic events, the finite element model of the aqueduct structure incorporates constitutive models for three different types of bearings: plate rubber bearings, pot rubber bearings and lead-core rubber bearings. These bearings are established based on their force–displacement relationships and maximum bearing capacities.
Stage 4: Pursuant to the Code for Seismic Design of Hydraulic Structures (GB 51247-2018) [23] and the ATC-63 (2008) report [24], 15 representative seismic ground motion records were extracted from the PEER strong motion database and evaluated against the code-specified response spectrum to verify their relevance and precision.
Stage 5: The incremental dynamic analysis (IDA) method is employed to input amplitude-scaled seismic ground motion records into the finite element model for nonlinear dynamic time–history analysis. This approach simulates the aqueduct structure’s response up to its ultimate failure state, elucidating the damage progression and failure mechanisms.
Stage 6: The engineering demand parameters (EDPs) for each structural component of the aqueduct have been extracted based on the findings of nonlinear time history studies which were performed. The log-linear regression methodology was utilized in conjunction with certain damage indicators in order to construct capacity demand ratio (CDR) models for the thin-walled hollow piers as well as the three different types of bearings.
Stage 7: The seismic fragility curves of each component were constructed using the failure probability formula, and the seismic fragility analysis of the elevated long-span U-shaped aqueduct was conducted to evaluate the damage probabilities of its components.
3. Project Synopsis and Finite Element Modeling
3.1. Project Synopsis
This research examines the elevated large-span U-shaped aqueduct of an irrigation water diversion project as a case study. The superstructure of the 391.9 m long aqueduct consists of prestressed concrete U-shaped aqueduct channels made of C40 concrete, with a thickness of 0.8 m and aqueduct channel height of 2.75 m. The substructure consists of thin-walled hollow piers, with heights varied according to topographical circumstances, ranging up to 30 m. The aqueduct piers are fabricated from C30 concrete and HRB400 reinforcing steel, whilst the foundation used C25 concrete. The aqueduct top is fitted with a multitude of transverse tie rods, each of which has a cross-section of 0.2 m by 0.2 m. These tie rods are distributed at intervals of 1.7 m and are created using C40 concrete. Each single-span aqueduct segment is 23.96 m in length, and neighboring segments are linked by deformable water-stop bands. By using deformable water-stop bands, the interaction between adjacent aqueduct segments is greatly reduced. Consequently, the impact of neighboring spans may be disregarded, and just the effect of their mass on the pier is taken into account. This research focuses on a single-span aqueduct with a span length of 23.96 m and a pier height of 30 m for comprehensive investigation. Figure 2 illustrates the schematic diagram of the aqueduct structure.
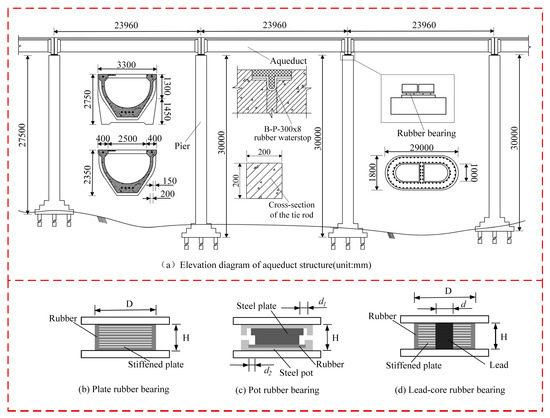
Figure 2.
Schematic diagram of the aqueduct structure (units: mm): (a) Elevation diagram of aqueduct structure; (b) Plate rubber bearing; (c) Pot rubber bearing; (d) Lead-core rubber bearing.
3.2. Finite Element Modeling
This research produced a three-dimensional finite element model of the aqueduct using ANSYS finite element software. It was comprised of 85,150 elements and 93,584 nodes, and the meshing was carried out with eight-node hexahedral elements, as shown in Figure 3. Due to the significant bedrock hardness and robust integrity of the prototype aqueduct engineering site, the soil–structure interaction (SSI) effect is disregarded in the finite element model. Fixed constraints are implemented at the base of the supporting structure, with all nodes at the bottom of the finite element model constrained in three directions to limit base movement. On the other hand, the aqueduct channel and tie rods are modeled with the SOLID45 solid element, the aqueduct piers and foundation with the SOLID65 solid element and the reinforcing steel with the LINK8 bar element. Reinforcing steel and concrete are modeled using a separated modeling approach, in which the steel and concrete elements are coupled as a single entity through constraint equations. The model uses Rayleigh damping with a damping ratio of 0.05 to accurately simulate the dynamic response of the structure. The bearing as an essential element linking the aqueduct trough to the thin-walled hollow pier, must guarantee the continuity and efficacy of force transmission during seismic loading [25]. The bearing is modeled with two horizontal COMBIN14 spring elements and one vertical COMBIN40 spring element to depict its mechanical behavior. Two nodes are first established at the upper and lower extremities of the bearing. Subsequently, three spring elements (two horizontal and one vertical) are configured between these nodes. The MPC184 element is used to connect the bearing’s spring components with the aqueduct’s solid elements (SOLID65), guaranteeing efficient force transmission and compatibility of deformation. The three-dimensional acoustic components FLUID30 are used to describe the aquatic moderate in the aqueduct, the medium is defined by a water density of 1000 kg/m3 and a longitudinal wave velocity of 1440 m/s. The water surface is considered to be a free surface, and a fluid–structure interaction interface is built between the inner wall of the aqueduct channel and the water body [26]. This interface is created to ensure that the degrees of freedom between the solid components of the inner wall and the fluid elements are coupled together. The interaction between the fluid and the structure is shown in pictorial form in Figure 3a.
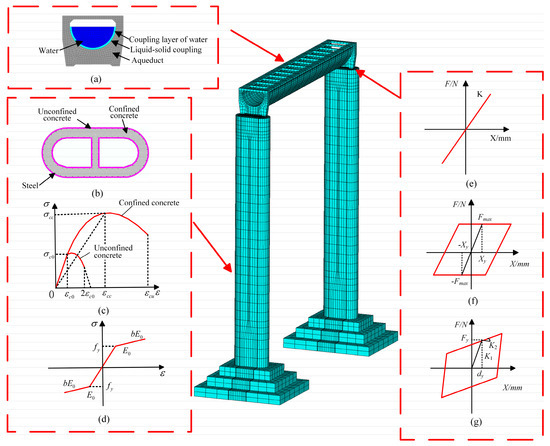
Figure 3.
Finite element model of aqueduct structure: (a) fluid–structure coupling schematic; (b) fiber section of aqueduct pier; (c) constitutive model of concrete; (d) constitutive model of reinforcement; (e) plate rubber bearing; (f) pot rubber bearing; (g) lead-core rubber bearing.
Finite element models of aqueduct structures with lead-core rubber bearings, pot rubber bearings and plate rubber bearings were created in order to examine the seismic isolation performance of various rubber bearing types. Of these, the shear stiffness of plate rubber bearings can be considered constant, and their horizontal force–displacement relationship shows stable mechanical features within a particular frequency range and under the condition of maximum shear strain. As a result, the mechanical behavior of laminated rubber bearings can be fairly simplified as a linear model in the finite element modeling method [27]. This study selected a GYZ350×74 plate rubber bearing, and the parameters of its linear model were computed according to Table 1.

Table 1.
Modeling equations for the linear model of bearings.
In alignment with the Seismic Design Specification for Highway Bridges (JTG/T2231-01-2020) [28], a bilinear idealized model is used to represent the mechanics of movable pot rubber bearings, as depicted in Figure 3f. The parameters of the bilinear idealized model for pot rubber bearings are computed as specified in Table 2.

Table 2.
Modeling equations for the bilinear ideal model of bearings.
This work used a bilinear model to mimic the stiffness-damping characteristics of lead-core rubber bearings [29], as illustrated in Figure 3g. The parameters of the bilinear model for lead-core rubber bearings are computed as specified in Table 3.

Table 3.
Modeling equations for the bilinear model of bearings.
3.3. The Uncertainty in Modeling
The accuracy of nonlinear time–history analysis results for aqueducts under seismic relies heavily on the precision of the finite element model. To ensure that the numerical analysis results accurately represent the aqueduct dynamic response under seismic loading, it is essential to accurately define the geometry of components, material characteristics and boundary conditions before building the finite element model of the aqueduct. Improving the model accuracy requires a comprehensive evaluation of the influence of uncertainty in structural parameters [30]. This work utilizes the Latin Hypercube Sampling methodology [31] to address uncertainties in structural parameters, producing a total of 10 aqueduct samples, as shown in Table 4.

Table 4.
Latin hypercube sampling results.
3.4. Natural Frequencies and Mode Shapes of the Aqueduct
Mode frequency analysis serves as the foundation for the dynamic time–history analysis of aqueduct structures, delineating their intrinsic vibrational characteristics in the absence of external stimuli. The elevated long-span aqueduct in the practical engineering case examined in this study is supported by plate rubber bearings. Consequently, the plate rubber bearing model was chosen as the primary analysis object in the modal analysis and the natural vibration characteristics were examined under three operating conditions: empty, half-full and design water level conditions. The cumulative effective mass in each direction must exceed 90% of the total structural mass, as stipulated in the Code for Seismic Design of Buildings (GB 50011-2010) [32]. The study’s cumulative mass participation rates for the first ten modes in the x, y and z directions all exceed 90%, indicating that there are enough extracted modes, as shown in Table 5. Figure 4 presents the lower-order vibration modes of the aqueduct structure. Overall longitudinal translation is exhibited by the aqueduct structure’s first mode, overall transverse translation by its second and transverse staggered rotation by its third.

Table 5.
Natural frequency of aqueduct structure.
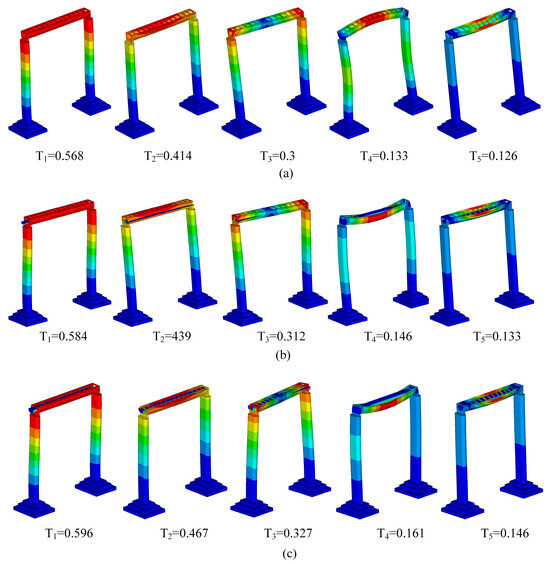
Figure 4.
Modal shapes of the aqueduct structure under three different conditions: (a) vibration mode of aqueduct structure under empty condition; (b) vibration mode of aqueduct structure under half-full condition; (c) vibration mode of aqueduct structure under design water level.
As the water level rises, the mass of the water body considerably augments the overall mass of the superstructure, resulting in an extension of the natural vibration time in comparison to the empty condition. Through dynamic analysis, this study indicates that the augmentation of water mass directly influences the total mass distribution of the structure, thereby modifying its dynamic response characteristics. The natural frequencies and mode forms that were calculated for the empty condition, the half-full condition and the design water level all match up with the basic rules of structure dynamics. This validates the validity and reasonableness of the existing model.
4. Theory and Methodology of Seismic Fragility Analysis
4.1. Theory of Seismic Fragility Analysis
The seismic fragility of aqueduct structures is defined as the conditional likelihood that the structure attains or surpasses a designated performance standard under seismic stress. Seismic fragility analysis assesses the failure risk of structures subjected to different intensities, serving as a foundation for the seismic design and risk evaluation of aqueducts. The capacity demand ratio curve fitting technique is used [33], with the assumption that the seismic fragility curve of a component follows a lognormal distribution. In contrast to the probabilistic seismic demand curve fitting approach [34], the DCR curve fitting methodology utilizes the ratio of seismic demand to structural capacity in conjunction with the seismic intensity measure for the purpose of conducting log-quadratic regression analysis. Using capacity demand ratio curve fitting methodology, the link between the capacity–demand ratio and seismic intensity is shown in a manner that is more approximate. The expression is calculated as follows:
where λ signifies the logarithmic mean of the capacity–demand ratio; σ indicates the logarithmic standard deviation of the capacity demand ratio; IM denotes the seismic intensity measure. Sr represents the summation of squared residuals of the sample points; N is the sufficient number of sample points; and a, b, c are the parameters of the regression equation.
The failure probability of a single component at various damage levels may be articulated as follows:
where Pf signifies the failure probability of the component; Sd represents the seismic demand of the component; Sc denotes the structural capacity; and Φ(x) is the cumulative distribution function of the standard normal distribution.
4.2. Selection of Seismic Motions
Seismic fragility analysis necessitates the selection of a sufficient quantity of ground motion recordings to effectively address the uncertainty of ground movements. For the incremental dynamic analysis approach, the selection of 10 to 20 ground motion data is enough to fulfill the accuracy criteria for the analysis [35]. The aqueduct engineering site is classified as a Type II site, with a soil shear wave velocity between 250 and 500 m/s and a seismic fortification intensity of 7.5. The target response spectrum is determined per the Code for Seismic Design of Hydraulic Structures (GB 51247-2018) [23]. Fifteen seismic ground motion records were extracted from the Pacific Earthquake Engineering Research (PEER) database, with the findings illustrated in Figure 5. The target response spectrum was compared to the mean response spectrum of the selected ground motions, and a satisfactory fit was observed. The peak ground acceleration (PGA) was used as the seismic intensity metric, and the PGA of the 15 ground motion records was scaled tenfold across a spectrum of 0.1 g to 1.0 g, resulting in a total of 150 seismic ground motion samples. The corresponding vibration response data for each ground motion were extracted by sequentially inputting these 150 samples into the finite element model along the transverse direction of the aqueduct.
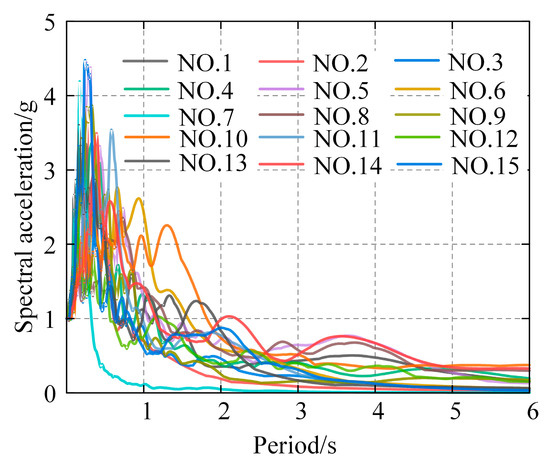
Figure 5.
Fifteen ground motion records.
4.3. Definition of Damage Limit States
The construction of the aqueduct is largely made up of three components: the aqueduct channel, bearings and piers. The bearings act as the connecting parts between the aqueduct channel and the piers, while the piers are responsible for sustaining both the aqueduct channel and the water load. When it comes to the uninterrupted functioning of the aqueduct structure, the safety of both components is of the utmost importance [9,36]. Under the influence of seismic motion, the failure of the bearings might result in the instability of the aqueduct channel, while damage to the piers could lead to the collapse or whole structural instability of the structure. For this reason, the failure probabilities of the bearings and piers, which are considered to be critical components, are stressed in the seismic fragility analysis of aqueduct structures in order to assess the seismic performance of these structural components.
Damage measure are metrics used to measure the degree of damage to structures or components across various damage stages. According to HAZUS [37], the damage statuses of aqueducts may be broken down into five distinct categories: no harm, slight damage, moderate damage, severe damage and complete damage. The deformation capacity of piers is often measured using critical indices, including displacement ratio [38], curvature [39] and displacement ductility ratio [40]. For the purpose of evaluating the damage states of thin-walled hollow piers, this study used the displacement ductility ratio (μd) as the damage measure. The displacement ductility ratio quantifies the deformation capacity of a structure under various loading situations, effectively indicating the damage extent of thin-walled hollow piers, and is generally acknowledged in earthquake engineering [41]. The displacement ductility ratio at the initial yield of longitudinal tensile reinforcement is used to determine the critical value for slight damage. The displacement ductility ratio at the section equivalent yield is used to calculate the critical value for moderate damage. With a compressive strain of 0.004 on the concrete, the displacement ductility ratio is used to establish the threshold for severe damage. The critical index for complete damage is defined as μ4 = μ3 + 3, according to the Seismic Retrofitting Manual for Highway Structures: Part 1—Bridges [42]. Prior to the calculation of the displacement ductility ratio, it is necessary to determine the plastic hinge length of the hollow thin-walled pier in order to accurately characterize its nonlinear deformation capacity under seismic loading. The plastic hinge length (Lp) represents the region where plastic deformations are concentrated after yielding, typically located at the pier base or other stress-concentrated zones. The calculation formula is given as follows [43]:
where L denotes the height of the pier, Lp represents the equivalent plastic hinge length, db1 is the diameter of the longitudinal reinforcement, and fy refers to the standard tensile strength of the longitudinal reinforcement.
The critical values of the damage measure can be determined by utilizing the moment-curvature (P-M-φ) analysis of reinforced concrete sections in X-TRACT software (https://www.xtract.app/, accessed on 4 August 2025), as illustrated in Figure 6. Table 6 provides specific results.
Figure 6.
M–ϕ relationship of thin-walled hollow bridge piers.

Table 6.
Limit state of aqueduct components.
In this study, the damage states of bearings are evaluated by selecting three representative types: lead-core rubber bearings (seismic isolation bearings), plate rubber bearings and pot rubber bearings (nonisolation bearings). In the current moment, there is a scarcity of seismic damage data for isolated aqueducts, and research into the damage of rubber isolation bearings rely mostly on data from experiments [27,44]. It was found by Zhang et al. [29] that shear strain properly characterizes the effectiveness of seismic isolation rubber bearings. This is because shear strain indicates the shear modulus and damping properties of the bearings. This research utilizes shear strain (γ) as the damage measure for lead-core rubber bearings. This study using damage indices that are predicated on the mechanical properties of plate rubber bearings and pot rubber bearings, respectively, to evaluate the damage of nonisolated bearings. For plate rubber bearings, Li et al. [45] proposed using the relative displacement ductility ratio (μd) as the Damage measure. For pot rubber bearings, this study selects pot rubber bearings with an allowable displacement of ±100 mm and uses the relative displacement (d) between the upper and lower parts of the bearing as the damage assessment index. Critical thresholds of 25 mm, 50 mm and 75 mm are established to correspond to slight damage, moderate damage and severe damage, respectively [46]. Table 6 illustrates the precise parameters of each damage measure.
4.4. Capacity Demand Ratio Model
This study uses seismic motions in the transverse direction of the aqueduct as input and produces response data for each aqueduct component using nonlinear time–history analysis. Scatter plots are constructed using the logarithm of peak ground acceleration on the x-axis and the logarithm of the capacity–demand ratio on the y-axis. A quadratic polynomial regression analysis is performed on the scatter data using the least squares method to fit the logarithmic capacity–demand ratio curves for each aqueduct component. Due to space constraints, only the fitted results of the logarithmic capacity–demand ratio with slight damage at the design water level are shown, as seen in Figure 7.
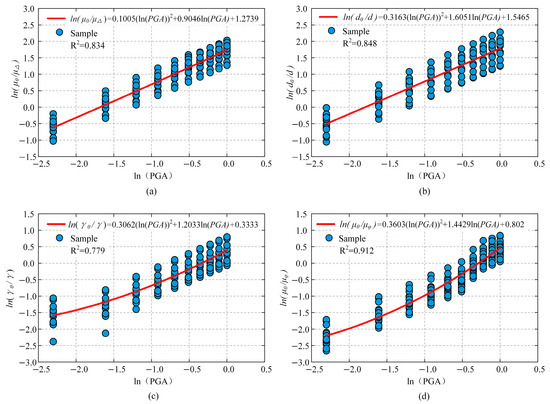
Figure 7.
Demand capacity ratio curves for slight damage of aqueduct components under design water level: (a) plate rubber bearing; (b) pot rubber bearing; (c) lead-core rubber bearing; (d) thin-walled hollow pier.
5. Seismic Fragility Analysis of Aqueduct Structures
5.1. Fragility Comparison of Aqueduct Components Under Three Water Level Conditions
The peak ground acceleration (PGA) was selected as the seismic intensity measure, according to the capacity–demand ratio model of the aqueduct components and the structural failure probability calculation method outlined in Equation (4). The seismic fragility curves of the rubber bearings and thin-walled hollow supports were subsequently established based on the exceedance probabilities of the components under various damage conditions. Water level fluctuations create supplementary mass effects, substantially affecting the dynamic properties and seismic response of large-span elevated U-shaped aqueduct. To further investigate this, the study compares fragility curves of aqueduct components under different water level conditions, with a specific emphasis on assessing how fluctuations in water level affect the seismic fragility of the structure. The aqueduct structure using plate rubber bearings is chosen as the typical model for fragility analysis across three water level circumstances, with the objective of clarifying the influence of water level fluctuations on the seismic fragility of large-span elevated U-shaped aqueduct structures.
5.1.1. Fragility Analysis of Plate Rubber Bearings Under Three Water Level Conditions
Figure 8 illustrates the fact that under the design water level, the seismic fragility curve for plate rubber bearings in the slight damage state has a steeper slope, signifying a significant rise in the chance of damage exceedance with rising peak ground acceleration. At a PGA of 0.2 g, the chance of slight damage exceedance for plate rubber bearings is 61.36% under the design water level, 34.76% under the half-full conditions, and 11.75% under the empty conditions. The analytical findings indicate that when the water level ascends from the empty conditions state to the design water level, the exceedance probability of slight damage for plate rubber bearings markedly escalates (from 11.75% to 61.36%). This occurs as a consequence of the increased mass of the superstructure that is brought about by the elevated water levels. This causes the dynamic properties of the structure to be altered, which in turn, increases the deformation demand placed on the bearings, accelerates their transition into the plastic deformation phase, and ultimately reduces their seismic performance.
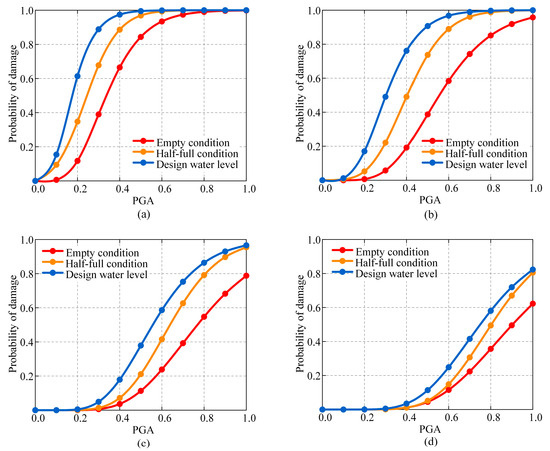
Figure 8.
Seismic fragility curves of plate bearing under three water level conditions: (a) slight damage; (b) moderate damage; (c) severe damage; (d) complete damage.
At the design water level, with a peak ground acceleration of 0.5 g, the exceedance probabilities for plate rubber bearings are 99.48% for slight damage, 90.68% for moderate damage, 37.89% for severe damage and 11.42% for complete damage. Conversely, in the half-full conditions, the exceedance probabilities for these damage states are 96.88%, 73.73%, 21.11% and 5.15%, indicating decreases of 2.60%, 16.95%, 16.78% and 6.27%, respectively. In the empty conditions, the probabilities are 84.35%, 38.71%, 11.31% and 4.49%, which equate to decreases of 15.13%, 51.97%, 26.59% and 6.93%, respectively. The results demonstrate that at the design water level, the damage exceedance probabilities of plate rubber bearings are more sensitive to increasing PGA, especially for slight and moderate damage states, where they are considerably higher than under half-full and empty conditions.
5.1.2. Fragility Analysis of the Hollow Thin-Walled Pier Under Three Water Level Conditions
The exceedance probabilities of slight damage, moderate damage, severe damage and complete failure for thin-walled hollow piers equipped with plate rubber bearings under three water level conditions (empty condition, half-full condition and design water level) gradually increase as PGA increases under seismic action, as illustrated in Figure 9. At a PGA of 0.4 g, under the empty conditions, the probability of slight, moderate, severe and complete damage to the piers are 15.1%, 8.5%, 2.58% and 1.41%, respectively. In the context of a half-full conditions, these odds rise to 19.04%, 10.42%, 5.57% and 2.85%, respectively. At the design water level, the odds increase to 28.06%, 16.33%, 6.38% and 2.91%, respectively.
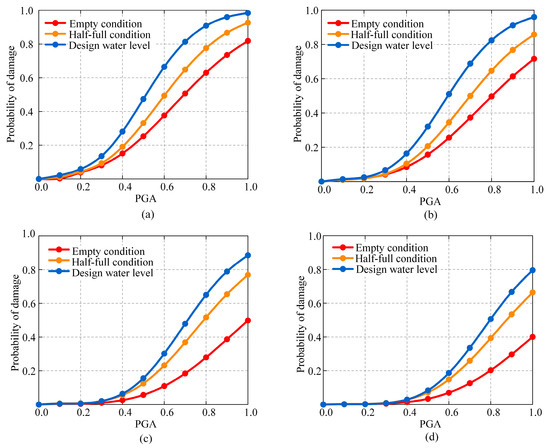
Figure 9.
Seismic fragility curves of thin-walled hollow pier under three water level conditions: (a) slight damage; (b) moderate damage; (c) severe damage; (d) complete damage.
This investigation demonstrates that the seismic fragility of thin-walled hollow piers is substantially influenced by fluctuations in water level within the aqueduct structure. The damage states are subject to variable impacts under various water level conditions. The exceedance probability of thin-walled hollow piers across various damage states increases considerably as the water level increases. The most pronounced increase is observed in minor damage states, followed by moderate damage states. The analysis suggests that the upper structure of the aqueduct experiences an increase in mass as a result of rising water levels. This leads to more substantial displacement responses and greater inertial forces under seismic action.
When the exceedance probability of damage for thin-walled hollow piers attains 70%, in the slight damage, the corresponding PGA values for the empty condition, half-full condition and design water level are 0.86 g, 0.74 g and 0.62 g. In the moderate damage, the PGA values for the empty condition, half-full condition and design water level are 0.98 g, 0.84 g and 0.71 g. When the damage exceeding probability of the thin-walled hollow pier is 30%, the PGA in the severe damage state is 0.82 g, 0.65 g and 0.6 g corresponding to the empty condition, half condition and design water level; and in the complete damage state, the PGA corresponding to the empty condition, half condition and design water level is 0.91 g, 0.73 g and 0.68 g, respectively. Under the same damage state, compared to the seismic damage probability of piers in the empty condition, the presence of water in the aqueduct enables the piers to reach the same exceedance probability at lower seismic intensities. Therefore, the influence of the water on the structure must not be overlooked in the seismic analysis of aqueduct structures.
5.2. Comparative Analysis of the Seismic Fragility of Aqueduct Structures with Three Types of Isolation Bearings Under the Design Water Level
The structural failure probability of the aqueduct under seismic is considerably increased by the increase in additional water mass, rendering the design water level the most disadvantageous seismic condition. Three typical seismic isolation and energy dissipation bearing types are selected for this condition: plate rubber bearings, pot rubber bearings and lead-core rubber bearings. Through a combination of finite element numerical simulation and seismic fragility analysis, the impact of different bearing types on the seismic fragility of the aqueduct structure is systematically evaluated, aiming to provide a basis for optimizing bearing selection and enhancing the seismic performance of the structure.
5.2.1. Seismic Fragility Assessment of Three Isolation Bearing Types Under the Design Water Level
Figure 10 shows the fact that under the design water level, the damage exceedance probabilities for plate rubber bearings and pot rubber bearings have comparable trends, both markedly surpassing those of lead-core rubber bearings. At a peak ground acceleration of 0.4 g, the exceedance probabilities for slight damage are 97.45% for plate rubber bearings and 80.68% for pot rubber bearings, much above the 8.64% for lead-core rubber bearings, with analogous patterns seen throughout various damage states. In contrast to nonisolated bearings, lead-core rubber bearings possess high damping characteristics, which allow them to effectively dissipate seismic energy, significantly reduce structural vibration amplitudes and internal force responses, and, as a result, reduce the risk of damage during seismic excitation. Comparing the two varieties of nonisolation bearings reveals that the damage exceedance probability of plate rubber bearings escalates more rapidly than that of pot rubber bearings at slight and moderate damage states, signifying a heightened vulnerability to damage in these conditions. Nonetheless, in instances of severe and complete harm states, the damage exceedance probabilities of the two bearing types converge and become identical.
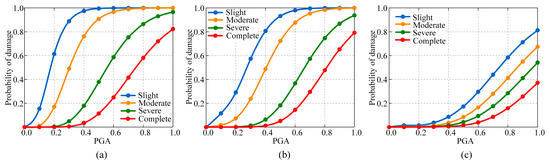
Figure 10.
Seismic fragility curves of three bearing types under the design water level: (a) plate rubber bearing; (b) pot rubber bearing; (c) lead-core rubber bearing.
The results show that, under the design water level, lead-core rubber bearings (seismic isolation bearings) exhibit enhanced seismic performance relative to nonisolation bearings owing to their exceptional energy dissipation capabilities. Among nonisolation bearings, pot rubber bearings have superior seismic performance compared to plate rubber bearings due to their enhanced stiffness and load-bearing capability. Consequently, given the impact of water level fluctuations and the stringent seismic performance criteria for aqueduct structures, it is advisable to prioritize lead-core rubber bearings as the preferred bearing type to guarantee safety and stability amid changing water levels and seismic events.
5.2.2. Fragility Analysis of the Thin-Walled Hollow Pier System with Three Bearing Types Under Design Water Level
Figure 11 shows that for the thin-walled hollow piers with plate rubber bearings, the exceedance probabilities for the slight, moderate, severe and complete damage states are 28.06%, 16.33% and 2.91%, respectively, under the design water level with a peak ground acceleration of 0.4 g. For piers equipped with pot rubber bearings, the likelihood of exceedance is 17.2%, 9.92%, 5.62% and 2.81%; for piers equipped with lead-core rubber bearings, it is 6.74%, 3.91%, 2.27% and 0.78%. A comparative analysis indicates that the exceedance probabilities for slight and moderate damage states are markedly elevated for piers equipped with nonisolation bearings in contrast to those with isolation bearings, primarily attributable to the energy dissipation and isolation properties of lead-core rubber bearings. A comparison examination of the two nonisolation bearings demonstrates that the exceedance probabilities for piers that use plate rubber bearings are consistently higher than those that use pot rubber bearings across all damage states.
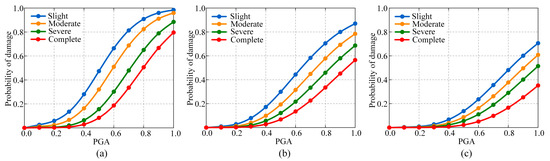
Figure 11.
Seismic fragility curves of thin-walled hollow piers with different bearing types under the design water level: (a) plate rubber bearing; (b) pot rubber bearing; (c) lead-core rubber bearing.
At a peak ground acceleration of 1.0 g, the exceedance probabilities for thin-walled hollow piers with lead-core rubber bearings are 70.59%, 60.84%, 51.43% and 35.21% for slight, moderate, severe and complete damage states, respectively. The exceedance probabilities for piers using pot rubber bearings rise by 16.42%, 17.6%, 17.22% and 21.31% over the four damage states, while those employing plate rubber bearings increase by 27.8%, 35.08%, 37.03% and 44.39%, respectively. The findings reveal that, under identical seismic loads, the failure probability of piers equipped with isolation bearings is much lower than that of piers with nonisolation bearings, indicating a considerable improvement in structural safety. The isolation bearings significantly reduce the possibility of seismic damage to the piers. Consequently, for thin-walled hollow piers, the seismic efficacy of lead-core rubber bearings significantly surpasses that of pot rubber bearings, which in turn, exceed plate rubber bearings.
6. Conclusions
This research develops a finite element model of an elevated large-span U-shaped aqueduct construction used ANSYS software, including fluid–structure interaction effects. The incremental dynamic analysis approach is used to assess the damage probability of aqueduct components, including bearings and piers under diverse seismic excitations. Upon comparing the damage possibilities of the aqueduct structure with various bearing types under conditions of empty, half-full and design water levels, then the failure probability of isolated vs. nonisolated piers subjected to seismic forces, the following findings are reached:
(1) The probability of injury to each component of the elevated large-span U-shaped aqueduct increases as seismic intensity increases. The development patterns of the seismic fragility curves range markedly across various damage states, with the exceedance probability for slight damage escalating more swiftly, whilst that for severe damage increases at a more moderate pace. Under transverse seismic loading, the bearings in the aqueduct structure fail before plastic hinges develop in the piers.
(2) Under the conditions of an empty condition, a half-full condition and the design water level, the likelihood of damage to the aqueduct construction increases with increasing peak ground acceleration. As the water level in the aqueduct rises, the mass of the superstructure alters the structure dynamic response characteristics, resulting in an increasing trajectory in the failure risk of aqueduct components throughout all damage states with rising water levels. This means that the influence of the water on the structure must be fully considered in the seismic research of aqueducts.
(3) Lead-core rubber bearings substantially reduce the displacement response of the aqueduct structure to seismic by exhibiting superior seismic isolation performance and lower damage exceedance probabilities under varying water level. In contrast, pot rubber bearings exhibit higher damage exceedance probabilities under the same conditions, while plate rubber bearings exhibit the weakest seismic performance.
(4) The failure probabilities of isolated piers across various damage states are inferior to those of nonisolated piers, demonstrating that seismic isolation bearings improve the isolation efficacy of the aqueduct, significantly diminishing the seismic response of the structure and consequently alleviating the severity of earthquake-induced damage. Seismic isolation bearings should be addressed in aqueduct projects situated in high-seismic-intensity areas.
Author Contributions
J.W.: writing—original draft preparation, formal analysis, investigation, methodology and data curation; X.Y.: conceptualization, supervision and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Special Project of Xinjiang Uygur Autonomous Region (2022B03024-3).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the project involves relevant confidentiality regulations.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sheng, J.C.; Zhang, R.Z.; Yang, H.Q. Inter-basin water transfers and water rebound effects: The South-North water transfer Project in China. J. Hydrol. 2024, 638, 10. [Google Scholar] [CrossRef]
- Xiao, J.L.; Yang, Y.; Zhuang, L.D.; Nie, X. A numerical and theoretical analysis of the structural performance for a new type of steel-concrete composite aqueduct. Eng. Struct. 2021, 245, 20. [Google Scholar] [CrossRef]
- Buonopane, S.G.; Gasparini, D.A.; John, A. Roebling’s 1845 Allegheny Aqueduct: Design, History and Performance. J. Bridge Eng. 2024, 29, 13. [Google Scholar] [CrossRef]
- Huang, L.; Hou, Y.J.; Wang, B.; Yao, J.C. Collision in the expansion joint effects on the seismic behavior of large-scale aqueduct. J. Asian Archit. Build. Eng. 2021, 20, 663–673. [Google Scholar] [CrossRef]
- Wang, H.B.; Li, C.L.; Zhao, L.J. Experimental Study on Dynamic Interaction between Large U-Shape Aqueduct and Water. KSCE J. Civ. Eng. 2022, 26, 1203–1213. [Google Scholar] [CrossRef]
- Liu, Y.H.; Dang, K.N.; Dong, J. Finite element analysis of the aseismicity of a large aqueduct. Soil. Dyn. Earthq. Eng. 2017, 94, 102–108. [Google Scholar] [CrossRef]
- Yan, J.L.; Liang, Y.; Du, X. Analysis of the importance coefficient of offshore bridges under earthquakes based on seismic fragility and incremental dynamic analysis. Soil. Dyn. Earthq. Eng. 2023, 171, 15. [Google Scholar] [CrossRef]
- Ellingwood, B.R.; Kinali, K. Quantifying and communicating uncertainty in seismic risk assessment. Struct. Saf. 2009, 31, 179–187. [Google Scholar] [CrossRef]
- Wu, C.; Xu, J.G.; Zhang, C.Y.; Wang, J.F. Overall seismic reliability analysis of aqueduct structure based on different levels under random earthquake. Structures 2023, 58, 11. [Google Scholar] [CrossRef]
- Xu, X.Y.; Liu, X.H.; Jiang, L.; Khan, M.Y.A. Dynamic Damage Mechanism and Seismic Fragility Analysis of an Aqueduct Structure. Appl. Sci. 2021, 11, 11709. [Google Scholar] [CrossRef]
- Wang, J.T.; Zhang, M.X.; Jin, A.Y.; Zhang, C.H. Seismic fragility of arch dams based on damage analysis. Soil. Dyn. Earthq. Eng. 2018, 109, 58–68. [Google Scholar] [CrossRef]
- Zhong, J.; Zhou, S.; Wang, H.; Hu, H.M. Regional seismic fragility of bridge network derived by covariance matrix model of bridge portfolios. Eng. Struct. 2024, 309, 13. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Seismic fragility analysis of concrete dams: A state-of-the-art review. Eng. Struct. 2016, 128, 374–399. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Xu, J.G.; Wang, B.; Wu, C. Nonlinear random seismic response analysis of the double-trough aqueduct based on fiber beam element model. Soil. Dyn. Earthq. Eng. 2021, 150, 10. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Xu, J.G.; Qian, Y.L.; Zhang, J.P.; Wang, R.; Wang, B. Seismic reliability analysis of random parameter aqueduct structure under random earthquake. Soil. Dyn. Earthq. Eng. 2022, 153, 10. [Google Scholar] [CrossRef]
- Du, M.; Zhang, S.R.; Wang, C.; She, L.; Li, J.B.; Lu, T. Seismic fragility assessment of aqueduct bent structures subjected to mainshock-aftershock sequences. Eng. Struct. 2023, 292, 19. [Google Scholar] [CrossRef]
- Zhang, S.R.; Du, M.; Wang, C.; Sun, B.B.; She, L.; Liu, W.J. Fragility analysis of high-span aqueduct structure under near-fault and far-field ground motions. Structures 2022, 46, 681–697. [Google Scholar] [CrossRef]
- Yina, Z.; Gege, C.; Shuai, Z.; Jianwei, Z.; Jinlin, H. Analysis of Seismic Fragility of Aqueduct Structure Based on Copula Function. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 042061. [Google Scholar]
- Ma, Y.; Wu, Z.B.; Liu, Z.S.; Zhang, M.Q.; Aibaidula, M. Seismic Fragility Analysis of Aqueduct Structural Systems Based on G-PCM Method. Sustainability 2022, 14, 13161. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Liu, C.; Zhang, A.J.; Zhu, H.D.; Li, J.W. Seismic Fragility Evaluation of Simply Supported Aqueduct Accounting for Water Stop’s Leakage Risk. Water 2021, 13, 1404. [Google Scholar] [CrossRef]
- Du, M.; Yang, X.H.; Zhang, S.R.; Wang, C.; Guo, R.; Yao, J.; Li, Z. Optimal intensity measures and probabilistic fragility assessment for the long-span aqueduct structure with four-column bents. Constr. Build. Mater. 2024, 455, 16. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, J.P.; Xu, J.G.; Zhang, C.Y.; Geng, Y.P. Nonlinear Response and Collapse Analysis of Double-Channel Aqueduct under Strong Earthquake. Adv. Civ. Eng. 2022, 2022, 16. [Google Scholar] [CrossRef]
- GB 51247-2018; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Seismic Design of Hydraulic Structures. China Planning Press: Beijing, China, 2018.
- ATC-63; Quantification of Building Seismic Performance Factors. Applied Technology Council: Redwood City, CA, USA, 2008.
- De Macêdo Wahrhaftig, A.; Eisenberger, M.; Baptista Elias, C.; Malheiros Filho, L.A. Seismic Response of Variable Section Column with a Change in Its Boundary Conditions. Buildings 2025, 15, 1456. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, C.W.; Wang, P.G. Seismic Fragility Analysis of Bridge Group Pile Foundations considering Fluid-Pile-Soil Interaction. Shock. Vib. 2020, 2020, 17. [Google Scholar] [CrossRef]
- Xiang, N.L.; Xu, H.X.; Wang, J.; Wu, X.X.; Chen, X. Seismic vulnerability assessment of laminated rubber bearing supported highway bridges with various bearing bonding alternatives. Eng. Struct. 2025, 326, 18. [Google Scholar] [CrossRef]
- JTG/T2231-01-2020; Ministry of Transport of the People’s Republic of China. Specifications for Seismic Design of Highway Bridges. China Communication Press: Beijing, China, 2020.
- Zhang, J.; Huo, Y.L. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method. Eng. Struct. 2009, 31, 1648–1660. [Google Scholar] [CrossRef]
- Du, M.; Yang, X.H.; Zhang, S.R.; Wang, C.; Guo, R.; Li, Z.; Yao, J. Probabilistic seismic performance assessment of aqueduct structures considering different sources of uncertainty. Structures 2024, 70, 16. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- GB 50011-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- Pan, Y.; Agrawal, A.K.; Ghosn, M. Seismic fragility of continuous steel highway bridges in New York state. J. Bridge Eng. 2007, 12, 689–699. [Google Scholar] [CrossRef]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.-A. Probabilistic Basis for 2000 SAC Federal Emergency Management Agency Steel Moment Frame Guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef]
- Shome, N.; Cornell, C.A. Probabilistic Seismic Demand Analysis of Nonlinear Structures; Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Peng, T.; Wang, G.H.; Lu, W.B.; Gao, Z.; Pan, X.H.; Shu, Y.Z. Blast resistance performance and failure modes of prestressed thin-walled aqueducts subjected to underwater contact explosion. Thin-Walled Struct. 2024, 201, 16. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. Multi-Hazard Loss Estimation Methodology. Earthquake Model; HAZUS99 User’s Manual; Federal Emergency Management Agency: Washington, DC, USA, 1999. [Google Scholar]
- Dutta, A.; Mander, J. Rapid and Detailed Seismic Fragility Analysis of Highway Bridges; Multidisciplinary Center for Earthquake Engineering Research: New York, NY, USA, 2001; pp. 1–152. [Google Scholar]
- Taskari, O.; Sextos, A. Multi-angle, multi-damage fragility curves for seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2015, 44, 2281–2301. [Google Scholar] [CrossRef]
- Hwang, H.; Liu, J.B.; Chiu, Y.H. Seismic Fragility Analysis of Highway Bridges. Mid-America Earthquake Center CD Release 01-06. 2001. Available online: https://mae.cee.illinois.edu/publications/reports/Report01-06.pdf (accessed on 4 August 2025).
- Liang, Y.; Yan, J.L.; Cheng, Z.Q.; Chen, P.; Ren, C. Time-Varying Seismic Fragility Analysis of Offshore Bridges with Continuous Rigid-Frame Girder under Main Aftershock Sequences. J. Bridge Eng. 2020, 25, 20. [Google Scholar] [CrossRef]
- Buckle, I.G.; Friedland, I.; Mander, J.; Martin, G.; Nutt, R.; Power, M. Seismic Retrofitting Manual for Highway Structures. Part 1, Bridges; Turner-Fairbank Highway Research Center: McLean, VA, USA, 2006. [Google Scholar]
- Pham, P.A.H.; Hung, C.-C.J.S.; Engineering, I. Assessment of plastic hinge length in reinforced concrete columns. Struct. Infrastruct. Eng. 2023, 21, 992–1007. [Google Scholar] [CrossRef]
- Xiang, N.L.; Huang, J.H.; Liu, X.X. Seismic performance upgrade of highway bridges using a novel hybrid placement of bonded and unbonded laminated rubber bearings. Structures 2024, 65, 15. [Google Scholar] [CrossRef]
- Li, L.F.; Wu, W.P.; Huang, J.M.; Wang, L. Research on the Seismic Vulnerability Analysis of Laminated Rubber Bearing. J. Hunan Univ. (Nat. Sci.) 2011, 38, 1–6. (In Chinese) [Google Scholar]
- Jangid, R.S. Seismic response of sliding structures to bidirectional earthquake excitation. Earthq. Eng. Struct. Dyn. 1996, 25, 1301–1305. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).