Analysis of Greenhouse Gas Emissions from Ships Visiting European Ports
Abstract
1. Introduction
- It requires progressive reductions in greenhouse gas (GHG) intensity, aiming for an 80% decrease by 2050.
- By 2034, a 2% sub-quota for renewable fuels of non-biological origin will be implemented based on market evaluations.
- Ships docking in EU ports must an utilize onshore power supply while berthed, except in cases where zero-emission technologies are employed.
- Low price signals for EU Allowances result in limited emissions reductions and could even lead to increased emissions.
- Reducing the EU ETS inclusion threshold from 5000 GT to 400 GT could lead to an additional 7–11% reduction in CO2eq emissions.
- The FuelEU Maritime regulation is expected to have minimal short-term effects until around 2030.
2. GHG Emissions Requirements of the EU and IMO
2.1. GHG Intensity According to FuelEU
2.2. Attained Annual GFI According to IMO
2.3. Comparisons of EU and IMO Requirements
3. GHG Intensity for the Main Ship Types According to FuelEU
- Total fuel consumption [m ton]–FC.
- Total emissions [m ton]–.
- emissions which occurred within ports under an MS jurisdiction at berth [m ton]–.
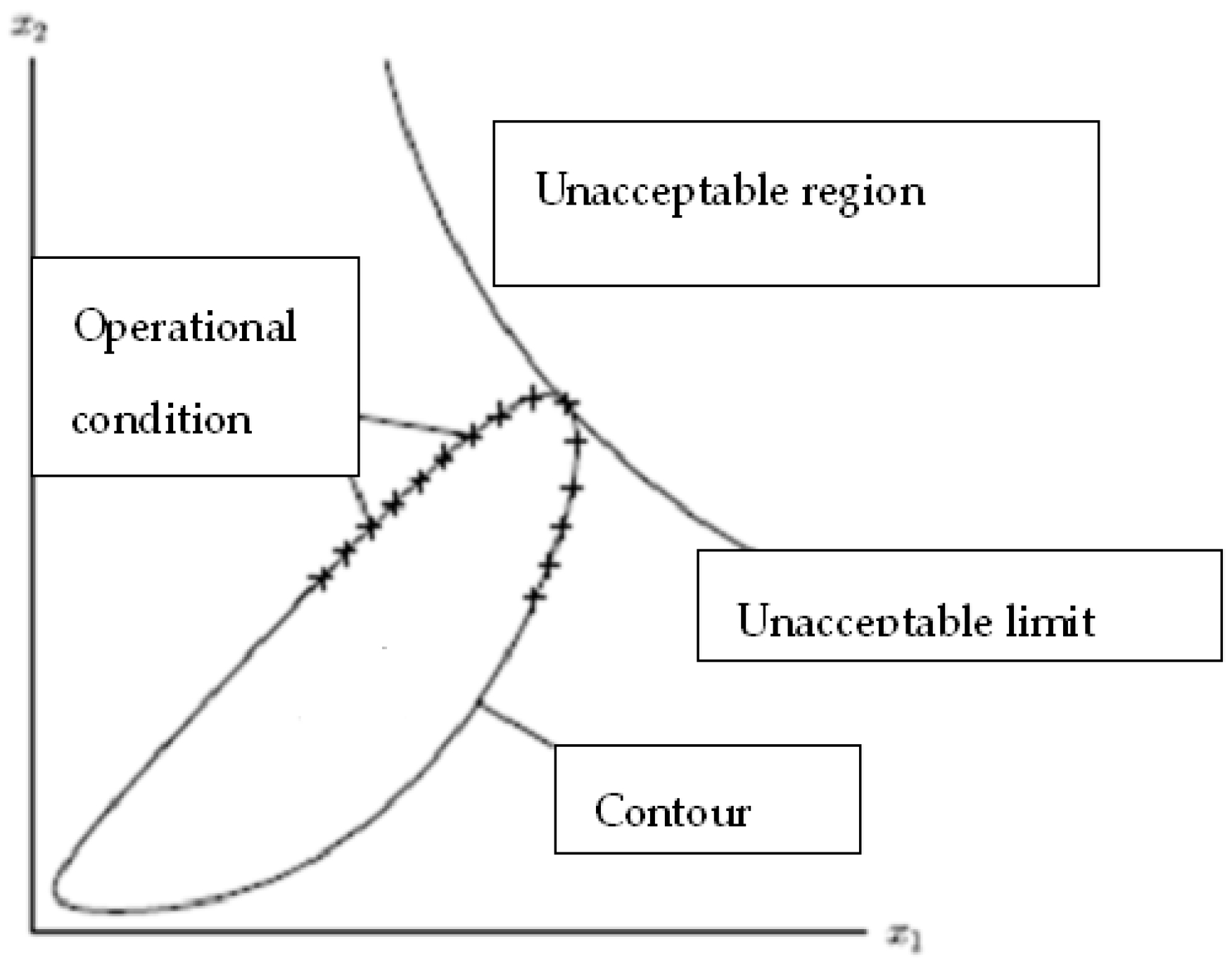
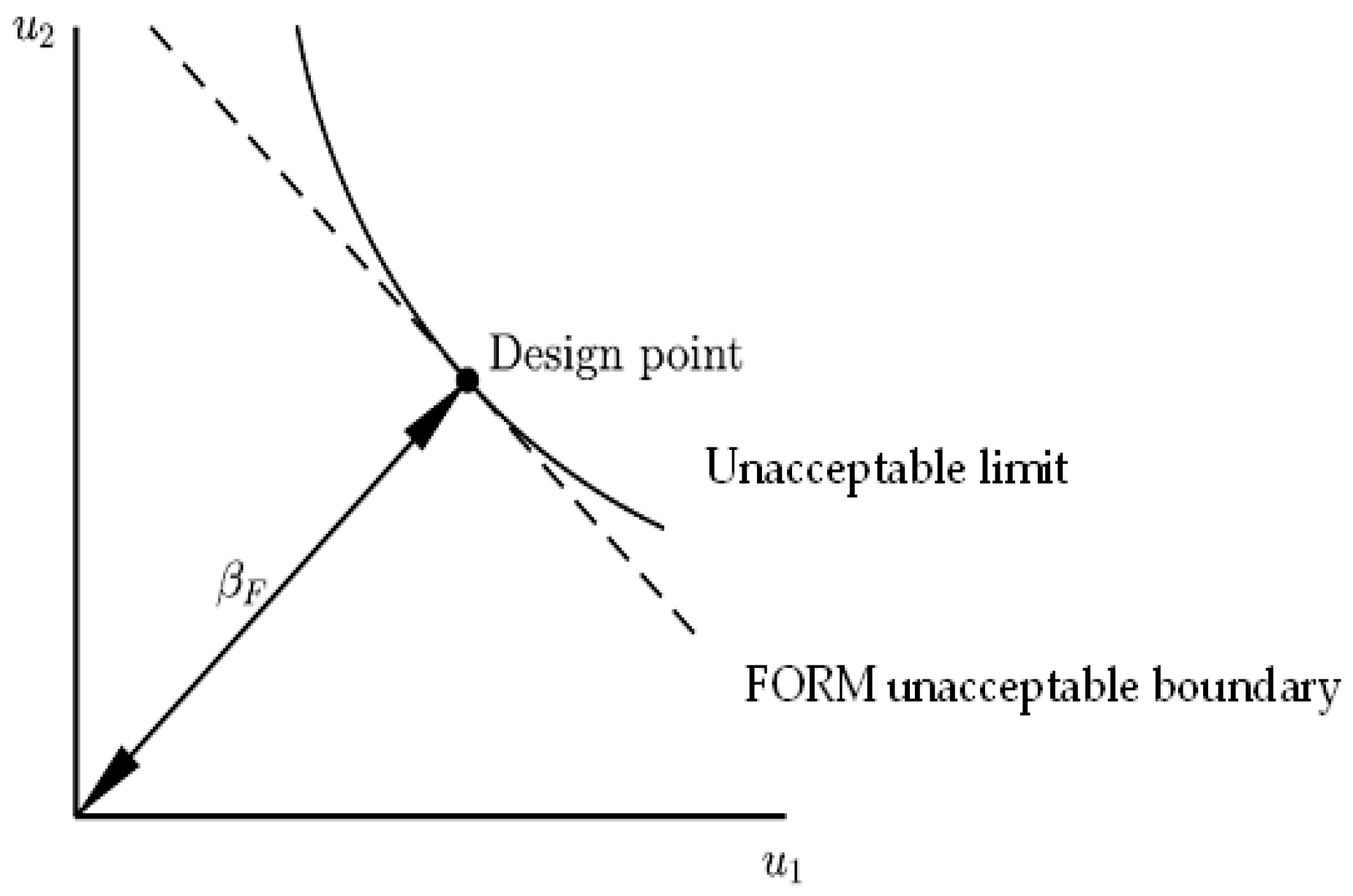
4. Contour Line Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DNV. Energy-Efficiency Measures and Technologies; DNV: Høvik, Norway, 2025. [Google Scholar]
- MEPC. Resolution MEPC.352(78). 2022 Guidelines on Operational Carbon Intensity Indicators and the Calculation Methods (CII Guidelines, G1); IMO: London, UK, 2022. [Google Scholar]
- MEPC. Resolution MEPC.353(78). 2022 Guidelines on the Reference Lines for Use with Operational Carbon Intensity Indicators (CII Reference Lines Guidelines, G2); IMO: London, UK, 2022. [Google Scholar]
- MEPC. Resolution MEPC.338(76). 2021 Guidelines on the Operational Carbon Intensity Reduction Factors Relative to Reference Lines (CII Reduction Factor Guidelines, G3); IMO: London, UK, 2021. [Google Scholar]
- MEPC. Resolution MEPC.354(78). 2022 Guidelines on the Operational Carbon Intensity Rating of Ships (CII Rating Guidelines, G4); IMO: London, UK, 2022. [Google Scholar]
- MEPC. Resolution MEPC.355(78). 2022 Interim Guidelines on Correction Factors and Voyage Adjustments for CII Calculations (CII Guidelines, G5); IMO: London, UK, 2022. [Google Scholar]
- MEPC. Resolution MEPC.400(83). Amendments to the 2021 Guidelines on the Operational Carbon Intensity Reduction Factors Relative to Reference Lines (CII Reduction Factors Guidelines, G3); IMO: London, UK, 2025. [Google Scholar]
- IMO. Circular Letter No.5005; IMO: London, UK, 2025. [Google Scholar]
- EU. Regulation (EU) 2023/1805 on the Use of Renewable and Low-Carbon Fuels in Maritime Transport and Amending Directive 2009/16/EC. Off. J. EU 2023, L 234, 48–100. [Google Scholar]
- EU. Directive 2003/87/EC of the European Parliament and of the Council of 13 October 2003. Establishing a Scheme for Greenhouse Gas Emission Allowance Trading Within the Community and Amending Council Directive 96/61/EC. Off. J. Eur. Union 2003, L 275/32. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32003L0087 (accessed on 8 August 2025).
- EU. Directive (EU) 2023/959 of the European Parliament and of the Council of 10 May 2023 amending Directive 2003/87/EC establishing a system for greenhouse gas emission allowance trading within the Union and Decision (EU) 2015/1814 concerning the establishment and operation of a market stability reserve for the Union greenhouse gas emission trading system. Off. J. Eur. Union 2023, L 130/134. [Google Scholar]
- EU. Commission Decision (EU) 2023/1575 of 27 July 2023 on the Union-wide quantity of allowances to be issued under the EU Emissions Trading System for 2024. Off. J. Eur. Union 2023, L 192/30. [Google Scholar]
- Homaio. European Carbon Market: Our Guide for 2025. Available online: https://www.homaio.com/post/eu-ets-definitions-updated-guide (accessed on 30 July 2025).
- von Malmborg, F. Advocacy coalitions and policy change for decarbonization of international maritime transport: The case of FuelEU maritime. Marit. Transp. Res. 2023, 4, 100091. [Google Scholar] [CrossRef]
- DTU. Power-to-X—From Green Energy to Green Fuel. Available online: https://www.dtu.dk/english/research/areas/energy-technology/power-to-x (accessed on 19 January 2025).
- Ingwersen, A.; Hahn Menacho, A.J.; Pfister, S.; Peel, J.N.; Sacchi, R.; Moretti, C. Prospective life cycle assessment of cost-effective pathways for achieving the FuelEU Maritime Regulation targets. Sci. Total Environ. 2025, 958, 177880. [Google Scholar] [CrossRef]
- Oh, J.; Kim, D.; Roussanaly, S.; Lim, Y. Greenhouse gas emissions of shipping with onboard carbon capture under the FuelEU Maritime regulation: A well-to-wake evaluation of different propulsion scenarios. Chem. Eng. J. 2024, 498, 155407. [Google Scholar] [CrossRef]
- Park, S.; Lee, H.; Kim, D. Regulatory compliance and operational efficiency in maritime transport: Strategies and insights. Transp. Policy 2024, 155, 161–177. [Google Scholar] [CrossRef]
- Trosvik, L.; Brynolf, S. Decarbonizing Swedish maritime transport: Scenario analyses of climate policy instruments. Transp. Res. Part D Transp. Environ. 2024, 136, 104457. [Google Scholar] [CrossRef]
- LR. IMO Marine Environment Protection Committee (MEPC 83). Summary Report; LR: London, UK, 2025. [Google Scholar]
- Myhre, G.; Shindell, D.; Bréon, F.-M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- MEPC. RESOLUTION MEPC.278(70). Amendments to MARPOL Annex VI (Data Collection System for Fuel Oil Consumption of Ships); IMO: London, UK, 2016. [Google Scholar]
- MEPC. Resolution MEPC.391(81). 2024 Guidelines on Life Cycle Ghg Intensity of Marine Fuels (2024 LCA Guidelines); IMO: London, UK, 2024. [Google Scholar]
- Bishnoi, R.; Thakur, Y. FuelEU and IMO Net-Zero Framework Explained. Available online: https://www.sustainable-ships.org/stories/qa-normec-verifavia (accessed on 24 July 2025).
- Jallal, C. Strategic Differences Between IMO and EU Decarbonization Regimes. Available online: https://www.rivieramm.com/news-content-hub/news-content-hub/strategic-differences-between-imo-and-eu-decarbonisation-regimes-84771 (accessed on 21 July 2025).
- BetterSea. IMO Net-Zero Framework: Impact on Different Fuel Types and Costs. Available online: https://www.bettersea.tech/post/imo-net-zero-framework-impact-on-different-fuel-types-and-costs (accessed on 27 July 2025).
- Winterstein, S.; Ude, T.C.; Cornell, C.A.; Bjerager, P.; Haver, S. Environmental Parameters for Extreme Response: Inverse FORM with omission Sensitivity. In Proceedings of the ICOSSAR-93, Innsbruck, Austria, 9–13 August 1993. [Google Scholar]
- Leira, B.J. A comparison of stochastic process models for definition of design contours. Struct. Saf. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Leira, B.J.; Chai, W.; Radhakrishnan, G. On Characteristics of Ice Ridges and Icebergs for Design of Ship Hulls in Polar Regions Based on Environmental Design Contours. Appl. Sci. 2021, 11, 5749. [Google Scholar] [CrossRef]
- Garbatov, Y.; Georgiev, P. Carbon Intensity Assessment of a Bulk Carrier Operating in Different Sea State Conditions. J. Mar. Sci. Eng. 2024, 12, 119. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. An exact and invariant first-order reliability format. J. Eng. Mech. Div. ASUE 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Rackwitz, R. First order reliability theories and stochastic models. In Proceedings of the International Conference ICOSSAR’77I, Munich, Germany, 19–21 September 1977. [Google Scholar]
- Rosenblatt, M. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. ASME J. Appl. Mech. Trans. Am. Eng. 1952, 19, 233–234. [Google Scholar] [CrossRef]
- DnV. Recommended Practice: RP-C205 Environmental Conditions and Environmental Loads. 2007. Available online: https://www.dnv.com/energy/standards-guidelines/dnv-rp-c205-environmental-conditions-and-environmental-loads/ (accessed on 7 May 2025).





| IMO | EU | ||
|---|---|---|---|
| Carbon Intensity Index (CII) | GHG Fuel Index (GFI) | FuelEU Maritime Regulation (FEUM) | Emission Trading System (ETS) |
| came into effect on 1 January 2023 | will come into force by March 2027 | came into force on 1 January 2025 | came into force on 1 January 2024 |
| MEPC.352(78) [2]; MEPC.353(78) [3]; MEPC.338(76) [4]; MEPC.354(78) [5]; MEPC.355(78) [6]; MEPC.400(83) [7]. | Circular letter No. 5005 [8] Expected to be formally adopted in October 2025. | Regulation (EU) 2023/1805 [9]. | Directive (EU) 2003/87/EC [10]; Directive (EU) 2023/959 [11]. |
| Aspect | FuelEU | GFS |
|---|---|---|
| Enforcement structures | Direct, legally binding requirements under EU law, which are enforced by member states and monitored by accredited third-party verifiers. | The framework depends on flag-state enforcement through the MARPOL Annex VI regulations. The compliance will be confirmed by the IMO-maintained Global Fuel Intensity (GFI) registry. |
| Economic incentives and penalties | FuelEU functions solely as a penalty-driven model. | GFS closely resembles FuelEU in structure, but it incorporates a global pricing system. |
| Pricing models | FuelEU imposes a fixed penalty of EUR 2400 for each metric ton of VLSFO-equivalent shortfall, irrespective of greenhouse gas intensity performance or global market conditions. | Under the IMO framework, Tier 1 remedial units are valued at USD 100 per metric ton of CO2eq, while Tier 2 remedial units are priced at USD 380 per metric ton. |
| Political drivers | FuelEU was created as part of the EU’s Fit for 55 legislative initiatives. It allows for only limited options for withdrawal or modification, requiring new actions from both the Commission and the Parliament. | IMO moved away from the consensus decision-making process and, by voting during MEPC (83), reached an agreement in response to global trade tensions. |
| Jurisdiction | Regional–Applies to ships using EU ports. | Global–Applies to all IMO member states. |
| Applicability | This applies to ships over 5000 GT operating within the EU, excluding non-commercial vessels, government vessels, and those that use non-mechanical propulsion systems. | Global application of MARPOL for vessels exceeding 5000 GT, with exceptions that may apply based on flag state, geographic region, and type of propulsion. |
| Target Year for Implementation | The regulations will take effect in 2027, with the first reporting period beginning in 2028. | This takes effect from 1 January 2025. |
| Fuel Certification | Fuel suppliers are required to adhere to EU fuel certification regulations, including RED II and FuelEU templates. | The GHG profile of the fuel must be certified according to the IMO Lifecycle Guidelines. |
| Ship Type | 2020 | 2021 | 2022 | 2023 |
|---|---|---|---|---|
| General cargo ship | 1226 | 1237 | 1220 | 1175 |
| Bulk carrier | 3566 | 3553 | 4067 | 3624 |
| Tanker | 1920 | 1994 | 2006 | 1908 |
| Container ship | 1827 | 1716 | 1854 | 1916 |
| Ship Type | Age (Avg), Year | DW (Avg), t |
|---|---|---|
| General cargo ship | 15.8 | 21,779.8 |
| Bulk carrier | 11.4 | 65,058.1 |
| Tanker | 10.8 | 111,305.2 |
| Containership | 14.8 | 80,260.6 |
| Ship Type | Q | , Metric Ton | , Years | ||
|---|---|---|---|---|---|
| Bulk carrier | 1041 (29%) | 0.202 | 0.8 | 56,557 | 5.56 |
| Container ship | 352 (18%) | 0.257 | 0.7 | 104,321 | 5.89 |
| Tanker | 445 (23%) | 0.229 | 0.7 | 149,519 | 3.25 |
| General cargo ship | 568 (48%) | 0.123 | 1.2 | 25,430 | 10.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, P.; Garbatov, Y.; Angelov, A. Analysis of Greenhouse Gas Emissions from Ships Visiting European Ports. Appl. Sci. 2025, 15, 9582. https://doi.org/10.3390/app15179582
Georgiev P, Garbatov Y, Angelov A. Analysis of Greenhouse Gas Emissions from Ships Visiting European Ports. Applied Sciences. 2025; 15(17):9582. https://doi.org/10.3390/app15179582
Chicago/Turabian StyleGeorgiev, Petar, Yordan Garbatov, and Angel Angelov. 2025. "Analysis of Greenhouse Gas Emissions from Ships Visiting European Ports" Applied Sciences 15, no. 17: 9582. https://doi.org/10.3390/app15179582
APA StyleGeorgiev, P., Garbatov, Y., & Angelov, A. (2025). Analysis of Greenhouse Gas Emissions from Ships Visiting European Ports. Applied Sciences, 15(17), 9582. https://doi.org/10.3390/app15179582







