Abstract
In the design of complex products, change propagation often leads to overlapping impact paths, structural conflicts, and decreased coordination efficiency, especially in multi-source change scenarios. These issues limit the effectiveness of existing path extraction and management methods. This study addresses the challenge of managing multi-source change propagation by proposing a novel optimization method. The method involves constructing a multi-layer propagation network model that integrates structural, functional, and form-level information and combines propagation risk assessment with frequency feedback mechanisms. By employing a path cost function based on node risks and propagation probabilities, the model accurately evaluates the costs of change propagation and identifies high-risk paths while prioritizing those with lower costs. Additionally, a multi-source path combination optimization approach is developed, and it dynamically adjusts path costs to reduce overlap and conflicts, improving coordination between paths in multi-source change scenarios. The proposed approach was validated through a case study based on the design data of an intelligent cabin system, where the constructed propagation network reflects real-world structural, functional, and form-level dependencies. The experimental results show that the proposed method reduces total propagation cost by an average of 27.3% and lowers node-level conflict rate by 41.6% compared with baseline methods. Tests on different complex products confirmed consistent advantages over baselines with , while also reducing redundancy and conflicts. The method maintained these advantages across networks of different sizes with linear scalability. Sensitivity analysis confirms that frequency-feedback weighting is the main driver for cost reduction, and the overlap penalty effectively suppresses node congestion. The method provides a robust solution for managing change propagation in complex product design and enhances overall propagation efficiency and system adaptability.
1. Introduction
The design process of complex products (such as aerospace systems, high-end equipment, etc.) usually involves multidisciplinary deep coupling, and its change propagation has significant multi-source and nonlinear conduction characteristics. Such changes form a complex dependency network in the design parameter space, and their dynamic propagation process may lead not only to local performance degradation but also to systemic risks, such as cascading failures. Existing research shows that more than 60% of quality defects and cost overruns in complex product development are due to change propagation control failures. Therefore, one of the key technologies is ensuring the stability and efficiency of the complex product design process by identifying and extracting the propagation path of design changes and then predicting and controlling the propagation impact.
In the design process of complex products, change propagation is a common phenomenon with systemic impacts. Due to multi-level and heterogeneous dependencies within product systems, a change in one design unit often triggers a chain reaction that affects other related units. Numerous studies have investigated change modeling and propagation path analysis. Zhang et al. [1] proposed a design change model that integrates multidisciplinary coupling and parameter information, enabling systematic identification of change propagation paths and supporting resolution decisions. A concept generation and selection framework was introduced to improve the flexibility of engineering changes across the lifecycle. In addition, Hu [2] developed sensitivity-based methods and risk susceptibility analysis to assess propagation impact and to prioritize system elements under uncertainty. Guenther et al. [3] emphasized early-stage change consideration by incorporating propagation analysis into modular platform design, improving product adaptability.
From a path evaluation perspective, Li et al. [4] formulated objective functions to assess multiple propagation routes under renewable resource constraints and optimized change scheduling using simulation and optimization integration. Liu et al. [5] constructed a multi-layer weighted propagation network based on the Function–Behavior–Structure (FBS) model, enriching path representation across design levels. For risk-aware modeling, Yeasin et al. [6] introduced a dynamic Bayesian network to quantify change risks and predict change durations, capturing temporal uncertainty. Li et al. [7] further considered incomplete source information by incorporating gray attack models into risk propagation networks. Ni and colleagues [8] built directed weighted networks of automotive components to model structural dependencies. Similarly, Li et al. [9] combined an enhanced DFMEA with knowledge graphs to evaluate component-level risks in complex systems. Efforts have also been made in predictive methods and design support tools. Tang et al. [10] proposed a change propagation algorithm for aircraft tool design and developed a computer-aided forecasting system. Shankar et al. [11] presented a validation planning method to mitigate change impacts during engineering design and manufacturing. Sarica [12] modeled propagation as an infinite regress problem and used eigenvector analysis to quantify component influence and sensitivity. Wynn et al. [13] developed iterative resource-demand models that consider concurrency and multi-source changes to assess schedule risks. In addition, formal modeling approaches have been explored. Gan et al. [14] constructed a Petri-Net-based model for attribute-level design changes and embedded optimization using ant colony algorithms. Chua and Hossain [15] introduced a predictive model based on stage-dependent change magnitudes to assess downstream impacts. Eltaief et al. [16] developed a matrix-based method for change risk quantification and built a structure–task network for risk evaluation in complex designs.
These studies have collectively advanced multi-source change modeling, propagation mechanism understanding, and risk quantification, forming a strong foundation for change impact management. However, a key challenge remains: existing models often lack integration of dynamic feedback mechanisms during propagation, making it difficult to characterize the temporal, nonlinear, and coupled effects of changes across product stages and design units. This limits their effectiveness in accurately predicting the scope and intensity of change propagation.
The extraction of change propagation paths forms the basis for identifying potential impact scopes, locating sensitive design regions, and enabling timely coordination among collaborative teams. Existing studies have developed various modeling and extraction techniques, including Design Structure Matrices (DSMs), complex network models, and Petri Nets. For path modeling and propagation structure analysis, Ma [17] constructed a semantic model of design features and a change analysis network, proposing an adaptive strategy to optimize parallel propagation paths in multi-source change scenarios. A multi-agent framework was also introduced to enable controllable mechanisms where propagation effects could be absorbed or neutralized. Li et al. [18] built a component association model based on small-world network theory, with edge weights capturing change intensity, cost, and response time. They applied ant colony optimization to address multi-objective path optimization in the context of motorcycle engine design. Zheng et al. [19] proposed a dual-layer mechanism combining upstream dynamic optimization and downstream path search to generate globally coordinated change paths within a feature-association network. In the domain of optimization algorithm design, Wang et al. [20] addressed configuration updates in sanitation vehicle design by constructing a change impact network and enhancing ant colony optimization with a penalty-based weight control mechanism to reduce inter-module conflicts. Song et al. [21] integrated reinforcement learning with differential evolution through a DDQN-DE algorithm, enabling dynamic selection of search strategies for multi-objective optimization with respect to cost, time, and performance. Zhan et al. [22] developed a temporal differential optimization algorithm based on an extension-theory-based parameter network, aiming to improve adaptability to time-varying design conditions through cost-sensitive path modeling. In terms of intelligent decision modeling, Xing et al. [23] introduced a process-driven decision model based on prospect theory, incorporating the psychological characteristics of design agents. A dual-layer encoding method was proposed to identify change paths with minimal cognitive disturbance, offering a new perspective on agent-aware propagation modeling. Regarding practical engineering validation, Chen et al. [24] developed a parallel search strategy tailored for large-scale, multi-source change environments, which significantly improved extraction efficiency in complex structures. Ricoh and Cadence [25] demonstrated the value of incremental extraction techniques in system-on-chip (SoC) design, allowing localized re-evaluation of affected network segments without full reanalysis.
Collectively, these studies have advanced the field in terms of network construction, propagation modeling, and optimization strategy development. However, several limitations persist. Although various approaches have been developed for change propagation modeling and path optimization, they differ significantly in network representation, integration of heterogeneous design layers, use of dynamic feedback mechanisms, and strategies for conflict control. Table 1 summarizes representative prior methods and compares their core features with those of the proposed method. Most optimization strategies rely on heuristic or evolutionary search and do not incorporate feedback mechanisms such as propagation frequency or historical change behaviors. In addition, existing methods for path coordination and conflict resolution in multi-source scenarios remain underdeveloped, which restricts the scalability and global optimality of path planning under concurrent change conditions.

Table 1.
Comparison of representative prior methods and the proposed method.
This study proposes a multi-source change propagation path optimization method for complex product design, which mainly includes three links: propagation network modeling, risk perception path extraction, and multi-source path optimization. Firstly, a communication network that integrates the information-dependent information of the structure, function, and form layers is constructed to expand the expression ability of the traditional communication graph model. Secondly, the node risk is estimated based on the topological structure features, and the path cost function is constructed based on the edge propagation probability so as to guide the path extraction process to identify more risk-sensitive propagation paths. On this basis, a multi-source path combination optimization method based on candidate path frequency feedback is designed, and it dynamically adjusts the propagation cost while extracting the paths, effectively reducing the conflict and overlap between paths, and improving the coordination of multi-source propagation.
The main contributions of this paper are reflected in two aspects:
- A novel multi-dimensional propagation network modeling framework is proposed, which integrates heterogeneous features and significantly improves the structural integrity and engineering interpretability of propagation dynamics.
- A risk-frequency-guided path optimization method is designed, achieving an optimal balance between conflict mitigation and cost efficiency in multi-source propagation scenarios.
The remainder of this paper is organized as follows: Section 2 presents the proposed multi-layer propagation network model, the path cost definition, and the multi-source path combination optimization method. Section 3 presents the experimental results from the intelligent cabin case study and additional validations on other complex product networks. Section 4 discusses the parameter sensitivity, computational aspects, applicability, and limitations of the method. Section 5 concludes the paper and highlights future research directions.
2. Materials and Methods
2.1. Change Network Construction
2.1.1. Change Network Layer
Constructing a design knowledge ontology model for complex product design changes can reveal the interaction mechanism between complex product components. Functional requirements often need to be carried and met through specific structures, and changes in structural elements will have an impact on the product design, so the product form will change accordingly. Structure is not only the main body of function realization, but it also constitutes the medium through which appearance changes are transmitted between function and form. Therefore, the design scheme during early design stages is divided into three layers: function, structure, and form. In order to further analyze the design status of complex products before the change, the design objects of complex products are divided according to the product modules and change requirements. Subsequently, the detailed design scheme of each design object is broken down into three types of design elements: function, form, and structure. On this basis, the three types of elements involved in the design object are extracted, and the correlation relationship within the same level and the mapping relationship between different levels are clarified. The extracted features are defined as network nodes, and the associations between them are used as edges in the network. Finally, the design scheme is mapped to a design change network model composed of object nodes, function nodes, structure nodes, form nodes, and the connecting edges between them, in which the function nodes, structure nodes, and form nodes belong to the design content nodes, as shown in Figure 1.
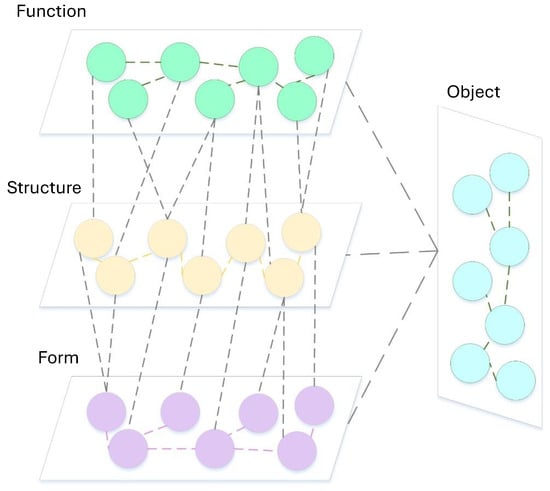
Figure 1.
Complex product network extracted from an intelligent cabin.
- (1)
- Construction of the structure-layer network framework
The structure is the core element that forms the detailed design scheme and is the bridge that connects function and form. Uncertainty in the structural layer mainly arises from incomplete or inconsistent design documentation, leading to missing or incorrect physical connection relationships between components. Since the structural layer determines network connectivity and feasible propagation paths, such inaccuracies can result in underestimation or overestimation of propagation risks, thereby affecting path cost calculation and optimization results. Structural information is cross-validated through multiple design documents, structured interviews with design teams, and relationship mining from historical change records. This ensures the completeness and reliability of network connections. The detailed design phase often results in a complete digital structure model. First, the connection structures in the scheme are extracted, and then the structure elements are derived from the connection parts at both ends of each connection structure. These structural elements are extracted as network nodes, and connecting edges are established based on their connection relationships. Subsequently, a structure-layer network model is generated.
- (2)
- Construction of the function-layer network framework
Uncertainty in the function layer often arises from unclear functional requirements, evolving user needs, or incomplete functional decomposition during early design stages. As the function layer defines logical dependencies between functions, any missing or incorrect dependency can alter the set of functional propagation chains and affect cross-layer mapping to the structural layer. This, in turn, impacts risk propagation assessment and optimization accuracy. Functional dependencies are verified by analyzing functional implementation scenarios. This involves requirement specification checks, validation against functional decomposition diagrams, and targeted discussions with functional engineers to capture missing or evolving relationships. Based on the availability of product features, the feature implementation process is subdivided into several scenarios in which users interact with the product, and each story contains an action. Function nodes are identified based on actions, and the behavior target of each action is the content of the function node. Subsequently, the interaction sequence is considered, and the relationship between functional elements is analyzed. When the implementation of function A is a necessary condition for the implementation of function B, the connection between the nodes of function A and function B is established to complete the construction of the network model of the function layer. Based on the function–behavior–structure mapping method, the structure required to achieve each function is analyzed, and the mapping relationship between the function layer and the structure layer is established.
- (3)
- Construction of the form-layer network framework
The detailed design scheme is presented in the form of design content through elements. The form layer is affected by uncertainty due to measurement errors in dimensions, missing material property data, or incomplete records of visual attributes. Since the form layer directly affects propagation probabilities and risk coefficients on its edges, such uncertainty can alter calculated path costs and influence the ranking of propagation paths in optimization. The process begins with the content of the form design and extracts form nodes from different dimensions. It then incorporates inspection and testing data and leverages historical quality records to avoid content omissions. The design content of form nodes includes properties such as material, color, and shape. Modules within the user’s visual range are extracted from the design scheme as form nodes, and connections are made when they share consistency in any of these properties.
- (4)
- Construction of the object-layer network framework
After constructing the hierarchical framework of function, structure, and form, the next step is to identify design object nodes that represent physical or functional modules affected by changes. These object nodes are extracted based on modular decomposition and change requirements in the design task. For each object, its associated design content—spanning function, structure, and form elements—is analyzed to determine influence relationships. If a content node exerts influence on an object, a link is established between them to capture potential change propagation.
2.1.2. Weighted Calculation
After constructing the function, form, and object layers, the network framework describes the relationships among different design elements. However, these relationships remain qualitative and do not capture variations in the strength of interactions. To make them quantitative, edge weights are introduced to represent the degree of dependency between different types of nodes. By incorporating weights, the framework can more accurately capture the influence among design elements and provide a solid basis for subsequent propagation analysis and optimization. The weight calculation method varies depending on the different nodes on both sides of the edge within the network. Depending on the design content node type, the network has five types of design content edges. The weights are calculated as follows:
- (1)
- Calculation of the weights of structure-to-structure edges
The implementation of a feature is closely related to the physical structure. The relationship between the structures in the design scheme mainly includes four aspects: contact mode, combination mode, combination of tool types, and connection degrees of freedom. These four indicators are assigned the same weighting factor. Quantitative evaluation criteria are shown in Table 2. The contact type refers to the contact mode between structural parts in the assembly state, such as point contact, line contact, or surface contact; the larger the contact area, the more stable the connection, and the greater the influence range when changing. The tool represents the type of tool required to disassemble the structural connection, and large or specialized tools usually mean that the disassembly is complex, which indirectly increases the probability of change propagation between structures. The disassembly method describes the assembly form of the structural connection, such as insertion, screw-in, non-detachable, etc., which determines its maintainability and change cost. Degrees of freedom represent the number of directions of motion that can be achieved before the connected parts are constrained, and the higher the degrees of freedom of constraints, the stronger the structural dependencies and the greater the influence on other structures. The correlation strength is a qualitative description after the comprehensive evaluation of the above factors, which reflects the overall coupling strength between the structures in terms of physical connection and design dependence.

Table 2.
Computation method for structure–structure edge weights.
- (2)
- Calculation of the weights of function–structure edges
The connotation of function–structure edge weights reflects the role of each structural component in achieving a given function. When a function is associated with only one structural element, the edge weight is assigned as 1.0 by definition. For functions associated with multiple structural elements, their relative importance is evaluated by comparing the contribution of each structure to achieving higher-level function. In this evaluation, designers were asked to assess a set of representative function–structure interaction scenarios. Consensus values were then assigned to each relation type based on the perceived functional contribution. This assessment aimed to capture the design rationale in which structural components may serve as enablers, constraints, or passive carriers of function, depending on their level of integration and operational role [8]. The final weight values were computed as the average of normalized scores assigned by a group of experienced industrial designers. The relationship types and their corresponding weight values used in the structural importance matrix are summarized in Table 3.

Table 3.
Relation types between structural elements and functional components.
- (3)
- Calculation of the function–function weight
In the functional-layer network framework, a connection with a weight of 1 is established between two functions if their implementations directly depend on each other. A DSM method is further employed to capture nuanced functional interdependencies by analyzing both task flow and information flow among functional units [26]. Each functional node is assessed for whether it provides information or task support to another, with DSM entries populated accordingly, and the strength of interactions is quantified through the frequency and depth of cross-functional exchanges recorded in the DSM. The sum of outgoing and incoming couplings is computed for each functional pair to capture how much a function sends and receives. These aggregated coupling degrees are then normalized to the range [0, 1] and used as edge weights in the functional network.
- (4)
- Calculation of the weights of structure–form edges
The structure–form edge weights indicate the extent to which formal elements influence corresponding structural components in the function implementation. These weights were derived through a combination of questionnaires and interviews with both professional designers and design students, who evaluated the impact of form on structure across different design scenarios. The correlation strength between form nodes and structure nodes is evaluated from two main perspectives: (1) mutual influence between structure and form, including both the structural constraints on aesthetic form and the form constraints on structural ergonomics; (2) the synergy of structure and form in supporting function realization. This synergy was examined through a survey involving both design professionals and students, where participants were asked to rate the degree of structure–form interaction in terms of these two perspectives. Ratings were given on a normalized scale from 0 to 1, where higher values indicate stronger correlation. The final values are shown in Table 4.

Table 4.
Scoring for structure–form correlation strength (two-direction model).
- (5)
- Calculation of form–form edge weight
The weight between form nodes is evaluated along three factors: shape, color, and material.
is the shape similarity assigned by designers; is the cosine similarity between color vectors; indicates whether the two forms use the same material in production. The division by 3 keeps without changing the relative ordering of edges. Together, these components define a unified weight that quantitatively represents the strength of relationships between form nodes.
- (6)
- Object-content edge weight calculation
Function, form, and structure are all industrial design content nodes, which are the attributes of each design object. The weight of the connection between the design object and the design content in the network is marked as 1, which means that the design task for the design object contains the design content.
2.2. Path Extract and Optimization
2.2.1. Path Cost Calculation
In the design network of complex products, change propagation often follows directed paths across related nodes. The propagation cost of such paths depends not only on the strength of the structural connections along the path but also on the vulnerability of the terminal node and the network-wide potential for uncontrolled continuation. A cost function is proposed to quantify the effectiveness and controllability of propagation paths by incorporating propagation probability, frequency-based structural feedback, and terminal-node risk. The cost model is derived from the basic mechanism of structural transmission and is mathematically coherent and physically interpretable.
Consider a propagation path (denoted as P), where , where each edge represents a potential transmission between two design elements. The cost of each edge is inversely related to its propagation probability , which characterizes the likelihood that a change successfully propagates from to . A higher value of implies lower resistance and, thus, lower cost. In this work, the propagation probability on edge is defined from the edge weight.
However, during path enumeration, certain edges may be repeatedly selected, forming structural bottlenecks and increasing design-level conflicts. Such high-usage edges are penalized by introducing a feedback variable , which denotes the frequency of edge usage across candidate paths. Its effect on the edge cost is modulated by a hyperparameter , and a small constant ensures numerical stability. The cost of edge is, thus, defined as
The total resistance of path is the sum of its edge costs:
This expression captures the cumulative difficulty of propagation through the path. However, it does not fully reflect the overall cost of change propagation. In real-world scenarios, change propagation starts at the source and terminates at a specific node . Whether the change stops at or continues to spread downstream depends on the structural robustness and containment capacity of .
If the terminal node has high modular independence or design redundancy, the change is more likely to be absorbed locally, limiting its overall impact. In contrast, if the node is tightly coupled with other components, unstable, or sensitive to perturbations, the change is more likely to spread beyond it. Therefore, the ability of the terminal node to block further propagation significantly affects the total cost of the path. This mechanism is modeled by introducing a terminal risk coefficient , which reflects the difficulty or cost associated with terminating propagation at . A higher value of implies that the path is less likely to stop at this node and, thus, incurs a higher termination cost. The terminal risk is computed as a weighted average of node-level structural impact over the path as follows:
Here, denotes the local structural weight of node , indicating its coupling intensity, and is the influence of the node, which is defined as
where is the clustering coefficient, and is the centrality of node . This formulation captures both the local structure and global influence, allowing to serve as a proxy for the propagation containment difficulty.
The overall cost of path is then defined by multiplying the cumulative edge resistance by the terminal-node risk.
In addition, when all nodes along the path belong to the same design object, the propagation is considered intra-object and less costly to coordinate. This is reflected by applying a half-weight adjustment to the total cost as follows:
2.2.2. Single-Source Path Extraction
Based on the proposed propagation cost model, this study extracts multiple feasible propagation paths for each change source node using a cost-based evaluation strategy. For a given set of source nodes , where each represents a potential origin of change, the algorithm employs the shortest_simple_paths method to enumerate candidate paths in non-decreasing order of cost.
In the initial extraction stage, the cost function is simplified by setting in Equation (2), meaning that only the propagation probability is considered, and frequency-based feedback is excluded. This ensures that the extracted paths reflect the inherent structural propagation potential. For each source node, only the top-K paths with the lowest initial cost are retained, which effectively controls the size of the candidate set while maintaining high-quality options.
During this process, an edge frequency map is maintained. Each time an edge appears in any extracted path from any source, its usage count is incremented. This global frequency profile records the reliance on each structural link and is later used for cost updating.
2.2.3. Cost Update
In the cost update phase, the usage frequency information is incorporated into the propagation cost function by updating in Equation (2). The updated edge costs are then used to recompute the path cost using Equation (6) (or Equation (7) for intra-object paths), where is the terminal-node risk defined in Equation (4). This update reflects both local propagation probabilities and global structural utilization patterns.
2.2.4. Multi-Source Path Optimization
After obtaining the updated candidate paths for all sources, an integer programming model is used to select an optimal subset of paths. The decision variable indicates whether candidate path is selected. Node visitation variables count how many selected paths pass through node v.
The primary objective follows a weighted-sum formulation,
where controls the penalty for node overlap. In practice, additional multi-objective optimization strategies such as the -constraint method and lexicographic optimization can be applied to explore the Pareto front of .
The following two constraints are enforced:
ensuring that exactly one path is selected for each source node s, and
ensuring correct node visitation counts for overlap penalty computation.
Together, these constraints ensure that the optimization process assigns one valid path to each change source while also accounting for node-level conflicts, which are penalized through the second term in the objective function. This mechanism allows the model to balance propagation efficiency with structural coordination in multi-source change scenarios.
The optimization method is implemented in Python (version 3.10.12) using the PuLP library (version 2.7.0). PuLP is employed to formulate and solve the integer programming model, in which node visitation variables are explicitly incorporated into the objective function to discourage the repeated use of the same nodes across different source paths. This mechanism reduces structural overlap and enhances the system’s capacity and scalability for handling concurrent changes. After solving the model, the implementation outputs the optimal propagation path for each source node along with the global node visitation distribution, thereby providing an automated computational workflow that integrates cost modeling, frequency-based feedback updating, and global optimization.
3. Results
The effectiveness of the proposed change propagation path extraction method under different conditions was evaluated through two experiments. The first experiment used a network derived from a real-world intelligent cabin design project, aiming to verify the method’s applicability in an actual engineering context. The second experiment was conducted on a simulated network, allowing for the systematic control of network structure and propagation characteristics for comparative analysis. All experiments were implemented in Python 3.11 and executed on a standard laptop without GPU acceleration (Intel Core i7 processor, 16 GB RAM, Windows 11 OS).
3.1. Experimental Validation on a Real-World Intelligent Cabin Network
The first experiment aims to evaluate the applicability and effectiveness of the proposed change propagation path extraction method in an actual engineering scenario. The experiments were conducted on a complex product network constructed from a real-world intelligent cabin design project. This network contains 115 nodes covering three design layers and the corresponding object layer; nodes 1–34 represent object nodes (indicated in blue), nodes 41–60 represent function nodes (represented in green), nodes 71–114 represent structure nodes (shown in orange), and nodes 120–136 represent form nodes (shown in purple), as shown in Figure 2. In the network, the color of each edge is the same as that of the nodes in its layer. Cross-layer edges are shown in gray. The thickness of the edges reflects the weight magnitude. This network incorporates actual structural modules, functional interactions, and form elements. The data were obtained through component analysis and design decomposition of the intelligent cabin configuration used in a commercial vehicle platform. Seven representative source nodes were selected from different levels to simulate realistic multi-source change propagation scenarios. All methods in this experiment were executed on the same network with identical source nodes.
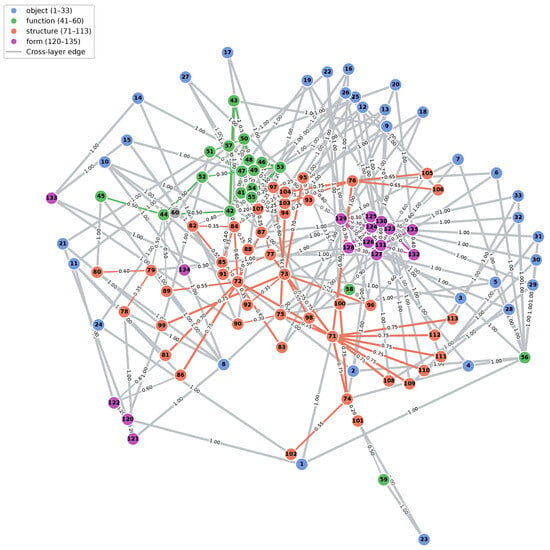
Figure 2.
Complex product network extracted from an intelligent cabin.
Figure 3, Figure 4 and Figure 5 present the path structures and node heat distributions for the proposed method, the Dijkstra method, and the DSM method. The three heatmaps use a unified color scale (0–4) to indicate visit counts: node colors represent how many times each node is traversed, while edge colors and widths represent edge visit counts. Darker colors and thicker edges indicate higher counts, whereas zero visits appear in lighter colors with thinner edges. Source nodes are highlighted with red outlines (other nodes have black outlines). By comparing the three heatmaps, one can observe the overlaps and differences in path usage across the methods.
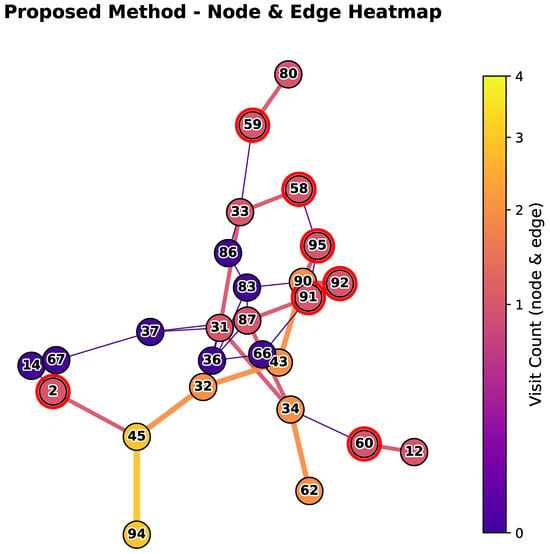
Figure 3.
Heatmap and path of the proposed method.
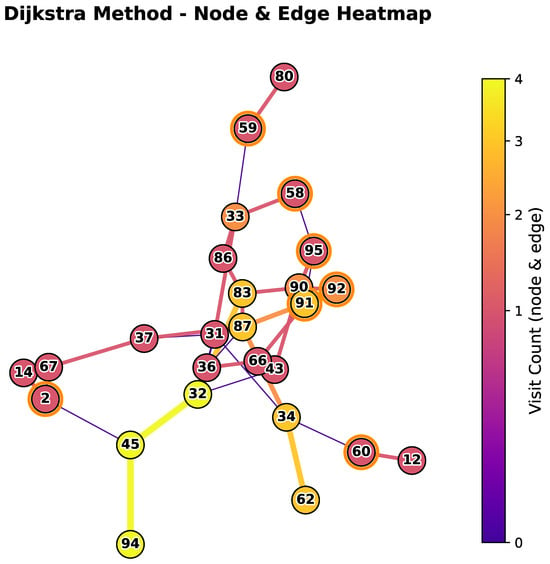
Figure 4.
Heatmap and path of the Dijkstra method.
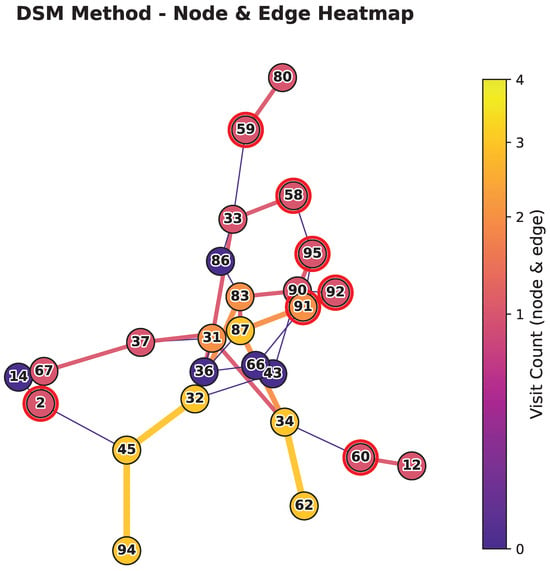
Figure 5.
Heatmap and path of the DSM method.
In Figure 3, the proposed method generates three relatively independent linear paths, covering node sequences such as 59–80, 2–45–94, and 58–33–95, with a main backbone connecting through nodes 34 and 31. The heatmap shows a band-like gradient in access frequency, with high-frequency nodes confined to internal segments of the paths and no visible hotspot concentration. The paths exhibit minimal overlap and form a compact structure, indicating effective control of node conflicts and balanced routing decisions.
Figure 4 shows the result of the Dijkstra method, where the paths form a dense and entangled network. Nodes such as 33, 90, and 86 display significantly high access frequencies and emerge as hotspot centers. The paths heavily overlap around these nodes, forming redundant cycles and small loops, which leads to spatial clutter and excessive path redundancy. Several source nodes (e.g., 59 and 60) must traverse long detours to connect to the main structure, resulting in a loose topology and high risk of conflict due to load concentration.
In Figure 5, the DSM method shows intermediate performance. The overall structure forms a Y-shape, with node 31 serving as a central junction connecting three major branches toward nodes 59, 2, and 60. The heatmap reveals that nodes such as 31 and 34 still carry relatively high access frequencies, but the hotspot area is more constrained than the Dijkstra method, while the paths are clearer and the number of redundant links is reduced; some path overlaps and local load concentration remain.
The effectiveness of the proposed path extraction method was evaluated by comparing it with the classical Dijkstra algorithm and the DSM method. Five evaluation metrics were employed to capture the structural and cost implications of change propagation. The average propagation cost measures the expected per-path impact of a single change, reflecting the average system cost per propagation event. A lower value suggests a reduced likelihood of secondary changes or reworking. The average path length corresponds to the number of hops or steps a change signal must traverse. Shorter paths reduce the risk of information attenuation, dependency accumulation, and uncontrolled spread. The node redundancy rate quantifies the degree of node overlap among selected paths, where high redundancy indicates shared bottlenecks and greater vulnerability to cascading failures. The max node conflict denotes the maximum concurrent access to any node across all paths, which is indicative of congestion or scheduling conflicts, with higher values suggesting potential delays and organizational disruption. Finally, the total cost aggregates the overall change impact across all selected paths, aligning with budgetary and scheduling constraints. Collectively, these indicators reflect propagation intensity, efficiency, structural resilience, congestion risk, and cumulative system burden.
As shown in Table 5, the proposed method consistently outperforms the baselines across all metrics. The average propagation cost is 0.2525, which is significantly lower than that of Dijkstra (0.5478) and DSM (0.3608), with corresponding p-values of 0.00013 and 0.00457, respectively. This indicates a clear improvement in propagation efficiency. The average path length of 3.67 is also significantly shorter than that of Dijkstra (6.83, p = 0.00087) and DSM (4.83, p = 0.0213), helping reduce the overall path complexity. In terms of node redundancy, the proposed method yields a rate of 0.2222, which is lower than that of Dijkstra (0.3846, p = 0.00132) and DSM (0.3500, p = 0.0184), suggesting more efficient node usage. The maximum node conflict is reduced to 2, whereas both Dijkstra and DSM have conflicts of 3, indicating better conflict control, although no statistical tests were applied here. When considering both the propagation cost and structural complexity, the proposed method achieves the lowest total cost of 1.5152, compared with 3.2869 for Dijkstra and 2.1649 for DSM. The p-values (0.00004 and 0.00210, respectively) confirm the significance of this improvement. In summary, the proposed method demonstrates statistically significant and consistent improvements in path compactness, propagation efficiency, and conflict reduction compared with existing methods.

Table 5.
Comparison of path extraction methods in intelligent cabin network.
3.2. Experimental Validation on a Simulated Propagation Network
The effectiveness and generality of the proposed method were evaluated through experiments on three representative multi-layered engineering networks: a wind turbine drivetrain system, an electric vehicle (EV) e-drive system, and an exoskeleton manipulator system. For each network, approximately 200 nodes were simulated according to product characteristics rather than using real-world data, ensuring that the connectivity patterns and layer distributions reflect realistic engineering architectures. Each network was organized into functional, structural, and formal layers based on domain knowledge, but with different dominant characteristics; the wind turbine network (210 nodes, 424 edges, average degree ≈ 4.0) emphasizes functional flows of energy and torque transmission, the EV e-drive network (240 nodes, 1400 edges, average degree ≈ 11.7) contains dense structural connections among components in the powertrain, and the exoskeleton manipulator network (270 nodes, 1700 edges, average degree ≈ 12.6) exhibits a pronounced formal hierarchy of joints and actuators.
In the data preparation stage, source nodes across all three layers were randomly selected to simulate realistic design-change scenarios involving multiple origins and cross-layer propagation. All experiments applied the same propagation evaluation model and cost computation procedures. In the path extraction stage, three methods were compared: the proposed method, the k-shortest simple paths approach (KSSP) [27], and a directed routing strategy (DRSP) [28]. After extracting candidate paths, the resulting propagation characteristics were assessed using quantitative indicators including path length, cumulative cost, and layer-wise propagation extent.
Table 6 presents the experimental results with 95% confidence intervals and significance annotations. Across all three networks, the proposed method consistently achieves the lowest average propagation cost and total cost, with statistically significant improvements () over both baselines. In the wind turbine and EV networks, the proposed method also outperforms the baselines in terms of average path length and node redundancy, indicating superior control over both propagation efficiency and structural dispersion. In particular, the reduced redundancy implies that the selected paths are more structurally diverse, mitigating risks of common bottlenecks and simultaneous failures. In the exoskeleton manipulator network, although the proposed method exhibits slightly longer path lengths than KSSP, it still achieves the best performance in cost-related metrics. The proposed method incorporates a structural risk avoidance mechanism during path extraction, actively bypassing highly coupled or high-centrality nodes, which may result in slightly longer paths. In return, the cost function, which integrates frequency feedback and structural centrality, effectively steers propagation away from high-risk regions, thereby significantly reducing the overall propagation cost.

Table 6.
Comparison of path extraction methods in simulated propagation network.
Overall, the proposed method demonstrates consistent and significant advantages across different network topologies. The improvements are observed not only in cost efficiency but also in the structural robustness of the propagation paths. These results validate the proposed mechanism’s adaptability and scalability, making it well suited for complex engineering systems with layered architectures and heterogeneous dependencies. The results also show that the proposed method consistently outperforms the baselines across all three datasets, with stable advantages in cases dominated by functional flows, dense structural connections, and pronounced formal hierarchies, indicating that the method maintains high sensitivity and adaptability to different dominant layer types.
4. Discussion
The experimental results demonstrate that the proposed method achieves significant improvements in both propagation efficiency and structural coordination compared with the baseline approaches. This section discusses the underlying factors contributing to these improvements and the practical implications for change management in complex product design.
4.1. Sensitivity to and
A systematic sensitivity analysis was conducted on two key hyperparameters, the frequency-feedback weight and the node-overlap penalty , to assess their impact on path extraction quality and multi-source coordination. The experiments were performed on a graph of size , with the number of candidate paths per source fixed at . Starting from the default setting , and were varied over the set . Each configuration was repeated times with different random seeds to control for stochastic variation, while keeping the graph structure and edge-weight perturbations fixed. The recorded metrics include average propagation cost, total propagation cost, maximum node conflict, and runtime (mean ± 95% CI), as shown in Table 7. Average path length and redundancy are omitted from the main table due to near-zero variance under this topology, which is dominated by one-hop selections.

Table 7.
Sensitivity and ablation at (, ). Lower is better.
The results show that is strongly associated with the propagation cost, while mainly affects node conflicts. Specifically, removing frequency feedback (i.e., ) leads to a substantial increase in both average and total costs, which rise to and , respectively, compared with the default values of and . This indicates that, in the absence of frequency guidance, path selection tends to overuse frequently traversed but structurally expensive regions. In contrast, setting results in the lowest observed costs ( average and total), without increasing node conflicts. This suggests that strong frequency feedback effectively encourages efficient path selection without compromising structural coordination.
On the other hand, the overlap penalty has limited influence on the propagation cost but plays an important role in conflict suppression. When , the maximum node conflict increases to , while the cost remains nearly unchanged at , close to the default setting. This confirms that successfully reduces structural congestion. Notably, further increasing beyond 1 does not yield additional conflict reduction, implying that a moderate penalty is sufficient to suppress most path overlap issues.
4.2. Computational Complexity
The scalability of the proposed method in product design networks is evaluated in this section by analyzing both time and space complexity. The estimation focuses on the core steps of the algorithm, namely path enumeration, search procedures, and the storage and management of candidate paths.
For a single source node s and target node t, the enumeration of propagation paths has a time complexity of
where n and m denote the number of nodes and edges, respectively, and U is the upper bound of candidate paths. Each path generation depends on shortest-path search and sorting operations, which introduce the factor. When the process is repeated across all source–target pairs, the total time complexity becomes
where S is the number of source nodes and L is the average path length. This indicates that the overall computational cost grows linearly with the candidate path bound U, the average path length L, and the source node scale S.
The space complexity is mainly determined by two parts: graph storage using adjacency lists and the storage of candidate paths. The former requires space. If each source–target pair retains K candidate paths with an average length of ℓ, the additional storage cost is
This shows that space consumption grows linearly with the graph size, while also being affected by the number and length of candidate paths.
From the theoretical derivation and the experimental results in Table 8, the method remains within polynomial complexity. For small- to medium-scale product networks, when the candidate path bound U, the retained path number K, and the average path length ℓ are reasonably constrained, both computational and storage costs remain manageable. The consistency between theoretical analysis and empirical results suggests that the proposed method achieves a balance between accuracy and efficiency and provides sufficient scalability for practical change propagation analysis in product design networks.

Table 8.
Scalability results on synthetic networks (mean ± 95% CI, ).
4.3. Convergence Analysis
After candidate paths are generated, the method applies a mixed-integer programming (MIP) model to select one path per source. This model is formulated as a 0–1 integer linear program and solved using an exact solver, which guarantees global optimality. Both the weighted-sum and epsilon-constraint formulations explore the approximate Pareto front within the fixed candidate pool without relying on initialization or gradient information, ensuring stable global search behavior. In addition, the lexicographic variant uses a two-phase strategy; it first minimizes the total cost and then minimizes the number of visited nodes within a cost tolerance range. This design provides explicit control over optimality. Overall, the proposed optimization stage has guaranteed convergence in theory and shows consistent solution quality in practice.
4.4. Computational Cost and Scalability
Table 8 reports the runtime and peak memory usage of the method on synthetic graphs of varying sizes. As the number of nodes increases from 200 to 1200, the runtime grows from about 1 s to around 20 s, and the memory usage increases from 0.7 MB to 2.4 MB. This trend indicates stable and acceptable computational costs under typical task sizes. The method also exhibits good structural scalability. Path generation for different pairs is independent and can be parallelized across threads or machines. Frequency aggregation and candidate merging are also simple to distribute. Overall, the method has a simple structure and controllable parameters and is well suited for deployment on a variety of platforms.
5. Conclusions
This study addresses the problem of organizing and optimizing multi-source change propagation paths in complex product design. A design propagation network model integrating functional, structural, and form-level information is constructed. By introducing a composite edge resistance function based on propagation probability and frequency feedback, along with a path cost function amplified by terminal-node risk, a coherent and interpretable mechanism for path evaluation and selection is developed. Furthermore, a mixed-integer programming model is applied to identify the optimal path set under global conflict constraints.
The experimental results demonstrate that the proposed method achieves significant improvements in multi-source path conflict control and propagation risk reduction compared with existing DSM-based approaches. Specifically, the total propagation cost is reduced by an average of 27.3%, and the node-level conflict rate is lowered by 41.6%, indicating the method’s suitability for structural coordination and propagation planning during the early stages of design. From a practical perspective, the proposed method provides designers with a systematic tool for analyzing and predicting the impact of changes in complex product design. The design network can be instantiated from requirement documents, bills of materials and change logs; observable measures are normalized into edge weights, and the proposed analysis is executed within the existing engineering change management workflow. Once the design network is constructed, the method enables the quantification of dependencies among different design elements and the computation of potential propagation paths, thereby identifying the critical nodes involved in a change and the range of elements that may be affected. By using this analysis to support design decisions, designers can plan change paths before implementation and avoid rework and resource waste caused by conflicts in change propagation. Consequently, the method not only enhances the transparency and controllability of the design process but also contributes to reducing iteration costs and improving the robustness and efficiency of complex product development. Overall, the method addresses the practical problem of unpredictable change propagation by making its impact visible and quantifiable, supporting prioritization and conflict avoidance, and thereby reducing rework and cycle time in complex product development.
Despite its theoretical and empirical advantages, several limitations remain. First, the model assumes that propagation probabilities and risk coefficients are accurately known, which may not hold in real-world design scenarios with uncertainty. Second, the current formulation focuses on static structural propagation and does not consider the temporal sequence of changes. Third, some edge weights are based on expert estimation, which may introduce subjectivity. External factors (e.g., regulations, market demands, and environmental conditions) are not explicitly modeled but can be indirectly incorporated via expert knowledge when defining relation strengths and risk parameters.
Future work will address these limitations by incorporating uncertainty modeling into key parameters, extending the model to dynamic change flows, and leveraging design data to calibrate edge weights in a more objective and transferable manner. In addition, future work will involve probabilistic modeling of external factors to enhance full life cycle applicability. Furthermore, the proposed approach will be validated and refined through practical case studies to ensure its robustness and effectiveness in real-world applications.
Author Contributions
Conceptualization, Y.S. and D.C.; methodology, Y.S.; software, H.W.; writing—original draft preparation, Y.S.; writing—review and editing, Y.Z.; visualization, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Shaanxi Province Key RD Program, Research on a Dynamic Three-dimensional Evaluation Model for Working Comfort in Manned Confined Cabins (2022GY-311), and the Shaanxi Provincial Special Branch Program Leading Talent Project (W099115). There was no additional external funding received for this study.
Data Availability Statement
Data are available upon request due to restrictions.
Acknowledgments
The authors thank the people or institutions that helped them in the preparation of the manuscript. The authors thank the reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, H.Z.; Ding, G.F.; Li, R.; Qin, S.F.; Yan, K.Y. Design Change Model for Effective Scheduling Change Propagation Paths. Chin. J. Mech. Eng. 2017, 30, 1081–1090. [Google Scholar] [CrossRef]
- Junfei, H.U. Flexible Engineering System Design with Multiple Exogenous Uncertainties and Change Propagation. Flex. Eng. Syst. Des. 2012, 6, 214–225. [Google Scholar]
- Schuh, G.; Riesener, M.; Breunig, S. Design for Changeability: Incorporating Change Propagation Analysis in Modular Product Platform Design. Procedia CIRP 2017, 61, 63–68. [Google Scholar] [CrossRef]
- Yuliang, L.; Wei, Z.; Jie, Z. Resource-constrained scheduling of design changes based on simulation of change propagation process in the complex engineering design. Res. Eng. Des. 2019, 30, 21–40. [Google Scholar]
- Liu, Q.; Li, C.; Chen, X.; Qu, T. Research on module partition of complex products considering influence of change propagation. Adv. Eng. Inform. 2024, 60, 102384. [Google Scholar] [CrossRef]
- Yeasin, F.N.; Grenn, M.; Roberts, B. A Bayesian Networks Approach to Estimate Engineering Change Propagation Risk and Duration. IEEE Trans. Eng. Manag. 2020, 67, 869–884. [Google Scholar] [CrossRef]
- Li, R.; Yang, N.; Yi, H.; Jin, N. The robustness of complex product development projects under design change risk propagation with gray attack information. Reliab. Eng. Syst. Saf. 2023, 235, 109248. [Google Scholar] [CrossRef]
- Ni, J.; Zhao, H. Multiobjective Optimization of Propagation Path in Automotive Product Design Change Based on MOPSO. Mob. Inf. Syst. 2022, 2022, 221–227. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Rong, J. Combining improved DFMEA with knowledge graph for component risk analysis of complex products. Reliab. Eng. Syst. Saf. 2024, 251, 310–340. [Google Scholar] [CrossRef]
- Tang, D.B.; Yin, L.L. Using an Engineering Change Propagation Method to Support Aircraft Assembly Tooling Design. In Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation—Core Theory and Applications of Industrial Engineering (Volume 1); Atlantis Press: Paris, France, 2015; Volume 1, pp. 939–951. [Google Scholar]
- Shankar, P.; Joshua, S.; Keith, P. A verification and validation planning method to address change propagation effects in engineering design and manufacturing. Concurr. Eng. 2017, 25, 151–162. [Google Scholar] [CrossRef]
- Su, S.; Luo, J. An Infinite Regress Model of Design Change Propagation in Complex Systems. IEEE Syst. J. 2019, 13, 3610–3618. [Google Scholar] [CrossRef]
- Wynn, D.; Caldwell, N.; Clarkson, P.J. Predicting Change Propagation in Complex Design Workflows. J. Mech. Des. 2014, 136, 257–269. [Google Scholar] [CrossRef]
- Gan, Y.; He, Y.; Gao, L.; He, W. Propagation path optimization of product attribute design changes based on Petri Net fusion ant colony algorithm. Expert Syst. Appl. 2021, 173, 146–164. [Google Scholar] [CrossRef]
- Chua, D.K.H.; Hossain, M.A. Predicting Change Propagation and Impact on Design Schedule Due to External Changes. IEEE Trans. Eng. Manag. 2012, 59, 483–493. [Google Scholar] [CrossRef]
- Eltaief, A.; Makhlouf, A.B.; Amor, S.B.; Remy, S.; Louhichi, B.; Eynard, B. Engineering Change Risk Assessment: Quantitative and qualitative change characterization. Comput. Ind. 2022, 140, 103656. [Google Scholar] [CrossRef]
- Ma, S. Research on Multi-Source Change Propagation Mechanism and Path Optimization in Complex Product Concurrent Design; Technical Report No. 51505254; National Natural Science Foundation of China: Beijing, China, 2016. [Google Scholar]
- Li, M.; Sheng, J.; Li, Y.; Qi, W. Multi-Objective Path Optimization for Design Change Propagation on Complex Product. J. Mach. Des. 2020, 37, 66–72. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, Y.; Zhang, N.; Jiao, Y. Dynamic Optimization of Engineering Change Propagation Path for Complex Products; Technical Report; State Key Laboratory of Mechanical Transmission, Chongqing University: Chongqing, China, 2024. [Google Scholar]
- Wang, Q.; Li, Y.; Zhang, N.; Cao, J. Optimization of Product Configuration Updating Path for Complex Product Oriented by Customer Requirements Change. Comput. Integr. Manuf. Syst. 2022, 28, 3789–3801. [Google Scholar]
- Song, X.; Yang, Y.; Zhang, Y.; Zheng, R. Multi-Objective Differential Evolution algorithm for Product Change Path Optimization Guided by Reinforcement Learning. Control Theory Appl. 2025, 2025, 109–117. [Google Scholar]
- Zhan, M.; Wang, Z.; Zhao, Y.; Ren, S.; Dong, W. Optimization of Change Propagation Path Based on Product Parameter Basic-Element Network. Comput. Integr. Manuf. Syst. 2022, 28, 2545–2556. [Google Scholar]
- Xing, Q.; Liang, C.; Liang, X. Optimization of Complex Product Design Change Decision Based on Process Correlation Considering Agent Psychological Perception. J. Syst. Manag. 2022, 33, 366. [Google Scholar]
- Chen, Z.; Wall, T.; Li, S. Parallel Search Method for Multi-Change Propagation Paths in Product Structures. Comput. Integr. Manuf. Syst. 2021, 27, 2981–2989. [Google Scholar]
- Cadence Newsroom. Ricoh Cuts Parasitic Extraction Design Closure Time in Half Using Cadence Quantus QRC Extraction Solution. Design-Reuse News, 15 July 2014.
- Hoffmann, M.; Steinbrenner, J.M.; Achurra, D.; Thomsen, M.D.; Jensen, O.M. Systemic Modeling for Urban Projects: A Multi-Domain DSM Approach. Urban Sci. 2020, 4, 28. [Google Scholar] [CrossRef]
- Kurz, D.; Mutzel, P. A sidetrack-based algorithm for finding the k shortest simple paths in a directed graph. Symmetry 2022, 14, 368. [Google Scholar] [CrossRef]
- Ren, Y.; Ma, Y.; Li, X.; Zhang, J.; Liu, Z.; Wang, H. Multi-source design change propagation path optimisation based on the multi-view complex network model. Res. Eng. Des. 2021, 32, 28–60. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).