Abstract
With the rapid growth of software scale, binary code similarity detection is of great significance in security analysis tasks, such as malicious code detection and vulnerability mining. However, due to differences in instruction sets and inconsistent intermediate languages used by different compilers, with existing methods it is difficult to effectively implement cross-architecture detection. To address the problem of insufficient cross-architecture feature extraction in existing methods, we propose a cross-architecture binary code similarity-detection method based on contextual information. We design an assembly instruction-classification method that maps instructions implementing the same function under different architectures to the same semantic space, and makes the model learn the common features of semantically similar instructions under different architectures more efficiently through comparative learning to better capture semantic context information. In order to better capture the contextual structural information between basic blocks, we introduce graph attention neural networks to reduce the interference of noisy nodes that contain fewer instructions. The combination of semantic contextual information as well as structural contextual information ultimately improves the detection accuracy. Experimental results show that compared with existing methods, the proposed method has better performance in accuracy, precision, recall and F1-score.
1. Introduction
With the continuous improvement of the level of digitalization, various new types of software have emerged. However, as the scale of the software industry expands, cyber-security threats continue to increase. The risks in software development and operation are also increasing, including software vulnerabilities, malware attacks, intellectual property infringement and software supply chain security issues [1]. In the process of software development, developers use a large number of third-party libraries to achieve code reuse [2], thereby improving development efficiency. However, improper code reuse will bring certain risks. If there are vulnerabilities in these codes that have not yet been discovered or fixed, they may be spread in different systems and scenarios, increasing the potential risks [3]. For example, the classic vulnerability “Heartbleed” [4] seriously affected the encryption protocol in the OpenSSL library, posing serious security risks to companies around the world, such as Yahoo, Imgur and other websites [5]. If it is possible to perform similarity analysis on existing codes and identify the parts containing vulnerabilities, it will help to better maintain the security of software.
As a core component of software, binary code plays an important role in software security. In actual application scenarios, software usually exists in the form of binary code and its source code cannot be obtained. Therefore, binary code analysis has become one of the key means to ensure software security. At the same time, with the successful application of machine learning and deep learning technologies in computer vision, natural language processing, data mining, recommendation systems and other fields, researchers have begun to apply machine learning methods to binary code similarity analysis [6]. However, a large amount of semantic information will be lost in the process of compiling source code into binary code, including function names, variable names and defined data structures [7], making binary code analysis more difficult. In addition, the same source code may generate completely different binary codes under compilation options such as different platforms and different instruction architectures. From a technical perspective, binary code similarity detection not only needs to solve the problem of code syntax structure matching, but also needs to consider the equivalence of instruction function semantics, which further brings huge challenges to binary code similarity detection and homology analysis. Figure 1 shows the difference in binary code generated by GNU (GNU’s Not Unix) functions under different CPU instruction set architectures.

Figure 1.
Binary code comparison across CPU instruction set architectures.
In summary, with the increase in software application scenarios and the continuous expansion of scale, the use of effective detection methods to determine whether the software contains known software vulnerabilities or whether it is malware has become important in the field of software security. Especially in the process of modern software development, the software may run on terminals with different CPU architectures, such as ARM, x86, etc. These architectures have unique instruction sets, which makes security detection between different CPU architectures more complicated. Therefore, cross-CPU instruction set architecture-detection technology is not only the key to software security protection, but also a necessary way to identify and analyze security issues such as malware and vulnerability codes. In response to the above problems, this paper proposes a new cross-CPU instruction set architecture binary code similarity-detection method. By performing semantic analysis, structural analysis and alignment on binary codes under different architectures, it can not only more accurately identify similar binary codes under different architectures, but also improve detection efficiency.
The contributions of this paper are as follows:
- We design an assembly instruction-classification method that can map instructions with the same function under different architectures into the same semantic space and use contrastive learning to make the model more effective in learning the common features of semantically similar instructions under different architectures.
- We use a Graph Attention Network to integrate basic block embeddings based on a control flow graph to generate function embeddings and transform the problem of binary function similarity into a similarity score-prediction problem for function-level embedding vectors.
- We evaluate our model on datasets of different function sizes and the result shows that our proposed model outperforms previous methods.
2. Related Work
2.1. Binary Code Similarity Detection Based on Traditional Methods
Hu et al. [8] proposed the CACompare model, which first extracts the parameters required for dynamic execution and the target of the switch statement jump from the function’s CFG, then converts the assembly functions of different architectures into a unified intermediate representation and simulates the execution, thereby extracting the semantic signature of the function, and finally judging whether it is similar through the semantic signature. Similarly, Alrabaee et al. [9] proposed the Fossil model, which captures the syntactic features of the function through the opcode frequency, captures the semantics of the function by extracting the interaction between nodes from the control flow graph, captures the behavior of the function by calculating the distribution of important opcodes and finally uses the Bayesian network to combine the results of the three components for similarity matching. Ren et al. [10] proposed the UnDiff model, which extracts statistical features related to compiler optimization from the control flow graph of the function, and compares the differences in binary code generated by the same source code under different compilation options through traditional statistical methods, thereby judging whether the binary code is compiled from the same source code. Han et al. [11] implemented a program-analysis model MalInsight for detecting malware, which analyzes the malware by considering its structural, low-level and high-level behavioral features. Although these methods perform well in specific scenarios, they are highly dependent on rule construction and lack robustness.
2.2. Binary Code Similarity Detection Based on Computer Vision
Moussas et al. [12] proposed a malware-detection method based on code visualization and two-layer artificial neural network. The method converts binary files into grayscale images and extracts image features such as correlation, contrast, average image intensity, etc., and finally classifies them according to the output of the trained artificial neural network. Zhong et al. [13] proposed a visual malware-classification framework VisMal, which converts malware samples into two-dimensional grayscale images and uses a contrast-limited adaptive histogram equalization algorithm to enhance the local contrast of the image area. It is then classified by a convolutional neural network (CNN). Marastoni et al. [14] designed a CNN-based framework that generates a large number of semantically equivalent but syntactically different binary code datasets using the Tigress C obfuscator, converts them into standardized image representations and then inputs them into the CNN model for training and classification. Liu et al. [15] further represented the raw bytes of the function as a matrix, extracted semantic information from it using a convolutional neural network and combined the function call relationship and the interaction features between the calling library functions to comprehensively evaluate the similarity of the functions. In addition, Keller et al. [16] proposed a semantic representation learning method based on code visualization, which visualizes code snippets as images and combines them with transfer learning techniques to extract their structural and semantic features using the pre-trained image-classification model ResNets. These methods can extract complex feature patterns from images and focus on capturing the underlying semantic information of the code, thereby capturing detailed features that may be overlooked by traditional static methods.
However, differences in techniques such as how to generate semantically equivalent images, how to select data-normalization methods and how to design models not only determine the ability to extract features, but also affect the model’s generalization capabilities in complex scenarios.
2.3. Binary Code Similarity Detection Based on Natural Language Processing
Early researchers widely borrowed technical methods from the field of natural language processing (NLP), treating opcodes and operands as words and assembly instructions as sentences, and detecting binary code similarity by modeling assembly code. For example, Massarelli et al. [17] proposed a function-embedding architecture based on self-attention neural network, directly analyzing a single function, effectively avoiding the high complexity of global code analysis, and introduced an attention mechanism to assign different weights to instructions, focusing on semantically important instructions. By modeling instruction sequences, they determined whether function codes were similar based on the function semantic embedding output by the model. Zuo et al. [18] were inspired by neural machine translation, and solved the code inclusion problem through path decomposition and the longest common subsequence algorithm, vectorized code fragments, and then detected the similarity of binary codes. Ding et al. [19] proposed a binary clone search method based on representation learning, which modeled the control flow graph of assembly code as multiple execution sequences, combined with the PV-DM model, and generated the semantic vector of the function through unsupervised learning and negative sampling technology.
Although the above methods have a high detection accuracy, they can only detect binary code of a single architecture and cannot detect across CPU architectures. Therefore, Luo et al. [20] proposed a cross-architecture binary code clone-detection method by converting binary code of different architectures into VEX intermediate representation and using the PV-DM model to generate semantic vectors for binary code similarity detection. This method can effectively handle the differences between different architectures, but it relies on VEX intermediate representation. Different binary analysis tools may generate different VEX intermediate representations, which makes the features extracted by different analysis tools different, resulting in poor robustness of the detection results. Yang et al. [21] improved the Skip-Gram model, extracted the semantic information of basic blocks from the interprocedural control-flow graph (ICFG), combined with the AANE and LINE algorithms, used different models to train binary code of different architectures, mapped binary functions into low-dimensional feature vectors and used LSH to quickly perform code similarity retrieval. Tian et al. [22] used IDA Pro to extract the instruction sequence of binary functions, vectorized it using the word2vec model, identified the type of function through a recurrent neural network classification model and selected an appropriate Siamese neural network model for similarity detection. However, training multiple models for different CPU architectures not only requires a lot of time and computing resources, resulting in low detection efficiency, but also requires a large amount of labeled datasets for training, which further consumes a lot of human resources.
With the emergence of pre-trained models, Li [23] and Wang [24] both improved the effect of binary code similarity detection by modifying the task design of pre-trained models. Specifically, Li et al. proposed a pre-trained assembly language model based on the BERT model, combining three pre-training tasks: Masked Language Model (MLM), Context Window Prediction (CWP) and Def-Use Prediction (DUP) to capture the internal structure, control flow dependency and data flow dependency of assembly instructions, thereby generating high-quality semantic embeddings suitable for a variety of downstream tasks. Ahn et al. [25] proposed a transferable similarity learning architecture BinShot based on the BERT model. This architecture removes the original NSP task in BERT and only models the semantics of assembly code through the MLM task combined with weighted distance and binary cross-entropy loss function. Finally, the weighted distance between code pairs is learned using a twin neural network to determine whether the binary function code is similar. Wang et al. designed a jump-aware module, which embeds the source address and target address of instruction jumps through a parameter sharing mechanism to better capture the control flow structure of binary code. In addition, a Jump Target Prediction (JTP) pre-training tasks are used to improve the model’s ability to understand the semantics and structure of binary code. However, these methods only consider the context information of the instruction sequence, and the model lacks the semantic understanding of the whole program.
2.4. Binary Code Similarity Detection Based on Graph Neural Network
Xu et al. [26] proposed a neural network-based control flow graph-embedding method called Gemini. This method first uses the Structure2Vec model to convert the control flow graph of a binary function into a high-dimensional vector representation, and then learns the features of the basic blocks in the control flow graph in an iterative manner. The embedding vector of the entire function is obtained by global aggregation, and finally, the similarity between binary function pairs is calculated using a Siamese network. Gao et al. [27] used a graph neural network to extract the semantic features of functions from CFG, and generated the semantic signature of functions through dynamic simulation, thereby performing vulnerability detection while maintaining a low time overhead. Massarelli et al. [28] automatically mapped assembly instructions into vectors through unsupervised learning technology, and used two strategies, weighted average based on attention and sequence processing based on recurrent neural network to aggregate instruction vectors. Then, the control flow graph was further embedded into the vector space through the Structure2Vec model. Bowman et al. [29] proposed a vulnerability code clone-detection system based on Code Property Graph (CPG) and code property triples. By abstracting the relationship between vulnerability code and repair code into positive triples, negative triples and context triples, and using a hierarchical graph matching algorithm, it can effectively tolerate changes in the text and structure of the code, thereby realizing the detection of highly modified vulnerability code clones. Wang et al. [30] introduced control flow and data flow information into the abstract syntax tree, constructed the FA-AST graph structure and used two models, Gated Graph Neural Network (GGNN) and Graph Matching Network (GMN), to learn the vector representation of code snippets, and measured the similarity of code pairs by cosine similarity. Kim et al. [31] transformed the cross-platform analysis problem into a graph alignment problem, extracted a Binary Disassembly Graph (BDG) containing rich contextual information from the binary code and used Graph Convolutional Networks (GCNs) to learn entity semantic embedding to perform cross-platform binary code detection. He et al. [32] constructed a Semantics-Oriented Graph (SOG) based on the internal structure of instructions, the relationship between instructions and implicit calling conventions, and used graph neural networks to capture local structural information, thereby generating function-embedding vectors and calculating similarity. Jia et al. [33] summarized three function inline patterns and trained three models respectively. They used Augmented Control Flow Graphs (ACFG) combined with instruction opcodes to represent the semantic information of binary functions, and used graph neural networks to embed ACFG into vector space to learn function similarity. However, representing the entire binary function only through a graph structure will ignore the contextual information between and within instructions, resulting in incomplete semantic expression and difficulty in accurately capturing the fine-grained features of the internal operations of the function. It will also be disturbed by noise nodes, thus affecting the detection results.
3. Method
3.1. Classification and Normalization of Assembly Instructions
The assembly instructions of different CPU architectures have significant differences in syntax structure, register and operand definitions, etc. These differences are one of the main obstacles to cross-architecture binary code analysis. In order to reduce the interference of these differences on the semantic consistency of model learning, this section designs a unified assembly instruction classification and normalization method to improve the efficiency of cross-architecture semantic modeling.
(1) Instruction classification
The semantic diversity of assembly instructions stems from the instruction set design principles of different architectures. To resolve this difference, a set of general instruction-classification rules is proposed based on the functional characteristics of instructions, and complex assembly instructions are classified into ten general categories. By reasonably classifying instruction semantics, a consistent input representation can be provided for subsequent instruction normalization and feature extraction. The specific classification categories are shown in Table 1.

Table 1.
Classification of assembly instructions for x86 architecture and ARM architecture.
By analyzing the instruction set characteristics of the x86 architecture and the ARM architecture, the following general classification categories are designed, which mainly divide complex assembly instructions into the following main categories:
Conditional Jump: includes conditional jump instructions, such as JZ, JNZ of x86 and B.EQ, B.NE of ARM, which are used to change the program-execution flow according to specific conditions.
Unconditional Jump: includes unconditional jump instructions, such as x86’s JMP and ARM’s B, which are used to jump to the specified address unconditionally.
Data Transfer: includes data transfer instructions, such as MOV, LEA of x86 and LDR, STR of ARM, which are used to transfer data between registers, memory and immediate values.
Arithmetic: includes numerical calculation instructions such as addition, subtraction, multiplication and division, such as ADD, SUB of x86 and ADD, SUB of ARM.
Logical: includes bitwise logical operation instructions, such as AND, OR of x86 and AND, ORR of ARM.
Shift and Rotate: includes displacement and bit rotation instructions, such as SHL, SAR of x86 and LSL, LSR of ARM.
Bit Operation: includes bit operation instructions, such as BT, BTS of x86 and TST, REV of ARM.
CPU and System: includes control registers, memory barriers and other instructions, such as HLT, CPUID of x86 and DMB, DSB of ARM.
Compare: Includes instructions for numerical or conditional comparison, such as CMP of x86 and CMP and CMN of ARM.
Conditional Set: Includes instructions for setting flags or register values according to conditions, such as SETZ of x86 and CSET of ARM.
However, the instruction classification here only focuses on the macro-function of the instruction, and does not go into too much detail on the specific implementation of the instruction function. For example, the CMP instruction actually performs a subtraction operation under the x86 architecture, and updates the relevant bits of the flag register (EFLAGS) according to the result of the subtraction, while its macro-function is to compare whether the values in two immediate numbers or registers are equal.
Through the instruction-classification method, instructions with the same semantics under different architectures are aligned, which can reduce the macro-function differences of binary codes under different architectures and lay the foundation for instruction normalization.
(2) Instruction normalization
On the basis of completing instruction classification, we further propose an opcode and operand normalization method to eliminate instruction differences between different CPU architectures to the greatest extent possible, mainly including opcode normalization and operand normalization.
The key to opcode normalization is to abstract the functional semantics of instructions and map opcodes with the same semantics but different representations in different architectures to common opcodes. For example, instructions with the same semantics such as MOV, LEA in the x86 architecture and LDR, STR in the ARM architecture are unified as “Data Transfer” opcodes; instructions such as OR, XOR in x86 and ORR, EOR in ARM are unified as “Logical” opcodes.
According to the expression and format of operands in different architectures, it can be divided into symbol normalization, string normalization, immediate normalization and memory address normalization. Symbol normalization normalizes the contents of the symbol table in the assembly instruction to “symbol”; string normalization normalizes the contents of the string table in the assembly instruction to “string”; immediate numbers may have different prefixes (such as 0x for hexadecimal) or suffixes in different architectures, and they are normalized to “immval” by removing these prefixes and suffixes; usually the address in the assembly code starts with “0x”, and its length can be used to determine whether it is a memory address. For the memory address normalization mentioned in this article, when the length of the string starting with 0x is greater than 6, it is considered to be a memory address and normalized to “address”.
Through the above normalization processing, the semantic differences of assembly instructions under different architectures are significantly reduced, so that instructions with the same semantics and their opcodes and operands can be input into the model in a consistent form, so that the model focuses on the assembly instruction itself, and does not pay attention to architecture-irrelevant information, which not only improves the model training efficiency, but also improves the model’s cross-architecture detection capabilities.
3.2. Model Design
3.2.1. Overview
Figure 2 shows the overall framework of the cross-architecture binary code similarity-detection model proposed in this study. The system mainly consists of three key modules: semantic context information-extraction module, structural context information-extraction module and similarity score calculation module.
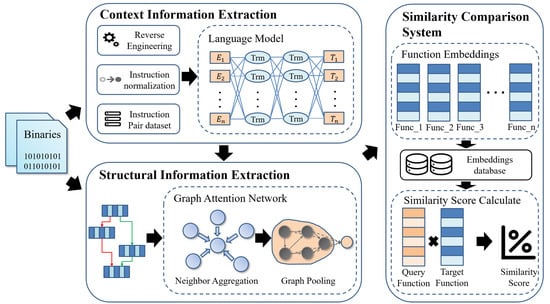
Figure 2.
The overview of our method, which consists of a contextual information extraction module, a structural information extraction module and a similarity comparison system.
First, in the semantic context information-extraction module, the system disassembles the input binary file and extracts the assembly instruction sequence in the function. In view of the large grammatical differences and diverse expressions between different architectures, this study designed a cross-architecture instruction alignment and normalization scheme. By uniformly mapping the opcodes and operands of binary functions, heterogeneous instructions with the same semantics are mapped to the same space, minimizing the impact of instruction differences caused by different architectures. Based on the BERT pre-trained language model, it is trained through tasks such as Masked Language Modeling (MLM), Next Sentence Prediction (NSP) and Contrastive Learning (CL), thereby obtaining. This process not only realizes architecture-independent instruction semantic modeling, but also provides a unified representation space for subsequent similarity learning.
Secondly, in the structural context information-extraction module, the program control flow graph (CFG) of the binary function is constructed, and the graph structure is encoded in combination with the graph attention neural network (GAT). Considering that the semantics of binary functions not only depends on a single instruction, but is also closely related to the control path in which it is located, this module uses graphs as basic units to model the control dependencies between basic blocks, which can effectively capture the structural context information of basic blocks; at the same time, the larger the binary function, the more basic blocks it contains, and there may be noisy basic blocks containing fewer instructions or irrelevant instructions. Therefore, GAT is used to make the model pay more attention to important nodes containing rich semantic information and reduce the interference of noise nodes on graph representation learning.
Finally, in the similarity score-calculation module, the function-level vector representation that integrates semantics and structural context is obtained, and its Euclidean distance is calculated. The preset threshold is used to determine whether the given two binary functions are similar.
3.2.2. Semantic Context Information Extraction Module
The semantic context information-extraction module mainly performs semantic embedding through three BERT model pre-training tasks, including the masked language model task, the next sentence-prediction task and the contrastive learning task. The specific design ideas and implementation details are as follows:
(1) Masked Language Model
The Mask Language Model (MLM) task is one of the basic tasks of BERT. Its core idea is to randomly mask some tokens in the input sequence so that the model can use the learned contextual semantic information to predict the masked content. In this module, the MLM task is applied to the normalized instruction sequence so that the model can learn the semantic information in the instruction.
Specifically, the input instruction sequence , for each instruction , consists of an opcode and 0 or more operands, and these opcodes and operands are regarded as tokens, that is, , then a certain proportion (15%) of tokens are randomly selected for masking. Among these selected tokens, 80% are replaced with a special mark “[MASK]”, 10% are replaced with a random token and the remaining 10% remain unchanged. The principle of this design is that the model cannot know which tokens are replaced by other tokens, forcing the model to learn the context information of all tokens. Through self-supervised training, the model can use the context information of Token to accurately predict the original content of the masked token. The training loss function is as follows.
represents the set of masked tokens in the instruction and the model outputs the predicted probability of each masked token. Through multiple masking and prediction, the model gradually learns to use global context information to restore the masked tokens, and then capture the semantic relationship within the instruction.
(2) Next sentence-prediction model
In assembly code, the order of instructions is crucial, and the execution logic of the program often relies on the synergy of a series of assembly instructions. For example, a conditional jump instruction is followed by a data transfer instruction or an arithmetic operation instruction. The combination not only affects the operation result, but also determines the choice of the program-execution path. By capturing the order information between instructions, the accuracy of model similarity detection can be further improved.
The Next Sentence Prediction (NSP) model is another basic task in BERT pre-training. Its main purpose is to train the model to determine whether two input sequences are adjacent in the original text. In this model, the NSP task is applied to the normalized binary instruction sequence to capture the contextual continuity and logical relationship between instructions.
Specifically, given instructions and instructions , if these two instructions are adjacent in the instruction sequence, they are marked with positive label 1, otherwise they are marked with negative label 0. The instruction pairs and are input into the model, and the predicted probability is output through a binary classification layer. The cross entropy function is selected as the training loss function, and the formula is as follows.
represents the probability that the model predicts and is continuous, represents the probability that the model predicts and is discontinuous, y is the actual label, 1 represents continuous and 0 represents discontinuous. Through the NSP task, the model can learn the sequential relationship and logical dependency of binary instructions during training, improving the model’s ability to understand complex binary code structures and detection accuracy.
(3) Contrastive learning task
The contrastive learning (CL) task is one of the core modules for cross-architecture binary code similarity detection. Its basic idea is to construct positive and negative sample pairs under different architectures so that the model can learn the semantic similarities and differences between different instructions in a unified embedding space, thereby achieving cross-architecture semantic alignment.
In the data preprocessing module, after the assembly instructions are normalized, the instructions that implement the same function in different CPU architectures (such as MOV in the x86 architecture and LDR in the ARM architecture) are classified into the same category. These instructions constitute positive sample pairs; while those instructions with obvious functional differences (such as ADD in x86 and AND in ARM) are used as negative sample pairs. Through the construction of such positive and negative sample pairs, the model can automatically adjust the spatial distribution of the embedded vectors during the training process, so that the distance between semantically similar instruction pairs in the vector space is as close as possible, while the distance between semantically inconsistent instruction pairs is enlarged. That is, for a sample pair, the embedding vectors generated after normalization are and respectively, and the contrast loss function can be expressed as follows.
represents the label of the i-th sample pair (1 for positive sample pair, 0 for negative sample pair), and respectively represent the embedding vectors of the two instructions in the i-th sample pair, represents the Euclidean distance between them, m is the interval parameter, which is used to ensure that the embedding distance of the negative sample pair is not less than the threshold, and N is the total number of sample pairs.
During the training process, the model continuously optimizes the distribution of the embedding space by minimizing the above loss function. The vector distance of the positive sample pair is gradually reduced during training, while the vector distance of the negative sample pair is expanded. In this way, the model can learn to map instructions from different architectures but with similar functions to a unified semantic representation, thereby improving the model’s ability and accuracy in cross-architecture detection.
The loss function of the entire model is the sum of the above three pre-training tasks, as shown in Equation (4).
Through the semantic embedding module, the model can fuse the internal semantic information of a single instruction and the contextual information between instructions, and combine it with comparative learning to effectively learn the common features of semantically similar instructions under different architectures, thereby converting the normalized instruction sequence into a unified semantic vector representation.
3.2.3. Structural Information Extraction Module
The purpose of structural information-extraction module is to extract feature vectors containing contextual structural information between basic blocks from the program control flow graph. In order to reduce the interference of noise nodes in the program control flow graph, this chapter uses the F1-score (GAT)-based attention mechanism-related ideas for design, that is, it includes an embedding layer, a multi-layer graph attention encoding layer and a feature-aggregation output layer.
Since the input is a graph structure containing a continuous instruction sequence, the relevant methods of the graph neural network are borrowed to first embed the instruction input-embedding layer in the basic block, so that each node carries the semantic information of its internal instructions, which is convenient for the subsequent extraction of structural features. After that, the embedded vector is used as the initial vector of the basic block node and input into the multi-layer graph attention encoding layer to obtain a vector containing its own weight and the structural information between nodes for each node. In order to make the model pay more attention to nodes with rich semantics, the multi-head graph attention mechanism in the graph attention neural network is designed as the multi-layer graph attention encoding layer. In order to obtain the embedding vector of the entire program control flow graph, the state concatenation and fully connected layers are used as feature-aggregation output layers at the end. The purpose is to output a vector as the final embedding vector of the binary function, which is convenient for the subsequent calculation of the similarity between functions.
I. Embedding layer
Since each basic block contains multiple instructions, the embedding module is used to generate a semantic embedding vector for each instruction, and the basic block is passed through the embedding layer to obtain the basic block-level embedding vector, which is convenient for subsequent multi-layer attention encoding layers to process. The embedding process is as follows. Given a basic block node containing N assembly instructions , the semantic embedding module is first used to convert each instruction into an embedding vector of d dimension, as follows:
In which, represents the embedding vector corresponding to each instruction, and represents the semantic embedding process. After obtaining the embedding vectors of all instructions in the basic block, all the embedding vectors are averaged and pooled, and merged into a basic block-level embedding vector, which is used as the initial embedding vector of the basic block node, as shown in Equation (6):
In which, is the final embedding vector of the basic block, which represents the average semantic information of all instructions in the basic block. The above operation is performed on each basic block in the program control flow graph, and the control flow information between basic blocks is combined for the subsequent multi-layer graph attention encoding layer to extract structural features.
II. Multi-layer graph attention encoding layer
The purpose of the multi-layer graph attention encoding layer is to use the graph attention neural network to extract the structural information between basic blocks from the program control flow graph, and to make the model pay more attention to important basic blocks containing rich features through the attention mechanism.
Assume that the program control flow graph is represented as , where V is the set of basic block nodes and E is the set of control flow edges. For each basic block node in the graph, the information of neighboring nodes is aggregated through the process of message passing to learn the structural information of the node context. During the message passing process, the attention weights between adjacent nodes are calculated to adaptively adjust the attention of each basic block of the model and reduce the impact of noise nodes. For any two adjacent basic blocks and , first use a learnable linear transformation w to project the features of the basic blocks and ; the formula is as follows:
To calculate the attention weights between and , we use LeakyReLU as the activation function. LeakyReLU is an improved activation function designed to address the ‘dying ReLU’ problem. Unlike the standard ReLU, which outputs 0 for all negative inputs (potentially causing neurons to stop learning), LeakyReLU introduces a small slope for negative values. This modification allows gradients to flow through negative inputs, ensuring that parameters can continue to update during training.The formula is as follows:
is a learnable attention, “ ” represents the vector concatenation operation, and is the Leaky ReLU activation function. The purpose of this operation is to calculate the attention of the basic block to its neighbor basic block , that is, the degree of influence between basic blocks. In order to ensure that the sum of the weights of different neighbors of the basic block is 1, the attention weights of all its neighbor basic blocks are then normalized by Softmax, the formula is as follows:
represents the set of all neighbor nodes of the basic block . Then, the features of the neighbor nodes are aggregated by attention weighted summation:
is a nonlinear activation function. This paper uses ReLU as the nonlinear activation function, and is the influence weight of the neighbor node on the node . Through the entire message passing process and attention mechanism, the features of each basic block not only contain its own information, but also integrate the information of its neighbor nodes, and can adaptively adjust the attention of each basic block to its neighbor nodes, reduce the influence of noise nodes and enhance the model’s understanding of the contextual structure information between basic blocks.
In order to improve the expressiveness of the model and enhance the stability of feature extraction, the K head attention mechanism is introduced. The formula is as follows:
In which, K represents the number of attention heads, each head independently calculates the attention weight , is the parameter matrix of the k-th attention head and “ ” represents the concatenation of the outputs of multiple attention heads. By calculating multi-head attention, not only can the stability of the model be increased and information loss caused by a single attention distribution be avoided, but also a variety of feature patterns can be captured, so that different attention heads can focus on different types of basic block relationships. We use GATLayer to aggregate information from multiple levels. GATLayer is a core component of F1-scores (GATs) and is designed specifically for graph structured data. It calculates node embeddings by dynamically assigning attention weights to neighbouring nodes, enabling the model to focus on more relevant neighbouring nodes.
After L layers of forward propagation, the final embedding vector of each basic block is aggregated from multiple levels of information:
In which, represents the node feature matrix of the l-th layer, A is the adjacency matrix of the entire program control flow graph, represents the calculation process of a GAT layer, and by stacking multiple GAT layers, the information of the basic block on the control flow graph can be transmitted to a farther range, that is, when there is only one GAT layer, the basic block can only receive information from direct neighbors; when there are two layers of GAT, the basic block can receive information from neighboring nodes (two jumps); when the level is deeper, the embedding vector of the basic block can integrate the context information of the entire program control flow graph, thereby gradually generating an embedding vector containing the structural information of the entire graph. After completing the calculation of multiple GAT layers, the structural feature vector of each basic block is finally obtained, but because the final similarity detection is at the binary function level, that is, the entire graph level, it is still necessary to integrate the information of the entire control flow graph into a global embedding vector. We use MLP (Multi-Layer Perceptron) as the deep learning model in this paper. MLP (Multi-Layer Perceptron) is a fully connected neural network consisting of multiple layers of neurons. It maps input features to outputs through a series of linear transformations. This paper uses state concatenation and fully connected layer for feature aggregation. The specific implementation method is as follows:
In which, is the feature of the starting basic block, is the feature of the final basic block and MLP (Multi-layer Perceptron) represents a small neural network. This paper uses a fully connected layer combined with a summation method to integrate global information and obtain the embedding vector of the entire program control flow graph. Through the aggregation operation, not only can the global information be strengthened to ensure that the embedding vector of the binary function contains the features of the entire control flow graph, but also information loss can be prevented. By connecting the starting and final basic block information, the structural information of the control flow graph is more complete.
3.2.4. Similarity Score Calculation Module
After obtaining the function-level embedding vectors under different architectures, this module first performs a distance measurement on the two embedding vectors. Specifically, the Euclidean distance is used to measure the difference between the two vectors. Let the two function-embedding vectors from architectures A and architectures B be and , with dimension N, and their Euclidean distance d is defined as follows.
The Euclidean distance is essentially an unbounded metric of difference, and its direct use fails to intuitively reflect similarity. Therefore, an exponential mapping is employed to transform it into the [0,1] interval. During the design process, we explored various mapping methods. Compared to linear mapping, which relies on normalization using maximum and minimum values, the absence of an upper bound in the Euclidean distance may lead to training instability; while functions like sigmoid are bounded, they tend to saturate in large-distance regions, causing the similarity of distant samples to approach 0, which weakens the model’s detection capability. Exponential mapping has the characteristics of being monotonically decreasing, having a value range restricted to the [0,1] interval and being sensitive to small-distance differences. It can maintain numerical stability while enhancing the distinguishability between highly similar samples, better aligning with the intuitive semantic meaning of similarity measurement. This paper ultimately selects the exponential mapping to convert the distance metric into a similarity score between 0 and 1. The specific conversion is shown in Equation (15).
s is the final similarity score. The smaller the distance, the closer is s to 1, indicating that the two binary functions are semantically consistent; conversely, the larger the distance, the closer is s to 0, indicating a greater semantic difference.
After obtaining the similarity score s, the detection result is further judged by the preset threshold . If s is higher than the threshold , the two binary functions are considered to be semantically consistent; otherwise, they are considered inconsistent. The threshold is determined by experimental parameter adjustment to achieve the best detection effect.
Through the above steps, the similarity score-calculation module can convert the embedding vector generated by the semantic embedding module into a quantitative similarity score to achieve the determination of cross-architecture binary codes. This module not only provides an intuitive scoring basis for the detection results, but also plays a key decision-making role in the overall model, which helps to improve the accuracy of cross-architecture detection.
4. Experimentation and Evaluation
4.1. Dataset
The experimental dataset is generated using the existing dataset generation tool Binkit [34]. Binkit is a large-scale binary code similarity-detection benchmark dataset that includes 51 GNU software packages, targeting 8 different CPU architectures (including x86, ARM, MIPS, etc.) and 9 different versions of compilers (GCC and Clang), covering 5 optimization levels (O0-O3, Os), and including compilation options such as position-independent execution (PIE), link-time optimization (LTO), and code obfuscation (OBFUSCATION). There are a total of 243,128 binary files and 75,230,573 functions. In order to facilitate comparative experiments, the Binkit dataset can be divided into six subdatasets. The number distribution of each dataset is shown in Table 2.

Table 2.
Distribution of subdataset numbers.
In order to verify the effectiveness of the proposed method in similarity detection of large-scale binary functions, the distribution of large-scale binary functions in the NORMAL subdataset is statistically analyzed, as shown in Table 3.

Table 3.
Binkit dataset function scale composition.
After comprehensive consideration, this paper selects the NORMAL subdataset as the experimental dataset, and uses the GCC compiler to generate experimental data for the two CPU architectures x86 and ARM, and selects O0–O3 level compilation optimization. This dataset contains complete binary code, without obfuscation or advanced optimization (such as LTO, PIE), and can fully retain the original semantic information, ensuring that the experiment only focuses on cross-architecture instruction differences, avoiding interference from optimization strategies and other factors on the instruction sequence, thereby providing a unified benchmark for subsequent research.
In this experimental dataset, there are a total of 208,590 binary functions, and the specific binary function size distribution is shown in Figure 3. The dataset is divided into training set, validation set and test set in a ratio of 80%, 10% and 10%.
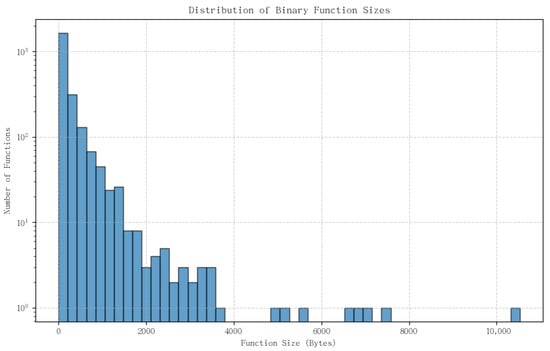
Figure 3.
Binary function size distribution.
4.2. Hardware and Software Environment
The experiments were conducted on an Ubuntu 22.04.5 LTS system using Python 3.8.19 and PyTorch 2.4.0 with CUDA 12.8. The hardware included one NVIDIA GeForce RTX 4090 GPU (24 GB) for accelerating GCN and BERT computations, two Intel Xeon Platinum 8468V processors with 192 cores (3.8 GHz) for data preprocessing and non-GPU tasks, and 503 GB RAM ensuring efficient handling of large-scale datasets. The system featured two NUMA nodes for optimized memory access, a hierarchical cache system (4.5 MB L1d, 3 MB L1i, 192 MB L2, 195 MB L3), and Intel VT-x support for hardware-assisted virtualization.
4.3. Experimental Settings
In order to evaluate the effectiveness of the proposed method, this section sets up three types of experimental questions:
Question 1: How to determine the optimal threshold of the similarity score while ensuring the stability of the detection effect?
Question 2: How does the proposed method perform on large-scale and normal-scale binary functions ?
Question 3: How significant is the impact of the semantic feature-extraction model and multi-feature combination on the performance of the proposed method?
Question 4: How efficient is the proposed method?
Based on the above three questions, three groups of experiments were set up respectively. Experiment 1 is used to determine the similarity score threshold for judging whether two binary functions are similar.
Experiment 2 evaluates the effectiveness and robustness of the proposed method by comparing it with other baseline models [23]. Experiment 3 verifies the importance of structural feature extraction through ablation experiments.
For the proposed method, the Adam optimizer is used, the learning rate is set to 0.0001, is 0.9, is 0.999 and the weight decay is set to . The graph neural network contains a 5-layer F1-score GATConv, the number of attention heads is set to 8, the hidden layer dimension is 128, the embedding vector dimension is 64, the attention mechanism dropout rate is 0.1 and the boundary threshold m of the model loss function is set to 10.
4.4. Evaluation
In response to the above three questions, the experiment is divided into three parts. The specific experimental steps are as follows:
(1) Determination of similarity score threshold
Question 1: How to determine the optimal threshold of similarity score while ensuring stable detection effect?
In order to obtain a threshold that can balance precision and recall, this section will calculate the changes in indicators such as accuracy, precision, recall and F1-score under different thresholds to obtain the optimal similarity score threshold result. The corresponding calculation formula is as follows:
Among them, TP (True Positive) means that binary function pairs with the same function in different architectures are correctly identified; TN (True Negative) means that binary function pairs with different functions in different architectures are correctly misidentified as having different functions; FP (False Positive) means that binary function pairs with different functions in different architectures are misidentified as having the same function, that is, false positive; FN (False Negative) means that binary function pairs with the same function in different architectures are misidentified as having different functions, that is, false negative.
The experiment randomly selects 1024 pairs of binary functions in the dataset, and calculates the similarity score of each function with the other 1024 functions, generating a total of 1,000,000 similarity scores, which are analyzed by various indicators. The distribution of similarity scores for 1,000,000 comparisons is shown in Figure 4.
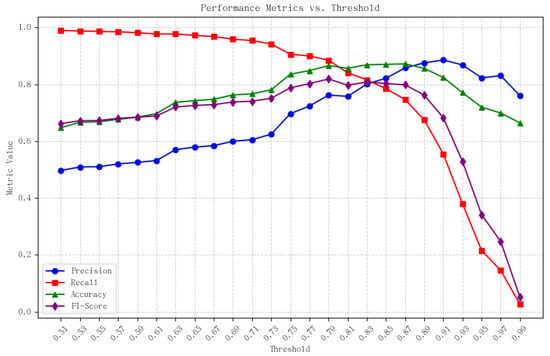
Figure 4.
Comparison of indicators and thresholds.
As can be seen from Figure 4, when the similarity threshold is below 0.75, the recall rate is very high, while the precision and F1-score show an upward trend. This indicates that when the similarity threshold is low, the accuracy of the model’s similarity-detection results is also low, so these results are not reliable for reference purposes. When the similarity threshold is between 0.75 and 0.87, the model’s precision and recall rate remain at a relatively high level. When the similarity threshold is set between 0.87 and 1.0, there is a rapid decline in the relationship between precision, F1-score and similarity threshold. In summary, setting the similarity threshold at a point between 0.75 and 0.87 achieves a balance between precision, recall rate and similarity threshold. When the threshold is 0.83, the model achieves a relatively balanced state between precision and recall, while the F1-score is also at a relatively high level, and the accuracy is close to the maximum value at this point, indicating that the overall prediction accuracy of the model is high. Therefore, subsequent experiments all use this threshold as the default setting for similarity judgment to ensure the robustness and reproducibility of the results.
(2) Comparison experiment with existing detection model
Question 2: How does the proposed method perform on large-scale and normal-scale binary functions?
In this experiment, we evaluated the performance of our model and the baseline model in binary function similarity detection on the Binkit dataset. As shown in Table 4 and Table 5, when comparing standard-scale and large-scale scenarios, most methods exhibit a decline in metrics at large scale (e.g., Safe in the O0 scenario, where recall rate decreases from 0.756 at normal scale to 0.690 at large scale), indicating that increased data scale poses challenges for binary function similarity-detection tasks. However, our proposed method maintains a relative advantage at the large-scale level, with an average F1-score of 0.865, demonstrating better robustness and adaptability. Similarly, under different compilation optimization levels (O0–O3), the performance of all models shows a downward trend, indicating that different optimization levels indeed pose significant challenges to the binary function similarity-detection task. However, our method significantly outperforms the comparison methods in evaluation metrics such as recall rate, precision rate, accuracy rate and F1-score, demonstrating superior overall performance with stable advantages across different scenarios. This highlights the advantages of our method, which considers both the contextual semantic information between instructions and the contextual structural information between basic blocks. Overall, the proposed method demonstrates superior comprehensive performance in binary function similarity-detection tasks of different scales and optimization levels.

Table 4.
Comparison between the proposed method and existing methods in normal scale.

Table 5.
Comparison between the proposed method and existing methods in large scale.
Question 3: How significant is the impact of the semantic feature-extraction model and multi-feature combination on the performance of the proposed method?
The experimental results are shown in Table 6. As can be seen from Table 6, compared with the single-feature model, the proposed method has better performance in binary function-detection tasks. On the large-scale binary function dataset, the semantic feature alone has an F1-score of only 0.810 due to ignoring the structural information, while the structural feature alone improves the F1-score to 0.760 by capturing the relationship between control flow and basic blocks. However, the proposed method greatly improves both the recall rate and precision by fusing instruction-level semantic information and structural information, and its F1-score also reaches 0.905, which is significantly improved compared with the single-feature model’s accuracy of 0.901. Through the analysis of experimental results, it can be concluded that the structural feature-extraction method proposed in this chapter can effectively make up for the limitations of the single feature method and improve the accuracy and stability of similarity detection on binary function datasets of different scales.

Table 6.
Performance of multi-feature combination result.
To validate the effectiveness of our various tasks, we conducted experiments on large-scale datasets. As shown in Table 7, the MLM (Masked Language Model), NSP (Next Sentence Prediction) and CL (Contrastive Learning) tasks all played a crucial role in improving model performance, demonstrating their necessity in learning the semantic representations of assembly code. Specifically, the MLM task helps the model learn the internal semantic features of individual assembly instructions; the NSP task is used to model the sequential relationships between instructions, thereby capturing contextual dependencies between adjacent instructions; and the CL task employs a contrastive learning mechanism to enable the model to identify assembly instructions with the same semantic functionality across different architectures. In summary, these three tasks work synergistically to effectively enhance the model’s semantic perception capabilities and generalization performance in cross-architecture binary similarity detection tasks.

Table 7.
Performance of semantic feature-extraction model result.
Question 4: How efficient is the proposed method?
To comprehensively evaluate the resource consumption and scalability of the proposed method, we conducted large-scale experiments on an RTX 4090 GPU, measuring the average training and inference times, GPU memory usage and scalability performance across different data scales. Figure 5 shows that as the data scale expands from 10 K, 50 K to 100 K, the memory usage increases gradually, while the training and inference times increase linearly, demonstrating good scalability and resource efficiency. This method not only has advantages in detection performance but also meets the requirements of large-scale applications in terms of computational resources and scalability.
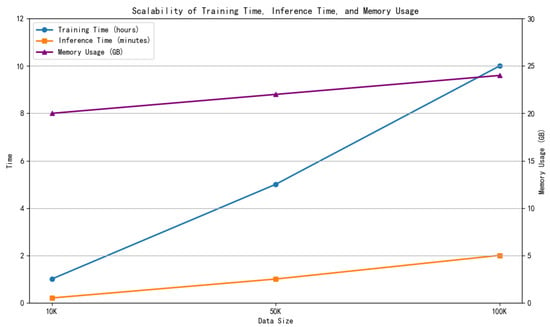
Figure 5.
Scalability of training time, inference time and memory usage.
5. Conclusions
This paper proposes a contextual semantic information-extraction method, which based on instruction relations at the instruction granularity to solve the problem that the existing cross-architecture binary code similarity-detection methods rely on intermediate languages. In combination with the BERT model, a contrastive learning task is designed to accurately detect cross-architecture binary functions without relying on intermediate languages. In detail, we first performed data preprocessing on binary functions, and the problem of binary code similarity detection is solved through the relevant ideas of natural language processing. Secondly, the assembly instruction function classification is designed to address the different problems of assembly instructions in syntax and structure under different architectures. Using the idea of contrastive learning, instructions with the same semantics under different architectures can be uniformly represented, enabling the model to extract common features. Subsequently, the optimal threshold is calculated based on the embedding vector output by the model, and the similarity score between the embedding vectors is calculated to determine whether two binary functions are similar. Finally, a structural feature-extraction method based on the attention mechanism is designed, which can be used to perform similarity detection on large-scale binary functions and reduce the impact of noise nodes. Experiments are set to verify the detection performance and robustness of the model. The experimental results show the effectiveness and superiority of the proposed method in dealing with binary function similarity-detection problems of different scales.
Author Contributions
Conceptualization, X.Z.; Data curation, Y.Y.; Formal analysis, X.Z. and Y.Y.; Software, X.Z. and Y.Y.; Supervision, Q.W. and S.Q.; Validation, X.Z., Y.Y. and S.Q.; Writing—original draft, X.Z.; Writing—review & editing, X.Z., Y.Y., Q.W. and S.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work research was funded by National Natural Science Foundation of China (Grant No. 62272056).
Data Availability Statement
The dataset used in this study was obtained from Binkit [34]. The code for this paper is publicly available on GitHub at https://github.com/smilestar/CACI-code-Similarity- (accessed on 19 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, J.; Zhang, C.; Chen, L.; Rong, Y.; Wu, Y.; Wang, H.; Tan, W.; Li, Q.; Li, Z. Improving ML-based Binary Function Similarity Detection by Assessing and Deprioritizing Control Flow Graph Features. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 4265–4282. [Google Scholar]
- Li, S.; Liu, J.; Wang, S.; Tian, H.; Ye, D. Survey on dependency conflict problem of third-party libraries. J. Softw. 2023, 34, 4636–4660. [Google Scholar]
- Gkortzis, A.; Feitosa, D.; Spinellis, D. Software reuse cuts both ways: An empirical analysis of its relationship with security vulnerabilities. J. Syst. Softw. 2021, 172, 110653. [Google Scholar] [CrossRef]
- Heartbleed Vulnerability. Available online: https://openssl-library.org/news/vulnerabilities/index.html#CVE-2014-0160 (accessed on 15 January 2025).
- Durumeric, Z.; Li, F.; Kasten, J.; Amann, J.; Beekman, J.; Payer, M.; Weaver, N.; Adrian, D.; Paxson, V.; Bailey, M. The matter of heartbleed. In Proceedings of the 2014 Conference on Internet Measurement Conference, Vancouver, BC, Canada, 5–7 November 2014; pp. 475–488. [Google Scholar]
- Han, Y.; Sun, Z.; Zhao, T.; Wang, B. A survey of binary code similarity detection techniques based on machine learning. Commun. Technol. 2022, 55, 1105–1111. [Google Scholar]
- Chen, B.; Liu, S.; Hu, A.; Yang, Q. Binary function similarity detection based on neural machine translation. J. Inf. Eng. Univ. 2021, 22, 675–682. [Google Scholar]
- Hu, Y.; Zhang, Y.; Li, J.; Gu, D. Binary code clone detection across architectures and compiling configurations. In Proceedings of the 2017 IEEE/ACM 25th International Conference on Program Comprehension (ICPC), Buenos Aires, Argentina, 22–23 May 2017; pp. 88–98. [Google Scholar]
- Alrabaee, S.; Shirani, P.; Wang, L.; Debbabi, M. Fossil: A resilient and efficient system for identifying foss functions in malware binaries. ACM Trans. Priv. Secur. (TOPS) 2018, 21, 1–34. [Google Scholar] [CrossRef]
- Ren, X.; Ho, M.; Ming, J.; Lei, Y.; Li, L. Unleashing the hidden power of compiler optimization on binary code difference: An empirical study. In Proceedings of the 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation, Virtual, 20–25 June 2021; pp. 142–157. [Google Scholar]
- Han, W.; Xue, J.; Wang, Y.; Huang, L.; Kong, Z.; Mao, L. MalDAE: Detecting and explaining malware based on correlation and fusion of static and dynamic characteristics. Comput. Secur. 2019, 83, 208–233. [Google Scholar] [CrossRef]
- Moussas, V.; Andreatos, A. Malware detection based on code visualization and two-level classification. Information 2021, 12, 118. [Google Scholar] [CrossRef]
- Zhong, F.; Chen, Z.; Xu, M.; Zhang, G.; Yu, D.; Cheng, X. Malware-on-the-brain: Illuminating malware byte codes with images for malware classification. IEEE Trans. Comput. 2022, 72, 438–451. [Google Scholar] [CrossRef]
- Marastoni, N.; Giacobazzi, R.; Dalla Preda, M. A deep learning approach to program similarity. In Proceedings of the 1st International Workshop on Machine Learning and Software Engineering in Symbiosis, Montpellier, France, 3 September 2018; pp. 26–35. [Google Scholar]
- Liu, B.; Huo, W.; Zhang, C.; Li, W.; Li, F.; Piao, A.; Zou, W. αdiff: Cross-version binary code similarity detection with dnn. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, Montpellier, France, 3–7 September 2018; pp. 667–678. [Google Scholar]
- Keller, P.; Kaboré, A.K.; Plein, L.; Klein, J.; Le Traon, Y.; Bissyandé, T.F. What you see is what it means! semantic representation learning of code based on visualization and transfer learning. ACM Trans. Softw. Eng. Methodol. (TOSEM) 2021, 31, 1–34. [Google Scholar] [CrossRef]
- Massarelli, L.; Di Luna, G.A.; Petroni, F.; Baldoni, R.; Querzoni, L. Safe: Self-attentive function embeddings for binary similarity. In Proceedings of the International Conference on Detection of Intrusions and Malware, and Vulnerability Assessment, Gothenburg, Sweden, 19–20 June 2019; pp. 309–329. [Google Scholar]
- Zuo, F.; Li, X.; Young, P.; Luo, L.; Zeng, Q.; Zhang, Z. Neural machine translation inspired binary code similarity comparison beyond function pairs. arXiv 2018, arXiv:1808.04706. [Google Scholar] [CrossRef]
- Ding, S.H.; Fung, B.C.; Charland, P. Asm2vec: Boosting static representation robustness for binary clone search against code obfuscation and compiler optimization. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (sp), San Francisco, CA, USA, 19–23 May 2019; pp. 472–489. [Google Scholar]
- Luo, Z.; Wang, B.; Tang, Y.; Xie, W. Semantic-based representation binary clone detection for cross-architectures in the internet of things. Appl. Sci. 2019, 9, 3283. [Google Scholar] [CrossRef]
- Yang, J.; Fu, C.; Liu, X.Y.; Yin, H.; Zhou, P. Codee: A tensor embedding scheme for binary code search. IEEE Trans. Softw. Eng. 2021, 48, 2224–2244. [Google Scholar] [CrossRef]
- Tian, D.; Jia, X.; Ma, R.; Liu, S.; Liu, W.; Hu, C. BinDeep: A deep learning approach to binary code similarity detection. Expert Syst. Appl. 2021, 168, 114348. [Google Scholar] [CrossRef]
- Li, X.; Qu, Y.; Yin, H. Palmtree: Learning an assembly language model for instruction embedding. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 15–19 November 2021; pp. 3236–3251. [Google Scholar]
- Wang, H.; Qu, W.; Katz, G.; Zhu, W.; Gao, Z.; Qiu, H.; Zhuge, J.; Zhang, C. Jtrans: Jump-aware transformer for binary code similarity detection. In Proceedings of the 31st ACM SIGSOFT International Symposium on Software Testing and Analysis, Virtual, 18–22 July 2022; pp. 1–13. [Google Scholar]
- Ahn, S.; Ahn, S.; Koo, H.; Paek, Y. Practical binary code similarity detection with bert-based transferable similarity learning. In Proceedings of the 38th Annual Computer Security Applications Conference, Austin, TX, USA, 5–9 December 2022; pp. 361–374. [Google Scholar]
- Xu, X.; Liu, C.; Feng, Q.; Yin, H.; Song, L.; Song, D. Neural network-based graph embedding for cross-platform binary code similarity detection. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 363–376. [Google Scholar]
- Gao, J.; Yang, X.; Fu, Y.; Jiang, Y.; Shi, H.; Sun, J. Vulseeker-pro: Enhanced semantic learning based binary vulnerability seeker with emulation. In Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Lake Buena Vista, FL, USA, 4–9 November 2018; pp. 803–808. [Google Scholar]
- Massarelli, L.; Di Luna, G.A.; Petroni, F.; Querzoni, L.; Baldoni, R. Investigating graph embedding neural networks with unsupervised features extraction for binary analysis. In Proceedings of the 2nd Workshop on Binary Analysis Research (BAR), San Diego, CA, USA, 24 February 2019; pp. 1–11. [Google Scholar]
- Bowman, B.; Huang, H.H. VGRAPH: A robust vulnerable code clone detection system using code property triplets. In Proceedings of the 2020 IEEE European Symposium on Security and Privacy (EuroS&P), Genoa, Italy, 7–11 September 2020; pp. 53–69. [Google Scholar]
- Wang, W.; Li, G.; Ma, B.; Xia, X.; Jin, Z. Detecting code clones with graph neural network and flow-augmented abstract syntax tree. In Proceedings of the 2020 IEEE 27th International Conference on Software Analysis, Evolution and Reengineering (SANER), London, ON, Canada, 18–21 February 2020; pp. 261–271. [Google Scholar]
- Kim, G.; Hong, S.; Franz, M.; Song, D. Improving cross-platform binary analysis using representation learning via graph alignment. In Proceedings of the 31st ACM SIGSOFT International Symposium on Software Testing and Analysis, Virtual, 18–22 July 2022; pp. 151–163. [Google Scholar]
- He, H.; Lin, X.; Weng, Z.; Zhao, R.; Gan, S.; Chen, L.; Ji, Y.; Wang, J.; Xue, Z. Code is not Natural Language: Unlock the Power of Semantics-Oriented Graph Representation for Binary Code Similarity Detection. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 1759–1776. [Google Scholar]
- Jia, A.; Fan, M.; Xu, X.; Jin, W.; Wang, H.; Liu, T. Cross-inlining binary function similarity detection. In Proceedings of the IEEE/ACM 46th International Conference on Software Engineering, Lisbon, Portugal, 14–20 April 2024; pp. 1–13. [Google Scholar]
- Kim, D.; Kim, E.; Cha, S.K.; Son, S.; Kim, Y. Revisiting binary code similarity analysis using interpretable feature engineering and lessons learned. IEEE Trans. Softw. Eng. 2022, 49, 1661–1682. [Google Scholar] [CrossRef]
- Yu, Z.; Cao, R.; Tang, Q.; Nie, S.; Huang, J.; Wu, S. Order matters: Semantic-aware neural networks for binary code similarity detection. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 1145–1152. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).