Abstract
A parallel efficient global optimization (EGO) algorithm with a pseudo expected improvement (PEI) multi-point sampling criterion, proposed in recent years, is developed to adapt the capabilities of modern parallel computing power. However, a comprehensive and clear discussion on the impact of different point-filling strategies on the optimization performance of the parallel EGO algorithm is still lacking, limiting its theoretical reference for practical applications and technological advancements. To address this gap, this study comprehensively investigates the optimization performance of the parallel EGO algorithm based on the PEI multi-point sampling criterion by analyzing the impact of different point-filling strategies under kriging surrogate models of varying fidelity. Therefore, nine benchmark test functions with different optimization problem characteristics were selected as optimization test objects, and the results were systematically analyzed from the perspectives of convergence performance, optimization efficiency, and algorithmic diversity. The analysis results indicate that the higher-fidelity kriging surrogate model enhances the stability of the parallel EGO algorithm in terms of convergence performance, optimization efficiency, and algorithmic diversity.
1. Introduction
In modern industrial design, engineers frequently encounter optimization tasks involving computationally expensive black-box problems, such as finite element analysis models and computational fluid dynamics models. With the rapid advancement of the algorithm field, numerous derivative-free and derivative-based algorithms have been developed to address this challenge [,]. Among them, traditional population-based algorithms such as particle swarm optimization, as well as emerging nature-inspired metaheuristic algorithms, are known to be highly reliable for optimizing black-box problems [,]. However, the direct application of such algorithms typically requires a large number of evaluations of the objective function, which is impractical for time-sensitive industrial product design.
To mitigate the high computational cost associated with directly applying intelligent algorithms to engineering optimization problems, surrogate-based optimization (SBO) methods have gained increasing attention over the past two decades []. Figure 1 illustrates the typical workflow of SBO methods. Leveraging the predictive capability of surrogate models and their low computational cost, the number of expensive objective function evaluations in the optimization process can be significantly reduced, thereby improving the overall efficiency of the optimization workflow. SBO methods have been extensively studied and applied to various problems, including aerodynamic performance optimization [,] and structural optimization [,].
Figure 1.
The fundamental process of surrogate-based optimization (SBO).
The kriging-based efficient global optimization (EGO) algorithm is one of the most successful SBO methods [,]. The kriging surrogate model not only provides predictions of the objective function but also quantifies the uncertainty of these predictions. Accordingly, the EGO algorithm incorporates an adaptive sampling criterion, known as expected improvement (EI), to guide the selection of new sample points. On one hand, the sampling criterion identifies candidate points with the highest probability of improvement; on the other hand, it enhances the predictive accuracy in the vicinity of the selected points. The optimization process terminates once the stopping criterion is met. The traditional EGO algorithm has been extensively studied and extended to address not only simple single-objective optimization problems [,] but also complex challenges such as multi-objective optimization [,,], numerical noise optimization [,], constrained optimization [,,], and gradient-based optimization []. However, a major limitation of the classical EGO algorithm is that it identifies only a single promising candidate point per optimization cycle. For automotive aerodynamic optimization problems, a complete point-filling process requires approximately 8 h of computational time [], including 5 h for CFD numerical simulations on a 576-core supercomputer and 3 h for mesh preparation and queuing delays prior to evaluation []. Under such circumstances, when only one design sample point can be evaluated per optimization cycle, despite abundant available computing resources, the approach fails to effectively utilize the parallel computing capacity. This limitation substantially restricts the potential reduction in wall-clock time and consequently hinders optimization efficiency improvement.
To overcome this limitation, researchers have explored various approaches to extend the classical serial EGO algorithm [,,], enabling the generation of multiple candidate points within a single optimization cycle. As a result, the overall optimization process can be significantly accelerated by reducing the number of required optimization cycles. Among various multi-point sampling criteria, the pseudo expected improvement (PEI) criterion exhibits relatively high reliability. It employs additional influence functions (IFs) to approximate the impact of newly sampled points on the original EI criterion, thereby avoiding costly evaluations of new points and frequent updates of the kriging model. Performance evaluations have demonstrated that the EGO algorithm based on the PEI criterion exhibits strong robustness and effective global optimization capability. However, it is known that a major limitation of the parallel EGO algorithm based on the PEI criterion is that as the number of candidate points increases within a single optimization cycle, the improvement in parallel optimization efficiency gradually slows down. A possible explanation proposed by researchers is that as more IFs are multiplied by the initial EI function, the reliability of the PEI function gradually decreases. Consequently, the likelihood of identifying high-quality candidate points diminishes. Currently, no systematic study has been conducted to investigate the impact of the number of candidate points per optimization cycle on the performance of the EGO algorithm. Key aspects such as the quality of the converged solution, convergence speed, and variations in algorithmic diversity remain unexplored. Furthermore, existing numerical studies are based on the ordinary kriging (OK) model, without exploring how the number of candidate points affects the performance of the EGO algorithm under different kriging models, such as the gradient-enhanced kriging (GEK) model.
This study aims to enhance the practical applicability and further development of the EGO algorithm based on the PEI criterion. A comparative analysis was conducted on nine analytical functions with different characteristics to investigate the impact of the number of candidate points on the performance of the PEI-based EGO algorithm using both the OK and GEK models. A systematic and in-depth evaluation was performed from multiple perspectives, including global optimization capability, convergence speed, optimization efficiency in achieving the desired convergence criteria, algorithmic diversity, and the balance between global exploration and local exploitation.
The remainder of this paper is organized as follows: Section 2 provides a brief overview of the methodology of the parallel EGO algorithm and details the design of the comparative numerical experiments. Section 3 presents the experimental results and discussion. Finally, Section 4 presents the conclusions and recommendations.
2. Materials and Methods
2.1. Ordinary Kriging
Kriging was first introduced by Sacks et al. as a surrogate for expensive computational models []. Given n initial training points, the response of the OK model can typically be expressed as follows:
Here, represents the mean term, which is determined by solving a weighted least squares problem:
Here, is the regression matrix representing the zero-order basis function. In the OK model, the polynomial vector of the basis function can be expressed as follows:
The correlation matrix characterizes the spatial correlation among all training points:
Here, the Gaussian function is selected as the modeling function for spatial correlation:
is a critical hyper-parameter in kriging, and its value directly influences the quality of the kriging fit. As seen from the expression, scales the influence of the design variable on the correlation between training points. Figure 2 illustrates the variation in correlation with respect to the distance between training points under different hyper-parameter values. The determination of hyper-parameters requires optimization using the maximum likelihood estimation (MLE) method to achieve the optimal fitting trend for the training points.
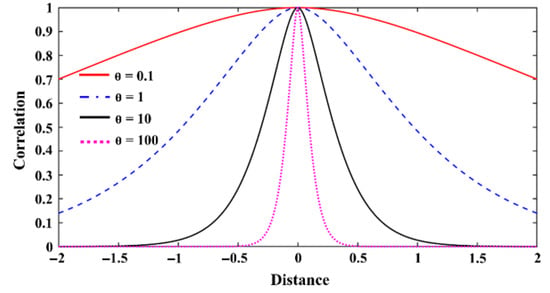
Figure 2.
The variation trend of spatial correlation between sample points under different hyper-parameter values (one-dimensional correlation function).
The error term in Equation (1) is treated as a realization of a stochastic process and can be expressed as follows:
Here, the correlation vector describes the spatial correlation between the training points and the prediction point:
The determination of requires solving a system of linear equations:
The final kriging predictor can be expressed as follows:
The mean square error of the prediction made by the kriging predictor is given by the following:
Here, represents the predicted system variance:
The objective function values at the unknown points can be predicted by solving the linear equation systems (2), (8), (10), and (11).
2.2. Gradient-Enhanced Kriging
If the objective function values and sensitivity information of the corresponding points are available, incorporating gradient information into the construction of the kriging model can significantly improve the accuracy of fitting []. Figure 3 presents an example of fitting the two-dimensional Griewank function using both OK and GEK, with the same number of training points. Clearly, the latter achieves higher fitting accuracy. The GEK model is an extension of the OK model. To fit the GEK model, the correlation terms are also extended to include the gradient terms. First, the correlation matrix is expanded as follows:
where is the correlation matrix that does not include gradient information:
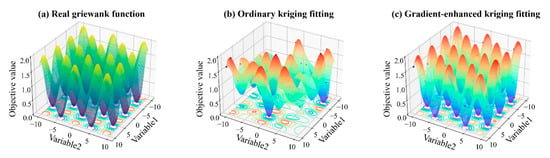
Figure 3.
Comparison of fitting accuracy between gradient-enhanced kriging (GEK) and ordinary kriging (OK). (a) Real two-dimensional Griewank function, (b) OK fitting, and (c) GEK fitting.
is the extended correlation matrix that includes the first-order gradient information of :
is the extended correlation matrix that includes the second-order gradient information of :
The spatial correlation between the prediction point and the training points is also extended in the same manner as follows:
Similarly, the extension of the function value vector also includes the gradient information of the response:
The extended expression for the regression matrix of the zero-order basis function is given by
The mean square error of the prediction made by the GEK predictor is given by
The predicted system variance is given by
The objective function values at the unknown points can be predicted by solving the linear equation systems (2), (8), (19), and (20). It is important to note that, because GEK improves fitting accuracy by augmenting the correlation vectors and matrices, the computational cost of constructing the GEK model increases accordingly. However, this cost remains relatively low compared to the expensive evaluation experiments and the wall-clock time costs associated with practical engineering optimization cycles.
2.3. Expected Improvement Multi-Points Infill Criterion
Kriging not only predicts the objective function values at unknown points but also provides the uncertainty of the predictions. This makes kriging well-suited to be paired with an acquisition function to enhance optimization efficiency. The kriging predictor treats the predicted objective function value at an unknown point as a realization of a stochastic process, which follows a normal distribution with a mean of and a variance of . Based on this, the criterion for identifying unknown points with potential for improvement can be expressed as []
Here, and represent the cumulative distribution function and the probability density function of the standard normal distribution, respectively. The EI function consists of two terms: the first term represents local exploitation near the current optimal value, while the second term represents global exploration in sparsely sampled regions. Therefore, the EI function maintains a perfect balance between local exploitation and global exploration. However, a significant limitation of the EI function is that it can only identify one candidate point within a single optimization cycle. This prevents it from fully utilizing external parallel computing resources to reduce the wall-clock time cost during the optimization process. To overcome this limitation, the PEI criterion proposes using an additional influence function to simulate the impact of the updated points on the behavior of the original EI function, thereby eliminating the costly evaluation of the update points and the Kriging model update within a single optimization cycle. As illustrated in Figure 4, a comparative analysis of the approximation and discrepancies between the EI and PEI functions during point infill on a one-dimensional Griewank’s function reveals several key observations. Figure 4a demonstrates that the EI function derived from the updated kriging model and the PEI function obtained using the IF function exhibit generally consistent variation trends. The IF function effectively captures the characteristic behavior of the EI function, where the influence of updated points on the EI function diminishes with increasing distance from the update location in the design space. More notably, in this particular case, the PEI function demonstrates superior convergence performance compared to its EI counterpart. This enhanced performance stems precisely from the subtle differences introduced by the approximation process, which enable the PEI function to overcome the well-documented limitation of conventional EI functions—their tendency to become trapped in local optima. The observed phenomenon suggests that the intentional approximation employed in the PEI formulation not only maintains the essential properties of the EI function but also introduces beneficial characteristics that improve global search capability. The expression for the PEI criterion is given by []
where represents the number of candidate points to be identified within a single optimization cycle. The IF function is used to simulate the impact of the updated points on the initial EI function and can be computed using the following expression:
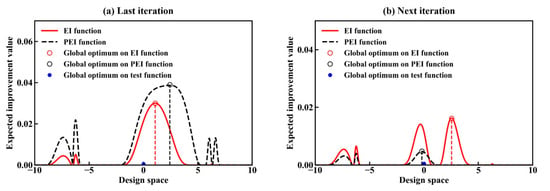
Figure 4.
Comparison of changes in EI and PEI functions in one cycle of point infills.
Here, denotes the position of the candidate point, and is the spatial correlation function used in the construction of kriging. The value of the PEI function at the update points is zero, and as the distance between the unknown point and the update point increases, the value of the PEI function gradually increases to one. This means that the EI function is significantly affected in the vicinity of the update point, while areas far from the update point are not noticeably impacted. This characteristic ensures that the variation of the PEI function across the entire search space closely approximates the influence of the update points on the initial EI function. In high-dimensional problems, where functional relationships exhibit extreme complexity, the current IF function considers only spatial correlations between sample points and therefore captures relatively limited information. During the approximation process, the IF function may potentially lose many critical pieces of information. Consequently, whether the IF function can perfectly approximate the true EI function in high-dimensional spaces remains an open question that warrants further investigation.
2.4. Kriging-Based Parallel EGO Algorithm System
The combination of the kriging surrogate model with the expected improvement sampling criterion constitutes an efficient global optimization (EGO) algorithm. Figure 5 presents the framework of the parallel EGO algorithm system based on the kriging surrogate model. First, a design of experiment (DOE) method is used to generate the initial sample points for evaluation. Then, computationally expensive experiments are conducted to evaluate the objective values of each sample point, forming the initial training dataset for fitting the kriging model. Next, an external optimizer is employed to optimize the hyper-parameters of the kriging model, thereby constructing the surrogate model. Subsequently, based on the current kriging model and the multi-points sampling criterion, the external optimizer is utilized to identify multiple promising candidate points. The objective values of these candidate points are then re-evaluated. If the optimization of the objective values meets the predefined requirements, the optimization process terminates. Otherwise, the kriging model is updated, and the iterative optimization continues until the stopping criterion of the optimization process is satisfied.
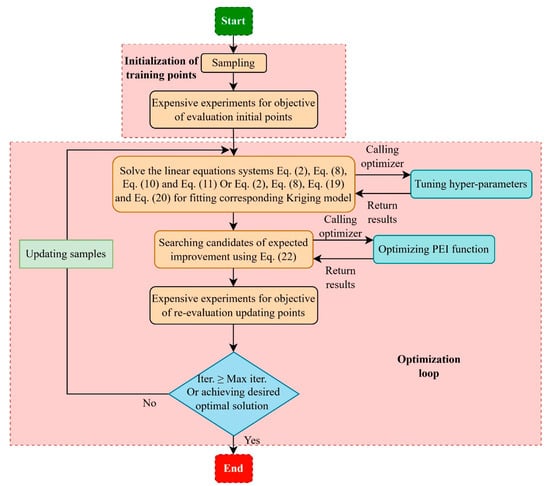
Figure 5.
Framework of the kriging-based parallel efficient global optimization (EGO) algorithm system.
2.5. Materials for Numerical Simulation Tests
To comprehensively investigate the impact of the number of infill points on the performance of the kriging-based EGO algorithm system, a comparative experimental study was conducted under different levels of infill points. The optimization performance of the EGO algorithm system based on both the OK model and the GEK model was systematically evaluated. Table 1 presents nine benchmark functions, selected from a benchmark function suit specifically designed for evaluating the performance of optimization algorithms [], including their mathematical formulations, design space specifications, and corresponding global optima, all of which are derived from authoritative references in the field. The tested functions all have a dimensionality of five. To reduce the impact of randomness in the initial points and stochastic parameters in the optimization process, the tested experiments were repeated 30 times using 30 sets of 40 initial points generated by optimal Latin hypercube design (OLHD) []. In each case, the EGO algorithm based on OK and GEK was allowed to perform an additional 240 and 120 evaluations, respectively, on the tested function. This configuration is implemented to ensure both OK-based and GEK-based EGO algorithms converge to relatively high-quality solutions, with the OK-based EGO algorithm’s iteration count set twice that of GEK-based EGO due to its comparatively slower convergence speed. In each optimization cycle, the EGO algorithm generates 2, 4, 6, 8, and 10 candidate points, respectively. This means that the EGO algorithm based on the OK model has a maximum of 120 optimization cycles, while the EGO algorithm based on the GEK model has a maximum of 60 optimization cycles.

Table 1.
Details of benchmark test functions.
In the numerical simulation tests, a Python (3.9.0) toolbox (0.6.2), named VAEOpy (Vehicular Aerodynamic Engineering Optimization in Python) [], was used to fit both OK and GEK models and to perform optimization using the parallel EGO algorithm. The corresponding parameter settings are as follows []:
- Regression function: regpoly0.
- Correlation function: corrgauss.
- Feasible domain of hyper-parameters: [10−5, 105].
- Optimizer for tuning hyper-parameters: GS-SQP; maximum number of iterations: 1000.
Optimizer for searching candidate points: MGBDE; population size: 50; maximum number of iterations: 500.
3. Experimental Results and Discussion
3.1. Comparative Analysis of the Optimization Performance of the Parallel EGO Algorithm
3.1.1. Optimization Solution Accuracy
A comparative analysis was conducted to examine the impact of different point-filling quantities on the optimization solution accuracy of the parallel EGO algorithm based on the OK model and the GEK model within a limited total number of evaluations. Table 2 presents the statistical results of the optimized solutions for all test cases, along with the Friedman ranking across the test cases []. A p-value less than 0.05 indicates statistically significant differences in solution accuracy between different point-filling strategies at the specified significance level, whereas values exceeding this threshold demonstrate no statistically significant performance variations.

Table 2.
Statistical results of the converged solutions obtained by the parallel EGO algorithms based on OK and GEK models under different point-filling strategies.
The results indicate that, for the case based on the OK model, filling two update points per optimization cycle achieved the most accurate converged solutions for test functions F1, F4, F6, F8, and F9. Furthermore, the significance levels (p-values) reveal statistically significant differences in solution accuracy among different point-filling strategies for these test functions. Additionally, for F5, it also obtained the second-highest ranked approximate optimal solution in terms of accuracy. The observed phenomenon may be attributed to the high-dimensional, multimodal characteristics of these functions, where a relatively small number of filling points effectively avoids local optima traps while maintaining convergence efficiency by preventing excessive exploration. In contrast, as the number of filled points increased to 10, the algorithm yielded the least accurate converged solutions for almost all test functions, except for F3 and F6. This suggests that the stability of the optimization performance of the parallel EGO algorithm based on the OK model deteriorates as the number of filled points increases. However, overall, as the number of filled points increased from 2 to 10, the change in the accuracy of the converged solutions did not follow a strictly linear decline; instead, there were fluctuations within certain intervals. For test functions F2 and F6, the performance with six filling points proves superior to that with four points. This phenomenon similarly manifests in functions F5 and F9, where eight filling points demonstrate better performance than six. The underlying rationale may lie in the fact that intermediate quantities (6–8 points) in certain specific problems enable the parallel EGO algorithm to escape particular types of local optima traps while maintaining an optimal balance between global exploration and local exploitation.
It is noteworthy that the impact of point-filling quantity on parallel EGO algorithm performance varies significantly across different functions. For instance, the performance differences between various filling quantities nearly disappear when comparing the original Griewank’s function (F2) with its rotated version (F3). This phenomenon likely stems from how rotation weakens the original function’s variable coupling structure (as illustrated in Figure 6, showing 3D maps of both versions), thereby reducing optimization process sensitivity to sampling strategies. A similar pattern emerges between the original Schwefel’s function (F6) and its rotated counterpart (F7). In contrast, for Rastrigin functions (F4, F5), the algorithm’s performance remains highly sensitive to filling quantities regardless of rotation, with two-point filling demonstrating consistent performance—a characteristic potentially related to the function’s strong multimodality (visualized in Figure 7’s 3D maps). An appropriate filling quantity balances avoidance of local optima traps with maintained exploration efficiency. These findings suggest that-filling strategy selection should consider objective function landscape characteristics: more flexible approaches may suit rotation-sensitive functions (e.g., Griewank-class), while rotation-invariant problems (e.g., Rastrigin-class) may benefit from the robust two-point-filling strategy.
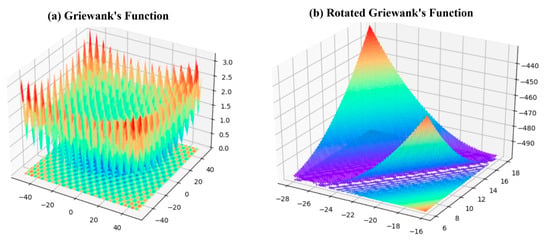
Figure 6.
Three-dimensional maps for two-dimensional Griewank and rotated Griewank functions.
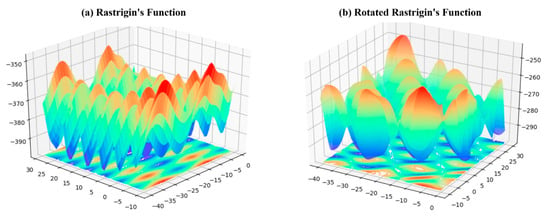
Figure 7.
Three-dimensional maps for two-dimensional Rastrigin and rotated Rastrigin functions.
For the case based on the GEK model, the optimization performance advantage of the strategy with two filled points decreased. It only achieved the best convergence accuracy on test functions F1, F3, and F5, while performing relatively poorly on several other test functions. Particularly, the convergence accuracy obtained on F2, F6, and F7 was the worst. Although the strategy with a point-filling number of 10 still performs poorly on most test functions compared to other filling strategies, the overall accuracy of its convergence solutions has improved, with a reduction in the differences. Additionally, except for F1 and F3, the variation in the accuracy of the convergence solutions does not exhibit a linear decrease as the point-filling number increases. It is worth noting that, based on the statistical decision metric p-value, the difference in the accuracy of the converged solutions has significantly reduced, compared to the case based on OK model, except for F1 and F3. This indicates that the stability of the optimization performance of the parallel EGO algorithm based on GEK model has been better ensured.
3.1.2. Convergence Speed of Optimization
To investigate the impact of different point-filling quantities on the convergence speed of the parallel EGO algorithm, Figure 8 and Figure 9 present the average convergence curves of the parallel EGO algorithm based on the OK and GEK models, respectively, under different point-filling strategies.
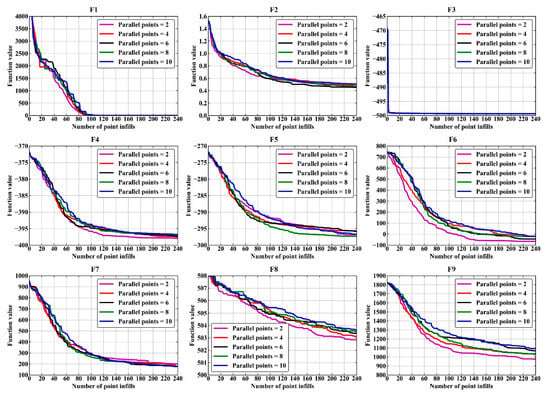
Figure 8.
Average convergence curves of the OK-based parallel EGO algorithm on all tested problems.
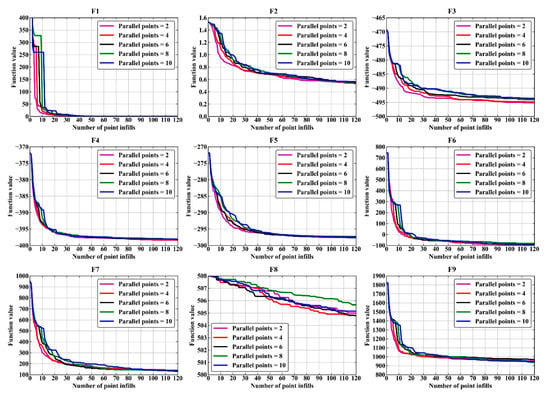
Figure 9.
Average convergence curves of the GEK-based parallel EGO algorithm on all tested problems.
From Figure 8, it can be observed that for the case based on the OK model, the convergence speed varies significantly across different point-filling quantities for almost all test functions, except for F3. A point-filling quantity of two exhibits an absolute performance advantage in terms of convergence speed for test functions F1, F4, F6, F8, and F9. This conclusion can be drawn from the fact that the average convergence curve for a point-filling quantity of two remains consistently below the other average convergence curves throughout the optimization process. In contrast, the average convergence speed for a point-filling quantity of 10 is relatively slower across most test functions. The average convergence speed for other point-filling quantities exhibits a certain degree of fluctuation between these two cases. This result is generally consistent with the findings on the accuracy of the optimized solutions presented above. This indicates that the optimization performance of the parallel EGO algorithm based on OK model is most reliable when the point-filling quantity is set to two. However, as the point-filling quantity gradually increases to 10, the stability of the parallel EGO algorithm’s optimization performance deteriorates significantly.
From the average convergence curves in Figure 9, it can be observed that in the case of the GEK model, the impact of different point-filling quantities on the convergence speed of the parallel EGO algorithm differs only in the early stages of the optimization process for almost all test functions, except for F3 and F8. Moreover, during this stage, the impact on the average convergence speed exhibits a trend that is essentially linearly correlated with the increase in point-filling quantity. As the optimization process progresses, the differences in average convergence speed among different point-filling quantities gradually diminish. The potential reason for this phenomenon is that, in the early stages of the optimization process, fewer point-filling quantities lead to more frequent updates of the surrogate model. This provides more reliable design space information for the EGO algorithm’s optimization. As the optimization process progresses and considering that GEK model has superior fitting performance compared to OK model, it can rapidly compensate for the loss of design space information due to fewer surrogate model updates in the early stages of the optimization process. This result also indicates that the convergence performance of the parallel EGO algorithm based on the GEK model is more stable and reliable. It is noteworthy that both OK-based and GEK-based parallel EGO algorithms demonstrate relatively poor convergence performance on test function F8 (rotated expanded Griewank plus Rosenbrock function), exhibiting slower convergence speeds. Analysis of F8’s functional characteristics reveals its highly oscillatory and multimodal nature, which can lead to significant deviations between the PEI function and the true EI function. Consequently, the PEI criterion may prove particularly susceptible to failure when applied to functions of this category.
As evidenced in Figure 8 and Figure 9, the GEK-based parallel EGO algorithm demonstrates superior convergence performance over its OK-based counterpart on test functions F1, F4–F7, and F9. This enhancement stems from GEK’s effective utilization of gradient information from the same number of sample points, enabling more comprehensive exploration of the design space when identifying promising candidate points. However, for functions F2, F3, and F8 (all belonging to the Griewank family), the GEK-based approach shows no performance advantage and even exhibits degraded convergence compared to the OK-based method. This phenomenon may be attributed to the Griewank functions’ characteristic local oscillations (illustrated in Figure 6), where gradients exhibit violent fluctuations near local optima. The GEK model’s strong dependence on gradient information may cause it to overemphasize local curvature at the expense of global trends, thereby misleading the search direction. Consequently, OK-based parallel EGO is recommended for problems exhibiting such functional characteristics. Furthermore, while the GEK model possesses powerful fitting capabilities, practical applications must consider the accessibility of gradient information, and potential noise contamination in gradient data—both critical factors when selecting GEK-based approaches.
3.2. Comparative Analysis of the Optimization Efficiency of the Parallel EGO Algorithm
In practical performance optimization problems, the primary source of time consumption is the wall-clock time cost. In a single optimization cycle, the wall-clock time cost primarily consists of three components: experimental model preparation, waiting gap, and experimental evaluation (Figure 10). An effective approach to significantly improving optimization efficiency is to achieve the desired optimization objective with as few optimization cycles as possible. Therefore, the multi-point infill criterion was proposed based on this principle.
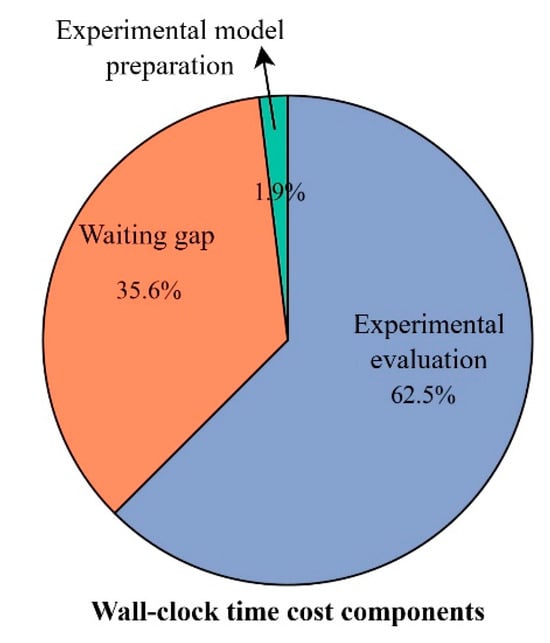
Figure 10.
Composition of the wall-clock time cost within a single optimization cycle for practical problems.
To investigate the impact of different infill point quantities on the optimization efficiency of the parallel EGO algorithm, Table 3 presents the relevant statistics on the number of optimization cycles required to achieve the predefined convergence criteria for the parallel EGO algorithm based on both OK and GEK models. For the case based on the OK model, the number of optimization cycles continuously decreases with an increasing number of infill points for almost all test functions, except for F3. This result is generally consistent with the findings presented in []. However, the reduction in the number of cycles required for the parallel EGO algorithm to reach the convergence criterion does not strictly follow a proportional relationship with the increase in the number of infill points. For example, on F1, taking the parallel EGO algorithm with an infill point count of 2 as the baseline, the parallel EGO algorithm with an infill point count of 4 accelerates the search by approximately 92.77/49.33 ≈ 1.88 times. However, for a strictly linear speedup, the expected factor should be 2. A possible explanation given in previous studies is that as the sequential selection process progresses within a single optimization cycle, an increasing number of IFs are multiplied by the initial EI criterion, making the PEI criterion increasingly unreliable. It is noteworthy that for F5, the parallel EGO algorithm with a point-filling number of 4 achieved an acceleration factor of approximately 53.13/26.63 ≈ 2.00 times.

Table 3.
The statistics of the number of cycles required to reach the expected stopping criterion under different point-filling strategies using parallel EGO algorithms based on OK and GEK, respectively.
To explain this phenomenon, Figure 11 illustrates the process of the PEI criterion searching for multiple potential improvement points within an optimization cycle. Strictly speaking, the fundamental principle of the PEI criterion remains a sequential process, rather than a true parallel point-filling criterion (its parallel concept is based on the parallelization of external computational resources, rather than the parallelization of the algorithm itself). The initial potential improvement point is identified using the original EI criterion, while subsequent points depend on the approximation accuracy between the current PEI function and the true EI function. When the discrepancy between PEI and true EI remains relatively small, the search process benefits from more reliable information. Conversely, significant deviations may lead to information loss, potentially misleading the EGO algorithm’s exploration direction. As the candidate selection process progresses, these approximation errors accumulate, ultimately affecting the overall optimization convergence rate. A truly parallel candidate selection approach would require completely independent selection of multiple points within each optimization cycle. Interestingly, the observed linear relationship between efficiency improvement and increased point-filling quantity in certain special cases may stem from how the influence function-induced differences between PEI and true EI functions provide beneficial algorithmic diversity. This diversity enhances the probability of escaping local optima while promoting faster convergence to higher-quality solutions.

Figure 11.
The process for searching multi-points using the PEI criterion within a single optimization cycle.
For the case based on the GEK model, compared to the parallel EGO algorithm with the OK model, the number of optimization cycles with the same number of point fillings significantly decreased in almost all test functions, except for F3 and F8. Because the fitting performance of the GEK model has been significantly improved, as a result, the effective spatial information relied upon during the search for potential improvement points is more reliable, which facilitates the convergence of the parallel EGO algorithm. However, the redundancy of the spatial information relied upon by multiple points in a single optimization cycle also increases, which means the bottleneck for achieving optimization efficiency improvements occurs more quickly than in the case of the OK model.
3.3. Comparative Analysis of the Optimizing Diversity of the Parallel EGO Algorithm
3.3.1. Population Diversity
When an optimization algorithm is prone to getting trapped in local optima, strategies can be employed to provide population diversity, helping the algorithm escape local optima and thereby increasing the probability of finding higher-quality solutions []. The classical EGO algorithm inherently achieves a perfect balance between local exploitation and global exploration; however, it is also prone to getting trapped in local optima. The introduction of the parallel EGO algorithm not only enhances the efficiency of the entire optimization process but also, by multiplying the corresponding number of IFs after the original EI function, can be seen as increasing the diversity of the optimization. Therefore, the impact of different point-filling quantities on the performance of the parallel EGO algorithm is analyzed from the perspective of algorithmic diversity. The calculation method for population diversity is as follows:
where n and D represent the total population size and the number of design variables, respectively. represents the position of the individual in the dimension, and denotes the average position of all individuals in the dimension. A low population diversity indicates that the search is exploring the design space near the local optimum. In contrast, a high population diversity suggests that the search is exploring regions of the design space farther from the local optimum.
Figure 12 and Figure 13 present the average population diversity curves of the parallel EGO algorithm based on the OK model and the GEK model, respectively, under different point-filling quantities during optimization process. For the case based on OK model, the parallel EGO algorithm with a larger point-filling quantity generally exhibits greater population diversity in the early stages of optimization, indicating that it explores a larger design space. As the optimization process progresses, population diversity gradually decreases. Meanwhile, the rate of decline in population diversity is relatively slower for the parallel EGO algorithm with a larger point-filling quantity. This also explains why its overall solution convergence speed is relatively slower (Figure 8). However, the advantage of having greater population diversity is that it can facilitate the parallel EGO algorithm in escaping local optima, thereby increasing the probability of discovering higher-quality optimal solutions. For example, in the case of test functions F2, F3, F5, and F7, higher-quality solutions were found when using a larger number of filled points.
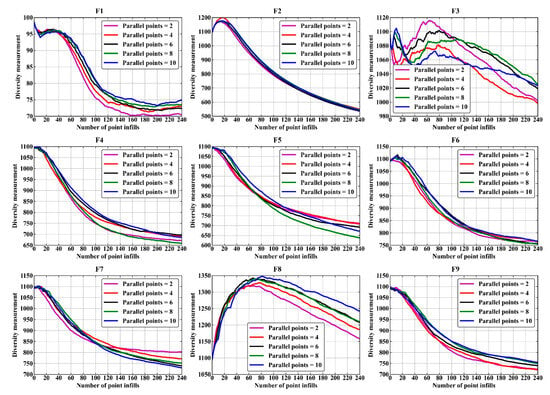
Figure 12.
Population diversity curves of the OK-based parallel EGO algorithm on all tested problems.
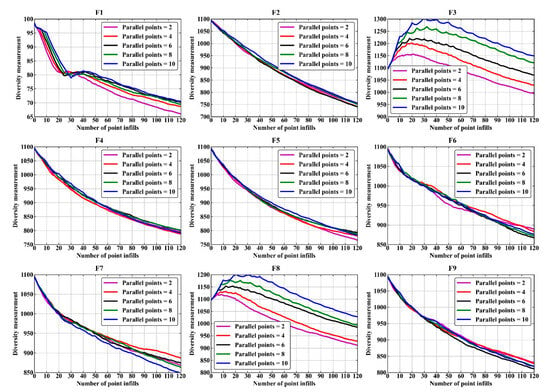
Figure 13.
Population diversity curves of the GEK-based parallel EGO algorithm on all tested problems.
For the case based on the GEK model, overall, the impact of different point-filling numbers on the population diversity of the parallel EGO algorithm is reduced, except for test functions F1, F3, and F8. Combining the average convergence curves for the corresponding test functions in Figure 6, it can also be observed that the differences in the impact of different point-filling numbers on the convergence speed of the parallel EGO algorithm are minimal. This may be due to the fact that the spatial design information provided by GEK to the parallel EGO algorithm is sufficiently reliable, which makes the search directions for potential improvement points more well-defined.
3.3.2. Exploitation and Exploration
Almost all global optimization algorithms aim to achieve a reasonable balance between local exploitation and global exploration, and the EGO algorithm is no exception. To evaluate the impact of different point-filling numbers on the balance between local exploitation and global exploration in the parallel EGO algorithm, the percentage change trends of exploitation–exploration throughout the optimization process were calculated using the following formula:
Here, is defined in Equation (24) and represents the diversity of the entire population.
Figure 14 and Figure 15 show the trends of the exploration–exploitation ratio over the process of optimization for the parallel EGO algorithm based on the OK and GEK models, respectively, under different point-filling quantities. Overall, it can be observed that the parallel EGO algorithm with different point-filling quantities maintains a high level of exploration during the early stages of optimization, allowing the algorithm to explore a broader design space for global optima. As the optimization progresses, the exploration rate gradually decreases while the exploitation rate increases, enabling the algorithm to continue improving the solution quality in the vicinity of local optima. For the case based on the OK model, as shown in Figure 8, the point-filling quantity of 2 consistently achieves the best convergence speed on F1, F4, F6, F8, and F9. Therefore, with a point-filling quantity of 2, the parallel EGO algorithm better maintains a reasonable balance between local exploitation and global exploration. This conclusion can be drawn from the trend of the exploration–exploitation curves in Figure 14, as the exploration–exploitation curves for the case with two points remain smaller and larger than those for the other point configurations throughout almost the entire optimization process.
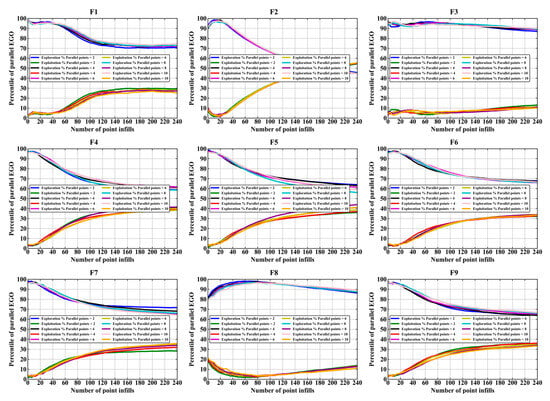
Figure 14.
Exploration and exploitation curves of the OK-based parallel EGO algorithm on all tested problems.
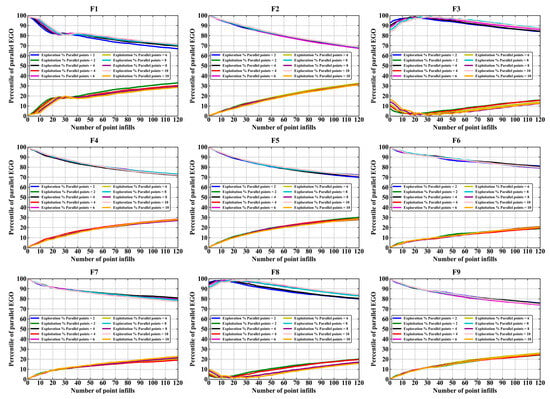
Figure 15.
Exploration and exploitation curves of the GEK-based parallel EGO algorithm on all tested problems.
For the case based on the GEK model, as shown in Figure 9, except for F1, F3, and F8, where there is a significant difference in convergence speed between different point-filling quantities, the convergence speed for the other test functions only shows slight differences in the early stages of optimization. As the optimization iterations progress, the convergence speed remains nearly consistent. Therefore, as shown in Figure 15, the differences in the impact of different point-filling quantities on the balance between local exploitation and global exploration of the parallel EGO algorithm are negligible for these test functions. This indicates that the GEK model provides greater reliability and stability to the parallel EGO algorithm.
4. Conclusions
This study conducts an in-depth investigation into how the optimization performance of the Kriging-based parallel EGO algorithm with the PEI multi-point sampling criterion is affected by different numbers of points filled in a single optimization cycle. Meanwhile, to obtain comprehensive numerical simulation results and conduct an in-depth comparative analysis, nine benchmark test functions with different optimization problem characteristics were selected as optimization targets. The point-filling levels within a single optimization cycle were set to five values: 2, 4, 6, 8, and 10. Different fidelity surrogate models were then constructed using both OK and GEK. Finally, the optimization tasks were performed using the parallel EGO algorithm with the PEI multi-point sampling criterion. Finally, a systematic comparative analysis of the results was conducted from the perspectives of the optimization performance, efficiency, and diversity of the parallel EGO algorithm, leading to the following conclusions:
- (a).
- The impact of different point-filling quantities on the optimization performance of the parallel EGO algorithm based on the OK model is significant. Filling two points per optimization cycle ensures the most stable optimization performance of the parallel EGO algorithm. However, as the number of filled points increases, the stability of the optimization performance gradually declines. In contrast, for the GEK model, the influence of different point-filling quantities on the optimization performance of the parallel EGO algorithm is only noticeable in the early stages of optimization. As the optimization process progresses, the performance differences gradually diminish.
- (b).
- For the parallel EGO algorithm based on the OK model, optimization efficiency improves as the point-filling quantity increases. However, the rate of improvement gradually slows with the increasing number of filled points. In the case of GEK, this slowdown in optimization efficiency becomes even more pronounced.
- (c).
- The point-filling quantity has a significant impact on the optimization diversity of the parallel EGO algorithm based on the OK model. In most cases, filling two points per optimization cycle ensures a reasonable level of optimization diversity and maintains a balance between local exploitation and global exploration. In contrast, for the GEK model, the influence of different point-filling quantities on the diversity of the parallel EGO algorithm is less pronounced.
- (d).
- For practical implementation, it is recommended to employ a smaller number of filling points per optimization cycle during the initial stages when design space information remains relatively limited. However, as iterations progress, gradually increasing the filling quantity may enhance algorithmic convergence speed and improve overall optimization efficiency.
Although the introduction of multi-point sampling criteria can significantly improve the efficiency of the EGO algorithm in solving practical optimization problems, its fundamental principle still follows a sequential point selection strategy within a single optimization cycle. Therefore, achieving true parallelization of the EGO algorithm requires decoupling the selection process of potential improvement points and reducing their mutual dependence. In the future, further research will focus on developing more efficient and stable point-filling strategies to better meet the needs of practical engineering optimization problems.
Author Contributions
Conceptualization, H.F. and M.T.; methodology, H.F. and Q.W.; software, H.F. and Q.W.; validation, H.F. and T.N.; formal analysis, H.F., R.B. and M.T.; writing—original draft preparation, H.F.; writing—review and editing, Q.W., T.N., R.B. and M.T.; supervision, M.T.; funding acquisition, M.T. and H.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by MEXT as “Program for Promoting Researches on the Supercomputer Fugaku” (JPMXP1020210316) and used the computational resources of supercomputer Fugaku provided by the RIKEN Center for Computational Science (Project ID: hp210262), as well as China Scholarship Council (CSC) Grant Number 202108500034.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the information required to reproduce the results is fully disclosed in Section 3. The same results can be obtained by employing the settings and the strategies discussed in this paper. The toolboxes developed by us cannot be provided due to the further application and the research. To help readers reproduce the results, the DACE or ooDACE toolboxes are suggested to generate all kinds of kriging models and expand the EGO and parallel EGO algorithms, which can be downloaded from the websites: https://www.omicron.dk/dace.html (accessed on 7 July 2022) and https://sumo.intec.ugent.be/?q=ooDACE (accessed on 7 July 2022).
Conflicts of Interest
Author Qingyu Wang was employed by the company BYD Auto Industry Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Larson, J.; Menickelly, M.; Wild, S.M. Derivative-Free Optimization Methods. Acta Numer. 2019, 28, 287–404. [Google Scholar] [CrossRef]
- Daoud, M.S.; Shehab, M.; Al-Mimi, H.M.; Abualigah, L.; Zitar, R.A.; Shambour, M.K.Y. Gradient-Based Optimizer (GBO): A Review, Theory, Variants, and Applications. Arch. Comput. Methods Eng. 2023, 30, 2431–2449. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Vinod Chandra, S.S.; Anand, H.S. Nature Inspired Meta Heuristic Algorithms for Optimization Problems. Computing 2022, 104, 251–269. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in Surrogate Based Modeling, Feasibility Analysis, and Optimization: A Review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- He, Z.; Xiong, X.; Yang, B.; Li, H. Aerodynamic Optimisation of a High-Speed Train Head Shape Using an Advanced Hybrid Surrogate-Based Nonlinear Model Representation Method. Optim. Eng. 2022, 23, 59–84. [Google Scholar] [CrossRef]
- Liu, B.; Liang, H.; Han, Z.-H.; Yang, G. Surrogate-Based Aerodynamic Shape Optimization of a Sliding Shear Variable Sweep Wing over a Wide Mach-Number Range with Plasma Constraint Relaxation. Struct. Multidiscip. Optim. 2023, 66, 43. [Google Scholar] [CrossRef]
- Li, S.; Trevelyan, J.; Wu, Z.; Lian, H.; Wang, D.; Zhang, W. An Adaptive SVD–Krylov Reduced Order Model for Surrogate Based Structural Shape Optimization through Isogeometric Boundary Element Method. Comput. Methods Appl. Mech. Eng. 2019, 349, 312–338. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, C.; Liu, B. Surrogate-Based Structural Optimization Design of Large-Scale Rectangular Pressure Vessel Using Radial Point Interpolation Method. Int. J. Press. Vessels Pip. 2022, 197, 104638. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Jones, D.R. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Sóbester, A.; Leary, S.J.; Keane, A.J. On the Design of Optimization Strategies Based on Global Response Surface Approximation Models. J. Glob. Optim. 2005, 33, 31–59. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C.; van Beers, W.; van Nieuwenhuyse, I. Expected Improvement in Efficient Global Optimization through Bootstrapped Kriging. J. Glob. Optim. 2012, 54, 59–73. [Google Scholar] [CrossRef]
- Keane, A.J. Statistical Improvement Criteria for Use in Multiobjective Design Optimization. AIAA J. 2006, 44, 879–891. [Google Scholar] [CrossRef]
- Zhan, D.; Cheng, Y.; Liu, J. Expected Improvement Matrix-Based Infill Criteria for Expensive Multiobjective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 956–975. [Google Scholar] [CrossRef]
- Wang, Q.; Nakashima, T.; Lai, C.; Hu, B.; Du, X.; Fu, Z.; Kanehira, T.; Konishi, Y.; Okuizumi, H.; Mutsuda, H. Enhanced Expected Hypervolume Improvement Criterion for Parallel Multi-Objective Optimization. J. Comput. Sci. 2022, 65, 101903. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J.; Bressloff, N.W. Design and Analysis of “Noisy” Computer Experiments. AIAA J. 2006, 44, 2331–2339. [Google Scholar] [CrossRef]
- Wang, Q.; Nakashima, T.; Lai, C.; Du, X.; Kanehira, T.; Konishi, Y.; Okuizumi, H.; Mutsuda, H. An Improved System for Efficient Shape Optimization of Vehicle Aerodynamics with “Noisy” Computations. Struct. Multidiscip. Optim. 2022, 65, 215. [Google Scholar] [CrossRef]
- Xu, Q.; Wehrle, E.; Baier, H. Adaptive Surrogate-Based Design Optimization with Expected Improvement Used as Infill Criterion. Optimization 2012, 61, 661–684. [Google Scholar] [CrossRef]
- Jiao, R.; Zeng, S.; Li, C.; Jiang, Y.; Jin, Y. A Complete Expected Improvement Criterion for Gaussian Process Assisted Highly Constrained Expensive Optimization. Inf. Sci. 2019, 471, 80–96. [Google Scholar] [CrossRef]
- Qian, J.; Cheng, Y.; Zhang, J.; Liu, J.; Zhan, D. A Parallel Constrained Efficient Global Optimization Algorithm for Expensive Constrained Optimization Problems. Eng. Optim. 2021, 53, 300–320. [Google Scholar] [CrossRef]
- Chen, L.; Qiu, H.; Gao, L.; Jiang, C.; Yang, Z. Optimization of Expensive Black-Box Problems via Gradient-Enhanced Kriging. Comput. Methods Appl. Mech. Eng. 2020, 362, 112861. [Google Scholar] [CrossRef]
- Ginsbourger, D.; Le Riche, R.; Carraro, L. Kriging Is Well-Suited to Parallelize Optimization. In Computational Intelligence in Expensive Optimization Problems; Tenne, Y., Goh, C.-K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 131–162. [Google Scholar] [CrossRef]
- Zhan, D.; Qian, J.; Cheng, Y. Pseudo Expected Improvement Criterion for Parallel EGO Algorithm. J. Glob. Optim. 2017, 68, 641–662. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wu, Y. Kriging-Based Unconstrained Global Optimization through Multi-Point Sampling. Eng. Optim. 2020, 52, 1082–1095. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Han, Z.-H.; Görtz, S.; Zimmermann, R. Improving Variable-Fidelity Surrogate Modeling via Gradient-Enhanced Kriging and a Generalized Hybrid Bridge Function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
- Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization. ResearchGate. Available online: https://www.researchgate.net/publication/256995189_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2013_Special_Session_on_Real-Parameter_Optimization (accessed on 20 August 2022).
- Wang, Q.; Nakashima, T.; Lai, C.; Mutsuda, H.; Kanehira, T.; Konishi, Y.; Okuizumi, H. Modified Algorithms for Fast Construction of Optimal Latin-Hypercube Design. IEEE Access 2020, 8, 191644–191658. [Google Scholar] [CrossRef]
- Wang, Q.; Nakashima, T.; Kanehira, T.; Mutsuda, H. A Python Toolbox for Surrogate-Based Optimization. In Proceedings of the 2022 IEEE 12th International Conference on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, 15–17 July 2022; pp. 80–84. [Google Scholar] [CrossRef]
- Fu, H.; Wang, Q.; Nakashima, T. Gradient-Enhanced Kriging-Based Parallel Efficient Global Optimization Algorithm and Its Application in Aerodynamic Shape Optimization. IEEE Access 2025, 13, 73848–73869. [Google Scholar] [CrossRef]
- Zimmerman, D.W.; Zumbo, B.D. Relative Power of the Wilcoxon Test, the Friedman Test, and Repeated-Measures ANOVA on Ranks. J. Exp. Educ. 1993, 62, 75–86. [Google Scholar] [CrossRef]
- Chauhan, D.; Yadav, A. Optimizing the Parameters of Hybrid Active Power Filters through a Comprehensive and Dynamic Multi-Swarm Gravitational Search Algorithm. Eng. Appl. Artif. Intell. 2023, 123, 106469. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).