Root Cause Analysis of Cast Product Defects with Two-Branch Reasoning Network Based on Continuous Casting Quality Knowledge Graph

Abstract

A variety of cast product defects may occur in the continuous casting process. By establishing a Continuous Casting Quality Knowledge Graph (C2Q-KG) focusing on the causes of cast product defects, enterprises can systematically sort out and express the relations between various production factors and cast product defects, which makes the reasoning process for the causes of cast product defects more objective and comprehensive. However, reasoning schemes for general KGs often use the same processing method to deal with different types of relations, without considering the difference in the number distribution of the head and tail entities in the relation, leading to a decrease in reasoning accuracy. In order to improve the reasoning accuracy of C2Q-KGs, this paper proposes a model based on a two-branch reasoning network. Our model classifies the continuous casting triples according to the number distribution of the head and tail entities in the relation and connects a two-branch reasoning network consisting of one connection layer and one capsule layer behind the convolutional layer. The connection layer is used to deal with the sparsely distributed entity-side reasoning task in the triple, while the capsule layer is used to deal with the densely distributed entity-side reasoning task in the triple. In addition, the Graph Attention Network (GAT) is introduced to enable our model to better capture the complex information hidden in the neighborhood of each entity and improve the overall reasoning accuracy. The experimental results show that compared with other cutting-edge methods on the continuous casting data set, our model significantly improves performance and infers more accurate root causes of cast product defects, which provides powerful guidance for enterprise production.

1. Introduction

In modern industrial manufacturing, continuous casting has been widely used in steel production. However, the continuous casting process is complex and involves many parameters and operation steps. Various cast product defects, such as cracks, segregation and pores, may occur, affecting quality of cast products and potentially causing production stagnation or equipment damage. Therefore, accurately identifying and analyzing the root causes of cast product defects are crucial.

Traditional cast product defect analysis mainly relies on experienced engineers who judge the causes of defects by observing the appearance of defects and combining their own experience [1]. This method is effective to a certain extent, but due to the complexity of the continuous casting process and the diversity of influencing factors, it is difficult to grasp all the potential defect causes comprehensively and systematically by manual experience alone. With the development of artificial intelligence and data analysis technology, how to use data-driven methods to analyze the root causes has become a research hotspot.

A knowledge graph (KG) is a model that represents knowledge in the form of a graph structure. It connects entities and relations in knowledge through nodes and edges, forming a networked knowledge system. A KG can not only express static relations among entities but also semantically reason about entities and their relations, so as to reveal hidden knowledge and information. With the development of technology, KGs have been widely used in various domains to form the so-called Domain-Specific KGs (DSKGs).

DSKGs can significantly improve the effect of information retrieval, knowledge discovery, decision support and other tasks in a specific domain [2]. For example, in the medical domain, DSKGs can help doctors diagnose diseases [3] and perform medical research and clinical practice [4] more accurately by integrating patient data. In the manufacturing domain, DSKGs can optimize production processes, predict equipment failures and improve product quality [5]. In the financial domain, DSKGs can assist in risk assessment and intelligent investment advisory [6].

In the root cause analysis of cast product defects, the Continuous Casting Quality Knowledge Graph (C2Q-KG) can integrate different process parameters, equipment status and environmental factors in the continuous casting process. Through the systematic analysis of the correlation of this information, the causes of cast product defects can be reasoned out more objectively.

However, existing knowledge graph reasoning methods often use the same reasoning method when dealing with different types of relation features and fail to fully consider the difference in the number distribution of head and tail entities in the relation. Applying the same treatment leads to uneven reasoning accuracy, and the reasoning performance is often unsatisfactory.

In order to solve this problem, this paper proposes a knowledge graph reasoning model based on a two-branch reasoning network (KGTBRN), which aims to improve the accuracy of root cause analysis for cast product defects and provide powerful decision support for quality control and process optimization in production for continuous casting enterprises.

Our contributions in this paper are as follows:

• We propose KGTBRN in the continuous casting domain. Aiming at the requirements of root cause analysis for cast product defects, one connection layer and one capsule layer are used to deal with different types of entity-side reasoning tasks, so as to improve both the adaptability of KGTBRN to different relation features and the reasoning accuracy.
• KGTBRN is experimentally verified on a continuous casting data set and compared with existing cutting-edge methods. The experimental results show that KGTBRN obtains the best mean reciprocal rank and the highest HITS@1, HITS@3 and HITS@10 on the continuous casting data set. It also demonstrates clear advantages on the benchmark data set FB15k-237 and shows good generalization performance on the WN18RR data set.

The rest of the paper is structured as follows: Section 2 reviews the related works on knowledge graph reasoning and Graph Attention Network (GAT). Section 3 introduces the proposed knowledge graph reasoning model, KGTBRN. Section 4 introduces the C2Q-KG and analyzes the experimental results. Section 5 gives the conclusions of this paper.

2. Related Works

2.1. Root Cause Traceability of Cast Product Defects

Defect cause traceability is one of the key links in product quality management. The core goal of traceability is to accurately locate the root cause of product defects through systematic analysis methods, so as to reduce the occurrence of problems at the source and improve the overall quality of products.

In the field of manufacturing, defect cause traceability is closely related to quality traceability. Most enterprises manage historical production data through big data technologies [7], primarily including key parameter prediction [8], the optimization of operational parameters [9] and big data management platforms. These efforts assist enterprises in quality management and process optimization, helping reduce the occurrence of issues and improve overall product quality.

In the continuous casting domain, tracing the cause of cast product defects is of great significance for improving product quality and optimizing production process. Zhang et al. [10] proposed a knowledge graph reasoning-based method for quality defect traceability in hot-rolled strip products which uses the interpretable method SHapley Additive exPlanations (SHAP) and the Bayesian network to infer the posterior probability of product quality defects caused by different process parameters. Wu et al. [11] employed an unsupervised deep learning approach to detect mold-level anomalies in continuous casting production, enabling the process traceability of billet production quality.

To address the issue of insufficient model transparency in machine learning-based quality reasoning analysis, Takalo-Mattila [12] proposed a steel quality analysis method based on gradient boosting trees. This method employs SHAP to infer the potential relationships between process input parameters and surface defects. Li et al. [13] used an improved Residual U-Shaped Network segmentation algorithm to learn the features of steel defects, which improved the recognition accuracy for steel defects.

Quality management has become one of the cores of intelligent manufacturing, constructing, and improving the root cause traceability system [14] of cast product defects not only helps to improve product quality but also effectively improves the market competitiveness and brand reputation of enterprises [15]. In the future, with the further development of artificial intelligence and big data analysis technology, the traceability of cast product defects in the continuous casting domain can become more intelligent and accurate, which can provide strong technical support for the transformation and upgrading of steel enterprises.

2.2. Industrial KGs

Continuous casting technology plays a pivotal role in the iron and steel industry. In the production process, the root cause analysis of cast product defects has always been the focus of academic and industrial attention. As an emerging knowledge representation and reasoning tool, the KG has been widely used in many domains. Compared with the general KG represented by Google knowledge graph [16], the DSKG is more professional and complex, with higher requirements for the depth and fine granularity of knowledge [17] and more stringent requirements for accuracy.

In recent years, researchers have begun to apply KGs to industrial production processes to achieve the intelligent management of production processes and quality control. For example, Zhou et al. [18] designed an ontology of petrochemical production processes and constructed a KG for diesel production, optimizing the production process of biodiesel to achieve optimal operating conditions under different market conditions. Similarly, Chen et al. [19] used multiple data sources to construct a KG for the problem of steel strip fracture in cold-rolling production process and effectively modeled steel strip fracture through embedding technology. Zheng et al. [20] designed the Self-X cognitive manufacturing network, which integrates an industrial KG and multi-agent reinforcement learning to achieve self-configuration, self-optimization, and self-adaptation capabilities within manufacturing systems. Mou et al. [21] proposed a general method framework for KG construction for process industry control systems to realize the management of cyber–physical assets. The aforementioned studies show that KGs can effectively integrate multi-source heterogeneous data in complex industrial scenarios and provide more intelligent decision support.

In the continuous casting domain, the application of KGs is not limited to the storage and retrieval of knowledge but also includes, more importantly, its reasoning ability in the root cause analysis of cast product defects. However, the current research on C2Q-KGs mainly focuses on the construction and static analyses and lacks in-depth research on the dynamic factors and complex relations in the continuous casting process. For example, the existing triple-embedding-based methods usually only consider the local semantic relations when dealing with continuous casting data and ignore the complex causal association between process parameters and production conditions.

In addition, although the path-based reasoning method can capture the chain relation between casting entities, its reasoning results are often not accurate enough when the path information is missing or incomplete. KG reasoning in the continuous casting domain is still in the development stage.

2.3. GATs

In recent years, Graph Convolutional Networks (GCNs) have been widely used in the realm of KGs. The typical representative is the relational GCN (R-GCN) [22], which is based on the representation of the surrounding nodes of the known entities or relations in the graph, and the representation of the unknown entities can be obtained by reasoning, so as to obtain the representation vector of the missing entities in the KG.

A GCN can deal with graph-structured data with complex relations and interdependence between data. The introduction of the GCN model enriches the representation of entities and relations in KGs, especially as it has a certain reasoning ability to obtain the representation of unknown entities and relations. However, the expressibility of a GCN is constrained by the fixed and immutable weights between nodes, so that the hidden information in the KG may be ignored. In order to solve the shortcomings of GCNs, Velickovi et al. [23] introduced GATs.

The GAT is a new GCN model that can assign different weights to different nodes in adjacent domains without any type of matrix operation and dynamically adjust the weights between nodes. For example, Wang et al. [24] used Graph-based Attention Networks for tasks such as link prediction and entity discovery. In addition, there are also GATs proposed by Wang et al. [25] which use node-level attention and semantic-level attention based on heterogeneous graphs.

In this paper, a GAT is introduced to make KGTBRN better capture the hidden information in the C2Q-KG and improve the reasoning accuracy.

2.4. Knowledge Graph Completion

In recent years, knowledge graph completion technology has received extensive attention and achieved in-depth development. At present, knowledge graph completion technology is abstracted as a link prediction problem which predicts the missing parts of the triple, such as head entity prediction $\left(?,r,t\right)$, tail entity prediction $\left(h,r,?\right)$ and relation prediction $\left(h,?,t\right)$, where $?$ indicates the part that needs to be predicted and the other two parts are known.

Among all knowledge completion methods, those based on knowledge representation learning have emerged as the most effective and widely adopted approaches and use linear or neural network models to predict the missing information in knowledge triples by learning low-dimensional vector representations of entities and relations on the basis of preserving the internal structure of the KG [26]. These methods can be roughly divided into three categories: triple-embedding-based methods, path-based methods, and graph-structure-based methods.

Triple-embedding-based methods map the entities and relations in the KG to a low-dimensional vector space and use the relations between the vectors to predict the associations between the entities [27]. For example, in the relational rotation model proposed by Sun et al. [28], each relation is represented as a rotation angle on the complex plane, and the association information between entities is captured by the rotation operation. Similarly, in the box-embedding model proposed by Abboud et al. [29], entities are embedded as points and relations are embedded as box-like hyperrectangles to capture relation rules and represent logical properties on KGs.

Path-based methods predict the relation by analyzing the path information between entities. Niu et al. [30] proposed a path representation method that combines semantic and data-driven approaches, which can integrate information from multiple paths to generate a more interpretable and generalized path representation. The reasoning method based on Graph Neural Networks (GNNs) learns the information of entities and their neighbors to predict the relation between entities by performing message passing and aggregation operations on the KG [31].

In the sequence relation Graph Convolutional Network method proposed by Wang et al. [32], the set of paths between entity pairs is constructed as a path graph, which is serialized into a series of subgraphs, and the reasoning task is performed by the GNN algorithm [33]. Marra et al. [34] proposed Relational Reasoning Networks (R2N), a neuro-symbolic model that integrates knowledge graph embeddings with logical reasoning. It can perform multi-hop relational reasoning in latent space, enhancing relational representation and reasoning capabilities under uncertainty.

However, the existing methods have limitations. Methods based on triple embedding mainly capture local semantic relations and lack a global understanding of complex graph structure [35]. Path-based methods consider path information, but their reasoning performance may be limited in the case of missing paths or incomplete information. Methods based on GNNs can aggregate the information of neighbor nodes, but they often ignore the differences in the characteristics of different relations in the KG.

In order to solve the problem that the existing knowledge graph completion methods cannot balance the reasoning accuracy of all relations, this paper proposes a knowledge graph reasoning model based on a two-branch reasoning network in the continuous casting domain.

KGTBRN classifies the triples in the C2Q-KG according to the number distribution of the head and tail entities and introduces a two-branch reasoning network structure following the GAT layer to select a more appropriate method for the knowledge graph completion task according to different entity distribution types, so as to improve the analysis accuracy of KGTBRN in the root cause analysis of cast product defects.

3. Methods

3.1. Problem Modeling

The task of the root cause analysis of cast product defects is formalized as a link prediction task of head entity or tail entity. The C2Q-KG is expressed in the form of triples as $G=\left\{\left(h,r,t\right)\right\}$, where $h,t\in E$ represent the continuous casting head entity and the continuous casting tail entity, respectively, and $r\in R$ represents the continuous casting relation between the continuous casting head entity and the tail entity. For a cast product defect head entity h and a continuous casting relation r, the triple is represented as $\left(defecth,r,t\right)$, and its reasoning task is to reason on the root cause tail entity t. On the other hand, for a continuous casting relation r and a cast product defect tail entity t, the triple is represented as $\left(h,r,defectt\right)$, and its reasoning task is to reason on the root cause head entity h.

3.2. Continuous Casting Triple-Embedding Module Based on GAT

Aiming at the existing C2Q-KG, we propose a continuous casting triple-embedding module based on the GAT, which makes KGTBRN better capture the complex information hidden in the neighborhood of each entity [21] and improves the accuracy of the subsequent reasoning layer. Specifically, this module consists of two parts: the continuous casting relation classification module and the GAT embedding module.

3.2.1. Continuous Casting Relation Classification Module

This module realizes the preprocessing task of continuous casting triples in the C2Q-KG and counts the number of entities and the number of different relations contained in it. Then, it classifies the relations according to the number distribution of head and tail entities. Specifically, the processing method for the classification of relations is detailed below.

The average number of continuous casting tail entities ${\eta }_t$ for each continuous casting head entity and the average number of continuous casting head entities ${\eta }_h$ for each continuous casting tail entity are counted. For a continuous casting triple $\left(h,r,t\right)$, if ${\eta }_h<1.5$ and ${\eta }_t<1.5$, the relation r is classified as a 1-1 type; if ${\eta }_h<1.5$ and ${\eta }_t\ge 1.5$, the relation r is classified as a 1-N type; if ${\eta }_h\ge 1.5$ and ${\eta }_t\le 1.5$, the relation r is classified as an N-1 type; and if ${\eta }_h\ge 1.5$ and ${\eta }_t\ge 1.5$, the relation r is classified as an N-N type.

In the subsequent reasoning task of triples, different types of relations are classified to improve the accuracy of reasoning about the causes of cast product defects on the C2Q-KG, and the problem that the existing knowledge graph reasoning methods cannot balance the reasoning accuracy of all continuous casting relations is solved.

3.2.2. GAT Embedding Module

In this module, we input the relations obtained by the continuous casting classification module and the feature vectors of its neighborhood into the GAT. Then, we capture the hidden neighborhood information between the entities and relations through the two-layer GAT. Finally, we obtain the updated embedding vectors of head entity, tail entity and relation. Figure 1 shows the structural diagram of this module.

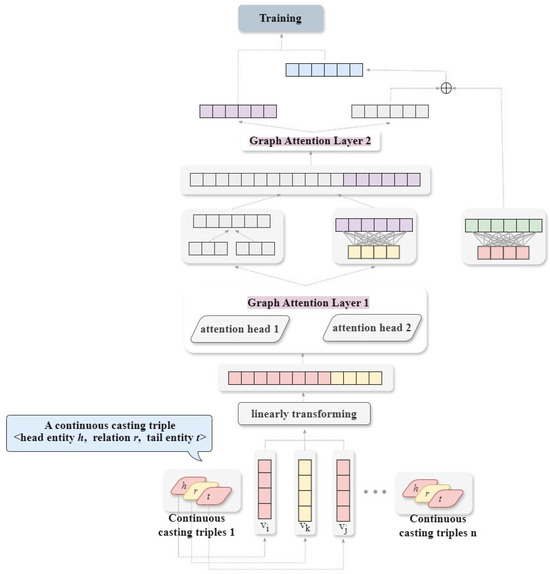
Figure 1. The embedding module structure of the two-layer GAT.

For a continuous casting triple $\tau =\left(h,r,t\right)$, similar to Nathani et al. [35], we first obtain the representation of each continuous casting triple associated with the continuous casting head entity h, tail entity t and relation r by performing a linear transformation on the cascade of its three feature vectors, as shown in Equation (1).

$$\overrightarrow{M_{hrt}}=W_1\left[\left.\overrightarrow{v_h}\right|\left.\overrightarrow{v_r}\right|\overrightarrow{v_t}\right],$$

(1)

where $\overrightarrow{v_{\mathrm{h}}},\overrightarrow{v_{\mathrm{r}}},\overrightarrow{v_t}$ denote the embeddings of head entity $h$, tail entity $t$ and relation $r$, respectively; $\overrightarrow{M_{hrt}}$ is the embedding vector representation of a continuous casting triple $\tau$; and $W_1$ denotes the linear transformation matrix.

We perform a linear transformation on $\overrightarrow{M_{hrt}}$, and the attention coefficient $b_{hrt}$ of a specific triple $\tau$ is obtained through the nonlinear activation function LeakyReLU. $b_{hrt}$ represents the importance of the continuous casting triple in the cast product defect reasoning task, as shown in Equation (2). LeakyReLU is determined based on common practice in the existing literature and empirical performance during preliminary experiments. Then, we perform the normalization operation on $b_{hrt}$ and get the normalized attention coefficient $a_{hrt}$, as shown in Equation (3).

$$b_{hrt}=LeakyReLU(W_2\overrightarrow{M_{hrt}}),$$

(2)

$$a_{hrt}=softmax(b_{hrt})={\displaystyle \frac{exp(b_{hrt})}{{\displaystyle \sum _{e\in E_t}{\displaystyle \sum _{r\in R_t}exp(b_{hrt})}}}},$$

(3)

where $E_{\tau }$ denotes the set of all neighborhood of the head entity $h$ and $R_{\tau }$ represents the set of relations $r$ connecting the entity in $E_{\tau }$ and head entity $h$.

After obtaining the normalized attention coefficient $a_{hrt}$, the new head entity embedding vector $\overrightarrow{h^{\prime }}$ is calculated by weighting, as shown in Equation (4). The attention values of each head are averaged and updated to obtain the final head entity embedding vector $\overrightarrow{h^{″}}$, as shown in Equation (5).

$$\overrightarrow{h^{\prime }}=\sigma ({\displaystyle \sum _{t\in E_{\tau }}{\displaystyle \sum _{r\in R_{\tau }}{a}_{hrt}\overrightarrow{M_{hrt}})}}.$$

(4)

$$\overrightarrow{h^{″}}=\sigma ({\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N{\displaystyle \sum _{t\in E_{\tau }}{\displaystyle \sum _{r\in R_{\tau }}{a}_{hrt}^n}{M}_{hrt}^n}}).$$

(5)

Similarly, the same update method is used to obtain the final tail embedding vector $\overrightarrow{t^{″}}$.

This module uses N independent attention mechanisms to calculate the embedding vectors of continuous casting triples and concatenates these embedding results to obtain a more expressive continuous casting triple-embedding representation.

3.3. Cast Product Defect Root Cause Reasoning Module of C2Q-KG Based on Two-Branch Reasoning Network

This module reasons on the root causes of cast product defects on the basis of the updated continuous casting triple-embedding vector obtained previously. It is composed of a convolutional layer and a reasoning layer and uses a flexible reasoning network to reason on the root causes for the different types of relations previously divided. We modify the convolutional layers of the ConvKB model [36]. The reasoning layer includes a two-branch network including a connection layer and a capsule layer.

The convolutional layer connects the updated embedding vectors of head entity, tail entity and relation to obtain the embedding matrix. Then, the Convolutional Neural Network (CNN) is used to perform a convolution operation. The structure is shown in Figure 2.

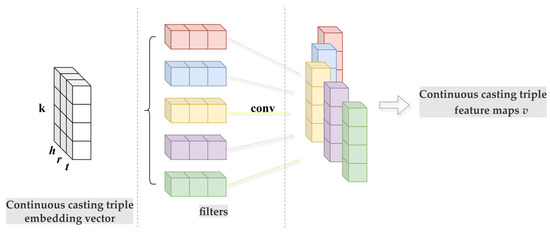
Figure 2. The structure of the convolutional layer.

The embedding form $(v_h,v_r,v_t)$ of each continuous casting triple $(h,r,t)$ is regarded as a continuous casting matrix $A=\left[V_h,V_r,V_t\right]\in {\mathbb{R}}^{k\times 3},$ where $A_i$ denotes the row of $A$ and $k\times 3$ denotes the dimension size of $(h,r,t)$. Referring to the transfer characteristics based on the transfer model, the convolutional layer uses filters of $\omega$ ∈ ${\mathbb{R}}^{1\times 3}$ size to study the overall relation between the embedded continuous casting triples $(v_h,v_r,v_t)$ in the same dimension. The filter $\omega$ repeats the operation on each row of $A$ and finally generates the set of feature maps $v=\left[v_1,v_2,\dots ,v_k\right]\in {\mathbb{R}}^k$, as shown in Equation (6).

$$v_i=ReLU(w\cdot A_i+b),$$

(6)

where $b\in R$ is a bias term.

For the KG link prediction task, CapSe [37] uses the capsule network to optimize accuracy. However, the capsule network only shows good performance when reasoning on the multi-terminal entity (N-side) of the triple, and its effect on the single-terminal entity (1-side) is not as good as those connection models. Therefore, we use the capsule layer, which consists of two capsule networks, to deal with the N-side continuous casting entity reasoning tasks, and use the connection layer to deal with the 1-side continuous casting entity reasoning tasks.

Through the two-branch reasoning network, the overall reasoning process of the root causes is refined, so that KGTBRN can better adapt to the diversified characteristics of relations in the continuous casting domain and improve the reasoning accuracy. Figure 3 shows the structure diagram of the two-branch reasoning network.

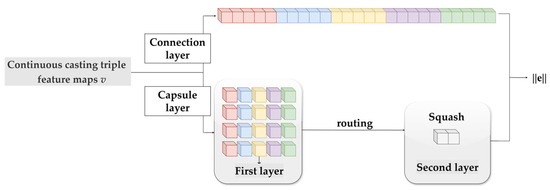
Figure 3. The structure of the two-branch reasoning network.

For 1-side continuous casting entity reasoning tasks (including the 1-1 and 1-N types of head entity reasoning tasks and the 1-1 and N-1 types of tail entity reasoning tasks), the feature-mapping vector can be input into the connection layer directly to form the output vector $e\in {\mathbb{R}}^{\tau k\times 1}$, where $\tau$ is the number of filters and $k$ is the embedding dimension of the vector in the convolutional layer.

For N-side continuous casting entity reasoning tasks (including the N-N and N-1 types of head entity reasoning tasks and the N-N and 1-N types of tail entity reasoning tasks), the feature-mapping vector can be reconstructed into the corresponding first capsule layer. It is reconstructed as a matrix and routed to the second capsule layer to generate the continuous casting triple vector compressed by the squash function.

K capsules are constructed in the first capsule layer, where the entries of the same dimension from all the continuous casting triple feature-mapping vectors are encapsulated into the same capsule, so that each capsule can capture many features between the entries of the corresponding dimension in the embedded continuous casting triple. These features are re-summarized through the routing process and squash function compression and finally recorded in the second capsule network.

Additionally, the routing process between the two capsule layers is as follows: Each capsule vector $u_i$ of the first capsule layer is multiplied by a weight matrix $W_i$ to obtain the updated capsule vector $\widehat{u_{\mathrm{i}}}$, as shown in Equation (7).

$$\widehat{u_i}=W_i{u}_i.$$

(7)

The weighted sum of all capsule vectors is performed, where the weighting coefficient $c_i$ is obtained by the output of softmax function in the first capsule layer. The routing result $s$ is obtained by weighted summation, and the final continuous casting triple output vector of this layer is obtained by the squash function, as shown in Equation (8).

$$s={\displaystyle \sum _i{c}_i\widehat{u_i}},e=squash(s),$$

(8)

where

$$squash(s)={\displaystyle \frac{{‖s‖}^2}{1+{‖s‖}^2}}{\displaystyle \frac{s}{‖s‖}}.$$

The modular length of the output vector $e$ obtained by the above two reasoning methods is the reasoning accuracy of the continuous casting triple. The scoring function f is operated by computing the modulus of e. Concat(*) denotes the connection layer, and capsnet(*) denotes the capsule layer, as shown in Equation (9).

$$f(h,r,t)=‖e‖,$$

(9)

where

$$e=\left\{\begin{array}{l}concat(g(\left[v_h,v_r,v_t\right]\ast \omega \left)\right)\\ capsnet(g(\left[v_h,v_r,v_t\right]\ast \omega \left)\right)\end{array}\right..$$

KGTBRN is trained by minimizing the loss function and is optimized by using the Adam optimizer. The loss function is as shown Equation (10), where ${\mathcal{G}}^{\prime }$ is the set of invalid continuous casting triples, which are generated by the head entity or tail entity that damages the triples in the valid set $\mathcal{G}$.

$$\mathcal{L}={\displaystyle \sum _{(h,r,t)\in \left\{\mathcal{G}{\displaystyle \cup {\mathcal{G}}^{\prime }}\right\}}\log (1+\exp (-t_{(h,r,t)}}\cdot f(h,r,t))),$$

(10)

where

$$t_{(h,r,t)}=\left\{\begin{array}{l}1,when(h,r,t)\in \mathcal{G}\\ -1,when(h,r,t)\in {\mathcal{G}}^{\prime }\end{array}\right..$$

The overall structure of KGTBRN is shown in Figure 4. KGTBRN consists of two main components: the embedding module and the reasoning module. The embedding module includes a continuous casting relation classification module and a two-layer GAT, which together capture structural and semantic information from triples in the C2Q-KG. The reasoning module includes a convolutional layer and a two-branch reasoning network, designed to handle different distributed entity-side reasoning task and improve the accuracy of KGTBRN.

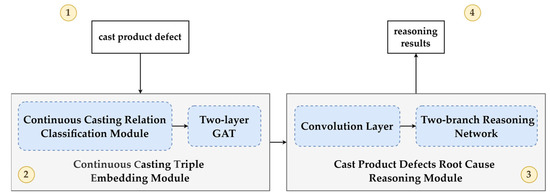
Figure 4. The overall structure of KGTBRN. The numbers indicate the steps of KGTBRN.

The specific classification of relations and the reasoning selection examples of the two-branch reasoning network are shown in Table 1.

Table 1. Relation classification and selection examples of two-branch reasoning network.

Continuous Casting Head Entity	Continuous Casting Relation	Continuous Casting Tail Entity	Relation Type	Reasoning Need	Reasoning Selection
Uneven water cooling in secondary cooling zone	Lead to	Columnar crystals grow faster	N-N	Continuous casting head entity reasoning	Capsule layer
Liquid steel enriched with solute elements is sucked into the void	Cause	Central segregation	1-N	Continuous casting head entity reasoning	Connection layer
Bridging	Lead to	The enriched solute element molten steel is sucked into the void	N-N	Continuous casting head entity reasoning	Capsule layer
Belly drum	Solution	Keep the clamp roller rigid	1-1	Continuous casting tail entity reasoning	Connection layer

According to the different types of relation obtained by the previous classification and the needs of the reasoning tasks, we randomly select another entity that is not equal to the current entity from the entity set for replacement to generate negative samples of continuous casting triples for model training. For example, for the 1-N type continuous casting triple, the following steps are necessary:

(i)

Replace the existing head entity, and retain the relation and tail entity to generate a negative sample of the 1-N type, which is used for training the reasoning tasks of the head entity in the 1-N type casting triple.

(ii)

Replace the existing tail entity, and retain the relation and head entity to generate a negative sample of the 1-N type, which is used for training the reasoning tasks of the tail entity in the 1-N type casting triple.

The above two steps are performed for all continuous casting triples to generate a set of all negative samples as the invalid continuous casting triple set ${\mathcal{G}}^{\prime }$.

4. Experiment and Analysis

4.1. C2Q-KG

The detailed metadata of the C2Q-KG used in this paper is shown in Table 2. The C2Q-KG contains 1626 continuous casting triples, involving 1144 entities and 5 types of relations.

Table 2. The detailed metadata of the C2Q-KG.

Parameter	Number
continuous casting entities	1144
continuous casting relations	5
continuous casting triples	1626
describe	144
lead to	349
feature is	261
solution	297
cause	575
total	2396

The “describe” relation denotes basic information about cast product defects, such as their location. The “feature is” relation denotes specific manifestations and related attributes of cast product defects, such as depth and temperature. The “cause” relation denotes that a certain root cause leads to a dynamic cast product defect phenomenon, while the “lead to” relation denotes a cause resulting in a static cast product defect. The “solution” relation denotes the optimization measures adopted for cast product defects.

These relations cover the four types of 1-1, 1-N, N-1 and N-N. The reasoning accuracy and stability of KGTBRN can be measured by using the standard knowledge graph reasoning evaluation indicators in the domain. The main indicators include hit probability among the top k results (HITS@K) and mean reciprocal rank (MRR), as shown in Equations (11) and (12), where ${\mathit{rank}}_i$ denotes the rank of the correct entity among all reasoning results and S denotes the number of data in the set.

$$HITS@K={\displaystyle \frac{1}{\left|S\right|}}{\displaystyle \sum _{i=1}^{\left|s\right|}I(ran{k}_i\le k)}$$

(11)

$$MRR={\displaystyle \frac{1}{\left|S\right|}}{\displaystyle \sum _{i=1}^{\left|s\right|}\frac{1}{ran{k}_i}}$$

(12)

4.2. Performance Evaluation of Root Cause Analysis Model for Cast Product Defects

Table 3 shows the reasoning accuracy of KGTBRN on the continuous casting data set and the comparison with TransE [38], DistMult [39], ComplEX [40], KGLM [41] and KERMIT [42].

Table 3. Comparison of reasoning accuracy of each model on continuous casting data set.

Model	MRR	HITS@1	HITS@3	HITS@10
TransE	0.492	19.5	24.7	56.8
DistMult	0.614	21.9	30.2	65.4
ComplEX	0.597	22.8	31.5	62.1
KGLM	0.712	31.4	42.2	67.5
KERMIT	0.697	30.3	45.4	71.3
Ours	0.893	37.2	51.6	76.9

On the task of the root cause analysis of cast product defects in the C2Q-KG, KGTBRN shows the highest accuracy. On the continuous casting data set, KGTBRN has the best performance on MRR, HITS@1, HITS@3 and HITS@10.

Compared with the comparison models, the improvement in HITS@1 means that the differentiated reasoning mode for different relation types adopted by KGTBRN is more in line with the diversified characteristics of triple relation types in the C2Q-KG. KGTBRN scores a 6.9% higher value than the optimal model KERMIT in HITS@1, and 6.2% and 5.6% higher values in HITS@3 and HITS@10, respectively. These findings prove that KGTBRN is effective in the task of the root cause analysis of cast product defects.

4.3. Ablation Experiment of Root Cause Analysis Model for Cast Product Defects

Table 4 shows the results of the ablation experiment of KGTBRN on the task of the root cause analysis of cast product defects. “Model-attention” is the model where the GAT layer of KGTBRN is removed, and only the two-branch reasoning network is used for the root cause analysis task. “Model-concat” is the model where the capsule layer in the two-branch reasoning network of KGTBRN is removed, and “Model-capsnet” is the model where the connection layer in the two-branch reasoning network of KGTBRN is removed.

Table 4. Ablation experiment results of KGTBRN on the task of the root cause analysis of cast product defects.

Ablation	HITS@1	HITS@3	HITS@10
Model-attention	31.5	43.7	69.8
Model-concat	32.6	46.9	71.0
Model-capsnet	35.2	48.2	73.4
All	37.2	51.6	76.9

It can be seen from Table 4 that the GAT layer, the connection layer and the capsule layer improve the reasoning accuracy. Taking the HITS@1 index as an example, the addition of the GAT layer improves HITS@1 by 5.7%. Using the connection layer to process the 1-side reasoning task improves HITS@1 by 2%, and using the two capsule layers to process the N-side reasoning task improves HITS@1 by 4.6%.

This shows that the two-branch reasoning network uses the idea of “classifying relation types, and using different reasoning methods to deal with different types of relations separately” is more suitable for the C2Q-KG. Meanwhile, the GAT layer can better identify the potential feature relations between relations and entities, so as to improve the reasoning accuracy of the overall model.

4.4. Experiments on Hyperparameters of GAT Layer and Reasoning Layer

Table 5 shows the experiment results of the hyperparameters of the GAT layer and the reasoning layer. In Table 5, “epoch_attention” represents the iteration number of the GAT layer and takes values of {500, 800, 1000}, and “epoch_reasoning” represents the iteration number of the reasoning layer and takes values of {150, 200, 250}. Experiments are carried out on these two hyperparameter permutations and combinations. When “epoch_attention” is 1000 and “epoch_reasoning” is 200, the reasoning accuracy of KGTBRN reaches the highest.

Table 5. Experimental results of hyperparameters of GAT layer and reasoning layer.

Hyperparameter	Number of Iterations	HITS@1	HITS@3	HITS@10
epoch_attention	1000	37.2	51.6	76.9
epoch_reasoning	200
epoch_attention	1000	33.8	46.7	72.0
epoch_reasoning	150
epoch_attention	1000	33.6	44.2	67.3
epoch_reasoning	250
epoch_attention	500	35.5	47.3	73.6
epoch_reasoning	200
epoch_attention	500	34.2	48.5	74.4
epoch_reasoning	150
epoch_attention	500	32.0	45.1	71.8
epoch_reasoning	250
epoch_attention	800	36.8	50.3	74.2
epoch_reasoning	200
epoch_attention	800	35.4	48.9	75.1
epoch_reasoning	150
epoch_attention	800	36.4	47.1	69.4
epoch_reasoning	250

Figure 5 shows the loss iteration values of the GAT layer and the two-branch reasoning network of KGTBRN with the optimal parameters, respectively. It can be seen that all parts have converged successfully, proving that both the GAT layer and the two-branch reasoning network successfully capture the knowledge information of the C2Q-KG.

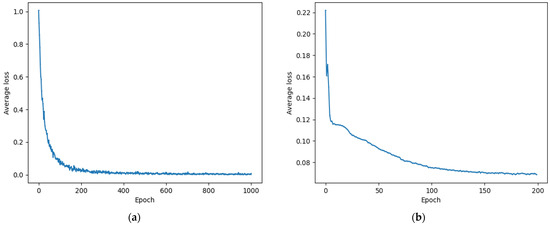
Figure 5. Loss iteration values of the GAT layer (a) and the two-branch reasoning network (b).

4.5. Generalization Experiment of Root Cause Analysis Model for Cast Product Defects

Table 6 and Table 7 show the experimental results of KGTBRN on the benchmark data sets FB15K-237 and WN18RR, respectively. The selected comparison models are ConvE [43], TransE [38], ConvKB [36], KGLM [41], KERMIT [42] and NBFNET [44].

Table 6. Experimental results on data set FB15K-237.

Model	HITS@1	HITS@3	HITS@10
ConvE	23.7	35.6	50.1
TransE	19.9	31.4	47.1
ConvKB	24.6	35.2	51.7
KGLM	20.0	31.4	46.8
KERMIT	26.6	39.6	54.7
NBFNET	32.1	45.4	59.9
Ours	34.8	47.3	58.3

Table 7. Experimental results on data set WN18RR.

Model	HITS@1	HITS@3	HITS@10
ConvE	41.5	46.3	50.1
TransE	38.7	44.1	53.8
ConvKB	53.5	44.5	56.8
KGLM	33.0	53.8	74.1
KERMIT	59.1	66.4	78.0
NBFNET	48.5	56.4	64.1
Ours	58.5	67.7	77.9

It can be seen that on the FB15K-237 data set, KGTBRN achieves the highest HITS@1 and HITS@3 and is suboptimal in HITS@10. Also, KGTBRN achieves the highest HITS@3 on WN18RR, indicating that the two-branch reasoning network can improve the overall reasoning accuracy of the KG by effectively handling different entity distribution patterns. Table 6 and Table 7 further reflect the robustness and generalization capability of KGTBRN.

Take FB15K-237 as an example, analyzing the triple distribution of and continuous casting data set, the results are shown in Table 8. The statistical results show that the proportions of 1-1-type and 1-N-type triples in the FB15K-237 data set are small: the 1-1-type triples represent only 0.94% and the 1-N-type ones only 6.32%. However, the distribution on the continuous casting data set is more uniform, so it is speculated that the uneven distribution of triples in the FB15K-237 affects the reasoning accuracy of the 1-side of KGTBRN; then, the overall reasoning results are reduced in the HITS@10 index, achieving suboptimal results.

Table 8. Statistical results of triple distribution of FB15K-237 and continuous casting data set.

Model	Percentage of Relation Type (%)
	1-1	1-N	N-1	N-N
FB15K-237	0.94	6.32	22.03	70.72
Continuous cast data set	8.9	21.5	34.3	35.3

Table 9 shows examples of actual reasoning results. According to the needs of the reasoning task, KGTBRN can use different reasoning methods according to the 1-side and N-side and give the top two root causes obtained by reasoning.

Table 9. Examples of actual reasoning results of root cause analysis task.

Casting Defect	Root Cause Analysis Task	Root Cause Analysis Results
		Root Cause 1	Root Cause 2
Cracks appear on the surface of the casting	<?, cause, surface cracks> Head entity reasoning	The first brittleness temperature zone moves towards low temperature	Deviation in critical stress appears
Casting belly bulging	<?, cause, bulge> Head entity reasoning	Casting shell thinning	Liquid molten steel static pressure deviation
The thickness of the solidified shell is uneven	<?, lead to, uneven thickness of solidified shell> Head entity reasoning	Mold liquid level fluctuation	The protective slag does not melt well
Air bubbles escape from the molten steel	<?, lead to, bubble escape> Head entity reasoning	Oxygen, nitrogen, hydrogen, argon and carbon are at the front of the solidification interface	Shear effect of molten steel

When researchers need to reason about the root cause based on the appearance of a certain cast product defect, they can use “cause” as the input relation of the root cause analysis task. When researchers need to reason about the root cause based on a certain production phenomenon, “lead to” can be used as the input relation.

From the first row of Table 9, it can be seen that when cracks appear on the surface of the casting, KGTBRN gives the top two root causes as “the first brittleness temperature zone moves towards low temperature” and “deviation in critical stress appears”. Based on these results, workers can make the corresponding adjustments to relevant continuous casting process parameters.

Figure 6 illustrates the cause reasoning results for “Crack”. KGTBRN identifies eight potential root causes for it, including “Stress concentration”, ”Shell unevenness”, ”Critical stress drop”, etc.

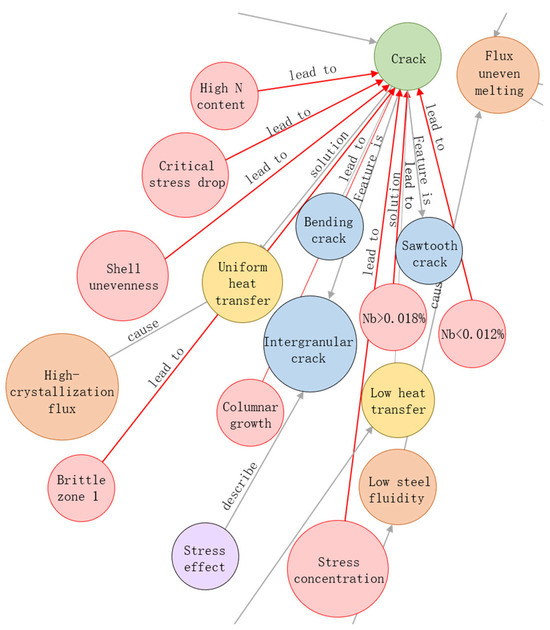
Figure 6. Reasoning results for cause of “Crack” defect.

5. Conclusions

This paper proposes a reasoning model of a C2Q-KG based on a GAT and a two-branch reasoning network. Firstly, KGTBRN classifies the continuous casting triples according to the number distribution of the head entities and tail entities for each relation in the C2Q-KG. For the triples with a sparse entity distribution (1-side), KGTBRN uses the connection layer to ensure that the relevant entities can still be accurately reasoned on in the case of lacking information. For the triples with a dense entity distribution (N-side), the capsule layer is used for reasoning.

In order to further improve the performance of KGTBRN, KGTBRN also introduces a GAT. By dynamically adjusting the attention distribution in different neighborhoods, the GAT enhances the ability of KGTBRN to capture the local neighborhood information of triples and enables it to better understand the implicit connections among entities, so that KGTBRN can still maintain high reasoning accuracy in the face of complex relations.

In the experimental part, we compare KGTBRN with other cutting-edge models on the C2Q-KG. The experiment results show that KGTBRN shows higher accuracy and reliability, improving by 6.9% on HITS@1, by 6.2% on HITS@3 and by 5.6% on HITS@10. This shows that KGTBRN can not only adapt to reasoning tasks under different entity distributions but also perform effective root cause analysis of cast product defects in complex continuous casting process scenarios.

We provide an effective knowledge graph reasoning model for the continuous casting domain. By combining the GAT and the two-branch reasoning network, the influence of the unbalanced distribution of entities on the reasoning accuracy is successfully solved. As KGTBRN is constructed based on the data characteristics of the C2Q-KG in the continuous casting domain, generalizing it to other industrial domains still presents challenges. Additionally, the two-branch reasoning network may increase model complexity and implementation difficulty. Future work will explore broader applications and introduce quality evaluation metrics to enhance the generalization capability of KGTBRN.

The application of this method can help enterprises to more accurately identify the potential root causes of cast product defects in the production process, thereby advancing quality management technologies in intelligent manufacturing. With strong scalability and application potential, it is expected to promote process optimization and product quality improvement, thus facilitating the intelligent and digital transformation of the manufacturing industry.