Abstract
The dynamic characteristics of fractured coal under cumulative impact are an important basis for evaluating the safety and stability of mining engineering. In order to study the dynamic mechanical properties of fractured coal under cumulative impact, the split-Hopkinson pressure bar (SHPB) device is used to conduct dynamic impact tests on fractured coal under cumulative impact. The wave velocity variation, dynamic compressive strength, fractal characteristics of fragmentation and energy dissipation properties of fractured coal samples under different impact times are analyzed. The results indicate that as the number of cumulative impacts increases, the decreasing trend of wave velocity of the coal samples conforms to the linear change relationship, and the rate of reduction varies with fracture inclination angles, demonstrating an inclination-dependent behavior. The dynamic compressive strength and energy dissipation rate of coal samples continuously decrease with the increase in cumulative impact times. The dynamic strength of the samples decreases approximately 25–40% after five time impacts. Coal samples with a fracture inclination angle of 30° show the largest decrease in dynamic compressive strength and are most prone to failure. As the number of cumulative impacts increases, the fractal dimension of the coal samples gradually increases, and the fragmentation mode transitions from large-size block failure to fine-grain pulverization. The failure mechanism converts from tensile failure to a mixed tensile–shear failure mode. The research findings provide a scientific basis for studying the mechanism of dynamic disasters in fractured coal samples under disturbance impact.
1. Introduction
Coal resources have long played a pivotal role in China’s energy system, with their safe and efficient extraction remaining a central issue in mining engineering [1,2]. As mining operations progressively extend to deeper geological strata, the frequent occurrence of dynamic hazards poses significant threats to coal safety extraction [3,4,5]. Coal-rock masses in deep mining progress are frequently subjected to complex dynamic disturbances, such as blasting vibrations, mechanical excavation and so on, which typically exhibit repetitive and cyclic cumulative characteristics [6,7,8]. These disturbances induce progressive crack propagation within coal-rock masses [9] and generate cumulative damage to coal seams [10,11]. The evolutionary pattern of major disasters induced by minor perturbations and multiple cycles demonstrates distinct time-dependent cumulative effects, presenting critical challenges in dynamic hazard prevention within deep mining operations. Moreover, coal seams subjected to long-term geological movements and external disturbances contain numerous discontinuities, which include fractures, joints and faults. In situ coal strata typically exhibit complex fracture networks [12,13]. These fracture networks significantly alter the mechanical and deformation properties of coal-rock masses [14], leading to more complex dynamic responses in fractured coal-rock systems. Under dynamic loading disturbances, such systems exhibit heightened susceptibility to triggering dynamic disasters, including rockbursts and coal–gas outbursts [15,16,17,18]. Therefore, investigating the dynamic characteristics of fractured coal rock under cumulative impacts holds substantial scientific and engineering significance.
Extensive research has been conducted on the mechanical properties of coal-rock masses, yielding substantial scientific achievements [19,20,21,22,23,24,25]. Yao et al. [26] performed uniaxial compression testing of coal under controlled moisture conditions, revealing moisture-dependent degradation of critical mechanical parameters: peak stress, elastic modulus, strain-softening modulus and post-peak modulus exhibited inverse correlations with hydration levels. Thermal–mechanical characterization through uniaxial compression testing of coal specimens under varying thermal conditions revealed temperature-dependent fracture propagation dynamics and micro-to-macro failure mechanism transitions (Yang et al. [27]). Through numerical simulations, Wang et al. [28] demonstrated that the joint influence on shear failure diminishes with increasing load intensity in coal masses. The dynamic behavior of coal rock under impact loading has attracted significant research attention [29,30,31,32]. The split-Hopkinson pressure bar (SHPB) device has become a standard experimental method for studying the dynamic responses of brittle geomaterials [33,34,35]. For example, a comprehensive research initiative has been conducted to decode cryogenic-conditioned dynamic mechanical responses of coal specimens under sub-zero thermal environments (Wang et al. [36]). Gong et al. [37] attempted to use the SHPB device to investigate the stress–strain behavior, dynamic peak stress, elastic modulus and energy distribution characteristics of coal-rock composites under varying loading rates. The experimental results revealed that bedding planes induce mechanical degradation in coal specimens, with the interfacial angle between bedding planes and loading direction demonstrating pronounced influence on mechanical behavior, particularly showing minimum compressive strength at 30°or 45° orientations (Tan et al. [38]). Hao et al. [39] utilized a modified SHPB device; the researchers conducted combined static–dynamic loading tests on coal specimens while systematically investigating the coupled effects of static axial pre-stress and loading rate on dynamic tensile strength and crack propagation behavior. Cheng et al. [40] performed triaxial dynamic loading tests on coal specimens across low, medium and high strain rate regimes, revealing that dynamic compressive strength demonstrates progressive enhancement with increasing loading rates, axial stress levels and confining pressure magnitudes. While significant progress has been made in coal-rock dynamics research, the existing studies predominantly focus on intact specimens. Although the literature [41] conducted dynamic impact experiments on coal samples with prefabricated fractures, it did not account for the effects of cumulative impact disturbance. Practically, fractured coal undergoing cumulative impacts follows a “damage accumulation–fracture coalescence–performance degradation” evolutionary path, critically impacting coal seam stability. However, there are few studies on the dynamic characteristics of fractured coal under the action of cumulative impact disturbances. Therefore, this necessitates comprehensive investigation into the dynamic responses of fractured coal subjected to cumulative impact disturbances.
On the basis of the research above, this study utilizes prefabricated fractured coal samples as the research subject, subjecting them to cyclic impact loading while monitoring wave velocity evolution characteristics. Then, the split-Hopkinson pressure bar (SHPB) device is used to carry out the dynamic impact on the fractured coal rock under the action of cumulative impact, followed by sieve analysis of fragmented particles. The research systematically evaluates cumulative impact effects on three critical aspects: dynamic compressive strength, fractal fragmentation characteristics and energy dissipation mechanisms of fractured coal-rock masses. The findings provide theoretical and technical references for mechanism exploration of coal-rock dynamic disasters and prevention strategies in deep mining operations.
2. Experimental Design
2.1. Specimen Preparation
The coal block samples are obtained from a coal mine in Xunyi County, Shaanxi Province. The depth of this coal mine is 377.5 m, and the coal seam thickness is 7 m, which is underlain by mudstone strata. Homogeneous coal specimens from the same mining batch are prepared, which use a 50 mm diameter core drilling system for initial sampling. Diamond wire cutting technology is utilized for cross-sectional processing to eliminate hydro-cutting-induced alterations in physical–mechanical properties. The stringent geometric tolerances of this technique require that the flatness error of the two ends of the coal sample is not larger than 0.05 mm and the diameter deviation of the two ends is not greater than 0.02 mm.
Prefabricated central fractures are created through wire cutting, with specimens preliminarily processed into 50 mm diameter × 17.5 mm height cylindrical units for operational feasibility. Controlled fracture parameters include 10 mm length discontinuities with dip angles of 30°, 60° and 90° relative to horizontal plane. Final specimens are assembled by bonding two 17.5 mm thick subunits using epoxy resin adhesive (Type AB). The flatness of the surfaces is crucial. When bonding with Type AB glue, a brush was used to lightly apply the adhesive to the surface, resulting in a negligible glue layer thickness, as illustrated in Figure 1. To ensure stress uniformity under stress wave propagation in SHPB tests, specimens are designed with a length-to-diameter ratio typically below 1.0 [42]. Specimens are specifically set to 50 mm × 35 mm in this study, ensuring compliance with the critical length-to-diameter ratio requirement for dynamic impact testing.

Figure 1.
Experimental procedures and equipment.
2.2. Experimental Procedure
A custom-designed drop-weight impact system is developed to deliver controlled energy inputs to fractured coal specimens. Such device features a hammer mass, striker bar, support frame with height-adjustable column, precision level gauge and vibration-damped baseplate. The hammer with 100 g mass is positioned at 80 cm vertical height above specimens, with impact cycles controlled at 1, 3 and 5 repetitions through a free-fall release mechanism. A layer of polymer foam cushioning material was placed at the bottom of the simple drop hammer impact device to ensure that the hammer delivered a single impact to the sample, thereby avoiding repeated impacts. Post-impact P-wave velocity measurements are conducted using ultrasonic pulse generator, with triplicate measurements at varied probe orientations for mean value calculation. SHPB dynamic impact tests are subsequently performed on cumulatively damaged specimens, followed by fragment collection and sieve analysis. Standard sieves with graded apertures (30, 20, 10, 5, 1, 0.5 mm) are employed, with fragment mass distribution recorded via precision electronic balance. The experimental workflow is schematically presented in Figure 1.
2.3. SHPB System Configuration and Stress Equilibrium Verification
Dynamic impact tests are conducted by using a 50 mm diameter split-Hopkinson pressure bar (SHPB) device, as shown in Figure 1. The SHPB device comprises three subsystems: a pressure bar assembly obtaining the striker, incident, transmission and absorber bars with elastic modulus of 210 GPa, a measurement system and a data acquisition–processing unit. Strain gauges are symmetrically bonded on incident and transmission bars, which are set at 1.8 m and 1.5 m from specimen interfaces, respectively, configured in full-bridge circuits for wave separation analysis. A constant gas pressure of 0.15 MPa is maintained for impact loading, with annular brass shim serving as a pulse shaper for waveform optimization.
The experimental principle follows the elastic stress wave propagation theory under two fundamental assumptions: uniaxial stress state and dynamic stress equilibrium. The first assumption concludes that the specimen only has axial stress under the action of stress waves, and the dynamic stress equilibrium states that the stress always remains equal when the stress waves are repeatedly acted on the specimen. During the dynamic impact process, the incident strain, reflected strain and transmitted strain are recorded in the strain acquisition instrument. Then, by organizing the strain data output from the test according to the three-wave method [43], the strain rate , average strain ε(t) and stress σ(t) of the specimen can be obtained, as in Formulae (1)–(3) [44]:
where t is the testing time (s); v is the P-wave velocity (m/s); l is the specimen length (m); εi is the incident strain; εr is the reflected strain; εt is the transmitted strain; A is the cross-sectional area of SHPB bars (mm2); E is the elastic modulus of SHPB bars (GPa); As is the specimen cross-sectional area (mm2).
Dynamic stress equilibrium verification is a prerequisite for dynamic impact testing, serving as a fundamental criterion for experimental validity. Validation was performed on a 30° inclined fractured coal specimen after five cumulative impacts, as shown in Figure 2. The low transmitted signal observed in Figure 2 is due to the significant increase in internal microcracks within the fractured coal sample caused by multiple impacts, which leads to a reduction in the overall impedance of the sample. As the stress wave propagates through the sample, the transmission of the stress wave is hindered. The superimposed waveform of incident and reflected stresses demonstrates close agreement with the transmitted stress profile, confirming dynamic equilibrium attainment.
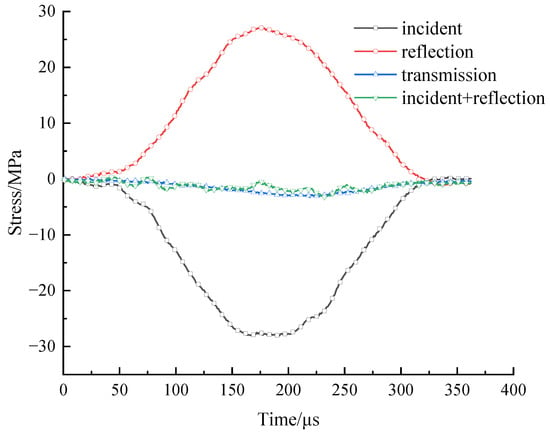
Figure 2.
Dynamic force balance during a SHPB test.
3. Results and Analysis
3.1. Wave Velocity Analysis
Generally, wave propagation velocity in solid materials increases with higher density and elastic modulus. Ultrasonic wave velocity measurement serves as an effective method for evaluating damage evolution in solids, as increased porosity and crack density significantly alter wave propagation characteristics. Cumulative impacts induce progressive damage in fractured coal samples, with wave velocity measurements providing a quantifiable indicator of damage severity under varying impact cycles. Figure 3 illustrates the wave velocity variations of coal samples with different fracture inclinations under cumulative impacts.
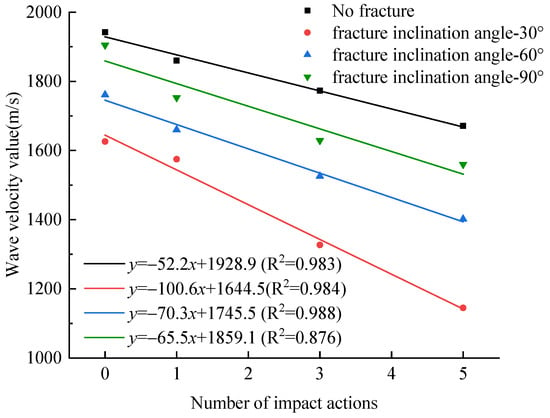
Figure 3.
The variation diagram of wave velocity of coal with different fracture angles under cumulative impact.
Figure 3 demonstrates that the wave velocity of coal samples decreases progressively with cumulative impacts under identical fracture inclination. For 30° inclined fractures, the initial wave velocity of 1626 m/s respectively declines to 1575 m/s, 1327 m/s and 1145 m/s after 1, 3 and 5 impacts. This reduction is attributed to microcrack propagation and porosity enhancement induced by cyclic impacts. Post-impact observations reveal secondary cracks around the prefabricated fractures and micro-debris detachment, indicating cumulative damage mechanisms. Prefabricated fractures reduce the initial wave velocity compared to intact specimens, with 90° inclined fractures exhibiting minimal reduction, which is parallel to wave direction, while 30° inclined fractures show the highest attenuation. The 90° aligned fractures minimally obstruct longitudinal wave propagation, whereas inclined fractures induce multi-path reflections and energy dissipation, elongating wave trajectories.
Furthermore, linear regression analysis reveals a well-defined linear correlation between cumulative impact cycles and wave velocity reduction across coal samples with varying fracture inclinations. The absolute slopes of fitting curves vary with fracture inclination: 100.6, 70.3 and 65.5 for 30°, 60° and 90° fractures, respectively, reflecting differential damage sensitivities. Under cumulative impact loading, the wave velocity decreases most rapidly when the crack inclination angle is 30°. This phenomenon primarily occurs because pre-existing cracks with a 30° inclination angle readily generate wing cracks and secondary cracks at their tips. The resulting complex crack network impedes wave propagation and introduces intricate wave path trajectories. Consequently, a significant acceleration in wave velocity attenuation is observed. The wave velocity of fractured coal specimens exhibits dip-angle dependency under cumulative impact loading. The slope of the fitted curve characterizes the sensitivity of crack dip angles to cumulative impact loading. A larger absolute slope value indicates higher sensitivity of the corresponding crack dip angle to cumulative impact loading. This demonstrates that crack dip-angle characteristics significantly influence wave velocity variations under cumulative impact loading.
3.2. Dynamic Compressive Strength Analysis
Dynamic stress–strain curves characterize the deformation and failure processes of fractured coal under dynamic loading conditions. Figure 4 presents these curves for coal samples with varying fracture inclinations subjected to cumulative impacts.
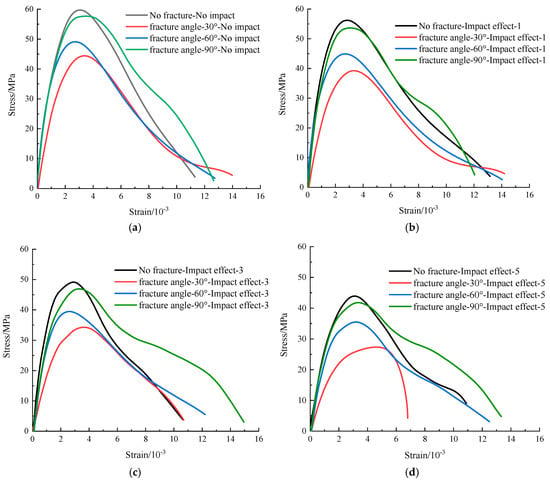
Figure 4.
Dynamic stress–strain curves of coal samples with different fracture angles under cumulative impact. (a) No impact effect; (b) Impact effect-1; (c) Impact effect-3; (d) Impact effect-5.
Figure 4 demonstrates that the dynamic stress–strain curves of fractured coal samples can be divided into three distinct phases: the elastic stage, yield stage and failure stage. Due to the narrow aperture of prefabricated fractures, rapid compression under impact loading eliminates a discernible compaction phase. The elastic stage exhibits near-linear stress escalation with minimal non-linearity. The yield stage corresponds to microcrack initiation and propagation, while the failure stage is characterized by gradual stress degradation. Under identical impact cycles, intact specimens exhibit the highest elastic modulus (slope), whereas 30° inclined fractures show the lowest values, indicating severely compromised deformation resistance. Progressive reduction in elastic modulus slope with cumulative impacts reflects accumulated internal damage, directly impairing the coal’s load-bearing capacity. The stress–strain curve of 30° fractured coal samples subjected to five cumulative impacts exhibits a shortened elastic stage with significant slope reduction and a marked decrease in peak strength. This demonstrates that damage accumulation from repeated impacts and fracture dip-angle characteristics critically govern the failure mechanism of fractured coal specimens.
Dynamic compressive strength quantifies fracture coal’s ability to resist failure under impact loads, with its degradation patterns providing critical insights into mechanical behavior and stability assessment. The dynamic compressive strength data extracted from Figure 4, summarized in Table 1, reveal systematic strength reduction with cumulative impacts. After five impacts, the dynamic strength decreases by approximately 25–40%, demonstrating severe material degradation. Furthermore, under identical impact cycles, coal specimens with 30° crack dip angle exhibit the lowest dynamic compressive strength values. For instance, after the initial impact, the strength reduction percentages were 5.9%, 11.7%, 8.5% and 7.0% for the corresponding specimens without pre-existing cracks and those with crack dip angles of 30°, 60° and 90°. The 30°dip-angle specimens demonstrate the most substantial strength degradation. This indicates that coal specimens containing 30° cracks possess the highest susceptibility to premature failure. The literature [45] revealed that variations in joint inclination significantly affect the impact resistance of specimens, with the weakest impact resistance observed at a joint inclination of 30°. The conclusions of this study are consistent with those findings, which also validate the reliability of the conclusions drawn in this research.

Table 1.
Dynamic compressive strength of fractured coal samples under cumulative impact (MPa).
Cumulative impact loading essentially subjects fractured coal specimens to cyclic disturbances, where the number of impacts corresponds to distinct levels of input disturbance energy. Impact cycles were configured as 0, 1, 3 and 5, with corresponding disturbance energies calculated via kinetic energy formulae as 0 J, 0.784 J, 2.352 J and 3.92 J, respectively. A quantitative relationship is established between disturbance energy and dynamic compressive strength to investigate their interdependence. Furthermore, correlative analysis between wave velocity reduction and strength degradation is conducted. Figure 5 illustrates the triaxial relationships among wave velocity, disturbance energy and dynamic compressive strength for 60° inclined fracture specimens.
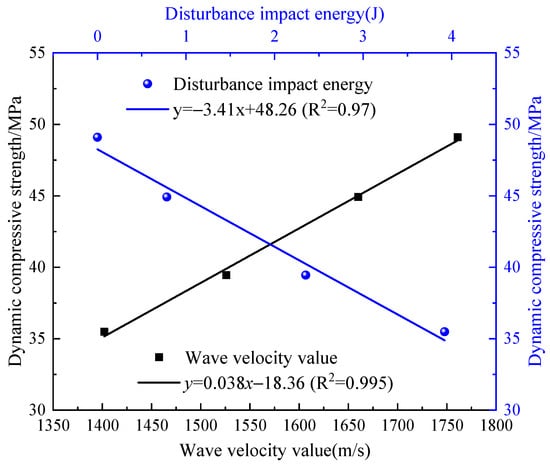
Figure 5.
Relationship diagram of wave velocity, disturbance impact energy and dynamic compressive strength.
The plot reveals a robust linear correlation: dynamic compressive strength decreases proportionally with wave velocity reduction, enabling strength prediction via wave velocity measurements given known fracture inclination. Furthermore, increased disturbance impact energy correlates with progressive deterioration in dynamic compressive strength of fractured coal specimens. This finding reveals that sustained energy absorption accelerates internal damage propagation within the material matrix, ultimately leading to strength degradation. Through data fitting, it is found that there is also a strong linear relationship between dynamic compressive strength and disturbance impact energy. It should be noted that the above relationship is based on the application mode of “lower single disturbance energy and more disturbance times”, and different input modes of disturbance impact energy may lead to different results.
3.3. Fractal Characteristics of Fragmentation
Macroscopic failure of fractured coal under dynamic loading arises from coalescence of microcracks, which nucleate from submicron-scale defects, exhibiting inherent self-similarity across multiple scales. The fractal theory provides a powerful framework for analyzing fragment size distribution, offering critical insights into failure mechanisms. The sieve analysis of post-impact fragments, as shown in Table 2, reveals systematic shifts in mass distribution with increasing impact cycles. Intact coal specimens without pre-existing cracks subjected to single impact loading exhibited residual coarse fragments with particle sizes exceeding 30 mm in post-SHPB test analysis. With increasing impact cycles, a progressive decrease in mass percentage of coarse fragments (>30 mm) was observed, accompanied by a corresponding increase in fine fragment proportion.

Table 2.
Screening results of fractured coal samples.
The fractal dimension provides an intuitive and quantitative measure of the degree of fragmentation in fractured coal samples. A larger fractal dimension indicates a higher number of fragments, smaller fragment sizes and a greater degree of sample fragmentation. Fragment size distribution follows the fractal mass–size relationship, as in Formula (4) [46]:
where x is the fragment size (mm); xm is the maximum fragment size (mm); M(x) is the cumulative mass of fragments with size less than x; MT is the total fragment mass; D is the fractal dimension. Taking the logarithm of both sides of Equation (4) yields Formula (5):
The relationship reveals that the slope k of the linear fit in the log–log coordinate system equals (3 − D), thus allowing the calculation of the fractal dimension D of fragmented coal, as in Formula (6).
As shown in Figure 6, the logarithmic curves of fragment mass distribution for fractured coal samples under cumulative impacts are presented. The SHPB test data points in Figure 6 demonstrate a linear relationship in log–log coordinates, with correlation coefficients exceeding 0.93, indicating strong statistical significance. This confirms that the fragmentation of fractured coal under cumulative impacts exhibits self-similarity across scales, satisfying fractal distribution characteristics.
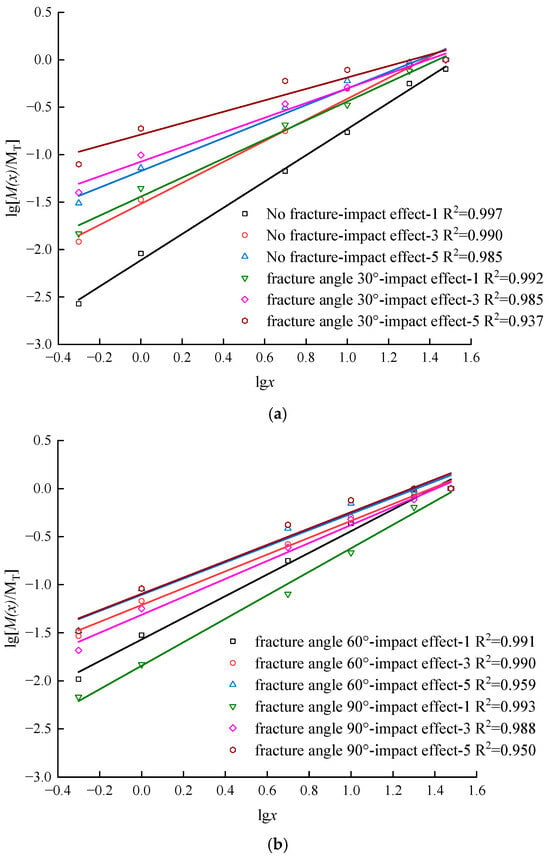
Figure 6.
Logarithmic curve of fragment mass distribution of fractured coal samples. (a) No fracture and fracture angle 30°; (b) Fracture angle 60° and fracture angle 90°.
The slopes of fitting curves in Figure 6 are extracted to calculate fractal dimensions, with the relationship between fractal dimension and prefabricated fracture inclination plotted in Figure 7. Under identical impact cycles, intact specimens exhibit the lowest fractal dimensions between 1.6 and 2.1, while 30° inclined fractures show the highest values, ranging from 1.8 to 2.4. As the fracture angle increases, the fractal dimension of fractured coal samples decreases, demonstrating that the crack propagation path is more complex and the degree of fragmentation is more severe in coal samples with a fracture angle of 30°. Furthermore, increasing fractal dimensions with cumulative impacts demonstrate progressive damage accumulation, rendering fractured coal more susceptible to comminution during SHPB failure.
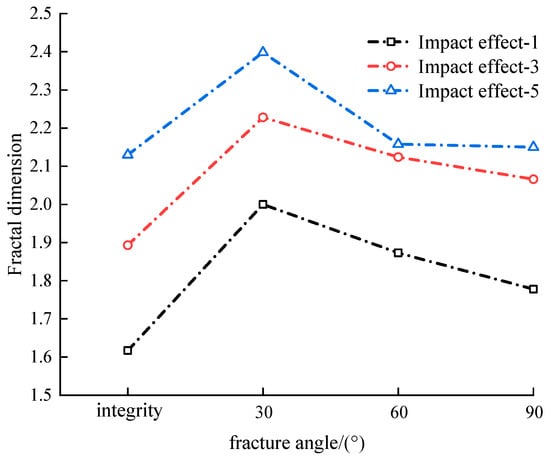
Figure 7.
Relationship diagram between fractal dimension and prefabricated fracture dip angle.
Combined with morphological analysis, the failure patterns under dynamic loading can be inferred from fragment geometries. Figure 8 displays typical fracture patterns of coal samples subjected to cumulative impacts. Post-SHPB specimens exhibit distinct fragmentation patterns: low-impact cycles (Figure 8a–d) predominantly yield large fragments (>10 mm), whereas high-impact cycles (Figure 8i–l) generate finer particles, demonstrating a transition from macro-fracture to pulverization with increasing impacts. Morphologically, low-impact fragments display elongated shapes, while high-impact debris exhibits polygonal geometries and powder-like particulates. This phenomenon arises from distinct failure mechanisms: elongated fragments result from axial-stress-induced tensile failure along dominant cracks, whereas polygonal/powdered debris forms through tension–shear interactions within complex crack networks generated by repeated impacts, where multi-directional stress fields and inter-fragment collisions induce mixed-mode failure.

Figure 8.
Morphological diagram of crushed coal samples under cumulative impact. (a) No fracture-impact effect-1; (b) Fracture angle 30°-impact effect-1; (c) Fracture angle 60°-impact effect-1; (d) Fracture angle 90°-impact effect-1; (e) No fracture-impact effect-3; (f) Fracture angle 30°-impact effect-3; (g) Fracture angle 60°-impact effect-3; (h) Fracture angle 90°-impact effect-3; (i) No fracture-impact effect-5; (j) Fracture angle 30°-impact effect-5; (k) Fracture angle 60°-impact effect-5; (l) Fracture angle 90°-impact effect-5.
3.4. Energy Dissipation Analysis
Macroscopic material failure is fundamentally an energy-driven process from micro-deformation to fragmentation. Based on the recorded incident strain εi, reflected strain εr and transmitted strain εt from SHPB tests, the incident energy Ei, reflected energy Er and transmitted energy Et can be calculated using Formulae (7)–(9) [45]:
The dissipated energy Ed during dynamic failure of fractured coal samples can be derived from the law of energy conservation as Formula (10) [47,48]:
Energy dissipation constitutes the fundamental mechanism of material failure. The dissipated energy comprises three components: fracture energy, kinetic energy of the ejected fragments and other auxiliary losses. The fracture energy is the energy used to produce cracks and crack propagation of materials, which is the energy absorbed by material damage in a strict sense. Fracture energy, accounting for over 90% of dissipated energy, strictly represents the energy absorbed during material disintegration. Neglecting fragment kinetic energy and auxiliary losses, fracture energy can be approximated as the total dissipated energy.
Under constant impact pressure, the incident energy remained consistent across tests. The energy dissipation ratio is defined as Formula (11):
The energy dissipation ratio variations in fractured coal samples under cumulative impacts are analyzed in Figure 9. Prefractured specimens exhibit lower energy dissipation rates compared to intact samples, though the influence of fracture inclination angles on the dissipation rates is statistically insignificant. Furthermore, as the number of impact cycles increases, the energy dissipation rate of coal samples continuously decreases. This occurs because repeated impacts inevitably increase the quantity of micro-fractures within the coal matrix. Consequently, the material’s compactness and homogeneity diminish, while internal damage accumulation intensifies. This structural degradation reduces the energy required to induce failure in fractured coal samples under dynamic impact loading. These observations substantiate the notion that cumulative impact loading induces significant damage deterioration effects in fractured coal specimens.
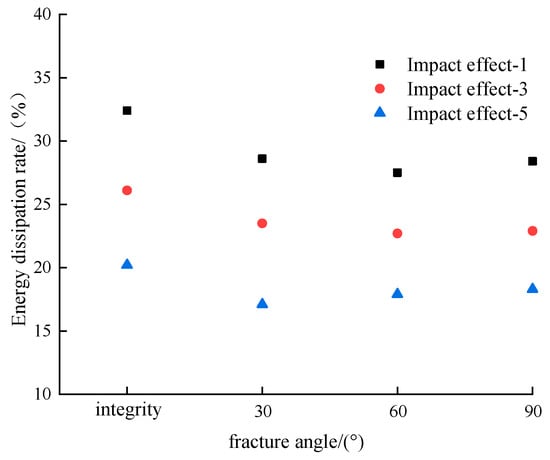
Figure 9.
Energy dissipation rate of fractured coal samples under cumulative impact.
4. Conclusions
This study investigates the effects of cumulative impacts on the wave velocity, dynamic compressive strength, fractal fragmentation characteristics and energy dissipation behavior of fractured coal through wave velocity measurement and dynamic impact tests. This study can, to some extent, reveal the dynamic failure mechanism of fractured coal samples under cumulative impact. The key conclusions are as follows:
- (1)
- As the number of cumulative impacts increases, the wave velocity of coal samples continuously decreases, following a linear relationship. The rate of wave velocity reduction varies with fracture dip angles, demonstrating angular dependence in fractured coal samples under cumulative impacts.
- (2)
- Dynamic compressive strength progressively decreases with cumulative impacts, showing 25–40% reduction after five impact cycles. Specimens with 30° fracture dip angles exhibit the most significant strength reduction and the highest failure probability under equivalent impact cycles.
- (3)
- Fractured coal fragments demonstrate remarkable self-similarity under cumulative impacts, conforming to fractal distribution characteristics. Increasing impact cycles elevate the fractal dimensions while transforming the fragmentation patterns from large-block tensile failure to small-particle crushing with tensile–shear hybrid failure modes.
- (4)
- A progressive reduction in the energy dissipation rate reveals that cumulative impacts induce significant damage degradation, reducing the energy consumption required for failure. Pre-existing fractures cause measurable energy dissipation reduction, though dip angles show limited influence on the dissipation rates.
The experimental data presented in this paper cannot yet be directly applied to the dynamic response analysis of actual coal-rock masses. However, the research conclusions reveal universal principles underlying the scientific problems studied. Future research will attempt to establish a correspondence between actual working conditions and experimental results, thereby providing a reference for further studies and engineering applications related to these issues.
Author Contributions
Conceptualization, J.M.; methodology, J.M.; software, L.S.; validation, J.M. and L.S.; formal analysis, L.S.; investigation, F.L.; resources, F.L.; data curation, J.M.; writing—original draft preparation, J.M.; writing—review and editing, J.M. and L.S.; visualization, F.L.; supervision, F.L.; project administration, F.L.; funding acquisition, F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Basic Research Plan in Shaanxi Province (No. 2023-YBGY-085) and the Scientific Research Program Funded by Shaanxi Provincial Education Department (No. 24JK0529) and Xi’an Jiaotong University City College potential cultivation project (No. 2024PY02), for which the authors are very thankful.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Jiachen Ma was employed by the company Shaanxi Coal Chemical Industry Technology Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, G.F.; Pan, Y.S.; Zhao, S.K. How to realize safe-efficient-intelligent mining of rock burst coal seam. Coal Sci. Technol. 2024, 52, 1–14. (In Chinese) [Google Scholar]
- Ram, S.; Singh, R.; Kumar, A.; Singh, A.K.; Kumar, R.; Rao, A.R.; Rao, V.S. Stability assessment of heightened rib/snook during extraction of a thick coal seam by continuous miner in single lift. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 74. [Google Scholar] [CrossRef]
- Remennikov, A.; Kalubadanage, D.M.; Yang, X.; Ren, T. The development of specialised modular protective structure on continuous miners against coal burst hazards. Int. J. Prot. Struct. 2022, 13, 182–208. [Google Scholar] [CrossRef]
- Dyrdin, V.V.; Oparin, V.N.; Fofanov, A.A.; Smirnov, V.G.; Kim, T.L. Possible Effect of Main Roof Settlement on Outburst Hazard in Case of Gas Hydrate Dissociation during Coal Mining. J. Min. Sci. 2017, 53, 801–810. [Google Scholar] [CrossRef]
- He, S.; Qin, M.; Qiu, L.; Song, D.; Zhang, X. Early warning of coal dynamic disaster by precursor of AE and EMR “quiet period”. Int. J. Coal Sci. Technol. 2022, 9, 46. [Google Scholar] [CrossRef]
- Roy, P.P.; Sawmliana, C.; Singh, R.K. Design of blasting patterns to induce effective caving in continuous miner depillaring panel—A case study. Min. Technol. 2021, 130, 209–220. [Google Scholar]
- Wang, X.; Wang, J.; Liu, X.; Zhou, X.; Li, N.; Feng, J.; Yang, H. Microcracking evolution and clustering fractal characteristics in coal failure under multi step and cyclic loading. Eng. Fract. Mech. 2024, 310, 110511. [Google Scholar]
- Zhou, X.; Liu, X.; Wang, X.; Xie, H.; Du, P. Failure characteristics and mechanism of coal under the coupling between different confining pressures and disturbance loading. B Eng. Geol. Environ. 2023, 82, 442. [Google Scholar] [CrossRef]
- Song, S.; Ren, T.; Dou, L.; Sun, J.; Yang, X.; Tan, L. Fracture features of brittle coal under uniaxial and cyclic compression loads. Int. J. Coal Sci. Technol. 2023, 82, 442. [Google Scholar] [CrossRef]
- Tan, T.J.; Wang, E.Y.; Wang, X.R.; Ma, L.Z.; Yao, W.L. Resistivity and damage of coal under cyclic loading and unloading. Eng. Geol. 2023, 323, 107234. [Google Scholar]
- Chai, S.; Jia, Y.; Du, Y.; Hu, B.; Li, X. Experimental study on compression mechanical characteristics of filled rock joints after multiple pre-impacts. Sci. Rep. 2022, 12, 13628. [Google Scholar] [CrossRef]
- Liu, X.; Tan, Y.; Ning, J.; Lu, Y.; Gu, Q. Mechanical properties and damage constitutive model of coal in coal-rock combined body. Int. J. Rock Mech. Min. 2018, 110, 140–150. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, G.; Li, M.; Zhang, D.; Deng, B.; Liu, C.; Lu, J. Anisotropic mechanical properties and the permeability evolution of cubic coal under true triaxial stress paths. Rock Mech. Rock Eng. 2019, 52, 2505–2521. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Zhang, C.; Canbulat, I.; Vardar, O.; Saydam, S. Computing the damage and fracture energy in a coal mass based on joint density. Int. J. Min. Sci. Technol. 2018, 28, 813–817. [Google Scholar] [CrossRef]
- Khan, M.; Xueqiu, H.; Jia, G.; Dazhao, S. Accurate prediction of indicators for engineering failures in complex mining environments. Eng. Fail. Anal. 2023, 155, 107736. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, A. Disturbance response instability theory of rock bursts in coal mines and its application. Geohazard Mech. 2022, 1, 1–17. [Google Scholar] [CrossRef]
- Pan, Y.S.; Song, Y.M.; Liu, J. Pattern, change and new situation of coal mine rockburst prevention and control in China. Chin. J. Rock Mech. Eng. 2023, 42, 2081–2095. [Google Scholar]
- Wojtecki, Ł.; Konicek, P.; Schreiber, J. Effects of torpedo blasting on rockburst prevention during deep coal seam mining in the Upper Silesian Coal Basin. J. Rock Mech. Geotech. 2017, 9, 694–701. [Google Scholar] [CrossRef]
- Shkuratnik, V.L.; Filimonov, Y.L.; Kuchurin, S.V. Experimental investigations into acoustic emission in coal samples under uniaxial loading. J. Min. Sci. 2004, 40, 458–464. [Google Scholar] [CrossRef]
- Xie, H.; Gao, M.; Zhang, R.; Peng, G.; Wang, W.; Li, A. Study on the Mechanical Properties and Mechanical Response of Coal Mining at 1000 m or Deeper. Rock Mech. Rock Eng. 2019, 52, 1475–1490. [Google Scholar] [CrossRef]
- Ranathunga, A.; Perera, M.; Ranjith, P. Influence of CO2 adsorption on the strength and elastic modulus of low rank Australian coal under confining pressure. Int. J. Coal Geol. 2016, 167, 148–156. [Google Scholar] [CrossRef]
- Klepaczko, J.; Bassim, M.; Hsu, T. Fracture toughness of coal under quasi-static and impact loading. Eng. Fail. Anal. 1984, 19, 305–316. [Google Scholar] [CrossRef]
- Klepaczko, J.R. On the role of microcracking inertia in rate sensitivity of coal at high strain rates. Arch. Mech. 1988, 40, 345–358. [Google Scholar]
- Krasnovyd, S.; Konchits, A.; Shanina, B.; Valakh, M.; Yukhymchuk, V.; Skoryk, M.; Molchanov, O.; Kamchatny, O. Coal from the outburst hazardous mine seams: Spectroscopic study. Min. Miner. Deposits. 2023, 17, 93–100. [Google Scholar] [CrossRef]
- Mullagaliyeva, L.; Baimukhametov, S.; Portnov, V.; Yurov, V. On the issue of thermal destruction of coal matter. Eng. J. Satbayev Univ. 2022, 144, 57–61. [Google Scholar] [CrossRef]
- Yao, Q.; Chen, T.; Ju, M.; Liang, S.; Liu, Y.; Li, X. Effects of water intrusion on mechanical properties of and crack propagation in coal. Rock Mech. Rock Eng. 2016, 49, 4699–4709. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, K.; Li, Z.; Li, Z.; Si, L.; Hou, S.; Duan, Y. Experimental study on pore-fracture evolution law in the thermal damage process of coal. Int. J. Rock Mech. Min. 2019, 116, 13–24. [Google Scholar] [CrossRef]
- Wang, X.; Kang, H.; Gao, F. Numerical investigation on the shear behavior of jointed coal mass. Comput. Geotech. 2018, 106, 274–285. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, B.; Zhao, S.; Wei, S. Experimental study on dynamic mechanical properties of multidirectional constrained water-bearing coal samples under dynamic-static coupling loading. Sci. Rep. 2024, 14, 20597. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Li, S.; Qin, G.; Lu, W.; Zhu, Z.; Jia, C.; Wen, H.; Yang, L. Experiments on Mechanical Response and Energy Dissipation Behavior of Rockburst-Prone Coal Samples Under Impact Loading. Shock Vib. 2021, 2021, 9924456. [Google Scholar] [CrossRef]
- Gu, Z.; Shen, R.; Liu, Z.; Zhao, E.; Chen, H.; Yuan, Z.; Chu, X.; Tian, J. Dynamic Characteristics of Coal under Triaxial Constraints Based on the Split–Hopkinson Pressure Bar Test System. Nat. Resour. Res. 2023, 32, 587–601. [Google Scholar] [CrossRef]
- Rahman, T.; Sarkar, K.; Singh, A.K. Correlation of Geomechanical and Dynamic Elastic Properties with the P-Wave Velocity of Lower Gondwana Coal Measure Rocks of India. Int. J. Geomech. 2020, 20, 04020189. [Google Scholar] [CrossRef]
- Chai, S.; Wang, H.; Yu, L.; Shi, J.; Abi, E. Experimental study on static and dynamic compression mechanical properties of filled rock joints. Lat. Am. J. Solids Struct. 2020, 17, 1–15. [Google Scholar] [CrossRef]
- Akdag, S.; Karakus, M.; Nguyen, G.D.; Taheri, A.; Zhang, Q.; Zhao, J. Dynamic response and fracture characteristics of thermally-treated granite under dynamic loading. Int. J. Rock Mech. Min. 2023, 170, 105482. [Google Scholar] [CrossRef]
- Tripathi, A.; Khan, M.M.; Pain, A.; Rai, N.; Iqbal, M.A. Compressive strength of thermally treated Barakar sandstone in Jharia coal mine fire region: Interplay of strength, strain rate, and temperature. Eng. Fract. Mech. 2025, 319, 111002. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Zhang, Y.; Wang, J. Dynamic mechanical properties of coals subject to the low Temperature-Impact load coupling effect. Sci. Rep. 2019, 9, 20218. [Google Scholar] [CrossRef]
- Gong, F.; Ye, H.; Luo, Y. The effect of high loading rate on the behaviour and mechanical properties of Coal-Rock combined body. Shock Vib. 2018, 2018, 4374530. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Yang, X.; He, X. A numerical simulation study on mechanical behaviour of coal with bedding planes under coupled static and dynamic load. Int. J. Min. Sci. Technol. 2018, 28, 791–797. [Google Scholar] [CrossRef]
- Hao, X.; Du, W.; Zhao, Y.; Sun, Z.; Zhang, Q.; Wang, S.; Qiao, H. Dynamic tensile behaviour and crack propagation of coal under coupled static-dynamic loading. Int. J. Min. Sci. Technol. 2020, 30, 659–668. [Google Scholar] [CrossRef]
- Cheng, C.; Xue, S.; Han, Y. Experimental Study on the Mechanical Behavior of Coal under Triaxial Dynamic Compression. Minerals 2022, 12, 1206. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, B.; Wei, Z.; Jiao, Z.; Song, Z.; Zhang, H. Dynamic mechanical responses and crack evolution of burst-prone coal with a single prefabricated fissure. Theor. Appl. Fract. Mech. 2022, 121, 103494. [Google Scholar] [CrossRef]
- Chai, S.; Liu, H.; Song, L.; Li, X.; Fu, X.; Zhou, Y. Static pressure and dynamic impact characteristics of filled jointed rock after frozen-thaw cycle damage. Front. Ecol. Evol. 2023, 11, 1222676. [Google Scholar] [CrossRef]
- Song, L.; Hu, S.S. Two-wave and three-wave method in SHPB data processing. Explos. Shock Waves 2005, 25, 368–373. [Google Scholar]
- Zhang, T.; Yu, L.; Su, H.; Zhang, Q.; Chai, S. Experimental and numerical investigations on the tensile mechanical behavior of marbles containing dynamic damage. Int. J. Min. Sci. Technol. 2021, 32, 89–102. [Google Scholar] [CrossRef]
- Liu, K.; Liu, H.; Zhou, Y.; Liang, G.; Xue, L. Experimental study on the dynamic mechanical and progressive fracture behavior of multi-jointed rock mass under repetitive impact loading. Theor. Appl. Fract. Mech. 2024, 131, 104416. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, W.; Zhao, G.; Meng, X.; Li, Y.; Wu, X.; Li, Y.; Cheng, X. Energy evolution law and fractal characteristics of different rock specimen sizes on dynamic compression. Geofluids 2022, 2022, 339603. [Google Scholar] [CrossRef]
- Panowicz, R.; Janiszewski, J.; Kochanowski, K. Effects of sample geometry imperfections on the results of split Hopkinson pressure bar experiments. Exp. Tech. 2018, 43, 397–403. [Google Scholar] [CrossRef]
- Stopka, G.; Gieleta, R.; Panowicz, R.; Wałach, D.; Kaczmarczyk, G.P. High Strain Rate Response of Sandstones with Different Porosity under Dynamic Loading Using Split Hopkinson Pressure Bar (SHPB). Appl. Sci. 2024, 14, 5347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).