Study on the Evolution Process of Snow Cover in Wind-Induced Railway Embankments and the Control Effect of Snow Fences

Abstract

Snowdrift, as a natural disaster, constantly compromises railway traffic by affecting how snow accumulates on the subgrade. This paper establishes a unified set of similarity criteria for wind tunnel testing, using viscous silica sand to simulate snow particles. By employing a geometric scale model (1:30) and similarity criteria (size, motion, dynamics, accumulation patterns, and time scales), it systematically investigates the evolution patterns of wind-induced snow accumulation on two types of roadbed structures: embankments and excavations. This study also evaluates the effectiveness of snow fences, proposing optimized placement distances and quantifying the effects of snow accumulation platform width. The results showed the following: (1) Snow on embankments has a “U”-shaped distribution, with the lowest wind speed (<0.5 m/s) and maximum accumulation at the leeward slope’s foot. In excavations, snow forms an “M”-shaped distribution, with significantly reduced wind speeds (<1 m/s) on the accumulation platform. (2) Snow fences effectively manage snow placement by lowering wind speed (below 1 m/s). A single-row snow fence with a porosity of 50% and a height of 3 m performs best when placed at seven times its height (7 H) from the slope’s toe. (3) A 5 m snow accumulation platform in excavations reduces surface snow accumulation (distribution coefficient drops to 1.6), outperforming scenarios without a platform (coefficient of 2.0). These findings contribute to the prevention and control of snowdrift disasters along railway lines in cold regions. They offer practical guidance for optimizing snow fence configurations, while also laying a foundation for future improvements in experimental accuracy through advanced techniques such as PIV and real-snow testing.

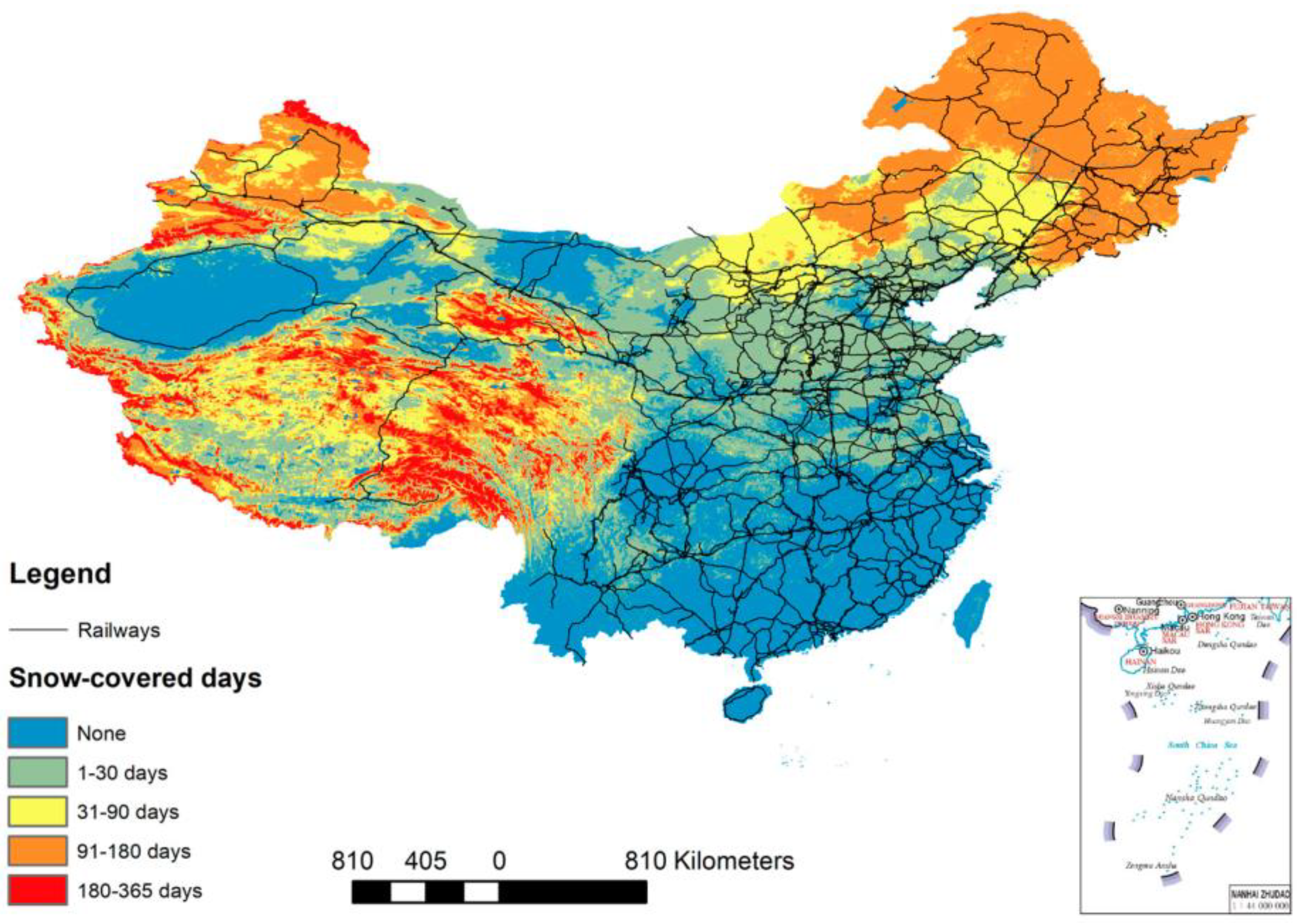
1. Introduction

Usually occurring in high-latitude regions, snowdrift is a natural disaster in which snow particles are blown by strong winds and accumulate in certain areas, posing a threat to railway traffic safety in northern China. This form of disaster brings challenges to the construction and operation of the road [1,2]. Figure 1 [3] shows the number of snow-covered days in China, overlaid with railway lines, where red areas represent regions experiencing the most severe snowfall throughout the year. A total of 11.83% of railways are situated in regions with over 180 snow-covered days. As a linear structure, railway traffic engineering spans complex terrains, and snowdrift disasters along the route are widespread, affecting multiple areas and causing significant harm [4].

In addressing snowdrifts and measures to prevent them, domestic and foreign research usually adopts the method of combining theoretical analysis, field observation, and simulation experiments. As wind and snow movement constitutes a complex atypical two-phase flow, its mechanism is difficult to interpret accurately [5,6,7]. In recent years, obtaining regional environment and snow field conditions through field observation, along with conducting quantitative analysis combined with simulation experiments, has become the main method for studying the phenomenon of wind-blown snow [8,9].

Existing studies primarily focus on wind speed, snow transport rate, and snow particle dynamics across different types of railway subgrades and structures. Wind tunnel experiments simulate a real environment by scaling down a solid model, enabling the study of the forces and motion states of snow particles. They allow for accurate control of wind speed, wind direction, and snow volume and closely replicate the natural flow field and the dynamics of snow particles. Compared with field monitoring, wind tunnel experiments have significant advantages in controlling experimental conditions. Early scholars laid a theoretical foundation for wind tunnel testing by examining initial wind speed, snow transport rate, and movement state, and discussed the corresponding experimental technology and material selection [10,11,12,13,14].

Current research on wind tunnel experiments involves varying scales and configurations of physical models to replicate real-world snowdrift phenomena, incorporating parameters such as wind velocity, snow particle characteristics, and terrain variations. At present, wind tunnel experiments mainly focus on wind engineering, building wind loads, sandstorm flow, and other fields, and analyze the wind load response and particle accumulation characteristics of special structures [15,16,17].

A series of prevention measures have been implemented for new railway projects in wind-blown snow areas, such as setting up snow fences, planting snow-proof forests, and building snow-proof corridors [18,19]. With its simple and effective characteristics, snow cover plays an important role in alleviating snow disasters and ensuring road safety, but its structural differences will affect the deposition effect of snow cover [20]. Due to the terrain, the design of the snow cover on the ridge needs to ensure that more snow is deposited on the windward side to effectively protect the facilities [21] below the mountain. In the study of the snowcover set at the bottom of Banihal Mountain, it was found that the snow deposition distance on the downwind side of the snowcover can reach 15 times the height of the plate, while the maximum snow depth behind the plate is almost equal to the height of the plate [22].

An indoor wind tunnel test was conducted using a scaled model. Unified similarity criteria were established for geometry, particle transition process, particle motion trajectory, time scale, and deposition morphology. Sticky silica gel particles were used to simulate particle density, resting angle, sedimentation velocity, starting velocity, threshold friction velocity, and Reynolds number. This experimental setup enabled detailed control over parameters such as wind direction, snow particle velocity, and environmental conditions, providing a clearer understanding of snow distribution and movement along railway subgrades. Effective control of wind speed, wind direction, and snow volume allowed for a comprehensive reproduction of natural flow fields, the force and motion of the scaled snow particles, the distribution characteristics of embankment snow, and wind-induced snow evolution. This study investigated the influence of the spacing between the snow fence and the subgrade on snow cover distribution within the subgrade. The variation in wind field and surface shear velocity around the snow fence and subgrade was also analyzed. This research provides theoretical and technical support for selecting subgrade forms in snowy areas and designing snowdrift mitigation measures in subgrade engineering.

The objective of this study was to investigate the characteristics of wind-induced snow accumulation over a typical railway embankment and to evaluate the effectiveness of different snow fence configurations under simulated snowdrift conditions. A 1:30 geometric scale model and fine silica sand were used to simulate snow in wind tunnel experiments, enabling the analysis of snow distribution patterns, wind field evolution, and the impact of fence spacing and porosity on snow control performance. The key innovation of this work lies in the development of a unified similarity framework—which includes geometric, kinematic, dynamic, and temporal scaling—to accurately replicate realistic snow deposition processes.

This work provides theoretical and practical insights for designing railway subgrades and snow control systems in cold regions, enhancing the optimization of snow fence configurations and improving operational safety and infrastructure resilience.

2. Methodology

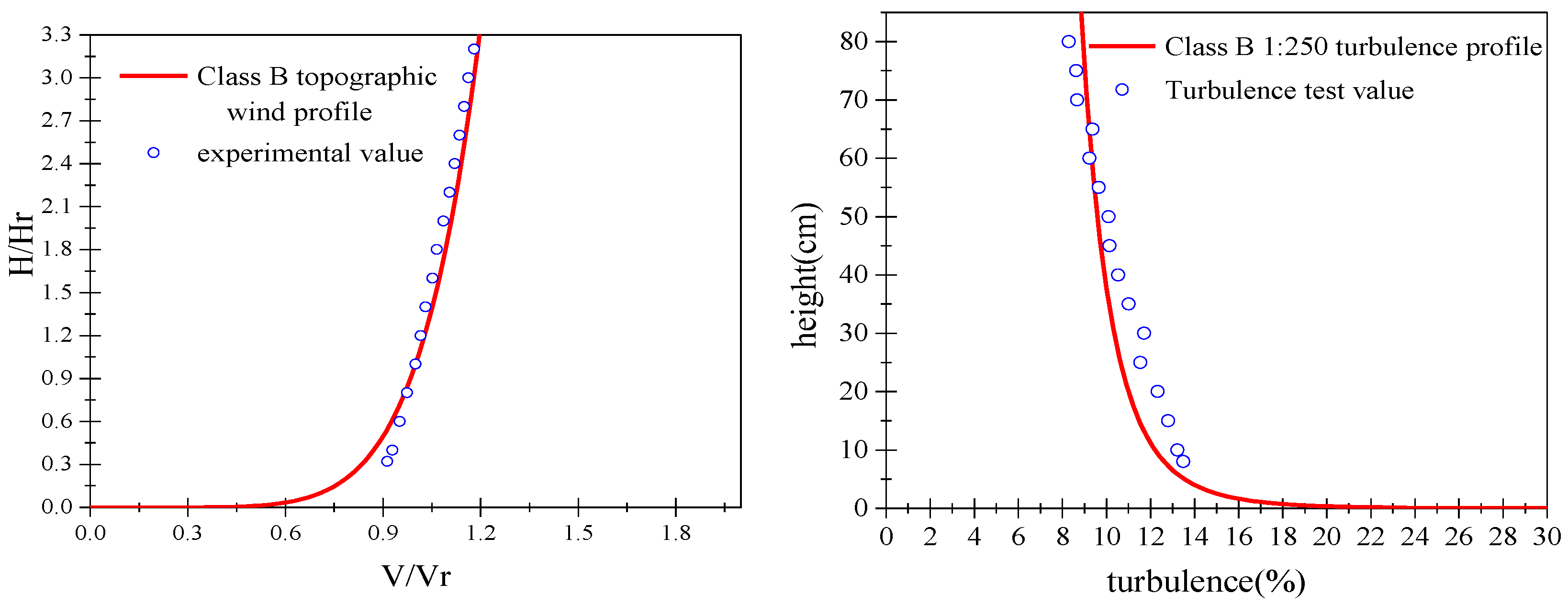
2.1. Wind Tunnel Testing Equipment and Parameter Settings

Snowdrift tests were conducted using the DC wind tunnel (shown in Figure 2) at Beijing Jiaotong University. The wind tunnel dimensions are 1.2 m (W) × 1.5 m (H) × 10.0 m (L). The free-stream wind speed ranges from 2 to 20 m/s, featuring smooth speed control. The main components of the wind tunnel include the wind flow area, the tunnel body, and the data acquisition and control system. The reference wind speed of the test flow field is measured and monitored using a fixed-spot micro pressure meter. The DC wind tunnel is equipped with the wind load and the corresponding testing devices, which include pressure measurement, force measurement, vibration measurement, and other functionalities that are capable of meeting diverse test conditions requirements.

The simulated wind field within the wind tunnel was characterized using a Cobra Probe wind speed measurement system from Turbulent Flow Instrumentation Pty. Ltd. (TFI, Tullamarine, VIC, Australia), integrated with a three-dimensional traverse system (accurate to 0.1 mm) to ensure accurate and reliable wind field measurements. The wind pressure on the structural surfaces was measured using electronic pressure scanning valves from Pressure Systems Inc. (PSI, Hampton, VA, USA), with pressure acquisition facilitated by eight PSI ESP-64HD miniature pressure scanning modules, enabling high-speed synchronous pressure measurements at 512 points.

Unlike previous studies that employed a self-designed wind tunnel with a test section height of 0.6 m and a geometric scale of 1:12 [23], our experiments utilized a validated, large-scale wind tunnel (1.5 m height) at Beijing Jiaotong University (Figure 2), achieving a refined geometric ratio of 1:150. This design minimizes boundary layer interference and enhances flow field accuracy, as evidenced by turbulence intensity stabilization at 11%, consistent with Class B terrain specifications (Figure 3). Additionally, our setup incorporated more wind speed sampling points across vertical profiles, enabling high-resolution analysis of near-surface velocity gradients critical for snow particle transport.

2.2. Similarity Criteria

Wind tunnel testing typically involves scaled models. To ensure the accuracy of the test results, maintaining similarity between the model and actual operating conditions is crucial. The influence of snow flow is primarily simulated using alternative materials. Due to the complexity of snow particles and the practicality of the experiment, it is impossible to meet all the similarity criteria. In this study, we considered similarities in size, kinematics, dynamics, accumulation pattern, and time scale, drawing upon relevant wind tunnel test methodologies [24,25,26,27].

Table 1. Similarity parameters and criteria for the wind tunnel test.

Similarity Parameters	Definition	Scale and Relationships	Purpose
Size	The geometric scale ratio of the model is equal to the prototype: ${\left({\displaystyle \frac{l}{L}}\right)}_m={\left({\displaystyle \frac{l}{L}}\right)}_p$	Geometric scale (1:30)	We ensure that the model is consistent with the geometry of the real operating conditions, and the spatial distribution of the flow field after the scale is similar.
Kinematics	Equal speed ratio: ${\left({\displaystyle \frac{u}{U}}\right)}_m={\left({\displaystyle \frac{u}{U}}\right)}_p$ Particle starting conditions are similar: $\begin{array}{l}\left\{\begin{array}{l}{({\displaystyle \frac{u_{*}}{U_{*t}}})}_m={({\displaystyle \frac{u_{*}}{U_{*t}}})}_p\\ {({\displaystyle \frac{u_{*}}{2g}})}_m={({\displaystyle \frac{u_{*}}{2g}})}_p\\ {({\displaystyle \frac{u_{*}}{2gv}})}_m\ge 30\end{array}\right.\\ \end{array}$ The settlement velocity is similar: ${\left({\displaystyle \frac{U}{w_f}}\right)}_m={\left({\displaystyle \frac{U}{w_f}}\right)}_p$ The Fr and Re is equal: Frm = Frp, Rem = Rep	The velocity field is scaled and the particle motion trajectory is aligned with the prototype.	Ensure that the dynamics of the starting suspension and sedimentation process of the model and the prototype are similar.
Dynamics	Pneumatic resistance is similar: ${\left(C_D{\displaystyle \frac{\rho L}{{\rho }_p{d}_p}}\right)}_m={\left(C_D{\displaystyle \frac{\rho L}{{\rho }_p{d}_p}}\right)}_p$	The resistance of the particle is in proportion to the inertial force.	Control the force balance of particles in the flow field, reflecting the interaction mechanism of air flow and particles.
Accumulation pattern	The rest Angle is equal: ${\left(\theta \right)}_m={\left(\theta \right)}_p$	Simulation material (silica sand) and snow The particle resting angle is consistent.	Ensure that the particle accumulation pattern (such as slope and density distribution) is consistent with the actual snow cover.
Time scale	Sedimentation time ratio: ${\left({\displaystyle \frac{\rho }{{\rho }_p}}{\displaystyle \frac{ut}{L}}\right)}_m={\left({\displaystyle \frac{\rho }{{\rho }_p}}{\displaystyle \frac{ut}{L}}\right)}_p$ ${\left({\displaystyle \frac{ut}{L}}\right)}_m={\left({\displaystyle \frac{ut}{L}}\right)}_p$	The deposition process time is scaled (shortened after scaling).	Ensure that the model agrees with the dynamic timescale of the snow cover evolution process in the prototype.

Note: The subscripts m and p represent the model and the prototype, respectively.

presents the specific parameters for each of the similarity criteria.

2.3. Test Materials

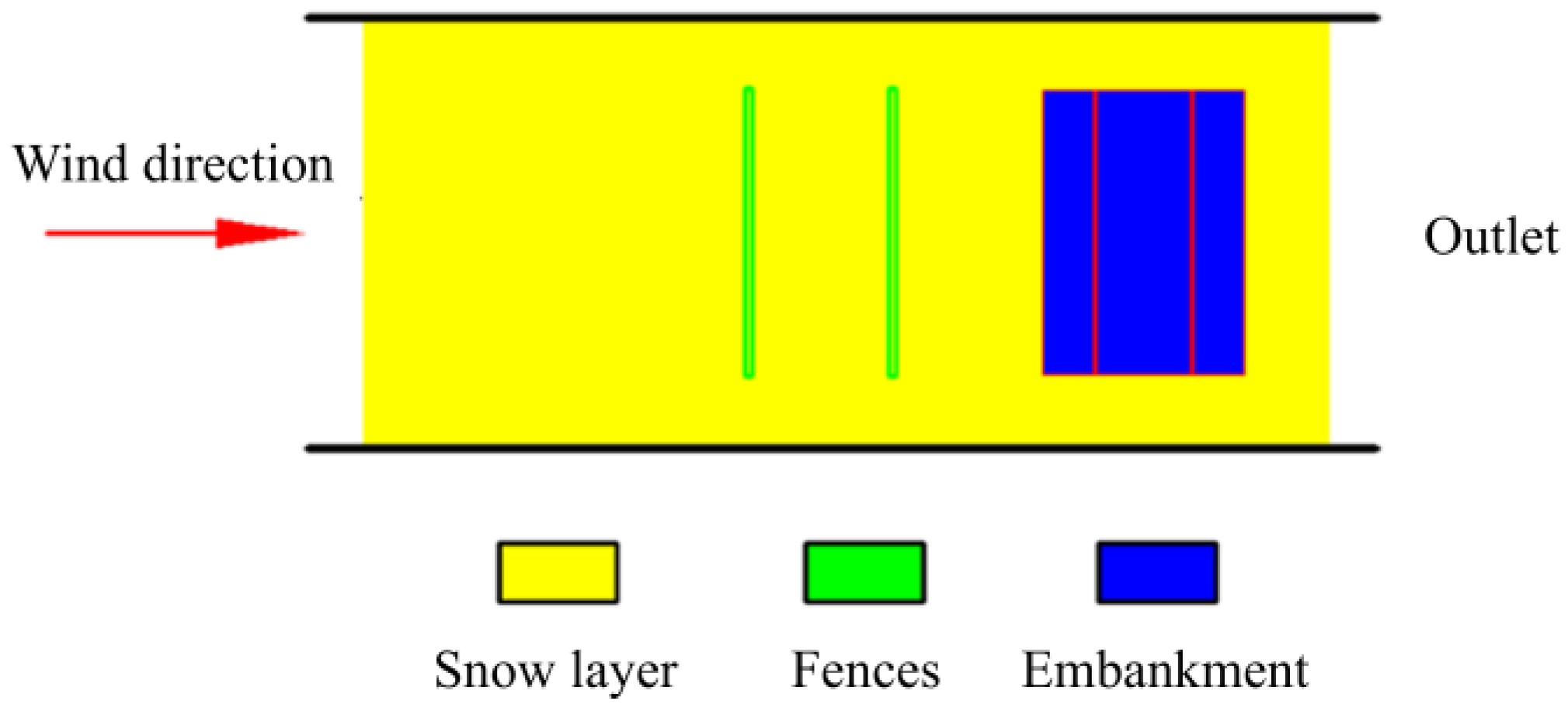
2.3.1. Test Model

The test model was designed based on the actual engineering structure, including the railway embankment and a snow fence model. The subgrade model was constructed of polished wood board, and the fence was made of single-line railway section model (Figure 4). The prototype dimensions were a depth of 3 m, a top width of 8 m, and a slope of 1:1.5. The fence was a snow grid with adjustable height and porosity; a single prototype panel featured a porosity of 50% and a height of 0.5 m. As illustrated in Figure 3, the wind tunnel test utilized a fence comprising six panels, resulting in a total height of 10 cm and an overall porosity of 75%. The model reduction ratio was 1/30, yielding a blockage ratio of 3.9% which meets the requirements outlined in JGJ/T 338-2014 “Wind tunnel test method Standard” [28].

2.3.2. Test Particles

The wind tunnel tests employed simulated material instead of actual snow particles. Prior to the test, several types of particles with characteristics resembling snow grains were selected based on similarity criteria, including snow grain density, particle size, angle of repose, and settling velocity. The physical properties of materials such as artificial snow, salt, and silicon sand of various grades were compared. Based on the results of air tests, fine silicon sand with a particle size of 0.2 mm was ultimately chosen as the substitute for snow particles.

Table 2. Main parameters of test particles.

Parameters	Snow	Thin Silicon Sand
Particle size (mm)	0.1~0.4	0.19
Density (g/cm3)	0.120~0.222	0.208
Reynolds Number	21.1~247	81
Drag-to-Inertia Ratio	14.37~16.32	1.54
Sedimentary Velocity (m/s)	1.08~1.3	1.24
Sedimentary Similarity	>30	36
Threshold Velocity (m/s)	0.12~0.28	0.224

shows a comparison of the physical and mechanical parameters of the selected fine silica sand particles used in the indoor wind tunnel test. The silica sand was sourced commercially as abrasive media for sandblasting.

2.4. Test Parameters

Prior to the test, a closed split tip was first used to adjust the flow field distribution and modify the outlet roughness of the wind tunnel to simulate the flow characteristics of Class B terrain (Figure 5), which is typical of regions prone to snowdrifts. The turbulence intensity of the flow field near the base height was stabilized at approximately 11%, meeting the requirements for Class B terrain (Figure 3) as defined in the GB 50009-2012 “Load Code for the Design of Building Structures” [29].

Snow was distributed in a uniform layer from the upstream end to the outlet of the wind tunnel test section, maintaining a specific distance from the side walls, as shown in Figure 6. The yellow area indicates the snow-covered area. The initial snow depth was set to 20 mm. To avoid the influence of the fan and other wind tunnel equipment on the flow field within the test chamber, a certain distance was maintained between the upstream end to the outlet.

In the context of the actual engineering project, flow field data were measured at four nominal driving wind speeds: 5.5 m/s, 6.5 m/s, 7.5 m/s, and 8.5 m/s. At a reference height of 30 cm above the ground, the corresponding reference wind speeds (u) were 3.9 m/s, 4.8 m/s, 5.3 m/s, and 6.0 m/s, respectively. As shown in Figure 4, when the driving wind speed was 6.5 m/s, particles experienced noticeable displacement. Subsequently, the driving wind speed was gradually decreased by 0.1 m/s increments. When the driving wind speed reached 6 m/s, a small number of particles still exhibited slight movement. Considering measurement errors, this study determined the particle initiation driving speed to be 5.5 m/s, corresponding to a wind speed of 3.9 m/s at a height of 30 cm. In the experiment, the corresponding blow-out time was recorded. After the blowing process, a snow gauge with graduation of 1 mm was used to measure the snow depth, and the interpolation method was used to obtain the snow depth distribution across the entire wind tunnel test section.

In the preliminary tests, strong airflow separation appeared at the edge of the line direction of the middle segment model (similar to the erosion phenomenon at the edge of the flat roof), resulting in a snow depth of nearly 0 m; the effective length influenced by this erosion was considerably larger than the distance between the fence and the subgrade. Therefore, these eroded edge areas were excluded from the measurement.

3. Results and Discuss

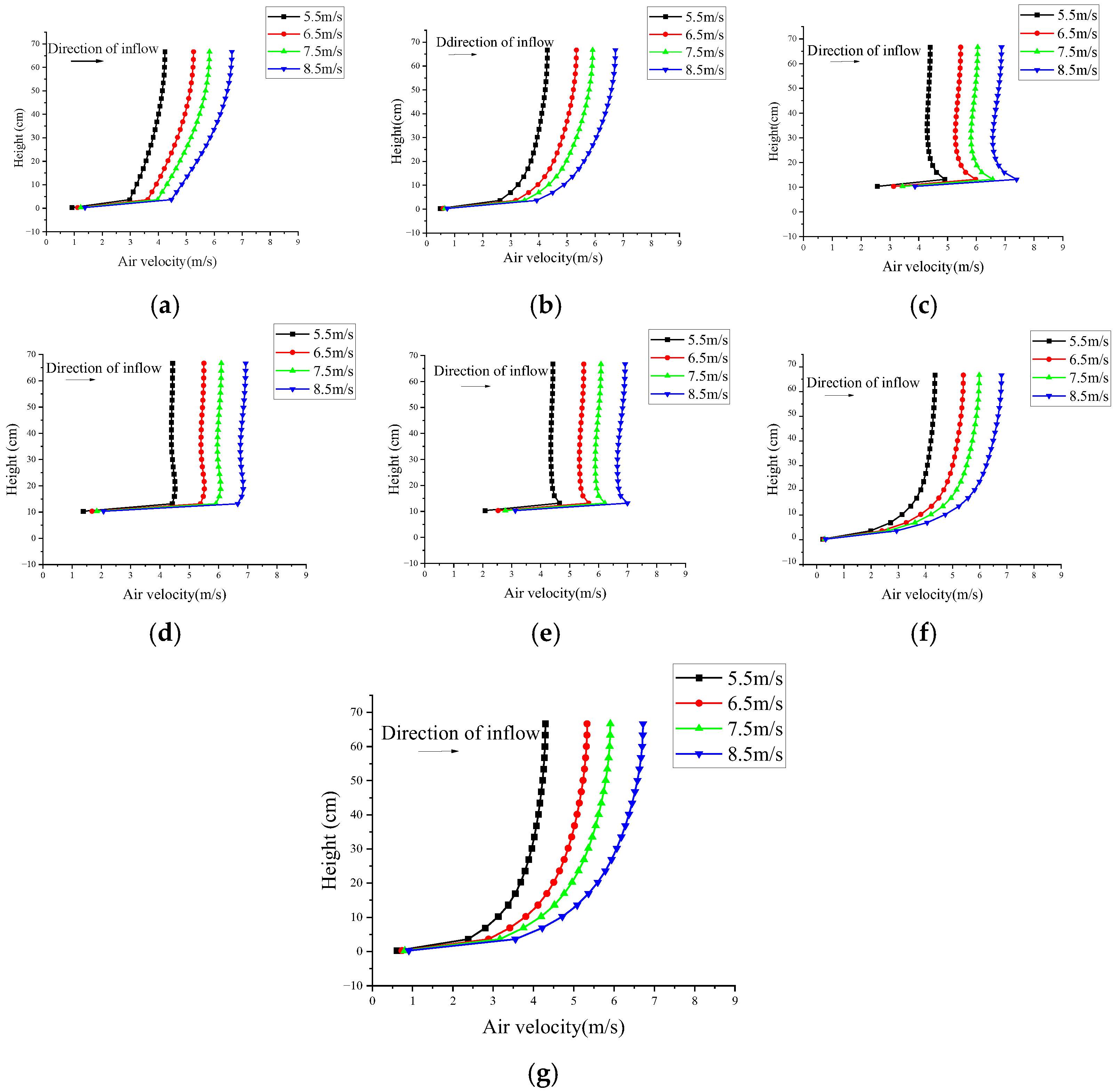
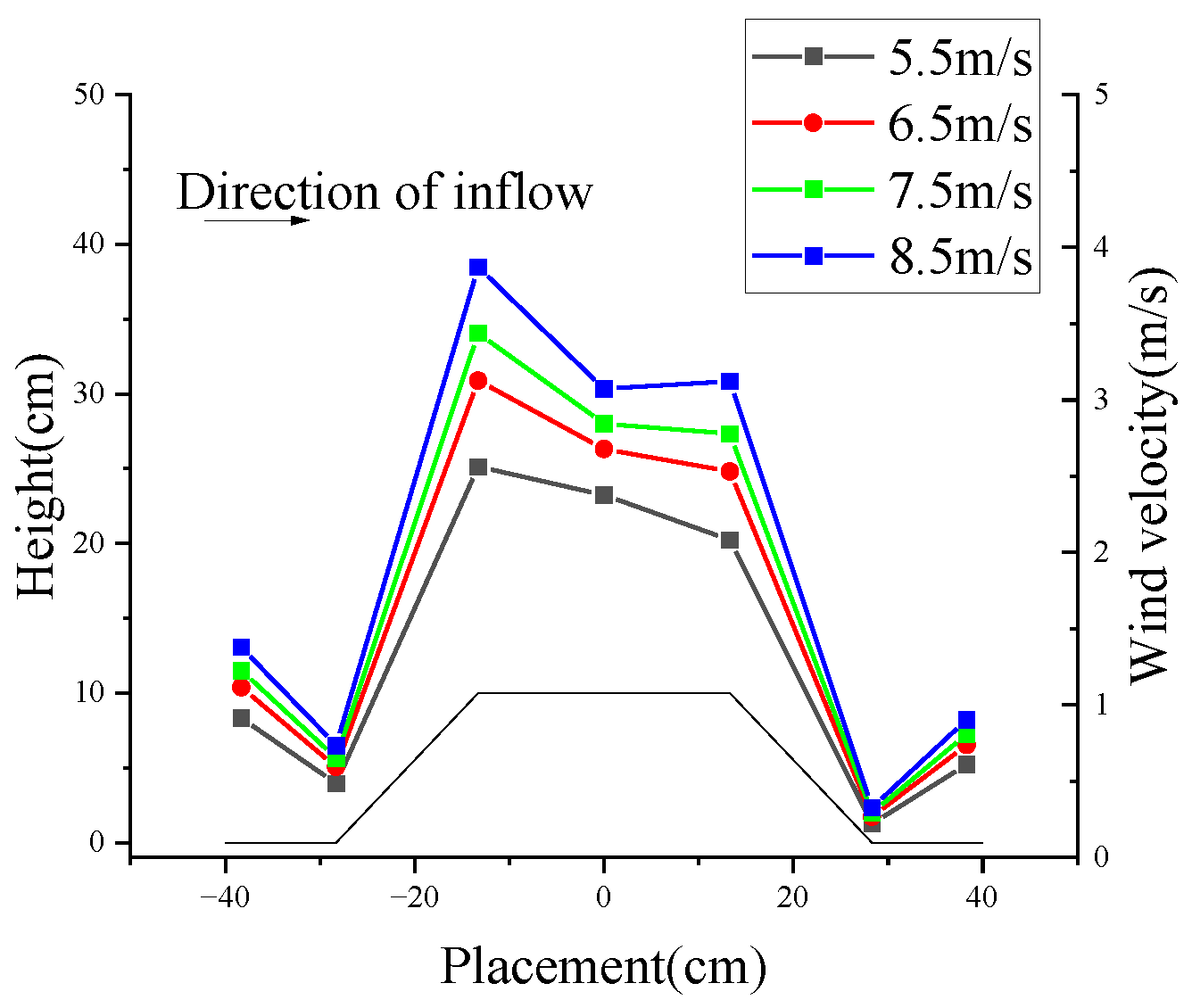
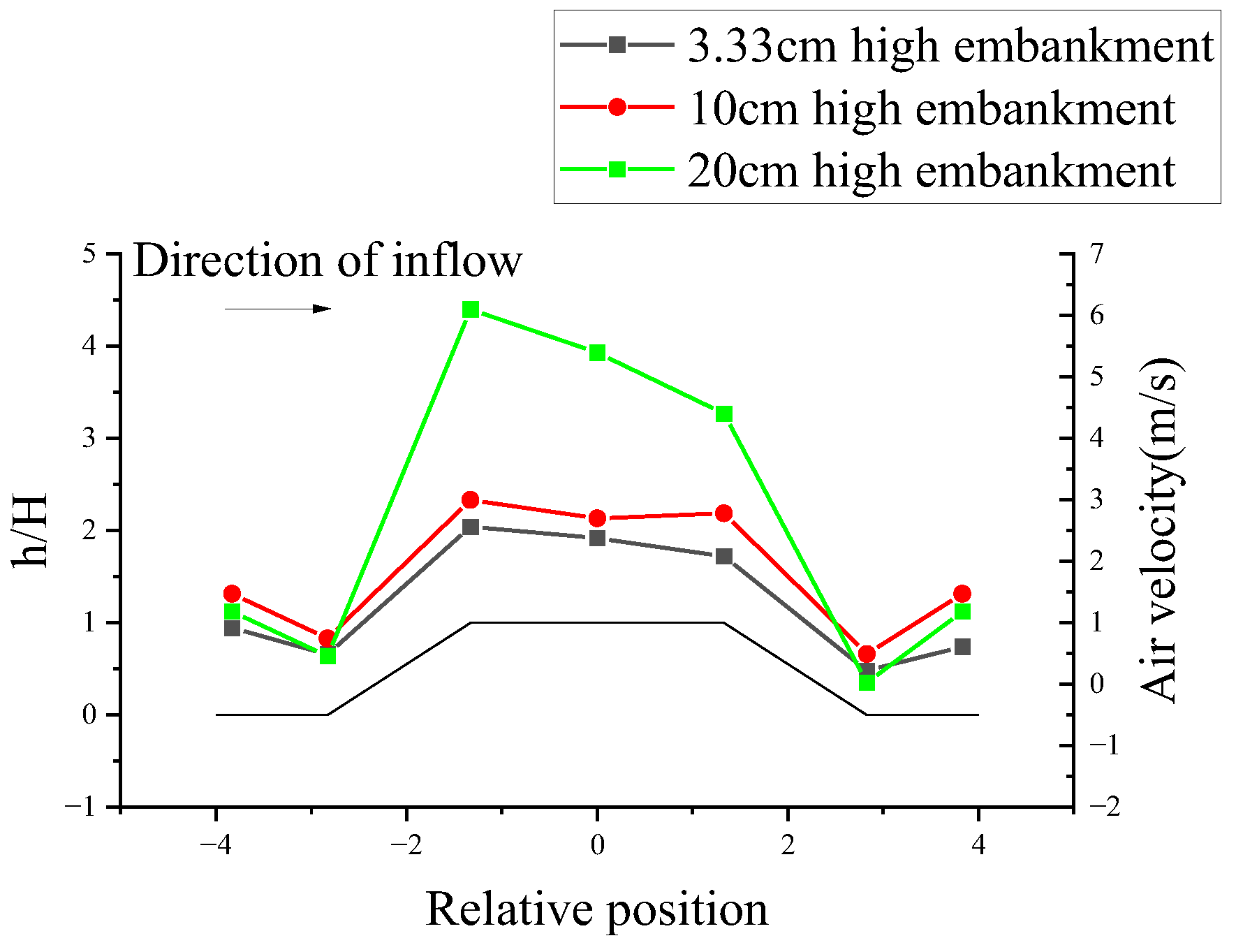
3.1. Wind Field Evolution Law

To measure wind speeds at different heights and positions, a wind speed measurement probe was developed and mounted on an adjustable support frame within the wind tunnel test section. This frame enabled vertical and horizontal movement of the probe, as shown in Figure 7. Figure 8 shows the distribution of the 10 cm high embankment and the corresponding wind fields, scaled to a real 3 m high embankment at different startup wind speeds. Measurements were taken at six horizontal positions: 10 cm outside the foot of the windward slope, windward slope top, subgrade center, leeward slope top, leeward slope foot, and 10 cm outside the leeward slope. At each horizontal position, wind speed was measured at vertical intervals corresponding to 0.9 m in the prototype, with a measurement point every 3 cm in the model. Due to experimental constraints, the lowest measuring point was set at 0.3 cm above the ground or subgrade surface, corresponding to an actual height of 0.09 m. At a wind speed of 3.9 m/s measured at 30 cm, the starting wind speed at 0.3 cm was 1.86 m/s.

As shown in Figure 8, at any given measurement location, with the increase of starting wind speed, the wind speed at each height increases accordingly, while the overall vertical profile trend remains consistent, with lower wind speeds near the ground, gradually increasing with height until stabilization. At the lowest measurement point (0.3 cm height), 10 cm outside the foot of the windward slope, the foot of the windward slope, the foot of the leeward slope, and 10 cm outside the foot of the leeward slope, the wind speed is low and exhibits minimal change with the increase of the inflow wind speed. The wind speed at the foot of the windward slope, the foot and 10 cm outside the foot of the leeward slope remains below 1 m/s across different inflow wind speeds, with the minimum wind speed recorded at the foot of the leeward slope (0.2 m/s). This suggests that this location is particularly susceptible to snow particle accumulation, which aligns with the findings of subsequent tests. Conversely, the top of the windward slope and the top of the leeward slope exhibit distinct wind acceleration, with wind speeds near the subgrade surface exceeding 2 m/s, followed by an initial increase then a decrease with height until stabilization. At the center of the subgrade, the wind speed near the surface ranges between 1 m/s and 2 m/s, indicating a relatively high potential for snow accumulation in this area, with minimal wind speed variation with increasing height.

To clearly compare the wind speeds across the embankment range, measurements were taken at 0.3 cm above the ground, corresponding to 0.09 m at actual height, as depicted in Figure 9. The figure reveals that, under identical wind speed conditions, the wind speed on the windward slope is greater than that on the leeward slope. The lowest wind speed is observed at the foot of the leeward slope, where snow accumulation is most probable. In contrast, the wind speed on the embankment surface is comparatively high, reducing the likelihood of snow accumulation in that area.

Figure 10 shows the comparison diagram of the wind speed at 3.3 cm (1 m actual height), 10 cm (3 m actual height), and 20 cm (6 m actual height) near the ground when the inflow wind speed is 5.5 m/s. The abscissa represents the actual corresponding position of each embankment. As shown in Figure 10, the wind speed is lowest at the foot of the leeward slope for all embankment heights, remaining below 0.5 m/s, indicating significant snow particle accumulation in the area. Notably, the wind speed at the foot of the leeward slope decreases with increasing embankment height. The wind speed on the subgrade surface increases with embankment height, suggesting that higher embankments are less prone to snow particle accumulation on the surface.

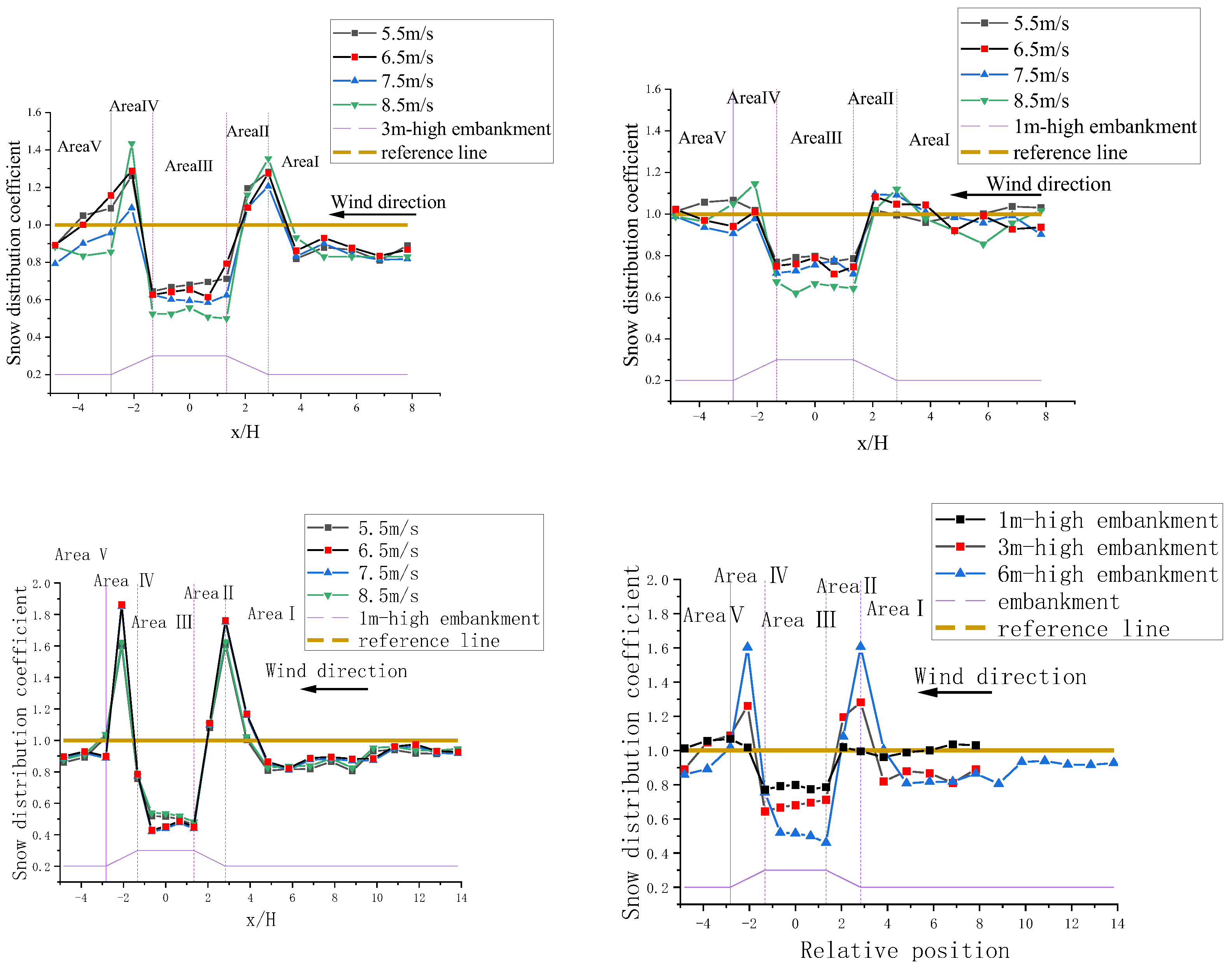
3.2. Snow Cover Distribution Pattern

This section examines the characteristics of snow distribution on the embankment section with a model height of 10 cm (corresponding to an actual height of 3 m) under nominal wind speeds of 5.5 m/s, 6.5 m/s, 7.5 m/s, and 8.5 m/s, respectively. Additionally, embankments with model heights of 3.3 cm (actual height of 1 m) and 20 cm (actual height of 6 m) were also considered. In the wind tunnel, a 20 mm thick layer of particles was uniformly distributed in the test section to simulate the initial snow cover, and each blowing test lasted for 10 min. Figure 11 shows the comparison of the snow distribution before and after each experiment.

Figure 12 depicts the particle distribution along the central axis of the embankment under different wind speeds and embankment heights. To provide a more intuitive representation of the particle accumulation depth distribution, the snow distribution coefficient is defined as follows:

$$r_s={\displaystyle \frac{h_s}{h_c}},$$

(1)

where, $h_s$ is the snow cover thickness measured after the test and $h_c$ is the snow cover thickness measured before the test.

Overall, the snow distribution is consistent across different embankment heights, and exhibits characteristics typical of five areas. Area I, extending from the windward front to the foot of the embankment slope, experiences significant erosion. The distribution coefficient of snow cover in this area is less than 1, indicating that snow particles were removed by the wind. Area II, located on the windward slope, is characterized by snow particle accumulation, which gradually decreases along the wind direction, reaching its maximum at the foot of the windward slope. Area III, the embankment surface area, undergoes the most severe erosion, with a substantial amount of particles being carried away by the wind, resulting in a snow cover distribution coefficient that is significantly less than 1. Area IV, the leeward slope surface, exhibits substantial particle accumulation, increasing along the wind direction and peaking at the foot of the slope. Area V, extending from the foot of the leeward slope outwards, shows a reappearance of erosion. Comparison with field-measured data reveals a similar “u” shaped distribution for the snow distribution coefficient in the wind tunnel tests. At lower wind speeds, particles initially accumulate at the foot of the embankment slope and gradually shift towards the subgrade surface. As the embankment height increases, the accelerated wind field causes particles on the embankment surface to be removed and deposited on the leeward slope. With increasing test wind speed, particle accumulation at the foot of the windward slope increases. However, at excessively high wind speeds, particles are more readily carried away by the wind, leading to increased accumulation at the foot of the leeward slope and reduced accumulation on the embankment surface. This indicates that, under strong wind conditions, particles are more likely to be transported away, hindering accumulation on the embankment surface.

The primary differences between the tested conditions are as follows: For a given embankment height, increasing wind speed leads to greater deposition at the front foot of the slope (Area II), increased erosion (and thus less deposition) on the embankment surface (Area III), and higher deposition in Area IV. For a given wind speed, increasing embankment height results in greater deposition in Areas II and IV, but also greater erosion (less deposition) in Area III. This is attributed to the significant influence of embankment height on the wind–snow flow field. As embankment height increases, the wind speed on the embankment surface also increases, facilitating the movement of particles across it and consequently reducing snow particle accumulation.

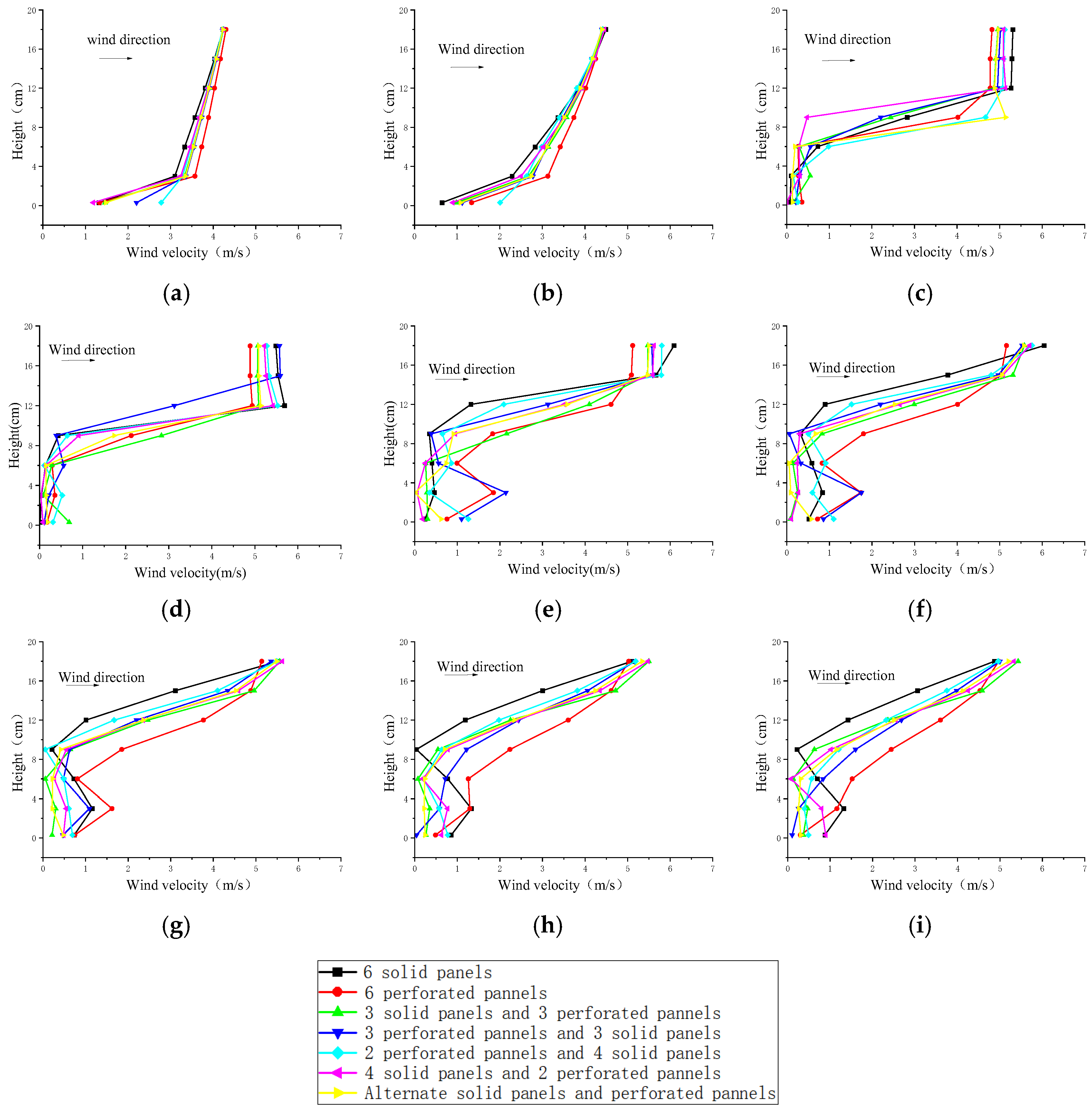
3.3. Flow Field Regulation Mechanism of Snow Prevention Fence

Figure 3 depicts the panel-type snow fence used in the wind tunnel tests, featuring a configuration of three solid panels and three perforated panels. Other configurations of the snow fence include six solid panels (where all six panels are solid), six perforated panels (where all six panels are perforated), as well as combinations such as three solid and three perforated, three perforated and three solid, four solid and two perforated, two perforated and four solid, and alternating configurations of solid and perforated panels.

Figure 13 shows the wind speed at different positions at a starting wind speed of 6.5 m/s for snow fences in different arrangements. Measurements were taken at horizontal intervals of 1 H (where H = 100 mm) within a range of 2 H upstream and 5 H downstream of the snow fence. Vertically, measurements were taken every 3 cm, corresponding to a prototype height of 0.9 m, with a total of seven measurement points up to 18 cm (equivalent to a prototype height of 6 m). Due to experimental limitations, the lowest measurement point was 0.3 cm above the ground or subgrade surface, corresponding to an actual height of 0.09 m.

As shown in Figure 13, the wind speed remains relatively consistent below a height of 10 cm for all tested snow fence types, and the wind speed patterns downstream of the different fences are also quite similar. The wind speed is lowest immediately upstream and downstream of the snow fences, generally below 1 m/s. Above 10 cm, the wind speed gradually recovers, and the effect of different configurations on the wind speed becomes less pronounced. A key difference is that when the bottom panel of the snow fence is perforated, the wind speed in the area below the height of the snow fence is higher than when the bottom panel is solid.

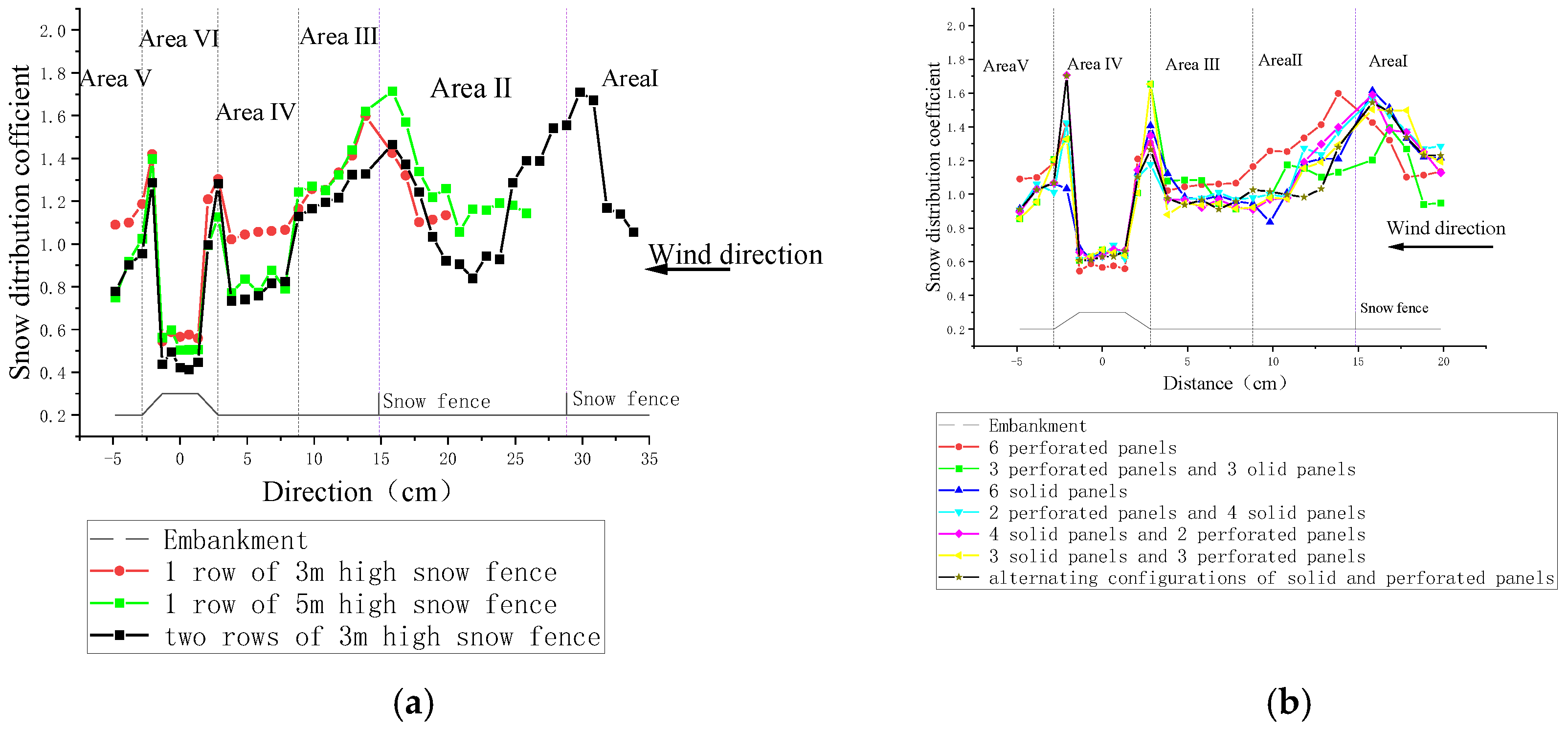
3.4. Analysis of Snow Fences and Snow Cover Distribution

Using the subgrade model as the basic line, various types of snow fences were introduced to investigate their influence on the snow distribution around the subgrade. By changing the configuration of snow fences, their role in protecting against railway snowdrifts was examined, and different snow fence placement strategies were explored. The initial thickness of the particle layer on the ground remained at 20 mm, the wind speed was set at 6.5 m/s, and the blowing duration was 10 min. Figure 14 shows the snow distribution around the fence before and after the wind tunnel test.

Figure 15 illustrates the particle distribution along the central axis of the lower embankment for different snow fence configurations, indicating that the presence of a snow fence did not alter the fundamental pattern of snow distribution around the embankment. Consistent with the previously established model, the test area was divided into five regions. Area I, the upstream zone of the snow fence, is characterized by particle accumulation, with significant accumulation starting approximately 2H upstream of the fence (where H is the height of the snow fence). This accumulation occurs because the fence obstructs the snow flow. Given that the standard snow fence is a free snow fence with a porosity of about 50%, some snow particles pass through and accumulate in this first area due to the fence’s impedance. The wind speed is substantially reduced downstream of the snow fence, preventing particles from reaching their initiation speed, thus promoting accumulation. Wind field analysis revealed a “vortex effect” at the corners of the snow fence, where reduced ground-level wind speeds allow wind-picked-up snow particles to settle. Consequently, the maximum particle accumulation occurs not immediately upstream or downstream of the fence, but at a certain distance downstream. The snow distribution gradually stabilizes beyond 6H downstream of the snow fence, entering Area V. In this region, as the influence of the snow fence on wind speed diminishes, particle accumulation gradually decreases and becomes relatively uniform across different positions. Both the upstream (Area I) and downstream (Area V) zones relative to the snow fence exhibit a “U” shaped distribution pattern similar to that observed around an embankment without a snow fence. When comparing the distribution coefficient to the case without a snow fence, a slight, but not substantial, decrease in the snow distribution coefficient on the embankment surface is observed.

By comparing the distribution coefficient of snow cover under different snow fence structural configurations, similar overall distribution characteristics can be observed upstream and downstream of the fence, regardless of the specific form. Accumulation patterns are consistent within 2–4 H upstream and 4–6 H downstream of the snow fence. Furthermore, the snow cover distribution coefficient on the subgrade surface does not vary significantly across different snow fence configurations. Comparing snow fences with solid and perforated bottom panels reveals that a solid bottom tends to promote greater particle accumulation upstream of the fence. When the entire snow fence is solid (effectively a snow wall), particle accumulation is maximized upstream, with minimal accumulation downstream. Therefore, by adjusting the structural form of snow fences according to different terrain and landform characteristics, the location of snow accumulation can be controlled to optimize space utilization. However, regardless of the configuration, snow fences should be positioned within a 7 H distance from the foot of the subgrade slope to prevent direct snow accumulation on the embankment.

By comparing the distribution coefficient of snow cover under conditions of different snow fence rows and height, it is observed that the overall distribution characteristics upstream and downstream of the fence remain similar across different arrangements, with accumulation typically forming within 2–4 H upstream and 4–6 H downstream. If a small snow distribution coefficient on the subgrade surface is considered the criterion for effective snow fence protection, then two rows of 3 m high snow fences are superior to one row of 5 m high snow fences, and also better than one row of 3 m high snow fences. This is because two rows of snow fences can intercept more snow particles. The first row causes initial accumulation and, after a stable zone, the second row further decelerates the airflow, leading to a second accumulation, thus blocking a large number of particles outside the subgrade area. The main disadvantage of two rows of snow fences is the requirement for a larger area, while the protective effect is not significantly enhanced. Therefore, in areas where snowdrift disasters are particularly severe, prioritizing an increase in the height of snow fences may be preferable to increasing the number of rows.

Previous studies [8,23] have emphasized the role of cutting geometry in snowdrift formation, reporting an “M-shaped” snow distribution in cuttings. In contrast, our findings reveal that embankments exhibit a “U-shaped” distribution, with maximum snow depth (38.3 mm) at the leeward slope foot. This divergence underscores the necessity of terrain-specific strategies: while cuttings benefit from snow platform widening (reducing distribution coefficients from 2.0 to 1.6), embankments require optimized snow fences to disrupt airflow and redirect snow deposition. For example, a 3 m-high fence with 50% porosity placed at 7 H reduces embankment surface snow depth by 60%, outperforming passive structural modifications alone.

As the driving force and material source of wind-blown snow movement, wind field characteristics and snow availability directly influence snow depth. During snowdrifting, snow particles continuously gain kinetic energy from the airflow, causing them to become mobile and move with the air, thus increasing the snow concentration in the airflow. Simultaneously, snow particles near the surface reduce the average wind speed, and some particles lose momentum and settle, decreasing the airborne snow concentration. Snow particles are both lifted from the ground and deposited onto it. The change in airflow energy exists in a dynamic equilibrium with the momentum changes of the snow particles, forming a bidirectional feedback system where the movement of snow grains affects the airflow, and changes in airflow also affect the movement of snow grains. This equilibrium state is dynamic due to the fluctuating airflow energy and snow grain movement.

The wind-blown snow movement causes both deposition on and erosion of the snow particle surface. In a state of dynamic balance, deposition and erosion can be considered equal. However, changes in flow conditions induced by snow prevention structures disrupt this balance, leading to a difference between the amounts of deposition and erosion, causing more snow particles to become airborne or settle on the ground. Under the influence of snow prevention structures, alterations in wind speed lead to changes in the flow field state. In areas of increased flow velocity, the wind-blown snow movement exhibits more pronounced erosion, and more snow particles become airborne. Conversely, in areas of weakened flow velocity, the wind-blown snow movement exhibits more deposition, and snow grains settle. Through the impact of snow-proof structures on the flow field and the direct blockage of snow particle movement, more snow particles are deposited within the functional area of the snow-proof structure, thereby reducing snow accumulation on traffic engineering lines and ultimately decreasing the likelihood of snowdrift disaster.

4. Conclusions

• When the snow flow passes over the embankment, the wind speed on the windward slope is greater than that on the leeward slope. At the same cross-section, wind speed increases with height until it stabilizes. The lowest wind speed is found at the foot of the leeward slope, while the wind speed is relatively high at the surface of the embankment. As the height of the embankment increases, the wind speed at the foot of the leeward slope decreases. The wind speed at the surface of the subgrade increases with the height of the embankment.
• The overall snow thickness exhibits a “U”-shaped distribution. Regardless of the height of the embankment, the overall snow distribution coefficient is less than 1. The higher the embankment, the smaller the snow distribution coefficient. The greater the wind speed, the thicker the snow accumulation on the subgrade.
• When the snow flow passes over fences, the wind speed remains relatively consistent within the height range on both sides for different types of fences. The wind speed is at its lowest immediately in front of and behind the fences. Above the height of the fences, the wind speed gradually recovers. The difference is that when the bottom of the snow barrier is of the “perforated” type, the wind speed in the area below the height of the barrier is greater than when the bottom is of the “solid” type.
• The influence range of the snow barrier on the embankment results in significant snow accumulation within the range of 4–6 times the height (h) of the barrier, while in areas beyond 6 h, the accumulation of snow particles remains relatively stable. Fences with a higher porosity provide better protection, corresponding to the 10 perforated snow fences on site. The influence range of the snow barrier in the ditch reaches a stable state with respect to the thickness of snow particle accumulation after 9–11 times the height (h) of the barrier. Fences with a higher porosity also provide better protection. In areas severely impacted by wind-blown snow disasters, single-row high snow fences may be prioritized over double-row low snow fences.
• By adopting a high-precision wind tunnel (1:150 scale ratio) and viscous silica sand (density: 0.208 g/cm³), we addressed the limitations of prior setups (1:12 ratio, artificial snow density: 0.5 g/cm³) that overestimated particle inertia [23]. We quantified the efficacy of snow fences (e.g., 50% porosity, 7 H placement) for embankments, a terrain type previously underexplored in favor of cuttings [8]. Our results advocate combining structural adjustments (e.g., snow platforms) with active snow fences, offering a holistic strategy for diverse railway terrains.

This study contributes to the prevention and control of snowdrift disasters along railways in cold regions. Future efforts can focus on enhancing the equipment and measurement technology for model experiments by incorporating Particle Image Velocimetry (PIV) in wind tunnels and utilizing real snow particles to simulate and analyze their behavior under wind-blown conditions. By comparing the experimental results of artificial snow with the behavior of natural snow, the reliability and accuracy of the research methods can be further improved.

5. Limitations and Future Work

Despite the insights gained, this study has certain limitations. First, it utilizes viscous silica sand as a snow analog, which, although controllable and reproducible, does not fully replicate the physical behavior of real snow particles, particularly in terms of cohesion, melting, and sublimation. Second, the scaling laws used in the geometric modeling (1:30 scale) may not perfectly capture complex full-scale interactions, especially turbulence near fence edges and particle rebound effects.

To improve accuracy, future work should address the following:

• Integrate Particle Image Velocimetry (PIV) in wind tunnel setups to obtain high-resolution velocity fields and enhance flow visualization around fences and embankments.
• Conduct comparative experiments using natural or artificial snow particles to better simulate real-world snow dynamics.
• Develop computational fluid dynamics (CFD) models calibrated by wind tunnel results to explore larger-scale and more varied scenarios.
• Investigate multi-factor coupling effects, such as wind-blown snow under thermal gradients, terrain complexity, and evolving snowpack densification.

These efforts will enhance the reliability of simulation methods and provide a more robust scientific basis for snowdrift control in railway engineering.