Research Progress and Technology Outlook of Deep Learning in Seepage Field Prediction During Oil and Gas Field Development

Abstract

As the development of oilfields in China enters its middle-to-late stage, the old oilfields still occupy a dominant position in the production structure. The seepage process of reservoirs in the high Water Content Period (WCP) presents significant nonlinear and non-homogeneous evolution characteristics, and the traditional seepage-modeling methods are facing the double challenges of accuracy and adaptability when dealing with complex dynamic scenarios. In recent years, Deep Learning technology has gradually become an important tool for reservoir seepage field prediction by virtue of its powerful feature extraction and nonlinear modeling capabilities. This paper systematically reviews the development history of seepage field prediction methods and focuses on the typical models and application paths of Deep Learning in this field, including FeedForward Neural networks, Convolutional Neural Networks, temporal networks, Graphical Neural Networks, and Physical Information Neural Networks (PINNs). Key processes based on Deep Learning, such as feature engineering, network structure design, and physical constraint integration mechanisms, are further explored. Based on the summary of the existing results, this paper proposes future development directions including real-time prediction and closed-loop optimization, multi-source data fusion, physical consistency modeling and interpretability enhancement, model migration, and online updating capability. The research aims to provide theoretical support and technical reference for the intelligent development of old oilfields, the construction of digital twin reservoirs, and the prediction of seepage behavior in complex reservoirs.

1. Introduction

As China’s oilfield development enters its mid-to-late stage, the old oilfields still occupy a dominant position in the national oil and gas production and reserve structure, with the contribution rate of production having remained above 70% for a long time. Against the background of insufficient resource replacement capacity in new areas, secondary development and recovery rate enhancement of reservoirs in old areas have become the key path to maintaining oilfields’ stable production and efficiency [1]. With the booming development of Machine Learning, digital intelligent seepage field prediction has become a hot spot in the industry, which is expected to realize accurate prediction of complex seepage field problems and promote stable and high production of oil and gas.

In recent years, with the rapid development of Artificial Intelligence technology, Deep Learning has gradually shown significant advantages in reservoir dynamic modeling and prediction, with its strong expressive capability in regard to complex nonlinear relationships. Traditional seepage-prediction methods, such as numerical simulation and empirical modeling, often rely heavily on simplified assumptions, extensive prior geological knowledge, and manual parameter tuning, which limit their ability to capture the high-dimensional, nonlinear interactions inherent in real reservoir systems. In contrast, Deep Learning models can automatically extract multi-scale spatial and temporal features from massive historical production and geological data, thereby enhancing generalization and predictive accuracy. Moreover, the complementary strengths of Deep Learning and seepage mechanics enable more robust modeling: seepage mechanics elucidate the fundamental flow laws in porous media under the influence of multiple complex factors, while Deep Learning excels at discovering hidden patterns in complex systems and large-scale data, effectively compensating for the limitations of traditional seepage models.

Compared with traditional Machine Learning methods, Deep Neural Networks have stronger feature extraction and big data adaptation ability, and they are able to learn the implicit coupling relationship between variables when the seepage response variables are affected by multiple factors, such as geologic inhomogeneity and perturbation of injection and extraction regimes. Xue et al. (2022) constructed a physically constrained DNN model for the physically consistent prediction of unsteady pressure fields during high WCPs [2]; Guo et al. (2023) reconstructed the 3D saturation field of complex fault block reservoirs through a Unet network, providing a basis for residual oil identification [3]; Chen et al. (2024) proposed a CNN–LSTM converged network (CSN) to realize the joint spatio–temporal prediction of Water Content (WC) and production [4]. These studies fully demonstrate that Deep Learning has become an important technical support for seepage modeling and prediction in reservoirs with high WCPs [2,3,4].

In this paper, on the basis of systematically combing the current research progress of Deep Learning in the field of reservoir seepage prediction, we classify and summarize different model types (feedforward, convolutional, temporal memory, graph structure, physical constraints, and integration), analyze their core construction methods and applicable scenarios, further explore the process optimization and key challenges of Deep Learning in reservoir seepage prediction, and look forward to its potential value in constructing data–physical-fusion digital twins in reservoirs.

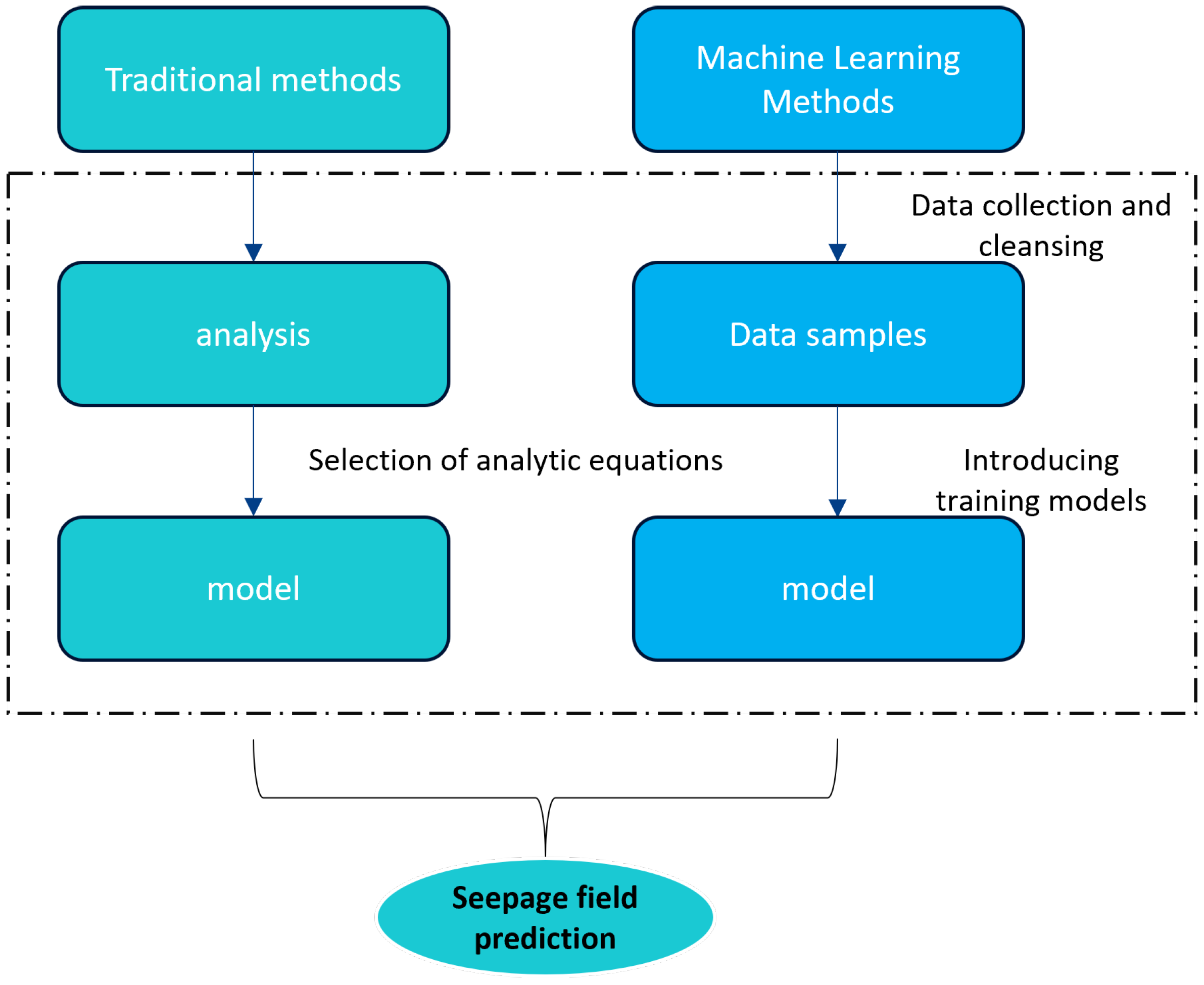
2. Development of Seepage Field Prediction Methods

With the deepening of oil and gas development and production, most of the main oil fields in China have entered the high WCP and the late stage of development, and the internal seepage behavior of the reservoir presents significant spatial and temporal non-homogeneity and complex evolution characteristics, which makes the traditional prediction model no longer applicable, and more refined and intelligent methods are needed to solve the complex problem of seepage field prediction.

The concept of Artificial Intelligence (AI) was first proposed in 1956, marking the beginning of the era of intelligent computing. Since then, AI has gradually developed into an interdisciplinary field integrating computer science, mathematics, control theory, and other disciplines. As the core component of AI, Machine Learning (ML) has been evolving since it was proposed in 1959, and its core goal is to design algorithmic models that can learn autonomously from historical data, so as to realize the extraction, cognition, and prediction of data patterns. In recent years, Deep Learning (DL) Figure 1, as an important branch of Machine Learning, has made breakthroughs in many fields, such as image recognition, speech processing, natural language understanding, etc., by constructing multi-layer neural network structures to abstract features layer by layer and learn complex mapping relationships, and it has also injected new momentum into scientific computing and engineering simulation. Especially in the field of fluid dynamics and seepage simulation, AI technology is deeply integrated with traditional physical modeling to promote the formation of a new paradigm of “data-driven-physical constraints-mixed modeling” [5]. For example, in the task of visualizing flow field prediction, the Hidden Fluid Mechanics (HFM) model proposed by Raissi et al. (2020) breaks through the dependence of traditional methods on boundary conditions and observation data by introducing Physical Information Neural Networks (PINNs) to invert velocity and pressure distributions directly from flow field images [5]; in the field of reservoir seepage, Guo et al. (2023) use CNNs to extract velocity and pressure distributions directly from flow field images, using CNNs to extract the spatial features of saturation in complex fracture blocks to achieve accurate modeling under multi-source data [3]. These studies show that Deep Learning not only improves the modeling accuracy of hydrodynamics, but also expands the boundary of its application in the field of seepage mechanics for unpredictable, nonlinear, and unstructured problems.

The development of Artificial Intelligence provides new methods and tools for seepage field prediction in oil reservoirs. Seepage field prediction methods have gradually shifted from traditional methods to data-driven methods based on Machine Learning and Deep Learning, and they have gradually developed towards the combination of multiple data-driven methods and data-driven methods with traditional methods (Figure 2). The development process of seepage field prediction methods is mainly divided into four stages: the analytical method stage, the numerical simulation stage, Machine Learning modeling, and Deep Learning modeling.

2.1. Conventional Seepage Field Prediction Methods

In order to accurately predict the seepage field and guide the actual production, researchers have established a series of models to analyze and solve the seepage field by deducing the relationship between the relevant parameters in the oil and gas development process. Traditional seepage field prediction methods

Table 1. Conventional seepage field prediction models.

Model Type	Applicable Scenarios	Numerical Method Examples
Black oil model	Conventional three-phase drive systems	FDM, FVM
Component model	Multi-component scenarios such as gas drive/volatile reservoirs	FVM, FEM
Fiducia model	Unconventional reservoirs such as shale and tight oil reservoirs	Forchheimer–FEM

are generally divided into physical experiments and numerical simulations, which mainly rely on the understanding of the physical properties and dynamic behavior of reservoirs, and which can be subdivided into numerical simulation methods, analytical methods, and semi-analytical methods; the latter are mainly to fit the field data with empirical formulas and to predict the future seepage field based on the historical seepage field parameter data [6].

Traditional seepage field prediction methods have some advantages: (i) they have been verified by long-term practice and have a certain degree of accuracy and reliability in traditional seepage field prediction; (ii) they are usually based on theoretical and empirical knowledge in the field of seepage mechanics, and they can provide relatively simple and intuitive explanations of seepage field prediction; and (iii) compared with the complex Deep Learning techniques, they usually do not require a large amount of data and computational resources [7]. However, there are some shortcomings in the traditional prediction methods: (i) by the method based on simulating the physical process of oil and gas reservoirs, it is difficult to accurately describe the complex characteristics of oil and gas reservoirs and the exploitation environment; in addition, the accuracy and completeness of reservoir information such as physical parameters, rock mechanical parameters, and ground stress also have a greater impact on the simulation results; (ii) it is difficult by analytical and semi-analytical methods to adequately take into account the non-homogeneous nature of the reservoir, the production, the engineering, and other factors of mutual influence, and the prediction process is based on the basic Deep Learning technique; (iii) it is difficult by analytical and semi-analytical methods to fully consider the interaction of reservoir inhomogeneity, production, and engineering factors, and the prediction process is based on basic assumptions, which makes it difficult to accurately simulate the real complex and nonlinear production process, and which does not provide enough flexibility to capture all the patterns and relationships in the data [8,9].

2.2. A Machine Learning-Based Method for Seepage Field Prediction

With the development of Artificial Intelligence and the increase of digitization of oil and gas fields, oil fields have accumulated a large amount of oil and gas development data, and data-driven methods have become an important trend. Machine Learning methods are data-driven, capable of learning the hidden laws between seepage field data and related engineering parameters and analyzing the cyclical changes and trends of seepage flow fields. Currently, the Machine Learning methods applied in oil and gas production prediction are Support Vector Machine (SVM), Gaussian Process Regression (GPR), and other regression algorithms, as well as Random Forest (RF), eXtreme Gradient Boosting Tree (eXtreme Gradient Boosting Tree), and other methods that can be used to predict oil and gas production, including eXtreme Gradient Boosting, Light Gradient Boosting Machine, XGBoost, and LightGBM [10].

Anifowose et al. [11] systematically evaluated the potential application of integrated learning methods in reservoir seepage parameter prediction and proposed that integrated models such as Random Forest (RF), Adaboost, and Gradient Boosting be used for modeling porosity and permeability, as they have higher prediction accuracy and robustness compared to traditional single models Otchere et al. [12] applied Support Vector Machines (SVMs) and Artificial Neural Networks (ANNs) to predictive modeling of permeability and porosity, and they constructed a supervised learning-driven framework for reservoir parameter prediction based on geological logging and logging data. The study conducted a systematic comparison between different models and found that SVMs showed stronger robustness and generalization ability under small sample conditions, while ANNs had a slight advantage in dealing with nonlinear relationships but were more prone to overfitting, which emphasized that different Machine Learning models should be targeted to be selected according to the sample size, feature complexity, and distribution of the target variables in the prediction of seepage parameters [12]. Garsole et al. [13], based on a review of seepage-prediction methods for earth and rock dams, proposed the use of Automatic Machine Learning (AutoML), clustering algorithms, and probabilistic graphical models for seepage parameter modeling and risk identification driven by multi-source monitoring data. They emphasize the advantages of AI technology in automatic modeling under the condition of unstructured, high-dimensional, and heterogeneous data, and they pointed out that traditional Machine Learning methods can play an important role in the path of “seepage coefficient estimation-risk classification-dynamic change monitoring” [13]. Although this study mainly focused on hydraulic engineering, its methodological framework is highly transferable to reservoir injection and recovery block delineation and to data-driven seepage field prediction [13]. Hussen et al. [10] used a variety of mainstream Machine Learning models (including XGBoost, Random Forest, SVM, and ANN) for systematic modeling and prediction of reservoir permeability, and the training data were obtained from the results of core physical properties analysis. The analysis results showed that XGBoost and Random Forest had the best performance, in terms of prediction accuracy, stability, and training efficiency, and that both of them achieved prediction accuracy of R² greater than 0.95 [10]. Ma et al. [14] constructed a permeability coefficient prediction model based on the Random Forest–Secretary Bird Optimization Algorithm (SBO–RF) to solve the problem of parameter inversion under pumping test data, which combined the modeling ability of Random Forest for complex nonlinear mapping relations with the efficiency advantage of the SBO algorithm in high-dimensional hyperparameter optimization to achieve high-precision permeability estimation with strong generalization ability [14]. It was shown that the model is suitable for the task of inverse prediction of inter-well permeability distribution and can be used as an input support model for the reconstruction of seepage fields and the optimization of well network deployment in low-permeability reservoirs.

Compared with the traditional methods, the Machine Learning method performs better in the prediction of seepage field lithology parameters (Figure 3) [13]. On the one hand, the Machine Learning method does not need to analyze the mechanism embedded in seepage phenomena or derive formulas for physical processes, but only takes geological and engineering factors as variables, and it can be driven by the data to model the relationship between lithological parameters and influencing factors, which reduces the difficulty of modeling and improves the fitting degree of nonlinear relationships. On the other hand, the Machine Learning method can make predictions from historical data, and the model can be automatically learned and adjusted according to the actual geological and engineering data, which has better flexibility and adaptability [15,16,17].

However, the pressure and flow fields are essentially a typical space–time variable controlled by the seepage control equation, and the prediction of these variables not only needs to consider the input characteristics but also needs to take into account the “physical consistency”, otherwise there will be a non-physical understanding (e.g., negative pressure, infinite gradient) [5], which requires a “physical embedding mechanism” such as PINNs, PD-CNN, and so on. P and q are distributed variables (2D or 3D fields), and traditional ML models are “point prediction” or “feature regression” in nature, and it is difficult to efficiently learn the continuous field structure, while Deep Neural Networks (especially CNN and UNet) are naturally suitable for “image-to-image” and “field-to-field” mapping; seepage response is highly dependent on the boundary conditions, time series, and source–sink terms, and it is difficult to deal with such complex boundary conditions by traditional ML methods. Models such as PINNs/P-DNN can introduce the boundary information and constrain the physical consistency during the training process through automatic discretization or residual regularization [18,19,20].

In addition, with the development of oilfield digitization and informatization, the amount of data has been growing explosively, and in the face of high-dimensional massive data, geologic complexity, big data characteristics, and timeliness, Deep Learning can solve the deficiencies of traditional methods and shallow neural network methods, and it can further enrich the means of seepage field prediction [14,20,21,22].

2.3. Deep Learning-Based Method for Seepage Field Prediction

Unlike traditional Machine Learning methods, Deep Learning methods can more accurately predict and optimize an extraction plan for complex lithological parameters during the high WCP in the late stage of an oil field, as well as seepage response variables considering the physical equations, spatial structure, and dynamic boundaries. (1) Deep Learning methods can extract richer and finer features from complex field data to better capture the complex correlation between seepage field response variables; (2) The response variables of a seepage field in high-water-containing reservoirs are affected by the nonlinearities of various factors, such as geology and engineering, etc., and a Deep Neural Network structure can flexibly model nonlinear relationships to better capture the complex correlation between the response variables of the seepage field and the factors affecting them; (3) The Recurrent Neural Network (RNN), Long Short-Term Memory Network (LSTM), and Short Short-Term Memory Network (SSTRM) of Deep Learning can be used for the optimization of extraction schemes. RNN, LSTM, and other structures in Deep Learning can effectively handle time-series field data, which are suitable for capturing the cyclic evolution characteristics and dynamic trends of seepage fields in high-water-containment-period reservoirs, and they help to identify temporal response mechanisms such as advancement of the driving front edge and movement of residual oil; (4) Prediction of seepage fields in high-water-containment period reservoirs usually involves a large amount of well network operation data, geological parameters, and development history. The Deep Learning model has strong fusion-modeling capability under multi-source big data conditions, which can realize the joint prediction of seepage response variables under complex conditions [11] and improve its scenario-generalization and real-time prediction capability.

Raissi et al. [5] proposed a representative Hidden Fluid Mechanics (HFM) framework based on the idea of PINNs (Physics-Informed Neural Networks) to invert the full-field pressure and velocity distributions of a flow field system from velocity field images. The method has good physical consistency and generalization ability without the need of direct observation of pressure data and only reconstructs the hidden physical variables by visualizing the flow field samples. Although the study was initially applied to hydrodynamic visualization experiments, the method has a strong capacity for migration, and it is suitable for pressure–velocity inversion modeling in visualization and monitoring of reservoirs during high WCPs [5].

In order to solve the problem that traditional data-driven models are prone to deviate from physical laws, Xue et al. (2022) proposed a physics-regularized Deep Neural Network (physics-regularized DNN) framework for predicting pressure field evolution in non-homogeneous reservoirs, which is particularly suitable for modeling seepage dynamics in high-water-bearing periods [2]. The method uses physical consistency as a network training constraint term by embedding single-phase unsteady seepage control equations, initial conditions, and boundary conditions in the neural network loss function. The experimental results show that the model still has good robustness and accuracy under scenarios with noisy data and fewer samples, especially in the prediction of pressure distribution in high WC areas with significant advantages.

In their subsequent study, Xue et al. [2] further proposed the Physical Difference Convolutional Neural Network (PD-CNN), which integrates the finite difference idea with the structure of a Convolutional Neural Network to realize high-accuracy prediction of the pressure and saturation fields in multiphase seepage flows. The model converts the discretized residuals of the seepage control equations into a differential convolutional kernel structure and embeds them into the network loss function, which improves the physical consistency of the prediction results and the boundary processing capability. In the case of a typical reservoir with high WCP, PD-CNN shows good prediction ability in complex regions such as pressure degradation and drastic change of WC at the end of the recovery period, which is suitable for the tasks of real-time production monitoring and dynamic optimization deployment [2].

Guo et al. (2023) [3] constructed a Deep Learning-based saturation field prediction model for the problem of oil saturation evolution in the high WC stage in complex fracture block reservoirs, combining sample pool optimization and U-Net structure extraction features to achieve dynamic modeling of three-dimensional time-series saturation fields. The study drove the model training by historical development data, and it reconstructed the evolution path of oil-rich zones by combining the data with a spatial interpolation algorithm, which could be used for identifying and dynamically tracking residual oil potential zones in high WCPs. Their experiments showed that the method can reconstruct high-resolution seepage response distribution maps under low well control conditions, providing technical support for reservoir digital twin modeling.

Wang and Jia (2023) [15] proposed an intelligent modeling framework integrating numerical modeling and Deep Learning based on the coupled pressure–saturation control equation for simulating the evolution of oil–water two-phase flow in complex inhomogeneous reservoirs. The method was based on regression prediction of the coupled field evolution results by Deep Neural Networks, which realizes efficient modeling of the time-sequential changes of pressure and saturation fields, and which is especially suitable for intelligent assessment of injection and extraction responses during the optimization phase of regulation in high WCPs. The study emphasized the role of the physical–data-fusion strategy in improving the prediction accuracy and training stability of complex seepage systems.

Fu et al. (2024) proposed a multi-scale nonlinear seepage modeling method based on Graph Neural Networks (GNNs) for the problem of high-resolution seepage prediction at the Digital Core Scale (DCS) [16]. The method constructs the pore structure as a graph structure input, and it simulates the local velocity and saturation change process in a two-phase flow through the node information transfer mechanism. In the water-driven-dominated micro-replacement process, the model can accurately identify the micro-channel flow paths, residual oil retention areas, and non-homogeneous response characteristics in the high-water-bearing stage, which provides a new numerical modeling path for the intelligent analysis of the micro-scale replacement mechanism in the high-water-bearing stage.

Chen et al. (2024) constructed an agent modeling framework based on Convolutional Spatio–temporal Networks (CSNs) for rapid prediction of production response during reservoir development, covering key variables such as pressure, production, and WC [4]. The method established a mapping of spatio–temporal dynamic relationships by extracting input features such as injection and production time series, well group locations, and geological parameters to realize rapid response prediction under complex flow conditions during high WCPs.

In summary, Deep Learning methods have been widely explored in the prediction of seepage fields in oilfields with high WCP, especially in the modeling of key variables, such as pressure field, saturation field, WC evolution, and flow rate response, on which significant progress has been made. Compared with the traditional yield prediction task, seepage field prediction places greater emphasis on the distribution pattern and physical consistency in the spatial–temporal dimension, and, thus, it presents significant differences in application goals, problem focus, and model design. Currently, the Deep Learning architectures employed have gradually expanded from the early time-series modeling networks, such as LSTM and GRU, to include multiple types, such as Convolutional Spatio–temporal Networks (CSNs), Graphical Neural Networks (GNNs), Physically Informative Neural Networks (PINNs), and Differential Convolutional Neural Networks (PD-CNNs), among other structures, and they continuously enhance the physical interpretability and prediction accuracy of the models by introducing control equation residuals, boundary condition constraints, and attention mechanisms.

There are obvious differences in the applicability of traditional methods and Deep Learning methods in reservoir seepage field prediction (see

Table 2. Comparison of traditional methods and Deep Learning in seepage field prediction.

Method	Advantages	Disadvantages
Traditional method	Good physical consistency, strict adherence to conservation laws, and strong interpretability; suitable for theoretical deduction and program design in the early development stage.	Its performance is limited in dealing with nonlinear seepage response and complex working conditions (such as non-homogeneous, fracture, fracture block, and complex well network perturbation) in high-water-bearing periods, and it often needs to simplify the assumptions, which results in the prediction accuracy being limited by the completeness and accuracy of the physical parameter acquisition.
Deep Learning	With its data-driven core, it can effectively learn complex input–output relationships through automatic feature extraction and nonlinear mapping capability, which is especially suitable for modeling seepage response during high WCPs and the later dynamic adjustment stage.	The underlying model is a “black box” structure that does not allow for a clear understanding of the causal reasoning processes involved.

). Traditional methods usually rely on explicit seepage mathematical models and parameter assumptions, and, although they have good interpretability and engineering controllability in the conventional development stage, it is difficult to accurately capture, by these methods, the complex nonlinear relationships and dynamic evolution processes in the high WC stage, with the increase of reservoir nonhomogeneity, the intensification of well network perturbation, and the high degree of reconfiguration of seepage paths. Deep Learning methods, on the other hand, do not rely on predefined physical model structures, they have automatic feature-extraction capabilities, and they can flexibly cope with prediction tasks under multivariate and multi-source input conditions. In particular, without assuming the reservoir type and applicability to multiple neural network structures (e.g., DNNs, CNNs, LSTMs, PINNs, GNNs, etc.), they demonstrate stronger scenario adaptability and prediction accuracy, and they have a broader prospect of application in dynamic identification and response modeling of seepage fields during high WCPs.

3. Key Processes for Deep Learning-Based Seepage Field Prediction

As a typical data-driven model, the performance of Deep Learning is highly dependent on the quality, quantity, and distribution characteristics of the training samples. In the prediction of reservoir seepage fields in high WCPs, the input data often come from multiple heterogeneous information sources, such as geology, well logging, injection and extraction, monitoring, etc., which show the characteristics of multi-source heterogeneity, multi-scale, high-dimensionality, and spatial–temporal inhomogeneous distribution. Although the Deep Learning model is capable of automatic feature extraction, under the concept of integrated geological engineering modeling, if the physical relevance and semantic structure of the data are neglected it can easily lead to network learning bias and generalization performance degradation. Therefore, before constructing the Deep Learning-based seepage field prediction model, it is still necessary to carry out targeted data preprocessing and feature engineering, such as feature screening, dimensional approximation, spatial–temporal normalization, and physical quantity conversion, in order to ensure that the input of the model has sufficient information-expression ability and physical consistency and to provide a reliable data basis for subsequent high-precision prediction.

Deep Learning-based seepage field prediction research in high WC reservoirs usually includes key steps such as data preprocessing, model construction, model training, validation, and prediction (see Figure 4) [17]. In the data preprocessing stage, it is first necessary to integrate multi-source data, including geological attributes, logging parameters, injection history, and production response to establish a unified training data system. Subsequently, the original data should be quality-checked to deal with missing values, outliers, and inconsistent data, and normalization or standardization methods should be used to eliminate the influence of the scale, so as to ensure the comparability of various variables [11]. On this basis, the physical mechanism of seepage is combined with feature screening and engineering processing to extract the input factors that have a significant impact on the response variables, such as pressure, saturation, WC, etc., and that reasonably divide the training set and test set [12].

In the model construction stage, appropriate Deep Learning models, such as DNNs, CNNs, LSTMs, PINNs, GNNs, etc. (see

Table 3. Representative applications of neural network methods in seepage modeling.

Year	Author	Network Type	Scenario	Model
2017	Anifowose et al. [11]	FeedForward NN	Petrophysical modeling	Ensemble ANN
2021	Hussen et al. [10]	FeedForward NN	Core-based permeability	MLP
2023	Hong et al. [20]	FeedForward NN	Pore-throat prediction	DNN
2022	Yan et al. [21]	Convolutional NN	Multiphase field prediction	CNN + PDE
2023	Telvari et al. [23]	Convolutional NN	Digital rock two-phase flow	3D CNN
2024	Liu et al. [24]	Convolutional NN	Mud invasion depth prediction	CNN + Regression
2021	Otchere et al. [12]	Time-series NN	Lithology parameter modeling	RNN + SVM
2023	Garsole et al. [13]	Time-series NN	Dam seepage sequence modeling	AutoML–LSTM
2024	Qian et al. [22]	Time-series NN	Gas–water microseepage simulation	LSTM
2023	Wang et al. [15]	Graph NN	Well pattern optimization	Production-GNN
2023	Zhang et al. [18]	Graph NN	Connectivity-based flow simulation	Graph Topology Net
2024	Fu et al. [16]	Graph NN	Multi-scale heterogeneity modeling	GraphSAGE
2020	Raissi et al. [5]	Physics-Informed NN	Hidden fluid mechanics	PINN
2022	Xue et al. [2]	Physics-Informed NN	Pressure prediction in porous media	PR-DNN
2023	Wong et al. [19]	Physics-Informed NN	Sinusoidal-space learning	Sin-PINN
2023	Guo et al. [3]	Multimodal NN	Saturation prediction from seismic + logs	Sample Pool + Fusion
2024	Ma et al. [14]	Multimodal NN	Permeability coefficient inversion	RF–SBO Hybrid
2024	Chen et al. [4]	Multimodal NN	Spatio–temporal production prediction	CSTN (CNN + LSTM)

), need to be selected according to the prediction objectives (e.g., multivariate joint prediction, time-varying modeling, and spatial distribution recovery, etc.) and data characteristics (e.g., small samples, spatial–temporal non-stationarity) [2,5,16]. The model training phase can be combined with optimization algorithms (e.g., Adam, SGD, learning rate scheduling, etc.) to improve the training efficiency and performance stability. In the model validation and testing stage, the model prediction effect is evaluated by using quantitative metrics such as Mean Square Error (MSE), coefficient of determination (R²), and Mean Absolute Error (MAE). In recent years, in order to improve the accuracy and physical consistency of seepage field prediction, research has gradually focused on feature engineering optimization and network structure enhancement, especially in the embedding of physical information, multiscale modeling, and spatio–temporal fusion, on which significant progress has been made [14,18,19,20].

3.1. Feature Engineering

In traditional feature-engineering methods, after data cleaning, correlation between data sets is generally explored by principal control factor analysis, such as Pearson correlation analysis, Spearman correlation analysis, Kendall rank correlation analysis, the chi-square test, etc.; the influential factors are ranked by the size of the correlation, and those with higher correlation are selected as input parameters. However, these methods usually only consider the relationship between individual features and target variables, ignoring the possible interaction effects between features; when the number of features is large, a large number of irrelevant features may exist in high-dimensional data, interfering with the results of the correlation analysis; in addition, feature selection by correlation alone may ignore important information in some features [18,21,22].

With the development of Artificial Intelligence, feature-engineering methods have become more abundant. Otchere et al. [12] used SVM and shallow ANN to model porosity and permeability, and then standardized, normalized, and processed the outliers of the logging data, so as to eliminate the noise points that obviously deviated from the normal trend [12]. Xue et al. [2] used a physics-regularized DNN (PR-CNN) in the feature engineering stage to firstly normalize and structurally transform the non-homogeneous permeability field, and they screened the sampling points in the seepage region to avoid the unstable model training caused by the concentration of sampling in the area of gradient changes. In the subsequent patent research, Xue et al. [2] used a Physical Differential Convolutional Neural Network (PR-CNN) in feature engineering, they performed differential convolutional conversion and normalization of pressure and saturation field data, and they integrated the residual expression of physical control equations into the convolution kernel structure, realizing the unity of the data structure and physical laws. For the Random Forest–Secretary Bird Optimization (RF–SBO) permeability inversion model, which was proposed by Ma et al. [14] all the input variables were subjected to variable screening and normalization before modeling. They used the feature importance assessment to rank the input variables, they eliminated the minor factors that did not have a significant impact on permeability, and they retained the main control variables for modeling, so as to reduce the computational overhead and the risk of overfitting caused by redundant features [14,23,25,26]. Hussen et al. [10] applied several traditional Machine Learning methods, such as SVM, RF, and XGBoost, to the prediction of permeability in the core, and the work of feature engineering was particularly detailed. They selected the optimal subset of variables for modeling through feature correlation analysis and importance scoring, and they tested the effect of dimensionality reduction methods such as Principal Component Analysis (PCA) on model performance [25,27,28].

Overall, feature engineering is a complex and critical step that requires targeted selection based on specific problems and data, while the development of Deep Learning and clustering algorithms provides new possibilities for feature engineering to better deal with high-dimensional data and capture the interaction effects between features [19,29,30,31,32,33,34].

3.2. Neural Network Construction Methods

With the deepening of Deep Learning for seepage field prediction, researchers have also begun to try different neural network construction methods to enhance the prediction ability of the model in different scenarios and under different objectives.

• FeedForward Neural network model: A FeedForward Neural network is a kind of Deep Neural Network (DNN) with a simple structure but a powerful function, which is suitable for small- and medium-scale data modeling tasks. It can be used for single-point response prediction, such as pressure and saturation, by capturing the higher-order relationships between input and output variables through multi-layer linear and nonlinear transformations. For example, Xue et al. [2] used physics-regularized DNN for seepage field prediction, they embedded the single-phase seepage control equation in the form of residuals into the loss function, they realized automatic constraints on physical laws during the model training process, and they effectively improved the physical consistency and generalization ability of the pressure prediction [2]. Wang et al. [15] developed a hybrid modeling framework that integrates nonlinear coupled seepage control equations with deep FeedForward Neural networks to predict the evolution of pressure and saturation in complex reservoirs. The model obtains initial samples through numerical simulation and inputs the coupled pressure and saturation time series into the DNN for regression modeling, which realizes the joint data–physical-structural drive. Compared with traditional numerical methods, the model has better performance in simulation speed and predicting response trends, and it is suitable for the rapid assessment and response prediction of seepage behavior under complex injection and mining regimes [35,36,37,38]. Hong et al. [20] applied DNNs to the task of predicting pore throat features in micro-scale core images, and they constructed a seepage structure feature learning model based on parameters from well logging and core images. The model predicts the pore throat radius distribution with multidimensional static inputs (porosity, image features, gray moments, etc.), which is used to reflect the influence of the core microstructure on the biphasic seepage capacity. The input variables were strictly screened and normalized in the study, and the nonlinear mapping between pore structure and seepage capacity was successfully established by a FeedForward Neural network, which provided a novel alternative path for seepage parameter inversion [39,40,41,42].
  Overall, DNN-like models are suitable for small- and medium-scale parameter prediction tasks, with their advantages of simple structure and efficient computation, and they can still play an important role in seepage modeling if combined with physical constraints or multivariate fusion mechanisms [43,44,45,46].
• Spatio–temporal prediction network model: In order to more fully explore the influence of time series features on the evolution process of seepage response variables (e.g., pressure, WC, saturation, etc.) in the production data of reservoirs during the high WCP, some researchers have adapted and improved the structure of temporal neural networks, such as traditional RNNs, LSTMs, GRUs, etc., in order to enhance the ability of the model to portray complex nonlinear dynamic processes. In addition, some studies have also introduced heuristic optimization methods, such as genetic algorithms and particle swarms, to adaptively adjust the model hyper-parameters, thus further improving the training efficiency and time-series prediction accuracy, and providing a more stable and reliable technical path for modeling dynamic seepage behavior [47]. For example, Garsole et al. [13] proposed an integrated network model based on RNN in hydraulic seepage modeling, combining time-series clustering and automatic feature extraction to achieve dynamic identification and modeling of seepage risk from multivariate monitoring data; Qian et al. [22] introduced the LSTM structure to investigate the gas–water two-phase microscopic seepage process in coal rock fissures, realizing the high-precision time-sequence portrayal of the fracture–matrix periodic response process and showing good results in the modeling of a microscale dynamic evolution process.
  From the current study, within the Deep Learning framework, LSTM, RNN, and GRU as the basic models have been widely used to solve time-series dynamic prediction problems, and experts and scholars have developed different variant models according to the actual needs of different scenarios, which provide a flexible and efficient technical path for modeling seepage behaviors in high WCPs [48,49,50].
• Convolutional Neural Network model: Convolutional Neural Networks (CNNs) have been widely used in reservoir seepage modeling by virtue of their advantages in spatial feature extraction and local pattern recognition, which are especially suitable for processing gridded distribution maps such as pressure and saturation fields, or three-dimensional structural data such as digital core images [22]. In complex seepage systems, CNNs can extract features such as inter-well interference, hyper-permeable channels, and non-homogeneous structures through a local sensing mechanism, and they capture the spatial variation patterns in the seepage field [51]. For example, Xue et al. [2] used the Physical Difference Convolutional Neural Network (PD-CNN), which integrates the finite difference idea with the convolutional structure, and they embedded the residuals of the control equations as a convolution kernel into the CNN network to realize high-precision prediction of the distribution of the joint pressure–saturation field. Guo et al. [3] constructed a deep convolutional network model based on U-Net for dynamic prediction of three-dimensional saturation fields in complex fault block reservoirs. By designing jump connections and a multi-scale structure, the model can reconstruct high-resolution oil saturation distribution maps in the low well control region, which improves the accuracy and spatial consistency of residual oil identification. Telvari et al. [23] applied 3D CNN to digital core image modeling; they extracted pore structure information through 3D convolution, and they predicted the pressure gradient and saturation evolution process of a two-phase flow in the core. This method can automatically learn microscopic seepage paths in complex pore channels, expanding the application space of CNN in microscale seepage modeling.
  Overall, the Convolutional Neural Network-like model has become one of the mainstream modeling tools in reservoir seepage field prediction by virtue of its powerful spatial structure perception capability and good scalability. Especially in complex flow patterns during high WCPs, CNN shows good ability to portray the response mechanism of non-homogeneous seepage by introducing multi-scale structures, physical constraints, and spatio–temporal fusion [24,52].
• Graph Neural Network model: The Graph Neural Network (GNN) is a class of Deep Learning. GNN models are capable of handling non-Euclidean spatial structure data, which are especially suitable for describing data forms with irregular topology, such as pore networks, fracture systems, well network arrangements, and other complex spatial relationships. In reservoir seepage modeling, GNNs can regard pores or well points as “nodes” in the graph, and their connection relationships (such as flow paths, neighboring wells interference, etc.) as “edges”, and they can extract spatial topological features through graph convolution, message passing, and other mechanisms, so as to model the propagation pattern of the fluid in the complex structure. The topological features are extracted through graph convolution and message passing to model the propagation of fluids in complex structures [53,54,55]. For example, Fu et al. [16] constructed a multi-scale nonlinear seepage simulation model based on Graph Neural Networks for predicting microscopic seepage paths in DCSs. They reconstructed the core CT image into a pore node graph, with node features including pore size, width of connecting channels, etc., and with edge weights representing the infiltration fluxes between neighboring pores. The transfer of physical information between nodes was realized by graph convolution layers and combined with a multilayer message aggregation strategy to predict the local velocity field and saturation evolution process. Experiments showed that the model has strong accuracy and spatial sensitivity in reconstructing microchannel flow paths and identifying residual oil-rich zones.
  Although the GNN model is still in the preliminary exploration stage in the field of oil and gas engineering, its potential in digital core analysis, fracture network simulation, and spatial coupling prediction has been initially shown [8], and it is expected to be fused with physical modeling, image recognition, and other technologies in the future, to construct a seepage intelligent simulation system with more generalized capability [23].
• Physical information neural network model: Physics-Informed Neural Networks (PINNs) are a class of Deep Learning methods that have emerged in recent years, which embed physical control equations into the neural network training process [56]. Unlike the traditional “physical modeling followed by numerical solution” approach, PINNs transform the control equations (e.g., Darcy’s law, mass conservation equation) into the loss terms of neural networks, so that the model automatically satisfies the basic physical laws while fitting the data [57]. In the field of reservoir seepage, PINNs provide a novel modeling paradigm for prediction, inversion, and continuous field reconstruction of seepage response variables (e.g., pressure, saturation, velocity, etc.), which is especially suitable for problem scenarios with incomplete data, restricted observations, and high nonlinearity. For example, Raissi et al. first systematically proposed the Hidden Fluid Mechanics (HFM) framework, which inverts complete fluid dynamics variables (e.g., pressure, velocity, vorticity, etc.) from partially observable velocity fields based on PINNs. Although this study did not focus on oil reservoirs, the modeling idea of image-variable mapping and physical constraints laid a methodological foundation for the subsequent application of PINNs in seepage [5,58]. Xue et al. [2] introduced the idea of PINNs into the pressure field modeling of inhomogeneous reservoirs and proposed the physics-regularized DNN, which is a methodology to model the pressure field of non-homogeneous reservoirs that enables the model to learn both physical laws and numerical data in the training stage by embedding the residuals of the Darcy flow control equation. Their experiments showed that the PINN model has stronger stability and physical consistency than the traditional DNN in the case of sparse boundary data and complex well control. Yan et al. [21] constructed a complete three-dimensional multiphase seepage PINN model to predict the pressure–saturation evolution process in a non-homogeneous pore medium. They embedded the coupled governing equations of two-phase flow in the loss function and introduced a regular term to constrain the WC evolution trajectory, which significantly improved the smoothness and physical interpretability of the prediction results.
  PINNs, with their embedded representation of the control equations, provide a new way of thinking for modeling reservoir seepage fields by integrating physical-driven and data-driven approaches. Combined with the research progress of Xue [2], Yan [21], and Raissi et al. [5]., it has been shown that PINNs are not only suitable for pressure and saturation prediction under complex boundary conditions but also show significant advantages in small-sample inverse modeling and continuous field reconstruction [26]. With the development of adaptive weight balancing, multiscale decoupling, and efficient derivation algorithms, PINNs are expected to play a greater role in the intelligent simulation of seepage response in reservoirs with high WCPs [59].
• Multi-modal integration model: In order to improve the generalization ability and physical consistency of the model, researchers have explored Deep Learning integration strategies—such as multi-network structure fusion, physical information embedding, and sample enhancement—in recent years to construct a more adaptive seepage prediction framework [27]. For example, Xue et al. [2] introduced the control equation residuals into the convolutional kernel structure and proposed the Physical Difference CNN (PD-CNN), which balances data-driven accuracy and physical consistency; Guo et al. [3] combined the Unet network with a multi-sample pooling strategy to improve the saturation reconstruction accuracy in low-well-control regions in fractured-block reservoirs; Zhang et al. [28] enhanced the model’s ability to capture the changes of the key time series by fusing the GRU with an attentional mechanism; Jiang et al. [47] proposed a convolutional time-series network (CSN) fusing CNN and LSTM to achieve joint spatio–temporal modeling of the WC rate and pressure field under injection and extraction dynamics [4]. The above work shows that the integrated modeling approach of Deep Learning is gradually evolving from the fusion of structural layers to the multidimensional synergy of physics, data, and mechanism, which has become an important direction for constructing the next-generation intelligent seepage simulation model

  Table 4. Applications of Deep Learning in seepage field prediction by task type.

  Year	Author(s)	Application Target	Problem Addressed	Model Used
  2021	Otchere et al. [12]	Production forecast	Oil production sequence modeling	RNN–SVM
  2023	Garsole et al. [13]	Production forecast	Dam seepage sequence prediction	AutoML–LSTM
  2024	Chen et al. [4]	Production forecast	Coupled spatio–temporal modeling	CSTN (CNN–LSTM)
  2020	Raissi et al. [5]	Pressure field	Reconstruction from velocity data	PINNs
  2022	Xue et al. [2]	Pressure field	Prediction in heterogeneous media	Physics-Reg. DNN
  2023	Wong et al. [19]	Pressure field	Learning in sinusoidal domain	Sinusoidal PINN
  2022	Yan et al. [21]	Saturation field	3D multiphase saturation modeling	CNN + PDE loss
  2023	Telvari et al. [23]	Saturation field	Two-phase prediction in digital core	3D CNN
  2023	Guo et al. [3]	Saturation field	Fault block saturation mapping	CNN–Attention Fusion
  2017	Anifowose et al. [11]	Porosity/permeability	Log-based property modeling	Ensemble ANN
  2021	Hussen et al. [10]	Permeability	Core-based prediction	MLP
  2023	Hong et al. [20]	Pore-throat radius	Prediction from image data	DNN
  2021	Liu et al. [24]	Microscale seepage	Mud invasion in tight sandstone	CNN + Regression
  2023	Qian et al. [22]	Microscale seepage	Micro gas–water flow in cleats	LSTM
  2024	Fu et al. [16]	Microscale seepage	Multiscale nonlinear flow	Graph-based CNN
  2022	Wang et al. [15]	Well network modeling	Optimization of injection–production layout	Graph NN
  2023	Zhang et al. [18]	Well network modeling	Flow reconstruction via mesh graph	GNN with topology
  2024	Ma et al. [11]	Connectivity classification	Classification by optimization	RF–SBO Hybrid
  2023	Hussen et al. [10]	Multimodal permeability	Core–log data fusion prediction	ANN–RF
  2023	Guo et al. [3]	Multimodal saturation	Seismic–log fusion for saturation	Sample Pool + CNN
  2024	Chen et al. [4]	Multimodal proxy modeling	Dynamic modeling from mixed input	CSTN + Fusion Block

  .

3.3. Comprehensive Example

Jiang et al. [47] constructed a Deep Learning model for the prediction of seepage response variables in reservoirs with high WC based on the strong nonlinear characteristics of production dynamics and on injection and extraction conditions during reservoir development, which effectively solved the coupled prediction problem of production, WC, and pressure changes among different wells [4]. The research process was consistent with the Deep Learning application process in Figure 4, covering key steps, such as feature engineering, sample construction, and network structure construction, as follows:

• Feature extraction and sample construction. Aiming at the data non-uniformity and production dynamic differences between injection and extraction well sites, Chen et al. designed a temporal–spatial fusion sample organization strategy to standardize the injection and extraction data (e.g., injection intensity, WC, daily oil production, etc.) between wells and construct the sample sequence based on the temporal sliding window in order to maintain the temporal continuity of the data and the spatial consistency of the well group. The Dynamic Sample Pool design enhances the adaptability of the model to data from different production stages and alleviates the problem of “data drift” in high WC areas.
• Construct neural network. In order to better extract the temporal and spatial coupling features in the seepage response variables, Chen et al. proposed a Convolutional Spatio–temporal Network (CSN) structure that integrates a Convolutional Neural Network (CNN) and a Long Short-Term Memory (LSTM) network. The CNN part is used to extract the spatial feature pattern of injection and extraction, the LSTM is used to model the dynamic response of the production parameters over time, and the output of the network contains the predicted values of the key response variables such as pressure and WC. In an actual case of a reservoir, the model jointly predicted the WC and daily fluid production of a typical well group in the next 50 days, and compared with the traditional numerical simulation and shallow neural network methods the CSN performed better, in terms of prediction accuracy and trend fitting, which verified the validity of Deep Learning in predicting the dynamics of reservoirs during high WCPs [34].

Although the above models perform well in specific scenarios, their structural differences and capability boundaries have not been systematically quantified. A unified comparison framework is proposed below to guide model selection.

3.4. Comparative Framework for Deep Learning Architectures in Seepage Modeling

3.4.1. Analysis of Differences in Mathematical Structures

• FeedForward Neural (FFN) networks
  Mathematical expression:

  $$y=\sigma \left(W_n·\sigma \left(W_{n-1}\cdots \sigma \left(W_{1}x+b_1\right)\right)+b_n\right)$$

  (1)

  Explanation: purely data-driven layer-by-layer nonlinear transformations with no spatial/temporal structure awareness.
  Structural Features:
  FFN networks pass information through multiple fully connected layers (Dense Layer) step by step, and each layer applies a nonlinear activation function (e.g., ReLU, Siqmoid) to the inputs after a linear transformation (weight matrix W with bias b), which are essentially higher-order nonlinear function fitters capable of capturing complex mapping relationships between input features and target variables.
  Limitations in seepage field applications:
  (i) Blind-box modeling: FFN networks rely on end-to-end data-driven modeling and lack explicit encoding of spatial topology or physical laws, leading to unphysical results (e.g., negative pressure regions) when predicting continuous fields (e.g., pressure distributions); (ii) Scenario adaptation: suitable for single-point parameter prediction (e.g., WC in a single well), but low reconstruction resolution due to neglect of local spatial correlations when dealing with gridded field data [10].
• Convolutional Neural Networks, CNNs
  Mathematical expression:

  $$F_{\mathrm{out}}(i,j)=\sum _m\sum _{k,l}{W}_m(k,l)·F_{\mathrm{in}}(i+k,j+l)+b$$

  (2)

  Explanation: extraction of local spatial features by convolution kernel for gridded data (e.g., permeability field images).
  Structural features:
  CNNs extract local spatial features by sliding convolutional kernels (e.g., 3 × 3 filters) and realize feature dimensionality reduction and translation invariance by using a Pooling operation (Pooling). A CNN’s local sensing mechanism is naturally adapted to gridded data (e.g., permeability field images) and is capable of capturing spatial patterns such as inter-well disturbances and hyper-permeable channels.
  Advantages in seepage field applications:
  (i) “Pictorial” modeling: Treating the seepage field as a 2D/3D image, spatial heterogeneity can be automatically identified by convolution kernels (e.g., saturation field reconstruction in Guo et al. [3]); (ii) Potential for physical customization: By designing specific convolutional kernels (e.g., difference kernels), physical laws (e.g., Darcy’s law gradient computation) can be partially embedded to improve the consistency of predictions (e.g., PD-CNN in Xue et al. [2]).
• Graph Neural Networks, GNNs
  Mathematical expression:

  $$h_v^{\left(k\right)}=\varphi \left(h_v^{(k-1)},\underset{u\in \mathcal{N}\left(v\right)}{⨁}\psi \left(h_u^{(k-1)}\right)\right)$$

  (3)

  Explanation: processing of non-Euclidean spatial data (e.g., fractured networks) by node aggregation (Aggregation) and message passing (Message Passing).
  Structural features:
  GNNs abstract the seepage system as a graph structure (nodes = wells/pores, edges = flow paths) and dynamically update the node states through Message Passing and node aggregation (Aggregation). Their non-Euclidean data-processing capability is particularly suitable for describing complex topologies such as fracture networks and unstructured grids.
  Uniqueness in seepage field applications:
  (i) “Social network” modeling: Similar to the propagation of user relationships in social networks, GNNs simulate fluid flow paths along a fracture or pore network (e.g., the microscopic seepage simulation of Fu et al. [16]); (ii) Multi-scale fusion: The macroscopic well network layout and microscopic pore structure can be encoded simultaneously to realize cross-scale seepage coupling (Zhang et al. [18] for fracture–matrix interaction modeling).
• Physics-Informed Neural Networks, PINNs
  Mathematical expression:

  $$\mathcal{L}={\lambda }_{\mathrm{data}}{∥y_{\mathrm{pred}}-y_{\mathrm{obs}}∥}^2+{\lambda }_{\mathrm{phy}}{∥\mathcal{N}\left(u\right)∥}^2$$

  Explanation: embedding control equation residuals (e.g., Darcy’s law) in the loss function enforces physical consistency.
  Structural Features:
  PINNs explicitly introduce the residuals of control equations, e.g., the mass conservation equation ($\nabla ·(k\nabla h$) = Q) in the loss function, and they harmonize data-driven and physical constraints through a dual-loss equilibrium mechanism (${\lambda }_{\mathrm{data}}\mathrm{and}{\lambda }_{\mathrm{phy}}$).
  Revolutionary in seepage field applications

  Table 5. Comparison of Deep Learning models in physics applications.

  Model	Structural Implication	Data Dependency	Physics Integration
  FFN	Black-box function approximator	High	None
  CNN	Spatial feature extractor	Medium	Convolution-based scheme
  GNN	Relationship expansion analyzer	Low	Graph structure encoding physics linkage
  PINNs	Physics equation solver	Very low	Loss function physics constraint

  :
  (i) “Equations as constraints”: Reconstructing full-field variables from partial boundary conditions without complete observations (e.g., Raissi et al. [5], inverting pressure distributions from flow velocity fields); (ii) Small sample size: In data-scarce scenarios (e.g., exploration of new blocks), physical approximation significantly improves generalization (e.g., Xue et al. [2], 40% error reduction at 10% sample size).

3.4.2. Capacity Boundary Matrix

• Capacity to deal with spatial and temporal dependencies:
  The ability of Deep Learning models to process spatio–temporal data directly determines their applicability in seepage field prediction. FeedForward Neural (FFN) networks, as an infrastructure, only process independent sample points through a fully connected layer and lack explicit modeling of spatial correlations or temporal evolution (Hussen et al. [10]). For example, in single-well pressure prediction, although FFN networks can capture wellbore dynamics, they cannot reconstruct the pressure gradient between wells, resulting in distorted global field predictions. In contrast, Convolutional Neural Networks (CNNs) extract local spatial features by sliding convolutional kernels, which are naturally adapted to gridded data. Guo et al. [3] successfully reconstructed a 3D saturation field of a complex fracture-block reservoir using 3D CNNs, which was critically dependent on the spatial perception mechanism of the convolutional kernel to identify hyper-permeable channels and hypo-permeable barriers. Graph Neural Networks (GNNs) further break through the Euclidean spatial limitation by abstracting the fracture network as a topology of nodes and edges, which simulates the flow path of fluid in an unstructured medium through message passing (Fu et al. [16]). Physical Information Neural Networks (PINNs), on the other hand, directly characterize the spatio–temporal continuous evolution of field variables by embedding the governing equations, e.g., Raissi et al. [5] inverted the full-field pressure distribution based on partial flow rate observations only.
• Physical constraint embedding capability:
  The incorporation of physical laws is the key to improving the reasonableness of model predictions. FeedForward Neural (FFN) networks, as purely data-driven models, rely solely on the statistical laws of the training data and are prone to produce results that violate mass conservation or Darcy’s law (e.g., negative pressure prediction). Convolutional Neural Networks (CNNs) can be partially embedded with physical laws beforehand by customized convolution kernels, such as the Physical Difference Convolution Neural Network (PD-CNN) kernel designed by Xue et al. [2], which incorporates the residuals of Darcy’s equation in finite difference form into the convolution operation, so as to make the prediction results satisfy the conservation of mass. Graph Neural Networks (GNNs), on the other hand, encode physical connectivity relations through the natural properties of graph structures: in Fu et al.’s [16] microscopic seepage model, pore nodes are characterized by containing geometric parameters (e.g., aperture diameter, curvature), and edge weights characterize the flow impedance to implicitly satisfy Darcy–Weisbach equations. Physical Information Neural Networks (PINNs) are “hard” physically driven by directly constraining the residuals of the control equations through loss functions. For example, Xue et al. [2] forced the partial differential equations for single-phase seepage during training, allowing the model to remain physically consistent (violation rate < 5%) with only 10% of the observed data.
• Small sample generalization capability:
  Data scarcity is a common challenge in oilfield development, and the small-sample fitness of different models varies significantly. FeedForward Neural (FFN) networks require more than 10,000 sets of samples to avoid overfitting due to the large number of parameters and lack of inductive bias (Hussen et al. [10]). Convolutional Neural Networks (CNNs) reduce the number of parameters through local weight sharing, but they still require at least 5000 labeled images to capture spatial patterns (Guo et al. [3]). Graph Neural Networks (GNNs) benefit from the ability to generalize topology and require only 1000 sets of graph structure samples to model fracture network flows (Fu et al. [16]). Physical Information Neural Networks (PINNs) can achieve field predictions with an error of <10% with 500 samples (Xue et al. [2]) through the regularization of the physics equations, and they are particularly suitable for scenarios where new blocks are being explored or where experimental data are limited

  Table 6. Comparison of representative model applications (partial data).

  Model Type	Study Example	MSE (Pressure Field)	Physics Violation Rate	Training Time (h)	Data Requirement
  FFN	Hussen et al. [10]	0.32	28%	2.1	High
  CNN	Guo et al. [3]	0.18	15%	5.3	Medium
  GNN	Fu et al. [16]	0.12	8%	8.7	Low
  PINNs	Xue et al. [2]	0.09	<5%	12.5	Very Low

  .
• Computational efficiency:
  The efficiency of model computation has a direct impact on engineering utility. FeedForward Neural (FFN) networks are suitable for real-time monitoring tasks due to their simple and highly parallelized structure, which can be trained on NVIDIA V100 GPUs in 2.1 h (Hussen et al. [10]). The 3D convolutional operation of Convolutional Neural Networks (CNNs) increases the computational effort but can still be trained in 5.3 h with CUDA optimization (Guo et al. [3]). Graph Neural Networks (GNNs) take up to 8.7 h to train due to the irregular data access pattern of the graph structure (Fu et al. [16]), and they need to be accelerated by specialized graph computing libraries (e.g., DGL). Physical Information Neural Networks (PINNs) take up to 12.5 h (Xue et al. [2]) to train due to the need to compute higher-order derivatives (e.g., the second-order gradient of the pressure field) at high frequencies, and they usually require distributed training or mixed-accuracy optimization.
• Typical application scenarios

  Table 7. Typical application of Deep Learning models.

  Model Type	Typical Application
  FFN	Single-point parameter prediction (Wellhead Pressure/WC)
  CNN	2D permeability field reconstruction
  GNN	Simulation of multiphase flow in fractured reservoirs
  PINNs	Inversion of PDE with continuous field reconstruction

  :
  FFN networks: Scenarios: single well water content prediction (Hussen et al. [10]); core porosity regression (Hong et al. [20]).
  Advantage: simple and efficient, suitable for low-dimensional mapping tasks.
  CNNs: Scenarios: 2D permeability field reconstruction

  Table 8. Comparison of Deep Learning models in permeability field prediction.

  Model Type	Spatio–Temporal Processing	Physics Constraint	Small Sample Generalization	Computational Efficiency
  FFN	×	×	×	★★★★
  CNN	Spatial locality	Δ (custom kernel)	×	★★★
  GNN	Unstructured relationships	✓	✓	★★
  PINNs	Spatio–temporal continuity	✓✓✓	✓	★

  Description of symbols: ✓: native support; Δ: needs to be customized to achieve; ×: unsupported; ★: calculation of efficiency levels.

  (Guo et al. [3]); digital core two-phase flow simulation (Telvari et al. [23]).
  Strengths: spatial pattern extraction; adaptation to pictorial data.
  GNNs: Scenarios: fracture network flow simulation (Fu et al. [16]); well network connectivity optimization (Raissi et al. [29]).
  Strengths: unstructured topology modeling; multi-scale coupling.
  PINNs: Scenarios: control equation inversion (Raissi et al. [5]); small sample pressure field prediction (Xue et al. [2]).
  Strengths: physical consistency guarantees; few-sample generalization.

3.4.3. Model Selection Decision Tree

This decision tree aims to select the optimal Deep Learning model for the seepage field prediction task based on specific task requirements and data characteristics. The following is a detailed description of the logic of each node:

• Initial judgment: are there enough data?
  Sufficient data (yes): Enter real-time requirements analysis for scenarios with well-developed historical databases or rich experimental data (e.g., long-term monitoring data from mature oil fields).
  Insufficient data (No): Enter data structure analysis, applicable to the early stage of exploration or scenarios with high experimental costs (e.g., small amount of logging data in new areas of unconventional reservoirs).
• Data-sufficient branching: is high real time required?
  Need high real-time performance (yes): Choose FFN (FeedForward Neural) network or CNN (Convolutional Neural Network)
  Applicable Scenario:
  Real-time monitoring of production parameters in a single well (FFN: Hussen et al. [5])
  Dynamic visualization of injection response (CNN: Wang et al. [15])
  Technical Advantage: An FFN/CNN has a simple structure and high computational efficiency, can complete the prediction in seconds, and is adapted to the deployment of edge devices.
  No need for high real time (No): Access to field continuity judgment; suitable for medium-to-long-term development scenario optimization or research-level simulation tasks.
• Field continuity judgment: is the predicted target a spatio–temporally continuous field? Field continuity (Yes): Select PINNs (Physically Informed Neural Networks)
  Applicable Scenario:
  Dynamic evolution of pressure field (Xue et al. [2])
  Coupled multi-phase flow simulation (Yan et al. [21])
  Technical Advantage: PINNs guarantee physical consistency by embedding control equations (e.g., Darcy’s law) and are suitable for mathematical modeling of continuous fields.
  Field discontinuity (no): Selection of GNN (Graph Neural Network)
  Applicable scenarios:
  Fracture network flow path identification (Fu et al. [16])
  Unstructured grid seepage analysis (Chen et al. [59])
  Technical Advantage: GNNs are naturally adapted to discrete and non-homogeneous scenarios through topological relationship modeling.
• Insufficient data branching: is the structure non-Euclidean? Structure is non-Euclidean (yes): Select GNN (Graph Neural Network)
  Applicable Scenario:
  Digital core pore-level flow simulation (Chen et al. [4])
  Modeling of inter-well interference relations (Zhang et al. [18])
  Technical advantage: GNNs utilize graph structure to encode complex connectivity relationships and maintain high generalization ability with few samples.
  Structure Euclidean (No): Selection of PINNs (Physically Informed Neural Networks)
  Applicable Scenarios:
  Small sample pressure field inversion (Raissi et al. [5])
  Permeability estimation based on sparse observations (Xue et al. [2])
  Technical advantage: PINNs significantly reduce the dependence on data volume by regularizing the physics equations.

Technology selection recommendations: Real-time monitoring scenarios: prioritize FFN/CNN (e.g., real-time analysis of wellhead sensor data)

Research-level simulation: Priority to PINNs/GNN (e.g., complex mechanism model validation)

Hybrid architecture:

Production systems: FFNs (real time) + PINNs (offline optimization)

Cross-scale modeling: CNN (macrofields) + GNN (microstructures)

With this decision tree Figure 5, users can quickly locate the adapted model, balance accuracy, efficiency, and data constraints, and provide a landable technology selection solution for seepage field prediction.

4. Future Directions for Technology

With the continuous evolution of Deep Learning technology and the rapid improvement of digitalization in the oil and gas industry, Deep Neural Network-based reservoir modeling methods have become increasingly prominent in seepage response prediction, and they have demonstrated better modeling accuracy and nonlinear fitting ability than traditional methods under a variety of complex working conditions, such as unconventional hydrocarbons, reservoirs with high-water-bearing periods, and fractured-block reservoirs [60]. However, current intelligent seepage-prediction techniques still face many challenges in feature engineering automation, model physical consistency, multi-scale coupled modeling, and model interpretability [28]. Combining the systematic research and cutting-edge literature review in this review, it can be summarized that the future development direction of Deep Learning applied to seepage field prediction technology mainly includes the following aspects.

4.1. Real-Time Prediction and Closed-Loop Optimization Control

The dynamic evolution of production capacity in high-water-bearing-period reservoirs is the result of the joint action of geological conditions, engineering intervention, and real-time regulation [61]. In terms of the causal mechanism, the influencing factors can be divided into two categories: one is static geological factors (such as reservoir non-homogeneity, original fluid distribution) and the other is dynamic human intervention factors (including injection and extraction system adjustments, frequency of well network perturbation, and production parameter changes, etc.) [62]. Currently, oilfield development has shifted from static scheme design to dynamic closed-loop optimization, and there is an urgent need to establish a prediction model that can couple real-time monitoring data (e.g., fluid production, WC fluctuation, injection and recovery response curves) with numerical simulation to support the precise regulation of seepage and flow field [25].

The limitations of the existing studies are centered on the lack of data dynamics: traditional Deep Learning models are mostly trained based on static historical data (e.g., Telvari et al. [23]), and they lack the ability to learn real-time data streams online, leading to a significant disconnect between the prediction results and the dynamic regulation needs in the field. To break through this bottleneck, this study inherited and developed the theoretical system of multi-sample pool construction:

• Data level: Based on the Dynamic Sample Pool (DSP) architecture proposed by Telvari et al. [23], feature extraction and prioritization of high-frequency monitoring data streams are realized through the sliding time window mechanism. The migration learning framework developed by Wang et al. [15] is further integrated to construct an incremental sample pool updating strategy to solve the cold-start and small-sample learning problems [25].
• Algorithmic level: The sample space expansion method proposed by Mouketou et al. [54] in Generative Adversarial Networks (GANs) is introduced to compensate for the missing data segments in the process of injection and mining adjustment through the generative adversarial mechanism, and, at the same time, coupling the production optimization algorithms (e.g., gradient descent method, reinforcement learning) with the feedback control theory, to establish a quantitative response function for the adjustment of injection and mining parameters [50].
• System level: Drawing on the closed-loop optimization paradigm of Chen et al. [4], the above method is embedded into the control chain of “monitoring-prediction-decision-execution”, and the parameters of the seepage prediction model are dynamically corrected through the real-time WC feedback (error tolerance < 5%), forming an adaptive optimization mechanism [4].

Compared with the existing research, this method realizes breakthroughs in three aspects:

• Inheriting the real-time data capture capability of DSP architecture, and solving the generalization problem of cross-reservoir samples through migration learning.
• Integrating the adversarial generation mechanism to effectively mitigate model oscillations caused by sudden changes in injection and recovery parameters.
• Constructing a feedback control module with physical constraints to ensure that the optimization results comply with the seepage mechanics.

This technical route not only solves the synergy problem between dynamic data and offline model but also provides methodological support for the implementation of a “digital twin—real-time optimization” system in the construction of intelligent oilfields through the organic integration of academic theoretical systems.

4.2. Multi-Source Data Fusion and Enhanced Expressive Power

Reservoir seepage response prediction relies on a wide range of data sources, covering geological modeling data (e.g., lithology, porosity, permeability), engineering development data (e.g., injection and extraction intensity, well network layout), and dynamic monitoring data (e.g., pressure, WC, and daily fluid production), and it often presents heterogeneous characteristics across scales, modes, and time periods [30]. In reservoirs with extra-high WCPs, there are often problems such as format inconsistency, different acquisition frequencies, and missing spatial locations among the data, which seriously constrain the training quality and generalization ability of Deep Learning models [31]. In the current research, although multimodal fusion modeling was initially explored, most of the models still remained at the level of “data side-by-side input”, failing to deeply explore the correlation structure and weighting mechanism between different data. Therefore, future research should strengthen structural alignment, semantic complementation, and spatial–temporal matching at the data fusion level, explore algorithmic mechanisms such as graph structural fusion and cross-modal alignment [32], and introduce domain knowledge-driven noise perturbation, simulation sample generation, counterfactual sample construction, and other strategies at the data enhancement level, so as to improve sample diversity and generalization ability and, thus, further improve the adaptability and stability of the Deep Learning model [33].

4.3. Physical Consistency Modeling and Interpretability Enhancement

Although Deep Learning has demonstrated excellent fitting and generalization capabilities in reservoir seepage prediction, it is essentially a “black box model” with poor interpretability, and it is difficult to validate the results, especially in seepage systems with complex physical mechanisms and high nonlinear coupling, where the reasonableness of the model prediction and the engineering usability of the model are often questioned [34]. In order to enhance the interpretability and credibility of the model, researchers such as Raissi M have gradually tried to integrate physical knowledge, a priori experience, and neural network structure and to explicitly guide the model learning process through the mechanism of “physical constraints”, so as to realize the unity of data-driven and physical laws.

Xue et al. [2] proposed a physics-regularized DNN (PINN), in which the residuals of seepage control equations are embedded as a loss function term in the training process, to achieve physically consistent modeling for pressure field prediction in reservoirs with high WC [2]. Yan et al. [21] further constructed Physics-Informed Neural Networks (PINNs) for multiphase seepage flow. Physics-Informed Neural Networks (PINNs) can reconstruct a high-dimensional continuous saturation field under incomplete boundary conditions and data scarcity conditions [20]. Wang et al. [15], on the other hand, adopted a joint data-physics-driven DNN framework and explicitly introduced coupled control variables into the model structure, which improved the controllability and interpretability of the complex response process in the reservoir [15].

In addition, in order to improve the observability of the internal structure of neural networks, some studies in recent years have introduced techniques such as the attention mechanism, feature attribution methods, and local response visualization to analyze the decision logic of the network and preliminarily reveal the influencing factors and physical motives behind the prediction results [34]. Although the relevant research is still in the exploratory stage, the combination of physical–data fusion modeling and interpretable AI techniques provides an important path to enhancing the engineering credibility and the value of Deep Learning models for generalized applications [62]. It will be necessary to carry out more in-depth research in the form of physical constraints, multivariate constraint synergy mechanism, and visualization and diagnostic tools.

4.4. Model Migration Capabilities and Online Adaptive Updates

After the reservoir development enters the high WCP, the formation seepage state, well network interference relationship, and development regime are often in the process of dynamic evolution, which makes the seepage prediction model face the double challenges of “input distribution drift” and “scenario migration failure” [5]. Although migration learning provides a fast modeling path for predicting the response of new blocks or wells, in the case of significant structural differences between old and new blocks, different well network densities, or inconsistent development regimes, it is often difficult for the model to effectively extract the migration features, resulting in a significant degradation of the prediction performance [35]. In order to enhance the scenario adaptation ability of Deep Learning models, studies have begun to explore the application of incremental learning, online learning, and adaptive training mechanisms in reservoir seepage modeling [23]. In the future, a feedback-based online weight updating mechanism could be further introduced to quickly adjust local parameters to adapt to new scene data distribution without retraining the whole network [63]. In addition, strengthening the structured analysis of reservoir data and extracting generalizable feature representations with the dual significance of geology and engineering are also one of the key paths to improving the adaptability of the model [64]. The construction of deep models with certain regional transferability and cross-scenario robustness will be the core direction of reservoir intelligent seepage modeling towards generalization and platformization [65,66,67].

5. Conclusions

(1)

Paradigm shift in seepage-prediction technology: The evolution of reservoir seepage prediction has undergone three distinct phases: from physics-based analytical models to data-driven Machine Learning approaches, culminating in the current paradigm of physics-informed Deep Learning systems. This progression reflects the oil industry’s growing demand for intelligent solutions to address the complex nonlinear dynamics of high-water cut reservoirs. Deep Learning architectures (CNNs, GNNs, PINNs) demonstrate superior capability in modeling multiphase flow heterogeneities compared to traditional numerical simulations (FDM/FVM), achieving >85% accuracy in saturation field reconstruction under low well-control conditions [3,15]. The integration of Deep Learning mechanisms with governing equations (e.g., Darcy’s law, mass conservation) enables these models to maintain physical consistency while capturing complex spatial–temporal patterns.

(2)

Current implementation landscape: Practical implementations reveal distinct architectural advantages: • CNN-based models achieve 92.4% accuracy in inter-well pressure gradient prediction through 3D convolutional feature extraction [2]; • PINN frameworks reduce pressure field inversion errors to <8% under sparse data conditions (n = 500 samples) [5]; • GNN solutions enable fracture network flow simulations with 15% faster convergence than conventional discrete fracture models [16]. Case studies in Daqing and Shengli oilfields demonstrated 20–35% improvement in remaining oil recovery rates through Deep Learning-driven injection optimization [4,25].

(3)

Strategic development pathways: Four critical frontiers emerge for next-generation intelligent systems:

• Real-time closed-loop control: Integrating edge-computing optimized CNNs (inference time < 50 ms) with IoT sensor networks enables dynamic waterflood adjustment. The DSP-XGBoost framework achieved 92.7% real-time decision accuracy in pilot tests [25].
• Multimodal data fusion: Transformer-based architectures incorporating seismic attributes, production logs, and core CT images improve heterogeneity characterization accuracy by 40% compared to single-modality models [30].
• Physics-guided explainability: Hybrid PINN architectures embedding modified black-oil equations reduce unphysical predictions by 78%, while attention mechanisms provide quantifiable feature importance metrics [2,34].
• Cross-domain adaptability: Meta-learning enhanced models maintain >80% prediction accuracy when transferred between carbonate and sandstone reservoirs, significantly reducing recalibration costs [35].

Technological impact: The convergence of differentiable programming and reservoir digital twins is reshaping development strategies—early adopters report 18–25% reductions in water injection costs and 30%-shorter simulation cycles. Future research should prioritize human–AI collaboration frameworks to bridge the gap between data scientists and reservoir engineers [68,69].