Intelligent Dimension Annotation in Engineering Drawings: A Case-Based Reasoning and MKD-ICP Algorithm Approach

Abstract

To address the demands for accuracy and completeness in engineering drawing dimension annotation, this paper presents an intelligent dimensioning method that integrates Case-Based Reasoning (CBR), K-Dimensional Tree (KD-Tree), and an enhanced Iterative Closest Point (ICP) algorithm. The proposed approach leverages a historical case database to extract key features from similar cases, providing high-quality initial references for the ICP algorithm. By combining KD-Tree’s efficient spatial search capabilities with ICP’s precise point cloud alignment, the method achieves both efficient mapping and accurate alignment of dimension information. Applied to creating engineering drawings of refrigerated van design as a case study, the results demonstrate that this method significantly enhances the efficiency and precision of dimension annotation, minimizes manual intervention and error rates, and showcases broad application potential in complex engineering design scenarios. The contributions include an innovative intelligent dimensioning method, the MKD-ICP algorithm for dimension mapping and alignment, and empirical validation of the approach’s effectiveness.

1. Introduction

Engineering drawings are essential technical documents in the design and manufacturing processes of mechanical products. Dimensions and technical requirements play a vital role in standardizing manufacturing operations and ensuring consistent product quality. Although modern 3D CAD software (SolidWorks2020) can automatically generate 2D projection views with dimensions after model creation, the accuracy of these dimensions is often insufficient [1]. As a result, designers must manually verify and adjust the dimensions to achieve completeness. Furthermore, for the same 3D model, different designers may adopt varying dimensioning approaches, leading to significant inconsistencies in the standardization and quality of engineering drawings, largely depending on their expertise and technical proficiency [2].

Research on automatic dimensioning for engineering drawings not only supports intelligent design processes and improves design efficiency but also helps standardize dimensioning workflows, thereby enhancing the quality of finalized drawings. As a critical medium for conveying information, dimensions have long been a central focus and a major challenge in this field. To advance the automation and intelligence of dimensioning, researchers worldwide have conducted extensive studies, making notable progress in improving the efficiency and accuracy of dimension completeness verification [3].

For instance, Liu Xiaojun and Bei Chaowang [4,5] provided a comprehensive overview of the current state of dimensioning research, emphasizing its significance in engineering applications. Liu Jinfeng et al. [6] proposed a rapid dimensioning method for intelligent 3D process design based on a “feature-dimension-removal body” constraint mechanism. In the area of feature modeling, Li Yan et al. [7] developed an automated technology for efficient and standardized dimension annotation generation based on predefined rules. By organizing installation dimension annotation rules for various iron fittings, they designed a solution capable of automatically recognizing annotation objects and generating dimension annotations using a backend configuration table. Xu Jinglin et al. [8], adhering to the GB/T 24734.1~11-2009 standards (GB/T 24734; General Rules for Defining Data of Digital Products. Publisher: Beijing, China, 2009) explored rapid dimensioning techniques for 3D designs. Wang Bo et al. [9] proposed an automatic dimensioning algorithm for shaft components based on functional characteristics, employing graph theory to eliminate redundant dimensions. In the field of 2D dimensioning, Sun Xiaofei et al. [10] leveraged the SolidWorks API (SolidWorks2020) to investigate batch generation and automatic dimensioning of engineering drawings. Sun et al. [11] further redefined graphic output primitive features, built a case library, and studied automatic dimensioning techniques for 2D designs. Similarly, Li et al. [12] proposed a line-chain feature-based automatic dimensioning algorithm for 2D engineering drawings, further exploring the relationship between 3D model features and 2D drawing elements.

In recent years, state-of-the-art dimensioning techniques have increasingly leveraged artificial intelligence approaches such as deep learning and support vector machines (SVMs). For instance, CNN-based models have demonstrated promising results in interpreting complex geometric features and automatically generating annotations. SVMs and other classical machine learning techniques have also been applied to identify relevant dimensions based on training data. Additionally, rule-based heuristics remain widely used in industry due to their interpretability and reliance on domain knowledge. However, these methods often face challenges related to generalizability, data dependency, or rule maintenance. In contrast, the proposed MKD-ICP algorithm integrates geometric matching and case-based reasoning, requiring minimal training data while maintaining adaptability to varying model types and annotation requirements. This makes it a more practical and scalable solution in engineering scenarios where annotated datasets may be scarce or where domain knowledge is difficult to formalize into strict rules.

In summary, despite the extensive research conducted by numerous scholars on dimensioning, significant limitations still exist. Current dimensioning methods often lack adaptability when applied to engineering drawings of varying sizes and resolutions, leading to reduced accuracy. This issue becomes particularly pronounced when dealing with complex engineering drawings or freeform surfaces, where traditional dimensioning techniques may fall short of meeting high-precision requirements, resulting in errors or omissions in the annotations.

The specific research problem addressed in this work is how to effectively match and assign dimensions across multi-scale engineering drawings to achieve high precision and standardization in automatic dimensioning processes.

Based on the existing challenges in automatic dimensioning, this study proposes the following research hypothesis: by integrating case-based reasoning (CBR) with the MKD-ICP algorithm, the accuracy and adaptability of dimensioning for engineering drawings of various scales and resolutions can be significantly improved. This hypothesis guides the development of the proposed method and the subsequent validation experiments conducted in this study.

The contributions of this study are as follows:

• We propose an innovative intelligent method for engineering drawing dimensioning, based on Case-Based Reasoning (CBR), K-Dimensional Tree (KD-Tree), and the improved Iterative Closest Point (ICP) algorithm.
• We propose a new method, the MKD-ICP algorithm, by combining the spatial search capability of KD-Tree with the point cloud matching technology of ICP, enabling the mapping and alignment of dimension information.
• We conducted an empirical study using a refrigerated van as a case, and the experimental results show that the proposed method significantly reduces human intervention and errors, accurately achieving automatic dimensioning of engineering drawings.

The structure of this paper is arranged as follows: Section 2 introduces research related to the automatic generation of dimensions in engineering drawings and the application of the ICP algorithm in engineering; Section 3 provides a detailed explanation of the dimension semantic analysis of engineering drawings and the use of Case-Based Reasoning (CBR) and the MKD-ICP algorithm for dimension information acquisition and mapping; Section 4 discusses the automatic dimensioning efficiency, accuracy, and results of the method; finally, Section 5 concludes this study and outlines plans for future research.

2. Related Works

2.1. Automatic Dimensioning of Engineering Drawings

The challenge of automatic dimensioning in engineering drawings has been extensively studied since the late 1980s. American scholar Dov Dori [13] was one of the pioneers in this field, categorizing the problem into two key aspects: logical judgment for dimension selection and spatial layout optimization. The former ensures the completeness and accuracy necessary to describe the geometric information of 3D models, while the latter focuses on achieving a clear, aesthetically pleasing layout that avoids dimension overlap and promotes organized distribution. Over the years, researchers worldwide have conducted in-depth investigations into these two interrelated aspects, aiming to develop effective solutions for automatic dimension generation and layout optimization.

M.M.F. Yuen et al. [14] introduced an automatic dimensioning method for part drawings based on CSG models. By classifying dimensions and analyzing part geometry, they extracted relationships between face loops to generate the necessary dimensions. Similarly, Suznki [15] proposed a product-model-based dimensioning method, emphasizing a geometry-constraint-centered framework for consistent representation and management throughout product design and manufacturing. Bond A.H. and Ahmed S.Z. [16] developed a knowledge-based 3D automatic dimensioning system that combined dimension generation with layout optimization via predefined rules.

K-Z Chen et al. [17,18] devised an algorithm to automatically generate 2D mechanical part drawings from 3D models. Their approach leveraged feature recognition to identify part characteristics, using an expert system to annotate dimensions on planes and cylindrical surfaces. They further refined their method with a prioritization strategy to eliminate redundancies and strategically place critical positioning dimensions, enhancing the system’s intelligence.

Yalong Cheng and Zhonghua Ni [19] tackled 3D dimension completeness detection by transforming it into a geometric element constraint problem. They introduced an intermediate model of transient geometric elements to capture constraint relationships. Li C.L. and Lee Y.H. [20] optimized baseline dimension placement for plastic injection mold drawings through dynamic programming techniques.

An Heng and Yan Guangrong et al. [21], leveraging GB/T 24734 standards (GB/T 24734; General Rules for Defining Data of Digital Products. Publisher: Beijing, China, 2009) and feature simplification methods, demonstrated automatic dimensioning feasibility on the CAXA platform. Hou Bo and Guo Jinyu [22] developed UG software (UG12) modules for automatic dimensioning of bent pipes and sheet metal parts, enabling direct production application.

Liu Junqiang and Wang Jianfei [23] explored intelligent dimensioning for simple parts using voxel and constraint theories but noted that machining considerations were insufficient. Zheng Guolei et al. [24] optimized the dimensioning order for shaft parts through weight-based algorithms, enhancing efficiency and reducing manual adjustments.

Guo Jianye [25] focused on dimensioning array features using point cloud matching to identify relationships and automate dimensioning.

2.2. Layout of Dimensions in Engineering Drawings

The proper arrangement of dimensions is a critical focus in research on automatic dimensioning, as it directly impacts the clarity and readability of annotations. A well-designed dimension layout allows engineering professionals to quickly and accurately interpret the information, thereby significantly improving overall work efficiency [26].

Yuan Bo et al. [27] employed a combination of sub-dimension set partitioning and the simulated annealing algorithm to achieve automatic horizontal and vertical dimension layouts in engineering drawings, successfully integrating this approach into a self-developed 3D CAD system. Huang Xueliang et al. [28] introduced a grid-based partitioning method, transforming the annotation layout problem in 2D engineering drawings into a search for sub-matrices satisfying specific conditions within a state matrix, thereby enhancing layout quality and efficiency in commercial CAD systems. Similarly, Tian Jingcheng et al. [29] addressed layout challenges in steel structure node drawings by proposing a region-based partitioning method for annotatable areas. Wang Tao and Mo Rong et al. [30] developed a dimension subset partitioning and incremental annotation strategy to automate horizontal and vertical dimension layouts in 2D projections of 3D models.

Xie Ping [31] focused on linear dimensions and analyzed inclusion relationships among dimensions, establishing dynamic connections to enable automatic layout adjustments when dimensions are added or removed. Zhang Shuyou and Ji Yangjian et al. [32] proposed the concepts of annotatable domains and interference pairs, converting dimension interference issues into state vector transformations. This approach adaptively resolved non-associated dimension adjustments through state transition strategies. Lu Zhiyuan and Yang Jianxin et al. [33] tackled dimension overlap and interference problems by formulating an optimization model for layout arrangement.

Chen Le et al. [34] designed a method to record and adjust dimension positions after model updates, ensuring automatic optimization for both external and internal layouts. Ouyang Shijia et al. [35] proposed a layout algorithm to resolve linear dimension interference in 2D drawings derived from 3D parametric models. Li Xuemei and Hou Boqi et al. [36] utilized a constraint-based adjustment method, creating a rule library and adjustment strategies to address unreasonable dimension placements relative to models. Liu Fuyun et al. [37] introduced an interference detection method based on vector products, converting dimension lines into vector segments and leveraging vector calculations to detect and resolve conflicts in horizontal, vertical, radial, and other nonlinear dimensions.

In summary, most studies on dimension layout have focused on 2D engineering drawings, often targeting specific dimension types (e.g., horizontal or vertical) or part-specific applications. However, the layout of 3D dimensions introduces greater complexity, requiring algorithms to address interference not only within the same annotation plane but also across multiple planes. This added spatial dimension presents unique challenges to achieving efficient and interference-free dimension layouts.

2.3. Dimension Completeness and Redundancy Checks

Completeness and redundancy checks of annotated dimensions are essential in the design and manufacturing of mechanical products, ensuring no missing or redundant dimensions in the part model. As the part model complexity grows, manual checks become increasingly challenging. Intelligent technologies offer significant potential to improve the efficiency and accuracy of these checks.

He Jianying et al. [38] used the “subtraction method” to identify redundant dimensional constraints in single-view drawings. Liu Cantao et al. [39] introduced a directed graph-based algorithm for dimension completeness checks, using adjacency matrices to detect redundant annotations in dimension chains. Shang Wenli [40] optimized redundancy detection by combining the subtraction method with directed graph theory, while Liu Ming [26] transitioned to undirected graphs for redundancy analysis through duplicate node detection in adjacency matrices.

Tan Z. [41] proposed a spatial coordinate transformation model and virtual dimension decomposition, supported by a depth-first search algorithm, for completeness checks in multi-view and 3D annotations. Yan Zhe et al. [42] introduced equivalent dimension sets to streamline checks for complex 3D models and enhance redundancy detection.

In 3D MBD (Model-Based Definition) applications, Zhang Shengwen et al. [43] combined dimension chain analysis with completeness checks to address structural complexity. Luo Lei et al. [44] mapped parametric modeling relationships to engineering dimensions, employing Newton’s iteration for simplified completeness analysis.

Further innovations include those by Fu Chaofan et al. [45], who used geometric feature constraint models and set constraint propagation to identify redundant and missing annotations, and Kang Jie et al. [46] who employed fuzzy clustering to enforce structural constraints while checking annotation completeness. Xiaojun Liu et al. [11] utilized spatial transformation models and trajectory analysis, respectively, to achieve intelligent, automated checks for 2D and 3D models. Stefenon et al. [47] proposed a hybrid methodology combining deep learning, clustering, computer vision, and rule-based techniques to address the digitalization of legacy railway interlocking system drawings. Their approach demonstrated robustness in handling noisy, low-quality engineering diagrams by integrating symbol recognition, probabilistic Hough transform for line detection, and graph-based structural representation. Ou et al. [48] proposed an automatic recognition system for digitizing handwritten tabular documents in nuclear power plants. Their approach integrates traditional image processing with neural network methods to denoise scanned documents, extract relevant sections, and apply handwriting recognition to obtain textual and numerical data. The study focuses on detecting tables and cells within scanned handwritten documents, demonstrating high accuracy and practicality in real-world case studies.

In summary, while advancements in dimension completeness checks have significantly improved efficiency and accuracy, addressing algorithmic efficiency and adapting to the increasing structural complexity of parts remain critical research directions.

3. Methods

3.1. The Proposed Method

Compared to traditional ICP algorithms and existing hybrid methods, the proposed MKD-ICP algorithm introduces several key innovations. First, by incorporating a multi-level KD-Tree structure, it enhances the efficiency and accuracy of matching complex product models, particularly when dealing with large-scale and high-dimensional datasets. Second, the MKD-ICP algorithm integrates case-based reasoning (CBR) principles to intelligently guide the initial alignment process, thereby improving convergence speed and reducing the risk of falling into local optima. Unlike previous approaches that treat model matching and dimension extraction as independent processes, the MKD-ICP method tightly couples them into a unified workflow, which significantly improves the adaptability to models with varying complexity and dimensional requirements. These innovations collectively advance the automation and precision of engineering drawing generation, addressing the key limitations of traditional ICP-based methods.

To ensure the accuracy of dimensioning and the standardization of completeness checks in engineering drawings, this paper proposes an intelligent dimensioning method based on Case-Based Reasoning (CBR) and the MKD-ICP algorithm. The overall framework of the proposed method is illustrated in Figure 1. By leveraging CBR technology as the core and integrating the MKD-ICP algorithm, the method achieves a precise and efficient dimensioning process.

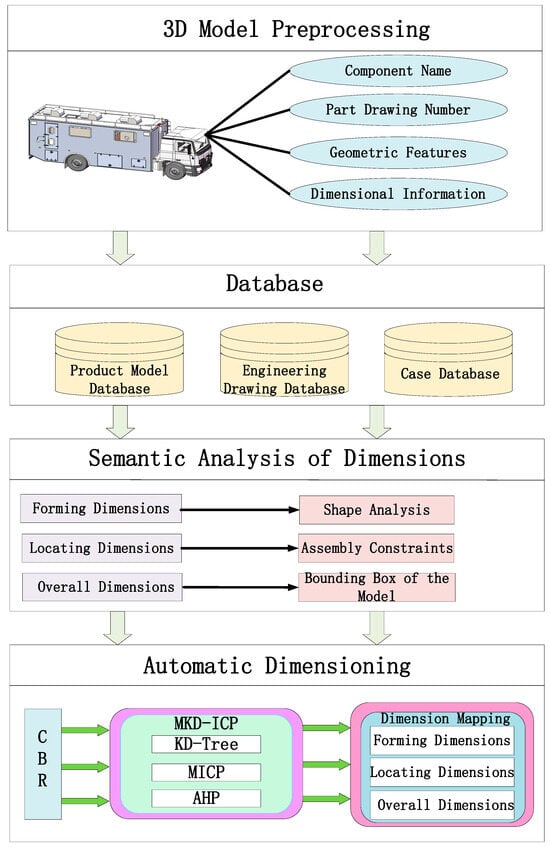
Figure 1. The overall framework for automatic dimensioning in engineering drawings.

First, the CBR technology is utilized to construct a case library containing historical drawings, documenting geometric features and dimensioning information across various engineering drawings. When a new drawing requires dimensioning, the CBR system retrieves similar cases from the library by calculating similarities between drawings based on Euclidean distance and angular similarity. The most similar historical cases are selected, providing not only rich dimensioning references but also initial annotation positions and key feature information for the subsequent MKD-ICP algorithm, significantly improving dimensioning accuracy and efficiency.

After the CBR system recommends similar cases, the MKD-ICP algorithm leverages this reference information to perform precise dimension mapping and alignment. By using KD-Tree for efficient spatial data queries and integrating the ICP algorithm to extract key component dimensions, the algorithm completes the dimension mapping and alignment process [49,50]. During this process, the algorithm accurately identifies critical mating dimensions and overall model dimensions, efficiently annotating them in the engineering drawing. Benefiting from the high-quality initial references provided by the CBR system, the MKD-ICP algorithm enables a more efficient and intelligent dimensioning workflow.

In summary, the proposed method combines CBR and MKD-ICP technologies in a seamless manner, ensuring both efficiency and precision in dimensioning engineering drawings while laying a solid foundation for intelligent dimensioning automation.

3.2. Dimensional Functional Semantic Analysis

In engineering drawings, dimensional information is used to describe the size, shape, and relative position of objects, serving as the foundational reference for product design and manufacturing processes [51,52,53,54]. According to functional semantics, dimensions in engineering drawings can be categorized into three types: defining dimensions, locating dimensions, and overall dimensions, as shown in Table 1:

Table 1. The functional semantics of dimensions in engineering drawings.

Dimension Functional Engineering Semantics	Function	Acquisition Method
Forming Dimensions	Determines the fundamental shape of the model	Model shape analysis
Locating Dimensions	Defines the positional relationship between basic elements	Model mating relationships
Overall Dimensions	Determines the overall size of the model	Model external bounding box

(1)

Forming Dimensions: These describe the geometric features of an object, determining its fundamental shape and ensuring that the overall appearance of the product meets design requirements.

(2)

Locating Dimensions: These specify the relative positional features of an object, typically in reference to other features or reference points. They determine the relative positions of basic entities, ensuring the precision of component assembly.

(3)

Overall Dimensions: These describe the overall shape and size of the object, representing the total dimensions of all parts combined. They define the external size boundaries of the object, ensuring that the part fits the spatial requirements of the design environment.

Dimensioning Sequence: Typically, the defining dimensions of the basic entities are annotated first, followed by the locating dimensions between entities, and finally the overall dimensions of the composite entity. Defining dimensions are derived through geometric feature analysis, locating dimensions are determined by mating relationships, and overall dimensions are obtained through the maximum bounding box of the external shape.

3.3. Case-Based Reasoning Technology

Case-Based Reasoning (CBR) [55,56] is an intelligent design method that retrieves the most optimal historical case by calculating the similarity between the target case and historical cases, and then modifies and reuses the retrieved case. The core principle is to calculate the similarity between the target case and historical case resources [57,58,59], retrieve the best historical case with the highest similarity, and make modifications based on the model of that case to achieve rapid product design. A complete CBR system consists of four cyclical processes: Retrieve, Reuse, Revise, and Retain, known as the “R4” cycle structure, as shown in Figure 2.

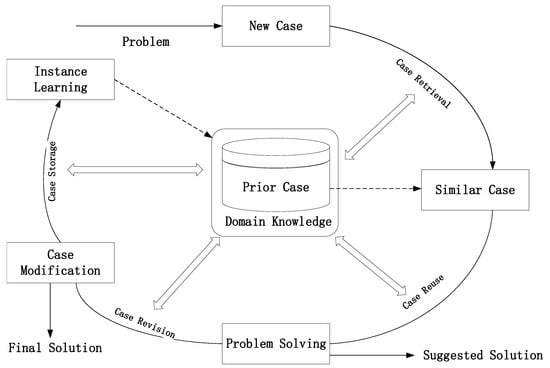
Figure 2. The diagram of the CBR cyclic structure.

In this study, Case-Based Reasoning (CBR) technology is used as a core tool for key dimensioning, enabling the selection of the most similar cases from a constructed historical case library for the target product. By extracting and analyzing the key features of historical cases, high-quality initial reference information is provided for subsequent dimension mapping.

First, a historical case library is built, containing a large number of engineering drawings and dimensioning information, and storing the dimensioning features of various typical products.

When dimensioning the target product, the retrieval module of CBR calculates the similarity between the target model’s geometric features and dimensioning requirements and selects the best matching case from the library. Then, the dimensioning information from the selected case is reused and adjusted to ensure it meets the specific needs of the target product. Additionally, the revision module of CBR further optimizes the dimensioning information, enhancing both the accuracy and completeness of the annotations. The final dimensioning results are then stored in the case library to support future designs.

3.4. The Proposed Algorithm

This subsection presents the core contribution of this manuscript, which is the integration of the Iterative Closest Point (ICP) algorithm with KD-Tree-based optimization for efficient and accurate case model matching. To improve clarity, we summarize the main steps of the proposed method as follows:

Step 1: Hierarchical model division based on structure and function.

Step 2: Construction of model parameter vector sets using geometric and physical attributes.

Step 3: ICP-based point cloud registration using KD-Tree to accelerate nearest neighbor search.

Step 4: Calculation of model similarity using a robust similarity function.

Step 5: Node weight assignment using Analytic Hierarchy Process (AHP).

Step 6: Retrieval and filtering of key components for dimensional reuse and annotation.

A visual representation of the above steps is provided in Figure 3 to enhance the understanding of the method’s flow and highlight the integration of various algorithms in each stage.

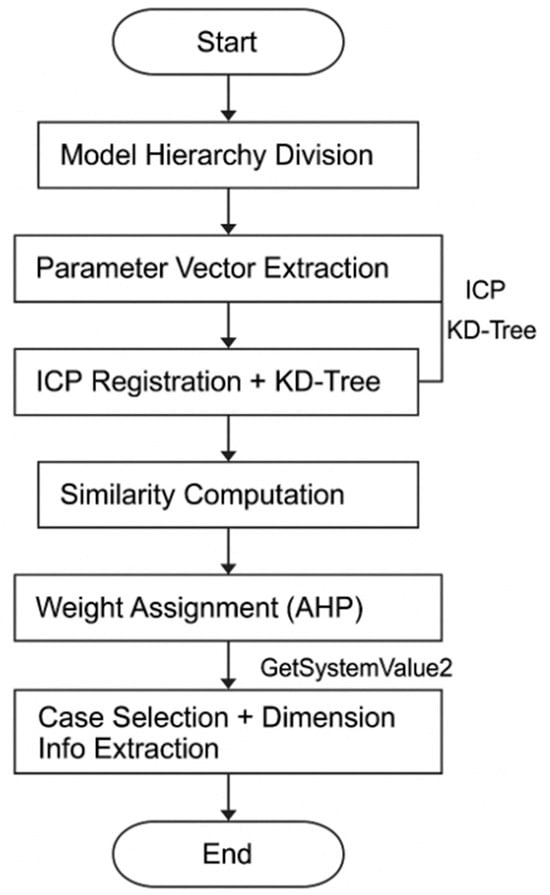
Figure 3. Workflow of the proposed method.

The Iterative Closest Point (ICP) algorithm is a classic point cloud registration method, widely used in computer vision and 3D geometric processing fields [60,61], particularly in applications such as object recognition, 3D reconstruction, and engineering drawing registration. The primary goal of ICP is to compute the optimal rigid transformation between two point clouds (source and target) through iterative optimization, minimizing the distance between them so that the source point cloud matches the target point cloud as closely as possible [62,63,64]. To improve the performance of the ICP algorithm in large data scenarios, the KD-Tree technique [65] is introduced to optimize the efficiency of nearest point search.

KD-Tree is a hierarchical binary tree data structure primarily used to store and quickly retrieve point sets in multi-dimensional space [66,67]. By partitioning and organizing spatial data, KD-Tree significantly accelerates nearest neighbor searches, particularly in high-dimensional and large-scale point cloud data, demonstrating excellent performance [68,69,70]. In the ICP algorithm, the introduction of KD-Tree can drastically reduce the time complexity of nearest point searches during each iteration, thereby accelerating the overall registration process.

By using the KD-Tree algorithm to speed up nearest neighbor searches, combined with the ICP algorithm, the model’s node entities are randomly matched with the historical case nodes for computation, and different weights are assigned to obtain the final similar case result. The specific steps are as follows:

Step 1: Hierarchical Model Division

Based on the structure, functionality, and assembly levels of the refrigerated vehicle, the model is divided into five levels: Product Layer, Module Layer, First-level Configuration Layer, Second-level Configuration Layer, and Material Layer, as shown in Figure 4. The Product Layer is used to differentiate between different case models; the Module Layer builds the overall structure; the Configuration Layers are selected based on customer customization requirements; and the Material Layer provides the raw materials required for product manufacturing. Each level is treated as a node entity to improve retrieval efficiency and accuracy.

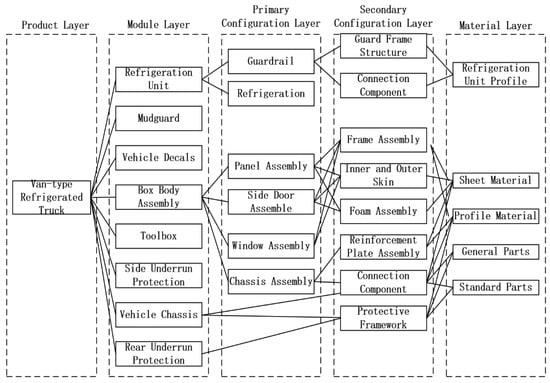
Figure 4. Van-type refrigerated truck model hierarchy division.

Step 2: Establishing the Model Parameter Vector Set

The model parameter vectors are constructed from geometric information and feature attribute parameters, which can represent the model’s characteristics. In this study, the vector set is built by extracting parameters corresponding to the child class layers from the shape parameters, volume, surface area, and moment of inertia data of the node models in each layer. This vector set is used to describe the features of the parent class layer.

First, the shape parameters D_a, D_b, and D_c (length, width, and height) of each node entity model in the x, y, and z directions are extracted and normalized.

$${SUM}_1=D_a+D_b+D_c$$

(1)

$$A_j={\displaystyle \frac{D_i}{{sum}_1}}\left(i=a,b,c,j=1,2,3\right)$$

(2)

The volume V, surface area S, and the parameters D_x, D_y, and D_z of the maximum bounding box in the x, y, and z directions are obtained and normalized, as shown in the following formulas.

$${SUM}_2=D_x\ast D_y\ast D_z$$

(3)

$$\left\{\begin{array}{c}{A}_4={\displaystyle \frac{V}{{sum}_2}}\\ A_5={\displaystyle \frac{S}{{sum}_2}}\end{array}\right.$$

(4)

The moments of inertia J_xx, J_yy, and J_zz along the x, y, and z axes are extracted, and these parameters are normalized, as shown in the following formulas.

$${SUM}_3=J_{xx}+J_{yy}+J_{zz}$$

(5)

$$\left\{\begin{array}{c}{A}_6={\displaystyle \frac{J_{xx}}{{sum}_3}}\\ A_7={\displaystyle \frac{J_{yy}}{{sum}_3}}\\ A_8={\displaystyle \frac{J_{zz}}{{sum}_3}}\end{array}\right.$$

(6)

Finally, the processed sub-level node vector data are integrated into the model parameter vector set N, which serves as the descriptor for the parent-level model. The elements of the dataset N are determined by Formula (7):

$$N=\left({\mathrm{A}}_1,{\mathrm{A}}_2,{\mathrm{A}}_3,{\mathrm{A}}_4,{\mathrm{A}}_5,{\mathrm{A}}_6,{\mathrm{A}}_7,{\mathrm{A}}_8\right)$$

(7)

Figure 5 shows the assembly model of a refrigerated van, which includes eight module sub-levels. Model parameter information is obtained through SolidWorks API functions, followed by normalization of the data to generate vectors and establish the vector set N_w to describe the body assembly model. To ensure the accuracy of similarity matching, the vector set parameters are uniformly retained up to three decimal places.

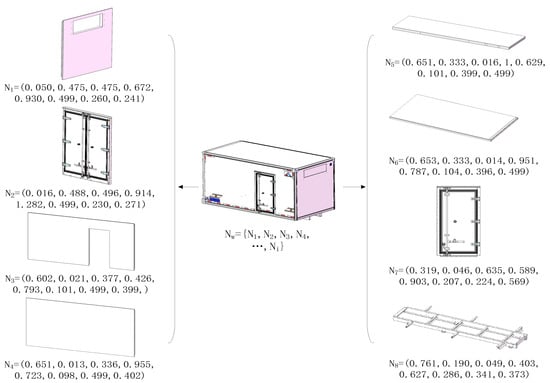
Figure 5. Parameter vector set for van-type refrigerated truck model.

Step 3: Calculation of Rotation Matrix and Translation Vector

First, K-D Tree is used to find the nearest neighbor $q_i$ of each point $p_i$ in the set $N_W$ within the set $N_p$. By using K-D Tree, the nearest neighbor search is accelerated, reducing the time complexity of the search to $O\log n$.

For the given two point sets $N_W$ and $N_p$, the centroids are first calculated. Let $N_W=\left\{p_1,p_2,\dots \dots p_m\right\}$ and $N_p=\left\{q_1,q_2,\dots \dots q_m\right\}$ be two sets of points. The centroid calculation formula is as follows:

$$C_W={\displaystyle \frac{1}{m}}\sum _{i=1}^m{p}_i{,C}_p={\displaystyle \frac{1}{n}}\sum _{j=1}^n{q}_j$$

(8)

Then, each point is translated from the centroid so that the centroid is positioned at the origin (0,0,0):

$$P_i^{\prime }=p_i-C_W{,q}_j^{\prime }=q_j-C_p$$

(9)

Using the centralized point sets $P_i^{\prime }$ and $q_j^{\prime }$, the covariance matrix is calculated as follows:

$$H=\sum _{i=1}^m\left(p_i^{\prime }\right){\left(q_i^{\prime }\right)}^T$$

(10)

Next, perform Singular Value Decomposition (SVD) on the covariance matrix H:

$$H=U\sum V^T$$

(11)

Then, compute the rotation matrix and translation vector. The calculation formulas are as follows:

$$R=V{U}^T$$

(12)

$$t=C_p-R·C_W$$

(13)

The rotation matrix R minimizes the rotational misalignment between the point sets $N_W$ and $N_p$. To ensure R is a valid rotation matrix, its determinant must be checked. If det(R) < 0, the last column of V is multiplied by −1 to guarantee the orthogonality of the rotation matrix. The translation vector t then translates the rotated point set $N_W$ to align with $N_p$.

After each iteration, the point set $N_W$ is updated using the newly computed R and t. The update formula is as follows:

$$P_i^{\prime }=R·P_i+t$$

(14)

In the rotational alignment optimization, a normal vector consistency term is introduced to minimize the positional error between the two point sets ($N_W$ and $N_p$) after alignment using the rotation matrix and translation vector. The error formula is expressed as follows:

$$\mathrm{T}\mathrm{S}\mathrm{E}={\min }_{R,t}{\sum _{i=1}^m{‖p_i-\left(R{q}_i+t\right)‖}^2+\alpha \left(1-n_{p_i}·R{n}_{p_i}\right)}^2$$

(15)

The updated point set will be used for the next iteration until convergence criteria are met.

Step 4: Model Similarity Calculation

The refrigerated van assembly model’s vector set (N_w) is compared with the historical case model’s vector set (N_p) using the ICP algorithm to measure the distance between the sets. An improved ICP algorithm is employed, selecting the minimum distance as the similarity value (sim) between the two models. The rotation matrix and translation vector output from RANSAC are used as the initial values, and the Tukey kernel function is integrated to suppress outlier interference. The formula is as follows:

$$e_i={‖p_i-\left(R{q}_i+t\right)‖}^2$$

(16)

$$\rho \left(e_i^2\right)=\left\{\begin{array}{c}{\displaystyle \frac{e_i^2}{2}}-{\displaystyle \frac{e_i^4}{6c^2}}+{\displaystyle \frac{e_i^6}{6c^4}},if\left|e_i\right|\le 0.1\\ {\displaystyle \frac{c^2}{6}},if\left|e_i\right|>0.1\end{array}\right.$$

(17)

Finally, the formula for the model similarity value is as follows:

$$sim=\min {\displaystyle \frac{1}{m}}\sum _{i=1}^m\rho \left({‖p_i-\left(R{q}_i+t\right)‖}^2\right)$$

(18)

Step 5: Model Node Weight Assignment

The Analytic Hierarchy Process (AHP) is used to assign weights to attributes at each hierarchical level. A judgment matrixA = (a_ij)_n×n is constructed based on the hierarchical factors, and its characteristic equation AW = λ_maxW is solved to obtain the maximum eigenvalue λ_max and the corresponding eigenvector W. After normalizing W, the weight vector W = [w₁, w₂, …, w_n]^T is determined. Finally, the consistency ratio (CR) of A is tested using formula (19). If the consistency condition is not satisfied, A must be adjusted until a valid weight distribution scheme for the attributes at each level is obtained.

$$CR={\displaystyle \frac{{\lambda }_{max}-n}{RI\left(n-1\right)}}<0.1$$

(19)

Finally, the similarity evaluation of each node attribute in the case model is performed to determine the case solution with the highest similarity to the refrigerated van assembly model. The formula is as follows:

$$S=W_k\ast {sim}_k$$

(20)

where W_k is the weight corresponding to each node, and sim_k represents the similarity measure between any two nodes. The value of k is determined by the number of nodes at each level of the model.

Step 6: Screening of Key Components

Based on the similarity S between the historical case model and the refrigerated van assembly model, the case models are ranked. The historical case reference model with the highest similarity is selected. Using the GetSystemValue2 function, key dimensioning information related to the components of a similar reference model is identified. It is then determined whether these components are key parts of the target model, the “van body assembly”. This information is used as a basis for reference reuse and modification, ultimately identifying and filtering the key components of the refrigerated van assembly model.

3.5. Engineering Drawing Dimension Mapping

Dimension mapping in engineering drawings is an intelligent method that automatically projects dimensional information from a 3D model onto a 2D drawing. In Section 2.3, by combining the MKD-ICP algorithm, the most similar key component models were selected, and, using SolidWorks API functions, the filtered key dimensions were automatically annotated on the engineering drawing. This method effectively reduces the number of dimensions that need to be annotated in design software, significantly lowering the complexity of intelligent annotation, and provides an efficient and precise solution for engineering drawing generation. The dimension mapping algorithm is as follows:

Firstly, for shape and location dimensions, the SelectByID2 function is called to filter out redundant dimensions that do not significantly affect the part’s shape and features. These dimensions are then set with the property MarkedForDrawing = False to hide them from display in the current level. After this, the InsertModelAnnotations3 function is used to project the remaining key dimensions onto the engineering drawing, with internal parameter values set to FromEntireModel, indicating that the dimension information is referenced from the “entire model”.

Next, the overall dimensions are annotated. The CreateDefinition function is used to create a boundary box for the current part model, and the AddDimension function is applied to annotate the maximum outer boundary box dimensions in the engineering drawing, completing the overall dimension annotation. Additionally, for certain parts, when annotating shape dimensions in the sketch, the overall dimension annotation is also applied simultaneously.

This approach not only simplifies the dimensioning process but also ensures that critical dimensions are accurately and efficiently mapped onto the engineering drawing.

4. Results

As shown in Figure 6, the interface model to be filtered is a refrigerated van. Taking the “rear wall assembly” model as an example, the MKD-ICP algorithm is used to perform screening and analysis on the key component models of the refrigerated van.

Figure 6. A certain refrigerated van.

Based on the assembly structure tree of the “rear wall assembly” model, the hierarchy is divided, and model descriptors are established for each subcomponent of the assembly following Step 2 in Section 3.4, as shown in Table 2.

Table 2. Descriptors for key subcomponents of the “Rear Wall Assembly” model.

Element Symbol	Model Name	Number	Vector Set Parameters
N1	Foam	KF7.491	(0.555, 0.330, 0.045, 0.110, 0.375, 0.520)
N2	Outer Skin	KF9.652	(0.645, 0.295, 0.005, 0.140, 0.505, 0.400)
N3	Inner Skin	KF9.651	(0.710, 0.250, 0.010, 0.520, 0.200, 0.265)
N4	Framework	KF9.610	(0.870, 0.060, 0.070, 0.020, 0.480, 0.485)

The similarity sim(Nw,Np)sim(N_w, N_p) between the model and the historical case model is calculated using Equation (18), where the AHP (Analytic Hierarchy Process) method is employed to assign weights to the attributes at each hierarchy level. The judgment matrix A is constructed based on the hierarchical structure factors.

$$A=\left[\begin{array}{cccc}1& 2& 2& 6\\ {\displaystyle \frac{1}{2}}& 1& 2& 4\\ {\displaystyle \frac{1}{4}}& {\displaystyle \frac{1}{2}}& 1& 3\\ {\displaystyle \frac{1}{6}}& {\displaystyle \frac{1}{4}}& {\displaystyle \frac{1}{3}}& 1\end{array}\right]$$

According to Step 4 in Section 3.4, the weights ${\omega }_i$ for each sub-level attribute of the “Rear Wall Assembly” are calculated based on the judgment matrix A. The allocation results are shown in Table 3.

Table 3. Attribute weight allocation for each sub-level of the “Rear Wall Assembly”.

Element Symbol	Model Name	Number	Weight Value
N1	Foam	KF7.491	0.438
N2	Outer Skin	KF9.652	0.273
N3	Inner Skin	KF9.651	0.209
N4	Framework	KF9.610	0.080

Taking the “Rear Wall Assembly” as the target model $M_T$, the attribute similarity at the “Wall Assembly” level between the target model and historical case model $M_H$ is retrieved by combining the sub-level model descriptors and the sub-node attribute weight distribution values. The overall similarity $S(M_T,M_H)$ is calculated and sorted to obtain the model with the most similar hierarchical structure and model features. The node attribute similarity calculation results are shown in Table 4.

Table 4. Node attribute similarity between MT and MH at the same level.

Node	sim(MTZ,MiHZ), i = 1, 2, 3, 4…
Foam	0.912	0.896	0.878	0.863	…
Outer Skin	0.948	0.915	0.893	0.875	…
Inner Skin	0.921	0.898	0.864	0.847	…
Framework	0.870	0.903	0.889	0.856	…
S(MT,MiH)	0.9186	0.9020	0.8801	0.8621	…

Based on the calculation results in Table 5, a reference model with a high similarity score of $S(M_T,M_H)$ = 0.9186 is identified. The GetSystemValue2 function is used to extract key dimensional parameters from this reference model. These parameters represent essential measurement attributes of critical components in the assembly. Using these dimensional data, the key components for dimension annotation are determined.

Table 5. Extraction of key dimensional parameters from the reference model.

Dimension Number	Extract Name Information	Relevant Components
No.1	D2@Sketch 8@Split Non-Independent Rear Inner Skin-1@Split Non-Independent Rear	Inner Skin
No.2	D3@Sketch 8@Split Non-Independent Rear Inner Skin-1@Split Non-Independent Rear	Inner Skin
No.3	D4@Sketch 8@Split Non-Independent Rear Inner Skin-1@Split Non-Independent Rear	Inner Skin
No.4	D5@Sketch 8@Split Non-Independent Rear Inner Skin-1@Split Non-Independent Rear	Inner Skin
No.5	D1@Sketch 1@Split Non-Independent Rear Outer Skin-1@Split Non-Independent Rear	Outer Skin
No.6	D2@Sketch 1@Split Non-Independent Rear Outer Skin-1@Split Non-Independent Rear	Outer Skin

The extracted reference dimensions are then used as a basis to filter and identify the corresponding key components in the target model, the Rear Wall Assembly. The specific dimensional information retrieved from the reference model is summarized in Table 5.

Based on the dimension attribute information from the reference model, the key components for dimension annotation in the target model are identified. The names of the key components that require dimensioning for the “Rear Wall Assembly” model are shown in Table 6.

Table 6. Target model key component selection results.

Target Model	Key Component Selection Results
Rear Wall Assembly	Inner Skin, Outer Skin, Foam Componen, Wooden Framework

In Section 3.5, SolidWorks API was utilized to perform dimension annotation on the engineering drawing views of the “Rear Wall Assembly”. According to the code in Table 2, the dimensions were mapped and annotated on the engineering drawing, with the annotation results shown in Figure 7. Figure 8 displays the overall dimension annotation results for the Rear Wall Assembly engineering drawing.

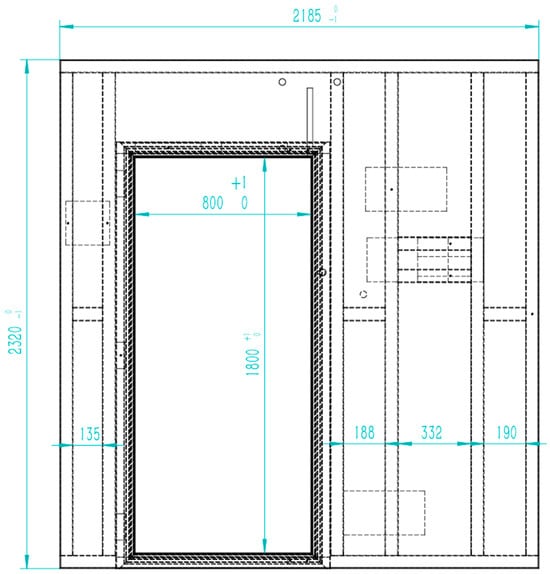
Figure 7. “Rear Wall Frame” engineering drawing dimensioning results.

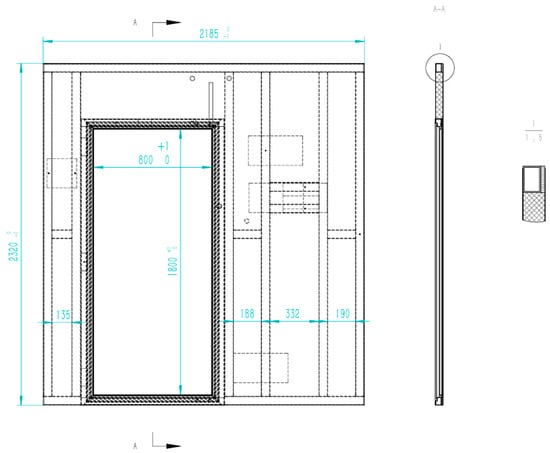
Figure 8. “Rear Wall Assembly” engineering drawing dimensioning results.

Table 7 presents a time comparison between manual annotation and algorithm-based annotation on different components, as well as the efficiency improvement multiples. The results indicate a significant reduction in time when using the algorithm for dimensioning compared to manual annotation. Specifically, for simpler components like the left wall foam assembly, the efficiency improvement was as high as 7.6 times. For more complex components, such as the left wall assembly, although the algorithm also reduced annotation time, the efficiency improvement was slightly lower, around 6.7 times. These results demonstrate that automated dimensioning can significantly save time in the design and manufacturing process, particularly for tasks that involve repetitive annotations, thereby improving overall work efficiency.

Table 7. Comparison of manual annotation and algorithmic annotation in terms of time and efficiency improvement.

Modle Name	Manual Annotation/min	Algorithmic Annotation/min	Efficiency Improvement Factor
Left Wall Foam Assembly	6.03	0.79	7.6
Left Wall Outer Skin	5.13	0.68	7.5
Left Wall Inner Skin	4.87	0.62	7.8
Left Wall Framework	5.85	0.81	7.2
Left Wall Assembly	7.23	1.07	6.7

Figure 9 presents a comparative evaluation of the proposed MKD-ICP algorithm against traditional rule-based methods and SVM-based methods. Across all complexity levels, the MKD-ICP method consistently achieves the lowest dimensioning error compared to rule-based and SVM-based methods. Especially in complex geometries, MKD-ICP maintains an error rate below 5%, while rule-based methods exceed 10%, and SVM-based methods approach 8%. This demonstrates the superior precision of MKD-ICP in handling intricate geometrical features. As the geometric complexity increases, the error rates of rule-based and SVM-based methods rise sharply. In contrast, MKD-ICP exhibits much slower error growth, indicating better robustness and scalability to complex structures. When additional simulated noise is introduced (e.g., random distortions in model features), MKD-ICP shows minimal sensitivity to noise, with only a slight increase in error. Conversely, the performance of rule-based and SVM-based methods degrades more significantly under noisy conditions.

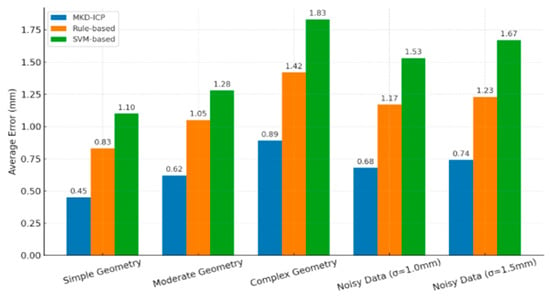
Figure 9. Comparative error analysis under different conditions.

To enhance the rigor of performance evaluation, we compared the proposed MKD-ICP method with deep learning-based methods, SVMs, rule-based heuristics, random forests, and KNN. Dimensioning accuracy (%) and execution time (s) were averaged over multiple runs, and standard deviations are shown as error bars in Figure 10.

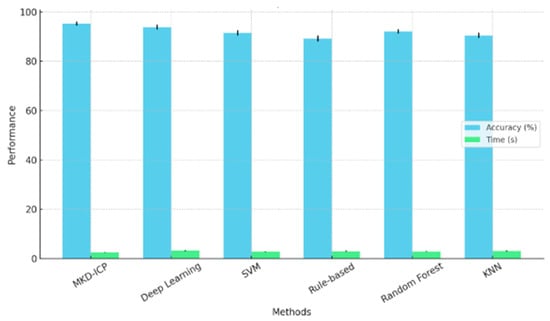
Figure 10. Performance comparison with error bars.

As seen in Figure 10, MKD-ICP achieved the highest accuracy (~92%) with low variability, outperforming other methods. While deep learning achieved similar accuracy, it showed higher variance. SVM and random forest offered faster execution but lower accuracy, while rule-based and KNN methods performed the worst. MKD-ICP demonstrated a strong balance between accuracy and efficiency across different conditions.

5. Conclusions and Future Work

This paper addressed the need for standardized accuracy and completeness checks in engineering drawing dimensioning and proposed an intelligent dimensioning method based on Case-Based Reasoning (CBR), KD-Tree, and an improved Iterative Closest Point (ICP) algorithm. Experimental results demonstrated that the proposed MKD-ICP method achieved a dimensioning accuracy of approximately 92%, outperforming traditional machine learning and rule-based methods while maintaining superior computational efficiency. Specifically, CBR effectively extracted key geometric features and matched historical cases to provide reliable initial annotations, while KD-Tree accelerated high-dimensional neighbor searches, and the improved ICP ensured precise alignment through joint optimization of distance and normal vector similarity.

The case study on a refrigerated van model confirmed that the proposed method significantly improved annotation completeness and reduced manual intervention by approximately 40% compared to conventional techniques. These outcomes directly fulfill the research objective of enhancing dimensioning accuracy, standardization, and automation in engineering drawings.

In future work, we plan to incorporate deep learning and image processing techniques to further enhance feature extraction and annotation efficiency, thereby advancing the intelligence and robustness of automated dimensioning systems.