Abstract
The durability of reinforced concrete structures in aggressive environments is strongly influenced by the ingress of chloride and other harmful ions, which is further complicated under partially saturated conditions, due to the coexistence of liquid and gas phases within the pore network. This study aimed to develop a predictive moisture–chemical–temperature model and to elucidate the mechanisms governing ion transport in partially saturated concrete. A multi-species hygro-chemo-thermo transport model was formulated based on the Nernst–Planck equation, incorporating electroneutrality, zero current conditions, and the coupled effects of moisture and temperature gradients. The model was numerically implemented using a parallel FE method with the Crank–Nicolson scheme, supported by domain decomposition and SPMD techniques for high computational efficiency. As a result, experimental validation was performed through chloride ponding tests under varying temperature conditions (20 °C, 35 °C, 50 °C), water-to-cement ratios (0.55, 0.65), and relative humidity differences (100%, 60%). The simulation results showed good agreement with the experimental data and confirmed that the proposed model can effectively predict chloride penetration under both isothermal and non-isothermal conditions. Additionally, the simulations revealed that moisture gradients accelerate ion transport, as the inward migration of the moisture front enhances the diffusion rates of chloride, sodium, and calcium ions until a steady-state moisture distribution is reached.
1. Introduction
Concrete is the most widely used construction material in the world, due to its cost-effectiveness and structural performance. Over its designed service life, concrete develops cracks due to internal stresses and external conditions. The causes of these cracks can be broadly categorized into three main types. The first is chemical attack, where substances like sulfates and magnesium infiltrate the concrete, causing expansion and resulting in cracks. The second is physical actions, such as freezing–thawing cycles and wave action. The third is corrosion of the rebar, which occurs at the interface between the rebar and concrete due to chloride infiltration. Among these, rebar corrosion is one of the most common causes of durability issues in reinforced concrete structures. Especially when concrete structures are built in marine environments rich in chloride or when deicing salts are widely used during winter, the concentration of chloride ions reaches a critical level, initiating rebar corrosion. Once rust forms on the rebar surface, its volume expands, causing cracks in the concrete, and as it grows and spreads, it can lead to significant degradation in durability, reducing the structure’s load-bearing capacity [1,2,3].
To reduce the deterioration and improve the durability performance of concrete, there are several techniques: (1) surface treatment, (2) corrosion inhibitors, (3) autonomic self-healing with expansive agents, admixtures, and fibers, and (4) mineral additives (called supplementary cementitious materials). In practical fields, these techniques are widely adopted to increase the design lifespan of concrete structures with the passing of penetration time. The design life takes into account chloride and carbon dioxide penetration rates, which are closely related to the protective ability against rebar corrosion. Both penetration rates rely on the porosity of the matrix, and the distribution of pore sizes in terms of the material aspect [4].
Additionally, for predicting the long-term durability of concrete structures, a mathematical model that characterizes the deterioration process needs to be developed. The process of various ions penetrating concrete has been studied by many researchers over several decades. Fick’s law of diffusion is well known for describing the movement of molecules from a higher concentration to a lower concentration region. Chloride penetration follows Fick’s law in fully saturated concrete, where chloride penetrates due to the concentration gradient. In partially saturated concrete, the degree of moisture diffusion is a significant factor affecting chloride ingress [5,6,7].
Li et al. presented a mathematical model and numerical results for the simulation of electrochemical chloride transport in saturated concrete. The concentration profiles of ion species charged at various current densities in the electric field were demonstrated, considering the activities of ions in the concentration solution [8]. Subsequently, the transport behavior of ions in saturated concrete was simulated using a finite element model. This model was developed based on the Nernst–Planck equation, related to the interactions of multiple ions in the concrete pore solution. The effects of boundary conditions, current density, and the diffusion coefficient of concrete were integrated into the study [9,10,11,12]. An electrochemical chloride removal model was also proposed for concrete that considers electrostatic coupling of ions, adsorption, porosity of the pore structure, and tortuosity effects [13,14]. Yogarajah et al. investigated the influence of C-S-H tortuosity and surface electrical properties on chloride transport in slag-blended cement systems through a combination of modeling and experimental analysis. The simulation results showed good agreement with the experimental data, and the findings contribute to a better understanding of corrosion risk in reinforced concrete incorporating slag-blended cement [15].
Researchers presented a mathematical model of ion diffusion in porous media. This model, based on the Nernst–Planck equation, included the Poisson equation to evaluate the electrostatic coupling between ions [16]. Subsequently, the model was expanded to consider chemical activity effects by including ions in non-ideal solutions. A mathematical model was developed by considering the chemical activity terms in the governing equations [17]. More recently, a model was developed for unsaturated cement-based materials related to external sulfate or calcium and hydroxide leaching, based on a set of Nernst–Planck/Poisson equations, considering diffusion, electrostatic coupling, chemical activity, and convective mechanisms under isothermal conditions [18]. Nielsen et al. proposed a chloride diffusion coefficient in partially saturated cementitious materials by combining composite theory and Power’s model instead of the Nernst–Planck equation [19].
Recently, a numerical model was developed to analyze mass transport and electrode polarization in concrete under an externally applied voltage, accounting for multi-species electromigration, time-dependent overpotential, and non-equilibrium binding. The model incorporated the Tafel equation to represent overpotential at electrode interfaces and dynamically updated boundary conditions to accurately simulate the ion distribution. Its reliability was validated against experimental data. The results showed that electrode polarization reduced the effective potential across the concrete, significantly influencing chloride penetration and the spatial-temporal distribution of ionic species [20]. Furthermore, multi-species reactive transport modeling (RTM) has been advanced to better understand the deterioration mechanisms of cement-based materials under various environmental conditions. Sharmilan et al. developed an RTM for saturated systems, incorporating multi-ionic transport via modified Poisson–Nernst–Planck equations, chemical equilibrium, and evolving pore structure, with validated predictions for chloride and ion distribution in mortar exposed to NaCl and seawater. This approach was extended to unsaturated conditions, coupling multi-ionic and moisture transport with a two-phase moisture model driven by capillary pressure. The numerical results under wetting–drying cycles showed that prolonged wetting increased the chloride penetration and deterioration depth, with Friedel’s salt formation limiting deeper chloride ingress. An additional study focused on carbonation processes, modeling how pore solution composition and phase changes affect steel corrosion. It revealed alkali ion depletion and migration toward carbonated zones, increased sulfur and chloride concentrations from solid phase decomposition, and enhanced calcite formation due to calcium migration [21,22,23].
The actual boundary conditions of concrete structures are often exposed to climate changes, facing periodic moisture and temperature boundary conditions. Moreover, temperature fluctuations and moisture diffusion affect chloride penetration. This effect has previously been integrated with BET isotherms and the Arrhenius law [24,25].
To better predict the transport of chloride ions in concrete materials, it is necessary to develop a robust mathematical model that considers temperature effects. In general, concrete structures are subject to non-isothermal conditions, and temperature fluctuations can significantly affect the chemical reactions of ions. In other words, the temperature gradient is one of the most important driving forces [26].
A governing equation should be derived for chloride ion penetration based on temperature effects under partially saturated concrete conditions, which has been studied by many researchers based on experimental and numerical studies. Bazant et al. and Saetta et al. mentioned the relationship between temperature and moisture movement in saturated and unsaturated concrete using mathematical models, experimental data, and numerical programs. In particular, Bazant et al. reported on the relationship of adsorption isotherms, the dependence of permeability on temperature, and the change in porosity due to dehydration [27,28]. Sih et al. simulated the combined effect of heat and moisture diffusion on transient stress [29]. Lien et al. studied mass transport influenced by moisture and temperature gradients. As a result, they found that the presence of temperature gradients could induce internal pressure gradients in porous media with sufficiently low permeability [30].
Many researchers have studied a coupled thermo-chemo-mechanical model to simulate critical phenomena in concrete, in terms of hydration behavior in early age, creep, shrinkage, cracking, and so on. These models have been constructed with a thermodynamic basis, associated with the reactive porous media theory and microprestress-solidifications theory [31,32]. Recently, a 3D chemo-hygro-thermo mechanical model was proposed to predict the degradation and reinforcement depassivation in a bridge exposed to an aggressive environment. The results underlined the need for incorporating damage and cracking into service life prediction for reliable long-term durability assessments [33]. Isgor et al. developed a 2D finite element computational program, CONDUR, considering the coupled effects of moisture, heat, and carbon dioxide transport in concrete. The proposed finite element model and program can handle all aspects, including cracks, prescribed initial and boundary conditions, and related material nonlinearities [34]. In addition, Isteita et al. investigated that increasing temperature accelerates the chloride penetration rate in concrete and proposed coupling parameters for chloride penetration concerning temperature effects [35].
In this study, we aimed to explain and propose prediction methods for the penetration phenomena of chloride ions and other ions (Na+, Ca2+, K+, OH−) diffusing into partially saturated concrete based on mathematical models and numerical analysis techniques. To this end, we intended to derive the interactions of chloride ions and ions (Na+, K+, OH−) in the concrete pore solution based on the Nernst–Planck equation. This mathematical model utilized the FEM method and the Parallel algorithm to derive the results, and the reliability of the model was verified using experimental data.
2. Basic Transport Formulation of Unsaturated Concrete
2.1. Governing Equation
Concrete is made up of three physical phases: aggregate, cement paste, and porosity. Due to the dense and hard nature of the aggregate, the diffusivity of ionic species is minimal within it. However, the pore system of cement paste provides a pathway for the migration of ionic species. The presence of multi-species ions (Cl−, Na+, Ca2+, K+, OH−) in pore solutions depends on the type of cement and mineral admixtures used. The total chloride content includes both bound and free chlorides. Once the water-soluble free chlorides reach a certain threshold, the passive film on the reinforced rebar surface can be damaged.
To predict the service life of concrete structures, the content of chloride ions is computed with a mathematical model. While this implementation is simple and convenient, it is not able to demonstrate the deterioration of concrete including ionic interactions inside the pore system of concrete under micro-climate conditions. Therefore, a mathematical model that accurately reflects the diffusion of ionic species in the system may be necessary to better understand real-world phenomena.
For the flux of each species in the pore solution of saturated concrete, the Nernst–Planck equation is used, as follows:
where denotes the flux of ions, represent the diffusion coefficient, specifies the concentration of multi-species (Cl−, Na+, Ca2+, K+, OH−), is the charge number, F is Faraday’s constant, R is the gas constant, T refers to the temperature, Φ indicates the electrostatic potential, and index i corresponds to the i-th species [36].
When subjected to an internally induced electric field, all ionic species in the pore solution influence the electro-neutrality condition. There are two physical requirements of the electro-neutrality condition: one is that the total charge should be zero at every point of the domain, and the other is that no electric current should pass through the domain [36]. To account for the electrical potential (Φ) inherently caused by the movement of all species, two conditions are required, as follows:
Eletroneutrality
Null current
To solve Equation (1), the null current assumption from Equation (3) is employed. The expression for the electro potential can be obtained as in Equation (4).
The formulation of chloride ions (Cl−) and other species (Na+, Ca2+, K+, OH−) in non-saturated concrete is based on the Nernst–Planck equation. The transport of all ionic species is associated with the coupled effect of temperature and moisture in concrete. The heat flow is described by Fourier’s law of heat conduction.
The governing equation of multi-species diffusion in partially saturated concrete affected by the coupling of moisture gradient and temperature gradient (Soret effect) can be written as follows:
where is the flux of ions, denotes the diffusion coefficient, represents the concentration of multi-species (Cl−, Na+, Ca2+, K+, OH−), is the charge number, F is Faraday’s constant, R is the gas constant, T is the temperature, Φ is the electrostatic potential, and index i represents the i-th species. and are the coupling parameters of the effect of moisture and temperature on ion diffusion, respectively. In Equation (1), the first term in the right-hand side is the diffusion due to the concentration gradient, and the second term is the migration or the electrical coupling between ions.
The moisture and temperature transport can be described as follows:
where and are the flux of relative humidity and temperature, and are the diffusion coefficients, H is relative humidity, and T is temperature.
The mass balance equations for each ionic species can be expressed as
Substituting Equation (5) into Equation (8) yields
where
In the same way, the mass balance equations for moisture and temperature are
where,
Finally, Equations (9)–(11) can be combined and simplified into matrix form,
where is the concentration of multi species (Cl−, Na+, Ca2+, K+, OH−). The total degree of freedom in this matrix form has seven unknowns.
2.2. Material Models
2.2.1. Capacity and Diffusivity Coefficients of Multi-Species in Non-Saturated Concrete
The moisture capacity of concrete can be calculated as the average of the moisture capacities of the cement paste and aggregate [37]. The chloride binding capacity is defined as the ratio of the change in the free chloride content to the total chloride content [38]. The other species (Na+, Ca2+, K+, OH−) and temperature capacity are employed as one. The heat capacity of concrete is assumed to have a specific heat and density. The change in moisture due to temperature is negligible under normal temperature conditions and can be ignored.
The temperature diffusion coefficient refers to the thermal diffusivity of concrete, which is approximately on the order of m2/s. This can vary depending on factors such as moisture content, porosity, and the type of aggregate used.
The moisture diffusion coefficient of concrete is derived using composite theory and can be computed through the relationship with the diffusion coefficient of aggregate and cement paste [39]. The ion diffusion coefficient is adopted in references [14,34,38]. The diffusion coefficient of chloride ions in concrete can be estimated using the multifactor method [38]. This coefficient depends on factors such as water–cement ratio, the composite action of aggregates, relative humidity, temperature, and free chloride concentration. The diffusion coefficient of other species (Na+, Ca2+, K+, OH−) can be obtained from various references [14,34]. The remaining coupling parameters are discussed in the following section.
2.2.2. Coupling Parameters
The coupling parameters in the diffusivity matrix have been studied by many researchers. The Soret effect (thermal diffusion) is the occurrence of a diffusion flux due to a temperature gradient. The Dufour effect is the reciprocal phenomenon, where heat flux occurs due to a chemical potential gradient. The temperature effect on chloride diffusion was reported by Isteita [35]. The effect of moisture due to chloride diffusion and the influence of chloride due to the moisture gradient were demonstrated by Ababneh et al. and Homan et al. [5,40]. More detailed information is described below.
and
The humidity diffusion coefficient of concrete depends on the diffusion coefficients of both the aggregate and the cement paste. The diffusion coefficient of the aggregates is considered negligible, as the pores within the aggregates are discontinuous and surrounded by cement paste. The humidity diffusion coefficient of cement paste can be evaluated using the empirical formula proposed by Xi et al. [25]. Although the coupling parameters in the diffusivity matrix of Equation (14) for the effect of temperature on moisture diffusion and the effect of moisture on temperature diffusion were introduced by Bazant et al. [26,27], the flux driven by the temperature gradient (Soret flux) is relatively small based on the limited experimental data available; that is, approximately . In addition, the coupled heat flux may be neglected in this numerical model.
and
In Equation (14), the coupling parameter of temperature’s effect on chloride diffusion was as proposed by Isteita, following Equation (15), which was evaluated based on the experimental study of the effect of temperature on chloride penetration into saturated concrete [35]. This depends on the effect of aging and temperature.
where is the coefficient , which depends on the concrete composition; is the free chloride concentration (%); is a factor that accounts for the effect of the aging of concrete, which is due to hydration reactions in cement; and is the factor of temperature’s effect.
where the of is the curing age of concrete, U is the activation energy of the diffusion process, R is the gas constant, and T and Tref are the current and reference temperature, respectively. Based on the Soret effect, the heat flow in concrete can carry chloride ions and other ions in concrete pore solution. Therefore, this coupling parameter may be applied to other ionic species (Na+, Ca2+, K+, OH−), and can be used in Equation (18).
Material models for the coupling parameters between ion transport and moisture diffusion in concrete have not been sufficiently developed and researched. According to the research by Ababneh and Xi, both coupling parameters and depend on the free chloride concentration [5]. For the other species and moisture coupling parameters, a reasonable assumption is needed, as moisture movement can transport ions in the same way it transports chloride ions; that is, the coupling parameters are proportional to the ratio of the ion’s diffusion coefficient to the diffusion coefficient of chloride.
3. Implementation of Parallel Finite Element Method
3.1. Numerical Modeling with Finite Element Method
To solve the multispecies transport problem using a coupled hygro-chemo-thermo model over time, a large linear system of equations is derived using the parallel finite element method. The finite element formulation is briefly outlined in this section. The continuous variables in the coupled moisture–chemical–temperature diffusion equations, free chloride, other species (Na+, Ca2+, K+, OH−), relative humidity (), and temperature are spatially discretized over the space domain, . The discretization of the domain is presented in Equation (19),
where represents the total number of elements in the spatial domain, and refers to an individual element. Additionally, is defined as the boundary of the computational domain, while is the boundary of a subdomain.
The unknown variables in Equations (20)–(22) are expressed in terms of nodal values, , , and :
where is the shape function for the triangle element. The notations and represent row and column vectors, respectively. The element shape functions are expressed in Equation (23)
in which is the shape function for node j, and n is the total number of nodes in an element. The unknown vectors for temperature , relative humidity , and multi-species can be defined as follows:
The nodal variables of relative humidity, ion concentrations, and temperature are determined by substituting the approximated values from Equations (20)–(22) into the governing Equations (9)–(11). The Galerkin method is then applied to the weak forms, which leads to the finite element matrix as presented in Equation (27):
where the element matrices and the variable vector are given by Equations (28)–(30) and the element matrices and the variable vector are given in Appendix A.
Finally, Equation (44) is discretized in time with a time interval, , as shown below:
The value of the parameter is related to the solution method used in the PFE program. Typical values of , namely 0, ½, and 1, correspond to the fully explicit, semi-implicit, and fully implicit methods, respectively. In this study, the semi-implicit method, known as the Crank–Nicholson method, is used.
Equation (31) is simplified into a linear system of equations.
where
3.2. Framework of Parallel Finite Element Method
For the implementation of the multispecies transport in this study, the framework of the parallel finite element (PFE) program was coded with C++ and some numerical algorithms from several programs, such as Triangle for mesh generation, ParMETIS, PETSc, and MPI that were included in [41,42,43,44]. The key issue in a parallel computing environment is balancing the workload across processors and minimizing the time spent exchanging data between processors.
In this study, to solve the multispecies transport problem, a PFE program was developed using the single-program-multiple-data (SPMD) paradigm, as well as domain decomposition techniques. Each processor worked on a separate part (subdomain) of the problem, and processors communicated with each other through message passing.
The mesh of triangle elements was generated using Triangle, a program designed to create exact Delaunay triangulations, which are suitable for finite element analysis [41].
Since the problem involved large-scale simulations, ParMETIS was used to handle the mesh decompositions efficiently. ParMETIS applied a parallel graph-partitioning algorithm, optimizing inter-process communication during these decompositions and making it particularly useful for unstructured meshes in large-scale numerical simulations [44].
The numerical solution of the partial differential equations (PDEs) was achieved with the PETSc (3.14.6) library. PETSc, primarily written in C, can be accessed through user codes written in C, Fortran, or C++ [42]. For message-passing communication between processors, the MPI (Message Passing Interface) was utilized, ensuring portability and functionality across various parallel computing platforms.
To accurately simulate the movement of multiple ions in concrete, especially in the thin layer between the concrete surface and steel rebar, a fine mesh was required. Triangle was used to generate the node and element data for the mesh. To check and visualize the size and shape of the mesh, ParaView was used [45]. ParaView is an open-source tool that can handle large datasets and analyze them using multiple computers working together.
For handling large-scale information, the VTK file format was employed, as it is easy to read and write programmatically or by hand. The VTK input file is automatically generated once the program runs. Figure 1 illustrates a flow chart for the parallel pre-processing and finite element solver.
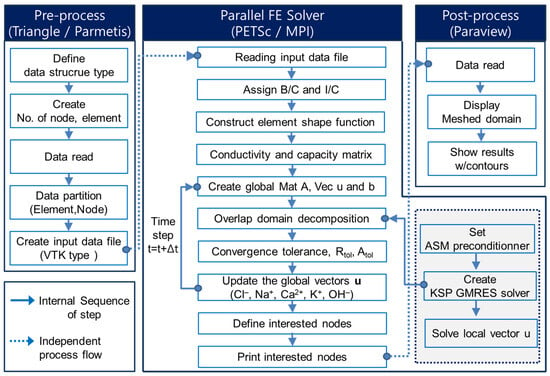
Figure 1.
Framework of parallel FEM with hygro-chemo-thermo transport model.
3.3. Overlapping Domain Decomposition Method
In this study, a parallel program was developed by dividing the program into multiple fragments, each of which could execute simultaneously on its own processor. This was achieved using the domain decomposition (DD) method, which is well suited for parallel finite element computations. The DD method is commonly employed to solve large-scale system equations, enabling sub-domain operations to be executed concurrently on separate processors [7].
There are two main types of domain decomposition methods: overlapping and non-overlapping. In this study, the overlapping method was preferred for solving the linear sparse matrix. This method offers a simpler implementation for algebraic approaches and results in faster convergence compared to the non-overlapping DD method. Additionally, the extended subdomains in the overlapping approach have smoother boundaries than those of non-overlapping subdomains, leading to a better overall performance.
To create the algorithm structure, the overlapping DD method consists of four parts: subdomain preparation, subdomain solver, data exchange, and global management. The process starts with a set of overlapping subdomains, each with its own solver. During each iteration, the boundary conditions need to be updated, requiring data to be exchanged between neighboring subdomains. To coordinate the solvers and data exchange, the global management part controls the progress of the DD iterations, monitors overall convergence, starts the subdomain solvers, and manages the data exchange [46].
To solve the system of equations required by the DD method, an iterative solver is necessary. In this study, the GMRES (Generalized Minimal Residual) method was primarily used, as it is particularly effective for solving non-symmetric linear systems that involve both global and local matrices. Furthermore, to improve the convergence in solving the multi-species transport problem, the additive Schwarz preconditioner was applied.
The mathematical formulations of the overlapping domain decomposition (DD) method, along with details of the preconditioned Schwarz method, can be found in [46,47]. To achieve overlapping decomposition of the domain, each subdomain is extended into a larger domain , where, . The overlap is uniform and is the discretized space over . Therefore, Equation (19) can be rewritten as below:
where denotes a finite dimensional subspace of the Sobolev space , and subscript represents the number of subspaces, and superscript is the element size.
Equation (32) is simplified as follows:
Since Equation (37) is typically ill-conditioned, a preconditioner such as the additive Schwarz preconditioner is necessary to solve it using any iterative method.
The additive Schwarz preconditioned system can be written as
denotes the operators and can be written in matrix form as , where is the restriction matrix and is the solver for the subdomain problem. In the PFE program, for the additive scheme, the number of subdomains, , is typically set as equal to the number of available processors.
4. Results
4.1. Validation of Hygro-Chemo-Thermo Transport Model
4.1.1. Experimental Validation of Chloride Ingress Under Temperature Gradient
To validate the derived numerical model, the experimental test data produced by Isteita et al. were adopted [35]. The experiments were conducted using a chloride ponding method under varying initial temperature conditions to investigate the effects of temperature variation on chloride penetration. The key test variables were the initial temperature conditions, the water–cement ratio, and the relative humidity differences between the top surface and the interior of the concrete. Concrete specimens were prepared with two different water–cement ratios, 0.55 and 0.65, and the concrete mix design was as shown in Table 1. All specimens were stored in the air for 24 days to create varying humidity conditions, considering the effect of the moisture gradient. To enhance the chloride ingress into concrete, a ponding reservoir was located on the top surface of the concrete specimen with a plastic sleeve and was filled with 5% sodium chloride (NaCl) solution. A steel clamp and silicone were used to secure the plastic sleeve. For the initial temperature condition, the top chloride solution was heated using a heating stick to 35 °C and 50 °C, establishing temperature gradients as driving forces. The numerical and experimental results were compared for specimens exposed to 5% NaCl under these temperature gradients over 3, 6, 12, and 24 days. Figure 2 illustrates the experimental setup, and Table 2 presents the total chloride profile based on varying water–cement ratios, temperatures, and exposure durations across different depths. Each specimen was embedded with two SHT75 Sensirion humidity and temperature sensors. The sensors were positioned at depths of approximately 20 mm and 40 mm from the top surface, to measure the internal temperature of the concrete. Data were recorded at 15 min intervals using an EK-H3 Sensirion data logger.

Table 1.
Concrete mix designs.
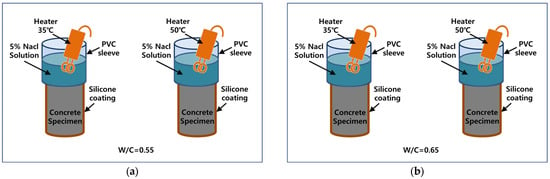
Figure 2.
Experimental plan for chloride penetration under two different temperatures, 35 °C and 50 °C: (a) W/C = 0.55, 5% of NaCl (b) W/C = 0.65, 5% of NaCl.

Table 2.
Total chloride profile associated with two different water–cement ratios, temperature, time period, and depth.
4.1.2. Comparison of Experimental and Numerical Results
According to the experimental results of Isteita et al., the concrete specimens exposed to a 5% chloride solution reached a steady-state temperature after 14 days at 35 °C when using a heater, while those exposed to 50 °C required approximately 23 days to reach a steady state [35]. Additionally, at a depth of 42 mm from the surface, the temperature was measured to be the same as that of the distilled water on the top surface of the concrete specimens. Since temperature effects were considered negligible beyond this period, the experimental results up to 24 days were used for comparison with the numerical analysis. The total chloride content profile was measured at 6 mm intervals from the surface, and the numerical analysis was conducted under the same boundary conditions as the experiment.
Figure 3 and Figure 4 compare the total chloride profiles obtained from the experiments and numerical analysis based on the water–cement (W/C) ratio and measurement time. These results highlight the influence of the W/C ratio and temperature gradient on chloride penetration in the unsaturated concrete.
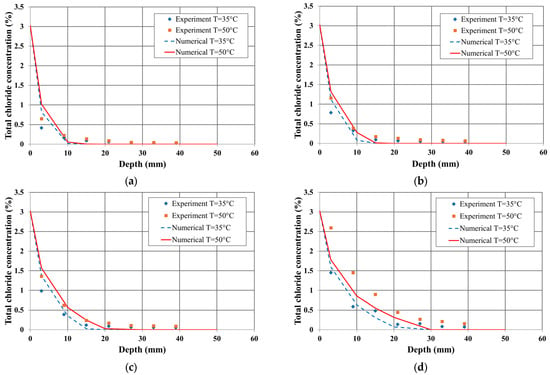
Figure 3.
Chloride profile in concrete sample (0.55 w/c): (a) duration = 3 days, (b) 6 days, (c) 12 days, (d) 24 days.
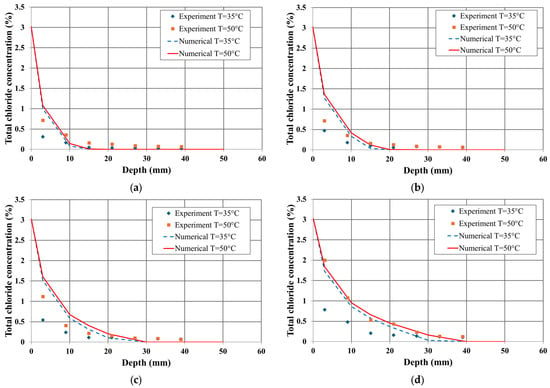
Figure 4.
Chloride profile in concrete sample (0.65 w/c): (a) duration = 3 days, (b) 6 days, (c) 12 days, (d) 24 days.
In terms of the W/C ratio, the numerical analysis results for a 0.55 W/C ratio showed better agreement with the experimental data. This trend remained consistent over time. However, at 24 days, the numerical results for a 0.65 W/C ratio also exhibited a similar tendency to the experimental data. Furthermore, for the same measurement duration, both the experimental and numerical results indicated that the total chloride content was higher for the 0.65 W/C ratio than for the 0.55 W/C ratio.
Regarding the effect of the temperature gradient, the numerical results closely matched the experimental data under both 35 °C and 50 °C conditions. Over time, the influence of the temperature gradient was more significant in specimens with a 0.55 W/C ratio, whereas the effect was relatively smaller in specimens with a 0.65 W/C ratio.
These findings confirm that the proposed transport model, which accounts for diffusion mechanisms, ion interactions, and combined temperature effects, can effectively predict chloride penetration in concrete structures under both isothermal and non-isothermal conditions.
4.2. Numerical Prediction with Hygro-Chemo-Thermo Transport Model
In the previous section, a Parallel Finite Element (FE) program was developed using the Hygro-Chemo-Thermo transport model and validated through comparison with experimental studies. In this section, the developed transport model was used to examine the effects of temperature and relative humidity (RH) on the diffusion of various ions.
The geometry of the concrete specimen used for numerical analysis is shown in Figure 5a, with dimensions of 15 cm in height and 30 cm in width. The boundary conditions were set to reflect real environmental conditions, where various types of deicing salts are commonly used. Accordingly, the specimen was assumed to be exposed to a 3% NaCl and 3% CaCl2 solution. The external temperature conditions were set at 20 °C, 35 °C, and 50 °C, while the internal concrete temperature was maintained at 20 °C. Additionally, the initial concentrations of Na+ and K+ ions in the pore solution were determined based on the chemical composition of cement provided by the manufacturer [48]. All surfaces except the top were assumed to be silicone-coated to prevent moisture exchange, and the internal relative humidity (RH) was set at 60%.
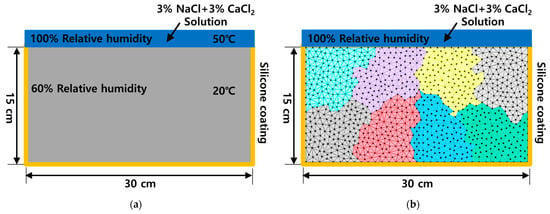
Figure 5.
Information of the numerical analysis. (a) Geometry information, (b) mesh generation with subdomain.
The numerical model assumed a long-term ponding condition, where chloride and moisture diffusion occurred in the same direction. The total analysis duration was 400 days, with a time step of 0.5 days. To ensure numerical accuracy, two convergence tolerance conditions were applied: a relative tolerance (Rtol) of 10−4 and an absolute tolerance (Atol) of 10−10. To solve the large sparse matrix, the Krylov Subspace Method (KSP) GMRES solver with an additive Schwarz preconditioner was employed, as detailed in Figure 1 of the previous section.
The mesh structure used for numerical analysis is shown in Figure 5b. It consisted of approximately 3000 nodes and 6000 triangular elements. The entire mesh was divided into eight sub-meshes, each containing an approximately equal number of elements. Additionally, the number of nodes at the subdomain boundaries was minimized to enhance the computational efficiency during parallel processing. A parallel finite element method was employed to solve the coupled moisture, temperature, and multi-ion diffusion problem. In this analysis, relative humidity (Hm) and five ionic species (Cl−, Na+, Ca2+, K+, OH −), defined by the Nernst–Planck equation, were spatially discretized. For time integration, the semi-implicit Crank–Nicholson method was applied.
The key material parameters and input data used in the analysis are summarized in Table 3. These include the diffusion coefficients, initial concentrations at the top surface and in the pore solution, the water-to-cement ratio (W/C ratio), the volume fraction of aggregates, relative humidity, and temperature. The numerical simulations were conducted under unsaturated conditions, where the relative humidity inside and outside the concrete differed. All ion concentrations were expressed in mol/L as input parameters, whereas the total ionic concentration was expressed as the percentage of ion mass per unit mass of the solution (%).

Table 3.
Material parameters and input data for numerical analysis.
To evaluate the performance of the parallel FE algorithm, it is necessary to consider the concepts of speed-up and efficiency. The definitions of speed-up, , and efficiency, , are shown in Equations (39) and (40).
where is the time taken by the code to execute on a single processor, is the time taken for the same code to execute on p processors, and is the number of processors.
To evaluate the scalability of the parallel algorithm, meshes with 3000, 6000, 12,000, and 24,000 nodes were used, while increasing the number of processors up to 32. As shown in Figure 6, when the number of processors increased, the problem size assigned to each processor decreased, and the speed-up gradually improved. For instance, in the case of 24,000 nodes, the speed-up achieved with eight processors approached the ideal conditions, and the efficiency was nearly one, as illustrated in Figure 7. In contrast, for the 3000-node case, the speed-up increased more slowly when more than two processors were used, due to the cost of communication between processors.
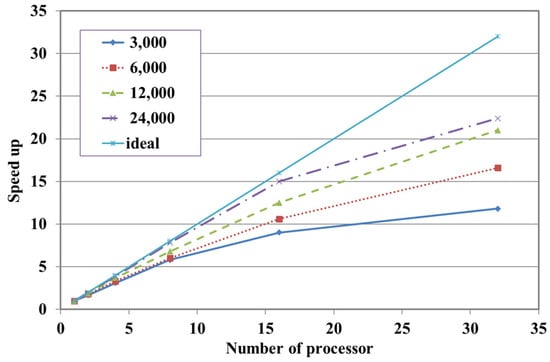
Figure 6.
Speed-up according to the number of nodes and processors.
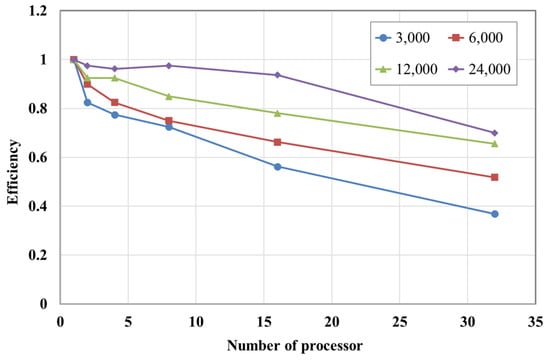
Figure 7.
Efficiency according to the number of nodes and processors.
In unsaturated concrete, the relative humidity (RH) significantly influences the diffusion of ionic species [5]. As shown in Figure 5, to observe the ingress of various ions from the top surface of the concrete, a boundary condition consisting of a mixture of sodium chloride (NaCl) and calcium chloride (CaCl2) was applied. Specifically, the top surface of the concrete specimen was exposed to 3% NaCl and 3% CaCl2 solutions. Additionally, the initial conditions included the presence of K+, Na+, and OH− ions in the concrete’s pore solution.
Figure 8 presents the simulation results of the relative humidity profile over depth under unsaturated conditions for the different durations (20, 50, 100, 200, and 400 days) of numerical analysis. A moisture gradient was established from the external RH of 100% toward the internal RH of 60%, indicating that a gradient was formed from the exposed surface toward the interior of the concrete. The results demonstrate that the moisture front migrated inward over time and eventually converged to 100% RH, reaching a steady-state condition. In practice, this moisture gradient enhanced the transport of chloride, sodium, and calcium ions, thereby accelerating their penetration rates.
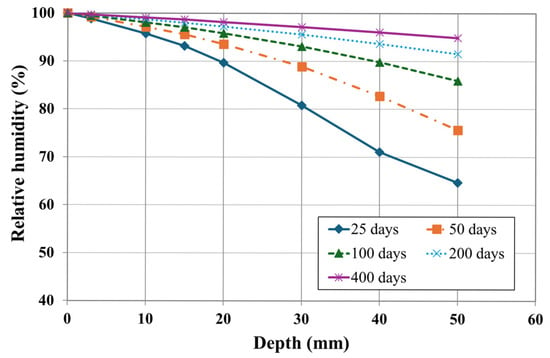
Figure 8.
Profile of relative humidity over time.
Figure 9 shows the total chloride concentration profiles with respect to depth. Figure 9a illustrates the effect of the water–cement (W/C) ratio, while Figure 9b demonstrates the effect of temperature on chloride ion ingress. The results indicate that although the W/C ratio influenced the rate of ion transport, temperature played a more dominant role in accelerating the diffusion rate under the same W/C ratio.
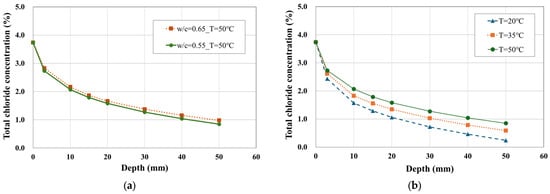
Figure 9.
Profile of total chloride concentration over depth. (a) Effect of W/C, (b) effect of temperature.
Figure 10 presents the ion concentration profiles of Na+, Ca2+, K+, and OH− after 400 days. It was observed that externally sourced ions such as Ca2+ and Na+ increased in concentration inside the concrete compared to their initial values. In contrast, internally originated ions like K+ and OH− showed a reduction in concentration, indicating outward diffusion. These findings confirm that both the moisture gradients and temperature gradients contributed to enhancing the transport of ionic species within the unsaturated concrete.
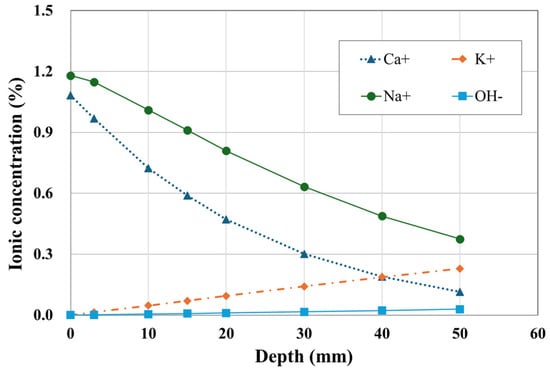
Figure 10.
Profile of various ionic concentration.
5. Conclusions
The durability of concrete structures exposed to aggressive environments is significantly affected by the ingress of deleterious ions, particularly chloride ions, which are a primary cause of reinforcement corrosion. In partially saturated concrete, the transport mechanisms of chloride (Cl−) and other ions (Na+, Ca2+, K+, OH−) become complex, due to the coexistence of liquid and gas phases within the pore structure. Accurate and reliable prediction of ion transport under these multiphase conditions is essential for evaluating the service life and long-term performance of reinforced concrete structures. This study aimed to clarify the mechanisms of ion diffusion in partially saturated concrete and to propose predictive methods based on mathematical modeling and numerical simulation. The key findings are as follows:
A multi-species transport model was developed based on the Nernst–Planck equation and implemented using a parallel finite element method. The model was formulated under the assumptions of electroneutrality and zero current, and it incorporated the coupled effects of moisture and temperature gradients in concrete. Material properties such as moisture and heat capacities were obtained from the literature, while coupling parameters for ion diffusivity were calibrated using experimental data.
A hygro-chemo-thermo transport model was numerically implemented within a parallel finite element framework. A large linear system of equations was derived and discretized using the Crank–Nicolson semi-implicit method. A computational framework was developed in C++ and integrated numerical algorithms from libraries including Triangle, ParMETIS, PETSc, and MIP. The code was parallelized using the Single Program Multiple Data (SPMD) model and overlapping domain decomposition techniques.
Experimental validation was conducted to ensure model reliability. Chloride ponding tests were performed under varying initial temperature conditions (20 °C, 35 °C, and 50 °C), water-to-cement ratios (0.55 and 0.65), and relative humidity differences (100% and 60%) between the concrete surface and interior. The results confirmed that the proposed transport model, accounting for diffusion mechanisms, ion interactions, and temperature effects, accurately predicted chloride ingress under both isothermal and non-isothermal conditions. Additionally, numerical simulations revealed the inward migration of the moisture front, which eventually stabilized at 100% relative humidity, indicating a steady-state condition. This moisture gradient was found to significantly enhance the transport of chloride, sodium, and calcium ions, thereby accelerating their penetration rates.
The model proposed in this study was developed to account for the effects of relative humidity and temperature on ion penetration in concrete. Its significance lies in the implementation of a parallel algorithm combined with the finite element method. Moreover, the model is advantageous in that it can be applied for the simulation and analysis of entire large-scale structures. However, additional experimental validation of the coupling parameter is necessary to enhance the reliability of prediction results.
Author Contributions
Conceptualization, G.L. and O.N.; data curation, O.N.; formal analysis, O.N.; funding acquisition, G.L.; investigation, G.L. and O.N.; methodology, G.L. and O.N.; supervision, G.L.; validation, O.N.; visualization, O.N.; writing—original draft, O.N.; writing—review and editing, G.L. and O.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
Author Okpin Na was employed by the company Hyundai E&C Technology Research Center. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
The Galerkin method is then applied to the weak forms, which leads to the finite element matrix as presented in Equation (A1):
where the element matrices and the variable vector are given by Equations (A2)–(A4)
Specifically, the components of the element matrices are given by Equations (A5)–(A17),
References
- Mehta, P.K. Durability of Concrete in Marine Environment—A Review. In Performance of Concrete in Marine Environment; Malhotra, V.M., Ed.; ACI Publication: Farmington Hills, MI, USA, 1980; pp. 1–20. [Google Scholar]
- Thomas, M.D.A.; Moffatt, E.G. The Performance of Concrete in a Marine Environment. In Proceedings of the ICDCS 2018, Vienna, Austria, 2–5 July 2018. [Google Scholar]
- Pratiwi, W.D.; Putra, F.D.D.; Triwulan; Tajunnisa, Y.; Husin, N.A.; Wulandari, K.D. A Review of Concrete Durability in Marine Environment; (IOP Conference Series: Materials Science and Engineering); IOP Publishing Ltd.: Bristol, UK, 2021. [Google Scholar]
- Coppola, L.; Beretta, S.; Bignozzi, M.C.; Bolzoni, F.; Brenna, A.; Cabrini, M.; Candamano, S.; Caputo, D.; Carsana, M.; Cioffi, R.; et al. The Improvement of Durability of Reinforced Concretes for Sustainable Structures: A Review on Different Approaches. Materials 2022, 15, 2728. [Google Scholar] [CrossRef]
- Ababneh, A.; Xi, Y. An Experimental Study on the Effect of Chloride Penetration on Moisture Diffusion in Concrete. Mater. Struct. 2002, 35, 659–664. [Google Scholar] [CrossRef]
- Ababneh, A.; Benboudjema, F.; Xi, Y. Chloride penetration in Nonsaturated concrete. J. Mater. Civ. Eng. 2003, 15, 183–191. [Google Scholar] [CrossRef]
- Suwito, A.; Cai, X.C.; Xi, Y. Parallel finite element method for coupled chloride moisture diffusion in concrete. Int. J. Numer. Anal. Model. 2006, 3, 481–503. [Google Scholar]
- Li, L.Y.; Page, C.L. Modelling of electrochemical chloride extraction from concrete: Influence of ionic activity coefficients. Comput. Mater. Sci. 1998, 9, 303–308. [Google Scholar] [CrossRef]
- Li, L.Y.; Page, C.L. Finite element modeling of chloride removal from concrete by an electrochemical method. Corros. Sci. 2000, 42, 2145–2165. [Google Scholar] [CrossRef]
- Truc, O.; Olliver, J.P.; Nillson, L.O. Numerical simulation of multi-species diffusion. Mater. Struct. 2000, 33, 566–573. [Google Scholar] [CrossRef]
- Lorente, S.; Carcassè, M.; Ollivier, J. Penetration of ionic species into saturated porous media: The case of concrete. Int. J. Energy Res. 2003, 27, 907–917. [Google Scholar]
- Nguyen, T.Q.; Baroghel-Bouny, V.; Dangla, P. Prediction of chloride ingress into saturated concrete on the basis of multi-species model by numerical calculations. Comput. Concr. 2006, 3, 401–422. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.-Y.; Page, C. A two-dimensional model of electrochemical chloride removal from concrete. Comput. Mater. Sci. 2001, 20, 196–212. [Google Scholar]
- Wang, Y.; Li, L.-Y.; Page, C. Modelling of chloride ingress into concrete from a saline environment. Build. Environ. 2005, 40, 1573–1582. [Google Scholar] [CrossRef]
- Yogarajah, E.; Hatanaka, A.; Kurumisawa, K.; Nawa, T. Modelling of Chloride Ion Transport in Slag Blended Cementitious Materials: Influence of Tortuosity and Surface Electrical Properties. In Proceedings of the 3rd International Congress on Durability of Concrete, Adelaide, Australia, 22–25 October 2017. [Google Scholar]
- Samson, E.; Lemaire, G.; Marchand, J.; Beaudoin, J. Modeling chemical activity effects in strong ionic solutions. Comput. Mater. Sci. 1999, 15, 285–294. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Numerical Solution of the Extended Nernst–Planck Model. J. Colloid Interface Sci. 1999, 215, 1–8. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Modeling the transport of ions in unsaturated cement-based materials. Comput. Struct. 2007, 85, 1740–1756. [Google Scholar] [CrossRef]
- Nielsen, E.P.; Geiker, M.R. Chloride diffusion in partially saturated cementitious material. Cem. Concr. Res. 2003, 33, 133–138. [Google Scholar] [CrossRef]
- Mao, L.; Li, L.; Kim, B. Modelling of Multi-species Transport in Concrete Under the Action of External Electric Field: Influence of the Overpotential at Electrode-electrolyte. J. Electroanal. Chem. 2022, 159, 116079. [Google Scholar] [CrossRef]
- Sharmilan, S.; Stang, H.; Michel, A. A Multi-species Reactive Transport Model Based on Ion-solid Phase Interaction for Saturated Cement-based Materials. Cem. Concr. Res. 2022, 159, 106861. [Google Scholar] [CrossRef]
- Sharmilan, S.; Stang, H.; Michel, A. Enhancement of a Multi-species Reactive Transport Model for Cement-based Materials under Cyclic Wetting and Drying Conditions. J. Build. Eng. 2023, 77, 107532. [Google Scholar] [CrossRef]
- Sharmilan, S.; Stang, H.; Michel, A. A Multi-species Reactive Transport Model Based on Gas-ion-solid Phase Interaction for the Carbonation of Cement-based Materials. Cem. Concr. Res. 2024, 175, 107349. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials: Adsorption isotherm. Adv. Cem.Based Mater. 1994, 1, 248–257. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials: Moisture capacity and diffusivity. Adv. Cem. Based Mater. 1994, 1, 258–266. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Thonguthai, W. Pore Pressure and Drying of concrete at high temperature. J. Eng. Mech. Div. 1978, 5, 1059–1079. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Chern, J.; Thonguthai, W. Finite element program for moisture and heat transfer in heated concrete. Nucl. Eng. Des. 1981, 68, 61–70. [Google Scholar] [CrossRef]
- Saetta, A.V.; Schrefler, B.A.; Vitaliani, R. The carbonation of concrete and the mechanism of moisture, heat and carbonation dioxide flow through porous materials. Cem. Concr. Res. 1993, 23, 761–772. [Google Scholar] [CrossRef]
- Sih, G.C.; Shih, M.T. Transient hygrothermal stresses in composites: Coupling of moisture and heat with temperature varying diffusivity. Int. J. Eng. Sci. 1980, 18, 19–42. [Google Scholar] [CrossRef]
- Lien, H.P.; Wittmann, F.H. Mass transfer in inhomogeneous porous media under thermal gradients. Nucl. Eng. Des. 1998, 179, 179–189. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-Chemo-Mechanical Model for Concrete. I: Hydration and Aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Gasch, T.; Malm, R.; Ansell, A. A Coupled Hygro-thermo-mechanical Model for Concrete Subjected to Variable Environmental Conditions. Int. J. Solids Struct. 2016, 91, 143–156. [Google Scholar] [CrossRef]
- Maric, M.K.; Ozbolt, J.; Balabanic, G. Application of the 3D Chemo-hygro-thermo Mechanical Model on Existing Bridges Exposed to Chlorides and Mechanical Damages. In Proceedings of the 7th International Conference on Euro Asia Civil Engineering Forum, Stuttgart, Germany, 30 September–2 October 2019. [Google Scholar]
- Isgor, O.B.; Razaqpur, A.G. Finite element modelling of coupled heat transfer, moisture transport and carbonation processes in concrete structures. Cem. Concr. Compos. 2004, 26, 57–73. [Google Scholar] [CrossRef]
- Isteita, M.; Xi, Y. The Effect of Temperature Variation on Chloride Penetration in Concrete. Constr. Build. Mater. 2017, 156, 73–82. [Google Scholar] [CrossRef]
- Tabrizinejadas, S.; Carrayrou, J.; Saaltink, M.W.; Baalousha, H.M.; Fahs, M. On the Validity of the Null Current Assumption for Modeling Sorptive Reactive Transport and Electro-Diffusion in Porous Media. Water 2021, 13, 2221. [Google Scholar] [CrossRef]
- Xi, Y.; Willam, K.; Frangopol, D.M. Multiscale modeling of interactive diffusion processes in concrete. J. Eng. Mech. 2003, 126, 258–265. [Google Scholar] [CrossRef]
- Xi, Y.; Bažant, Z.P. Modeling Chloride Penetration in Saturated Concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Homan, L.; Ababneh, A.N.; Xi, Y. The effect of moisture transport on chloride penetration in concrete. Constr. Build. Mater. 2016, 125, 1189–1195. [Google Scholar] [CrossRef]
- Triangle. Available online: https://www.cs.cmu.edu/~quake/triangle.html (accessed on 19 March 2025).
- Balay, S.; Buschelman, K.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; Smith, B.F.; Zhang, H. PETSc-Users Manual. In Technical Report ANL-95/11—Revision 2.1.5; Argonne National Laboratory: Lemont, IL, USA, 2008. [Google Scholar]
- MPICH Team. MPICH: A Portable Implementation of MPI. 1996–2005. Available online: https://www.anl.gov/mcs/mpich-a-highperformance-portable-implementation-of-mpi (accessed on 19 March 2025).
- Karypis, G. ParMETIS: Parallel Graph Partitioning and Sparse Matrix Ordering. 1996–2005. Available online: https://github.com/KarypisLab/ParMETIS (accessed on 19 March 2025).
- Paraview. Available online: https://www.paraview.org/ (accessed on 19 March 2025).
- Cai, X.-C. Overlapping domain decomposition methods. In Advanced Topics in Computational Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003; Chapter 2; pp. 57–95. [Google Scholar]
- Cai, X.-C.; Saad, Y. Overlapping domain decomposition algorithms for general sparse matrices. Numer. Linear Algebra Appl. 1996, 3, 221–237. [Google Scholar] [CrossRef]
- Damrongwiriyanupap, N.; Li, L.; Limkatanyu, S.; Xi, Y. Temperature effect on multi-ionic species diffusion in saturated concrete. Int. J. Comput. Concr. 2014, 13, 149–171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).