Abstract
Damage assessment methods fall into contact and non-contact approaches. Contact methods, like physical measurements, material sampling, and ultrasonic testing, provide detailed data but are time-consuming and require specialized equipment. In contrast, non-contact methods assess damage remotely, allowing for faster, safer, and large-scale evaluations, especially useful in post-disaster scenarios. However, there are currently no standardized non-contact methods for assessing damage levels in confined masonry walls after damaging seismic events in Peru. On the other hand, an experimental database of cyclic loading tests on confined masonry walls is available, supporting numerical simulations with calibrated mathematical models to estimate damage levels. This research extends the application of this database by analyzing the crack pattern imagery from the tested walls and correlating it with the lateral deformation (drift) to identify the damage levels. A high-accuracy crack measurement technique was developed, combining a convolutional neural network to generate a binary crack mask and a binary search algorithm to extract polylines and convert them into length measurements, achieving a detection accuracy of 78%. The measured crack patterns were normalized into an index, which was then correlated with the amplitude of the lateral deformation in each hysteretic loop. Finally, a relationship was established between drift and the damage level index. These findings contribute to the development of a rapid, non-contact damage assessment method for confined masonry walls in seismic-prone regions.
1. Introduction
Peru is located within a highly seismically active region known as the Pacific Ring of Fire, along the western coast of South America. Throughout history, three major earthquakes have significantly impacted the Lima Metropolitan Area, occurring in 1746, 1966, and 1974, with estimated magnitudes of 8.9, 7.9, and 7.8, respectively [1]. The 1746 earthquake is considered one of the most catastrophic events in Peruvian history, almost completely destroying the city of Lima and its port, Callao, which was subsequently devastated by a massive tsunami, resulting in thousands of fatalities and widespread destruction. The 1966 earthquake, with its epicenter located offshore near Huacho, although less severe than the 1746 disaster, caused substantial structural damage across Lima and nearby provinces, resulting in several casualties and exposing the vulnerability of modern urban development to seismic hazards. The 1974 earthquake, which struck the coastal regions of Lima and Ica, despite its relatively lower magnitude compared to historical megathrust events, caused moderate infrastructure damage and served as a stark reminder to both authorities and the public of the persistent seismic threat along the Peruvian coastline. An updated seismic hazard map [2] clearly delineates six distinct seismicity zones, with Lima located within the zone of highest seismic hazard. Figure 1 presents the seismic hazard map corresponding to probabilities of exceedance of 10% and 2% in 50 years, which are equivalent to return periods of 475 and 2475 years, respectively [2].
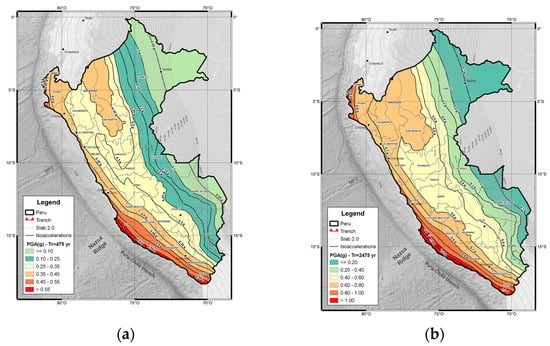
Figure 1.
Seismicity hazard map. (a) Tr = 475 years; (b) Tr = 2475 years [2].
Central Peru is located within a seismic gap, posing a significant risk of a megathrust earthquake with a magnitude between 8.5 and 8.9 [3], similar to that of the 1746 Lima earthquake. The Lima metropolitan area is particularly vulnerable, as it lies within the seismic gap and contains 83% of dwellings constructed with masonry [4], which have a high susceptibility to seismic damage.
Given this risk, the development of rapid damage assessment methods is crucial following destructive earthquakes. Direct crack measurement techniques can be challenging due to the anxiety of screeners caused by subsequent aftershocks, potentially compromising their safety. In this context, non-contact methods for surveying damaged walls and estimating the damage levels of confined masonry structures are urgently needed, as Peru currently lacks such survey techniques.
Rapid screening surveys for damage assessment expose inspectors to unsafe conditions, incur time costs, and increase the anxiety of occupants to return home. Moreover, detecting crack patterns can provide valuable insights into the reached maximum lateral displacement of the walls, which is essential for assessing economic losses and estimating retrofitting costs.
The experimental database of cyclic loading tests on confined masonry walls was collected by the Laboratory of Structures of CISMID [5]; this experimental database supported several investigations to approach the damage level by conducting numerical simulations with calibrated mathematical models [6,7] and photographic panels during the history of lateral deformations. The application of this database can be extended to the use of imagery of crack patterns of tested confined masonry walls to determine the corresponding drift and to identify the damage level.
Previous studies have investigated the impact of various crack patterns on masonry walls under seismic loads. The authors in [8] found that diagonal cracks are more likely to cause early collapse than vertical or horizontal cracks, emphasizing the need to assess diagonal cracking in seismic evaluations. Another research [9] introduced damage index equations based on crack pattern evolution, providing a quantitative approach to assessing seismic damage in masonry structures.
Non-contact methods for structural damage assessment have gained significant attention in recent years, particularly for post-disaster scenarios where rapid and safe evaluation is crucial. These approaches include photogrammetry, laser scanning, infrared thermography, and image-based crack detection using computer vision algorithms. Compared to traditional contact-based inspections, non-contact methods offer the advantage of minimizing human exposure to hazardous environments while enabling large-scale and efficient data acquisition [10,11]. Despite these advancements, standardized procedures for non-contact assessment of confined masonry walls are still lacking, particularly in regions highly prone to seismic hazards, such as Peru.
Machine learning and deep learning techniques, particularly convolutional neural networks (CNNs), have been widely applied to identify patterns in structural response data, enabling rapid post-earthquake damage assessment and accurate prediction of building safety conditions [12,13,14]. The detection and assessment of structural damage in confined masonry walls after an earthquake is a critical challenge in structural engineering. Recent advances in deep learning techniques have significantly improved the identification and quantification of cracks in various infrastructures, including buildings, pavements, and bridges. The application of CNNs has proven to be highly effective in automating crack detection, with methodologies leveraging both traditional CNN architectures and modern transformer-based networks. For instance, U-Net has been successfully applied to detect cracks in concrete surfaces, demonstrating robustness under different lighting conditions and complex backgrounds [15]. Similarly, deep learning approaches have been integrated with machine learning techniques to enhance the segmentation of bricks and the detection of cracks in masonry walls, improving automation and accuracy [16]. Moreover, transformer-based networks such as CrackFormer have been introduced for fine-grained crack detection, achieving state-of-the-art results by leveraging attention mechanisms and improving contextual feature extraction [17]. More recently, Hacıefendioğlu et al. [18] developed the CAM-K-SEG model, integrating Grad-CAM visualization and K-means clustering to automatically detect and segment cracks in historical masonry structures, outperforming traditional segmentation models like U-Net. Furthermore, Lazaridis and Thomoglou [19] proposed a machine learning-based ensemble approach combining XGBoost and CatBoost algorithms to accurately predict the shear capacity of TRM-strengthened unreinforced masonry walls, demonstrating the potential of machine learning for structural performance evaluation. These advancements highlight the growing role of deep learning in structural health monitoring, offering reliable and scalable solutions for post-earthquake damage assessment in masonry structures.
The analysis of crack patterns, together with experimentally measured restoring forces and corresponding drift values, was performed using two distinct methodologies. The first methodology relied on manual crack pattern surveys conducted throughout the experimental procedure. These hand-drawn surveys facilitated the detailed quantification and investigation of crack propagation relative to drift, resulting in the creation of crack propagation curves and a comprehensive database for further analysis. The second methodology involved the application of photographic image analysis leveraging advanced deep learning techniques, specifically a novel segmentation model utilizing convolutional neural networks. The CNN-based segmentation model was rigorously validated against the manually obtained results from the first methodology, confirming its accuracy, reliability, and potential for automated analysis.
The objective of this research is to develop a digital engineering tool designed for accurately estimating damage levels in confined masonry walls. By employing deep learning techniques, the tool analyzes images of damaged walls to calculate the crack length ratio—a normalized measure of crack presence. Subsequently, drift values are computed and integrated into a newly proposed equation to determine the damage index. Finally, the resulting damage index is classified based on a damage level derived from previous experimental databases. This innovative approach aims to offer an economical, user-friendly, and rapid method for conducting structural assessments and evaluating post-disaster damage.
Additionally, this study presents and thoroughly describes the experimental database of confined masonry walls utilized in this research. Furthermore, it investigates the relationship between the extent of cracking and the corresponding experimental drift by employing both conventional numerical methods and advanced deep learning techniques.
2. Experimental Basis and Structural Characterization of Confined Masonry Walls
This section presents the experimental database compiled for this study. The section is structured into subsections to distinguish between construction practice details, material characterization, and relevant experimental results. This organization aims to provide a comprehensive understanding of the confined masonry typology and its representative behavior under seismic conditions, based on available experimental studies.
2.1. Construction Practice
Confined masonry walls are used in buildings regulated by National Standards, such as the Earthquake-Resistant Design (E.030) [20] and the Masonry Technical Standard (E.070) [21]. A confined masonry wall consists of a masonry panel and reinforced concrete tie-columns and tie-beam. Typically, the masonry panels are constructed first and inter-locked with the tie-columns, which are then cast to enclose and confine the masonry panel.
In the Lima Metropolitan Area, masonry dwellings constitute the predominant building typology, with burned clay bricks being the principal masonry units [4]. Peruvian confined masonry construction incorporates three principal types of bricks: industrial vertical hollow bricks (K-type), handmade solid bricks (S-type), and industrial horizontal hollow or tubular bricks (T-type), as illustrated in Figure 2a–c, respectively. According to the current masonry standard [21], only K-type and S-type bricks are authorized for use in structural walls, whereas T-type bricks are designated for non-structural partition walls, particularly in high seismic hazard zones. Representative masonry dwellings in the region are predominantly non-engineered, often utilizing K-type or S-type bricks at lower floors for load-bearing purposes, while upper floors frequently incorporate T-type bricks. For instance, Figure 2d presents a typical confined masonry dwelling exhibiting S-type bricks on the first and second floors and T-type bricks on the third floor. This construction typology is recognized for its high seismic vulnerability [22].
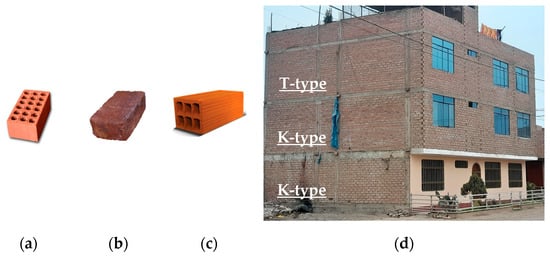
Figure 2.
Representative confined masonry dwelling in the Lima Metropolitan Area. (a) K-type brick, (b) S-type brick, (c) T-type brick, and (d) one of the representative dwellings.
2.2. Cyclic Lateral Loading Test on Full-Scale Confined Masonry Walls
The cyclic lateral loading test for confined masonry walls involves the application of incremental horizontal loads and uniform vertical loads in a quasi-static manner, simulating lateral reversal forces and axial loads on the wall. The number of cycles is determined based on the displacement protocol, as illustrated in Figure 3.
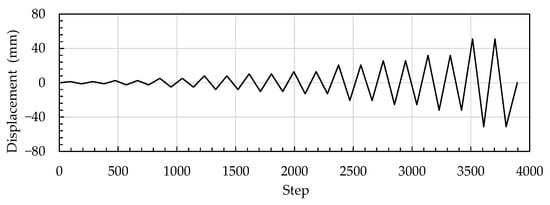
Figure 3.
Displacement protocol for cyclic lateral loading tests of confined masonry walls.
The cyclic loading test setup includes four hydraulic static jacks manufactured by Riken Seiki, model TCLP-500KNB-D, each capable of exerting a 500 kN load with a stroke range of ±250 mm. Two of these jacks are used to apply lateral cyclic forces, simulating seismic loads, while the remaining two jacks impose vertical loads to represent the gravitational effects of upper floors.
The horizontal jacks were anchored to the reaction wall and linked to a steel frame assembly to facilitate load transfer, as illustrated in Figure 4. Similarly, the vertical jacks were supported by the reaction floor and connected to the steel assemblage. The measurement system comprised load cells integrated into the jacks (CH-00 to CH-03) and LVDT displacement transducers positioned on the specimen (CH-04 to CH-20). All sensors and load cells were connected to a universal scanning system, the Tokyo Sokki TDS-530 data logger, as depicted in Figure 4.
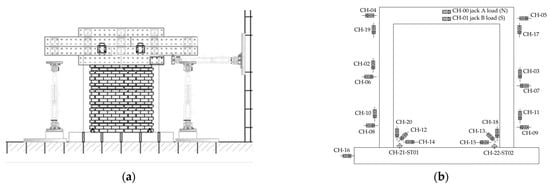
Figure 4.
Test setup. (a) Loading system for cyclic loading tests; (b) measuring system for cyclic loading tests.
2.3. Selected Confined Masonry Walls Database and Crack Amount
2.3.1. Description of the Experimental Database
The Laboratory of Structures of CISMID developed a database containing experimental results from cyclic lateral loading tests on confined masonry walls [6]. The database includes hysteresis and skeleton curves, sensor distribution data, and detailed records of crack patterns, including drawings and images captured at each step and peak displacement according to the displacement protocol (Figure 2).
In this study, fourteen full-scale specimens were selected to represent typical confined masonry dwelling construction in the Lima Metropolitan Area. Full-scale specimens were chosen to accurately replicate the construction practices and structural behavior of real housing units, ensuring that the observed failure mechanisms and performance outcomes are applicable to actual conditions.
The specimens selected for this study were obtained from three different research projects. Ten specimens were funded by the National Training Service for the Construction Industry (SENCICO) in 2017, two were funded by the Program for the Reduction of Vulnerability and Emergency Attention for Disasters (PP0068), and the remaining two were supported by the National Council of Science, Technology, and Technological Innovation under contract 115-2018-FONDECYT (project VIRVI-ALB).
Two types of masonry units were used in these tests: handmade solid bricks (S) and industrial tubular bricks (T), which are among the most representative masonry units in the Lima Metropolitan Area [4].
The confined masonry walls generally measured 2500 mm in height and 2600 mm in width. Their confinement system comprised reinforced concrete tie-columns and a tie-beam. The tie-columns were 200 mm long, while the tie-beam had a height of 300 mm. Both the columns and the beam matched the masonry wall thickness in width. Reinforcement for each tie-column and tie-beam included four longitudinal #4 bars (12.7 mm) and #2 stirrups (6.0 mm), arranged as follows: 1@50 mm, 4@100 mm, and then spaced at 250 mm intervals. Additionally, the specimen featured a foundation designed to connect it to the reaction floor, with a cross-section of 900 mm × 300 mm and a total length of 3200 mm.
2.3.2. Cumulative Crack Length
Crack patterns were recorded throughout the testing process following a cyclic lateral displacement protocol. The number, location, and evolution of cracks were documented at each step, supported by detailed sketches and photographic records. This allowed for an accurate quantification of damage propagation and correlation with the target drift.
After reaching the target drift, a photographic image corresponding to that specific drift level is captured. Subsequently, to document crack propagation, the damage observed on the walls is digitized using V.72.0.0 AutoCAD 2025.0.1 software. The cracks are represented as polylines, allowing for precise measurement of their lengths at each target drift, as shown in Figure 5. Additionally, the relationship between crack length and the corresponding drift for the specimens presented in Table 1 is illustrated in Figure 6.
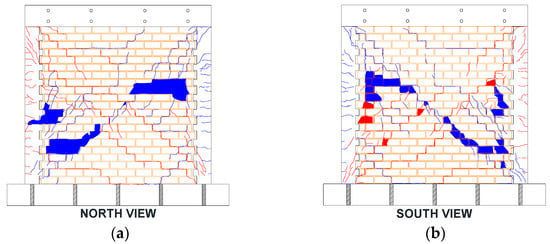
Figure 5.
Digitized crack pattern of the masonry wall using AutoCAD software: (a) north-facing view; (b) south-facing view.

Table 1.
Selected confined masonry walls tested under cyclic lateral loading.
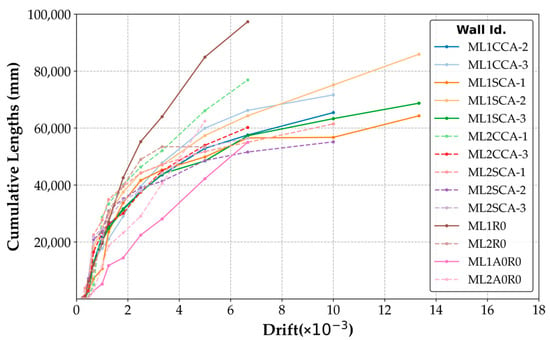
Figure 6.
Crack propagation in the confined masonry walls of database.
The evolution of crack pattern was systematically documented during each loading cycle, based on the predefined displacement protocol. At each increment, visible cracks were recorded on the specimen surface, photographed, and digitized for further analysis. This process enabled a detailed assessment of crack initiation, propagation, and accumulation throughout the test.
The primary metric used in this section is the total number of cracks observed at target drift for each wall. This indicator provides a comparative view of the cracking intensity between different specimen configurations and construction practices.
To facilitate visualization, Figure 6 presents the distribution of crack types across all specimens, highlighting trends according to brick type. In general, walls constructed with solid bricks exhibited a higher number of diagonal cracks, which are commonly associated with shear-dominant failure mechanisms. Conversely, T-type brick walls tended to develop fewer cracks but exhibited a larger number of horizontal or flexural-type cracks at earlier drift stages.
2.4. Damage Level Classification
Non-engineered masonry dwellings often exhibit significant structural irregularities, particularly due to variations in the type of brick across different stories, as illustrated in Figure 2. These material differences lead to varying inelastic behavior at each story, depending on the type of brick used in its construction.
Confined masonry walls constructed with handmade solid bricks exhibit a higher lateral deformation capacity compared to those constructed with tubular bricks, as shown in Table 2. The drift limits used in Table 2 for damage level classification were derived from the experimental presented by Diaz et al. [23] and from specimens listed in Table 1. As a result, the most damaged story is not necessarily the one with the highest drift but rather the one that reaches its drift limit first.

Table 2.
Drift limits at damage levels for confined masonry walls.
To efficiently identify the most damaged story in confined masonry dwellings with material variations, drift values obtained at each floor were normalized based on the type of brick used in construction. This normalization process involves determining a damage index, which allows for the identification of the most affected story regardless of material inconsistencies along the dwelling’s height. Additionally, the index provides insight into the extent of damage sustained by each story.
The damage levels associated with this index are categorized as Undamaged or Slight, Light, Moderate, Extensive, and Collapse, as illustrated in Figure 7. It is important to note that the ultimate stage is defined as 80% of the maximum restoring force. Beyond this threshold, confined masonry walls are considered to have undergone total collapse. The collapse category indicates that while the walls may still support gravity loads, they have lost their lateral load-bearing capacity.
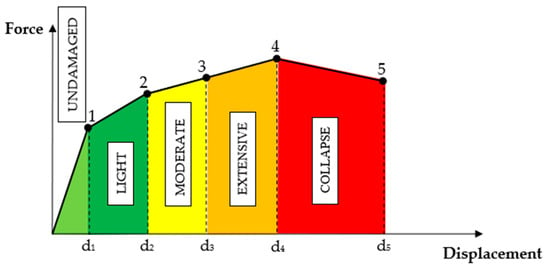
Figure 7.
Damage levels and corresponding damage index.
The damage levels are represented in the capacity curve, as shown in Figure 7. The Undamaged level indicates that the confined masonry wall remains below the cracking stage (Point 1). The Slight Damage level indicates that the wall is within the cracking stage and the yielding stage (Point 2). The Moderate Damage level indicates that the wall is within the yielding stage and the extensive damage stage (Point 3), with this threshold varying depending on the type of confined masonry wall. The Extensive Damage level signifies that the wall lies between the extensive damage stage and the maximum stage (Point 4). Finally, the Collapse level indicates that the wall has surpassed the maximum stage. The drift limits corresponding to each damage level are provided in Table 2, and the index value ranges are presented in Table 3 [24].

Table 3.
Index values for damage level [24].
The following equations [24] enable the calculation of the damage index of confined masonry walls, based on the maximum drift reached () by the wall and the type of brick unit used in their construction. These index values provide information about the damage level of the wall.
where represents the damage index, while , , , and denotate the drift limit for the Undamaged or Slight, Light, Moderate, Extensive, and Collapse level, respectively. When the damage index exceeds a value of 5, it indicates that the story has surpassed its ultimate stage, resulting in the total collapse of the wall.
3. Crack Pattern Identification
3.1. Crack Labeling
A critical aspect of evaluating the seismic performance of confined masonry walls is the precise identification of crack patterns throughout different drift states. During quasi-static testing, each specimen is subjected to incremental lateral displacements until failure. At each increment—often referred to as a drift level—high-resolution images are captured to document emerging or expanding cracks. These visual records serve as the foundation for mapping the evolution of damage and correlating it with structural performance indicators such as lateral strength, stiffness degradation, and energy dissipation.
To facilitate the labeling and cataloging of cracks, a custom software tool named Crack Labeler version 1.0 [25] was developed using Python Version 3.8 [26]. This application features a user-friendly graphical interface that enables operators to open images of wall specimens and manually draw lines over the regions where cracks are observed. Each annotated line is recorded along with a color label indicating the direction of the hydraulic actuator’s action: red for pushing and blue for pulling. In this context, pushing refers to a shear stress flow along the blue-marked cracks, whereas pulling corresponds a shear stress flow along the red-marked cracks as show in Figure 5 and Figure 8a. Once the labeling process is completed, the software generates both a graphical mask and a corresponding numerical record in a separate file. This binary mask can then be passed to a skeletonization algorithm for finer delineation of the cracks, enabling a more precise and streamlined analysis of crack trajectories in subsequent stages of the research.

Figure 8.
Crack labeling process. (a) Cracks labeled during pull (red) and push (blue) phases; (b) corresponding binary mask.
Within the program, each labeled stroke is recorded in a history log, enabling iterative refinement of the crack labeling without losing previously annotated information. Once all cracks in a particular image are labeled, the software automatically generates both a colored composite mask (highlighting different crack groups) and a binary mask for further image processing tasks. The resulting information can then be used to quantify crack density, trace propagation paths, and even link specific cracking sequences to the moment in the test protocol when they occurred. This automated labeling approach ensures reproducibility, minimizes the risk of overlooking subtle cracks, and considerably reduces the time required to process large sets of images from extensive experimental campaigns.
3.2. Deep Learning Model
A brief review of crack segmentation models based on convolutional neural networks was conducted, prioritizing the accuracy of the final mask concerning the labeled data. Among these models, the application of the following stands out: DeepCrack [27], Crack Segmentation [28], a UAV-based method using deep learning and binocular vision [29], which performed well during both the training and validation processes. As shown in Figure 9, although two of the models perform well in smooth surface areas, clearly their inferences in rough surface areas reveal confusion between the mortar joints and the presence of cracks. This occurs because the training images predominantly feature cracks on smooth surfaces. Therefore, these models are not suitable for the objectives of this research. As a result, it was decided to train a new model using a dataset generated through an implemented tool.

Figure 9.
Current state-of-the-art applied to tested wall images. (a) Tested image. (b) DeepCrack. (c) Crack Segmentation. (d) Pavimendonia.
At the initial stage of the research, the objective was to determine three parameters (number, length, and slope) of the cracks or fissures in the confined masonry walls tested in laboratory. Crack width is widely recognized in structural assessments as a relevant indicator of damage severity; however, this parameter was not included in the present analysis due to the inability of the neural network to accurately detect it, primarily because of the limited resolution of the available damage imagery. This led to the choice of an instance segmentation model instead of a semantic segmentation model, due to the need for differentiation between detected objects. Mask2Former [30], Mask R-CNN [31], and YOLOv11 [32] were selected to fulfill this purpose.
3.3. Experimental Setup
The development environment for this phase of segmentation and crack length ratio calculation utilized Python 3.8 [26], PyTorch 2.1 [33], CUDA 12.4, CuDNN 9.2, and several libraries such as OpenCV [34] and Pillow [35]. Given the limited physical computational capacity available, a virtual machine with a GPU was rented on the RunPod platform, equipped with 32vCPUs, 32 GB RAM, and two 24 GB RTX 4090 graphics cards.
3.4. Hyper Parameter Details
The image size was determined based on the requirements of the selected model for the training process. Training was conducted over 120 epochs with a batch size of 16. The loss function employed was Cross-Entropy, and the optimization algorithm used was AdamW [36]. The initial learning rate was set to 0.001, with a decay factor of 10−1 applied every 10 epochs.
After multiple preliminary trials and comparative analyses, the selected hyperparameters demonstrated superior performance in training the deep learning models. A batch size of 16 was found optimal for balancing computational efficiency with model stability. The initial learning rate of 0.001 consistently achieved stable convergence without overshooting minima, further refined through a scheduled decay by a factor of 10 every 10 epochs to enhance training precision. The training spanned 120 epochs employing the AdamW optimizer, which effectively managed overfitting and ensured robust learning. A summary of training parameters is showed in Table 4.

Table 4.
Summary of training parameters for the deep learning model.
3.5. Dataset and Training
The dataset used for training the models described in the previous section was obtained from the results of the Crack Labeler version 1.0 software. This dataset was subdivided into smaller images of 640 × 640 pixels, including both the original image and the corresponding binary mask. The labeled images are not homogeneous in terms of size or resolution, making it necessary to adapt the subdivision at the edges by default. Furthermore, it is important to consider that lighting conditions [37], camera angles, and perspectives vary across the labeled samples. Given these variations, a data augmentation process will be applied. The split of the dataset by class for training and validation is shown in Table 5.
where represents the number of classes and Intersection over Union () also known as the Jaccard Index (Figure 10), which is a critical metric for evaluating segmentation models, as it measures the model’s ability to differentiate objects from the background effectively. Table 6 show models performance for training and validations prosses.

Table 5.
Labeled reference data used for training, validation of DCNNs.

Figure 10.
Intersection over Union (IoU).

Table 6.
Performance metrics of instance segmentation models.
Figure 11 shows a batch from the validation dataset, where the left side illustrates the manual labeling of cracks using the conventional method and the right side presents the images processed by the instance segmentation model. Additionally, it is highlighted that despite some images having incorrect or missing labels, the model demonstrates the ability to identify these cracks effectively.

Figure 11.
Crack segmentation. (a) Batch of labeled images; (b) batch of corresponding inferenced images.
3.6. Skeleton Algorithm
Following the generation of binary masks, the next phase involves converting the labeled crack regions into refined polylines using a skeleton algorithm, sometimes referred to as skeletonization. This procedure aims to reduce each crack to a single-pixel-wide centerline while retaining its principal geometry and connectivity. In this work, the skeletonization approach is partially inspired by the open-source implementation provided in the skeleton-tracing library by LingDong [38], which applies a set of morphological operations to iteratively trim away outer pixels until only the essential “skeleton” remains (Figure 12).

Figure 12.
Results of thinning algorithm for drift values.
Once the skeleton is obtained, each crack is represented as a polyline with clearly defined nodes and edges (Figure 13). This representation confers two critical advantages for subsequent analysis. First, it enables straightforward computation of total crack length, since each segment in the polyline can be measured precisely and summed to yield a global metric of damage. Second, the directional data encapsulated within the polyline facilitate more nuanced assessments of crack orientation, propagation trends, and potential localization of damage. These attributes become increasingly valuable when correlating observed crack patterns with structural responses, such as lateral drift or load capacity, across different stages of quasi-static testing. By integrating the skeleton-tracing technique into the crack analysis workflow, researchers can more accurately quantify crack progression and better visualize the complexity of damage evolution (Figure 14).

Figure 13.
Pipeline for crack detection and skeletonization: (a) quasi-static test wall, (b) binary crack mask from crack-labeler, (c) skeletonization of the mask, and (d) polyline representation of crack structures (each polyline is represented by one color).
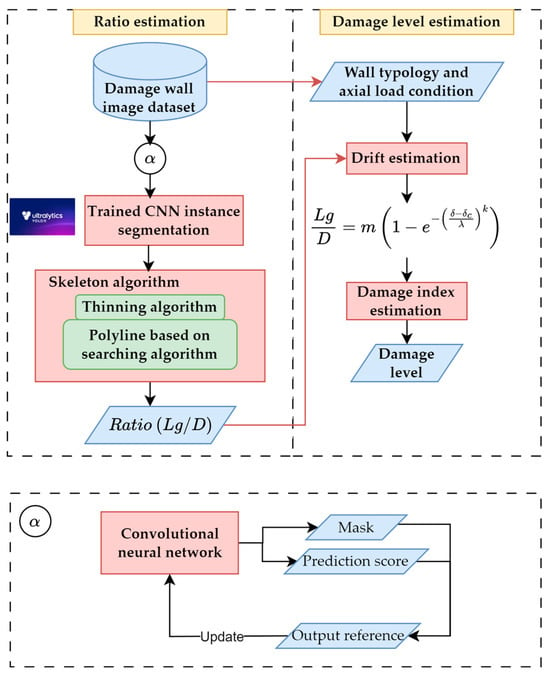
Figure 14.
Methodology flowchart for crack length ratio ( and damage level estimation.
4. Crack Length Ratio and Damage Index Correlation
To determine the damage level of a confined masonry wall based on the observed cracks, a relationship was established between the amount of cracks and the corresponding drift level using the database presented in Table 1. Confined masonry walls predominantly exhibit shear deformation, characterized by diagonal crack patterns across confined masonry wall. To a lesser extent, these walls also display flexural deformation, indicated by horizontal cracks in the tie-columns [39], as illustrated in Figure 13. Nevertheless, the developed deep learning model considers all crack patterns due to the predominance of shear deformation. The total crack length in the wall was calculated and standardized by normalizing it with the length of the main diagonal, defining the crack length ratio () as the relationship between the total crack length and the diagonal length of the wall.
Analysis of the database shows that the crack length ratio depends on both the type of bricks used in the confined masonry walls and the axial stress applied, as shown in Figure 15. The axial stress refers to stress effect due to vertical constant load applied on the wall. Figure 15a illustrates that the ML1A0R0 wall exhibits a different crack length ratio curve compared to the other walls in the same figure. This difference arises because, in the ML1A0R0 wall, cracks predominantly formed within the bricks, leading to damage concentration in a few cracks. In contrast, for the other walls, cracks were distributed between both the mortar and the bricks, resulting in a greater number of cracks spread throughout the wall. Consequently, the analysis and formulations for calculating the crack length ratio will focus on cases where cracks are uniformly distributed across the entire wall surface.
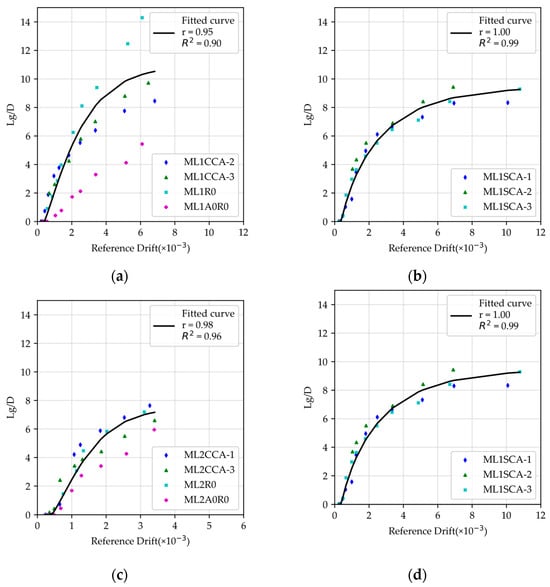
Figure 15.
Crack length ratio in confined masonry wall. (a) Handmade solid brick walls with axial load. (b) Handmade solid brick walls without axial load. (c) Tubular industrial bricks wall with axial load. (d) Tubular industrial bricks wall without axial load.
Figure 15a–d show that the crack length ratio at ultimate stage () remains approximately constant on average when considering the same type of brick regardless of the type of brick. However, the drift value at the ultimate stage varies depending on the axial stress applied on the walls, and it can be seen that the distortion for the ultimate state is lower in the case of high axial stresses, or walls with lower axial stress exhibit greater lateral deformation capacity. It is also important to note that walls made with tubular brick (T) have lower deformation capacity compared to walls made with solid handmade brick (S), both for high and low axial stresses.
Therefore, the crack length ratio at ultimate stage can be expressed as a parameter that depends on the type of brick used in the confined masonry wall, as shown in Equation (8). This parameter () represents the total energy dissipated through the damage, reflected in the cracking pattern, at the ultimate stage or Collapse level.
Since the crack length increases with wall deformation, a mathematical expression based on the Weibull probability distribution was used to determine the crack length ratio, as written in Equation (9). This function depends solely on the maximum drift reached () and includes the calibration parameters , , and , which adjust Equation (9) to match the experimental values for each wall type. Parameters for evaluating the crack length ratio in structural assessments are shown in Table 7. The parameter represents the drift at the onset of cracking and is expressed in units of 1/1000. For all wall cases , a value of 0.4 is assigned.

Table 7.
Parameters for evaluating the crack length ratio in structural assessments.
5. Results and Discussion
5.1. Model Validation
In the laboratory tests, a manual crack identification process was conducted for each damage level of every wall specimen. Initially, existing cracks were marked directly on the physical specimens using distinct colors. Subsequently, photographs capturing both the wall specimens and the marked cracks were digitized using V.72.0.0 AutoCAD 2025.0.1 software, ensuring the images were accurately scaled to the actual dimensions of the specimens.
This setup enabled precise tracing of crack paths, facilitating accurate measurement of their total lengths. From these measurements, the parameter was derived, serving as the reference value for this investigation.
To assess the reliability of the deep learning approach in estimating the dimensionless parameter , comparisons were conducted between the predicted and reference values of the crack length ratio. This evaluation was performed for each wall specimen across all damage levels. To quantify the accuracy of these predictions, several statistical indicators were computed, including the Mean Squared Error (MSE), Root Mean Squared Error (RMSE), correlation coefficient (r), and coefficient of determination (R²). These metrics, summarized in Table 8, illustrate the extent of agreement between the deep learning predictions and the experimentally measured data.

Table 8.
Metrics for every confined masonry wall; both directions are joined.
The data presented in Table 8 clearly demonstrate that most specimens consistently achieve low values of Mean Squared Error (MSE) and Root Mean Squared Error (RMSE), along with high correlation coefficients (r) and coefficients of determination (R²), as illustrated in Figure 16. For example, specimen Wall ML1A0R0 shows an MSE of 0.118, an RMSE of 0.343, and high correlation metrics (r = 0.994, R2 = 0.983), indicating an outstanding agreement between the predicted and reference crack length ratios.
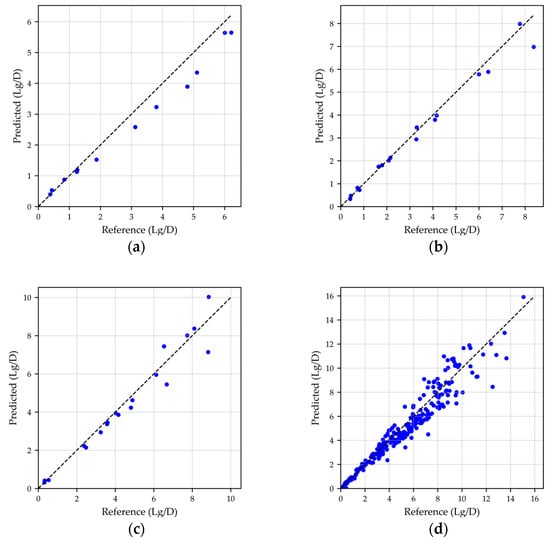
Figure 16.
Comparison of predicted and reference ratios. (a) ML1SCA-1; (b) ML1A0R0; (c) ML2CCA-3; and (d) all specimens.
To further validate these findings, individual scatter plots were produced for each specimen, combining data from both the north and south faces. In these plots, the horizontal axis represents the reference ratio measured using AutoCAD, while the vertical axis depicts the predicted ratio derived from the deep learning model. Observations from these plots reveal that nearly all data points cluster closely around the 1:1 reference line, confirming a robust alignment between the actual and estimated values across various loading protocol stages.
While the manual crack measurement process using AutoCAD provided highly de-tailed crack traces, it proved to be labor-intensive and time-consuming, requiring an average of three hours per specimen, considering both sides of the wall for every drift value. In contrast, the proposed deep learning-based segmentation model significantly reduced time processing to approximately one minute per specimen, demonstrating a substantial improvement in evaluation speed without compromising accuracy.
Both methods achieved highly correlated measurement results, as evidenced by an average coefficient of determination (R2) of 0.944 (Table 8). However, the deep learning approach provides additional critical advantages over the manual method. Specifically, it ensures greater consistency in crack detection and effectively eliminates human-induced biases, such as fatigue or subjective judgments, which are common during extensive manual evaluations.
Therefore, incorporating deep learning techniques into post-earthquake damage assessment processes represents a scalable, robust, and efficient alternative to traditional manual inspection methods.
5.2. Damage Index Validation
To validate the proposed method, the damage index was calculated using drift values derived from crack length ratios predicted by the deep learning model (predicted value). Specifically, images of damaged confined masonry walls were analyzed to estimate the crack length ratio through the deep learning method; subsequently, drift values were computed using Equation (9), and finally, the damage index was determined based on Table 3. These results were then compared to the damage index obtained from drift values experimentally measured during the tests (reference value).
To demonstrate the accuracy of the damage index estimates, Figure 17 compares the reference and predicted damage index for four selected cases. Figure 17a contains the complete dataset, including all walls and their deformation states, resulting in an RMSE of 0.71. This indicates that, on average, predictions closely align with the 1:1 reference line, representing an acceptable estimation of the damage index. Figure 17b contains the case of wall ML2A0R0, whose RMSE error is 0.61, closely matching the average RMSE calculated across all walls (see Table 8). Figure 17c illustrates the results for wall ML1A0R0, exhibiting the highest RMSE (1.35) among the 14 walls evaluated. This elevated error can be attributed to the distinct cracking pattern observed in ML1A0R0, characterized predominantly by brick cracks that concentrated damage into fewer, larger cracks. Figure 17d shows the results for wall ML2R0, which achieved the lowest RMSE value (0.25) within the sample analyzed.
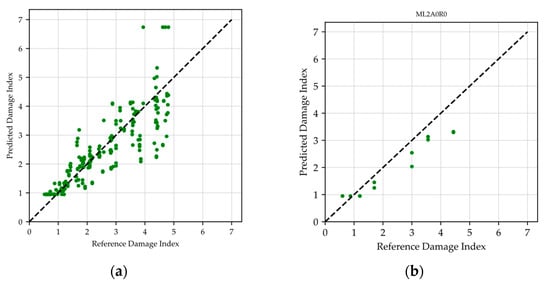
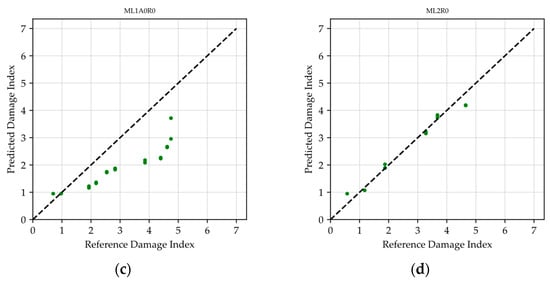
Figure 17.
Damage index comparison (a) all walls, (b) mean MRSE case, (c) maximum MRSE case wall, and (d) minimum MRSE case.
Table 9 presents the statistical error metrics and the dispersion coefficients r and R2 for the reference and predicted damage indices of each sample wall. It can be observed that the individual values of r and R2 are close to 1, which indicates that individually the dispersion of the estimated values is low, but not necessarily close to the reference values. Then, to analyze the pressure of the method, the RMSE errors were used, where good results of damage index are found for RMSE values lower than 0.5, while regular estimates are found for RMSE values higher than 0.5 and lower than 0.8.

Table 9.
Statistical metrics of damage index prediction.
Figure 18a presents the confusion matrix in terms of occurrence, emphasizing a higher predominance in the Slight and Moderate damage levels. In contrast, Figure 18b illustrates the accuracy of the method, showing higher precision for the Undamaged or Slight, Light, and Moderate damage levels, with values of 82.50%, 72.58%, and 71.74%, respectively. For the Severe Damage and Collapse level, the percentage of correct estimations is 50% and 52.5%, respectively.
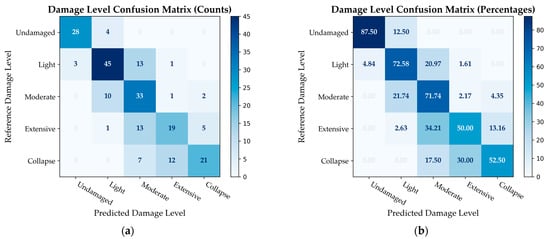
Figure 18.
Confusion matrices of damage levels. (a) Number of occurrences. (b) Relative proportions.
6. Conclusions
A rapid, non-contact method for assessing damage in confined masonry walls was developed using photographic image analysis enhanced by deep learning techniques trained on an experimental dataset. The deep learning model created within this study effectively quantifies crack lengths, whether cracks in smooth face walls or raw face walls. Additionally, one proposed equation to estimate crack length ratio based on the maximum drift experienced during seismic events was validated, demonstrating its potential as a reliable tool for rapid damage assessment post-earthquake.
The results obtained from the training metrics indicate that the YOLOv11 instance segmentation model outperforms the other models, achieving an mAP@0.5 of 0.62 and an mAP@0.5–0.95 of 0.31. Although these values suggest relatively low precision in the predicted mask, the model demonstrates a high capability in crack detection and length estimation. This is supported by a strong correlation between the predicted and reference values, with a mean R2 of 0.944 across all tested walls.
The proposed equation to calculate the crack length ratio in terms of the confined masonry wall drift demonstrates high precision for Slight, Light, and Moderate damage levels, achieving success rates above 70%. For Severe Damage and Collapse levels, the prediction accuracy decreases to approximately 50%; however, significant damage in such cases is typically evident through visual inspection. Despite this limitation, the proposed methodology greatly supports damage assessments, especially in instances where expert judgment alone may be inadequate.
This approach offers a promising alternative for rapid structural damage assessment, particularly when direct visual inspection is subjective or limited. Further research is recommended to validate its applicability to other confined masonry wall types and enhance overall accuracy. Additionally, other crack pattern characteristics, such as slope, location, concentration, and failure mechanism, should be incorporated into damage assessments. Integrating these parameters into the dataset could further enhance the predictive performance of the deep learning model.
Moreover, the presented methodology constitutes an automated procedure that could be integrated into a practical tool or software for real-world applications. Building on this automation, future research could explore the use of unmanned aerial vehicles (UAVs) to perform real-time damage detection during seismic events, further enhancing operational efficiency while minimizing human exposure to hazardous conditions in post-earthquake environments.
Author Contributions
Conceptualization, M.D.; Data curation, M.A.; Funding acquisition, M.D.; Investigation, M.D., L.L., M.A. and I.I.; Methodology, M.D., L.L. and E.F.; Project administration, I.I.; Software, J.S. and S.I.; Supervision, E.M.; Writing—review and editing, E.F. and E.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research project (24-2024-003040-VRI-UNI) was funded by the Office of the Vice-Rectorate for Research at the National University of Engineering.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the National Training Service for the Construction Industry (SENCICO), the Program for the Reduction of Vulnerability and Emergency Response to Disasters (PP0068), and the National Council of Science, Technology, and Technological Innovation (FONDECYT), under contract No. 115-2018-FONDECYT (project VIRVI-ALB), for providing experimental data through their funded research programs.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional Neural Network |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| CISMID | Peruvian–Japanese Center of Seismic Research and Disaster Mitigation |
| SENCICO | National Training Service for the Construction Industry |
| FONDECYT | Technology, and Technological Innovation under contract |
References
- Silgado, E. Historia de los Sismos más Notables Ocurridos en el Perú (1513–1974); Serie C: Geodinámica e Ingeniería Geológica; Instituto de Geología y Minería del Perú: San Borja, Perú, 1978. [Google Scholar]
- Aguilar, Z.; Tarazona, J.C. New Seismicity Based Seismic Sources and Hazard Model for Peru. In Proceedings of the 18th World Conference on Earthquake Engineering–WCEE, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
- Pulido, N.; Aguilar, Z.; Tavera, H.; Chlieh, M.; Calderón, D.; Sekiguchi, T.; Nakai, S.; Yamazaki, F. Scenario Source Models and Strong Ground Motion for Future Mega-earthquakes: Application to Lima, Central Peru. Bull. Seismol. Soc. Am. 2015, 105, 368–386. [Google Scholar] [CrossRef]
- Diaz, M.; Zavala, C.; Estrada, M.; Matsuoka, M. Characterization of the Structural Typologies of Buildings in the Lima Metropolitan Area. J. Disaster Res. 2023, 18, 329–337. [Google Scholar] [CrossRef]
- CISMID Experimental Wall Database 2015. Available online: https://www.cismid.uni.edu.pe/base-de-datos-del-laboratorio-de-estructuras-satreps-project-jica-gobierno-del-peru-ppr-068/ (accessed on 6 July 2024).
- Sugano, S.; Saito, T.; Zavala, C.; Cardenas, L. Strength and Deformation of Confined Brick Masonry Walls Subjected to Lateral Forces—Review of Existing Test Data in Japan and Peru—. J. Disaster Res. 2014, 9, 984–992. [Google Scholar] [CrossRef]
- Cardenas, L.; Reyna, R.; Estacio, L.; Zavala, C. Implementation of Database of Masonry Walls Test—Review of Existing Test Data in Peru. J. Disaster Res. 2014, 9, 993–1000. [Google Scholar] [CrossRef]
- Choi, Y.; Park, D.; Kim, S.; Hong, J.-W. Seismic Performance of Crack-Damaged Masonry Wall Structures via Shaking Table Tests. Structures 2022, 45, 2272–2291. [Google Scholar] [CrossRef]
- Sarhosis, V.; Dais, D.; Smyrou, E.; Bal, İ.E.; Drougkas, A. Quantification of Damage Evolution in Masonry Walls Subjected to Induced Seismicity. Eng. Struct. 2021, 243, 112529. [Google Scholar] [CrossRef]
- Kim, M.-K.; Wang, Q.; Li, H. Non-Contact Sensing Based Geometric Quality Assessment of Buildings and Civil Structures: A Review. Autom. Constr. 2019, 100, 163–179. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Huang, C.-W. Non-Contact Measurement of Inter-Story Drift in Three-Layer RC Structure under Seismic Vibration Using Digital Image Correlation. Mech. Syst. Signal Process. 2020, 136, 106500. [Google Scholar] [CrossRef]
- Oh, B.K.; Park, Y.; Park, H.S. Seismic Response Prediction Method for Building Structures Using Convolutional Neural Network. Struct. Control Health Monit. 2020, 27, e2519. [Google Scholar] [CrossRef]
- Oh, B.K.; Kim, J. Optimal Architecture of a Convolutional Neural Network to Estimate Structural Responses for Safety Evaluation of the Structures. Measurement 2021, 177, 109313. [Google Scholar] [CrossRef]
- Alcantara, E.A.M.; Saito, T. Machine Learning-Based Rapid Post-Earthquake Damage Detection of RC Resisting-Moment Frame Buildings. Sensors 2023, 23, 4694. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, Y.; Wang, Y.; Wang, W. Computer Vision-Based Concrete Crack Detection Using U-Net Fully Convolutional Networks. Autom. Constr. 2019, 104, 129–139. [Google Scholar] [CrossRef]
- Loverdos, D.; Sarhosis, V. Automatic Image-Based Brick Segmentation and Crack Detection of Masonry Walls Using Machine Learning. Autom. Constr. 2022, 140, 104389. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y. CrackFormer: Transformer Network for Fine-Grained Crack Detection. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 18–24 June 2022; IEEE: New York, NY, USA; pp. 1–8. [Google Scholar]
- Haciefendioğlu, K.; Altunişık, A.C.; Abdioğlu, T. Deep Learning-Based Automated Detection of Cracks in Historical Masonry Structures. Buildings 2023, 13, 3113. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Thomoglou, A.K. Rapid Shear Capacity Prediction of TRM-Strengthened Unreinforced Masonry Walls through Interpretable Machine Learning Deployed in a Web App. J. Build. Eng. 2024, 98, 110912. [Google Scholar] [CrossRef]
- E.030; Earthquake-Resistant Design. SENCICO Technical Standard of Buildings. SENCICO: Lima, Peru, 2018.
- E.070; Masonry. SENCICO Technical Standard of Buildings. SENCICO: Lima, Peru, 2006.
- Diaz, M.; Zavala, C.; Lopez, L.; Amancio, M. Analysis of Adaptive Pushover in Confined Masonry Dwellings with Height Irregularity in the Lima Metropolitan Area. J. Disaster Res. 2023, 18, 350–358. [Google Scholar] [CrossRef]
- Diaz, M.; Zavala, C.; Gallardo, J.; Lavado, L. Experimental Study of Non-Engineered Confined Masonry Walls Retrofitted with Wire Mesh and Cement-Sand Mortar. In Proceedings of the 16th World Conference on Earthquake, 16WCEE 2017, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Lopez, L.; Diaz, M. Análisis de la Eficacia del Reforzamiento de Viviendas de Albañilería Confinada Usando Malla de Acero y Mortero en Lima Metropolitana; Universidad Nacional de Ingeniería: Lima, Peru, 2023. [Google Scholar]
- CISMID. Crack Labeler 2025, Version 1.0. Available online: https://github.com/tic-cismid/Crack_labeler (accessed on 6 July 2024).
- Python Software Foundation. Python Language Reference, Version 3.8 ed; Python Software Foundation: Beaverton, OR, USA, 2025. [Google Scholar]
- Zou, Q.; Zhang, Z.; Li, Q.; Qi, X.; Wang, Q.; Wang, S. Deepcrack: Learning Hierarchical Convolutional Features for Crack Detection. IEEE Trans. Image Process. 2019, 28, 1498–1512. [Google Scholar] [CrossRef]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic Crack Detection from Pavement Images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, H.; Li, P.; Zhang, K.; Hong, W.; Guo, R. A Pavement Crack Detection Method via Deep Learning and a Binocular-Vision-Based Unmanned Aerial Vehicle. Appl. Sci. 2024, 14, 1778. [Google Scholar] [CrossRef]
- Cheng, B.; Misra, I.; Schwing, A.G.; Kirillov, A.; Girdhar, R. Masked-Attention Mask Transformer for Universal Image Segmentation. In Proceedings of the CVPR, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Wu, Y.; Kirillov, A.; Massa, F.; Lo, W.-Y.; Girshick, R. Detectron2. 2019. Available online: https://github.com/facebookresearch/detectron2 (accessed on 18 August 2024).
- Khanam, R.; Hussain, M. YOLOv11: An Overview of the Key Architectural Enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’s Journal of Software Tools 2000. Available online: https://opencv.org/ (accessed on 18 August 2024).
- Clark, A. Pillow (PIL Fork) Documentation. 2015. Available online: http://python-pillow.org/ (accessed on 18 August 2024).
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Yang, S.; Xiao, W.; Zhang, M.; Guo, S.; Zhao, J.; Shen, F. Image Data Augmentation for Deep Learning: A Survey. arXiv 2023, arXiv:2204.08610. [Google Scholar]
- Dong, L. Skeleton Tracing 2020. Available online: https://github.com/LingDong-/skeleton-tracing (accessed on 18 August 2024).
- Kato, H.; Goto, T.; Mizuno, H. Cyclic Loading Test of Confined Masonry Wall Elements for Structural Design Development of Apartment Houses in the Third World. In Proceedings of the Tenth World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).