Securing Internet of Things Applications Using Software-Defined Network-Aided Group Key Management with a Modified One-Way Function Tree

Abstract

Group management is practiced to deploy access control and to ease multicast and broadcast communication. However, the devices that constitute the Internet of Things (IoT) are resource-constrained, and the network of IoT is heterogeneous with variable topologies interconnected. Hence, to tackle heterogeneity, SDN-aided centralized group management as a service framework is proposed to provide a global network perspective and administration. Group management as a service includes a group key management function, which can be either centralized or decentralized. Decentralized approaches use complex cryptographic primitives, making centralized techniques the optimal option for the IoT ecosystem. It is also necessary to use a safe, scalable approach that addresses dynamic membership changes with minimal overhead to provide a centralized group key management service. A group key management strategy called a one-way Function Tree (OFT) was put forth to lower communication costs in sizable dynamic groups. The technique, however, is vulnerable to collusion attacks in which an appending and withdrawing device colludes and conspires to obtain unauthorized keys for an unauthorized timeline. Several collusion-deprived improvements to the OFT method are suggested; however, they come at an increased cost for both communication and computation. The Modified One-Way Function Tree (MOFT), a novel technique, is suggested in this proposed work. The collusion resistance of the proposed MOFT system was demonstrated via security analysis. According to performance studies, MOFT lowers communication costs when compared to the original OFT scheme. In comparison to the OFT’s collusion-deprived upgrades, the computation cost is smaller.

1. Introduction

The Internet of Things (IoT) emerged when everyday objects began connecting to the Internet and interacting with each other autonomously without human intervention. IoT devices follow the IEEE 802.15.4 standard [1] to enable network connectivity for resource-constrained devices using short-range, lightweight communication protocols [1]. Due to the limited availability of device resources in addition to the bandwidth problem, the IoT ecosystem prefers multicast communication instead of unicast messages to send updates and patch-ups [2,3]. To send multicast messages securely, a common secret key need to be shared between the devices in the multicast group. To efficiently distribute the keys to all group devices, a vast amount of group key management techniques have been proposed in the literature. Group key management enables the group to operate with integrity and confidentiality [4]. There are three methods for managing group keys. The Key Management Server (KMS), a trustworthy third party, is utilized for key distribution in the centralized key management technique [5,6]. In decentralized key management, both the server and group member devices contribute to key management [7,8,9]. In distributed key management, there is no centralized trust, but every member participates in key management [10,11,12,13]. Among all three methods, centralized key management offers less communication and computation overhead on the member devices with simpler functions. Hence, the proposed work focuses on centralized key management techniques, considering them to be most suitable for resource-constrained IoT devices. Centralized key management relies on a dependable third-party server for key management and key distribution. The proposed group management server uses an SDN controller to obtain centralized control over the heterogeneous network. The controller provides opinions on whether to forward network traffic, while the routers just obey the controller [14]. The advantages of SDN in comparison with traditional networks [15,16,17] are,

• Easy patching and upgradation
• Knowledge of the sleep/wake cycle of IoT devices
• Supports security services by routing traffic through virtualized service functions known as Virtual Service Functions (VSF)

The distribution of a common group key or key materials needed for group key generation occurs during the rekeying procedure. Rekeying ensures the group’s confidentiality by putting forward and backward secrecy into action. When a group member leaves, the departing member should not have any access to any key materials that could be used to access any unapproved group data after the member exit event. This is termed forward secrecy. Similarly, when a new member enters an existing group, the joining member ought not to receive any key materials to obtain any unauthorized group data preceding the member join event. This is termed backward secrecy. A collusion attack is when two or more members join to obtain key material to access the group’s data that are unauthorized for the colluding members. An efficient key management technique should ensure both forward secrecy and backward secrecy, as well as resistance to collusion attacks. Chinese Remainder Theorem (CRT)-based methods [18] offer the lowest communication costs out of all the centralized group key management techniques that have been proposed in the literature. However, because of its limited scalability, the method cannot be applied to dynamic groups.

A group key management strategy called OFT [19] lowers the communication cost for rekeying by a factor of log₂n. However, a collusion attack is possible on this approach. There are many proposed collusion-resistant OFT-based methods; however, they come at a higher communication cost. In the proposed MOFT, the binary tree’s neighboring nodes share a second key, which is termed adjacent secret. Additionally, the method employs both a top-down and bottom-up strategy for group key generation, making it collusion-resistant with lower communication costs than the original OFT scheme. The suggested approach’s performance analysis demonstrates that it has less communication overhead and better computation overhead than collusion-resistant OFTs. The existence of forward and backward secrecy in the MOFT approach is verified via security analysis. The existence of collusion resistance in MOFT is verified by a new proposition. Our main contributions are as follows:

➢

A novel technique, MOFT, for centralized group key management.

➢

A new proposition that proves the collusion resistance property of MOFT.

➢

The evaluation of MOFT proves MOFT reduces network traffic, with limited storage cost and optimal computation cost, proving it is scalable.

The remainder of the manuscript is organized as follows: Section 2 depicts the works that are related to SDN-based security for IoT and group key management techniques; Section 3 describes the proposed framework for group management using SDN, provides a brief on the original OFT scheme, and finally, elucidates on the proposed MOFT scheme; Section 4 verifies the security strength of the proposed approach; Section 5 evaluates the proposed approach in terms of computation, storage, and communication cost; finally, Section 6 depicts the IoT tailored version of MOFT; and Section 7 gives the conclusion.

2. Related Works

2.1. SDN-Centered Security for IoT

An architecture for furnishing network security services like an internet content filtering system, firewall, Intrusion Detection System (IDS), Intrusion Prevention System (IPS), and packet inspection using SDN is proposed. The network traffic can be routed through the services based on the needs of the user. The use of SDN for IoT networks to mitigate attacks by limiting the rate of suspicious traffic flow is proposed in [20]. An SDN-based framework for designing cyber resilience for the Industrial IoT (IIoT) is proposed in [21]. The ontology is designed to create pre-programmed failover paths that become activated in the event of failure. This maintains the equilibrium resilience of the IIoT network for effective failure recovery. A similar SDN-based ontology design for cyber resilience in smart manufacturing applications is proposed in [22]. To implement incident response in the IIoT, the use of SDN is proposed in [23] due to its dynamic routing policies. The preconfigured incident–response policy is enforced using SDN in the event of an attack. Invariant-based anomaly detection using SDN for IIoT is proposed in [24]. Invariant is a property of the IIoT network that remains the same in any situation. A change in this property is identified as an anomaly by adding the invariant algorithm to the SDN-controlled switches. An Intrusion Detection and Prevention System (IDPS) is proposed in [25] that exploits SDN and a Genetic Algorithm (GA) to extract features for effective intrusion detection in IoT applications. Advanced reservation-based access control using SDN is proposed in [26]. The advanced reservation of bandwidth for a certain period is employed using SDN. SDN extends the reservation from border routers to the end devices with tokens for authorization. Another SDN-based architecture for smart home networks is proposed in [27]. With SDN, all smart home devices are connected via a gateway. KNOT and Orchestrator are used with the aid of SDN to detect Advanced Persistent Threats and saturation attacks and mitigate them effectively. HanGaurd SDN-based fine-grained protection for a smart home from malicious apps running on authorized devices like a smartphone is proposed in [28]. An SDN-based firewall called FORTRESS is proposed in [29]. The stateful flow data are obtained from the data plane, and the Mealy machine is exploited to perform state table updations based on the routing decision made. An SDN-centered defense mechanism for IoT networks is proposed in [30]. The IoT devices are classified as easily patchable or non-patchable, vulnerable or hard-to-exploit, and a proactive defense mechanism is provided by changing the attack surface in case the device is vulnerable and non-patchable. The features of SDN are exploited to provide a honeypot as a service by steering the traffic through Virtualized Functions (VF) as proposed in [31]. The honeypot acts as a proactive as well as a reactive defense mechanism against attacks. The honeypots are virtualized and provided as a service using SDN. SDN for effective intrusion detection as well as for mitigation of attacks like Distributed Denial of Service (DDoS) in the habitat of the IoT is proposed in [32,33]. DDoS detection system that exploits the convenience of SDN using machine learning techniques is proposed in [34]. The proposed work uses an adaptive multilayered feed-forwarding scheme that uses different algorithms in five layers. The third layer computes the live, real-time network traffic for DDoS attack detection, and SDN mitigates the attacks using Open Flow switches.

2.2. Group Key Management Techniques

SKDC follows a very simple approach, where all the existing participants of the group share an individual secret key with the KMS. When there is a change in the number of group members, the new group key is handed out by KMS to existing participants of the group individually, encrypted using the shared secret key, in sequential order. Hence, the communication cost is linear, which is highly inefficient for large dynamic groups. The group Diffie–Hellman (DH) proposed in [35] uses asymmetric encryption for key distribution, with higher computation overhead. Logical Key Hierarchy (LKH) [36] is a familiar centralized, hierarchy-based key management approach for dynamic groups. LKH uses a balanced binary tree-based data structure with member devices’ keys as leaf nodes. The root node contains the group key. The intermediate nodes along the path of the member devices to the root hold the key encryption keys with which the devices can obtain the group key. The overall overhead of the approach is 2 log n.

Yet another centralized, hierarchy-based key management approach for groups is the OFT, which reduces the communication cost to log n. Hence, the approach reduces bandwidth consumption considerably. The approach is similar to LKH, with the member device’s individual keys as leaf nodes. The root key is the group key. The intermediate nodes hold the key-encryption key, which is calculated using a one-way and mixing function on the child node’s keys. However, the approach fails to provide collusion resistance where two expelled members collide and can gain access to unauthorized group data. Several advancements to the OFT-based approach are proposed [37,38] to enhance the collusion resistance property, but in turn, the advancements increase the overall overhead. To impart collusion resistance in OFT, two more approaches are proposed in [39]; both approaches successfully impart collusion resistance with the same communication cost as OFT but with higher computation costs.

A centralized key management approach for the group that uses Diffie-Hellman for generating the key-encryption key is proposed in [40]. The group key can be decrypted using the key-encryption key. However, the use of public key cryptography increases the computation cost greatly. Moreover, without authentication, the use of Diffie-Hellman is liable to man-in-the-middle attack. A lightweight key management approach for groups formed in IoT applications is proposed in. The approach uses a hybrid technique with a combination of CRT and LKH. The intermediate node keys are calculated by hashing the device’s ID. Although the ID of a device is unique, tracking the ID of the device is simple for malicious users to perform forgery-based attacks. Group key management using the Chinese Reminder Theorem (CRT) is proposed in. The approach is efficient, with the least communication cost of a single broadcast. When the group size exceeds the preset n value, the individual keys for the entire group must be renewed. A blockchain-based solution for key management in groups for autonomous aerial vehicles has earlier been proposed. The approach uses LKH along with blockchain for group key updations and reduces delay. The approach also assures forward and backward secrecy. However, the use of blockchain in a resource-constrained environment would be a problem. Another lightweight asymmetric group key management approach for VANETS is proposed in [41]. The approach uses a combination of CRT and asymmetric cryptography in contrast to the traditional symmetric group key management techniques. The scheme is comparatively scalable and has minimal computation overhead compared to its predecessor, CRT-based group key management techniques for VANETS. Still, the approach cannot use variable key sizes since the key sizes are chosen based on constraints. Further, a collusion-resistant approach to group key management is proposed in [42], which makes use of tokens to avoid collusions. The approach distributes group keys with a single broadcast with minimal communication load. Still, the storage overhead is high as the devices store the tokens belonging to a device’s cognate nodes. A novel protocol, GKMP, for key management in groups, is proposed in [43] to avoid collusion attacks during file sharing in the cloud. The scheme uses a group key generated by participants and not by a centralized cloud server, adding security in terms of file sharing. But the scheme uses RSA for key generation, which is expensive for IoT devices. Yet another communication-aware key management protocol for IoT networks is proposed in [44]. The scheme uses hyperelliptic curve cryptography for authentication along with bilateral generalization in a homogeneous short integer-based solution for effective key management in IoT groups. The scheme has lower computational time compared to its previous similar schemes; still, public key cryptography-based schemes increase the complexity and device overload in IoT networks.

When evaluated in terms of computation, communication, storage load, scalability, and secrecy, the existing techniques in the literature attain efficiency in one parameter with a trade-off in other parameters. OFT reduces the communication cost but does not ensure secrecy. CRT reduces the overall computation, communication, and storage costs but lacks scalability. Public-key cryptography-based schemes increase the computation load on the device to a greater extent. To provide group key management as a service, a centralized group key management technique should offer the following properties:

➢

Secrecy, ensuring forward secrecy, backward secrecy, and collusion resistance.

➢

Reduced communication costs, leading to reduced network traffic.

➢

Limited usage of resources in IoT devices.

➢

The technique should be scalable even though the group is large and dynamic.

3. Proposed Work

3.1. SDN-Based Group Management Framework

The architecture for group management service is depicted in Figure 1. The devices that communicate frequently and form a communication pattern are united as a group. The Group Management Server (GMS) is built-in with an authentication service function, a key management service function, and an SDN controller. Service functions are virtualized functions that can be provided as a service. The GMS stores the attributes of the group, including the group ID, group member ID, application ID, IP address, MAC address, and location. The key management function stores the key materials of the group. The authentication function authenticates the devices by collaborating with the GMS.

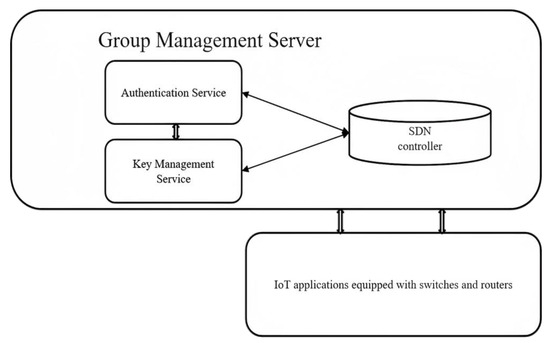
Figure 1. Group management server (GMS).

The authenticated devices will then be allowed to form a group. The key management service function will then distribute the key materials. Using SDN, the communication link is set up in such a way that only group members can communicate. This ensures security against the spread of node-capture attacks and phishing-based attacks by cutting off unnecessary communications.

3.2. Use Case

The proposed group management framework is applied to smart home applications, as depicted in Figure 2. The smart home application is built up of embedded devices and sensors that collaborate via LAN or WAN connections to improve the comfort of the house members. The components of a smart home system include an entertainment system consisting of a music system, home theater, TV, etc., a security surveillance system with cameras, alarms, door locks, etc., and an energy management system with a connection to a smart grid to optimize electricity usage [45,46]. The segregation of smart home applications into groups helps prevent the spread of attacks from a vulnerable part of a system to other parts of the system. An authenticated key agreement protocol for groups in home-based sensor networks is proposed in [47], which uses an authentication token for authentication between mobile stations and serving networks. The scheme shows robustness when the mobile stations move between different serving networks. Another group-based authenticated key agreement protocol for machine-to-machine communication is proposed in [48], which selects a leader device first to perform full authentication. The remaining member devices authenticate using the vector provided by the leader device. The proposed work assumes that the smart home application contains an admin device that is trustable with enough resources to communicate with service functions and establish a secure connection. The steps involved in group initialization are depicted in Figure 3. Resource-constrained smart home devices can connect with the admin device via 5G networks or Bluetooth LE that supports device authentication. After mutual authentication, the admin devices send the device IP, MAC address, ID, Group ID, individual key ${\mathrm{K}}_{\mathrm{L}}$, and adjacent shared secret ${\mathrm{K}}_{\mathrm{a}}$ to the authentication service function encrypted using the key shared between them. After authentication, the authentication service function forwards the request to the key management service function. The key management service function forwards the adjacent shared secret and key materials needed to obtain the group key to the device encrypted using ${\mathrm{K}}_{\mathrm{L}}$, which was already obtained by the device from the admin. This ensures the message is from a trusted source. The member devices only know the group key of their respective groups. But the admin will have all the group keys as they generate ${\mathrm{K}}_{\mathrm{a}}$, which is consequently used to extract the group key in the proposed group key management approach. The flow rules are set in the switches and routers using an SDN controller so that only devices in the same groups communicate. Thus, if a malicious person compromises the music system, they cannot proceed further to compromise the door lock since the device will be in another group, and using SDN, these devices can be segmented.

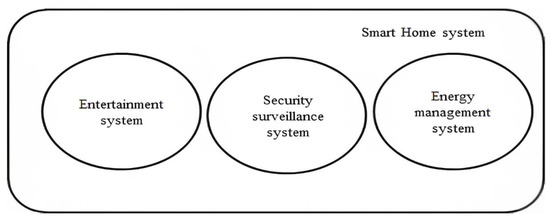
Figure 2. Grouping of the smart home system.

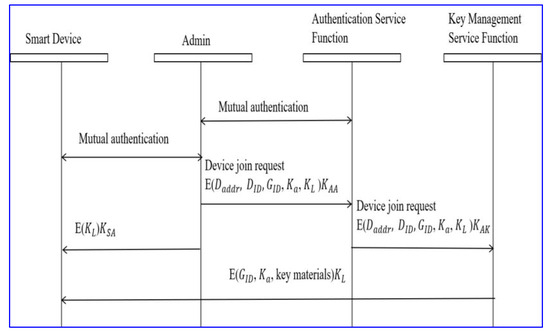
Figure 3. Steps in group initialization.

3.3. Existing OFT

Table 1 gives the notations used in the proposed work. The group key $\mathrm{G}\mathrm{K}$ is commonly shared among all group devices to share data and resources within the group. The node key ${\mathrm{n}}_{\mathrm{k}}$ is the individual key possessed by every node. An adjacent secret ${\mathrm{K}}_{\mathrm{a}}$(l,r) is a secret key shared between two adjacent nodes, i.e., the left and right child of a parent node. The intermediate node is the node between the leaf and the root node that contains the group key. The intermediate node secret ${\mathrm{S}\mathrm{I}}_{\mathrm{i}}$ is the secret calculated and known only to the intermediate node, whereas the blinded secret ${\mathrm{b}\mathrm{l}}_{\mathrm{i}}$ is distributed to other nodes for group key generation.

Table 1. Notations used.

$\mathrm{G}\mathrm{K}$	Group key
${\mathrm{n}}_{\mathrm{k}}$	node key
${\mathrm{b}\mathrm{l}}_{\mathrm{i}}$	Blinded secret of node i
${\mathrm{I}}_{\mathrm{i}}$	Intermediate node
${\mathrm{K}}_{\mathrm{a}}$(l,r)	Adjacent shared secret of node l and r
${\mathrm{K}}_{\mathrm{i}}$	Individual secret key of user i
$\mathrm{f}\left(\mathrm{x}\right)$	One-way function
$\mathrm{g}\left(\mathrm{x}\right)$	Mixing function
$\mathrm{L}$	Length of key
$\mathrm{n}$	No. of users
${\mathrm{S}\mathrm{I}}_{\mathrm{i}}$	Node secret of Intermediate node i
${\mathrm{K}}_{\mathrm{L}}$	Individual key between GMS and user
${\mathrm{K}}_{\mathrm{A}\mathrm{A}}$	Key shared between authentication service function and admin
${\mathrm{K}}_{\mathrm{A}\mathrm{K}}$	Key shared between authentication service function and key management service function
${\mathrm{K}}_{\mathrm{S}\mathrm{A}}$	Key shared between
${\mathrm{G}}_{\mathrm{I}\mathrm{D}}$	Group ID
${\mathrm{D}}_{\mathrm{I}\mathrm{D}}$	Device ID

Before looking into the working of MOFT, the working of the earliest OFT scheme is discussed. The OFT scheme uses a binary tree data structure, which is balanced for key management. Each leaf node of the binary tree denotes a group member and is assigned a node key. The group members already possess a shared secret with the KMS with which the node key can be encrypted and distributed to the respective group member. The one-way function on the key is the blinded secret of the leaf node. The mixing function of the left and right child’s blinded node secret gives the intermediate node secret. In this way, the intermediate node secrets are calculated in a bottom-up fashion to compute the group key.

In Figure 4, the numbers represent the nodes of the binary tree, whereas the intermediate nodes are represented using the symbol $\mathrm{I}$. When a user exits or joins, the keys on the trail of the leaving or joining node are changed. As in Figure 5, when user 7 leaves, node 8 takes the position of ${\mathrm{I}}_3$ as the leaf node. Node 3 is issued a new node key ${\mathrm{n}}_{\mathrm{k}3}$. Node 3 then calculates its new blinded node secret ${\mathrm{b}\mathrm{l}}_3$, thus leading to a new ${\mathrm{S}\mathrm{I}}_1$ intermediate node secret and group key $\mathrm{G}\mathrm{K}$. Users 9 and 10 are issued the new ${\mathrm{b}\mathrm{l}}_3$ encrypted using ${\mathrm{S}\mathrm{I}}_4$. Hence, users 9 and 10 calculate ${\mathrm{S}\mathrm{I}}_1=\mathrm{g}\left({\mathrm{b}\mathrm{l}}_3,{\mathrm{b}\mathrm{l}}_4\right)$. Users 11 and 12 are issued new ${\mathrm{b}\mathrm{l}}_{\mathrm{k}1}$ encrypted using ${\mathrm{S}\mathrm{I}}_2$. Now, the group key is calculated as $\mathrm{G}\mathrm{K}=\mathrm{g}\left({\mathrm{b}\mathrm{l}}_1,{\mathrm{b}\mathrm{l}}_2\right)$.

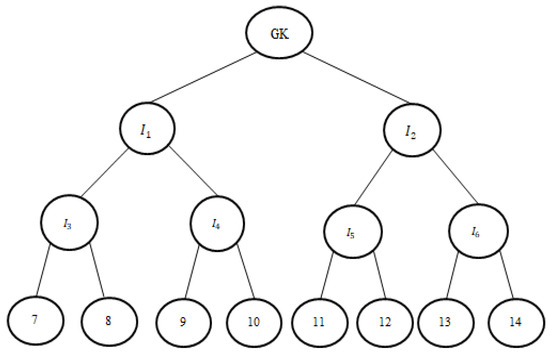
Figure 4. Group tree structure.

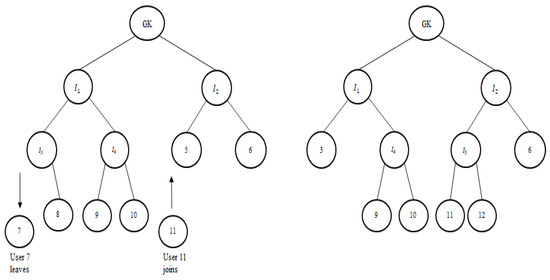
Figure 5. User leave and join event.

Now, as in Figure 5, if user 11 joins, the user is issued the node secret ${\mathrm{n}}_{\mathrm{k}11}$. User 11 will calculate its blinded secret ${\mathrm{b}\mathrm{l}}_{11}$. User 12 is issued ${\mathrm{b}\mathrm{l}}_{11}$ encrypted using its own node secret ${\mathrm{n}}_{\mathrm{k}12}$. Users 11 and 12 calculate $=\mathrm{g}\left({\mathrm{b}\mathrm{l}}_{11},{\mathrm{b}\mathrm{l}}_{12}\right)$. Users 11, 12, and 6 calculate ${\mathrm{S}\mathrm{I}}_2=\mathrm{g}\left({\mathrm{b}\mathrm{l}}_5,{\mathrm{b}\mathrm{l}}_6\right)$. Then, users 3, 9, and 10 are supplied with the blinded secret of node ${\mathrm{I}}_2$ so that the group key $\mathrm{G}\mathrm{K}$ can be calculated. Although the scheme has the advantage of reduced communication costs, it is prone to collusion attacks. Several enhanced OFT-based approaches are proposed [38,39] to attain collusion resistance but with higher communication cost or computation cost.

Collusion Attack in OFT

When two users collude to obtain unauthorized information, it can be termed a collusion attack. For instance, when user 7 leaves at time t1, they know the ${\mathrm{b}\mathrm{l}}_1$ value. Now, new user 11 joins at time t2. User 11 knows the ${\mathrm{b}\mathrm{l}}_1$ value. Now, the left user 7 colludes with malicious user 11 and uses ${\mathrm{b}\mathrm{l}}_2$, which is known to user 7, and ${\mathrm{b}\mathrm{l}}_1$, which is known to user 11, to compute the group key $\mathrm{G}\mathrm{K}=\mathrm{g}\left({\mathrm{b}\mathrm{l}}_1,{\mathrm{b}\mathrm{l}}_2\right)$ for the timeline between t1 and t2. Thus, OFT is prone to collusion attacks. There are works based on OFT that avoid collusion attacks often but with an enhanced cost. Our work attempts to provide a collusion-resistant OFT-based scheme but with a reduced cost.

3.4. MOFT

The proposed MOFT scheme uses a binary tree just like OFT maintained by a key management server. The proposed scheme also assumes that the users joining the group have an individual secret key $\mathrm{K}$ pre-established with the KMS. In the modified OFT, instead of leaf nodes being issued with the node key, the adjacent leaf nodes are issued with a common adjacent shared secret ${\mathrm{K}}_{\mathrm{a}(\mathrm{l},\mathrm{r})}$.

Now, as in Figure 6, the left and right leaf nodes share a common adjacent shared secret ${\mathrm{K}}_{\mathrm{a}(\mathrm{l},\mathrm{r})}$. The first intermediate node nearest to the leaf nodes ${\mathrm{I}}_{\mathrm{i}+2}$ will have the same ${\mathrm{K}}_{\mathrm{a}(\mathrm{l},\mathrm{r})}$ as node secret, and the blinded node secret of ${\mathrm{I}}_{\mathrm{i}+2}$ is calculated as ${\mathrm{f}(\mathrm{K}}_{\mathrm{a}(\mathrm{l},\mathrm{r})})$. The next intermediate node secret ${\mathrm{I}}_{\mathrm{I}}$ is calculated as $\mathrm{g}({\mathrm{b}\mathrm{l}}_{\mathrm{i}+2},{\mathrm{b}\mathrm{l}}_{\mathrm{i}+3})$. Further node secrets are calculated in a bottom-up style as in OFT to compute the group key $\mathrm{G}\mathrm{K}$.

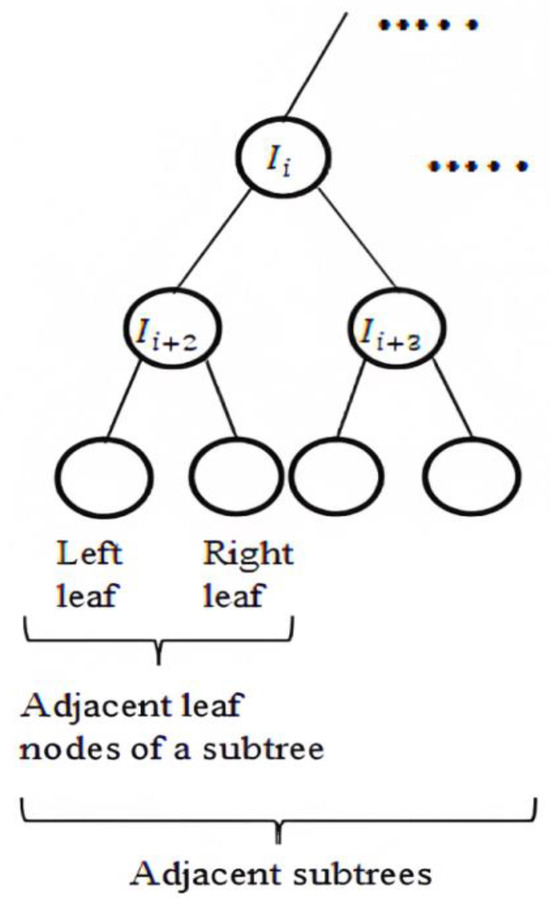
Figure 6. Adjacent subtree structure.

3.4.1. Top-Down Growth

As in Figure 7, when a new user $\mathrm{u}1$ arrives, the $\mathrm{l}$ node performs a mixing function $\mathrm{g}({\mathrm{K}}_{\mathrm{a}\left(\mathrm{l},\mathrm{r}\right)},{\mathrm{K}}_{\mathrm{l}})$ in which ${\mathrm{K}}_{\mathrm{l}}$ is the pre-established secret of user $\mathrm{l}$, and ${\mathrm{K}}_{\mathrm{a}\left(\mathrm{l},\mathrm{r}\right)}$ is the adjacent shared secret between nodes $\mathrm{l}$ and $\mathrm{r}$. This is the new adjacent secret for $\mathrm{l}$ and $\mathrm{u}1$. The $\mathrm{r}$ node’s blinded node secret becomes $\mathrm{f}\left({\mathrm{K}}_{\mathrm{a}\left(\mathrm{l},\mathrm{r}\right)}\right)$. Similarly, when a new user arrives on the right side of the tree, $\mathrm{g}({\mathrm{K}}_{\mathrm{a}\left(\mathrm{l},\mathrm{r}\right)},{\mathrm{K}}_{\mathrm{r}})$ is calculated and issued to the new user as an adjacent secret. In this way, a certain amount of communication cost is cut off.

Figure 7. Top-down growth during new user join.

3.4.2. User Leave and Join Event

When user 7 leaves, as in Figure 8, node 8 becomes leaf node 3. In the modified OFT node, 3 is issued with a new adjacent shared secret value ${\mathrm{K}}_{\mathrm{a}3}$. The adjacent secret is blinded using a one-way function to obtain the blinded secret of node 3. Users 9 and 10 are supplied with a new blinded secret of node 3. $\mathrm{S}{\mathrm{I}}_2$ is calculated as $\left(\mathrm{g}\right({\mathrm{b}\mathrm{l}}_3,{\mathrm{b}\mathrm{l}}_4)$. Users 7, 8, 9, and 10 are supplied with the blinded secret of ${\mathrm{I}}_2$. The keys that change during the user leave event are highlighted in Figure 8.

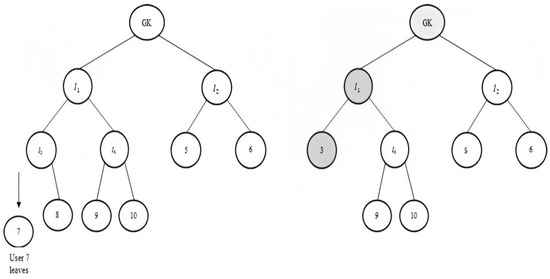
Figure 8. User leave event, keys that change during leave event.

When user 11 joins as in Figure 9, node 5’s adjacent shared secret is changed to $\mathrm{g}({\mathrm{K}}_{\mathrm{a}\left(\mathrm{5,6}\right)},{\mathrm{K}}_5)$. The changed adjacent secret is issued to user 11 as ${\mathrm{K}}_{\mathrm{a}\left(\mathrm{11,12}\right)}$ encrypted using its individual secret key ${\mathrm{K}}_{11}$. The blinded secret of ${\mathrm{I}}_5$ is calculated as ${\mathrm{f}(\mathrm{K}}_{\mathrm{a}\left(\mathrm{11,12}\right)})$. User 6’s adjacent secret ${\mathrm{K}}_{\mathrm{a}\left(\mathrm{5,6}\right)}$ is blinded using a one-way function $\mathrm{f}\left(\mathrm{x}\right)$ and becomes its blinded secret ${\mathrm{b}\mathrm{l}}_6=\mathrm{f}\left({\mathrm{K}}_{\mathrm{a}\left(\mathrm{5,6}\right)}\right)$. User 11 is issued with the blinded secret ${\mathrm{b}\mathrm{l}}_6.$ Users 6, 11, and 12 calculate ${\mathrm{S}\mathrm{I}}_2=\mathrm{g}({\mathrm{b}\mathrm{l}}_5,{\mathrm{b}\mathrm{l}}_6)$. Users 7, 8, 9, and 10 are supplied with SI₂, which is encrypted using the node secret of ${\mathrm{I}}_1$. As in ROFT [39], another one-way function is performed on each one of the blinded node secrets along the trail of the joining user and supplied to them as a new blinded secret. This makes the MOFT collusion-resistant. The keys that change during the user join event are highlighted in Figure 9. Hence, the new users entering the group do not know any previously used keys, assuring backward secrecy. The modified OFT reduces the communication cost compared to the original OFT.

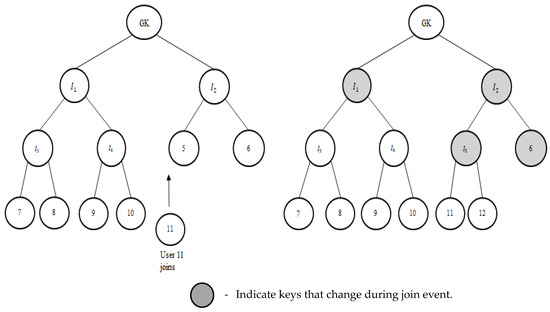
Figure 9. User join event.

4. Security Analysis

The work one way function tree (OFT) proposes a new generic definition for collusion resistance. Although our scheme follows ROFT to be collusion-resistant, a new proposition is made to prove the collusion resistance of our scheme.

Proposition 1. 

The OFT scheme is collusion-resistant if the leaving users at the time $t1$ and joining users at time $t2$ cannot compute any unknown node secrets if the intersection of their set of known secrets does not contain any adjacent pair node secrets, i.e., the leaving users at time $t1$ known key set $t_{leave}$ and the joining users at time $t2$ known key set $t_{join}$ should not contain the secrets of adjacent pairs ${t_{leave} \cup t_{join }\ne secrets of pair\{I}_{oi}, I_{oi+1}\}$ where $oi\in \{set of odd numbers\}$, $t_{leave}$ is the key set known in the time duration between $t1$ and the first key update after the user leaves $t_{MIN}$, $t_{join }$ is the key set known in the time interval between the last key update that happened before the user join $t_{MAX }$ and $t2$.

Proof. 

The group key is calculated in a bottom-up fashion using a mixing function $\mathrm{g}\left(\mathrm{x}\right)$ of adjacent blinded node secrets ${\mathrm{b}\mathrm{l}}_{\mathrm{o}\mathrm{i}},{\mathrm{b}\mathrm{l}}_{\mathrm{o}\mathrm{i}+1}$. So, to compute any parent intermediate node secret SI_i, both the child’s adjacent blinded secrets and adjacent secrets should be known. Hence, if the chain of knowing adjacent secrets and adjacent blinded secrets is broken then the colluding users cannot compute any intermediate key or the group key for an unauthorized time. □

Theorem 1. 

MOFT is collusion-resistant.

Proof of Theorem. 

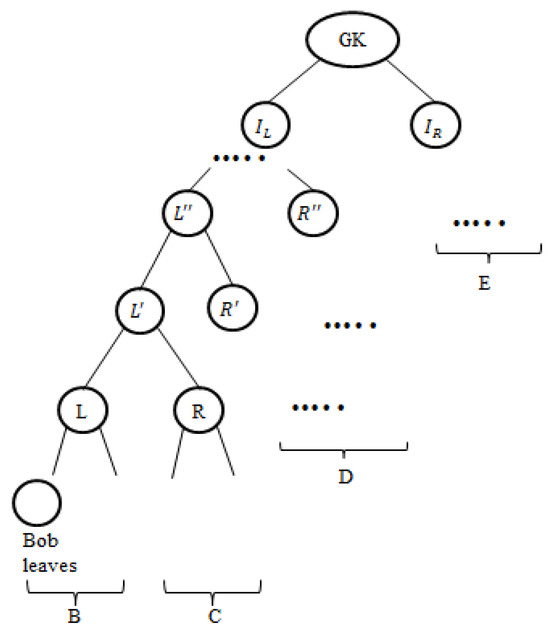
According to Proposition 1, the OFT scheme is collusion-resistant if the leaving users ${\mathrm{t}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{v}\mathrm{e}}$ and the joining users ${\mathrm{t}}_{\mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}}$ cannot collude to contain any $\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\{\mathrm{S}{\mathrm{I}}_{\mathrm{o}\mathrm{i}},\mathrm{S}{\mathrm{I}}_{\mathrm{o}\mathrm{i}+1}\}$. Consider user Bob leaves at the time ${\mathrm{t}}_{\mathrm{l}}$, as in Figure 10 (B–E) subtree sections. The set of keys Bob knows after time ${\mathrm{t}}_{\mathrm{l}}$, ${\mathrm{t}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{v}\mathrm{e}}= \mathrm{s}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{t} \mathrm{k}\mathrm{e}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s}\{\mathrm{R},{\mathrm{R}}^{\prime },{\mathrm{R}}^{″},{\mathrm{I}}_{\mathrm{R}}\}$. To perform a collusion attack, Bob has to collude with any of the joining users at the time ${\mathrm{t}}_{\mathrm{j}}$. Consider Alice joining at the time ${\mathrm{t}}_{\mathrm{j}}$ at any of the sections B, C, D, or E. The known key set of Alice that existed before time ${\mathrm{t}}_{\mathrm{j}}$, ${\mathrm{t}}_{\mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}}=\left\{\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{l}\right\}$ since all the node secrets on the path are hashed using the one-way function before being distributed to Alice. The collusion of Alice and Bob known key sets ${\mathrm{t}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{v}\mathrm{e}}\cup {\mathrm{t}}_{\mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}}=\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{t} \mathrm{k}\mathrm{e}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s}\{\mathrm{R},{\mathrm{R}}^{\prime },{\mathrm{R}}^{″},{\mathrm{I}}_{\mathrm{R}}\}$. Hence, according to Proposition 1, the proposed MOFT confirms collusion resistance. □

Figure 10. Collusion attack.

5. Performance Evaluation

The proposed MOFT is evaluated by comparing it with the prevailing OFT-based group key management approaches in terms of computation and communication cost.

From Table 2 and Table 3, it is evident that the proposed MOFT approach attains the least communication cost, and the cost is even less than the OFT approach itself. The proposed MOFT reduces the communication cost by 39% than the earliest OFT. Although the computation cost is higher than the OFT scheme, it is comparatively less than the existing collusion-resistant OFT schemes. Figure 11 depicts the evaluation of the proposed approach with the existing approaches regarding total communication cost. The schemes OFT and ROFT share the same communication cost. Ku and Chen’s and Xu’s schemes share the same communication cost, whereas the proposed work’s communication cost is less with ${(2\mathrm{l}\mathrm{o}\mathrm{g}}_2\mathrm{n}+3)\times \mathrm{L}$ messages, which is lesser than the original OFT. The number of messages transferred is equal to the number of keys needed to be distributed.

Table 2. User join event.

KMS	OFT [19]	Ku and Chen [37]	Xu [38]	ROFT [39]	MOFT
Comm. Cost KMS	$\left(2{log}_{2}n+1\right)\times L$	$\left(2{log}_{2}n+1\right)\times L$	$\left(2{log}_{2}n+1\right)\times L$ OR ${{\left(\right(log}_{2}n)}^2+\left(2{log}_{2}n+1\right))\times L$	$\left(2{log}_{2}n+1\right)\times L$	${(log}_{2}n+2)\times L$
Comp. Cost KMS	$\left(2{log}_{2}n+1\right)\times C_e+\left({log}_{2}n+1\right)\times C_h$	$\left(2{log}_{2}n+1\right)\times C_e+\left({log}_{2}n+1\right)\times C_h$	$\left(2{log}_{2}n+1\right)\times C_e+\left({log}_{2}n+1\right)\times C_h$ OR ($\left({{log}_{2}n)}^2+2{log}_{2}n+1\right)\times C_e+\left({{(log}_{2}n)}^2+{log}_{2}n+1\right)\times C_h$	$\left(2{log}_{2}n+1\right)\times C_e+\left({2log}_{2}n\right)\times C_h$	${(log}_{2}n+2)\times$ $C_e+\left({2log}_{2}n-1\right)\times C_h$
Comp. Cost member device	$2C_d+{log}_{2}n\times C_h$	$2C_d+{log}_{2}n\times C_h$	$2C_d+{log}_{2}n\times C_h$ OR $\left(log2n+1\right)\times C_d+0.5\times {(log}_{2}n)\times C_h$	$2C_d+(2{log}_{2}n-1)\times C_h$	$C_d+(2{log}_{2}n-1)\times C_h$

Table 3. User leave event.

KMS	OFT [19]	Ku and Chen [37]	Xu [38]	ROFT [39]	MOFT
Comm. Cost KMS	$\left({log}_{2}n+1\right)\times L$	$\left({{{(log}_{2}n)}^2+log}_{2}n+1\right)\times L$	$\left({log}_{2}n+1\right)\times L$	$\left({log}_{2}n+1\right)\times L$	$\left({log}_{2}n+1\right)\times L$
Comp. Cost KMS	$\left({log}_{2}n+1\right)\times C_e+\left({log}_{2}n\right)\times C_h$	$\left({{{(log}_{2}n)}^2+log}_{2}n+1\right)\times C_e+\left({{{(log}_{2}n)}^2+log}_{2}n\right)\times C_h$	$\left({log}_{2}n+1\right)\times C_e+\left({log}_{2}n\right)\times C_h$	$\left({log}_{2}n+1\right)\times C_e+\left({log}_{2}n\right)\times C_h$	$\left({log}_{2}n+1\right)\times C_e+\left({log}_{2}n\right)\times C_h$
Comp. Cost member device	$C_d+{log}_{2}n\times C_h$	${{\left({log}_{2}n\right)\times C_d+(log}_{2}n)}^2\times C_h$	$C_d+{log}_{2}n\times C_h$	$C_d+{log}_{2}n\times C_h$	$C_d+{log}_{2}n\times C_h$

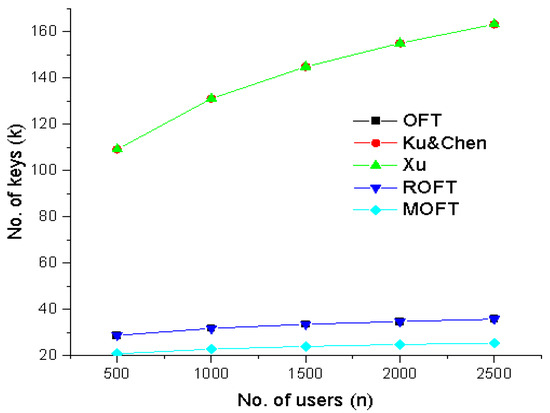
Figure 11. Comparison of proposed MOFT communication cost with OFT [19], Ku & Chen [37], Xu [38] and ROFT [39].

5.1. Load on SDN-Centered KMS

Group rekeying occurs in the event of the user joining or exiting the group. For static applications of IoT like smart home, the devices joining and leaving the smart home network are less frequent. For dynamic applications like retail, healthcare, etc., the rekeying frequency is high. Figure 12a–c depict the communication load on SDN-centered KMS for different rekeying frequencies $\mathrm{f}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$120$}\right.,\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$480$}\right.,$ and $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1920$}\right.$ respectively.

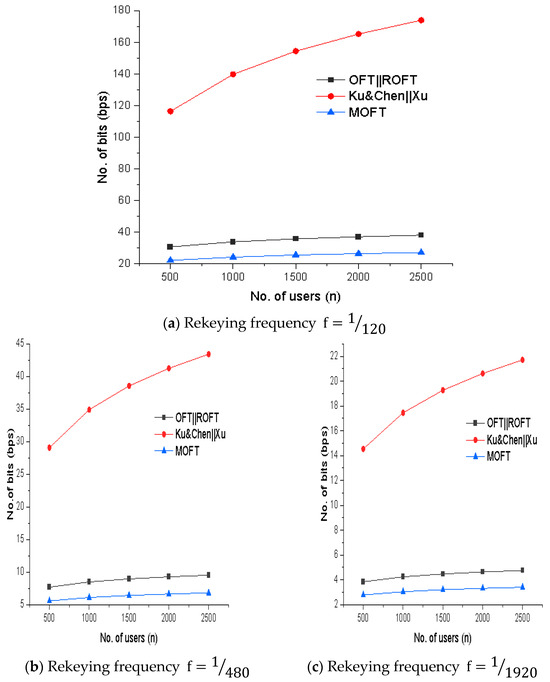
Figure 12. Rekeying frequency comparison of proposed MOFT with OFT [19], Ku & Chen [37], Xu [38] and ROFT [39].

5.2. Storage Cost

The maximum storage cost of the OFT scheme is $2({\mathrm{l}\mathrm{o}\mathrm{g}}_2\mathrm{n}+1)$. The proposed work uses an adjacent secret shared between adjacent nodes instead of the individual node secret; hence, the storage cost of MOFT is ${2\mathrm{l}\mathrm{o}\mathrm{g}}_2\mathrm{n}$.

6. MOFT Tailored for IoT

Since the adjacent secret for the device is generated by the admin and shared with the centralized server, the admin can generate all the key materials subsequently needed to obtain the group key of all groups in the application. To reduce the overhead on the centralized key management server, the admin device can act as an edge device and take part in the key distribution part. The devices on the left side of the root node can obtain group keys from the centralized server, and the right-side devices can obtain their keys from the admin or vice versa. This will further reduce the overhead on the centralized server. To sum up, even though the group exhibits regular rekeying with membership changes, the suggested MOFT minimizes the communication cost and thus reduces the network traffic to a significant extent. The proposed MOFT also offers lower storage overhead on group member devices. The suggested solution additionally provides collusion resistance using basic cryptographic primitives such as a one-way function and mixing function. The computation overhead is lower than the collusion-deprived enhancements of OFT. All these features make MOFT secure and adaptable to the IoT environment.

The proposed work using the SDN controller, switches, and routers are simulated using the Mininet [49] simulator installed in an oracle VM. The topology is created with 30 hosts, an SDN controller, and 2 switches. The flow rule is set using python script. The hosts are grouped into three groups with each group consisting of ten hosts. The communication link is set only for the hosts of the same group. This restricts the communication between hosts of different groups.

7. Conclusions

Unlike traditional networks, the IoT’s network is heterogeneous, with different lightweight communication protocols for communication with lesser bandwidth. Treating this heterogeneous network as a single network and providing it with essential security solutions is inevitable. Hence, a group management framework with an SDN-centered server as a trusted third party is proposed to tackle heterogeneity and aid in secure key distribution. For key distribution to dynamic groups, a cost-efficient, scalable, and centralized key management technique is undeniable. Although CRT-based schemes are efficient, they lack scalability. LKH and OFT are the earliest, most familiar, and most widely used centralized key management techniques. OFT was proposed as an enhancement to LKH with reduced communication costs, yet it suffers from collusion attacks. The proposed MOFT technique is novel, has minimal communication overhead, and reduces network traffic by 39% compared to OFT. The new proposition defined for security analysis proves that MOFT is collusion-resistant with optimal computation overhead.