Area and Performance Estimates of Finite State Machines in Reconfigurable Systems

Abstract

Modern reconfigurable systems are typically implemented in field-programmable gate arrays (FPGAs) based on look-up tables (LUTs). Finite state machines (FSMs) perform the functions of control devices and are integral to reconfigurable systems. When designing reconfigurable systems, the problem of optimizing the area and performance of FSMs often arises. The FSM synthesis and state encoding methods generally use only one estimate of the FSM area or performance. However, regardless of the computational complexity of the FSM synthesis or state encoding method, if the estimate incorrectly reflects the optimization aim, the result is far from the optimal solution. This paper proposes several estimates of the area and performance of FSMs implemented in LUT-based FPGAs. The effectiveness of the proposed estimates was investigated using the sequential method for FSM state encoding. Experimental studies on benchmarks showed that the FSM area decreases on average from 3.8% to 6.5%, compared to known approaches (for some cases by 33.3%), while the performance increases on average from 3.5% to 7.3% (for some cases by 27.6%). Recommendations for the practical use of the proposed estimates are also provided. The Conclusions section highlights promising directions for future research.

1. Introduction

Currently, various reconfigurable systems are widely used in all spheres of human activity [1]. A distinctive feature of modern reconfigurable systems is the intensive use of field-programmable gate array (FPGA) based on a look-up table (LUT) [2]. When developing reconfigurable systems, there is often a need to improve the design parameters, such as the area (implementation cost), performance (speed), and power consumption. Because finite state machines (FSMs) are an integral part of most reconfigurable systems (FSMs act as controllers of digital devices and systems), it is important to reduce the number of LUTs [3], increase the performance [4], and reduce the power consumption [5] of FSMs.

To solve these problems, it is vital to estimate the area, performance, and power consumption of FSMs with the highest accuracy. The power consumption estimates of the FSMs implemented in FPGAs are given in [6,7]. However, it is much more difficult to estimate the area and performance of FSMs implemented in reconfigurable systems. The methods of minimization and decomposition of Boolean functions used by design tools are usually unknown to developers. In addition, design tools typically use various logical and physical synthesis techniques, for example, to satisfy timing constraints. Therefore, even exact estimates of the expected area and performance usually differ from the area and performance of the implemented FSM circuit.

When implementing FSMs in an LUT-based FPGA, an area is measured by the number of LUTs in the FSM circuit. Performance is determined by the delay of signals in the critical (longest) signal path from input to output of the circuit, which is measured by the number of levels (depth) of LUTs in the FSM circuit. Both of these parameters (area and depth) are usually minimized in FSM synthesis methods for reconfigurable systems.

This paper considers several estimates of the area and performance of FSMs, as well as other estimates that are not directly related to the computation of the area or performance of an FSM. The proposed estimates were investigated using the sequential method for FSM state encoding [8].

Note that the results of FSM synthesis or state encoding depend significantly on the estimates used (area, speed, or power consumption). Because (regardless of the computational complexity of the method) if the estimate does not correctly reflect the optimization aim, the synthesis results will not be optimal. Therefore, it is very important in FSM synthesis methods to use efficient estimates that contribute optimization and more exactly reflect the synthesis results.

The main goal of this paper is to reduce the area and increase the performance of FSMs for reconfigurable systems by using the most efficient or exact estimates in synthesis methods or state encoding of FSMs.

The main contribution of this paper is a new approach to synthesizing and state encoding FSMs for reconfigurable systems, when several different estimates, rather than one, are applied in determining the area and performance of the FSM. To this end:

• Several area and performance estimates of FSMs, as well as estimates that are not directly related to the computation of the area or performance estimates of FSMs, are presented;
• For each estimate, and the expressions and algorithm for its computation are given;
• The efficiency of the estimates is verified on benchmarks of FSMs using the estimates in the sequential method of FSM state encoding [8];
• A comparison of different estimates was performed to determine their efficiency for optimizing the area and performance of FSMs;
• It has been shown that the use of the considered estimates in the method [8] allows to obtain solutions on average better in comparison with known methods;
• Recommendations on the practical use of the proposed estimates are given.

The rest of the paper is organized as follows. Section 2 includes a short analysis of related works. Section 3 discusses essential information about the FSM representations and presented FSM estimations. Section 4 includes the experimental results and their analysis. Section 5 shows a short summary.

2. Related Works

The most common area and delay estimation is performed when mapping Boolean functions (design logic) into an FPGA structure [9,10,11]. The classical study [9] presents algorithms for multilevel synthesis and minimization of combinational logic in the case of its implementation on gates. In [9], the area (complexity) of a Boolean function was determined by the number of literals required to represent the function in factorized form. Here, a literal is a Boolean variable or its inverse. The delay in [9] is determined by the time taken for the signal to pass along the critical path. In [10], the area estimate a(f) and delay d(f) of a Boolean function f are defined by the same expression (1):

$$a\left(f\right)=d\left(f\right)=\left\{\begin{array}{c}1, L\le n;\\ L-n+1, L>n;\end{array}\right.,$$

(1)

where L is the number of arguments of the function f; and n is the number of LUT inputs. In [11], the delay estimate is also calculated according to (1).

Area and delay estimates are widely used in decomposition methods of Boolean functions [12,13]. In [12], the area and delay estimates are defined by the same expression (1). In [13], the area is described by expression (2):

$$a\left(f\right)=⌈{\log }_2\mu ⌉+1,$$

(2)

where µ is the number of unique variables in the decomposition of the function f; and ⌈A⌉ is the smallest integer greater than or equal to A.

Area and delay estimates are often used in synthesis methods of combinational and sequential circuits. For example, in the method [14] of symbolic RTL (register transfer level) synthesis in LUT-based FPGAs, a multilevel logic network of LUTs is constructed, the area of which is determined by expression (3):

$$a\left(F\right)=⌈{\displaystyle \frac{L}{n}}⌉·⌈{\displaystyle \frac{N}{m}}⌉,$$

(3)

where L and N are the number of inputs and outputs of the Boolean function system F; and n and m are the number of inputs and outputs of the LUT.

In [15,16], the upper and lower bounds on the area and delay estimates of the Boolean function when implemented in an LUT-based FPGA are given. These estimates can be used in synthesis methods to determine the measure to which the resulting solution differs from the optimal solution. In [15], the lower bound on the number of LUTs is defined by inequality (4), and the upper bound is defined by inequality (5):

$$a_l(f)\ge ⌈{\displaystyle \frac{L-1}{n-1}}⌉,$$

(4)

$$a_u\left(f\right)\le 2^{L-n+1},$$

(5)

where L is the number of inputs of the function f. In [15], the upper area bound of the function f represented in the sum-of-products (SOP) form is also given:

$$a_u(f)\le ⌊{\displaystyle \frac{l-1+(c+1)·(n-2)}{n-1}}⌋,$$

(6)

where l is the number of literals; c is the number of cubes [9] in the SOP of the function f; and ⌊A⌋ is the largest integer less than or equal to A.

In [16], the lower bound of the area is defined by inequality (7), and the upper bound of the area is defined by inequality (8):

$$a_l(f)\ge ⌊{\displaystyle \frac{L+1}{n-1}}⌋,$$

(7)

$$a_u\left(f\right)\le 2^{L-n+1}-1.$$

(8)

• In addition, in [16], the lower delay bound is defined by inequality (9), and the upper delay bound is defined by inequality (10):

  $$d_l(f)\ge {\log }_n(L),$$

  (9)

  $$d_u\left(f\right)\le \left\{\begin{array}{c}1, L\le n;\\ L-n+1, L>n;\end{array}\right..$$

  (10)

• In [17], when implementing FSMs in LUT-based FPGAs, the state number minimization method uses area, delay, and power consumption estimates. Here, the area of function f is calculated using expression (11), and the delay is calculated using expression (12):

  $$a\left(f\right)=⌈{\displaystyle \frac{L}{n-1}}⌉+1,$$

  (11)

  $$d\left(f\right)=⌈{\displaystyle \frac{L-n}{n-1}}⌉+1.$$

  (12)

Note that in the FSM synthesis method [18] in FPGAs, the Hamming distance between the state codes is taken into account in the area estimation.

FSMs are sometimes realized in complex programmable logic devices (CPLDs). In [19], the area estimate of a CPLD was measured by the number of PAL (programmable array logic) blocks used.

The analysis of the known area and performance estimates has shown that in all considered methods only one area or delay estimate is used. Almost all estimates consider only the number L of Boolean function arguments and the number n of LUT inputs, with the exception of estimates (2) and (6). None of the considered methods compares the different area or performance estimates with each other to select the most efficient or more exact estimate. Therefore, it can be assumed that selecting the most efficient estimate (i.e., the estimate that contributes to the optimization of a certain FSM parameter) or a more exact estimate will modify the result of the synthesis method and bring the result closer to the optimal solution.

3. Materials and Methods

This section discusses the representation of FSMs in the form of a transition list, which is widely used in practice and will be used to compute FSM estimates. The estimates are described for the area and performance of FSMs, as well as other estimates. For each estimate, expressions and an algorithm for its computation are given.

3.1. Representation of FSMs

The main parameters of an FSM are as follows: L is the number of inputs (input variables); N is the number of outputs (output variables); M is the number of states; and T is the number of transitions between states. Let X = {x₀,…,x_L−1} be the set of FSM input variables; Y = {y₀,…,y_N−1} be the set of FSM output variables; S = {s₀,…,s_M−1} be the set of FSM states, where s₀ is the initial state; D = {d₀,…,d_R−1} be the set of FSM transition functions; and E = {e₀,…,e_R−1} is the set of FSM feedback variables, where R = ⌈log₂M⌉ is the number of code bits (code length) in case of encoding the FSM states by a binary code. The structural model of the FSM with the above notations is shown in Figure 1, where Φ is the combinational circuit realizing the FSM transition functions of the set D; Ψ is the combinational circuit realizing the FSM output functions of the set Y; and RG is the register (memory of the FSM), at the outputs of which the values of feedback variables of the set E are formed.

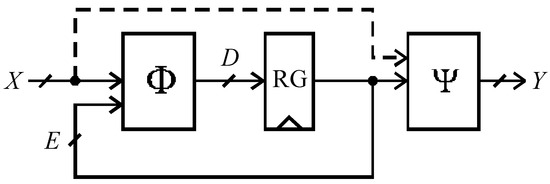
Figure 1. Generalized structural model of an FSM.

In practice, during synthesis, the FSM is often represented in the form of a transition list (Table 1), which is sometimes called a transition table.

Table 1. Transition list of the FSM.

t	pst	Xt	nst	Yt
0	s0	---	s1	001
1	s1	--0	s2	110
2	s1	-01	s3	101
3	s1	011	s4	100
4	s1	111	s5	010
5	s2	0--	s4	100
6	s2	1--	s5	010
7	s3	---	s0	100
8	s4	---	s0	000
9	s5	---	s0	000

One line of the transition list corresponds to one transition between the FSM states, where X^t is the input vector; Y^t is the output vector; ps_t is the initial state of the transition (present state); and ns_t is the final state of the transition (next state).

The input vector X^t is L bits long and corresponds to a conjunction of input variables, the value 1 of which initiates the transition t, t = $\overline{0,T-1}$. Each j-th bit of the vector X^t takes the value “1” when the conjunction contains the literal x_j, the value “0” when the conjunction contains the literal $\overline{x_j}$, and the value “-” when the variable x_j does not affect the transition t, t = $\overline{0,T-1}$.

3.2. Estimates of FSMs

Because the FSM state encoding affects the area and delay of only the transition functions of the set D, all the estimates considered in this paper concern only the transition functions. If necessary, the proposed estimates can also be applied to the output functions of the set Y.

3.2.1. Area Estimates

When FSMs are implemented in FPGAs, the area is usually measured by the number of LUTs used in the FSM circuit. Let n be the number of LUT inputs; X(d_r) be the set of input variables that are arguments of function d_r, d_r ∈ D; X(t,j) be the j-th bit of the input vector X^t; K(s_i) be the code of the state s_i; K(s_i,r) be the r-th bit of the code of the state s_i; and X(p_t) be the set of input variables affecting the t-th transition.

The e_FPGA estimate. The e_FPGA estimate is often used when FSMs are implemented in FPGAs. For this estimate, the area of each transition function d_r is calculated using expression (13):

$$area\left(d_r\right)=\left\{\begin{array}{c}1, rank\left(d_r\right)\le n;\\ ⌈{\displaystyle \frac{rank\left(d_r\right)-n}{n-1}}⌉+1, rank(d_r)>n;\end{array}\right.$$

(13)

where rank(d_r) denotes the rank of the transition function d_r, d_r ∈ D. The rank rank(d_r) is determined by the number of arguments of function d_r as follows:

$$rank\left(d_r\right)=\left|X(d_r)\right|+R,$$

(14)

where |A| denotes the cardinality of set A.

The e_FPGA estimate according to (13) and (14) is calculated using Algorithm 1.

Algorithm 1. Calculation of e_FPGA estimate.

INPUT: transition list.

OUTPUT: area.

area = 0;

for all r = 0 to R − 1 do     // loop by transition functions of set D

X(dr) = Ø;         // define the set X(dr), Ø is an empty set

for all t = 0 to T − 1 do     // loop by FSM transitions

if K(nst,r) = 1 then    // code K(nst,r) has one in bit r

for all j = 0 to L − 1 do   // loop by input variables

if X(t,j) = 1 or X(t,j) = 0 then   // xj affects the transition t

X(dr) = X(dr) U {xj};    // include xj in the set X(dr)

end if

end for

end if

end for

rank(dr) = |X(dr)| + R;    // determine the rank of the function dr

if (rank(dr) <= n) then    // calculate the area of the function dr

area(dr) = 1;

else

$area(d_r)=⌈(rang\left(d_r\right)-n)/(n-1)⌉$;

end if

area = area + area(dr);    // increasing the total area

end for

Return area.

The disadvantage of the e_FPGA estimate is that it only considers the number of arguments of each transition function d_r, and it does not consider the number of FSM transitions. Therefore, the e_FPGA estimate can be considered a lower bound on the number of LUTs in the realization of FSM transition functions.

The e_CPLD estimate. For this estimate, the area of each transition function d_r is defined as the number of cubes (minterms) in the SOP of the function d_r, d_r ∈ D:

$$d_r=m_{0 }^r+\dots +m_{Q-1}^r;$$

(15)

where $m_q^r$ is the q-th minterm of function d_r; and Q is the number of minterms in the SOP of the function d_r, d_r ∈ D. In this case, the area of function d_r is defined as follows:

area(d_r) = Q.

(16)

The computation of the e_CPLD estimate, according to (15) and (16), is described by Algorithm 2.

Algorithm 2. Calculation of the e_CPLD estimate.

INPUT: transition list. OUTPUT: area. area = 0; for all r = 0 to R − 1 do               // loop by transition functions of the set D     area(dr) = 0;                 // determine the area of the function dr    for all t = 0 to T − 1 do          // loop by FSM transitions       if K(nst,r) = 1 then         // nst state code contains 1          area(dr) = area(dr) + 1;    // increase the area of the function dr       end if    end for    area = area + area(dr);          // increasing the total area end for Return (area).

The e_CPLD estimate has the following disadvantages: the number of arguments of function d_r is not considered; the complexity of each minterm is not considered; and the LUT parameters are not considered. However, despite these disadvantages, the e_CPLD estimate has shown high efficiency in the implementation of FSMs in CPLDs [19], so it is called e_CPLD.

The classic estimate. Most of the e_CPLD estimate disadvantages were absent in the classic estimate. The classic estimate corresponds to the number of gate inputs when function f is realized on elements of small and medium degrees of integration.

The SOP of each transition function d_r, d_r ∈ D, can be represented as follows:

$$d_r={\sum }_{t=0}^{T-1}{X}^t·E^t·flag(r,t),$$

(17)

where X^t is the conjunction of input variables initiating the t-th transition; E^t is the conjunction of feedback variables defining the state code ps_t; and flag(r, t) = 1 if the minterm $X^t·E^t$ is included in the SOP of the function d_r, otherwise flag(r, t) = 0. It follows from (17) that the number of literals in each minterm is equal to

$$\left|X^t\right|+R.$$

(18)

The computation of the classic estimate, based on (17) and (18), is described by Algorithm 3.

Algorithm 3. Calculation of the classic estimate.

INPUT: transition list. OUTPUT: area. area = 0; for all r = 0 to R − 1 do        // loop on transition functions of the set D     area(dr) = 0;          // determine the estimate of the function dr     for all t = 0 to T−1 do    // loop by transitions of a finite automaton        if K(nst,r) = 1 then      // state code nst contains 1            area(dr) = area(dr) + 1;     // count the number of minterms            X(pt) = Ø;          // define the set X(pt)            for all j = 0 to L − 1 do                if X(t,j) = 1 or X(t,j) = 0 then    // xj affects the transition t                    X(pt) = X(pt) U {xj};       // xj is included in X(pt)                end if            end for           area(dr) = area(dr) + | X(pt) | + R;      // increase area(dr)        end if      area = area + area(dr);     // increase the total area end for Return area.

Note that the classic estimate does not consider the LUT parameters.

The terms estimate. The terms estimate assumes that each minterm of transition functions is implemented in the FPGA as a separate Boolean function. The terms estimate assumes, in advance, the use of a redundant number of LUTs, but it takes into account more properties of the transition functions. In the terms estimate, the area is computed as the sum of the areas of all the minterms of each transition function d_r, d_r ∈ D:

$$area\left(d_r\right)={\sum }_{q=0}^{Q-1}area(m_q^r),$$

(19)

where $area(m_q^r)$ is the area of the minterm $m_q^r$ of the function d_r, d_r ∈ D.

The value of area $area(m_q^r)$ of minterm $m_q^r$ is determined by expression (13), only instead of the rank $rank\left(d_r\right)$ of function d_r the rank $rank\left(m_q^r\right)$ of minterm $m_q^r$ is used, which is calculated by expression (20):

$$rank\left(m_q^r\right)=\left|X(m_q^r)\right|+R,$$

(20)

where $X(m_q^r)$ is the set of input variables that are arguments of the minterm $m_q^r$.

The computation of the terms estimate, according to (13), (19), and (20), is described by Algorithm 4.

Algorithm 4. Calculation of the terms estimate.

INPUT: transition list. OUTPUT: area. area = 0; for all r = 0 to R − 1 do      // loop on transition functions of the set D     area(dr) = 0;      // determine the estimate of the function dr     for all t = 0 to T − 1 do      // loop by transitions of the FSM       if K(nst,r) = $1 \mathbf{then} \hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{state} \mathrm{code} {\mathrm{ns}}_t \mathrm{contains} 1$          $X(m_t^r)=Ø; \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{define} \mathrm{the} \mathrm{set} X(m_t^r$$), Ø \mathrm{is} \mathrm{an} \mathrm{empty} \mathrm{set}$          $\mathbf{for} \mathbf{all} \mathrm{j}=0 \mathbf{to} L-1 \mathbf{do} \hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{loop} \mathrm{by} \mathrm{bits} \mathrm{of} \mathrm{input} \mathrm{vector} X^t$             $\mathbf{if} X(t,\mathrm{j})=1 \mathbf{or} X(t,\mathrm{j})=0 \mathbf{then}$               $X(m_t^r)=X(m_t^r) \mathrm{U} \left\{{\mathrm{x}}_{\mathrm{j}}\right\}; \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{include} {\mathrm{x}}_{\mathrm{j}} \mathrm{in} X(m_t^r)$             end if          end for          $rank(m_t^r)=| X(m_t^r$$) |+R; \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{determine} \mathrm{the} \mathrm{rank} \mathrm{of} \mathrm{minterm}{ m}_t^r$          $\mathbf{if} (\mathrm{rank}(m_t^r$$) \text{<}=n) \mathbf{then}$            $area(m_t^r)=1;$          else            $area(m_t^r)=⌈(rank\left(m_t^r\right)-n)/(n-1)⌉;$          end if          $area(d_r)=area(d_r)+area(m_t^r$);      // increase area(dr)        end if        area = area + area(dr);           // increase the total area     end for end for Return area.

A special feature of the terms estimate is that it considers the area of each minterm of each transition function. Despite the redundancy of the terms estimate, in an FSM encoding and synthesis methods, this redundancy is an advantage over other estimates because it takes into account more properties of the transition functions.

3.2.2. Performance Estimates

The performance of an FSM is determined by the maximum operation frequency of the FSM circuit. At the logic synthesis level, performance is often associated with the critical path length (cpl). When FSMs are implemented in LUT-based FPGAs, the path length is determined by the number of LUTs through which signals pass from the input to the output of the circuit.

There are two main ways of decomposing complex Boolean functions: sequential (Figure 2a) and parallel (Figure 2b).

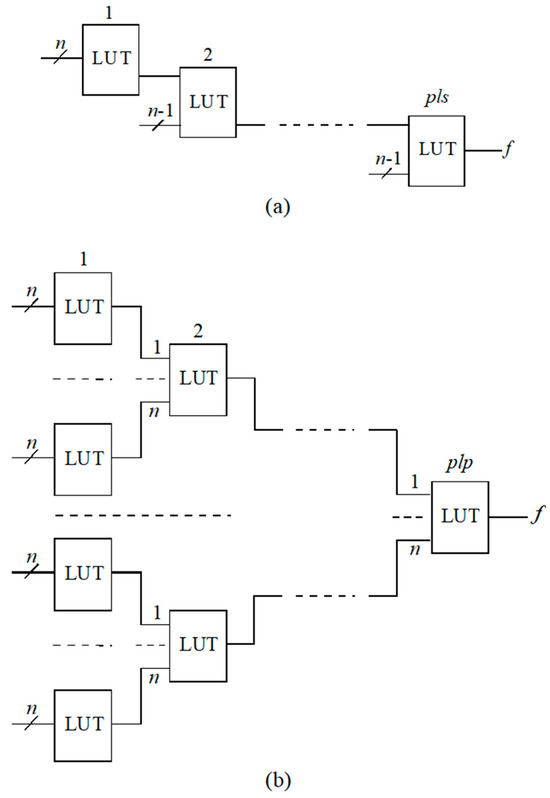
Figure 2. Generalized decomposition structures: (a) sequential; (b) parallel.

The number pls of LUT levels in the case of the sequential decomposition of the Boolean function f is determined by expression (21):

$$pls(f)=\left\{\begin{array}{c}1, rank\left(f\right)\le n;\\ ⌈{\displaystyle \frac{rank\left(f\right)-n}{n-1}}⌉+1, rank\left(f\right)>n;\end{array}\right.,$$

(21)

where rank(f) is the number of arguments of function f.

The number plp of LUT levels in the case of parallel decomposition of the Boolean function f is determined by expression (22):

$$plp(f)=⌈{\log }_n(rank(f))⌉=⌈{\displaystyle \frac{{\log }_{e}rank(f)}{{\log }_{e}n}}⌉.$$

(22)

The seq_dec estimate. The seq_dec estimate determines the critical path length of FSM transition functions for the case of the sequential decomposition of Boolean functions when the signal path length is computed using expression (21). Let pls(d_r) be the signal path length of a transition function d_r, d_r ∈ D. The computation of the critical path length cpl of the seq_dec estimate is described by Algorithm 5.

Algorithm 5. Calculation of the seq_dec estimate.

INPUT: transition list. OUTPUT: cpl. cpl = 0; for all r = 0 to R − $1 \mathbf{do} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{loop} \mathrm{by} \mathrm{function} d_r$;    Determine the set X(dr) as in Algorithm 1;    rank(dr) = |X(dr)| + R;     // determine the rank of the function dr    if rank(dr) <= n then     // calculate the path length pls(dr) of the function dr      pls(dr) = 1;    else      pls(dr) = ⌈(rang(dr) − n)/(n − 1)⌉;    end if    if pls(dr) > cpl then      // determine the length of the critical path      cpl = pls(dr);    end if end for Return cpl.

The par_dec estimate. The par_dec estimate determines the critical path length of the FSM functions for the case of parallel decomposition of Boolean functions when the signal path length is computed using expression (22). Let plp(d_r) be the signal path length of a transition function d_r. The computation of the critical path length cpl of the par_dec estimate is described by Algorithm 6.

Algorithm 6. Calculation of the par_dec estimate.

INPUT: transition list. OUTPUT: cpl. cpl = 0; for all r = 0 to R − $1 \mathbf{do} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}// \mathrm{loop} \mathrm{by} \mathrm{function} d_r$     Determine the set X(dr) as in Algorithm 1;     rank(dr) = |X(dr)| + R;         // determine the rank of the function dr     plp(dr) = ⌈log⁡(rang(dr))/log⁡n⌉;    // calculate the path length plp(dr) for dr     if (plp(dr) > cpl) then         // determine the length of the critical path        cpl = plp(dr);     end if end for Return cpl.

The disadvantage of the seq_dec and par_dec estimates is that they do not take into account the number of transitions T and the number of states M of the FSMs.

The avg_dec estimate. The avg_dec estimate is calculated as the arithmetic mean of the seq_dec and par_dec estimations according to Equation (23):

$$avg\_dec=⌈(seq\_dec+par\_dec)/2⌉.$$

(23)

3.2.3. Other Estimates for FSMs

In addition to estimates directly aimed at determining the area or performance of the FSM being designed, other estimates can be proposed that are not directly aimed at computing the area or performance of the FSM.

The diff_w estimate. The diff_w estimate is based on the following assumption: if all transition functions d_r, d_r ∈ D, have approximately the same complexity, which is determined by the weight w(d_r), then the depth and possibly the area of the FSM will be minimized.

Let the weight of function d_r, d_r ∈ D, be defined as the number of cubes [9] in the SOP of the function d_r, i.e., using expression (24):

$$w\left(d_r\right)={\sum }_{i=0}^{M-1}C\left(s_i\right)·K\left(s_i,r\right),$$

(24)

where C(s_i) is the number of transitions ending in state s_i, s_i ∈ S.

The value of the diff_w estimate is determined by expression (25):

$$\mathit{diff\_w}=\underset{d_r\in D}{\max }\left(w\left(d_r\right)\right)-\underset{d_r\in D}{\min }(w(d_r)).$$

(25)

The computation of the diff_w estimate, according to (24) and (25), is described by Algorithm 7.

Algorithm 7. Calculation of the diff_w estimate.

INPUT: transition list. OUTPUT: max(w(dr)) − min(w(dr)). for all i = 0 to M − 1 do       // determine the set of values C(si)     C(si) = 0;       // determine the number of transitions to the state si     for all t = 0 to T − 1 do       if nst = si then          C(si) = C(si) + 1;       end if     end for end for for all r = 0 to R − 1 do       // determine weights of functions dr     w(dr) = 0;     for all i = 0 to M − 1 do       // loop on the FSM states       if K(si,r) = 1 then       // state code si has 1 in bit r          w(dr) = w(dr) + C(si);       end if     end for end for max_w = −1; min_w = 10,000;       // find the maximum and minimum values of weight for all r = 0 to R−1 do          // loop by weights of functions dr     if w(dr) > max_w then max_w = w(dr) end if     if w(dr) < min_w then min_w = w(dr) end if end for Return (max_w − min_w);

The max_w estimate. The max_w estimate is based on the assumption that in order to increase the speed of FSMs, it is reasonable to minimize the length of the critical path, which is defined by the weight w(d_r), d_r ∈ D.

In the max_w estimate, the result is the maximum weight value of all transition functions d_r, d_r ∈ D. Therefore, the value of max_w estimate is determined by expression (26):

$$\mathit{max\_w}=\underset{d_r\in D}{\max }(w(d_r)).$$

(26)

The computation of the max_w estimate, according to (24) and (26), is described by Algorithm 8.

Algorithm 8. Calculation of the max_w estimate.

INPUT: transition list. OUTPUT: max(w(dr)). Determine the set of values C(si), si ∈ S, as in Algorithm 7; Determine the weights w(dr) of functions dr, dr ∈ D, as in Algorithm 7; max_w = −1;            // find the maximum value of weight for all r = 0 to R − 1 do       // loop by weights of functions dr     if w(dr) > max_w then       max_w = w(dr);     end if end for Return max_w.

In the diff_w and max_w estimates, the weight w(d_r) of the transition function d_r, d_r ∈ D, can be computed in different ways, not necessarily using expression (24). By defining other weights of the function d_r, other estimates can be defined to increase the performance or reduce the area of the FSMs. Depending on the selected weight of the function d_r, the optimization criteria can be changed. For example, to minimize the area, one can choose e_FPGA, e_CPLD, classic, or terms estimate as the weight w(d_r), and to increase performance, one can choose seq_dec, par_dec, or avg_dec estimate as the weight w(d_r).

In this way new estimates of the area and performance of FSMs can be created based on the diff_w and max_w estimates. In Algorithms 7 and 8, the number of cubes [9] in the SOP of function d_r is used as the weight w(d_r), which corresponds to the e_CPLD estimate.

Table 2 presents the parameters of FSMs that are considered (directly or indirectly) in the above estimates, where “+”—the parameter is taken into account; “-”—the parameter is not taken into account.

Table 2. The parameters of FSMs that are taken into account in the presented estimates.

Estimates	L	M	T	R	n
e_FPGA	+	-	-	+	+
e_CPLD	-	-	+	+	-
classic	+	-	+	+	-
terms	+	-	+	+	+
seq_dec	+	-	-	+	+
par_dec	+	-	-	+	+
avg_dec	+	-	-	+	+
diff_w	-	+	+	+	-
max_w	-	+	+	+	-

Table 2 shows that all estimates consider the number of code bits R. Most estimates consider the number of FSM inputs L and the number of LUT inputs n. The estimates e_CPLD, classic, and terms consider the number of transitions T. The estimates diff_w and max_w consider both the number of transitions T and the number of states M.

The e_FPGA, e_CPLD, classic, diff_w, and max_w estimates were used in [8] to determine the implementation cost of the FSM; the seq_dec and par_dec estimates were used in [4] to determine the performance of the FSM; and the terms and avg_dec estimates are new.

3.3. Example of Calculating FSM Evaluations

For example, consider the FSM whose transition list is presented in Table 1. Our FSM has 6 states s0,…,s5. Let the FSM states be encoded by a sequential binary code: s0—000, s1—001, s2—010, s3—011, s4—100, and s5—101. For convenience in demonstrating the computation of the considered estimates, the columns K(ps_t) and K(ns_t) with the codes of the initial and final states of the transitions have been added in Table 1. Moreover, the row with the variables of sets E, X, D, and Y has been added to the header of Table 1. The modified transitions list of the FSM (also called the structural transition table) is presented in Table 3.

Table 3. Transitions list of the FSM with the state codes.

t	pst	K(pst) e2e1e0	Xt x2x1x0	nst	K(nst) d2d1d0	Yt y2y1y0
0	s0	000	---	s1	001	001
1	s1	001	--0	s2	010	110
2	s1	001	-01	s3	011	101
3	s1	001	011	s4	100	100
4	s1	001	111	s5	101	010
5	s2	010	0--	s4	100	100
6	s2	010	1--	s5	101	010
7	s3	011	---	s4	100	100
8	s4	100	---	s0	000	000
9	s5	101	---	s0	000	000

Based on the structural transition table, the following logical equations in SOP forms can be written for the FSM transition functions:

$$\begin{array}{l}{d}_0=\overline{e_2}·\overline{e_1}·\overline{e_0}+\overline{x_1}·x_0·\overline{e_2}·\overline{e_1}·e_0+x_2·x_1·x_0·\overline{e_2}·\overline{e_1}·e_0+x_2·\overline{e_2}·e_1·\overline{e_0};\\ d_1=\overline{x_0}·\overline{e_2}·\overline{e_1}·e_0+\overline{x_1}·x_0·\overline{e_2}·\overline{e_1}·e_0;\\ d_2=\overline{x_2}·x_1·x_0·\overline{e_2}·\overline{e_1}·e_0+x_2·x_1·x_0·\overline{e_2}·\overline{e_1}·e_0+\overline{x_2}·\overline{e_2}·e_1·e_0+x_2·\overline{e_2}·e_1·\overline{e_0}+\overline{e_2}·e_1·e_0.\end{array}$$

(27)

In Equation (27), the sign “∙” denotes logical AND, and the sign “+” denotes logical OR.

The area values for the transition functions d₀,…,d₂ as well as the total area of the FSM for the e_FPGA, e_CPLD, classic, and terms estimates are given in Table 4.

Table 4. Values of the estimates for area.

	e_FPGA	e_CPLD	classic	terms
area(d0)	2	4	22	6
area(d1)	2	2	11	3
area(d2)	2	5	23	7
area	6	11	56	16

Table 4 shows that the e_FPGA estimate does not distinguish the area of the transition functions for our example. However, other estimates indicate differences in the area of each transition function. Each of these estimates indicates that the area of function d₁ is half the area of function d₀, and the area of function d₂ is larger than the area of function d₀.

Table 5 presents the ranks of the transition functions in computing the performance estimates, the number of LUT levels pls(d_r) or plp(d_r) for each function d_r, d_r ∈ D, and the value of the critical path length cpl.

Table 5. The rank values, the number of levels, and the critical path length of the FSM transition functions in calculating performance estimates.

	rank(dr)	seq_dec	par_dec	avg_dec
pls/plp(d0)	6	2	2	2
pls/plp(d1)	5	2	2	2
pls/plp(d2)	6	2	2	2
cpl		2	2	2

For our simple example, the ranks of the transition functions differ only slightly. Therefore, the value of the estimates as well as the value of the critical path length match. Nevertheless, for large and complex FSMs, the seq_dec, par_dec, and avg_dec estimates can be useful in the FSM state encoding.

In computing the diff_w and max_w estimates, we have the following values for the weights of the transition functions: w(d₀) = 4, w(d₁) = 2, and w(d₂) = 5. Therefore, diff_w = 3 and max_w = 5. The diff_w and max_w estimates are not computed for each transition function. However, the diff_w and max_w estimates can evaluate the intermediate results of FSM state encoding and can positively influence finding the best solution.

4. Results and Discussions

The considered estimates were used in the sequential method of FSM state encoding [8]. The studies were performed using design tool Quartus from Intel version 24.1 while implementing the FSM benchmarks of the Microelectronics Center of North Carolina (MCNC) [20] in FPGAs of family Cyclone 10 LP. The selection of states to encode was performed in P_C mode [8], when for encoding the state s_i, s_i ∈ S, with the maximum number of connections to already encoded states is selected. The search for the most appropriate code was performed using the considered estimates.

4.1. Results with Respect to the FSM Area

The experimental results with respect to the FSM area are shown in Table 6 and Table 7, where L1, …,L7 are the number of LUTs in the FSM circuit when using the corresponding estimate; Lmin is the minimum value of area for a particular example; Best is the number of best solutions; Unique is the number of unique solutions; L1/Lmin, …,L7/Lmin are the ratios of the corresponding parameters; and Av is the arithmetic mean of the parameter. Here, the unique solution is understood as the best solution, which is achieved using a particular estimate and which is not achieved using other estimates.

Table 6. Area (number of LUTs) of FSMs when using the considered estimates in the sequential state coding method [8] (the best solutions are in bold).

FSM	e_FPGA L1	classic L2	diff_w L3	max_w L4	seq_dec L5	par_dec L6	avg_dec L7	Lmin
bbara	32	26	37	28	32	32	32	26
bbsse	61	61	65	54	57	66	57	54
beecount	18	19	20	19	18	18	18	18
cse	86	83	85	80	86	86	86	80
dk14	48	40	45	45	48	48	48	40
dk15	15	15	14	15	15	15	15	14
dk16	86	86	87	115	86	86	86	86
dk17	12	13	12	21	12	12	12	12
dk512	15	15	18	14	15	15	15	14
ex1	109	108	112	103	109	106	106	103
ex4	33	31	41	30	33	33	33	30
ex5	18	20	26	21	18	18	18	18
ex6	55	58	52	53	55	55	55	52
ex7	20	23	36	26	20	20	20	20
keyb	73	72	100	75	73	73	73	72
lion9	11	15	22	13	11	11	11	11
planet	199	201	203	199	195	190	195	190
planet1	199	201	203	199	195	190	195	190
pma	148	153	149	154	162	141	162	141
s1	190	146	180	147	190	190	190	146
s1488	228	226	227	237	220	220	220	220
s1494	218	234	223	226	223	223	223	218
s298	929	954	1075	991	929	929	929	929
s386	54	48	60	55	56	56	56	48
s510	136	143	155	149	130	103	103	103
s820	132	129	144	130	129	132	132	129
s832	132	133	144	129	134	131	131	129
sand	199	231	228	220	199	199	199	199
sse	61	61	65	54	57	66	57	54
styr	190	186	183	186	190	190	190	183
tbk	274	265	273	262	274	274	274	262
tma	98	96	96	93	99	98	99	93
train11	28	25	25	30	28	28	28	25
Best	9	8	5	9	10	13	10
Unique	1	5	3	9	0	3	0

Table 7. Comparison of the FSM area using different estimates with the best solution Lmin.

FSM	e_FPGA L1/Lmin	classic L2/Lmin	diff_w L3/Lmin	max_w L4/Lmin	seq_dec L5/Lmin	par_dec L6/Lmin	avg_dec L7/Lmin
bbara	1.231	1.000	1.423	1.077	1.231	1.231	1.231
bbsse	1.130	1.130	1.204	1.000	1.056	1.222	1.056
beecount	1.000	1.056	1.111	1.056	1.000	1.000	1.000
cse	1.075	1.038	1.063	1.000	1.075	1.075	1.075
dk14	1.200	1.000	1.125	1.125	1.200	1.200	1.200
dk15	1.071	1.071	1.000	1.071	1.071	1.071	1.071
dk16	1.000	1.000	1.012	1.337	1.000	1.000	1.000
dk17	1.000	1.083	1.000	1.750	1.000	1.000	1.000
dk512	1.071	1.071	1.286	1.000	1.071	1.071	1.071
ex1	1.058	1.049	1.087	1.000	1.058	1.029	1.029
ex4	1.100	1.033	1.367	1.000	1.100	1.100	1.100
ex5	1.000	1.111	1.444	1.167	1.000	1.000	1.000
ex6	1.058	1.115	1.000	1.019	1.058	1.058	1.058
ex7	1.000	1.150	1.800	1.300	1.000	1.000	1.000
keyb	1.014	1.000	1.389	1.042	1.014	1.014	1.014
lion9	1.000	1.364	2.000	1.182	1.000	1.000	1.000
planet	1.047	1.058	1.068	1.047	1.026	1.000	1.026
planet1	1.047	1.058	1.068	1.047	1.026	1.000	1.026
pma	1.050	1.085	1.057	1.092	1.149	1.000	1.149
s1	1.301	1.000	1.233	1.007	1.301	1.301	1.301
s1488	1.036	1.027	1.032	1.077	1.000	1.000	1.000
s1494	1.000	1.073	1.023	1.037	1.023	1.023	1.023
s298	1.000	1.027	1.157	1.067	1.000	1.000	1.000
s386	1.125	1.000	1.250	1.146	1.167	1.167	1.167
s510	1.320	1.388	1.505	1.447	1.262	1.000	1.000
s820	1.023	1.000	1.116	1.008	1.000	1.023	1.023
s832	1.023	1.031	1.116	1.000	1.039	1.016	1.016
sand	1.000	1.161	1.146	1.106	1.000	1.000	1.000
sse	1.130	1.130	1.204	1.000	1.056	1.222	1.056
styr	1.038	1.016	1.000	1.016	1.038	1.038	1.038
tbk	1.046	1.011	1.042	1.000	1.046	1.046	1.046
tma	1.054	1.032	1.032	1.000	1.065	1.054	1.065
train11	1.120	1.000	1.000	1.200	1.120	1.120	1.120
Av	1.072	1.072	1.193	1.104	1.068	1.063	1.059

In the sequential state coding method [8], the e_CPLD, classic, and terms estimates lead to the same results when the code with the minimum number of ones is selected at each step of the algorithm. Therefore, in Table 6 and Table 7, the values for the classic estimate only are given.

Table 7 shows that with respect to the best area solution on average (parameter Av), the estimates can be arranged in the following order:

avg_dec—1.059;

par_dec—1.063;

seq_dec—1.068;

e_FPGA—1.072;

classic—1.072;

max_w—1.104;

diff_w—1.193.

Unexpectedly, the avg_dec, par_dec, and seq_dec estimates, which are designed to measure the performance rather than the area of FSMs, are the best in terms of area on average. Of these, the par_dec estimate achieves the largest number (13) of best solutions (Table 6). The e_FPGA estimate, which is designed to most accurately measure the area when implementing FSMs in FPGAs, achieves 9 best solutions and follows immediately after the avg_dec, par_dec, and seq_dec estimates. This is followed by the estimates of classic, max_w, and diff_w. Note that the max_w estimate unexpectedly reaches the highest number of unique solutions (9). The diff_w estimate ranks last in the order given, but it achieves the best 5 solutions, among which 3 solutions are unique.

Given the reported results, we recommend that when searching for the best area solution using the sequential state coding method [8], all estimates should be considered, since each estimate can achieve the best solution.

Figure 3 shows the graphs of the efficiency of the considered estimates in terms of area. Here, the estimates are assigned place numbers by the average area value (Average) according to the order given above, with the avg_dec estimate having the highest number 7 and the diff_w estimate having the lowest number 1.

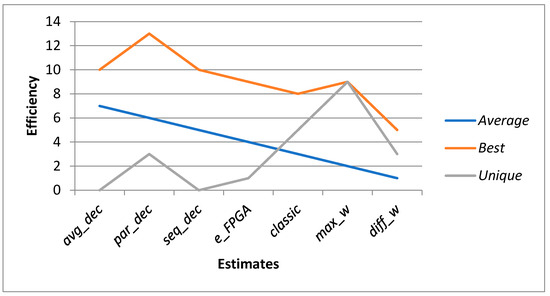
Figure 3. Efficiency by area of the estimates considered: Average is the place in order by average value area; Best is the number of best solutions; Unique is the number of unique solutions.

According to Figure 3, the ranking in terms of average area value (Average) approximately corresponds to the number of best solutions (Best).

4.2. Results with Respect to the FSM Performance

The results of the studies with respect to performance are summarized in Table 8 and Table 9, where F1,…,F7 are the maximum frequency of the FSM operation (in megahertz) using the corresponding estimate; Fmax is the maximum frequency value for a particular example; Fmax/F1,…, Fmax/F7 are the ratios of the corresponding parameters; and Best, Unique, and Av meaning as before.

Table 8. Performance of FSMs when using the considered estimates in the sequential state coding method [8] (the best solutions are in bold).

FSM	e_FPGA F1	classic F2	diff_w F3	max_w F4	seq_dec F5	par_dec F6	avg_dec F7	Fmax
bbara	430	529	414	453	430	430	430	529
bbsse	324	335	321	349	357	320	357	357
beecount	633	632	601	632	633	633	633	633
cse	298	323	300	322	298	298	298	323
dk14	457	423	576	479	457	457	457	576
dk15	869	869	796	869	869	869	869	869
dk16	375	371	398	262	375	375	375	398
dk17	648	712	711	647	648	648	648	712
dk512	578	640	639	654	578	578	578	654
ex1	317	307	307	320	317	339	339	339
ex4	464	545	393	496	464	464	464	545
ex5	504	521	505	480	504	504	504	521
ex6	384	358	408	381	384	384	384	408
ex7	472	551	383	487	472	472	472	551
keyb	328	335	273	341	329	329	329	341
lion9	636	587	461	606	636	636	636	636
planet	243	236	234	249	235	239	235	249
planet1	243	236	234	249	235	239	235	249
pma	223	245	246	265	249	277	249	277
s1	241	255	256	256	241	241	241	256
s1488	235	239	223	233	227	227	227	239
s1494	219	234	206	228	232	232	232	234
s298	128	121	126	122	128	128	128	128
s386	343	368	315	372	357	357	357	372
s510	250	246	226	241	233	303	303	303
s820	243	239	233	230	231	247	247	247
s832	229	246	262	264	250	234	234	264
sand	244	230	226	229	244	244	244	244
sse	324	335	321	349	357	320	357	357
styr	241	242	230	250	241	241	241	250
tbk	192	206	199	188	192	192	192	206
tma	290	315	284	290	287	290	287	315
train11	435	451	518	469	435	435	435	518
Best	5	11	5	9	6	7	9
Unique	1	10	4	7	0	1	0

Table 9. Comparison of FSM performance using different estimates with the best solution Fmax.

FSM	e_FPGA Fmax/F1	classic Fmax/F2	diff_w Fmax/F3	max_w Fmax/F4	seq_dec Fmax/F5	par_dec Fmax/F6	avg_dec Fmax/F7
bbara	1.230	1.000	1.278	1.168	1.230	1.230	1.230
bbsse	1.102	1.066	1.112	1.023	1.000	1.116	1.000
beecount	1.000	1.002	1.053	1.002	1.000	1.000	1.000
cse	1.084	1.000	1.077	1.003	1.084	1.084	1.084
dk14	1.260	1.362	1.000	1.203	1.260	1.260	1.260
dk15	1.000	1.000	1.092	1.000	1.000	1.000	1.000
dk16	1.061	1.073	1.000	1.519	1.061	1.061	1.061
dk17	1.099	1.000	1.001	1.100	1.099	1.099	1.099
dk512	1.131	1.022	1.023	1.000	1.131	1.131	1.131
ex1	1.069	1.104	1.104	1.059	1.069	1.000	1.000
ex4	1.175	1.000	1.387	1.099	1.175	1.175	1.175
ex5	1.034	1.000	1.032	1.085	1.034	1.034	1.034
ex6	1.063	1.140	1.000	1.071	1.063	1.063	1.063
ex7	1.167	1.000	1.439	1.131	1.167	1.167	1.167
keyb	1.040	1.018	1.249	1.000	1.036	1.036	1.036
lion9	1.000	1.083	1.380	1.050	1.000	1.000	1.000
planet	1.025	1.055	1.064	1.000	1.060	1.042	1.060
planet1	1.025	1.055	1.064	1.000	1.060	1.042	1.060
pma	1.242	1.131	1.126	1.045	1.112	1.000	1.112
s1	1.062	1.004	1.000	1.000	1.062	1.062	1.062
s1488	1.017	1.000	1.072	1.026	1.053	1.053	1.053
s1494	1.068	1.000	1.136	1.026	1.009	1.009	1.009
s298	1.000	1.058	1.016	1.049	1.000	1.000	1.000
s386	1.085	1.011	1.181	1.000	1.042	1.042	1.042
s510	1.212	1.232	1.341	1.257	1.300	1.000	1.000
s820	1.016	1.033	1.060	1.074	1.069	1.000	1.000
s832	1.153	1.073	1.008	1.000	1.056	1.128	1.128
sand	1.000	1.061	1.080	1.066	1.000	1.000	1.000
sse	1.102	1.066	1.112	1.023	1.000	1.116	1.000
styr	1.037	1.033	1.087	1.000	1.037	1.037	1.037
tbk	1.073	1.000	1.035	1.096	1.073	1.073	1.073
tma	1.086	1.000	1.109	1.086	1.098	1.086	1.098
train11	1.191	1.149	1.000	1.104	1.191	1.191	1.191
Av	1.088	1.055	1.113	1.072	1.080	1.071	1.069

Table 9 shows that with respect to the best performance solution on average (parameter Av), the estimates can be arranged in the following order:

classic—1.055;

avg_dec—1.069;

par_dec—1.071;

max_w—1.072;

seq_dec—1.080;

e_FPGA—1.088;

diff_w—1.113.

Unexpectedly, the best in terms of performance on average is the classic estimate, which is designed to determine the FSM area. The classic estimate also achieves the highest number of best (11) and unique (10) solutions (Table 8). The classic estimate is expectedly followed by the avg_dec and par_dec estimates, which on average perform reasonably well in terms of performance. This is followed by the max_w, seq_dec, and e_FPGA estimates. The diff_w estimate shows noticeably worse results (1.113). However, the diff_w estimate reaches the 5 best solutions, among which 4 solutions are unique.

Given the reported results, we recommend that to find the best solution in terms of performance, all estimates should be applied because each estimate can achieve the best unique solution. Of the avg_dec, par_dec, and seq_dec estimates, only one avg_dec estimate can be applied because it achieves the largest number of best solutions.

Figure 4 shows the graphs of the efficiency of the considered estimates in terms of performance. Here, the estimates are assigned place numbers by the average performance value (Average) according to the order given above, with classic estimate having the highest number 7, and diff_w estimate having the lowest number 1.

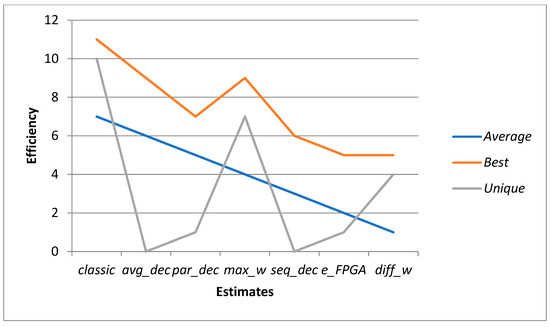
Figure 4. Efficiency by performance of the estimates considered: Average is the place in order by average value performance; Best is the number of best solutions; Unique is the number of unique solutions.

Figure 4 shows that the ranking in terms of average performance value (Average) approximately corresponds to the number of best solutions (Best).

4.3. Comparison of the Sequential State Coding Method Using Presented Estimates with Known Methods

To verify the effectiveness of the proposed estimates, let us compare the results of the sequential method (s_method) with simple binary coding (seq_code method), the Sequential mode of the Quartus system (Quartus method), and the JEDI program [21] (JEDI method). The results of this comparison are shown in Table 10 and Table 11, where LS, LQ, and LJ are the number of LUTs in the FSM circuit synthesized using the seq_code, Quartus, and JEDI methods; Lmin is the minimum area value from Table 6 for the particular example obtained using the s_method method; LS/Lmin, LQ/Lmin, and LJ/Lmin are the ratios of the corresponding parameters; FS, FQ, and FJ are the maximum operation frequency in megahertz of the FSM synthesized using the seq_code, Quartus, and JEDI methods; Fmax is the maximum frequency value from Table 8 for a particular example, obtained using the s_method method; Fmax/FS, Fmax/FQ, and Fmax/FJ are the ratios of the corresponding parameters; Max is the maximum value of the parameters; and Av, Best, and Unique meaning as before.

Table 10. Comparison of the sequential state encoding method using presented estimates with known FSM state encoding methods in terms of area (the best solutions are in bold).

FSM	seq_code LS	Quartus LQ	JEDI LJ	s_method Lmin	LS/Lmin	LQ/Lmin	LJ/Lmin
bbara	27	25	24	26	1.038	0.962	0.923
bbsse	60	59	62	54	1.111	1.093	1.148
beecount	18	18	21	18	1.000	1.000	1.167
cse	86	86	83	80	1.075	1.075	1.038
dk14	44	37	40	40	1.100	0.925	1.000
dk15	15	15	14	14	1.071	1.071	1.000
dk16	81	81	87	86	0.942	0.942	1.012
dk17	14	13	11	12	1.167	1.083	0.917
dk512	15	16	13	14	1.071	1.143	0.929
ex1	107	108	117	103	1.039	1.049	1.136
ex4	33	36	30	30	1.100	1.200	1.000
ex5	24	19	14	18	1.333	1.056	0.778
ex6	57	56	58	52	1.096	1.077	1.115
ex7	26	19	22	20	1.300	0.950	1.100
keyb	72	72	81	72	1.000	1.000	1.125
lion9	11	11	9	11	1.000	1.000	0.818
planet	201	218	201	190	1.058	1.147	1.058
planet1	201	218	201	190	1.058	1.147	1.058
pma	147	140	164	141	1.043	0.993	1.163
s1	147	137	140	146	1.007	0.938	0.959
s1488	218	226	232	220	0.991	1.027	1.055
s1494	227	233	234	218	1.041	1.069	1.073
s298	965	788	981	929	1.039	0.848	1.056
s386	58	55	49	48	1.208	1.146	1.021
s510	103	106	130	103	1.000	1.029	1.262
s820	123	131	133	129	0.953	1.016	1.031
s832	122	135	135	129	0.946	1.047	1.047
sand	222	220	228	199	1.116	1.106	1.146
sse	60	59	62	54	1.111	1.093	1.148
styr	175	215	185	183	0.956	1.175	1.011
tbk	266	266	282	262	1.015	1.015	1.076
tma	97	93	92	93	1.043	1.000	0.989
train11	28	26	22	25	1.120	1.040	0.880
Av					1.065	1.044	1.038
Max					1.333	1.200	1.262
Best	8	8	9	16
Unique	4	5	7	11

Table 11. Comparison of the sequential state encoding method using presented estimates with known FSM state encoding methods in terms of performance (the best solutions are in bold).

FSM	seq_code FS	Quartus FQ	JEDI FJ	s_method Fmax	Fmax/FS	Fmax/FQ	Fmax/FJ
bbara	430	451	547	529	1.230	1.173	0.967
bbsse	345	397	341	357	1.035	0.899	1.047
beecount	633	636	637	633	1.000	0.995	0.994
cse	291	302	319	323	1.110	1.070	1.013
dk14	471	595	596	576	1.223	0.968	0.966
dk15	869	911	799	869	1.000	0.954	1.088
dk16	374	372	333	398	1.064	1.070	1.195
dk17	637	712	717	712	1.118	1.000	0.993
dk512	642	642	668	654	1.019	1.019	0.979
ex1	302	315	317	339	1.123	1.076	1.069
ex4	539	539	545	545	1.011	1.011	1.000
ex5	485	531	581	521	1.074	0.981	0.897
ex6	387	454	393	408	1.054	0.899	1.038
ex7	463	465	532	551	1.190	1.185	1.036
keyb	318	318	313	341	1.072	1.072	1.089
lion9	636	640	684	636	1.000	0.994	0.930
planet	230	235	221	249	1.083	1.060	1.127
planet1	230	235	221	249	1.083	1.060	1.127
pma	237	217	237	277	1.169	1.276	1.169
s1	243	269	254	256	1.053	0.952	1.008
s1488	224	230	206	239	1.067	1.039	1.160
s1494	205	223	224	234	1.141	1.049	1.045
s298	126	144	127	128	1.016	0.889	1.008
s386	387	365	406	372	0.961	1.019	0.916
s510	303	270	265	303	1.000	1.122	1.143
s820	257	252	260	247	0.961	0.980	0.950
s832	233	221	242	264	1.133	1.195	1.091
sand	215	219	231	244	1.135	1.114	1.056
sse	345	397	341	357	1.035	0.899	1.047
styr	247	237	224	250	1.012	1.055	1.116
tbk	215	215	202	206	0.958	0.958	1.020
tma	290	307	288	315	1.086	1.026	1.094
train11	435	467	545	518	1.191	1.109	0.950
Av					1.073	1.035	1.040
Max					1.230	1.276	1.195
Best	1	7	11	16
Unique	0	6	10	15

Table 10 shows that using the proposed estimates in the s_method method reduces the FSM area by 6.5% on average compared to the seq_code method, by 4.4% compared to the Quartus method, and by 3.8% compared to the JEDI method. The largest area improvement by the s_method method is observed over the seq_code method in example ex5 (33.3% better), over the Quartus method in example ex4 (20.0% better), and over the JEDI method in example s510 (26.2% better). The s_method method achieves the largest number (16) of best solutions, of which 11 solutions are unique.

According to Table 11, using the proposed estimates in the s_method method on average improves the FSM performance by 7.3% over the seq_code method, 3.5% over the Quartus method, and 4.0% over the JEDI method. The greatest performance superiority of the s_method method is observed over the seq_code method in example bbara (23.0% better), over the Quartus method in example pma (27.6% better), and over the JEDI method in example dk16 (19.5% better). The s_method method achieves the largest number (16) of best area solutions, of which 15 solutions are unique.

5. Conclusions

In this paper, four FSM area estimates are proposed to estimate the quality of FSM state encoding: e_FPGA for implementing FSMs in FPGAs; e_CPLD for implementing FSMs in CPLDs; classic for implementing FSMs on elements of small and medium degree of integration; and terms for considering the largest number of FSM parameters. Three estimates of FSM performance are proposed: seq_dec, when sequential decomposition of Boolean functions is used; par_dec, when parallel decomposition of Boolean functions is used; and avg_dec, when an unknown method of Boolean function decomposition is used. In addition, two estimates that do not directly aim at computing area or delay are proposed: diff_w to ensure that the complexity of the FSM transition functions is approximately equal and max_w to minimize the maximum complexity of the FSM transition functions. It is shown how new estimates of the area and performance of FSMs can be generated from the diff_w and max_w estimates. The expressions and algorithms for the computation of each estimate are given.

A comparison of the efficiency of the estimates between each other on the benchmark of FSMs when using the proposed estimates in the sequential state coding method [8] is performed. The use of the considered estimates reduces the area of FSMs on average from 3.8% to 6.5%, compared to known approaches (for some cases by 33.3%), and increases the performance on average from 3.5% to 7.3% (for some cases by 27.6%).

Future research will be directed to the development of new estimates of the area and performance of FSMs, which should take into account more parameters of the FSM, as well as take into account the peculiarities of synthesis methods or state encoding of FSMs. The development of estimates based on other principles of measuring FSM parameters (e.g., based on information measures) is also seen as a promising direction.