A Novel FECAM-iTransformer Algorithm for Assisting INS/GNSS Navigation System during GNSS Outages

Abstract

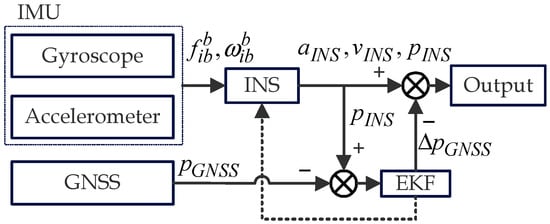
In the field of navigation and positioning, the inertial navigation system (INS)/global navigation satellite system (GNSS) integrated navigation system is known for providing stable and high-precision navigation services for vehicles. However, in extreme scenarios where GNSS navigation data are completely interrupted, the positioning accuracy of these integrated systems declines sharply. While there has been considerable research into using neural networks to replace the GNSS signal output during such interruptions, these approaches often lack targeted modeling of sensor information, resulting in poor navigation stability. In this study, we propose an integrated navigation system assisted by a novel neural network: an inverted-Transformer (iTransformer) and the application of a frequency-enhanced channel attention mechanism (FECAM) to enhance its performance, called an INS/FECAM-iTransformer integrated navigation system. The key advantage of this system lies in its ability to simultaneously extract features from both the time and frequency domains and capture the variable correlations among multi-channel measurements, thereby enhancing the modeling capabilities for sensor data. In the experimental part, a public dataset and a private dataset are used for testing. The best experimental results show that compared to a pure INS inertial navigation system, the position error of the INS/FECAM-iTransformer integrated navigation system reduces by up to 99.9%. Compared to the INS/LSTM (long short-term memory) and INS/GRU (gated recurrent unit) integrated navigation systems, the position error of the proposed method decreases by up to 82.4% and 78.2%, respectively. The proposed approach offers significantly higher navigation accuracy and stability.

1. Introduction

Highly accurate and reliable positioning, navigation, and timing technologies are essential for the safe operation of mobile smart devices [1]. Inertial navigation systems (INS) are characterized by short-term high accuracy and independence from environmental influences. However, standalone INS solutions degrade over time due to the significant errors inherent in the raw measurements of inertial measurement units (IMUs) [2]. This degradation is especially pronounced and drastic in INS systems that use small, low-cost IMU devices, which many mobile devices are compelled to use due to space constraints. The integration of global navigation satellite systems (GNSSs) and INS has been widely used to improve the accuracy and reliability of positioning [3,4], because GNSSs can provide long-term accurate and continuous positioning signals under decent visibility conditions [5], compensating for the defect of low-cost INS. However, the GNSS has one almost inevitable drawback: it relies heavily on stable signals for high-precision positioning. In areas with ambiguous signals, such as cities, forests, and tunnels, GNSS signals can become unstable or even lost [6,7]. If the GNSS signal is interrupted for a prolonged period, the GNSS/INS integrated navigation system will inevitably revert to a pure INS, leading to the rapid accumulation of positioning errors and compromising the safety and efficiency of vehicle operation [8].

There are many solutions to this problem, typically involving the addition of extra sensors such as barometers, odometers, cameras, LIDAR, etc., to collect richer environmental data [9,10,11]. However, this approach results in higher hardware costs and a more complicated data fusion process, making it less economical for general application scenarios [12]. In recent years, machine learning algorithms have been shown to improve the performance of GNSS/INS integrated navigation systems by modeling the mathematical relationship between navigation parameters and vehicle dynamic data during GNSS outages [13].

Sharaf et al. used a radial basis function neural network to model INS positions and the mathematical relationship between INS and GNSS for stable and reliable navigation performance [14,15]. Tan et al. employed support vector machines (SVM) optimized by genetic algorithms (GAs) to address neural network overfitting and local minimum problems [16]. Static neural networks have limited navigation performance due to their inability to remember long-term time features, leading to the application of more advanced deep learning models. Long short-term memory (LSTM), as a dynamic neural network, uses past and present information to predict future states and was applied to obtain stable GNSS navigation data during interruptions [17]. X. Meng et al. proposed a convolutional neural networks-gated recurrent unit (CNNs-GRU) hybrid model combined with an improved robust adaptive Kalman filter to enhance navigation accuracy during GNSS failures [18]. Despite solving the basic degradation problem, these deep neural networks still face accuracy and long-term stability issues. To further explore artificial intelligence in this field, large-scale deep learning models have been integrated into INS/GNSS systems. For example, the Transformer [19] was used to improve navigation reliability during GNSS outages [20], and the time convolutional network (TCN) was applied for its feature extraction and time modeling capabilities, achieving multi-task learning when combined with other neural networks like GRU [21].

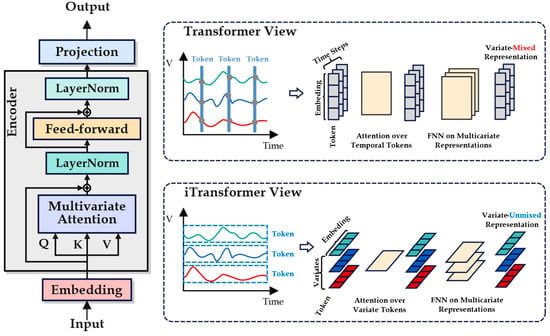
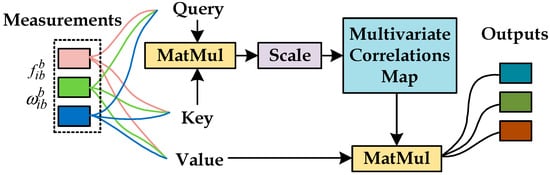
It is worth noting that the models mentioned above are significant research advancements in time-series prediction, which raises the question of whether other models could also improve navigation stability. In time-series prediction, recurrent neural networks such as LSTM [22] and GRU [23] are well suited for capturing long-term dependencies due to their gating mechanisms and memory units. However, they lack specialized feature extraction units. For time-series data rich in motion and noise features, such as IMU data, LSTM and GRU may struggle to learn effective features. The attention-based Transformer [19] model has become a popular research direction in time-series prediction. Its well-designed attention mechanism can effectively learn both temporal and spatial characteristics. However, like most time-series prediction models, the Transformer is sensitive to inconsistencies in the timing of events. The Transformer treats each variable at the same timestamp as a token, which can introduce noise if the timestamps are misaligned or if there is a shift in the statistical distribution of the data [24]. The iTransformer [25] addresses this issue effectively by inputting the entire time series for each input channel into the model as a token, thereby avoiding the noise introduced by misaligned timestamps or non-stationary information. Additionally, the inclusion of the attention mechanism makes iTransformer more effective in capturing variable relationships between sequences. This model is particularly suitable for modeling multi-channel IMU data in INS/GNSS combined systems.

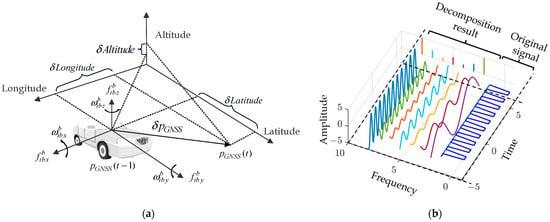
Navigation data possess unique characteristics. In addition to their rich kinematic features, they also contain a significant amount of noise, which can mislead AI algorithms into learning invalid features. Therefore, a critical challenge is to enable AI to correctly understand and analyze the features of navigation data to achieve optimal prediction performance. The core sensor of the INS is IMU, which includes gyroscopes and accelerometers. Numerous studies have demonstrated that frequency analysis is an effective method for analyzing data from these devices. Wang et al. analyzed the relationship between IMU measurement noise and inertial guidance system noise from a frequency-domain perspective to improve the positioning accuracy of the INS/DVL integrated navigation system [26]. Zihajehzadeh et al. used Gaussian process regression, combining both time-domain and frequency-domain features of the IMU to estimate a human’s walking speed [27]. Bolotin et al. proposed a low-cost calibration method for IMUs, utilizing fast Fourier transform (FFT) to obtain frequency-domain data and find the frequency, amplitude, and phase at the spectrum’s peak [28]. Frequency analysis methods are also widely used in time-series forecasting to extract compact and rich temporal features, such as FNet, frequency-enhanced decomposed transformer (FEDformer), and a frequency interpolation time-series analysis baseline (FITS) [29,30,31].

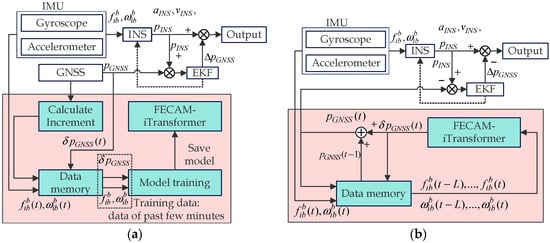
In this paper, a novel AI-assisted INS/GNSS integrated navigation system is proposed to address the rapid accuracy degradation of the INS/GNSS integrated navigation system during a GNSS outage. The iTransformer is introduced and optimized based on considerations of computational accuracy and data characteristics to make it more suitable for navigation.

The main contributions of this paper are as follows:

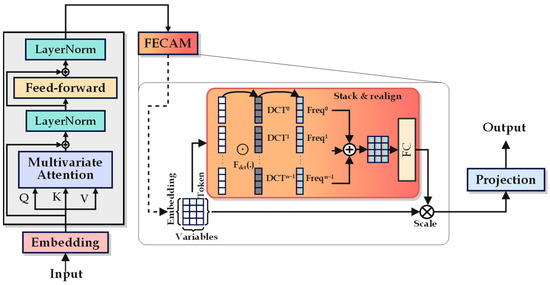
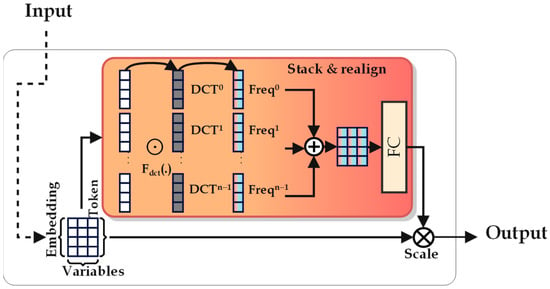
• Proposing FECAM-iTransformer: To extract more comprehensive information from IMU data, we introduce the frequency-enhanced channel attention mechanism (FECAM) [32] into the iTransformer. This mechanism applies attention across multiple frequency-domain channels to capture more compact, richer, and more comprehensive time features in navigation data. This enhancement broadens the iTransformer’s perspective and improves its ability to model multi-channel IMU data effectively.
• Proposing INS/FECAM-iTransformer Integrated Navigation System: This system provides pseudo-GNSS signals to the extended Kalman filter in case of a GNSS outage.
• Conducting Extensive Experiments: We conduct experiments using both a high-precision public dataset and a low-precision personal dataset to evaluate the model’s performance in two different scenarios: professional integrated navigation sensors and low-cost, small sensors, and the effectiveness of the proposed method is verified.

The remainder of this paper is structured as follows: In Section 2, we describe the theory of the INS/GNSS integrated navigation system in detail, including its mathematical model [17,33,34]. Section 3 introduces the design of the proposed FECAM-iTransformer and the INS/FECAM-iTransformer integrated navigation system. Section 4 presents the experiments conducted, along with a comprehensive comparative analysis. Section 5 discusses the results and significance of this research. Lastly, Section 6 makes a conclusion.

2. Theory of INS/GNSS Integrated Navigation System

The INS and GNSS loosely integrated navigation system combines the high-frequency, short-term accuracy of the INS and the long-term stability of the GNSS to achieve long-term, high-precision, and stable navigation. Initially, both the INS and GNSS independently measure position, velocity, and attitude. A Kalman filter algorithm is then employed to estimate the position, velocity, and attitude errors of the INS relative to the GNSS. These estimated errors are used to correct the INS, thereby reducing the navigation bias caused by the accumulation of errors in the INS system. In this subsection, we first derive the error propagation model of the inertial guidance system and then introduce the combined navigation model based on the extended Kalman filter. The INS/GNSS navigation system used in this paper is shown in Figure 1.

Figure 1. INS/GNSS integrated navigation system. $f_{ib}^b$ and ${\omega }_{ib}^b$ represent the specific acceleration and angular velocity vectors measured by the IMU, respectively. The variables $a_{INS}$, $v_{INS}$, and $p_{INS}$ are the attitude, velocity, and position of the vehicle calculated by INS. $p_{GNSS}$ is the positions obtained with the GNSS. $\Delta p_{GNSS}$ is the position correction value obtained from the EKF calculations. The remaining parts of the EKF calculation are also used to correct errors in the INS.

The INS is the backbone of the INS/GNSS integrated navigation system. In the system, the positioning information provided by GNSS and AI is primarily used to correct the positioning errors of the INS. The sensor used by the INS is IMU, and the raw data from the IMU serve as the input feature for the AI algorithm [35]. The INS outputs information on the attitude, position, and velocity of the vehicle. There are errors in this information before applying the extended Kalman filter, which is then corrected by the positioning information from the GNSS receiver.

The selection of reference frames is crucial for the navigation system. In this paper, the navigation frame is set as the East-North-Up (ENU) geographic coordinate, while the body frame is set as the Right-Front-Up (RFU) frame. The navigation coordinate system is called the n-frame, and the earth coordinate system is called the e-frame. Based on the established reference frames, the INS error model can be derived, incorporating elements such as attitude, velocity, and position errors. These elements are also included in state estimation as components of the state transition matrix of the EKF. The attitude error equation is shown in Equation (1) [33]:

$$\dot{\theta }=\theta \times {\omega }_{in}^n+△{\omega }_{in}^n-{\epsilon }^n$$

(1)

where $\theta$ is the attitude error vector. ${\omega }_{in}^n$ and $△{\omega }_{in}^n$ are the angular velocity of the navigation frame to the inertial frame and its error. ${\epsilon }^n$ is the drift vector of the gyroscopes.

The velocity error equation is shown in Equation (2) [33]:

$$\Delta {\dot{V}}^n=f^n\times {\theta }^n+V^n\times (\Delta {\omega }_{en}^n+2\Delta {\omega }_{ie}^n)+\Delta V^n\times ({\omega }_{en}^n+2{\omega }_{ie}^n)+{\nabla }^n$$

(2)

where $V^n$ represents the kinematic velocity vector of the vehicle, while $\Delta V^n$ denotes the associated errors. $f^n$ stands for the specific force vector. ${\omega }_{en}^n$ and $\Delta {\omega }_{en}^n$ represent the angular velocity and its errors relative to the n-frame with respect to the e-frame. ${\omega }_{ie}^n$ and $\Delta {\omega }_{ie}^n$ represent the angular velocity and errors associated with the earth’s rotation. Finally, ${\nabla }^n$ denotes the accelerometer bias vector.

The position error equation is shown in Equations (3)–(5) [33]:

$$\Delta \dot{L}=-{\displaystyle \frac{V_N}{{(R_M+h)}^2}}\Delta h+{\displaystyle \frac{1}{R_M+h}}\Delta V_N$$

(3)

$$\Delta \dot{\lambda }={\displaystyle \frac{V_E\tan L\sec L}{R_N+h}}\Delta L+{\displaystyle \frac{\sec L}{R_N+h}}\Delta V_E-{\displaystyle \frac{V_E\sec L}{{(R_N+h)}^2}}\Delta h$$

(4)

$$\Delta \dot{h}=\Delta V_U$$

(5)

where $L$, $\lambda$, and $h$ represent the latitude, longitude, and height of the vehicle in the n-frame, respectively, while $\Delta L$, $\Delta \lambda$, and $\Delta h$ denote their corresponding errors. $V_N$, $V_E$, and $V_U$ indicate the velocities in the north, east, and upward directions within the n-frame, with $\Delta V_N$, $\Delta V_E$, and $\Delta V_U$ representing their respective errors. The terms $R_M$ and $R_N$ are the radius of the curvature of the meridian and the prime vertical, respectively.

In an INS/GNSS integrated navigation system, a 15-dimensional state vector is commonly used for state estimation, which is defined as follows [17]:

$$X=[{\theta }_R,{\theta }_P,{\theta }_H,\Delta V_E,\Delta V_N,\Delta V_U,\Delta L,\Delta \lambda ,\Delta h,{\nabla }_x,{\nabla }_y,{\nabla }_z,{\epsilon }_x,{\epsilon }_y,{\epsilon }_z]$$

(6)

where ${\theta }_R$, ${\theta }_P$, and ${\theta }_H$ are the roll, pitch, and yaw angle errors, respectively. ${\epsilon }_x$, ${\epsilon }_y$ and ${\epsilon }_z$ are the gyroscopes’ drifts in the three directions in the body frame. ${\nabla }_x$, ${\nabla }_y$, and ${\nabla }_z$ are the accelerometers’ biases in the three directions in the body frame.

The discrete expressions of the state and measurement models for the INS/GNSS loosely coupled navigation are defined as follows [17]:

$$\left\{\begin{array}{l}{X}_k=F_{k,k-1}{X}_{k-1}+G_{k-1}{W}_{k-1}\hfill \\ Z_k=H_k{X}_k+V_k\hfill \end{array}\right.$$

(7)

where vectors $X_k$ and $X_{k-1}$ represent the states at moments $k$ and $k-1$, $F_{k,k-1}$ is the state transition matrix, $H_k$ is the measurement matrix, $G_{k-1}$ is the noise input matrix, $W_{k-1}$ is the system process noise sequence, $V_k$ is the system measurement noise sequence, and $Z_k$ is the measurement vector.

The filtering algorithm is the core of the INS/GNSS integrated navigation system, providing more accurate positioning results through state estimation. In this paper, we use the extended Kalman filter, a nonlinear version of the Kalman filter, which is better suited for working in real-world nonlinear environments. The computation is shown in Algorithm 1 [34].

Algorithm 1: Extended Kalman Filter.

Required:         Nonlinear model:                 $x(t)=f(x(t-1),u(t-1))+w(t-1)$                 $z(t)=h(x(t))+v(t)$         Initial value: ${\widehat{x}}_0,P_0,Q,R$ for i = 1,2,3,…,N do         Prediction phase:         $x^{-}(t)=f(\tilde{x}(t-1),u(t-1),w(t-1))$         $\mathrm{\Phi }(t-1)={\displaystyle \frac{\partial }{\partial x}}(f(x^{-}(t-1),u(t-1)))$         $P^{-}(t)=\mathrm{\Phi }(t-1)P(t-1)\mathrm{\Phi }{(t-1)}^T+Q$         Update phase:         $y(t)=z(t)-h(x^{-}(t))$         $H(t)={\displaystyle \frac{\partial }{\partial x}}h(x^{-}(t))$         $K(t)=P^{-}(t)H{(t)}^T{\left[H(t)P^{-}(t)H{(t)}^T+R\right]}^{-1}$         $\tilde{x}(t)=x^{-}(t)+K(t)y(t)$         $P(t)=(I-K(t)H(t))P^{-}(t)$ end for

3. Design of Integrated Navigation System Based on FECAM-iTransformer

3.1. Features of IMU and GNSS Signals

As shown in Figure 2a, when the vehicle’s motion state changes, the IMU measurement data displaying the specific acceleration and angular velocity values correspond to the vehicle’s state changes. Meanwhile, GNSS receiver outputs the location of the vehicle, and the change between successive locations also indicates the vehicle’s state changes. This suggests a potential correlation between IMU data and GNSS position changes. Ideally, the vehicle’s position could be directly calculated by integrating the IMU measurements, but noise in the IMU signals introduces significant errors [14]. Thus, we propose utilizing neural networks to learn this potential correlation and the AI will be used to output the GNSS position increment $\delta p_{GNSS}$.

Figure 2. Relationship and features of IMU signal and GNSS. (a) IMU measurements correspond to changes in the vehicle’s GNSS position, $f_{ibx}^b$, $f_{iby}^b$, $f_{ibz}^b$ are the measurement from accelerometer of IMU, ${\omega }_{ibx}^b$, ${\omega }_{iby}^b$, ${\omega }_{ibz}^b$ are the measurement from gyroscope of IMU, $p_{GNSS}(t)$ and $p_{GNSS}(t-1)$ are the GNSS position at time t and t − 1, $\delta p_{GNSS}=\left\{\delta Longitude,\delta Latitude,\delta Altitude\right\}$ is the GNSS position increment from time t − 1 to t; (b) The IMU signal can be represented as the superposition of several sine waves, each characterized by its amplitude, frequency, and phase.

Furthermore, the multi-channel measurements from the IMU collectively reflect the vehicle’s state changes, and they exhibit kinematic interdependencies [36]. Therefore, we require a neural network that can model the correlations between these multi-channel input sequences, rather than simply focusing on the temporal progression of the inputs. After various attempts, we selected the iTransformer for this task, which is thoroughly explained in Section 3.3.2.

Additionally, we suggest addressing the noise in IMU measurements and exploring potential kinematic features from a frequency-domain perspective. Treating time series as signals allows it to be decomposed into a linear combination of sinusoidal components without losing any information. Each component has a unique frequency, initial phase, and amplitude, as shown in Figure 2b. Thus, the frequency domain provides another view of the IMU signal. Each IMU signal in the time domain can be transformed into the frequency domain using a Fourier transform. This conversion provides a more compact and elegant representation, typically expressed in a complex number, and can be mathematically represented by the following formula [31]:

$$X(f)=\left|X(f)\right|e^{j\theta (f)}=\left|X(f)\right|\left(\cos \theta (f)+j\sin \theta (f)\right)$$

(8)

where $X(f)$ is the complex number associated with the frequency component at frequency $f$, $\left|X(f)\right|$ is the amplitude of the frequency component, and $\theta (f)$ is the phase of the frequency component.

In the frequency domain of IMU signals, the high-frequency components tend to be noisier, while the low-frequency components contain more valuable information. However, these two elements are often intertwined across all frequencies, making it challenging to separate them. To amplify the impact of useful information within the frequency components, we propose utilizing neural networks, specifically incorporating FECAM. By integrating FECAM into the iTransformer, we aim to strengthen its ability to capture and express frequency-domain features. Subsequent experiments have demonstrated the effectiveness of this approach, with notable improvements observed. The detailed workings of FECAM are outlined in Section 3.3.3.

3.2. The Overall Architecture of INS/FECAM-iTransformer Integrated Navigation System

The overall architecture of our approach is illustrated in Figure 3, which corresponds to the training model and the prediction model of the system, respectively. This paper presents a loosely integrated navigation scheme that combines artificial intelligence with an extended Kalman filter (EKF). In this scheme, the EKF module provides high-precision error information to the system, which is then used to correct the attitude, speed, and position. The AI module, the FECAM-iTransformer, temporarily supplies the EKF with essential GNSS positioning data during GNSS outages. The principle and framework of the FECAM-iTransformer will be described in detail in Section 3.3.

Figure 3. INS/FECAM-iTransformer integrated navigation system: (a) The training mode of the system. $\delta p_{GNSS}(t)$ and $\delta p_{GNSS}(t-1)$ are the increments of GNSS position at time t and t − 1. $f_{ib}^b,{\omega }_{ib}^b$ is IMU measured value. (b) The predicting mode of the system. At this moment, the real GNSS signal is missed. $p_{GNSS}(t)$ is the pseudo GNSS position at time t. $L$ is the length of lookback window; $t$ is present moment. All of data at each moment are saved in data memory.

The training mode of the system is shown in Figure 3a. When the GNSS works, the FECAM-iTransformer model is trained. Data memory store IMU measurements, GNSS position measurements, and GNSS position increments at each moment. The features and labels required for model training are $f_{ib}^b$, ${\omega }_{ib}^b$, and $\delta p_{GNSS}$ of the past few minutes. The reason for using the FECAM-iTransformer to predict GNSS position increments is to establish a more interpretable relationship with IMU measurements, which reflect changes in the vehicle’s state over time, corresponding to the vehicle’s position change during this period. The training process is conducted periodically, and the training data are taken from the past few minutes, so as to ensure that the latest model is used to output GNSS position increments in the GNSS outage.

The predicting mode of the system is shown in Figure 3b. During a GNSS outage, the FECAM-iTransformer provides the GNSS location information to the EKF. First, the IMU measurement data from the recent period are retrieved from the data memory. Then, these data will be fed to the FECAM-iTransformer to predict the GNSS increment $\delta p_{GNSS}$ for the next time step. $\delta p_{GNSS}$ will be added to the $p_{GNSS}(t-1)$ (GNSS position at time t − 1) to determine the $p_{GNSS}(t)$ (GNSS position at time t). Finally, the GNSS positions will be saved and fed to the EKF. The total process is shown in Algorithm 2.

Algorithm 2: INS/FECAM-iTransformer integrated navigation system.

while(1) if GNSS works: (During GNSS outage, stop and switch to predicting mode)         Integrated navigation using GNSS and INS measured value;         if t = (time to train the model)                    Training mode: (Concurrent with integrated navigation)                      Obtain $f_{\mathit{ib}}^b$$, {\omega }_{\mathit{ib}}^b$$\mathrm{and} \delta p_{GNSS}$ of past few minutes from data memory;                      Train FECAM-iTransformer;                      Save model and all variables;           end if       end if       if GNSS outage:             Predicting mode:             Obtain $f_{ib}^b,{\omega }_{ib}^b$ from the past L seconds from data memory;             Predicting $\delta p_{GNSS}(t)$ by feeding $f_{ib}^b,{\omega }_{ib}^b$ into FECAM-iTransformer;             Obtain $p_{GNSS}(t-1)$ from data memory;          $p_{GNSS}(t)=p_{GNSS}(t-1)+\delta p_{GNSS}(t)$;          Feeding $p_{GNSS}(t)$ into EKF;          Save all variables: $p_{GNSS}(t)$, $\delta p_{GNSS}(t)$$, f_{ib}^b$$, {\omega }_{ib}^b$ to data memory;       end if end while

3.3. FECAM-iTransformer

3.3.1. The Framework of FECAM-iTransformer

The positions of the FECAM within the FECAM-iTransformer and their respective internal structures are shown in Figure 4. After passing through the iTransformer encoder, each token undergoes a discrete cosine transform (DCT) via FECAM to obtain its corresponding frequency-domain representation. This representation is then selectively enhanced within the FECAM by focusing on channels that contain effective frequency bands, a process achieved through a Squeeze and Excitation Block (SE-Block). Finally, the enhanced multi-channel frequency-domain information is combined back into the time-domain channel.

Figure 4. The framework of FECAM-iTransformer and FECAM.

3.3.2. iTransformer

We introduce iTransformer [25], a high-performing model in time-series prediction, to output the GNSS pseudo-location information. The network structure of this deep learning model is illustrated in Figure 5.

Figure 5. The framework of iTransformer.

Unlike the traditional Transformer, iTransformer introduces a new approach to processing time-series data. Instead of treating the multivariate representation of a single time step as a token, iTransformer considers the entire input sequence of each variable as a token. The design can avoid the noise problems introduced by the time-stamp dislocation or the distribution deviation of the sequence [25]. More importantly, this approach allows the model to make predictions with a more global perspective, enhancing its ability to represent and describe multivariate correlations. The multi-head self-attention mechanism primarily accomplishes this task. When each measurement sequence is treated as a token, the multi-head attention mechanism evaluates the similarity between measured values by comparing the query and key derived from the input measurements. It then extracts the essential features of the sequence through the value, revealing multiple correlations among all measured values, as shown in Figure 6.

Figure 6. Multivariate attention revealing multivariate correlations between the measurements.

iTransformer retains the encoder structure of the Transformer while discarding the decoder structure. Its encoder includes layer normalization, a feedforward layer, and a multi-head attention mechanism. First, the data are embedded to obtain a tensor where the entire time step serves as the token. This tensor is then fed into the encoder, and finally, the result is projected to the output through a linear transformation. The process can be simply represented by the following formula [25]:

$$\begin{array}{l}{h}_n^0=\mathrm{Embedding}(X_{:,n}),\\ H^{l+1}=\mathrm{Encoder}(H^l),l=0,\dots ,L-1,\\ {\widehat{Y}}_{:,n}=\mathrm{Projection}(h_n^L),\end{array}$$

(9)

where $X$ represents the time series within the sliding window and $X_{:,n}$ represents a token of $X$, ${\widehat{Y}}_{:,n}$ denotes a token of the predicted future series $\widehat{Y}$, $H$ is the tensor after embedding, and $h$ represents each token of the tensor $H$, with the superscripts indicating the layer index. To enable the inverting operation, the designers of iTransformer have significantly modified each module within the encoder.

Layer Normalization: Layer normalization standardizes each sample across all features of its current layer, ensuring that these features follow a Gaussian distribution. The normalized data are then adjusted using learnable scaling (scale) and shifting (shift) parameters, which restore the original distributional properties of the data. This process enhances the convergence and training stability of the deep network. The process can be represented by the following formula [25]:

$$\mathrm{LayerNorm}(H)=\left.\left\{\left.{\displaystyle \frac{h_n-\mathrm{mean}(h_n)}{\sqrt{\mathrm{var}(h_n)}}}\right|\right.n=1,\dots ,N\right\}$$

(10)

where $h_n$ is each token of $H$, $\mathrm{mean}\left(\right)$ represents the function of finding the mean, and $\mathrm{var}()$ represents the function of finding the variance.

Feedforward Network: Due to changes in the way tokens are obtained, the feedforward neural network (FNN) in the iTransformer has been redesigned to represent each variate token rather than each time-step token as in the traditional Transformer model. This redesign avoids the limitations caused by the misalignment of time steps and the over-localization of the receptive field.

Self-Attention Mechanism: The attention mechanism assigns different weights to different parts of the input data, allowing the model to focus more on important information when making predictions or inferences. In the classic Transformer model, the self-attention mechanism is used to simplify time-dependent modeling by enabling the model to process each element of a sequence while considering all other elements in the sequence, thereby capturing more comprehensive contextual information. In the iTransformer, the self-attention mechanism treats the entire sequence of each variable as an independent process to capture the correlations between multiple variables, expressed by the following formula [25]:

$$A\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{softmax}({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}})V$$

(11)

where $Q$ represents the query, $K$ represents the key, $V$ represents the value, and $\sqrt{d_k}$ represents a scaling factor. Both of them are important variables in the self-attention mechanism [25]. $\mathrm{softmax}\left(\right)$ is the activation function. $Attention(Q,K,V)$ are attention scores.

3.3.3. FECAM: Frequency-Enhanced Channel Attention Mechanism

FECAM [32] learns the frequency-domain representation of a time series by modeling it in the frequency domain, assigning weights to different channels, and determining the importance of each channel at various frequencies. The most notable feature of FECAM is its use of the discrete cosine transform (DCT) to address the high-frequency noise caused by the Gibbs phenomenon [32], which often arises when using Fourier transform in time-series prediction. This approach allows the model to adaptively capture frequency dependencies between channels, effectively reducing prediction errors. The framework of FECAM is shown in Figure 7.

Figure 7. The framework of FECAM.

First, FECAM divides the input feature maps into $n$ groups along the channel dimension, effectively separating each token. Subsequently, a DCT operation is performed on each token to obtain the frequency representation of the response [32]:

$$Fre{q}^i=DC{T}_j(V^i)={\displaystyle {\sum }_{j=0}^{j=L_S-1}(V_{:,l}^i)B_l^j}$$

(12)

where $V$ represents each input token, $L_S$ is the length of the input token, $B_l^j$ is the function of one-dimensional DCT, which can be expressed as [32]:

$$Freq=DCT(V)=stack([Fre{q}^0,Fre{q}^1,\dots Fre{q}^{n-1}])$$

(13)

Next, the attention weights for these frequency channel vectors are learned through neural structure as SE-block. The mathematical expression for the frequency channel-enhanced attention mechanism is as follows [32]:

$$att=\sigma (W_2\delta (W_{1}DCT(V))$$

(14)

where $att$ is the attention weight learned by the neural structure of SE-block, $\delta$ and $\sigma$ are the sigmoid and ReLU activation functions, respectively, $W_1$ and $W_2$ are the linear layer weights learned by the neural structure of SE-block.

4. Results and Analyses

The effectiveness of the proposed model is evaluated using both public and private datasets in the experimental section of this paper. Public datasets, obtained with high-precision equipment, are used to assess the model’s performance on higher-quality data. In contrast, private datasets, collected using low-cost sensors and mobile robot platforms, are employed to test the model’s performance on lower-quality, interference-prone devices.

4.1. Configuration of Model

In addition to INS, the original iTransformer, and the FECAM-iTransformer, two existing deep neural networks, LSTM and GRU, commonly used to address the GNSS loss-of-lock problem, are selected for comparison. The configurations and training parameters of each model are determined using the grid search method and are summarized in Table 1.

Table 1. The configurations and training parameters of each model.

	FECAM-iTransformer	iTransformer	LSTM	GRU
learning rate	0.0001	0.0001	0.001	0.001
batch size	32	32	64	64
training epochs	10	10	50	50
input length	8	8	4	4
encoder layers	2	2	\	\
number of heads	8	8	\	\
number channels	512	\	\	\
hidden size	\	\	64	64
number of layers	\	\	2	2
learning rate decay	\	\	0.0001	0.0001

The computer used for training and testing is configured with a Windows 11 operating system, an Intel i5-12500H CPU, and 16 GB of memory.

Additionally, due to the large error associated with INS, it is neither practical nor desirable to display comparisons using images. Therefore, when presenting the test results, the trajectory of the INS should be plotted, but its results will not be included in line charts, box plots, or bar charts. Instead, comparisons between the INS and other methods will be presented in tabular form.

4.2. Experiment on Public Datasets

4.2.1. Description of Public Datasets

The public dataset provided by Dalian University of Technology can be accessed at the following: http://www.psins.org.cn/newsinfo/1508278.html accessed on 29 February 2024. The dataset was uploaded to the open-source website on 24 May 2021. The data collection route was located on an open road with strong GNSS signal reception in Tongzhou District, Beijing, China. The dataset was collected using the MTI710, a high-precision INS/GNSS integrated navigation device, and a vehicle with an average speed of 3.5 m/s. The parameters of MTI710 are detailed in Table 2 below. To avoid repetition of the experimental route, half of the dataset, with a duration of 6000 s, is used in this paper. The trajectory of the dataset is shown in Figure 8, where the yellow segment represents the training set, with a duration of 4800 s, accounting for 80% of the data. The green segment represents the test set, with a duration of 1200 s, accounting for 20% of the data, as shown in Figure 8a. Within the test set, two representative sections with different durations are selected as test tracks and marked in red, with durations of 100 s and 200 s, called Path #1 and Path #2, respectively, as shown in Figure 8b. The longitude, latitude, and altitude measurements obtained from the GNSS receiver are used as ground truth values for testing.

Table 2. The parameters of MTI710.

Sensor	Bias Drift	Noise	Frequency	Position Error
Gyroscope	${10}^{\mathrm{o}}/\mathrm{h}$	$0.01/\mathrm{s}/\sqrt{\mathrm{Hz}}$	$100 \mathrm{Hz}$	\
Accelerometer	$15 \mathrm{ug}$	$60 \mathrm{ug}/\sqrt{\mathrm{Hz}}$	$100 \mathrm{Hz}$	\
GNSS	\	\	$5 \mathrm{Hz}$	$0~2 \mathrm{m}$

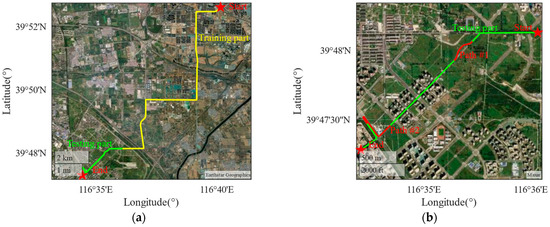
Figure 8. The trajectory of public datasets: (a) the trajectory of training part and testing part of public datasets; (b) the trajectory of Path #1 and Path #2.

4.2.2. The Results of Experiment on Public Dataset

Path #1 has a duration of 100 s and follows a gentle curve, with the movement of the vehicle being relatively stable and smooth. Figure 9a presents a comparison of the test tracks and the horizontal errors for each method on Path #1. It is evident from the trajectory diagram that all integrated navigation methods based on neural networks closely fit the real path, with minimal differences among the various methods. The same path results in similar trajectories and errors for each method. In contrast, the INS approach significantly deviates from the true path, particularly when the vehicle changes direction. Figure 9b shows the comparison of horizontal position errors for the different methods, excluding pure INS (since the INS error is excessively large, making it difficult to display alongside other methods, a graphical comparison would be meaningless here; instead, a quantitative comparison will be provided in tabular form later). From the 8th second onward, the positioning errors of each method begin to change significantly, though the differences between the methods remain relatively small. Among these, the method proposed in this paper demonstrates the least error. Figure 10 shows the error values of each method in three different directions, showing small differences along the stable route. Since the vehicle is in a horizontal motion, the altitude error is very small.

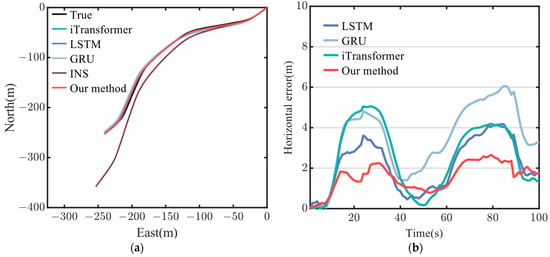
Figure 9. Trajectory diagram and horizontal position errors diagram: (a) the trajectory of each method on Path #1; (b) the horizontal position errors of each method on Path #1.

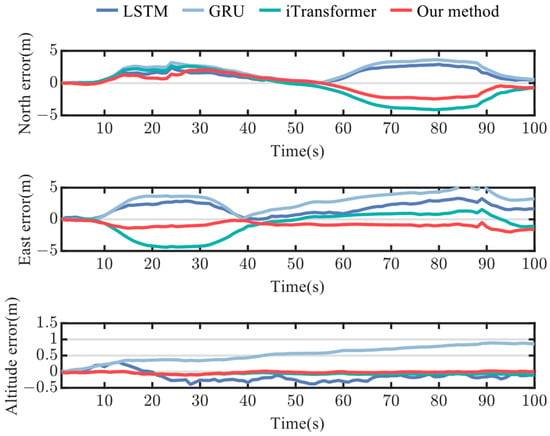
Figure 10. Position errors of north, east, and altitude on Path #1.

Figure 11a presents the horizontal position error distribution of each method in the form of a box plot. The error distribution of the method proposed in this paper is more concentrated, with most of the errors and the median below 3 m indicating greater stability compared to other methods. Figure 11b shows the root mean square error (RMSE) and maximum error (MAX Error) of the horizontal position for each method, presented in a bar chart. Our method yields strong results, with an RMSE of 1.7 m and a MAX Error of 2.7 m after 100 s of GNSS outage. While the iTransformer’s error is slightly higher than that of the LSTM, the difference is minimal. On the more moderate route, both the LSTM and GRU perform well, but on routes with more drastic changes in a motion state, the effectiveness of each method needs further verification. This will be explored in experiments on Path #2.

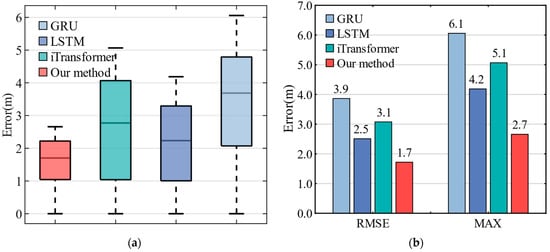
Figure 11. The box plot and bar chart of position error on Path #1: (a) The box plot shows the horizontal position error distribution of each method; (b) The bar chart shows the RMSE and MAX Error of each method.

Table 3 provides a detailed comparison of the RMSE and MAX Error for the east, north, and horizontal position errors of each method on Path #1. The proposed method, the FECAM-iTransformer, demonstrates superior performance across all directions, with significant reductions in absolute position errors in the east, north, and horizontal directions:

• Compared to INS: The RMSE decreased by 98%, 80.3%, and 96.5%, and the MAX Error decreased by 98.1%, 81.9%, and 97.5%, respectively;
• Compared to iTransformer: The RMSE is reduced by 51.4%, 39%, and 44.1%, and the MAX Error decreased by 54.7%, 40.5%, and 47.5%, respectively;
• Compared to LSTM: The RMSE decreased by 49.3%, 11%, and 31.5%, and the MAX Error decreased by 31.2%, 26.3%, and 36.4%, respectively;
• Compared to GRU: The RMSE is reduced by 69%, 35.6%, and 55.5%, and the MAX Error decreased by 44.8%, 52.9%, and 56.1%, respectively.

Table 3. MAX Error and RMSE of different methods on Path #1.

	Method	East Error (m)	North Error (m)	Horizontal Error (m)
MAX Error	Our method	1.9959	2.4495	2.6581
	iTransformer	4.4082	4.1171	5.0657
	LSTM	2.9022	3.3230	4.1863
	GRU	3.6161	5.1970	6.0572
	INS	106.6452	13.5499	107.5026
RMSE	Our method	0.9880	1.4085	1.7205
	iTransformer	2.0331	2.3087	3.0763
	LSTM	1.9485	1.5821	2.5099
	GRU	3.1849	2.1873	3.8636
	INS	48.9940	7.1497	49.5129

Table 3. MAX Error and RMSE of different methods on Path #1.

	Method	East Error (m)	North Error (m)	Horizontal Error (m)
MAX Error	Our method	1.9959	2.4495	2.6581
	iTransformer	4.4082	4.1171	5.0657
	LSTM	2.9022	3.3230	4.1863
	GRU	3.6161	5.1970	6.0572
	INS	106.6452	13.5499	107.5026
RMSE	Our method	0.9880	1.4085	1.7205
	iTransformer	2.0331	2.3087	3.0763
	LSTM	1.9485	1.5821	2.5099
	GRU	3.1849	2.1873	3.8636
	INS	48.9940	7.1497	49.5129

Path #2 has a duration of 200 s and involves straight lines, right-angle turns, and U-shaped bends, making the vehicle’s motion state more complex than that of Path #1. Figure 12 presents the comparison of test tracks and horizontal errors for each method on Path #2. As shown in Figure 12a, the INS trajectory deviates completely from the true path, with an error exceeding 400 m. In contrast, the other methods remain much closer to the true trajectory. The specific horizontal error values are depicted in Figure 12b with a line chart (excluding the INS error, as it is too large and would interfere with the normal display of the other methods). After the first right-angle turn at 60 s, all methods experience some error amplification. However, the iTransformer and our proposed method do not continue to accumulate errors, while the errors for the LSTM and GRU begin to increase further, likely due to the significant impact of the maneuver on the vehicle’s state. A second change in positioning error occurs at 165 s when the vehicle navigates a U-turn. Among all the methods, the proposed method exhibits the smallest horizontal error, demonstrating its ability to maintain high positioning accuracy during complex vehicle maneuvers. The comparison of positioning errors in the east, north, and vertical directions is shown in Figure 13, where our method consistently outperforms the others in all directions. It is worth noting that at the U-turn point, the horizontal positioning error briefly decreases before increasing again. This occurs because the northbound and eastbound prediction results of the neural network fluctuate at the vehicle’s turning point. As shown in Figure 13, the northbound prediction error increases, while the eastbound prediction error decreases around the 165 s mark. This leads to a temporary reduction in the accumulation of horizontal errors at that point. Subsequently, both the northbound and eastbound prediction errors stabilize, causing the overall horizontal error to increase again. In addition, the vehicle typically travels at a low speed during the U-turn, which reduces the complexity of the model’s prediction. This is another reason for the decrease in the horizontal positioning error.

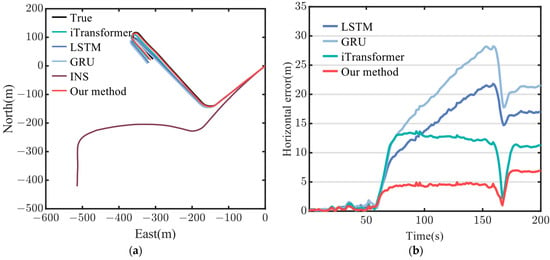
Figure 12. Trajectory diagram and horizontal position errors diagram on Path #2: (a) the trajectory of each method on Path #2; (b) the horizontal position errors of each method on Path #2.

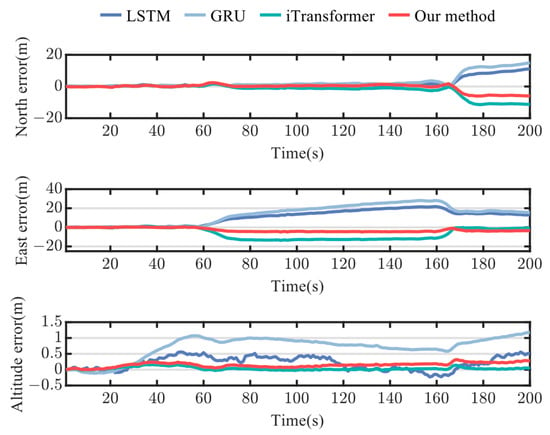
Figure 13. Position errors of north, east, and altitude on Path #2.

Figure 14a shows the horizontal position error distribution for each method in the form of a box plot. The error distribution of the method proposed in this paper is more concentrated, with most errors and the median falling below 5 m, indicating greater stability and accuracy compared to other methods. Figure 14b presents the RMSE and MAX Error of the horizontal absolute position for each method in the form of a bar chart. The proposed method demonstrates strong performance, achieving an RMSE of 4.1 m and a MAX Error of 7.0 m after 200 s of GNSS outage.

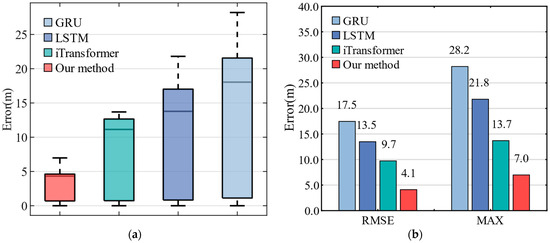
Figure 14. The box plot and bar chart of position error on Path #2: (a) The box plot shows the horizontal position error distribution of each method; (b) The bar chart shows the RMSE and MAX Error of each method.

Table 4 provides a detailed comparison of the RMSE and MAX Error for the east, north, and horizontal position errors of each method on Path #2. The reductions in position errors in the east, north, and horizontal directions are as follows:

• Compared to INS: The RMSE decreased by 98.5%, 97.2%, and 98.3%, and the MAX Error decreased by 98.9%, 97.1%, and 98.6%, respectively;
• Compared to iTransformer: The RMSE is reduced by 61.1%, 46.4%, and 57.8%, and the MAX Error decreased by 64.2%, 47.1%, and 49%, respectively;
• Compared to LSTM: The RMSE decreased by 73.8%, 36.2%, and 69.6%, and the MAX Error decreased by 77.5%, 46.7%, and 68%, respectively;
• Compared to GRU: The RMSE is reduced by 79.6%, 55.6%, and 76.5%, and the MAX Error decreased by 82.6%, 59.7%, and 75.3%, respectively.

Table 4. MAX Error and RMSE of different methods on Path #2.

	Method	East Error (m)	North Error (m)	Horizontal Error (m)
MAX Error	Our method	4.8879	6.0308	6.9790
	iTransformer	13.6634	11.3954	13.6902
	LSTM	21.7570	11.3180	21.8038
	GRU	28.0816	14.9659	28.2057
	INS	444.8387	207.2744	490.7587
RMSE	Our method	3.3980	2.3024	4.1046
	iTransformer	8.7338	4.2948	9.7326
	LSTM	12.9937	3.6071	13.4851
	GRU	16.6707	5.1831	17.4579
	INS	226.1042	83.2790	240.9533

Table 4. MAX Error and RMSE of different methods on Path #2.

	Method	East Error (m)	North Error (m)	Horizontal Error (m)
MAX Error	Our method	4.8879	6.0308	6.9790
	iTransformer	13.6634	11.3954	13.6902
	LSTM	21.7570	11.3180	21.8038
	GRU	28.0816	14.9659	28.2057
	INS	444.8387	207.2744	490.7587
RMSE	Our method	3.3980	2.3024	4.1046
	iTransformer	8.7338	4.2948	9.7326
	LSTM	12.9937	3.6071	13.4851
	GRU	16.6707	5.1831	17.4579
	INS	226.1042	83.2790	240.9533

Experiments on public datasets demonstrate that the proposed model effectively addresses the rapid accumulation of positioning errors caused by the GNSS outage in professional strapdown inertial navigation systems, outperforming existing methods such as the LSTM and GRU. The model will also be further tested on a low-cost INS/GNSS integrated navigation system and a mobile robot.

4.3. Experiment on Private Dataset

A low-cost INS/GNSS integrated navigation system and a small mobile robot platform were used to collect the private dataset at 13:03 on 11 July 2024, at a university located in Pudong New Area, Shanghai, China. The robot’s moving speed was about 0~1.5 m/s, compared to the 3 m/s speed used for the public dataset. Furthermore, the robot’s size is $726\times 617\times 273\mathrm{mm}$, and its net weight is $40\mathrm{kg}$. The IMU sensor is the JY901B, and the GNSS module is the ATGM336H-5N-71. The sensors’ and mobile robot’s parameters are detailed in Table 5. The total duration of the dataset is 2800 s, with 80% (2240 s) used as training data and the remaining 20% (560 s) as test data. Within the test data, a 250 s route is selected as the test track, as shown in Figure 15, in which yellow represents the training part, green represents the testing part, and red indicates the testing path named Path #3. The longitude, latitude, and altitude measurements obtained from the GNSS receiver are used as ground truth values for testing.

Table 5. The parameters of JY901B, ATGM336H-5N-71, and mobile robot.

Sensor	Bias Drift	RMS Noise	Frequency	Position Error
Gyroscope	${2.24}^{\mathrm{o}}/\mathrm{h}$	$0.028~{0.07}^{\mathrm{o}}/\mathrm{s}$	$100 \mathrm{Hz}$	\
Accelerometer	$\pm 20~40 \mathrm{mg}$	$0.75~1 \mathrm{mg}$	$100 \mathrm{Hz}$	\
ATGM336H-5N-71	\	\	$1 \mathrm{Hz}$	$0~2.5 \mathrm{m}$

Figure 15. Data acquisition platform and trajectory of datasets: (a) The appearance and electrical connection diagram of the data acquisition platform are provided; (b) The data acquisition path covers the entire route with a strong GNSS signal throughout, lasting a total of 2800 s. Of this, 2240 s are used for the training set, 560 s for the test set, and a 25 s segment is designated as the test path called Path #3.

For the test on the private dataset, we first compare the RMSE and MAX Errors. An intuitive comparison of RMSE and MAX Errors is shown in Figure 16. Table 6 provides a detailed comparison of the RMSE and MAX Error for each method in the east, north, and horizontal directions. It can be seen that the method proposed in this paper achieved excellent results in all directions, with the reduction in absolute position error in the east, north, and horizontal directions as follows:

• Compared to INS: The RMSE and MAX Error decreased by 99.9% in all directions, respectively;
• Compared to iTransformer: The RMSE is reduced by 55%, −32.4%, and 37.2%, and the MAX Error decreased by 51.6%, −13.6%, and 37.4%, respectively;
• Compared to LSTM: The RMSE decreased by 85.9%, 74.3%, and 82.4%, and the MAX Error decreased by 86.1%, 78.4%, and 82%, respectively;
• Compared to GRU: The RMSE is reduced by 55.5%, 83.4%, and 78.2%, and the MAX Error decreased by 53.3%, 87.9%, and 81.7%, respectively.

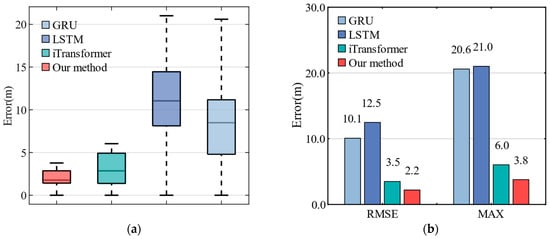
Figure 16. The box plot and bar chart of position error on Path #3: (a) The box plot shows the horizontal position error distribution of each method; (b) The bar chart shows the RMSE and MAX Error of each method.

Table 6. MAX Error and RMSE of different methods on Path #3.

	Method	East Error (m)	North Error (m)	Horizontal Error (m)
MAX Error	Our method	2.9107	2.4888	3.7739
	iTransformer	6.0123	2.1510	6.0318
	LSTM	20.9941	11.4996	21.0050
	GRU	6.2305	20.5142	20.5985
	INS	200,340	1,493,000	1,495,300
RMSE	Our method	1.5307	1.5734	2.1951
	iTransformer	3.3269	1.0635	3.4928
	LSTM	10.8684	6.1222	12.4741
	GRU	3.4413	9.4653	10.0715
	INS	4959	2684	5639

Table 6. MAX Error and RMSE of different methods on Path #3.

	Method	East Error (m)	North Error (m)	Horizontal Error (m)
MAX Error	Our method	2.9107	2.4888	3.7739
	iTransformer	6.0123	2.1510	6.0318
	LSTM	20.9941	11.4996	21.0050
	GRU	6.2305	20.5142	20.5985
	INS	200,340	1,493,000	1,495,300
RMSE	Our method	1.5307	1.5734	2.1951
	iTransformer	3.3269	1.0635	3.4928
	LSTM	10.8684	6.1222	12.4741
	GRU	3.4413	9.4653	10.0715
	INS	4959	2684	5639

Among these, the iTransformer achieved the best performance in the north direction, slightly outperforming the method proposed in this paper. However, its performance in the east direction was weaker, leading to a lower overall score in horizontal positioning. Our method achieved the best overall performance. Additionally, due to the high noise and low stability of the low-cost sensors, the error in pure INS inertial navigation was so large that its trajectory and error values could not be properly displayed alongside the other methods. Therefore, the INS is excluded from further comparisons.

It is worth noting that on Path #3, the neural network performs better than on Path #2 due to differences in the operating environments of the public and private datasets, as well as the speeds of the acquisition vehicles and robots. The faster the vehicle and the more complex the operating environment, there will be more pronounced changes in motion during acceleration, deceleration, and turning. The neural network must adapt to these rapid changes, which can introduce fluctuations. The acquisition vehicle for the public dataset operates in a more complex environment and at higher speeds. In contrast, the robots using private datasets operate at a lower, steady speed, resulting in relatively smaller error fluctuations.

Nevertheless, noise in the low-cost sensor measurements persisted and affected the performance of the LSTM and GRU models. However, the iTransformer and FECAM-iTransformer, with their attention mechanisms, mitigated the impact of these noises, achieving positioning accuracy comparable to the smooth driving on Path #1.

Figure 17 shows the comparison of test tracks and horizontal errors for each method on Path #3. The test route includes multiple right-angle turns, and due to the mobile robot lacking a shock absorber, it experiences relatively high noise levels, posing a significant challenge for the neural network models. As seen in Figure 17a, LSTM and GRU are significantly affected, deviating considerably from the actual trajectory, while the iTransformer and FECAM-iTransformer align more closely with the real trajectory. Figure 17b shows that the fluctuations in the error graph are caused by the mobile robot’s turns. The horizontal positioning errors accumulate more noticeably with the LSTM and GRU, whereas the FECAM-iTransformer shows a smaller overall error than the iTransformer, consistently maintaining its horizontal positioning error below 5 m. This is because the attention mechanism of the iTransformer and FECAM-iTransformer filters out invalid information in the time series, and some noise that causes error accumulation is no longer considered. The FECAM-iTransformer further enhances the effective frequency channel from the frequency domain and weakens the adverse effects brought by the invalid frequencies, so its performance is better than the iTransformer. Figure 18 shows the error values of each method in three different directions on Path #3.

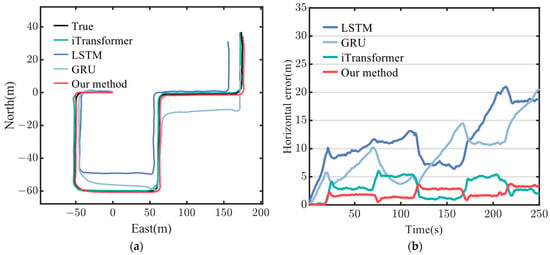
Figure 17. Trajectory diagram and horizontal position errors diagram on Path #3: (a) the trajectory of each method on Path #3; (b) the horizontal position errors of each method on Path #3.

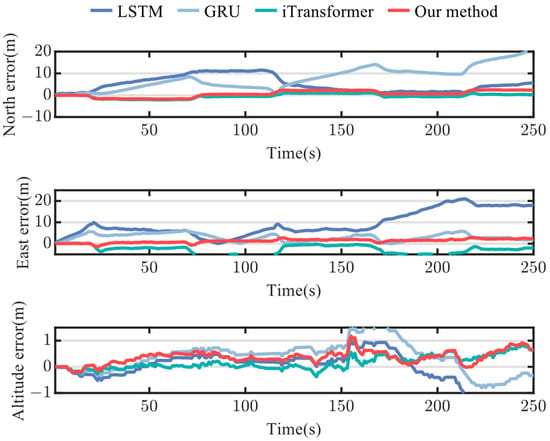
Figure 18. Position errors of north, east, and altitude on Path #3.

5. Discussion

In this paper, an INS/FECAM-iTransformer integrated navigation system is proposed to address the rapid accumulation of INS errors during GNSS outages. Experimental results demonstrate that the FECAM-iTransformer offers higher accuracy and stability compared to existing neural network solutions. The main advantages of the FECAM-iTransformer are as follows:

(1)

The iTransformer can model the entire input sequence in the time domain across multiple tokens, effectively capturing the variable correlations between the multi-channel data from the IMU.

(2)

The FECAM enables the FECAM-iTransformer to model in the frequency domain. By using an SE-Block, the FECAM enhances the effective frequency information of the IMU, allowing the model to capture rich frequency-domain features from the IMU data.

In this experiment, two datasets were used: a public dataset and a private dataset. From each dataset, three representative routes were selected for testing, referred to as Path #1, Path #2, and Path #3.

The experiments on Path #1 demonstrate that neural networks can effectively mitigate error amplification during GNSS outages. However, on the stable Path #1, the performance gap between all models is minimal, with the proposed method in this paper reducing the error by 97.5% compared to the INS system.

Experiments on Path #2 show that during sharp turns in the trajectory, the attention mechanism plays a significant role in modeling IMU and GNSS signals. The performance of LSTM and GRU on this route is notably inferior to that of the iTransformer and FECAM-iTransformer. The FECAM-iTransformer, which places additional emphasis on multi-channel frequency-domain features, achieved higher positioning accuracy than the iTransformer. Compared to INS, the positioning error of the FECAM-iTransformer is reduced by 98.3%.

Experiments on Path #3 demonstrate that neural networks with attention mechanisms perform better on low-cost sensor platforms, regardless of whether the vehicle is turning or traveling in a straight line. The FECAM-iTransformer reduced the positioning error by 99.9% compared to the INS.

Compared to traditional deep learning models, the FECAM-iTransformer demonstrates superior navigation accuracy and stability. Current neural network solutions generally fail to deeply and specifically capture and extract the time and frequency characteristics of the IMU data, as they typically model all sequence information solely in the time domain. Therefore, further research in this area, focusing on detailed feature analysis and extraction of sensor data, represents a promising direction for improvement.

However, there are areas for further enhancement in this work: the training and test datasets do not cover all possible application scenarios. Although experiments have shown that the method is effective on both professional and low-cost equipment platforms for land vehicles, future studies could extend experimental vehicles to surface, underwater, aerial, and other scenarios. As the volume of data increases, the proposed method is expected to achieve even better adaptability.

6. Conclusions

In this paper, a novel method for estimating the GNSS location measurements using the FECAM-iTransformer algorithm is proposed to mitigate the accumulated INS errors during GNSS signal interruptions. The iTransformer and FECAM algorithms are employed to extract time-domain and frequency-domain features from multi-channel IMU sensor data, enabling the stable output of reliable GNSS positioning signals even in the event of a complete GNSS outage. This approach significantly reduces vehicle position errors. Additionally, this study provides a detailed analysis of the model’s input features and outputs. The model dynamically learns and predicts changes in vehicle position using IMU inputs, specifically triaxial acceleration and triaxial angular velocity. Compared to existing LSTM and GRU models, the FECAM-iTransformer achieves more accurate and stable navigation prediction results.