Multi-Objective Real-Time Planning of Evacuation Routes for Underground Mine Fires

Abstract

When a fire occurs underground, pre-existing emergency escape routes may become ineffective. Such scenarios necessitate the real-time planning of escape routes that consider evolving conditions and prioritize safety. This paper proposes a multi-objective real-time search method for emergency escape routes using dynamic programming to address these challenges. Firstly, this paper discusses how the evacuation of an underground mine fire caused by external factors depends on the fire monitoring system, personnel positioning system, and emergency evacuation system, as well as the modeling and solution methods of evacuation route planning. Then, based on fire smoke, CO, and temperature sensor data from the mine ventilation network structure and monitoring system, the possible smoke spread in the event of an underground fire was calculated. The objectives are to optimize both the shortest equivalent length of the path and the shortest time to walk through the smoke flow while ensuring that temporary escape time does not exceed the rated protection time of the self-rescuer. A mathematical model for emergency escape route planning is established under these conditions. A labeling algorithm based on dynamic programming is employed to find the Pareto optimal solution set of emergency evacuation routes that meet emergency requirements. Finally, two path evaluation indicators, namely “escape target priority” and “personnel temporary escape time”, are introduced to re-rank the solutions in the Pareto optimal set, thereby obtaining disaster evacuation routes with different priorities. Example verification shows that the algorithm can quickly solve the disaster evacuation routes that meet the actual disaster evacuation needs in complex networks. Example verification shows that the algorithm can quickly solve the emergency escape routes in complex networks that meet actual emergency escape needs.

1. Introduction

The mining industry is an important way for humans to obtain resources and is one of the most dangerous industrial sectors. For both coal mines and metallic non-metallic mines, underground mining is as important as open pit mining. The main accidents in underground mining include mine fires, poisoning and suffocation, explosions, mine inundation, collapse, roof falls, and rock collapse. Of these, mine fires, although not the most frequent, have a large impact area and on average cause a high number of casualties in a single incident. From 2008 to 2021, 29 fire accidents occurred in Chinese coal mines, killing 203 people [1]. In 2021, a fire accident occurred in the Listvyazhnaya coal mine in Siberia, Russia, due to a coal dust explosion, killing 51 people. The fires that occur more frequently in metallic non-metallic underground mines are exogenous fires caused by fires from manual welding operations or spontaneous combustion of cables. Exogenous fires in metal mines refer to fires formed by igniting underground combustibles under the action of external ignition sources. They also include exogenous fires induced by improper treatment of internal fires [2]. For example, improper electric welding operation, aging cables, spontaneous combustion of mining trucks, etc. The occurrence of external fires underground is sudden and develops rapidly. In addition to causing burns or heat illnesses, the high-temperature smoke flow generated by fires also causes a large amount of toxic and harmful gases such as carbon monoxide in the smoke flow to spread to the downwind side of the fire area through the ventilation system, reducing visibility and causing poisoning and suffocation. It also creates the risk of airflow disturbances in the ventilation system [3]. Therefore, when an exogenous fire occurs in an underground mine, it is particularly important to promptly detect and handle the fire and safely evacuate personnel. However, the current emergency response model necessitates extensive communication and feedback between underground workers, surface dispatch centers, and emergency rescue teams, which often leads to delayed responses and inefficient evacuations. Consequently, optimizing the use of underground monitoring systems and risk-avoidance infrastructure to enable automated evacuation route planning is of significant importance.

The successful evacuation of underground personnel in the event of a disaster must take into account the layout of the mine’s ventilation system, the exact location of the underground personnel, the location and type of underground fires, the protective capacity and layout of underground shelters, and the self-rescue capacity of personal protective equipment [4,5]. Underground personnel must be familiar with the layout of the mine ventilation system and know the common escape routes and safe exits. The location of the underground personnel should be determined by various sensors and transmitted to the emergency rescue control platform on the ground to help the rescue team on the ground carry out rescue and command. Through monitoring and active reporting, knowledge of the location of underground fires, the type of combustible materials, the development of the fire, and the assessment of the impact of high-temperature smoke streams, CO, and other toxic gases generated by the fire can help reduce and avoid the threat to the health and safety of underground fire [6]. Self-rescuers and refuges ensure the survival and mobility of personnel in the event of a fire, when they have to enter a fire-affected hazardous area, or when it is difficult for them to escape to the surface.

Currently, more and more countries have realized the importance of underground emergency evacuation systems and have put forward standards and requirements for the construction of underground emergency evacuation systems. For example, in 2010, China proposed to build six underground emergency evacuation systems, including monitoring and surveillance systems, emergency evacuation systems, compressed air self-rescue systems, water supply and rescue systems, personnel positioning systems, and communication systems, which greatly improved the emergency rescue capabilities when disasters occur in underground mines. What is more, the United States, Australia, South Africa, and other countries have also stipulated the relevant requirements for underground safety evacuation in the form of laws [7]. Underground safety systems make it possible to identify hazards at an early stage of a disaster and to quickly communicate with personnel and respond to the disaster. When a disaster cannot be controlled in time and personnel need to be evacuated from the well, the system provides guidance on evacuation information, ensures that current evacuation routes are feasible, and revises evacuation routes in real time in response to developments in the disaster. In addition, many researchers have studied different aspects of underground refuge systems, such as fire monitoring and identification methods, parameters of underground refuge chambers, and layout methods [8]. Zujing Zhang conducted a study on the dynamic coupled heat transfer characteristics between rock and air within refuge chambers under ventilated conditions [9]. Yong Li et al. investigated the physiological and psychological responses of individuals to high temperature, relative humidity, and carbon dioxide concentration within refuge chambers [10]. Katherine et al. proposed a pre-emptive training program aimed at helping miners acclimate to the environmental conditions of refuge chambers, thereby preparing them to cope with the physical and psychological stresses that may arise during an emergency [11]. While these studies have significantly contributed to the understanding of the safety of refuge facilities, human–environment interactions, and emergency preparedness training, there remains a lack of comprehensive research that integrates both the performance of refuge facilities and human responses into disaster management decision-making.

The current research on disaster avoidance route planning tends to focus on the simulation of disasters and route planning before the occurrence of a disaster, the auxiliary escape decision making in the event of a disaster is not fully considered, and the research on the multi-objective route planning problem, which takes into account the efficiency of the path and the safety factors, is not in-depth enough. Therefore, our proposed method utilizes real-time fire sensor data from underground during a disaster to assist in path planning, incorporating both safety and access efficiency. Drawing from the experience of actual projects, we have developed path selection criteria to determine the disaster avoidance routes that best align with the practical needs of evacuation and rescue operations.

Our approach is exemplified by applying it to a case study of an underground metal mine fire, where we generate a roadway accessibility network based on real-time sensor data. Based on the mathematical model of the resource-constrained shortest path, with the rated protection time of the self-rescuer as the constraint and with the shortest equivalent length of the roadway and the shortest time for personnel to walk in the smoke flow as the optimization goal, a mathematical model for escape route planning during mine fire was established. Then, the Pareto optimal solution set of the evacuation path from underground workers to the surface safety exit and the underground refuge chamber was solved based on the labeling algorithm of dynamic programming. The Pareto optimal solutions of all safety exits were re-ranked based on the safety exit priority and the time to escape from the dangerous area. An example verification was carried out in a metal mine. The results showed that the algorithm proposed in this paper can quickly obtain disaster avoidance routes that meet actual safety needs, thereby assisting and guiding emergency risk avoidance decisions in underground mines.

The rest of the paper is organized as follows. Section 2 introduces the related work on emergency escape systems and emergency escape route planning. Section 3 presents an algorithm for assigning equivalent lengths to underground roadways. Section 4 develops a mathematical model for evacuation routes and provides a solution algorithm along with a strategy for optimizing the solutions. Section 5 simulates disasters, solves evacuation paths, and discusses the obtained results. Finally, Section 6 draws a conclusion of the study.

2. Related Works

Externally caused fires in underground mines are a highly random disaster. The cause of the fire is often factors such as improper operation or aging of cables. In addition, the smoke and toxic gases such as CO generated by underground fires will spread rapidly along the mine ventilation system, causing greater disasters. Therefore, in order to achieve effective emergency evacuation when an external fire occurs in an underground mine, it is necessary to plan an emergency plan and formulate an evacuation route in advance on the premise of accurately grasping the development of the disaster and the distribution of underground personnel. In order to ensure the planning of a safe and reliable evacuation route, it is necessary to rely on a reliable monitoring system, underground personnel positioning system, and emergency evacuation system.

2.1. Fire Monitoring System

A monitoring and control system is a software and hardware system with information collection and processing as well as sound and light alarms that can monitor the concentration of poisonous and harmful gases, wind speed, wind pressure, temperature, smoke, fan starting and stopping status, ground pressure, and other objects in underground mines. In coal mines, a monitoring and control system is one of the effective measures to prevent and control mine gas, mine fire, rock burst, and other serious accidents [12]. The current monitoring methods for exogenous fires in mines can be mainly classified into temperature monitoring, indicator gas monitoring, and image recognition methods based on visual features. Fire temperature monitoring mainly includes the use of temperature sensors such as RTDs, thermocouples, and infrared thermometers. Indicator gas monitoring mainly refers to the use of gas sensors to monitor CO, CO₂, HCL, and other electrical equipment and tape pyrolysis combustion of a variety of iconic gases. Visible light and infrared video image detection methods are also widely used because of their large monitoring range and fast response speed [13]. WANG et al. proposed using a deep learning algorithm to predict the heat release rate of transient fires based on fire scene images, providing an alternative method for fire heat release rate measurement [14]. Li et al. designed an autonomous patrol firefighting robot based on SLAM, infrared thermal imager, and YOLOv4 deep learning algorithm. This robot can perform autonomous inspections and execute firefighting actions in indoor spaces, thereby reducing the probability of fire occurrence [15].

2.2. Underground Personnel Positioning System

When various underground disasters occur, underground personnel positioning and communication are the key to timely understanding the development of underground disasters and implementing rescue efficiently. Especially when disasters such as fires and floods occur, the reliability of traditional wired communication methods is not high, so it is necessary to use stable and reliable wireless communication methods to locate underground personnel [16]. Underground personnel positioning is an indoor positioning technology. Due to factors such as signal scattering caused by the complex indoor environment, indoor positioning requires higher accuracy than outdoor positioning technology [17]. Traditional GPS, manual reporting, IEEE802.11b-based, and IP-based wireless video positioning methods have shortcomings such as being unsuitable for underground confined spaces and low accuracy [18]. The literature [19] demonstrates that high-accuracy indoor positioning is achievable in large realistic environments, using wearable sensors without the need for beacons, with performance evaluated through empirical testing across various competition tracks, yielding accuracy scores between 0.90 m and 11.70 m. The Ultra-Wide Band (UWB) refers to signals with a relative bandwidth greater than or equal to 0.20 or a bandwidth greater than or equal to 500 MHz. UWB technology offers high positioning accuracy in 2D and 3D, lightweight positioning tags, and the ability to track multiple objects simultaneously in 3D space. The use of UWB technology to locate underground personnel in real time is the basis for accurate disaster route planning.

2.3. Emergency Refuge System

According to the Regulations for Construction of Emergency Refuge System in Metal and Non-metallic Underground Mines, the emergency refuge system refers to the emergency escape routes, emergency refuge facilities, and equipment and measures to provide protection for the underground personnel to avoid danger in the event of an accident in the underground mine [20]. In order to improve the emergency response capacity of mines and safeguard the safety of underground workers, metal and non-metal underground mines should build a perfect emergency refuge system. Emergency refuge facilities (ERAs) are spaces that can be used to keep people safe in the event of a fire, collapse, or other disaster and include permanent refuge chambers and a mobile refuge chamber. A number of studies have been carried out on the temperature, humidity, and air quality of underground refuges, as well as their protection capabilities [21,22,23]. In addition, many researchers have investigated the location of underground refuge chambers. For example, Shao Zhixuan et al. used a tree network-based algorithm to select the optimal location for underground refuge chambers [24]. Zhang et al. used Fluent to establish the diffusion of CO gas when a fire broke out in a coal mine belt roadway and established a speed model for the escape of people in the roadway, thereby determining the layout position of the escape cabin in the roadway [25].

The self-rescuer is an isolated oxygen generator carried by personnel entering the well to prevent poisoning and suffocation [26]. Mines should be equipped with self-rescuers with a rated protection time of not less than 30 min for downhole personnel, and 10 per cent of the total number of people entering the well should be equipped with spare self-rescuers. Underground personnel should be proficient in wearing the self-rescuer, when disaster occurs, they can quickly wear the self-rescuer to escape.

2.4. Optimal Emergency Escape Route Planning

Many disaster evacuation scholars have studied the problem of underground disaster evacuation route planning. One of the most mainstream research methods is to use optimization ideas to model it as a shortest path problem or a maximum flow problem. Nguyen DUY HUY et al. used VentSim software to simulate the mine ventilation system of a coal mine and used the software to predict the escape route [27]. Lotero et al. simulated an exogenous fire under a room-and-pillar coal mine based on VentSim software and used a lightweight network flow algorithm to compute the lowest-exposure as well as the shortest-path avoidance routes under the disaster [4]. Xiuli Shi et al. proposed a bi-objective optimization model with minimum rescue time and minimum hazard level for selecting emergency routes in underground mine fires [28]. In 2023, Salmi reviewed the problem of underground mine fires and emergency evacuation, and pointed out two research routes for this problem: the optimization method based on graph theory and the risk assessment method based on multi-agent modeling and computational fluid dynamics [29]. In more complexity multi-objective optimization problems, Man-Fai Leung et al. proposed a collaborative neurodynamic approach, utilizing neural networks and particle swarm optimization to achieve both Pareto optimality and solution diversity, outperforming other leading algorithms on benchmark datasets [30]. However, due to the cost requirements of underground sensor placement, fire sensors are often not placed in each and every roadway underground. Therefore, the above studies are simulated in software, and path planning is performed by calculating the weights of each roadway in the ventilation network based on the simulated data. Using software simulation, especially CFD simulation, firstly, the type of combustible materials and the location of the fire need to be known in detail for modeling, and it is often not possible to measure and obtain real data when the disaster occurs. Secondly, underground fires develop rapidly, and CFD simulation requires a certain amount of calculation time, which is difficult to meet the needs of emergency rescue.

3. Sensor-Based Network Weight Update Methodology

3.1. Calculation of the Equivalent Length of a Roadway

When a disaster occurs underground, the planning of the evacuation route should not only consider the length of the roadway, but also the conventional properties that affect the traffic efficiency, such as the roadway type, slope, width, and other structures that affect traffic. It should also consider whether there is smoke flow in the roadway and the smoke flow’s concentration, temperature, visibility and other properties during the disaster period. In order to comprehensively measure the impact of these parameters on the difficulty of roadway, the ratio of the roadway speed when affected by a certain factor to the roadway speed when not affected by a certain factor is used to define the roadway difficulty coefficient of a certain factor [31]. The formula is as follows:

$$k_{attr}={\displaystyle \frac{v_{attr}}{v_{norm}}}$$

(1)

where $k_{atrr}$ is the travel difficulty coefficient affected by a certain factor. $v_{norm}$ is the speed when it is not affected by a certain factor. $v_{attr}$ is the speed of traffic affected by a certain factor.

The equivalent length of a roadway is used to measure the efficiency of a roadway under the influence of all factors. The main factors affecting the efficiency of the roadway are combined and converted into the accessibility coefficient and the equivalent length of the roadway is obtained by multiplying the actual length by the accessibility coefficient and adding the sum of the equivalent lengths of the local obstacles inside the roadway. The equivalent length of the roadway $(i,j)$ from node $i$ to node $j$ is expressed as $w_{ij}$, then the equivalent length of the roadway is given by,

$$w_{ij}=k_h{k}_w{k}_g{k}_v{k}_s{l}_{ij}+{\displaystyle \sum _{m=1}^n{l}_m}$$

(2)

where $k_h$ is the travel difficulty coefficient of the roadway height. $k_w$ is the travel difficulty coefficient of the roadway width. $k_g$ is the travel difficulty coefficient of the roadway slope. $k_v$ is the travel difficulty coefficient of the wind speed in the roadway. $k_s$ is the visibility difficulty coefficient of the roadway. $l_{ij}$ is the actual length of the roadway, m. $n$ is the number of obstacles in the roadway from $i$ to $j$. $l_m$ is the equivalent length value of the obstacle in the roadway from $i$ to $j$, m.

3.2. Network Weight Update Algorithm

When a fire occurs underground, as the fire smoke spreads, the passability and efficiency of the downwind side of the roadway decreases as the smoke stream encroaches. In this case, the weights on the edges of the graph increase with the concentration of the smoke stream in the roadway or decrease as the smoke stream is expelled. The roadway network is represented as a directed graph $G=(V,E)$, where $V$ denotes the set of all points in the graph and $E$ denotes the set of all pairs of points in the graph, i.e., the set of edges. For any edge $(i,j)\in E$, there is an equivalent length $w_{ij}$. The path is a finite set of nodes, denoted by P, then $P=\left(v_0,v_1,\dots ,v_p\right)$. For any road $P$, the sum of equivalent lengths is denoted as $W$.

Equivalent length is a measure of roadway passability. Parameters related to roadway passability during catastrophic periods are mainly obtained in real time through real-time monitoring by underground monitoring and surveillance systems, in addition to reporting by underground personnel. The monitoring and control system monitors various toxic and hazardous gases underground through sensors such as carbon monoxide, nitrogen dioxide, and smoke. The arrangement of sensors is the key to disaster monitoring, and the arrangement method is based on the type of mine and the characteristics of the disaster. Coal mines mainly arrange carbon monoxide sensors to monitor fire in the return-airway and the downwind side of the belt conveyor, the observation point of spontaneous combustion, and the firewall of the closed fire zone [32]. In addition to carbon monoxide and smoke sensors on the downwind side of the belt conveyor, metal mines are encouraged to arrange carbon monoxide or nitrogen dioxide sensors for blasting smoke in the middle of production, in the sectional inlet and return airways, and in the return airway of the excavation roadway.

However, due to cost considerations, it is impossible to deploy sensors in every roadway downhole, so the smoke flow arrival times of all sensor downstream nodes are derived based on Dijkstra’s algorithm, and a network of roadway passability is generated. The specific implementation of the algorithm is shown in Figure 1.

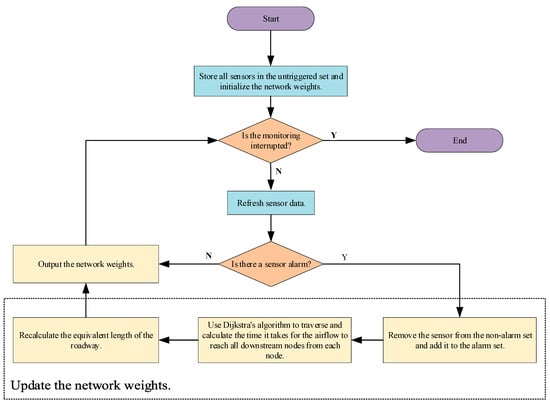
Figure 1. Emergency escape network weighting algorithm.

The specific steps of the algorithm are described as follows:

Step 1: Obtain the position of all sensors and initialize them to the non-alarm state. Add all sensors to the non-alarm set and initialize the roadway network weights;

Step 2: Determine whether to interrupt sensor monitoring. If not, refresh the sensor data and execute the next step; if yes, jump to step 7.

Step 3: Determine whether there is a sensor alarm, if yes, execute the next step; if no, jump to step 2;

Step 4: Move the alarming sensor out of the non-alarm set and add it to the alarm set;

Step 5: Use the Dijkstra algorithm to traverse the downstream nodes of each alarm sensor and calculate the arrival time of the downstream node smoke flow. If the node is downstream of multiple alarm sensors, take the first arrival time of the smoke flow;

Step 6: Recalculate the equivalent length of the roadway and output the network weight, jump to step 2;

Step 7: Complete the time-varying network weight solution.

4. Mathematical Models and Algorithms for Emergency Escape Routes

4.1. Shortest Path Problem with Resource with Constraints

The shortest path problem with resource with constraints (SPPRC) is a variant of the shortest path problem [33]. The problem intends to find a path from a network that goes from an origin to an end point and satisfies a set of constraints based on a set of resources, where resources refer to traveling time, cost, etc. For any path in the graph, from the start point $i$ of one of the edges to the end point $j$ of this edge, resource extension functions (REFs) should be satisfied for any kind of resource on the edge. Resource extension functions are generally defined as

$$f_{ij(T_i)}=T_i+t_{ij}$$

(3)

where $T_i$ is the resource vector on node. $t_{ij}$ is the resource weight on directed edge $<i,j>$. $f_{ij(T_i)}$ is the new resource vector starting from the resource vector $T_i$ on point $i$, extending to point through the directed edge $<i,j>$.

For any path $P=(v_0,v_1,\mathrm{\dots },v_p)$ in the graph, define the resource vector $T_p\in [a_{v_p},b_{v_p}]$ at the end point of $p$ the path, where $a_{v_p},b_{v_p}$ are the lower and upper limits of the resource at that point. Define $\mathsf{\Gamma }(P)$ as the set of all feasible resource vectors at the end point $v_p$ of path $P=(v_0,v_1,\mathrm{\dots },v_p)$. Then, the resource-constrained shortest path problem can be expressed as follows: in a path $P$, if the resource vector at its end point $p$ satisfies the upper and lower limits and for all points other than the end point $i=0,\mathrm{\dots },p-1$ on the path, there exists a resource vector that satisfies the resource upper and lower limits on each point, that is $T_i\in [a_{v_i},a_{v_{i+1}}]$; and so that for all $i=0,\mathrm{\dots },p-1$, $f_{v_i,v_{i+1}}(T_i)\le T_{i+1}$ holds true and the path $P$ is resource feasible. The classic SPPRC can be expressed as

$$\mathsf{\Gamma }(P)=\{T_p\in [a_{v_p},b_{v_p}]:\exists T_i\in [a_{v_i},b_{v_i}],f_{v_i,v_{i+1}}(T_i)\le T_{i+1},i=0,\mathrm{\dots },p-1\}$$

(4)

where $i=0,\mathrm{\dots },p-1$ is the node other than the end point and $T_i\in [a_{v_i},b_{v_i}]$ is the resource vector on node $i$ that meets the upper and lower limit constraints. $f_{v_i,v_{i+1}}(T_i)\le T_{i+1}$ is the constraint that the resource vector extending from node $i$ to node $j$ is less than or equal to the resource vector at node $j$, ensuring that the resource consumption in the current extension direction of the path is minimal.

4.2. Mathematical Model of Emergency Escape Routes

When searching for an underground escape route, feasible exits include the main and secondary shaft exits and in times of emergency, the return air shafts can also be used as an escape route. When the situation is serious and it is not possible to reach the surface exits in time, the underground personnel should enter the refuge in time to escape and wait for rescue. In the event of a disaster, the first step is to wear a self-rescuer. According to the regulations, self-rescuers should be rated for a minimum of 30 min, and when two self-rescuers cannot be relied upon to reach the surface, an emergency refuge system, such as a removable refuge, or a temporary or permanent refuge should be installed underground.

In general, the downhole shortest emergency escape route problem considering downhole avoidance facilities can be described as follows: for a network $G=\left(N,E\right)$, $N$ is the set of nodes, and $E$ is the set of edges. $\left|N\right|=n,\left|E\right|=e$. Using $i$ and $j$ to represent any pair of nodes, the directed edge from $i$ to $j$ is denoted as $\left(i,j\right)$. The equivalent weight of the directed edge $\left(i,j\right)$ is denoted as $w_{ij}$ and the time of passage is denoted as $t_{ij}$. $w_{ij}$ and $t_{ij}$ are both non-negative real numbers. For any path $P$ from the start to the end, the sum of the equivalent lengths of the path is $W$, and the total time spent traveling through the smoke stream is $T$. The logic variable $x_{ij}$ represents whether the directed edge $(i,j)$ is on the path from the personnel position to the goal position, taking 1 if it is and 0 if it is not. At most, each node passes through once. The shortest path that satisfies the requirements that the time in the smoke flow from the start of escape does not exceed the rated protection time of the self-rescuer must be found, and the escape path is relatively short and has the shortest escape time in the smoke flow.

To sum up, the mathematical model of the underground emergency escape route considering the underground emergency facilities can be described as follows,

$$\begin{array}{lll}\min W=& {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}}}{w}_{ij}& \\ \min T=& {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{y}_{ij}{x}_{ij}{t}_{ij}}}& \\ s.t.& \sum _j{x}_{ij}-\sum _j{x}_{ji}=& \{\begin{array}{ll}1& \mathrm{if}i=0\\ -1& \mathrm{if} i=D \forall i\in N\\ 0& \mathrm{otherwise}\end{array}\\ & {\displaystyle \sum _j{x}_{ij}}\le 1& \forall i\in N\\ & {\displaystyle \sum _{(i,j)}{x}_{ij}t(i,j)\le T}& \forall (i,j)\in E\\ & x_{ij}\in \{0,1\}& \forall (i,j)\in E\\ & y_{ij}\in \{0,1\}& \forall (i,j)\in E\end{array}$$

(5)

4.3. Labeling Algorithm Based on Dynamic Programming

A general algorithm for solving constrained shortest circuits is the labeling algorithm based on dynamic programming [34]. The algorithm degenerates into Dijkstra’s algorithm when there is only one type of weight on the edges of the network and only one objective function for the shortest path model. The labels in this algorithm refer to the data structure that stores the paths as well as the distances of the paths and the traveling time in the smoke stream. The algorithm starts from the starting point and gradually searches for feasible paths and records them in the labels. The same node will generate different labels when it is reached through different paths. The REFs are used to generate and determine whether the labels are legal and construct the solution set space of feasible paths; the dominance function is used to determine the dominant relationship between the labels on the same node. If a label is dominated, it means that the path represented by the label is not the shortest path or cannot constitute the shortest path to the end point. Then, in order to speed up the solution, the label should be discarded. A reasonable dominance function is the key to accelerating the algorithm solution.

Label data structure:

struct Label{

  Vector<int> Path;//Path

  int Equal_Distance;//Equivalent length

  int Time_in_smoke;//Time spent walking in the smoke

  int Time_escape_smoke_area;//Time to leave the smoke area

}

Resource Expansion Function(REFs): The Resource Expansion Function specifies the change in each resource (path length, cost, etc.) from the start point to the end point on each edge. It provides a lower bound on the resource value at the end point based on the start point to resource value. For any resource $r$, the resource consumption at the node $i$ is $T_i$, and the weight of that resource on the edge $<i,j>$ is $t_{ij}$; hence, the resource consumption at the node is $j$

$${f_{ij}}^r(T_i)={T_i}^r+{t_{ij}}^r$$

(6)

where $f_{ij}^r\left(T_i\right)$ is the resource consumption of resource $r$ based on the resource consumption at node $i$ expanded along edges $<i,j>$.

Dominance function: The two attributes of the path equivalent length and the travel time in the smoke flow in this problem are represented by the vector $<W,T>$. Since the two resource attributes in this problem are non-negative, the resource expansion function is non-decreasing. Therefore, for labels ${\mathrm{L}}_1=<W_1,T_1>$ and labels ${\mathrm{L}}_2=<{\mathrm{W}}_2,{\mathrm{T}}_2>$, if ${\mathrm{W}}_1\le W_2$ and ${\mathrm{T}}_1\le T_2$, then label ${\mathrm{L}}_1$ is dominated by label ${\mathrm{L}}_2$. All non-dominated labels on a node form a Pareto optimal set [35].

A constrained shortest path example based on two resources is shown in Figure 2. Starting from the starting point S, there are two labels, s-2-1 and s-1 at node 1, and the resource vectors are (1,2) and (2,1), respectively, and there is no dominance relationship; at node 2, there are two labels, s-1-2 and s-2, and the resource vectors are (2.5,2) and (0.5,1), respectively, and the former is dominated by the latter. Therefore, the path s-1-2 is abandoned and no longer expanded. Finally, at node t, there are three labels, s-2-t, s-2-1-t, and s-1-t, and the resource vectors are (3,3), (4,2), and (5,1), respectively, and there is no dominant relationship between them. Therefore, all three paths are Pareto optimal solutions.

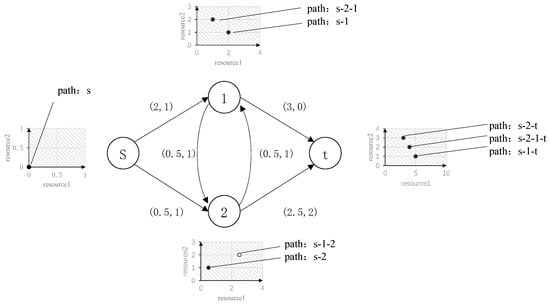
Figure 2. Case of the shortest path problem with constraints on two resources.

The algorithm flow of the constrained shortest path model emergency route planning problem is shown in Figure 3.

Figure 3. The flow chart of the RCSPP algorithm.

The specific steps are as follows.

Step 1: Firstly, read the roadway and mine ventilation network information to construct the escape and emergency escape information network $G$; obtain the personnel position $s$ as well as the escape target $d$; define the set of unprocessed labels as $U=\left\{\right(s\left)\right\}$, containing only one path; and define the set of labels that have been processed as $P=\left\{\right\}$, which is initialized to be the empty set.

Step 2: Determine whether the set $U$ is empty. If yes, the procedure ends and outputs all labels on the target node $d$. If not, take out the labels $L_t$ on $v$ of the node from the set $U$.

Step 3: Determine whether the label $L_t$ is dominated by other labels on node $i$. If yes, delete the label $L_t$ and go back to step (2) and if no, perform the next step.

Step 4: Iterate to judge and delete all labels on node $i$ that are dominated by label $L_t$. Add the label $L_t$ to the set $P$. Compute the new labels from node $i$ to all adjacent nodes and determine whether the REFs is satisfied. If yes, proceed to the next step. If no, remove the new label $L_i$ and go back to step 3.

Step 5: Add the new label $L_i$ to the set $U$.

4.4. Path Optimization Strategy

The above algorithm yields a Pareto optimal set, in which any path is not dominant in terms of the two attributes of equivalent length and time spent walking in the smoke relative to other paths. In order to achieve real-time path-assisted decision making, it is also necessary to consider parameters such as the choice of disaster escape exits and the time to escape the disaster area. The target of the escape exit is to prioritize surface exits such as the auxiliary shaft and the main shaft. When no solution can be found for all surface exits, the refuge chamber is used as the escape exit.

In addition, in order to ensure that the underground personnel escape from the potentially affected area as soon as possible, not only should the route with the least time of exposure to the disaster be chosen but also the route with the fastest access to the roadway that is not attacked by the smoke flow should be chosen. Taking a feasible solution of an emergency escape route $<v_0,v_1,\dots v_n>$ as an example, if all the edges after the path reaches node $i$ are safe edges, the time to reach point $i$ is defined as a temporary escape time. For paths arriving at the same end point, the path with shorter temporary de-risking time is taken as the better path. The path optimization strategy is shown in Figure 4.

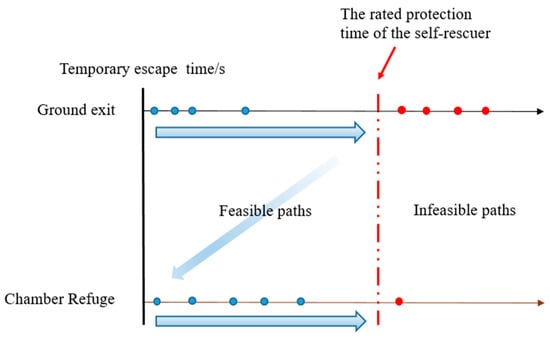
Figure 4. Path optimization strategy.

5. Case Studies

5.1. Experimental Model of Ventilation System

The iVent 3D Mine Ventilation System is a mine ventilation system software with functions such as ventilation network drawing, 3D visualization, ventilation network solution, ventilation facility control, etc. It can design mine ventilation systems and help ventilation engineers dynamically maintain ventilation systems during mine production [36].

The ventilation network of an iron ore mine is modeled as an example. The ventilation network graph of this mine has 494 nodes and 660 edges. The ventilation method is forced ventilation, with air entering through the west shaft and returning through the east return shaft as well as the main and auxiliary shafts. Workers can escape to the surface through the main and secondary shafts, inclined shafts, and the intake shaft. All draw raises, return air shafts, etc., are made impassable. One refuge is located at Level −330 and one at Level −175. These chambers will allow workers to escape to the surface if they are unable to do so. The mine ventilation system for the mine is shown in Figure 5 and Figure 6:

Figure 5. A mine ventilation network of an iron ore mine.

Figure 6. Three-dimensional mine ventilation diagram of an iron ore mine.

5.2. Simulation Result and Discussion

It is assumed that the location of an underground evacuee is in a roadway at the lowest elevation of the underground mine, Level −245. CO and smoke sensors are mainly located in the inlet and return airways of each production section and sub-section, as well as in the return air outlets of forced ventilation roadways.

Assume that a fire occurs in the −110 horizontal transport roadway at the bottom of the west wind shaft underground due to the aging of electromechanical equipment, and the smoke spreads along the ventilation system. The time sequence of the underground sensors alarming in sequence since the fire occurred is shown in Table 1. The range of the underground contaminated by smoke obtained by the algorithm search is shown in Figure 7. As shown in the table, the earliest smoke sensors located in the inlet airway detected the fire 11 s after its ignition. If no effective control measures, such as air reversing, are implemented or if these measures fail, all underground sensors will gradually trigger alarms over the course of approximately 1771 s. This indicates that carbon monoxide and smoke from the fire will spread to all underground locations.

Table 1. Sensor alarm time and sequence.

Sensor Serial Number	Alarm Time/s	Sensor Serial Number	Alarm Time/s
2	11	19	847
3	30	7	868
15	233	5	1042
20	288	12	1222
16	314	1	1266
8	346	13	1283
9	496	18	1324
6	621	14	1442
11	818	17	1771
4	846

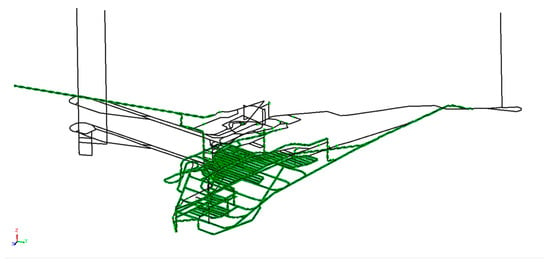
Figure 7. Smoke diffusion pollution range of underground fire.

Based on the attributes such as smoke diffusion time generated by sensor data, the passability network of the underground roadways is assigned; then, the location of the underground personnel is taken as the starting point and the four surface safety exits of the main shaft, auxiliary shaft, inclined shaft, and air intake shaft and the two underground refuge chambers are used as escape targets. The route-finding process is constrained by the self-rescuer-rated protection time of 30 min according to the safety regulations. The equivalent length of the route and the hazardous time attribute are used as the path dominance attributes to obtain the routes for underground personnel to reach each escape location. Based on the dynamic programming labeling algorithm, the optimal route that meets the rated protection time of the self-rescuer and has a shorter equivalent length and travel time in the smoke stream is found. By prioritizing escape targets and escaping from the danger zone as early as possible, feasible evacuation routes are sorted. In addition, to investigate the effect of response time on route planning, we explored feasible avoidance routes for the same personnel location after 12 s, 300 s, and 1200 s of the disaster, respectively. The path visualization results are shown in Figure 8; the path sorting results are shown in Table 2:

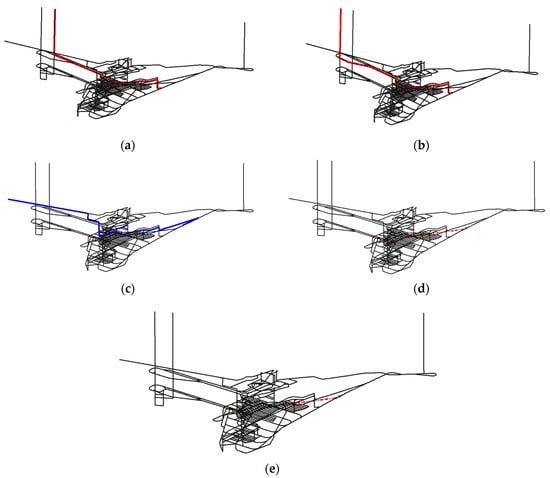
Figure 8. Evacuation routes to different destinations. (a) Route to the main shaft. (b) Route to the auxiliary shaft. (c) Route to the incline shaft. (d) Route to the chamber refuge1. (e) Route to the chamber refuge2.

Table 2. Ranked results of evacuation routes.

Respond Time	Priorities	Targets	Paths	Temporary Escape Time/s	Equal Distance/m	Time in Smoke/s
12 s	1	Main shaft	[446, 472, 467, 466, 385, 409, 422, 421, 419, 43, 442]	-	1811	0
	2	Second shaft	[446, 472, 467, 466, 385, 409, 422, 421, 419, 376, 430, 414, 382, 381, 32, 441]	-	1991	0
	3	Inclined shaft	[446, 405, 445, 27, 26, 28, 25, 24, 35, 444]	825	1657	681
	4	−245 level refuge	[446, refuge2]	-	187	0
	5	−230 level refuge	[446, 472, 467, 466, 385, refuge 1]	-	839	0
300 s	1	Second shaft	[446, 472, 467, 466, 385, 409, 422, 421, 389, 416, 415, 414, 382, 381, 32, 441]	927	2395	379
	2	Inclined shaft	[446, 405, 445, 27, 26, 28, 25, 24, 35, 444]	1276	1902	954
	3	−245 level refuge	[446, refuge2]	424	187	424
	4	−230 level refuge	[446, 472, 467, 466, 385, ‘chamber1’]	927	1180	379
1200	1	−245 level refuge	[446, ‘chamber2’]	1324	187	1324

If the evacuation command is issued immediately after the sensor alarm (12 s), a total of five feasible avoidance routes can be obtained at this point. In this case, a total of five paths were obtained. The escape targets of Paths 1, 2, and 3 are the main and second shafts and the east return air shaft, respectively, and they are surface exits, so they are prioritized over the routes with the refuge chamber as the target; because the fire occurred in the −110 horizontal transport roadway under the west wind shaft, most of the paths with the west wind shaft as the escape target are in the smoke flow, and the algorithm cannot find a feasible solution that meets the rated protection time of the self-rescuer. Among all feasible solutions, Path 1 and Path 2 do not go through the smoke stream and have the highest security, but the equivalent length is relatively long. Path 3 has to walk in the smoke for about 681 s and it takes about 825 s to completely escape the smoke invasion area, so paths 1 and 2 should be given priority; when a path leading to a safe exit on the surface is available, the refuge chamber is generally not used as an escape target; on the contrary, when the disaster situation is out of control, that is, all surface exits cannot be solved and only the route with the refuge chamber as the target point has a feasible solution, the refuge chamber should be used as the escape target.

Delays in evacuation can lead to a reduction in the number of possible routes and a deterioration in the safety of those routes. Evacuating immediately at the first sensor alarm, at 12 s, allows escape to all surface exits and refuge chambers. By evacuating at 300 s, all routes are affected by the smoke flow for a longer period of time and the route to the main shaft becomes impassable. At 1200 s, it is no longer safe to evacuate to the surface area and the only option is to go to the nearest refuge and wait for help.

Since the resource vector in the label data structure of this algorithm is less than the equivalent length, the walking time in the smoke flow increases, which contains only two elements, and it is easy to form a dominant relationship between any two labels. Therefore, for any escape target, only one feasible path with the shortest length, the shortest walking time in the smoke flow, and meeting the rated protection time of the self-rescuer is obtained. We also compared planning algorithms with the classical disaster avoidance route and the results show that in scenarios with a small range of disaster impacts, the results of the present method are basically the same as those of the classical methods; in scenarios with severe disaster development and long distances between the avoidance starting point and the target point, the present algorithm has the potential to obtain multiple better solutions. Compared to traditional models, our approach integrates two critical safety indices: path length and path safety. In the event of a large-scale underground disaster, this method assesses the safety of available exits and plans feasible evacuation routes. Ultimately, it prioritizes these routes based on the safety indices, guiding underground personnel in making informed and rational decisions to evacuate.

6. Conclusions

This study investigates the planning of emergency escape routes for underground personnel in the event of an exogenous fire in an underground mine. It considers real-time disaster development, personnel location, the protective capacity of self-rescuers, and the location of underground refuge chambers. Using alarm sensor data and Dijkstra’s algorithm, we predicted the arrival time of smoke flow at each underground location. We then established a bi-objective optimization model that aims to minimize both the shortest equivalent length of the emergency escape route and the time that personnel are affected by smoke flow, thereby ensuring the efficiency and safety of the escape routes. A dynamic programming-based labeling algorithm is employed to solve the model, facilitating the identification of optimal routes across all emergency escape options. This is achieved through the inclusion of two labeled elements in the model and the application of a stricter dominance rule. For multiple feasible emergency escape routes that consist of various exits and Pareto-optimal sets for the same exit, a path preference strategy is implemented. This strategy prioritizes surface exits and minimizes temporary escape time in accordance with safety requirements. Ultimately, the route with the shortest path length and highest safety is selected from all feasible options. This approach avoids the influence of decision makers’ risk preferences, which can occur with traditional weighting methods.

However, the prediction of fire development in this study is based on the premise that the fire development is in a stable stage and there is no airflow reversal in the ventilation system. How to integrate all the sensor data from underground to predict the trend of the disaster and the change in the ventilation system will be the key point to be solved in the future. Moreover, the reliability of sensor data, which this study assumes to be consistently accurate, presents another limitation. In real-world scenarios, sensor failures, inaccuracies, or delays in data transmission could significantly impact the model’s effectiveness. Future work should address these issues by incorporating sensor reliability factors into the model, as well as developing strategies to mitigate the effects of potential data inaccuracies. In our future work, we will investigate how to predict fire development and changes in the state of the ventilation system based on sensor data at the time of the fire and to provide a more accurate assessment of the risk at various locations underground during a fire. We hope that our work will provide a new perspective to other scholars in the area of evacuation of people from exogenous fires in underground mines.