Privacy-Preserving Byzantine-Resilient Swarm Learning for E-Healthcare

Abstract

An automatic medical diagnosis service based on deep learning has been introduced in e-healthcare, bringing great convenience to human life. However, due to privacy regulations, insufficient data sharing among medical centers has led to many severe challenges for automated medical diagnostic services, including diagnostic accuracy. To solve such problems, swarm learning (SL), a blockchain-based federated learning (BCFL), has been proposed. Although SL avoids single-point-of-failure attacks and offers an incentive mechanism, it still faces privacy breaches and poisoning attacks. In this paper, we propose a new privacy-preserving Byzantine-resilient swarm learning (PBSL) that is resistant to poisoning attacks while protecting data privacy. Specifically, we adopt threshold fully homomorphic encryption (TFHE) to protect data privacy and provide secure aggregation. And the cosine similarity is used to judge the malicious gradient uploaded by malicious medical centers. Through security analysis, PBSL is able to defend against a variety of known security attacks. Finally, PBSL is implemented by uniting deep learning with blockchain-based smart contract platforms. Experiments based on different datasets show that the PBSL algorithm is practical and efficient.

1. Introduction

In recent years, online medical diagnosis services [1] have attracted considerable interest due to their ability to overcome geographical restrictions and reduce the waiting time of seeing doctors [2,3]. To discover hidden diseases from collected medical data, deep learning (DL) has been applied to e-healthcare systems [4,5,6]. DL can process huge amounts of medical data and automatically find valid patterns that are too complex for human-led analysis. DL intrinsically relies on large amounts of training data. Unfortunately, in traditional healthcare systems, medical data tend to be distributed among different hospitals, and the small amount of medical data collected by individual hospitals are often insufficient to train reliable models [7,8]. Therefore, data centralization is an effective way to address the lack of training data [9]. Although the centralized model has brought many benefits, it still faces many challenges, including surge in data traffic, disclosure of local data, confidentiality of global models, and data monopolies [10].

As shown in Figure 1a, Google’s federated Learning (FL) [11,12] is implemented with the help of a centralized server that aggregates all local model gradients and takes an overall average to produce a global model update. Although the problems of local data storage and local data confidentiality have been solved, the global model parameters are still processed and stored by the centralized server. Furthermore, such centralized architectures decrease fault tolerance. To solve these problems, Stefanie et al. [13] proposed swarm learning (SL), in which multiple medical centers share their local gradients through blockchain peer-to-peer networks, and the medical center that wins the consensus mechanism replaces the centralized parameter server to update the global parameters according to collected gradients.

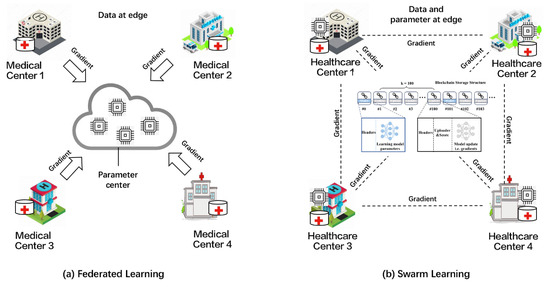
Figure 1. (a) Traditional federated learning (FL) architecture and (b) swarm learning (SL) architecture.

As shown in Figure 1b, despite the move away from centralized servers, SL still faces data security and privacy breaches. First, SL does not protect the privacy of hospital data and guarantee the confidentiality of the global model. While local model updates and global models are already recorded on blockchain, blockchain itself does not guarantee the privacy of local data and the confidentiality of the global model. For example, any curious medical center participating in swarm learning can infer the original training data of other medical centers according to the gradient and model parameters stored in the blockchain [14,15]. Secondly, in the process of gradient collection and parameter updating, the malicious behavior of dishonest medical centers can destroy the swarm learning process and poison the federated model. In particular, malicious medical centers (e.g., Byzantine attackers) can easily disrupt swarm learning systems by spreading false information over the network [16]. For example, Bagdasaryan et al. demonstrated that dishonest edge devices can poison collaborative models by replacing updated models with its exquisitely designed one [17].

Therefore, we propose a privacy-preserving Byzantine-robust swarm learning (PBSL), which ensures the confidentiality of the local gradient, the privacy of the global model, and the robustness of Byzantine attacks. Specifically, after the blockchain-based point-to-point network is established, each medical center calculates its local gradients according to the local training data. Then, the local gradients encrypted by the fully homomorphic encryption (FHE) scheme, CKKS, are broadcast to all other medical centers on the blockchain-based network. If medical centers on the blockchain reach a consensus, the winning medical center uses a proposed Byzantine attack tolerant aggregation scheme based on secure cosine similarity, which supports lossless collaborative model learning while protecting the privacy of the medical center.

In short, the main contributions of this paper include the following three aspects:

• PBSL can not only protect the privacy of local sensitive data, but also ensure the confidentiality of the global collaborative model. Using the fully homomorphic encryption (FHE) scheme CKKS, PBSL encrypts the local gradient submitted by the medical center and aggregates to generate a global collaborative model without decryption.
• PBSL can achieve swarm learning (SL) that resists Byzantine attacks. In order to resist Byzantine attacks, we propose a privacy-protecting Byzantine-robust aggregation method, which uses secure cosine similarity to punish malicious $\mathbf{MC}s$.
• PBSL prototype is implemented by integrating deep learning and blockchain-based smart contract. Moreover, PBSL is tested using real medical datasets to evaluate its effectiveness. Experimental results show that PBSL is effective.

The remainder of this paper is organized as follows. We review related works in Section 2. We review some primitives in Section 3, and introduce our system model and design goals in Section 4. Then, we introduce our scheme in Section 5. Next, we present the security and performance analyses in Section 6 and Section 7, respectively. Finally, we conduct a summary of our work in Section 8.

2. Related Work

In this section, we focus on related works about privacy-preserving FL, Byzantine-robust FL, blockchain-based FL, and swarm learning.

2.1. Privacy-Preserving Federated Learning

Although the training dataset is divided and stored separately, federated learning (FL) cannot protect training data privacy because the exchanged global model and local gradients still contain a large amount of sensitive information. Three popular privacy-protecting federal learning (PPFL), i.e., differential privacy (DP), homomorphic encryption (HE), and secure multi-party computation (MPC), have been proposed to address this problem.

DP-based PPFL protects the local updates against inference attacks through adding random noises [18,19,20]. However, it is challenging to bring a trade-off of accuracy loss. SMC-based PPFL collaboratively computes the aggregated values between multi-parties’ inputs through secure multi-party computing in nature [21,22,23,24,25,26]. SMC-based PPFL has been constructed in one [27], two [28], three [29], and four [30] servers. However, although SMC, which is a cryptographic primitive, has powerful privacy, it is inefficient. HE-based PPFL uses homomorphic encryption to support aggregation operation on cipher-texts, and protects training data privacy from curious parameter servers without external learning accuracy loss [31]. EaSTFLy [32] uses $(T,N)$-Shamir’ secret sharing and Paillier partially homomorphic encryption (PHE). BatchCrypt [33] encodes quantized gradients into signed integers and then encrypts them, achieving training speedup compared with full-precision encryption. However, most of them contain massive, complicated arithmetical operations, which brings considerable computation overhead.

In this paper, threshold fully homomorphic encryption (TFHE), which combines $(T,N)$-Shamir’ secret sharing and CKKS fully homomorphic encryption (FHE) [34], is used as a privacy protection mechanism, which greatly reduces the computing and communication overheads.

2.2. Byzantine-Robust Federated Learning

2.2.1. Byzantine Attack

As we all know, federated learning is vulnerable to Byzantine attacks [35,36,37]. In order to map the specified feature to the target class, the Byzantine attacker tries to modify the classification boundary of the trained model. It has been proven that an attacker can control the entire training process and steal user privacy [16].

According to the goals of the attackers, Byzantine attacks can be divided into targeted attacks [17] and untargeted attacks [35]. Targeted attacks target only one or a few data categories in the dataset, while maintaining the accuracy of other categories. Untargeted attacks are undifferentiated attacks that aim to reduce the accuracy of all data categories. And according to the abilities of the adversaries, Byzantine attacks can also be divided into data attacks [37] and model attacks [35]. In data attacks, the attackers indirectly poison the global model by poisoning the client’s local data. For example, the label-flipping attack flips the label of the normal features to the target class. And the backdoor attack is an attempt to seek a set of parameters to establish a strong link between the trigger and the target label while minimizing the impact on benign input classification. In model attacks, the attackers can directly manipulate and control the model updates of communication between the clients and the server, which directly affects the accuracy of the global model.

2.2.2. Byzantine-Robust Federated Learning

Typical FLs, such as FedSGD [38] and FedAvg, are not resistant to poisoning attacks, resulting in untrustworthy and inaccurate global models. By comparing local gradients received from different parties, Byzantine-robust federated learning (BRFL) [16,39,40,41] excludes abnormal gradients to protect the training model from poisoning attacks. Based on the Euclidean distance between any two gradients, Krum [16] excludes the outlier gradients. Specifically, in each training round, a candidate model would be selected. Similarly, Trim-mean [39] first sorts the received local gradients, then removes the larger and smaller gradients among them, and finally takes the mean of the remaining gradients as the global gradient. GeoMed [42] updates the FL model by selecting a gradient based on the geographic median to realize gradient aggregation. Bulyan [43] first implements the Krum-based aggregation and then updates the global model by averaging the gradient closest to the median value. Meanwhile, based on the cosine similarity between the parties’ historical gradients, FoolsGold [35] sets the weights of parties to ward off Sybil attacks in FL.

However, these schemes do not consider privacy threats, which directly aggregate the global model directly in plaintext. In order to solve this problem, the FL scheme [40] using DP and SMC can not only prevent inference attack during training, but also improve model accuracy. However, because it is difficult to calculate the similarity between the encrypted gradients, the FL scheme [40] is vulnerable to malicious gradients. To this end, privacy-enhanced federated learning (PEFL), which employs HE as the underlying technology, punishes malicious parties via the logarithmic function of gradient data. However, the PEFL scheme still does not avoid malicious behaviors of the servers and inference attacks onto clients.

To develop a Byzantine-resilient, and at the same time, privacy-preserving federated learning framework, we use TFHE to protect user privacy, cosine similarity to remove malicious gradients, and blockchain to avoid malicious behavior of servers.

2.3. Blockchain-Based Federated Learning and Swarm Learning

By heavily relying on a single server, traditional FL cannot protect against a single point of failure and resist malicious attacks. As the infrastructure of Bitcoin, blockchain has attracted a lot of attention because of its decentralization and reliability. Several blockchain-based FL protocols [44,45,46,47] replace servers with blockchain, enabling privacy protection and enhancing trust among parties. BAFFLE [44] uses blockchain to avoid single points of failure and aggregates local models using smart contracts (SCs). Similarly, through blockchain smart contracts, BlockFL [46] exchanges and validates local model updates. By providing incentives associated with training samples, BlockFL can integrate more equipment and more training samples. Meanwhile, as a state-of-the-art BCFL, swarm learning (SL) [13,48] combines edge computing, blockchain networking, and federated learning while maintaining confidentiality without a central coordinator. In the e-heath field, SL has been successfully applied to the diagnosis of COVID-19, tuberculosis, leukemia and lung diseases [13], skin lesion classification fairness [49], genomics data sharing [50], and risk prediction of cardiovascular events [51].

However, the above schemes impose heavy computation and communication costs on the blockchain nodes and cannot distinguish the malicious gradients. To address these issues, the blockchain-based federated learning framework with committee consensus (BFLC) [45] can effectively reduce consensus computing and prevent malicious attacks through innovative committee consensus mechanisms.

Finally, Table 1 shows a comparison of our PBSL scheme with the various FL schemes described above. The results show that our scheme can not only resist poisoning attacks and be robust to users dropping out, but also has high privacy and computational efficiency. The compared results point out that PBSL can not only resist Byzantine attacks and be robust to parties dropping out, but also protect privacy and improve computing efficiency.

Table 1. A comparative summary between our scheme and previous schemes.

Schemes	Privacy Protection	Poisoning Defense	Central Server or Blockchain	Robust to Off-Line	Lightweight Computation
SecProbe [20]	DP-based	×	Central server	√	√
PPDL [31]	HE-based	×	Central server	×	×
PPML [27]	MPC-based	×	Central server	√	×
Krum [16]	×	√	Central server	×	√
Trim-mean [39]	×	√	Central server	×	√
FoolsGold [35]	×	√	Central server	×	√
PEFL [41]	HE-based Paillier	√	Central server	√	×
BAFFLE [44]	×	×	Blockchain	×	×
BlockFL [46]	×	×	Blockchain	×	×
Swarm Learning [46]	×	×	Blockchain	×	×
BFLC [45]	×	√	Blockchain	×	√
PBSL	HE-based CKKS	√	Blockchain	√	√

3. Preliminaries

In this section, we review the basics of PBSL, namely swarm learning and full homomorphic encryption.

3.1. Swarm Learning

As the state-of-the-art BCFL, discarding the centralized server, swarm learning (SL) shares local gradients through the swarm network, and independently builds models on local data at the swarm edge nodes. SL ensures the confidentiality, privacy, and security of sensitive data with the help of blockchain. Unlike clients in traditional FL, edge nodes not only perform training tasks, but also execute transactions. The workflow of SL is as follows. A new edge node is first registered to the smart contract (SM) pre-deployed on the blockchain. Then, the swarm edge nodes perform a new training round, including downloading the global model and performing localized training. And then, all swarm edge nodes commit the local gradients to the SM through the swarm network. Finally, the SM aggregates all local gradients to create an updated model.

Suppose there are K parties $\{P_1,P_2,\dots ,P_K\}$ that constitute a collaborative group, in which each party $P_k$ holds its local dataset $D_k$ ($k=1,2,3,\dots ,K$). $D=\{D_1,D_2,\dots ,D_K\}$ denotes the joint dataset. Without disclosing their local sensitive data, K parties aim to cooperatively train a global general classifier $f(\mathbf{x};\mathbf{w})$ from the complete dataset D. As illustrated in Figure 1b, in tth iteration, the party $P_k$ downloads the global model ${\mathbf{w}}_{t-1}$ from the blockchain and trains the local model based on the local dataset $D_k$. Equation (1) describes the objective function optimized by training:

$$F({\mathbf{x}}_i,\mathbf{w},y_i)=\underset{\mathbf{w}}{min}{\mathbb{E}}_{({\mathbf{x}}_i,y_i)\backsim \tilde{D}}L(f({\mathbf{x}}_i;\mathbf{w}),y_i)$$

(1)

where $({\mathbf{x}}_i,y_i)$ is the training sample, $L(·,·)$ is the empirical error function, and $\tilde{D}$ is the training sample distribution. We adopt stochastic gradient descent (SGD) to solve this minimization problem. Using ${\mathbf{w}}_{t-1}$ and $D_k$, each party $P_k$ computes its local gradient $▿g_k\left({\mathbf{w}}_t\right)$ via Equation (2):

$$▿g_k\left({\mathbf{w}}_t\right)=\sum _{i=1}^{|D_k|}\frac{d}{d{\mathbf{w}}_t}L(f({\mathbf{x}}_i^k;{\mathbf{w}}_{t-1}),y_i^k)$$

(2)

Through the consensus mechanism, the winning party performs the model update operation with Equation (3):

$${\mathbf{w}}_t={\mathbf{w}}_{t-1}-\gamma \sum _{k=1}^K{\zeta }_i^j▿g_k\left({\mathbf{w}}_t\right)$$

(3)

where ${\zeta }_i^j=\frac{|D_j|}{\left|D\right|}$, ${\sum }_{j=1}^N{\zeta }_i^j=1$, and $\gamma$ is the local learning rate. Once the update operation is completed, the winning party then sends the updated results through transactions to all parties.

3.2. The CKKS Scheme

As a typical fully homomorphic encryption (FHE), the Cheon–Kim–Kim–Song (CKKS) scheme [34] is a cryptographic technique in which addition and multiplication operations on plaintext are equivalent to corresponding operations on cipher-text. With the unique encoding, decoding, and rescaling mechanisms, CKKS can encrypt float numbers and vectors. CKKS consists of the following functions:

(1)

Key Generation: $(sk,pk,evk)\leftarrow KeyGen\left(1^{\lambda }\right)$. This procedure generates a public key $pk$ for encryption, a corresponding secret key $sk$ for decryption, and a key $evk$ for evaluation.

(2)

Encoding: $m\leftarrow Ecd(\mathbf{z},s)$. Taking an $N/2$-dimensional vector $\mathbf{z}={\left(z_j\right)}_{j\in \mathcal{T}}$ and a scaling factor s as inputs, the procedure transforms $\mathbf{z}$ to a polynomial m by encoding, i.e., $m={\sigma }^{-1}\circ {\pi }^{-1}(\mathbf{z}·s)$, where ${\sigma }^{-1}$ and ${\pi }^{-1}$ are the inverses of $\sigma$ and $\pi$, respectively.

(3)

Encryption: $c\leftarrow Enc(m,pk)$. Taking the given polynomial $m\in \mathcal{R}$ and public key $pk$ as inputs, the procedure outputs the cipher-text $c\in {\mathcal{R}}_{q_{L^{\prime }}}^k$.

(4)

Addition: $\widehat{c}\leftarrow Add(c_1,c_2)$. Taking the cipher-texts $c_1$ and $c_2$ as inputs, the procedure outputs $\widehat{c}=c_1\oplus c_2$.

(5)

Multiplication: $\tilde{c}\leftarrow Mult(c_1,c_2,evk)$. Taking the cipher-texts $c_1$ and $c_2$ and the evaluation key $evk$ as inputs, the procedure outputs $\tilde{c}=c_1\otimes c_2\in {\mathcal{R}}_{q_l}^k$.

(6)

Rescaling: $c^{\prime }\leftarrow RS\left(c\right)$. Taking a cipher-text $c\in {\mathcal{R}}_{q_l}^k$ at level l as inputs, the procedure outputs the cipher-text $c^{\prime }\leftarrow \lfloor \frac{q_{l^{\prime }}}{q_l}c\rceil$ in ${\mathcal{R}}_{q_{l^{\prime }}}^k$, where $\lfloor x\rceil$ represents the integer closest to the real number x.

(7)

Decryption: $m\leftarrow Dec(c,sk)$. Taking the cipher-text c and the secret key $sk$ as inputs, the procedure outputs the polynomial m.

(8)

Decoding: $\mathbf{z}\leftarrow Dcd(m,s)$. Taking the plaintext polynomial $m\in \mathcal{R}$ as inputs, the procedure transforms $m\in \mathcal{R}$ into a vector $\mathbf{z}$ using $\mathbf{z}=\pi \circ \sigma (s^{-1}·m)$.

3.3. Threshold Fully Homomorphic Encryption

To construct distributed FHE, threshold fully homomorphic encryption (TFHE) [52] has been proposed, in which each participant has a share of a secret key corresponding to an FHE public key.

Let $P=\{P_1,\dots ,P_N\}$ be a set of parties. Threshold fully homomorphic encryption scheme (TFHE) is tuple of PPT algorithms $TFHE=(TFHE.Setup,TFHE.Encrypt,TFHE.Eval,TFHE.PartDec,TFHE.FinDec)$ satisfying the following specifications:

• $(pk,s{k}_1,\dots ,s{k}_N)\leftarrow TFHE.Setup(1^{\lambda },1^d,\mathbb{A})$: The algorithm inputs a security parameter $\lambda$, a circuit depth d, and an access structure $\mathbb{A}$, and outputs a public key $pk$, and secret key shares $s{k}_1,\dots ,s{k}_N$.
• $ct\leftarrow TFHE.Encrypt(pk,\mu )$: The algorithm inputs a public key $pk$ and a single-bit plaintext $\mu \in \{0,1\}$, and outputs a cipher-text $ct$.
• $\widehat{ct}\leftarrow TFHE.Eval(pk,C,c{t}_1,\dots ,c{t}_k)$: The algorithm inputs a public key $pk$, a boolean circuit $C:{\{0,1\}}^k\to \{0,1\}\in C_{\lambda }$ of $depth\le d$ and cipher-texts $c{t}_1,\dots ,c{t}_k$ encrypted under the same public key, and outputs an evaluation cipher-text $\widehat{ct}$.
• $p_i\leftarrow TFHE.PartDec(pk,ct,s{k}_i)$: The algorithm inputs a public key $pk$, a cipher-text $ct$ and a secret key share $s{k}_i$. and outputs a partial decryption $p_i$ related to the party $P_i$.
• $\widehat{\mu }\leftarrow TFHE.FinDec(pk,B)$: The algorithm inputs a public key $pk$, a set $B={\left\{p_i\right\}}_{i\in S}$ for some $S\subseteq \{P_1,\dots ,P_N\}$ where we recall that we identify a party $P_i$ with its index i, and deterministically outputs a plaintext $\widehat{\mu }\{0,1,\perp \}$.

And we construct $TFHE$ using the schemes, $FHE=(FHE.Setup,FHE.Encrypt,FHE.Eval,FHE.Decrypt)$ and $SS=(SS.Share,SS.Combine)$ as follows:

• $TFHE.Setup(1^{\lambda },1^d,{\mathbb{A}}_t)$: The algorithm inputs $\lambda$, d, and ${\mathbb{A}}_t\in TAS$, and generates $(fhepk,fhesk)\leftarrow FHE.Setup(1^{\lambda },1^d)$. Then, $fhesk$ is divided into shares using $(fhes{k}_1,\dots ,fhes{k}_N)\leftarrow SS.Share(fhesk,{\mathbb{A}}_t)$.
• $TFHE.Encrypt(pk,\mu )$: The algorithm inputs $pk$ and $\mu \in \{0,1\}$, computes $ct\leftarrow FHE.Encrypt(pk,\mu )$, and output $ct$.
• $TFHE.Eval(pk,C,c{t}_1,\dots ,c{t}_k)$: The algorithm inputs $pk$, C and $c{t}_1,\dots ,c{t}_k$, computes $\widehat{ct}\leftarrow FHE.Eval(C,c{t}_1,\dots ,c{t}_k)$, and outputs $\widehat{ct}$.
• $TFHE.PartDec(pk,ct,s{k}_i)$: The algorithm inputs $pk$, $ct$, and $s{k}_i\in {\mathbb{Z}}_q^n$, computes $p_i=FHE.Decod{e}_0(s{k}_i,ct)+{(N!)}^2·e\in {\mathbb{Z}}_p$, and outputs $p_i$.
• $TFHE.FinDec(pk,B)$: The algorithm inputs $pk$ and ${\left\{p_i\right\}}_{i\in S}$, and checks if $S\in \mathbb{A}$. If this is not the case, then it outputs ⊥. Otherwise, it arbitrarily chooses a satisfying set $S^{\prime }\subseteq S$ of size t and computes the Lagrange coefficients ${\lambda }_{i,0}^{S^{\prime }}$ for all $i\in S^{\prime }$. Then, it computes $\mu \leftarrow FHE.Decod{e}_1({\sum }_{i\in S^{\prime }}{\lambda }_{i,0}^{S^{\prime }})$, and outputs $\mu$.

4. Problem Statement

In this section, we formulate our system model, threat model, and design goals.

4.1. System Model

As shown in Figure 2, our PBSL includes three entities: trusted authorities ($\mathbf{TAs}$), medical centers ($\mathbf{MC}s$), and blockchain ($\mathbf{BC}$)-based peer-to-peer network. Each $\mathbf{MC}$ is equipped with a PC server, and $\mathbf{MC}$s are interconnected through blockchain ($\mathbf{BC}$)-based peer-to-peer networks. The three entities involved in the system are shown below.

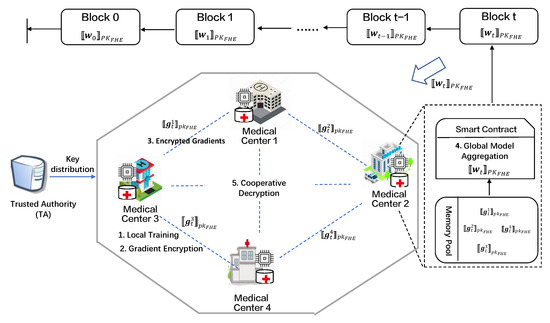
Figure 2. System model of PBSL.

• $\mathbf{TA}$ stands for Trusted Authority and is responsible for generating initial parameters and public/secret key pairs and distributing them to $\mathbf{MC}s$.
• $\mathbf{MC}s=\{{\mathbf{MC}}_1,{\mathbf{MC}}_2,\dots ,{\mathbf{MC}}_K\}$ represents K medical centers participating in swarm learning. In our system, each ${\mathbf{MC}}_k\in \mathbf{MC}s$ trains the model using its local medical dataset, encrypts the gradient, shares the encrypted gradient to the blockchain, and cooperatively trains with other $\mathbf{MC}s$ to achieve a more accurate global model.
• $\mathbf{BC}$ represents a blockchain platform made up of self-organizing networks of interconnected medical centers ($\mathbf{MC}s$). Every node (i.e., $\mathbf{MC}s$) on blockchain has the opportunity to aggregate the global model, so $\mathbf{BC}$ can replace a central aggregator. Smart contract (SC) deployed on the blockchain homomorphically aggregates the encrypted gradients to obtain the global collaboration model.

4.2. Threat Model

$\mathbf{TA}$ is a trusted third party. Considering the autonomy of $\mathbf{MC}s$ in swarm learning, we select the “curious-and-malicious” threat model, which is weaker than the “honest-and-curious” threat model. Specifically, curious $\mathbf{MC}s$ are honest in uploading true gradients trained on their local datasets, while attempting to obtain more information from gradients shared by other $\mathbf{MC}s$ stored on the blockchain, thus compromising users’ data privacy. In order to reduce the global model accuracy, malicious $\mathbf{MC}s$ can perform malicious operations or deliberately abandon local training. The potential threats to our PBSL are as follows:

• Privacy: Since local gradients contain $\mathbf{MC}s$’ private information, if the $\mathbf{MC}s$ directly upload the local gradients in plaintext, the adversaries can infer the private information of honest $\mathbf{MC}s$, which leads to data leakage of $\mathbf{MC}s$.
• Byzantine Attacks: Byzantine attack refers to the arbitrary behavior of the system participant who does not follow the designed protocol. For example, a Byzantine $\mathbf{MC}$ randomly sends a vector in place of the local gradient, or mistakenly aggregates the local gradient of all $\mathbf{MC}s$.
• Poisoning Attacks: Poison attack refers to various malicious behaviors launched by the $\mathbf{MC}s$. For example, an $\mathbf{MC}$ flips the label of the sample and uploads the toxic gradient.

4.3. Design Goals

Under the system and threat models mentioned above, aiming to design a privacy-preserving swarm learning (PBSL) scheme, the proposed scheme should provide confidentiality and privacy guarantees, resist Byzantine attacks, and reduce computational overheads. And our scheme should achieve the same precision as classical swarm learning (SL). Specifically, the following goals are achieved:

• Confidentiality: Guaranteeing the confidentiality of the global model stored in the blockchain. Specifically, after swarm learning, only $\mathbf{MC}s$ can access the global model stored in the blockchain.
• Privacy: Guaranteeing the privacy of each $\mathbf{MC}s$’ local sensitive information. Specifically, during swarm learning, every $\mathbf{MC}s$’ local training data cannot be leaked to other $\mathbf{MC}s$.
• Robustness: Detecting malicious $\mathbf{MC}s$ and discarding their local gradients during swarm learning. Specifically, a mechanism is constructed to identify malicious medical centers and discard their submitted local model gradients.
• Accuracy: While protecting data privacy and resisting malicious attacks, the model accuracy of PBSL training should be the same as that of the original SL training.
• Efficiency: Reducing the high computational and communication cost of encryption operations in a privacy-preserving SL scheme.
• Tolerance to $\mathbf{MC}$ drop-out: Guaranteeing the privacy and convergence even if up to D $\mathbf{MC}s$ are delayed or dropped.

5. Our Privacy-Preserving Swarm Learning

As shown in Figure 3, our PBSL described in this section mainly includes four stages: (I) system initialization, (II) local computation, (III) model aggregation, and (IV) global model decryption and updating.

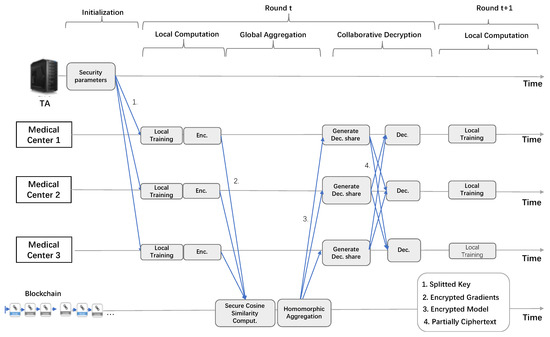
Figure 3. An overview of proposed PBSL.

Firstly, $\mathbf{TA}$ sets initialization parameters, generates key pairs $<s{k}_{FHE},p{k}_{FHE}>$, divides $s{k}_{FHE}$ into K shares through Shamir’s secret sharing, and distributes K shares to K $\mathbf{MC}s$, respectively.

Then, $\mathbf{MC}s$ train their model on its local dataset and encrypt their gradients by fully homomorphic encryption technology CKKS [34], which are broadcasted to the blockchain-based network.

Furthermore, the $\mathbf{MC}$ that wins the consensus mechanism uses a cosine similarity-based strategy to punish malicious gradient vectors, obtain the encrypted global model through homomorphically aggregating the encrypted local gradients, and stores the encrypted collaborative learning results on the blockchain.

Finally, $\mathbf{MC}s$ obtain the encrypted global models from the blockchain and cooperatively decrypt the encrypted global models to obtain the global models. We summarize PBSL in Algorithm 1, and illustrate the details of each process in the following. Table 2 lists the description of notations in our PBSL.

Algorithm 1: PBSL

Table 2. Summary of notations in PBSL.

Notation	Implications
K	the number of medical centers
m	the threshold of Sharmir secret sharing
${\mathbf{MC}}_1,\dots ,{\mathbf{MC}}_K$	a set of K medical centers
$p{k}_k^{psu},s{k}_k$	pseudo public key and secret key of medical center ${\mathbf{MC}}_k$
$\alpha$	the security parameter
$p{k}_{FHE},s{k}_{FHE}$	the keys of CKKS cryptosystem
$s{k}_{FHE}^k$	the distributed secret keys splited from $s{k}_{FHE}$
$ke{y}_{kl}$	the symmetric encryption key between medical center ${\mathbf{MC}}_k$ and ${\mathbf{MC}}_l$
$En{c}_{ke{y}_{kl}}(·),De{c}_{ke{y}_{kl}}(·)$	the symmetric key encryption or decryption algorithm using $ke{y}_{kl}$
${\mathbf{w}}_t$	the weight of the global model after the $t-1$-th iteration of training
${\left[[·]\right]}_{p{k}_{FHE}}$	the cipher-text generated by CKKS algorithm
v	the size of decryption set $DS$

5.1. System Initialization

5.1.1. Blockchain P2P Network Construction

$\mathbf{MC}s=\{{\mathbf{MC}}_1,{\mathbf{MC}}_2,\dots ,{\mathbf{MC}}_K\}$ form blockchain-based peer-to-peer network. $\mathbf{MC}s$ have pseudonymity, i.e., pseudo public keys $p{k}_1^{psu},p{k}_2^{psu},\dots ,p{s}_K^{psu}$, and their corresponding secret keys $s{k}_1,s{k}_2,\dots ,s{k}_K$ are privately kept, respectively.

5.1.2. Cryptosystem Initialization

Firstly, $\mathbf{TA}$ generates a key pair $<s{k}_{FHE},p{k}_{FHE}>\leftarrow KeyGen\left(1^{\lambda }\right)$. $\mathbf{TA}$ sets a security parameter $\lambda$, and chooses a power-of-two $M=m(\lambda ,q_L)$, an integer $h=h(\lambda ,q_L)$, an integer $P=P(\lambda ,q_L)$, and a real value $\sigma =\sigma (\lambda ,q_L)$. Then, $\mathbf{TA}$ samples $s\leftarrow \mathcal{HWT}\left(h\right)$, $a\leftarrow {\mathcal{R}}_{q_L}$, and $e\leftarrow \mathcal{DG}\left({\sigma }^2\right)$, where $\mathcal{HWT}\left(h\right)$ is the set of signed binary vectors whose Hamming weight is exactly h and $\mathcal{DG}\left({\sigma }^2\right)$ samples a vector in ${\mathbb{Z}}^N$ by drawing its coefficient independently from the discrete Gaussian distribution of variance ${\sigma }^2$. The private key is set as $s{k}_{FHE}\leftarrow (1,s)$ and the public key as $p{k}_{FHE}\leftarrow (b,a)\in {\mathcal{R}}_{q_L}^2$ where $b\leftarrow -as+e\left(mod{q}_L\right)$.

Secondly, $\mathbf{TA}$ randomly divides $s{k}_{FHE}$ into K parts. $\mathbf{TA}$ computes $\delta =\eta ·\lambda$, s.t., $\eta ·\lambda \equiv 1mod{N}^2$, sets a threshold m, s.t., $(m-1)\le N$, and defines a polynomial function of secret sharing protocol $f\left(x\right)=\lambda +{\sum }_{i=1}^m{a}_i{x}^i$, where $a_1,a_2,\dots ,a_{m-1}{\in }_R{\mathbb{Z}}_{\lambda }^{*}$. $\mathbf{TA}$ divides $s{k}_{FHE}$ into K parts through calculating $f\left(i\right)$. $\mathbf{TA}$ broadcasts $<g,p{k}_{FHE},\eta >$ to all $\mathbf{MC}s$ through blockchain-based network.

Finally, each ${\mathbf{MC}}_k\in \mathbf{MC}$ asks $\mathbf{TA}$ for its own private key $s{k}_{FHE}^k=f\left(k\right)$.

5.1.3. Registration

To participate in swarm learning, ${\mathbf{MC}}_k\in \mathbf{MC}s$ need to register to smart contract (SC) published on the blockchain, which specifies the entire deep learning task. Each ${\mathbf{MC}}_k$ constructs a zero-knowledge proof $proo{f}_{s{k}_k}$ of its private key $s{k}_k$. The $proo{f}_{s{k}_k}$ is defined as $<c,r>$, where $v{\in }_R{\mathbb{Z}}_q$, $t=g^v$, $c=H(g,p{k}_k^{psu},t)$, and $r=(v-c·s{k}_k)modq$. Then, ${\mathbf{MC}}_k$ submits “Registration” transaction $<p{k}_k^{psu},proo{f}_{s{k}_k}>$ to the blockchain. And then, each ${\mathbf{MC}}_k$ on the blockchain verifies $proo{f}_{s{k}_k}$, i.e., $proo{f}_{s{k}_k}\stackrel{?}{=}H(g,p{k}_k^{psu},g^r{\left(p{k}_k^{psu}\right)}^c)$ to prevent an adversary from registering itself with $p{k}_k^{psu}$ copied from an honest ${\mathbf{MC}}_l$. If the verification is passed, ${\mathbf{MC}}_k$ is registered as a member of the learning group and stores its $p{k}_k^{psu}$ to the blockchain.

And in order to protect public broadcast channels, we can construct the symmetric encryption key $ke{y}_{kl}={\left(p{k}_k^{psu}\right)}^{s{k}_l}={\left(p{k}_l^{psu}\right)}^{s{k}_k}$ and use the symmetric key encryption algorithm $En{c}_{ke{y}_{kl}}(·)$ to encrypt the traffic data between ${\mathbf{MC}}_k$ and ${\mathbf{MC}}_l$.

5.1.4. Parameter Initialization

In order to initialize the system parameters, a randomly selected ${\mathbf{MC}}_l$ sets the initial parameters $\mathbf{p}=(\eta ,b,{\mathbf{w}}_0)$, where $\eta$ is the learning rate, b is batch size, and ${\mathbf{w}}_0$ is initial model parameters. Then, ${\mathbf{MC}}_l$ broadcasts the encrypted parameters $\overline{{\mathbf{p}}_{l\to k}}=En{c}_{ke{y}_{lk}}\left(\mathbf{p}\right)$ to all other ${\mathbf{MC}}_k$ ($k\ne l$). Upon receiving $\overline{{\mathbf{p}}_{l\to k}}$ from ${\mathbf{MC}}_l$, ${\mathbf{MC}}_k$ decrypts $\overline{{\mathbf{p}}_{l\to k}}$ to obtain $\mathbf{p}=De{c}_{ke{y}_{lk}}\left(\overline{{\mathbf{p}}_{l\to k}}\right)$. Finally, all $\mathbf{MC}s$ obtained uniform initial parameters $\mathbf{p}$.

5.2. Local Computation

Algorithm 2 describes the procedure of $\mathbf{Local}\_\mathbf{Computation}$ in detail. In a local computation procedure, there are four parts: local model training, normalization, encryption, and sharing. The four parts are described in detail below.

5.2.1. Local Model Training

In the tth iteration, each ${\mathbf{MC}}_k$ obtains the encrypted global model ${\left[\left[{\mathbf{w}}_{t-1}\right]\right]}_{p{k}_{FHE}}$ from the latest block $B_{t-1}$ on the blockchain. Then, each ${\mathbf{MC}}_k$ calls $\mathbf{Collab}\_\mathbf{Decryption}(·)$ to obtain the local model ${\mathbf{w}}_{t-1}$. Finally, using $D_k$ and ${\mathbf{w}}_{t-1}^k$, each MC computes the local gradient ${\mathbf{g}}_t^k$, as shown in Equation (4):

$${\mathbf{g}}_t^k=▿L({\mathbf{w}}_{t-1}^k,D_k)$$

(4)

where $L({\mathbf{w}}_{t-1}^k,D_k)$ represents the experical loss function and ▿ represents the derivation operation.

Algorithm 2: Local_Computation

5.2.2. Normalization

In order to directly apply our cosine-similarity-based aggregation rule to cipher-text and mitigate the effects of malicious gradients with a larger magnitudes, these local gradients ${\left\{{\mathbf{g}}_t^k\right\}}_{k=1}^K$ need to be normalized. For each ${\mathbf{MC}}_k$, we use Equation (5) to normalize the local gradients ${\mathbf{g}}_t^k$:

$${\tilde{\mathbf{g}}}_t^k=\frac{{\mathbf{g}}_t^k}{|{\mathbf{g}}_t^k|}$$

(5)

where ${\tilde{\mathbf{g}}}_t^k$ is the unit vector.

5.2.3. Encryption

To ensure the confidentiality of local model updates, as shown in Algorithm 3, each ${\mathbf{MC}}_k$ encrypts ${\tilde{\mathbf{g}}}_t^k$ using $p{k}_{FHE}$. Because gradients are signed the floating-point vector, gradients are encrypted using the CKKS scheme [34] instead of the Paillir scheme [53] with high computation overheads. ${\tilde{\mathbf{g}}}_t^k$ is treated as vectors and encrypted using $p{k}_{FHE}$.

Algorithm 3: Global_Aggregation

5.2.4. Message Encapsulation and Sharing

Each ${\mathbf{MC}}_k$ encapsulates $p{k}_k^{psu}$, ${\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{pk}$, and timestamp t into the following message:

$${\mathbb{M}}_t^k=(p{k}_k^{psu},{\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{pk},t)$$

(6)

and broadcasts ${\mathbb{M}}_t^k$ to other $\mathbf{MC}s$.

5.3. Global Aggregation

5.3.1. PoW Competition

In order to compete for the right to append blocks to the blockchain, all $\mathbf{MC}s$ that make up the blockchain execute any consensus algorithm (e.g., PoW). The only winner ${\mathbf{MC}}_j$ has the right to construct a block and add it to the blockchain.

5.3.2. Homomorphic Aggregation

In the tth iteration, the winner ${\mathbf{MC}}_j$ is responsible for aggregating all the encrypted gradients stored in the memory pool. ${\mathbf{MC}}_j$ decodes $\{{\mathbb{M}}_t^1,{\mathbb{M}}_t^2,\dots ,{\mathbb{M}}_t^K\}$ and homomorphically aggregates encrypted gradients to generate the encrypted global model ${\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}$ without the need for decryption by the following equation:

$${\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}=\frac{1}{K}\sum _{k=1}^K{\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}$$

(7)

5.3.3. Secure Cosine Similarity Computation

Then, we compute the cosine similarity $c{s}_t^k$ between two gradients ${\tilde{\mathbf{g}}}_t=[p_1,p_2,\dots ,p_n]$ and ${\tilde{\mathbf{g}}}_t^k=[q_1,q_2,\dots ,q_n]$. And the encrypted gradients ${\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}$ and ${\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}$ are obtained as ${\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}=En{c}_{p{k}_{FHE}}\left([p_1,p_2,\dots ,p_n]\right)$ and ${\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}=En{c}_{p{k}_{FHE}}\left([q_1,q_2,\dots ,q_n]\right)$. The encrypted cosine similarity ${\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}$ between ${\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}$ and ${\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}$ can be transformed to the inner product, which is described as follows:

$$\begin{array}{cc}\hfill {\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}& ={\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}\odot {\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}\hfill \\ \hfill & ={\left[[p_1{q}_1+p_2{q}_2+\dots +p_n{q}_n]\right]}_{p{k}_{FHE}}\hfill \end{array}$$

If $c{s}_t^k<0$, it means that the angle between ${\tilde{\mathbf{g}}}_t^k$ and ${\tilde{\mathbf{g}}}_t$ is greater than ${90}^{°}$, that is, ${\tilde{\mathbf{g}}}_t^k$ has a negative impact on ${\tilde{\mathbf{g}}}_t$. The trust score $S_t^k$ of ${\mathbf{MC}}_j$ is defined by Equation (7) to punish the malicious gradients

$$S_t^k=ReLU\left(c{s}_t^k\right)$$

(8)

Equation (8) gives the definition of the $ReLU$ function.

$$ReLU\left(a\right)=\left\{\begin{array}{cc}a,\hfill & \mathrm{if}a>0\hfill \\ 0,\hfill & \mathrm{if}a\le 0\hfill \end{array}\right.$$

According to the previous work [54], the cipher-text homomorphism operation of $ReLU$ function is given below:

$$\begin{array}{cc}\hfill & {{\left[\left[S_t^k\right]\right]}^{\prime }}_{p{k}_{FHE}}=ReL{U}^{\prime }\left({\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}\frac{1}{2}({\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}+{\left[\left[1\right]\right]}_{p{k}_{FHE}}),\hfill & \\ \mathrm{if}\frac{1}{2}({\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}+{\left[\left[1\right]\right]}_{p{k}_{FHE}})>{\left[\left[\frac{1}{2}\right]\right]}_{p{k}_{FHE}}\hfill \\ \left[\right[\frac{1}{2}]{]}_{p{k}_{FHE}},\hfill & \\ \mathrm{if}\frac{1}{2}({\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}+{\left[\left[1\right]\right]}_{p{k}_{FHE}})\le {\left[\left[\frac{1}{2}\right]\right]}_{p{k}_{FHE}}\hfill \end{array}\right.\hfill \end{array}$$

To compare the cipher-text of $\frac{1}{2}({\left[\left[c{s}_t^k\right]\right]}_{p{k}_{FHE}}+{\left[\left[1\right]\right]}_{p{k}_{FHE}})$ and ${\left[\left[\frac{1}{2}\right]\right]}_{p{k}_{FHE}}$, the numerical method for the comparison of homomorphic ciphers in the range of $[0,1]$ is called [54]. The encrypted score ${\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}$ is set by

$${\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}=2·{{\left[\left[S_t^k\right]\right]}^{\prime }}_{p{k}_{FHE}}-{\left[\left[1\right]\right]}_{p{k}_{FHE}}$$

(9)

5.3.4. Model Aggregation and Updating

In the tth epoch, the winner ${\mathbf{MC}}_j$ homomorphically aggregates the local gradients weighted by their trust score according to the following equation:

$$\begin{array}{cc}\hfill & {\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}=\frac{{\sum }_{k=1}^K{\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}·{\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}}{{\sum }_{k=1}^K{\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}}\hfill \\ \hfill & =\frac{{\sum }_{k=1}^{K}ReLU({\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}\odot {\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}})·{\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}}{{\sum }_{k=1}^K{\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}}\hfill \end{array}$$

and subsequently updates the global model:

$${\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}}={\left[\left[{\mathbf{w}}_{t-1}\right]\right]}_{p{k}_{FHE}}-\gamma {\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}$$

(10)

5.3.5. Construction of New Block

${\mathbf{MC}}_k$ constructs the new block $B_t$ that contains the following:

$$B_t=({\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}},[{\mathbb{M}}_t^1,{\mathbb{M}}_t^2,\dots ,{\mathbb{M}}_t^K])$$

(11)

and appends $B_t$ to the blockchain.

5.4. Collaborative Global Model Decryption

As described in Algorithm 4, each ${\mathbf{MC}}_k$ downloads the generated block $B_t$ from the blockchain. ${\mathbf{MC}}_k$ executes the partial decryption algorithm to obtain ${\mathbf{w}}_t^k$, i.e.,

$${\mathbf{w}}_t^k={\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}}·s{k}_{FHE}^k$$

(12)

Then, each device ${\mathbf{MC}}_k$ broadcasts the encrypted

$$\overline{{\left({\mathbf{w}}_t^k\right)}_{k\to j}}=En{c}_{ke{y}_{kj}}\left({\mathbf{w}}_t^k\right)$$

(13)

for other ${\mathbf{MC}}_j$ ($j\ne k$). And then, upon receiving $\overline{{\left({\mathbf{w}}_t^k\right)}_{k\to j}}$ from ${\mathbf{MC}}_k$, ${\mathbf{MC}}_j$ computes ${\mathbf{w}}_t^k=De{c}_{k_{ij}}\left(\overline{{\left({\mathbf{w}}_t^k\right)}_{k\to j}}\right)$. Furthermore, ${\mathbf{MC}}_j$ randomly selects v $(v\ge m)$ numbers from the set $\{1,2,\dots ,K\}$ to form a decryption set $DS$. Finally, ${\mathbf{MC}}_j$ executes the final decryption algorithm to obtain ${\mathbf{w}}_t$, i.e.,

$${\mathbf{w}}_t=\sum _{k\in DS}{\lambda }_k{\mathbf{w}}_t^k$$

(14)

where ${\lambda }_k$ ($k\in DS$) is the Lagrange coefficient.

Algorithm 4: Collab_Decryption

6. Security Analysis of PBSL

In this section, we review our security requirements of PBSL, described in Section 2, and analyze the security of PBSL.

6.1. Privacy and Confidentiality

Theorem 1.

PBSL can achieve the privacy of local model gradient ${\mathbf{g}}_t^k$ and the confidentiality of global model ${\mathbf{w}}_t$.

Proof. 

We show that ${\mathbf{g}}_t^k$ and ${\mathbf{w}}_t$ are able to be guaranteed at different stages of swarm learning.

• In the stage of local computation, ${\mathbf{g}}_t^k$ is encrypted with $p{k}_{FHE}$, i.e.,

  $${\left[\left[{\mathbf{g}}_t^k\right]\right]}_{p{k}_{FHE}}=Enc({\mathbf{g}}_t^k,p{k}_{FHE})$$

  (15)

  where $t=\{1,2,\dots ,T\}$ and $k=\{1,2,\dots ,K\}$, and $TA$ splits $s{k}_{FHE}$ into K distributed secret keys $s{k}_{FHE}^1,s{k}_{FHE}^2,\dots ,s{k}_{FHE}^K$ for $\mathbf{MC}s$. Because any ${\mathbf{MC}}_k$ with only a single $s{k}_{FHE}^k$ cannot decrypt ${\left[\left[{\mathbf{g}}_t^k\right]\right]}_{p{k}_{FHE}}$, PBSL can protect the privacy of ${\mathbf{g}}_t^k$ at this stage.
• At the stage of global model aggregation, the winning ${\mathbf{MC}}_k$ homomorphically aggregates ${\left\{{\left[\left[{\mathbf{g}}_t^k\right]\right]}_{p{k}_{FHE}}\right\}}_{k=1,2,\dots ,K}$ to generate ${\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}$, then homomorphically calculates ${\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}$ by ${\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}=2·ReLU({\left[\left[{\tilde{\mathbf{g}}}_t\right]\right]}_{p{k}_{FHE}}\odot {\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}{)}^{\prime }-{\left[\left[1\right]\right]}_{p{k}_{FHE}}$, and updates

  $${\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}}={\left[\left[{\mathbf{w}}_{t-1}\right]\right]}_{p{k}_{FHE}}-\gamma \frac{{\sum }_{k=1}^K{\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}·{\left[\left[{\tilde{\mathbf{g}}}_t^k\right]\right]}_{p{k}_{FHE}}}{{\sum }_{k=1}^K{\left[\left[S_t^k\right]\right]}_{p{k}_{FHE}}}$$

  (16)
  The whole process is performed on cipher-text. And ${\mathbf{MC}}_k$ with only a single $s{k}_{FHE}^k$ cannot decrypt ${\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}}$. Therefore, PBSL can protect the confidentiality of ${\mathbf{w}}_t$ in the stage.
• At the stage of collaborative global model decryption, all $\mathbf{MC}s$ decrypt the ${\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}}$ distributedly, and each ${\mathbf{MC}}_k$ shares its partially decryption result ${\mathbf{w}}_t^k$. Because any ${\mathbf{MC}}_k$ with only a single $s{k}_{FHE}^k$ cannot decrypt ${\left[\left[{\mathbf{w}}_t\right]\right]}_{p{k}_{FHE}}$, PBSL can protect the privacy of ${\mathbf{w}}_t$ in the stage.

□

6.2. Byzantine-Robust

Theorem 2.

For an arbitrary number of malicious $\mathbf{MC}s$, in the $t$ iteration, the loss between the learned model ${\mathbf{w}}_t$ and the optimal model $\widehat{\mathbf{w}}$ under no attacks is bounded, i.e.,

$$\left|\right|{\mathbf{w}}_t-\widehat{\mathbf{w}}\left|\right|\le {(1-\rho )}^t\left|\right|{\mathbf{w}}^0-\widehat{\mathbf{w}}\left|\right|+12\beta {\Delta }_1\rho +error$$

(17)

with probability at least $1-\delta$, where $error$ is caused by CKKS.

Proof. 

Our PBSL improves the encryption algorithm of FLTrust [55] and extends FLTrust to blockchain, so we directly apply FLTrust’s security analysis to PBSL. According to FLTrust, in our PBSL, the loss between the learned model ${\mathbf{w}}_t$ in the $t$ iteration and the optimal model $\widehat{\mathbf{w}}$ is

$$\left|\right|{\mathbf{w}}_t-\widehat{\mathbf{w}}\left|\right|\le {(1-\rho )}^t\left|\right|{\mathbf{w}}^0-\widehat{\mathbf{w}}\left|\right|+12\beta {\Delta }_1\rho +error$$

(18)

with probability at least $1-\delta$, where $error$ is caused by CKKS. As described in CKKS [34], Equation (19) gives the bound of the encoding and encryption errors.

$$B=8\sqrt{2}\sigma N+6\sigma \sqrt{N}+16\sigma \sqrt{hN}$$

(19)

Therefore, $error$ generated by the cipher-text operation of our PBSL can be expressed as follows:

$$error=B+B_1+B_2+v_1{B}_2+v_2{B}_1+B_1{B}_2+B_{mult\left(l\right)}$$

(20)

where $error$ from ⊕ is $B_1+B_2$, $error$ from ⊗ is $v_1{B}_2+v_2{B}_1+B_1{B}_2+B_{mult\left(l\right)}$, $B_{mult\left(l\right)}=P^{-1}·q_l·B_{ks}+B_{scale}$, $B_{ks}=8\sigma N/\sqrt{3}$, $P=P(\lambda ,q_{L^{\prime }})$, and $B_{scale}=\sqrt{N/3}·(3+8\sqrt{h})$. Then, when $|1-\rho |<1$, we have $li{m}_{t\to \infty }\left|\right|{\mathbf{w}}_t-{\mathbf{w}}^{*}\left|\right|\le 12\beta {\Delta }_1/\rho +error$. □

Therefore, the loss between the learned model ${\mathbf{w}}_t$ and the optimal model $\widehat{\mathbf{w}}$ is bounded.

7. Evaluation

In this section, we evaluate our scheme and present the experimental results to analyze the performance of our PBSL from two perspectives: defense effectiveness against attacks, and resource overhead in terms of computation.

7.1. Experimental Setup

7.1.1. Experimental Environment

Implementation Settings: In order to evaluate the integrated performance, we implement the PBSL scheme on a private Ethereum blockchain setup with real medical datasets. In our experiment, smart contract performs secure a global gradient aggregation algorithm instead of the centralized server.

• A blockchain system uses Ethereum, a blockchain-based smart contracts platform [56,57,58]. Smart contracts developed in the Solidity programming language are deployed to private blockchains using Truffle v5.10And Ethereum is deployed on a desktop computer with 3.3 GHz Intel(R) Xeon(R) CPU, 16 GB memory, and Windows 10.
• CKKS Scheme is deployed using the TenSEAL library, which is a library for carrying out homomorphic encryption operations on tensors, and its code is available on Github (https://github.com/OpenMined/TenSEAL, accessed on 9 June 2024).

Dataset: Our PBSL scheme was evaluated using two widely used datasets, the MNIST dataset and the FashionMNIST dataset.

• MNIST dataset consists of handwritten digital pictures of 250 different people. Every sample is a black and white image with $28\times 28$ pixels. The dataset is divided into a training set with 60,000 samples and a test set with 10,000 samples. We distributed the entire dataset evenly across 10 $\mathbf{MC}s$.
• FashionMNIST dataset constitutes images in 10 categories. The whole dataset contains 60,000 samples (50,000 for training and 10,000 for testing). The dataset was also evenly distributed to 10 $\mathbf{MC}s$.

7.1.2. Byzantine Attacks

In our experiments, the following Byzantine attacks were considered:

• Label Flipping Attack: By changing the label of the training sample to another category, the label flipping attacker misleads the classifier. To simulate this attack, the labels of the samples on each malicious ${\mathbf{MC}}_k$ are modified from l to $N-l-1$, where N is the total number of labels and $l\in \{0,1,\dots ,N-1\}$.
• Backdoor Attack: Backdoor attackers force classifiers to make bad decisions about samples with specific characteristics. To simulate the attack, we choose $6\times 6$ pixels as the trigger, and randomly select a number of training images on each malicious $\mathbf{MC}s$, and overwrite the $6\times 6$ pixels at the top left of each selected images. Then, we reset the labels of all the selected images to the target class.
• Arbitrary Model Attack: The model attacker arbitrarily tampers with some of the local model parameters. To reproduce the arbitrary model attack, malicious ${\mathbf{MC}}_k$ select a random number as its jth local model parameter.
• Untargeted Model Poisoning: The model attacker constructs the toxic local model that is similar to benign local models but causes the correct global gradient to reverse, or is much bigger (or smaller) than the maximum (or minimum) benign local models.

7.1.3. Evaluation Metrics

To verify that our PSDL scheme improves model accuracy, we use test accuracy and test error rate as evaluation measures on different training datasets. In the case of different numbers of malicious $\mathbf{MC}s$, the results of our PBSL scheme were verified by using the no-attack FedSGD scheme [38] as the baseline, and the Krum scheme [16], Bulyan [16], Trim-mean [39] as the control.

7.1.4. SL Settings

In our experiment, the total number K of $\mathbf{MC}s$ is set to 10, and all $\mathbf{MC}s$ are selected in each iteration during training. And we selected the models derived from convolutional neural networks (CNNs) with structure: $Input\to Conv\to FC\to Output$, to train three different datasets using Python, Numpy, and Tensorflow. Then, the training data are evenly distributed to each $\mathbf{MC}$, i.e., for both MNIST and FashionMNIST datasets, the size of each local dataset is 6000. We considered the proportion of different malicious $\mathbf{MC}s$ from $10\%$ to $50\%$. Our PBSL scheme is compared with SL and Krum. And the batch size b is set as 128.

7.2. Experimental Results

To demonstrate that the PBSL scheme meets our goals of accuracy, robustness, privacy, efficiency, and reliability, we conduct the following experiments. The experimental results show that PBSL can achieve the expected goals, which are discussed below.

7.2.1. Experimental Results on Defense Performance

Impact of Number of $\mathbf{MC}s$: The test accuracy was measured by increasing the number of $\mathbf{MC}s$ involved in collaborative training. The experiments were run with different numbers of $\mathbf{MC}s$ from 1 to 10. Figure 4 shows that the more $\mathbf{MC}s$ participate, the higher the training accuracy.

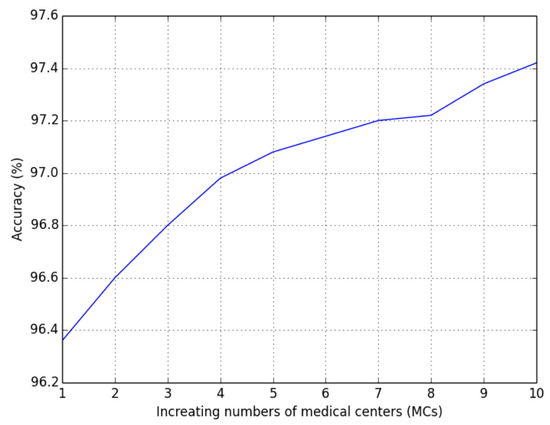
Figure 4. The impact of the number of $\mathbf{MC}s$.

Impact of Different Proportions of Malicious $\mathbf{MC}s$: To check the robustness of our PBSL scheme, we evaluate the accuracy loss caused by the ratio change in malicious $\mathbf{MC}s$. Figure 5 and Figure 6 show the results of PBSL training on two different datasets in the presence of different proportions of malicious $\mathbf{MC}s$. The experiment shows that the proposed basic scheme is reasonable and robust.

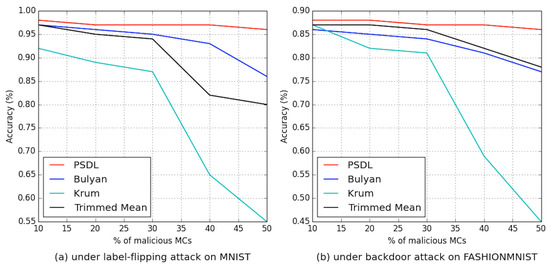
Figure 5. Comparison of accuracy with different numbers of malicious $\mathbf{MC}s$ under different attacks on different datasets.

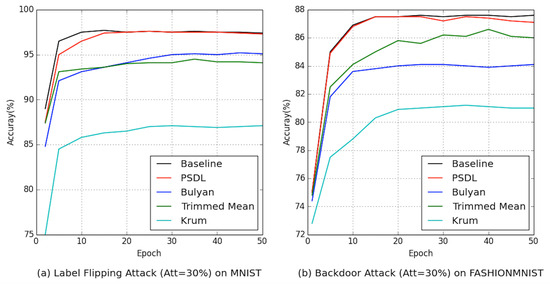
Figure 6. Comparison of accuracy with different epochs under different attacks on different datasets.

Impact of different attacks: To prove Byzantine robustness against different typical Byzantine attacks, we performed targeted attacks and untargeted attacks to our PBSL scheme. Table 3 shows the training results on MNIST and FashionMNIST datasets in the presence of different proportions of malicious $MCs$ under targeted and untargeted attacks. The results show that PBSL still keeps the same accuracy as baseline for different typical attacks, achieving the goal of robustness and accuracy.

Table 3. Accuracy of PBSL and Bulyan with different numbers of malicious MCs under untargeted attack and targeted attack on different datasets.

Dataset	Scheme (Attacks)	% of Malicious MCs
		10%	20%	30%	40%	50%
MNIST	PBSL (Untargeted)	$98.0$	$98.0$	$97.0$	$97.0$	$96.0$
	Bulyan (Untargeted)	$97.0$	$95.0$	$94.0$	$80.0$	$58.0$
	PBSL (Targeted)	$98.0$	$97.0$	$97.0$	$97.0$	$96.0$
	Bulyan (Targeted)	$97.0$	$96.0$	$94.0$	$84.0$	$78.0$
FashionMNIST	PBSL (Untargeted)	$87.0$	$87.0$	$86.0$	$85.0$	$85.0$
	Bulyan (Untargeted)	$85.0$	$84.0$	$83.0$	$79.0$	$54.0$
	PBSL (Targeted)	$88.0$	$88.0$	$87.0$	$87.0$	$86.0$
	Bulyan (Targeted)	$87.0$	$87.0$	$85.0$	$80.0$	$72.0$

7.2.2. Efficiency Comparison with Related FL Approaches

Comparison of PBSL with alternative privacy protection schemes. In the PBSL scheme, all operations, including similarity calculations and model aggregation, are computed in cipher-text. No participant can recover the original plaintext of the $\mathbf{MC}s$’ from the cipher-text. Therefore, the PBSL scheme meets the $\mathbf{MC}s$’ requirements for data privacy. To verify the efficiency of PBSL, using the Paillier-based federated learning scheme, i.e., PEFL [41], as a benchmark, we evaluated PBSL and BatchCrypt, where BatchCrypt [33] is a federated learning scheme based on HE. For each $\mathbf{MC}$, we use the time required for encryption and decryption of each iteration as a criterion. As shown in Figure 7, PBSL greatly improves computational efficiency and reduces computational costs compared to baseline and BatchCrypt. PBSL adopts a novel encryption scheme, i.e., CKKS [34], which has its unique advantages in encrypting large-scale floating-point vectors and network models with many parameters.

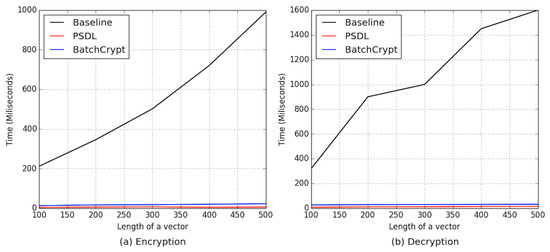
Figure 7. Comparison of the cost time of encryption and decryption in baseline, BatchCrypt, and PBSL.

Comparison of PBSL with alternative blockchain-based schemes.Table 4 compares the model accuracy and mining overhead on the FashionMNIST dataset between LearningChain in [59], BCFL [45], and PBSL, where $\alpha$ denotes training time per iteration and $\beta$ denotes mining time per block. First, we observe that the proposed PBSL achieves the highest model accuracy, compared with LearningChain and BCFL. This is because the privacy protection of PBSL uses fully homomorphic encryption (FHE) instead of differential privacy, which improves the accuracy of the model. Second, the mining overhead of PBSL is less than that of LearningChain but more than that of BCFL. This is due to the fact that LearningChain defends against Byzantine attacks at the cost of resource consumption for mining, while BCFL reduces the mining overhead at the expense of model robustness.

Table 4. Comparison of accuracy and mining overhead on FashionMNIST dataset.

$(\mathit{\alpha },\mathit{\beta })$	LearningChain		BCFL		PBSL
	Accuracy	Overhead	Accuracy	Overhead	Accuracy	Overhead
$(1,10)$	$73.3\%$	100	$76.5\%$	70	$86.3\%$	90
$(1,8)$	$72.8\%$	94	$75.7\%$	70	$85.2\%$	84
$(1,6)$	$76.4\%$	98	$77.5\%$	74	$87.4\%$	88
$(2,10)$	$67.9\%$	90	$72.2\%$	52	$82.1\%$	80
$(5,10)$	$51.8\%$	70	$56.5\%$	46	$74.2\%$	60

And the model aggregation is implemented as functions of smart contract, and the computational cost of a function in a smart contract is assessed in gas units. Therefore, we measure the computational consumption of PBSL in gas. Using the CNN model, gas costs are tested in each iteration with 10 $\mathbf{MC}s$. After all the $\mathbf{MC}s$ have submitted their local updates in cipher-text, SC obtains the global gradient at $30,500,242$ gas per transaction by homomorphically aggregating all local updates.

8. Conclusions

In the article, we review the shortcomings of swarm learning (SL) and further propose a new privacy-protection Byzantine-resilient swarm learning for e-heath, called PBSL, which ensures the privacy of local gradient and the tolerance toward Byzantine attacks. With the CKKS cryptosystem based on threshold decryption and decentralized computing based on blockchain, each $\mathbf{MC}$ can safely aggregate other $\mathbf{MC}s$’ gradients to generate a more accurate global model, while the confidentiality of the final global model can be ensured. And in the process of global model aggregation, our proposed Byzantine-robust aggregation method uses secure cosine similarity to punish malicious $\mathbf{MC}s$. Detailed security analysis and extensive experiments show that PBSL has privacy protection capability and efficiency.

In this paper, our attack detection strategy is based on cosine similarity between the local model gradient and the global model gradient. In future work, in order to prevent new attack vectors, we will continue to study new attack detection strategies that are suitable for blockchain platforms and take into account privacy protection, so as to deal with unforeseen threats in future-proofing systems.