Thermal Analysis and Junction Temperature Estimation under Different Ambient Temperatures Considering Convection Thermal Coupling between Power Devices

Abstract

The convection thermal coupling between adjacent power devices in power converters is dependent on the ambient temperature. When the ambient temperature changes, the convection thermal coupling also changes. This results in an inaccurate thermal model that causes errors in the prediction of the thermal distribution and junction temperature based on a fixed ambient temperature for power devices in converters application. To solve this variable-ambient-temperature-related issue, a thermal coupling experiment for semiconductor power devices (the MOSFET and diode) was performed to discuss the influence of the thermal coupling effect between adjacent devices and the FEM (Finite Element Method) thermal models for the power devices considering the convection thermal coupling are established. Through these simulations, the junction temperatures of devices under different ambient temperatures were obtained, and the relationships between the junction temperature and ambient temperatures were established. Moreover, the junction temperatures of power devices under different ambient temperatures were calculated and temperature distributions are analyzed in this paper. This method shows a strong significance and has potential applications for high-efficiency and high-power density converter designs.

1. Introduction

1.1. Literature Review

The existing thermal analysis models [1,2] are often based on fixed ambient temperature values, such as 25 °C or 30 °C [3,4]. However, the ambient temperature is widely variable [5,6]. Different ambient temperatures have different effects on the convection thermal coupling between power devices [7,8]. Meanwhile, the convection thermal coupling also changes the temperature distribution and junction temperature of devices [9,10]. When the ambient temperature changes, the traditional thermal analysis models for power devices may cause errors to calculate the temperature distribution and junction temperature prediction [11,12].

The calculation formula of junction temperature is derived in [3] which considers the conduction thermal coupling effect while the derivation is based on a fixed ambient temperature and the analysis is based on the ideal air region. Here the parameters and ambient temperature are considered independent of the temperature, while the ambient temperatures are not constant, and the parameters are ambient temperature dependent.

The short-term and long-term electro-thermal models are analyzed in [6], and the long-term one is considered to be affected by the ambient temperature. Moreover, the junction and case temperatures of power devices can be estimated by these models. The device model estimates the voltage drop and switching energy of the device by considering the device current, the blocking voltage of the off state and the junction temperature change. The thermal models consider the conduction thermal coupling between MOSFETs and diodes integrated with the same package and the effect of the junction temperature of devices at the ambient temperatures of 25 °C and 30 °C. In this reference, it is pointed out that different ambient temperatures have different influences on the thermal coupling and the junction temperature, while only two ambient temperature points are considered, and the mentioned thermal model is only for one power device.

In [13], the dynamic ambient profile is analyzed, and a thermal analysis model based on the profile is established, while the thermal coupling effect among power devices in the system is not considered [14]. In the electrical grid network where the power devices are commonly located in the outdoor environment and the ambient temperature is not constant as discussed in [15].

The self-thermal resistance (case-to-ambient thermal resistance, R_ca) of the power devices, the measured values of R_ca in the datasheet in [16] show that the value will vary from the range of 190 °C/W to 310 °C/W [17] when the devices packaged with SO-8 with different forms of a substrate (P-DSO-14-4 and P-TO252-3-1) insulate. Meanwhile, the manufacturer, Infineon, has provided the variation curves for the junction-to-ambient thermal resistance (R_ja) packaged under the two conditions of natural convection and forced air cooling, which indicates that the R_ca is variable and the values depend on the package, working conditions and the boundary conditions.

Therefore, different ambient temperatures analysis will help the thermal coupling between power devices be better well-analyzed which can decrease the erroneous junction temperature calculation [18,19,20] and a better understanding of the ambient which is one of the important factors of the thermal coupling calculation can assist the practical design guidelines for impact power converters.

1.2. Main Contributions

The major contributions of this paper are as follows: thermal coupling experiment for semiconductor power devices (the MOSFET and diode) is performed to discuss the influence of thermal coupling effect between adjacent devices; FEM models for power devices considering convection thermal coupling are established; the junction temperatures of devices under different ambient temperatures and the temperature distribution have been given; and the relationships between junction temperature and ambient temperatures are obtained.

1.3. Outline

The paper is organized as follows. First, the variation of the ambient temperature after the analysis of the thermal transfer process and thermal coupling experiment to show the influence of the thermal coupling effect between adjacent devices is discussed in Section 2. Thermal models and FEM simulations for adjacent power devices considering convection thermal coupling are established in Section 3. The relationships between junction temperatures and ambient temperatures are presented in Section 4. After that, thermal models in new ambient temperatures are built to verify the proposed model in Section 5. Finally, the main conclusion is drawn in Section 6.

2. Variation of Ambient Temperature

2.1. Thermal Transfer Process

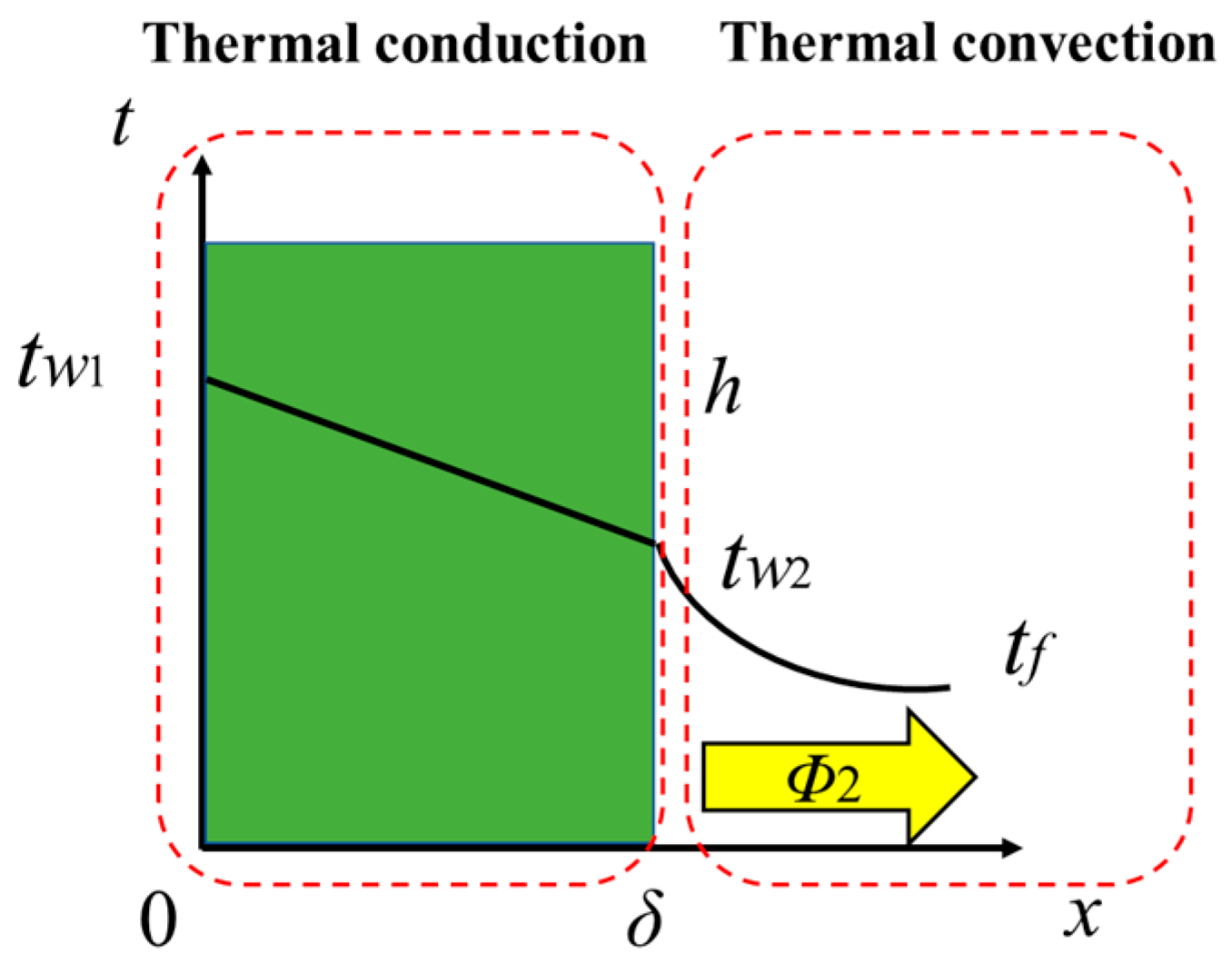
The thermal transfer process refers to the process that the thermal is transferred from the interior of the solid to the other side of the fluid through the solid wall, that is, the thermal transfers from the heating solid (chip) to the surrounding air, as shown in Figure 1. In the figure, tw₁, tw₂, t_f are the temperatures and h is the convection coefficient. It is assumed that tw₁, tw₂, t_f and h do not change with time and λ is a constant [21].

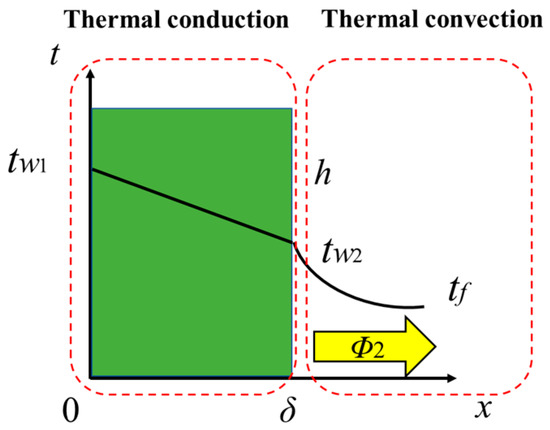
Figure 1. Thermal transfer.

The thermal conduction equation of a flat wall can be obtained based on the steady-state thermal transfer

$${\varnothing }_1=A\lambda \frac{t_{w1}-t_{w2}}{\delta }=\frac{t_{w1}-t_{w2}}{\frac{\delta }{A\lambda }}=\frac{t_{w1}-t_{w2}}{R_{\lambda }}$$

(1)

Furthermore, the thermal convection equation can be expressed as

$${\varnothing }_2=A{h}_2\frac{t_{w2}-t_f}{\delta }=\frac{t_{w2}-t_f}{\frac{1}{Ah}}=\frac{t_{w2}-t_f}{R_h}$$

(2)

When the thermal transfer reaches a steady state, it can be obtained by energy conservation

$${\varnothing =\varnothing }_1={\varnothing }_2$$

(3)

That is

$$\left\{\begin{array}{c}\varnothing =\frac{t_{w1}-t_f}{\frac{\delta }{A\lambda }+\frac{1}{Ah}}=\frac{t_{w1}-t_f}{R_{\lambda }+R_h}=\frac{t_{w1}-t_f}{R_k}\\ R_k=R_{\lambda }+R_h\end{array}\right.$$

(4)

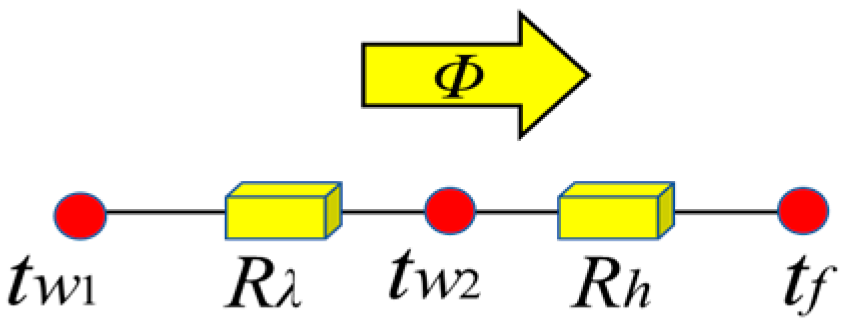
where R_k is the total thermal transfer resistance, $R_{\lambda }$ is conduction thermal resistance and R_h is convection thermal resistance.

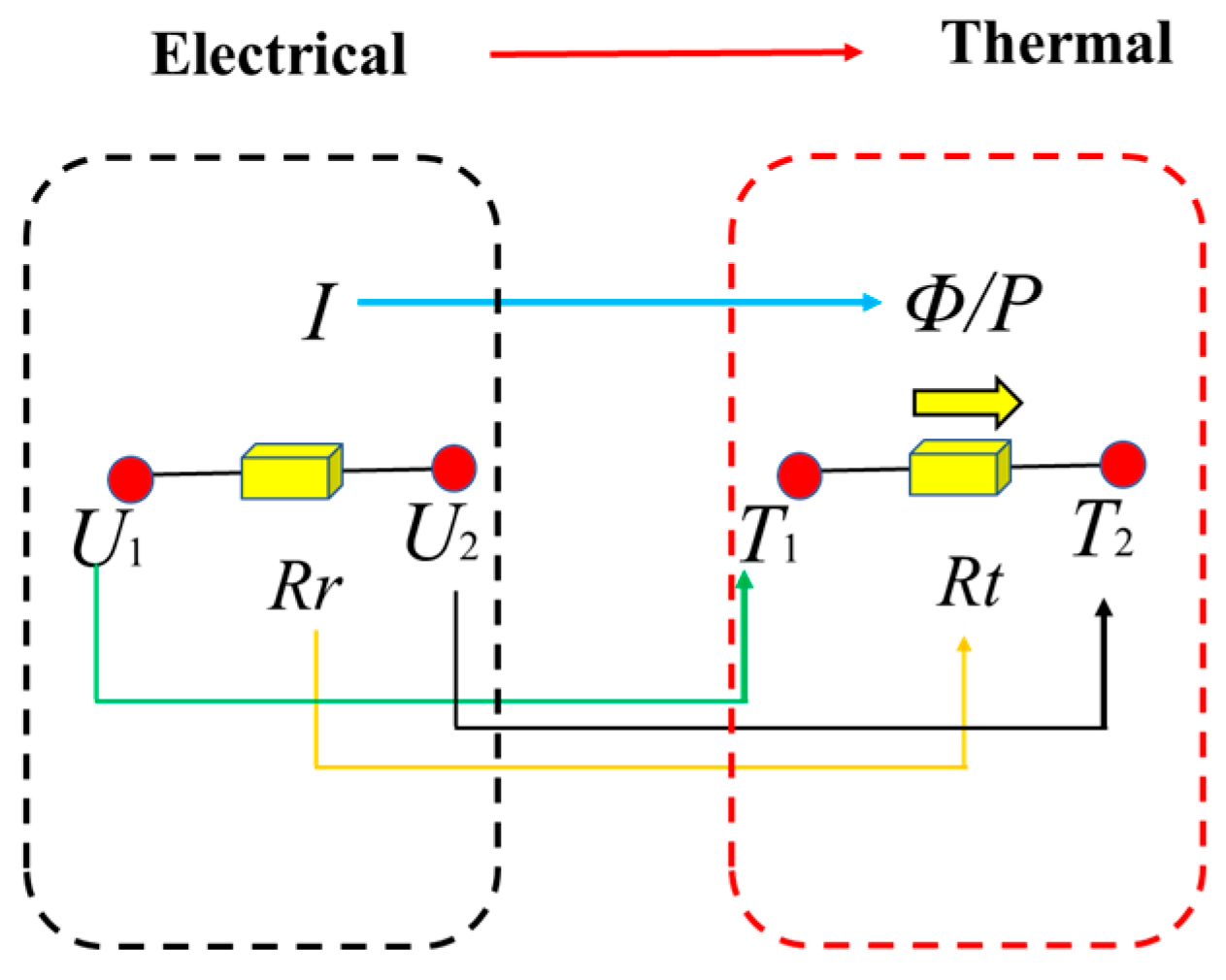
Based on the theory of electrical to thermal, as shown in Figure 2: the resistance corresponds to the thermal resistance; the voltage difference corresponds to the temperature difference and the current corresponds to the power loss. The corresponding thermal resistance network in the thermal transfer process is shown in Figure 3.

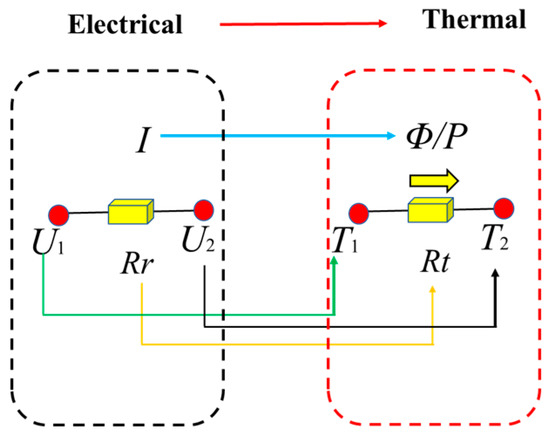
Figure 2. The theory of electrical to thermal.

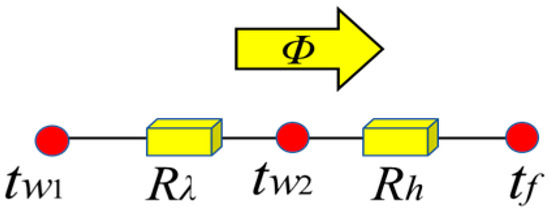
Figure 3. Thermal resistance network.

2.2. Thermal Coupling Experiments

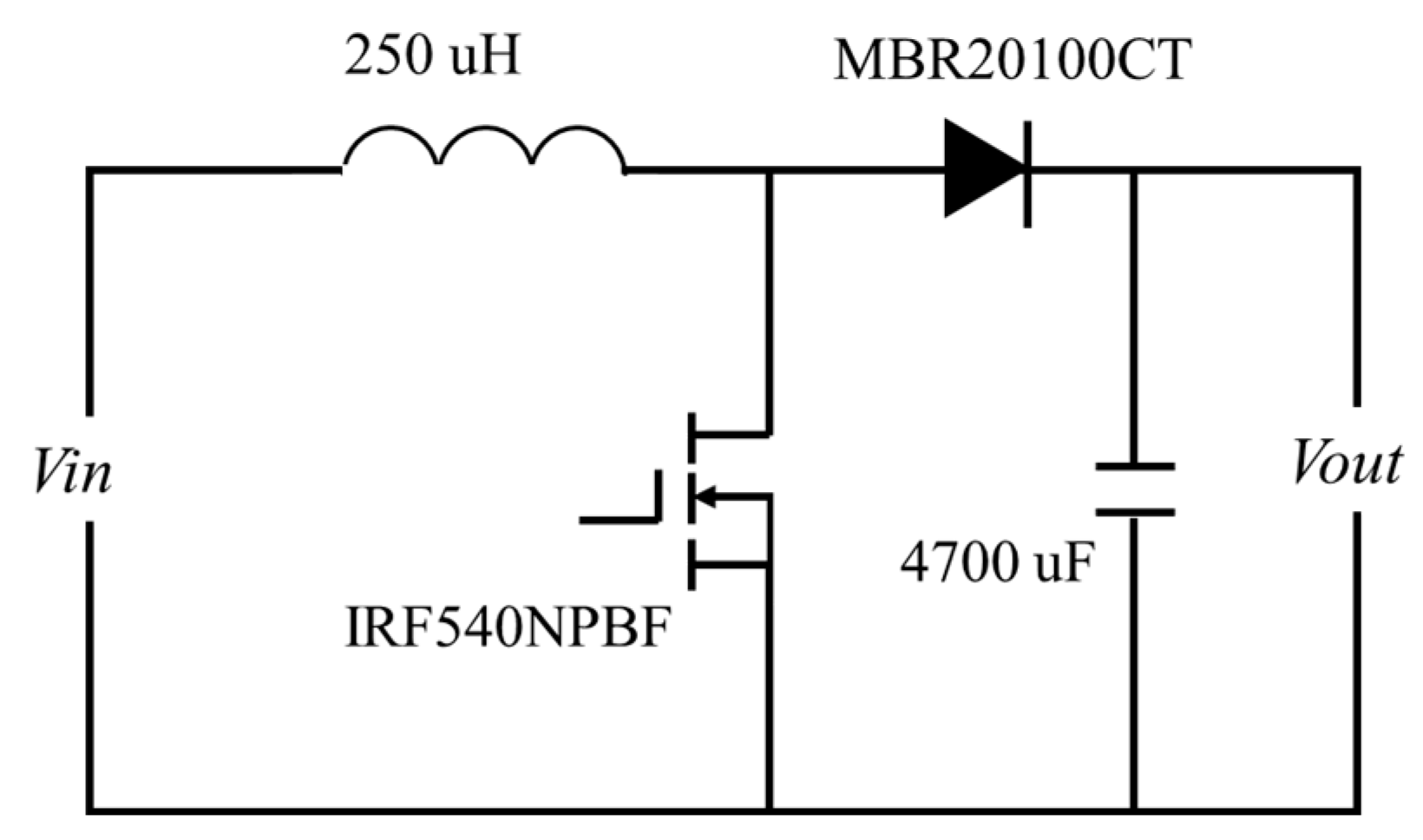
In this section, a thermal coupling testing platform for the power converter is established as shown in Figure 4, and its circuit diagram is shown in Figure 5. In this experimental platform, the selected switching frequencies of the power converters are commonly used, which are 10 kHz, 25 kHz and 50 kHz, respectively. The duty cycle is set to 0.5, and the load resistances are 8 Ω, 6 Ω and 5 Ω, respectively. The type of the power device MOSFET is IRF540 NPBF, the diode model is MBR20100CT, and both the semiconductor devices are in the TO-220 package. The capacitor is MAL215050472E3-35 V and the value of its capacitance is 4700 UF. The inductance is MCAP115018047A and the value of its inductance is 250 μH.

Figure 4. Thermal coupling testing platform of the power converter.

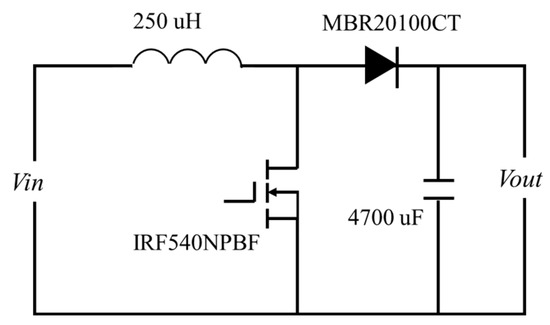
Figure 5. The circuit diagram of the power converter.

In order to study the influence of the thermal coupling effect (the convection thermal coupling and conduction thermal coupling are included) of adjacent devices under different working conditions, the two different types of power converters are tested and compared as follows, type I with large device spacing and type II with small device spacing, as shown in Figure 6. The MOSFET is controlled by the PWM wave and its on state and off state are controlled by the given duty cycle and switching frequencies. During the testing of the converter system, the input voltage and output voltage of the circuit is 12 V and 24 V, respectively. The case temperature of the power devices of the converter system is collected by changing the load resistances.

Figure 6. Two different types of power converters: (a) type I with large device spacing; (b) type II with small device spacing.

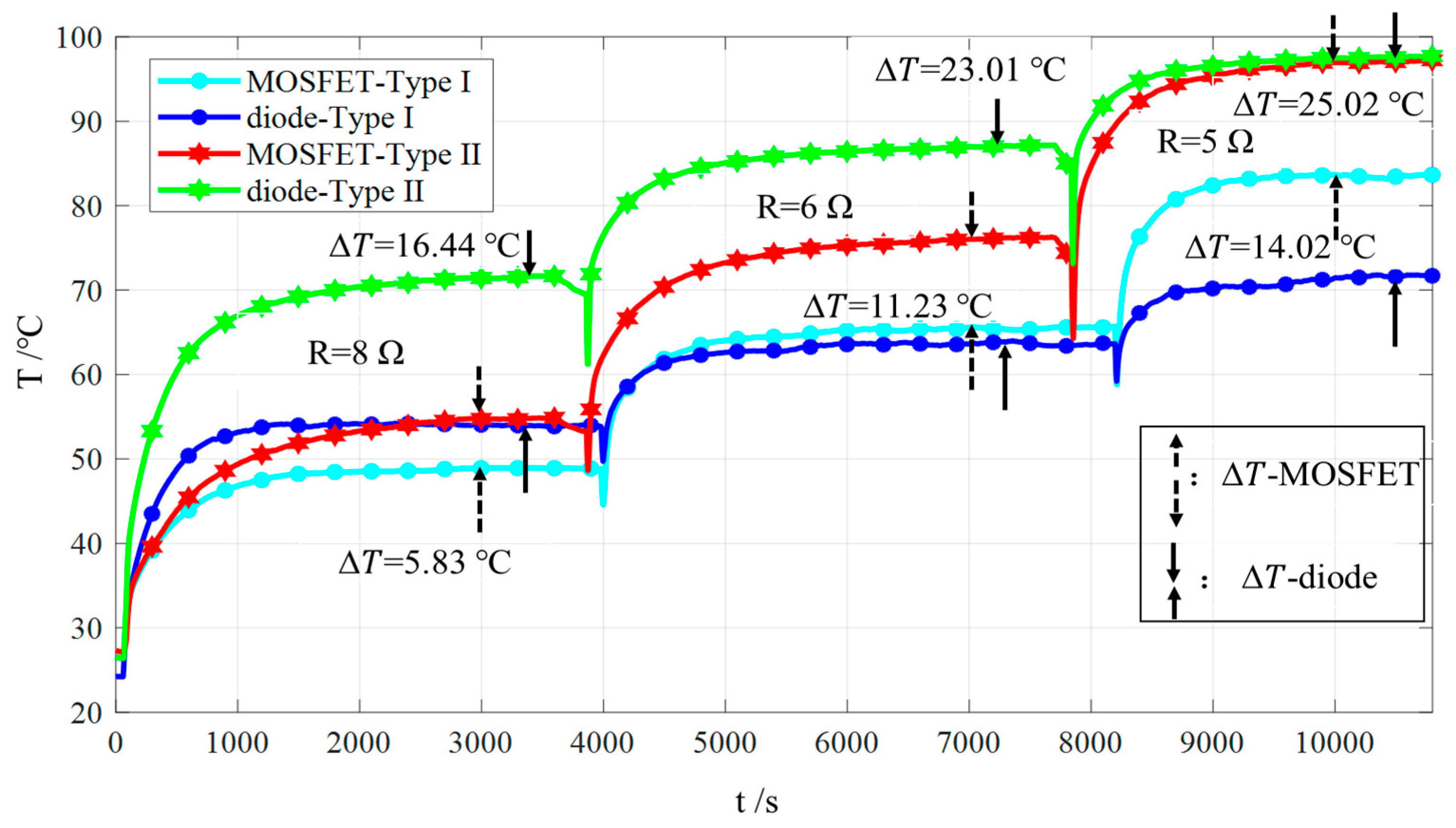
Figure 7 shows the measurement results of the case temperatures and the calculation results of the temperature difference of the two power devices with different types of spacing. In this figure, the case temperature of the MOSFET and diode with two types of devices spacing (type I: large spacing, dot mark on the blue and cyan solid line; type II: small spacing, six-star mark on red and green solid line) are compared at the switching frequency of 25 kHz and the load resistances which are 8 Ω, 6 Ω and 5 Ω, respectively.

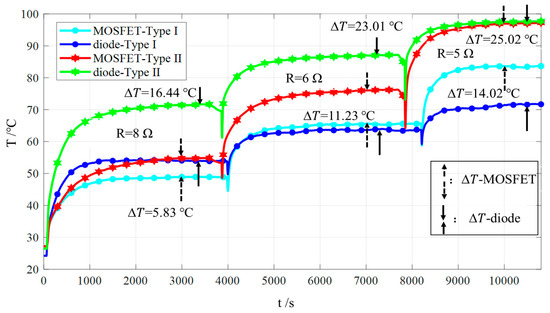
Figure 7. The comparisons of the case temperatures and the temperature differences of the power devices with different spacing types.

It can be seen from the comparisons that, for both MOSFET and diode, with the decrease in device spacing the case temperature of the device increases under the same working condition. This shows that the thermal coupling effect between adjacent devices is affected by the device spacing, and with the decrease in the spacing, the thermal coupling effect increases. In addition, according to the comparison results of the case temperature difference in Table 1, when the load resistance decreases, the current flowing through the semiconductor device increases. At this time, the case temperature difference of the two devices changes with the change of current, which shows that the thermal coupling effect between adjacent devices is affected by the working current, and with the increase in the current the thermal coupling effect increases. It is verified that the thermal coupling effect obtained from the thermal coupling testing platform (the MOSFET and diode are tested) of devices can also be applied to the case where multiple devices exist in the power converter system.

Table 1. The temperature differences of case temperature under different load resistances.

R/Ω	8	6	5
ΔTc_M/°C	5.83	11.23	14.02
ΔTc_D/°C	16.44	23.01	25.02

The calculation formula of the steady-state case-to-ambient thermal resistance, R_ca in the convection thermal transfer is obtained as

$$R_{\mathrm{ca}}=\frac{\Delta T}{P}$$

(5)

The steady-state thermal resistance of the devices under different working conditions is analyzed. By bringing the measured steady-state T_c into (5), the R_ca of the MOSFET and diode can be obtained. The calculation results are shown in Table 2 and Table 3, respectively. According to the two tables above, when the power loss (the working current) increases and the T_c rises, the values of R_ca decrease. This shows that the R_ca is not constant, and its value depends on the power loss and environmental factors.

Table 2. R_ca for the MOSFET.

Tc_M [°C]	Rca_M [°C/W]
25.75	69.32
34.43	62.73
53.27	61.76
80.01	54.27
146.85	45.15

Table 3. R_ca for the diode.

Tc_D [°C]	Rca_D [°C/W]
50.66	60.39
79.59	58.89
105.85	54.35
129.26	52.24
149.19	49.60

2.3. Finite Element Method (FEM) models

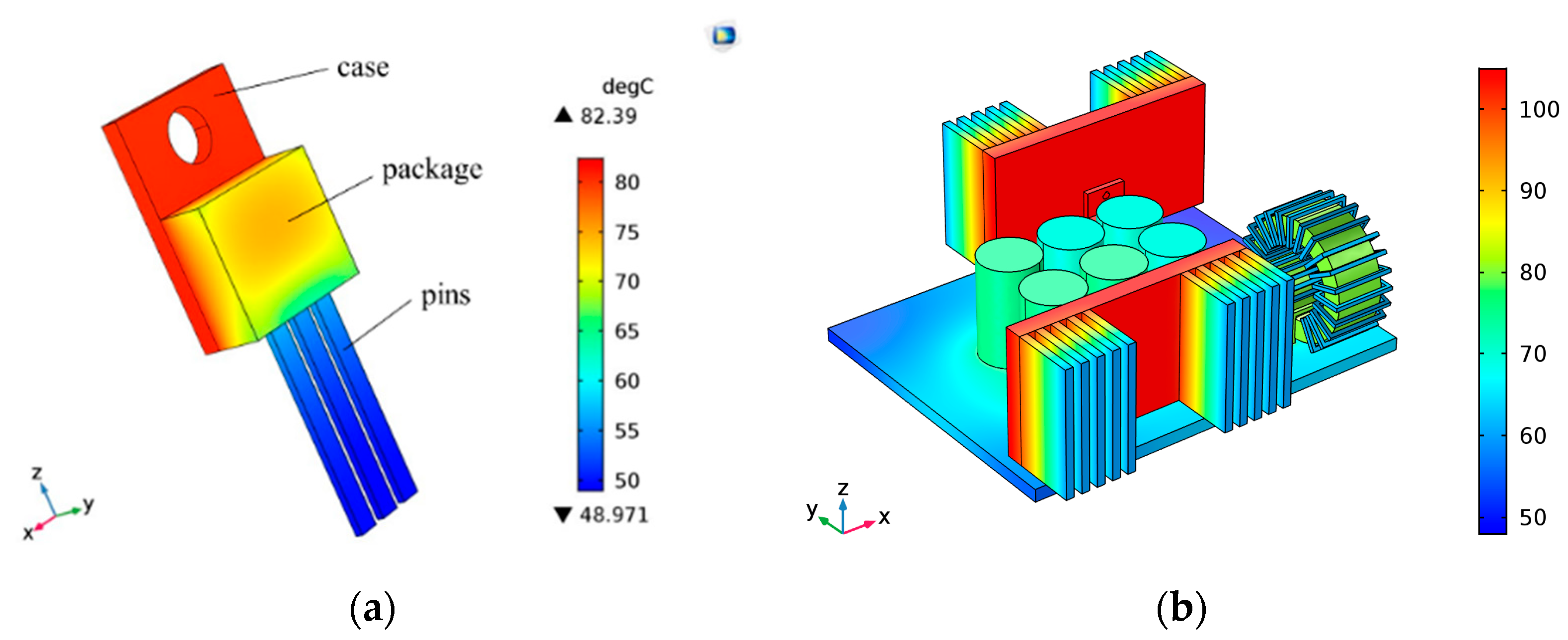
Thermal dissipation has a negative impact on the performance and lifetime of semiconductor devices and power converters. As shown in Figure 8, different colors constitute the thermal map and this simulation can be used to obtain the junction temperature (T_j) and case temperature (T_c), and the temperature at the chip and copper substrate layer is the highest.

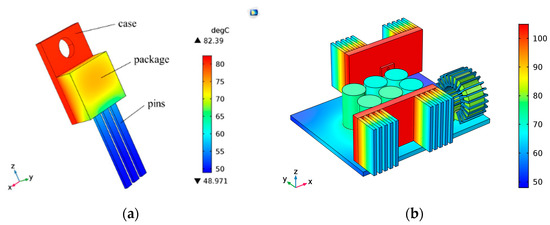
Figure 8. FEM thermal analysis model: (a) three-dimensional thermal calculation model for a MOSFET; (b) temperature distributions of a power converter.

Therefore, thermal analysis modeling under different load conditions is essential, and it is necessary to seek the temperature calculation methods of power converters and the optimal distribution schemes of thermal distribution. As the size of a single traditional silicon-based device approaches its basic limit, a better understanding of the thermal distribution of adjacent devices under different operating conditions can help the system carry out reasonable thermal management, thus improving the performance of the converter system, and optimizing the overall structure of the converter [22]. The accuracy of the thermal analysis model has a significant impact on the thermal management and reliability of devices and systems.

For semiconductor devices and power converter systems, the commonly used thermal modeling methods mainly include the physical model calculation method, numerical calculation method, finite element method (FEM), thermal resistance network method, etc. [23,24]. FEM can be used for the thermal calculation of devices or power converter systems, and the simulated structures can be simplified within the range of accuracy allowed. The FEM results can be used to analyze the temperature distribution directly by different colors, and the junction/case temperature can be extracted by adding virtual thermal probes to the corresponding components. Unlike the real probes or temperature sensors, the virtual probes are considered to have absolutely ideal thermal conductivity and insulation properties, which can be attached to the device surface or injected inside the devices, or anywhere in the air region [24,25].

However, it has difficulties when using FEM to establish thermal models for the semiconductor devices, because you should be familiar with the specific parameters of internal structures for power devices or modules. The FEM analysis needs 3D modeling of the devices or systems. Although the structures can be simplified, the structures of the devices and systems need to be better understood. In addition, in order to obtain a more accurate FEM analysis model, boundary conditions and the ambient domains are also essential [24,26]. In this paper, the FEM method is used to analyze the convection thermal coupling of adjacent semiconductor devices considering different ambient domains in different cities.

2.4. Ambient Domain

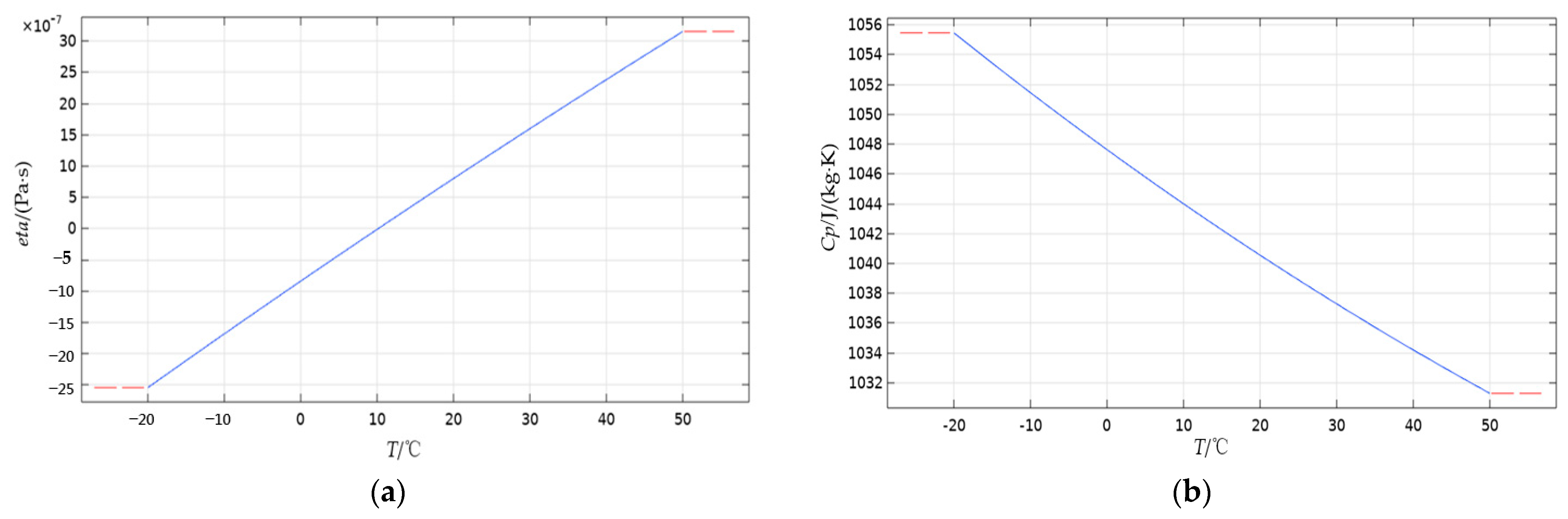
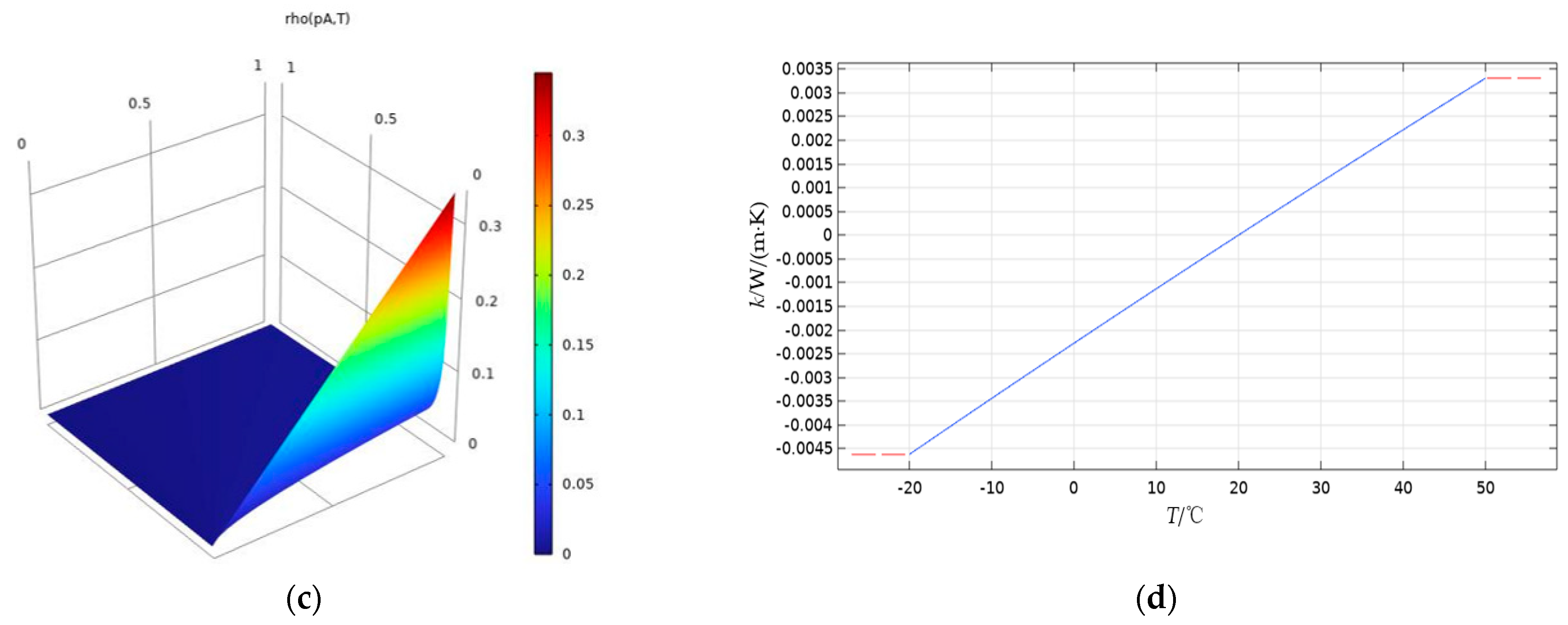
In addition to the power losses factor, the junction temperature of power devices is also affected by environmental factors. The parameters of the outside surrounding ambient domain of power devices, such as kinetic viscosity, constant pressure heat capacity, density, and thermal conductivity, are all functions of ambient temperature and will be changed when the temperature [13,27] changes. The aforementioned parameters and their parametric relationships are shown in Table 4 and Figure 9.

Table 4. Ambient domain parameters.

Name	Symbol	Unit
kinetic viscosity	eta (T)	Pa·s
constant pressure heat capacity	Cp (T)	J/(kg·K)
density	ρ (pA,T)	kg/m3
thermal conductivity	k (T)	W/(m·K)

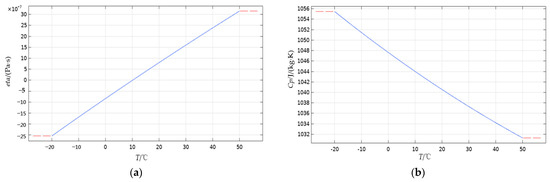
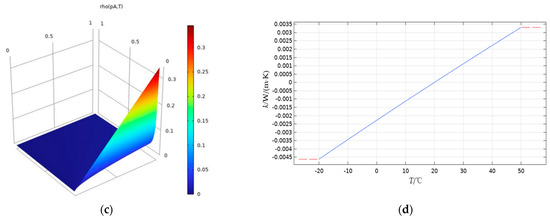
Figure 9. Ambient domain parameters: (a) kinetic viscosity; (b) constant pressure heat capacity; (c) density; (d) thermal conductivity of air.

2.5. Analysis and Selection of the Ambient Temperatures

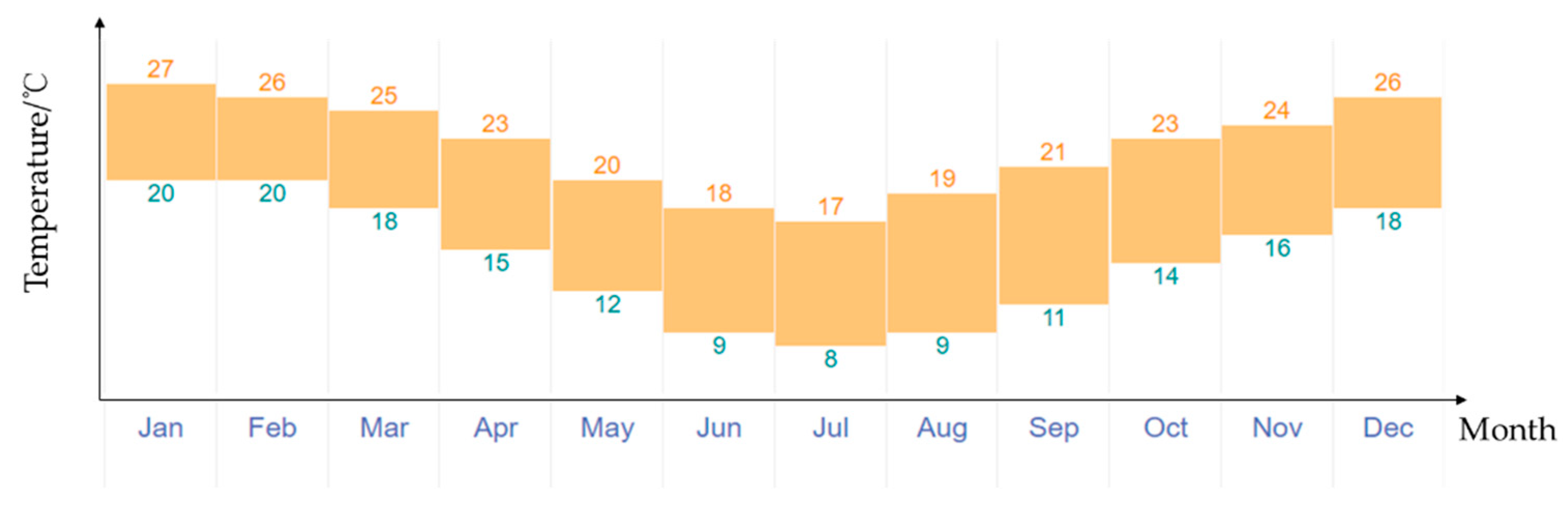
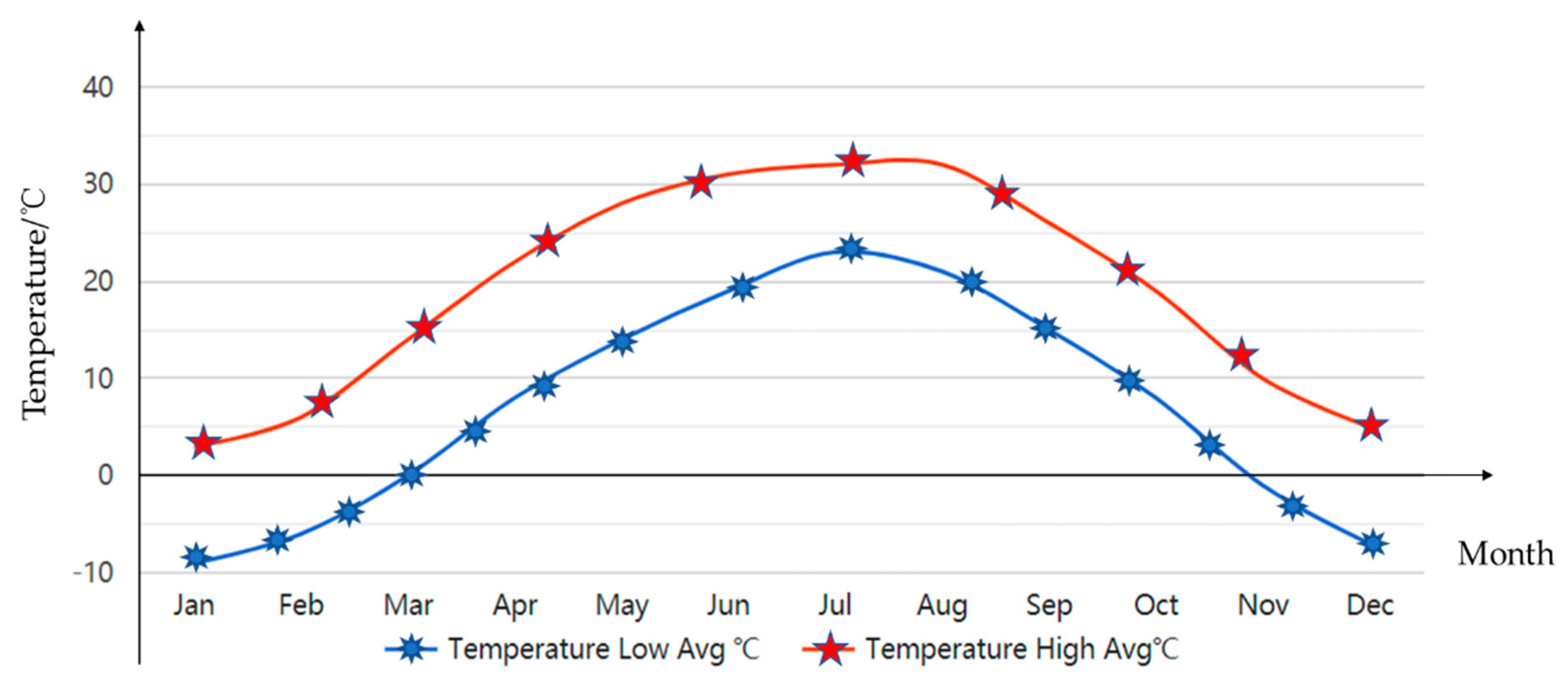
Figure 10 shows the all-year climate (annual weather averages) in Sydney. The averages performed are based on weather reports collected in the period 1985–2015 for Sydney Airport which is 9 km from Sydney. The temperatures from the months of December, January and February are the highest, with a temperature of 26–27 °C in the daytime and 18–20 °C in the evening; the temperatures from June to August are the lowest, with a temperature of about 17–19 °C in the daytime and 8–9 °C in the evening which are the worst-case scenarios. Furthermore, in the season of Autumn, from March to May, the temperatures decrease from 25 °C to 20 °C in the daytime, and 18–12 °C in the evening, respectively. In the season of Spring (from September to November) the temperatures increase from 21 to 24 °C in the daytime and 11 to 16 °C at night, respectively. Figure 11 gives the temperature changes in 2022 in Beijing, China. The highest temperatures occur in the season of summer from June to August which are around 32 °C in the daytime and 23 °C in the evening, respectively. In wintertime, the highest temperatures are 3 to 5 °C in the daytime and −7 to −9 °C in the evening, respectively.

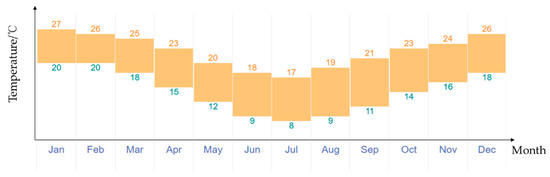
Figure 10. The all-year climate (annual weather averages) in Sydney.

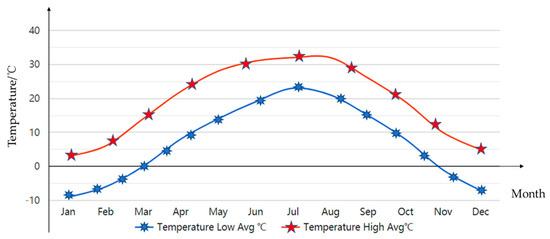
Figure 11. The temperature change in 2022 in Beijing.

Based on the above temperatures, a series of ambient temperatures can be selected, which are −10 °C, 0 °C, 10 °C, 20 °C and 30 °C. In addition, high temperatures from 38 °C to 42 °C often occur in summer in Sydney. Therefore, 40 °C is also selected in this paper and an added temperature of 50 °C is the upper limit of the maximum ambient temperature.

3. Convection Thermal Coupling Modeling of Adjacent Devices

3.1. FEM Modeling

The calculation method of the thermal coupling effect for adjacent devices is complex. The calculation method of thermal conduction coupling in [11] is based on the principle of linear superposition: a power loss P is applied to one device (device I) and the temperature rise of the adjacent device (device II) is supposed to be caused by the thermal conduction coupling from device I. Then a power loss is applied to device II to observe the thermal coupling effect on device I. The conduction thermal coupling between device I and device II can be obtained by this method. However, it has limitations which are only applicable to linear relations [11,28]. The thermal coupling between power devices contains non-linear convection terms. Therefore, this causes errors if the superposition principle is still adopted [21]. Based on the above, FEM modeling is established in this paper to simulate the convection thermal coupling between adjacent power devices and to calculate the junction temperature at different ambient temperatures.

The boundary conditions are as follows [29,30,31]: (1) the packed side is considered to be insulated; (2) all thermal will flow from the copper substrate (case) and pins into the surrounding air; and (3) the thermal transferring mode is thermal conduction and natural convection. Probes are added at the key points to extract and compare the device temperature. The simulation runs for 1000 s until the device temperature reaches a stable state for a certain time.

This paper simplifies the structures of the power devices (MOSFET and diode) to better analyze the convective thermal coupling effect between adjacent devices. In addition, in order to obtain more accurate results and reduce simulation time, a multi-level grid meshing method is adopted where in the key layer (chip layer) finer mesh is given and in other layers such as substrate and PCB, a coarse mesh is used [32,33,34].

3.2. Convection Thermal Coupling Simulation and Junction Temperature Calculation

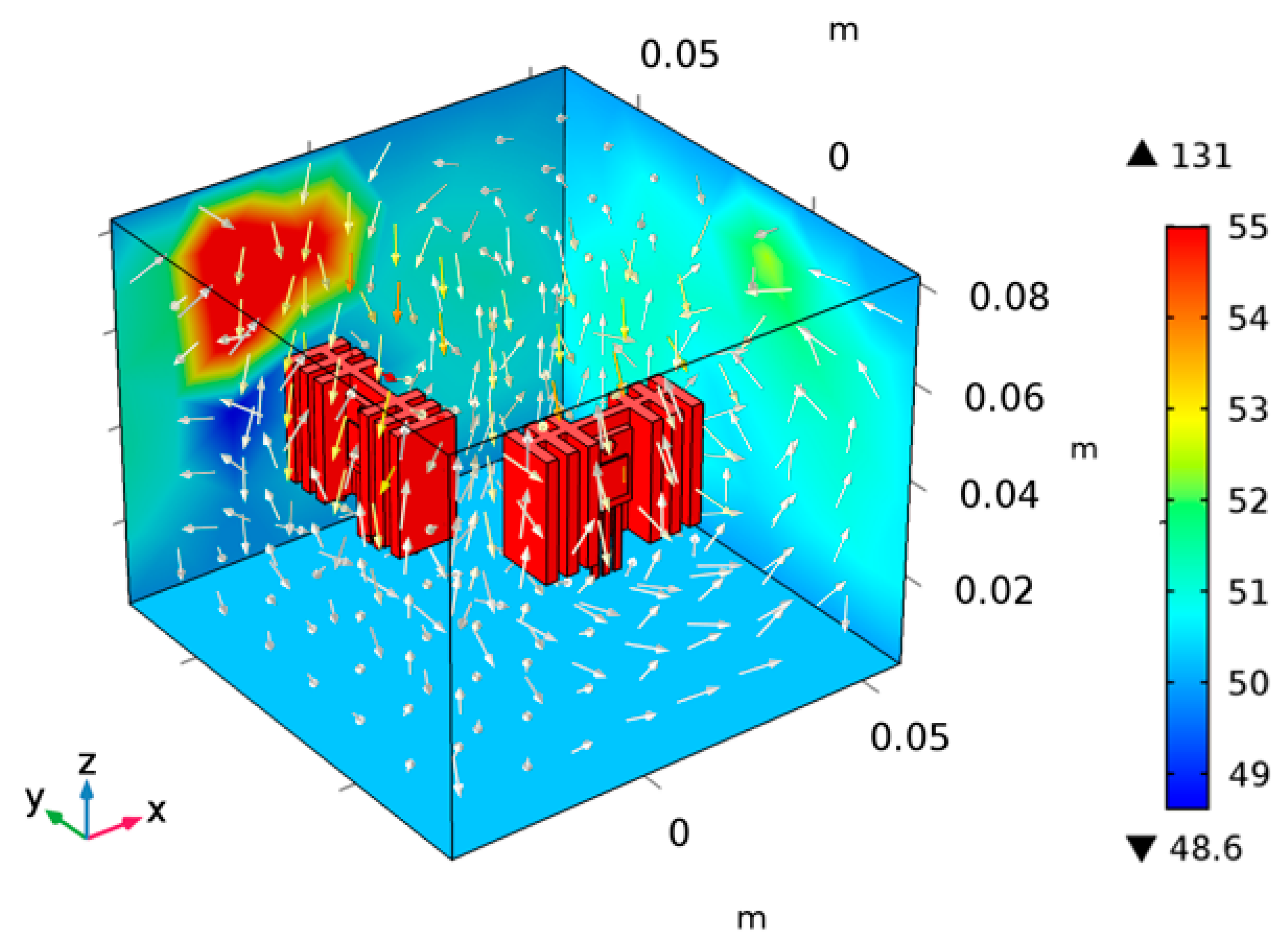
The power loss of the MOSFET is set to 5 W and the diode to 2 W. As the value of power loss for MOSFET is higher than that of the diode, the surrounding ambient temperature for MOSFET is also higher than that for the diode, and the color table shows the thermal distribution, as shown in Figure 12.

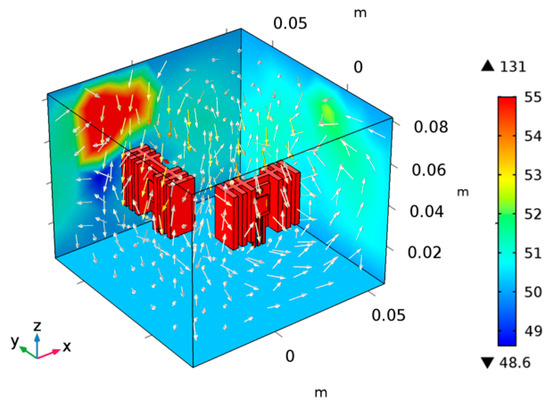
Figure 12. The temperature distribution of convection thermal coupling.

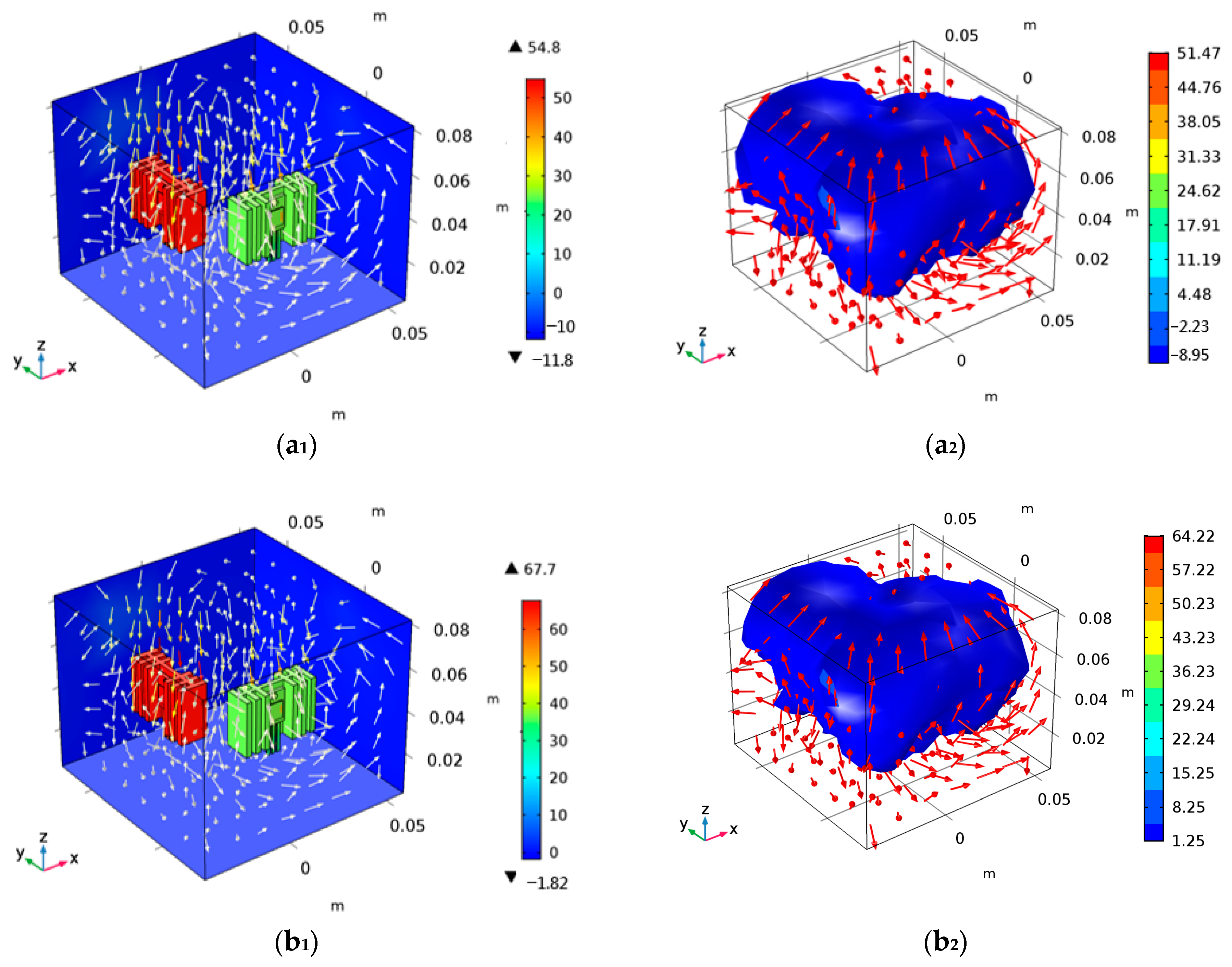
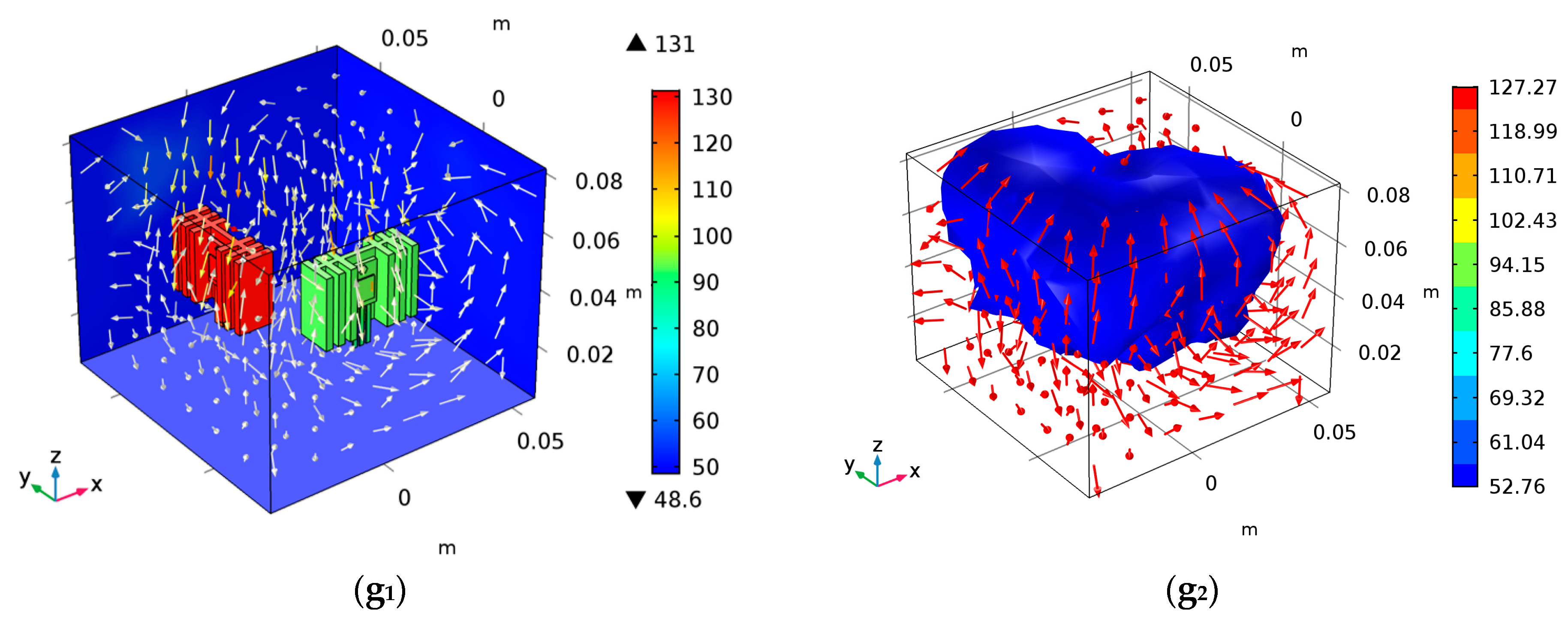
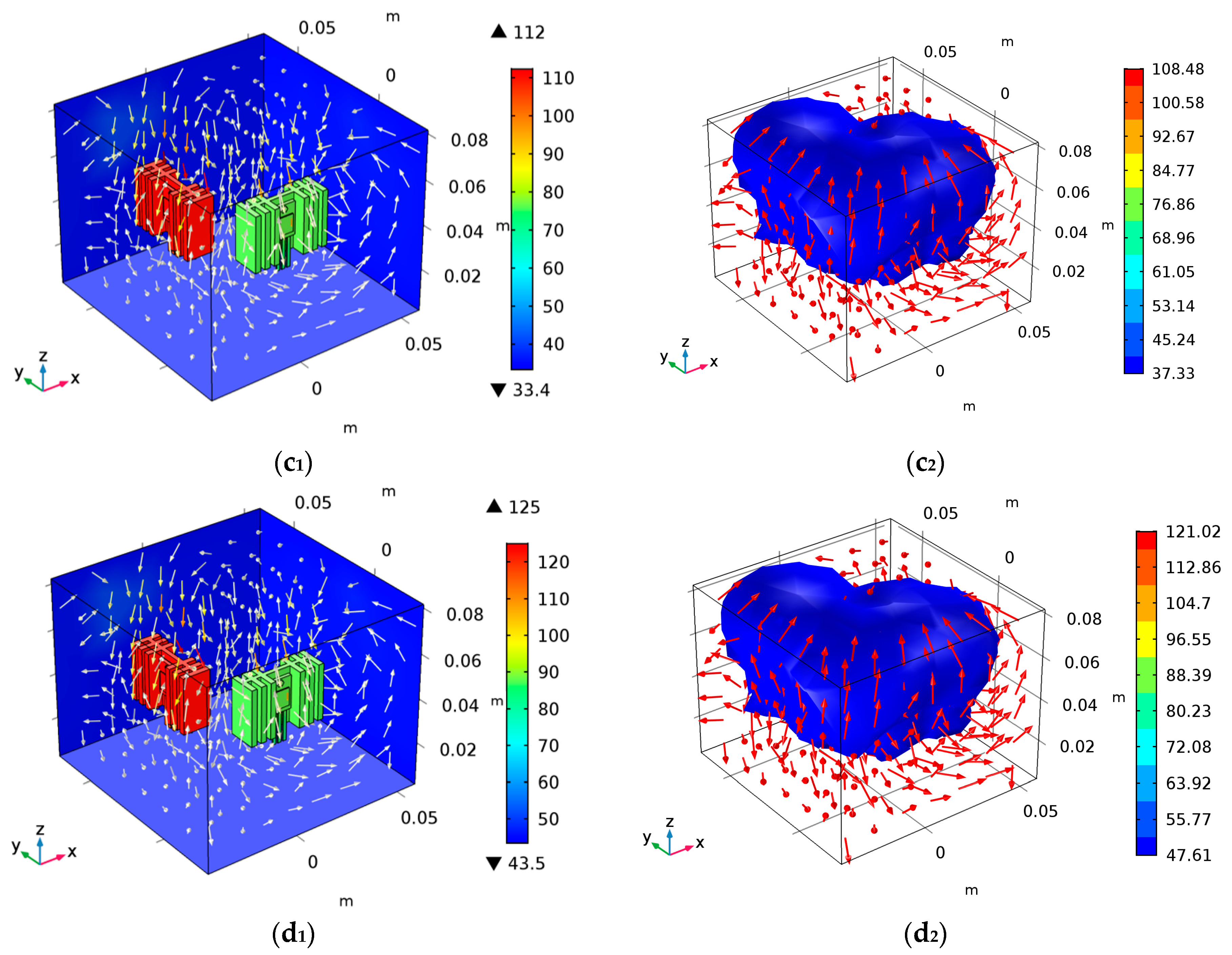
Through the FEM analysis, the temperature distribution and iso-surface distribution of power devices under different ambient temperatures are obtained, as shown in Figure 13. In the figures below, the color tables show the difference in the distribution.

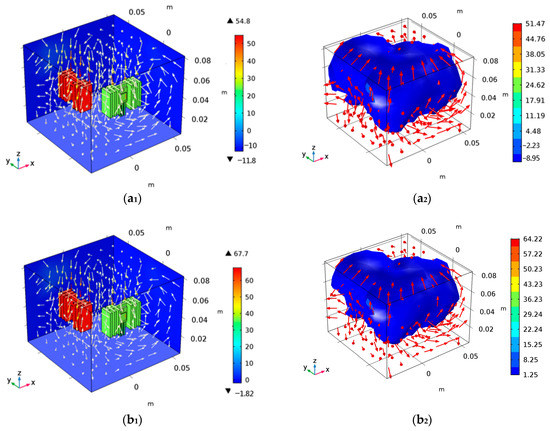
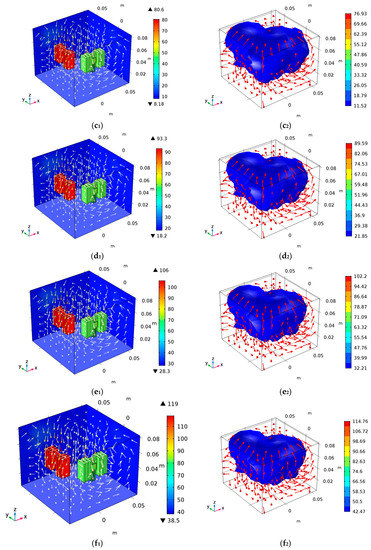
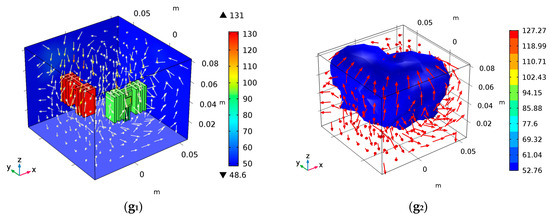
Figure 13. Simulation analysis of convection thermal coupling. (a₁,a₂) are temperature distribution and iso-surface distribution when T_a = −10 °C; (b₁,b₂) are temperature distribution and iso-surface distribution when T_a = 0 °C; (c₁,c₂) are temperature distribution and iso-surface distribution when T_a = 10 °C; (d₁,d₂) are temperature distribution and iso-surface distribution at T_a = 20 °C; (e₁,e₂) are temperature distribution and iso-surface distribution at T_a = 30 °C; (f₁,f₂) are temperature distribution and iso-surface distribution at T_a = 40 °C; (g₁,g₂) are temperature distribution and iso-surface distribution at T_a = 50 °C.

In the simulation, the junction temperature of the devices can be directly detected by adding a virtual probe. The junction temperatures of the devices under different ambient temperatures can be obtained considering the convection thermal coupling between the power devices, as shown in Table 5.

Table 5. The junction temperatures at different ambient temperatures.

Ta/°C	−10	0	10	20	30	40	50
Tj_M/°C	54.81	67.70	80.54	93.33	106.07	118.76	131.40
Tj_D/°C	25.35	36.82	46.65	59.66	71.03	82.37	93.67

4. The Relationships between the Junction and Ambient Temperatures

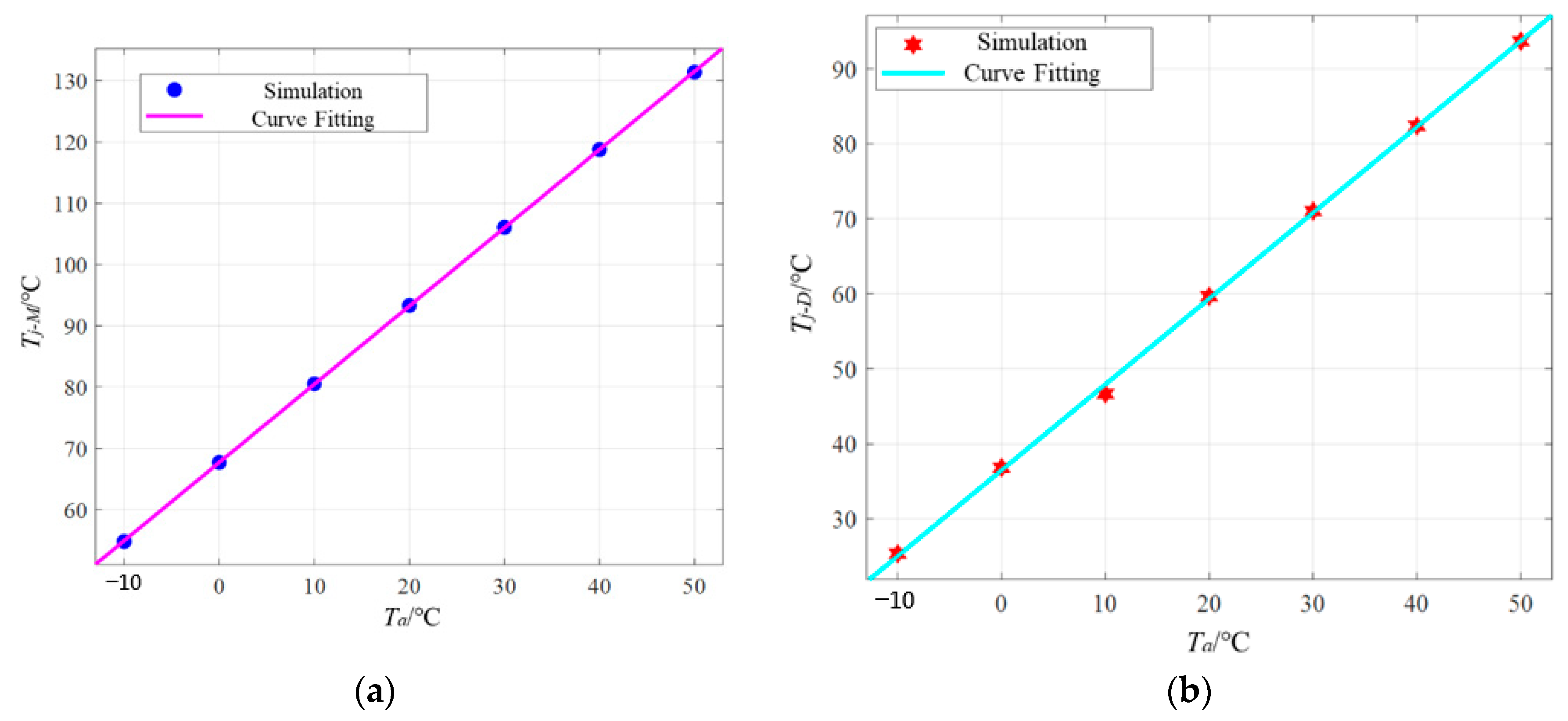
The steady-state junction temperatures of the power devices in Table 5 are used to fit the relationships between junction temperatures and ambient temperatures, and the relationships for MOSFET and diode are shown in Figure 14 and (6).

$$\left\{\begin{array}{c}f\left(T_{j\text{-}M}\right)=p_1{T}_a+p_2\\ f\left(T_{j\text{-}D}\right)=p_3{T}_a+p_4\end{array}\right.$$

(6)

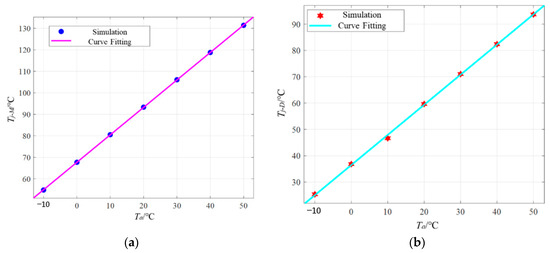
Figure 14. The relationships between junction and ambient temperatures: (a) for MOSFET, (b) for diode.

The fitting coefficients of the relationships for MOSFET and diode are

$$\left\{\begin{array}{c}{p}_1=1.28\\ p_2=67.73\\ p_3=1.14\\ p_4=36.48\end{array}\right.$$

As the ambient temperature will change with time changes, then when the ambient changes as a function of time [7], the relationships between the junction and ambient temperature can be expressed as

$$\left\{\begin{array}{c}f\left(T_{j\text{-}M}(t)\right)=p_1{T}_a\left(t\right)+p_2\\ f\left(T_{j\text{-}D}(t)\right)=p_3{T}_a\left(t\right)+p_4\end{array}\right.$$

(7)

5. Modeling Verification

5.1. The Simulation Analysis under New Temperature Profile

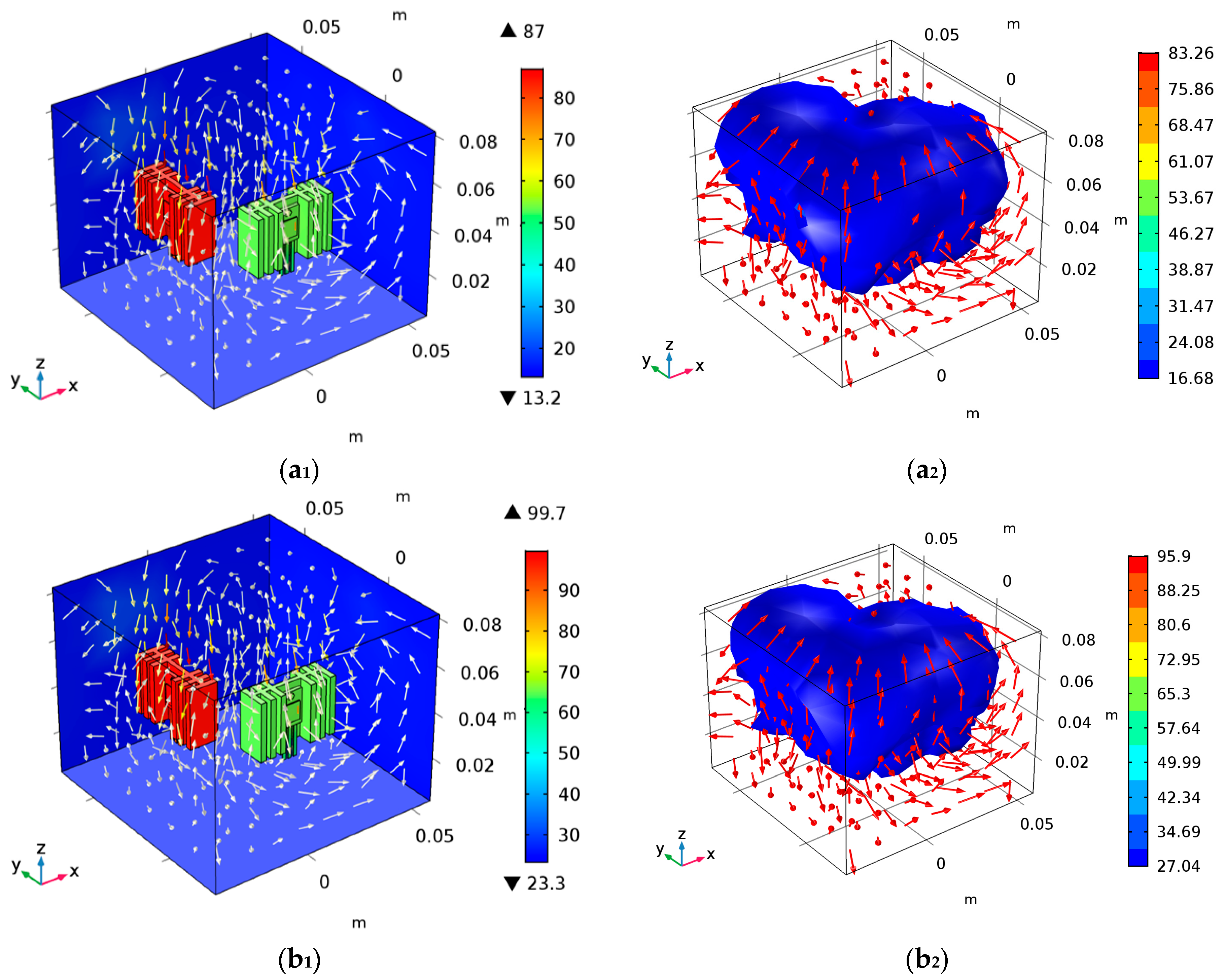
To verify the correctness of the model and the relationship between device junction temperature and ambient temperature, a new finite element simulation model based on (5) and (2) and under the ambient temperature profile is established. The ambient temperature is 15 °C, 25 °C, 35 °C, 45 °C, respectively. The simulated temperature distribution and iso-surface distribution are shown in Figure 15.

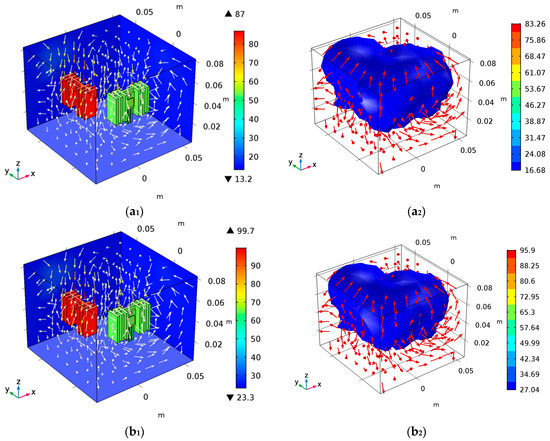
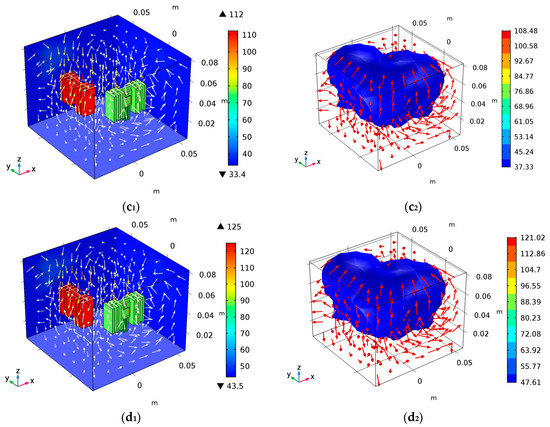
Figure 15. The simulation analysis of convective heat coupling: (a₁,a₂) are the temperature distribution and iso-surface distribution at T_a = 15 °C, (b₁,b₂) are the temperature distribution and iso-surface distribution at T_a = 25 °C, (c₁,c₂) are the temperature distribution and iso-surface distribution at T_a = 35 °C, and (d₁,d₂) are the temperature distribution and iso-surface distribution at T_a = 45 °C.

5.2. Junction Temperature Calculation and Comparisons

The new junction temperatures can be obtained from FEM simulations in Figure 8 and the junctions at new ambient temperatures can be obtained through (6). The comparisons of the junction temperatures by simulation and calculation for MOSFET and diode are given in Table 6 and Table 7, respectively. By comparison, the maximum error of MOSFET is 0.08% and the maximum error of diode is 0.70%, which shows the feasibility and effectiveness of the proposed method.

Table 6. The junction temperature comparisons of the calculation and simulation for the MOSFET.

Ta/°C	15	25	35	45
Tc_M/°C (Calculation)	86.87	99.63	112.39	125.15
Tc_M/°C (FEM)	86.94	99.71	112.42	125.08
Error/%	0.08	0.08	0.03	0.06

Table 7. The junction temperature comparisons of the calculation and simulation for the diode.

Ta/°C	15	25	35	45
Tc_D/°C (Calculation)	53.58	64.98	76.38	87.78
Tc_D/°C (FEM)	53.96	65.35	76.70	88.02
Error/%	0.70	0.57	0.42	0.27

6. Conclusions

In view of the dependence of the convection thermal dissipation of the device itself and the convection thermal coupling effect between adjacent devices on the surrounding air region, a FEM simulation model of convection thermal coupling of adjacent devices at different ambient temperatures is established. By changing the environmental temperature profiles, the temperature distribution, iso-surface distribution, and junction temperature of the devices under different ambient temperatures are obtained, and the relationships between junction temperature and ambient temperature are deduced. The relationships are verified by the junction temperature of the device at the new ambient temperatures. The junction temperatures of the device at other ambient temperatures can be calculated by the proposed relationship. Moreover, a better understanding of the environmentally dependent temperatures will be desirable to assist in terms of power converter optimization.